update

next.config.mjs

@@ -7,7 +7,7 @@ const withNextra = nextra({
     renderer: 'katex',
     options: {
       // suppress warnings from katex for `\\`
-      strict: false,
+      // strict: false,
       // macros: {
       //   '\\RR': '\\mathbb{R}'
       // }
@@ -17,9 +17,9 @@ const withNextra = nextra({
 
 export default withNextra({
   output: 'standalone',
-  eslint: {
+  // eslint: {
-    ignoreDuringBuilds: true,
+  //   ignoreDuringBuilds: true,
-  },
+  // },
   experimental: {
     // optimize memory usage: https://nextjs.org/docs/app/building-your-application/optimizing/memory-usage
     webpackMemoryOptimizations: true,

pages/CSE559A/CSE559A_L12.md

@@ -0,0 +1,159 @@
+# CSE559A Lecture 12
+
+## Transformer Architecture
+
+### Outline
+
+**Self-Attention Layers**: An important network module, which often has a global receptive field
+
+**Sequential Input Tokens**: Breaking the restriction to 2d input arrays
+
+**Positional Encodings**: Representing the metadata of each input token
+
+**Exemplar Architecture**: The Vision Transformer (ViT)
+
+**Moving Forward**: What does this new module enable? Who wins in the battle between transformers and CNNs?
+
+### The big picture
+
+CNNs
+
+- Local receptive fields
+- Struggles with global content
+- Shape of intermediate layers is sometimes a pain
+
+Things we might want:
+
+- Use information from across the image
+- More flexible shape handling
+- Multiple modalities
+
+Our Hero: MultiheadAttention
+
+Use positional encodings to represent the metadata of each input token
+
+## Self-Attention layers
+
+### Comparing with ways to handling sequential data
+
+#### RNN
+
+![Image of RNN](https://notenextra.trance-0.com/CSE559A/RNN.png)
+
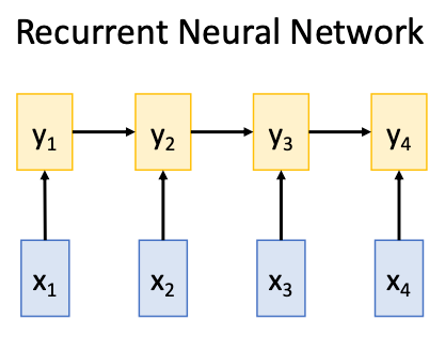
+Works on **Ordered Sequences**
+
+- Good at long sequences: After one RNN layer $h_r$ sees the whole sequence
+- Bad at parallelization: need to compute hidden states sequentially
+
+#### 1D conv
+
+![Image of 1D conv](https://notenextra.trance-0.com/CSE559A/1D_Conv.png)
+
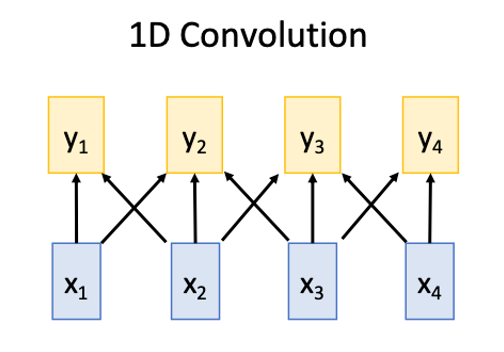
+Works on **Multidimensional Grids**
+
+- Bad at long sequences: Need to stack may conv layers or outputs to see the whole sequence
+- Good at parallelization: Each output can be computed in parallel
+
+#### Self-Attention
+
+![Image of self-attention](https://notenextra.trance-0.com/CSE559A/Self_Attention.png)
+
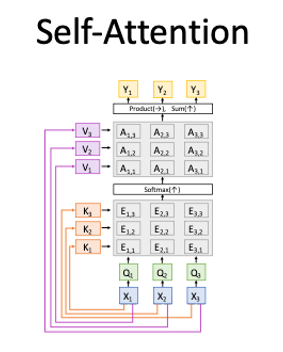
+Works on **Set of Vectors**
+
+- Good at Long sequences: Each output can attend to all inputs
+- Good at parallelization: Each output can be computed in parallel
+- Bad at saving memory: Need to store all inputs in memory
+
+### Encoder-Decoder Architecture
+
+The encoder is constructed by stacking multiple self-attention layers and feed-forward networks.
+
+#### Word Embeddings
+
+Translate tokens to vector space
+
+```python
+class Embedder(nn.Module):
+    def __init__(self, vocab_size, d_model):
+        super().__init__()
+        self.embed=nn.Embedding(vocab_size, d_model)
+
+    def forward(self, x):
+        return self.embed(x)
+```
+
+#### Positional Embeddings
+
+The positional encodings are a way to represent the position of each token in the sequence.
+
+Combined with the word embeddings, we get the input to the self-attention layer with information about the position of each token in the sequence.
+
+> The reason why we just add the positional encodings to the word embeddings is _perhaps_ that we want the model to self-assign weights to the word-token and positional-token.
+
+#### Query, Key, Value
+
+The query, key, and value are the three components of the self-attention layer.
+
+They are used to compute the attention weights.
+
+```python
+class SelfAttention(nn.Module):
+    def __init__(self, d_model, num_heads):
+        super().__init__()
+        self.d_model = d_model
+        self.d_k = d_k
+        self.q_linear = nn.Linear(d_model, d_k)
+        self.k_linear = nn.Linear(d_model, d_k)
+        self.v_linear = nn.Linear(d_model, d_k)
+        self.dropout = nn.Dropout(dropout)
+        self.out = nn.Linear(d_k, d_k)
+
+    def forward(self, q, k, v, mask=None):
+
+        bs = q.size(0)
+
+        k = self.k_linear(k)
+        q = self.q_linear(q)
+        v = self.v_linear(v)
+
+        # calculate attention weights
+        outputs = attention(q, k, v, self.d_k, mask, self.dropout)
+
+        # apply output linear transformation
+        outputs = self.out(outputs)
+
+        return outputs
+```
+
+#### Attention
+
+```python
+def attention(q, k, v, d_k, mask=None, dropout=None):
+    scores = torch.matmul(q, k.transpose(-2, -1)) / math.sqrt(d_k)
+
+    if mask is not None:
+        mask = mask.unsqueeze(1)
+        scores = scores.masked_fill(mask == 0, -1e9)
+
+    scores = F.softmax(scores, dim=-1)
+
+    if dropout is not None:
+        scores = dropout(scores)
+
+    outputs = torch.matmul(scores, v)
+
+    return outputs
+```
+
+The query, key are used to compute the attention map, and the value is used to compute the attention output.
+
+#### Multi-Head self-attention
+
+The multi-head self-attention is a self-attention layer that has multiple heads.
+
+Each head has its own query, key, and value.
+
+### Computing Attention Efficiency
+
+- the standard attention has a complexity of $O(n^2)$
+- We can use sparse attention to reduce the complexity to $O(n)$

pages/CSE559A/CSE559A_L13.md

@@ -0,0 +1,7 @@
+# CSE559A Lecture 13
+
+## Positional Encodings
+
+## Vision Transformer (ViT)
+
+## Moving Forward

pages/CSE559A/_meta.js

@@ -14,4 +14,5 @@ export default {
     CSE559A_L9: "Computer Vision (Lecture 9)",
     CSE559A_L10: "Computer Vision (Lecture 10)",
     CSE559A_L11: "Computer Vision (Lecture 11)",
+    CSE559A_L12: "Computer Vision (Lecture 12)",
 }

pages/Math4121/Math4121_L16.md

@@ -1 +1,94 @@
-# Lecture 16
+# Math 4121 Lecture 16
+
+## Continue on Patches for Riemann Integrals
+
+### Harnack's Mistake
+
+#### Theorem 3.6 Heine-Borel Theorem
+
+If $\{U_\alpha\}_{\alpha \in A}$ is a collection of open sets which cover $[a, b]$, then there exists a finite subcover, i.e. $\{U_{\alpha_1}, U_{\alpha_2}, \cdots, U_{\alpha_n}\}$ such that $[a, b] \subseteq \bigcup_{i=1}^n U_{\alpha_i}$.
+
+Using the fact that $[a, b]$ is compact.
+
+Proof:
+
+Define $S = \{x \in [a, b] : \exists U_\alpha \text{ s.t. } [a, x] \subseteq \bigcup_{i=1}^n U_{\alpha_i}\}$.
+
+If we can show that $b\in S$, then we are done.
+
+Clearly $S\neq \emptyset$ since $a\in S$.
+
+Let $\beta=\sup S\geq a$. If we can show that $\beta \geq b$, then we are done. (taking $x=b$ to take finite subcover)
+
+Suppose toward contradiction that $\beta < b$.
+
+Then $\exists U_\alpha$ and $(c,d)\subseteq U_\alpha$ such that $a<c<\beta<d<b$.
+
+Since $c<\beta$, $\exists U_{\alpha_1},\ldots,U_{\alpha_n}$ s.t. $[a,x]\subseteq \bigcup_{i=1}^n U_{\alpha_i}$.
+
+So $[a,d]\subseteq U_\alpha\cup \bigcup_{i=1}^n U_{\alpha_i}$.
+
+So $d\in S$, this contradicts the definition of $\beta$ as the supremum of $S$.
+
+So $\beta \geq b$.
+
+EOP
+
+### Reviewing sections for Math 4111
+
+#### Definition: Cardinality
+
+Two sets $A$ and $B$ have the same cardinality if there exists a bijection $f:A\to B$.
+
+_We can imaging the cardinality as the number of elements in the set. However, this is not rigorous, for example, the set of rational and irrational numbers are both infinite, but the set of rational numbers are countable while the set of irrational numbers are uncountable._
+
+- the cardinality of a finite set is the number of elements in the set.
+- the cardinality of $\mathbb{N}$ is $\aleph_0$, such a set is called "countable".
+
+#### Definition: Countable
+
+A set is countable if there exists an injection $f:\mathbb{N}\to A$.
+
+Example:
+
+1. The set of integers $\mathbb{Z}$ is countable.
+
+    We can construct a bijection $f:\mathbb{N}\to \mathbb{Z}$ by mapping $f(n)=\begin{cases}
+    \frac{n}{2} & \text{if } n \text{ is even} \\
+    -\frac{n+1}{2} & \text{if } n \text{ is odd}
+    \end{cases}$
+
+2. The set of rational numbers $\mathbb{Q}$ is countable.
+
+    We can construct a bijection $f:\mathbb{N}\to \mathbb{Q}$ using the 
+
+
+3. The algebraic numbers $\mathbb{A}$ (roots of polynomials with integer coefficients) are countable.
+
+    Proof using [the union of countable sets is countable](https://notenextra.trance-0.com/Math4111/Math4111_L6#theorem-212).
+
+#### Definition: Uncountable
+
+A set is uncountable if it is not countable.
+
+#### Theorem: $\mathbb{R}$ is uncountable
+
+Easy proof using[Cantor's diagonal argument](https://notenextra.trance-0.com/Math4111/Math4111_L6#theorem-214).
+
+A new one
+
+Proof:
+
+Suppose $\mathbb{R}=\{r_1,r_2,\ldots\}$. Let $a_0<b_0$ be the first two entries $a_0,b_0\in \{r_1,r_2,\ldots\}$ in our list which lie in $(0,1)$.
+
+Let $a_1<b_1$ be the first two entries such that $a_1,b_1\in (a_0,b_0)$.
+
+Continue this process, we can construct $[0,1]\supsetneq [a_0,b_0]\supsetneq [a_1,b_1]\supsetneq \cdots$ sets.
+
+> By the nested interval theorem of real numbers, $\bigcap_{n=1}^\infty [a_n,b_n]\neq \emptyset$.
+
+Setting $r=\sup a_n$ (by the least upper bound property of real numbers), $r\in [a_n,b_n]$ for all $n\in\mathbb{N}$. Since $r\in \mathbb{R}$, $r=r_m$ for some $m\in\mathbb{N}$. Then find $a_n,b_n$  which come after $r_m$ in the list.
+
+This contradicts the assumption that $a_n,b_n$ as the first element in the list.
+
+EOP

pages/Math416/Math416_L12.md

@@ -75,4 +75,46 @@ So $I\to 0$ as $\zeta_1\to\zeta$.
 
 Therefore, $g'(\zeta_1)=f(\zeta_1)$ for all $\zeta_1\in U$.
 
-EOP
+EOP
+
+### Cauchy's Theorem for a disk
+
+Let $U$ be the open set, $f\in O(U)$. Let $C$ be a circle inside $U$ and $\zeta$ be a point inside $C$.
+
+Then
+
+$$
+f(\zeta)=\frac{1}{2\pi i}\int_C\frac{f(\xi)d\xi}{\xi-\zeta} d\xi
+$$
+
+Proof:
+
+Let $C_\epsilon$ be a circle with center $\zeta$ and radius $\epsilon$ inside $C$.
+
+Claim:
+
+$$
+\int_{C_\epsilon}\frac{f(\xi)d\xi}{\xi-\zeta}=\int_{C}\frac{f(\xi)d\xi}{\xi-\zeta}
+$$
+
+We divide the integral into four parts:
+
+![Integral on a disk](https://notenextra.trance-0.com/Math416/Cauchy_disk.png)
+
+Notice that $\frac{f(\xi)}{\xi-\zeta}$ is holomorphic whenever $f(\xi)\in U$ and $\xi\in \mathbb{C}\setminus\{\zeta\}$.
+
+So we can apply Cauchy's theorem to the integral on the inside square.
+
+$$
+\int_{C_\epsilon}\frac{f(\xi)d\xi}{\xi-\zeta}=0
+$$
+
+Since $\frac{1}{2\pi i}\int_{C_\epsilon}\frac{1}{\xi-\zeta}d\xi=1$, $\sigma=\epsilon e^{it}+\zeta_0$ and $\sigma'=\epsilon e^{it}$, we have
+
+/* TRACK LOST*/
+
+$$
+\int_{C_\epsilon}\frac{f(\xi)d\xi}{\xi-\zeta}=\int_0^{2\pi}\frac{f(\sigma)d\sigma}{\sigma-\zeta}=2\pi i f(\zeta)
+$$
+
+EOP