updates

pages/Math401/Math401_T4.md

@@ -96,6 +96,101 @@ Story of light polarization and violation of Bell's inequality.
 
 > An interesting story will be presented here.
 
+#### Polarization of light
+
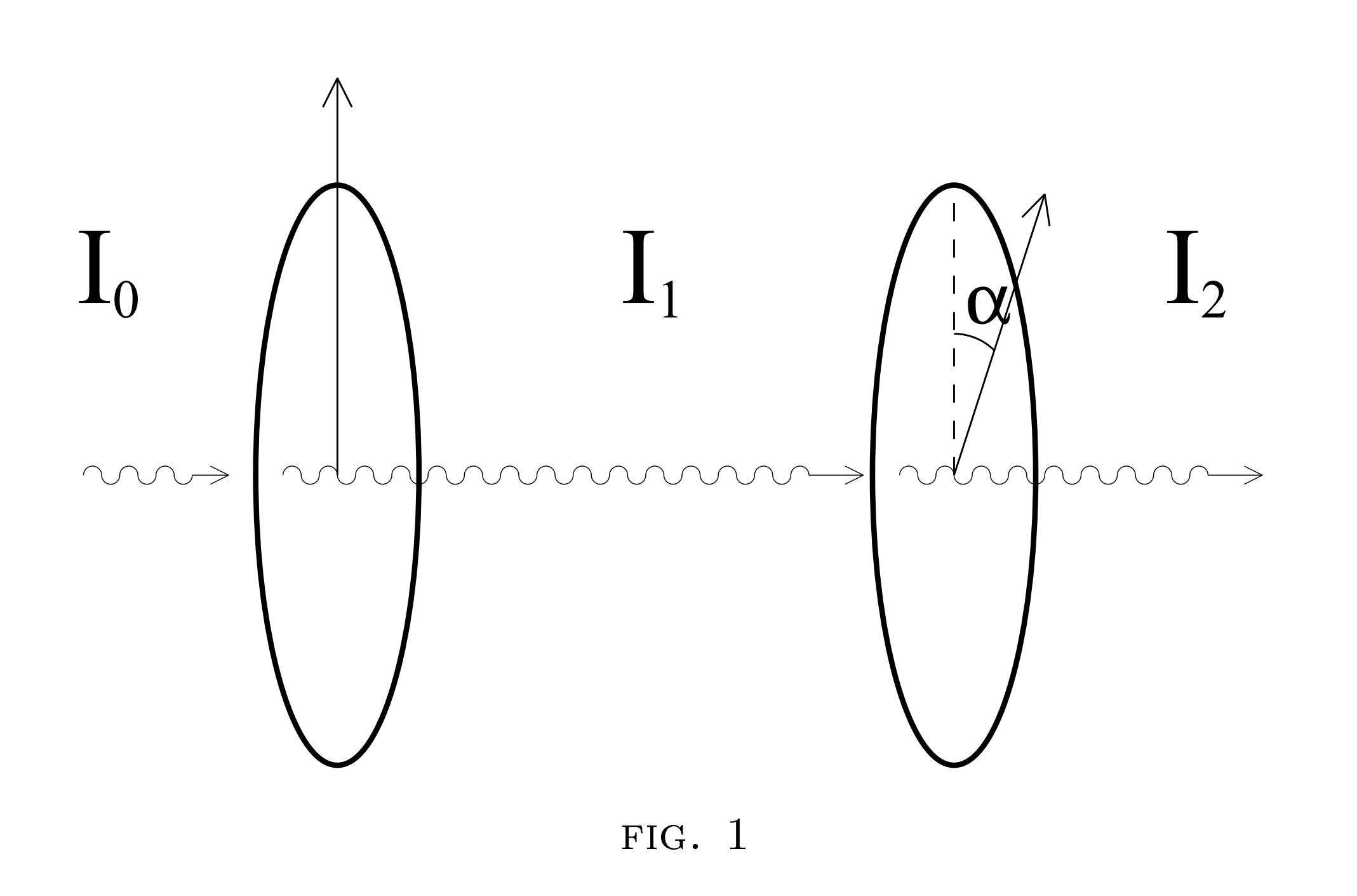
+The light which comes through a polarizer is polarized in a certain direction. If we fixed the first filter and rotate the second filter, we will observe the intensity of the light will change.
+
+The light intensity decreased with $\alpha$ (the angle between the two filters). The light should vanished when $\alpha=\pi/2$.
+
+![Filter figure](https://notenextra.trance-0.com/Math401/Filter_figure.png)
+
+By experimental measurement, the intensity of the light passing the first filter is half the beam intensity (Assume the original beam is completely unpolarized).
+
+Then $I_1=I_0/2$, and
+
+$$
+I_2=I_0\cos^2\alpha
+$$
+
+Claim: there exist a smallest package of monochromatic light, which is a photon.
+
+We can model the behavior of each individual photon passing through the filter with direction $\alpha$ with random variable $P_\alpha$. The $P_\alpha(\omega)=1$ if the photon passes through the filter, and $P_\alpha(\omega)=0$ if the photon does not pass through the filter.
+
+Then, the probability of the photon passing through the two filters with direction $\alpha$ and $\beta$ is given by
+
+$$
+\mathbb{E}(P_\alpha P_\beta)=\operatorname{Prob}(P_\alpha=1 \text{ and } P_\beta=1)=\frac{1}{2}\cos^2(\alpha-\beta)
+$$
+
+However, for system of 3 polarizing filters $F_1,F_2,F_3$, having direction $\alpha_1,\alpha_2,\alpha_3$. If we put them on the optical bench in pairs, Then we will have three random variables $P_1,P_2,P_3$.
+
+#### Bell's 3 variable inequality
+
+$$
+\operatorname{Prob}(P_1=1,P_3=0)\leq \operatorname{Prob}(P_1=1,P_2=0)+\operatorname{Prob}(P_2=1,P_3=0)
+$$
+
+Proof:
+
+By the law of total probability, (The event that the photon passes through the first filter but not the third filter is the union of the event that the photon did not pass through the second filter and the event that the photon passed the second filter and did not pass through the third filter) we have
+
+$$
+\begin{aligned}
+\operatorname{Prob}(P_1=1,P_3=0)&=\operatorname{Prob}(P_1=1,P_2=0,P_3=0)+\operatorname{Prob}(P_1=1,P_2=1,P_3=0)\\
+&=\operatorname{Prob}(P_1=1,P_2=0)\operatorname{Prob}(P_3=0)+\operatorname{Prob}(P_2=1,P_3=0)\operatorname{Prob}(P_1=1)\\
+&\leq\operatorname{Prob}(P_1=1,P_2=0)+\operatorname{Prob}(P_2=1,P_3=0)
+\end{aligned}
+$$
+
+However, according to our experimental measurement, for any pair of polarizers $F_i,F_j$, by the complement rule, we have
+
+$$
+\begin{aligned}
+\operatorname{Prob}(P_i=1,P_j=0)&=\operatorname{Prob}(P_i=1)-\operatorname{Prob}(P_i=1,P_j=1)\\
+&=\frac{1}{2}-\frac{1}{2}\cos^2(\alpha_i-\alpha_j)\\
+&=\frac{1}{2}\sin^2(\alpha_i-\alpha_j)
+\end{aligned}
+$$
+
+This leads to a contradiction if we apply the inequality to the experimental data.
+
+$$
+\frac{1}{2}\sin^2(\alpha_1-\alpha_3)\leq\frac{1}{2}\sin^2(\alpha_1-\alpha_2)+\frac{1}{2}\sin^2(\alpha_2-\alpha_3)
+$$
+
+If $\alpha_1=0,\alpha_2=\frac{\pi}{6},\alpha_3=\frac{\pi}{3}$, then
+
+$$
+\begin{aligned}
+\frac{1}{2}\sin^2(-\frac{\pi}{3})&\leq\frac{1}{2}\sin^2(-\frac{\pi}{6})+\frac{1}{2}\sin^2(\frac{\pi}{6}-\frac{\pi}{3})\\
+\frac{3}{8}&\leq\frac{1}{8}+\frac{1}{8}\\
+\frac{3}{8}&\leq\frac{1}{4}
+\end{aligned}
+$$
+
+Other revised experiments (eg. Aspect's experiment, Calcium entangled photon experiment) are also conducted and the inequality is still violated.
+
+#### The true model of light polarization
+
+The full description of the light polarization is given belows:
+
+State of polarization of a photon: $\psi=\alpha|0\rangle+\beta|1\rangle$, where $|0\rangle$ and $|1\rangle$ are the two orthogonal polarization states in $\mathbb{C}^2$.
+
+Polarization filter (generalized 0,1 valued random variable): orthogonal projection $P_\alpha$ on $\mathbb{C}^2$ corresponding to the direction $\alpha$. (operator satisfies $P_\alpha^*=P_\alpha=P_\alpha^2$.)
+
+The matrix representation of $P_\alpha$ is given by
+
+$$
+P_\alpha=\begin{pmatrix}
+\cos^2(\alpha) & \cos(\alpha)\sin(\alpha)\\
+\cos(\alpha)\sin(\alpha) & \sin^2(\alpha)
+\end{pmatrix}
+$$
+
+Probability of a photon passing through the filter $P_\alpha$ is given by $\langle P_\alpha\psi,\psi\rangle$, this is $\cos^2(\alpha)$ if we set $\psi=|0\rangle$.
+
+Since the probability of a photon passing through the three filters is not commutative, it is impossible to discuss $\operatorname{Prob}(P_1=1,P_3=0)$ in the classical setting.
+
 ## Section 5: The non-commutative (_quantum_) probability theory
 
 Let $\mathscr{H}$ be a Hilbert space. $\mathscr{H}$ consists of complex-valued functions on a finite set $\Omega=\{1,2,\cdots,n\}$. and that the functions $(e_1,e_2,\cdots,e_n)$ form an orthonormal basis of $\mathscr{H}$. We use Dirac notation $|k\rangle$ to denote the basis vector $e_k$.