update
This commit is contained in:
240
content/CSE510/CSE510_L3.md
Normal file
240
content/CSE510/CSE510_L3.md
Normal file
@@ -0,0 +1,240 @@
|
||||
# CSE510 Lecture 3
|
||||
|
||||
## Introduction and Definition of MDPs
|
||||
|
||||
### Definition and Examples
|
||||
|
||||
#### Reinforcement Learning
|
||||
|
||||
A computational framework for behavior
|
||||
learning through reinforcement
|
||||
|
||||
- RL is for an agent with the capacity to act
|
||||
- Each action influences the agent’s future observation
|
||||
- Success is measured by a scalar reward signal
|
||||
- Goal: find a policy that maximizes expected total rewards
|
||||
|
||||
Mathematical Model: Markov Decision Processes (MDP)
|
||||
|
||||
#### Markov Decision Processes (MDP)
|
||||
|
||||
A Finite MDP is defined by:
|
||||
|
||||
- A finite set of states $s \in S$
|
||||
- A finite set of actions $a \in A$
|
||||
- A transition function $T(s, a, s')$
|
||||
- Probability that a from s leads to s', i.e.,
|
||||
$P(s'| s, a)$
|
||||
- Also called the model or the dynamics
|
||||
- A reward function $R(s)$ ( Sometimes $R(s,a)$ or $R(s, a, s')$ )
|
||||
- A start state
|
||||
- A start state
|
||||
- Maybe a terminal state
|
||||
|
||||
A model for sequential decisionmaking problem under uncertaint
|
||||
|
||||
#### States
|
||||
|
||||
- **Stat is a snapshot of everything that matters for the next decision**
|
||||
- _Experience_ is a sequence of observations, actions, and rewards.
|
||||
- _Observation_ is the raw input of the agent's sensors
|
||||
- The state is a summary of the experience.
|
||||
|
||||
$$
|
||||
s_t=f(o_1, r_1, a_1, \ldots, a_{t-1}, o_t, r_t)
|
||||
$$
|
||||
|
||||
- The state can **include immediate "observations," highly processed observations, and structures built up over time from sequences of observations, memories** etc.
|
||||
- In a fully observed environment, $s_t= f(o_t)$
|
||||
|
||||
#### Action
|
||||
|
||||
- **Action = choice you make now**
|
||||
- They are used by the agent to interact with the world.
|
||||
- They can have many different temporal granularities and abstractions.
|
||||
- Actions can be defined to be
|
||||
- The instantaneous torques on the gripper
|
||||
- The instantaneous gripper translation, rotation, opening
|
||||
- Instantaneous forces applied to the objects
|
||||
- Short sequences of the above
|
||||
|
||||
#### Rewards
|
||||
|
||||
- **Reward = score you get as a result**
|
||||
- They are scalar values provided by the environment to the agent that indicate whether goals have been achieved,
|
||||
- e.g., 1 if goal is achieved, 0 otherwise, or -1 for overtime step the goal is not achieved
|
||||
- Rewards specify what the agent needs to achieve, not how to achieve it.
|
||||
- The simplest and cheapest form of supervision, and surprisingly general.
|
||||
- **Dense rewards are always preferred if available**
|
||||
- e.g., distance changes to a goal.
|
||||
|
||||
#### Dynamics or the Environment Model
|
||||
|
||||
- **Transition = dice roll** the world makes after your choice.
|
||||
- How the state change given the current state and action
|
||||
|
||||
$$
|
||||
P(S_{t+1}=s'|S_t=s_t, A_t=a_t)
|
||||
$$
|
||||
|
||||
- Modeling the uncertainty
|
||||
- Everyone has their own "world model", capturing the physical laws of the world.
|
||||
- Human also have their own "social model", by their values, beliefs, etc.
|
||||
- Two problems:
|
||||
- Planning: the dynamics model is known
|
||||
- Reinforcement learning: the dynamics model is unknown
|
||||
|
||||
#### Assumptions we have for MDP
|
||||
|
||||
**First-Order Markovian dynamics** (history independence)
|
||||
|
||||
- Next state only depend on current state and current action
|
||||
|
||||
$$
|
||||
P(S_{t+1}=s'|S_t=s_t,A_t=a_t,S_1,A_1,\ldots,S_{t-1},A_{t-1}) = P(S_{t+1}=s'|S_t=s_t,A_t=a_t)
|
||||
$$
|
||||
|
||||
**State-dependent** reward
|
||||
|
||||
- Reward is a deterministic function of current state
|
||||
|
||||
**Stationary dynamics**: do not depend on time
|
||||
|
||||
$$
|
||||
P(S_{t+1}=s'|A_t,S_t) = P(S_{k+1}=s'|A_k,S_k),\forall t,k
|
||||
$$
|
||||
|
||||
**Full observability** of the state
|
||||
|
||||
- Though we can't predict exactly which state we will reach when we execute an action, after the action is executed, we know the new state.
|
||||
|
||||
### Examples
|
||||
|
||||
#### Atari games
|
||||
|
||||
- States: raw RGB frames (one frame is not enough, so we use a sequence of frames, usually 4 frames)
|
||||
- Action: 18 actions in joystick movement
|
||||
- Reward: score changes
|
||||
|
||||
#### Go
|
||||
|
||||
- States: features of the game board
|
||||
- Action: place a stone or resign
|
||||
- Reward: win +1, lose -1, draw 0
|
||||
|
||||
#### Autonomous car driving
|
||||
|
||||
- States: speed, direction, lanes, traffic, weather, etc.
|
||||
- Action: steer, brake, throttle
|
||||
- Reward: +1 for reaching the destination, -1 for honking from surrounding cars, -100 for collision (exmaple)
|
||||
|
||||
#### Grid World
|
||||
|
||||
A maze-like problem
|
||||
|
||||
- The agent lives in a grid
|
||||
|
||||
- States: position of the agent
|
||||
- Noisy actions: east, south, west, north
|
||||
- Dynamics: actions not always go as planned
|
||||
- 80% of the time, the action North takes the agent north (if there is a wall, it stays)
|
||||
- 10% of the time, the action North takes the agent west and 10% of the time, the action North takes the agent east
|
||||
- Reward the agent receives each time step
|
||||
- Small "living" reward each step (can be negative)
|
||||
- Big reward for reaching the goal
|
||||
|
||||
> [!NOTE]
|
||||
>
|
||||
> Due to the noise in the actions, it is insufficient to just output a sequence of actions to reach the goal.
|
||||
|
||||
### Solution and its criterion
|
||||
|
||||
### Solution to an MDP
|
||||
|
||||
- Actions have stochastic effects, so the state we end up in is uncertain
|
||||
- This means that we might end up in states where the remainder of the action sequence doesn't apply or is a bad choice
|
||||
- A solution should tell us what the best action is for any possible situation/state that might arise
|
||||
|
||||
### Policy as output to an MDP
|
||||
|
||||
A stationary policy is a mapping from states to actions
|
||||
|
||||
- $\pi: S \to A$
|
||||
- $\pi(s)$ is the action to take in state $s$ (regardless of the time step)
|
||||
- Specifies a continuously reactive controller
|
||||
|
||||
We don't want to output just any policy
|
||||
|
||||
We want to output a good policy
|
||||
|
||||
One that accumulates a lot of rewards
|
||||
|
||||
### Value of a policy
|
||||
|
||||
Value function
|
||||
|
||||
$V:S\to \mathbb{R}$ associates value with each state
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
V^\pi(s) &= \mathbb{E}\left[\sum_{t=0}^\infty \gamma^t R(s_t)|s_0=s,a_t=\pi(s_t), s_{t+1}|s_t,a_t\sim P\right] \\
|
||||
&= \mathbb{E}\left[R(s_t) + \gamma \sum_{t=1}^\infty \gamma^{t-1} R(s_{t+1})|s_0=s,a_t=\pi(s_t), s_{t+1}|s_t,a_t\sim P\right] \\
|
||||
&= R(s) + \gamma \sum_{s'\in S} P(s'|s,\pi(s)) V^\pi(s')
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Future rewards "discounted" by $\gamma$ per time step
|
||||
|
||||
We value the state by the expected total rewards from this state onwards, discounted by $\gamma$ for each time step.
|
||||
|
||||
> A small $\gamma$ means model would short-sighted and reduce computation complexity.
|
||||
|
||||
#### Bellman Equation
|
||||
|
||||
Basically, it gives one step lookahead value of a policy.
|
||||
|
||||
$$
|
||||
V^\pi(s) = R(s) + \gamma \sum_{s'\in S} P(s'|s,\pi(s)) V^\pi(s')
|
||||
$$
|
||||
|
||||
Today's value = Today's reward + discounted future value
|
||||
|
||||
### Optimal Policy and Bellman Optimality Equation
|
||||
|
||||
The goal for a MDP is to compute or learn an optimal policy.
|
||||
|
||||
- An optimal policy is one that achieves the highest value at any state
|
||||
|
||||
$$
|
||||
\pi^* = \arg\max_\pi V^\pi(s)
|
||||
$$
|
||||
|
||||
We define the optimal value function suing Bellman Optimality Equation (Proof left as an exercise)
|
||||
|
||||
$$
|
||||
V^*(s) = R(s) + \gamma \max_{a\in A} \sum_{s'\in S} P(s'|s,a) V^*(s')
|
||||
$$
|
||||
|
||||
The optimal policy is
|
||||
|
||||
$$
|
||||
\pi^*(s) = \arg\max_{a\in A} \sum_{s'\in S} P(s'|s,a) V^*(s')
|
||||
$$
|
||||
|
||||
|
||||
|
||||
> [!NOTE]
|
||||
>
|
||||
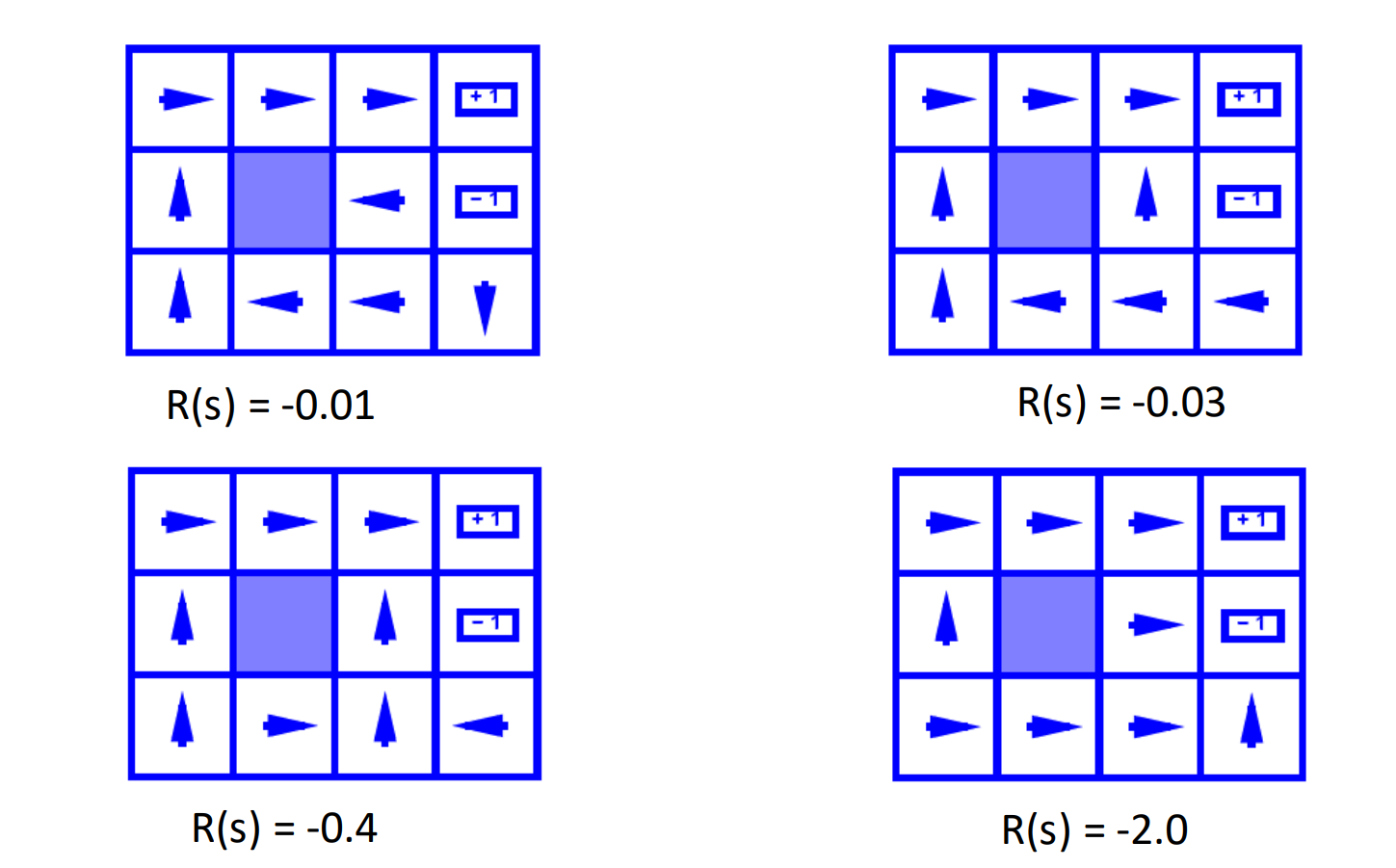
> When $R(s)$ is small, the agent will prefer to take actions that avoids punishment in short term.
|
||||
|
||||
### The existence of the optimal policy
|
||||
|
||||
Theorem: for any Markov Decision Process
|
||||
|
||||
- There exists an optimal policy
|
||||
- There can be many optimal policies, but all optimal policies achieve the same optimal value function
|
||||
- There is always a deterministic optimal policy for any MDP
|
||||
|
||||
## Value Iteration
|
||||
|
||||
## Policy Iteration
|
||||
@@ -5,4 +5,5 @@ export default {
|
||||
},
|
||||
CSE510_L1: "CSE510 Deep Reinforcement Learning (Lecture 1)",
|
||||
CSE510_L2: "CSE510 Deep Reinforcement Learning (Lecture 2)",
|
||||
CSE510_L3: "CSE510 Deep Reinforcement Learning (Lecture 3)",
|
||||
}
|
||||
BIN
public/CSE510/MDP-optimal-policy.png
Normal file
BIN
public/CSE510/MDP-optimal-policy.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 71 KiB |
Reference in New Issue
Block a user