update old paper links

content/CSE5313/Exam_reviews/CSE5313_F1.md

@@ -32,241 +32,8 @@ Please refer to the syllabus for our policy regarding the use of GenAI.
 >
 > This notation system is annoying since in mathematics, $A^*$ is the transpose of $A$, but since we are using literatures in physics, we keep the notation of $A^*$. In this report, I will try to make the notation consistent as possible and follows the **physics** convention in this report. So every vector you see will be in $\ket{\psi}$ form. And we will avoid using the $\langle v,w\rangle$ notation for inner product as it used in math, we will use $\langle v|w\rangle$ or $\langle v,w\rangle$ to denote the inner product.
 
-A quantum error-correcting code is defined to be a unitary mapping (encoding) of $k$ qubits (two-state quantum systems) into a subspace of the quantum state space of $n$ qubuits such that if any $t$ of the qubits undergo arbitary decoherence, not necessarily independently, the resulting $n$ qubit state can be used to faithfully reconstruct the original quantum state of the $k$ encoded qubits.
-
-Asymptotic rate $k/n=1-2H_2(2t/n)$, where $H_2$ is the binary entropy function
-
-$$
-H_2=-p\log_2(p)-(1-p)\log_2(1-p)
-$$
-
-### Problem setting and motivation
-
-#### Linear algebra 102
-
-The main vector space we are interested in is $\mathbb{C}^n$, therefore, all the linear operator we defined are from $\mathbb{C}^n$ to $\mathbb{C}^n$.
-
-We denote a vector in vector space as $\ket{\psi}=(z_1,\cdots,z_n)$ (might also be infinite dimensional, and $z_i\in\mathbb{C}$).
-
-A natural inner product space defined on $\mathbb{C}^n$ is given by the Hermitian inner product:
-
-$$
-\langle\psi|\varphi\rangle=\sum_{i=1}^n z_i\bar{z}_i
-$$
-
-This satisfies the following properties:
-1. $\bra{\psi}\sum_i \lambda_i\ket{\varphi}=\sum_i \lambda_i \langle\psi|\varphi\rangle$ (linear on the second argument)
-2. $\langle\varphi|\psi\rangle=(\langle\psi|\varphi\rangle)^*$
-3. $\langle\psi|\psi\rangle\geq 0$ with equality if and only if $\ket{\psi}=0$
-
-Here $\psi$ is just a label for the vector and you don't need to worry about it too much. This is also called the ket, where the counterpart:
-
-- $\langle\psi\rangle$ is called the bra, used to denote the vector dual to $\psi$, such element is a linear functional if you really wants to know what that is.
-- $\langle\psi|\varphi\rangle$ is the inner product between two vectors, and $\bra{\psi} A\ket{\varphi}$ is the inner product between $A\ket{\varphi}$ and $\bra{\psi}$, or equivalently $A^\dagger \bra{\psi}$ and $\ket{\varphi}$.
-- Given a complex matrix $A=\mathbb{C}^{n\times n}$,
-  - $A^*$ is the complex conjugate of $A$.
-    - i.e., $A=\begin{bmatrix}1+i & 2+i & 3+i\\4+i & 5+i & 6+i\\7+i & 8+i & 9+i\end{bmatrix}$, $A^*=\begin{bmatrix}1-i & 2-i & 3-i\\4-i & 5-i & 6-i\\7-i & 8-i & 9-i\end{bmatrix}$
-  - $A^\top$ is the transpose of $A$.
-    - i.e., $A=\begin{bmatrix}1+i & 2+i & 3+i\\4+i & 5+i & 6+i\\7+i & 8+i & 9+i\end{bmatrix}$, $A^\top=\begin{bmatrix}1+i & 4+i & 7+i\\2+i & 5+i & 8+i\\3+i & 6+i & 9+i\end{bmatrix}$
-  - $A^\dagger=(A^*)^\top$ is the complex conjugate transpose, referred to as the adjoint, or Hermitian conjugate of $A$.
-    - i.e., $A=\begin{bmatrix}1+i & 2+i & 3+i\\4+i & 5+i & 6+i\\7+i & 8+i & 9+i\end{bmatrix}$, $A^\dagger=\begin{bmatrix}1-i & 4-i & 7-i\\2-i & 5-i & 8-i\\3-i & 6-i & 9-i\end{bmatrix}$
-  - $A$ is unitary if $A^\dagger A=AA^\dagger=I$.
-  - $A$ is hermitian (self-adjoint in mathematics literatures) if $A^\dagger=A$.
-
-#### Motivation of Tensor product
-
-Recall from the traditional notation of product space of two vector spaces $V$ and $W$, that is, $V\times W$, is the set of all ordered pairs $(\ket{v},\ket{w})$ where $\ket{v}\in V$ and $\ket{w}\in W$.
-
-The space has dimension $\dim V+\dim W$.
-
-We want to define a vector space with notation of multiplication of two vectors from different vector spaces.
-
-That is
-
-$$
-(\ket{v_1}+\ket{v_2})\otimes \ket{w}=(\ket{v_1}\otimes \ket{w})+(\ket{v_2}\otimes \ket{w})
-$$
-$$
-\ket{v}\otimes (\ket{w_1}+\ket{w_2})=(\ket{v}\otimes \ket{w_1})+(\ket{v}\otimes \ket{w_2})
-$$
-
-and enables scalar multiplication by
-
-$$
-\lambda (\ket{v}\otimes \ket{w})=(\lambda \ket{v})\otimes \ket{w}=\ket{v}\otimes (\lambda \ket{w})
-$$
-
-And we wish to build a way associates the basis of $V$ and $W$ to the basis of $V\otimes W$. That makes the tensor product a vector space with dimension $\dim V\times \dim W$.
-
-#### Definition of linear functional
-
-> [!TIP]
->
-> Note the difference between a linear functional and a linear map.
->
-> A generalized linear map is a function $f:V\to W$ satisfying the condition
->
-> 1. $f(\ket{u}+\ket{v})=f(\ket{u})+f(\ket{v})$
-> 2. $f(\lambda \ket{v})=\lambda f(\ket{v})$
-
-A linear functional is a linear map from $V$ to $\mathbb{F}$.
-
-#### Definition of bilinear functional
-
-A bilinear functional is a bilinear function $\beta:V\times W\to \mathbb{F}$ satisfying the condition that $\ket{v}\to \beta(\ket{v},\ket{w})$ is a linear functional for all $\ket{w}\in W$ and $\ket{w}\to \beta(\ket{v},\ket{w})$ is a linear functional for all $\ket{v}\in V$.
-
-The vector space of all bilinear functionals is denoted by $\mathcal{B}(V,W)$.
-
-#### Definition of tensor product
-
-Let $V,W$ be two vector spaces.
-
-Let $V'$ and $W'$ be the dual spaces of $V$ and $W$, respectively, that is $V'=\{\psi:V\to \mathbb{F}\}$ and $W'=\{\phi:W\to \mathbb{F}\}$, $\psi, \phi$ are linear functionals.
-
-The tensor product of vectors $v\in V$ and $w\in W$ is the bilinear functional defined by $\forall (\psi,\phi)\in V'\times W'$ given by the notation
-
-$$
-(v\otimes w)(\psi,\phi)\coloneqq\psi(v)\phi(w)
-$$
-
-The tensor product of two vector spaces $V$ and $W$ is the vector space $\mathcal{B}(V',W')$
-
-Notice that the basis of such vector space is the linear combination of the basis of $V'$ and $W'$, that is, if $\{e_i\}$ is the basis of $V'$ and $\{f_j\}$ is the basis of $W'$, then $\{e_i\otimes f_j\}$ is the basis of $\mathcal{B}(V',W')$.
-
-That is, every element of $\mathcal{B}(V',W')$ can be written as a linear combination of the basis.
-
-Since $\{e_i\}$ and $\{f_j\}$ are bases of $V'$ and $W'$, respectively, then we can always find a set of linear functionals $\{\phi_i\}$ and $\{\psi_j\}$ such that $\phi_i(e_j)=\delta_{ij}$ and $\psi_j(f_i)=\delta_{ij}$.
-
-Here $\delta_{ij}=\begin{cases}
-1 & \text{if } i=j \\
-0 & \text{otherwise}
-\end{cases}$ is the Kronecker delta.
-
-$$
-V\otimes W=\left\{\sum_{i=1}^n \sum_{j=1}^m a_{ij} \phi_i(v)\psi_j(w): \phi_i\in V', \psi_j\in W'\right\}
-$$
-
-Note that $\sum_{i=1}^n \sum_{j=1}^m a_{ij} \phi_i(v)\psi_j(w)$ is a bilinear functional that maps $V'\times W'$ to $\mathbb{F}$.
-
-This enables basis free construction of vector spaces with proper multiplication and scalar multiplication.
-
-This vector space is equipped with the unique inner product $\langle v\otimes w, u\otimes x\rangle_{V\otimes W}$ defined by
-
-$$
-\langle v\otimes w, u\otimes x\rangle=\langle v,u\rangle_V\langle w,x\rangle_W
-$$
-
-In practice, we ignore the subscript of the vector space and just write $\langle v\otimes w, u\otimes x\rangle=\langle v,u\rangle\langle w,x\rangle$.
-
-> [!NOTE]
->
-> All those definitions and proofs can be found in Linear Algebra Done Right by Sheldon Axler.
-
-#### Definition of two-state quantum system
-
-The finite dimensional Hilbert space $\mathcscr{H}
-
-#### Definition of Coherent states from the view of physics
-
-#### Side node: Why quantum error-correcting code is hard
-
-Decoherence process
-
-#### No-cloning theorem
-
-> Reference from P.532 of the book
-
-Suppose we have a quantum system with two slots $A$, and $B$, the data slot, starts out in an unknown but pure quantum state $\ket{\psi}$. This is the state which is to be copied into slot $B$m the target slot. We assume that the target slot starts out in some standard pure state $\ket{s}$. Thus the initial state of the copying machine is $\ket{\psi}\otimes \ket{s}$.
-
-Assume there exists some unitary operator $U$ such that $U(\ket{\psi}\otimes \ket{s})=\ket{\psi}\otimes \ket{\psi}$.
-
-Consider two pure states $\ket{\psi}$ and $\ket{\varphi}$, such that $U(\ket{\psi}\otimes \ket{s})=\ket{\psi}\otimes \ket{\psi}$ and $U(\ket{\varphi}\otimes \ket{s})=\ket{\varphi}\otimes \ket{\varphi}$. The inner product of the two equation yields:
-
-$$
-\langle \psi|\varphi\rangle =(\langle \psi|\varphi\rangle)^2
-$$
-
-This equation has only two solutions, either $\langle \psi|\varphi\rangle=0$ or $\langle \psi|\varphi\rangle=1$.
-
-If $\langle \psi|\varphi\rangle=0$, then $\ket{\psi}=\ket{\varphi}$, no cloning for trivial case.
-
-If $\langle \psi|\varphi\rangle=1$, then $\ket{\psi}$ and $\ket{\varphi}$ are orthogonal.
-
-#### Proposition: Encoding 8 to 9 that correct 1 errors
-
-Recover 1 qubit from a 9 qubit quantum system. (Shor code, 1995)
-
-![Shore code](https://notenextra.trance-0.com/CSE5313/Shore_code.png)
-
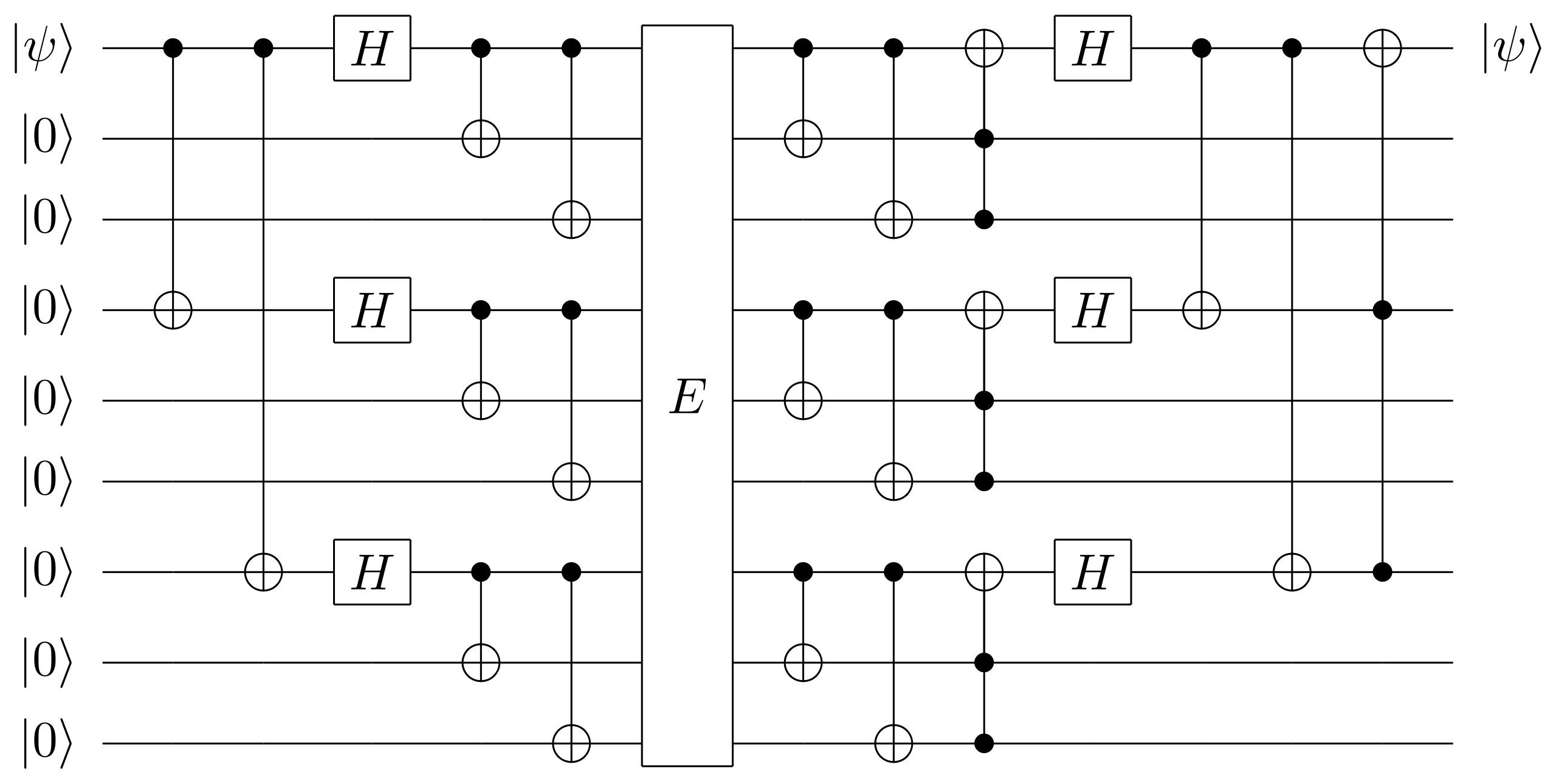
-### Tools and related topics
-
-#### Theoretical upper bound for quantum error-correcting code
-
-From quantum information capacity of a quantum channel
-
-$$
-\min\{1-H_2(2t/3n),H_2(\frac{1}{2}+\sqrt{(1-t/n)t/n})\}
-$$
-
-#### Definition of quantum error-correcting code from binary linear error-correcting code
-
-All the operations will be done in $\mathbb{F}_2=\{0,1\}$.
-
-Consider two binary vectors $v=[v_1,...,v_n],v_i\in\{0,1\}$ and $w=[w_1,...,w_n],w_i\in\{0,1\}$ with size $n$.
-
-Recall from our lecture that
-
-$d$ denotes the Hamming weight of a vector.
-
-$d_H(v,w)=\sum_{i=1}^{n}\begin{cases} 0 & \text{if } v_i=w_i \\ 1 & \text{if } v_i\neq w_i \end{cases}$ denotes the Hamming distance between $v$ and $w$.
-
-$\operatorname{supp}(v)=\{i\in[n]:v_i\neq 0\}$ denotes the support of $v$.
-
-$v|_S$ denotes the projection of $v$ onto the subspace $S$, we usually denote the $S$ by a set of coordinates, that is $S\subseteq[n]$.
-
-When projecting a vector $v$ onto a another vector $w$, we usually write $v|_E\coloneqq v|_{\operatorname{supp} w}$.
-
-When we have two vector we may use $v\leqslant w$ (Note that this is different than $\leq$ sign) to mean $\operatorname{supp}(v)\subseteq \operatorname{supp}(w)$.
-
-<details>
-<summary>Example</summary>
-
-Let $v=[1,0,0,1,1,1,1]$ and $w=[1,0,0,1,0,0,1]$, then $\operatorname{supp}(v)=\{1,4,5,6,7\}$, $\operatorname{supp}(w)=\{1,4,7\}$. Therefore $w\leqslant v$.
-
-$v|_w=[v_1,v_4,v_7]=[1,1,0]$
-</details>
-
-$\mathcal{C}$ denotes the code, a set of arbitrary binary vectors with length $n$.
-
-$d(\mathcal{C})=\{d(v,w)|v,w\in\mathcal{C}\}$ denotes the minimum distance of the code.
-
-If $\mathcal{C}$ is linear then the minimum distance is the minimum Hamming weight of a non-zero codeword.
-
-A $[n,k,d]$ linear code is a linear code of $n$ bits codeword with $k$ message bits that can correct $d$ errors.
-
-$R\coloneqq\frac{\operatorname{dim}\mathcal{C}}{n}$ is the rate of code $\mathcal{C}$.
-
-$\mathcal{C}^{\perp}\coloneqq\{v\in\mathbb{F}_2^n:v\cdot w=0\text{ for all }w\in\mathcal{C}\}$ is the dual code of a code $\mathcal{C}$. From linear algebra, we know that $\dim\mathcal{C}^{\perp}+\dim\mathcal{C}=n$.
-
-<details>
-<summary>Example used in the paper</summary>
-
-Consider the $[7,4,3]$ Hamming code with generator matrix $G$.
-
-</details>
-
-#### Proposition: Encoding $k$ to $n$ that correct $t$ errors
-
-### Evaluation of paper
-
-### Limitation and suggestions
-
-### Further direction and research
-
-#### Toric code, surface code
-
-This is the topic I really want to dig into.
-
-This method gives a [2nm+n+m+1, 1, min(n,m)] error correcting code with only needs local stabilizer checks and really interests me.
-
-### References
+<iframe src="https://git.trance-0.com/Trance-0/CSE5313F1/raw/branch/main/latex/ZheyuanWu_CSE5313_FinalAssignment.pdf" width="100%" height="600px" style="border: none;" title="Embedded PDF Viewer">
+  <!-- Fallback content for browsers that do not support iframes or PDFs within them -->
+  <iframe src="https://git.trance-0.com/Trance-0/CSE5313F1/raw/branch/main/latex/ZheyuanWu_CSE5313_FinalAssignment.pdf" width="100%" height="500px">
+  <p>Your browser does not support iframes. You can <a href="https://git.trance-0.com/Trance-0/CSE5313F1/raw/branch/main/latex/ZheyuanWu_CSE5313_FinalAssignment.pdf">download the PDF</a> file instead.</p>
+</iframe>

content/Math401/Extending_thesis/Math401_R4.md

@@ -53,4 +53,4 @@ $$
 
 This part is intentionally left blank and may be filled near the end of the semester, by assignments given in CSE5313.
 
-[Link to self-contained report](../../CSE5313/Exam_reviews/CSE5313_F1.md)
+[Link to self-contained report](https://notenextra.trance-0.com/CSE5313/Exam_reviews/CSE5313_F1/)

content/Math401/Math401_H1.md

@@ -4,6 +4,7 @@ I made this little book for my Honor Thesis, showing the relevant parts of my wo
 
 Contents updated as displayed and based on my personal interest and progress with Prof.Feres.
 
+
 <iframe src="https://git.trance-0.com/Trance-0/HonorThesis/raw/branch/main/main.pdf" width="100%" height="600px" style="border: none;" title="Embedded PDF Viewer">
   <!-- Fallback content for browsers that do not support iframes or PDFs within them -->
   <iframe src="https://git.trance-0.com/Trance-0/HonorThesis/raw/branch/main/main.pdf" width="100%" height="500px">