update
This commit is contained in:
@@ -3,7 +3,7 @@ services:
|
||||
build:
|
||||
context: ./
|
||||
dockerfile: ./Dockerfile
|
||||
image: trance0/notenextra:v1.1.7
|
||||
image: trance0/notenextra:v1.1.8
|
||||
restart: on-failure:5
|
||||
ports:
|
||||
- 13000:3000
|
||||
|
||||
@@ -92,6 +92,8 @@ SSD is a multi-resolution object detection
|
||||
|
||||
RetinaNet combine feature pyramid network with focal loss to reduce the standard cross-entropy loss for well-classified examples.
|
||||
|
||||
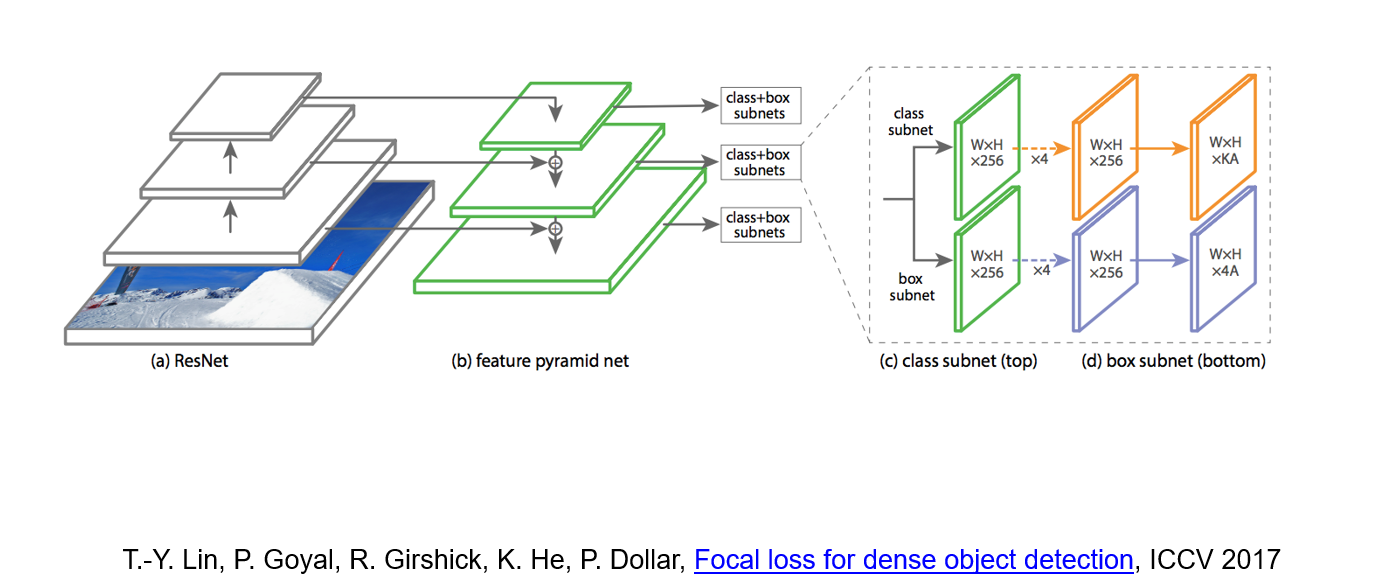
|
||||
|
||||
> Cross-entropy loss:
|
||||
> $$CE(p_t) = - \log(p_t)$$
|
||||
|
||||
|
||||
114
pages/CSE559A/CSE559A_L16.md
Normal file
114
pages/CSE559A/CSE559A_L16.md
Normal file
@@ -0,0 +1,114 @@
|
||||
# CSE559A Lecture 16
|
||||
|
||||
## Dense image labelling
|
||||
|
||||
### Semantic segmentation
|
||||
|
||||
Use one-hot encoding to represent the class of each pixel.
|
||||
|
||||
### General Network design
|
||||
|
||||
Design a network with only convolutional layers, make predictions for all pixels at once.
|
||||
|
||||
Can the network operate at full image resolution?
|
||||
|
||||
Practical solution: first downsample, then upsample
|
||||
|
||||
### Outline
|
||||
|
||||
- Upgrading a Classification Network to Segmentation
|
||||
- Operations for dense prediction
|
||||
- Transposed convolutions, unpooling
|
||||
- Architectures for dense prediction
|
||||
- DeconvNet, U-Net, "U-Net"
|
||||
- Instance segmentation
|
||||
- Mask R-CNN
|
||||
- Other dense prediction problems
|
||||
|
||||
### Fully Convolutional Networks
|
||||
|
||||
"upgrading" a classification network to a dense prediction network
|
||||
|
||||
1. Covert "fully connected" layers to 1x1 convolutions
|
||||
2. Make the input image larger
|
||||
3. Upsample the output
|
||||
|
||||
Start with an existing classification CNN ("an encoder")
|
||||
|
||||
Then use bilinear interpolation and transposed convolutions to make full resolution.
|
||||
|
||||
### Operations for dense prediction
|
||||
|
||||
#### Transposed Convolutions
|
||||
|
||||
Use the filter to "paint" in the output: place copies of the filter on the output, multiply by corresponding value in the input, sum where copies of the filter overlap
|
||||
|
||||
We can increase the resolution of the output by using a larger stride in the convolution.
|
||||
|
||||
- For stride 2, dilate the input by inserting rows and columns of zeros between adjacent entries, convolve with flipped filter
|
||||
- Sometimes called convolution with fractional input stride 1/2
|
||||
|
||||
#### Unpooling
|
||||
|
||||
Max unpooling:
|
||||
|
||||
- Copy the maximum value in the input region to all locations in the output
|
||||
- Use the location of the maximum value to know where to put the value in the output
|
||||
|
||||
Nearest neighbor unpooling:
|
||||
|
||||
- Copy the maximum value in the input region to all locations in the output
|
||||
- Use the location of the maximum value to know where to put the value in the output
|
||||
|
||||
### Architectures for dense prediction
|
||||
|
||||
#### DeconvNet
|
||||
|
||||
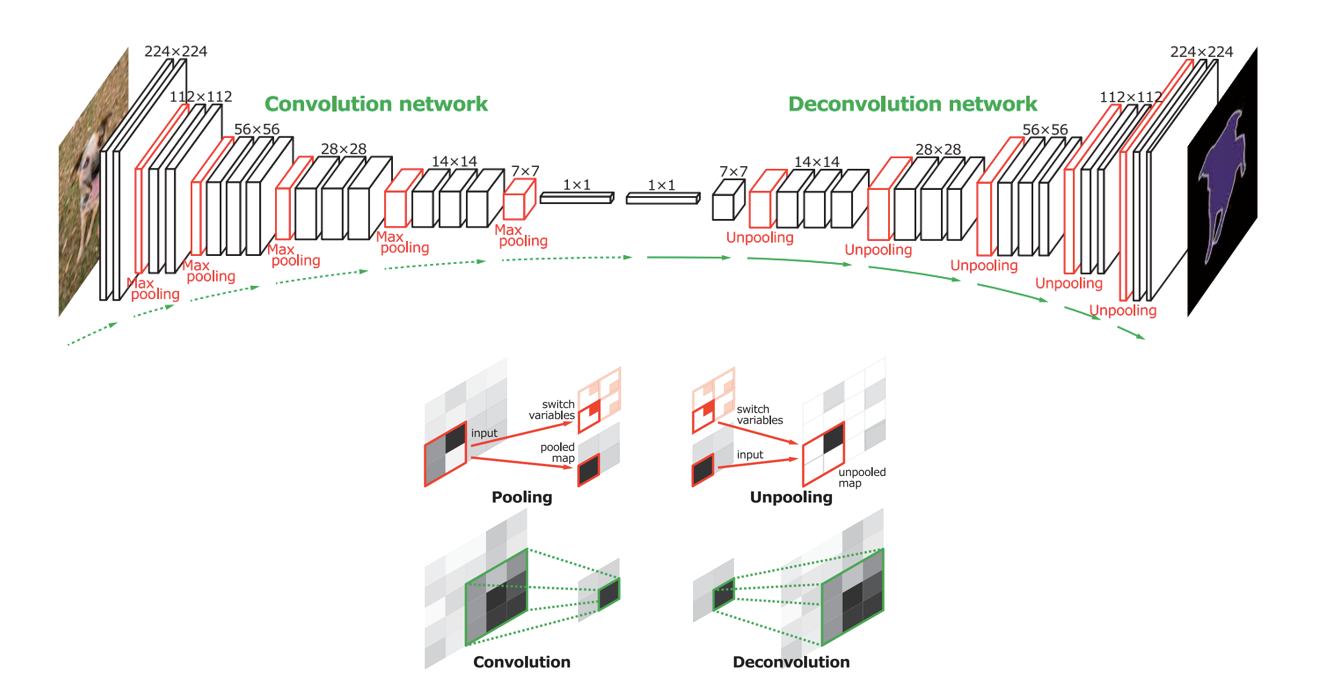
|
||||
|
||||
_How the information about location is encoded in the network?_
|
||||
|
||||
#### U-Net
|
||||
|
||||
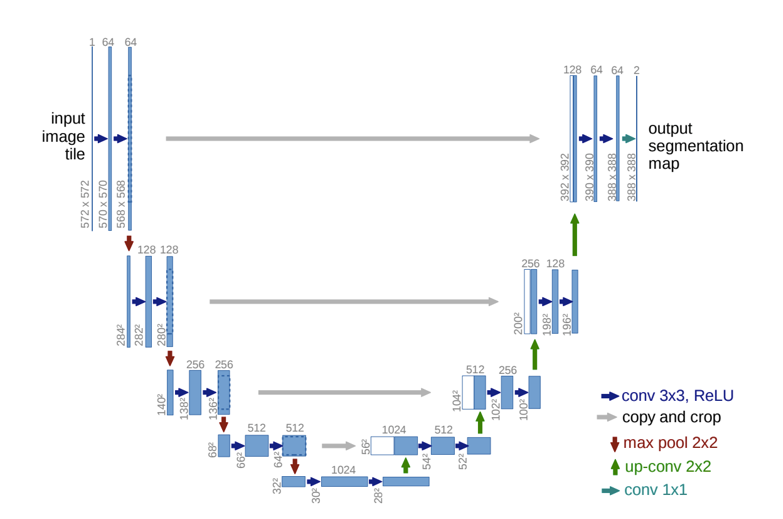
|
||||
|
||||
- Like FCN, fuse upsampled higher-level feature maps with higher-res, lower-level feature maps (like residual connections)
|
||||
- Unlike FCN, fuse by concatenation, predict at the end
|
||||
|
||||
#### Extended U-Net Architecture
|
||||
|
||||
Many variants of U-Net would replace the "encoder" of the U-Net with other architectures.
|
||||
|
||||
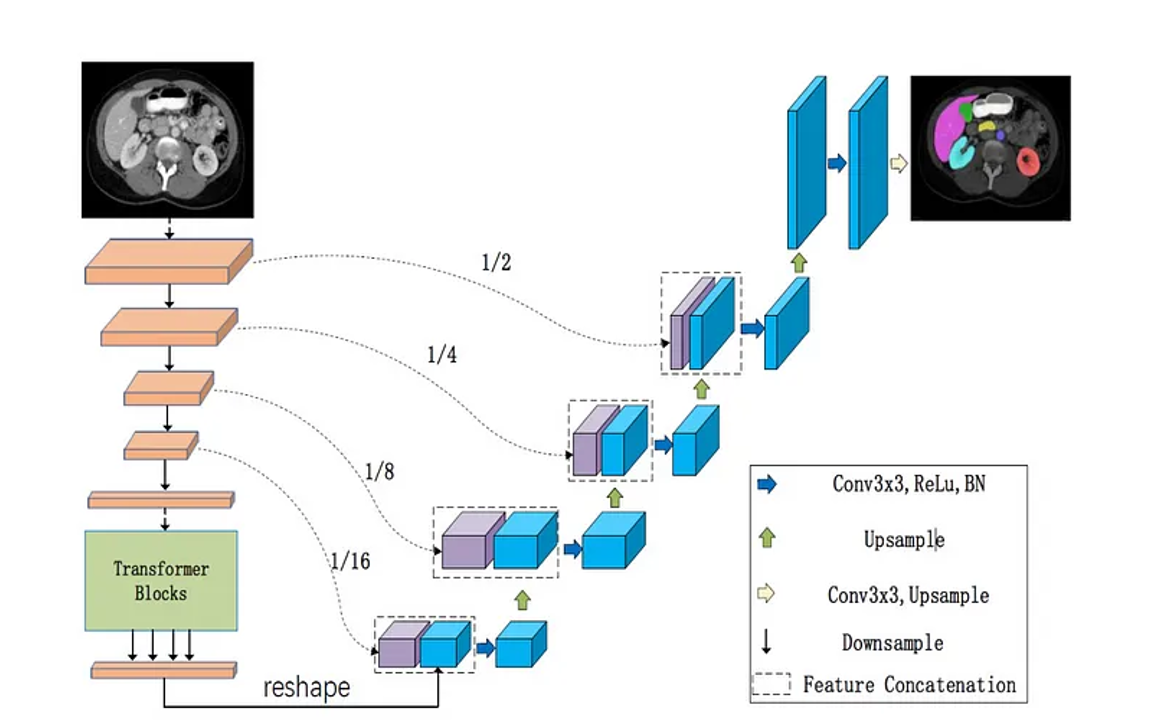
|
||||
|
||||
##### Encoder/Decoder v.s. U-Net
|
||||
|
||||
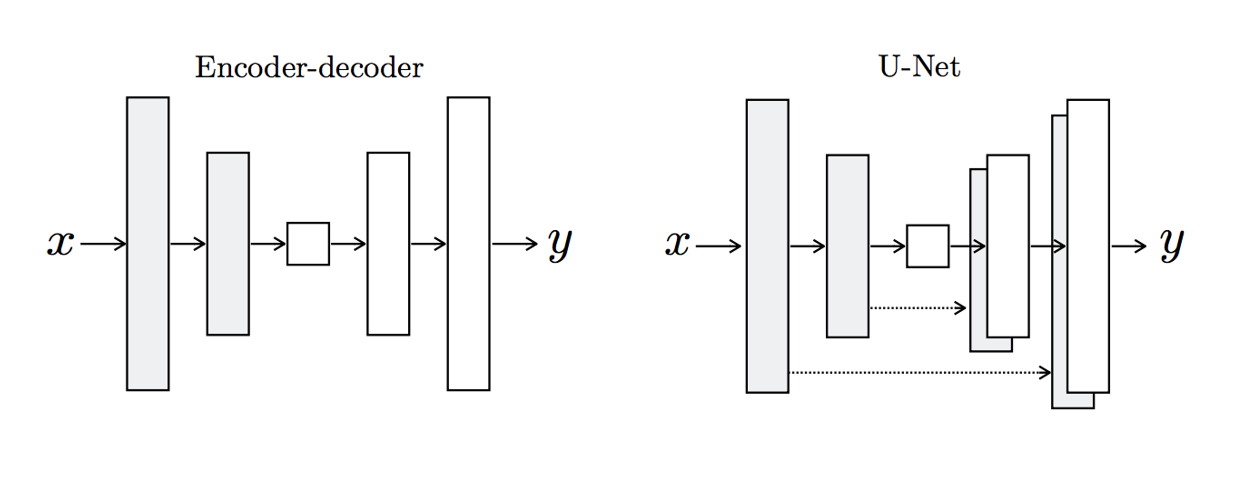
|
||||
|
||||
### Instance Segmentation
|
||||
|
||||
#### Mask R-CNN
|
||||
|
||||
Mask R-CNN = Faster R-CNN + FCN on Region of Interest
|
||||
|
||||
### Extend to keypoint prediction?
|
||||
|
||||
- Use a similar architecture to Mask R-CNN
|
||||
|
||||
_Continue on Tuesday_
|
||||
|
||||
### Other tasks
|
||||
|
||||
#### Panoptic feature pyramid network
|
||||
|
||||
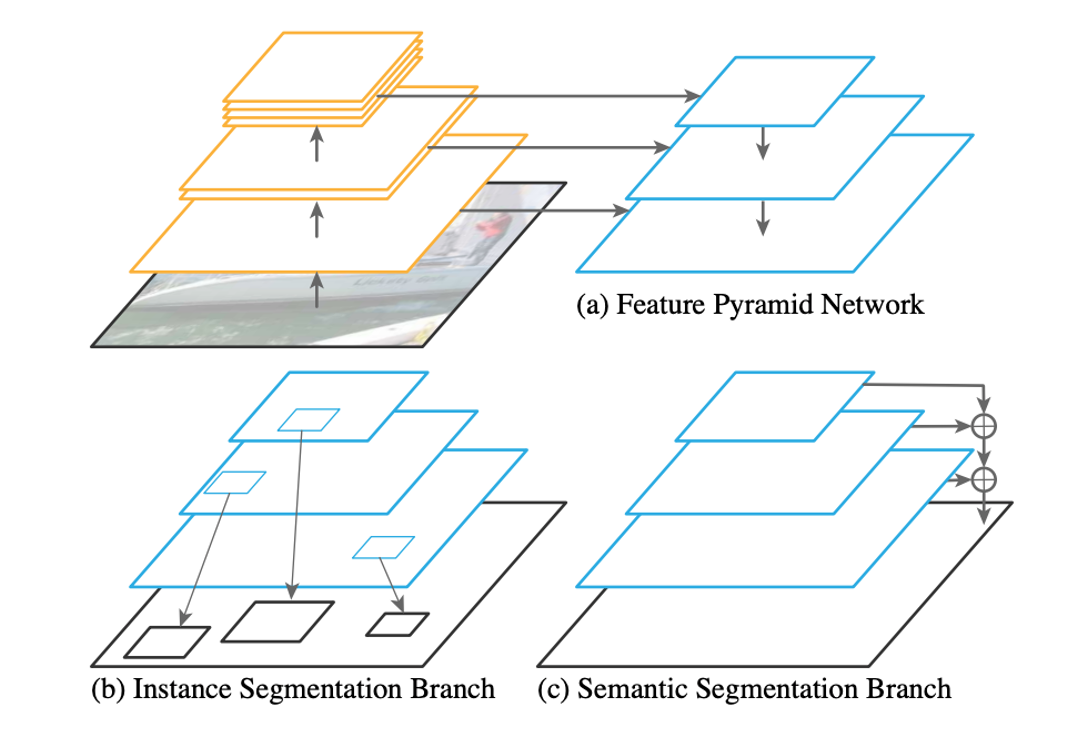
|
||||
|
||||
#### Depth and normal estimation
|
||||
|
||||
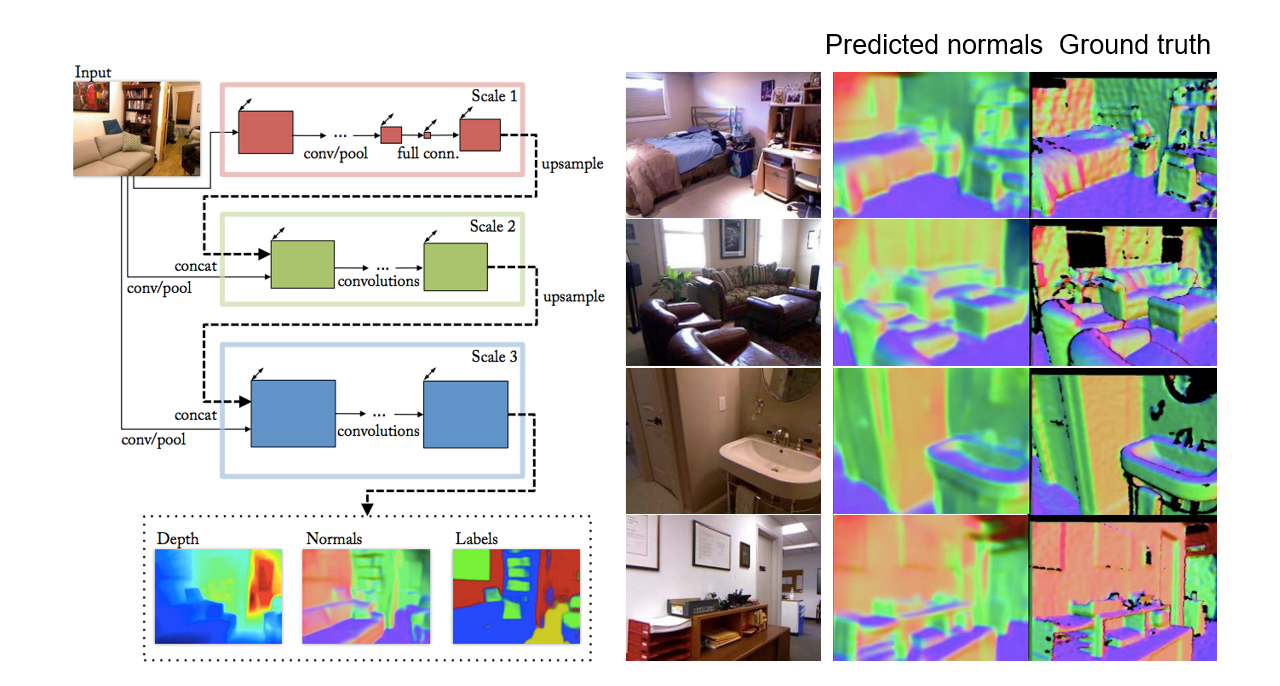
|
||||
|
||||
D. Eigen and R. Fergus, Predicting Depth, Surface Normals and Semantic Labels with a Common Multi-Scale Convolutional Architecture, ICCV 2015
|
||||
|
||||
#### Colorization
|
||||
|
||||
R. Zhang, P. Isola, and A. Efros, Colorful Image Colorization, ECCV 2016
|
||||
@@ -18,4 +18,5 @@ export default {
|
||||
CSE559A_L13: "Computer Vision (Lecture 13)",
|
||||
CSE559A_L14: "Computer Vision (Lecture 14)",
|
||||
CSE559A_L15: "Computer Vision (Lecture 15)",
|
||||
CSE559A_L16: "Computer Vision (Lecture 16)",
|
||||
}
|
||||
|
||||
@@ -1 +1,105 @@
|
||||
# Lecture 24
|
||||
# Math4121 Lecture 24
|
||||
|
||||
## Chapter 5: Measure Theory
|
||||
|
||||
### Jordan Measurable
|
||||
|
||||
#### Proposition 5.1
|
||||
|
||||
A bounded set $S\subseteq \mathbb{R}^n$ is Jordan measurable if
|
||||
|
||||
$$
|
||||
c_e(S)=c_i(S)+c_e(\partial S)
|
||||
$$
|
||||
|
||||
where $\partial S$ is the boundary of $S$ and $c_e(\partial S)=0$.
|
||||
|
||||
Example:
|
||||
|
||||
1. $S=\mathbb{Q}\cap [0,1]$ is not Jordan measurable.
|
||||
|
||||
Since $c_e(S)=0$ and $\partial S=[0,1]$, $c_i(S)=1$.
|
||||
|
||||
So $c_e(\partial S)=1\neq 0$.
|
||||
|
||||
2. SVC(3) is Jordan measurable.
|
||||
|
||||
Since $c_e(S)=0$ and $\partial S=0$, $c_i(S)=0$. The outer content of the cantor set is $0$.
|
||||
|
||||
> Any set or subset of a set with $c_e(S)=0$ is Jordan measurable.
|
||||
|
||||
3. SVC(4)
|
||||
|
||||
At each step, we remove $2^n$ intervals of length $\frac{1}{4^n}$.
|
||||
|
||||
So $S=\bigcap_{n=1}^{\infty} C_i$ and $c_e(C_k)=c_e(C_{k-1})-\frac{2^{k-1}}{4^k}$. $c_e(C_0)=1$.
|
||||
|
||||
So
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
c_e(S)&\leq \lim_{k\to\infty} c_e(C_k)\\
|
||||
&=1-\sum_{k=1}^{\infty} \frac{2^{k-1}}{4^k}\\
|
||||
&=1-\frac{1}{4}\sum_{k=0}^{\infty} \left(\frac{2}{4}\right)^k\\
|
||||
&=1-\frac{1}{4}\cdot \frac{1}{1-\frac{2}{4}}\\
|
||||
&=1-\frac{1}{4}\cdot \frac{1}{\frac{1}{2}}\\
|
||||
&=1-\frac{1}{2}\\
|
||||
&=\frac{1}{2}.
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
And we can also claim that $c_i(S)\geq \frac{1}{2}$. Suppose not, then $\exists \{I_j\}_{j=1}^{\infty}$ such that $S\subseteq \bigcup_{j=1}^{\infty} I_j$ and $\sum_{j=1}^{\infty} \ell(I_j)< \frac{1}{2}$.
|
||||
|
||||
Then $S$ would have gaps with lengths summing to greater than $\frac{1}{2}$. This contradicts with what we just proved.
|
||||
|
||||
So $c_e(SVC(4))=\frac{1}{2}$.
|
||||
|
||||
> General formula for $c_e(SVC(n))=\frac{n-3}{n-2}$, and since $SVC(n)$ is nowhere dense, $c_i(SVC(n))=0$.
|
||||
|
||||
### Additivity of Content
|
||||
|
||||
Recall that outer content is sub-additive. Let $S,T\subseteq \mathbb{R}^n$ be disjoint.
|
||||
|
||||
$$
|
||||
c_e(S\cup T)\leq c_e(S)+c_e(T)
|
||||
$$
|
||||
|
||||
The inner content is super-additive. Let $S,T\subseteq \mathbb{R}^n$ be disjoint.
|
||||
|
||||
$$
|
||||
c_i(S\cup T)\geq c_i(S)+c_i(T)
|
||||
$$
|
||||
|
||||
#### Proposition 5.2
|
||||
|
||||
Finite additivity of Jordan content:
|
||||
|
||||
Let $S_1,\ldots,S_N\subseteq \mathbb{R}^n$ are pairwise disjoint Jordan measurable sets, then
|
||||
|
||||
$$
|
||||
c(\bigcup_{i=1}^N S_i)=\sum_{i=1}^N c(S_i)
|
||||
$$
|
||||
|
||||
Proof:
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\sum_{i=1}^N c_i(S_i)&\leq c_i(\bigcup_{i=1}^N S_i)\\
|
||||
&\leq c_e(\bigcup_{i=1}^N S_i)\\
|
||||
&\leq \sum_{i=1}^N c_e(S_i)\\
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Since $\sum_{i=1}^N c(S_i)=\sum_{i=1}^N c_e(S_i)=\sum_{i=1}^N c_i(S_i)$, we have
|
||||
|
||||
$$
|
||||
c(\bigcup_{i=1}^N S_i)=\sum_{i=1}^N c(S_i)
|
||||
$$
|
||||
|
||||
QED
|
||||
|
||||
##### Failure for countable additivity for Jordan content
|
||||
|
||||
Notice that each singleton $\{q\}$ is Jordan measurable and $c(\{q\})=0$. But take $a\in \mathbb{Q}\cap [0,1]$, $Q\cap [0,1]=\bigcup_{q\in Q\cap [0,1]} \{q\}$, but $\mathbb{Q}\cap [0,1]$ is not Jordan measurable.
|
||||
|
||||
Issue is a countable union of Jordan measurable sets is not necessarily Jordan measurable.
|
||||
|
||||
@@ -25,12 +25,8 @@ export default {
|
||||
Math4121_L20: "Introduction to Lebesgue Integration (Lecture 20)",
|
||||
Math4121_L21: "Introduction to Lebesgue Integration (Lecture 21)",
|
||||
Math4121_L22: "Introduction to Lebesgue Integration (Lecture 22)",
|
||||
Math4121_L23: {
|
||||
display: 'hidden'
|
||||
},
|
||||
Math4121_L24: {
|
||||
display: 'hidden'
|
||||
},
|
||||
Math4121_L23: "Introduction to Lebesgue Integration (Lecture 23)",
|
||||
Math4121_L24: "Introduction to Lebesgue Integration (Lecture 24)",
|
||||
Math4121_L25: {
|
||||
display: 'hidden'
|
||||
},
|
||||
|
||||
154
pages/Math416/Math416_L17.md
Normal file
154
pages/Math416/Math416_L17.md
Normal file
@@ -0,0 +1,154 @@
|
||||
# Math416 Lecture 17
|
||||
|
||||
## Continue on Chapter 7
|
||||
|
||||
### Harmonic conjugates
|
||||
|
||||
#### Theorem 7.18
|
||||
|
||||
Existence of harmonic conjugates.
|
||||
|
||||
Let $u$ be a harmonic function on $\Omega$ a convex open subset in $\mathbb{C}$. Then there exists $g\in O(\Omega)$ such that $\text{Re}(g)=u$ on $\Omega$.
|
||||
|
||||
Moreover, $g$ is unique up to an imaginary additive constant.
|
||||
|
||||
Proof:
|
||||
|
||||
Let $f=2\frac{\partial u}{\partial z}=\frac{\partial u}{\partial x}-i\frac{\partial u}{\partial y}$
|
||||
|
||||
$f$ is holomorphic on $\Omega$
|
||||
|
||||
Since $\frac{\partial u}{\partial \overline{z}}=0$ on $\Omega$, $f$ is holomorphic on $\Omega$
|
||||
|
||||
So $f=g'$, fix $z_0\in \Omega$, we can choose $q(z_0)=u(z_0)$ and $g=u_1+iv_1$, $g'=\frac{\partial u_1}{\partial x}+i\frac{\partial v_1}{\partial x}=\frac{\partial v_1}{\partial y}-i\frac{\partial u_1}{\partial y}=\frac{\partial u}{\partial x}-i\frac{\partial u}{\partial y}$, given that $\frac{\partial u_1}{\partial x}=\frac{\partial u}{\partial x}$ and $\frac{\partial u_1}{\partial y}=\frac{\partial u}{\partial y}$
|
||||
|
||||
So $u_1=u$ on $\Omega$
|
||||
|
||||
$\text{Re}(g)=u_1=u$ on $\Omega$
|
||||
|
||||
If $u+iv$ is holomorphic, $v$ is harmonic conjugate of $u$
|
||||
|
||||
QED
|
||||
|
||||
### Corollary For Harmonic functions
|
||||
|
||||
#### Theorem 7.19
|
||||
|
||||
Harmonic functions are $C^\infty$
|
||||
|
||||
$C^\infty$ is a local property.
|
||||
|
||||
#### Theorem 7.20
|
||||
|
||||
Mean value property for harmonic functions.
|
||||
|
||||
Let $u$ be harmonic on an open set of $\Omega$
|
||||
|
||||
Then $u(z_0)=\frac{1}{2\pi}\int_0^{2\pi}u(z_0+re^{i\theta})d\theta$
|
||||
|
||||
Proof:
|
||||
|
||||
$\text{Re}g(z_0)=\frac{1}{2\pi}\int_0^{2\pi}\text{Re}g(z_0+re^{i\theta})d\theta$
|
||||
|
||||
QED
|
||||
|
||||
#### Theorem 7.21
|
||||
|
||||
Identity theorem for harmonic functions.
|
||||
|
||||
Let $u$ be harmonic on a domain $\Omega$. If $u=0$ on some open set $G\subset \Omega$, then $u\equiv 0$ on $\Omega$.
|
||||
|
||||
_If $u=v$ on $G\subset \Omega$, then $u=v$ on $\Omega$._
|
||||
|
||||
Proof:
|
||||
|
||||
We proceed by contradiction.
|
||||
|
||||
Let $H=\{z\in \Omega:u(z)=0\}$ be the interior of $G$
|
||||
|
||||
$H$ is open and nonempty. If $H\neq \Omega$, then $\exists z_0\in \partial H\cap \Omega$. Then $\exists r>0$ such that $B_r(z_0)\subset \Omega$ such that $\exists g\in O(B_r(z_0))$ such that $\text{Re}g=u$ on $B_r(z_0)$
|
||||
|
||||
Since $H\cap B_r(z_0)$ is nonempty open set, then $g$ is constant on $H\cap B_r(z_0)$
|
||||
|
||||
So $g$ is constant on $B_r(z_0)$
|
||||
|
||||
So $u$ is constant on $B_r(z_0)$
|
||||
|
||||
So $D(z_0,r)\subset H$. This is a contradiction that $z_0\in \partial H$
|
||||
|
||||
QED
|
||||
|
||||
#### Theorem 7.22
|
||||
|
||||
Maximum principle for harmonic functions.
|
||||
|
||||
A non-constant harmonic function on a domain cannot attain a maximum or minimum on the interior of the domain.
|
||||
|
||||
Proof:
|
||||
|
||||
We proceed by contradiction.
|
||||
|
||||
Suppose $u$ attains a maximum at $z_0\in \Omega$.
|
||||
|
||||
For all $z$ in the neighborhood of $z_0$, $u(z)<u(z_0)$. We can choose $r>0$ such that $B_r(z_0)\subset \Omega$.
|
||||
|
||||
By the mean value property, $u(z_0)=\frac{1}{2\pi}\int_0^{2\pi}u(z_0+re^{i\theta})d\theta$
|
||||
|
||||
So $0= \frac{1}{2\pi}\int_0^{2\pi}u[z_0+re^{i\theta}-u(z_0)]d\theta$
|
||||
|
||||
We can prove the minimum is similar.
|
||||
|
||||
QED
|
||||
|
||||
> Maximum/minimum (modulus) principle for holomorphic functions.
|
||||
>
|
||||
> If $f$ is holomorphic on a domain $\Omega$ and attains a maximum on the boundary of $\Omega$, then $f$ is constant on $\Omega$.
|
||||
>
|
||||
> Except at $z_0\in \Omega$ where $f'(z_0)=0$, if $f$ attains a minimum on the boundary of $\Omega$, then $f$ is constant on $\Omega$.
|
||||
|
||||
### Dirichlet problem for domain $D$
|
||||
|
||||
Let $h: \partial D\to \mathbb{R}$ be a continuous function. Is there a harmonic function $u$ on $D$ such that $u$ is continuous on $\overline{D}$ and $u|_{\partial D}=h$?
|
||||
|
||||
We can always solve the problem for the unit disk.
|
||||
|
||||
$$
|
||||
u(z)=\frac{1}{2\pi}\int_0^{2\pi}h(e^{i t})\text{Re}\left(\frac{e^{it}+z}{e^{it}-z}\right)dt
|
||||
$$
|
||||
|
||||
Let $z=re^{i\theta}$
|
||||
|
||||
$$
|
||||
\text{Re}\left(\frac{e^{it}+re^{i\theta}}{e^{it}-re^{i\theta}}\right)=\frac {1-r^2}{1-2r\cos(\theta-t)+r^2}
|
||||
$$
|
||||
|
||||
_This is called Poisson kernel._
|
||||
|
||||
$Pr(\theta, t)>0$ and $\int_0^{2\pi}Pr(\theta, t)dt=1$, $\forall r,t$
|
||||
|
||||
## Chapter 8 Laurent series
|
||||
|
||||
when $\sum_{n=-\infty}^{\infty}a_n(z-z_0)^n$ converges?
|
||||
|
||||
Claim $\exists R>0$ such that $\sum_{n=-\infty}^{\infty}a_n(z-z_0)^n$ converges if $|z-z_0|<R$ and diverges if $|z-z_0|>R$
|
||||
|
||||
Proof:
|
||||
|
||||
Let $u=\frac{1}{z-z_0}$
|
||||
|
||||
$\sum_{n=0}^{\infty}a_n(z-z_0)^n$ has radius of convergence $\frac{1}{R}$
|
||||
|
||||
So the series converges if $|u|<\frac{1}{R}$
|
||||
|
||||
So $|z-z_0|=\frac{1}{|u|}>\frac{1}{\frac{1}{R}}=R$
|
||||
|
||||
QED
|
||||
|
||||
### Laurent series
|
||||
|
||||
A Laurent series is a series of the form $\sum_{n=-\infty}^{\infty}a_n(z-z_0)^n$
|
||||
|
||||
The series converges in some annulus shape $A=\{z:r_1<|z-z_0|<r_2\}$
|
||||
|
||||
The annulus is called the region of convergence of the Laurent series.
|
||||
|
||||
@@ -20,4 +20,5 @@ export default {
|
||||
Math416_L14: "Complex Variables (Lecture 14)",
|
||||
Math416_L15: "Complex Variables (Lecture 15)",
|
||||
Math416_L16: "Complex Variables (Lecture 16)",
|
||||
Math416_L17: "Complex Variables (Lecture 17)",
|
||||
}
|
||||
|
||||
9
pages/Swap/Math401/Math401_N2.md
Normal file
9
pages/Swap/Math401/Math401_N2.md
Normal file
@@ -0,0 +1,9 @@
|
||||
# Node 2
|
||||
|
||||
## Random matrix theory
|
||||
|
||||
### Wigner's semicircle law
|
||||
|
||||
## h-Inversion Polynomials for a Special Heisenberg Family
|
||||
|
||||
###
|
||||
Reference in New Issue
Block a user