update

docker-compose.yaml

@@ -3,7 +3,7 @@ services:
     build:
       context: ./
       dockerfile: ./Dockerfile
-    image: trance0/notenextra:v1.1.7
+    image: trance0/notenextra:v1.1.8
     restart: on-failure:5
     ports:
       - 13000:3000

pages/CSE559A/CSE559A_L15.md

@@ -92,6 +92,8 @@ SSD is a multi-resolution object detection
 
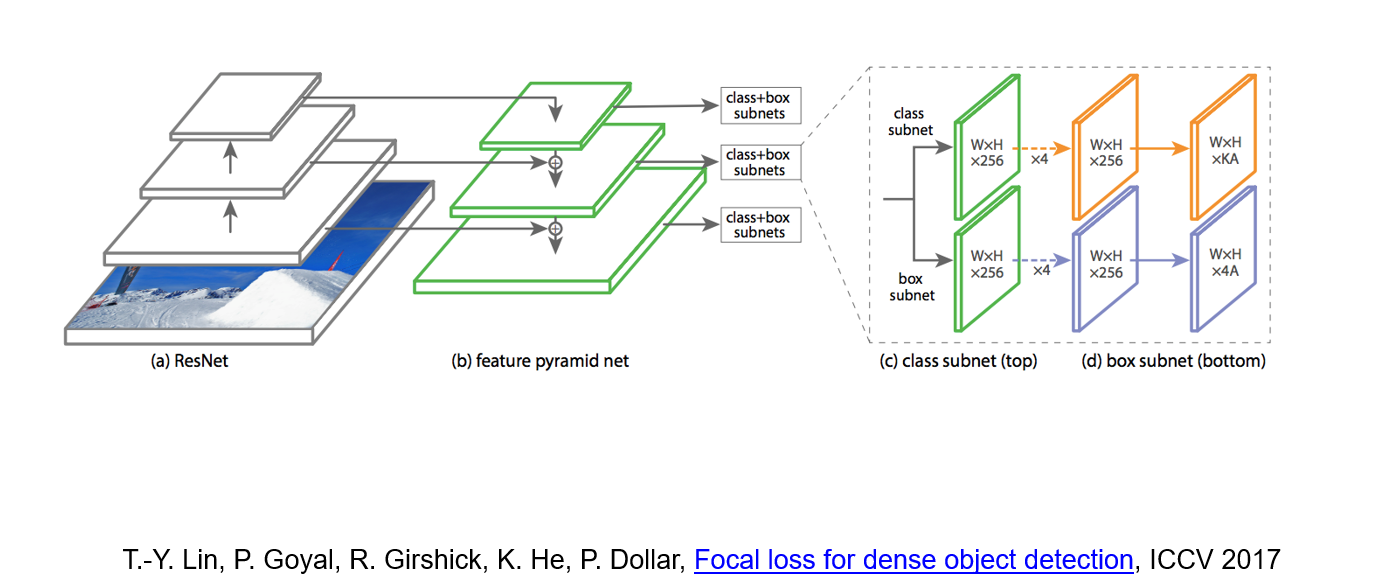
 RetinaNet combine feature pyramid network with focal loss to reduce the standard cross-entropy loss for well-classified examples.
 
+![RetinaNet](https://notenextra.trance-0.com/CSE559A/RetinaNet.png)
+
 > Cross-entropy loss:
 > $$CE(p_t) = - \log(p_t)$$
 

pages/CSE559A/CSE559A_L16.md

@@ -0,0 +1,114 @@
+# CSE559A Lecture 16
+
+## Dense image labelling
+
+### Semantic segmentation
+
+Use one-hot encoding to represent the class of each pixel.
+
+### General Network design
+
+Design a network with only convolutional layers, make predictions for all pixels at once.
+
+Can the network operate at full image resolution?
+
+Practical solution: first downsample, then upsample
+
+### Outline
+
+- Upgrading a Classification Network to Segmentation
+- Operations for dense prediction
+  - Transposed convolutions, unpooling
+- Architectures for dense prediction
+  - DeconvNet, U-Net, "U-Net"
+- Instance segmentation
+  - Mask R-CNN
+- Other dense prediction problems
+
+### Fully Convolutional Networks
+
+"upgrading" a classification network to a dense prediction network
+
+1. Covert "fully connected" layers to 1x1 convolutions
+2. Make the input image larger
+3. Upsample the output
+
+Start with an existing classification CNN ("an encoder")
+
+Then use bilinear interpolation and transposed convolutions to make full resolution.
+
+### Operations for dense prediction
+
+#### Transposed Convolutions
+
+Use the filter to "paint" in the output: place copies of the filter on the output, multiply by corresponding value in the input, sum where copies of the filter overlap
+
+We can increase the resolution of the output by using a larger stride in the convolution.
+
+- For stride 2, dilate the input by inserting rows and columns of zeros between adjacent entries, convolve with flipped filter
+- Sometimes called convolution with fractional input stride 1/2
+
+#### Unpooling
+
+Max unpooling:
+
+- Copy the maximum value in the input region to all locations in the output
+- Use the location of the maximum value to know where to put the value in the output
+
+Nearest neighbor unpooling:
+
+- Copy the maximum value in the input region to all locations in the output
+- Use the location of the maximum value to know where to put the value in the output
+
+### Architectures for dense prediction
+
+#### DeconvNet
+
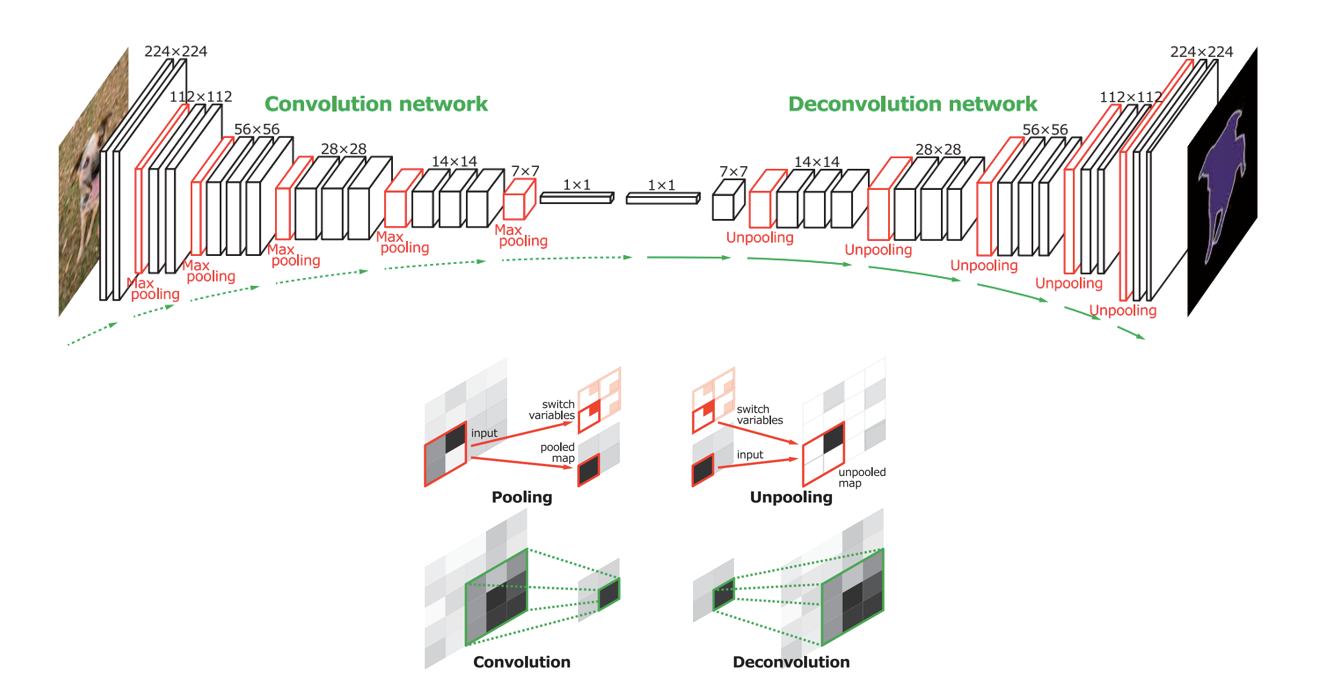
+![DeconvNet](https://notenextra.trance-0.com/CSE559A/DeconvNet.png)
+
+_How the information about location is encoded in the network?_
+
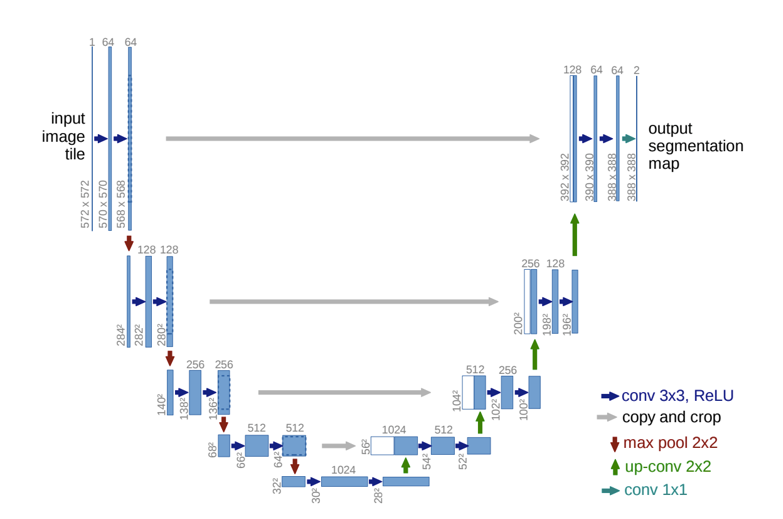
+#### U-Net
+
+![U-Net](https://notenextra.trance-0.com/CSE559A/U-Net.png)
+
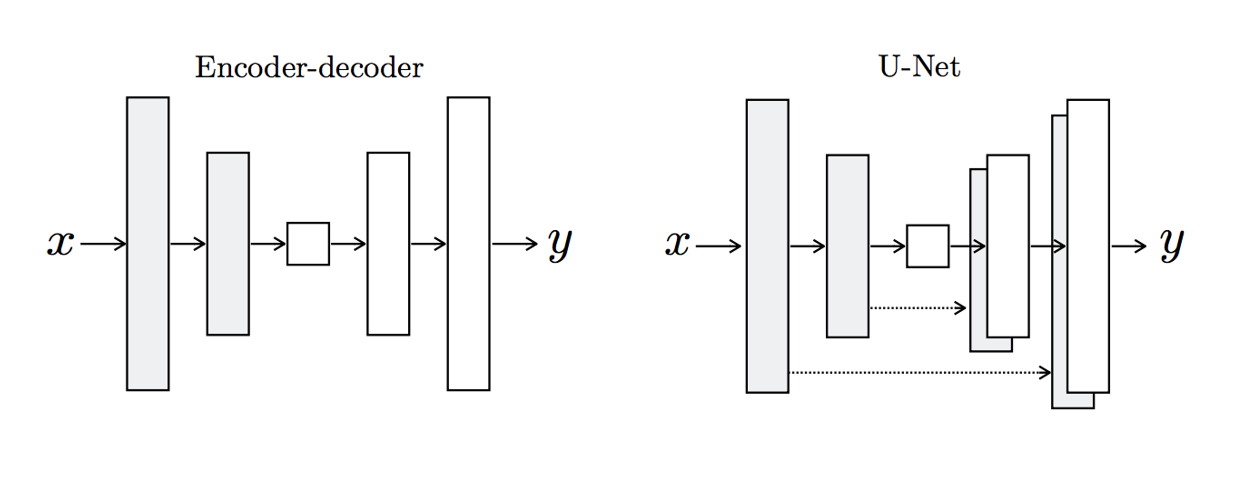
+- Like FCN, fuse upsampled higher-level feature maps with higher-res, lower-level feature maps (like residual connections)
+- Unlike FCN, fuse by concatenation, predict at the end
+
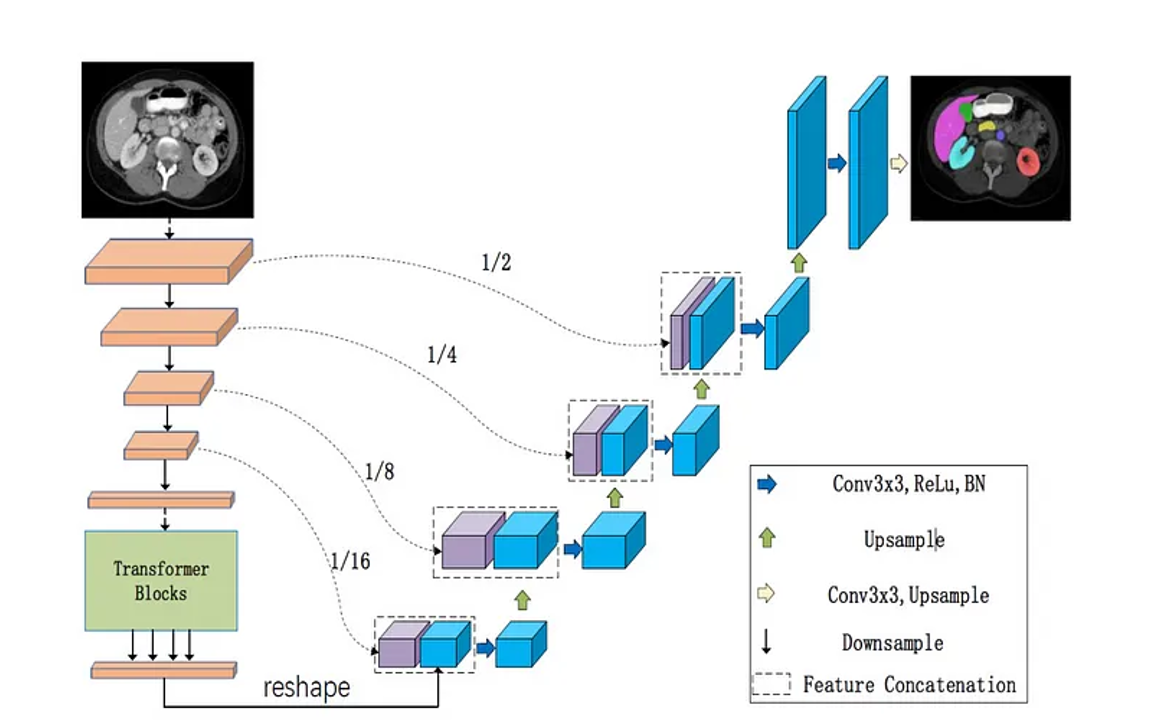
+#### Extended U-Net Architecture
+
+Many variants of U-Net would replace the "encoder" of the U-Net with other architectures.
+
+![Extended U-Net Architecture Example](https://notenextra.trance-0.com/CSE559A/ExU-Net.png)
+
+##### Encoder/Decoder v.s. U-Net
+
+![Encoder/Decoder v.s. U-Net](https://notenextra.trance-0.com/CSE559A/EncoderDecoder_vs_U-Net.png)
+
+### Instance Segmentation
+
+#### Mask R-CNN
+
+Mask R-CNN = Faster R-CNN + FCN on Region of Interest
+
+### Extend to keypoint prediction?
+
+- Use a similar architecture to Mask R-CNN
+
+_Continue on Tuesday_
+
+### Other tasks
+
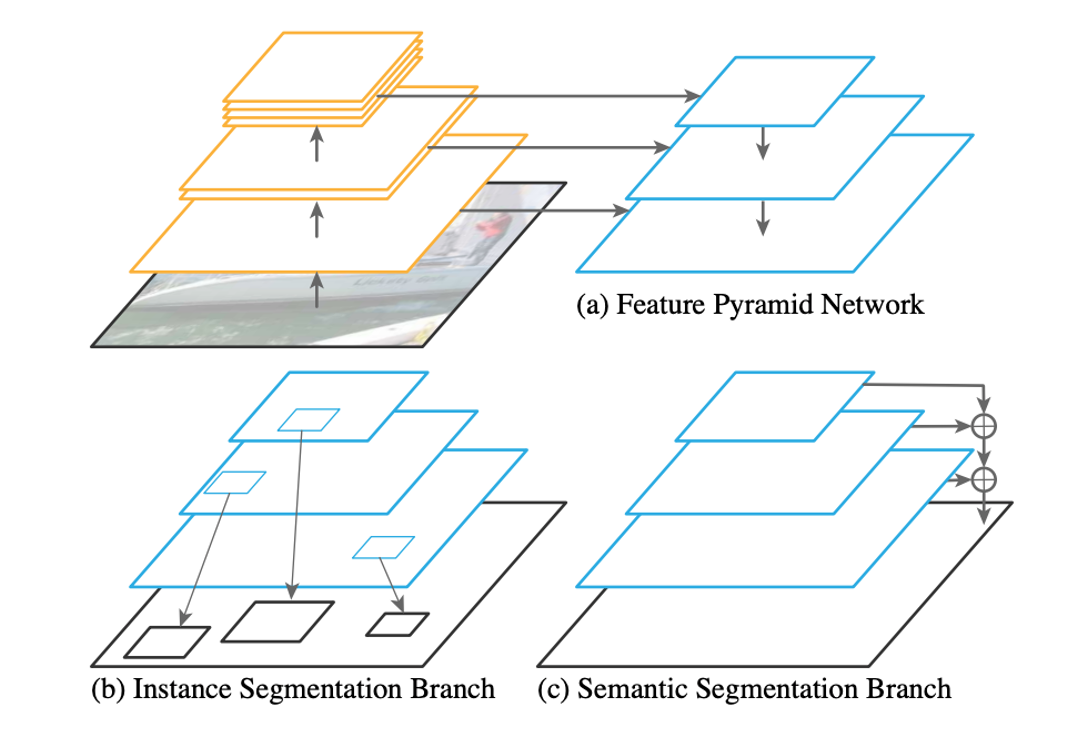
+#### Panoptic feature pyramid network
+
+![Panoptic Feature Pyramid Network](https://notenextra.trance-0.com/CSE559A/Panoptic_Feature_Pyramid_Network.png)
+
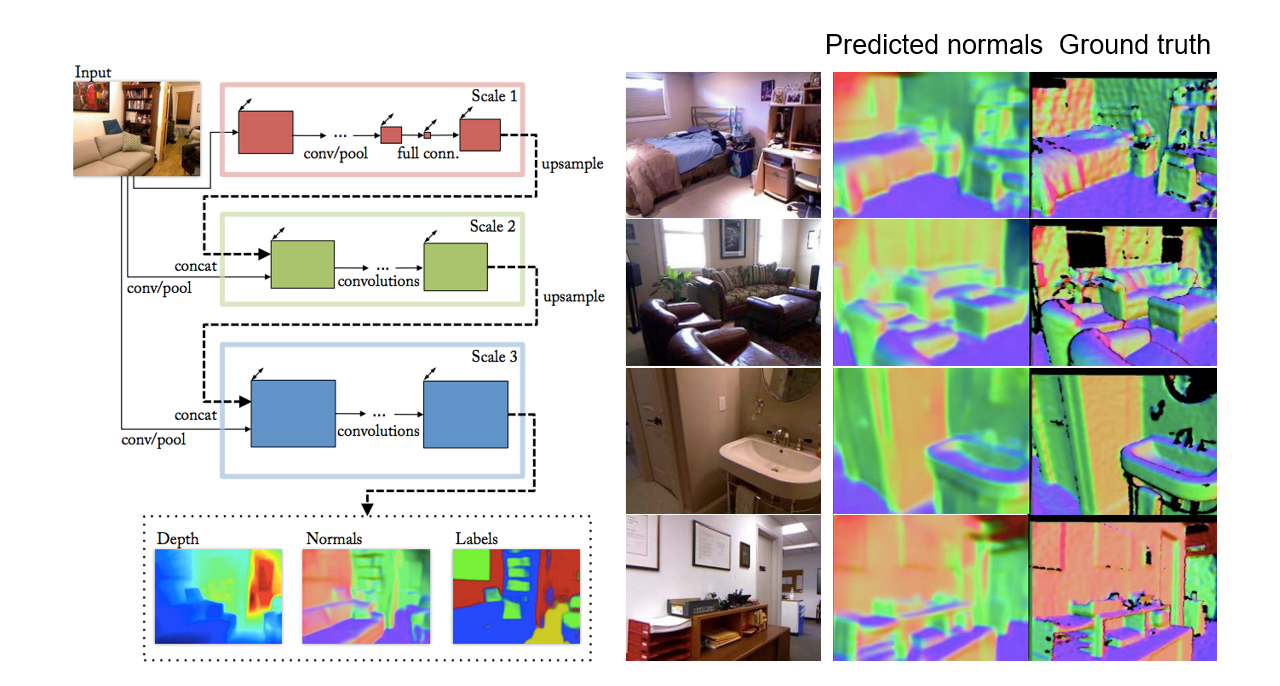
+#### Depth and normal estimation
+
+![Depth and Normal Estimation](https://notenextra.trance-0.com/CSE559A/Depth_and_Normal_Estimation.png)
+
+D. Eigen and R. Fergus, Predicting Depth, Surface Normals and Semantic Labels with a Common Multi-Scale Convolutional Architecture, ICCV 2015
+
+#### Colorization
+
+R. Zhang, P. Isola, and A. Efros, Colorful Image Colorization, ECCV 2016

pages/CSE559A/_meta.js

@@ -18,4 +18,5 @@ export default {
     CSE559A_L13: "Computer Vision (Lecture 13)",
     CSE559A_L14: "Computer Vision (Lecture 14)",
     CSE559A_L15: "Computer Vision (Lecture 15)",
+    CSE559A_L16: "Computer Vision (Lecture 16)",
 }

pages/Math4121/Math4121_L24.md

@@ -1 +1,105 @@
-# Lecture 24
+# Math4121 Lecture 24
+
+## Chapter 5: Measure Theory
+
+### Jordan Measurable
+
+#### Proposition 5.1
+
+A bounded set $S\subseteq \mathbb{R}^n$ is Jordan measurable if
+
+$$
+c_e(S)=c_i(S)+c_e(\partial S)
+$$
+
+where $\partial S$ is the boundary of $S$ and $c_e(\partial S)=0$.
+
+Example:
+
+1. $S=\mathbb{Q}\cap [0,1]$ is not Jordan measurable.
+
+Since $c_e(S)=0$ and $\partial S=[0,1]$, $c_i(S)=1$.
+
+So $c_e(\partial S)=1\neq 0$.
+
+2. SVC(3) is Jordan measurable.
+
+Since $c_e(S)=0$ and $\partial S=0$, $c_i(S)=0$. The outer content of the cantor set is $0$.
+
+> Any set or subset of a set with $c_e(S)=0$ is Jordan measurable.
+
+3. SVC(4)
+
+At each step, we remove $2^n$ intervals of length $\frac{1}{4^n}$.
+
+So $S=\bigcap_{n=1}^{\infty} C_i$ and $c_e(C_k)=c_e(C_{k-1})-\frac{2^{k-1}}{4^k}$. $c_e(C_0)=1$.
+
+So
+
+$$
+\begin{aligned}
+c_e(S)&\leq \lim_{k\to\infty} c_e(C_k)\\
+&=1-\sum_{k=1}^{\infty} \frac{2^{k-1}}{4^k}\\
+&=1-\frac{1}{4}\sum_{k=0}^{\infty} \left(\frac{2}{4}\right)^k\\
+&=1-\frac{1}{4}\cdot \frac{1}{1-\frac{2}{4}}\\
+&=1-\frac{1}{4}\cdot \frac{1}{\frac{1}{2}}\\
+&=1-\frac{1}{2}\\
+&=\frac{1}{2}.
+\end{aligned}
+$$
+
+And we can also claim that $c_i(S)\geq \frac{1}{2}$. Suppose not, then $\exists \{I_j\}_{j=1}^{\infty}$ such that $S\subseteq \bigcup_{j=1}^{\infty} I_j$ and $\sum_{j=1}^{\infty} \ell(I_j)< \frac{1}{2}$.
+
+Then $S$ would have gaps with lengths summing to greater than $\frac{1}{2}$. This contradicts with what we just proved.
+
+So $c_e(SVC(4))=\frac{1}{2}$.
+
+> General formula for $c_e(SVC(n))=\frac{n-3}{n-2}$, and since $SVC(n)$ is nowhere dense, $c_i(SVC(n))=0$.
+
+### Additivity of Content
+
+Recall that outer content is sub-additive. Let $S,T\subseteq \mathbb{R}^n$ be disjoint.
+
+$$
+c_e(S\cup T)\leq c_e(S)+c_e(T)
+$$
+
+The inner content is super-additive. Let $S,T\subseteq \mathbb{R}^n$ be disjoint.
+
+$$
+c_i(S\cup T)\geq c_i(S)+c_i(T)
+$$
+
+#### Proposition 5.2
+
+Finite additivity of Jordan content:
+
+Let $S_1,\ldots,S_N\subseteq \mathbb{R}^n$ are pairwise disjoint Jordan measurable sets, then
+
+$$
+c(\bigcup_{i=1}^N S_i)=\sum_{i=1}^N c(S_i)
+$$
+
+Proof:
+
+$$
+\begin{aligned}
+\sum_{i=1}^N c_i(S_i)&\leq c_i(\bigcup_{i=1}^N S_i)\\
+&\leq c_e(\bigcup_{i=1}^N S_i)\\
+&\leq \sum_{i=1}^N c_e(S_i)\\
+\end{aligned}
+$$
+
+Since $\sum_{i=1}^N c(S_i)=\sum_{i=1}^N c_e(S_i)=\sum_{i=1}^N c_i(S_i)$, we have
+
+$$
+c(\bigcup_{i=1}^N S_i)=\sum_{i=1}^N c(S_i)
+$$
+
+QED
+
+##### Failure for countable additivity for Jordan content
+
+Notice that each singleton $\{q\}$ is Jordan measurable and $c(\{q\})=0$. But take $a\in \mathbb{Q}\cap [0,1]$, $Q\cap [0,1]=\bigcup_{q\in Q\cap [0,1]} \{q\}$, but $\mathbb{Q}\cap [0,1]$ is not Jordan  measurable.
+
+Issue is a countable union of Jordan measurable sets is not necessarily Jordan measurable.

pages/Math4121/_meta.js

@@ -25,12 +25,8 @@ export default {
     Math4121_L20: "Introduction to Lebesgue Integration (Lecture 20)",
     Math4121_L21: "Introduction to Lebesgue Integration (Lecture 21)",
     Math4121_L22: "Introduction to Lebesgue Integration (Lecture 22)",
-    Math4121_L23: {
-        display: 'hidden'
-    },
-    Math4121_L24: {
-        display: 'hidden'
-    },
+    Math4121_L23: "Introduction to Lebesgue Integration (Lecture 23)",
+    Math4121_L24: "Introduction to Lebesgue Integration (Lecture 24)",
     Math4121_L25: {
         display: 'hidden'
     },

pages/Math416/Math416_L17.md

@@ -0,0 +1,154 @@
+# Math416 Lecture 17
+
+## Continue on Chapter 7
+
+### Harmonic conjugates
+
+#### Theorem 7.18
+
+Existence of harmonic conjugates.
+
+Let $u$ be a harmonic function on $\Omega$ a convex open subset in $\mathbb{C}$. Then there exists $g\in O(\Omega)$ such that $\text{Re}(g)=u$ on $\Omega$.
+
+Moreover, $g$ is unique up to an imaginary additive constant.
+
+Proof:
+
+Let $f=2\frac{\partial u}{\partial z}=\frac{\partial u}{\partial x}-i\frac{\partial u}{\partial y}$
+
+$f$ is holomorphic on $\Omega$
+
+Since $\frac{\partial u}{\partial \overline{z}}=0$ on $\Omega$, $f$ is holomorphic on $\Omega$
+
+So $f=g'$, fix $z_0\in \Omega$, we can choose $q(z_0)=u(z_0)$ and $g=u_1+iv_1$, $g'=\frac{\partial u_1}{\partial x}+i\frac{\partial v_1}{\partial x}=\frac{\partial v_1}{\partial y}-i\frac{\partial u_1}{\partial y}=\frac{\partial u}{\partial x}-i\frac{\partial u}{\partial y}$, given that $\frac{\partial u_1}{\partial x}=\frac{\partial u}{\partial x}$ and $\frac{\partial u_1}{\partial y}=\frac{\partial u}{\partial y}$
+
+So $u_1=u$ on $\Omega$
+
+$\text{Re}(g)=u_1=u$ on $\Omega$
+
+If $u+iv$ is holomorphic, $v$ is harmonic conjugate of $u$
+
+QED
+
+### Corollary For Harmonic functions
+
+#### Theorem 7.19
+
+Harmonic functions are $C^\infty$
+
+$C^\infty$ is a local property.
+
+#### Theorem 7.20
+
+Mean value property for harmonic functions.
+
+Let $u$ be harmonic on an open set of $\Omega$
+
+Then $u(z_0)=\frac{1}{2\pi}\int_0^{2\pi}u(z_0+re^{i\theta})d\theta$
+
+Proof:
+
+$\text{Re}g(z_0)=\frac{1}{2\pi}\int_0^{2\pi}\text{Re}g(z_0+re^{i\theta})d\theta$
+
+QED
+
+#### Theorem 7.21
+
+Identity theorem for harmonic functions.
+
+Let $u$ be harmonic on a domain $\Omega$. If $u=0$ on some open set $G\subset \Omega$, then $u\equiv 0$ on $\Omega$.
+
+_If $u=v$ on $G\subset \Omega$, then $u=v$ on $\Omega$._
+
+Proof:
+
+We proceed by contradiction.
+
+Let $H=\{z\in \Omega:u(z)=0\}$ be the interior of $G$
+
+$H$ is open and nonempty. If $H\neq \Omega$, then $\exists z_0\in \partial H\cap \Omega$. Then $\exists r>0$ such that $B_r(z_0)\subset \Omega$ such that $\exists g\in O(B_r(z_0))$ such that $\text{Re}g=u$ on $B_r(z_0)$
+
+Since $H\cap B_r(z_0)$ is nonempty open set, then $g$ is constant on $H\cap B_r(z_0)$
+
+So $g$ is constant on $B_r(z_0)$
+
+So $u$ is constant on $B_r(z_0)$
+
+So $D(z_0,r)\subset H$. This is a contradiction that $z_0\in \partial H$
+
+QED
+
+#### Theorem 7.22
+
+Maximum principle for harmonic functions.
+
+A non-constant harmonic function on a domain cannot attain a maximum or minimum on the interior of the domain.
+
+Proof:
+
+We proceed by contradiction.
+
+Suppose $u$ attains a maximum at $z_0\in \Omega$.
+
+For all $z$ in the neighborhood of $z_0$, $u(z)<u(z_0)$. We can choose $r>0$ such that $B_r(z_0)\subset \Omega$.
+
+By the mean value property, $u(z_0)=\frac{1}{2\pi}\int_0^{2\pi}u(z_0+re^{i\theta})d\theta$
+
+So $0= \frac{1}{2\pi}\int_0^{2\pi}u[z_0+re^{i\theta}-u(z_0)]d\theta$
+
+We can prove the minimum is similar.
+
+QED
+
+> Maximum/minimum (modulus) principle for holomorphic functions.
+>
+> If $f$ is holomorphic on a domain $\Omega$ and attains a maximum on the boundary of $\Omega$, then $f$ is constant on $\Omega$.
+>
+> Except at $z_0\in \Omega$ where $f'(z_0)=0$, if $f$ attains a minimum on the boundary of $\Omega$, then $f$ is constant on $\Omega$.
+
+### Dirichlet problem for domain $D$
+
+Let $h: \partial D\to \mathbb{R}$ be a continuous function. Is there a harmonic function $u$ on $D$ such that $u$ is continuous on $\overline{D}$ and $u|_{\partial D}=h$?
+
+We can always solve the problem for the unit disk.
+
+$$
+u(z)=\frac{1}{2\pi}\int_0^{2\pi}h(e^{i t})\text{Re}\left(\frac{e^{it}+z}{e^{it}-z}\right)dt
+$$
+
+Let $z=re^{i\theta}$
+
+$$
+\text{Re}\left(\frac{e^{it}+re^{i\theta}}{e^{it}-re^{i\theta}}\right)=\frac {1-r^2}{1-2r\cos(\theta-t)+r^2}
+$$
+
+_This is called Poisson kernel._
+
+$Pr(\theta, t)>0$ and $\int_0^{2\pi}Pr(\theta, t)dt=1$, $\forall r,t$
+
+## Chapter 8 Laurent series
+
+when $\sum_{n=-\infty}^{\infty}a_n(z-z_0)^n$ converges?
+
+Claim $\exists R>0$ such that $\sum_{n=-\infty}^{\infty}a_n(z-z_0)^n$ converges if $|z-z_0|<R$ and diverges if $|z-z_0|>R$
+
+Proof:
+
+Let $u=\frac{1}{z-z_0}$
+
+$\sum_{n=0}^{\infty}a_n(z-z_0)^n$ has radius of convergence $\frac{1}{R}$
+
+So the series converges if $|u|<\frac{1}{R}$
+
+So $|z-z_0|=\frac{1}{|u|}>\frac{1}{\frac{1}{R}}=R$
+
+QED
+
+### Laurent series
+
+A Laurent series is a series of the form $\sum_{n=-\infty}^{\infty}a_n(z-z_0)^n$
+
+The series converges in some annulus shape $A=\{z:r_1<|z-z_0|<r_2\}$
+
+The annulus is called the region of convergence of the Laurent series.
+

pages/Math416/_meta.js

@@ -20,4 +20,5 @@ export default {
     Math416_L14: "Complex Variables (Lecture 14)",
     Math416_L15: "Complex Variables (Lecture 15)",
     Math416_L16: "Complex Variables (Lecture 16)",
+    Math416_L17: "Complex Variables (Lecture 17)",
 }

pages/Swap/Math401/Math401_N2.md

@@ -0,0 +1,9 @@
+# Node 2
+
+## Random matrix theory
+
+### Wigner's semicircle law
+
+## h-Inversion Polynomials for a Special Heisenberg Family
+
+###