update graphs

content/CSE5313/CSE5313_L24.md

@@ -2,7 +2,7 @@
 
 ## Continue on coded computing
 
-[!Coded computing scheme](https://notenextra.trance-0.com/CSE5313/Coded_computing_scheme.png)
+![Coded computing scheme](https://notenextra.trance-0.com/CSE5313/Coded_computing_scheme.png)
 
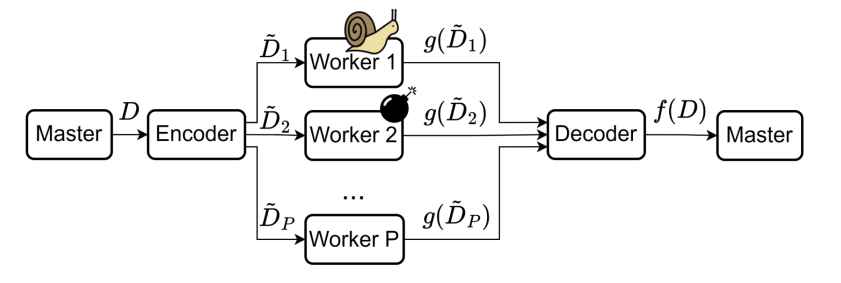
 Matrix-vector multiplication: $y=Ax$, where $A\in \mathbb{F}^{M\times N},x\in \mathbb{F}^N$
 

content/CSE5313/Exam_reviews/CSE5313_F1.md

@@ -30,7 +30,7 @@ Please refer to the syllabus for our policy regarding the use of GenAI.
 
 > [!WARNING]
 >
-> This notation system is annoying since in mathematics, $A^*$ is the transpose of $A$, but since we are using literatures in physics, we keep the notation of $A^*$. In this report, I will try to make the notation consistent as possible and follows the **physics** convention in this report. So every vector you see will be in $\ket{\psi}$ form. And we will avoid using the $\langle v,w\rangle$ notation for inner product as it used in math, we will use $\langle v|w\rangle$ to denote the inner product.
+> This notation system is annoying since in mathematics, $A^*$ is the transpose of $A$, but since we are using literatures in physics, we keep the notation of $A^*$. In this report, I will try to make the notation consistent as possible and follows the **physics** convention in this report. So every vector you see will be in $\ket{\psi}$ form. And we will avoid using the $\langle v,w\rangle$ notation for inner product as it used in math, we will use $\langle v|w\rangle$ or $\langle v,w\rangle$ to denote the inner product.
 
 A quantum error-correcting code is defined to be a unitary mapping (encoding) of $k$ qubits (two-state quantum systems) into a subspace of the quantum state space of $n$ qubuits such that if any $t$ of the qubits undergo arbitary decoherence, not necessarily independently, the resulting $n$ qubit state can be used to faithfully reconstruct the original quantum state of the $k$ encoded qubits.
 
@@ -170,9 +170,33 @@ In practice, we ignore the subscript of the vector space and just write $\langle
 
 Decoherence process
 
+#### No-cloning theorem
+
+> Reference from P.532 of the book
+
+Suppose we have a quantum system with two slots $A$, and $B$, the data slot, starts out in an unknown but pure quantum state $\ket{\psi}$. This is the state which is to be copied into slot $B$m the target slot. We assume that the target slot starts out in some standard pure state $\ket{s}$. Thus the initial state of the copying machine is $\ket{\psi}\otimes \ket{s}$.
+
+Assume there exists some unitary operator $U$ such that $U(\ket{\psi}\otimes \ket{s})=\ket{\psi}\otimes \ket{\psi}$.
+
+Consider two pure states $\ket{\psi}$ and $\ket{\varphi}$, such that $U(\ket{\psi}\otimes \ket{s})=\ket{\psi}\otimes \ket{\psi}$ and $U(\ket{\varphi}\otimes \ket{s})=\ket{\varphi}\otimes \ket{\varphi}$. The inner product of the two equation yields:
+
+$$
+\langle \psi|\varphi\rangle =(\langle \psi|\varphi\rangle)^2
+$$
+
+This equation has only two solutions, either $\langle \psi|\varphi\rangle=0$ or $\langle \psi|\varphi\rangle=1$.
+
+If $\langle \psi|\varphi\rangle=0$, then $\ket{\psi}=\ket{\varphi}$, no cloning for trivial case.
+
+If $\langle \psi|\varphi\rangle=1$, then $\ket{\psi}$ and $\ket{\varphi}$ are orthogonal.
+
+
+
 #### Proposition: Encoding 8 to 9 that correct 1 errors
 
-Recover 1 qubit from a 9 qubit quantum system. (Shor code)
+Recover 1 qubit from a 9 qubit quantum system. (Shor code, 1995)
+
+![Shore code](https://notenextra.trance-0.com/CSE5313/Shore_code.png)
 
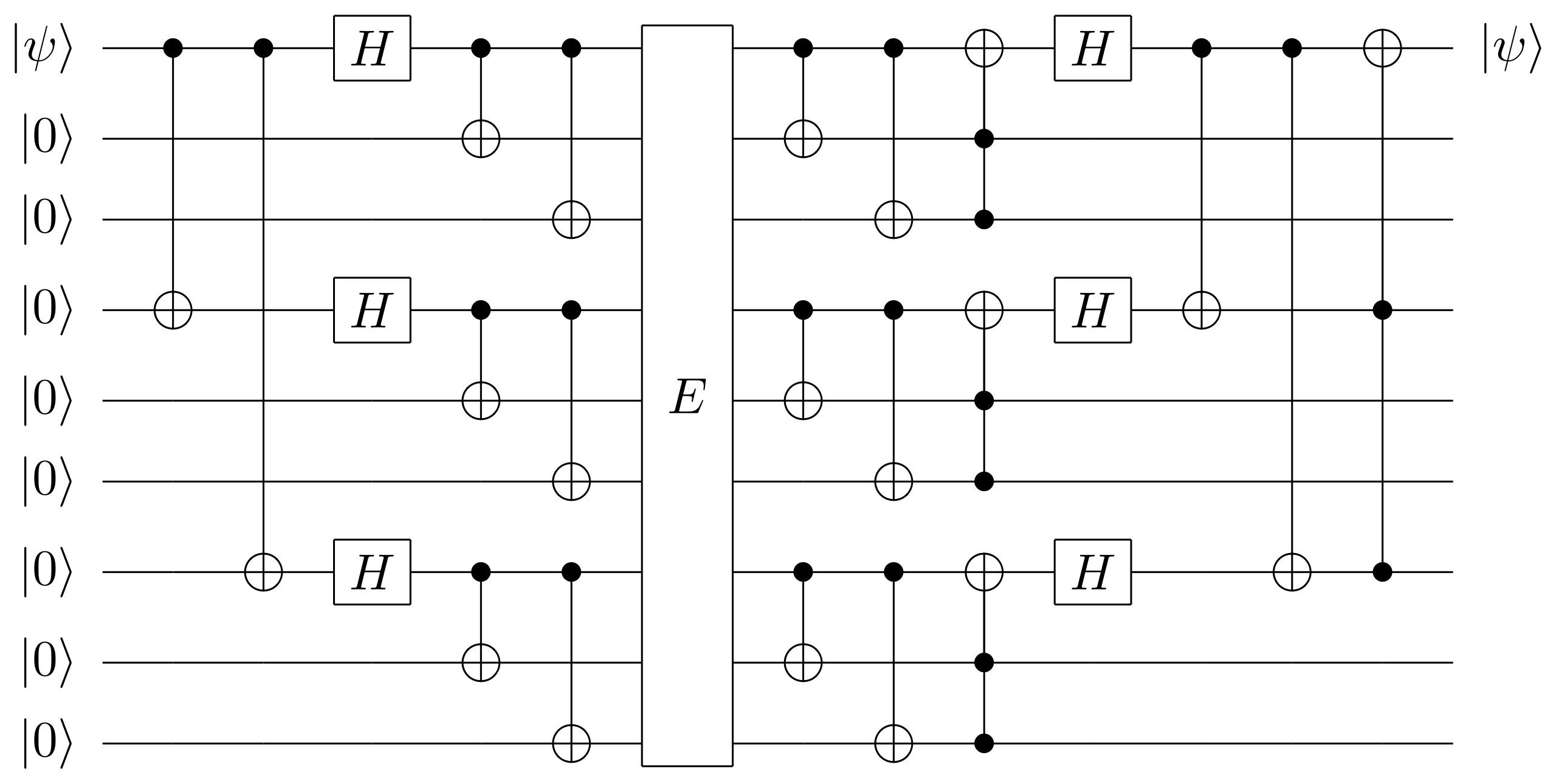
 ### Tools and related topics
 
@@ -229,16 +253,6 @@ $\mathcal{C}^{\perp}\coloneqq\{v\in\mathbb{F}_2^n:v\cdot w=0\text{ for all }w\in
 
 Consider the $[7,4,3]$ Hamming code with generator matrix $G$.
 
-$$
-G=
-\begin{bmatrix} 
-1 &  0 & 0 & 0 & 1 & 0 & 1\\
-0 &  1 & 0 & 0 & 1 & 1 & 1\\
-0 &  0 & 1 & 0 & 0 & 1 & 1\\
-0 &  0 & 0 & 1 & 0 & 1 & 1\\
-\end{bmatrix}
-$$
-
 </details>
 
 #### Proposition: Encoding $k$ to $n$ that correct $t$ errors