Merge branch 'main' of https://github.com/Trance-0/NoteNextra

pages/CSE559A/CSE559A_L10.md

@@ -0,0 +1,148 @@
+# CSE559A Lecture 10
+
+## Convolutional Neural Networks
+
+### Convolutional Layer
+
+Output feature map resolution depends on padding and stride
+
+Padding: add zeros around the input image
+
+Stride: the step of the convolution
+
+Example:
+
+1. Convolutional layer for 5x5 image with 3x3 kernel, padding 1, stride 1 (no skipping pixels)
+   - Input: 5x5 image
+   - Output: 3x3 feature map, (5-3+2*1)/1+1=5
+2. Convolutional layer for 5x5 image with 3x3 kernel, padding 1, stride 2 (skipping pixels)
+   - Input: 5x5 image
+   - Output: 2x2 feature map, (5-3+2*1)/2+1=2
+
+_Learned weights can be thought of as local templates_
+
+```python
+import torch
+import torch.nn as nn
+
+# suppose input image is HxWx3 (assume RGB image)
+
+conv_layer = nn.Conv2d(in_channels=3, # input channel, input is HxWx3
+                        out_channels=64, # output channel (number of filters), output is HxWx64
+                        kernel_size=3, # kernel size
+                        padding=1, # padding, this ensures that the output feature map has the same resolution as the input image, H_out=H_in, W_out=W_in
+                        stride=1) # stride
+```
+
+Usually followed by a ReLU activation function
+
+```python
+conv_layer = nn.Conv2d(in_channels=3, out_channels=64, kernel_size=3, padding=1, stride=1)
+relu = nn.ReLU()
+```
+
+Suppose input image is $H\times W\times K$, the output feature map is $H\times W\times L$ with kernel size $F\times F$, this takes $F^2\times K\times L\times H\times W$ parameters
+
+Each operation $D\times (K^2C)$ matrix with $(K^2C)\times N$ matrix, assume $D$ filters and $C$ output channels.
+
+### Variants 1x1 convolutions, depthwise convolutions
+
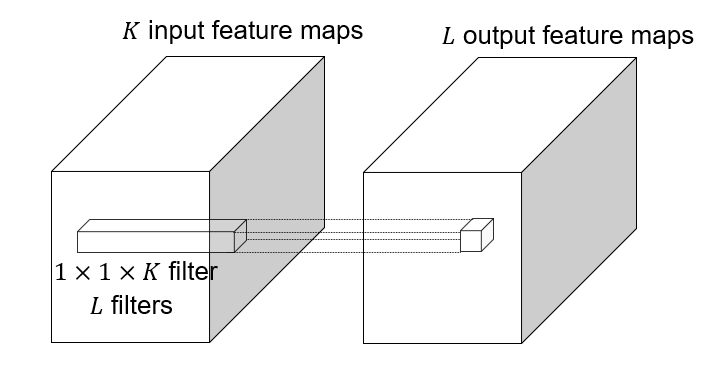
+#### 1x1 convolutions
+
+![1x1 convolution](https://notenextra.trance-0.com/CSE559A/1x1_layer.png)
+
+1x1 convolution: $F=1$, this layer do convolution in the pixel level, it is **pixel-wise** convolution for the feature.
+
+Used to save computation, reduce the number of parameters.
+
+Example: 3x3 conv layer with 256 channels at input and output.
+
+Option 1: naive way:
+
+```python
+conv_layer = nn.Conv2d(in_channels=256, out_channels=256, kernel_size=3, padding=1, stride=1)
+```
+
+This takes $256\times 3 \times 3\times 256=524,288$ parameters.
+
+Option 2: 1x1 convolution:
+
+```python
+conv_layer = nn.Conv2d(in_channels=256, out_channels=64, kernel_size=1, padding=0, stride=1)
+conv_layer = nn.Conv2d(in_channels=64, out_channels=64, kernel_size=3, padding=1, stride=1)
+conv_layer = nn.Conv2d(in_channels=64, out_channels=256, kernel_size=1, padding=0, stride=1)
+```
+
+This takes $256\times 1\times 1\times 64 + 64\times 3\times 3\times 64 + 64\times 1\times 1\times 256 = 16,384 + 36,864 + 16,384 = 69,632$ parameters.
+
+This lose some information, but save a lot of parameters.
+
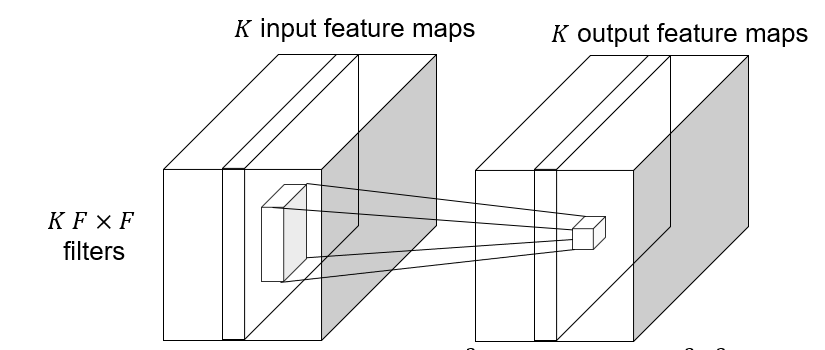
+#### Depthwise convolutions
+
+Depthwise convolution: $K\to K$ feature map, save computation, reduce the number of parameters.
+
+![Depthwise convolution](https://notenextra.trance-0.com/CSE559A/Depthwise_layer.png)
+
+#### Grouped convolutions
+
+Self defined convolution on the feature map following the similar manner.
+
+### Backward pass
+
+Vector-matrix form:
+
+$$
+\frac{\partial e}{\partial x}=\frac{\partial e}{\partial z}\frac{\partial z}{\partial x}
+$$
+
+Suppose the kernel is 3x3, the feature map is $\ldots, x_{i-1}, x_i, x_{i+1}, \ldots$, and $\ldots, z_{i-1}, z_i, z_{i+1}, \ldots$ is the output feature map, then:
+
+The convolution operation can be written as:
+
+$$
+z_i = w_1x_{i-1} + w_2x_i + w_3x_{i+1}
+$$
+
+The gradient of the kernel is:
+
+$$
+\frac{\partial e}{\partial x_i} = \sum_{j=-1}^{1}\frac{\partial e}{\partial z_i}\frac{\partial z_i}{\partial x_i} = \sum_{j=-1}^{1}\frac{\partial e}{\partial z_i}w_j
+$$
+
+### Max-pooling
+
+Get max value in the local region.
+
+#### Receptive field
+
+The receptive field of a unit is the region of the input feature map whose values contribute to the response of that unit (either in the previous layer or in the initial image) 
+
+## Architecture of CNNs
+
+### AlexNet (2012-2013)
+
+Successor of LeNet-5, but with a few significant changes
+
+- Max pooling, ReLU nonlinearity
+- Dropout regularization
+- More data and bigger model (7 hidden layers, 650K units, 60M params)
+- GPU implementation (50x speedup over CPU)
+  - Trained on two GPUs for a week
+
+#### Key points
+
+Most floating point operations occur in the convolutional layers.
+
+Most of the memory usage is in the early convolutional layers.
+
+Nearly all parameters are in the fully-connected layers.
+
+### VGGNet (2014)
+
+### GoogLeNet (2014)
+
+### ResNet (2015)
+
+### Beyond ResNet (2016 and onward): Wide ResNet, ResNeXT, DenseNet
+
+

pages/CSE559A/_meta.js

@@ -12,4 +12,5 @@ export default {
     CSE559A_L7: "Computer Vision (Lecture 7)",
     CSE559A_L8: "Computer Vision (Lecture 8)",
     CSE559A_L9: "Computer Vision (Lecture 9)",
+    CSE559A_L10: "Computer Vision (Lecture 10)",
 }

pages/Math4121/Math4121_L1.md

@@ -1,4 +1,4 @@
-# Lecture 1
+# Math4121 Lecture 1
 
 ## Chapter 5: Differentiation
 

pages/Math4121/Math4121_L10.md

@@ -1,4 +1,4 @@
-# Lecture 10
+# Math 4121 Lecture 10
 
 ## Recap
 

pages/Math4121/Math4121_L13.md

@@ -1 +1,103 @@
-# Lecture 13
+# Math4121 Lecture 13
+
+## New book Chapter 2
+
+Riemann's motivation: Fourier series
+
+$$
+F(x) = \frac{a_0}{2} + \sum_{k=1}^{\infty} a_k \cos(kx) + b_k \sin(kx)
+$$
+
+$a_k = \frac{1}{\pi} \int_{-\pi}^{\pi} f(x) \cos(kx) dx$
+
+$b_k = \frac{1}{\pi} \int_{-\pi}^{\pi} f(x) \sin(kx) dx$
+
+To study the convergence of the Fourier series, we need to study the convergence of the sequence of partial sums. (Riemann integration)
+
+Why Riemann integration?
+
+Let
+
+$$
+((x)) = \begin{cases} 
+x-\lfloor x \rfloor & x \in [\lfloor x \rfloor, \lfloor x \rfloor + \frac{1}{2}) \\
+0 & x=\lfloor x \rfloor + \frac{1}{2}\\
+x-\lfloor x \rfloor - 1 & x \in (\lfloor x \rfloor + \frac{1}{2}, \lfloor x \rfloor + 1] \end{cases}
+$$
+
+We define
+
+$$
+f(x) = \sum_{n=1}^{\infty} \frac{((nx))}{n^2}=\lim_{N\to\infty}\sum_{n=1}^{N} \frac{((nx))}{n^2}
+$$
+
+(i) The series converges uniformly over $x\in[0,1]$.
+
+$$
+\left|f(x)-\sum_{n=1}^{N} \frac{((nx))}{n^2}\right|\leq \sum_{n=N+1}^{\infty}\frac{|((nx))|}{n^2}\leq \sum_{n=N+1}^{\infty} \frac{1}{n^2}<\epsilon
+$$
+
+As a consequence, $f(x)\in \mathscr{R}$.
+
+(ii) $f$ has a discontinuity at every rational number with even denominator.
+
+$$
+\begin{aligned}
+\lim_{h\to 0^+}f(\frac{a}{2b}+h)-f(\frac{a}{2b})&=\lim_{h\to 0^+}\sum_{n=1}^{\infty}\frac{((\frac{na}{2b}+h))}{n^2}-\sum_{n=1}^{\infty}\frac{((\frac{na}{2b}))}{n^2}\\
+&=\lim_{h\to 0^+}\sum_{n=1}^{\infty}\frac{((\frac{na}{2b}+h))-((\frac{na}{2b}))}{n^2}\\
+&=\sum_{n=1}^{\infty}\lim_{h\to 0^+}\frac{((\frac{na}{2b}+h))-((\frac{na}{2b}))}{n^2}\\
+&>0
+\end{aligned}
+$$
+
+### Back to the fundamental theorem of calculus
+
+Suppose $f$ is integrable on $[a,b]$, then
+
+$$
+F(x)=\int_a^x f(t)dt
+$$
+
+$F$ is continuous on $[a,b]$.
+
+if $f$ is continuous at $x_0$, then $F$ is differentiable at $x_0$ and $F'(x_0)=f(x_0)$.
+
+#### Theorem (Darboux's theorem)
+
+If $\lim_{x\to a^-}f(x)=L^-$, then $\lim_{h\to 0} \frac{f(a+h)-f(a)}{h}=L^-$.
+
+Proof:
+
+$$
+h\sup_{x\in [0,h]}f(x)\geq F(a+h)\geq \inf_{x\in [0,h]}f(x)h
+$$
+
+Consequently,
+
+$$
+f(x)=\sum_{n=1}^{\infty} \frac{((nx))}{n^2}
+$$
+
+then
+
+$$
+F(x)=\int_0^x f(t)dt
+$$
+
+is continuous on $[0,1]$.
+
+However, since $\lim_{x\to 0^+}f(x)\neq \lim_{x\to 0^-}f(x)$ holds for all the rational numbers with even denominator, $F$ is not differentiable at all the rational numbers with even denominator.
+
+Moral: There exists a continuous function on $[0,1]$ that is not differentiable at any rational number with even denominator. (Dense set)
+
+#### Weierstrass function
+
+$$
+g(x)=\sum_{n=0}^{\infty} a^n \cos(b^n \pi x)
+$$
+
+where $0<a<1$ and $ab>1+\frac{3}{2}\pi$.
+
+$g(x)$ is continuous on $\mathbb{R}$ but nowhere differentiable.
+
+_If we change our integral, will be differentiable at most points?_

pages/Math4121/Math4121_L14.md

@@ -1 +1,19 @@
-# Lecture 14
+# Math 4121 Lecture 14
+
+## Recap
+
+### Hankel developedn Riemann's integrabilty criterion.
+
+#### Definition 
+
+Given an interval $I\subset[a,b]$, $f:[a,b]\to\mathbb{R}$ the oscillation of $f$ at $I$ is
+
+$$
+\omega(f,I) = \sup_I f - \inf_I f
+$$
+
+#### Theorem 
+
+A bounded function $f$ is Riemann integrable if and only if
+
+

pages/Math4121/Math4121_L2.md

@@ -1,4 +1,4 @@
-# Lecture 2
+# Math4121 Lecture 2
 
 ## Chapter 5: Differentiation
 

pages/Math4121/Math4121_L3.md

@@ -1,4 +1,4 @@
-# Lecture 3
+# Math4121 Lecture 3
 
 ## Continue on Differentiation
 

pages/Math4121/Math4121_L4.md

@@ -1,4 +1,4 @@
-# Lecture 4
+# Math4121 Lecture 4
 
 ## Chapter 5. Differentiation
 

pages/Math4121/Math4121_L5.md

@@ -1,4 +1,4 @@
-# Lecture 5
+# Math4121 Lecture 5
 
 ## Continue on differentiation
 

pages/Math4121/Math4121_L6.md

@@ -1,4 +1,4 @@
-# Lecture 6
+# Math4121 Lecture 6
 
 ## Chapter 6: Riemann-Stieltjes Integral
 

pages/Math4121/Math4121_L7.md

@@ -1,4 +1,4 @@
-# Lecture 7
+# Math4121 Lecture 7
 
 ## Continue on Chapter 6
 

pages/Math4121/Math4121_L8.md

@@ -1,4 +1,4 @@
-# Lecture 8
+# Math4121 Lecture 8
 
 ## Continue on Riemann-Stieltjes Integral
 

pages/Math4121/Math4121_L9.md

@@ -1,4 +1,4 @@
-# Lecture 9
+# Math 4121 Lecture 9
 
 Exam next week.
 

pages/Math416/Math416_L10.md

@@ -0,0 +1,190 @@
+# Math416 Lecture 10
+
+## Fast reload on Power Series
+
+Suppose $\sum_{n=0}^\infty a_n$ converges absolutely. ($\sum_{n=0}^\infty |a_n|<\infty$)
+
+Then rearranging the terms of the series does not affect the sum of the series.
+
+For any permutation $\sigma$ of the set of positive integers, $\sum_{n=0}^\infty a_{\sigma(n)}=\sum_{n=0}^\infty a_n$.
+
+Proof:
+
+Let $\epsilon>0$, then $\exists N\in\mathbb{N}$ such that $\forall n\geq N$,
+
+$$
+\sum_{n=N}^\infty |a_n|<\epsilon
+$$
+
+So there exists $N_0$ such that if $M\geq N_0$, then
+
+$$
+\sum_{n=N_0}^M |a_n|<\epsilon
+$$
+
+_for any first $M$ terms of $\sigma$, we choose $N_0$ such that all the terms (no overlapping with the first $M$ terms) on the tail is less than $\epsilon$_.
+
+$$
+\sum_{n=1}^{\infty} a_n=\sum_{n=1}^{M} a_n+\sum_{n=M+1}^\infty a_n
+$$
+
+Let $K>N$, $L>N_0$,
+
+$$
+\left|\sum_{n=1}^{K}a_n-\sum_{n=1}^{L}a_{\sigma(n)}\right|<2\epsilon
+$$
+
+EOP
+
+## Chapter 4 Complex Integration
+
+### Complex Integral
+
+#### Definition 4.1
+
+If $\phi(t)$ is a complex function defined on $[a,b]$, then the integral of $\phi(t)$ over $[a,b]$ is defined as
+
+$$
+\int_a^b \phi(t) dt = \int_a^b \text{Re}\{\phi(t)\} dt + i\int_a^b \text{Im}\{\phi(t)\} dt
+$$
+
+#### Theorem 4.3 (Triangle Inequality)
+
+If $\phi(t)$ is a complex function defined on $[a,b]$, then
+
+$$
+\left|\int_a^b \phi(t) dt\right| \leq \int_a^b |\phi(t)| dt
+$$
+
+Proof:
+
+Let $\lambda(t)=\frac{\left|\int_a^t \phi(t) dt\right|}{\int_a^t |\phi(t)| dt}$, then $\left|\lambda(t)\right|=1$.
+
+$$
+\begin{aligned}
+\left|\int_a^b \phi(t) dt\right|&=\lambda\int_a^b \phi(t) dt\\
+&=\int_a^b \lambda(t)\phi(t) dt\\
+&=\text{Re} \{\int_a^b \lambda(t)\phi(t) dt\}\\
+&\leq\int_a^b |\lambda(t)\phi(t)| dt\\
+&=\int_a^b |\phi(t)| dt
+\end{aligned}
+$$
+
+Assume $\phi$ is continuous on $[a,b]$, the equality means $\lambda(t)\phi(t)$ is real and positive everywhere on $[a,b]$, which means $\arg \phi(t)$ is constant.
+
+EOP
+
+#### Definition 4.4 Arc Length
+
+Let $\gamma$ be a curve in the complex plane defined by $\gamma(t)=x(t)+iy(t)$, $t\in[a,b]$. The arc length of $\gamma$ is given by
+
+$$
+\Gamma=\int_a^b |\gamma'(t)| dt=\int_a^b \sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2} dt
+$$
+
+N.B. If $\int_{\Gamma} f(\zeta) d\zeta$ depends on orientation of $\Gamma$, but not the parametrization.
+
+We define
+
+$$
+\int_{\Gamma} f(\zeta) d\zeta=\int_{\Gamma} f(\gamma(t))\gamma'(t) dt
+$$
+
+Example:
+
+Suppose $\Gamma$ is the circle centered at $z_0$ with radius $R$
+
+$$
+\int_{\Gamma} \frac{1}{\zeta-z_0} d\zeta
+$$
+
+Parameterize the unit circle:
+
+$$
+\gamma(t)=z_0+Re^{it}\quad
+\gamma'(t)=iRe^{it}, t\in[0,2\pi]
+$$
+
+$$
+f(\zeta)=\frac{1}{\zeta-z_0}
+$$
+
+$$
+f(\gamma(t))=\frac{1}{(z_0+Re^{it})-z_0}
+$$
+
+$$
+\int_{\Gamma} f(\zeta) d\zeta=\int_0^{2\pi} f(\gamma(t))\gamma'(t) dt=\int_0^{2\pi} \frac{1}{Re^{-it}}iRe^{it} dt=2\pi i
+$$
+
+#### Theorem 4.11 (Uniform Convergence)
+
+If $f_n(z)$ converges uniformly to $f(z)$ on $\Gamma$, assume length of $\Gamma$ is finite, then
+
+$$
+\lim_{n\to\infty} \int_{\Gamma} f_n(z) dz = \int_{\Gamma} f(z) dz
+$$
+
+Proof:
+
+Let $\epsilon>0$, since $f_n(z)$ converges uniformly to $f(z)$ on $\Gamma$, there exists $N\in\mathbb{N}$ such that for all $n\geq N$,
+
+$$
+\left|f_n(z)-f(z)\right|<\epsilon
+$$
+
+$$
+\begin{aligned}
+\left|\int_{\Gamma} f_n(z) dz - \int_{\Gamma} f(z) dz\right|&=\left|\int_{\Gamma} (f_n(\gamma(t))-f(\gamma(t)))\gamma'(t) dt\right|\\
+&\leq \int_{\Gamma} |f_n(\gamma(t))-f(\gamma(t))||\gamma'(t)| dt\\
+&\leq \int_{\Gamma} \epsilon|\gamma'(t)| dt\\
+&=\epsilon\text{length}(\Gamma)
+\end{aligned}
+$$
+
+EOP
+
+#### Theorem 4.6 (Integral of derivative)
+
+Suppose $\Gamma$ is a closed curve, $\gamma:[a,b]\to\mathbb{C}$ and $\gamma(a)=\gamma(b)$.
+
+$$
+\begin{aligned}
+\int_{\Gamma} f'(z) dz &= \int_a^b f'(\gamma(t))\gamma'(t) dt\\
+&=\int_a^b \frac{d}{dt}f(\gamma(t)) dt\\
+&=f(\gamma(b))-f(\gamma(a))\\
+&=0
+\end{aligned}
+$$
+
+EOP
+
+Example:
+
+Let $R$ be a rectangle $\{-a,a,ai+b,ai-b\}$, $\Gamma$ is the boundary of $R$ with positive orientation.
+
+Let $\int_{R} e^{-\zeta^2}d\zeta$.
+
+Is $e^{-\zeta^2}=\frac{d}{d\zeta}f(\zeta)$?
+
+Yes, since
+
+$$
+e^{\zeta^2}=1-\frac{\zeta^2}{1!}+\frac{\zeta^4}{2!}-\frac{\zeta^6}{3!}+\cdots=\frac{d}{d\zeta}\left(\frac{\zeta}{1!}-\frac{1}{3}\frac{\zeta^3}{2!}+\frac{1}{5}\frac{\zeta^5}{3!}-\cdots\right)
+$$
+
+This is polynomial, therefore holomorphic.
+
+So
+
+$$
+\int_{R} e^{\zeta^2}d\zeta = 0
+$$
+
+with some limit calculation, we can get
+
+<!--TODO: Fill the parts-->
+
+$$
+\int_{R} e^{-\zeta^2}d\zeta = 2\pi i
+$$

pages/Math416/Math416_L3.md

@@ -1,4 +1,4 @@
-# Lecture 3
+# Math416 Lecture 3
 
 ## Differentiation of functions in complex variables
 

pages/Math416/Math416_L4.md

@@ -1,4 +1,4 @@
-# Lecture 4
+# Math416 Lecture 4
 
 ## Review
 

pages/Math416/Math416_L5.md

@@ -1,4 +1,4 @@
-# Lecture 5
+# Math416 Lecture 5
 
 ## Review
 

pages/Math416/Math416_L6.md

@@ -1,4 +1,4 @@
-# Lecture 6
+# Math416 Lecture 6
 
 ## Review
 

pages/Math416/Math416_L7.md

@@ -1,4 +1,4 @@
-# Lecture 7
+# Math416 Lecture 7
 
 ## Review
 

pages/Math416/Math416_L8.md

@@ -1,4 +1,4 @@
-# Lecture 8
+# Math416 Lecture 8
 
 ## Review
 

pages/Math416/_meta.js

@@ -11,5 +11,6 @@ export default {
     Math416_L6: "Complex Variables (Lecture 6)",
     Math416_L7: "Complex Variables (Lecture 7)",
     Math416_L8: "Complex Variables (Lecture 8)",
-    Math416_L9: "Complex Variables (Lecture 9)"
+    Math416_L9: "Complex Variables (Lecture 9)",
+    Math416_L10: "Complex Variables (Lecture 10)",
 }

pages/Swap/Math401/index.md

@@ -2,4 +2,4 @@
 
 This is a course about symmetrical group and bunch of applications in other fields of math.
 
-Prof. Fere is teaching this course.
+Prof. Renado Fere is teaching this course.