updates

content/CSE510/CSE510_L19.md

@@ -0,0 +1,100 @@
+# CSE510 Deep Reinforcement Learning (Lecture 19)
+
+## Model learning with high-dimensional observations
+
+- Learning model in a latent space with observation reconstruction
+- Learning model in a latent space without reconstruction
+
+### Learn in Latent Space: Dreamer
+
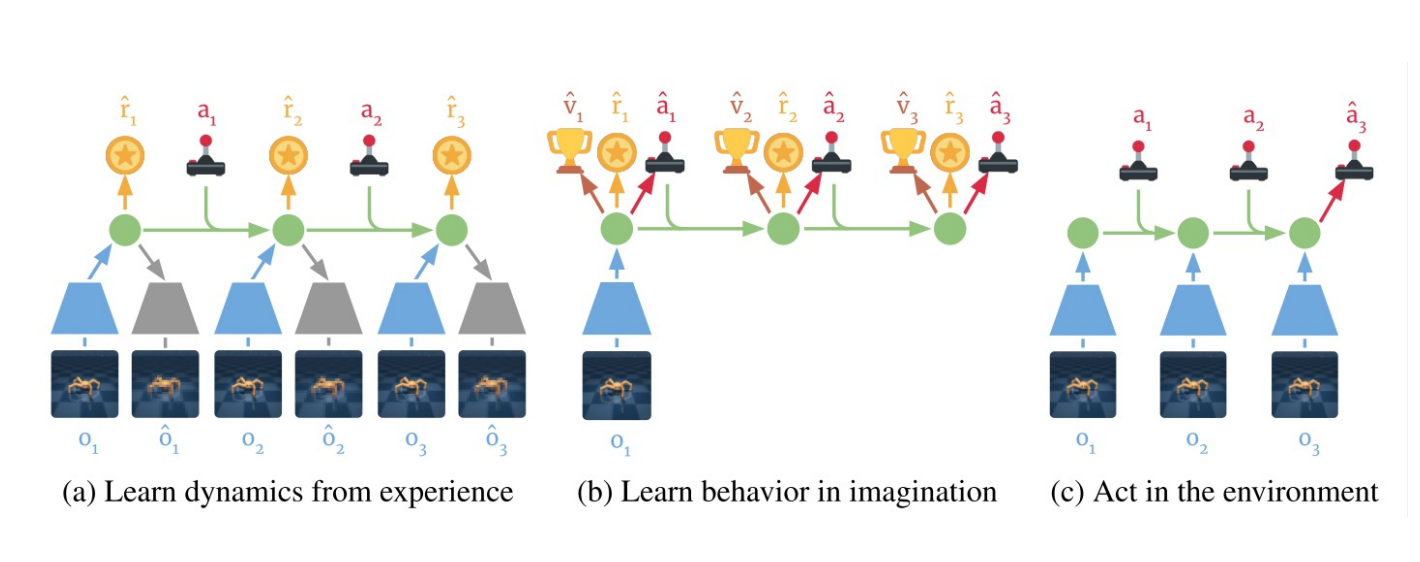
+Learning embedding of images & dynamics model (jointly)
+
+![Dreamer](https://notenextra.trance-0.com/CSE510/Dreamer.png)
+
+Representation model: $p_\theta(s_t|s_{t-1}, a_{t-1}, o_t)$
+
+Observation model: $q_\theta(o_t|s_t)$
+
+Reward model: $q_\theta(r_t|s_t)$
+
+Transition model: $q_\theta(s_t| s_{t-1}, a_{t-1})$.
+
+Variational evidence lower bound (ELBO) objective:
+
+$$
+\mathcal{J}_{REC}\doteq \mathbb{E}_{p}\left(\sum_t(\mathcal{J}_O^t+\mathcal{J}_R^t+\mathcal{J}_D^t)\right)
+$$
+
+where
+
+$$
+\mathcal{J}_O^t\doteq \ln q(o_t|s_t)
+$$
+
+$$
+\mathcal{J}_R^t\doteq \ln q(r_t|s_t)
+$$
+
+$$
+\mathcal{J}_D^t\doteq -\beta \operatorname{KL}(p(s_t|s_{t-1}, a_{t-1}, o_t)||q(s_t|s_{t-1}, a_{t-1}))
+$$
+
+#### More versions for Dreamer
+
+Latest is V3, [link to the paper](https://arxiv.org/pdf/2301.04104)
+
+### Learn in Latent Space
+
+- Pros
+  - Learn visual skill efficiently (using relative simple networks)
+- Cons
+  - Using autoencoder might not recover the right representation
+  - Not necessarily suitable for model-based methods
+  - Embedding is often not a good state representation without using history observations
+
+### Planning with Value Prediction Network (VPN)
+
+Idea: generating trajectories by following $\epsilon$-greedy policy based on the planning method
+
+Q-value calculated from $d$-step planning is defined as:
+
+$$
+Q_\theta^d(s,o)=r+\gamma V_\theta^{d}(s')
+$$
+
+$$
+V_\theta^{d}(s)=\begin{cases}
+V_\theta(s) & \text{if } d=1\\
+\frac{1}{d}V_\theta(s)+\frac{d-1}{d}\max_{o} Q_\theta^{d-1}(s,o)& \text{if } d>1
+\end{cases}
+$$
+
+![VPN](https://notenextra.trance-0.com/CSE510/VPN.png)
+
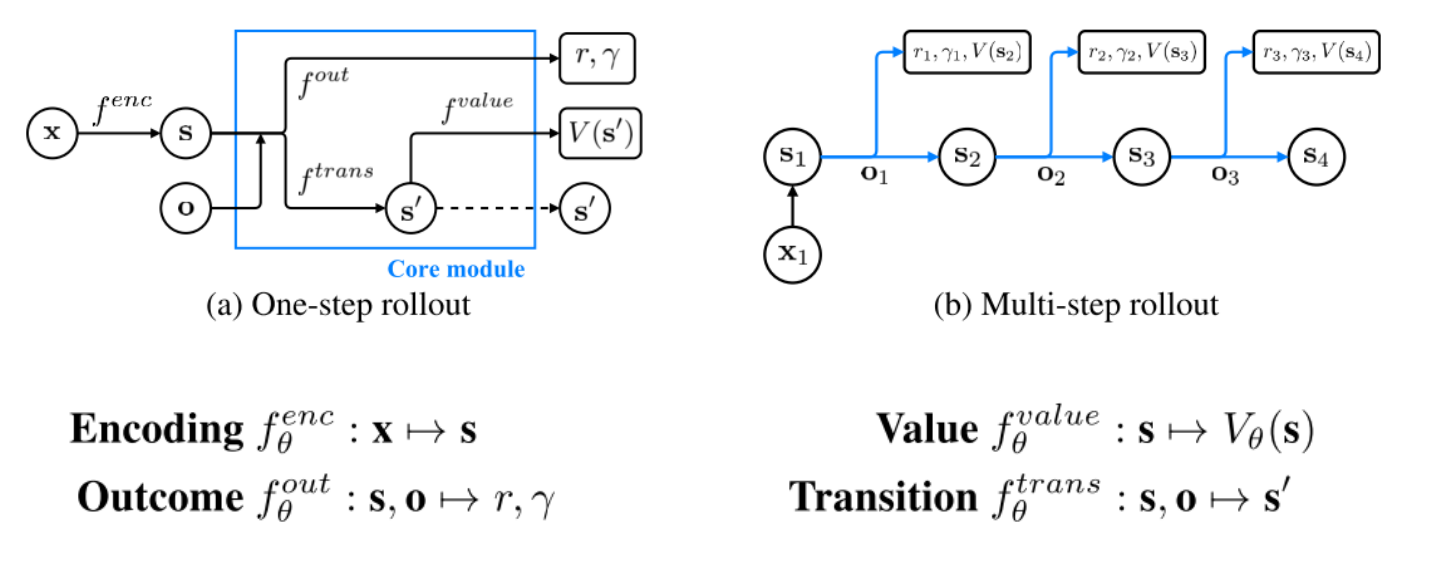
+Given an n-step trajectory $x_1, o_1, r_1, \gamma_1, x_2, o_2, r_2, \gamma_2, ..., x_{n+1}$ generated by the $\epsilon$-greedy policy, k-step predictions are defined as follows:
+
+$$
+s_t^k=\begin{cases}
+f^{enc}_\theta(x_t) & \text{if } k=0\\
+f^{trans}_\theta(s_{t-1}^{k-1},o_{t-1}) & \text{if } k>0
+\end{cases}
+$$
+
+$$
+v_t^k=f^{value}_\theta(s_t^k)
+$$
+
+$$
+r_t^k,\gamma_t^k=f^{out}_\theta(s_t^{k-1},o_t)
+$$
+
+$$
+\mathcal{L}_t=\sum_{l=1}^k(R_t-v_t^l)^2+(r_t-r_t^l)^2+(\gamma_t-\gamma_t^l)^2\text{ where } R_t=\begin{cases}
+r_t+\gamma_t R_{t+1} & \text{if } t\leq n\\
+\max_{o} Q_{\theta-}^d(s_{n+1},o)& \text{if } t=n+1
+\end{cases}
+$$
+
+### MuZero
+
+beats AlphaZero

content/CSE510/_meta.js

@@ -21,4 +21,5 @@ export default {
     CSE510_L16: "CSE510 Deep Reinforcement Learning (Lecture 16)",
     CSE510_L17: "CSE510 Deep Reinforcement Learning (Lecture 17)",
     CSE510_L18: "CSE510 Deep Reinforcement Learning (Lecture 18)",
+    CSE510_L19: "CSE510 Deep Reinforcement Learning (Lecture 19)",
 }