updates

content/CSE510/CSE510_L19.md

@@ -0,0 +1,100 @@
+# CSE510 Deep Reinforcement Learning (Lecture 19)
+
+## Model learning with high-dimensional observations
+
+- Learning model in a latent space with observation reconstruction
+- Learning model in a latent space without reconstruction
+
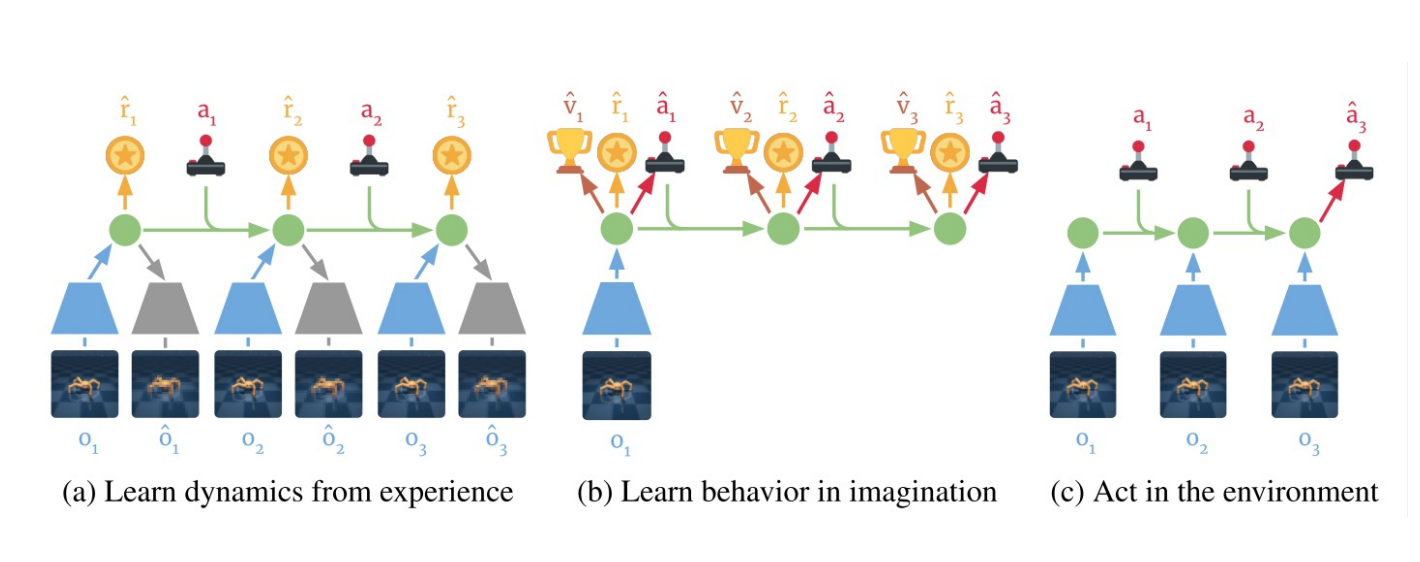
+### Learn in Latent Space: Dreamer
+
+Learning embedding of images & dynamics model (jointly)
+
+![Dreamer](https://notenextra.trance-0.com/CSE510/Dreamer.png)
+
+Representation model: $p_\theta(s_t|s_{t-1}, a_{t-1}, o_t)$
+
+Observation model: $q_\theta(o_t|s_t)$
+
+Reward model: $q_\theta(r_t|s_t)$
+
+Transition model: $q_\theta(s_t| s_{t-1}, a_{t-1})$.
+
+Variational evidence lower bound (ELBO) objective:
+
+$$
+\mathcal{J}_{REC}\doteq \mathbb{E}_{p}\left(\sum_t(\mathcal{J}_O^t+\mathcal{J}_R^t+\mathcal{J}_D^t)\right)
+$$
+
+where
+
+$$
+\mathcal{J}_O^t\doteq \ln q(o_t|s_t)
+$$
+
+$$
+\mathcal{J}_R^t\doteq \ln q(r_t|s_t)
+$$
+
+$$
+\mathcal{J}_D^t\doteq -\beta \operatorname{KL}(p(s_t|s_{t-1}, a_{t-1}, o_t)||q(s_t|s_{t-1}, a_{t-1}))
+$$
+
+#### More versions for Dreamer
+
+Latest is V3, [link to the paper](https://arxiv.org/pdf/2301.04104)
+
+### Learn in Latent Space
+
+- Pros
+  - Learn visual skill efficiently (using relative simple networks)
+- Cons
+  - Using autoencoder might not recover the right representation
+  - Not necessarily suitable for model-based methods
+  - Embedding is often not a good state representation without using history observations
+
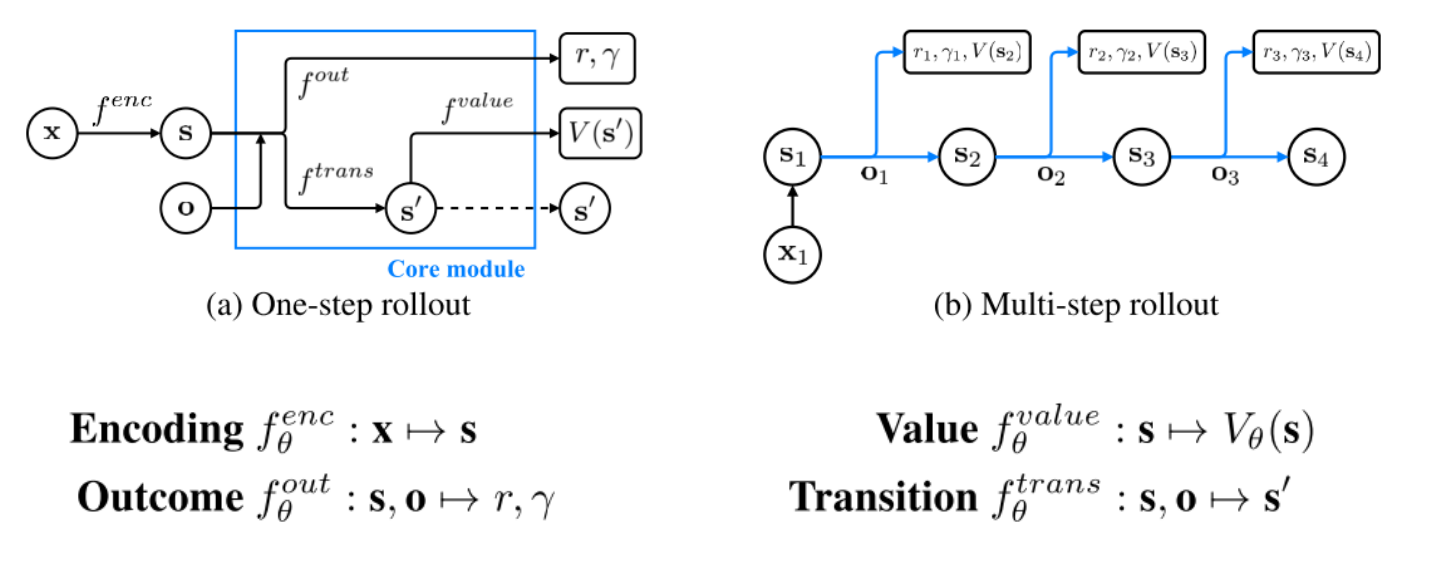
+### Planning with Value Prediction Network (VPN)
+
+Idea: generating trajectories by following $\epsilon$-greedy policy based on the planning method
+
+Q-value calculated from $d$-step planning is defined as:
+
+$$
+Q_\theta^d(s,o)=r+\gamma V_\theta^{d}(s')
+$$
+
+$$
+V_\theta^{d}(s)=\begin{cases}
+V_\theta(s) & \text{if } d=1\\
+\frac{1}{d}V_\theta(s)+\frac{d-1}{d}\max_{o} Q_\theta^{d-1}(s,o)& \text{if } d>1
+\end{cases}
+$$
+
+![VPN](https://notenextra.trance-0.com/CSE510/VPN.png)
+
+Given an n-step trajectory $x_1, o_1, r_1, \gamma_1, x_2, o_2, r_2, \gamma_2, ..., x_{n+1}$ generated by the $\epsilon$-greedy policy, k-step predictions are defined as follows:
+
+$$
+s_t^k=\begin{cases}
+f^{enc}_\theta(x_t) & \text{if } k=0\\
+f^{trans}_\theta(s_{t-1}^{k-1},o_{t-1}) & \text{if } k>0
+\end{cases}
+$$
+
+$$
+v_t^k=f^{value}_\theta(s_t^k)
+$$
+
+$$
+r_t^k,\gamma_t^k=f^{out}_\theta(s_t^{k-1},o_t)
+$$
+
+$$
+\mathcal{L}_t=\sum_{l=1}^k(R_t-v_t^l)^2+(r_t-r_t^l)^2+(\gamma_t-\gamma_t^l)^2\text{ where } R_t=\begin{cases}
+r_t+\gamma_t R_{t+1} & \text{if } t\leq n\\
+\max_{o} Q_{\theta-}^d(s_{n+1},o)& \text{if } t=n+1
+\end{cases}
+$$
+
+### MuZero
+
+beats AlphaZero

content/CSE510/_meta.js

@@ -21,4 +21,5 @@ export default {
     CSE510_L16: "CSE510 Deep Reinforcement Learning (Lecture 16)",
     CSE510_L17: "CSE510 Deep Reinforcement Learning (Lecture 17)",
     CSE510_L18: "CSE510 Deep Reinforcement Learning (Lecture 18)",
+    CSE510_L19: "CSE510 Deep Reinforcement Learning (Lecture 19)",
 }

content/CSE5313/CSE5313_L18.md

@@ -0,0 +1,270 @@
+# CSE5313 Coding and information theory for data science (Lecture 18)
+
+## Secret sharing
+
+The president and the vice president must both consent to a nuclear missile launch.
+
+We would like to share the nuclear code such that:
+
+- $Share1, Share2 \mapsto Nuclear Code$
+- $Share1 \not\mapsto Nuclear Code$
+- $Share2 \not\mapsto Nuclear Code$
+- $Share1 \not\mapsto Share2$
+- $Share2 \not\mapsto Share1$
+
+In other words:
+
+- The two shares are everything.
+- One share is nothing.
+
+<details>
+<summary>Solution</summary>
+
+Scheme:
+
+- The nuclear code is a field element $m \in \mathbb{F}_q$, chosen at random $m \sim M$ (M arbitrary).
+- Let $p(x) = m + rx \in \mathbb{F}_q[x]$.
+  - $r \sim U$, where $U = Uniform \mathbb{F}_q$, i.e., $Pr(\alpha = 1/q)$ for every $\alpha \in \mathbb{F}_q$.
+- Fix $\alpha_1, \alpha_2 \in \mathbb{F}_q$ (not random).
+- $s_1 = p(\alpha_1) = m + r\alpha_1, s_1 \sim S_1$.
+- $s_2 = p(\alpha_2) = m + r\alpha_2, s_2 \sim S_2$.
+
+And then:
+
+- One share reveals nothing about $m$.
+- I.e., $I(S_i; M) = 0$ (gradient could be anything)
+- Two shares reveal $p \Rightarrow reveal p(0) = m$.
+- I.e., $H(M|S_1, S_2) = 0$ (two points determine a line).
+
+</details>
+
+### Formalize the notion of secret sharing
+
+#### Problem setting
+
+A dealer is given a secret $m$ chosen from an arbitrary distribution $M$.
+
+The dealer creates $n$ shares $s_1, s_2, \cdots, s_n$ and send to $n$ parties.
+
+Two privacy parameters: $t,z\in \mathbb{N}$ $z<t$.
+
+**Requirements**:
+
+For $\mathcal{A}\subseteq[n]$ denote $S_\mathcal{A} = \{s_i:i\in \mathcal{A}\}$.
+
+- Decodability: Any set of $t$ shares can reconstruct the secret.
+  - $H(M|S_\mathcal{T}) = 0$ for all $\mathcal{T}\subseteq[n]$ with $|\mathcal{T}|\geq t$.
+- Security: Any set of $z$ shares reveals no information about the secret.
+  - $I(M;S_\mathcal{Z}) = 0$ for all $\mathcal{Z}\subseteq[n]$ with $|\mathcal{Z}|\leq z$.
+
+This is called $(n,z,t)$-secret sharing scheme.
+
+#### Interpretation
+
+- $\mathcal{Z} \subseteq [n]$, $|\mathcal{Z}| \leq z$ is a corrupted set of parties.
+- An adversary which corrupts at most $z$ parties cannot infer anything about the secret.
+
+#### Applications
+
+- Secure distributed storage.
+  - Any $\leq z$ hacked servers reveal nothing about the data.
+- Secure distributed computing with a central server (e.g., federated learning).
+  - Any $\leq z$ corrupted computation nodes know nothing about the data.
+- Secure multiparty computing (decentralized).
+  - Any $\leq z$ corrupted parties cannot know the inputs of other parties.
+
+### Scheme 1: Shamir secret sharing scheme
+
+Parameters $n,t$, and $z=t-1$.
+
+Fix $\mathbb{F}_q$, $q>n$ and distinct points $\alpha_1, \alpha_2, \cdots, \alpha_n \in \mathbb{F}_q\setminus \{0\}$. (public, known to all).
+
+Given $m\sim M$ the dealer:
+
+- Choose $r_1, r_2, \cdots, r_z \sim U_1, U_2, \cdots, U_z$ (uniformly random from $\mathbb{F}_q$).
+- Defines $p\in \mathbb{F}_q[x]$ by $p(x) = m + r_1x + r_2x^2 + \cdots + r_zx^z$.
+- Send share $s_i = p(\alpha_i)$ to party $i$.
+
+#### Theorem valid encoding scheme
+
+This is an $(n,t-1,t)$-secret sharing scheme.
+
+Decodability:
+
+- $\deg p=t-1$, any $t$ shares can reconstruct $p$ by Lagrange interpolation.
+
+<details>
+<summary>Proof</summary>
+
+Specifically, any $t$ parties $\mathcal{T}\subseteq[n]$ can define the interpolation polynomial $h(x)=\sum_{i\in \mathcal{T}} s_i \delta_{i}(x)$, where $\delta_{i}(x)=\prod_{j\in \mathcal{T}\setminus \{i\}} \frac{x-\alpha_j}{\alpha_i-\alpha_j}$. ($\delta_{i}(\alpha_i)=1$, $\delta_{i}(\alpha_j)=0$ for $j\neq i$).
+
+$\deg h=\deg p=t-1$, so $h(x)=p(x)$ for all $x\in \mathcal{T}$.
+
+Therefore, $h(0)=p(0)=m$.
+</details>
+
+Privacy:
+
+Need to show that $I(M;S_\mathcal{Z})=0$ for all $\mathcal{Z}\subseteq[n]$ with $|\mathcal{Z}|=z$.
+
+> that is equivalent to show that $M$ and $s_\mathcal{Z}$ are independent for all $\mathcal{Z}\subseteq[n]$ with $|\mathcal{Z}|=z$.
+
+<details>
+<summary>Proof</summary>
+
+We will show that $\operatorname{Pr}(s_\mathcal{Z}|M=m)=\operatorname{Pr}(M=m)$, for all $s_\mathcal{Z}\in S_\mathcal{Z}$ and $m\in M$.
+
+Let $m,\mathcal{Z}=(i_1,i_2,\cdots,i_z)$, and $s_\mathcal{Z}$.
+
+$$
+\begin{bmatrix}
+m & U_1 & U_2 & \cdots & U_z
+\end{bmatrix} = \begin{bmatrix}
+1 & 1 & 1 & \cdots & 1 \\
+\alpha_{i_1} & \alpha_{i_2} & \alpha_{i_3} & \cdots & \alpha_{i_n} \\
+\alpha_{i_1}^2 & \alpha_{i_2}^2 & \alpha_{i_3}^2 & \cdots & \alpha_{i_n}^2 \\
+\vdots & \vdots & \vdots & \ddots & \vdots \\
+\alpha_{i_1}^{z} & \alpha_{i_2}^{z} & \alpha_{i_3}^{z} & \cdots & \alpha_{i_n}^{z}
+\end{bmatrix}=s_\mathcal{Z}=\begin{bmatrix}
+s_{i_1} \\ s_{i_2} \\ \vdots \\ s_{i_z}
+\end{bmatrix}
+$$
+
+So,
+
+$$
+\begin{bmatrix}
+U_1 & U_2 & \cdots & U_z
+\end{bmatrix} = (s_\mathcal{Z}-\begin{bmatrix}
+m & m & m & \cdots & m
+\end{bmatrix})
+\begin{bmatrix}
+\alpha_{i_1}^{-1} & \alpha_{i_2}^{-1} & \alpha_{i_3}^{-1} & \cdots & \alpha_{i_n}^{-1} \\
+\end{bmatrix}
+
+\begin{bmatrix}
+1 & 1 & 1 & \cdots & 1 \\
+\alpha_1 & \alpha_2 & \alpha_3 & \cdots & \alpha_n \\
+\alpha_1^2 & \alpha_2^2 & \alpha_3^2 & \cdots & \alpha_n^2 \\
+\vdots & \vdots & \vdots & \ddots & \vdots \\
+\alpha_1^{z-1} & \alpha_2^{z-1} & \alpha_3^{z-1} & \cdots & \alpha_n^{z-1}
+\end{bmatrix}^{-1}
+$$
+
+So exactly one solution for $U_1, U_2, \cdots, U_z$ is possible.
+
+So $\operatorname{Pr}(U_1, U_2, \cdots, U_z|M=m)=\frac{1}{q^z}$ for all $m\in M$.
+
+Recall the law of total probability:
+
+$$
+\operatorname{Pr}(s_\mathcal{Z})=\sum_{m'\in M} \operatorname{Pr}(s_\mathcal{Z}|M=m') \operatorname{Pr}(M=m')=\frac{1}{q^z}\sum_{m'\in M} \operatorname{Pr}(M=m')=\frac{1}{q^z}
+$$
+
+So $\operatorname{Pr}(s_\mathcal{Z}|M=m)=\operatorname{Pr}(M=m)\implies I(M;S_\mathcal{Z})=0$.
+
+</details>
+
+### Scheme 2: Ramp secret sharing scheme (McEliece-Sarwate scheme)
+
+- Any $z$ know nothing
+- Any $t$ knows everything
+- Partial knowledge for $z<s<t$
+
+Parameters $n,t$, and $z<t$.
+
+Fix $\mathbb{F}_q$, $q>n$ and distinct points $\alpha_1, \alpha_2, \cdots, \alpha_n \in \mathbb{F}_q\setminus \{0\}$. (public, known to all)
+
+Given $m_1, m_2, \cdots, m_n \sim M$, the dealer:
+
+- Choose $r_1, r_2, \cdots, r_z \sim U_1, U_2, \cdots, U_z$ (uniformly random from $\mathbb{F}_q$).
+- Defines $p(x) = m_1+m_2x + \cdots + m_{t-z}x^{t-z-1} + r_1x^{t-z} + r_2x^{t-z+1} + \cdots + r_zx^{t-1}$.
+- Send share $s_i = p(\alpha_i)$ to party $i$.
+
+Decodability
+
+Similar to Shamir scheme, any $t$ shares can reconstruct $p$ by Lagrange interpolation.
+
+Privacy
+
+Similar to the proof of Shamir, exactly one value of $U_1, \cdots, U_z$
+is possible!
+
+$\operatorname{Pr}(s_\mathcal{Z}|m_1, \cdots, m_{t-z}) = \operatorname{Pr}(U_1, \cdots, U_z) = the above = 1/q^z$
+
+($U_i$'s are uniform and independent).
+
+Conclude similarly by the law of total probability.
+
+$\operatorname{Pr}(s_\mathcal{Z}|m_1, \cdots, m_{t-z}) = \operatorname{Pr}(s_\mathcal{Z}) \implies I(S_\mathcal{Z}; M_1, \cdots, M_{t-z}) = 0.
+
+### Conditional mutual information
+
+The dealer needs to communicate the shares to the parties.
+
+Assumed: There exists a noiseless communication channel between the dealer and every party.
+
+From previous lecture:
+
+- The optimal number of bits for communicating $s_i$ (i'th share) to the i'th party is $H(s_i)$.
+- Q: What is $H(s_i|M)$?
+
+Tools:
+- Conditional mutual information.
+- Chain rule for mutual information.
+
+#### Definition of conditional mutual information
+
+The conditional mutual information $I(X;Y|Z)$ of $X$ and $Y$ given $Z$ is defined as:
+
+$$
+\begin{aligned}
+I(X;Y|Z)&=H(X|Z)-H(X|Y,Z)\\
+&=H(X|Z)+H(X)-H(X)-H(X|Y,Z)\\
+&=(H(X)-H(X|Y,Z))-(H(X)-H(X|Z))\\
+&=I(X; Y,Z)- I(X; Z)
+\end{aligned}
+$$
+
+where $H(X|Y,Z)$ is the conditional entropy of $X$ given $Y$ and $Z$.
+
+#### The chain rule of mutual information
+
+$$
+I(X;Y,Z)=I(X;Y|Z)+I(X;Z)
+$$
+
+Conditioning reduces entropy.
+
+#### Lower bound for communicating secret
+
+Consider the Shamir scheme ($z = t - 1$, one message).
+
+Q: What is $H(s_i)$ with respect to $H(M)$ ?
+A: Fix any $\mathcal{T} = \{i_1, \cdots, i_t\} \subseteq [n]$ of size $t$, and let $\mathcal{Z} = \{i_1, \cdots, i_{t-1}\}$.
+
+$$
+\begin{aligned}
+H(M) &= I(M; S_\mathcal{T}) + H(M|S_\mathcal{T}) \text{(by def. of mutual information)}\\
+&= I(M; S_\mathcal{T}) \text{(since S_\mathcal{T} suffice to decode M)}\\
+&= I(M; S_{i_t}, S_\mathcal{Z}) \text{(since S_\mathcal{T} = S_\mathcal{Z} ∪ S_{i_t})}\\
+&= I(M; S_{i_t}|S_\mathcal{Z}) + I(M; S_\mathcal{Z}) \text{(chain rule)}\\
+&= I(M; S_{i_t}|S_\mathcal{Z}) \text{(since \mathcal{Z} ≤ z, it reveals nothing about M)}\\
+&= I(S_{i_t}; M|S_\mathcal{Z}) \text{(symmetry of mutual information)}\\
+&= H(S_{i_t}|S_\mathcal{Z}) - H(S_{i_t}|M,S_\mathcal{Z}) \text{(def. of conditional mutual information)}\\
+\leq H(S_{i_t}|S_\mathcal{Z}) \text{(entropy is non-negative)}\\
+\leq H(S_{i_t}|S_\mathcal{Z}) \text{(conditioning reduces entropy). \\
+\end{aligned}
+$$
+
+So the bits used for sharing the secret is at least the bits of actual secret.
+
+In Shamir we saw: $H(s_i) \geq H(M)$.
+
+- If $M$ is uniform (standard assumption), then Shamir achieves this bound with equality.
+- In ramp secret sharing we have $H(s_i) \geq \frac{1}{t-z}H(M_1, \cdots, M_{t-z})$ (similar proof).
+- Also optimal if $M$ is uniform.
+
+#### Downloading file with lower bandwidth from more servers
+
+[link to paper](https://arxiv.org/abs/1505.07515)

content/CSE5313/_meta.js

@@ -21,4 +21,5 @@ export default {
     CSE5313_L15: "CSE5313 Coding and information theory for data science (Lecture 15)",
     CSE5313_L16: "CSE5313 Coding and information theory for data science (Exam Review)",
     CSE5313_L17: "CSE5313 Coding and information theory for data science (Lecture 17)",
+    CSE5313_L18: "CSE5313 Coding and information theory for data science (Lecture 18)",
 }

content/CSE5519/CSE5519_D4.md

@@ -1,2 +1,21 @@
 # CSE5519 Advances in Computer Vision (Topic D: 2024: Image and Video Generation)
 
+## Autoregressive Model Beats Diffusion: Llama for Scalable Image Generation
+
+[link to the paper](https://arxiv.org/pdf/2406.06525)
+
+This paper shows that the autoregressive model can outperform the diffusion model in terms of image generation.
+
+### Novelty in the autoregressive model
+
+Use Llama 3.1 as the autoregressive model.
+
+Use code book and downsampling to reduce the memory footprint.
+
+> [!TIP]
+>
+> This paper shows that the autoregressive model can outperform the diffusion model in terms of image generation.
+>
+> And in later works, we showed that usually the image can be represented by a few code words; for example, 32 tokens may be enough to represent most of the images (that most humans need to annotate). However, I doubt the result if it can be generalized to more complex image generation tasks, for example, the image generation with a human face, since I found it difficult to describe people around me distinctively without calling their name.
+> 
+> For more real-life videos, to ensure contextual consistency, we may need to use more code words. Is such a method scalable to video generation to produce realistic results? Or will there be an exponential memory cost for the video generation?