final updates
This commit is contained in:
217
pages/CSE559A/CSE559A_L25.md
Normal file
217
pages/CSE559A/CSE559A_L25.md
Normal file
@@ -0,0 +1,217 @@
|
||||
# CSE559A Lecture 25
|
||||
|
||||
## Geometry and Multiple Views
|
||||
|
||||
### Cues for estimating Depth
|
||||
|
||||
#### Multiple Views (the strongest depth cue)
|
||||
|
||||
Two common settings:
|
||||
|
||||
**Stereo vision**: a pair of cameras, usually with some constraints on the relative position of the two cameras.
|
||||
|
||||
**Structure from (camera) motion**: cameras observing a scene from different viewpoints
|
||||
|
||||
Structure and depth are inherently ambiguous from single views.
|
||||
|
||||
Other hints for depth:
|
||||
|
||||
- Occlusion
|
||||
- Perspective effects
|
||||
- Texture
|
||||
- Object motion
|
||||
- Shading
|
||||
- Focus/Defocus
|
||||
|
||||
#### Focus on Stereo and Multiple Views
|
||||
|
||||
Stereo correspondence: Given a point in one of the images, where could its corresponding points be in the other images?
|
||||
|
||||
Structure: Given projections of the same 3D point in two or more images, compute the 3D coordinates of that point
|
||||
|
||||
Motion: Given a set of corresponding points in two or more images, compute the camera parameters
|
||||
|
||||
#### A simple example of estimating depth with stereo:
|
||||
|
||||
Stereo: shape from "motion" between two views
|
||||
|
||||
We'll need to consider:
|
||||
|
||||
- Info on camera pose ("calibration")
|
||||
- Image point correspondences
|
||||
|
||||
|
||||
|
||||
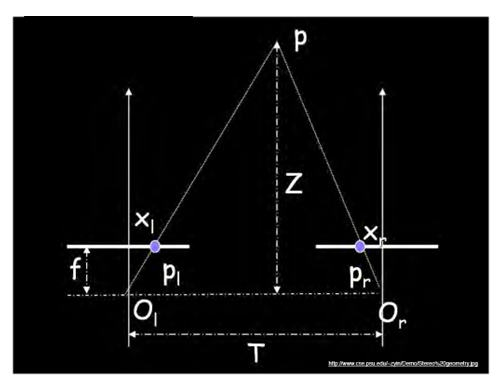
Assume parallel optical axes, known camera parameters (i.e., calibrated cameras). What is expression for Z?
|
||||
|
||||
Similar triangles $(p_l, P, p_r)$ and $(O_l, P, O_r)$:
|
||||
|
||||
$$
|
||||
\frac{T-x_l+x_r}{Z-f}=\frac{T}{Z}
|
||||
$$
|
||||
|
||||
$$
|
||||
Z = \frac{f \cdot T}{x_l-x_r}
|
||||
$$
|
||||
|
||||
### Camera Calibration
|
||||
|
||||
Use an scene with known geometry
|
||||
|
||||
- Correspond image points to 3d points
|
||||
- Get least squares solution (or non-linear solution)
|
||||
|
||||
Solving unknown camera parameters:
|
||||
|
||||
$$
|
||||
\begin{bmatrix}
|
||||
su\\
|
||||
sv\\
|
||||
s
|
||||
\end{bmatrix}
|
||||
= \begin{bmatrix}
|
||||
m_{11} & m_{12} & m_{13} & m_{14}\\
|
||||
m_{21} & m_{22} & m_{23} & m_{24}\\
|
||||
m_{31} & m_{32} & m_{33} & m_{34}
|
||||
\end{bmatrix}
|
||||
\begin{bmatrix}
|
||||
X\\
|
||||
Y\\
|
||||
Z\\
|
||||
1
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
Method 1: Homogenous linear system. Solve for m's entries using least squares.
|
||||
|
||||
$$
|
||||
\begin{bmatrix}
|
||||
X_1 & Y_1 & Z_1 & 1 & 0 & 0 & 0 & 0 & -u_1X_1 & -u_1Y_1 & -u_1Z_1 & -u_1 \\
|
||||
0 & 0 & 0 & 0 & X_1 & Y_1 & Z_1 & 1 & -v_1X_1 & -v_1Y_1 & -v_1Z_1 & -v_1 \\
|
||||
\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots\\
|
||||
X_n & Y_n & Z_n & 1 & 0 & 0 & 0 & 0 & -u_nX_n & -u_nY_n & -u_nZ_n & -u_n \\
|
||||
0 & 0 & 0 & 0 & X_n & Y_n & Z_n & 1 & -v_nX_n & -v_nY_n & -v_nZ_n & -v_n
|
||||
\end{bmatrix}
|
||||
\begin{bmatrix} m_{11} \\ m_{12} \\ m_{13} \\ m_{14} \\ m_{21} \\ m_{22} \\ m_{23} \\ m_{24} \\ m_{31} \\ m_{32} \\ m_{33} \\ m_{34} \end{bmatrix} = 0
|
||||
$$
|
||||
|
||||
Method 2: Non-homogenous linear system. Solve for m's entries using least squares.
|
||||
|
||||
**Advantages**
|
||||
|
||||
- Easy to formulate and solve
|
||||
- Provides initialization for non-linear methods
|
||||
|
||||
**Disadvantages**
|
||||
|
||||
- Doesn't directly give you camera parameters
|
||||
- Doesn't model radial distortion
|
||||
- Can't impose constraints, such as known focal length
|
||||
|
||||
**Non-linear methods are preferred**
|
||||
|
||||
- Define error as difference between projected points and measured points
|
||||
- Minimize error using Newton's method or other non-linear optimization
|
||||
|
||||
#### Triangulation
|
||||
|
||||
Given projections of a 3D point in two or more images (with known camera matrices), find the coordinates of the point
|
||||
|
||||
##### Approaches 1: Geometric approach
|
||||
|
||||
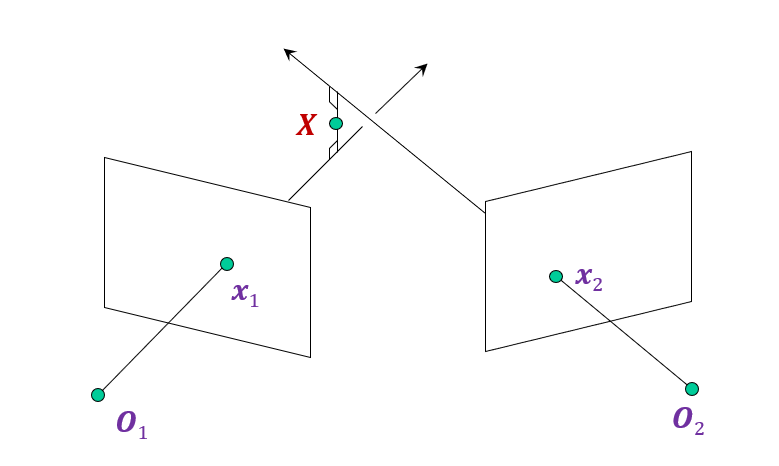
Find shortest segment connecting the two viewing rays and let $X$ be the midpoint of that segment
|
||||
|
||||
|
||||
|
||||
##### Approaches 2: Non-linear optimization
|
||||
|
||||
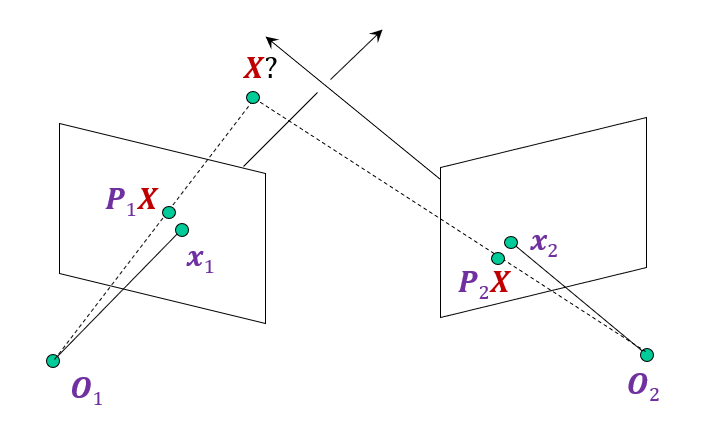
Minimize error between projected point and measured point
|
||||
|
||||
$$
|
||||
||\operatorname{proj}(P_1 X) - x_1||_2^2 + ||\operatorname{proj}(P_2 X) - x_2||_2^2
|
||||
$$
|
||||
|
||||
|
||||
|
||||
##### Approaches 3: Linear approach
|
||||
|
||||
$x_1\simeq P_1X$ and $x_2\simeq P_2X$
|
||||
|
||||
$x_1\times P_1X = 0$ and $x_2\times P_2X = 0$
|
||||
|
||||
$[x_{1_{\times}}]P_1X = 0$ and $[x_{2_{\times}}]P_2X = 0$
|
||||
|
||||
Rewrite as:
|
||||
|
||||
$$
|
||||
a\times b=\begin{bmatrix}
|
||||
0 & -a_3 & a_2\\
|
||||
a_3 & 0 & -a_1\\
|
||||
-a_2 & a_1 & 0
|
||||
\end{bmatrix}
|
||||
\begin{bmatrix}
|
||||
b_1\\
|
||||
b_2\\
|
||||
b_3
|
||||
\end{bmatrix}
|
||||
=[a_{\times}]b
|
||||
$$
|
||||
|
||||
Using **singular value decomposition**, we can solve for $X$
|
||||
|
||||
### Epipolar Geometry
|
||||
|
||||
What constraints must hold between two projections of the same 3D point?
|
||||
|
||||
Given a 2D point in one view, where can we find the corresponding point in the other view?
|
||||
|
||||
Given only 2D correspondences, how can we calibrate the two cameras, i.e., estimate their relative position and orientation and the intrinsic parameters?
|
||||
|
||||
Key ideas:
|
||||
|
||||
- We can answer all these questions without knowledge of the 3D scene geometry
|
||||
- Important to think about projections of camera centers and visual rays into the other view
|
||||
|
||||
#### Epipolar Geometry Setup
|
||||
|
||||
|
||||
|
||||
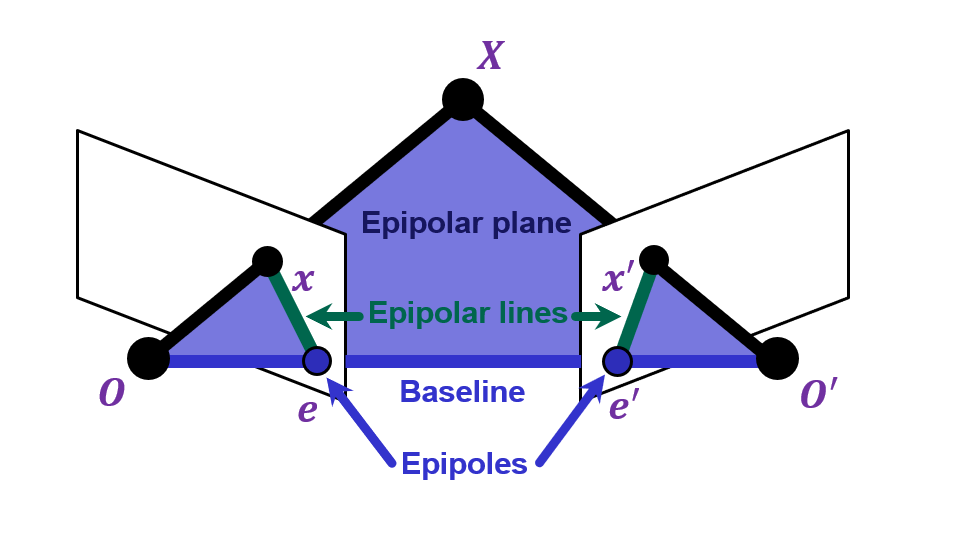
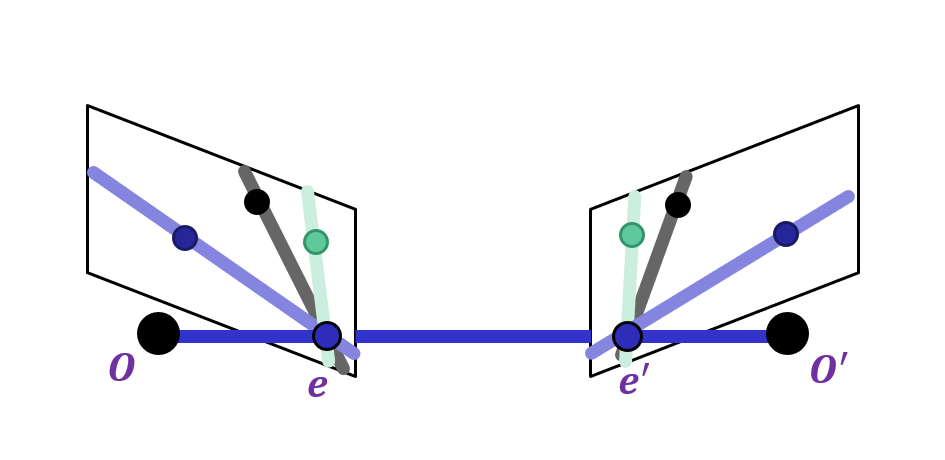
Suppose we have two cameras with centers $O,O'$
|
||||
|
||||
The baseline is the line connecting the origins
|
||||
|
||||
Epipoles $e,e'$ are where the baseline intersects the image planes, or projections of the other camera in each view
|
||||
|
||||
Consider a point $X$, which projects to $x$ and $x'$
|
||||
|
||||
The plane formed by $X,O,O'$ is called an epipolar plane
|
||||
There is a family of planes passing through $O$ and $O'$
|
||||
|
||||
Epipolar lines are projections of the baseline into the image planes
|
||||
|
||||
**Epipolar lines** connect the epipoles to the projections of $X$
|
||||
Equivalently, they are intersections of the epipolar plane with the image planes – thus, they come in matching pairs.
|
||||
|
||||
**Application**: This constraint can be used to find correspondences between points in two camera. by the epipolar line in one image, we can find the corresponding feature in the other image.
|
||||
|
||||
|
||||
|
||||
Epipoles are finite and may be visible in the image.
|
||||
|
||||
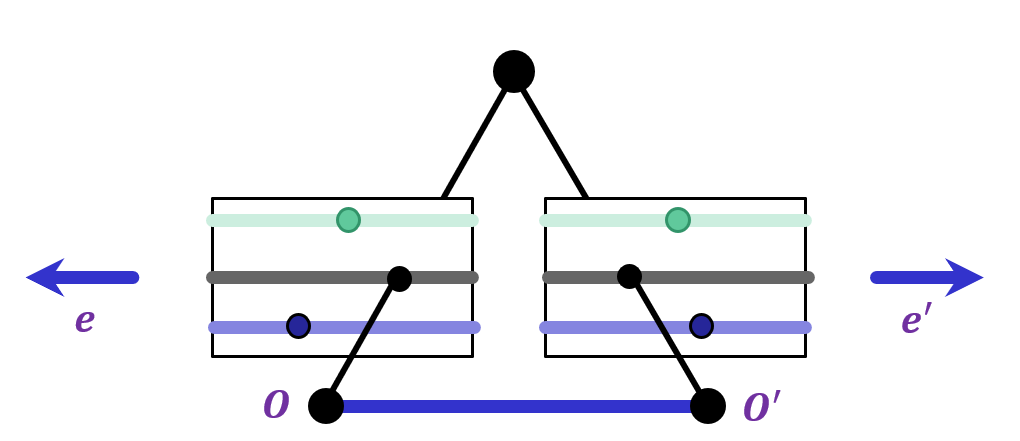
|
||||
|
||||
Epipoles are infinite, epipolar lines parallel.
|
||||
|
||||
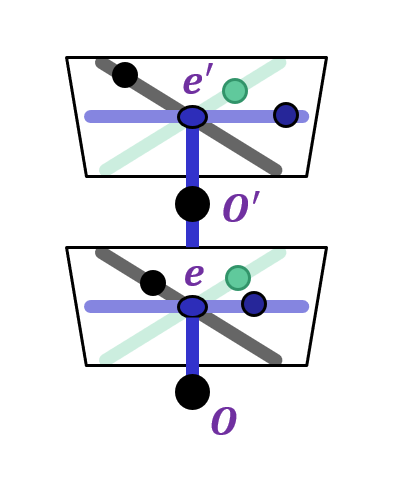
|
||||
|
||||
Epipole is "focus of expansion" and coincides with the principal point of the camera
|
||||
|
||||
Epipolar lines go out from principal point
|
||||
|
||||
Next class:
|
||||
|
||||
### The Essential and Fundamental Matrices
|
||||
|
||||
### Dense Stereo Matching
|
||||
|
||||
|
||||
0
pages/CSE559A/CSE559A_L26.md
Normal file
0
pages/CSE559A/CSE559A_L26.md
Normal file
@@ -26,5 +26,7 @@ export default {
|
||||
CSE559A_L21: "Computer Vision (Lecture 21)",
|
||||
CSE559A_L22: "Computer Vision (Lecture 22)",
|
||||
CSE559A_L23: "Computer Vision (Lecture 23)",
|
||||
CSE559A_L24: "Computer Vision (Lecture 24)"
|
||||
CSE559A_L24: "Computer Vision (Lecture 24)",
|
||||
CSE559A_L25: "Computer Vision (Lecture 25)",
|
||||
CSE559A_L26: "Computer Vision (Lecture 26)",
|
||||
}
|
||||
|
||||
@@ -94,7 +94,7 @@ $$
|
||||
|
||||
QED
|
||||
|
||||
## Application ot valuating definite integrals
|
||||
## Application to evaluating definite integrals
|
||||
|
||||
Idea:
|
||||
|
||||
|
||||
@@ -1 +1,148 @@
|
||||
# Math416 Lecture 26
|
||||
|
||||
## Continue on Application to evaluating definite integrals
|
||||
|
||||
Note: Contour can never go through a singularity.
|
||||
|
||||
Recall the semi annulus contour.
|
||||
|
||||
Know that $\int_\gamma f(z)dz=0$.
|
||||
|
||||
So $\int_A+\int_B+\int_C+\int_D=0$.
|
||||
|
||||
From last lecture, we know that $\int_D=0$ and $\int_A+\int_C=2i\int_0^\infty \frac{\sin x}{x}dx$.
|
||||
|
||||
### Integrating over $B$
|
||||
|
||||
Do $B$, we have $\gamma(t)=\epsilon e^{it}$ for $t\in[0,\pi]$.
|
||||
|
||||
$\int_B=-\int_0^\pi f(\epsilon e^{it})\epsilon i e^{it}dt$.
|
||||
|
||||
$f(z)=\frac{e^{iz}}{z}=\frac{1}{z}(1+iz-\frac{z^2}{2!}+\cdots)$.
|
||||
|
||||
So $z f(z)=1+O(\epsilon)$ and $f(z)=\frac{1}{z}+O(\frac{\epsilon}{z})$.
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\int_B&=-\int_0^\pi (\frac{1}{\epsilon}e^{it}+O(1))\epsilon i e^{it}dt\\
|
||||
&=-i\int_0^\pi 1dt+O(\epsilon)\\
|
||||
&=-i\pi+O(\epsilon)
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
### Integrating over $D$
|
||||
|
||||
#### Method 1: Using estimate
|
||||
|
||||
$z=Re^{it}$ for $t\in[0,\pi]$.
|
||||
|
||||
$f(z)=\frac{e^{iz}}{z}=\frac{e^{iRe^{it}}}{Re^{it}}$.
|
||||
|
||||
$Re^{it}=R(\cos t+i\sin t)$, $iRe^{it}=-R(\sin t-i\cos t)$.
|
||||
|
||||
$e^{iRe^{it}}=e^{-R\sin t}e^{iR\cos t}$.
|
||||
|
||||
$\max|f(z)|=\max\frac{|e^{iR\cos t}|}{|R e^{it}|}=\frac{1}{R}$.
|
||||
|
||||
This only bounds the function $|\int_D|\leq \pi R\frac{1}{R}=\pi$.
|
||||
|
||||
This is not a good estimate.
|
||||
|
||||
#### Method 2: Hard core integration
|
||||
|
||||
$\gamma(t)=Re^{it}$ for $t\in[0,\pi]$.
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\int_D&=\int_0^\pi \frac{e^{iRe^{it}}}{R e^{it}}iR e^{it}dt\\
|
||||
&=i\int_0^\pi e^{iR\cos t}e^{-R\sin t}dt\\
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Notice that we can use $\frac{2}{\pi}t$ to replace $\sin t$.
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\left|\int_D\right|&\leq\int_0^\pi e^{-R\sin t}dt\\
|
||||
&=2\int_0^{\pi/2} e^{-R\sin t}dt\\
|
||||
&\leq 2\int_0^{\pi/2} e^{-2Rt/\pi}dt\\
|
||||
&=-\frac{2\pi}{R}(e^{-\frac{R\pi}{2}t})|_0^{\pi/2}\\
|
||||
&\leq\frac{\pi}{R}
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
As $R\to\infty$, $\left|\int_D\right|\to 0$.
|
||||
|
||||
So $\int_D=0$.
|
||||
|
||||
So we have $\int_A+\int_C=2i\int_0^\infty \frac{\sin x}{x}dx=i\pi$.
|
||||
|
||||
So $\int_0^\infty \frac{\sin x}{x}dx=\frac{\pi}{2}$.
|
||||
|
||||
## Application to evaluate $\int_{-\infty}^\infty \frac{\cos x}{1+x^4}dx$
|
||||
|
||||
$f(z)=\frac{e^{iz}}{1+z^4}=\frac{\cos z+i\sin z}{1+z^4}$.
|
||||
|
||||
Our desired integral can be evaluated by $\int_{-R}^R f(z)dz$
|
||||
|
||||
To evaluate the singularity, $z^4=-1$ has four roots by the De Moivre's theorem.
|
||||
|
||||
$z^4=-1=e^{i\pi+2k\pi i}$ for $k=0,1,2,3$.
|
||||
|
||||
So $z=e^{i\theta}$ for $\theta=\frac{\pi}{4}+\frac{k\pi}{2}$ for $k=0,1,2,3$.
|
||||
|
||||
So the singularities are $z=e^{i\pi/4},e^{i3\pi/4},e^{i5\pi/4},e^{i7\pi/4}$.
|
||||
|
||||
Only $z=e^{i\pi/4},e^{i3\pi/4}$ are in the upper half plane.
|
||||
|
||||
So we can use the semi-circle contour to evaluate the integral. Name the path as $\gamma$.
|
||||
|
||||
$\int_\gamma f(z)dz=2\pi i\left[\operatorname{Res}_{z=e^{i\pi/4}}(f)+\operatorname{Res}_{z=e^{i3\pi/4}}(f)\right]$.
|
||||
|
||||
The two poles are simple poles.
|
||||
|
||||
$\operatorname{Res}_{z_0}(f)=\lim_{z\to z_0}(z-z_0)f(z)$.
|
||||
|
||||
So
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\operatorname{Res}_{z=e^{i\pi/4}}(f)&=\lim_{z\to e^{i\pi/4}}(z-e^{i\pi/4})\frac{e^{iz}}{1+z^4}\\
|
||||
&=\frac{(z-e^{i\pi/4})e^{iz}}{(z-e^{i\pi/4})(z-e^{i3\pi/4})(z-e^{i5\pi/4})(z-e^{i7\pi/4})}\\
|
||||
&=\frac{e^{ie^{i\pi/4}}}{(e^{i\pi/4}-e^{i3\pi/4})(e^{i\pi/4}-e^{i5\pi/4})(e^{i\pi/4}-e^{i7\pi/4})}
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
A short cut goes as follows:
|
||||
|
||||
We know $p(z)=1+z^4$ has four roots $z_1,z_2,z_3,z_4$.
|
||||
|
||||
$$
|
||||
\lim_{z\to z_0}\frac{(z-z_0)}{p(z)}=\frac{1}{p'(z_0)}
|
||||
$$
|
||||
|
||||
So
|
||||
|
||||
$$
|
||||
\operatorname{Res}_{z=e^{i\pi/4}}(f)=\frac{e^{ie^{i\pi/4}}}{4e^{i3\pi/4}}
|
||||
$$
|
||||
|
||||
Similarly,
|
||||
|
||||
$$
|
||||
\operatorname{Res}_{z=e^{i3\pi/4}}(f)=\frac{e^{ie^{i3\pi/4}}}{4e^{i\pi/4}}
|
||||
$$
|
||||
|
||||
So the sum of the residues is
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\operatorname{Res}_{z=e^{i\pi/4}}(f)+\operatorname{Res}_{z=e^{i3\pi/4}}(f)&=\frac{e^{ie^{i\pi/4}}}{4e^{i3\pi/4}}+\frac{e^{ie^{i3\pi/4}}}{4e^{i\pi/4}}\\
|
||||
&=\frac{e^{\frac{i}{\sqrt{2}}} e^{-\frac{1}{\sqrt{2}}}}{4[-\frac{1}{\sqrt{2}}+i\frac{1}{\sqrt{2}}]}+\frac{e^{-\frac{i}{\sqrt{2}}}-e^{-\frac{1}{\sqrt{2}}}}{4[\frac{1}{\sqrt{2}}+i\frac{1}{\sqrt{2}}]}\\
|
||||
&=\frac{\pi\sqrt{2}}{2}e^{-\frac{1}{\sqrt{2}}}(\cos\frac{1}{\sqrt{2}}+\sin\frac{1}{\sqrt{2}})
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
SKIP
|
||||
|
||||
Review on next lecture.
|
||||
|
||||
Reference in New Issue
Block a user