seems working on this small batch
This commit is contained in:
@@ -1,264 +0,0 @@
|
||||
# Math4121 Exam 1 Review
|
||||
|
||||
Range: Chapter 5 and 6 of Rudin. We skipped (and so you will not be tested on)
|
||||
|
||||
- Differentiation of Vector Valued Functions (pp. 111-113)
|
||||
- Integration of Vector-Valued Function and Rectifiable Curves (pp.135-137)
|
||||
|
||||
You will also not be tested on Uniform Convergence and Integration, which we cover in class on Monday 2/10.
|
||||
|
||||
## Chapter 5: Differentiation
|
||||
|
||||
### Definition of the Derivative
|
||||
|
||||
Let $f$ be a real function defined on an closed interval $[a,b]$. We say that $f$ is differentiable at a point $x \in [a,b]$ if the following limit exists:
|
||||
|
||||
$$
|
||||
f'(x) = \lim_{t\to x} \frac{f(t) - f(x)}{t - x}
|
||||
$$
|
||||
|
||||
If the limit exists, we call it the derivative of $f$ at $x$ and denote it by $f'(x)$.
|
||||
|
||||
#### Theorem 5.2
|
||||
|
||||
Every differentiable function is [continuous](https://notenextra.trance-0.com/Math4111/Math4111_L22#definition-45).
|
||||
|
||||
The converse is not true, consider $f(x) = |x|$.
|
||||
|
||||
#### Theorem 5.3
|
||||
|
||||
If $f,g$ are differentiable at $x$, then
|
||||
|
||||
1. $(f+g)'(x) = f'(x) + g'(x)$
|
||||
2. $(fg)'(x) = f'(x)g(x) + f(x)g'(x)$
|
||||
3. If $g(x) \neq 0$, then $(f/g)'(x) = (f'(x)g(x) - f(x)g'(x))/g(x)^2$
|
||||
|
||||
#### Theorem 5.4
|
||||
|
||||
Constant function is differentiable and its derivative is $0$.
|
||||
|
||||
#### Theorem 5.5
|
||||
|
||||
Chain rule: If $f$ is differentiable at $x$ and $g$ is differentiable at $f(x)$, then the composite function $g\circ f$ is differentiable at $x$ and
|
||||
|
||||
$$
|
||||
(g\circ f)'(x) = g'(f(x))f'(x)
|
||||
$$
|
||||
|
||||
#### Theorem 5.8
|
||||
|
||||
The derivative of local extremum ($\exists \delta > 0$ s.t. $f(x)\geq f(y)$ or $f(x)\leq f(y)$ for all $y\in (x-\delta,x+\delta)$) is $0$.
|
||||
|
||||
#### Theorem 5.9
|
||||
|
||||
Generalized mean value theorem: If $f,g$ are differentiable on $(a,b)$, then there exists a point $x\in (a,b)$ such that
|
||||
|
||||
$$
|
||||
(f(b)-f(a))g'(x) = (g(b)-g(a))f'(x)
|
||||
$$
|
||||
|
||||
If we put $g(x) = x$, we get the mean value theorem.
|
||||
|
||||
$$
|
||||
f(b)-f(a) = f'(x)(b-a)
|
||||
$$
|
||||
|
||||
for some $x\in (a,b)$.
|
||||
|
||||
#### Theorem 5.12
|
||||
|
||||
Intermediate value theorem:
|
||||
|
||||
If $f$ is differentiable on $[a,b]$, for all $\lambda$ between $f'(a)$ and $f'(b)$, there exists a $c\in (a,b)$ such that $f'(x) = \lambda$.
|
||||
|
||||
#### Theorem 5.13
|
||||
|
||||
L'Hôpital's rule: If $f,g$ are differentiable in $(a,b)$ and $g'(x) \neq 0$ for all $x\in (a,b)$, where $-\infty \leq a < b \leq \infty$,
|
||||
|
||||
Suppose
|
||||
$$
|
||||
\frac{f'(x)}{g'(x)} \to A \text{ as } x\to a
|
||||
$$
|
||||
|
||||
If
|
||||
$$
|
||||
f(x) \to 0, g(x) \to 0 \text{ as } x\to a
|
||||
$$
|
||||
|
||||
or if
|
||||
|
||||
$$
|
||||
g(x) \to \infty \text{ as } x\to a
|
||||
$$
|
||||
|
||||
then
|
||||
|
||||
$$
|
||||
\lim_{x\to a} \frac{f(x)}{g(x)} = A
|
||||
$$
|
||||
|
||||
#### Theorem 5.15
|
||||
|
||||
Taylor's theorem: If $f$ is $n$ times differentiable on $[a,b]$, $f^{(n-1)}$ is continuous on $[a,b]$, and $f^{(n)}$ exists on $(a,b)$, for any distinct points $\alpha, \beta \in [a,b]$, there exists a point $x\in (\alpha, \beta)$ such that
|
||||
|
||||
$$
|
||||
f(\beta) =\left(\sum_{k=0}^{n-1} \frac{f^{(k)}(\alpha)}{k!}(\beta-\alpha)^k\right) + \frac{f^{(n)}(x)}{n!}(\beta-\alpha)^n
|
||||
$$
|
||||
|
||||
## Chapter 6: Riemann-Stieltjes Integration
|
||||
|
||||
### Definition of the Integral
|
||||
|
||||
Let $\alpha$ be a monotonically increasing function on $[a,b]$.
|
||||
|
||||
A partition of $[a,b]$ is a set of points $P = \{x_0, x_1, \cdots, x_n\}$ such that
|
||||
|
||||
$$
|
||||
a = x_0 < x_1 < \cdots < x_n = b
|
||||
$$
|
||||
|
||||
Let $\Delta \alpha_i = \alpha(x_{i}) - \alpha(x_{i-1})$ for $i = 1, \cdots, n$.
|
||||
|
||||
Let $m_i = \inf \{f(x) : x_{i-1} \leq x \leq x_{i}\}$ and $M_i = \sup \{f(x) : x_{i-1} \leq x \leq x_{i}\}$ for $i = 1, \cdots, n$.
|
||||
|
||||
The lower sum of $f$ with respect to $\alpha$ is
|
||||
|
||||
$$L(f,P,\alpha) = \sum_{i=1}^{n} m_i \Delta \alpha_i$$
|
||||
|
||||
The upper sum of $f$ with respect to $\alpha$ is
|
||||
|
||||
$$U(f,P,\alpha) = \sum_{i=1}^{n} M_i \Delta \alpha_i$$
|
||||
|
||||
Let $\overline{\int_a^b} f(x) d\alpha(x)=\sup_P L(f,P,\alpha)$ and $\underline{\int_a^b} f(x) d\alpha(x)=\inf_P U(f,P,\alpha)$.
|
||||
|
||||
If $\overline{\int_a^b} f(x) d\alpha(x) = \underline{\int_a^b} f(x) d\alpha(x)$, we say that $f$ is Riemann-Stieltjes integrable with respect to $\alpha$ on $[a,b]$ and we write
|
||||
|
||||
$$
|
||||
\int_a^b f(x) d\alpha(x) = \overline{\int_a^b} f(x) d\alpha(x) = \underline{\int_a^b} f(x) d\alpha(x)
|
||||
$$
|
||||
|
||||
#### Theorem 6.4
|
||||
|
||||
Refinement of partition will never make the lower sum smaller or the upper sum larger.
|
||||
|
||||
$$
|
||||
L(f,P,\alpha) \leq L(f,P^*,\alpha) \leq U(f,P^*,\alpha) \leq U(f,P,\alpha)
|
||||
$$
|
||||
|
||||
#### Theorem 6.5
|
||||
|
||||
$\underline{\int_a^b} f(x) d\alpha(x) \leq \overline{\int_a^b} f(x) d\alpha(x)$
|
||||
|
||||
#### Theorem 6.6
|
||||
|
||||
$f\in \mathscr{R}(\alpha)$ on $[a,b]$ if and only if for every $\epsilon > 0$, there exists a partition $P$ of $[a,b]$ such that
|
||||
|
||||
$$
|
||||
U(f,P,\alpha) - L(f,P,\alpha) < \epsilon
|
||||
$$
|
||||
|
||||
#### Theorem 6.8
|
||||
|
||||
Every continuous function on a closed interval is Riemann-Stieltjes integrable with respect to any monotonically increasing function.
|
||||
|
||||
#### Theorem 6.9
|
||||
|
||||
If $f$ is monotonically increasing on $[a,b]$ and **$\alpha$ is continuous on $[a,b]$**, then $f\in \mathscr{R}(\alpha)$ on $[a,b]$.
|
||||
|
||||
Key: We can repartition the interval $[a,b]$ using $f$.
|
||||
|
||||
#### Theorem 6.10
|
||||
|
||||
If $f$ is bounded on $[a,b]$ and has only **finitely many discontinuities** on $[a,b]$, then $f\in \mathscr{R}(\alpha)$ on $[a,b]$.
|
||||
|
||||
Key: We can use the bound and partition around the points of discontinuity to make the error arbitrary small.
|
||||
|
||||
#### Theorem 6.11
|
||||
|
||||
If $f\in \mathscr{R}(\alpha)$ on $[a,b]$, and $m\leq f(x) \leq M$ for all $x\in [a,b]$, and $\phi$ is a continuous function on $[m,M]$, then $\phi\circ f\in \mathscr{R}(\alpha)$ on $[a,b]$.
|
||||
|
||||
_Composition of bounded integrable functions and continuous functions is integrable._
|
||||
|
||||
#### Theorem 6.12
|
||||
|
||||
Properties of the integral:
|
||||
|
||||
Let $f,g\in \mathscr{R}(\alpha)$ on $[a,b]$, and $c$ be a constant. Then
|
||||
|
||||
1. $f+g\in \mathscr{R}(\alpha)$ on $[a,b]$ and $\int_a^b (f(x) + g(x)) d\alpha(x) = \int_a^b f(x) d\alpha(x) + \int_a^b g(x) d\alpha(x)$
|
||||
2. $cf\in \mathscr{R}(\alpha)$ on $[a,b]$ and $\int_a^b cf(x) d\alpha(x) = c\int_a^b f(x) d\alpha(x)$
|
||||
3. $f\in \mathscr{R}(\alpha)$ on $[a,b]$ and $c\in [a,b]$, then $\int_a^b f(x) d\alpha(x) = \int_a^c f(x) d\alpha(x) + \int_c^b f(x) d\alpha(x)$.
|
||||
4. **Favorite Estimate**: If $|f(x)| \leq M$ for all $x\in [a,b]$, then $\left|\int_a^b f(x) d\alpha(x)\right| \leq M(\alpha(b)-\alpha(a))$.
|
||||
5. If $f\in \mathscr{R}(\beta)$ on $[a,b]$, then $\int_a^b f(x) d(\alpha+\beta) = \int_a^b f(x) d\alpha + \int_a^b f(x) d\beta$.
|
||||
|
||||
#### Theorem 6.13
|
||||
|
||||
If $f,g\in \mathscr{R}(\alpha)$ on $[a,b]$, then
|
||||
|
||||
1. $fg\in \mathscr{R}(\alpha)$ on $[a,b]$
|
||||
2. $|f|\in \mathscr{R}(\alpha)$ on $[a,b]$ and $\left|\int_a^b f(x) d\alpha(x)\right| \leq \int_a^b |f(x)| d\alpha(x)$
|
||||
|
||||
Key: (1), use Theorem 6.12, 6.11 to build up $fg$ from $(f+g)^2-f^2-g^2$. (2), take $\phi(x) = |x|$ in Theorem 6.11.
|
||||
|
||||
#### Theorem 6.14
|
||||
|
||||
Integration over indicator functions:
|
||||
|
||||
If $a<s<b$, $f$ is bounded on $[a,b]$, and $f$ is continuous at $s$, and $\alpha(x)=I(x-s)$, then
|
||||
|
||||
$$
|
||||
\int_a^b f(x) d\alpha(x) = f(s)
|
||||
$$
|
||||
|
||||
Key: Note the max difference can be made only occurs at $s$.
|
||||
|
||||
#### Theorem 6.15
|
||||
|
||||
Integration over step functions:
|
||||
|
||||
If $\alpha(x) = \sum_{i=1}^{n} c_i I(x-x_i)$ for $x\in [a,b]$, then
|
||||
|
||||
$$
|
||||
\int_a^b f(x) d\alpha(x) = \sum_{i=1}^{n} c_i f(x_i)
|
||||
$$
|
||||
|
||||
#### Theorem 6.21
|
||||
|
||||
Fundamental theorem of calculus:
|
||||
|
||||
Let $f\in \mathscr{R}(\alpha)$ on $[a,b]$, and $F(x) = \int_a^x f(t) d\alpha(t)$. Then
|
||||
|
||||
1. $F$ is continuous on $[a,b]$
|
||||
2. If $f$ is continuous at $x\in [a,b]$, then $F$ is differentiable at $x$ and $F'(x) = f(x)$
|
||||
|
||||
## Chapter 7: Sequence and Series of Functions
|
||||
|
||||
### Example of non-Riemann integrable function
|
||||
|
||||
$\lim_{m\to \infty} \lim_{n\to \infty} (\cos(m!\pi x))^{2n}=\begin{cases} 1 & x\in \mathbb{Q} \\ 0 & x\notin \mathbb{Q} \end{cases}$
|
||||
|
||||
This function is everywhere discontinuous and not Riemann integrable.
|
||||
|
||||
### Uniform Convergence
|
||||
|
||||
#### Definition 7.7
|
||||
|
||||
A sequence of functions $\{f_n\}$ converges uniformly to $f$ on $E$ if for every $\epsilon > 0$, there exists a positive integer $N$ such that
|
||||
|
||||
$$
|
||||
|f_n(x) - f(x)| < \epsilon \text{ for all } x\in E \text{ and } n\geq N
|
||||
$$
|
||||
|
||||
If $E$ is a point, then that's the common definition of convergence.
|
||||
|
||||
If we have uniform convergence, then we can swap the order of limits.
|
||||
|
||||
#### Theorem 7.16
|
||||
|
||||
If $\{f_n\}\in \mathscr{R}(\alpha)$ on $[a,b]$, and $\{f_n\}$ converges uniformly to $f$ on $[a,b]$, then
|
||||
|
||||
$$
|
||||
\int_a^b f(x) d\alpha(x) = \lim_{n\to \infty} \int_a^b f_n(x) d\alpha(x)
|
||||
$$
|
||||
|
||||
Key: Use the definition of uniform convergence to bound the difference between the integral of the limit and the limit of the integral. $\int_a^b (f-f_n)d\alpha \leq |f-f_n| \int_a^b d\alpha = |f-f_n| (\alpha(b)-\alpha(a))$.
|
||||
@@ -1,279 +0,0 @@
|
||||
# Math4121 Exam 2 Review
|
||||
|
||||
Range: Chapter 2-4 of Bressoud's A Radical Approach to Lebesgue's Theory of Integration
|
||||
|
||||
## Chapter 2
|
||||
|
||||
### The Riemann-Stieltjes Integral
|
||||
|
||||
#### Definition of the Riemann-Stieltjes Integral
|
||||
|
||||
Let $f$ be a bounded function on $[a,b]$ and $\alpha$ be a bounded function on $[a,b]$.
|
||||
|
||||
We say that $f$ is Riemann-Stieltjes integrable with respect to $\alpha$ on $[a,b]$ if there exists a number $I$ such that for every $\epsilon > 0$, there exists a $\delta > 0$ such that for every partition $P = \{a = x_0, x_1, \ldots, x_n = b\}$ of $[a,b]$ with $||P|| < \delta$, we have
|
||||
|
||||
$$
|
||||
\left| \int_a^b f \, d\alpha - I \right| < \epsilon
|
||||
$$
|
||||
|
||||
If $f$ is Riemann-Stieltjes integrable with respect to $\alpha$ on $[a,b]$, we write
|
||||
|
||||
$$
|
||||
\int_a^b f \, d\alpha = I
|
||||
$$
|
||||
|
||||
#### Darboux Sums
|
||||
|
||||
Let $P = \{a = x_0, x_1, \ldots, x_n = b\}$ be a partition of $[a,b]$.
|
||||
|
||||
The upper Darboux sum of $f$ with respect to $\alpha$ is
|
||||
|
||||
$$
|
||||
U(f, \alpha, P) = \sum_{i=1}^n M_i (x_i - x_{i-1})
|
||||
$$
|
||||
|
||||
where $M_i = \sup_{x \in [x_{i-1}, x_i]} f(x)$ and $\alpha_i = \sup_{x \in [x_{i-1}, x_i]} \alpha(x)$.
|
||||
|
||||
The lower Darboux sum of $f$ with respect to $\alpha$ is
|
||||
|
||||
$$
|
||||
L(f, \alpha, P) = \sum_{i=1}^n m_i (x_i - x_{i-1})
|
||||
$$
|
||||
|
||||
where $m_i = \inf_{x \in [x_{i-1}, x_i]} f(x)$ and $\alpha_i = \inf_{x \in [x_{i-1}, x_i]} \alpha(x)$.
|
||||
|
||||
### Fail of Riemann-Stieltjes Integration
|
||||
|
||||
Consider the function
|
||||
|
||||
$$
|
||||
((x)) = \begin{cases}
|
||||
x-\lfloor x \rfloor & x \in [\lfloor x \rfloor, \lfloor x \rfloor + \frac{1}{2}) \\
|
||||
0 & x=\lfloor x \rfloor + \frac{1}{2}\\
|
||||
x-\lfloor x \rfloor - 1 & x \in (\lfloor x \rfloor + \frac{1}{2}, \lfloor x \rfloor + 1] \end{cases}
|
||||
$$
|
||||
|
||||
).png)
|
||||
|
||||
We define
|
||||
|
||||
$$
|
||||
f(x) = \sum_{n=1}^{\infty} \frac{((nx))}{n^2}=\lim_{N\to\infty}\sum_{n=1}^{N} \frac{((nx))}{n^2}
|
||||
$$
|
||||
|
||||
).png)
|
||||
|
||||
(i) The series converges uniformly over $x\in[0,1]$.
|
||||
|
||||
$$
|
||||
\left|f(x)-\sum_{n=1}^{N} \frac{((nx))}{n^2}\right|\leq \sum_{n=N+1}^{\infty}\frac{|((nx))|}{n^2}\leq \sum_{n=N+1}^{\infty} \frac{1}{n^2}<\epsilon
|
||||
$$
|
||||
|
||||
As a consequence, $f(x)\in \mathscr{R}$.
|
||||
|
||||
(ii) $f$ has a discontinuity at every rational number with even denominator.
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\lim_{h\to 0^+}f(\frac{a}{2b}+h)-f(\frac{a}{2b})&=\lim_{h\to 0^+}\sum_{n=1}^{\infty}\frac{((\frac{na}{2b}+h))}{n^2}-\sum_{n=1}^{\infty}\frac{((\frac{na}{2b}))}{n^2}\\
|
||||
&=\lim_{h\to 0^+}\sum_{n=1}^{\infty}\frac{((\frac{na}{2b}+h))-((\frac{na}{2b}))}{n^2}\\
|
||||
&=\sum_{n=1}^{\infty}\lim_{h\to 0^+}\frac{((\frac{na}{2b}+h))-((\frac{na}{2b}))}{n^2}\\
|
||||
&>0
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
|
||||
#### Some integrable functions are not differentiable (violates the fundamental theorem of calculus)
|
||||
|
||||
Solve:
|
||||
|
||||
Define the oscilation of $f$ on $[x_{i-1}, x_i]$ as
|
||||
|
||||
$$
|
||||
\omega(f, [x_{i-1}, x_i]) = \sup_{x,y \in [x_{i-1}, x_i]} |f(x) - f(y)|-\inf_{x,y \in [x_{i-1}, x_i]} |f(x) - f(y)|
|
||||
$$
|
||||
|
||||
And define continuous functions as those functions that have oscilation 0 on every subinterval of their domain.
|
||||
|
||||
that is, the function $f$ is continuous at $c$ if $\omega(f,c) = 0$.
|
||||
|
||||
And we claim that the function is integrable on $[a,b]$ if and only if the outer measure of the set of discontinuities of $f$ is 0.
|
||||
|
||||
> Finite cover:
|
||||
>
|
||||
> Given a set $S$, an **finite cover** of $S$ is a **finite** collection of open/ or closed/ or half-open intervals $\{I_1, I_2, \ldots, I_n\}$ such that $S \subseteq \bigcup_{i=1}^n I_i$. The set of all finite covers of $S$ is denoted by $\mathcal{C}_S$.
|
||||
|
||||
> Length of a cover:
|
||||
>
|
||||
> The **length** of a cover $\ell(C)$ is the sum of the lengths of the intervals in the cover. (open/closed/half-open doesn't matter.)
|
||||
|
||||
> Outer content:
|
||||
>
|
||||
> The **outer content** of a set $S$ is the infimum of the lengths of all **finite covers** of $S$. $c_e(S) = \inf_{C\in \mathcal{C}_S}\ell(C)$. (e denotes "exterior")
|
||||
|
||||
Homework question: You cannot cover an interval $[a,b]$ with length $k$ with a finite cover of length strictly less than $k$.
|
||||
|
||||
Proceed by counting the intervals $I_i = [l_i, r_i]$ in the cover, and $r_n-l_0$ is less than or equal to $c_e(S)$ and $l_0\leq a$ and $r_n\leq b$.
|
||||
|
||||
#### Theorem 2.5
|
||||
|
||||
Given a bounded function $f$ defined on the interval $[a,b]$, let $S_\sigma$ be the points in $[a,b]$ with oscilation greater than $\sigma$.
|
||||
|
||||
The function $f$ is Riemann-Stieltjes integrable over $[a,b]$ if and only if $\lim_{\sigma \to 0} |S_\sigma| = 0$. That is, for every $\sigma > 0$, the outer content of $S_\sigma$ is 0.
|
||||
|
||||
Extra terminology:
|
||||
|
||||
> Dense:
|
||||
>
|
||||
> A set $S$ is **dense** in the interval $I$ is every open subinterval of $I$ contains a point of $S$.
|
||||
>
|
||||
> This is equivalent to saying that $S$ is dense in $I$ if every point of $I$ is a limit point of $S$ or a point of $S$. (proved in homework)
|
||||
|
||||
> Totally discontinuous:
|
||||
>
|
||||
> A discontinuous function is **totally discontinuous** in an interval if the set of points of continuity is not dense in that interval.
|
||||
>
|
||||
> In other words, there exists an open interval $I$ such that the set of points of continuity of $f$ in $I$ is empty.
|
||||
|
||||
> Pointwise discontinuity:
|
||||
>
|
||||
> A discontinuous function is **pointwise discontinuous** if the set of points of discontinuity is dense in the domain of $f$.
|
||||
|
||||
> Accumulation point (limit point):
|
||||
>
|
||||
> A point $p$ is an **accumulation point** of a set $S$ if every neighborhood of $p$ contains a point of $S$ other than $p$ itself. (That is, there exists a convergent sequence $\{p_n\}_{n=1}^\infty$ in $S$ such that $\lim_{n\to\infty} p_n = p$ and $p_n \neq p$ for all $n \in \mathbb{N}$. Proved in Rudin)
|
||||
|
||||
> Derived set:
|
||||
>
|
||||
> The **derived set** of a set $S$ is the set of all accumulation points of $S$. $S' = \{p \in \mathbb{R} \mid \forall \epsilon > 0, \exists x \in S \text{ s.t. } 0 < |x-p| < \epsilon\}$.
|
||||
|
||||
> Type 1 set:
|
||||
>
|
||||
> A set $S$ is a **type 1 set** if $S'\neq \emptyset$ and $S''=\emptyset$.
|
||||
|
||||
> Type $n$ set:
|
||||
>
|
||||
> A set $S$ is a **type $n$ set** if $S'$ is a type $n-1$ set.
|
||||
|
||||
> First species:
|
||||
>
|
||||
> A set $S$ is of **first species** if it is type $n$ for some $n\geq 0$, otherwise it is of **second species**.
|
||||
|
||||
$\mathbb{Q}$ is not first species since it is dense in $\mathbb{R}$ and $\mathbb{Q}' = \mathbb{R}$.
|
||||
|
||||
$\mathbb{R}$ is not first species.
|
||||
|
||||
## Chapter 3
|
||||
|
||||
### Topology of $\mathbb{R}$
|
||||
|
||||
> Open set:
|
||||
>
|
||||
> A set $S$ is **open** if for every $x \in S$, there exists an $\epsilon > 0$ such that $B_\epsilon(x) \subseteq S$.
|
||||
|
||||
> Closed set:
|
||||
>
|
||||
> A set $S$ is **closed** if its complement is open.
|
||||
>
|
||||
> Equivalently, a set $S$ is closed if it contains all of its limit points. That is $S' \subseteq S$.
|
||||
|
||||
> Interior of a set:
|
||||
>
|
||||
> The **interior** of a set $S$ is the set of all points in $S$ such that there exists an $\epsilon > 0$ such that $B_\epsilon(x) \subseteq S$. $S^\circ = \{x \in S \mid \exists \epsilon > 0 \text{ s.t. } B_\epsilon(x) \subseteq S\}$. (It is also the union of all open sets contained in $S$.)
|
||||
|
||||
> Closure of a set:
|
||||
>
|
||||
> The **closure** of a set $S$ is the set of all points that for every $\epsilon > 0$, $B_\epsilon(x) \cap S \neq \emptyset$. $\overline{S} = \{x \in \mathbb{R} \mid \forall \epsilon > 0, B_\epsilon(x) \cap S \neq \emptyset\}$.
|
||||
|
||||
> Boundary of a set:
|
||||
>
|
||||
> The **boundary** of a set $S$ is the set of all points in $S$ that are not in the interior of $S$. $\partial S = \overline{S} \setminus S^\circ$.
|
||||
|
||||
#### Theorem 3.4
|
||||
|
||||
Bolzano-Weierstrass Theorem:
|
||||
|
||||
Every bounded infinite set has an accumulation point.
|
||||
|
||||
Proof:
|
||||
|
||||
Let $S$ be a bounded infinite set. Cut the interval $[a,b]$ into two halves, and let $I_1$ be one with infinitely many points of $S$. (such set exists since $S$ is infinite.)
|
||||
|
||||
Let $I_2$ be the one half with infinitely many points of $I_1$.
|
||||
|
||||
By induction, we can cut the interval into two halves, and let $I_{n+1}$ be the one half with infinitely many points of $I_n$.
|
||||
|
||||
By the nested interval property, there exists a point $c$ that is in all $I_n$.
|
||||
|
||||
$c$ is an accumulation point of $S$.
|
||||
|
||||
QED
|
||||
|
||||
#### Theorem 3.6 (Heine-Borel Theorem)
|
||||
|
||||
For any open cover of a compact set, there exists a finite subcover.
|
||||
|
||||
> Compact set:
|
||||
>
|
||||
> A set $S$ is **compact** if every open cover of $S$ has a finite subcover. In $\mathbb{R}$, this is equivalent to being closed and bounded.
|
||||
|
||||
> Cardinality:
|
||||
>
|
||||
> The **cardinality** of $\mathbb{R}$ is $\mathfrak{c}$.
|
||||
>
|
||||
> The **cardinality** of $\mathbb{N}$, $\mathbb{Z}$, and $\mathbb{Q}$ is $\aleph_0$.
|
||||
|
||||
## Chapter 4
|
||||
|
||||
### Nowhere Dense set
|
||||
|
||||
A set $S$ is **nowhere dense** if there are no open intervals in which $S$ is dense.
|
||||
|
||||
That is equivalent to **$S'$ contains no open intervals**.
|
||||
|
||||
Note: If $S$ is nowhere dense, then $S^c$ is dense. But if $S$ is dense, $S^c$ is not necessarily nowhere dense. (Consider $\mathbb{Q}$)
|
||||
|
||||
### Perfect Set
|
||||
|
||||
A set $S$ is **perfect** if $S'=S$.
|
||||
|
||||
Example: open intervals, Cantor set.
|
||||
|
||||
#### Cantor set
|
||||
|
||||
The Cantor set ($SVC(3)$) is the set of all real numbers in $[0,1]$ that can be represented in base 3 using only the digits 0 and 2.
|
||||
|
||||
The outer content of the Cantor set is 0.
|
||||
|
||||
#### Generalized Cantor set (SVC(n))
|
||||
|
||||
The outer content of $SVC(n)$ is $\frac{n-3}{n-2}$.
|
||||
|
||||
#### Lemma 4.4
|
||||
|
||||
Osgood's Lemma:
|
||||
|
||||
Let $G$ be a closed, bounded set and Let $G_1\subseteq G_2\subseteq \ldots$ and $G=\bigcup_{n=1}^{\infty} G_n$. Then $\lim_{n\to\infty} c_e(G_n)=c_e(G)$.
|
||||
|
||||
Key: Using Heine-Borel Theorem.
|
||||
|
||||
#### Theorem 4.5
|
||||
|
||||
Arzela-Osgood Theorem:
|
||||
|
||||
Let $\{f_n\}_{n=1}^{\infty}$ be a sequence of continuous, uniformly bounded functions on $[0,1]$ that converges pointwise to $0$. It follows that
|
||||
|
||||
$$
|
||||
\lim_{n\to\infty}\int_0^1 f_n(x) \, dx = \int_0^1 \lim_{n\to\infty} f_n(x) \, dx=0
|
||||
$$
|
||||
|
||||
Key: Using Osgood's Lemma and do case analysis on bounded and unbounded parts of the Riemann-Stieltjes integral.
|
||||
|
||||
#### Theorem 4.7
|
||||
|
||||
Baire Category Theorem:
|
||||
|
||||
An open interval cannot be covered by a countable union of nowhere dense sets.
|
||||
|
||||
|
||||
|
||||
@@ -1,370 +0,0 @@
|
||||
# Math4121 Final Review
|
||||
|
||||
## Guidelines
|
||||
|
||||
There is one question from Exam 2 material.
|
||||
|
||||
3 T/F from Exam 1 material.
|
||||
|
||||
The remaining questions cover the material since Exam 2 (Chapters 5 and 6 of Bressoud and my lecture notes for the final week).
|
||||
|
||||
The format of the exam is quite similar to Exam 2, maybe a tad longer (but not twice as long, don't worry).
|
||||
|
||||
## Chapter 5: Measure Theory
|
||||
|
||||
### Jordan Measure
|
||||
|
||||
> Content
|
||||
>
|
||||
> Let $\mathcal{C}_S^e$ be the set of all finite covers of $S$ by closed intervals ($S\subset C$, where $C$ is a finite union of closed intervals).
|
||||
>
|
||||
> Let $\mathcal{C}_S^i$ be the set of disjoint intervals that contained in $S$ ($\bigcup_{i=1}^n I_i\subset S$, where $I_i$ are disjoint intervals).
|
||||
>
|
||||
> Let $c_e(S)=\sup_{C\in\mathcal{C}_S^e} \sum_{i=1}^n |I_i|$ be the outer content of $S$.
|
||||
>
|
||||
> Let $c_i(S)=\inf_{I\in\mathcal{C}_S^i} \sum_{i=1}^n |I_i|$ be the inner content of $S$.
|
||||
>
|
||||
> _Here we use $|I|$ to denote the length of the interval $I$, in book we use volume but that's not important here._
|
||||
>
|
||||
> The content of $S$ is defined if $c(S)=c_e(S)=c_i(S)$
|
||||
|
||||
Note that from this definition, **for any pairwise disjoint collection of sets** $S_1, S_2, \cdots, S_N$, we have
|
||||
|
||||
$$
|
||||
\sum_{i=1}^N c_i(S_i)\leq c_i(\bigcup_{i=1}^N S_i)\leq c_e(\bigcup_{i=1}^N S_i)\leq \sum_{i=1}^N c_e(S_i)
|
||||
$$
|
||||
|
||||
by $\sup$ and $\inf$ in the definition of $c_e(S)$ and $c_i(S)$.
|
||||
|
||||
#### Proposition 5.1
|
||||
|
||||
$$
|
||||
c_e(S)=c_i(S)+c_e(\partial S)
|
||||
$$
|
||||
|
||||
Note the boundary of $S$ is defined as $\partial S=\overline{S}\setminus S^\circ$ (corrected by Nathan Zhou).
|
||||
|
||||
> Some common notations for sets:
|
||||
>
|
||||
> $S^\circ$ is the interior of $S$. $S^\circ=\{x\in S| \exists \epsilon>0, B(x,\epsilon)\subset S\}$ (largest open set contained in $S$)
|
||||
>
|
||||
> $S'$ is the set of limit points of $S$ (derived set of $S$). $S'=\{x\in \mathbb{R}^n|\forall \epsilon>0, B(x,\epsilon)\setminus \{x\}\cap S\neq \emptyset\}$ (Topological definition of limit point).
|
||||
>
|
||||
> $\overline{S}$ is the closure of $S$. $\overline{S}=S\cup S'$ (smallest closed set containing $S$)
|
||||
|
||||
Equivalently, $\forall x\in \partial S$, $\forall \epsilon>0$, $\exists p\notin S$ and $q\notin S$ s.t. $d(x,p)<\epsilon$ and $d(x,q)<\epsilon$.
|
||||
|
||||
So the content of $S$ is defined if and only if $c_e(\partial S)=0$.
|
||||
|
||||
> Jordan Measurable
|
||||
>
|
||||
> A set $S$ is Jordan measurable if and only if $c_e(\partial S)=0$, ($c(S)=c_e(S)=c_i(S)$)
|
||||
|
||||
#### Proposition 5.2
|
||||
|
||||
Finite additivity of content:
|
||||
|
||||
Let $S_1, S_2, \cdots, S_N$ be a finite collection of pairwise disjoint Jordan measurable sets.
|
||||
|
||||
$$
|
||||
c(\bigcup_{i=1}^N S_i)=\sum_{i=1}^N c(S_i)
|
||||
$$
|
||||
|
||||
Example for Jordan measure of sets
|
||||
|
||||
| Set | Inner Content | Outer Content | Content |
|
||||
| --- | --- | --- | --- |
|
||||
| $\emptyset$ | 0 | 0 | 0 |
|
||||
| $\{q\},q\in \mathbb{R}$ | 0 | 0 | 0 |
|
||||
| $\{\frac{1}{n}\}_{n=1}^\infty$ | 0 | 0 | 0 |
|
||||
| $\{[n,n+\frac{1}{2^n}]\}_{n=1}^\infty$ | 1 | 1 | 1 |
|
||||
| $SVC(3)$ | 0 | 1 | Undefined |
|
||||
| $SVC(4)$ | 0 | $\frac{1}{2}$ | Undefined |
|
||||
| $Q\cap [0,1]$ | 0 | 1 | Undefined |
|
||||
| $[0,1]\setminus Q$ | 0 | 1 | Undefined |
|
||||
| $[a,b], a<b\in \mathbb{R}$ | $b-a$ | $b-a$ | $b-a$ |
|
||||
| $[a,b),a<b\in \mathbb{R}$ | $b-a$ | $b-a$ | $b-a$ |
|
||||
| $(a,b],a<b\in \mathbb{R}$ | $b-a$ | $b-a$ | $b-a$ |
|
||||
| $(a,b),a<b\in \mathbb{R}$ | $b-a$ | $b-a$ | $b-a$ |
|
||||
|
||||
### Borel Measure
|
||||
|
||||
Our desired property of measures:
|
||||
|
||||
1. Measure of interval is the length of the interval. $m([a,b])=m((a,b))=m([a,b))=m((a,b])=b-a$
|
||||
|
||||
2. Countable additivity: If $S_1, S_2, \cdots, S_N$ are pairwise disjoint Borel measurable sets, then $m(\bigcup_{i=1}^N S_i)=\sum_{i=1}^N m(S_i)$
|
||||
|
||||
3. Closure under set minus: If $S$ is Borel measurable and $T$ is Borel measurable, then $S\setminus T$ is Borel measurable with $m(S\setminus T)=m(S)-m(T)$
|
||||
|
||||
#### Borel Measurable Sets
|
||||
|
||||
$\mathcal{B}$ is the smallest $\sigma$-algebra that contains all closed intervals.
|
||||
|
||||
> Sigma algebra: A $\sigma$-algebra is a collection of sets that is closed under **countable** union, intersection, and complement.
|
||||
>
|
||||
> That is:
|
||||
>
|
||||
> 1. $\emptyset\in \mathcal{B}$
|
||||
> 2. If $A\in \mathcal{B}$, then $A^c\in \mathcal{B}$
|
||||
> 3. If $A_1, A_2, \cdots, A_N\in \mathcal{B}$, then $\bigcup_{i=1}^N A_i\in \mathcal{B}$
|
||||
|
||||
#### Proposition 5.3
|
||||
|
||||
Borel measurable sets does not contain all Jordan measurable sets.
|
||||
|
||||
Proof by cardinality of sets.
|
||||
|
||||
Example for Borel measure of sets
|
||||
|
||||
| Set | Borel Measure |
|
||||
| --- | --- |
|
||||
| $\emptyset$ | 0 |
|
||||
| $\{q\},q\in \mathbb{R}$ | 0 |
|
||||
| $\{\frac{1}{n}\}_{n=1}^\infty$ | 0 |
|
||||
| $\{[n,n+\frac{1}{2^n}]\}_{n=1}^\infty$ | 1 |
|
||||
| $SVC(3)$ | 0 |
|
||||
| $SVC(4)$ | 0 |
|
||||
| $Q\cap [0,1]$ | 0 |
|
||||
| $[0,1]\setminus Q$ | 1 |
|
||||
| $[a,b], a<b\in \mathbb{R}$ | $b-a$ |
|
||||
| $[a,b),a<b\in \mathbb{R}$ | $b-a$ |
|
||||
| $(a,b],a<b\in \mathbb{R}$ | $b-a$ |
|
||||
| $(a,b),a<b\in \mathbb{R}$ | $b-a$ |
|
||||
|
||||
|
||||
### Lebesgue Measure
|
||||
|
||||
> Lebesgue measure
|
||||
>
|
||||
> Let $\mathcal{C}$ be the set of all countable covers of $S$.
|
||||
>
|
||||
> The Lebesgue outer measure of $S$ is defined as:
|
||||
>
|
||||
> $$m_e(S)=\inf_{C\in\mathcal{C}} \sum_{i=1}^\infty |I_i|$$
|
||||
>
|
||||
> If $S\subset[a,b]$, then the inner measure of $S$ is defined as:
|
||||
>
|
||||
> $$m_i(S)=(b-a)-m_e([a,b]\setminus S)$$
|
||||
>
|
||||
> If $m_i(S)=m_e(S)$, then $S$ is Lebesgue measurable.
|
||||
|
||||
#### Proposition 5.4
|
||||
|
||||
Subadditivity of Lebesgue outer measure:
|
||||
|
||||
For any collection of sets $S_1, S_2, \cdots, S_N$,
|
||||
|
||||
$$m_e(\bigcup_{i=1}^N S_i)\leq \sum_{i=1}^N m_e(S_i)$$
|
||||
|
||||
#### Theorem 5.5
|
||||
|
||||
If $S$ is bounded, then any of the following conditions imply that $S$ is Lebesgue measurable:
|
||||
|
||||
1. $m_e(S)=0$
|
||||
2. $S$ is countable (measure of countable set is 0)
|
||||
3. $S$ is an interval
|
||||
|
||||
> Alternative definition of Lebesgue measure
|
||||
>
|
||||
> The outer measure of $S$ is defined as the infimum of all the open sets that contain $S$.
|
||||
>
|
||||
> The inner measure of $S$ is defined as the supremum of all the closed sets that are contained in $S$.
|
||||
|
||||
#### Theorem 5.6
|
||||
|
||||
Caratheodory's criterion:
|
||||
|
||||
A set $S$ is Lebesgue measurable if and only if for any set $X$ with finite outer measure,
|
||||
|
||||
$$m_e(X-S)=m_e(X)-m_e(X\cap S)$$
|
||||
|
||||
#### Lemma 5.7
|
||||
|
||||
Local additivity of Lebesgue outer measure:
|
||||
|
||||
If $I_1, I_2, \cdots, I_N$ are any countable collection of **pairwise disjoint intervals** and $S$ is a bounded set, then
|
||||
|
||||
$$
|
||||
m_e\left(S\cup \bigcup_{i=1}^N I_i\right)=\sum_{i=1}^N m_e(S\cap I_i)
|
||||
$$
|
||||
|
||||
#### Theorem 5.8
|
||||
|
||||
Countable additivity of Lebesgue outer measure:
|
||||
|
||||
If $S_1, S_2, \cdots, S_N$ are any countable collection of pairwise disjoint Lebesgue measurable sets, **whose union has a finite outer measure,** then
|
||||
|
||||
$$
|
||||
m_e\left(\bigcup_{i=1}^N S_i\right)=\sum_{i=1}^N m_e(S_i)
|
||||
$$
|
||||
|
||||
#### Theorem 5.9
|
||||
|
||||
Any finite union or intersection of Lebesgue measurable sets is Lebesgue measurable.
|
||||
|
||||
#### Theorem 5.10
|
||||
|
||||
Any countable union or intersection of Lebesgue measurable sets is Lebesgue measurable.
|
||||
|
||||
#### Corollary 5.12
|
||||
|
||||
Limit of a monotone sequence of Lebesgue measurable sets is Lebesgue measurable.
|
||||
|
||||
If $S_1\subseteq S_2\subseteq S_3\subseteq \cdots$ are Lebesgue measurable sets, then $\bigcup_{i=1}^\infty S_i$ is Lebesgue measurable. And $m(\bigcup_{i=1}^\infty S_i)=\lim_{i\to\infty} m(S_i)$
|
||||
|
||||
If $S_1\supseteq S_2\supseteq S_3\supseteq \cdots$ are Lebesgue measurable sets, **and $S_1$ has finite measure**, then $\bigcap_{i=1}^\infty S_i$ is Lebesgue measurable. And $m(\bigcap_{i=1}^\infty S_i)=\lim_{i\to\infty} m(S_i)$
|
||||
|
||||
#### Theorem 5.13
|
||||
|
||||
Non-measurable sets (under axiom of choice)
|
||||
|
||||
Note that $(0,1)\subseteq \bigcup_{q\in \mathbb{Q}\cap (-1,1)}(\mathcal{N}+q)\subseteq (-1,2)$
|
||||
|
||||
$$
|
||||
\bigcup_{q\in \mathbb{Q}\cap (-1,1)}(\mathcal{N}+q)
|
||||
$$
|
||||
|
||||
is not Lebesgue measurable.
|
||||
|
||||
## Chapter 6: Lebesgue Integration
|
||||
|
||||
### Lebesgue Integral
|
||||
|
||||
Let the partition on y-axis be $l=l_0<l_1<\cdots<l_n=L$, and $S_i=\{x|l_i<f(x)<l_{i+1}\}$
|
||||
|
||||
The Lebesgue integral of $f$ over $[a,b]$ is bounded by:
|
||||
|
||||
$$
|
||||
\sum_{i=0}^{n-1} l_i m(S_i)\leq \int_a^b f(x) \, dx\leq \sum_{i=0}^{n-1} l_{i+1} m(S_i)
|
||||
$$
|
||||
|
||||
> Definition of measurable function:
|
||||
>
|
||||
> A function $f$ is measurable if for all $c\in \mathbb{R}$, the set $\{x\in [a,b]|f(x)>c\}$ is Lebesgue measurable.
|
||||
>
|
||||
> Equivalently, a function $f$ is measurable if any of the following conditions hold:
|
||||
>
|
||||
> 1. For all $c\in \mathbb{R}$, the set $\{x\in [a,b]|f(x)>c\}$ is Lebesgue measurable.
|
||||
> 2. For all $c\in \mathbb{R}$, the set $\{x\in [a,b]|f(x)\geq c\}$ is Lebesgue measurable.
|
||||
> 3. For all $c\in \mathbb{R}$, the set $\{x\in [a,b]|f(x)<c\}$ is Lebesgue measurable.
|
||||
> 4. For all $c\in \mathbb{R}$, the set $\{x\in [a,b]|f(x)\leq c\}$ is Lebesgue measurable.
|
||||
> 5. For all $c<d\in \mathbb{R}$, the set $\{x\in [a,b]|c\leq f(x)<d\}$ is Lebesgue measurable.
|
||||
>
|
||||
> Prove by using the fact$\{x\in [a,b]|f(x)\geq c\}=\bigcap_{n=1}^\infty \{x\in [a,b]|f(x)>c-\frac{1}{n}\}$
|
||||
|
||||
#### Proposition 6.3
|
||||
|
||||
If $f,g$ is a measurable function, and $k\in \mathbb{R}$, then $f+g,kf,f^2,fg,|f|$ is measurable.
|
||||
|
||||
> Definition of almost everywhere:
|
||||
>
|
||||
> A property holds almost everywhere if it holds everywhere except for a set of Lebesgue measure 0.
|
||||
|
||||
#### Proposition 6.4
|
||||
|
||||
If $f_n$ is a sequence of measurable functions, then $\limsup_{n\to\infty} f_n, \liminf_{n\to\infty} f_n$ is measurable.
|
||||
|
||||
#### Theorem 6.5
|
||||
|
||||
Limit of measurable functions is measurable.
|
||||
|
||||
> Definition of simple function:
|
||||
>
|
||||
> A simple function is a linear combination of indicator functions of Lebesgue measurable sets.
|
||||
|
||||
#### Theorem 6.6
|
||||
|
||||
Measurable function as limit of simple functions.
|
||||
|
||||
$f$ is a measurable function if and only if ffthere exists a sequence of simple functions $f_n$ s.t. $f_n\to f$ almost everywhere.
|
||||
|
||||
### Integration
|
||||
|
||||
#### Proposition 6.10
|
||||
|
||||
Let $\phi,\psi$ be simple functions, $c\in \mathbb{R}$ and $E=E_1\cup E_2$ where $E_1\cap E_2=\emptyset$.
|
||||
|
||||
Then
|
||||
|
||||
1. $\int_E \phi(x) \, dx=\int_{E_1} \phi(x) \, dx+\int_{E_2} \phi(x) \, dx$
|
||||
2. $\int_E (c\phi)(x) \, dx=c\int_E \phi(x) \, dx$
|
||||
3. $\int_E (\phi+\psi)(x) \, dx=\int_E \phi(x) \, dx+\int_E \psi(x) \, dx$
|
||||
4. If $\phi\leq \psi$ for all $x\in E$, then $\int_E \phi(x) \, dx\leq \int_E \psi(x) \, dx$
|
||||
|
||||
> Definition of Lebesgue integral of simple function:
|
||||
>
|
||||
> Let $\phi$ be a simple function, $\phi=\sum_{i=1}^n l_i \chi_{S_i}$
|
||||
>
|
||||
> $$\int_E \phi(x) \, dx=\sum_{i=1}^n l_i m(S_i\cap E)$$
|
||||
|
||||
> Definition of Lebesgue integral of measurable function:
|
||||
>
|
||||
> Let $f$ be a nonnegative measurable function, then
|
||||
>
|
||||
> $$\int_E f(x) \, dx=\sup_{\phi\leq f} \int_E \phi(x) \, dx$$
|
||||
>
|
||||
> If $f$ is not nonnegative, then
|
||||
>
|
||||
> $$\int_E f(x) \, dx=\int_E f^+(x) \, dx-\int_E f^-(x) \, dx$$
|
||||
>
|
||||
> where $f^+(x)=\max(f(x),0)$ and $f^-(x)=\max(-f(x),0)$
|
||||
|
||||
#### Proposition 6.12
|
||||
|
||||
Integral over a set of measure 0 is 0.
|
||||
|
||||
#### Theorem 6.13
|
||||
|
||||
If a nonnegative measurable function $f$ has integral 0 on a set $E$, then $f(x)=0$ almost everywhere on $E$.
|
||||
|
||||
#### Theorem 6.14
|
||||
|
||||
Monotone convergence theorem:
|
||||
|
||||
If $f_n$ is a sequence of monotone increasing measurable functions and $f_n\to f$ almost everywhere, and $\exists A>0$ s.t. $|\int_E f_n(x) \, dx|\leq A$ for all $n$, then $f(x)=\lim_{n\to\infty} f_n(x)$ exists almost everywhere and it's integrable on $E$ with
|
||||
|
||||
$$
|
||||
\int_E f(x) \, dx=\lim_{n\to\infty} \int_E f_n(x) \, dx
|
||||
$$
|
||||
|
||||
#### Theorem 6.19
|
||||
|
||||
Dominated convergence theorem:
|
||||
|
||||
If $f_n$ is a sequence of integrable functions and $f_n\to f$ almost everywhere, and there exists a nonnegative integrable function $g$ s.t. $|f_n(x)|\leq g(x)$ for all $x\in E$ and all $n$, then $f(x)=\lim_{n\to\infty} f_n(x)$ exists almost everywhere and it's integrable on $E$ with
|
||||
|
||||
$$
|
||||
\int_E f(x) \, dx=\lim_{n\to\infty} \int_E f_n(x) \, dx
|
||||
$$
|
||||
|
||||
#### Theorem 6.20
|
||||
|
||||
Fatou's lemma:
|
||||
|
||||
If $f_n$ is a sequence of nonnegative integrable functions, then
|
||||
|
||||
$$
|
||||
\int_E \liminf_{n\to\infty} f_n(x) \, dx\leq \liminf_{n\to\infty} \int_E f_n(x) \, dx
|
||||
$$
|
||||
|
||||
> Definition of Hardy-Littlewood maximal function
|
||||
>
|
||||
> Given integrable $f$m and an interval $I$, look at the averaging operator $A_I f(x)=\frac{\chi_I(x)}{m(I)}\int_I f(y)dy$.
|
||||
>
|
||||
> The maximal function is defined as
|
||||
>
|
||||
> $$f^*(x)=\sup_{I \text{ is an open interval}} A_I f(x)$$
|
||||
|
||||
### Lebesgue's Fundamental theorem of calculus
|
||||
|
||||
If $f$ is Lebesgue integrable on $[a,b]$, then $F(x) = \int_a^x f(t)dt$ is differentiable **almost everywhere** and $F'(x) = f(x)$ **almost everywhere**.
|
||||
|
||||
Outline:
|
||||
|
||||
Let $\lambda,\epsilon > 0$. Find $g$ continuous such that $\int_{\mathbb{R}}|f-g|dm < \frac{\lambda \epsilon}{5}$.
|
||||
|
||||
To control $A_I f(x)-f(x)=(A_I(f-g)(x))+(A_I g(x)-g(x))+(g(x)-f(x))$, we need to estimate the three terms separately.
|
||||
|
||||
Our goal is to show that $\lim_{r\to 0^+}\sup_{I\text{ is open interval}, m(I)<r, x\in I}|A_I f(x)-f(x)|=0$. For $x$ almost every $x\in[a,b]$.
|
||||
|
||||
@@ -1,111 +0,0 @@
|
||||
# Math4121 Lecture 1
|
||||
|
||||
## Chapter 5: Differentiation
|
||||
|
||||
### The derivative of a real function
|
||||
|
||||
#### Definition 5.1
|
||||
|
||||
Let $f$ be a real-valued function on an interval $[a,b]$ ($f: [a,b] \to \mathbb{R}$).
|
||||
|
||||
We say that $f$ is _differentiable_ at a point $x\in [a,b]$ if the limit
|
||||
|
||||
$$
|
||||
\lim_{t\to x} \frac{f(t)-f(x)}{t-x}
|
||||
$$
|
||||
|
||||
exists.
|
||||
|
||||
Then we defined the derivative of $f$, $f'$, a function whose domain is the set of all $x\in [a,b]$ at which $f$ is differentiable, by
|
||||
|
||||
$$
|
||||
f'(x) = \lim_{t\to x} \frac{f(t)-f(x)}{t-x}
|
||||
$$
|
||||
|
||||
#### Theorem 5.2
|
||||
|
||||
Let $f:[a,b]\to \mathbb{R}$. If $f$ is differentiable at $x\in [a,b]$, then $f$ is continuous at $x$.
|
||||
|
||||
Proof:
|
||||
|
||||
> Recall [Definition 4.5](https://notenextra.trance-0.com/Math4111/Math4111_L22#definition-45)
|
||||
>
|
||||
> $f$ is continuous at $x$ if $\forall \epsilon > 0, \exists \delta > 0$ such that if $|t-x| < \delta$, then $|f(t)-f(x)| < \epsilon$.
|
||||
>
|
||||
> Whenever you see a limit, you should think of this definition.
|
||||
|
||||
We need to show that $\lim_{t\to x} f(t) = f(x)$.
|
||||
|
||||
Equivalently, we need to show that
|
||||
|
||||
$$
|
||||
\lim_{t\to x} (f(t)-f(x)) = 0
|
||||
$$
|
||||
|
||||
So for $t\ne x$, since $f$ is differentiable at $x$, we have
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\lim_{t\to x} (f(t)-f(x)) &= \lim_{t\to x} \left(\frac{f(t)-f(x)}{t-x}\right)(t-x) \\
|
||||
&= \lim_{t\to x} \left(\frac{f(t)-f(x)}{t-x}\right) \lim_{t\to x} (t-x) \\
|
||||
&= f'(x) \cdot 0 \\
|
||||
&= 0
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Therefore, differentiable is a stronger condition than continuous.
|
||||
|
||||
> There exists some function that is continuous but not differentiable.
|
||||
>
|
||||
> For example, $f(x) = |x|$ is continuous at $x=0$, but not differentiable at $x=0$.
|
||||
>
|
||||
> We can see that the left-hand limit and the right-hand limit are not the same.
|
||||
>
|
||||
> $$ \lim_{t\to 0^-} \frac{|t|-|0|}{t-0} = -1 \quad \text{and} \quad \lim_{t\to 0^+} \frac{|t|-|0|}{t-0} = 1 $$
|
||||
>
|
||||
> Therefore, the limit does not exist. for $f(x) = |x|$ at $x=0$.
|
||||
|
||||
#### Theorem 5.3
|
||||
|
||||
Suppose $f$ is differentiable at $x\in [a,b]$ and $g$ is differentiable at a point $x\in [a,b]$. Then $f+g$, $fg$ and $f/g$ are differentiable at $x$, and
|
||||
|
||||
(a) $(f+g)'(x) = f'(x) + g'(x)$
|
||||
(b) $(fg)'(x) = f'(x)g(x) + f(x)g'(x)$
|
||||
(c) $\left(\frac{f}{g}\right)'(x) = \frac{f'(x)g(x) - f(x)g'(x)}{g(x)^2}$, provided $g(x)\ne 0$
|
||||
|
||||
Proof:
|
||||
|
||||
Since the limit of product is the product of the limits, we can use the definition of the derivative to prove the theorem.
|
||||
|
||||
(a)
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
(f+g)'(x) &= \lim_{t\to x} \frac{(f+g)(t)-(f+g)(x)}{t-x} \\
|
||||
&= \lim_{t\to x} \frac{f(t)-f(x)}{t-x} + \lim_{t\to x} \frac{g(t)-g(x)}{t-x} \\
|
||||
&= f'(x) + g'(x)
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
(b)
|
||||
|
||||
Since $f$ is differentiable at $x$, we have $\lim_{t\to x} f(t) = f(x)$.
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
(fg)'(x) &= \lim_{t\to x} \left(\frac{f(t)g(t)-f(x)g(x)}{t-x}\right) \\
|
||||
&= \lim_{t\to x} \left(f(t)\frac{g(t)-g(x)}{t-x} + g(x)\frac{f(t)-f(x)}{t-x}\right) \\
|
||||
&= f(t) \lim_{t\to x} \frac{g(t)-g(x)}{t-x} + g(x) \lim_{t\to x} \frac{f(t)-f(x)}{t-x} \\
|
||||
&= f(x)g'(x) + g(x)f'(x)
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
(c)
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\left(\frac{f}{g}\right)'(x) &= \lim_{t\to x}\left(\frac{f(t)g(x)}{g(t)g(x)} - \frac{f(x)g(x)}{g(t)g(x)}\right) \\
|
||||
&= \frac{1}{g(t)g(x)}\left(\lim_{t\to x} (f(t)g(x)-f(x)g(t))\right) \\
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
@@ -1,109 +0,0 @@
|
||||
# Math4121 Lecture 10
|
||||
|
||||
## Recap
|
||||
|
||||
### Properties of Riemann-Stieltjes Integral
|
||||
|
||||
#### Linearity (Theorem 6.12 (a))
|
||||
|
||||
If $f,g\in \mathscr{R}(\alpha)$ on $[a, b]\subset \mathbb{R},c,d\in \mathbb{R}$, then $cf+dg\in \mathscr{R}(\alpha)$ on $[a, b]$ and
|
||||
|
||||
$$
|
||||
\int_a^b (cf+dg)d\alpha = c\int_a^b f d\alpha + d\int_a^b g d\alpha
|
||||
$$
|
||||
|
||||
#### Composition (Theorem 6.11)
|
||||
|
||||
Suppose $f\in \mathscr{R}(\alpha)$ on $[a, b]$, $m\leq f(x)\leq M$ for all $x\in [a, b]$, and $\phi$ is continuous on $[m, M]$, and let $h(x)=\phi(f(x))$ on $[a, b]$. Then $h\in \mathscr{R}(\alpha)$ on $[a, b]$.
|
||||
|
||||
#### Monotonicity (Theorem 6.12 (b))
|
||||
|
||||
If $f,g\in \mathscr{R}(\alpha)$ on $[a, b]$, and $f(x)\leq g(x),\forall x\in [a, b]$, then $\int_a^b f d\alpha \leq \int_a^b g d\alpha$.
|
||||
|
||||
## Continue on Chapter 6
|
||||
|
||||
### Properties of Integrable Functions
|
||||
|
||||
#### Theorem 6.13
|
||||
|
||||
Suppose $f,g\in \mathscr{R}(\alpha)$ on $[a, b]$, and $c\in (a, b)$. Then
|
||||
|
||||
(a) $fg\in \mathscr{R}(\alpha)$ on $[a, b]$.
|
||||
|
||||
Proof:
|
||||
|
||||
By linearity, $f+g,f-g\in \mathscr{R}(\alpha)$ on $[a, b]$.
|
||||
|
||||
Moreover, let $\phi(x)=x^2$, which is continuous on $\mathbb{R}$.
|
||||
|
||||
By **Theorem 6.11**, $f^2,g^2\in \mathscr{R}(\alpha)$ on $[a, b]$.
|
||||
|
||||
By linearity, $fg=1/4((f+g)^2-(f-g)^2)\in \mathscr{R}(\alpha)$ on $[a, b]$.
|
||||
|
||||
QED
|
||||
|
||||
(b) $|f|\in \mathscr{R}(\alpha)$ on $[a, b]$, and $|\int_a^b f d\alpha|\leq \int_a^b |f| d\alpha$.
|
||||
|
||||
Proof:
|
||||
|
||||
Let $\phi(x)=|x|$, which is continuous on $\mathbb{R}$.
|
||||
|
||||
By **Theorem 6.11**, $|f|\in \mathscr{R}(\alpha)$ on $[a, b]$.
|
||||
|
||||
Let $c=-1$ or $c=1$. such that $c\int_a^b f d\alpha=| \int_a^b f d\alpha|$.
|
||||
|
||||
By linearity, $c\int_a^b f d\alpha=\int_a^b cfd\alpha$. Since $cf\leq |f|$, by monotonicity, $|\int_a^b cfd\alpha|=\int_a^b cfd\alpha\leq \int_a^b |f| d\alpha$.
|
||||
|
||||
QED
|
||||
|
||||
### Indicator Function
|
||||
|
||||
#### Definition 6.14
|
||||
|
||||
The unit step function is defined as
|
||||
|
||||
$$
|
||||
I(x)=\begin{cases}
|
||||
0, & x\le 0 \\
|
||||
1, & x>0
|
||||
\end{cases}
|
||||
$$
|
||||
|
||||
#### Theorem 6.15
|
||||
|
||||
Let $a<s<b$. $f$ is bounded on $[a, b]$ and continuous at $s$. Define $\alpha(x)=I(x-s)$ on $[a, b]$. Then $f\in \mathscr{R}(\alpha)$ on $[a, b]$, and $\int_a^b f d\alpha=f(s)$.
|
||||
|
||||
Proof:
|
||||
|
||||
Under the hypothesis, $f$ is bounded on $[a, b]$ and continuous at $s$.
|
||||
|
||||
We can choose partition $P=\{x_0,x_1,x_2,x_3\}$ such that $a=x_0<x_1=s<x_2<x_3=b$.
|
||||
|
||||
Then,
|
||||
$$
|
||||
\begin{aligned}
|
||||
U(P,f,\alpha)&=\sum_{i=1}^3 M_i(\alpha(x_i)-\alpha(x_{i-1}))\\
|
||||
&=M_1(0-0)+M_2(1-0)+M_3(1-1)\\
|
||||
&=\sup_{x\in [s,x_2]}f(x)(\alpha(x_2)-\alpha(s))\\
|
||||
&=\sup_{x\in [s,x_2]}f(x)(1-0)\\
|
||||
&=M_2 \\
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
L(P,f,\alpha)&=\sum_{i=1}^3 m_i(\alpha(x_i)-\alpha(x_{i-1}))\\
|
||||
&=m_1(0-0)+m_2(1-0)+m_3(1-1)\\
|
||||
&=\inf_{x\in [s,x_2]}f(x)(\alpha(x_2)-\alpha(s))\\
|
||||
&=\inf_{x\in [s,x_2]}f(x)(1-0)\\
|
||||
&=m_2 \\
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Since $f$ is continuous at $s$, when $x\to s$, $U(P,f,\alpha)\to f(s)$ and $L(P,f,\alpha)\to f(s)$.
|
||||
|
||||
Therefore, $U(P,f,\alpha)-L(P,f,\alpha)\to 0$, $f\in \mathscr{R}(\alpha)$ on $[a, b]$, and $\int_a^b f d\alpha=f(s)$.
|
||||
|
||||
QED
|
||||
|
||||
|
||||
@@ -1,110 +0,0 @@
|
||||
# Lecture 11
|
||||
|
||||
## Recap
|
||||
|
||||
$$
|
||||
I(x)=\begin{cases}
|
||||
0 & x\leq 0 \\
|
||||
1 & x>0
|
||||
\end{cases}
|
||||
$$
|
||||
|
||||
## Continue on Chapter 6
|
||||
|
||||
### The step function
|
||||
|
||||
#### Theorem 6.16
|
||||
|
||||
If $\sum c_n$ converges and $\{s_n\}$ is a sequence of distinct elements of $(a,b)$, and $f$ is continuous on $[a,b]$, and $\alpha(x)=\sum_{n=1}^{\infty}c_nI(x-s_n)$, then $\int_a^bf \ d\alpha=\sum_{n=1}^{\infty}c_nf(s_n)$.
|
||||
|
||||
Proof:
|
||||
|
||||
For each $x$, $I(x-s_n)\leq 1$ so $\sum_{n=1}^{\infty}c_nI(x-s_n)\leq \sum_{n=1}^{\infty}c_n$ converges (by comparison test).
|
||||
|
||||
Let $\epsilon>0$. We can find $N$ such that $\sum_{n=N+1}^{\infty}c_n<\epsilon$. (Recall that the series $\sum_{n=1}^{\infty}c_n$ converges if and only if $\lim_{N\to\infty}\sum_{n=1}^{N}c_n$ exists.)
|
||||
|
||||
Set $\alpha_1(x)=\sum_{n=1}^{N}c_nI(x-s_n)$, and $\alpha_2(x)=\sum_{n=N+1}^{\infty}c_nI(x-s_n)$.
|
||||
|
||||
Using the linearity of the integral, we have
|
||||
|
||||
$$
|
||||
\int_a^b f\ d\alpha_1= \sum_{n=1}^{N}c_n\int_a^b fd(I(x-s_n))= \sum_{n=1}^{N}c_nf(s_n)
|
||||
$$
|
||||
|
||||
On the other hand, with $M=\sup|f|$,
|
||||
|
||||
$$
|
||||
\left|\int_a^b f\ d\alpha_2\right|\leq \int_a^b |f|\ d\alpha_2\leq M\int_a^b \alpha_2\ dx=M\sum_{n=N+1}^{\infty}c_n(b-s_n)<\epsilon
|
||||
$$
|
||||
|
||||
So,
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\left|\int_a^b f\ d\alpha-\sum_{n=1}^{\infty}c_nf(s_n)\right|&= \left|\int_a^b f\ d\alpha_2-\sum_{n=N+1}^{\infty}c_nf(s_n)\right|\\
|
||||
&\leq |M\epsilon-\sum_{n=N+1}^{\infty}|c_n|M(b-s_n)|\\
|
||||
&<2M\epsilon
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Since $\epsilon$ is arbitrary, we have $\int_a^b f\ d\alpha=\sum_{n=1}^{\infty}c_nf(s_n)$.
|
||||
|
||||
### Integration and differentiation
|
||||
|
||||
#### Theorem 6.20 Fundamental theorem of calculus
|
||||
|
||||
Let $f\in \mathscr{R}$ for $x\in [a,b]$. We define $F(x)=\int_a^x f(t)\ dt$. Then $F$ is continuous and if $f$ is continuous at $x_0\in [a,b]$, then $F$ is differentiable at $x_0$ and $F'(x_0)=f(x_0)$.
|
||||
|
||||
Proof:
|
||||
|
||||
Let $x<y,x,y\in [a,b]$. Then,
|
||||
|
||||
$$
|
||||
|F(y)-F(x)|=\left|\int_a^y f(t)\ dt-\int_a^x f(t)\ dt\right|=\left|\int_x^y f(t)\ dt\right|\leq \sup|f|\cdot (y-x)
|
||||
$$
|
||||
|
||||
So, $F$ is continuous on $[a,b]$.
|
||||
|
||||
Now, let $f$ be continuous at $x_0\in (a,b)$ and $\epsilon>0$. Then we can find $\delta>0$ such that $a<x_0-\delta<s<x_0<t<x_0+\delta<b$ and $|f(u)-f(x_0)|<\epsilon$ for all $u\in (x_0-\delta,x_0+\delta)$.
|
||||
|
||||
So,
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\left|\frac{F(s)-F(x_0)}{s-x_0}-f(x_0)\right|&=\left|\frac{1}{s-x_0}\left(\int_a^s f(u)\ du-\int_a^{x_0} f(u)\ du\right)-f(x_0)\right|\\
|
||||
&=\left|\frac{1}{s-x_0}\left(\int_s^{x_0} f(u)\ du\right)-\frac{1}{s-x_0}\left(\int_s^{x_0} f(x_0)\ dv\right)-f(x_0)\right|\\
|
||||
&=\left|\frac{1}{x_0-s}\left(\int_s^{x_0} [f(u)-f(x_0)]\ du\right)\right|\\
|
||||
&\leq \frac{1}{x_0-s}\epsilon(x_0-s)\\
|
||||
&= \epsilon
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
QED
|
||||
|
||||
If $f\in \mathscr{R}$, and there exists a differentiable function $F:[a,b]\to \mathbb{R}$ such that $F'=f$ on $(a,b)$, then
|
||||
|
||||
$$
|
||||
\int_a^b f(x)\ dx=F(b)-F(a)
|
||||
$$
|
||||
|
||||
Proof:
|
||||
|
||||
Let $\epsilon>0$ and $P=\{x_0,x_1,\cdots,x_n\}$ be a partition of $[a,b]$.
|
||||
|
||||
By the mean value theorem, on each subinterval $[x_{i-1},x_i]$, there exists $t_i\in (x_{i-1},x_i)$ such that
|
||||
|
||||
$$
|
||||
F(x_i)-F(x_{i-1})=F'(t_i)(x_i-x_{i-1})=f(t_i)\Delta x_i
|
||||
$$
|
||||
|
||||
Since $m_i\leq f(t_i)\leq M_i$, notices that $\sum_{i=1}^n f(t_i)\Delta x_i=F(b)-F(a)$.
|
||||
|
||||
So,
|
||||
|
||||
$$
|
||||
L(P,f)\leq F(b)-F(a)\leq U(P,f)
|
||||
$$
|
||||
|
||||
So, $f\in \mathscr{R}$ and $\int_a^b f(x)\ dx=F(b)-F(a)$.
|
||||
|
||||
QED
|
||||
@@ -1,139 +0,0 @@
|
||||
# Math4121 Lecture 12
|
||||
|
||||
## Chapter 7: Uniform Convergence and Integrals
|
||||
|
||||
Our goal is to solve problems like this:
|
||||
|
||||
Let
|
||||
|
||||
$$
|
||||
s_{n,m}=\frac{m}{m+n}
|
||||
$$
|
||||
|
||||
The different order of computation gives different results:
|
||||
|
||||
$$
|
||||
\lim_{n\to\infty}\lim_{m\to\infty}s_{n,m}=1
|
||||
$$
|
||||
|
||||
$$
|
||||
\lim_{m\to\infty}\lim_{n\to\infty}s_{n,m}=0
|
||||
$$
|
||||
|
||||
We cannot always switch the order of limits. We cannot also do this on derivatives.
|
||||
|
||||
### Examples
|
||||
|
||||
#### Example 7.4
|
||||
|
||||
$$
|
||||
f_m(x)=\lim_{n\to\infty}cos(m!x\pi)^{2n}
|
||||
$$
|
||||
|
||||
|
||||
If $cos(m!x\pi)^{2n}=\pm 1$, then $f_m(x)=1$.
|
||||
|
||||
If not, then $|cos(m!x\pi)^{2n}|<1$.
|
||||
|
||||
$$
|
||||
f_m(x)=\begin{cases}
|
||||
1 & \text{if } m!x\text{ is an integer} \\
|
||||
0 & \text{if } \text{otherwise}
|
||||
\end{cases}
|
||||
$$
|
||||
|
||||
This function "raise" the fractions with all denominators less than $m$.
|
||||
|
||||
$$
|
||||
\lim_{m\to\infty}f_m(x)=
|
||||
\begin{cases}
|
||||
1 & \text{if } x\text{ is an rational number} \\
|
||||
0 & \text{if } \text{otherwise}
|
||||
\end{cases}
|
||||
$$
|
||||
|
||||
So this function is not Riemann integrable. (show in homework)
|
||||
|
||||
But
|
||||
|
||||
$$
|
||||
g_{n,m}(x)=cos(m!x\pi)^{2n}
|
||||
$$
|
||||
|
||||
is continuous, and
|
||||
|
||||
$$
|
||||
\lim_{m\to\infty}\lim_{n\to\infty}g_{n,m}(x)=f(x)
|
||||
$$
|
||||
|
||||
So the function is not Riemann integrable.
|
||||
|
||||
#### Definition 7.7
|
||||
|
||||
A sequence of functions $\{f_n\}$ **converges uniformly** to $f$ on set $E$ if
|
||||
|
||||
$$
|
||||
\forall \epsilon>0, \exists N, \forall n\geq N, \forall x\in E, |f_n(x)-f(x)|<\epsilon
|
||||
$$
|
||||
|
||||
If $E$ is just a point, then it is the common definition of convergence.
|
||||
|
||||
_If you have uniform convergence, then you can switch the order of limits._
|
||||
|
||||
### Uniform Convergence and Integrals
|
||||
|
||||
#### Theorem 7.16
|
||||
|
||||
Suppose $\{f_n\}\in\mathscr{R}(\alpha)$ on $[a,b]$ that converges uniformly to $f$ on $[a,b]$. Then $f\in\mathscr{R}(\alpha)$ on $[a,b]$ and
|
||||
|
||||
$$
|
||||
\int_a^b f(x)d\alpha=\lim_{n\to\infty}\int_a^b f_n(x)d\alpha
|
||||
$$
|
||||
|
||||
#### Proof
|
||||
|
||||
Define $\epsilon_n=\sup_{x\in[a,b]}|f_n(x)-f(x)|$.
|
||||
|
||||
By uniform convergence, $\epsilon_n\to 0$ as $n\to\infty$.
|
||||
|
||||
$$
|
||||
f_n(x)-\epsilon_n\leq f(x)\leq f_n(x)+\epsilon_n
|
||||
$$
|
||||
|
||||
$$
|
||||
\int_a^b f_n-\epsilon_nd\alpha\leq\overline{\int_a^b}fd\alpha\leq\int_a^bf_n+\epsilon_nd\alpha
|
||||
$$
|
||||
|
||||
|
||||
$$
|
||||
\int_a^b f_n-\epsilon_n d\alpha\leq\underline{\int_a^b}fd\alpha\leq\int_a^b f_n+\epsilon_n d\alpha
|
||||
$$
|
||||
|
||||
So,
|
||||
|
||||
$$
|
||||
0\leq\overline{\int_a^b}fd\alpha-\underline{\int_a^b}fd\alpha\leq\int_a^b \epsilon_n d\alpha+\int_a^b \epsilon_n d\alpha=2\epsilon_n[\alpha(b)-\alpha(a)]
|
||||
$$
|
||||
|
||||
So $f\in\mathscr{R}(\alpha)$ and
|
||||
|
||||
$$
|
||||
\int_a^b fd\alpha\leq \int_a^b f_n d\alpha+\int_a^b \epsilon_n d\alpha\leq \int_a^b fd\alpha+2\epsilon_n d\alpha
|
||||
$$
|
||||
|
||||
So,
|
||||
|
||||
$$
|
||||
\int_a^b fd\alpha-\int_a^b \epsilon_n d\alpha\leq \int_a^b f_n d\alpha\leq \int_a^b fd\alpha+\int_a^b \epsilon_n d\alpha
|
||||
$$
|
||||
|
||||
Since $\int_a^b \epsilon_n d\alpha\to 0$ as $n\to\infty$, by the squeeze theorem, we have
|
||||
|
||||
by the squeeze theorem, we have
|
||||
|
||||
$$
|
||||
\lim_{n\to\infty}\int_a^b f_nd\alpha=\int_a^b fd\alpha
|
||||
$$
|
||||
|
||||
_Key is that $\int_a^b (f-f_n)d\alpha\leq \sup_{x\in[a,b]}|f-f_n|(\alpha(b)-\alpha(a))$_
|
||||
|
||||
@@ -1,171 +0,0 @@
|
||||
# Math4121 Lecture 13
|
||||
|
||||
## Hidden Chapter 1
|
||||
|
||||
This chapter is not covered in the lecture but I still want to mention it here.
|
||||
|
||||
At first, when the integral was first invented, it was thought to be the area under the curve or above the curve, using intuitive geometric definition from the mysterious common sense of the homo-sapiens. There was not a rigorous definition of the integral from the eighteenth century, when it was first invented, to the nineteenth century, when Riemann, Lebesgue, and others rigorously defined the integral.
|
||||
|
||||
The integral was thought to be the anti-derivative, for the general publics.
|
||||
|
||||
However, we want to apply the integral to more general functions, rather than just the differentiable functions.
|
||||
|
||||
So, we need a rigorous definition of the integral, one potential solution is the Cauchy-Riemann integral.
|
||||
|
||||
### Riemann integral
|
||||
|
||||
Recall from the previous lectures, we have the following definition of the Riemann integral:
|
||||
|
||||
A function $f$ is Riemann integrable on $[a,b]$ if there exists a number $V$ such that for every $\epsilon>0$, there exists a $\delta>0$ such that for every partition $P=\{x_0=a,x_1,\cdots,x_n=b\}$ of $[a,b]$ with mesh less than $\delta$, we have
|
||||
|
||||
$$
|
||||
\left|\sum_{i=1}^{n}f(x_i^*)(x_i-x_{i-1})-V\right|<\epsilon
|
||||
$$
|
||||
|
||||
where $x_i^*$ is a point in the $i$-th subinterval $[x_{i-1},x_i]$.
|
||||
|
||||
This sum only exists if the Darboux's sum defined by the following is small:
|
||||
|
||||
### Darboux's sum
|
||||
|
||||
Let $M_i=\sup_{x\in [x_{i-1},x_i]}f(x)$ and $m_i=\inf_{x\in [x_{i-1},x_i]}f(x)$.
|
||||
|
||||
Then, the Darboux's sum is defined as
|
||||
|
||||
$$
|
||||
\underline{S}(f,P)=\sum_{i=1}^{n}m_i(x_i-x_{i-1})
|
||||
$$
|
||||
|
||||
and
|
||||
|
||||
$$
|
||||
\overline{S}(f,P)=\sum_{i=1}^{n}M_i(x_i-x_{i-1})
|
||||
$$
|
||||
|
||||
In this case, small means that $\forall \epsilon>0$, there exists a $\delta>0$ such that if $x_i-x_{i-1}<\delta$, then
|
||||
|
||||
$$
|
||||
\sum_{i=1}^{n}(M_i-m_i)(x_i-x_{i-1})<\epsilon
|
||||
$$
|
||||
|
||||
$(M_i-m_i)$ is the oscillation of $f$ on the $i$-th subinterval $[x_{i-1},x_i]$.
|
||||
|
||||
#### Theorem 2.1: Riemann's Integrability Criterion (corollary version)
|
||||
|
||||
A function $f$ is Riemann integrable on $[a, b]$ if and only if for every $\sigma>0$ be the bound for the oscillation of $f$, and for any $\epsilon>0$, we can find a subinterval length $\delta$, such that for any partition $P$ of $[a, b]$ with each subinterval has length less than $\delta$, the length of the sum of the lengths of the subintervals where the oscillation exceeds $\sigma$ is less than $\epsilon$.
|
||||
|
||||
That is, mathematically, $\forall \sigma,\epsilon>0$, a function $f$ is Riemann integrable on $[a, b]$ if there exists $\delta>0$ such that $\forall P=\{x_0=a,x_1,\ldots,x_n=b\}$ where $x_i-x_{i-1}<\delta$.
|
||||
|
||||
$$
|
||||
\sum_{x_i\in J}\Delta x_i<\epsilon,\quad \text{where} \quad J=\{x_i|(M_i-m_i)>\sigma\}
|
||||
$$
|
||||
|
||||
#### Theorem 2.2: Darboux Integrability Condition
|
||||
|
||||
Let $f$ be a bounded function on $[a,b]$. This function is Riemann integrable on $[a, b]$ if and only if for every $\epsilon > 0$, there exists a partition $P$ of $[a, b]$ such that the upper sum $\overline{S}(P;f)-\underline{S}(P;f)<\epsilon$
|
||||
|
||||
## New book Chapter 2
|
||||
|
||||
Riemann's motivation: Fourier series
|
||||
|
||||
$$
|
||||
F(x) = \frac{a_0}{2} + \sum_{k=1}^{\infty} a_k \cos(kx) + b_k \sin(kx)
|
||||
$$
|
||||
|
||||
$a_k = \frac{1}{\pi} \int_{-\pi}^{\pi} f(x) \cos(kx) dx$
|
||||
|
||||
$b_k = \frac{1}{\pi} \int_{-\pi}^{\pi} f(x) \sin(kx) dx$
|
||||
|
||||
To study the convergence of the Fourier series, we need to study the convergence of the sequence of partial sums. (Riemann integration)
|
||||
|
||||
Why Riemann integration?
|
||||
|
||||
Let
|
||||
|
||||
$$
|
||||
((x)) = \begin{cases}
|
||||
x-\lfloor x \rfloor & x \in [\lfloor x \rfloor, \lfloor x \rfloor + \frac{1}{2}) \\
|
||||
0 & x=\lfloor x \rfloor + \frac{1}{2}\\
|
||||
x-\lfloor x \rfloor - 1 & x \in (\lfloor x \rfloor + \frac{1}{2}, \lfloor x \rfloor + 1] \end{cases}
|
||||
$$
|
||||
|
||||
).png)
|
||||
|
||||
We define
|
||||
|
||||
$$
|
||||
f(x) = \sum_{n=1}^{\infty} \frac{((nx))}{n^2}=\lim_{N\to\infty}\sum_{n=1}^{N} \frac{((nx))}{n^2}
|
||||
$$
|
||||
|
||||
).png)
|
||||
|
||||
(i) The series converges uniformly over $x\in[0,1]$.
|
||||
|
||||
$$
|
||||
\left|f(x)-\sum_{n=1}^{N} \frac{((nx))}{n^2}\right|\leq \sum_{n=N+1}^{\infty}\frac{|((nx))|}{n^2}\leq \sum_{n=N+1}^{\infty} \frac{1}{n^2}<\epsilon
|
||||
$$
|
||||
|
||||
As a consequence, $f(x)\in \mathscr{R}$.
|
||||
|
||||
(ii) $f$ has a discontinuity at every rational number with even denominator.
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\lim_{h\to 0^+}f(\frac{a}{2b}+h)-f(\frac{a}{2b})&=\lim_{h\to 0^+}\sum_{n=1}^{\infty}\frac{((\frac{na}{2b}+h))}{n^2}-\sum_{n=1}^{\infty}\frac{((\frac{na}{2b}))}{n^2}\\
|
||||
&=\lim_{h\to 0^+}\sum_{n=1}^{\infty}\frac{((\frac{na}{2b}+h))-((\frac{na}{2b}))}{n^2}\\
|
||||
&=\sum_{n=1}^{\infty}\lim_{h\to 0^+}\frac{((\frac{na}{2b}+h))-((\frac{na}{2b}))}{n^2}\\
|
||||
&>0
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
### Back to the fundamental theorem of calculus
|
||||
|
||||
Suppose $f$ is integrable on $[a,b]$, then
|
||||
|
||||
$$
|
||||
F(x)=\int_a^x f(t)dt
|
||||
$$
|
||||
|
||||
$F$ is continuous on $[a,b]$.
|
||||
|
||||
if $f$ is continuous at $x_0$, then $F$ is differentiable at $x_0$ and $F'(x_0)=f(x_0)$.
|
||||
|
||||
#### Theorem (Darboux's theorem)
|
||||
|
||||
If $\lim_{x\to a^-}f(x)=L^-$, then $\lim_{h\to 0} \frac{f(a+h)-f(a)}{h}=L^-$.
|
||||
|
||||
Proof:
|
||||
|
||||
$$
|
||||
h\sup_{x\in [0,h]}f(x)\geq F(a+h)\geq \inf_{x\in [0,h]}f(x)h
|
||||
$$
|
||||
|
||||
Consequently,
|
||||
|
||||
$$
|
||||
f(x)=\sum_{n=1}^{\infty} \frac{((nx))}{n^2}
|
||||
$$
|
||||
|
||||
then
|
||||
|
||||
$$
|
||||
F(x)=\int_0^x f(t)dt
|
||||
$$
|
||||
|
||||
is continuous on $[0,1]$.
|
||||
|
||||
However, since $\lim_{x\to 0^+}f(x)\neq \lim_{x\to 0^-}f(x)$ holds for all the rational numbers with even denominator, $F$ is not differentiable at all the rational numbers with even denominator.
|
||||
|
||||
Moral: There exists a continuous function on $[0,1]$ that is not differentiable at any rational number with even denominator. (Dense set)
|
||||
|
||||
#### Weierstrass function
|
||||
|
||||
$$
|
||||
g(x)=\sum_{n=0}^{\infty} a^n \cos(b^n \pi x)
|
||||
$$
|
||||
|
||||
where $0<a<1$ and $ab>1+\frac{3}{2}\pi$.
|
||||
|
||||
$g(x)$ is continuous on $\mathbb{R}$ but nowhere differentiable.
|
||||
|
||||
_If we change our integral, will be differentiable at most points?_
|
||||
@@ -1,103 +0,0 @@
|
||||
# Math4121 Lecture 14
|
||||
|
||||
## Recap
|
||||
|
||||
### Hankel developed Riemann's integrability criterion
|
||||
|
||||
#### Definition: Oscillation
|
||||
|
||||
Given an interval $I\subset[a,b]$, $f:[a,b]\to\mathbb{R}$ the oscillation of $f$ at $I$ is
|
||||
|
||||
$$
|
||||
\omega(f,I) = \sup_I f - \inf_I f
|
||||
$$
|
||||
|
||||
#### Theorem 2.5: Riemann's Integrability Criterion
|
||||
|
||||
A bounded function $f$ is Riemann integrable if and only if for every $\sigma,\epsilon>0$ there exists a partition $P$ of $[a,b]$ such that
|
||||
|
||||
$$
|
||||
\sum_{i\in \mathcal{P}}\Delta x_i<\epsilon
|
||||
$$
|
||||
|
||||
where $\mathcal{P}=\{i:\omega(f,I_i)>\sigma\}$.
|
||||
|
||||
Proof:
|
||||
|
||||
To prove Riemann's Integrability Criterion, we need to show that a bounded function $f$ is Riemann integrable if and only if for every $\sigma, \epsilon > 0$, there exists a partition $P$ of $[a, b]$ such that the sum of the lengths of the intervals where the oscillation exceeds $\sigma$ is less than $\epsilon$.
|
||||
|
||||
QED
|
||||
|
||||
#### Proposition 2.4
|
||||
|
||||
For point $c\in[a,b]$, define the oscillation at $c$ as
|
||||
|
||||
$$
|
||||
\omega(f,c) = \inf_{c\in I}\omega(f,I)
|
||||
$$
|
||||
|
||||
Homework question 6: $f$ is continuous at $c$ if and only if $\omega(f,c)=0$.
|
||||
|
||||
So we can restate the previous theorem as:
|
||||
|
||||
Given $\sigma>0$, define $S_\sigma=\{c\in[a,b]:\omega(f,c)>\sigma\}$.
|
||||
|
||||
Restate the theorem as:
|
||||
|
||||
$f\in\mathscr{R}[a,b]$ if and only if for every $\sigma,\epsilon>0$ there exists intervals $I_1,I_2,\cdots,I_n$ such that $S_\sigma\subset\bigcup_{i=1}^{n}I_i$ and $\sum_{i=1}^{n}\ell(I_i)<\epsilon$. where $\ell(I)$ is the length of the interval $I$.
|
||||
|
||||
#### Definition: Outer content
|
||||
|
||||
Given a set $S$, a **finite cover** of $S$ is a collection of intervals $C=\{I_1,I_2,\cdots,I_n\}$ such that $S\subseteq\bigcup_{i=1}^{n}I_i$.
|
||||
|
||||
The length of the cover $C$ is $\ell(C)=\sum_{i=1}^{n}\ell(I_i)$.
|
||||
|
||||
The **outer content** of $S$ is
|
||||
|
||||
$$
|
||||
c_e(S) = \inf_{c\in C_s}\ell(C)
|
||||
$$
|
||||
|
||||
where $C_s$ is the set of all finite covers of $S$.
|
||||
|
||||
Example:
|
||||
|
||||
$S=\{x_1,\ldots,x_n\}$, then $c_e(S)=0$.
|
||||
|
||||
- Let $I_i=(x_i-\frac{\epsilon}{2n},x_i+\frac{\epsilon}{2n})$, so $\sum_{i=1}^{n}\ell(I_i)=\epsilon$
|
||||
|
||||
$S=\{\frac{1}{n}\}_{n=1}^{\infty}$, then $c_e(S)=0$.
|
||||
|
||||
- In this case, we can only use finite cover, however, there is only one "accumulation point", so we can cover it with a single interval, and the remaining points can be covered by finite intervals. (for any $\epsilon>0$, we can construct a **finite cover** with length $\epsilon$ that covers all points.)
|
||||
|
||||
$S=\mathbb{Q}\cap[0,1]$, then $c_e(S)=1$.
|
||||
|
||||
- In this case, by covering the interval with $[0,1]$, we can get the length of the cover is at most 1.
|
||||
- Suppose there exists a cover $C$ with $\sum_{I\in C}\ell(I)<1$, then there must be a gap in the intervals, however, since the $\mathbb{Q}$ is dense in $\mathbb{R}$, there must be a point in the gap, which is a contradiction.
|
||||
|
||||
#### Theorem 2.5: Hankel's criterion for Riemann integrability
|
||||
|
||||
A function $f\in\mathscr{R}[a,b]$ if and only if $c_e(S_\sigma)=0$ for all $\sigma>0$.
|
||||
|
||||
_The idea is that if the oscillation of a function can be bounded by a finite set that the total length is small, then the function is Riemann integrable._
|
||||
|
||||
Hankel's idea was to apply this theorem to determining how discontinuous a function could be a Riemann integrable function.
|
||||
|
||||
> A set $S$ is dense in $X$ if every point of $X$ is a limit point of $S$.
|
||||
|
||||
#### Definition: Totally discontinuous
|
||||
|
||||
$f$ is **totally discontinuous** if the points of continuity of $f$ are not dense.
|
||||
|
||||
For example, $f(x)=\begin{cases}
|
||||
0 & x\in\mathbb{Q}\\
|
||||
1 & x\notin\mathbb{Q}
|
||||
\end{cases}$ is totally discontinuous.
|
||||
|
||||
#### Definition: Pointwise discontinuity
|
||||
|
||||
$f$ is **pointwise discontinuous** if they are dense in $[a,b]$.
|
||||
|
||||
Hankel's conjecture: $f$ is pointwise discontinuous, then $f$ is integrable.
|
||||
|
||||
|
||||
@@ -1,83 +0,0 @@
|
||||
# Math4121 Lecture 15
|
||||
|
||||
## Continue on patches for Riemann integral
|
||||
|
||||
### Hankel's conjecture
|
||||
|
||||
If $f$ is pointwise discontinuous (set of points of continuity is dense), then $f\in\mathcal{R}$.
|
||||
|
||||
Why the conjecture is believable:
|
||||
|
||||
- $\{w(f)\leq \sigma\}=\bigcup_{a\in D} I_a$, so then $S_{\sigma}$ contains no intervals, so the outer content _maybe_ zero.
|
||||
|
||||
However, it turns out that the complement of the set of points of continuity can be large.
|
||||
|
||||
#### Definition: Accumulation point
|
||||
|
||||
Given a set $S$, $x$ is an accumulation point of $S$ if every open interval containing $x$ also contains infinitely many points of $S$.
|
||||
|
||||
The derived set of $S$, denoted $S'$, is the set of all accumulation points of $S$.
|
||||
|
||||
#### Lemma
|
||||
|
||||
$$
|
||||
c_e(S)\leq c_e(S')
|
||||
$$
|
||||
|
||||
Proof:
|
||||
|
||||
Given $\epsilon > 0$, we can find open intervals $I_1, I_2, \ldots$ such that $S'\subseteq \bigcup_{i=1}^{n} I_i$ and
|
||||
|
||||
$$
|
||||
\sum_{i=1}^{n} \ell(I_i) \leq c_e(S') + \frac{\epsilon}{2}
|
||||
$$
|
||||
|
||||
So $S\setminus \bigcup_{i=1}^{n} I_i$ contains only finitely many points, say $N$, so we can cover $S\setminus \bigcup_{i=1}^{n} I_i$ by $N$ intervals of length $\frac{\epsilon}{2N}$. We call these intervals $J_1, J_2, \ldots, J_N$. Then $S$ is covered by the intervals $C=\bigcup_{i=1}^{n} I_i \cup \bigcup_{i=1}^{N} J_i$. and $\ell(C)\leq c_e(S') + \frac{\epsilon}{2} + \frac{N\epsilon}{2N}=c_e(S')+\epsilon$.
|
||||
|
||||
So $c_e(S)\leq \ell(C)\leq c_e(S')+\epsilon$.
|
||||
|
||||
QED
|
||||
|
||||
#### Corollary: sef of first species
|
||||
|
||||
There exists $n\in \mathbb{N}$ such that $S^{(n)'}=\phi$.
|
||||
|
||||
If $S$ is of the first species, then $c_e(S)=0$. This leads to further credence to Hankel's conjecture, but it begs the question is the complement of $\bigcup_{a\in D} I_a$ indeed of first species?
|
||||
|
||||
#### Theorem (Baire Category Theorem)
|
||||
|
||||
Every open set in $\mathbb{R}$ is a countable union of disjoint open intervals.
|
||||
|
||||
Proof:
|
||||
|
||||
Let $U$ be open and for each $t\in U$, set $a=\inf \{x:(x,t]\subseteq U\}$ and $b=\sup \{x:[t,x)\subseteq U\}$.
|
||||
|
||||
We define $I(t)=(a,b)$, $U\subseteq \bigcup_{t\in U} I(t)$.
|
||||
|
||||
Notice that if $I(t)\cap I(s)\neq \emptyset$, then there exists rational $r\in U$ such that $I(t)\cap I(s)\subseteq (r,r)$.
|
||||
|
||||
> Take a dense, contable set in $[0,1]$, say $D=\{a_n\}_{n=1}^{\infty}$. Let $\epsilon>0$ and define $I_n=(a_n-\frac{\epsilon}{2^{n+1}}, a_n+\frac{\epsilon}{2^{n+1}})$. Can the entire interval $[0,1]$ be placed inside a union of intervals whose lengths add up to $\epsilon$?
|
||||
|
||||
$$
|
||||
\sum_{n=1}^{\infty} \ell(I_n) = \sum_{n=1}^{\infty} \frac{2\epsilon}{2^{n+1}} = \epsilon
|
||||
$$
|
||||
|
||||
_Harnack believed that the complement of a countable union of intervals is another countable union of intervals._
|
||||
|
||||
Borel found the flaw in Harnack's argument. In fact, $[0,1]\setminus \bigcup_{n=1}^{\infty} I_n$ is uncountable.
|
||||
|
||||
#### Theorem (Heine-Borel)
|
||||
|
||||
If $\{U_\alpha\}_{\alpha\in A}$ is a collection of open sets (countable or uncountable) such that
|
||||
|
||||
$$
|
||||
[a,b]\subseteq \bigcup_{\alpha\in A} U_\alpha
|
||||
$$
|
||||
|
||||
then there exists a finite or countable subcollection $\{U_{\alpha_n}\}_{n=1}^{\infty}$ such that
|
||||
|
||||
$$
|
||||
[a,b]\subseteq \bigcup_{n=1}^{\infty} U_{\alpha_n}
|
||||
$$
|
||||
|
||||
Continue on next lecture.
|
||||
@@ -1,94 +0,0 @@
|
||||
# Math4121 Lecture 16
|
||||
|
||||
## Continue on Patches for Riemann Integrals
|
||||
|
||||
### Harnack's Mistake
|
||||
|
||||
#### Theorem 3.6 Heine-Borel Theorem
|
||||
|
||||
If $\{U_\alpha\}_{\alpha \in A}$ is a collection of open sets which cover $[a, b]$, then there exists a finite subcover, i.e. $\{U_{\alpha_1}, U_{\alpha_2}, \cdots, U_{\alpha_n}\}$ such that $[a, b] \subseteq \bigcup_{i=1}^n U_{\alpha_i}$.
|
||||
|
||||
Using the fact that $[a, b]$ is compact.
|
||||
|
||||
Proof:
|
||||
|
||||
Define $S = \{x \in [a, b] : \exists U_\alpha \text{ s.t. } [a, x] \subseteq \bigcup_{i=1}^n U_{\alpha_i}\}$.
|
||||
|
||||
If we can show that $b\in S$, then we are done.
|
||||
|
||||
Clearly $S\neq \emptyset$ since $a\in S$.
|
||||
|
||||
Let $\beta=\sup S\geq a$. If we can show that $\beta \geq b$, then we are done. (taking $x=b$ to take finite subcover)
|
||||
|
||||
Suppose toward contradiction that $\beta < b$.
|
||||
|
||||
Then $\exists U_\alpha$ and $(c,d)\subseteq U_\alpha$ such that $a<c<\beta<d<b$.
|
||||
|
||||
Since $c<\beta$, $\exists U_{\alpha_1},\ldots,U_{\alpha_n}$ s.t. $[a,x]\subseteq \bigcup_{i=1}^n U_{\alpha_i}$.
|
||||
|
||||
So $[a,d]\subseteq U_\alpha\cup \bigcup_{i=1}^n U_{\alpha_i}$.
|
||||
|
||||
So $d\in S$, this contradicts the definition of $\beta$ as the supremum of $S$.
|
||||
|
||||
So $\beta \geq b$.
|
||||
|
||||
QED
|
||||
|
||||
### Reviewing sections for Math 4111
|
||||
|
||||
#### Definition: Cardinality
|
||||
|
||||
Two sets $A$ and $B$ have the same cardinality if there exists a bijection $f:A\to B$.
|
||||
|
||||
_We can imaging the cardinality as the number of elements in the set. However, this is not rigorous, for example, the set of rational and irrational numbers are both infinite, but the set of rational numbers are countable while the set of irrational numbers are uncountable._
|
||||
|
||||
- the cardinality of a finite set is the number of elements in the set.
|
||||
- the cardinality of $\mathbb{N}$ is $\aleph_0$, such a set is called "countable".
|
||||
|
||||
#### Definition: Countable
|
||||
|
||||
A set is countable if there exists an injection $f:\mathbb{N}\to A$.
|
||||
|
||||
Example:
|
||||
|
||||
1. The set of integers $\mathbb{Z}$ is countable.
|
||||
|
||||
We can construct a bijection $f:\mathbb{N}\to \mathbb{Z}$ by mapping $f(n)=\begin{cases}
|
||||
\frac{n}{2} & \text{if } n \text{ is even} \\
|
||||
-\frac{n+1}{2} & \text{if } n \text{ is odd}
|
||||
\end{cases}$
|
||||
|
||||
2. The set of rational numbers $\mathbb{Q}$ is countable.
|
||||
|
||||
We can construct a bijection $f:\mathbb{N}\to \mathbb{Q}$ using the
|
||||
|
||||
|
||||
3. The algebraic numbers $\mathbb{A}$ (roots of polynomials with integer coefficients) are countable.
|
||||
|
||||
Proof using [the union of countable sets is countable](https://notenextra.trance-0.com/Math4111/Math4111_L6#theorem-212).
|
||||
|
||||
#### Definition: Uncountable
|
||||
|
||||
A set is uncountable if it is not countable.
|
||||
|
||||
#### Theorem: $\mathbb{R}$ is uncountable
|
||||
|
||||
Easy proof using [Cantor's diagonal argument](https://notenextra.trance-0.com/Math4111/Math4111_L6#theorem-214).
|
||||
|
||||
A new one
|
||||
|
||||
Proof:
|
||||
|
||||
Suppose $\mathbb{R}=\{r_1,r_2,\ldots\}$. Let $a_0<b_0$ be the first two entries $a_0,b_0\in \{r_1,r_2,\ldots\}$ in our list which lie in $(0,1)$.
|
||||
|
||||
Let $a_1<b_1$ be the first two entries such that $a_1,b_1\in (a_0,b_0)$.
|
||||
|
||||
Continue this process, we can construct $[0,1]\supsetneq [a_0,b_0]\supsetneq [a_1,b_1]\supsetneq \cdots$ sets.
|
||||
|
||||
> By the nested interval theorem of real numbers, $\bigcap_{n=1}^\infty [a_n,b_n]\neq \emptyset$.
|
||||
|
||||
Setting $r=\sup a_n$ (by the least upper bound property of real numbers), $r\in [a_n,b_n]$ for all $n\in\mathbb{N}$. Since $r\in \mathbb{R}$, $r=r_m$ for some $m\in\mathbb{N}$. Then find $a_n,b_n$ which come after $r_m$ in the list.
|
||||
|
||||
This contradicts the assumption that $a_n,b_n$ as the first element in the list.
|
||||
|
||||
QED
|
||||
@@ -1,69 +0,0 @@
|
||||
# Math4121 Lecture 17
|
||||
|
||||
## Continue on Last lecture
|
||||
|
||||
### Countability
|
||||
|
||||
#### Theorem: $\mathbb{R}$ is uncountable
|
||||
|
||||
We denote the cardinality of $\mathbb{N}$ be $\aleph_0$
|
||||
|
||||
We denote the cardinality of $\mathbb{R}$ be $\mathfrak{c}$
|
||||
|
||||
> Continuum Hypothesis:
|
||||
>
|
||||
> If there a cardinality between $\aleph_0$ and $\mathfrak{c}$
|
||||
|
||||
### Power set
|
||||
|
||||
#### Definition: Power set
|
||||
|
||||
Given a set $S$, the power set of $S$, denoted $\mathscr{P}(S)$ or $2^S$, is the collection of all subsets of $S$.
|
||||
|
||||
#### Theorem 3.10 (Cantor's Theorem)
|
||||
|
||||
Cardinality of $2^S$ is not equal to the cardinality of $S$.
|
||||
|
||||
<details>
|
||||
<summary>Proof of Cantor's Theorem</summary>
|
||||
|
||||
Assume they have the same cardinality, then $\exists \psi: S \to 2^X$ which is one-to-one and onto. (this function returns a subset of $S$)
|
||||
|
||||
$$
|
||||
T=\{a\in S:a\notin \psi (a)\}\subseteq S
|
||||
$$
|
||||
|
||||
Thus, $\exists b\in S$ such that $\psi(b)=T$.
|
||||
|
||||
If $b\in T$, then by definition of $T$, $b \notin \psi(b)$, but $\psi(b) = T$, which is a contradiction. So $b\notin T$.
|
||||
|
||||
If $b \notin T$, then $b \in \psi(b)$, which is also a contradiction since $b\in T$. Therefore, $2^S$ cannot have the same cardinality as $S$.
|
||||
|
||||
</details>
|
||||
|
||||
### Back to Hankel's Conjecture
|
||||
|
||||
$$
|
||||
T=\bigcup_{n=1}^\infty \left(a_n-\frac{\epsilon}{2^{n+1}},a_n+\frac{\epsilon}{2^{n+1}}\right)
|
||||
$$
|
||||
|
||||
is small
|
||||
|
||||
What is the structure of $S=[0,1]\setminus T$? (or Sparse)
|
||||
|
||||
- Cardinality (countable)
|
||||
- Topologically (not dense)
|
||||
- Measure, for now meaning small or zero outer content.
|
||||
|
||||
## Chapter 4: Nowhere Dense Sets and the Problem with the Fundamental Theorem of Calculus
|
||||
|
||||
### Nowhere Dense Sets
|
||||
|
||||
#### Definition: Nowhere Dense Set
|
||||
|
||||
A set $S$ is **nowhere dense** if there are no open intervals in which $S$ is dense.
|
||||
|
||||
#### Corollary: A set is nowhere dense if and only if $S$ contains no open intervals
|
||||
|
||||
$S'$ contains no open intervals
|
||||
|
||||
@@ -1,77 +0,0 @@
|
||||
# Math4121 Lecture 18
|
||||
|
||||
## Continue
|
||||
|
||||
### Small sets
|
||||
|
||||
A set that is nowhere dense, has zero outer content yet is uncountable.
|
||||
|
||||
By modifying this example, we can find similar with any outer content between 0 and 1.
|
||||
|
||||
#### Definition: Perfect Set
|
||||
|
||||
$S\subseteq[0,1]$ is perfect if $S=S'$.
|
||||
|
||||
<details>
|
||||
<summary>Examples of perfect set</summary>
|
||||
|
||||
- $[0,1]$ is perfect
|
||||
- perfect sets are closed
|
||||
- Finite collection of points is not perfect because they do not have limit points.
|
||||
- perfect sets are uncountable (no countable sets can be perfect)
|
||||
|
||||
</details>
|
||||
|
||||
#### Middle third Cantor set
|
||||
|
||||
We construct the set by removing the middle third of the interval.
|
||||
|
||||
Let $C_0=[0,1]$, $C_1=[0,\frac{1}{3}]\cup[\frac{2}{3}]$ ...
|
||||
|
||||
Continuing this process indefinitely, we define the Cantor set as
|
||||
|
||||
$$
|
||||
C=\bigcap_{n=0}^{\infty}C_n
|
||||
$$
|
||||
|
||||
1. $C_n\subseteq C_{n-1}$
|
||||
2. $\ell(C_n)=\ell(C_{n-1})$
|
||||
3. Each $C_n$ is closed.
|
||||
|
||||
> The algebraic expression for $C_n$, where $a\in[0,1]$, we write as a decimal expansion in base $3$.
|
||||
>
|
||||
> $$ a=\sum_{n=1}^{\infty} \frac{a_n}{3^n}$$, where $a_n\in\{0,1,2\}$.
|
||||
>
|
||||
> In this case, $C_0\to C_1$ means deleting all numbers with $a_1=1$. (the same as deleting the interval $[\frac{1}{3},\frac{2}{3}]$)
|
||||
>
|
||||
> $C_1\to C_2$ means deleting all the numbers with $a_2=1$.$
|
||||
>
|
||||
> So we can write the set as $$C=\left\{\sum_{n=1}^{\infty}\frac{a_n}{3^n},a_n\in\{0,2\}\right\}$$
|
||||
|
||||
#### Proposition 4.1
|
||||
|
||||
$C$ is perfect and nowhere dense, and outer content is 0.
|
||||
|
||||
<details>
|
||||
<summary>Proof</summary>
|
||||
|
||||
(i) $c_e(C)=0$
|
||||
|
||||
Let $\epsilon>0$, then $\exists n$ such that $\left(\frac{2}{3}\right)<\epsilon$. Then $C_n$ is a cover of $C$, and $\ell(C_n)<\epsilon$.
|
||||
|
||||
(ii) $C$ is perfect
|
||||
|
||||
Since $C_n$ is closed, $C$ is closed (any intersection of closed set is closed) so $C'\subseteq C$.
|
||||
|
||||
Let $a\in C$, and we need to show $a$ is a limit point. Let $\epsilon>0$, and we need to find $a^*\in C\setminus\{a\}$ and $|a^* - a| < \epsilon$. Suppose $a=\sum_{n=1}^{\infty} \frac{a_n}{3^n}, a_n \in \{0, 2\}$, Notive that if $a^*\in C$ has the expansion as $a$ except the k-th term.
|
||||
|
||||
So $|a^*-a|=\frac{2}{3^k}$, which can be made arbitrarily small by choosing a sufficiently large $k$. Thus, $a$ is a limit point of $C$, proving that $C$ is perfect.
|
||||
|
||||
(iii) $C$ is nowhere dense
|
||||
|
||||
It is sufficient to show $C$ contains no intervals.
|
||||
|
||||
Any open intervals has a real number with 1 in it's base 3 decimal expansion (proof in homework)
|
||||
|
||||
_take some interval in $(a,b)$ we can change the digits that is small enough and keep the element still in the set_
|
||||
</details>
|
||||
@@ -1,57 +0,0 @@
|
||||
# Math4121 Lecture 19
|
||||
|
||||
## Continue on the "small set"
|
||||
|
||||
### Cantor set
|
||||
|
||||
#### Theorem: Cantor set is perfect, nowhere dense
|
||||
|
||||
Proved last lecture.
|
||||
|
||||
_Other construction of the set by removing the middle non-zero interval $(\frac{1}{n},n>0)$ and take the intersection of all such steps is called $SVC(n)$_
|
||||
|
||||
Back to $\frac{1}{3}$ Cantor set.
|
||||
|
||||
Every step we delete $\frac{2^{n-1}}{3^n}$ of the total "content".
|
||||
|
||||
Thus, the total length removed after infinitely many steps is:
|
||||
|
||||
$$
|
||||
\sum_{n=1}^{\infty} \frac{2^{n-1}}{3^n} = \frac{1}{3}\sum_{n=0}^{\infty} \left(\frac{2}{3}\right)^n=1
|
||||
$$
|
||||
|
||||
However, the quarter cantor set removes $\frac{3^{n-1}}{4^n}$ of the total "content", and the total length removed after infinitely many steps is:
|
||||
|
||||
Every time we remove $\frac{1}{4^n}$ of the remaining intervals. So on each layer, we remove $\frac{2^{n-1}}{4^n}$ of the total "content".
|
||||
|
||||
So the total length removed is:
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
1-\frac{1}{4}-\frac{2}{4^2}-\frac{2^2}{4^3}-\cdots&=1-\frac{1}{4}\sum_{n=0}^{\infty} \left(\frac{2}{4}\right)^n\\
|
||||
&=1-\frac{1}{4}\cdot\frac{1}{1-\frac{2}{4}}\\
|
||||
&=1-\frac{1}{4}\cdot\frac{4}{2}\\
|
||||
&=1-\frac{1}{2}\\
|
||||
&=\frac{1}{2}
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
#### Generalized Cantor set (SVC(n))
|
||||
|
||||
The outer content of $SVC(n)$ is $\frac{n-3}{n-2}$.
|
||||
|
||||
#### Monotonicity of outer content
|
||||
|
||||
If $S\subseteq T$, then $c_e(S)\leq c_e(T)$.
|
||||
|
||||
<details>
|
||||
<summary>Proof of Monotonicity of outer content</summary>
|
||||
|
||||
If $C$ is cover of $T$, then $S\subseteq T\subseteq C$, so $C$ is a cover of $S$. Since $c_e(s)$ takes the inf over a larger set that $c_e(T)$, $c_e(S) \leq c_e(T)$.
|
||||
|
||||
</details>
|
||||
|
||||
#### Theorem Osgood's Lemma
|
||||
|
||||
Let $S$ be a closed, bounded set in $\mathbb{R}$, and $S_1\subseteq S_2\subseteq \ldots$, and $S=\bigcup_{n=1}^{\infty} S_n$. Then $\lim_{k\to\infty} c_e(S_k)=c_e(S)$.
|
||||
|
||||
@@ -1,138 +0,0 @@
|
||||
# Math4121 Lecture 2
|
||||
|
||||
## Chapter 5: Differentiation
|
||||
|
||||
### Continue on Differentiation
|
||||
|
||||
#### Theorem 5.5: Chain Rule
|
||||
|
||||
Suppose
|
||||
|
||||
1. $f:[a,b]\to \mathbb{R}$ is continuous on $[a,b]$ (or some neighborhood of $x$)
|
||||
2. $f'(x)$ exists at some point $x\in (a,b)$ ($f$ is differentiable at $x$)
|
||||
3. $g$ is defined on an interval $[c,d]$ containing the range of $f$, ($f([a,b])\subset [c,d]$)
|
||||
4. $g$ is differentiable at the point $f(x)$
|
||||
|
||||
Let $h=g\circ f$ ($h=g(f(x))$) where $f$ is differentiable at $x$ and $g$ is differentiable at $f(x)$. Then $h$ is differentiable at $x$ and
|
||||
|
||||
$$
|
||||
h'(x) = g'(f(x))f'(x)
|
||||
$$
|
||||
|
||||
Proof:
|
||||
|
||||
Let $y=f(x)$ and $u(t)=\frac{f(t)-f(x)}{t-x}-f'(x)$ for $t\neq x,t\in [a,b]$, $v(s)=\frac{g(s)-g(y)}{s-y}-g'(y)$ for $s\neq y,s\in [c,d]$.
|
||||
|
||||
Notice that $u(t)\to 0$ as $t\to x$ and $v(s)\to 0$ as $s\to y$.
|
||||
|
||||
Pick $s=f(t)$ for $t\in [a,b]$ so that $s\to y$ as $t\to x$. Then
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
h(t)-h(x) &= g(f(t))-g(f(x)) \\
|
||||
&= g(t)-g(y) \\
|
||||
&= (s-y)(g'(y)+v(s)) \\
|
||||
&= (f(t)-f(x))(g'(y)+v(s)) \\
|
||||
&= (t-x)(f'(x)+u(t))(g'(y)+v(s)) \\
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
So $h'(x)=\frac{h(t)-h(x)}{t-x}=(f'(x)+u(t))(g'(y)+v(s))$. Since $u(t)\to 0$ and $v(s)\to 0$ as $t\to x$ and $s\to y$, we have $h'(x)=g'(y)f'(x)$.
|
||||
|
||||
QED
|
||||
|
||||
#### Example 5.6
|
||||
|
||||
(a) Let $f(x)=\begin{cases}
|
||||
x\sin\frac{1}{x} & x\neq 0 \\
|
||||
0 & x=0
|
||||
\end{cases}$
|
||||
|
||||
For $x\neq 0$,
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
f'(x) &= 1\cdot\sin\frac{1}{x}+x\cos\frac{1}{x}\cdot\frac{-1}{x^2} \\
|
||||
&= \sin\frac{1}{x}-\frac{\cos\frac{1}{x}}{x}
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
For $x=0$,
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
f'(0) &= \lim_{x\to 0}\frac{f(x)-f(0)}{x-0} \\
|
||||
&= \lim_{x\to 0}\frac{x\sin\frac{1}{x}}{x} \\
|
||||
&= \lim_{x\to 0}\sin\frac{1}{x}
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
This limit does not exist, so $f$ is not differentiable at $x=0$.
|
||||
|
||||
(b) Let $f(x)=\begin{cases}
|
||||
x^2 \sin\frac{1}{x} & x\neq 0 \\
|
||||
0 & x=0
|
||||
\end{cases}$
|
||||
|
||||
For $x\neq 0$,
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
f'(x) &= 2x\sin\frac{1}{x}+x^2\cos\frac{1}{x}\cdot\frac{-1}{x^2} \\
|
||||
&= 2x\sin\frac{1}{x}-\cos\frac{1}{x}
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
For $x=0$,
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
f'(0) &= \lim_{x\to 0}\frac{f(x)-f(0)}{x-0} \\
|
||||
&= \lim_{x\to 0}\frac{x^2\sin\frac{1}{x}}{x} \\
|
||||
&= \lim_{x\to 0}x\sin\frac{1}{x}\\
|
||||
&= 0
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
So $f'(x)=\begin{cases}
|
||||
2x\sin\frac{1}{x}-\cos\frac{1}{x} & x\neq 0 \\
|
||||
0 & x=0
|
||||
\end{cases}$.
|
||||
|
||||
Notice that $f'(x)$ is not continuous at $x=0$ since $\lim_{x\to 0}f'(x)$ is undefined.
|
||||
|
||||
### Mean Value Theorem
|
||||
|
||||
#### Definition 5.7: Local Extrema
|
||||
|
||||
Let $f:[a,b]\to \mathbb{R}$. We say that $f$ has a local maximum (or minimum) at $x\in [a,b]$ if there exists some $\delta>0$ such that
|
||||
|
||||
$$
|
||||
f(x)\geq f(t) \text{ for all }|x-t|<\delta
|
||||
$$
|
||||
|
||||
for local maximum, and
|
||||
|
||||
$$
|
||||
f(x)\leq f(t) \text{ for all }|x-t|<\delta
|
||||
$$
|
||||
|
||||
for local minimum.
|
||||
|
||||
#### Theorem 5.8
|
||||
|
||||
If $f:[a,b]\to \mathbb{R}$ has a local maximum (or minimum) at $x\in (a,b)$ and $f$ is differentiable at $x$, then $f'(x)=0$.
|
||||
|
||||
Proof:
|
||||
|
||||
We can find $\delta>0$ such that $a<x-\delta<x<x+\delta<b$.
|
||||
|
||||
And for all $x-\delta<t<x+\delta$,
|
||||
|
||||
If $x-\delta<t<x$, then $f(x)\geq f(t)$ so $\frac{f(t)-f(x)}{t-x}\leq 0$.
|
||||
|
||||
If $x<t<x+\delta$, then $f(x)\geq f(t)$ so $\frac{f(t)-f(x)}{t-x}\geq 0$.
|
||||
|
||||
So $\lim_{t\to x}\frac{f(t)-f(x)}{t-x}=0$.
|
||||
|
||||
QED
|
||||
@@ -1,110 +0,0 @@
|
||||
# Math4121 Lecture 20
|
||||
|
||||
## Continue on Chapter 4
|
||||
|
||||
### Properties of the Cantor Set
|
||||
|
||||
Monotonicity: If $S\subseteq T$, then $c_e(S)\leq c_e(T)$.
|
||||
|
||||
Sub-additivity: $c_e(S\cup T)\leq c_e(S)+c_e(T)$.
|
||||
|
||||
Example: $S=\mathbb{Q}\cap[0,1]$, $T=[0,1]\setminus\mathbb{Q}$.
|
||||
|
||||
Then $c_e(S)=1$, $c_e(T)=1$, even though $S\cap T=\emptyset$.
|
||||
|
||||
$S\cup T=[0,1]$, $c_e(S\cup T)=1\leq 1+1=c_e(S)+c_e(T)$
|
||||
|
||||
The above example shows that:
|
||||
|
||||
> The following is **not true**: $c_e(S\cup T)=c_e(S)+c_e(T)$ if $S\cap T=\emptyset$.
|
||||
|
||||
However, the following is true:
|
||||
|
||||
(In $\mathbb{R}$)
|
||||
|
||||
If $S=\bigcup_{n=1}^{\infty} I_n$, $T=\bigcup_{n=1}^{\infty} J_n$, where $I_n$ and $J_n$ are intervals, and $S\cap T=\emptyset$, then $c_e(S\cup T)=c_e(S)+c_e(T)$.
|
||||
|
||||
### Back to Osgood's Lemma
|
||||
|
||||
#### Osgood's Lemma
|
||||
|
||||
Let $S$ be a closed, bounded set in $\mathbb{R}$, and $S_1\subseteq S_2\subseteq \ldots$, and $S=\bigcup_{n=1}^{\infty} S_n$. Then $\lim_{k\to\infty} c_e(S_k)=c_e(S)$.
|
||||
|
||||
<details>
|
||||
<summary>Proof of Osgood's Lemma</summary>
|
||||
|
||||
Trivial that $c_e(S_k)\leq c_e(S)$.
|
||||
|
||||
We need to show that $\forall \epsilon>0, \exists K$ such that $c_e(S_k)>c_e(S)-\epsilon$ for all $k\geq K$.
|
||||
|
||||
Let $U_k$ be finite union of open intervals containing $S_k$ such that $c_e(U_k)<c_e(S_k)+\frac{\epsilon}{2^k}$.
|
||||
|
||||
So $\{U_k\}_{k=1}^{\infty}$ are an open cover of $S$.
|
||||
|
||||
Since $S$ is closed and bounded in $\mathbb{R}$, it is compact.
|
||||
|
||||
So, $\exists N$ such that $S\subseteq \bigcup_{k=1}^{N} U_k$.
|
||||
|
||||
Then we split the $U_k$ into two parts:
|
||||
|
||||
$U_k=(U_k\cap U_N)\cup (U_k\setminus U_N)$, we denote $U_k^{(1)}=U_k\cap U_N$, $U_k^{(2)}=U_k\setminus U_N$, for $k\leq N$.
|
||||
|
||||
So, since $U_k^{(1)}, U_k^{(2)}$ disjoint intervals, and $S_k\subseteq U_k^{(1)}$, we have
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
c_e(U_k^{(1)})+c_e(U_k^{(2)})&=c_e(U_k)\\
|
||||
c_e(S_k)+c_e(U_k^{(2)})&<c_e(S_k)+\frac{\epsilon}{2^k}\\
|
||||
c_e(U_k^{(2)})&<\frac{\epsilon}{2^k}\\
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
So,
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
c_e(S)&\leq c_e(U)\\
|
||||
&\leq c_e(U_N)+\sum_{k=1}^{N-1} c_e(U_k^{(2)})\\
|
||||
&<c_e(S_N)+\frac{\epsilon}{2^{N}}+\sum_{k=1}^{N-1}\frac{\epsilon}{2^k}\\
|
||||
&\leq c_e(S_N)+\epsilon\\
|
||||
&<c_e(S_N)
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
</details>
|
||||
|
||||
### Convergence Theorems for sequences of functions
|
||||
|
||||
Is
|
||||
|
||||
$$
|
||||
\lim_{n\to\infty}\int f_n(x)\ dx=\int \lim_{n\to\infty} f_n(x)\ dx
|
||||
$$
|
||||
|
||||
?
|
||||
|
||||
Yes when $f_n\to f$ uniformly.
|
||||
|
||||
Uniform convergence also means $\lim_{n\to\infty} \sup_{x\in [a,b]}|f_n(x)-f(x)|=0$.
|
||||
|
||||
But there exists some cases that does not converge to the limit but still satisfies the above condition.
|
||||
|
||||
#### Theorem 4.5 (Arzela-Osgood Theorem)
|
||||
|
||||
If $\{f_n\}_{n=1}^{\infty}$ is a sequence of continuous, uniformly bounded function and $f(x)=\lim_{n\to\infty} f_n(x)$ exists for all $x\in [a,b]$ (pointwise convergence), then
|
||||
|
||||
$$
|
||||
\lim_{n\to\infty}\int_a^b f_n(x)\ dx=\int_a^b f(x)\ dx
|
||||
$$
|
||||
|
||||
<details>
|
||||
<summary>Proof of Arzela-Osgood Theorem (incomplete)</summary>
|
||||
|
||||
Define $\Gamma_{\alpha}=\{x:\forall m\in \mathbb{N} \textup{ and }\forall \delta>0, \exists n\geq m \textup{ s.t. } |y-x|<\delta \textup{ and } |f_n(y)-f_m(y)|>\alpha\}$.
|
||||
|
||||
_$\Gamma_{\alpha}$ is the negation of $(\alpha,\delta)$ definition of limit._
|
||||
|
||||
$\Gamma_{\alpha}$ is closed and nowhere dense.
|
||||
|
||||
Continue on next lecture.
|
||||
</details>
|
||||
@@ -1,75 +0,0 @@
|
||||
# Math4121 Lecture 21
|
||||
|
||||
## Rolling from last lecture
|
||||
|
||||
### Convergence of integrals
|
||||
|
||||
#### Arzela-Osgood Theorem
|
||||
|
||||
Let $\{f_n\}$ be a sequence of function, $f(x)=\lim_{n\to\infty}f_n(x)$ for every $x\in [0,1]$, if $f\in \mathscr{R}[0,1]$, and $\exists B>0$ such that $|f_n(x)|\leq B \forall x\in [0,1]$. (uniformly bounded and integrable)
|
||||
|
||||
$$
|
||||
\lim_{n\to\infty}\int_0^1 f_n(x) dx = \int_0^1 f(x) dx
|
||||
$$
|
||||
|
||||
If we let $\Gamma_{\alpha}$ be the set of intervals where $f_n$ is not continuous,
|
||||
|
||||
$$
|
||||
\Gamma_{\alpha} = \{x\in [0,1] : \textup{ for any }m\in \mathbb{N}, \delta > 0, \exists n\geq m, y\in (x-\delta, x+\delta) \text{ s.t. } |f_n(y)-f(y)|>\alpha\}
|
||||
$$
|
||||
|
||||
Fact: $\Gamma_{\alpha}$ is closed and nowhere dense.
|
||||
|
||||
<details>
|
||||
<summary>Proof</summary>
|
||||
|
||||
Without loss of generality, we can assume $f=0$. Given any $\alpha > 0$, $\exists N$ such that
|
||||
|
||||
$$
|
||||
\left|\int_0^1 f_n(x) dx \right| < \alpha
|
||||
$$
|
||||
|
||||
for all $n\geq N$.
|
||||
|
||||
Consider the set $\Gamma_{\alpha/2} = \bigcup_{n=1}^{\infty} E_n$, for each $g\in \Gamma_{\alpha/2}$, we still have $\lim_{n\to\infty}f_n(g) = 0$.
|
||||
|
||||
So we define
|
||||
|
||||
$$
|
||||
G_i=\{g\in \Gamma_{\alpha/2} :|f_n(g)|<\frac{\alpha}{2} \text{ for all }n\geq i\}
|
||||
$$
|
||||
|
||||
So $G_1\subset G_2\subset \cdots$ and $\Gamma_{\alpha/2} = \bigcup_{i=1}^{\infty} G_i$.
|
||||
|
||||
By Osgood Lemma, since $\Gamma_{\alpha/2}$ is closed, $\exists K$ such that $c_e(G_K)>c_e(\Gamma_{\alpha/2})-\frac{\alpha}{4B}$.
|
||||
|
||||
By definition of $c_e$, we cna find open $I_1,\ldots,I_N$ which cover $\Gamma_{\alpha/2}$ and
|
||||
|
||||
$$
|
||||
\sum_{i=1}^N \ell(I_i) < c_e(\Gamma_{\alpha/2})+\frac{\alpha}{4B}
|
||||
$$
|
||||
|
||||
Let $\mathcal{U}=\bigcup_{i=1}^N I_i$, and $\mathcal{C}=[0,1]\setminus \mathcal{U}$.
|
||||
|
||||
Part 1: Control the integral on $\mathcal{C}$
|
||||
|
||||
for each $x\in \mathcal{C}$, $x\notin \Gamma_{\alpha/2}$, so $\exists$ and open interval $I(x)$ and an integer $m(x)$ such that $|f_{m(x)}(x)|<\frac{\alpha}{2}$ and $\forall n\geq m(x), y\in I(x)$
|
||||
|
||||
So $\mathcal{C}\subset \bigcup_{x\in \mathcal{C}} I(x)$, and $\mathcal{C}$ is closed and bounded, $\exists x_1,\ldots,x_J$ such that $\mathcal{C}\subset \bigcup_{j=1}^J I(x_j)$. So if $n\geq \max_{j=1,\ldots,J} m(x_j)$, and $x\in \mathcal{C}$, then $|f_n(x)|<\frac{\alpha}{2}$.
|
||||
|
||||
So $\int_\mathcal{C} |f_n(x)| dx < \frac{\alpha}{2} c_e(\mathcal{C})$.
|
||||
|
||||
Part 2: Control the integral on $\mathcal{U}$
|
||||
|
||||
If $[x_i,x_{i+1}]\cap G_k\neq \emptyset$, then $\inf_{x\in [x_i,x_{i+1}]} |f_n(x)| < \frac{\alpha}{2}$ for all $n\geq K$. Denote such set as $P_1$.
|
||||
|
||||
Otherwise, we denote such set as $P_2$.
|
||||
|
||||
So $\ell(\mathcal{U})=\ell(P_1)+\ell(P_2)\geq c_e(G_K)+\ell(P_2)$.
|
||||
|
||||
This implies $\ell(P_2)\leq \frac{\alpha}{4B}$.
|
||||
|
||||
Continue on Friday.
|
||||
|
||||
</details>
|
||||
|
||||
@@ -1,126 +0,0 @@
|
||||
# Math 4121 Lecture 22
|
||||
|
||||
## Continue on Arzela-Osgood Theorem
|
||||
|
||||
<details>
|
||||
<summary>Proof continuation of Arzela-Osgood Theorem</summary>
|
||||
|
||||
Part 2: Control the integral on $\mathcal{U}$
|
||||
|
||||
If $[x_i,x_{i+1}]\cap G_k\neq \emptyset$, then $\inf_{x\in [x_i,x_{i+1}]} |f_n(x)| < \frac{\alpha}{2}$ for all $n\geq K$. Denote such set as $P_1$.
|
||||
|
||||
Otherwise, we denote such set as $P_2$.
|
||||
|
||||
So $\ell(\mathcal{U})=\ell(P_1)+\ell(P_2)\geq c_e(G_K)+\ell(P_2)$.
|
||||
|
||||
This implies $\ell(P_2)\leq \frac{\alpha}{4B}$ since $c_e(G_K)\leq c_e(\mathcal{U})+\frac{\alpha}{2B}$.
|
||||
|
||||
Thus, for $n\geq K$,
|
||||
|
||||
$$
|
||||
L(P,f_n)\leq \ell(P_1)\frac{\alpha}{2}+\ell(P_2)B
|
||||
$$
|
||||
|
||||
So
|
||||
|
||||
$$
|
||||
\int_\mathcal{U} |f_n(x)| dx \leq c_e(\mathcal{U})\frac{\alpha}{2}+\frac{\alpha}{2}
|
||||
$$
|
||||
|
||||
All in all,
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\left\vert \int_\mathcal{U} f_n(x) dx\right\vert &\leq \frac{\alpha}{2}+\frac{\alpha}{2}\\
|
||||
&= \int_0^1 |f_n(x)| dx\\
|
||||
&\leq \int_\mathcal{U} |f_n(x)| dx + \int_\mathcal{C} |f_n(x)|dx\\
|
||||
&\leq c_e(\mathcal{U})\frac{\alpha}{2}+\frac{\alpha}{2}+c_e(\mathcal{C})\frac{\alpha}{2}\\
|
||||
&= \alpha
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
$\forall N\geq K$.
|
||||
|
||||
</details>
|
||||
|
||||
### Baire Category Theorem
|
||||
|
||||
Nowhere dense sets can be large, but they canot cover an open (or closed) interval.
|
||||
|
||||
#### Theorem 4.7 (Baire Category Theorem)
|
||||
|
||||
An open interval cannot be covered by a countable union of nowhere dense sets.
|
||||
|
||||
<details>
|
||||
<summary>Proof</summary>
|
||||
|
||||
Suppose $(0,1)\subset \bigcup_{n=1}^\infty S_n$ where each $S_n$ is nowhere dense. In particular, $\exists I_1$ closed interval such that $I_1\subset (0,1)$ and $I_1\cap S_1=\emptyset$.
|
||||
|
||||
Now for each $k\geq 2$, $S_k$ is not dense in $I_{k-1}$ so $\exists I_k\subsetneq I_{k-1}$ such that $I_k\cap S_k=\emptyset$ for all $j\leq k$.
|
||||
|
||||
By nested interval property, $\exists x\in \bigcap_{n=1}^\infty I_n$.
|
||||
|
||||
Then $x\in (0,1)$ and $x\notin \bigcup_{n=1}^\infty S_n$.
|
||||
|
||||
Contradiction with the assumption that $(0,1)\subset \bigcup_{n=1}^\infty S_n$.
|
||||
|
||||
</details>
|
||||
|
||||
#### Definition First Category
|
||||
|
||||
A countable union of nowhere dense sets is called a set of **first category**.
|
||||
|
||||
#### Corollary 4.8
|
||||
|
||||
Complement of a set of first category in $\mathbb{R}$ is dense in $\mathbb{R}$.
|
||||
|
||||
<details>
|
||||
<summary>Proof</summary>
|
||||
|
||||
We need to show that for every interval $I$, $\exists x\in I\cap S^c$. ($\exists x\in I$ and $x\notin S$)
|
||||
|
||||
This is equivalent to the Baire Category Theorem.
|
||||
|
||||
</details>
|
||||
|
||||
Recall a function is pointwise discontinuous if $\mathcal{C}=\{c\in [a,b]: f\text{ is continuous at } c\}$ is dense in $[a,b]$.
|
||||
|
||||
$\mathcal{D}=[a,b]\setminus \mathcal{C}$ is called the set of points of discontinuity of $f$.
|
||||
|
||||
#### Corollary 4.9
|
||||
|
||||
$f$ is pointwise discontinuous if and only if $\mathcal{D}$ is of first category.
|
||||
|
||||
<details>
|
||||
<summary>Proof</summary>
|
||||
|
||||
Part 1: If $\mathcal{D}$ is of first category, then $f$ is pointwise discontinuous.
|
||||
|
||||
Immediate from Corollary 4.8.
|
||||
|
||||
Part 2: If $f$ is pointwise discontinuous, then $\mathcal{D}$ is of first category.
|
||||
|
||||
Let $P_k=\{x\in [a,b]: w(f;x)\geq \frac{1}{k}\}$, $\mathcal{D}=\bigcup_{k=1}^\infty P_k$.
|
||||
|
||||
Need to show that each $P_k$ is nowhere dense. (under the assumption that $\mathcal{C}$ is dense).
|
||||
|
||||
Let $I\subseteq [a,b]$ so $\exists c\in \mathcal{C}\cap I$. So by definition of $w(f;c)$, $\exists J\subseteq I$ and $c\in J$ such that $w(f;J)\leq \frac{1}{k}$ so for all $x\in J$, $w(f;x)\leq \frac{1}{k}$. so $J\subseteq P_k=\emptyset$.
|
||||
|
||||
Thus, $P_k$ is nowhere dense.
|
||||
|
||||
</details>
|
||||
|
||||
#### Corollary 4.10
|
||||
|
||||
Let $\{f_n\}$ be a sequence of pointwise discontinuous functions. The set of points at which all $f_n$ are simultaneously continuous is dense (it's also uncountable).
|
||||
|
||||
<details>
|
||||
<summary>Proof</summary>
|
||||
|
||||
$$
|
||||
\bigcap_{n=1}^\infty \mathcal{C}_n=\left(\bigcup_{n=1}^\infty \mathcal{D}_n\right)^c
|
||||
$$
|
||||
|
||||
The complement of a set of first category is dense.
|
||||
|
||||
</details>
|
||||
@@ -1,140 +0,0 @@
|
||||
# Math 4121 Lecture 23
|
||||
|
||||
## Chapter 5 Measure Theory
|
||||
|
||||
### Weierstrass idea
|
||||
|
||||
Define
|
||||
|
||||
$$
|
||||
S_f(x) = \{(x,y)\in \mathbb{R}^2: 0\leq y\leq f(x)\}
|
||||
$$
|
||||
|
||||
We take the outer content in $\mathbb{R}^2$ of $S_f(x)$ to be the area of the largest rectangle that can be inscribed in $S_f(x)$.
|
||||
|
||||
$$
|
||||
(w)\int_a^b f(x) dx = c_e(S_f(x))
|
||||
$$
|
||||
|
||||
We can generalize this to higher dimensions.
|
||||
|
||||
#### Definition volume of rectangle
|
||||
|
||||
Let $R=I_1\times I_2\times \cdots \times I_n\in \mathbb{R}^n$ be a rectangle.
|
||||
|
||||
The volume of $R$ is defined as
|
||||
|
||||
$$
|
||||
\text{vol}(R) = \prod_{i=1}^n \ell(I_i)
|
||||
$$
|
||||
|
||||
#### Definition of outer content
|
||||
|
||||
For $S\subseteq \mathbb{R}^n$, we define the outer content of $S$ as
|
||||
|
||||
$$
|
||||
c_e(S) = \inf_{\{R_j\}_{j=1}^N} \sum_{j=1}^N \text{vol}(R_j)
|
||||
$$
|
||||
|
||||
where $S\subseteq \bigcup_{j=1}^N R_j$ and $R_j$ are rectangles.
|
||||
|
||||
Note: $\overline{\int}f(x) dx=c_e(S_f(x))$
|
||||
|
||||
#### Definition of inner content
|
||||
|
||||
For $S\subseteq \mathbb{R}^n$, we define the inner content of $S$ as
|
||||
|
||||
$$
|
||||
c_i(S) = \sup_{\{R_j\}_{j=1}^N} \sum_{j=1}^N \text{vol}(R_j)
|
||||
$$
|
||||
|
||||
where $R_j$ are disjoint rectangles $\in \mathbb{R}^n$ and $\bigcup_{j=1}^N R_j\subseteq S$.
|
||||
|
||||
Note: $\underline{\int}f(x) dx=c_i(S_f(x))$
|
||||
|
||||
#### Definition of Jordan measurable set
|
||||
|
||||
A set $S\subseteq \mathbb{R}^n$ is said to be _Jordan measurable_ if $c_e(S)=c_i(S)$.
|
||||
|
||||
and we denote the common value **content** as $c_e(S)=c_i(S)=c(S)$.
|
||||
|
||||
#### Definition of interior of a set
|
||||
|
||||
The interior of a set $S\subseteq \mathbb{R}^n$ is defined as
|
||||
|
||||
$$
|
||||
S^\circ = \{x\in \mathbb{R}^n: B_\delta(x)\subseteq S \text{ for some } \delta > 0\}
|
||||
$$
|
||||
|
||||
_It is the largest open set contained in $S$._
|
||||
|
||||
#### Definition of closure of a set
|
||||
|
||||
The closure of a set $S\subseteq \mathbb{R}^n$ is defined as
|
||||
|
||||
$$
|
||||
\overline{S} = S\cup S'
|
||||
$$
|
||||
|
||||
or equivalently,
|
||||
|
||||
$$
|
||||
\overline{S} = \{x\in \mathbb{R}^n: B_\delta(x)\cap S\neq \emptyset \text{ for all } \delta > 0\}
|
||||
$$
|
||||
|
||||
where $S'$ is the set of all limit points of $S$.
|
||||
|
||||
_It is the smallest closed set containing $S$._
|
||||
|
||||
Homework problem: Complement of the closure of $S$ is the interior of the complement of $S$, i.e.,
|
||||
|
||||
$$
|
||||
(\overline{S})^c = (S^c)^\circ
|
||||
$$
|
||||
|
||||
#### Definition of boundary of a set
|
||||
|
||||
The boundary of a set $S\subseteq \mathbb{R}^n$ is defined as
|
||||
|
||||
$$
|
||||
\partial S = \overline{S}\setminus S^\circ
|
||||
$$
|
||||
|
||||
#### Proposition 5.1 (Criterion for Jordan measurability)
|
||||
|
||||
Let $S\subseteq \mathbb{R}^n$ be a bounded set. Then
|
||||
|
||||
$$
|
||||
c_e(S) = c_i(S)+c_e(\partial S)
|
||||
$$
|
||||
|
||||
So $S$ is Jordan measurable if and only if $c_e(\partial S)=0$.
|
||||
|
||||
<details>
|
||||
<summary>Proof</summary>
|
||||
|
||||
Let $\epsilon > 0$, and $\{R_j\}_{j=1}^N$ be an open cover of $\partial S$. such that $\sum_{j=1}^N \text{vol}(R_j) < c_e(\partial S)+\frac{\epsilon}{2}$.
|
||||
|
||||
We slightly enlarge each $R_j$ to $Q_j$ such that $R_j\subseteq Q_j$ and $\text{vol}(Q_j)\leq \text{vol}(R_j)+\frac{\epsilon}{2N}$.
|
||||
|
||||
and $dis(R_j,Q_j^c)>\delta > 0$
|
||||
|
||||
If we could construct such $\{Q_j\}_{j=N+1}^M$ disjoint and
|
||||
|
||||
$$
|
||||
\bigcup_{j=N+1}^M Q_j\subseteq S\subseteq \bigcup_{j=1}^M Q_j
|
||||
$$
|
||||
|
||||
then we have
|
||||
|
||||
$$
|
||||
c_e(S)\leq \sum_{j=1}^M \text{vol}(\partial S)+\epsilon +c_i(S)
|
||||
$$
|
||||
|
||||
We can do this by constructing a set of square with side length $\eta$. We claim:
|
||||
|
||||
If $\eta$ is small enough (depends on $\delta$), then $\mathcal{C}_\eta=\{Q\in K_\eta:Q\subset S\}$, $\mathcal{C}_\eta\cup \left(\bigcup_{j=1}^N Q_j\right)$ is a cover of $S$.
|
||||
|
||||
Suppose $\exists x\in S$ but not in $\mathcal{C}_\eta$. Then $x$ is closed to $\partial S$ so in some $Q_j$. (This proof is not rigorous, but you get the idea. Also not clear in book actually.)
|
||||
|
||||
</details>
|
||||
@@ -1,109 +0,0 @@
|
||||
# Math4121 Lecture 24
|
||||
|
||||
## Chapter 5: Measure Theory
|
||||
|
||||
### Jordan Measurable
|
||||
|
||||
#### Proposition 5.1
|
||||
|
||||
A bounded set $S\subseteq \mathbb{R}^n$ is Jordan measurable if
|
||||
|
||||
$$
|
||||
c_e(S)=c_i(S)+c_e(\partial S)
|
||||
$$
|
||||
|
||||
where $\partial S$ is the boundary of $S$ and $c_e(\partial S)=0$.
|
||||
|
||||
<details>
|
||||
<summary>Examples for Jordan measurable</summary>
|
||||
|
||||
1. $S=\mathbb{Q}\cap [0,1]$ is not Jordan measurable.
|
||||
|
||||
Since $c_e(S)=0$ and $\partial S=[0,1]$, $c_i(S)=1$.
|
||||
|
||||
So $c_e(\partial S)=1\neq 0$.
|
||||
|
||||
2. $SVC(3)$ is Jordan measurable.
|
||||
|
||||
Since $c_e(S)=0$ and $\partial S=0$, $c_i(S)=0$. The outer content of the cantor set is $0$.
|
||||
|
||||
> Any set or subset of a set with $c_e(S)=0$ is Jordan measurable.
|
||||
|
||||
3. $SVC(4)$
|
||||
|
||||
At each step, we remove $2^n$ intervals of length $\frac{1}{4^n}$.
|
||||
|
||||
So $S=\bigcap_{n=1}^{\infty} C_i$ and $c_e(C_k)=c_e(C_{k-1})-\frac{2^{k-1}}{4^k}$. $c_e(C_0)=1$.
|
||||
|
||||
So
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
c_e(S)&\leq \lim_{k\to\infty} c_e(C_k)\\
|
||||
&=1-\sum_{k=1}^{\infty} \frac{2^{k-1}}{4^k}\\
|
||||
&=1-\frac{1}{4}\sum_{k=0}^{\infty} \left(\frac{2}{4}\right)^k\\
|
||||
&=1-\frac{1}{4}\cdot \frac{1}{1-\frac{2}{4}}\\
|
||||
&=1-\frac{1}{4}\cdot \frac{1}{\frac{1}{2}}\\
|
||||
&=1-\frac{1}{2}\\
|
||||
&=\frac{1}{2}.
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
And we can also claim that $c_i(S)\geq \frac{1}{2}$. Suppose not, then $\exists \{I_j\}_{j=1}^{\infty}$ such that $S\subseteq \bigcup_{j=1}^{\infty} I_j$ and $\sum_{j=1}^{\infty} \ell(I_j)< \frac{1}{2}$.
|
||||
|
||||
Then $S$ would have gaps with lengths summing to greater than $\frac{1}{2}$. This contradicts with what we just proved.
|
||||
|
||||
So $c_e(SVC(4))=\frac{1}{2}$.
|
||||
|
||||
> General formula for $c_e(SVC(n))=\frac{n-3}{n-2}$, and since $SVC(n)$ is nowhere dense, $c_i(SVC(n))=0$.
|
||||
|
||||
</details>
|
||||
|
||||
### Additivity of Content
|
||||
|
||||
Recall that outer content is sub-additive. Let $S,T\subseteq \mathbb{R}^n$ be disjoint.
|
||||
|
||||
$$
|
||||
c_e(S\cup T)\leq c_e(S)+c_e(T)
|
||||
$$
|
||||
|
||||
The inner content is super-additive. Let $S,T\subseteq \mathbb{R}^n$ be disjoint.
|
||||
|
||||
$$
|
||||
c_i(S\cup T)\geq c_i(S)+c_i(T)
|
||||
$$
|
||||
|
||||
#### Proposition 5.2
|
||||
|
||||
Finite additivity of Jordan content:
|
||||
|
||||
Let $S_1,\ldots,S_N\subseteq \mathbb{R}^n$ are pairwise disjoint Jordan measurable sets, then
|
||||
|
||||
$$
|
||||
c(\bigcup_{i=1}^N S_i)=\sum_{i=1}^N c(S_i)
|
||||
$$
|
||||
|
||||
<details>
|
||||
<summary>Proof</summary>
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\sum_{i=1}^N c_i(S_i)&\leq c_i(\bigcup_{i=1}^N S_i)\\
|
||||
&\leq c_e(\bigcup_{i=1}^N S_i)\\
|
||||
&\leq \sum_{i=1}^N c_e(S_i)\\
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Since $\sum_{i=1}^N c(S_i)=\sum_{i=1}^N c_e(S_i)=\sum_{i=1}^N c_i(S_i)$, we have
|
||||
|
||||
$$
|
||||
c(\bigcup_{i=1}^N S_i)=\sum_{i=1}^N c(S_i)
|
||||
$$
|
||||
|
||||
</details>
|
||||
|
||||
##### Failure for countable additivity for Jordan content
|
||||
|
||||
Notice that each singleton $\{q\}$ is Jordan measurable and $c(\{q\})=0$. But take $a\in \mathbb{Q}\cap [0,1]$, $Q\cap [0,1]=\bigcup_{q\in Q\cap [0,1]} \{q\}$, but $\mathbb{Q}\cap [0,1]$ is not Jordan measurable.
|
||||
|
||||
Issue is a countable union of Jordan measurable sets is not necessarily Jordan measurable.
|
||||
@@ -1,78 +0,0 @@
|
||||
# Math4121 Lecture 25
|
||||
|
||||
## Continue on Measure Theory
|
||||
|
||||
### Borel Measure
|
||||
|
||||
Finite additivity of Jordan content, i.e. for any $\{S_j\}_{j=1}^N$ pairwise disjoint sets and Jordan measurable, then
|
||||
|
||||
$$
|
||||
\sum_{j=1}^N c(S_j)=c\left(\bigcup_{j=1}^N S_j\right)
|
||||
$$
|
||||
|
||||
This fails for countable unions.
|
||||
|
||||
#### Definition of Borel measurable
|
||||
|
||||
Borel introduced a new measure, called _Borel measure_, was net only finitely addition, but also _countably additive_, meaning $\{S_j\}_{j=1}^\infty$ pairwise disjoint and Borel measurable, then
|
||||
|
||||
$$
|
||||
m\left(\bigcup_{j=1}^\infty S_j\right) = \sum_{j=1}^\infty m(S_j)
|
||||
$$
|
||||
|
||||
#### Definition of Borel measure
|
||||
|
||||
Borel measure satisfies the following properties:
|
||||
|
||||
1. $m(I)=\ell(I)$ if $I$ is open, closed, or half-open interval
|
||||
2. countable additivity is satisfied
|
||||
3. If $R, S$ are Borel measurable and $R\subseteq S$, then $S\setminus R$ is Borel measurable and $m(S\setminus R)=m(S)-m(R)$
|
||||
|
||||
### Borel sets
|
||||
|
||||
#### Definition of sigma-algebra
|
||||
|
||||
A collection of sets $\mathcal{A}$ is called a sigma-algebra if it satisfies the following properties:
|
||||
|
||||
1. $\emptyset \in \mathcal{A}$
|
||||
2. If $\{A_j\}_{j=1}^\infty \subset \mathcal{A}$, then $\bigcup_{j=1}^\infty A_j \in \mathcal{A}$
|
||||
3. If $A \in \mathcal{A}$, then $A^c \in \mathcal{A}$
|
||||
|
||||
#### Definition of Borel sets
|
||||
|
||||
The Borel sets in $\mathbb{R}$ is the smallest sigma-algebra containing all closed intervals.
|
||||
|
||||
#### Proposition
|
||||
|
||||
The Borel sets are Borel measurable.
|
||||
|
||||
(proof in the following lectures)
|
||||
|
||||
<details>
|
||||
<summary>Examples for Borel measurable</summary>
|
||||
|
||||
1. Let $S=\{x\in [0,1]: x\in \mathbb{Q}\}$
|
||||
|
||||
$S=\{q_j\}_{j=1}^\infty=\bigcup_{j=1}^\infty \{q_j\}$ (by countability of $\mathbb{Q}$)
|
||||
|
||||
Since $m[q_j,q_j]=0$, $m(S)=0$.
|
||||
|
||||
2. Let $S=SVC(4)$
|
||||
|
||||
Since $c_e(SVC(4))=\frac{1}{2}$ and $c_i(SVC(4))=0$, it is not Jordan measurable.
|
||||
|
||||
$S$ is Borel measurable with $m(S)=\frac{1}{2}$. (use setminus and union to show)
|
||||
|
||||
</details>
|
||||
|
||||
#### Proposition 5.3
|
||||
|
||||
Let $\mathcal{B}$ be the Borel sets in $\mathbb{R}$. Then the cardinality of $\mathcal{B}$ is $2^{\aleph_0}=\mathfrak{c}$. But the cardinality of the set of Jordan measurable sets is $2^{\mathfrak{c}}$.
|
||||
|
||||
Sketch of proof:
|
||||
|
||||
SVC(3) is Jordan measurable, but $|SVC(3)|=\mathfrak{c}$. so $|\mathscr{P}(SVC(3))|=2^\mathfrak{c}$.
|
||||
|
||||
But for any $S\subset \mathscr{P}(SVC(3))$, $c_e(S)\leq c_e(SVC(3))=0$ so $S$ is Jordan measurable.
|
||||
|
||||
However, there are $\mathfrak{c}$ many intervals and $\mathcal{B}$ is generated by countable operations from intervals.
|
||||
@@ -1,93 +0,0 @@
|
||||
# Math4121 Lecture 26
|
||||
|
||||
## Lebesgue Measure
|
||||
|
||||
### Lebesgue's Integration
|
||||
|
||||
Partition on the y-axis, let $l$ be the minimum of $f(x)$ on the $y$-axis, $L$ be the maximum of $f(x)$ on the $y$-axis.
|
||||
|
||||
$l=l_0<l_1<\cdots<l_n=L$
|
||||
|
||||
Define $S_i=\{x\in[a,b]:l_{i-1}\leq f(x)<l_i\}$
|
||||
|
||||
Defined the characteristic function of set $S$ is $\chi_S(x)=1$ if $x\in S$ and $0$ otherwise.
|
||||
|
||||
Then $f$ lies between the following simple functions:
|
||||
|
||||
$$
|
||||
\sum_{i=1}^n l_{i-1}\chi_{S_i}\leq f(x)\leq \sum_{i=1}^n l_i\chi_{S_i}
|
||||
$$
|
||||
|
||||
_This representation allows us to measure some weird sets on the $x$-axis by constraining the $y$-axis._
|
||||
|
||||
This is still kind of Riemann sum, but $S_i$ can be very weird (not just intervals).
|
||||
|
||||
If we can "measure" each $S_i$, then we could define the integral of $f$ by
|
||||
|
||||
$$
|
||||
\sup_{l_0,\cdots,l_n}\sum_{i=1}^n l_{i-1}m(S_i)\quad \inf_{l_0,\cdots,l_n}\sum_{i=1}^n l_i m(S_i)
|
||||
$$
|
||||
|
||||
If we used Jordan content, for $m$ here, this is just a different perspective of Riemann integral.
|
||||
|
||||
If we use Borel measure maybe things would be different (perhaps, better)?
|
||||
|
||||
As we discussed last time, this limits the measurable sets significantly.
|
||||
|
||||
Nonetheless, let's try
|
||||
|
||||
1. Characteristic function of the rational numbers
|
||||
|
||||
$$
|
||||
f(x)=\begin{cases}
|
||||
1 & x\in\mathbb{Q}\cap[0,1]\\
|
||||
0 & \text{otherwise}
|
||||
\end{cases}
|
||||
$$
|
||||
|
||||
Take partition $0=x_0<x_1<\cdots<x_n=1$
|
||||
|
||||
$S_1=\{x:0\leq f(x)<\epsilon\}=[0,1]\setminus\mathbb{Q}$
|
||||
|
||||
$S_2=\{x:\epsilon\leq f(x)<1\}=\emptyset$
|
||||
|
||||
$S_3=\{x:1\leq f(x)<1+\epsilon\}=\mathbb{Q}\cap[0,1]$
|
||||
|
||||
$$
|
||||
\sum_{i=1}^n l_{i-1}m(S_i)=0\cdot 1+\epsilon\cdot 0+1\cdot 0=0
|
||||
$$
|
||||
|
||||
$$
|
||||
\sum_{i=1}^n l_i m(S_i)=\epsilon\cdot 1+1\cdot 0+(1+\epsilon)\cdot 0=\epsilon
|
||||
$$
|
||||
|
||||
So, $0\leq\int_0^1 f(x)dm\leq\epsilon$, here $m$ means the measure we used.
|
||||
|
||||
As $\epsilon$ is arbitrary, we have $\int_0^1 f(x)dm=0$.
|
||||
|
||||
_This shows that $\int \chi_S(x)dm=m(S)$ for any measurable set $S$._
|
||||
|
||||
### Lebesgue's Measure
|
||||
|
||||
#### Definition of Lebesgue measure
|
||||
|
||||
Outer Measure:
|
||||
|
||||
Given $S\subset [a,b]$, let $\mathcal{C}$ be the collection of all countable covers of $S$ by open intervals.
|
||||
|
||||
$$
|
||||
m_e(S)=\inf_{C\in\mathcal{C}}m(C)
|
||||
$$
|
||||
|
||||
where $m(C)$ is the Borel measure.
|
||||
|
||||
Recall such $C$ are Boreal measurable because open interval are in $\mathcal{B}$ and $\mathcal{B}$ (being a sigma algebra) is closed under countable unions.
|
||||
|
||||
Properties:
|
||||
|
||||
1. Translation invariant: $m_e(S+a)=m_e(S)$
|
||||
2. Countable additivity: $m_e(S\cup T)=m_e(S)+m_e(T)$ if $S\cap T=\emptyset$
|
||||
3. $m([0,1])=1$
|
||||
|
||||
**Notice we don't have the difference property here.**
|
||||
|
||||
@@ -1,149 +0,0 @@
|
||||
# Math4121 Lecture 27
|
||||
|
||||
## Lebesgue Measure
|
||||
|
||||
### Outer Measure
|
||||
|
||||
$$
|
||||
m_e(S)=\inf\left\{\sum_{n=1}^\infty \ell(I_n): S\subset \bigcup_{n=1}^\infty I_n\right\}
|
||||
$$
|
||||
|
||||
where $I_j$ is an open interval
|
||||
|
||||
**Properties:**
|
||||
|
||||
1. $m_e(I)=\ell(I)$
|
||||
2. Countably sub-additive: $m_e\left(\bigcup_{n=1}^\infty S_n\right)\leq \sum_{n=1}^\infty m_e(S_n)$ (Prove today)
|
||||
3. does not respect complementation (Build in to Borel measure)
|
||||
|
||||
Why does Jordan content respect complementation?
|
||||
|
||||
$(\text{Finite union of intervals })^C=\text{another finite union of intervals}$
|
||||
|
||||
We know this failed for countable unions.
|
||||
|
||||
Example:
|
||||
|
||||
$$
|
||||
\bigcup_{n=1}^\infty \left(q_n-\frac{\epsilon}{2^n},q_n+\frac{\epsilon}{2^n}\right)
|
||||
$$
|
||||
|
||||
Where $q_n$ is dense.
|
||||
|
||||
### Inner Measure
|
||||
|
||||
Say $S\subset I$
|
||||
|
||||
$$
|
||||
m_i(S)=m(I)-m_e(I\setminus S)
|
||||
$$
|
||||
|
||||
where $m(I)=\ell(I)$
|
||||
|
||||
Say $S$ is (Lebesgue) measurable if $m_i(S)=m_e(S)$, call this value $m(S)=m_e(S)=m_i(S)$ the (Lebesgue) measure of $S$.
|
||||
|
||||
#### Corollary of measurability of subsets
|
||||
|
||||
If $S$ is measurable, and $S\subset T$, then
|
||||
|
||||
$$
|
||||
m(S)=m_e(S)=m(I)-m_e(I\setminus S)
|
||||
$$
|
||||
|
||||
$$
|
||||
m(I\setminus S)=m(I)-m(S)
|
||||
$$
|
||||
|
||||
$I\setminus S$ is Lebesgue measurable and $m(I)=m(S)+m(I\setminus S)$
|
||||
|
||||
#### Proposition 5.8 (Countable additivity over measurable sets)
|
||||
|
||||
If $S_n$ are measurable, then
|
||||
|
||||
$$
|
||||
m_e\left(\bigcup_{n=1}^\infty S_n\right)\leq\sum_{n=1}^\infty m(S_n)
|
||||
$$
|
||||
|
||||
<details>
|
||||
<summary>Proof</summary>
|
||||
|
||||
Let $\epsilon>0$ and for each $j$, let $\{I_{i,j}\}_{i=1}^\infty$ be a cover of $S_j$ s.t.
|
||||
|
||||
$$
|
||||
\sum_{i=1}^\infty \ell(I_{i,j})<m(S_j)+\frac{\epsilon}{2^j}
|
||||
$$
|
||||
|
||||
Then $\bigcup_{j=1}^\infty \bigcup_{i=1}^\infty I_{i,j}$ is a countable cover of $\bigcup_{j=1}^\infty S_j$ and
|
||||
|
||||
$$
|
||||
m_e\left(\bigcup_{j=1}^\infty S_j\right)\leq \sum_{j=1}^\infty \sum_{i=1}^\infty \ell(I_{i,j})<\sum_{j=1}^\infty \left(m_e(S_j)+\frac{\epsilon}{2^j}\right)=\sum_{j=1}^\infty m_e(S_j)+\epsilon
|
||||
$$
|
||||
|
||||
Since $\epsilon$ is arbitrary, we have
|
||||
|
||||
$$
|
||||
m_e\left(\bigcup_{j=1}^\infty S_j\right)\leq\sum_{j=1}^\infty m_e(S_j)=\sum_{j=1}^\infty m(S_j)
|
||||
$$
|
||||
|
||||
</details>
|
||||
|
||||
#### Corollary: inner measure is always less than or equal to outer measure
|
||||
|
||||
$$
|
||||
m_i(S)\leq m_e(S)
|
||||
$$
|
||||
|
||||
<details>
|
||||
<summary>Proof</summary>
|
||||
|
||||
$$
|
||||
m_i(S)=m(I)-m_e(I\setminus S)\leq m(I)-m_i(I\setminus S)=m_e(S)
|
||||
$$
|
||||
|
||||
</details>
|
||||
|
||||
### Caratheodory's Criterion
|
||||
|
||||
#### Lemma 5.7 (Local additivity)
|
||||
|
||||
If $\{I_j\}_{j=1}^\infty$ are pairwise disjoint open intervals, then
|
||||
|
||||
$$
|
||||
m_e\left(S\cap \left(\bigcup_{j=1}^\infty I_j\right)\right)=m_e\left(\bigcup_{j=1}^\infty (S\cap I_j)\right)=\sum_{j=1}^\infty m_e(S\cap I_j)
|
||||
$$
|
||||
|
||||
<details>
|
||||
<summary>Proof</summary>
|
||||
|
||||
For each $j$, let $\{J_i\}_{i=1}^\infty$ be a cover of $S\cap \left(\bigcup_{j=1}^\infty I_j\right)$ such that $\sum_{i=1}^\infty \ell(J_i)<c_e(S\cap \left(\bigcup_{j=1}^\infty I_j\right))+\epsilon$. Since $\{I_j\}_{j=1}^\infty$ are pairwise disjoint, so is $\{J_i\cap I_j\}_{j=1}^\infty$ for each $i$.
|
||||
|
||||
$$
|
||||
\sum_{j=1}^\infty m_e(J_i\cap I_j)=m_e(J_i)
|
||||
$$
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
m_e\left(S\cap \left(\bigcup_{j=1}^\infty I_j\right)\right)&\leq \sum_{j=1}^\infty m_e(S\cap I_j)\\
|
||||
&\leq \sum_{j=1}^\infty m_e(\bigcup_{i=1}^\infty J_i\cap I_j)\\
|
||||
&= \sum_{j=1}^\infty m_e(J_i)+\epsilon
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Since $\epsilon$ is arbitrary, we have
|
||||
|
||||
$$
|
||||
m_e\left(S\cap \left(\bigcup_{j=1}^\infty I_j\right)\right)\leq \sum_{j=1}^\infty m_e(S\cap I_j)
|
||||
$$
|
||||
|
||||
</details>
|
||||
|
||||
#### Theorem 5.6 (Caratheodory's Criterion)
|
||||
|
||||
A set $S$ is measurable if and only if for every set $X\in \mathbb{R}$ of finite outer measure,
|
||||
|
||||
$$
|
||||
m_e(X)=m_e(X\cap S)+m_e(X\setminus S)
|
||||
$$
|
||||
|
||||
Lebesgue: $X=I$ and $S\subset I$ we can cut any set by a measurable set to get a measurable set. (no matter how big the set is)
|
||||
|
||||
@@ -1,134 +0,0 @@
|
||||
# Math4121 Lecture 28
|
||||
|
||||
## Continue from last lecture
|
||||
|
||||
### Lebesgue Measure
|
||||
|
||||
#### Outer Measure
|
||||
|
||||
$$
|
||||
m_e(S) = \inf_{S \subseteq \bigcup_{j=1}^{\infty} I_j} \sum_{j=1}^{\infty} \ell(I_j)
|
||||
$$
|
||||
|
||||
If $S\subseteq I$ is measurable, then $m_i(S)=m_e(I)-m_e(I\setminus S)$
|
||||
|
||||
#### Lebesgue criterion for measurability
|
||||
|
||||
$S\subseteq I$ is measurable if and only if $m_e(I)=m_e(S)+m_e(I\setminus S)$
|
||||
|
||||
#### Caratheodory's criteria
|
||||
|
||||
Lebesgue criterion holds if and only if for any $X$ of finite outer measure,
|
||||
|
||||
$$
|
||||
m_e(X)=m_e(X\cap S)+m_e(X\setminus S)
|
||||
$$
|
||||
|
||||
> **Local additivity**
|
||||
>
|
||||
> $\{I_j\}_{j=1}^{\infty}$ is a collection of disjoint intervals, then
|
||||
>
|
||||
> $$m_e\left(S\cap \bigcup_{j=1}^{\infty} I_j\right) = \sum_{j=1}^{\infty} m_e(S\cap I_j)$$
|
||||
> Proved on Friday
|
||||
|
||||
<details>
|
||||
<summary>Proof</summary>
|
||||
|
||||
$\implies$ If Lebesgue criterion holds for $S$, then for any $X$ of finite outer measure,
|
||||
|
||||
$$
|
||||
m_e(X)=m_e(X\cap S)+m_e(X\setminus S)
|
||||
$$
|
||||
|
||||
First, we extend Lebesgue criterion to intervals $I$ that may not contain $S$. Then we can find $J,K$ intervals neighboring $I$ such that $S\subseteq \tilde{I}=J\cup I\cup K$.
|
||||
|
||||
By Lebesgue criterion,
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
m_e(\tilde{I})&=m_e(\tilde{I}\cap S)+m_e(\tilde{I}\setminus S)\\
|
||||
&=m_e(S)+m_e(\tilde{I}\setminus S)\\
|
||||
&=m_e(S^c\cap \tilde{I})+m_e(S\cap \tilde{I})\\
|
||||
&=\sum_{L\in \{J,I,K\}}m_e(L\cap S^c)+m_e(L\cap S)\\
|
||||
&\geq \sum_{L\in \{J,I,K\}}m_e(L)\\
|
||||
&=m_e(\tilde{I})
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Therefore, $m_e(I)=m_e(S^c\cap I)+m_e(S\cap I)$.
|
||||
|
||||
Now, let $X$ has finite outer measure, let $\epsilon>0$, we can find $\{I_j\}_{j=1}^{\infty}$ covering $X$ and
|
||||
|
||||
$$
|
||||
\sum_{j=1}^{\infty} \ell(I_j)<m_e(X)+\epsilon
|
||||
$$
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
m_e(X)&\leq m_e(X\cap S)+m_e(S^c\cap X)\\
|
||||
&\leq m_e\left(\bigcup_{j=1}^{\infty} I_j\cap S\right)+m_e\left(\bigcup_{j=1}^{\infty} I_j\cap S^c\right)\\
|
||||
&\leq \sum_{j=1}^{\infty} m_e(I_j\cap S)+m_e(I_j\cap S^c)\\
|
||||
&=\sum_{j=1}^{\infty} m_e(I_j)\\
|
||||
&<m_e(X)+\epsilon
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
</details>
|
||||
|
||||
### Revisit Borel's criterion
|
||||
|
||||
1. $m(I)=\ell(I)$
|
||||
2. If $\{S_j\}_{j=1}^{\infty}$ is a sequence of disjoint measurable sets, then $m\left(\bigcup_{j=1}^{\infty} S_j\right)=\sum_{j=1}^{\infty} m(S_j)$
|
||||
3. If $R\subseteq S$, then $m(S\setminus R)=m(S)-m(R)$
|
||||
|
||||
#### Theorem 5.8 (Countable additivity for Lebesgue measure)
|
||||
|
||||
If $\{S_j\}_{j=1}^{\infty}$ is a sequence of disjoint measurable sets, whose union $S=\bigcup_{j=1}^{\infty} S_j$, has finite outer measure, then
|
||||
|
||||
$$
|
||||
m_e(S)=\sum_{j=1}^{\infty} m_e(S_j)
|
||||
$$
|
||||
|
||||
<details>
|
||||
<summary>Proof</summary>
|
||||
|
||||
First we prove $m_e(\bigcup_{j=1}^{\infty} S_j)=\sum_{j=1}^{\infty} m(S_j)$ by induction.
|
||||
|
||||
$n=1$ is trivial.
|
||||
|
||||
Let $n>1$ and suppose the statement holds for $n-1$. Take $X=\bigcup_{j=1}^{n-1} S_j$, then $S_n\cap X=S_n, X\setminus S_n=\bigcup_{j=1}^{n-1} (S_j)$.
|
||||
|
||||
By Caratheodory's criteria,
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
m_e(X)&=m_e(S_n)+m_e(\bigcup_{j=1}^{n-1} S_j)\\
|
||||
m_e(\bigcup_{j=1}^{n} S_j)&=m(S_n)+\sum_{j=1}^{n-1} m(S_j)\\
|
||||
&=\sum_{j=1}^{n} m(S_j)
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Take the limit as $n\to\infty$, and justify this.
|
||||
|
||||
$\sum_{j=1}^{\infty} m(S_j)=m_e(\bigcup_{j=1}^{\infty} S_j)\leq m_e(S)$
|
||||
|
||||
Since $m_e(S)$ is finite and $m(S_j)$ is monotone, the limit exists.
|
||||
|
||||
Therefore, $\sum_{j=1}^{\infty} m(S_j)\leq m_e(S)\leq \sum_{j=1}^{\infty} m(S_j)$
|
||||
|
||||
So $S$ is measurable.
|
||||
|
||||
</details>
|
||||
|
||||
#### Proposition 5.9 (Preview)
|
||||
|
||||
Any finite union (and intersection) of measurable sets is measurable.
|
||||
|
||||
<details>
|
||||
<summary>Proof</summary>
|
||||
|
||||
Let $S_1, S_2$ be measurable sets.
|
||||
|
||||
We prove by verifying the Caratheodory's criteria for $S_1\cup S_2$.
|
||||
|
||||
</details>
|
||||
@@ -1,120 +0,0 @@
|
||||
# Math4121 Lecture 29
|
||||
|
||||
## Continue on Measure Theory
|
||||
|
||||
### Lebesgue Measure
|
||||
|
||||
Caratheodory's criterion:
|
||||
|
||||
$S$ is Lebesgue measurable if for all $A\subset S$,
|
||||
|
||||
$$
|
||||
m_e(X) = m_e(X\cap S) + m_e(X\cap S^c)
|
||||
$$
|
||||
|
||||
Let $\mathfrak{M}$ be the collection of all Lebesgue measurable sets.
|
||||
|
||||
1. $\phi\in\mathfrak{M}$
|
||||
2. $\mathfrak{M}$ is closed under countable unions (proved last lecture)
|
||||
3. $\mathfrak{M}$ is closed under complementation ($\mathfrak{M}$ is a $\sigma$-algebra) (goal today)
|
||||
|
||||
> Desired properties of a measure:
|
||||
>
|
||||
> 1. $m(I)=\ell(I)$ for all intervals $I$
|
||||
> 2. If $\{S_n\}_{n=1}^{\infty}$ is a set of pairwise disjoint Lebesgue measurable sets, then
|
||||
>
|
||||
> $$ m\left(\bigcup_{n=1}^{\infty}S_n\right) = \sum_{n=1}^{\infty}m(S_n)$$
|
||||
> 3. If $R\subset S$, then $m(S\setminus R) = m(S) - m(R)$
|
||||
|
||||
Recall the Borel $\sigma$-algebra $\mathcal{B}$ was the smallest $\sigma$-algebra containing closed intervals. Therefore $\mathcal{B}\subset\mathfrak{M}$.
|
||||
|
||||
Towards proving $\mathfrak{M}$ is closed under countable unions:
|
||||
|
||||
#### Theorem 5.9 (Finite union/intersection of Lebesgue measurable sets is Lebesgue measurable)
|
||||
|
||||
Any finite union/intersection of Lebesgue measurable sets is Lebesgue measurable.
|
||||
|
||||
<details>
|
||||
<summary>Proof</summary>
|
||||
|
||||
Suppose $S_1, S_2$ is a measurable, and we need to show that $S_1\cup S_2$ is measurable. Given $X$, need to show that
|
||||
|
||||
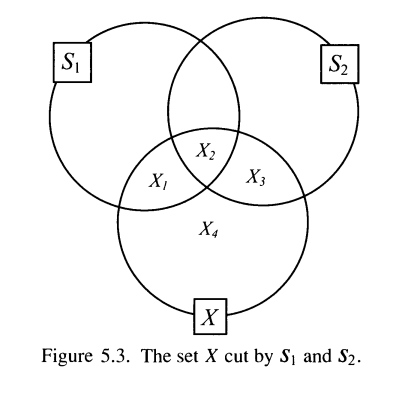
|
||||
|
||||
$$
|
||||
m_e(X) = m_e(X_1\cup X_2\cup X_3)+ m_e(X_4)
|
||||
$$
|
||||
|
||||
Since $S_1$ measurable, $m_e(X_1\cup X_2\cup X_3)=m_e(X_3)+m_e(X_1\cup X_2)$.
|
||||
|
||||
Since $S_2$ measurable, $m_e(X_3\cup X_4)=m_e(X_3)+m_e(X_4)$.
|
||||
|
||||
Therefore,
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
m_e(X) &= m_e(X_1\cup X_2\cup X_3) + m_e(X_4) \\
|
||||
&= m_e(X_1\cup X_2) + m_e(X_3)+m_e(X_4) \\
|
||||
&= m_e(X_1\cup X_2) + m_e(X_3\cup X_4) \\
|
||||
&= m_e(X)
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
by measurability of $S_1$ again.
|
||||
|
||||
</details>
|
||||
|
||||
#### Theorem 5.10 (Countable union/intersection of Lebesgue measurable sets is Lebesgue measurable)
|
||||
|
||||
Any countable union/intersection of Lebesgue measurable sets is Lebesgue measurable.
|
||||
|
||||
<details>
|
||||
<summary>Proof</summary>
|
||||
|
||||
Let $\{S_j\}_{j=1}^{\infty}\subset\mathfrak{M}$. Definte $T_j=\bigcup_{k=1}^{j}S_k$ such that $T_{j-1}\subset T_j$ for all $j$.
|
||||
|
||||
And $U_1=T_1$, $U_j=T_j\setminus T_{j-1}$ for $j\geq 2$.
|
||||
|
||||
Then $\bigcup_{j=1}^{\infty}S_j=\bigcup_{j=1}^{\infty}T_j=\bigcup_{j=1}^{\infty}U_j$. Notice that $\{U_j\}_{j=1}^{\infty}$ are pairwise disjoint, and $\{T_j\}_{j=1}^{\infty}$ are monotone.
|
||||
|
||||
Let $X$ have finite outer measure. Since $U_n$ is measurable,
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
m_e(X\cap T_n) &= m_e(X\cap T_n\cap U_n)+ m_e(X\cap T_n\cap U_n^c) \\
|
||||
&= m_e(X\cap U_n)+ m_e(X\cap T_{n-1}) \\
|
||||
&= \sum_{j=1}^{n}m_e(X\cap U_j)
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Since $T_n$ is measurable and $T_n\subset S$, $S^c\subset T_n^c$. $m_e(X\cap T_n^c)\geq m_e(X\cap S^c)$.
|
||||
|
||||
Therefore,
|
||||
|
||||
$$
|
||||
m_e(X)=m_e(X\cap T_n)+m_e(X\cap T_n^c)\\
|
||||
\geq \sum_{j=1}^{n}m_e(X\cap U_j)+m_e(X\cap S^c)
|
||||
$$
|
||||
|
||||
Take the limit as $n\to\infty$,
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
m_e(X) &\geq \sum_{j=1}^{\infty}m_e(X\cap U_j)+m_e(X\cap S^c) \\
|
||||
&= m_e(\bigcup_{j=1}^{\infty}(X\cap U_j))+m_e(X\cap S^c) \\
|
||||
&= m_e(X\cap S)+m_e(X\cap S^c) \\
|
||||
&\geq m_e(X)
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Therefore, $m_e(X\cap S)=m_e(X)$.
|
||||
|
||||
Therefore, $S$ is measurable.
|
||||
|
||||
</details>
|
||||
|
||||
#### Corollary from the proof
|
||||
|
||||
Every open or closed set is Lebesgue measurable.
|
||||
|
||||
(Every open set is a countable union of disjoint open intervals)
|
||||
@@ -1,86 +0,0 @@
|
||||
# Math4121 Lecture 3
|
||||
|
||||
## Continue on Differentiation
|
||||
|
||||
### Mean Value Theorem
|
||||
|
||||
#### Theorem 5.9 Generalized Mean Value Theorem
|
||||
|
||||
If $f,g:[a,b]\to \mathbb{R}$ are continuous on $[a,b]$ and differentiable in $(a,b)$, then there exists a point $x\in (a,b)$ such that
|
||||
|
||||
$$
|
||||
[f(b)-f(a)]g'(x)=[g(b)-g(a)]f'(x)
|
||||
$$
|
||||
|
||||
Proof:
|
||||
|
||||
Define $h(x)=[f(b)-f(a)]g(x)-[g(b)-g(a)]f(x)$, $t\in [a,b]$.
|
||||
|
||||
We need to show that there exists a point $x\in (a,b)$ such that $h'(x)=0$.
|
||||
|
||||
By previous theorem, it's enough to show that $h$ has a local minimum or maximum in $(a,b)$. By [Extreme Value Theorem](https://notenextra.trance-0.com/Math4111/Math4111_L24#theorem-416-extreme-value-theorem)
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
h(a)&=[f(b)-f(a)]g(a)-[g(b)-g(a)]f(a)\\
|
||||
&=f(b)g(a)-f(a)g(b)\\
|
||||
h(b)&=[f(b)-f(a)]g(b)-[g(b)-g(a)]f(b)\\
|
||||
&=g(a)f(b)-g(b)f(a)
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
So $h(a)=h(b)$.
|
||||
|
||||
Consider three cases:
|
||||
|
||||
1. $h$ is constant on $[a,b]$. Then $h'(x)=0$ for all $x\in (a,b)$.
|
||||
2. $\exists t\in (a,b)$ such that $h(t)>h(a)=h(b)$. Since every continuous function on a compact interval attains its supremum, and $h(t)>h(a)=h(b)$, the supremum of $h$ on $[a,b]$ is attained at some point $x\in (a,b)$. (Apply [Extreme Value Theorem](https://notenextra.trance-0.com/Math4111/Math4111_L24#theorem-416-extreme-value-theorem) to $h$ on $[a,b]$.)
|
||||
3. $\exists t\in (a,b)$ such that $h(t)<h(a)=h(b)$. Since every continuous function on a compact interval attains its infimum, and $h(t)<h(a)=h(b)$, the infimum of $h$ on $[a,b]$ is attained at some point $x\in (a,b)$. (Apply [Extreme Value Theorem](https://notenextra.trance-0.com/Math4111/Math4111_L24#theorem-416-extreme-value-theorem) to $h$ on $[a,b]$.)
|
||||
|
||||
In all cases, $h$ has a local minimum or maximum in $(a,b)$.
|
||||
|
||||
QED
|
||||
|
||||
#### Theorem 5.10 Mean Value Theorem
|
||||
|
||||
The mean value theorem is a special case of the generalized mean value theorem when $g(x)=x$ (the identity function).
|
||||
|
||||
If $f:[a,b]\to \mathbb{R}$ is continuous on $[a,b]$ and differentiable on $(a,b)$, then there exists a point $x\in (a,b)$ such that
|
||||
|
||||
$$
|
||||
f(b)-f(a)=f'(x)(b-a)
|
||||
$$
|
||||
|
||||
### Intermediate Value Theorem
|
||||
|
||||
#### Definition 5.12.1 Intermediate Value
|
||||
|
||||
We say that $f:[a,b]\to \mathbb{R}$ attains the intermediate values if for each $\lambda\in (f(a),f(b))$ there exists a point $x\in (a,b)$ such that $f(x)=\lambda$.
|
||||
|
||||
#### Theorem 5.12.2 Continuous Function attains Intermediate Values
|
||||
|
||||
If $f:[a,b]\to \mathbb{R}$ is continuous on $[a,b]$, then $f$ attains every value between $f(a)$ and $f(b)$.
|
||||
|
||||
#### Theorem 5.12 Intermediate Value Theorem
|
||||
|
||||
If $f:[a,b]\to \mathbb{R}$ is differentiable on $[a,b]$. Then $f'$ attains intermediate values.
|
||||
|
||||
Proof:
|
||||
|
||||
Let $\lambda\in (f'(a),f'(b))$.
|
||||
|
||||
Let our auxiliary function be $g(t)=f(t)-\lambda t$.
|
||||
|
||||
Since $g'(t)=f'(t)-\lambda$, it suffices to find $x\in (a,b)$ such that $g'(x)=0$.
|
||||
|
||||
$g'(a)<0$ and $g'(b)>0$.
|
||||
|
||||
We claim that $\exists t_1\in (a,b)$ such that $g(t_1)<g(a)$.
|
||||
|
||||
If this were false, then for all $t\in (a,b)$ we would have $g(t)\geq g(a)$.
|
||||
|
||||
$$
|
||||
\frac{g(t)-g(a)}{t-a}\geq 0\\
|
||||
$$
|
||||
|
||||
Continue on Monday.
|
||||
@@ -1,96 +0,0 @@
|
||||
# Math4121 Lecture 30
|
||||
|
||||
## Lebesgue Measure
|
||||
|
||||
$\mathfrak{M}=\{S\subseteq\mathbb{R}:S\text{ is Lebesgue measurable}\}$ is a $\sigma$-algebra on $\mathbb{R}$ (closed under complementation and countable unions).
|
||||
|
||||
### Consequence of Lebesgue Measure
|
||||
|
||||
Every open set and closed set is Lebesgue measurable.
|
||||
|
||||
#### Inner and Outer Regularity of Lebesgue Measure
|
||||
|
||||
Outer regularity:
|
||||
$$
|
||||
m_e(S)=\inf_{U\text{ open},S\subseteq U}m(U)
|
||||
$$
|
||||
|
||||
Inner regularity:
|
||||
$$
|
||||
m_i(S)=\sup_{K\text{ closed},K\subseteq S}m(K)
|
||||
$$
|
||||
|
||||
<details>
|
||||
<summary>Proof</summary>
|
||||
|
||||
Inner regularity:
|
||||
|
||||
Since $m_i(S)=m(I)-m_e(I\setminus S)$, $S\subseteq I$ for some closed interval $I$. Let $\epsilon>0$ and $U$ be an open set such that $I\setminus S\subseteq U$ and $m(U)<m(I\setminus S)+\epsilon$.
|
||||
|
||||
Take $K=I\setminus U$. Then $K\subseteq S$ and $K$ is closed and
|
||||
|
||||
$$
|
||||
m(K)=m(I)-m(U)>m(I)-m(I\setminus S)-\epsilon
|
||||
$$
|
||||
|
||||
So $m_i(S)<m(K)+\epsilon$. Since $\epsilon$ is arbitrary, $m_i(S)\leq m_e(S)$.
|
||||
|
||||
</details>
|
||||
|
||||
We can approximate $m(S)$ from outside by open sets. If we are just concerned with "approximating" $m(S)$, we can use finite union of intervals.
|
||||
|
||||
#### Symmetric difference
|
||||
|
||||
The symmetric difference of two sets $S$ and $T$ is defined as
|
||||
|
||||
$$
|
||||
S\Delta T=(S\setminus T)\cup(T\setminus S)
|
||||
$$
|
||||
|
||||
_The XOR operation on two sets._
|
||||
|
||||
#### Theorem
|
||||
|
||||
If $S\subset I$ is measurable, then for every $\epsilon>0$, $\exists I_1,I_2,\cdots,I_n\subset I$ open intervals such that
|
||||
|
||||
$$
|
||||
m(S\Delta U)<\epsilon
|
||||
$$
|
||||
|
||||
where $U=\bigcup_{j =1}^n I_j$.
|
||||
|
||||
<details>
|
||||
<summary>Proof</summary>
|
||||
|
||||
Let $\epsilon>0$ and $m(V)<m(S)+\frac{\epsilon}{2}$. Let $K\subseteq S$ be closed set such that $m(S)-\frac{\epsilon}{2}<m(K)$. $V$ is an open cover of closed and bounded set $K$. By Heine-Borel theorem, $K$ has a finite subcover. Let $I_1,I_2,\cdots,I_n$ be the open intervals in the subcover.
|
||||
|
||||
Check:
|
||||
|
||||
$$
|
||||
m(S\Delta U)=m(S\setminus U)+m(U\setminus S)\leq m(S\setminus K)+m(U\setminus S)<\epsilon
|
||||
$$
|
||||
|
||||
</details>
|
||||
|
||||
Recall $\{T_j\}_{j=1}^\infty$ are disjoint measurable sets. Then $T=\bigcup_{j=1}^\infty T_j$ is measurable and
|
||||
|
||||
$$
|
||||
m(T)=\sum_{j=1}^\infty m(T_j)
|
||||
$$
|
||||
|
||||
#### Corollary (Better osgood's theorem on Lebesgue measure)
|
||||
|
||||
If $S_1\subseteq S_2\subseteq S_3\subseteq\cdots$ are measruable (no need to be closed and bounded) and $S=\bigcup_{j=1}^\infty S_j$, then
|
||||
|
||||
$$
|
||||
m(S)=\lim_{j\to\infty}m(S_j)
|
||||
$$
|
||||
|
||||
Proof:
|
||||
|
||||
Let $T_1=S_1$ and $T_i=S_i\setminus S_{i-1}$ for $i\geq 2$. Still have $S=\bigcup_{j=1}^\infty T_j$.
|
||||
|
||||
Where $T_i$ are disjoint measurable sets. So $m(S)=\sum_{j=1}^\infty m(T_j)$.
|
||||
|
||||
So $\lim_{j\to\infty}m(S_j)=\sum_{j=1}^\infty m(T_j)=m(S)$.
|
||||
|
||||
@@ -1,92 +0,0 @@
|
||||
# Math4121 Lecture 31
|
||||
|
||||
## Chapter 3: Lebesgue Integration
|
||||
|
||||
### Non-measurable sets
|
||||
|
||||
#### Definition: Vitali's construction
|
||||
|
||||
Step 1. Define an equivalence relation on $\mathbb{R}$ as follows:
|
||||
|
||||
Recall a relation is an equivalence relation if it is reflexive, symmetric, and transitive.
|
||||
|
||||
1. Reflexive: $x\sim x$ for all $x\in\mathbb{R}$
|
||||
2. Symmetric: $x\sim y$ implies $y\sim x$ for all $x,y\in\mathbb{R}$
|
||||
3. Transitive: $x\sim y$ and $y\sim z$ implies $x\sim z$ for all $x,y,z\in\mathbb{R}$
|
||||
|
||||
Say $x\sim y$ if $x-y\in\mathbb{Q}$.
|
||||
|
||||
This is an equivalence relation, easy to show by the properties above.
|
||||
|
||||
We denote the equivalence class of $x$ by $\mathbb{R}/\sim$, where $[x]=\{x+q:q\in\mathbb{Q}\}$.
|
||||
|
||||
If $z\in [x]$, then so is the fractional part of $z$, i.e. $z-\lfloor z\rfloor\in [x]$. So in every equivalence class $[x]$ we can find an element in $[x]\cap (0,1)$. Take one such real number from every equivalence class, and call the set of all such numbers $\mathcal{N}$.
|
||||
|
||||
Step 2. Show that $\mathcal{N}$ is not Lebesgue measurable.
|
||||
|
||||
We defined the translation of $S$ as follows:
|
||||
|
||||
Given a set $S\subseteq\mathbb{R}$ and a real number $a\in\mathbb{R}$, the translation of $S$ by $a$ is defined as
|
||||
|
||||
$$
|
||||
S+a=\{x+a:x\in S\}
|
||||
$$
|
||||
|
||||
Outer measure is translation invariant, i.e. $m_e(S+a)=m_e(S)$ for all $S\subseteq\mathbb{R}$ and $a\in\mathbb{R}$, which also holds for inner measure.
|
||||
|
||||
Properties of $\mathcal{N}$:
|
||||
|
||||
1. $(0,1)\subseteq\bigcup_{q\in \mathbb{Q}\cap (-1,1)} (\mathcal{N}+q)\subseteq (-1,2)$
|
||||
2. $\{\mathcal{N}+q:q\in\mathbb{Q}\cap (-1,1)\}$ is pairwise disjoint.
|
||||
|
||||
Suppose $\mathcal{N}$ is measurable. Then by (1)
|
||||
$$
|
||||
\begin{aligned}
|
||||
1&\leq \sum_{q\in\mathbb{Q}\cap (-1,1)} (\mathcal{N}+q)\\
|
||||
&=\sum_{q\in\mathbb{Q}\cap (-1,1)} m(\mathcal{N})
|
||||
\end{aligned}
|
||||
$$
|
||||
So $m(\mathcal{N})\neq 0$.
|
||||
|
||||
By (2), we have
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
3&\geq \sum_{q\in\mathbb{Q}\cap (-1,1)} m(\mathcal{N}+q)\\
|
||||
&=\sum_{q\in\mathbb{Q}\cap (-1,1)} m(\mathcal{N})\\
|
||||
&=m(\mathcal{N})\sum_{q\in\mathbb{Q}\cap (-1,1)} 1\\
|
||||
&=\infty
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
This is a contradiction. So $\mathcal{N}$ is not Lebesgue measurable.
|
||||
|
||||
QED
|
||||
|
||||
Appendix:
|
||||
|
||||
(1) $I\subseteq\bigcup_{q\in\mathbb{Q}\cap (-1,1)} (\mathcal{N}+q)$
|
||||
|
||||
Let $x\in I$. We need to find $q\in\mathbb{Q}\cap (-1,1)$ such that $x-q\in\mathcal{N}$. $\exists y\in\mathcal{N}$ such that $y\in (0,1)\cap [x]$. Then $x-y=q\in \mathbb{Q}$ and since $x,y\in I$, we have $q\in (-1,1)$.
|
||||
|
||||
(2) $\{\mathcal{N}+q:q\in\mathbb{Q}\cap (-1,1)\}$ is pairwise disjoint.
|
||||
|
||||
Suppose $\mathcal{N}+q_1=\mathcal{N}+q_2$ for some $q_1,q_2\in\mathbb{Q}\cap (-1,1)$. We want to show $q_1=q_2$.
|
||||
|
||||
Take $x$ in the intersection, then this means $y=x-q_1, z=x-q_2\in\mathcal{N}$.
|
||||
|
||||
But $y\sim z$, this contradicts the fact that $\mathcal{N}$ contains only one element from each equivalence class. So $q_1=q_2$.
|
||||
|
||||
#### Axiom of choice
|
||||
|
||||
Given a set $S$, $\exists \psi:\mathscr{P}(S)\to S$ such that $\psi(T)\in T, \forall T\subseteq\mathscr{P}(S)$.
|
||||
|
||||
For any set $S$, there exists a map that maps every non-empty subset of $S$ to an element of that subset.
|
||||
|
||||
This leads to some weird results, e.g. Banach-Tarski paradox.
|
||||
|
||||
_Godel showed that the axiom of choice is not contradictory to ZF set theory._ You have ZFC
|
||||
|
||||
_Cohen showed that the negation of the axiom of choice is not contradictory to ZF set theory._ You have ZF
|
||||
|
||||
You can choose the axiom or not.
|
||||
@@ -1,99 +0,0 @@
|
||||
# Math4121 Lecture 32
|
||||
|
||||
## Chapter 6: The Lebesgue Integral
|
||||
|
||||
### Measurable Functions
|
||||
|
||||
Definition: A function $f:\mathbb{R}\to\mathbb{R}$ is measurable on the interval $[a,b]$ if $\{x\in [a,b]:f(x) > c\}$ is measurable for all $c\in\mathbb{R}$, called the **super level set** of $f$.
|
||||
|
||||
Denote $\{f> c\}$
|
||||
|
||||
#### Proposition 6.1
|
||||
|
||||
The following are equivalent:
|
||||
|
||||
For all $c\in\mathbb{R}$,
|
||||
|
||||
1. $\{x\in [a,b]:f(x) > c\}$ is measurable.
|
||||
2. $\{x\in [a,b]:f(x) < c\}$ is measurable.
|
||||
3. $\{x\in [a,b]:f(x) \geq c\}$ is measurable.
|
||||
4. $\{x\in [a,b]:f(x) \leq c\}$ is measurable.
|
||||
5. $\{x\in \mathbb{R}:c \leq f(x) < d\}$ is measurable for all $c,d\in\mathbb{R}$.
|
||||
|
||||
Proof:
|
||||
|
||||
Since the complement of a measurable set is measurable. (1) $\iff$ (4). and (2) $\iff$ (3).
|
||||
|
||||
We only need to show (1) $\implies$ (2).
|
||||
|
||||
Since $\{f>c\}=\bigcup_{n=1}^{\infty}\{f\geq c+\frac{1}{n}\}$.
|
||||
|
||||
So (1) $\implies$ (2).
|
||||
|
||||
Since (2) $\implies$ (1)-(4) $\implies$ (5).
|
||||
|
||||
To see (5) $\implies$ (1), we have $\{f\geq c\}=\bigcup_{n=1}^{\infty}\{x\in\mathbb{R}:c \leq f(x) < c+n\}$
|
||||
|
||||
QED
|
||||
|
||||
#### Proposition 6.3
|
||||
|
||||
Let $f,g$ be measurable on $[a,b]$ and $\alpha\in\mathbb{R}$. Then the following are measurable:
|
||||
|
||||
1. $f+g$
|
||||
2. $fg$
|
||||
3. $\alpha f$
|
||||
4. $|f|^\alpha$
|
||||
|
||||
Proof:
|
||||
|
||||
If $\alpha=0$, then $\alpha f$ and $|f|^\alpha$ are constant functions, hence measurable.
|
||||
|
||||
But for constant functions $h$, $\{h>c\}=\begin{cases}
|
||||
\emptyset & \text{if } c\geq h \\
|
||||
\mathbb{R} & \text{if } c < h
|
||||
\end{cases}$
|
||||
|
||||
For $a\neq 0$, $\{x\in \mathbb{R}:\alpha f(x) > c\}=\{x\in \mathbb{R}:f(x) > \frac{c}{\alpha}\}$
|
||||
|
||||
Similarly, $\{x\in \mathbb{R}:|f(x)|^\alpha > c\}=\{x\in \mathbb{R}:|f(x)| > c^{1/\alpha}\}=\{x\in \mathbb{R}:f(x) > c^{1/\alpha}\}\cup\{x\in \mathbb{R}:f(x) < -c^{1/\alpha}\}$
|
||||
|
||||
We want to show $\{f+g>c\}=\bigcup_{q\in \mathbb{Q}}\{f>q\}\cap\{g>c-q\}$
|
||||
|
||||
$\{f+g>c\}\supseteq \bigcup_{q\in \mathbb{Q}}\{f>q\}\cap\{g>c-q\}$
|
||||
|
||||
if $x$ is in the RHS, then $\exists q\in \mathbb{Q}$ such that $f(x) > q$ and $g(x) > c-q$, therefore $f(x)+g(x) > c$.
|
||||
|
||||
So $x$ is in the LHS.
|
||||
|
||||
$\{f+g>c\}\subseteq \bigcup_{q\in \mathbb{Q}}\{f>q\}\cap\{g>c-q\}$
|
||||
|
||||
Let $x\in \mathbb{R}$ such that $f(x)+g(x) > c$. Need to find $q\in \mathbb{Q}$ such that $f(x) > q$ and $g(x) > c-q$.
|
||||
|
||||
Since $f(x)>c-g(x)$, by the density of $\mathbb{Q}$ in $\mathbb{R}$, $\exists q\in \mathbb{Q}$ such that $q > c-g(x)$.
|
||||
|
||||
For $fg$, we have $fg=\frac{1}{4}((f+g)^2-(f-g)^2)$
|
||||
|
||||
So $fg$ is measurable.
|
||||
|
||||
QED
|
||||
|
||||
### Limit of Measurable Functions
|
||||
|
||||
#### Proposition 6.4
|
||||
|
||||
Let $\{f_n\}$ be a sequence of measurable functions on $[a,b]$. Then,
|
||||
|
||||
$$
|
||||
g(x)=\sup_{n\geq 1}f_n(x),\inf_{n\geq 1}f_n(x),\limsup_{n\to\infty}f_n(x),\liminf_{n\to\infty}f_n(x)
|
||||
$$
|
||||
|
||||
are all measurable functions
|
||||
|
||||
#### Corollary of Proposition 6.4
|
||||
|
||||
If $\{f_n\}_{n=1}^{\infty}$ are measurable functions and $f(x)=\lim_{n\to\infty}f_n(x)$ exists for all $x\in[a,b]$, then $f$ is measurable. (pointwise limit of measurable functions is measurable)
|
||||
|
||||
#### Definition of almost everywhere
|
||||
|
||||
A property holds **almost everywhere** if it holds everywhere except for a set of measure zero.
|
||||
@@ -1,107 +0,0 @@
|
||||
# Math4121 L33
|
||||
|
||||
## Continue on Lebegue integration
|
||||
|
||||
### Sequence of functions
|
||||
|
||||
#### Proposition 6.4
|
||||
|
||||
Let $f_n$ be a sequence of measurable functions, then $\sup_n f_n,\inf_n f_n, \limsup_n f_n, \liminf_n f_n$ are measurable.
|
||||
|
||||
Proof:
|
||||
|
||||
Consider the set $\{x\in \mathbb{R}, \sup_n f_n\leq c\}$.
|
||||
This is the set of $x$ such that $f_n(x)\leq c$ for all $n$.
|
||||
|
||||
$\bigcap_{n=1}^{\infty} \{x\in \mathbb{R}, f_n(x)\leq c\} \subset \{x\in \mathbb{R}, \sup_n f_n(x)\leq c\}$, by the definition of least upper bound.
|
||||
|
||||
Since the set on the right is intersection of measurable sets, it is measurable.
|
||||
|
||||
Therefore, $\sup_n f_n$ is measurable.
|
||||
|
||||
The proof for $\inf_n f_n, \limsup_n f_n, \liminf_n f_n$ are similar.
|
||||
|
||||
Consider ${x\in \mathbb{R}, \inf_n f_n\leq c}=\bigcap_{n=1}^{\infty} \{x\in \mathbb{R}, f_n(x)\geq c\}$.
|
||||
|
||||
$\limsup_n f_n(x)=\inf_n \sup_{k\geq n} f_k(x)$ is measurable by $\sup_{k\geq n} f_k(x)$ is measurable.
|
||||
|
||||
$\liminf_n f_n(x)=\sup_n \inf_{k\geq n} f_k(x)$ is measurable by $\inf_{k\geq n} f_k(x)$ is measurable.
|
||||
|
||||
QED
|
||||
|
||||
#### Lemma of function of almost everywhere
|
||||
|
||||
If $f$ is measurable function and $f(x)=g(x)$ for almost every $x$ (on a set which the complement has Lebesgue measure $0$), then $g$ is measurable.
|
||||
|
||||
Proof:
|
||||
|
||||
Let $c\in \mathbb{R}$, $F_1=\{x\in \mathbb{R}, f(x)>c\}$, $F_2=\{x\in \mathbb{R}, g(x)>c\}$.
|
||||
|
||||
Recall the symmetric difference $F_1\triangle F_2=\{x\in \mathbb{R}, f(x)\neq g(x)\}$. By the definition of $g$, $F_1\triangle F_2$ has a measure $0$.
|
||||
|
||||
In particular, all subsets of the $F_1\triangle F_2$ are measurable.
|
||||
|
||||
Notice that $F_2=(F_1\setminus F_2)\cup (F_1\setminus (F_1\setminus F_2))$.
|
||||
|
||||
Since $F_1\setminus F_2$ is measurable and $F_1$ is measurable, then $F_2$ is measurable.
|
||||
|
||||
QED
|
||||
|
||||
Example of measurable functions:
|
||||
|
||||
- Continuous functions are measurable.
|
||||
|
||||
$\{x:f(x)>c\}=\{x:f(x)\in (c,\infty)\}=f^{-1}(c,\infty)$ is open (by open mapping theorem, or the definition of continuity in topology).
|
||||
|
||||
- Riemann integrable functions are measurable.
|
||||
|
||||
Outer content of the discontinuity of the function is $0$.
|
||||
|
||||
$\forall \sigma>0$, where $S_\sigma=\{x\in [a,b]: w(f,x)>\sigma\}$, $m(S_\sigma)=0$.
|
||||
|
||||
$S=\bigcup_{n=1}^{\infty} S_{\frac{1}{n}}$ has a measure $0$. So $f$ is continuous outside a set of measure $0$.
|
||||
|
||||
$m(S)\leq \sum_{n=1}^{\infty} m(S_{\frac{1}{n}})=0$. ~~So $f$ agrees with a continuous function outside a set of measure $0$. (almost everywhere)~~ (detailed proof in the textbook)
|
||||
|
||||
#### Theorem 6.6
|
||||
|
||||
Let $f_n$ be a sequence of measurable functions and $f$ is a function satisfying $\lim_{n\to\infty} f_n(x)=f(x)$ for almost every $x$ (holds for sets which the complement has Lebesgue measure $0$).
|
||||
|
||||
Then $f(x)=\lim_{n\to\infty} f_n(x)$ is a measurable function.
|
||||
|
||||
_Notice that $f(x)$ is defined "everywhere"_
|
||||
|
||||
Proof:
|
||||
|
||||
Apply the lemma of function of almost everywhere to the sequence $f_n$.
|
||||
|
||||
QED
|
||||
|
||||
#### Definition of simple function
|
||||
|
||||
A measurable function $\phi:\mathbb{R}\to\mathbb{R}$ is called a simple function if it takes only finitely many values.
|
||||
|
||||
$$
|
||||
\text{range}(\phi)=\{d(x):x\in \mathbb{R}\}\subset \mathbb{R}
|
||||
$$
|
||||
|
||||
has finitely many values.
|
||||
|
||||
Equivalently, $\exists \{a_1,a_2,\cdots,a_n\}\subset \mathbb{R}$ and disjoint measurable sets $S_1,S_2,\cdots,S_n$ such that
|
||||
|
||||
$$
|
||||
\phi(x)=\sum_{i=1}^{n} a_i \chi_{S_i}(x)
|
||||
$$
|
||||
|
||||
where $\chi_{S_i}$ is the indicator function of $S_i$.
|
||||
|
||||
#### Theorem 6.7
|
||||
|
||||
A function $f$ is measurable if and only if there exists a sequence of simple functions $\{\phi_n\}$ such that $\lim_{n\to\infty} \phi_n(x)=f(x)$ for almost every $x$.
|
||||
|
||||
$f$ is a limit of almost everywhere convergent sequence of simple functions.
|
||||
|
||||
(already proved backward direction)
|
||||
|
||||
Continue on Monday.
|
||||
|
||||
@@ -1,141 +0,0 @@
|
||||
# Math4121 Lecture 34
|
||||
|
||||
> Important:
|
||||
>
|
||||
> $\mathfrak{M}=\{S\subset \mathbb{R}: S \text{ satisfies the caratheodory condition}\}$, that is, for any $X$ of finite outer measure,
|
||||
>
|
||||
> $$m_e(X)=m_e(X\cap S)+m_e(X\cap S^c)$$
|
||||
>
|
||||
> In particular, the measure of sets can be infinite, not necessarily bounded. (We want to make the real line measurable.)
|
||||
|
||||
## Lebesgue Integral
|
||||
|
||||
### Simple Function
|
||||
|
||||
A function $\phi$ is called a simple function if
|
||||
|
||||
$$
|
||||
\phi(x)=\sum_{i=1}^{n} a_i \chi_{S_i}(x)
|
||||
$$
|
||||
|
||||
where $a_i\in \mathbb{R}$ and $\chi_{S_i}=\begin{cases}1, & x\in S_i \\ 0, & x\notin S_i\end{cases}$
|
||||
|
||||
where $\{S_i\}_{i=1}^{n}$ are pairwise disjoint each having finite measure.
|
||||
|
||||
**constant function** is not simple ($\mathbb{R}$ is not finite measurable sets.)
|
||||
|
||||
#### Theorem 6.6
|
||||
|
||||
A function $f$ is measurable on $[a,b]$ if and only if there exists a sequence of simple functions $\{\phi_n\}$ such that $\lim_{n\to\infty} \phi_n(x)=f(x)$ almost everywhere on $[a,b]$.
|
||||
|
||||
Proof:
|
||||
|
||||
Partition $[-n,n]$ into $n2^{n+1}$ pieces.
|
||||
|
||||
(These are just horizontal strips from $-n$ to $n$ with width $\frac{1}{2^n}$.)
|
||||
|
||||
$$
|
||||
E_{n,k}=\{x\in[-n,n]:\frac{k}{2^n}\leq f(x)<\frac{k+1}{2^n}\}
|
||||
$$
|
||||
|
||||
for $-n2^n<k<n2^n$
|
||||
|
||||
$$
|
||||
E_{n,n2^n}=\{x\in[-n,n]:f(x)\geq n\}
|
||||
$$
|
||||
|
||||
$$
|
||||
E_{n,-n2^n}=\{x\in[-n,n]:f(x)<\frac{-n2^n+1}{2^n}\}
|
||||
$$
|
||||
|
||||
$$
|
||||
\phi_n(x)=\frac{k}{2^n}\chi_{E_{n,k}}(x)
|
||||
$$
|
||||
|
||||
is a simple function.
|
||||
|
||||
We need to justify that $\phi_n(x)\to f(x)$ for all $x\in\mathbb{R}$.
|
||||
|
||||
Let $x\in\mathbb{R}$. And choose $n_0$ large such that $x\in [-n_0,n_0]$ and $f(x)\in [-n_0,n_0]$.
|
||||
|
||||
Then, for $n\geq n_0$,
|
||||
|
||||
$$
|
||||
|\phi_n(x)-f(x)|<\frac{1}{2^n}\to 0
|
||||
$$
|
||||
|
||||
as $n\to\infty$.
|
||||
|
||||
QED
|
||||
|
||||
### Integration
|
||||
|
||||
Given a measurable set $E$ and a simple function $\phi$, we define
|
||||
|
||||
$$
|
||||
\int_E \phi dm=\sum_{i=1}^{n} a_i m(E\cap S_i)
|
||||
$$
|
||||
|
||||
#### Properties 6.10
|
||||
|
||||
Let $\phi$ and $\psi$ be simple functions, $c\in \mathbb{R}$, and $E=E_1\cup E_2$ where $E_1\cap E_2=\emptyset$ and $E_1,E_2\in \mathfrak{M}$. Then,
|
||||
|
||||
1. $\int_E c\phi dm=c\int_E \phi dm$ (linearity)
|
||||
2. $\int_E (\phi+\psi)dm=\int_E \phi dm+\int_E \psi dm$ (additivity of simple functions)
|
||||
3. if $\phi(x)\leq \psi(x)$ for all $x\in E$, then $\int_E \phi dm\leq \int_E \psi dm$ (monotonicity)
|
||||
4. $\int_E \phi(x)dm=\int_{E_1} \phi(x)dm+\int_{E_2} \phi(x)dm$ (additivity over **disjoint** measurable sets)
|
||||
|
||||
Proof:
|
||||
|
||||
Let $\phi(x)=\sum_{i=1}^{n} a_i \chi_{S_i}(x)$ and $\psi(x)=\sum_{j=1}^{m} b_j \chi_{T_j}(x)$.
|
||||
|
||||
2.
|
||||
|
||||
$$
|
||||
\phi+\psi=\sum_{i=1}^{n} a_i \chi_{S_i}+\sum_{j=1}^{m} b_j \chi_{T_j}
|
||||
$$
|
||||
|
||||
Without loss of generality, we may assume that $x\in E$, $\bigcup_{i=1}^{n} S_i=\bigcup_{j=1}^{m} T_j=E$.
|
||||
|
||||
So
|
||||
|
||||
$$
|
||||
\phi+\psi=\sum_{i,j=1}^{n,m}(a_i+b_j) \chi_{S_i\cup T_j}
|
||||
$$
|
||||
|
||||
is a simple function.
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\int_E (\phi+\psi)dm&=\sum_{i,j=1}^{n,m}(a_i+b_j) m(E\cap S_i\cup T_j) \\
|
||||
&=\sum_{i=1}^{n} a_i \sum_{j=1}^{m} m(E\cap S_i\cup T_j)+\sum_{j=1}^{m} b_j \sum_{i=1}^{n} m(E\cap S_i\cup T_j) \\
|
||||
&=\sum_{i=1}^{n} a_i m(E\cap S_i)+\sum_{j=1}^{m} b_j m(E\cap T_j) \\
|
||||
&=\int_E \phi dm+\int_E \psi dm
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
3.
|
||||
|
||||
$$
|
||||
\phi(x)=\sum_{i=1}^{n} a_i\sum_{j=1}^{m} \chi_{S_i\cap T_j}(x)
|
||||
$$
|
||||
|
||||
$$
|
||||
\psi(x)=\sum_{i=1}^{n} b_i\sum_{j=1}^{m} \chi_{S_i\cap T_j}(x)
|
||||
$$
|
||||
|
||||
If $x\in S_i\cap T_j$, then $\phi(x)=a_i$ and $\psi(x)=b_j$, therefore $a_i\leq b_j$.
|
||||
|
||||
So,
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\int_E \phi dm&=\sum_{i=1}^{n} \sum_{j=1}^{m} a_i m(E\cap S_i\cap T_j) \\
|
||||
&\leq \sum_{i=1}^{n} \sum_{j=1}^{m} b_i m(E\cap S_i\cap T_j) \\
|
||||
&=\int_E \psi dm
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
QED
|
||||
|
||||
Back on Wednesday.
|
||||
@@ -1,114 +0,0 @@
|
||||
# Math4121 Lecture 35
|
||||
|
||||
## Continue on Lebesgue Integration
|
||||
|
||||
### Lebesgue Integration
|
||||
|
||||
#### Definition of Lebesgue Integral
|
||||
|
||||
For simple functions $\phi = \sum_{i=1}^{n} a_i \chi_{S_i}$, given a measure $E$, the Lebesgue integral is defined as:
|
||||
|
||||
$$
|
||||
\int_{\mathbb{R}^n} \phi \, dm = \sum_{i=1}^{n} a_i m(S_i\cap E)
|
||||
$$
|
||||
|
||||
|
||||
Given a non-negative measurable function $f$ and a measurable set $E$.
|
||||
|
||||
Define $\int_E f \, dm = \sup \left\{ \int_E \phi \, dm : \phi \text{ is a simple function and } \phi \leq f \right\}$
|
||||
|
||||
(**We do allows $\int_E f \, dm = \infty$**)
|
||||
|
||||
For general measurable function $f$, we can define $f^-(x)=\max\{0,-f(x)\}$, $f^+(x)=\max\{0,f(x)\}$. (The positive part of the function and the negative part of the function, both non-negative)
|
||||
|
||||
Then $f=f^+-f^-$.
|
||||
|
||||
We say $f$ is integrable if $\int_E f^+ \, dm < \infty$ and $\int_E f^- \, dm < \infty$. (both finite) If at least one is finite, define
|
||||
|
||||
$$
|
||||
\int_E f \, dm = \int_E f^+ \, dm - \int_E f^- \, dm
|
||||
$$
|
||||
|
||||
We allow for $A-\infty = -\infty$ and $A+\infty = \infty$ for any $A\in \mathbb{R}$. But not $\infty-\infty$.
|
||||
|
||||
#### Immediate Properties of Lebesgue Integral
|
||||
|
||||
If $f$ is measurable and $m(E)=0$, then $\int_E f \, dm = 0$.
|
||||
|
||||
If $E=E_1\cup E_2$ and $E_1\cap E_2=\emptyset$, then $\int_E f \, dm = \int_{E_1} f \, dm + \int_{E_2} f \, dm$.
|
||||
|
||||
#### Corollary
|
||||
|
||||
If $f\leq g$ almost everywhere, ($f\leq g$ except for a set of measure 0), then $\int_E f \, dm \leq \int_E g \, dm$.
|
||||
|
||||
Proof:
|
||||
|
||||
Let $F=\{x\in E: f(x)>g(x)\}$. Then $m(F)=0$.
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\int_E f \, dm &= \int_{E\setminus F} f \, dm + \int_F f \, dm\\
|
||||
&\leq \int_{E\setminus F} g \, dm+\int_E g \, dm\\
|
||||
&= \int_E g \, dm
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
QED
|
||||
|
||||
#### Proposition 6.13
|
||||
|
||||
If $f$ is non-negative and $\int_E f \, dm =0$, then $f=0$ almost everywhere on $E$, $f(x)=0$ $\forall x\in E\setminus F$, where $m(F)=0$.
|
||||
|
||||
Proof:
|
||||
|
||||
Let $E_n=\{x\in E: f(x)\geq \frac{1}{n}\}$. Then $\frac{1}{n}\chi_{E_n}(x)\leq f(x)$ for all $x\in E$.
|
||||
|
||||
By definition $\frac{1}{n}m(E_n)=\int_E \frac{1}{n}\chi_{E_n} \, dm \leq \int_E f \, dm =0$.
|
||||
|
||||
Therefore, $m(E_n)=0$ for all $n$.
|
||||
|
||||
Now $U=\{x\in E: f(x)>0\}=\bigcup_{n=1}^{\infty} E_n$, and $E_n\subseteq E_{n+1}$ for all $n$.
|
||||
|
||||
Therefore, $m(U)=m(\bigcup_{n=1}^{\infty} E_n)=\lim_{n\to\infty} m(E_n)=0$.
|
||||
|
||||
QED
|
||||
|
||||
### Convergence Theorems
|
||||
|
||||
When does $\lim_{n\to\infty} \int_E f_n \, dm = \int_E \lim_{n\to\infty} f_n \, dm$?
|
||||
|
||||
#### Theorem 6.14 Monotone Convergence Theorem
|
||||
|
||||
Let $\{f_n\}$ be a monotone increasing sequence of measurable functions on $E$ and $f_n\to f$ almost everywhere on $E$. ($f_n(x)\leq f_{n+1}(x)$ for all $x\in E$ and $n$)
|
||||
|
||||
If there exists $A>0$ such that $\left|\int_E f_n \, dm\right|\leq A$ for all $n\in \mathbb{N}$, then $f(x)=\lim_{n\to\infty} f_n(x)$ exists for almost every $x\in E$ and it is integrable on $E$ and
|
||||
|
||||
$$
|
||||
\int_E f \, dm = \lim_{n\to\infty} \int_E f_n \, dm
|
||||
$$
|
||||
|
||||
Proof:
|
||||
|
||||
First to show the limit exists almost everywhere. It suffices to show
|
||||
|
||||
$$
|
||||
\mathcal{U}=\{x\in E: f_n(x) \text{ is unbounded}\}
|
||||
$$
|
||||
|
||||
has measure 0.
|
||||
|
||||
Let $\epsilon>0$ and write
|
||||
|
||||
$$
|
||||
U=\bigcup_{n=1}^{\infty} E_n
|
||||
$$
|
||||
|
||||
where $E_n=\{x\in E: |f_n(x)|\geq \epsilon\}$.
|
||||
|
||||
Then $U\subseteq \mathcal{U}$ and $m(U)<\epsilon$.
|
||||
|
||||
|
||||
CONTINUE NEXT TIME.
|
||||
|
||||
QED
|
||||
|
||||
@@ -1,133 +0,0 @@
|
||||
# Math 4121 Lecture 36
|
||||
|
||||
## Random visit for Lebesgue Integration
|
||||
|
||||
### Convergence Theorem
|
||||
|
||||
#### Theorem 6.14 Monotone Convergence Theorem
|
||||
|
||||
Let $\{f_n\}$ be a monotone increasing sequence of measurable functions on $E$ and $f_n\to f$ almost everywhere on $E$. ($f_n(x)\leq f_{n+1}(x)$ for all $x\in E$ and $n$)
|
||||
|
||||
If there exists $A>0$ such that $\left|\int_E f_n \, dm\right|\leq A$ for all $n\in \mathbb{N}$, then $f(x)=\lim_{n\to\infty} f_n(x)$ exists for almost every $x\in E$ and it is integrable on $E$ and
|
||||
|
||||
$$
|
||||
\int_E f \, dm = \lim_{n\to\infty} \int_E f_n \, dm
|
||||
$$
|
||||
|
||||
Proof:
|
||||
|
||||
To show the limit exists almost everywhere, let $\epsilon>0$, set $E_n=\{x\in E: f_n(x)>\frac{A}{\epsilon}\}$. We will show $U=\bigcup_{n=1}^{\infty} E_n$ has measure $<\epsilon$. $f_n(x)\geq \frac{A}{\epsilon}\chi_{E_n}(x)$, so
|
||||
|
||||
$$
|
||||
\frac{A}{\epsilon}m(E_n)=\int_E \frac{A}{\epsilon}\chi_{E_n}dm\leq \int_E f_n dm\leq A
|
||||
$$
|
||||
|
||||
In particular, $m(E_n)<\epsilon$. Since $E_n\subset E_{n+1}$ for all $n$, $m(U)=\lim_{n\to\infty} m(E_n)<\epsilon$.
|
||||
|
||||
$\lim_{n\to\infty} \int_E f_n dm\leq \int_E f dm\leq \lim_{n\to\infty}$. To show the reverse inequality, let $\phi$ be a simple function $\leq f$ of the form $\phi=\sum_{i=1}^{k} a_i\chi_{S_i}$ where $S_i$ is sidjoint and $\bigcup_{i=1}^{k} S_i\subseteq E$.
|
||||
|
||||
Let $\alpha\in (0,1)$ and set $A_n=\{x\in S:f_n(x)-\alpha\phi(x)>0\}$. This ensures that $f_n(x)\geq \alpha\phi(x)$ for all $x\in A_n$.
|
||||
|
||||
Notice that $A_n\subset A_{n+1}$ for all $n$ and $U=\bigcup_{n=1}^{\infty} A_n$. $lim_{n\to\infty} m(A_n\cap S_i)=m(S_i)$ for all $i$.
|
||||
|
||||
$\int_{A_n} \phi dm=\sum_{i=1}^{k} a_i m(S_i\cap A_n)$.
|
||||
|
||||
As $n\to\infty$, $m(A_n\cap S_i)\to m(S_i)$ and $\sum_{i=1}^{k} a_i m(S_i\cap A_n)\to \int_E \phi dm$.
|
||||
|
||||
Let $\epsilon>0$. There exists $n_0$ large such that $\int_{A_n} \phi dm>\int_E \phi dm-\epsilon$ for all $n\geq n_0$.
|
||||
|
||||
Then for such $n\geq n_0$,
|
||||
|
||||
$$
|
||||
\int_E f_n dm\geq \int_{A_n} f_n dm\geq \int_{A_n} \alpha \phi dm>\alpha(\int_E \phi dm-\epsilon)
|
||||
$$
|
||||
|
||||
So, $\lim_{n\to\infty} \int_E f_n dm\geq \alpha(\int_E \phi dm-\epsilon)$.
|
||||
|
||||
Since $\alpha,\epsilon$ are arbitrary, set $\alpha\to 1$ and $\epsilon\to 0$ to get $\lim_{n\to\infty} \int_E f_n dm\geq \int_E \phi dm$.
|
||||
|
||||
For any simple function $\phi\leq f$, taking sup over all simple functions $\phi\leq f$ gives $\lim_{n\to\infty} \int_E f_n dm\geq \int_E f dm$.
|
||||
|
||||
QED
|
||||
|
||||
#### Lemma Absolute Integrability
|
||||
|
||||
$f$ is integrable on $E$ if and only if $|f|$ is integrable on $E$ and $\left|\int_E f \, dm\right|\leq \int_E |f| \, dm$.
|
||||
|
||||
Proof:
|
||||
|
||||
If $f^+$ and $f^-$ are integrable and $|f|=f^+-f^-$. So setting $E_1=\{x\in E: f(x)\geq 0\}$ and $E_2=\{x\in E: f(x)<0\}$, these are disjoint and $E=E_1\cup E_2$.
|
||||
|
||||
$$
|
||||
\int_E |f| dm=\int_{E_1} f^+ dm+\int_{E_2} f^- dm
|
||||
$$
|
||||
|
||||
For the reverse inequality, note that
|
||||
|
||||
$$
|
||||
\int_E f^+ dm\leq \int_E |f| dm
|
||||
$$
|
||||
|
||||
and
|
||||
|
||||
$$
|
||||
\int_E f^- dm\leq \int_E |f| dm
|
||||
$$
|
||||
|
||||
QED
|
||||
|
||||
#### Corollary Properties of Integrals
|
||||
|
||||
Let $f$ and $g$ be integrable on $E$, and $c\in \mathbb{R}$.
|
||||
|
||||
1. $\int_E (cf) dm=c\int_E f dm$
|
||||
2. $\int_E (f+g) dm=\int_E f dm+\int_E g dm$
|
||||
|
||||
Proof:
|
||||
|
||||
First we prove it for $f,g$ nonnegative and $c\geq 0$.
|
||||
|
||||
Take simple functions $\phi_n\to f$ and $\psi_n\to g$ pointwise. Then $c\phi_n\to cf$ and $\phi_n+\psi_n\to f+g$ pointwise.
|
||||
|
||||
By Monotone Convergence Theorem,
|
||||
|
||||
$$
|
||||
\int_E cf dm=\lim_{n\to\infty} \int_E c\phi_n dm=c\lim_{n\to\infty} \int_E \phi_n dm=c\int_E f dm
|
||||
$$
|
||||
|
||||
Second part leave as homework.
|
||||
|
||||
QED
|
||||
|
||||
### Theorem 6.8
|
||||
|
||||
Riemann integrable functions are Lebesgue integrable and the values of the integrals are the same.
|
||||
|
||||
Proof:
|
||||
|
||||
Say $f$ is Riemann integrable on $[a,b]$. $m\leq f(x)\leq M$ for all $x\in [a,b]$.
|
||||
|
||||
We can find a partition $P_n\subseteq P_{n+1}$ of $[a,b]$ such that $L(P_n,f)\nearrow \int_a^b f dx$ and $U(P_n,f)\searrow \int_a^b f dx$.
|
||||
|
||||
Let $\phi_n=\sum_{i=1}^{k} m_i \chi_{I_i}$ and $\psi_n=\sum_{i=1}^{k} M_i \chi_{I_i}$ where $I_i$ is an interval in $P_n$.
|
||||
|
||||
So $\int_a^b \phi_n dm=L(P_n,f)$ and $\int_a^b \psi_n dm=U(P_n,f)$.
|
||||
|
||||
$m\leq \phi_n\leq f\leq \psi_n\leq M$ for all $n$. almost everywhere.
|
||||
|
||||
By Monotone Convergence Theorem, to $\phi_{n-m}$ we have $g(x)=\lim_{n\to\infty} \phi_n(x)$, $h(x)=\lim_{n\to\infty} \psi_n(x)$ exists for almost every $x\in [a,b]$.
|
||||
|
||||
$g(x)\leq f(x)\leq h(x)$ almost everywhere.
|
||||
|
||||
So
|
||||
|
||||
$$
|
||||
\int_a^b g dm= \int_a^b f dm= \int_a^b h dm =\int_a^b f dx
|
||||
$$
|
||||
|
||||
So $h(x)=f(x)=g(x)$ almost everywhere.
|
||||
|
||||
QED
|
||||
|
||||
|
||||
|
||||
@@ -1,121 +0,0 @@
|
||||
# Math4121 Lecture 37
|
||||
|
||||
## Extended fundamental theorem of calculus with Lebesgue integration
|
||||
|
||||
### Density of continuous functions
|
||||
|
||||
#### Lemma for density of continuous functions
|
||||
|
||||
Let $K\subseteq U$ be bounded sets in $\mathbb{R}$, $K$ is closed and $U$ is open. Then there is a continuous function $g$ such that $\chi_K\leq g\leq \chi_U$.
|
||||
|
||||
Proof in homework.
|
||||
|
||||
Hint: Consider the basic intervals cases.
|
||||
|
||||
#### Theorem for continuous functions
|
||||
|
||||
Let $f$ be integrable. For each $\epsilon>0$, there is a continuous function $g:\mathbb{R}\to\mathbb{R}$ such that $\int_{\mathbb{R}}|f-g|dm<\epsilon$.
|
||||
|
||||
Proof:
|
||||
|
||||
First where $f=\chi_S$ for some bounded means set $S$. then extended to all $f$ integrable.
|
||||
|
||||
First, assume $f=\chi_S$. Let $\epsilon>c$, we can find $K\subseteq S\subseteq U$. and $K$ is closed and $U$ is open such that (by definition of Lebesgue outer measure)
|
||||
|
||||
$$
|
||||
m(K)+\frac{\epsilon}{2}>m(S)>m(U)-\frac{\epsilon}{2}
|
||||
$$
|
||||
|
||||
In particular, $m(U\setminus K)=m(U)-m(K)<\epsilon$.
|
||||
|
||||
By lemma, there is a continuous function $g$ such that $\chi_K\leq g\leq \chi_U$.
|
||||
|
||||
So
|
||||
|
||||
$$
|
||||
\int_E |\chi_S -g|dm=\int_{U\setminus K} |\chi_S -g|dm\leq m(U\setminus K)<\epsilon
|
||||
$$
|
||||
|
||||
For the general case,
|
||||
|
||||
By the Monotone Convergence Theorem (use $|f|\chi_{[-N,N]}$ to approximate $|f|$), we can find $N$ large such that
|
||||
|
||||
$$
|
||||
\int_{E_N^c}|f|dm<\frac{\epsilon}{3}
|
||||
$$
|
||||
|
||||
where $E_N=E\cap [-N,N]$.
|
||||
|
||||
Notice that by the definition of Lebesgue integral, $\int f^+ dm=\sup\{\int \phi^+ dm:\phi\text{ is simple and } \phi\leq f^+\}$ and $\int f^- dm=\sup\{\int \phi^- dm:\phi\text{ is simple and } \phi\leq f^-\}$.
|
||||
|
||||
By considering $f^+$ and $f^-$ separately, we can find a simple function $\phi$ such that
|
||||
|
||||
$$
|
||||
\int_{E_N} |f-\phi|dm<\frac{\epsilon}{3}
|
||||
$$
|
||||
|
||||
For each $i=1,2,\cdots,n$, we can find $g_i$ continuous such that
|
||||
|
||||
$$
|
||||
\int_{E}|\chi_{S_i}-g_i|dm<\frac{\epsilon}{3M}
|
||||
$$
|
||||
|
||||
where $M=\sum_{i=1}^n |\alpha_i|$.
|
||||
|
||||
Take $g=\sum_{i=1}^n \alpha_i g_i$,
|
||||
|
||||
$$
|
||||
\int_E |\phi-g|dm\leq \sum_{i=1}^n |\alpha_i|\int_E |g_i-\chi_{S_i}|dm<\frac{\epsilon}{3}
|
||||
$$
|
||||
|
||||
$\phi-g=\sum_{i=1}^n \alpha_i (\chi_{S_i-g_i})$
|
||||
|
||||
All in all,
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\int_E |f-g|dm&\leq \int_E|f-\phi|dm+\int_E |\phi-g|dm\\
|
||||
&=\int_{E_N^c}|f|dm+\int_E |f-\phi|dm+\int_E |\phi-g|dm\\
|
||||
&<\frac{\epsilon}{3}+\frac{\epsilon}{3}+\frac{\epsilon}{3}\\
|
||||
&=\epsilon
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
QED
|
||||
|
||||
### Road map for proving the fundamental theorem of calculus in Lebesgue integration
|
||||
|
||||
Recall the Riemann-Stieltjes integral:
|
||||
|
||||
If $g\in \mathscr{R}(\alpha)$ on $[a,b]$,
|
||||
|
||||
$G(x)=\int_a^x g d\alpha$,
|
||||
|
||||
then:
|
||||
|
||||
1. $G$ is continuous on $[a,b]$
|
||||
2. If $g$ is continuous at $x\in [a,b]$, then $G$ is differentiable at $x$ with $G'(x)=g(x)$.
|
||||
|
||||
To extend this to the case where $g$ is Lebesgue integrable, we use the Hardy-Littlewood maximal function.
|
||||
|
||||
#### Definition of the Hardy-Littlewood maximal function
|
||||
|
||||
Given an interval $I\subseteq \mathbb{R}$, define the averaging operator $A_I f(x)=\frac{\chi_I(x)}{m(I)}\int_I f(x)dm$.
|
||||
|
||||
(This function takes the average of $f$ over the interval $I$.)
|
||||
|
||||
The Hardy-Littlewood maximal function is defined as:
|
||||
|
||||
$$
|
||||
f^*(x)=\sup_{I\text{ is open interval}}A_I f(x)
|
||||
$$
|
||||
|
||||
We will show that $f^*$ is not that such worse than $f$. (Prove on Wednesday)
|
||||
|
||||
Relates to the Fundamental Theorem of Calculus in Lebesgue integration.
|
||||
|
||||
$$
|
||||
\frac{G(x+h)-G(x)}{h}=\frac{1}{h}\int_x^{x+h} g(t)dt=A_{[x,x+h]}g(x)
|
||||
$$
|
||||
|
||||
If we can control all the averages, we can control the function.
|
||||
@@ -1,140 +0,0 @@
|
||||
# Math4121 Lecture 38
|
||||
|
||||
## Extended fundamental theorem of calculus with Lebesgue integration
|
||||
|
||||
### Hardy-Littlewood maximal function
|
||||
|
||||
Given integrable $f$m and an interval $I$, look at the averaging operator $A_I f(x)=\frac{\chi_I(x)}{m(I)}\int_I f(y)dy$.
|
||||
|
||||
The maximal function is defined as
|
||||
|
||||
$$
|
||||
f^*(x)=\sup_{I \text{ is an open interval}} A_I f(x)
|
||||
$$
|
||||
|
||||
#### Theorem Hardy-Littlewood Maximal Function Theorem
|
||||
|
||||
Fix $f$ integrable. For each $\lambda>0$, we define
|
||||
|
||||
$$
|
||||
E_\lambda^*=\{x\in\mathbb{R}: |f^*(x)|>\lambda\}
|
||||
$$
|
||||
|
||||
Then
|
||||
|
||||
$$
|
||||
m(E_\lambda^*)\leq \frac{2}{\lambda}\int_\mathbb{R} |f| dm
|
||||
$$
|
||||
|
||||
To give context for the maximal estimate, for any $f$ integrable, $\lambda>0$,
|
||||
|
||||
$$
|
||||
E_\lambda=\{x\in\mathbb{R}: |f(x)|>\lambda\}
|
||||
$$
|
||||
|
||||
Then we have Marknov's inequality, $m(E_\lambda)\leq \frac{1}{\lambda}\int_\mathbb{R} |f| dm$. We know $|f(x)|>\lambda \chi_{E_\lambda}(x)$ so Markov's inequality follows by integrating.
|
||||
|
||||
Proof:
|
||||
|
||||
Let $f^*(x)=\sup_{I \text{ is an open interval such that } x\in I} \frac{1}{m(I)}\int_I f \, dm$.
|
||||
|
||||
If $x\in E_\lambda^*$, then $\exists I$ open interval such that $x\in I$ and $\frac{1}{m(I(x))}\left|\int_{I(x)} f \, dm\right|>\lambda$.
|
||||
|
||||
Take $K\subset E_\lambda^*$ compact. Then $K\subset \bigcup_{x\in K} I(x)$. Taking the finite subcover, we have $I_1, \ldots, I_n$ open intervals such that $K\subset \bigcup_{i=1}^n I_i$.
|
||||
|
||||
If three intervals, $I,J,K$ have non-empty intersection, then one is contained in the union of the other two.
|
||||
|
||||
In particular, we can find another subcover for $K$, $J_1, \ldots, J_N$ such that they have overlap of at most 2 (otherwise, we can remove the cover). We can state this as
|
||||
|
||||
$$
|
||||
\sum_{j=1}^N \chi_{J_j}(x)\leq 2
|
||||
$$
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
m(K)&\leq \sum_{j=1}^N m(J_j)\\
|
||||
&\leq \sum_{j=1}^N \frac{1}{\lambda}\left|\int_{J_j} f \, dm\right|\\
|
||||
&\leq \frac{1}{\lambda}\int_\mathbb{R} \sum_{j=1}^N \chi_{J_j}(x) |f(x)| \, dx\\
|
||||
&\leq \frac{2}{\lambda}\int_\mathbb{R} |f(x)| \, dx
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Since $A_I f(x)$ is measurable, $f^*$ is measurable function and $E_\lambda$ is measurable, we have
|
||||
|
||||
$$
|
||||
m(E_\lambda^*)\leq \frac{2}{\lambda}\int_\mathbb{R} |f(x)| \, dx
|
||||
$$
|
||||
|
||||
QED
|
||||
|
||||
## 3 Big Convergence Theorems
|
||||
|
||||
### Theorem L.1 (Monotone Convergence Theorem)
|
||||
|
||||
[Monotone convergence theorem](https://notenextra.trance-0.com/Math4121/Math4121_L36#theorem-614-monotone-convergence-theorem)
|
||||
|
||||
### Theorem L.2 (Fatou's Lemma)
|
||||
|
||||
Let $\{f_n\}_{n=1}^\infty$ be a sequence of non-negative measurable functions on $E$. Then
|
||||
|
||||
$$
|
||||
\int_E \liminf_{n\to\infty} f_n \, dm\leq \liminf_{n\to\infty} \int_E f_n \, dm
|
||||
$$
|
||||
|
||||
Proof:
|
||||
|
||||
Let $g_n=\inf_{k\geq n} f_k$ is a monotone increasing nonnegative, and the following properties holds:
|
||||
|
||||
$$
|
||||
\lim_{n\to\infty} g_n(x)=\sup_{n\geq 1} \inf_{k\geq n} f_k(x)=\liminf_{n\to\infty} f_n(x)
|
||||
$$
|
||||
|
||||
$$
|
||||
\int_E g_n \, dm\leq \inf_{k\geq n} \int_E f_k\, dm
|
||||
$$
|
||||
|
||||
So,
|
||||
|
||||
$$
|
||||
\int_E g_n \, dm\leq \inf_{k\geq n} \int_E f_k \, dm
|
||||
$$
|
||||
|
||||
Apply the monotone convergence theorem to $g_n$, we have
|
||||
|
||||
$$
|
||||
\lim_{n\to\infty} \int_E g_n \, dm\leq \liminf_{n\to\infty} \int_E f_n \, dm
|
||||
$$
|
||||
|
||||
QED
|
||||
|
||||
### Theorem L.3 (Dominated Convergence Theorem)
|
||||
|
||||
Let $\{f_n\}_{n=1}^\infty$ be a sequence of measurable functions on $\mathbb{R}$ converging to $f$ almost everywhere. If there exists integrable $g$ such that $|f_n|\leq |g|$ for all $n$, then
|
||||
|
||||
$$
|
||||
\int_E f \, dm=\lim_{n\to\infty} \int_E f_n \, dm
|
||||
$$
|
||||
|
||||
Proof:
|
||||
|
||||
Consider the function $g+f_n$ and $g-f_n$, these are non-negative sequences of measurable functions. By Fatou's lemma, we have
|
||||
|
||||
$$
|
||||
\int g\,dm+\int f\,dm=\int_E \liminf_{n\to\infty} (g+f_n) \, dm\leq \liminf_{n\to\infty} \int_E (g+f_n) \, dm=\int_E g\,dm+\liminf_{n\to\infty} \int_E f_n\,dm
|
||||
$$
|
||||
|
||||
So, $\int_E f\,dm\leq \liminf_{n\to\infty} \int_E f_n\,dm$.
|
||||
|
||||
Similarly, we have
|
||||
|
||||
$$
|
||||
\int g\,dm-\int f\,dm=\int_E \liminf_{n\to\infty} (g-f_n) \, dm\leq \liminf_{n\to\infty} \int_E (g-f_n) \, dm=\int_E g\,dm-\limsup_{n\to\infty} \int_E f_n\,dm
|
||||
$$
|
||||
|
||||
So, $\limsup_{n\to\infty} \int_E f_n\,dm\leq \int_E f\,dm$.
|
||||
|
||||
So $\limsup_{n\to\infty} \int_E f_n\,dm\leq \int_E f\,dm\leq \liminf_{n\to\infty} \int_E f_n\,dm$.
|
||||
|
||||
Since $\limsup_{n\to\infty} \int_E f_n\,dm\geq \liminf_{n\to\infty} \int_E f_n\,dm$, we have $\int_E f\,dm=\lim_{n\to\infty} \int_E f_n\,dm$.
|
||||
|
||||
QED
|
||||
@@ -1,77 +0,0 @@
|
||||
# Math4121 Lecture 39
|
||||
|
||||
## Fundamental theorem of calculus (In Lebesgue integration)
|
||||
|
||||
### Preliminary results
|
||||
|
||||
#### Lemma 1
|
||||
|
||||
Riemann integrable functions are Lebesgue integrable
|
||||
$$\int_a^b f(x)dx = \int_{[a,b]} f dm$$
|
||||
|
||||
#### Lemma 2
|
||||
|
||||
Density of continuous functions: Given $f$ integrable, then $\exists \epsilon > 0$ there is $g$ continuous such that $\int_{[a,b]} |f-g| dm < \epsilon$
|
||||
|
||||
#### Lemma 3
|
||||
|
||||
Maximal function: $f^*(x) = \sup_{I\text{ is open intervals}}A_I f(x)$, where $A_I = \frac{\chi_I}{m(I)} \int_I f dm$. Then $|\{x\in\mathbb{R}:f^*(x)>\lambda\}|<\frac{2}{\lambda}\int_{\mathbb{R}}|f|dm$
|
||||
|
||||
#### Lemma 4
|
||||
|
||||
$I=[a,b]$, $I_\delta = [a+\delta, b-\delta]$, $\delta>0$, $\lim_{\delta\to 0^+} A_{I_\delta} f(x) = A_I f(x)$. (Prove via dominated convergence theorem)
|
||||
|
||||
> Riemann's Fundamental theorem of calculus:
|
||||
>
|
||||
> If $g$ is continuous on $[a,b]$, then $G(x) = \int_a^x g(t)dt$ is differentiable on $(a,b)$ and $G'(x) = g(x)$ for all $x\in(a,b)$.
|
||||
|
||||
### Lebesgue's Fundamental theorem of calculus
|
||||
|
||||
If $f$ is Lebesgue integrable on $[a,b]$, then $F(x) = \int_a^x f(t)dt$ is differentiable almost everywhere and $F'(x) = f(x)$ almost everywhere.
|
||||
|
||||
Outline:
|
||||
|
||||
Let $\lambda,\epsilon > 0$. Find $g$ continuous such that $\int_{\mathbb{R}}|f-g|dm < \frac{\lambda \epsilon}{5}$.
|
||||
|
||||
To control $A_I f(x)-f(x)=(A_I(f-g)(x))+(A_I g(x)-g(x))+(g(x)-f(x))$, we need to estimate the three terms separately.
|
||||
|
||||
Our goal is to show that $\lim_{r\to 0^+}\sup_{I\text{ is open interval}, m(I)<r, x\in I}|A_I f(x)-f(x)|=0$. For $x$ almost every $x\in[a,b]$.
|
||||
|
||||
This implies the fundamental theorem of calculus.
|
||||
|
||||
Since $\frac{F(x+h)-F(x)}{h}=\frac{1}{m(I_h)}\int_{I_h}f dm$, if the above condition holds, then $\forall \eta>0$, we can find $r>0$ such that $\sup_{I\text{ is open interval}, m(I)<r, x\in I}|A_I f(x)-f(x)|<\frac{\eta}{2}$.
|
||||
|
||||
Now given $h<\min\{r, x-a\}$, we can find by [4](https://notenextra.trance-0.com/Math4121_L39.html#Lemma-4) an interval $I_h^*$ such that
|
||||
|
||||
$$
|
||||
\left|\frac{1}{h}\int_{I_h^*}f dm - \frac{1}{m(I_h^*)}\int_{I_h^*}f dm\right|<\frac{\eta}{2}
|
||||
$$
|
||||
|
||||
Proof:
|
||||
|
||||
Let
|
||||
|
||||
$$
|
||||
F=\left\{x\in [a,b]:\limsup_{r\to 0^+}\sup_{I\text{ is open interval}, m(I)<r, x\in I}|A_I f(x)-f(x)|>\lambda \right\}
|
||||
$$
|
||||
|
||||
Need to show $m(F)<\epsilon$.
|
||||
|
||||
Since $F\subseteq \{(f-g)^*>\frac{\lambda}{2}\}\cup \{(f-g)>\frac{\lambda}{2}\}$
|
||||
|
||||
$$
|
||||
\limsup_{r\to 0^+}\sup_{I\text{ is open interval}, m(I)<r, x\in I}|A_I f(x)-f(x)|\leq \limsup_{r\to 0^+}\sup_{I\text{ is open interval}, m(I)<r, x\in I}|A_I (f-g)(x)|+|g(x)-f(x)|
|
||||
\leq |(f-g)^*(x)|+|(f-g)(x)|
|
||||
$$
|
||||
|
||||
By maximal inequality and Markov's inequality,
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
m(F)&\leq \frac{4}{\lambda}\int_{\mathbb{R}}|f-g|dm+\frac{1}{\lambda}\int_{\mathbb{R}}|f-g|dm\\
|
||||
&=\frac{5}{\lambda}\frac{\lambda \epsilon}{5}\\
|
||||
&=\epsilon
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
QED
|
||||
@@ -1,139 +0,0 @@
|
||||
# Math4121 Lecture 4
|
||||
|
||||
## Chapter 5. Differentiation
|
||||
|
||||
### The continuity of the derivative
|
||||
|
||||
#### Theorem 5.12
|
||||
|
||||
Suppose $f$ is differentiable on $[a,b]$, Then $f'$ attains intermediate values between $f'(a)$ and $f'(b)$.
|
||||
|
||||
Proof:
|
||||
|
||||
Let $\lambda\in (f'(a),f'(b))$. We need to show that there exists $x\in (a,b)$ such that $f'(x)=\lambda$.
|
||||
|
||||
Let $g(x)=f(x)-\lambda x$. Then $g$ is differentiable on $(a,b)$ and
|
||||
|
||||
$$
|
||||
g'(x)=f'(x)-\lambda.
|
||||
$$
|
||||
|
||||
So $g'(a)=f'(a)-\lambda<0$ and $g'(b)=f'(b)-\lambda>0$.
|
||||
|
||||
We need to show that $g'(x)=0$ for some $x\in (a,b)$.
|
||||
|
||||
Since $g'(a)<0$, $\exists t_1\in (a,b)$ such that $g'(t_1)<g(a)$.
|
||||
|
||||
If not, then $g(t)\geq g(a)$ for all $t\in (a,b)$. But then $g'(a)\gets \frac{g(t)-g(a)}{t-a}\geq 0$, which contradicts $g'(a)<0$.
|
||||
|
||||
With the loss of generality, since $g'(b)>0$, $\exists t_2\in (a,b)$ such that $g'(t_2)<g(b)$.
|
||||
|
||||
Hence, $g$ attains its infimum on $[a,b]$ at some $x\in (a,b)$. Then this $x$ is a local minimum of $g$ on $(a,b)$.
|
||||
|
||||
So $g'(x)=0$ and $f'(x)=\lambda$.
|
||||
|
||||
QED
|
||||
|
||||
### L'Hôpital's Rule
|
||||
|
||||
#### Theorem 5.13
|
||||
|
||||
Suppose $f$ and $g$ are differentiable on $(a,b)$ and $g'(x)\neq 0$ for all $x\in (a,b)$, where $-\infty\leq a<b\leq \infty$. Suppose
|
||||
|
||||
$$
|
||||
\frac{f'(x)}{g'(x)}\to A \text{ as } x\to a\dots
|
||||
$$
|
||||
|
||||
If
|
||||
|
||||
$$
|
||||
f(x)\to 0 \text{ and } g(x)\to 0 \text{ as } x\to a,
|
||||
$$
|
||||
|
||||
or
|
||||
|
||||
$$
|
||||
g(x)\to \infty \text{ as } x\to a,
|
||||
$$
|
||||
|
||||
then
|
||||
|
||||
$$
|
||||
\frac{f(x)}{g(x)}\to A \text{ as } x\to a.
|
||||
$$
|
||||
|
||||
Note that all these numbers $A$ can be $\infty$ or $-\infty$ (on extended real line).
|
||||
|
||||
We're using the open neighborhood definition of $\to$ here. An open neighborhood of $\infty$ is an interval of the form $(c,\infty)$ for some $c\in \mathbb{R}$.
|
||||
|
||||
> Recall the [Definition 3.1](https://notenextra.trance-0.com/Math4111/Math4111_L13#definition-31).
|
||||
|
||||
Proof:
|
||||
|
||||
Main step:
|
||||
|
||||
Suppose $-\infty\leq A\leq \infty$, and let $q>A$ with neighborhood $(-,\infty,q)$. Then $\exists c\in \mathbb{R}$ such that $\frac{f(x)}{g(x)}<q,\forall x\in (a,c)$.
|
||||
|
||||
Proof of the main step:
|
||||
|
||||
Fix $A<r<q$. Then $\exists c\in (a,b)$ such that $\frac{f'(x)}{g'(x)}<r,\forall x\in (a,c)$.
|
||||
|
||||
Now, for any $a<x<y<c$, by generalized mean value theorem, $\exists t\in (x,y)$ such that
|
||||
|
||||
$$
|
||||
\frac{f(x)-f(y)}{g(x)-g(y)}=\frac{f'(t)}{g'(t)}
|
||||
$$
|
||||
|
||||
Since $t\in (a,c)$, $\frac{f'(t)}{g'(t)}<r$.
|
||||
|
||||
Case 1: $f(x)\to 0$ and $g(x)\to 0$ as $x\to a$.
|
||||
|
||||
As $x\to a$, $f(x)\to 0$ and $g(x)\to 0$. So
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\lim_{x\to a}\frac{f(x)-f(y)}{g(x)-g(y)}&=\lim_{x\to a}\frac{0-f(y)}{0-g(y)}\\
|
||||
&=\lim_{x\to a}\frac{f(y)}{g(y)}\\
|
||||
&=\frac{f'(y)}{g'(y)}\\
|
||||
&\leq r<q
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
$\forall y\in (a,c)$, $\frac{f(y)}{g(y)}<q$.
|
||||
|
||||
Case 2: $g(x)\to \infty$ as $x\to a$.
|
||||
|
||||
We can find $c_1\in (a,y)$ such that $g(x)>g(y)$ for all $x\in (a,c_1)$.
|
||||
|
||||
Therefore,
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\frac{f(x)-f(y)}{g(x)}&<\frac{r[g(x)-g(y)]}{g(x)}\\
|
||||
\frac{f(x)}{g(x)}&<r-\frac{rg(y)}{g(x)}+\frac{f(y)}{g(x)}
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
To make the right side less than $q$, we need
|
||||
|
||||
$$
|
||||
\frac{|rg(y)|+|f(y)|}{|g(x)|}<q-r
|
||||
$$
|
||||
|
||||
so,
|
||||
|
||||
$$
|
||||
|g(x)|>\frac{|rg(y)|+|f(y)|}{q-r}
|
||||
$$
|
||||
|
||||
There exists $c_2\in (a,c_1)$ such that $|g(x)|>\frac{|rg(y)|+|f(y)|}{q-r},\forall x\in (a,c_2)$.
|
||||
|
||||
So $\forall x\in (a,c_2)$,
|
||||
|
||||
$$
|
||||
\frac{f(x)}{g(x)}<\frac{rg(y)+f(y)}{g(x)}<r+(q-r)=q
|
||||
$$
|
||||
|
||||
$\forall x\in (a,c_2)$, $\frac{f(x)}{g(x)}<q$.
|
||||
|
||||
QED
|
||||
@@ -1,119 +0,0 @@
|
||||
# Math4121 Lecture 5
|
||||
|
||||
## Continue on differentiation
|
||||
|
||||
### L'Hôpital's Rule
|
||||
|
||||
Suppose $f$ and $g$ are real differentiable on $(a,b)$ and $g'(x)\neq 0$ for all $x\in (a,b)$.
|
||||
|
||||
Suppose $\frac{f'(x)}{g'(x)}\to A$ as $x\to a$,
|
||||
|
||||
If $f(x)\to 0$ and $g(x)\to 0$ as $x\to a$,
|
||||
|
||||
or $g(x)\to \infty$ as $x\to a$,
|
||||
|
||||
then $\frac{f(x)}{g(x)}\to A$ as $x\to a$.
|
||||
|
||||
Proof:
|
||||
|
||||
**Main step: Let $-\infty<a<b<\infty$.for any $q>A$, there exists $c\in (a,b)$ such that $\frac{f(x)}{g(x)}<q$ for all $x\in (a,c)$.**
|
||||
|
||||
> Topological definition of limit:
|
||||
>
|
||||
> $h(x)\to A$ as $x\to a$ if $\forall \epsilon>0$, $\exists \delta>0$ such that $|x-a|<\delta$ implies $|h(x)-A|<\epsilon$.
|
||||
>
|
||||
> In other words, if for any open neighborhood $V$ of $A$, there exists an open neighborhood $U$ of $a$ such that $h(U)\subseteq V$.
|
||||
|
||||
Case 1: $A=-\infty$, for any $q>A$, there exists $\delta>0$ such that $x\in (a,a+\delta)$ implies $\frac{f(x)}{g(x)}<q$.
|
||||
|
||||
Case 2: $A=\infty$, we change the function $F(x)=-f(x)$ and apply the case 1.
|
||||
|
||||
Case 3: $A\in \mathbb{R}$, Let $\epsilon>0$ and take $q=A+\epsilon$. $\exists c_1\in (a,b)$ such that $\forall x\in (a,c_1)$, $\frac{f(x)}{g(x)}<q$.
|
||||
|
||||
Set $F(x)=-f(x)$. and $q=-A+\epsilon>-A$. Apply main step, $\exists c_2\in (a,b)$ such that $\forall x\in (a,c_2)$, $\frac{F(x)}{g(x)}<-A+\epsilon$. so $\forall x\in (a,c_2)$, $\frac{f(x)}{g(x)}>A-\epsilon$.
|
||||
|
||||
We take $c=\min(c_1,c_2)$. Then $\forall x\in (a,c)$, $\frac{f(x)}{g(x)}<q$.
|
||||
|
||||
QED
|
||||
|
||||
### Higher Order Derivatives
|
||||
|
||||
#### Definition 5.14
|
||||
|
||||
If $f$ is differentiable on $(a,b)$, then we define $f'(x)=\lim_{t\to x}\frac{f(t)-f(x)}{t-x}$.
|
||||
|
||||
If $f'$ is differentiable on $(a,b)$, then we define $f''(x)=(f')'(x)$.
|
||||
|
||||
If $f^{(k)}$ is differentiable on $(a,b)$, then we define $f^{(k+1)}(x)=(f^{(k)})'(x)$.
|
||||
|
||||
#### Theorem 5.15 Taylor's Theorem
|
||||
|
||||
Let $f:[a,b]\to \mathbb{R}$, and $n$ be a positive integer.
|
||||
|
||||
Let $f^{(n-1)}$ be continuous on $[a,b]$, and differentiable on $(a,b)$.
|
||||
|
||||
For $\alpha\in [a,b]$, define the Taylor polynomial of order $n-1$ at $\alpha$ by
|
||||
|
||||
$$
|
||||
P(t)=\sum_{k=0}^{n-1}\frac{f^{(k)}(\alpha)}{k!}(t-\alpha)^k
|
||||
$$
|
||||
|
||||
Example:
|
||||
|
||||
When $n=1$, $P(t)=f(\alpha)$.
|
||||
|
||||
When $n=2$, $P(t)=f(\alpha)+f'(\alpha)(t-\alpha)$.
|
||||
|
||||
When $n=3$, $P(t)=f(\alpha)+f'(\alpha)(t-\alpha)+\frac{f''(\alpha)}{2}(t-\alpha)^2$.
|
||||
|
||||
**Key property:**
|
||||
|
||||
$$
|
||||
P^{(k)}(\alpha)=f^{(k)}(\alpha)\quad \forall k=0,1,\cdots,n-1
|
||||
$$
|
||||
|
||||
For each $\beta\in [a,b]$, there exists $x$ between $\alpha$ and $\beta$ such that
|
||||
|
||||
$$
|
||||
f(\beta)=P(\beta)+\frac{f^{(n)}(x)}{n!}(\alpha-\beta)^n
|
||||
$$
|
||||
|
||||
_On rudin, it is_
|
||||
|
||||
$$
|
||||
f(\beta)=P(\beta)+\frac{f^{(n)}(x)}{n!}(\beta-\alpha)^n
|
||||
$$
|
||||
|
||||
Proof:
|
||||
|
||||
Let $M=\frac{f(\beta)-P(\beta)}{(\beta-\alpha)^n}$.
|
||||
|
||||
So that $f(\beta)=P(\beta)+M(\beta-\alpha)^n$.
|
||||
|
||||
Need to show that $n!M=f^{(n)}(x)$. for some $x\in (\alpha,\beta)$. Defined $g(t)=f(t)-P(t)-M(t-\alpha)^n$.
|
||||
|
||||
By our choice of $M$, $g(\alpha)=g(\beta)=0$.
|
||||
|
||||
$$
|
||||
g(t)=f(t)-P(t)-M(n(n-1)(n-2)\cdots(n-k+1)(t-\alpha)^{n-k})
|
||||
$$
|
||||
|
||||
for $k=1,2,\cdots,n-1$. And when $k=n$, $g^{(n)}(t)=f^{(n)}(t)-0-M(n!)$.
|
||||
|
||||
Need to show that $\exists x\in (\alpha,\beta)$ such that $g^{(n)}(x)=0$.
|
||||
|
||||
By Mean Value Theorem, $\exists x_1\in (\alpha,\beta)$ such that $g'(x_1)=0$.
|
||||
|
||||
By Mean Value Theorem, $\exists x_2\in (\alpha,x_1)$ such that $g''(x_2)=0$.
|
||||
|
||||
By Mean Value Theorem, $\exists x_3\in (\alpha,x_2)$ such that $g^{(3)}(x_3)=0$.
|
||||
|
||||
$\cdots$
|
||||
|
||||
By Mean Value Theorem, $\exists x_n\in (\alpha,x_{n-1})$ such that $g^{(n)}(x_n)=0$.
|
||||
|
||||
Since $g^{(n)}(\alpha)=0$ for $k=0,1,2,\cdots,n-1$, we can find $x_n\in (\alpha,x_{n-1})$ such that $g^{(n)}(x_n)=0$.
|
||||
|
||||
QED
|
||||
|
||||
## Chapter 6: Riemann-Stieltjes Integral
|
||||
@@ -1,122 +0,0 @@
|
||||
# Math4121 Lecture 6
|
||||
|
||||
## Chapter 6: Riemann-Stieltjes Integral
|
||||
|
||||
> A nice point to restart your learning, LOL.
|
||||
|
||||
### Differentiation and existence of the integral
|
||||
|
||||
#### Definition 6.1
|
||||
|
||||
Let $[a,b]\subseteq \mathbb{R}$. A partition of $[a,b]$ is a finite sequence of points $\{x_0,x_1,\cdots,x_n\}\subseteq [a,b]$ such that $x_0<x_1<\cdots<x_n$.
|
||||
|
||||
Let $\alpha:[a,b]\to \mathbb{R}$ be monotone increasing. ($\alpha(x)\leq \alpha(y)$ for $x\leq y$)
|
||||
|
||||
_We will use $\alpha$ for monotone increasing function in later sections._
|
||||
|
||||
#### Definition 6.2
|
||||
|
||||
For a partition $P$ of $[a,b]$, we define $\Delta \alpha_i=\alpha(x_i)-\alpha(x_{i-1})$ for $i=1,2,\cdots,n$.
|
||||
|
||||
Let $f:[a,b]\to \mathbb{R}$ be bounded.
|
||||
|
||||
Then we define
|
||||
|
||||
$$
|
||||
m_i=\inf_{x\in [x_{i-1},x_i]}f(x),\quad M_i=\sup_{x\in [x_{i-1},x_i]}f(x).
|
||||
$$
|
||||
|
||||
Defined the lower and upper Riemann sum by
|
||||
|
||||
$$
|
||||
L(P,f,\alpha)=\sum_{i=1}^n m_i\Delta \alpha_i,\quad U(P,f,\alpha)=\sum_{i=1}^n M_i\Delta \alpha_i.
|
||||
$$
|
||||
|
||||
Defined the lower and upper integral by
|
||||
|
||||
$$
|
||||
\underline{\int_a^b}f(x)d\alpha=\sup_P L(P,f,\alpha),\quad \overline{\int_a^b}f(x)d\alpha=\inf_P U(P,f,\alpha).
|
||||
$$
|
||||
|
||||
If $\underline{\int_a^b}f(x)d\alpha=\overline{\int_a^b}f(x)d\alpha$, then we say $f$ is Riemann-Stieltjes integrable with respect to $\alpha$ on $[a,b]$, written as $f\in \mathscr{R}(\alpha)$, and the common value is called the Riemann-Stieltjes integral of $f$ with respect to $\alpha$ on $[a,b]$, denoted by
|
||||
|
||||
$$
|
||||
\int_a^b f(x)d\alpha=\underline{\int_a^b}f(x)d\alpha=\overline{\int_a^b}f(x)d\alpha.
|
||||
$$
|
||||
|
||||
If $\alpha(x)=x$, then we write $\int_a^b f(x)dx$ instead of $\int_a^b f(x)d\alpha$.
|
||||
|
||||
> Damn, that's a really loooong definition.
|
||||
|
||||
#### Definition 6.3
|
||||
|
||||
A partition $P^*$ is called a **refinement** of $P$ if $P\subseteq P^*$.
|
||||
|
||||
Given two partitions $P_1$ and $P_2$, we define their common refinement $P^*=P_1\cup P_2$. _we can merge two partitions by adding all points in both partitions._
|
||||
|
||||
#### Theorem 6.4
|
||||
|
||||
If $P^*$ is a refinement of $P$, then
|
||||
|
||||
$$
|
||||
L(P^*,f,\alpha)\geq L(P,f,\alpha)
|
||||
$$
|
||||
|
||||
_Refinement of a partition will never make the lower sum smaller._
|
||||
|
||||
$$
|
||||
U(P^*,f,\alpha)\leq U(P,f,\alpha)
|
||||
$$
|
||||
|
||||
_Refinement of a partition will never make the upper sum larger._
|
||||
|
||||
Proof:
|
||||
|
||||
Main idea:
|
||||
|
||||
Let $P=P_0\subset P_1\subset P_2\subset \cdots \subset P_K=P^*$.
|
||||
|
||||
Where $P_k$ has more points than $P_{k-1}$.
|
||||
|
||||
It suffices to show that $L(P_k,f,\alpha)\geq L(P_{k-1},f,\alpha)$ for all $k=1,2,\cdots,K$.
|
||||
|
||||
Let $P_{k-1}=\{y_0,y_1,\cdots,y_J\}$ and $P_k=\{y_0,y_1,\cdots,y_{j-1},y^*,y_j,\cdots,y_J\}$.
|
||||
|
||||
Then, since $\alpha$ is monotone increasing, we have $y_{j-1}\leq y^*\leq y_j$.
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
L(P_k,f,\alpha)-L(P_{k-1},f,\alpha)&=\sum_{i=1}^{j+1}\inf_{x\in [y_{i-1},y_i]}f(x)(\alpha(y_i)-\alpha(y_{i-1}))-\sum_{i=1}^j\inf_{x\in [y_{i-1},y_i]}f(x)(\alpha(y_i)-\alpha(y_{i-1}))\\
|
||||
&=\inf_{x\in [y^*,y_j]}f(x)(\alpha(y_j)-\alpha(y^*))+\inf_{x\in [y_{j-1},y^*]}f(x)(\alpha(y^*)-\alpha(y_{j-1}))-\inf_{x\in [y_{j-1},y_j]}f(x)(\alpha(y_j)-\alpha(y_{j-1}))\\
|
||||
&\geq m_j(\alpha(y_j)-\alpha(y^*))+m_j(\alpha(y^*)-\alpha(y_{j-1}))-m_{j-1}(\alpha(y_j)-\alpha(y_{j-1}))\\
|
||||
&=0
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Same for $U(P_k,f,\alpha)\geq U(P_{k-1},f,\alpha)$.
|
||||
|
||||
QED
|
||||
|
||||
#### Theorem 6.5
|
||||
|
||||
$$
|
||||
\underline{\int_a^b}f(x)d\alpha\leq \overline{\int_a^b}f(x)d\alpha
|
||||
$$
|
||||
|
||||
Proof:
|
||||
|
||||
Let $P^*$ be a common refinement of $P_1$ and $P_2$.
|
||||
|
||||
By **Theorem 6.4**, we have
|
||||
|
||||
$$
|
||||
L(P_1,f,\alpha)\leq L(P^*,f,\alpha)\leq U(P^*,f,\alpha)\leq U(P_2,f,\alpha)
|
||||
$$
|
||||
|
||||
Fixing $P_1$ and take the supremum over all $P_2$, we have
|
||||
|
||||
$$
|
||||
\underline{\int_a^b}f(x)d\alpha\leq \sup_{P_1}L(P_1,f,\alpha)\leq \inf_{P_2}U(P_2,f,\alpha)=\overline{\int_a^b}f(x)d\alpha
|
||||
$$
|
||||
|
||||
QED
|
||||
@@ -1,96 +0,0 @@
|
||||
# Math4121 Lecture 7
|
||||
|
||||
## Continue on Chapter 6
|
||||
|
||||
### Riemann integrable
|
||||
|
||||
#### Theorem 6.6
|
||||
|
||||
A function $f$ is Riemann integrable with respect to $\alpha$ on $[a, b]$ if and only if for every $\epsilon > 0$, there exists a partition $P$ of $[a, b]$ such that $U(f, P, \alpha) - L(f, P, \alpha) < \epsilon$.
|
||||
|
||||
Proof:
|
||||
|
||||
$\impliedby$
|
||||
|
||||
For every $P$,
|
||||
|
||||
$$
|
||||
L(f, P, \alpha) \leq \underline{\int}_a^b f d\alpha \leq \overline{\int}_a^b f d\alpha \leq U(f, P, \alpha)
|
||||
$$
|
||||
|
||||
So if $f$ is Riemann integrable with respect to $\alpha$ on $[a, b]$, then for every $\epsilon > 0$, there exists a partition $P$ such that
|
||||
|
||||
$$
|
||||
0 \leq \overline{\int}_a^b f d\alpha - \underline{\int}_a^b f d\alpha \leq U(f, P, \alpha) - L(f, P, \alpha) < \epsilon
|
||||
$$
|
||||
|
||||
Thus $0 \leq \overline{\int}_a^b f d\alpha - \underline{\int}_a^b f d\alpha < \epsilon,\forall \epsilon > 0$.
|
||||
|
||||
Then, $\overline{\int}_a^b f d\alpha = \underline{\int}_a^b f d\alpha$.
|
||||
|
||||
So, $f$ is Riemann integrable with respect to $\alpha$ on $[a, b]$.
|
||||
|
||||
$\implies$
|
||||
|
||||
If $f\in \mathscr{R}(\alpha)$ on $[a, b]$, then $f$ is Riemann integrable with respect to $\alpha$ on $[a, b]$.
|
||||
|
||||
Then by the definition of Riemann integrable, $\sup_{P} L(f, P, \alpha) =\int^b_a f d\alpha = \inf_{P} U(f, P, \alpha)$.
|
||||
|
||||
Given any $\epsilon > 0$, by definition of infimum and supremum, there exists a partition $P_1,P_2$ such that
|
||||
|
||||
$$
|
||||
\int^b_a f d\alpha - \frac{\epsilon}{2} < L(f, P_1, \alpha) \leq \sup_{P} L(f, P, \alpha) = \inf_{P} U(f, P, \alpha) < \int^b_a f d\alpha + \frac{\epsilon}{2}
|
||||
$$
|
||||
|
||||
Taking $P = P_1 \cup P_2$, by [Theorem 6.4](https://notenextra.trance-0.com/Math4121/Math4121_L6#theorem-64) we have
|
||||
|
||||
$$
|
||||
U(f, P, \alpha) - L(f, P, \alpha) \leq \left( \int^b_a f d\alpha + \frac{\epsilon}{2} \right) - \left( \int^b_a f d\alpha - \frac{\epsilon}{2} \right) = \epsilon
|
||||
$$
|
||||
|
||||
So $f$ is Riemann integrable with respect to $\alpha$ on $[a, b]$.
|
||||
|
||||
QED
|
||||
|
||||
#### Theorem 6.8
|
||||
|
||||
If $f$ is continuous on $[a, b]$, then $f$ is Riemann integrable with respect to $\alpha$ on $[a, b]$.
|
||||
|
||||
Proof:
|
||||
|
||||
> Main idea:
|
||||
>
|
||||
> $$U(f, P, \alpha) - L(f, P, \alpha) = \sum_{i=1}^n \left( M_i - m_i \right) \Delta \alpha_i$$
|
||||
>
|
||||
> If we can make $M_i - m_i$ small enough, then $U(f, P, \alpha) - L(f, P, \alpha)$ can be made arbitrarily small.
|
||||
>
|
||||
> Since $M_i=\sup_{x\in [t_{i-1}, t_i]} f(x)$ and $m_i=\inf_{x\in [t_{i-1}, t_i]} f(x)$, we can make $M_i - m_i$ small enough by making the partition $P$ sufficiently fine.
|
||||
|
||||
Suppose we can find a partition $P$ such that $M_i - m_i < \eta$. Then $U(f, P, \alpha) - L(f, P, \alpha) \leq\eta\sum_{i=1}^n \Delta \alpha_i = \eta (\alpha(b)-\alpha(a))$.
|
||||
|
||||
> Let $\epsilon >0$ and choose $\eta = \frac{\epsilon}{\alpha(b)-\alpha(a)}$. Then there exists a partition $P$ such that $U(f, P, \alpha) - L(f, P, \alpha) < \epsilon$.
|
||||
|
||||
Since $f$ is continuous on $[a, b]$ (a compact set), then $f$ is uniformly continuous on $[a, b]$. [Theorem 4.19](https://notenextra.trance-0.com/Math4111/Math4111_L24#theorem-419)
|
||||
|
||||
> If $f$ is continuous on $x$, then $\forall \epsilon > 0$, $\exists \delta > 0$ such that $|x-y| < \delta \implies |f(x)-f(y)| < \epsilon$.
|
||||
>
|
||||
> If $f$ is continuous on $[a, b]$, then $f$ is continuous at $x,\forall x\in [a, b]$.
|
||||
|
||||
So, there exists a $\delta > 0$ such that for all $x, t\in [a, b]$ with $|x-t| < \delta$, we have $|f(x)-f(t)| < \eta$.
|
||||
|
||||
Let $P=\{x_0, x_1, \cdots, x_n\}$ be a partition of $[a, b]$ such that $\Delta x_i < \delta$ for all $i$.
|
||||
|
||||
So, $\sup_{x,t\in [x_{i-1}, x_i]} |f(x)-f(t)| < \eta$ for all $i$.
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\sup_{x,t\in [x_{i-1}, x_i]} |f(x)-f(t)| &= \sup_{x,t\in [x_{i-1}, x_i]} f(x)-f(t) \\
|
||||
&= \sup_{x\in [x_{i-1}, x_i]} f(x)-\sup_{t\in [x_{i-1}, x_i]} -f(t) \\
|
||||
&=\sup_{x\in [x_{i-1}, x_i]} f(x)-\inf_{t\in [x_{i-1}, x_i]} f(t) \\
|
||||
&= M_i - m_i
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
So, $f$ is Riemann integrable with respect to $\alpha$ on $[a, b]$.
|
||||
|
||||
QED
|
||||
@@ -1,83 +0,0 @@
|
||||
# Math4121 Lecture 8
|
||||
|
||||
## Continue on Riemann-Stieltjes Integral
|
||||
|
||||
### Integrable Functions
|
||||
|
||||
#### Theorem 6.9
|
||||
|
||||
If $f$ is monotonic (increasing) on $[a, b]$ and $\alpha$ is continuous on $[a, b]$, then $f\in \mathscr{R}(\alpha)$ on $[a, b]$.
|
||||
|
||||
Proof:
|
||||
|
||||
Given a partition $P = \{a = x_0, x_1, \cdots, x_n = b\}$, we have
|
||||
|
||||
$$
|
||||
M_i = \sup_{x\in [x_{i-i}, x_i]} f(x)\leq f(x_{i})
|
||||
$$
|
||||
|
||||
$$
|
||||
m_i = \inf_{x\in [x_{i-1}, x_i]} f(x)\geq f(x_{i-1})
|
||||
$$
|
||||
|
||||
So,
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
U(P,f,\alpha) - L(P,f,\alpha) &= \sum_{i=1}^{n} (M_i - m_i)\Delta \alpha_i \\
|
||||
&\leq \sum_{i=1}^{n} \left[ f(x_i) - f(x_{i-1}) \right] \left[ \alpha(x_i) - \alpha(x_{i-1}) \right] \\
|
||||
|
||||
&\leq \sum_{i=1}^{n} \left[ f(x_i) - f(x_{i-1}) \right](\sup_{x\in [x_{i-1}, x_i]} \alpha(x) - \inf_{x\in [x_{i-1}, x_i]} \alpha(x)) \\
|
||||
&=U(P,\alpha,f) - L(P,\alpha,f)
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
By Theorem 6.8, $\alpha\in \mathscr{R}(f)$, so for any $\epsilon > 0$, there exists a partition $P$ such that
|
||||
|
||||
$$
|
||||
U(P,\alpha,f) - L(P,\alpha,f) < \epsilon
|
||||
$$
|
||||
|
||||
Therefore, $U(P,f,\alpha) - L(P,f,\alpha)<U(P,\alpha,f) - L(P,\alpha,f) < \epsilon$, so $f\in \mathscr{R}(\alpha)$ on $[a, b]$.
|
||||
|
||||
QED
|
||||
|
||||
#### Theorem 6.10
|
||||
|
||||
Suppose $f$ is bounded on $[a, b]$ and has finitely many points $\{y_1, y_2, \cdots, y_J\}$ of discontinuity, and $\alpha$ is continuous on $[a, b]$. Then $f\in \mathscr{R}(\alpha)$ on $[a, b]$.
|
||||
|
||||
Proof:
|
||||
|
||||
Since $f$ is bounded, there exists a $M>0$ such that $|f(x)|\leq M$ for all $x\in [a, b]$.
|
||||
|
||||
Let $\epsilon > 0$. Since $\alpha$ is continuous on $[a, b]$, we can find some intervals $[u_j,v_j]\subset (a,b)$ and $y_j\in [u_j,v_j]$ and $|\alpha(u_j) - \alpha(v_j)| < \epsilon$ for all $j=1,2,\cdots,J$.
|
||||
|
||||
Set $K=[a,b]\setminus \bigcup_{j=1}^{J}(u_j,v_j)$. Since $K$ is compact, $f$ is uniformly continuous on $K$. Hence, there exists a $\delta > 0$ such that for any $s,t\in K$ and $|s-t|<\delta$, we have $|f(s)-f(t)|<\epsilon$.
|
||||
|
||||
Let $P=\{x_0,x_1,\cdots,x_n=b\}$ containing all the points $u_j,v_j,\forall j=1,2,\cdots,J$ and $\Delta x_i<\delta,\forall x_i\notin \{u_j,v_j,\forall j=1,2,\cdots,J\}$.
|
||||
|
||||
Then,
|
||||
|
||||
If $x_i=u_j$ for some $j=1,2,\cdots,J$, then $M_i-m_i\leq M:=2\sup|f_x|$. But $\Delta \alpha_i\leq \epsilon$ for all $i=1,2,\cdots,n$.
|
||||
|
||||
If $x_i\neq u_j$ for all $j=1,2,\cdots,J$, then by uniform continuity of $f$ on $K$, we have $M_i-m_i\leq \epsilon$.
|
||||
|
||||
In either case, we have
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
U(P,f,\alpha) - L(P,f,\alpha) &= \sum_{i=1}^{n} (M_i - m_i)\Delta \alpha_i \\
|
||||
&\leq J M\epsilon + \sum_{i=1}^{n} \epsilon \Delta \alpha_i \\
|
||||
&= \epsilon(J M + \sum_{i=1}^{n} \Delta \alpha_i)
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Since $\epsilon$ is arbitrary, we have $U(P,f,\alpha) - L(P,f,\alpha) < \epsilon$.
|
||||
|
||||
Therefore, $f\in \mathscr{R}(\alpha)$ on $[a, b]$.
|
||||
|
||||
QED
|
||||
|
||||
#### Theorem 6.11
|
||||
|
||||
Suppose $f\in \mathscr{R}(\alpha)$ on $[a, b]$, $m\leq f(x)\leq M$ for all $x\in [a, b]$, and $\phi$ is continuous on $[m, M]$, and let $h(x)=\phi(f(x))$ on $[a, b]$. Then $h\in \mathscr{R}(\alpha)$ on $[a, b]$.
|
||||
@@ -1,162 +0,0 @@
|
||||
# Math4121 Lecture 9
|
||||
|
||||
Exam next week.
|
||||
|
||||
Transition to new book.
|
||||
|
||||
## Continue on Chapter 6
|
||||
|
||||
### Integrable Functions
|
||||
|
||||
#### Theorem 6.11
|
||||
|
||||
Suppose $f\in \mathscr{R}(\alpha)$ on $[a, b]$, $m\leq f(x)\leq M$ for all $x\in [a, b]$, and $\phi$ is continuous on $[m, M]$, and let $h(x)=\phi(f(x))$ on $[a, b]$. Then $h\in \mathscr{R}(\alpha)$ on $[a, b]$.
|
||||
|
||||
Proof:
|
||||
|
||||
Since $\phi$ is uniformly continuous on $[m, M]$, for any $\epsilon > 0$, there exists a $\delta > 0$ such that if $s, t\in [m, M]$ and $|s-t| < \delta$, then $|\phi(s)-\phi(t)| < \epsilon$.
|
||||
|
||||
Since $f\in \mathscr{R}(\alpha)$ on $[a, b]$, we can find a partition $P=\{x_0, x_1, \cdots, x_n\}$ of $[a, b]$ such that $U(f, P, \alpha)-L(f, P, \alpha) < \epsilon \delta$.
|
||||
|
||||
Set $M_i=\sup \{f(x): x\in [x_{i-1}, x_i]\}$ and $m_i=\inf \{f(x): x\in [x_{i-1}, x_i]\}$. $M_i^*=\sup \{h(x): x\in [x_{i-1}, x_i]\}$ and $m_i^*=\inf \{h(x): x\in [x_{i-1}, x_i]\}$.
|
||||
|
||||
We call a index $i$ good if $M_i-m_i < \delta$.
|
||||
|
||||
If $i$ is good, then $\forall x, y\in [x_{i-1}, x_i]$, $|f(x)-f(y)| < \delta$ and by uniform continuity of $\phi$, $|\phi(f(x))-\phi(f(y))| < \epsilon$.
|
||||
|
||||
Therefore, $|M_i^*-m_i^*| < \epsilon$.
|
||||
|
||||
If $i$ is bad, then $M_i-m_i\geq \delta$.
|
||||
|
||||
Notice that
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\delta\sum_{i\in\text{bad}} \Delta \alpha_i &\leq \sum_{i\in\text{bad}} (M_i-m_i) \Delta \alpha_i \\
|
||||
&\leq \sum_{i=1}^n (M_i-m_i) \Delta \alpha_i \\
|
||||
&\leq U(f, P, \alpha)-L(f, P, \alpha) \\
|
||||
&< \epsilon\delta
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Therefore, $\sum_{i=1}^n (M_i^*-m_i^*) \Delta \alpha_i < \epsilon$.
|
||||
|
||||
So,
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
U(P,h,\alpha)-L(P,h,\alpha) &= \sum_{i=1}^n (M_i^*-m_i^*) \Delta \alpha_i \\
|
||||
&\leq \sum_{i\in\text{good}} \epsilon \Delta \alpha_i + \sum_{i\in\text{bad}}2 \sup \{|h(x)-h(y)|: x, y\in [x_{i-1}, x_i]\} \Delta \alpha_i \\
|
||||
&\leq \epsilon [\alpha(b)-\alpha(a)] + 2\epsilon \sup \{|h(x)-h(y)|: x, y\in [a, b]\}\\
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Since $\epsilon$ is arbitrary, $h\in \mathscr{R}(\alpha)$ on $[a, b]$.
|
||||
|
||||
QED
|
||||
|
||||
### Properties of Integrable Functions
|
||||
|
||||
#### Theorem 6.12
|
||||
|
||||
Let $f,g\in \mathscr{R}(\alpha)$ on $[a, b]$.
|
||||
|
||||
(a) $f+g\in \mathscr{R}(\alpha)$ on $[a, b]$, $\int_a^b (f+g)d\alpha = \int_a^b f d\alpha + \int_a^b g d\alpha$. (Linearity of the integral)
|
||||
|
||||
(aa) If $c\in \mathbb{R}$, then $cf\in \mathscr{R}(\alpha)$ on $[a, b]$, and $\int_a^b cf d\alpha = c\int_a^b f d\alpha$.
|
||||
|
||||
(b) If $f(x)\leq g(x),\forall x\in [a, b]$, then $\int_a^b f d\alpha \leq \int_a^b g d\alpha$.
|
||||
|
||||
(c) $c\in [a, b]$, then $\int_a^c f d\alpha + \int_c^b f d\alpha = \int_a^b f d\alpha$.
|
||||
|
||||
(d) If $|f(x)|\leq M$, then $|\int_a^b f d\alpha| \leq M(\alpha(b)-\alpha(a))$.
|
||||
|
||||
(e) If $f\in \mathscr{R}(\beta)$ then $f\in \mathscr{R}(\alpha+\beta)$ and $\int_a^b f d(\alpha+\beta) = \int_a^b f d\alpha + \int_a^b f d\beta$.
|
||||
|
||||
Proof:
|
||||
|
||||
**Property (aa), (b), (e) holds for Riemann Sums themselves.**
|
||||
|
||||
**For (a)**, Set $h(x)=f(x)+g(x)$. Then $h\in \mathscr{R}(\alpha)$ on $[a, b]$ and we will show $\int_a^b h d\alpha \leq \int_a^b f d\alpha + \int_a^b g d\alpha$.
|
||||
|
||||
Since $f,g\in \mathscr{R}(\alpha)$ on $[a, b]$, for any $\epsilon > 0$, there exists a partition $P_1,P_2$ of $[a, b]$ such that $U(f,P_1,\alpha)-L(f,P_1,\alpha) < \epsilon$ and $U(g,P_2,\alpha)-L(g,P_2,\alpha) < \epsilon$.
|
||||
|
||||
Let $P=P_1\cup P_2$. Then $U(P,f,\alpha)\leq U(P_1,f,\alpha)< \int_a^b f d\alpha + \epsilon$ and $U(P,g,\alpha)\leq U(P_2,g,\alpha)< \int_a^b g d\alpha + \epsilon$.
|
||||
|
||||
So $U(P,h,\alpha)\leq U(P,f,\alpha)+U(P,g,\alpha)\leq \int_a^b f d\alpha + \int_a^b g d\alpha + 2\epsilon$.
|
||||
|
||||
Since $\epsilon$ is arbitrary, $\int_a^b h d\alpha \leq \int_a^b f d\alpha + \int_a^b g d\alpha$.
|
||||
|
||||
|
||||
$$
|
||||
\sup cf(x) = c\sup f(x)\quad \forall c\in \mathbb{R}
|
||||
$$
|
||||
|
||||
$$
|
||||
U(P,cf, \alpha) = cU(P,f,\alpha)
|
||||
$$
|
||||
|
||||
**For (b)**, notice that if $f(x)\leq g(x)$, then $\sup f(x)\leq \sup g(x)$, $U(P,f,\alpha)\leq U(P,g,\alpha)$. and $L(P,f,\alpha)\leq L(P,g,\alpha)$.
|
||||
|
||||
**For (c)**, if $f\in \mathscr{R}(\alpha)$ on $[a,b]$, and if $a<c<b$, then $f\in \mathscr{R}$ on $[a,c]$ and $[c,b]$, and
|
||||
|
||||
$$
|
||||
\int_a^c f d\alpha + \int_c^b f d\alpha=\int_a^b f d\alpha
|
||||
$$
|
||||
|
||||
For every partition $P=\{x_0,x_1,\cdots,x_n\}$ of $[a,b]$, we have a refinement $P^*=P\cup\{c\}$ of $[a,b]$. Let $P_1=\{x_0,x_1,\cdots,x_j,c\}$ and $P_2=\{c,x_{j+1},\cdots,x_n\}$ be the partitions of $[a,c]$ and $[c,b]$ respectively. So
|
||||
$$
|
||||
\begin{aligned}
|
||||
U(P^*,f,\alpha)&=\sum_{i=0}^{n}M_i(x_i-x_{i+1})\\
|
||||
&=M_c(c-x_j)+\sum_{i=0}^{j-1}M_i(x_i-x_{i+1})+\sum_{i=j+1}^{n}M_i(x_i-x_{i+1})\\
|
||||
&=U(P_1,f,\alpha)+U(P_2,f,\alpha)
|
||||
\end{aligned}
|
||||
$$
|
||||
and
|
||||
$$
|
||||
\begin{aligned}
|
||||
L(P^*,f,\alpha)&=\sum_{i=0}^{n}m_i(x_i-x_{i+1})\\
|
||||
&=m_c(x_j-c)+\sum_{i=0}^{j-1}m_i(x_i-x_{i+1})+\sum_{i=j+1}^{n-1}m_i(x_i-x_{i+1})\\
|
||||
&=L(P_1,f,\alpha)+L(P_2,f,\alpha)
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Since $P^*$ is a refinement of $P$, by \textbf{Theorem 6.4}, we have $U(P^*,f,\alpha)\leq U(P,f,\alpha)$ and $L(P^*,f,\alpha)\geq L(P,f,\alpha)$.
|
||||
|
||||
So $\int_a^c f d\alpha+\int_c^b f d\alpha\leq U(P^*,f,\alpha)\leq U(P,f,\alpha)=\int_a^b f d\alpha$.
|
||||
|
||||
Similarly, we have $\int_a^c f d\alpha+\int_c^b f d\alpha\geq L(P^*,f,\alpha)\geq L(P,f,\alpha)=\int_a^b f d\alpha$.
|
||||
|
||||
Therefore, $\int_a^c f d\alpha+\int_c^b f d\alpha=\int_a^b f d\alpha$.
|
||||
|
||||
**For (d)**, if $f\in \mathscr{R}(\alpha)$ on $[a,b]$, and if $|f(x)| \leq M$ on $[a,b]$, then
|
||||
$$
|
||||
\left|\int_a^b f d\alpha\right| \leq M(\alpha(b)-\alpha(a))
|
||||
$$
|
||||
|
||||
Since $|f(x)|\leq M$ on $[a,b]$, $\forall x\in [a,b]$, we have $f(x)\in [-M,M]$ on $[a,b]$. So $\sup|f(x)|\leq M$ and $\inf|f(x)|\leq M$. Since $L(P,f,\alpha)\leq \int_a^b f d\alpha\leq U(P,f,\alpha)$, we have
|
||||
|
||||
So
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\left|\int_a^b f d\alpha\right|&\leq \max\left\{|L(P,f,\alpha)|,|U(P,f,\alpha)|\right\}\\
|
||||
&=\max\left\{\sum_{i=0}^{n-1}|M_i|\Delta x_i,\sum_{i=0}^{n-1}|m_i|\Delta x_i\right\}\\
|
||||
&\leq \sum_{i=0}^{n-1}\max\{|M_i|,|m_i|\}\Delta x_i\\
|
||||
&\leq \sum_{i=0}^{n-1}M\Delta x_i\\
|
||||
&=M(\alpha(b)-\alpha(a))
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Therefore, $\left|\int_a^b f d\alpha\right| \leq M(\alpha(b)-\alpha(a))$.
|
||||
|
||||
**For (e)**, notice that
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\Delta (\alpha+\beta)_i &= \alpha(x_i)-\alpha(x_{i-1})+\beta(x_i)-\beta(x_{i-1}) \\
|
||||
&= \Delta \alpha_i + \Delta \beta_i
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
QED
|
||||
@@ -1,46 +0,0 @@
|
||||
export default {
|
||||
index: "Course Description",
|
||||
"---":{
|
||||
type: 'separator'
|
||||
},
|
||||
Exam_reviews: "Exam reviews",
|
||||
Math4121_L1: "Introduction to Lebesgue Integration (Lecture 1)",
|
||||
Math4121_L2: "Introduction to Lebesgue Integration (Lecture 2)",
|
||||
Math4121_L3: "Introduction to Lebesgue Integration (Lecture 3)",
|
||||
Math4121_L4: "Introduction to Lebesgue Integration (Lecture 4)",
|
||||
Math4121_L5: "Introduction to Lebesgue Integration (Lecture 5)",
|
||||
Math4121_L6: "Introduction to Lebesgue Integration (Lecture 6)",
|
||||
Math4121_L7: "Introduction to Lebesgue Integration (Lecture 7)",
|
||||
Math4121_L8: "Introduction to Lebesgue Integration (Lecture 8)",
|
||||
Math4121_L9: "Introduction to Lebesgue Integration (Lecture 9)",
|
||||
Math4121_L10: "Introduction to Lebesgue Integration (Lecture 10)",
|
||||
Math4121_L11: "Introduction to Lebesgue Integration (Lecture 11)",
|
||||
Math4121_L12: "Introduction to Lebesgue Integration (Lecture 12)",
|
||||
Math4121_L13: "Introduction to Lebesgue Integration (Lecture 13)",
|
||||
Math4121_L14: "Introduction to Lebesgue Integration (Lecture 14)",
|
||||
Math4121_L15: "Introduction to Lebesgue Integration (Lecture 15)",
|
||||
Math4121_L16: "Introduction to Lebesgue Integration (Lecture 16)",
|
||||
Math4121_L17: "Introduction to Lebesgue Integration (Lecture 17)",
|
||||
Math4121_L18: "Introduction to Lebesgue Integration (Lecture 18)",
|
||||
Math4121_L19: "Introduction to Lebesgue Integration (Lecture 19)",
|
||||
Math4121_L20: "Introduction to Lebesgue Integration (Lecture 20)",
|
||||
Math4121_L21: "Introduction to Lebesgue Integration (Lecture 21)",
|
||||
Math4121_L22: "Introduction to Lebesgue Integration (Lecture 22)",
|
||||
Math4121_L23: "Introduction to Lebesgue Integration (Lecture 23)",
|
||||
Math4121_L24: "Introduction to Lebesgue Integration (Lecture 24)",
|
||||
Math4121_L25: "Introduction to Lebesgue Integration (Lecture 25)",
|
||||
Math4121_L26: "Introduction to Lebesgue Integration (Lecture 26)",
|
||||
Math4121_L27: "Introduction to Lebesgue Integration (Lecture 27)",
|
||||
Math4121_L28: "Introduction to Lebesgue Integration (Lecture 28)",
|
||||
Math4121_L29: "Introduction to Lebesgue Integration (Lecture 29)",
|
||||
Math4121_L30: "Introduction to Lebesgue Integration (Lecture 30)",
|
||||
Math4121_L31: "Introduction to Lebesgue Integration (Lecture 31)",
|
||||
Math4121_L32: "Introduction to Lebesgue Integration (Lecture 32)",
|
||||
Math4121_L33: "Introduction to Lebesgue Integration (Lecture 33)",
|
||||
Math4121_L34: "Introduction to Lebesgue Integration (Lecture 34)",
|
||||
Math4121_L35: "Introduction to Lebesgue Integration (Lecture 35)",
|
||||
Math4121_L36: "Introduction to Lebesgue Integration (Lecture 36)",
|
||||
Math4121_L37: "Introduction to Lebesgue Integration (Lecture 37)",
|
||||
Math4121_L38: "Introduction to Lebesgue Integration (Lecture 38)",
|
||||
Math4121_L39: "Introduction to Lebesgue Integration (Lecture 39)",
|
||||
}
|
||||
@@ -1,30 +0,0 @@
|
||||
# Math4121
|
||||
|
||||
Riemann integration; measurable functions; Measures; the Lebesgue integral; integrable functions; $L^p$ spaces.
|
||||
|
||||
## Textbook
|
||||
|
||||
Principles of Mathematical Analysis by Walter Rudin
|
||||
|
||||
A radical Approach to Lebesgue's Theory of Integration by David
|
||||
|
||||
## Grade
|
||||
|
||||
| item | percentage |
|
||||
| --- | --- |
|
||||
| Homework | 40% |
|
||||
| Midterm 1 | 15% |
|
||||
| Midterm 2 | 15% |
|
||||
| Final | 30% |
|
||||
|
||||
## Homework
|
||||
|
||||
Due every Monday.
|
||||
|
||||
## Office Hour
|
||||
|
||||
Monday 1pm-2pm
|
||||
|
||||
Wednesday 12pm-1pm
|
||||
|
||||
Friday 11:30am-12:30pm
|
||||
Reference in New Issue
Block a user