seems working on this small batch
This commit is contained in:
@@ -1,840 +0,0 @@
|
||||
# Math 416 Midterm 1 Review
|
||||
|
||||
So everything we have learned so far is to extend the real line to the complex plane.
|
||||
|
||||
## Chapter 0 Calculus on Real values
|
||||
|
||||
### Differentiation
|
||||
|
||||
Let $f,g$ be function on real line and $c$ be a real number.
|
||||
|
||||
$$
|
||||
\frac{d}{dx}(f+g)=f'+g'
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}(cf)=cf'
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}(fg)=f'g+fg'
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}(f/g)=(f'g-fg')/g^2
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}(f\circ g)=(f'\circ g)\frac{d}{dx}g
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}x^n=nx^{n-1}
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}e^x=e^x
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}\ln x=\frac{1}{x}
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}\sin x=\cos x
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}\cos x=-\sin x
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}\tan x=\sec^2 x
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}\sec x=\sec x\tan x
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}\csc x=-\csc x\cot x
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}\sinh x=\cosh x
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}\cosh x=\sinh x
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}\tanh x=\operatorname{sech}^2 x
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}\operatorname{sech} x=-\operatorname{sech}x\tanh x
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}\operatorname{csch} x=-\operatorname{csch}x\coth x
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}\coth x=-\operatorname{csch}^2 x
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}\arcsin x=\frac{1}{\sqrt{1-x^2}}
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}\arccos x=-\frac{1}{\sqrt{1-x^2}}
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}\arctan x=\frac{1}{1+x^2}
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}\operatorname{arccot} x=-\frac{1}{1+x^2}
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}\operatorname{arcsec} x=\frac{1}{x\sqrt{x^2-1}}
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}\operatorname{arccsc} x=-\frac{1}{x\sqrt{x^2-1}}
|
||||
$$
|
||||
|
||||
### Integration
|
||||
|
||||
Let $f,g$ be function on real line and $c$ be a real number.
|
||||
|
||||
$$
|
||||
\int (f+g)dx=\int fdx+\int gdx
|
||||
$$
|
||||
|
||||
$$
|
||||
\int cfdx=c\int fdx
|
||||
$$
|
||||
|
||||
$$
|
||||
\int e^x dx=e^x
|
||||
$$
|
||||
|
||||
$$
|
||||
\int \ln x dx=x\ln x-x
|
||||
$$
|
||||
|
||||
$$
|
||||
\int \frac{1}{x} dx=\ln|x|
|
||||
$$
|
||||
|
||||
$$
|
||||
\int \sin x dx=-\cos x
|
||||
$$
|
||||
|
||||
$$
|
||||
\int \cos x dx=\sin x
|
||||
$$
|
||||
|
||||
$$
|
||||
\int \tan x dx=-\ln|\cos x|
|
||||
$$
|
||||
|
||||
$$
|
||||
\int \cot x dx=\ln|\sin x|
|
||||
$$
|
||||
|
||||
$$
|
||||
\int \sec x dx=\ln|\sec x+\tan x|
|
||||
$$
|
||||
|
||||
$$
|
||||
\int \csc x dx=\ln|\csc x-\cot x|
|
||||
$$
|
||||
|
||||
$$
|
||||
\int \sinh x dx=\cosh x
|
||||
$$
|
||||
|
||||
$$
|
||||
\int \cosh x dx=\sinh x
|
||||
$$
|
||||
|
||||
$$
|
||||
\int \tanh x dx=\ln|\cosh x|
|
||||
$$
|
||||
|
||||
$$
|
||||
\int \coth x dx=\ln|\sinh x|
|
||||
$$
|
||||
|
||||
$$
|
||||
\int \operatorname{sech} x dx=2\arctan(\tanh(x/2))
|
||||
$$
|
||||
|
||||
$$
|
||||
\int \operatorname{csch} x dx=\ln|\coth x-\operatorname{csch} x|
|
||||
$$
|
||||
|
||||
$$
|
||||
\int \operatorname{sech}^2 x dx=\tanh x
|
||||
$$
|
||||
|
||||
$$
|
||||
\int \operatorname{csch}^2 x dx=-\coth x
|
||||
$$
|
||||
|
||||
$$
|
||||
\int \frac{1}{1+x^2} dx=\arctan x
|
||||
$$
|
||||
|
||||
$$
|
||||
\int \frac{1}{x^2+1} dx=\arctan x
|
||||
$$
|
||||
|
||||
$$
|
||||
\int \frac{1}{x^2-1} dx=\frac{1}{2}\ln|\frac{x-1}{x+1}|
|
||||
$$
|
||||
|
||||
$$
|
||||
\int \frac{1}{x^2-a^2} dx=\frac{1}{2a}\ln|\frac{x-a}{x+a}|
|
||||
$$
|
||||
|
||||
$$
|
||||
\int \frac{1}{x^2+a^2} dx=\frac{1}{a}\arctan(\frac{x}{a})
|
||||
$$
|
||||
|
||||
$$
|
||||
\int \frac{1}{\sqrt{x^2-a^2}} dx=\ln|x+\sqrt{x^2-a^2}|
|
||||
$$
|
||||
|
||||
$$
|
||||
\int \frac{1}{\sqrt{x^2+a^2}} dx=\ln|x+\sqrt{x^2+a^2}|
|
||||
$$
|
||||
|
||||
## Chapter 1 Complex Numbers
|
||||
|
||||
### Definition of complex numbers
|
||||
|
||||
An ordered pair of real numbers $(x, y)$ can be represented as a complex number $z = x + yi$, where $i$ is the imaginary unit.
|
||||
|
||||
With operations defined as:
|
||||
|
||||
$$
|
||||
(x_1 + y_1i) + (x_2 + y_2i) = (x_1 + x_2) + (y_1 + y_2)i
|
||||
$$
|
||||
|
||||
$$
|
||||
(x_1 + y_1i) \cdot (x_2 + y_2i) = (x_1x_2 - y_1y_2) + (x_1y_2 + x_2y_1)i
|
||||
$$
|
||||
|
||||
#### Modulus
|
||||
|
||||
The modulus of a complex number $z = x + yi$ is defined as
|
||||
|
||||
$$
|
||||
|z| = \sqrt{x^2 + y^2}=|z\overline{z}|
|
||||
$$
|
||||
|
||||
### De Moivre's Formula
|
||||
|
||||
Every complex number $z$ can be written as $z = r(\cos \theta + i \sin \theta)$, where $r$ is the magnitude of $z$ and $\theta$ is the argument of $z$.
|
||||
|
||||
$$
|
||||
z^n = r^n(\cos n\theta + i \sin n\theta)
|
||||
$$
|
||||
|
||||
The De Moivre's formula is useful for finding the $n$th roots of a complex number.
|
||||
|
||||
$$
|
||||
z^n = r^n(\cos n\theta + i \sin n\theta)
|
||||
$$
|
||||
|
||||
### Roots of complex numbers
|
||||
|
||||
Using De Moivre's formula, we can find the $n$th roots of a complex number.
|
||||
|
||||
If $z=r(\cos \theta + i \sin \theta)$, then the $n$th roots of $z$ are given by:
|
||||
|
||||
$$
|
||||
z_k = r^{1/n}(\cos \frac{\theta + 2k\pi}{n} + i \sin \frac{\theta + 2k\pi}{n})
|
||||
$$
|
||||
|
||||
for $k = 0, 1, 2, \ldots, n-1$.
|
||||
|
||||
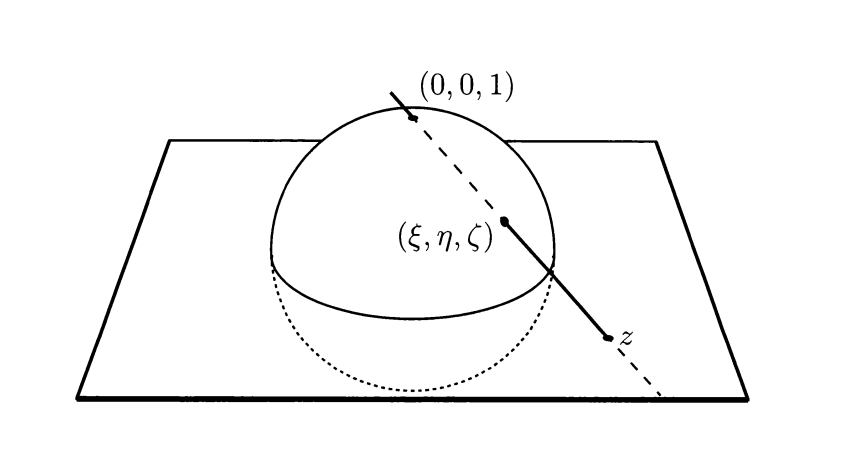
### Stereographic projection
|
||||
|
||||
|
||||
|
||||
The stereographic projection is a map from the unit sphere $S^2$ to the complex plane $\mathbb{C}\setminus\{0\}$.
|
||||
|
||||
The projection is given by:
|
||||
|
||||
$$
|
||||
z\mapsto \frac{(2Re(z), 2Im(z), |z|^2-1)}{|z|^2+1}
|
||||
$$
|
||||
|
||||
The inverse map is given by:
|
||||
|
||||
$$
|
||||
(\xi,\eta, \zeta)\mapsto \frac{\xi + i\eta}{1 - \zeta}
|
||||
$$
|
||||
|
||||
## Chapter 2 Complex Differentiation
|
||||
|
||||
### Definition of complex differentiation
|
||||
|
||||
Let the complex plane $\mathbb{C}$ be defined in an open subset $G$ of $\mathbb{C}$. (Domain)
|
||||
|
||||
Then $f$ is said to be differentiable at $z_0\in G$ if the limit
|
||||
|
||||
$$
|
||||
\lim_{z\to z_0} \frac{f(z)-f(z_0)}{z-z_0}
|
||||
$$
|
||||
|
||||
exists.
|
||||
|
||||
The limit is called the derivative of $f$ at $z_0$ and is denoted by $f'(z_0)$.
|
||||
|
||||
To prove that a function is differentiable, we can use the standard delta-epsilon definition of a limit.
|
||||
|
||||
$$
|
||||
\left|\frac{f(z)-f(z_0)}{z-z_0} - f'(z_0)\right| < \epsilon
|
||||
$$
|
||||
|
||||
whenever $0 < |z-z_0| < \delta$.
|
||||
|
||||
With such definition, all the properties of real differentiation can be extended to complex differentiation.
|
||||
|
||||
#### Differentiation of complex functions
|
||||
|
||||
1. If $f$ is differentiable at $z_0$, then $f$ is continuous at $z_0$.
|
||||
2. If $f,g$ are differentiable at $z_0$, then $f+g, fg$ are differentiable at $z_0$.
|
||||
$$
|
||||
(f+g)'(z_0) = f'(z_0) + g'(z_0)
|
||||
$$
|
||||
$$
|
||||
(fg)'(z_0) = f'(z_0)g(z_0) + f(z_0)g'(z_0)
|
||||
$$
|
||||
3. If $f,g$ are differentiable at $z_0$ and $g(z_0)\neq 0$, then $f/g$ is differentiable at $z_0$.
|
||||
$$
|
||||
\left(\frac{f}{g}\right)'(z_0) = \frac{f'(z_0)g(z_0) - f(z_0)g'(z_0)}{g(z_0)^2}
|
||||
$$
|
||||
4. If $f$ is differentiable at $z_0$ and $g$ is differentiable at $f(z_0)$, then $g\circ f$ is differentiable at $z_0$.
|
||||
$$
|
||||
(g\circ f)'(z_0) = g'(f(z_0))f'(z_0)
|
||||
$$
|
||||
5. If $f(z)=\sum_{k=0}^n c_k(z-z_0)^k$, where $c_k\in\mathbb{C}$, then $f$ is differentiable at $z_0$ and $f'(z_0)=\sum_{k=1}^n kc_k(z_0-z_0)^{k-1}$.
|
||||
$$
|
||||
f'(z_0) = c_1 + 2c_2(z_0-z_0) + 3c_3(z_0-z_0)^2 + \cdots + nc_n(z_0-z_0)^{n-1}
|
||||
$$
|
||||
|
||||
### Cauchy-Riemann Equations
|
||||
|
||||
Let the function defined on an open subset $G$ of $\mathbb{C}$ be $f(x,y)=u(x,y)+iv(x,y)$, where $u,v$ are real-valued functions.
|
||||
|
||||
Then $f$ is differentiable at $z_0=x_0+y_0i$ if and only if the partial derivatives of $u$ and $v$ exist at $(x_0,y_0)$ and satisfy the Cauchy-Riemann equations:
|
||||
|
||||
$$
|
||||
\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y}, \quad \frac{\partial u}{\partial y} = -\frac{\partial v}{\partial x}
|
||||
$$
|
||||
|
||||
On the polar form, the Cauchy-Riemann equations are
|
||||
|
||||
$$
|
||||
r\frac{\partial u}{\partial r} = \frac{\partial v}{\partial \theta}, \quad \frac{\partial u}{\partial \theta} = -r\frac{\partial v}{\partial r}
|
||||
$$
|
||||
|
||||
### Holomorphic functions
|
||||
|
||||
A function $f$ is said to be holomorphic on an open subset $G$ of $\mathbb{C}$ if $f$ is differentiable at every point of $G$.
|
||||
|
||||
#### Partial differential operators
|
||||
|
||||
$$
|
||||
\frac{\partial}{\partial z} = \frac{1}{2}\left(\frac{\partial}{\partial x} - i\frac{\partial}{\partial y}\right)
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{\partial}{\partial \bar{z}} = \frac{1}{2}\left(\frac{\partial}{\partial x} + i\frac{\partial}{\partial y}\right)
|
||||
$$
|
||||
|
||||
This gives that
|
||||
|
||||
$$
|
||||
\frac{\partial f}{\partial z} = \frac{1}{2}\left(\frac{\partial f}{\partial x} - i\frac{\partial f}{\partial y}\right)=\frac{1}{2}\left(\frac{\partial u}{\partial x} +\frac{\partial v}{\partial y}\right) + \frac{i}{2}\left(\frac{\partial v}{\partial x} - \frac{\partial u}{\partial y}\right)
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{\partial f}{\partial \bar{z}} = \frac{1}{2}\left(\frac{\partial f}{\partial x} + i\frac{\partial f}{\partial y}\right)=\frac{1}{2}\left(\frac{\partial u}{\partial x} - \frac{\partial v}{\partial y}\right) + \frac{i}{2}\left(\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}\right)
|
||||
$$
|
||||
|
||||
If the function $f$ is holomorphic, then by the Cauchy-Riemann equations, we have
|
||||
|
||||
$$
|
||||
\frac{\partial f}{\partial \bar{z}} = 0
|
||||
$$
|
||||
|
||||
### Conformal mappings
|
||||
|
||||
A holomorphic function $f$ is said to be conformal if it preserves the angles between the curves. More formally, if $f$ is holomorphic on an open subset $G$ of $\mathbb{C}$ and $z_0\in G$, $\gamma_1, \gamma_2$ are two curves passing through $z_0$ ($\gamma_1(t_1)=\gamma_2(t_2)=z_0$) and intersecting at an angle $\theta$, then
|
||||
|
||||
$$
|
||||
\arg(f\circ\gamma_1)'(t_1) - \arg(f\circ\gamma_2)'(t_2) = \theta
|
||||
$$
|
||||
|
||||
In other words, the angle between the curves is preserved.
|
||||
|
||||
An immediate consequence is that
|
||||
|
||||
$$
|
||||
\arg(f\cdot \gamma_1)'(t_1) =\arg f'(z_0) + \arg \gamma_1'(t_1)\\
|
||||
\arg(f\cdot \gamma_2)'(t_2) =\arg f'(z_0) + \arg \gamma_2'(t_2)
|
||||
$$
|
||||
|
||||
### Harmonic functions
|
||||
|
||||
A real-valued function $u$ is said to be harmonic if it satisfies the Laplace equation:
|
||||
|
||||
$$
|
||||
\frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = 0
|
||||
$$
|
||||
|
||||
## Chapter 3 Linear Fractional Transformations
|
||||
|
||||
### Definition of linear fractional transformations
|
||||
|
||||
A linear fractional transformation is a function of the form
|
||||
|
||||
$$
|
||||
\phi(z) = \frac{az+b}{cz+d}
|
||||
$$
|
||||
|
||||
where $a,b,c,d$ are complex numbers and $ad-bc\neq 0$.
|
||||
|
||||
### Properties of linear fractional transformations
|
||||
|
||||
#### Matrix form
|
||||
|
||||
A linear fractional transformation can be written as a matrix multiplication:
|
||||
|
||||
$$
|
||||
\phi(z) = \begin{bmatrix}
|
||||
a & b\\
|
||||
c & d\\
|
||||
\end{bmatrix}
|
||||
\begin{bmatrix}
|
||||
z\\
|
||||
1\\
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
#### Conformality
|
||||
|
||||
A linear fractional transformation is conformal.
|
||||
|
||||
$$
|
||||
\phi'(z) = \frac{ad-bc}{(cz+d)^2}
|
||||
$$
|
||||
|
||||
#### Three-fold transitivity
|
||||
|
||||
If $z_1,z_2,z_3$ are distinct points in the complex plane, then there exists a unique linear fractional transformation $\phi$ such that $\phi(z_1)=\infty$, $\phi(z_2)=0$, $\phi(z_3)=1$.
|
||||
|
||||
The map is given by
|
||||
|
||||
$$
|
||||
\phi(z) =\begin{cases}
|
||||
\frac{(z-z_2)(z_1-z_3)}{(z-z_1)(z_2-z_3)} & \text{if } z_1,z_2,z_3 \text{ are all finite}\\
|
||||
\frac{z-z_2}{z_3-z_2} & \text{if } z_1=\infty\\
|
||||
\frac{z_3-z_1}{z-z_1} & \text{if } z_2=\infty\\
|
||||
\frac{z-z_2}{z-z_1} & \text{if } z_3=\infty\\
|
||||
\end{cases}
|
||||
$$
|
||||
|
||||
So if $z_1,z_2,z_3$, $w_1,w_2,w_3$ are distinct points in the complex plane, then there exists a unique linear fractional transformation $\phi$ such that $\phi(z_i)=w_i$ for $i=1,2,3$.
|
||||
|
||||
#### Factorization
|
||||
|
||||
Every linear fractional transformation can be written as a composition of homothetic mappings, translations, inversions, and multiplications.
|
||||
|
||||
If $\phi(z)=\frac{az+b}{cz+d}$, then
|
||||
|
||||
$$
|
||||
\phi(z) = \frac{b-ad/c}{cz+d}+\frac{a}{c}
|
||||
$$
|
||||
|
||||
#### Clircle
|
||||
|
||||
A linear-fractional transformation maps circles and lines to circles and lines.
|
||||
|
||||
## Chapter 4 Elementary Functions
|
||||
|
||||
### Exponential function
|
||||
|
||||
The exponential function is defined as
|
||||
|
||||
$$
|
||||
e^z = \sum_{n=0}^\infty \frac{z^n}{n!}
|
||||
$$
|
||||
|
||||
Let $z=x+iy$, then
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
e^z &= e^{x+iy}\\
|
||||
&= e^x e^{iy}\\
|
||||
&= e^x\sum_{n=0}^\infty \frac{(iy)^n}{n!}\\
|
||||
&= e^x\sum_{n=0}^\infty \frac{(-1)^n y^{2n}}{(2n)!} + i \sum_{n=0}^\infty \frac{(-1)^n y^{2n+1}}{(2n+1)!}\\
|
||||
&= e^x(\cos y + i\sin y)\\
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
So we can rewrite the polar form of a complex number as
|
||||
|
||||
$$
|
||||
z = r(\cos \theta + i\sin \theta) = re^{i\theta}
|
||||
$$
|
||||
|
||||
#### $e^x$ is holomorphic
|
||||
|
||||
Let $f(z)=e^z$, then $u(x,y)=e^x\cos y$, $v(x,y)=e^x\sin y$.
|
||||
|
||||
$$
|
||||
\frac{\partial u}{\partial x} = e^x\cos y = \frac{\partial v}{\partial y}\\
|
||||
\frac{\partial u}{\partial y} = -e^x\sin y = -\frac{\partial v}{\partial x}
|
||||
$$
|
||||
|
||||
### Trigonometric functions
|
||||
|
||||
$$
|
||||
\sin z = \frac{e^{iz}-e^{-iz}}{2i}, \quad \cos z = \frac{e^{iz}+e^{-iz}}{2}, \quad \tan z = \frac{\sin z}{\cos z}
|
||||
$$
|
||||
|
||||
$$
|
||||
\sec z = \frac{1}{\cos z}, \quad \csc z = \frac{1}{\sin z}, \quad \cot z = \frac{1}{\tan z}
|
||||
$$
|
||||
|
||||
#### Hyperbolic functions
|
||||
|
||||
$$
|
||||
\sinh z = \frac{e^z-e^{-z}}{2}, \quad \cosh z = \frac{e^z+e^{-z}}{2}, \quad \tanh z = \frac{\sinh z}{\cosh z}
|
||||
$$
|
||||
|
||||
$$
|
||||
\operatorname{sech} z = \frac{1}{\cosh z}, \quad \operatorname{csch} z = \frac{1}{\sinh z}, \quad \operatorname{coth} z = \frac{1}{\tanh z}
|
||||
$$
|
||||
|
||||
### Logarithmic function
|
||||
|
||||
The logarithmic function is defined as
|
||||
|
||||
$$
|
||||
\ln z=\{w\in\mathbb{C}: e^w=z\}
|
||||
$$
|
||||
|
||||
#### Properties of the logarithmic function
|
||||
|
||||
Let $z=x+iy$, then
|
||||
|
||||
$$
|
||||
|e^z|=\sqrt{e^x(\cos y)^2+(\sin y)^2}=e^x
|
||||
$$
|
||||
|
||||
So we have
|
||||
|
||||
$$
|
||||
\log z = \ln |z| + i\arg z
|
||||
$$
|
||||
|
||||
### Power function
|
||||
|
||||
For any two complex numbers $a,b$, we can define the power function as
|
||||
|
||||
$$
|
||||
a^b = e^{b\log a}
|
||||
$$
|
||||
|
||||
> Example:
|
||||
>
|
||||
> $$i^i=e^{i\ln i}=e^{i(\ln 1+i\frac{\pi}{2})}=e^{-\frac{\pi}{2}} $$
|
||||
>
|
||||
> $$e^{i\pi}=-1$$
|
||||
|
||||
|
||||
## Chapter 5 Power Series
|
||||
|
||||
### Definition of power series
|
||||
|
||||
A power series is a series of the form
|
||||
|
||||
$$
|
||||
\sum_{n=0}^\infty a_n (z-z_0)^n
|
||||
$$
|
||||
|
||||
### Properties of power series
|
||||
|
||||
#### Geometric series
|
||||
|
||||
$$
|
||||
\sum_{n=0}^\infty z^n = \frac{1}{1-z}, \quad |z|<1
|
||||
$$
|
||||
|
||||
### Radius/Region of convergence
|
||||
|
||||
The radius of convergence of a power series is the largest number $R$ such that the series converges for all $z$ with $|z-z_0|<R$.
|
||||
|
||||
The region of convergence of a power series is the set of all points $z$ such that the series converges.
|
||||
|
||||
### Cauchy-Hadamard Theorem
|
||||
|
||||
The radius of convergence of a power series is given by
|
||||
|
||||
$$
|
||||
R=\frac{1}{\limsup_{n\to\infty} |a_n|^{1/n}}
|
||||
$$
|
||||
|
||||
### Derivative of power series
|
||||
|
||||
The derivative of a power series is given by
|
||||
|
||||
$$
|
||||
f'(z)=\sum_{n=1}^\infty n a_n (z-z_0)^{n-1}
|
||||
$$
|
||||
|
||||
### Cauchy Product (of power series)
|
||||
|
||||
Let $\sum_{n=0}^\infty a_n (z-z_0)^n$ and $\sum_{n=0}^\infty b_n (z-z_0)^n$ be two power series with radius of convergence $R_1$ and $R_2$ respectively.
|
||||
|
||||
Then the Cauchy product of the two series is given by
|
||||
|
||||
$$
|
||||
\sum_{n=0}^\infty c_n (z-z_0)^n
|
||||
$$
|
||||
|
||||
where
|
||||
|
||||
$$
|
||||
c_n = \sum_{k=0}^n a_k b_{n-k}
|
||||
$$
|
||||
|
||||
The radius of convergence of the Cauchy product is at least $\min(R_1,R_2)$.
|
||||
|
||||
## Chapter 6 Complex Integration
|
||||
|
||||
### Definition of Riemann Integral for complex functions
|
||||
|
||||
The complex integral of a complex function $\phi$ on the closed subinterval $[a,b]$ of the real line is said to be piecewise continuous if there exists a partition $a=t_0<t_1<\cdots<t_n=b$ such that $\phi$ is continuous on each open interval $(t_{i-1},t_i)$ and has a finite limit at each discontinuity point of the closed interval $[a,b]$.
|
||||
|
||||
If $\phi$ is piecewise continuous on $[a,b]$, then the complex integral of $\phi$ on $[a,b]$ is defined as
|
||||
|
||||
$$
|
||||
\int_a^b \phi(t) dt = \int_a^b \operatorname{Re}\phi(t) dt + i\int_a^b \operatorname{Im}\phi(t) dt
|
||||
$$
|
||||
|
||||
### Fundamental Theorem of Calculus
|
||||
|
||||
If $\phi$ is piecewise continuous on $[a,b]$, then
|
||||
|
||||
$$
|
||||
\int_a^b \phi'(t) dt = \phi(b)-\phi(a)
|
||||
$$
|
||||
|
||||
### Triangle inequality
|
||||
|
||||
$$
|
||||
\left|\int_a^b \phi(t) dt\right| \leq \int_a^b |\phi(t)| dt
|
||||
$$
|
||||
|
||||
### Integral on curve
|
||||
|
||||
Let $\gamma$ be a piecewise smooth curve in the complex plane.
|
||||
|
||||
The integral of a complex function $f$ on $\gamma$ is defined as
|
||||
|
||||
$$
|
||||
\int_\gamma f(z) dz = \int_a^b f(\gamma(t))\gamma'(t) dt
|
||||
$$
|
||||
|
||||
### Favorite estimate
|
||||
|
||||
Let $\gamma:[a,b]\to\mathbb{C}$ be a piecewise smooth curve, and let $f:[a,b]\to\mathbb{C}$ be a continuous complex-valued function. Let $M$ be a real number such that $|f(z)|\leq M$ for all $z\in\gamma$. Then
|
||||
|
||||
$$
|
||||
\left|\int_\gamma f(z) dz\right| \leq M\ell(\gamma)
|
||||
$$
|
||||
|
||||
where $\ell(\gamma)$ is the length of the curve $\gamma$.
|
||||
|
||||
## Chapter 7 Cauchy's Theorem
|
||||
|
||||
### Cauchy's Theorem
|
||||
|
||||
Let $\gamma$ be a closed curve in $\mathbb{C}$ and $U$ be a simply connected open subset of $\mathbb{C}$ containing $\gamma$ and its interior. Let $f$ be a holomorphic function on $U$. Then
|
||||
|
||||
$$
|
||||
\int_\gamma f(z) dz = 0
|
||||
$$
|
||||
|
||||
### Cauchy's Formula for a Circle
|
||||
|
||||
Let $C$ be a counterclockwise oriented circle and let $f$ be holomorphic function defined in an open set containing $C$ and its interior. Then for any $z$ in the interior of $C$,
|
||||
|
||||
$$
|
||||
f(z)=\frac{1}{2\pi i}\int_C \frac{f(\zeta)}{\zeta-z} d\zeta
|
||||
$$
|
||||
|
||||
### Mean Value Property
|
||||
|
||||
Let the function $f$ be holomorphic on a disk $|z-z_0|<R$. Then for any $0<r<R$, let $C_r$ denote the circle with center $z_0$ and radius $r$. Then
|
||||
|
||||
$$
|
||||
f(z_0)=\frac{1}{2\pi}\int_0^{2\pi} f(z_0+re^{i\theta}) d\theta
|
||||
$$
|
||||
|
||||
The value of the function at the center of the disk is the average of the values of the function on the boundary of the disk.
|
||||
|
||||
### Cauchy Integrals
|
||||
|
||||
Let $\gamma$ be a piecewise smooth curve in $\mathbb{C}$ and let $\phi$ be a continuous complex-valued function on $\gamma$. Then the Cauchy integral of $\phi$ on $\gamma$ is the function $f$ defined in $C\setminus\gamma$ by
|
||||
|
||||
$$
|
||||
f(z)=\int_\gamma \frac{\phi(\zeta)}{\zeta-z} d\zeta
|
||||
$$
|
||||
|
||||
Cauchy Integral Formula for circle $C_r$:
|
||||
|
||||
$$
|
||||
f(z)=\frac{1}{2\pi i}\int_{C_r} \frac{f(\zeta)}{\zeta-z} d\zeta
|
||||
$$
|
||||
|
||||
> Example:
|
||||
>
|
||||
> Evaluate $$\int_{|z|=2} \frac{z}{z-1} dz$$
|
||||
>
|
||||
> Note that if we let $f(\zeta)=\zeta$ and $z=1$ is inside the circle, then we can use Cauchy Integral Formula for circle $C_r$ to evaluate the integral.
|
||||
>
|
||||
> So we have
|
||||
>
|
||||
> $$\int_{|z|=2} \frac{z}{z-1} dz = 2\pi i f(1) = 2\pi i$$
|
||||
|
||||
General Cauchy Integral Formula for circle $C_r$:
|
||||
|
||||
$$
|
||||
f^{(n)}(z)=\frac{n!}{2\pi i}\int_{C_r} \frac{f(\zeta)}{(\zeta-z)^{n+1}} d\zeta
|
||||
$$
|
||||
|
||||
> Example:
|
||||
>
|
||||
> Evaluate $$\int_{C}\frac{\sin z}{z^{38}}dz$$
|
||||
>
|
||||
> Note that if we let $f(\zeta)=\sin \zeta$ and $z=0$ is inside the circle, then we can use General Cauchy Integral Formula for circle $C_r$ to evaluate the integral.
|
||||
>
|
||||
> So we have
|
||||
>
|
||||
> $$\int_{C}\frac{\sin z}{z^{38}}dz = \frac{2\pi i}{37!} f^{(37)}(0) = \frac{2\pi i}{37!} \sin ^{(37)}(0)$$
|
||||
>
|
||||
> Note that $\sin ^{(n)}(0)=\begin{cases} 0,& n\equiv 0 \pmod{4}\\
|
||||
1,& n\equiv 1 \pmod{4}\\
|
||||
0,& n\equiv 2 \pmod{4}\\
|
||||
-1,& n\equiv 3 \pmod{4}
|
||||
\end{cases}$
|
||||
>
|
||||
> So we have
|
||||
>
|
||||
> $$\int_{C}\frac{\sin z}{z^{38}}dz = \frac{2\pi i}{37!} \sin ^{(37)}(0) = \frac{2\pi i}{37!} \cdot 1 = \frac{2\pi i}{37!}$$
|
||||
|
||||
_Cauchy integral is a easier way to evaluate the integral._
|
||||
|
||||
### Liouville's Theorem
|
||||
|
||||
If a function $f$ is entire (holomorphic on $\mathbb{C}$) and bounded, then $f$ is constant.
|
||||
|
||||
### Finding power series of holomorphic functions
|
||||
|
||||
If $f$ is holomorphic on a disk $|z-z_0|<R$, then $f$ can be represented as a power series on the disk.
|
||||
|
||||
where $a_n=\frac{f^{(n)}(z_0)}{n!}$
|
||||
|
||||
> Example:
|
||||
>
|
||||
> If $q(z)=(z-1)(z-2)(z-3)$, find the power series of $q(z)$ centered at $z=0$.
|
||||
>
|
||||
> Note that $q(z)$ is holomorphic on $\mathbb{C}$ and $q(z)=0$ at $z=1,2,3$.
|
||||
>
|
||||
> So we can use the power series of $q(z)$ centered at $z=1$.
|
||||
>
|
||||
> To solve this, we can simply expand $q(z)=(z-1)(z-2)(z-3)$ and get $q(z)=z^3-6z^2+11z-6$.
|
||||
>
|
||||
> So we have $a_0=q(1)=-6$, $a_1=q'(1)=3z^2-12z+11=11$, $a_2=\frac{q''(1)}{2!}=\frac{6z-12}{2}=-3$, $a_3=\frac{q'''(1)}{3!}=\frac{6}{6}=1$.
|
||||
>
|
||||
> So the power series of $q(z)$ centered at $z=1$ is
|
||||
>
|
||||
> $$q(z)=-6+11(z-1)-3(z-1)^2+(z-1)^3$$
|
||||
|
||||
### Fundamental Theorem of Algebra
|
||||
|
||||
Every non-constant polynomial with complex coefficients has a root in $\mathbb{C}$.
|
||||
|
||||
Can be factored into linear factors:
|
||||
|
||||
$$
|
||||
p(z)=a_n(z-z_1)(z-z_2)\cdots(z-z_n)
|
||||
$$
|
||||
|
||||
We can treat holomorphic functions as polynomials.
|
||||
|
||||
$f$ has zero of order $m$ at $z_0$ if and only if $f(z)=(z-z_0)^m g(z)$ for some holomorphic $g(z)$ and $g(z_0)\neq 0$.
|
||||
|
||||
### Zeros of holomorphic functions
|
||||
|
||||
If $f$ is holomorphic on a disk $|z-z_0|<R$ and $f$ has a zero of order $m$ at $z_0$, then $f(z_0)=0$, $f'(z_0)=0$, $f''(z_0)=0$, $\cdots$, $f^{(m-1)}(z_0)=0$ and $f^{(m)}(z_0)\neq 0$.
|
||||
|
||||
And there exists a holomorphic function $g$ on the disk such that $f(z)=(z-z_0)^m g(z)$ and $g(z_0)\neq 0$.
|
||||
|
||||
> Example:
|
||||
>
|
||||
> Find zeros of $f(z)=\cos(z\frac{\pi}{2})$
|
||||
>
|
||||
> Note that $f(z)=0$ if and only if $z\frac{\pi}{2}=(2k+1)\frac{\pi}{2}$ for some integer $k$.
|
||||
>
|
||||
> So the zeros of $f(z)$ are $z=(2k+1)$ for some integer $k$.
|
||||
>
|
||||
> The order of the zero is $1$ since $f'(z)=-\frac{\pi}{2}\sin(z\frac{\pi}{2})$ and $f'(z)\neq 0$ for all $z=(2k+1)$.
|
||||
|
||||
If $f$ vanishes to infinite order at $z_0$ (that is, $f(z_0)=f'(z_0)=f''(z_0)=\cdots=0$), then $f(z)\equiv 0$ on the connected open set $U$ containing $z_0$.
|
||||
|
||||
### Identity Theorem
|
||||
|
||||
If $f$ and $g$ are holomorphic on a connected open set $U\subset\mathbb{C}$ and $f(z)=g(z)$ for all $z$ in a subset of $U$ that has a limit point in $U$, then $f(z)=g(z)$ for all $z\in U$.
|
||||
|
||||
Key: consider $h(z)=f(z)-g(z)$, prove $h(z)\equiv 0$ on $U$ by applying the zero of holomorphic function.
|
||||
|
||||
### Weierstrass Theorem
|
||||
|
||||
Limit of a sequence of holomorphic functions is holomorphic.
|
||||
|
||||
Let $f_n$ be a sequence of holomorphic functions on a domain $D\subset\mathbb{C}$ that converges uniformly to $f$ on every compact subset of $D$. Then $f$ is holomorphic on $D$.
|
||||
|
||||
### Maximum Modulus Principle
|
||||
|
||||
If $f$ is a non-constant holomorphic function on a domain $D\subset\mathbb{C}$, then $|f|$ does not attain a maximum value in $D$.
|
||||
|
||||
#### Corollary: Minimum Modulus Principle
|
||||
|
||||
If $f$ is a non-constant holomorphic function on a domain $D\subset\mathbb{C}$, then $\frac{1}{f}$ does not attain a minimum value in $D$.
|
||||
|
||||
### Schwarz Lemma
|
||||
|
||||
If $f$ is a holomorphic function on the unit disk $|z|<1$ and $|f(z)|\leq |z|$, then $|f'(0)|\leq 1$.
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
@@ -1,279 +0,0 @@
|
||||
# Math 416 Final Review
|
||||
|
||||
Story after Cauchy's theorem
|
||||
|
||||
## Chapter 7: Cauchy's Theorem
|
||||
|
||||
### Existence of harmonic conjugate
|
||||
|
||||
Suppose $f=u+iv$ is holomorphic on a domain $U\subset\mathbb{C}$. Then $u=\Re f$ is harmonic on $U$. That is $\Delta u=\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}=0$.
|
||||
|
||||
Moreover, there exists $g\in O(U)$ such that $g$ is unique up to an additive imaginary constant.
|
||||
|
||||
> Example:
|
||||
>
|
||||
> Find a harmonic conjugate of $u(x,y)=\log|\frac{z}{z-1}|$
|
||||
>
|
||||
> Note that $\log(\frac{z}{z-1})=\log \left|\frac{z}{z-1}\right|+i(\arg(z)-\arg(z-1))$ is harmonic on $\mathbb{C}\setminus\{1\}$.
|
||||
>
|
||||
> So the harmonic conjugate of $u(x,y)=\log|\frac{z}{z-1}|$ is $v(x,y)=\arg(z)-\arg(z-1)+C$ where $C$ is a constant.
|
||||
>
|
||||
> Note that the harmonic conjugate may exist locally but not globally. (e.g. $u(x,y)=\log|z(z-1)|$ has a local harmonic conjugate $i(\arg(z)+\arg(z-1)+C)$ but this is not a well defined function since $\arg(z)+\arg(z-1)$ is not single-valued.)
|
||||
|
||||
### Corollary for harmonic functions
|
||||
|
||||
#### Theorem 7.19
|
||||
|
||||
Harmonic function are infinitely differentiable.
|
||||
|
||||
#### Theorem 7.20
|
||||
|
||||
Mean value property of harmonic functions.
|
||||
|
||||
Let $u$ be harmonic on an open set of $\Omega$, then
|
||||
|
||||
$$u(z_0)=\frac{1}{2\pi}\int_0^{2\pi} u(z_0+re^{i\theta}) d\theta$$
|
||||
|
||||
for any $z_0\in\Omega$ and $r>0$ such that $D(z_0,r)\subset\Omega$.
|
||||
|
||||
#### Theorem 7.21
|
||||
|
||||
Identity theorem for harmonic functions.
|
||||
|
||||
Let $u$ be harmonic on a domain $\Omega$. If $u=0$ on some open set $G\subset\Omega$, then $u\equiv 0$ on $\Omega$.
|
||||
|
||||
#### Theorem 7.22
|
||||
|
||||
Maximum principle for harmonic functions.
|
||||
|
||||
Let $u$ be a non-constant real-valued harmonic function on a domain $\Omega$. Then $|u|$ does not attain a maximum value in $\Omega$.
|
||||
|
||||
## Chapter 8: Laurent Series and Isolated Singularities
|
||||
|
||||
### Laurent Series
|
||||
|
||||
Laurent series is a generalization of Taylor series.
|
||||
|
||||
Laurent series is a power series of the form
|
||||
|
||||
$$f(z)=\sum_{n=-\infty}^{\infty} a_n (z-z_0)^n$$
|
||||
|
||||
where
|
||||
|
||||
$$
|
||||
a_k=\frac{1}{2\pi i}\int_{C_r}\frac{f(z)}{(z-z_0)^{k+1}}dz
|
||||
$$
|
||||
|
||||
The series converges on an annulus $R_1<|z-z_0|<R_2$.
|
||||
|
||||
where $R_1=\limsup_{n\to\infty} |a_{-n}|^{1/n}$ and $R_2=\frac{1}{\limsup_{n\to\infty} |a_n|^{1/n}}$.
|
||||
|
||||
### Cauchy's Formula for an Annulus
|
||||
|
||||
Let $f$ be holomorphic on an annulus $R_1<r_1<|z-z_0|<r_2<R_2$. And $w\in A(z_0;R_1,R_2)$. Find the Annulus $w\in A(z_0;r_1,r_2)$
|
||||
|
||||
Then
|
||||
|
||||
$$
|
||||
f(w)=\frac{1}{2\pi i}\int_{C_{r_1}}\frac{f(z)}{z-w}dz-\frac{1}{2\pi i}\int_{C_{r_2}}\frac{f(z)}{z-w}dz
|
||||
$$
|
||||
|
||||
### Isolated singularities
|
||||
|
||||
Let $f$ be holomorphic on $0<|z-z_0|<R$ (The punctured disk of radius $R$ centered at $z_0$). If there exists a Laurent series of $f$ convergent on $0<|z-z_0|<R$, then $z_0$ is called an isolated singularity of $f$.
|
||||
|
||||
The series $f(z)=\sum_{n=-\infty}^{-1}a_n(z-z_0)^n$ is called the principle part of Laurent series of $f$ at $z_0$.
|
||||
|
||||
#### Removable singularities
|
||||
|
||||
If the principle part of Laurent series of $f$ at $z_0$ is zero, then $z_0$ is called a removable singularity of $f$.
|
||||
|
||||
Criterion for a removable singularity:
|
||||
|
||||
If $f$ is bounded on $0<|z-z_0|<R$, then $z_0$ is a removable singularity.
|
||||
|
||||
> Example:
|
||||
>
|
||||
> $f(z)=\frac{1}{e^z-1}$ has a removable singularity at $z=0$.
|
||||
>
|
||||
> The Laurent series of $f$ at $z=0$ is
|
||||
>
|
||||
> $$f(z)=\frac{1}{z}+\sum_{n=0}^{\infty}\frac{z^n}{n!}$$
|
||||
>
|
||||
> The principle part is zero, so $z=0$ is a removable singularity.
|
||||
|
||||
#### Poles
|
||||
|
||||
If the principle part of Laurent series of $f$ at $z_0$ is a finite sum, then $z_0$ is called a pole of $f$.
|
||||
|
||||
Criterion for a pole:
|
||||
|
||||
If $f$ has an isolated singularity at $z_0$, and $\lim_{z\to z_0}|f(z)|=\infty$, then $z_0$ is a pole of $f$.
|
||||
|
||||
> Example:
|
||||
>
|
||||
> $f(z)=\frac{1}{z^2}$ has a pole at $z=0$.
|
||||
>
|
||||
> The Laurent series of $f$ at $z=0$ is
|
||||
>
|
||||
> $$f(z)=\frac{1}{z^2}$$
|
||||
>
|
||||
> The principle part is $\frac{1}{z^2}$, so $z=0$ is a pole.
|
||||
|
||||
#### Essential singularities
|
||||
|
||||
If $f$ has an isolated singularity at $z_0$, and it is neither a removable singularity nor a pole, then $z_0$ is called an essential singularity of $f$.
|
||||
|
||||
"Criterion" for an essential singularity:
|
||||
|
||||
If the principle part of Laurent series of $f$ at $z_0$ has infinitely many non-zero coefficients corresponding to negative powers of $z-z_0$, then $z_0$ is called an essential singularity of $f$.
|
||||
|
||||
> Example:
|
||||
>
|
||||
> $f(z)=\sin(\frac{1}{z})$ has an essential singularity at $z=0$.
|
||||
>
|
||||
> The Laurent series of $f$ at $z=0$ is
|
||||
>
|
||||
> $$f(z)=\frac{1}{z}-\frac{1}{6z^3}+\frac{1}{120z^5}-\cdots$$
|
||||
>
|
||||
> Since there are infinitely many non-zero coefficients corresponding to negative powers of $z$, $z=0$ is an essential singularity.
|
||||
|
||||
#### Singularities at infinity
|
||||
|
||||
We say $f$ has a singularity (removable, pole, or essential) at infinity if $f(1/z)$ has an isolated singularity (removable, pole, or essential) at $z=0$.
|
||||
|
||||
> Example:
|
||||
>
|
||||
> $f(z)=\frac{z^4}{(z-1)(z-3)}$ has a pole of order 2 at infinity.
|
||||
>
|
||||
> Plug in $z=1/w$, we get $f(1/w)=\frac{1}{w^2}\frac{1}{(1/w-1)(1/w-3)}=\frac{1}{w^2}\frac{1}{(1-w)(1-3w)}=\frac{1}{w^2}(1+O(w))$, which has pole of order 2 at $w=0$.
|
||||
|
||||
#### Residue
|
||||
|
||||
The residue of $f$ at $z_0$ is the coefficient of the term $(z-z_0)^{-1}$ in the Laurent series of $f$ at $z_0$.
|
||||
|
||||
> Example:
|
||||
>
|
||||
> $f(z)=\frac{1}{z^2}$ has a residue of 0 at $z=0$.
|
||||
>
|
||||
> $f(z)=\frac{z^3}{z-1}$ has a residue of 1 at $z=1$.
|
||||
|
||||
Residue for pole with higher order:
|
||||
|
||||
If $f$ has a pole of order $n$ at $z_0$, then the residue of $f$ at $z_0$ is
|
||||
|
||||
$$
|
||||
\operatorname{res}(f,z_0)=\frac{1}{(n-1)!}\lim_{z\to z_0}\frac{d^{n-1}}{dz^{n-1}}((z-z_0)^nf(z))
|
||||
$$
|
||||
|
||||
## Chapter 9: Generalized Cauchy's Theorem
|
||||
|
||||
### Winding number
|
||||
|
||||
The winding number of a closed curve $C$ with respect to a point $z_0$ is
|
||||
|
||||
$$
|
||||
\operatorname{ind}_C(z_0)=\frac{1}{2\pi i}\int_C\frac{1}{z-z_0}dz
|
||||
$$
|
||||
|
||||
_the winding number is the number of times the curve $C$ winds around the point $z_0$ counterclockwise. (May be negative)_
|
||||
|
||||
### Contour integrals
|
||||
|
||||
A contour is a piecewise continuous curve $\gamma:[a,b]\to\mathbb{C}$ with integer coefficients.
|
||||
|
||||
$$
|
||||
\Gamma=\sum_{i=1}^p n_j\gamma_j
|
||||
$$
|
||||
|
||||
where $\gamma_j:[a_j,b_j]\to\mathbb{C}$ is continuous closed curve and $n_j\in\mathbb{Z}$.
|
||||
|
||||
### Interior of a curve
|
||||
|
||||
The interior of a curve is the set of points $z\in\mathbb{C}$ such that $\operatorname{ind}_{\Gamma}(z)\neq 0$.
|
||||
|
||||
The winding number of contour $\Gamma$ is the sum of the winding numbers of the components of $\Gamma$ around $z_0$.
|
||||
|
||||
$$
|
||||
\operatorname{ind}_{\Gamma}(z)=\sum_{j=1}^p n_j\operatorname{ind}_{\gamma_j}(z)
|
||||
$$
|
||||
|
||||
### Separation lemma
|
||||
|
||||
Let $\Omega\subseteq\mathbb{C}$ be a domain and $K\subset \Omega$ be compact. Then there exists a simple contour $\Gamma\subset \Omega\setminus K$ such that $K\subset \operatorname{int}_{\Gamma}(\Gamma)\subset \Omega$.
|
||||
|
||||
Key idea:
|
||||
|
||||
Let $0<\delta<d(K,\partial \Omega)$, then draw the grid lines and trace the contour.
|
||||
|
||||
### Residue theorem
|
||||
|
||||
Let $\Omega$ be a domain, $\Gamma$ be a contour such that $\Gamma\cap \operatorname{int}(\Gamma)\subset \Omega$. Let $f$ be holomorphic on $\Omega\setminus \{z_1,z_2,\cdots,z_p\}$ and $z_1,z_2,\cdots,z_p$ are finitely many points in $\Omega$, where $z_1,z_2,\cdots,z_p\notin \Gamma$. Then
|
||||
|
||||
$$
|
||||
\int_{\Gamma}f(z)dz=2\pi i\sum_{j=1}^p \operatorname{res}(f,z_j)
|
||||
$$
|
||||
|
||||
Key: Prove by circle around each singularity and connect them using two way paths.
|
||||
|
||||
|
||||
### Homotopy*
|
||||
|
||||
Suppose $\gamma_0, \gamma_1$ are two curves from
|
||||
$[0,1]$ to $\Omega$ with same end points $P,Q$.
|
||||
|
||||
A homotopy is a continuous function of curves $\gamma_t, 0\leq t\leq 1$, deforming $\gamma_0$ to $\gamma_1$, keeping the end points fixed.
|
||||
|
||||
Formally, if $H:[0,1]\times [0,1]\to \Omega$ is a continuous function satsifying
|
||||
|
||||
1. $H(s,0)=\gamma_0(s)$, $\forall s\in [0,1]$
|
||||
2. $H(s,1)=\gamma_1(s)$, $\forall s\in [0,1]$
|
||||
3. $H(0,t)=P$, $\forall t\in [0,1]$
|
||||
4. $H(1,t)=Q$, $\forall t\in [0,1]$
|
||||
|
||||
Then we say $H$ is a homotopy between $\gamma_0$ and $\gamma_1$. (If $\gamma_0$ and $\gamma_1$ are closed curves, $Q=P$)
|
||||
|
||||
#### Lemma 9.12 Technical Lemma
|
||||
|
||||
Let $\phi:[0,1]\times [0,1]\to \mathbb{C}\setminus \{0\}$ is continuous. Then there exists a continuous map $\psi:[0,1]\times [0,1]\to \mathbb{C}$ such that $e^\phi=\psi$. Moreover, $\psi$ is unique up to an additive constant in $2\pi i\mathbb{Z}$.
|
||||
|
||||
|
||||
### General approach to evaluate definite integrals
|
||||
|
||||
Choose a contour so that one side is the desired integral.
|
||||
|
||||
Handle the other sides using:
|
||||
|
||||
- Symmetry
|
||||
- Favorite estimate
|
||||
- Bound function by another function whose integral goes to 0
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
@@ -1,167 +0,0 @@
|
||||
# Math416 Lecture 1
|
||||
|
||||
## Chapter 1: Complex Numbers
|
||||
|
||||
### Preface
|
||||
|
||||
I don't know what happened to the first class. I will try to rewrite the notes from my classmates here.
|
||||
|
||||
#### Rigidity
|
||||
|
||||
Integral is preserved for any closed path.
|
||||
|
||||
#### Group
|
||||
|
||||
A set with a multiplication operator. $(G,\cdot)$ such that: for all $a,b,c\in G$:
|
||||
|
||||
1. $a\cdot b\in G$
|
||||
2. $a\cdot (b\cdot c)=(a\cdot b)\cdot c$
|
||||
3. $a\cdot 1=a$
|
||||
4. $a\cdot a^{-1}=1$
|
||||
|
||||
#### Ring
|
||||
|
||||
A group with two operations: addition and multiplication. $(R,+,\cdot)$ such that: for all $a,b,c\in R$:
|
||||
|
||||
1. Commutative under addition: $a+b=b+a$
|
||||
2. Associative under multiplication: $(a\cdot b)\cdot c=a\cdot (b\cdot c)$
|
||||
3. Distributive under addition: $a\cdot (b+c)=a\cdot b+a\cdot c$
|
||||
|
||||
Example:
|
||||
|
||||
$\{a+\sqrt{6}b\mid a,b\in \mathbb{Z}\}$ is a ring
|
||||
|
||||
#### Definition 1.1
|
||||
|
||||
the complex number is defined to be the set $\mathbb{C}$ of ordered pairs $(x,y)$ with $x,y\in \mathbb{R}$ and the operations:
|
||||
|
||||
- Addition: $(x_1,y_1)+(x_2,y_2)=(x_1+x_2,y_1+y_2)$
|
||||
- Multiplication: $(x_1,y_1)(x_2,y_2)=(x_1x_2-y_1y_2,x_1y_2+x_2y_1)$
|
||||
|
||||
#### Axiom 1.2
|
||||
|
||||
The operation of addition and multiplication on $\mathbb{C}$ satisfies the following conditions (The field axioms):
|
||||
|
||||
For all $z_1,z_2,z_3\in \mathbb{C}$:
|
||||
|
||||
1. $z_1+z_2=z_2+z_1$ (commutative law of addition)
|
||||
2. $(z_1+z_2)+z_3=z_1+(z_2+z_3)$ (associative law of addition)
|
||||
3. $z_1\cdot z_2=z_2\cdot z_1$ (commutative law of multiplication)
|
||||
4. $(z_1\cdot z_2)\cdot z_3=z_1\cdot (z_2\cdot z_3)$ (associative law of multiplication)
|
||||
5. $z_1\cdot (z_2+z_3)=z_1\cdot z_2+z_1\cdot z_3$ (distributive law)
|
||||
6. There exists an additive identity element $0=(0,0)$ such that $z+0=z$ for all $z\in \mathbb{C}$.
|
||||
7. There exists a multiplicative identity element $1=(1,0)$ such that $z\cdot 1=z$ for all $z\in \mathbb{C}$.
|
||||
8. There exists an additive inverse $-z=(-x,-y)$ for all $z=(x,y)\in \mathbb{C}$ such that $z+(-z)=0$.
|
||||
9. There exists a multiplicative inverse $z^{-1}=\left(\frac{x}{x^2+y^2},-\frac{y}{x^2+y^2}\right)$ for all $z=(x,y)\in \mathbb{C}$ such that $z\cdot z^{-1}=1$.
|
||||
|
||||
$$
|
||||
(a,b)^{-1}=\left(\frac{a}{a^2+b^2},-\frac{b}{a^2+b^2}\right)
|
||||
$$
|
||||
|
||||
#### Embedding of $\mathbb{R}$ in $\mathbb{C}$ 1.3
|
||||
|
||||
Let $z=x+iy\in \mathbb{C}$ where $a,b\in \mathbb{R}$.
|
||||
|
||||
- $x$ is called the real part of $z$ and
|
||||
- $y$ is called the imaginary part of $z$.
|
||||
- $|z|=\sqrt{x^2+y^2}$ is called the absolute value or modulus of $z$.
|
||||
- The angle between the positive real axis and the line segment from $0$ to $z$ is called the argument of $z$ and is denoted by $\theta$ (argument of $z$).
|
||||
- $\overline{z}=x-iy$ is called the conjugate of $z$. ($z\cdot \overline{z}=|z|^2$)
|
||||
- $z_1+z_2=(x_1+x_2,y_1+y_2)$ (vector addition)
|
||||
|
||||
#### Lemma 1.3
|
||||
|
||||
$$
|
||||
|z_1z_2|=|z_1||z_2|
|
||||
$$
|
||||
|
||||
#### Theorem 1.5 (Triangle Inequality)
|
||||
|
||||
$$
|
||||
|z_1+z_2|\leq |z_1|+|z_2|
|
||||
$$
|
||||
|
||||
<details>
|
||||
<summary>Proof</summary>
|
||||
|
||||
Geometrically, the triangle inequality states that the sum of the lengths of any two sides of a triangle is greater than the length of the third side.
|
||||
|
||||
Algebraically,
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
(|z_1+z_2|)^2-|z_1+z_2|^2&=|z_1+z_2|^2-2|z_1+z_2|-(z_1+z_2)(\overline{z_1}+\overline{z_2})\\
|
||||
&=|z_1|^2+|z_2|^2+2|z_1||z_2|-(|z_1|^2+|z_2|^2+\overline{z_1}z_2+\overline{z_2}z_1)\\
|
||||
&=2|z_1||z_2|-2Re(\overline{z_1}z_2)\\
|
||||
&=2(|z_1||z_2|-|z_1z_2|)\\
|
||||
&\geq 0
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
</details>
|
||||
|
||||
Suppose $2(|z_1||z_2|-|z_1z_2|)=0$, and $\overline{z_1}z_2$ is a non-negative real number $c$, then $|z_1||z_2|=|z_1z_2|$...
|
||||
|
||||
> What is the use of this?
|
||||
|
||||
Let $\arg(z)=\theta\in (-\pi,\pi]$, $z_1=r_1(\cos\theta_1+i\sin\theta_1)$, $z_2=r_2(\cos\theta_2+i\sin\theta_2)$.
|
||||
|
||||
$$
|
||||
z_1z_2=r_1r_2[cos(\theta_1+\theta_2)+i\sin(\theta_1+\theta_2)]
|
||||
$$
|
||||
|
||||
(Define $\text{cis}(\theta)=\cos\theta+i\sin\theta$)
|
||||
|
||||
#### Theorem 1.6 Parallelogram Equality
|
||||
|
||||
The sum of the squares of the lengths of the diagonals of a parallelogram equals the sum of the squares of the lengths of the sides.
|
||||
|
||||
<details>
|
||||
<summary>Proof</summary>
|
||||
|
||||
Let $z_1,z_2$ be two complex numbers representing the two sides of the parallelogram, then the sum of the squares of the lengths of the diagonals of the parallelogram is $|z_1-z_2|^2+|z_1+z_2|^2$, and the sum of the squares of the lengths of the sides is $2|z_1|^2+2|z_2|^2$.
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
|z_1-z_2|^2+|z_1+z_2|^2 &= (x_1-x_2)^2+(y_1-y_2)^2+(x_1+x_2)^2+(y_1+y_2)^2 \\
|
||||
&= 2x_1^2+2x_2^2+2y_1^2+2y_2^2 \\
|
||||
&= 2(|z_1|^2+|z_2|^2)
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
</details>
|
||||
|
||||
#### Definition 1.9
|
||||
|
||||
The argument of a complex number $z$ is defined as the angle $\theta$ between the positive real axis and the ray from the origin through $z$.
|
||||
|
||||
### De Moivre's Formula
|
||||
|
||||
#### Theorem 1.10 De Moivre's Formula
|
||||
|
||||
Let $z=r\text{cis}(\theta)$, then
|
||||
|
||||
$\forall n\in \mathbb{Z}$:
|
||||
|
||||
$$
|
||||
z^n=r^n\text{cis}(n\theta)
|
||||
$$
|
||||
|
||||
<details>
|
||||
<summary>Proof</summary>
|
||||
|
||||
For $n=0$, $z^0=1=1\text{cis}(0)$.
|
||||
|
||||
For $n=-1$, $z^{-1}=\frac{1}{z}=\frac{1}{r}\text{cis}(-\theta)=\frac{1}{r}(cos(-\theta)+i\sin(-\theta))$.
|
||||
|
||||
</details>
|
||||
|
||||
Application:
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
(\text{cis}(\theta))^3&=\text{cis}(3\theta)\\
|
||||
&=\cos(3\theta)+i\sin(3\theta)\\
|
||||
&=cos^3(\theta)-3cos(\theta)sin^2(\theta)+i(3cos^2(\theta)sin(\theta)-sin^3(\theta))\\
|
||||
\end{aligned}
|
||||
$$
|
||||
@@ -1,190 +0,0 @@
|
||||
# Math416 Lecture 10
|
||||
|
||||
## Fast reload on Power Series
|
||||
|
||||
Suppose $\sum_{n=0}^\infty a_n$ converges absolutely. ($\sum_{n=0}^\infty |a_n|<\infty$)
|
||||
|
||||
Then rearranging the terms of the series does not affect the sum of the series.
|
||||
|
||||
For any permutation $\sigma$ of the set of positive integers, $\sum_{n=0}^\infty a_{\sigma(n)}=\sum_{n=0}^\infty a_n$.
|
||||
|
||||
Proof:
|
||||
|
||||
Let $\epsilon>0$, then $\exists N\in\mathbb{N}$ such that $\forall n\geq N$,
|
||||
|
||||
$$
|
||||
\sum_{n=N}^\infty |a_n|<\epsilon
|
||||
$$
|
||||
|
||||
So there exists $N_0$ such that if $M\geq N_0$, then
|
||||
|
||||
$$
|
||||
\sum_{n=N_0}^M |a_n|<\epsilon
|
||||
$$
|
||||
|
||||
_for any first $M$ terms of $\sigma$, we choose $N_0$ such that all the terms (no overlapping with the first $M$ terms) on the tail is less than $\epsilon$_.
|
||||
|
||||
$$
|
||||
\sum_{n=1}^{\infty} a_n=\sum_{n=1}^{M} a_n+\sum_{n=M+1}^\infty a_n
|
||||
$$
|
||||
|
||||
Let $K>N$, $L>N_0$,
|
||||
|
||||
$$
|
||||
\left|\sum_{n=1}^{K}a_n-\sum_{n=1}^{L}a_{\sigma(n)}\right|<2\epsilon
|
||||
$$
|
||||
|
||||
QED
|
||||
|
||||
## Chapter 4 Complex Integration
|
||||
|
||||
### Complex Integral
|
||||
|
||||
#### Definition 6.1
|
||||
|
||||
If $\phi(t)$ is a complex function defined on $[a,b]$, then the integral of $\phi(t)$ over $[a,b]$ is defined as
|
||||
|
||||
$$
|
||||
\int_a^b \phi(t) dt = \int_a^b \text{Re}\{\phi(t)\} dt + i\int_a^b \text{Im}\{\phi(t)\} dt
|
||||
$$
|
||||
|
||||
#### Theorem 6.3 (Triangle Inequality)
|
||||
|
||||
If $\phi(t)$ is a complex function defined on $[a,b]$, then
|
||||
|
||||
$$
|
||||
\left|\int_a^b \phi(t) dt\right| \leq \int_a^b |\phi(t)| dt
|
||||
$$
|
||||
|
||||
Proof:
|
||||
|
||||
Let $\lambda(t)=\frac{\left|\int_a^t \phi(t) dt\right|}{\int_a^t |\phi(t)| dt}$, then $\left|\lambda(t)\right|=1$.
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\left|\int_a^b \phi(t) dt\right|&=\lambda\int_a^b \phi(t) dt\\
|
||||
&=\int_a^b \lambda(t)\phi(t) dt\\
|
||||
&=\text{Re} \{\int_a^b \lambda(t)\phi(t) dt\}\\
|
||||
&\leq\int_a^b |\lambda(t)\phi(t)| dt\\
|
||||
&=\int_a^b |\phi(t)| dt
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Assume $\phi$ is continuous on $[a,b]$, the equality means $\lambda(t)\phi(t)$ is real and positive everywhere on $[a,b]$, which means $\arg \phi(t)$ is constant.
|
||||
|
||||
QED
|
||||
|
||||
#### Definition 6.4 Arc Length
|
||||
|
||||
Let $\gamma$ be a curve in the complex plane defined by $\gamma(t)=x(t)+iy(t)$, $t\in[a,b]$. The arc length of $\gamma$ is given by
|
||||
|
||||
$$
|
||||
\Gamma=\int_a^b |\gamma'(t)| dt=\int_a^b \sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2} dt
|
||||
$$
|
||||
|
||||
N.B. If $\int_{\Gamma} f(z) dz$ depends on orientation of $\Gamma$, but not the parametrization.
|
||||
|
||||
We define
|
||||
|
||||
$$
|
||||
\int_{\Gamma} f(z) dz=\int_{\Gamma} f(\gamma(t))\gamma'(t) dt
|
||||
$$
|
||||
|
||||
Example:
|
||||
|
||||
Suppose $\Gamma$ is the circle centered at $z_0$ with radius $R$
|
||||
|
||||
$$
|
||||
\int_{\Gamma} \frac{1}{z-z_0} dz
|
||||
$$
|
||||
|
||||
Parameterize the unit circle:
|
||||
|
||||
$$
|
||||
\gamma(t)=z_0+Re^{it}\quad
|
||||
\gamma'(t)=iRe^{it}, t\in[0,2\pi]
|
||||
$$
|
||||
|
||||
$$
|
||||
f(z)=\frac{1}{z-z_0}
|
||||
$$
|
||||
|
||||
$$
|
||||
f(\gamma(t))=\frac{1}{(z_0+Re^{it})-z_0}
|
||||
$$
|
||||
|
||||
$$
|
||||
\int_{\Gamma} f(z) dz=\int_0^{2\pi} f(\gamma(t))\gamma'(t) dt=\int_0^{2\pi} \frac{1}{Re^{-it}}iRe^{it} dt=2\pi i
|
||||
$$
|
||||
|
||||
#### Theorem 6.11 (Uniform Convergence)
|
||||
|
||||
If $f_n(z)$ converges uniformly to $f(z)$ on $\Gamma$, assume length of $\Gamma$ is finite, then
|
||||
|
||||
$$
|
||||
\lim_{n\to\infty} \int_{\Gamma} f_n(z) dz = \int_{\Gamma} f(z) dz
|
||||
$$
|
||||
|
||||
Proof:
|
||||
|
||||
Let $\epsilon>0$, since $f_n(z)$ converges uniformly to $f(z)$ on $\Gamma$, there exists $N\in\mathbb{N}$ such that for all $n\geq N$,
|
||||
|
||||
$$
|
||||
\left|f_n(z)-f(z)\right|<\epsilon
|
||||
$$
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\left|\int_{\Gamma} f_n(z) dz - \int_{\Gamma} f(z) dz\right|&=\left|\int_{\Gamma} (f_n(\gamma(t))-f(\gamma(t)))\gamma'(t) dt\right|\\
|
||||
&\leq \int_{\Gamma} |f_n(\gamma(t))-f(\gamma(t))||\gamma'(t)| dt\\
|
||||
&\leq \int_{\Gamma} \epsilon|\gamma'(t)| dt\\
|
||||
&=\epsilon\text{length}(\Gamma)
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
QED
|
||||
|
||||
#### Theorem 6.6 (Integral of derivative)
|
||||
|
||||
Suppose $\Gamma$ is a closed curve, $\gamma:[a,b]\to\mathbb{C}$ and $\gamma(a)=\gamma(b)$.
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\int_{\Gamma} f'(z) dz &= \int_a^b f'(\gamma(t))\gamma'(t) dt\\
|
||||
&=\int_a^b \frac{d}{dt}f(\gamma(t)) dt\\
|
||||
&=f(\gamma(b))-f(\gamma(a))\\
|
||||
&=0
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
QED
|
||||
|
||||
Example:
|
||||
|
||||
Let $R$ be a rectangle $\{-a,a,ai+b,ai-b\}$, $\Gamma$ is the boundary of $R$ with positive orientation.
|
||||
|
||||
Let $\int_{R} e^{-z^2}dz$.
|
||||
|
||||
Is $e^{-z^2}=\frac{d}{dz}f(z)$?
|
||||
|
||||
Yes, since
|
||||
|
||||
$$
|
||||
e^{z^2}=1-\frac{z^2}{1!}+\frac{z^4}{2!}-\frac{z^6}{3!}+\cdots=\frac{d}{dz}\left(\frac{z}{1!}-\frac{1}{3}\frac{z^3}{2!}+\frac{1}{5}\frac{z^5}{3!}-\cdots\right)
|
||||
$$
|
||||
|
||||
This is polynomial, therefore holomorphic.
|
||||
|
||||
So
|
||||
|
||||
$$
|
||||
\int_{R} e^{z^2}dz = 0
|
||||
$$
|
||||
|
||||
with some limit calculation, we can get
|
||||
|
||||
<!--TODO: Fill the parts-->
|
||||
|
||||
$$
|
||||
\int_{R} e^{-z^2}dz = 2\pi i
|
||||
$$
|
||||
@@ -1,169 +0,0 @@
|
||||
# Math416 Lecture 11
|
||||
|
||||
## Continue on integration over complex plane
|
||||
|
||||
### Continue on last example
|
||||
|
||||
Last lecture we have:Let $R$ be a rectangular start from the $-a$ to $a$, $a+ib$ to $-a+ib$, $\int_{R} e^{-z^2}dz=0$, however, the integral consists of four parts:
|
||||
|
||||
Path 1: $-a\to a$
|
||||
|
||||
$\int_{I_1}e^{-z^2}dz=\int_{-a}^{a}e^{-z^2}dz=\int_{-a}^{a}e^{-x^2}dx$
|
||||
|
||||
Path 2: $a+ib\to -a+ib$
|
||||
|
||||
$\int_{I_2}e^{-z^2}dz=\int_{a+ib}^{-a+ib}e^{-z^2}dz=\int_{0}^{b}e^{-(a+iy)^2}dy$
|
||||
|
||||
Path 3: $-a+ib\to -a-ib$
|
||||
|
||||
$-\int_{I_3}e^{-z^2}dz=-\int_{-a+ib}^{-a-ib}e^{-z^2}dz=-\int_{a}^{-a}e^{-(x-ib)^2}dx$
|
||||
|
||||
Path 4: $-a-ib\to a-ib$
|
||||
|
||||
$-\int_{I_4}e^{-z^2}dz=-\int_{-a-ib}^{a-ib}e^{-z^2}dz=-\int_{b}^{0}e^{-(-a+iy)^2}dy$
|
||||
|
||||
> #### The reverse of a curve 6.9
|
||||
>
|
||||
> If $\gamma:[a,b]\to\mathbb{C}$ is a curve, then the rever of $\gamma$ is the curve $-\gamma:[-b,-a]\to\mathbb{C}$ defined by $(-\gamma)(t)=\gamma(a+b-t)$. It is the curve one obtains from $\gamma$ by traversing it in the opposite direction.
|
||||
>
|
||||
> - If $\gamma$ is piecewise in $C^1$, then $-\gamma$ is piecewise in $C^1$.
|
||||
> - $\int_{-\gamma}f(z)dz=-\int_{\gamma}f(z)dz$ for any function $f$ that is continuous on $\gamma([a,b])$.
|
||||
|
||||
If we keep $b$ fixed, and let $a\to\infty$, then
|
||||
|
||||
> #### Definition 6.10 (Estimate of the integral)
|
||||
>
|
||||
> Let $\gamma:[a,b]\to\mathbb{C}$ be a piecewise $C^1$ curve, and let $f:[a,b]\to\mathbb{C}$ be a continuous complex-valued function. Let $M$ be the maximum of $|f|$ on $\gamma([a,b])$. ($M=\max\{|f(t)|:t\in[a,b]\}$)
|
||||
>
|
||||
> Then
|
||||
>
|
||||
> $$\left|\int_{\gamma}f(z)dz\right|\leq L(\gamma)M$$
|
||||
|
||||
_Continue on previous example, we have:_
|
||||
|
||||
$$
|
||||
\left|\int_{\gamma}f(z)dz\right|\leq L(\gamma)\max_{z\in\gamma}|f(z)|\to 0
|
||||
$$
|
||||
|
||||
Since,
|
||||
|
||||
$$
|
||||
\int_{-\infty}^{\infty}e^{-x^2}dx-\int_{-\infty}^{\infty}e^{-x^2+b^2}(\cos 2bx+i\sin 2bx)dx=0
|
||||
$$
|
||||
|
||||
Since $\sin 2bx$ is odd, and $\cos 2bx$ is even, we have
|
||||
|
||||
$$
|
||||
\int_{-\infty}^{\infty}e^{-x^2}dx=\int_{-\infty}^{\infty}e^{-x^2+b^2}\cos 2bxdx=\sqrt{\pi}e^{-b^2}
|
||||
$$
|
||||
|
||||
##### Proof for the last step:
|
||||
|
||||
$$
|
||||
\int_{-\infty}^{\infty}e^{-x^2}dx=\sqrt{\pi}
|
||||
$$
|
||||
|
||||
Proof:
|
||||
|
||||
Let $J=\int_{-\infty}^{\infty}e^{-x^2}dx$
|
||||
|
||||
Then
|
||||
|
||||
$$J^2=\int_{-\infty}^{\infty}e^{-x^2}dx\int_{-\infty}^{\infty}e^{-y^2}dy=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}e^{-(x^2+y^2)}dxdy$$
|
||||
|
||||
We can evaluate the integral on the right-hand side by converting to polar coordinates. $x=r\cos\theta$, $y=r\sin\theta,dxdy=rdrd\theta$
|
||||
|
||||
$$
|
||||
J^2=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}e^{-(x^2+y^2)}dxdy=\int_{0}^{2\pi}\int_{0}^{\infty}e^{-r^2}rdrd\theta
|
||||
$$
|
||||
|
||||
$$
|
||||
J^2=\int_{0}^{2\pi}\int_{0}^{\infty}e^{-r^2}rdrd\theta=\int_{0}^{2\pi}\left[-\frac{1}{2}e^{-r^2}\right]_{0}^{\infty}d\theta
|
||||
$$
|
||||
|
||||
$$
|
||||
J^2=\int_{0}^{2\pi}\frac{1}{2}d\theta=\pi
|
||||
$$
|
||||
|
||||
$$
|
||||
J=\sqrt{\pi}
|
||||
$$
|
||||
|
||||
QED
|
||||
|
||||
## Chapter 7 Cauchy's theorem
|
||||
|
||||
### Cauchy's theorem (Fundamental theorem of complex function theory)
|
||||
|
||||
Let $\gamma$ be a closed curve in $\mathbb{C}$ and let $u$ be an open set _containing $\gamma^*$_. Let $f$ be a holomorphic function on $u$. Then
|
||||
|
||||
$$
|
||||
\int_{\gamma}f(z)dz=0
|
||||
$$
|
||||
|
||||
Note: What "containing $\gamma^*$" means? (Rabbit hole for topologists)
|
||||
|
||||
#### Lemma 7.1 (Goursat's lemma)
|
||||
|
||||
Cauchy's theorem is true if $\gamma$ is a triangle.
|
||||
|
||||
Proof:
|
||||
|
||||
We plan to keep shrinking the triangle until $f(z+h)=f(z)+hf'(z)+\epsilon(h)$ where $\epsilon(h)$ is a function of $h$ that goes to $0$ as $h\to 0$.
|
||||
|
||||
Let's start with a triangle $T$ with vertices $z_1,z_2,z_3$.
|
||||
|
||||
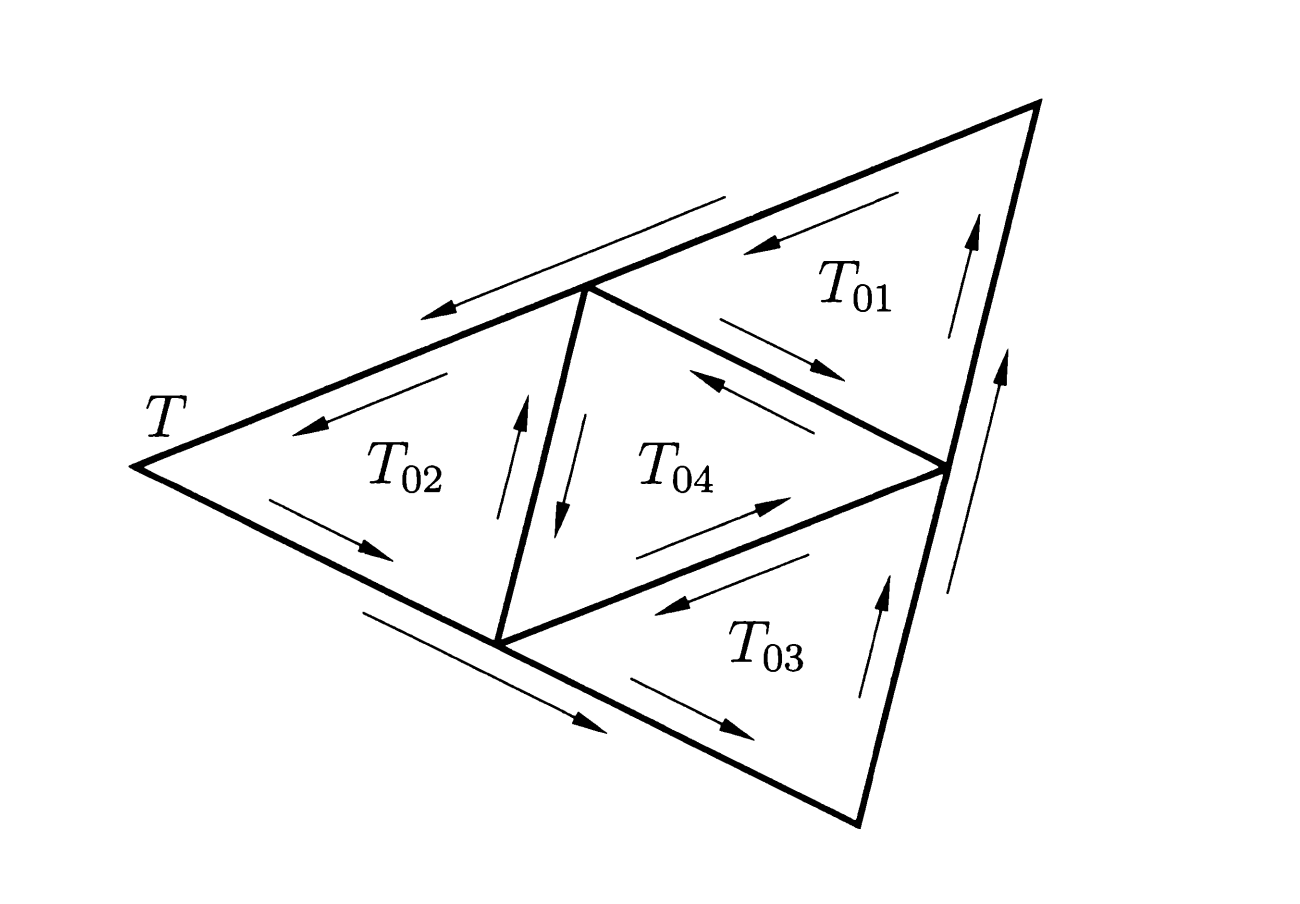
|
||||
|
||||
We divide $T$ into four smaller triangles by drawing lines from the midpoints of the sides to the opposite vertices.
|
||||
|
||||
Let $R_1,\ldots,R_4$ be the four smaller triangles.
|
||||
|
||||
For one $R_j$, $\left|\int_{R_j}f(z)dz\right|\geq\frac{1}{4}|I|$, we choose it then call it $T_1$.
|
||||
|
||||
There exists $T_1$ such that $\left|\int_{T_1}f(z)dz\right|\geq\frac{1}{4}|I|$.
|
||||
|
||||
Since $L(T_1)=\frac{1}{2}L(T)$, we iterate after $n$ steps, get a triangle $T_n$ such that $L(T_n)=\frac{L(T)}{2^n}$ and $\left|\int_{T_n}f(z)dz\right|\geq\frac{1}{4^n}|I|$.
|
||||
|
||||
Since $K_n=T_n\cup \text{interior}(T_n)$ is compact, we can find $K_n+1\subset K_n$ and $diam(K_n+1)<\frac{1}{2}diam(K_n)$. $diam(K_n)\to 0$ as $n\to\infty$. (Using completeness theorem)
|
||||
|
||||
Since $f$ is holomorphic on $u$, $\lim_{z\to z_0}\frac{f(z)-f(z_0)}{z-z_0}=f'(z_0)$ exists.
|
||||
|
||||
So $f(z)=f(z_0)+f'(z_0)(z-z_0)+R(z)$, we have
|
||||
|
||||
$$
|
||||
\int_{T_n}f(z)dz=\int_{T_n}f(z_0)dz+\int_{T_n}f'(z_0)(z-z_0)dz+\int_{T_n}R(z)dz
|
||||
$$
|
||||
|
||||
since $f(z_0)dz+\int_{T_n}f'(z_0)(z-z_0)$ is in form of Cauchy integral formula, we have
|
||||
|
||||
$$
|
||||
\int_{T_n}f(z_0)dz+\int_{T_n}f'(z_0)(z-z_0)dz=0
|
||||
$$
|
||||
|
||||
Let $e_n=\max\{\frac{R(z)}{z-z_0}:z_0\in T_n\}$
|
||||
|
||||
Since $diam(K_n)\to 0$ as $n\to\infty$, we have $e_n\to 0$ as $n\to\infty$.
|
||||
|
||||
So
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
|I|&\leq 4^n\left|\int_{T_n}f(z)dz\right|\\
|
||||
&\leq 4^n\left|\int_{T_n}R_n(z)dz\right|\\
|
||||
&\leq 4^n\cdot L(T_n)\cdot \max_{z\in T_n}|R_n(z)|\\
|
||||
&\leq 4^n\cdot \frac{L(T_0)}{2^n}\cdot e_n L(T_n)\\
|
||||
&\leq 4^n\cdot \frac{L(T_0)}{2^n}\cdot e_n\cdot \frac{L(T_0)}{2^n}\\
|
||||
&\leq e_n\cdot L(T_0)^2
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Since $e_n\to 0$ as $n\to\infty$, we have $I\to 0$ as $n\to\infty$.
|
||||
|
||||
So
|
||||
|
||||
$$
|
||||
\int_{T_n}f(z)dz\to 0
|
||||
$$
|
||||
|
||||
QED
|
||||
@@ -1,120 +0,0 @@
|
||||
# Math 416 Lecture 12
|
||||
|
||||
## Continue on last class
|
||||
|
||||
### Cauchy's Theorem on triangles
|
||||
|
||||
Let $T$ be a triangle in $\mathbb{C}$ and $f$ be holomorphic on $T$. Then
|
||||
|
||||
$$
|
||||
\int_T f(z) dz = 0
|
||||
$$
|
||||
|
||||
### Cauchy's Theorem for Convex Sets
|
||||
|
||||
Let's start with a simple case: $f(z)=1$.
|
||||
|
||||
For any closed curve $\gamma$ in $U$, we have
|
||||
|
||||
$$
|
||||
\int_\gamma f(z) dz = \int_a^b f(\gamma(t)) \gamma'(t) dt \approx \sum_{i=1}^n f(\gamma(t_i)) \gamma'(t_i) \Delta t_i
|
||||
$$
|
||||
|
||||
#### Definition of a convex set
|
||||
|
||||
A set $U$ is convex if for any two points $z_1, z_2 \in U$, the line segment $[z_1, z_2] \subset U$.
|
||||
|
||||
Let $O(U)$ be the set of all holomorphic functions on $U$.
|
||||
|
||||
#### Definition of primitive
|
||||
|
||||
Say $f$ has a primitive on $U$. If there exists a holomorphic function $g$ on $U$ such that $g'(z)=f(z)$ for all $z \in U$, then $g$ is called a primitive of $f$ on $U$.
|
||||
|
||||
#### Cauchy's Theorem for a Convex region
|
||||
|
||||
Cauchy's Theorem holds if $f$ has a primitive on a convex region $U$.
|
||||
|
||||
$$
|
||||
\int_\gamma f(z) dz = \int_\gamma \left[\frac{d}{dz}g(z)\right] dz = g(z_1)-g(z_2)
|
||||
$$
|
||||
|
||||
Since the curve is closed, $z_1=z_2$, so $\int_\gamma f(z) dz = 0$.
|
||||
|
||||
Proof:
|
||||
|
||||
It is sufficient to prove that if $U$ is convex, $f$ is holomorphic on $U$, then $f=g'$ for some $g$ holomorphic on $U$.
|
||||
|
||||
We pick a point $z_0\in U$ and define $g(z)=\int_{[z_0,z]}f(\xi)d\xi$.
|
||||
|
||||
We claim $g\in O(U)$ and $g'=f$.
|
||||
|
||||
Let $z_1$ close to $z$, since $f$ is holomorphic on $U$, using the Goursat's theorem, we can find a triangle $T$ with $\xi\in T$ and $z\in T$ and $T\subset U$.
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
0&=\int_{z_0}^{z}f(\xi)d\xi+\int_{z}^{z_1}f(\xi)d\xi\\
|
||||
&=g(z)-g(z_1)+\int_{z}^{z_1}f(\xi)d\xi+\int_{z_1}^{z_0}f(\xi)d\xi\\
|
||||
\frac{g(z)-g(z_1)}{z-z_1}&=-\frac{1}{z-z_1}\left(\int_{z}^{z_1}f(\xi)d\xi\right)\\
|
||||
\frac{g(z_1)-g(z_0)}{z_1-z_0}-f(z_1)&=-\frac{1}{z_1-z_0}\left(\int_{z}^{z_1}f(\xi)d\xi\right)-f(z_1)\\
|
||||
&=-\frac{1}{z_1-z_0}\left(\int_{z}^{z_1}f(\xi)-f(z_1)d\xi\right)\\
|
||||
&=I
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Use the fact that $f$ is holomorphic on $U$, then $f$ is continuous on $U$, so $\lim_{z\to z_1}f(z)=f(z_1)$.
|
||||
|
||||
There exists a $\delta>0$ such that $|z-z_1|<\delta$ implies $|f(z)-f(z_1)|<\epsilon$.
|
||||
|
||||
So
|
||||
|
||||
$$
|
||||
|I|\leq\frac{1}{z_1-z_0}\int_{z}^{z_1}|f(\xi)-f(z_1)|d\xi<\frac{\epsilon}{z_1-z_0}\int_{z}^{z_1}d\xi=\epsilon
|
||||
$$
|
||||
|
||||
So $I\to 0$ as $z_1\to z$.
|
||||
|
||||
Therefore, $g'(z_1)=f(z_1)$ for all $z_1\in U$.
|
||||
|
||||
QED
|
||||
|
||||
### Cauchy's Theorem for a disk
|
||||
|
||||
Let $U$ be the open set, $f\in O(U)$. Let $C$ be a circle inside $U$ and $z$ be a point inside $C$.
|
||||
|
||||
Then
|
||||
|
||||
$$
|
||||
f(z)=\frac{1}{2\pi i}\int_C\frac{f(\xi)d\xi}{\xi-z} d\xi
|
||||
$$
|
||||
|
||||
Proof:
|
||||
|
||||
Let $C_\epsilon$ be a circle with center $z$ and radius $\epsilon$ inside $C$.
|
||||
|
||||
Claim:
|
||||
|
||||
$$
|
||||
\int_{C_\epsilon}\frac{f(\xi)d\xi}{\xi-z}=\int_{C}\frac{f(\xi)d\xi}{\xi-z}
|
||||
$$
|
||||
|
||||
We divide the integral into four parts:
|
||||
|
||||
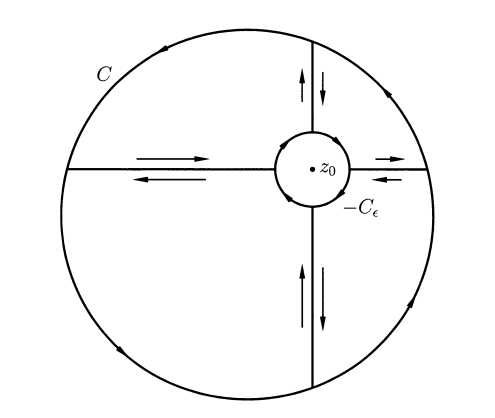
|
||||
|
||||
Notice that $\frac{f(\xi)}{\xi-z}$ is holomorphic whenever $f(\xi)\in U$ and $\xi\in \mathbb{C}\setminus\{z\}$.
|
||||
|
||||
So we can apply Cauchy's theorem to the integral on the inside square.
|
||||
|
||||
$$
|
||||
\int_{C_\epsilon}\frac{f(\xi)d\xi}{\xi-z}=0
|
||||
$$
|
||||
|
||||
Since $\frac{1}{2\pi i}\int_{C_\epsilon}\frac{1}{\xi-z}d\xi=1$, $\sigma=\epsilon e^{it}+z_0$ and $\sigma'=\epsilon e^{it}$, we have
|
||||
|
||||
/* TRACK LOST*/
|
||||
|
||||
$$
|
||||
\int_{C_\epsilon}\frac{f(\xi)d\xi}{\xi-z}=\int_0^{2\pi}\frac{f(\sigma)d\sigma}{\sigma-z}=2\pi i f(z)
|
||||
$$
|
||||
|
||||
QED
|
||||
@@ -1,182 +0,0 @@
|
||||
# Math416 Lecture 13
|
||||
|
||||
## Review on Cauchy's Theorem
|
||||
|
||||
Cauchy's Theorem states that if a function is holomorphic (complex differentiable) on a simply connected domain, then the integral of that function over any closed contour within that domain is zero.
|
||||
|
||||
Last lecture we proved the case for convex regions.
|
||||
|
||||
### Cauchy's Formula for a Circle
|
||||
|
||||
Let $C$ be a counterclockwise oriented circle, and let $f$ be a holomorphic
|
||||
|
||||
function defined in an open set containing $C$ and its interior. Then,
|
||||
|
||||
$$
|
||||
f(z_0)=\frac{1}{2\pi i}\int_C\frac{f(z)}{z-z_0}dz
|
||||
$$
|
||||
|
||||
for all points $z$ in the interior of $C$.
|
||||
|
||||
## New materials
|
||||
|
||||
### Mean value property
|
||||
|
||||
#### Theorem 7.6: Mean value property
|
||||
|
||||
Special case: Suppose $f$ is holomorphic on some $\mathbb{D}(z_0,R)\subset \mathbb{C}$, by cauchy's formula,
|
||||
|
||||
$$
|
||||
f(z_0)=\frac{1}{2\pi i}\int_{C_r}\frac{f(z)}{z-z_0}dz
|
||||
$$
|
||||
|
||||
Parameterizing $C_r$, we get $\gamma(t)=z_0+re^{it}$, $0\leq t\leq 2\pi$
|
||||
|
||||
$$
|
||||
\int f(z)dz=\int f(\gamma) \gamma'(t) d t
|
||||
$$
|
||||
|
||||
So,
|
||||
|
||||
$$
|
||||
f(z_0)=\frac{1}{2\pi i}\int_0^{2\pi}\frac{f(z_0+re^{it})}{re^{it}} ire^{it} dt=\frac{1}{2\pi}\int_{0}^{2\pi} f(z_0+re^{it}) dt
|
||||
$$
|
||||
|
||||
This concludes the mean value property for the holomorphic function
|
||||
|
||||
If $f$ is holomorphic, $f(z_0)$ is the mean value of $f$ on any circle centered at $z_0$
|
||||
|
||||
#### Area representation of mean value property
|
||||
|
||||
Area of $f$ on $\mathbb{D}(z_0,r)$
|
||||
|
||||
$$
|
||||
\frac{1}{\pi r^2}\int_{0}^{2\pi}\int_0^r f(z_0+re^{it})
|
||||
$$
|
||||
|
||||
/*Track lost*/
|
||||
|
||||
### Cauchy Integral
|
||||
|
||||
#### Definition 7.7
|
||||
|
||||
Let $\gamma:[a,b]\to \mathbb{C}$ be piecewise $\mathbb{C}^1$, let $\phi$ be condition on $\gamma$. Then the Cauchy interval of $\phi$ along $\gamma$ is
|
||||
|
||||
$$
|
||||
F(z)=\int_{\gamma}\frac{\phi(\zeta)}{\zeta-z}d \zeta
|
||||
$$
|
||||
|
||||
#### Theorem
|
||||
|
||||
Suppose $F(z)=\int_{\gamma}\frac{\phi(z)}{\zeta-z}d z$. Then $F$ has a local power series representation at all points $z_0$ not in $\gamma$.
|
||||
|
||||
Proof:
|
||||
|
||||
Let $R=B(z_0,\gamma)>0$, let $z\in \mathbb{D}(z_0,R)$
|
||||
|
||||
So
|
||||
|
||||
$$
|
||||
\frac{1}{\zeta-z}=\frac{1}{(\zeta-z_0)-(z-z_0)}=\frac{1}{1-z_0}\frac{1}{1-\frac{z-z_0}{\zeta-z_0}}
|
||||
$$
|
||||
|
||||
Since $|z-z_0|<R$ and $|\zeta-z_0|>R$, $|\frac{z-z_0}{\zeta-z_0}|<1$.
|
||||
|
||||
Converting it to geometric series
|
||||
|
||||
$$
|
||||
\frac{1}{1-z_0}\frac{1}{1-\frac{z-z_0}{\zeta-z_0}}=\sum_{n=0}^\infty \left(\frac{z-z_0}{\zeta-z_0}\right)^n
|
||||
$$
|
||||
|
||||
So,
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
F(z)&=\int_\gamma \frac{\phi(\zeta)}{\zeta - z} d\zeta\\
|
||||
&=\int_\gamma \frac{\phi(\zeta)}{z-z_0} \sum_{n=0}^\infty \left(\frac{z-z_0}{\zeta-z_0}\right)^n dz\\
|
||||
&=\sum_{n=0}^\infty (z-z_0)^n \int_\gamma \frac{\phi(\zeta)}{(\zeta-z_0)^{n+1}}
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Which gives us an power series representation if we set $a_n=\int_\gamma \frac{\phi(\zeta)}{(\zeta-z_0)^{n+1}}$
|
||||
|
||||
QED
|
||||
|
||||
#### Corollary 7.7
|
||||
|
||||
Suppose $F(z)=\int_\gamma \frac{\phi(\zeta)}{\zeta-z_0} dz$,
|
||||
|
||||
Then,
|
||||
|
||||
$$
|
||||
f^{(n)}(z)=n!\int_\gamma \frac{\phi(z)}{(\zeta-z_0)^{n+1}} d\zeta
|
||||
$$
|
||||
|
||||
where $z\in \mathbb{C}\setminus \gamma$.
|
||||
|
||||
Combine with Cauchy integral formula:
|
||||
|
||||
If $f$ is in $O(\Omega)$, then $\forall z\in \mathbb{D}(z_0,r)$.
|
||||
|
||||
$$
|
||||
f(z)=\frac{1}{2\pi i}\int_{C_r}\frac{f(\zeta)}{\zeta-z} d\zeta
|
||||
$$
|
||||
|
||||
We have proved that If $f\in O(\Omega)$, then $f$ is locally given by a convergent power series
|
||||
|
||||
power series has radius of convergence at $z_0$ that is $\geq$ dist($z_0$,boundary $\Omega$)
|
||||
|
||||
### Liouville's Theorem
|
||||
|
||||
#### Definition 7.11
|
||||
|
||||
A function that is holomorphic in all of $\mathbb{C}$ is called an entire function.
|
||||
|
||||
#### Theorem 7.11 Liouville's Theorem
|
||||
|
||||
Any bounded entire function is constant.
|
||||
|
||||
> Basic Estimate of integral
|
||||
>
|
||||
> $$\left|\int_\gamma f(z) dz\right|\leq L(\gamma) \max\left|f(z)\right|$$
|
||||
|
||||
Since,
|
||||
|
||||
$$
|
||||
f'(z)=\frac{1}{2\pi i} \int_{C_r} \frac{f(z)}{(\zeta-z)^2} dz
|
||||
$$
|
||||
|
||||
So the modulus of the integral is bounded by
|
||||
|
||||
$$
|
||||
\frac{1}{2\pi} |M|\cdot \frac{1}{R^2}=2\pi R\cdot M \frac{1}{R^2}=\frac{M}{R}
|
||||
$$
|
||||
|
||||
### Fundamental Theorem of Algebra
|
||||
|
||||
#### Theorem 7.12 Fundamental Theorem of ALgebra
|
||||
|
||||
Every nonconstant polynomial with complex coefficients can be factored over
|
||||
$\mathbb{C}$ into linear factors.
|
||||
|
||||
#### Corollary
|
||||
|
||||
For every polynomial with complex coefficients.
|
||||
|
||||
$$
|
||||
p(z)=c\prod_{j=i}^n(z-z_0)^{t_j}
|
||||
$$
|
||||
|
||||
where the degree of polynomial is $\sum_{j=0}^n t_j$
|
||||
|
||||
Proof:
|
||||
|
||||
Let $p(z)=a_0+a_1z+\cdots+a_nz^n$, where $a_n\neq 0$ and $n\geq 1$.
|
||||
|
||||
So
|
||||
|
||||
$$
|
||||
|p(z)|=|a_nz_n|\left[\left|1+\frac{a_{n-1}}{a_nz}+\cdots+\frac{a_0}{a_nz^n}\right|\right]
|
||||
$$
|
||||
|
||||
If $|z|\geq R$, $\left|1+\frac{a_{n-1}}{a_nz}+\cdots+\frac{a_0}{a_nz^n}\right|<\frac{1}{2}$
|
||||
@@ -1,148 +0,0 @@
|
||||
# Math 416 Lecture 14
|
||||
|
||||
## Review
|
||||
|
||||
### Holomorphic $\iff$ Analytic
|
||||
|
||||
#### Theorem 7.11 Liouville's Theorem
|
||||
|
||||
Any bounded entire function is constant.
|
||||
|
||||
## New Rollings
|
||||
|
||||
### Finding power series for holomorphic functions
|
||||
|
||||
Let $F$ be holomorphic on open set $U\subset \mathbb{C}$. Suppose $f(z_0)=0$, $f(z)=\sum_{n=0}^\infty a_n(z - z_0)^n$
|
||||
|
||||
Example,
|
||||
|
||||
$p(z)=(z-1)^3(z+i)^5(z-7)$
|
||||
|
||||
$p(z)=\sum_{n=0}^9 c_n(z-z_0)^n$
|
||||
|
||||
> Notice that:
|
||||
>
|
||||
> Since $f'(z)=\sum_{n=0}^\infty a_n n(z-z_0)^{n-1}$.
|
||||
> $a_0=f(z_0)$, $a_1=f'(z_0)$, $a_k=\frac{f^{(k)}(z_0)}{k!}$ for $k \geq 0$
|
||||
|
||||
So $c_0=0=f(1)$, $c_1=f'(1)=3(z-1)^2M=0$, $c_2=f''(1)=6(z-1)M=0$, $c_3=1$.
|
||||
|
||||
(i) The power series for $q(z)=(z-1)^3$ at $0$.
|
||||
|
||||
So $q(z)=\sum_{n=0}^3 a_nz^n$, you just expand it as $q(z)=z^3-3z^2+3z-1$
|
||||
|
||||
(ii) The power series for $q(z)=(z-1)^3$ at $-1$.
|
||||
|
||||
So $q(z)=\sum_{n=0}^3 a_n(z+1)^n$
|
||||
|
||||
$a_0=q(-1)=(-2)^3=-8$,
|
||||
|
||||
$a_1=q'(-1)=3(-2)^2=12$,
|
||||
|
||||
$a_2=\frac{1}{2}q''(-1)=\frac{6}{2} \cdot -2^1 = -6$,
|
||||
|
||||
$a_3=\frac{1}{6}q'''(-1)=\frac{6}{6} \cdot 1=1$.
|
||||
|
||||
All higher terms are zero
|
||||
|
||||
#### Definition: zero of multiplicity
|
||||
|
||||
Suppose $f$ is holomorphic on open $U$ and $f(\zeta_0)=0$ for some $z_0\in U$. Let $f(z)=\sum_{n=0}^\infty a_n(z-z_0)^n$ near $z_0$. Let $m$ be the smallest number such that $a_m\neq 0$. Then we say $f$ has a zero of multiplicity $m$ at $z_0$.
|
||||
|
||||
#### Theorem 7.12 Fundamental Theorem of Algebra
|
||||
|
||||
Every non-constant polynomial $f$ can be factored over $\mathbb{C}$ into linear factors
|
||||
|
||||
Proof:
|
||||
|
||||
Since $a_n=\frac{1}{n!}f^{(n)}(z_0)$, then $f$ has a zero of order $m$ $\iff$ $f^{(m)}(z_0) \neq 0$ and $f^{(k)}(z_0) = 0, \forall k < m$.
|
||||
|
||||
Suppose $f$ has a zero of order $m$ at $z_0$
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
f(z)&=a_m(z-z_0)^m+a_{m+1}(z-z_0)^{m+1}+\cdots\\
|
||||
&=(z-z_0)^m\left[a_{m+1}(z-z_0)^{m+1}+\cdots\right]\\
|
||||
&= (z-z_0)^m g(z)
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
So, if $f$ has a zero of order $m$ at $\zeta_0\iff$ $f(z)=(z-z_0)^mg(z)$ where $g$ is holomorphic and $g(z_0)\neq 0$.
|
||||
|
||||
QED
|
||||
|
||||
#### Definition: Connected Set
|
||||
|
||||
An open set $U$ is connected if whenever $U=U_1\cup U_2$ and $U_1, U_2$ are disjoint and open, then one of them is empty.
|
||||
|
||||
A domain is a connected open set.
|
||||
|
||||
#### Theorem 7.13 Zeros of Holomorphic Functions
|
||||
|
||||
Let $U$ be a open domain (in $\mathbb{C}$). Let $f$ be holomorphic on $U$ and vanish to infinite order at some point $z_0\in U$, then $f(z)=0$ on $U$.
|
||||
|
||||
> This is not true for $\mathbb{R}$. Consider the function $f(x) = e^{-1/x^2}$ for $x \neq 0$ and $f(0) = 0$, which is smooth and vanishes to infinite order at 0.
|
||||
|
||||
Proof:
|
||||
|
||||
Step 1:
|
||||
|
||||
Show any zero of finite order is isolated.
|
||||
|
||||
Let $z_0$ be a zero of order $m$, then by fundamental theorem of algebra, $f$ can be expressed as
|
||||
|
||||
$$
|
||||
f(z)=(z-z_0)^mg(z)
|
||||
$$
|
||||
|
||||
where $g$ is holomorphic and $g(z_0) \neq 0$. So $g$ is continuous.
|
||||
|
||||
Thus $\exists$ and open set $z_0\in V$ such that $g(z_0)\neq 0$ on all of $V$.
|
||||
|
||||
Let $U_1=\{z\in U\}$ such that $f$ vanishes to order infinity. and $U_2=U\setminus U_1$.
|
||||
|
||||
We need to show both $U_1$ and $U_2$ are open.
|
||||
|
||||
$U_1$:
|
||||
|
||||
Let $z_0\in U_1$. We know that $f$ is holomorphic thus it is analytic at $z_0$.
|
||||
|
||||
So $\exists \epsilon>0$ such that $\forall \mathbb{z}\in B_\epsilon(z_0)$
|
||||
|
||||
So $f(z)=\sum_{n=0}^{\infty} a_n(z-z_0)^n$ implies $f(z)=0$ on $B_\epsilon(z_0)$
|
||||
|
||||
We can expand $f$ in a power series centered at $z_1$ for any $z_1\in B_\epsilon(z_0)$, So $f(z)=\sum c_n(z-z_1)^n=0$
|
||||
|
||||
Therefore, $z_1 \in U_1$, proving that $U_1$ is open.
|
||||
|
||||
$U_2$:
|
||||
|
||||
Let $w\in U_2$, if $f(w)\neq 0$, then $\exists\epsilon > 0$ such that $f(z) \neq 0$ on $B_\epsilon(w)\subset U_2$.
|
||||
|
||||
If $f$ vanishes to finite order by Step 1, $\exists B_\epsilon(w)\subset U_2$
|
||||
|
||||
QED
|
||||
|
||||
#### Corollary 7.13.1 (Identity for holomorphic functions)
|
||||
|
||||
If $f,g$ are both holomorphic on domain $U$, and they have the same power series at some point $\zeta_0$, then $f \equiv g$ on $U$.
|
||||
|
||||
Proof:
|
||||
|
||||
Consider $f-g$.
|
||||
|
||||
QED
|
||||
|
||||
#### Corollary 7.13.2
|
||||
|
||||
Let $U$ be a domain, $f\in O(U)$, $f$ is not identically zero on $U$, $f^{-1}(0)$ has no limit point on $U$.
|
||||
|
||||
Proof:
|
||||
|
||||
We proceed by contradiction. Suppose $z_n\to w\in U$, $f(z_0)=0$, $f(w)=0$. $w$ is not an isolated zero. So $f$ is a zero of infinite order. Contradicting with our assumption that $f$ is not identically zero.
|
||||
|
||||
QED
|
||||
|
||||
#### Corollary 7.14: Identity principle
|
||||
|
||||
If $f,g\in O(U)$, $U$ is a domain and $\exists$ sequence $z_0$ that converges to $w\in U$, such that $f(z_n)=g(z_n)$, then $f\equiv g$ on U$.
|
||||
@@ -1,124 +0,0 @@
|
||||
# Math416 Lecture 15
|
||||
|
||||
## Review on Cauchy Integrals
|
||||
|
||||
The cauchy integral of function $\phi$ (may not be holomorphic) on curve $\Gamma$ (may not be closed) is
|
||||
|
||||
$$
|
||||
\int_{\Gamma}\frac{\phi(\zeta)}{\zeta-z}d\zeta
|
||||
$$
|
||||
|
||||
The Cauchy integral theorem states that if $f$ is holomorphic on a simply connected domain $D$, then the integral of $f$ over any closed curve $\gamma$ in $D$ is 0.
|
||||
|
||||
$$
|
||||
\int_{\gamma}f(z)dz = 0
|
||||
$$
|
||||
|
||||
The Cauchy integral formula states that if $f$ is holomorphic on a simply connected domain $D$, then $f$ over any closed curve $\gamma$ in $D$ is
|
||||
|
||||
$$
|
||||
f(z) = \frac{1}{2\pi i}\int_{\gamma}\frac{f(\zeta)}{\zeta-z}d\zeta
|
||||
$$
|
||||
|
||||
## Continue on Cauchy Integrals (Chapter 7)
|
||||
|
||||
### Convergence of functions
|
||||
|
||||
#### Theorem 7.15 Weierstrass Convergence Theorem
|
||||
|
||||
Limit of a sequence of holomorphic functions is holomorphic.
|
||||
|
||||
Let $G$ be an open subset of $\mathbb{C}$ and let $\left(f_n\right)_{n\in\mathbb{N}}$ be a sequence of holomorphic functions on $G$ that converges locally uniformly to $f$ on $G$. Then $f$ is holomorphic on $G$.
|
||||
|
||||
Proof:
|
||||
|
||||
Let $z_0\in G$. There exists a neighborhood $\overline{B_r(z_0)}\subset G$ of $z_0$ such that $\left(f_n\right)_{n\in\mathbb{N}}$ converges uniformly on $\overline{B_r(z_0)}$.
|
||||
|
||||
Let $C_r=\partial B_r(z_0)$.
|
||||
|
||||
By Cauchy integral formula, we have
|
||||
|
||||
$$
|
||||
f_n(z_0) = \frac{1}{2\pi i}\int_{C_r}\frac{f_n(\zeta)}{\zeta-z_0}d\zeta
|
||||
$$
|
||||
|
||||
$\forall z\in B_r(z_0)$, we have $\frac{f(w)}{w-\zeta}$ converges uniformly on $C_r$.
|
||||
|
||||
So $\lim_{n\to\infty}f_n(z_0) = f(z_0) = \frac{1}{2\pi i}\int_{C_r}\frac{f(w)}{w-z_0}dw$
|
||||
|
||||
So $f$ is holomorphic on $G$.
|
||||
|
||||
QED
|
||||
|
||||
#### Theorem 7.16 Maximum Modulus Principle
|
||||
|
||||
If $f$ is a non-constant holomorphic function on a domain $D$ (open and connected subset of $\mathbb{C}$), then $|f|$ does not attain a local maximum value on $D$.
|
||||
|
||||
Proof:
|
||||
|
||||
Assume at some point $z_0\in D$, $|f(z_0)|$ is a local maximum. $\exists r>0$ such that $\forall z\in \overline{B_r(z_0)}$, $|f(z)|\leq |f(z_0)|$.
|
||||
|
||||
If $f(z_0)=0$, then $f(z)$ is identically 0 on $B_r(z_0)$. (by identity theorem)
|
||||
|
||||
Else, we can assume that without loss of generality that $f(z_0)>0$. By mean value theorem,
|
||||
|
||||
$$
|
||||
f(z_0) = \frac{1}{2\pi}\int_0^{2\pi}f(z_0+re^{i\theta})d\theta
|
||||
$$
|
||||
|
||||
So $f(z_0) =$
|
||||
|
||||
/* TRACK LOST */
|
||||
|
||||
#### Corollary 7.16.1 Minimum Modulus Principle
|
||||
|
||||
If $f$ is a non-constant holomorphic function on a domain $D$ (open and connected subset of $\mathbb{C}$), and $f$ is non zero on $D$, then $\frac{1}{f}$ does not attain a local minimum value on $D$.
|
||||
|
||||
Proof:
|
||||
|
||||
Let $g(z) = \frac{1}{f(z)}$. $g$ is holomorphic on $D$.
|
||||
|
||||
QED
|
||||
|
||||
#### Theorem 7.17 Schwarz Lemma
|
||||
|
||||
Let $f$ be a holomorphic map of the open unit disk $D$ into itself, and $f(0)=0$. Then $\forall z\in D$, $|f(z)|\leq |z|$ and $|f'(0)|\leq 1$.
|
||||
|
||||
And the equality holds if and only if $f$ is a rotation, that is, $f(z)=e^{i\theta}z$ for some $\theta\in\mathbb{R}$.
|
||||
|
||||
Proof:
|
||||
|
||||
Let
|
||||
|
||||
$$
|
||||
g(z) = \begin{cases}
|
||||
\frac{f(z)}{z} & z\neq 0 \\
|
||||
f'(0) & z=0
|
||||
\end{cases}
|
||||
$$
|
||||
|
||||
We claim that $g$ is holomorphic on $D$.
|
||||
|
||||
For $z\neq 0$, $g(z)$ is holomorphic since $f$ is holomorphic on $D$.
|
||||
|
||||
For $z=0$, $g(z)$ is holomorphic since $f$'s power series expansion has $c_0=f(0)=0$. $g'(0)=f'(0)=c_1+c_2z+c_3z^2+\cdots$.
|
||||
|
||||
So $g$ is (analytic) thus holomorphic on $D$.
|
||||
|
||||
On the boundary of $D$, $|g(z)|\leq\frac{1}{r} \cdot 1$. By maximum modulus principle, $|g(z)|\leq 1$ on $D$.
|
||||
|
||||
So $|f(z)|\leq |z|$ on $D$.
|
||||
|
||||
And $|f'(0)|\leq 1$.
|
||||
|
||||
QED
|
||||
|
||||
#### Schwarz-Pick Lemma
|
||||
|
||||
Let $f$ be a holomorphic map of the open unit disk $D$ into itself, then for any $z,w\in D$,
|
||||
|
||||
$$
|
||||
\frac{|f(z)-f(w)|}{|1-\overline{f(w)}f(z)|}\leq\frac{|z-w|}{|1-\overline{w}z|}=\rho(z,w)
|
||||
$$
|
||||
|
||||
Prove after spring break.
|
||||
@@ -1,163 +0,0 @@
|
||||
# Math416 Lecture 16
|
||||
|
||||
## Answer checking for exam
|
||||
|
||||
### Q1
|
||||
|
||||
Cauchy riemann equations:
|
||||
|
||||
$$
|
||||
\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y}\quad\text{and}\quad\frac{\partial u}{\partial y} = -\frac{\partial v}{\partial x}
|
||||
$$
|
||||
|
||||
Liouville's Theorem:
|
||||
|
||||
Any non-constant entire function is unbounded.
|
||||
|
||||
So $\cos(z)$ is unbounded in $\mathbb{C}$.
|
||||
|
||||
$$
|
||||
\text{Log}(-e^2) = \ln|-e^2| + i\arg(-e^2) = -2 + \pi i
|
||||
$$
|
||||
|
||||
At any point $z_0\in \mathbb{C}\setminus\{0\}$, there is an open set $z_0\in U\subset \mathbb{C}$ and a branch of logarithm defined on $U$.
|
||||
|
||||
### Q2
|
||||
|
||||
Power series expansion
|
||||
|
||||
### Q3
|
||||
|
||||
limit superior
|
||||
|
||||
### Q4
|
||||
|
||||
Bound integral
|
||||
|
||||
### Q5
|
||||
|
||||
$f_n$ converges pointwise to $f$ on $U$ if $\forall z\in U$, $\forall \epsilon > 0$, $\exists N$ s.t. $\forall n\geq N$, $|f_n(z)-f(z)| < \epsilon$.
|
||||
|
||||
$f_n$ converges uniformly to $f$ on $U$ if $\forall \epsilon > 0$, $\exists N$ s.t. $\forall n\geq N$, $\forall z\in U$, $|f_n(z)-f(z)| < \epsilon$.
|
||||
|
||||
Show for $|z|<1$, $f_n(z)=z^n$ converges pointwise to $0$ but not uniformly to $0$.
|
||||
|
||||
(a) pointwise convergence:
|
||||
|
||||
$|z^n| = |z|^n < \epsilon$ if $n > \frac{\ln\epsilon}{\ln|z|}$.
|
||||
|
||||
(b) uniform convergence:
|
||||
|
||||
No matter how small $\epsilon$ is, there is always a $z$ s.t. $|z^n| > \epsilon$ for all $n$.
|
||||
|
||||
## Continue from last lecture
|
||||
|
||||
### Schwarz's Lemma
|
||||
|
||||
Let $f$ be an holomorphic function that maps the unit disk $D(0,1)$ to itself and $f(0)=0$. Then $|f(z)|\leq |z|$ for all $z\in D(0,1)$
|
||||
|
||||
#### Schwarz-Pick's Lemma
|
||||
|
||||
(see exercise 7.17.2)
|
||||
|
||||
Let $f$ be an holomorphic function that maps the unit disk $D(0,1)$ to itself. Then $\forall z,w\in D(0,1)$,
|
||||
|
||||
$$
|
||||
\left|\frac{f(z)-f(w)}{1-\overline{f(w)}f(z)}\right|\leq \left|\frac{z-w}{1-\overline{w}z}\right|
|
||||
$$
|
||||
|
||||
> Recall the Möbius map
|
||||
>
|
||||
> $$\phi_\alpha(z) = \frac{z-\alpha}{1-\overline{\alpha}z}$$
|
||||
>
|
||||
> is a homeomorphism of the unit disk.
|
||||
>
|
||||
> So we can use the Möbius to restate the Schwarz-Pick's Lemma as:
|
||||
>
|
||||
> $$|\phi_{f(w)}(f(z))|\leq |\phi_w(z)|$$
|
||||
|
||||
Suppose we defined $g=\phi_{f(w)}\circ f\circ \phi_{-w}$, then $g$ is a holomorphic function that maps the unit disk to itself and $g(0)=0$.
|
||||
|
||||
By Schwarz's Lemma, let $z\in D(0,1)$, $|g(z)|\leq |z|$.
|
||||
|
||||
$$
|
||||
|\phi_{f(w)}(f(\phi_{-w}(z)))|\leq |z|
|
||||
$$
|
||||
|
||||
Let $\zeta=\phi_{-w}(z)$, then $\zeta=\frac{z+w}{1+\overline{w}z}\in D(0,1)$, so $|\zeta|=\phi_w(z)$.
|
||||
|
||||
#### Extension of Schwarz-Pick's Lemma in hyperbolic metric
|
||||
|
||||
Suppose we defined the distance on $\mathbb{C}$ as $d(z,w)=|\frac{z-w}{1-\overline{w}z}|$.
|
||||
|
||||
We claim that this is a metric on $\mathbb{C}$. $\forall z,w,v\in \mathbb{C}$:
|
||||
|
||||
(a) $d(z,w)=0$ if and only if $z=w$ and $d(z,w)> 0$ otherwise.
|
||||
|
||||
(b) $d(z,w)=d(w,z)$.
|
||||
|
||||
(c) $d(z,w)\leq d(z,v)+d(v,w)$.
|
||||
|
||||
We call this metric the Pseudo hyperbolic metric.
|
||||
|
||||
> Hyperbolic metric:
|
||||
>
|
||||
> $$ \text{Hypdist}(z,w)=\tanh^{-1}(d(z,w))$$
|
||||
>
|
||||
> Where $d(z,w)=|\frac{z-w}{1-\overline{w}z}|$
|
||||
|
||||
So we can restate the Schwarz-Pick's Lemma as:
|
||||
|
||||
$$
|
||||
d(f(z),f(w))\leq d(z,w)
|
||||
$$
|
||||
|
||||
And in hyperbolic metric, it becomes:
|
||||
|
||||
$$
|
||||
\text{Hypdist}(f(z),f(w))\leq \text{Hypdist}(z,w)
|
||||
$$
|
||||
|
||||
Suppose the equality holds for Schwarz-Pick's Lemma, then $|g(z)|=\tau z$ where $|\tau|=1$.
|
||||
|
||||
Computation ignored here.
|
||||
|
||||
Then $f$ is a Möbius map that is automorphism of the unit disk.
|
||||
|
||||
### Existence of harmonic conjugate
|
||||
|
||||
Suppose $f=u+iv$ is holomorphic on a domain $U\subset \mathbb{C}$. Then $u=\text{Re}(f)$ is harmonic on $U$. That is $\Delta u=\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}=0$.
|
||||
|
||||
#### Theorem 7.18
|
||||
|
||||
Let $u$ be a real harmonic function on a convex domain $G\subset \mathbb{C}$. Then there exists $g\in O(G)$ such that $\text{Re}(g)=u$. Moreover, $g$ is unique up to an additive imaginary constant.
|
||||
|
||||
Proof:
|
||||
|
||||
Existence next time.
|
||||
|
||||
Uniqueness:
|
||||
|
||||
Suppose $g,h\in O(G)$ s.t. $\text{Re}(g)=\text{Re}(h)=u$.
|
||||
|
||||
$\text{Re}g=u=\text{Re}h$ on $G$.
|
||||
|
||||
If we can show that $(g-h)'=0$ on $G$, then we win.
|
||||
|
||||
Let $g=u+iv$, $h=u+iw$.
|
||||
|
||||
By the Cauchy-Riemann equations,
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\frac{\partial}{\partial x}(g-h)&=\frac{\partial}{\partial x}i(v-w)\\
|
||||
&=i\left(\frac{\partial u}{\partial y}-\frac{\partial u}{\partial y}\right)\\
|
||||
&=0
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Suppose $G=\mathbb{C}\setminus\{0\}$, then $u=\ln|z|=\frac{1}{2}\ln(x^2+y^2)$, which is harmonic.
|
||||
|
||||
Continue next time.
|
||||
|
||||
|
||||
@@ -1,154 +0,0 @@
|
||||
# Math416 Lecture 17
|
||||
|
||||
## Continue on Chapter 7
|
||||
|
||||
### Harmonic conjugates
|
||||
|
||||
#### Theorem 7.18
|
||||
|
||||
Existence of harmonic conjugates.
|
||||
|
||||
Let $u$ be a harmonic function on $\Omega$ a convex open subset in $\mathbb{C}$. Then there exists $g\in O(\Omega)$ such that $\text{Re}(g)=u$ on $\Omega$.
|
||||
|
||||
Moreover, $g$ is unique up to an imaginary additive constant.
|
||||
|
||||
Proof:
|
||||
|
||||
Let $f=2\frac{\partial u}{\partial z}=\frac{\partial u}{\partial x}-i\frac{\partial u}{\partial y}$
|
||||
|
||||
$f$ is holomorphic on $\Omega$
|
||||
|
||||
Since $\frac{\partial u}{\partial \overline{z}}=0$ on $\Omega$, $f$ is holomorphic on $\Omega$
|
||||
|
||||
So $f=g'$, fix $z_0\in \Omega$, we can choose $q(z_0)=u(z_0)$ and $g=u_1+iv_1$, $g'=\frac{\partial u_1}{\partial x}+i\frac{\partial v_1}{\partial x}=\frac{\partial v_1}{\partial y}-i\frac{\partial u_1}{\partial y}=\frac{\partial u}{\partial x}-i\frac{\partial u}{\partial y}$, given that $\frac{\partial u_1}{\partial x}=\frac{\partial u}{\partial x}$ and $\frac{\partial u_1}{\partial y}=\frac{\partial u}{\partial y}$
|
||||
|
||||
So $u_1=u$ on $\Omega$
|
||||
|
||||
$\text{Re}(g)=u_1=u$ on $\Omega$
|
||||
|
||||
If $u+iv$ is holomorphic, $v$ is harmonic conjugate of $u$
|
||||
|
||||
QED
|
||||
|
||||
### Corollary For Harmonic functions
|
||||
|
||||
#### Theorem 7.19
|
||||
|
||||
Harmonic functions are $C^\infty$
|
||||
|
||||
$C^\infty$ is a local property.
|
||||
|
||||
#### Theorem 7.20
|
||||
|
||||
Mean value property for harmonic functions.
|
||||
|
||||
Let $u$ be harmonic on an open set of $\Omega$
|
||||
|
||||
Then $u(z_0)=\frac{1}{2\pi}\int_0^{2\pi}u(z_0+re^{i\theta})d\theta$
|
||||
|
||||
Proof:
|
||||
|
||||
$\text{Re}g(z_0)=\frac{1}{2\pi}\int_0^{2\pi}\text{Re}g(z_0+re^{i\theta})d\theta$
|
||||
|
||||
QED
|
||||
|
||||
#### Theorem 7.21
|
||||
|
||||
Identity theorem for harmonic functions.
|
||||
|
||||
Let $u$ be harmonic on a domain $\Omega$. If $u=0$ on some open set $G\subset \Omega$, then $u\equiv 0$ on $\Omega$.
|
||||
|
||||
_If $u=v$ on $G\subset \Omega$, then $u=v$ on $\Omega$._
|
||||
|
||||
Proof:
|
||||
|
||||
We proceed by contradiction.
|
||||
|
||||
Let $H=\{z\in \Omega:u(z)=0\}$ be the interior of $G$
|
||||
|
||||
$H$ is open and nonempty. If $H\neq \Omega$, then $\exists z_0\in \partial H\cap \Omega$. Then $\exists r>0$ such that $B_r(z_0)\subset \Omega$ such that $\exists g\in O(B_r(z_0))$ such that $\text{Re}g=u$ on $B_r(z_0)$
|
||||
|
||||
Since $H\cap B_r(z_0)$ is nonempty open set, then $g$ is constant on $H\cap B_r(z_0)$
|
||||
|
||||
So $g$ is constant on $B_r(z_0)$
|
||||
|
||||
So $u$ is constant on $B_r(z_0)$
|
||||
|
||||
So $D(z_0,r)\subset H$. This is a contradiction that $z_0\in \partial H$
|
||||
|
||||
QED
|
||||
|
||||
#### Theorem 7.22
|
||||
|
||||
Maximum principle for harmonic functions.
|
||||
|
||||
A non-constant harmonic function on a domain cannot attain a maximum or minimum on the interior of the domain.
|
||||
|
||||
Proof:
|
||||
|
||||
We proceed by contradiction.
|
||||
|
||||
Suppose $u$ attains a maximum at $z_0\in \Omega$.
|
||||
|
||||
For all $z$ in the neighborhood of $z_0$, $u(z)<u(z_0)$. We can choose $r>0$ such that $B_r(z_0)\subset \Omega$.
|
||||
|
||||
By the mean value property, $u(z_0)=\frac{1}{2\pi}\int_0^{2\pi}u(z_0+re^{i\theta})d\theta$
|
||||
|
||||
So $0= \frac{1}{2\pi}\int_0^{2\pi}u[z_0+re^{i\theta}-u(z_0)]d\theta$
|
||||
|
||||
We can prove the minimum is similar.
|
||||
|
||||
QED
|
||||
|
||||
> Maximum/minimum (modulus) principle for holomorphic functions.
|
||||
>
|
||||
> If $f$ is holomorphic on a domain $\Omega$ and attains a maximum on the boundary of $\Omega$, then $f$ is constant on $\Omega$.
|
||||
>
|
||||
> Except at $z_0\in \Omega$ where $f'(z_0)=0$, if $f$ attains a minimum on the boundary of $\Omega$, then $f$ is constant on $\Omega$.
|
||||
|
||||
### Dirichlet problem for domain $D$
|
||||
|
||||
Let $h: \partial D\to \mathbb{R}$ be a continuous function. Is there a harmonic function $u$ on $D$ such that $u$ is continuous on $\overline{D}$ and $u|_{\partial D}=h$?
|
||||
|
||||
We can always solve the problem for the unit disk.
|
||||
|
||||
$$
|
||||
u(z)=\frac{1}{2\pi}\int_0^{2\pi}h(e^{i t})\text{Re}\left(\frac{e^{it}+z}{e^{it}-z}\right)dt
|
||||
$$
|
||||
|
||||
Let $z=re^{i\theta}$
|
||||
|
||||
$$
|
||||
\text{Re}\left(\frac{e^{it}+re^{i\theta}}{e^{it}-re^{i\theta}}\right)=\frac {1-r^2}{1-2r\cos(\theta-t)+r^2}
|
||||
$$
|
||||
|
||||
_This is called Poisson kernel._
|
||||
|
||||
$Pr(\theta, t)>0$ and $\int_0^{2\pi}Pr(\theta, t)dt=1$, $\forall r,t$
|
||||
|
||||
## Chapter 8 Laurent series
|
||||
|
||||
when $\sum_{n=-\infty}^{\infty}a_n(z-z_0)^n$ converges?
|
||||
|
||||
Claim $\exists R>0$ such that $\sum_{n=-\infty}^{\infty}a_n(z-z_0)^n$ converges if $|z-z_0|<R$ and diverges if $|z-z_0|>R$
|
||||
|
||||
Proof:
|
||||
|
||||
Let $u=\frac{1}{z-z_0}$
|
||||
|
||||
$\sum_{n=0}^{\infty}a_n(z-z_0)^n$ has radius of convergence $\frac{1}{R}$
|
||||
|
||||
So the series converges if $|u|<\frac{1}{R}$
|
||||
|
||||
So $|z-z_0|=\frac{1}{|u|}>\frac{1}{\frac{1}{R}}=R$
|
||||
|
||||
QED
|
||||
|
||||
### Laurent series
|
||||
|
||||
A Laurent series is a series of the form $\sum_{n=-\infty}^{\infty}a_n(z-z_0)^n$
|
||||
|
||||
The series converges in some annulus shape $A=\{z:r_1<|z-z_0|<r_2\}$
|
||||
|
||||
The annulus is called the region of convergence of the Laurent series.
|
||||
|
||||
@@ -1,194 +0,0 @@
|
||||
# Math416 Lecture 18
|
||||
|
||||
## Chapter 8: Laurent Series and Isolated Singularities
|
||||
|
||||
### 8.1 Laurent Series
|
||||
|
||||
#### Definition of Laurent Series
|
||||
|
||||
$$
|
||||
\sum_{n=-\infty}^{\infty} c_n (z-z_0)^n
|
||||
$$
|
||||
|
||||
where $c_n$ are complex coefficients.
|
||||
|
||||
Let $R_2=\frac{1}{\limsup_{n\to\infty} |c_n|^{1/n}}$, then the Laurent series converges on $|z-z_0|<R_2$
|
||||
|
||||
Where $R_1=\limsup_{n\to-\infty} |c_n|^{-1/n}$, if $|z-z_0|>R_1$, the Laurent series diverges.
|
||||
|
||||
If $R_1\leq R_2$, then the Laurent series converges on $A(z_0;R_1,R_2)=\{z:R_1<|z-z_0|<R_2\}$, the Laurent series converges absolutely on $A(z_0;R_1,R_2)$
|
||||
|
||||
By Weierstrass, the limit is a holomorphic function on $A(z_0;R_1,R_2)$
|
||||
|
||||
If $R_1<r<R_2$, then
|
||||
|
||||
$$
|
||||
\int_{C(z_0,r)} f(z) dz = \sum_{n=-\infty}^{\infty} c_n \int_{C(z_0,r)} (z-z_0)^n dz
|
||||
$$
|
||||
|
||||
<details>
|
||||
<summary>Additional Proof</summary>
|
||||
|
||||
$$
|
||||
\int_{C(z_0,r)} (z-z_0)^n dz = \begin{cases} 2\pi i, & n=-1 \\0, & n\neq -1\end{cases}
|
||||
$$
|
||||
|
||||
Proof:
|
||||
|
||||
$\gamma(t)=z_0+re^{it}, t\in[0,2\pi]$
|
||||
$$
|
||||
\begin{aligned}
|
||||
\int_{C(z_0,r)} (z-z_0)^n dz &= \int_0^{2\pi} (z_0+re^{it}-z_0)^n ire^{it} dt \\
|
||||
&= ir^{n+1} \int_0^{2\pi} e^{i(n+1)t} dt \\
|
||||
&= \begin{cases}
|
||||
2\pi i, & n=-1 \\
|
||||
\int_0^{2\pi} e^{i(n+1)t} dt = \frac{1}{i(n+1)}e^{i(n+1)t}\Big|_0^{2\pi} = 0, & n\neq -1
|
||||
\end{cases}
|
||||
\end{aligned}
|
||||
$$
|
||||
</details>
|
||||
|
||||
So,
|
||||
|
||||
$$
|
||||
\int_{C(z_0,r)} f(z) dz = \sum_{n=-\infty}^{\infty} c_n \int_{C(z_0,r)} (z-z_0)^n dz=c_{-1}2\pi i
|
||||
$$
|
||||
|
||||
And,
|
||||
|
||||
$$
|
||||
\int_{C(z_0,r)} f(z)(z-z_0)^k dz = \sum_{n=-\infty}^{\infty} c_n \int_{C(z_0,r)} (z-z_0)^{n+k} dz = c_{-1-k}2\pi i
|
||||
$$
|
||||
|
||||
So,
|
||||
|
||||
$$
|
||||
2\pi i c_j = \int_{C(z_0,r)} f(z)(z-z_0)^{-j-1} dz
|
||||
$$
|
||||
|
||||
### Cauchy integral
|
||||
|
||||
Recall Cauchy integral formula:
|
||||
|
||||
$$
|
||||
f(z) = \int_{\gamma} \frac{\phi(\xi)}{\xi-z} d\xi
|
||||
$$
|
||||
|
||||
where $\gamma$ is a closed curve.
|
||||
|
||||
Suppose $|z-z_0|>R$,
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\frac{1}{\xi-z}&=\frac{1}{\xi-z_0-(z-z_0)}\\
|
||||
&=-\frac{1}{z-z_0}\frac{1}{1-\frac{\xi-z_0}{z-z_0}}\\
|
||||
&=-\frac{1}{z-z_0}\sum_{n=0}^{\infty} \frac{(\xi-z_0)^n}{(z-z_0)^n}\\
|
||||
&=-\sum_{m=1}^{\infty} (\xi-z_0)^{m-1}(z-z_0)^{-m}
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
So,
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
f(z) &= \int_{\gamma} \frac{\phi(\xi)}{\xi-z} d\xi\\
|
||||
&= -\int_{\gamma} \sum_{m=1}^{\infty} (\xi-z_0)^{m-1}(z-z_0)^{-m}\phi(\xi) d\xi\\
|
||||
&=-\sum_{m=1}^{\infty} (z-z_0)^{-m} \int_{\gamma} (\xi-z_0)^{m-1} \phi(\xi) d\xi
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
So the Cauchy integral $\int_{\gamma} \frac{\phi(\xi)}{\xi-z} d\xi$ is a convergent power series in $B_{d(z_0,\gamma)}(z_0)$ and is a convergent Laurent series (with just negative powers) in $\mathbb{C}\setminus B_{\max_{\xi\in \gamma} d(z_0,\xi)}(z_0)$
|
||||
|
||||
#### Theorem 8.4 Cauchy Theorem for Annulus
|
||||
|
||||
Suppose $f$ is holomorphic on $A(z_0;R_1,R_2)$, Let $C_r=\{z:|z-z_0|=r\}$, oriented counterclockwise. Then $I(r)=\int_{C_r} f(z) dz$ is independent of $r$ for $R_1<r<R_2$
|
||||
|
||||
Proof:
|
||||
|
||||
If integrand is continuous with respect to $r$ and continuous with respect to $t$, then we can differentiate under the integral sign (Check after class, on Appendix 4?)
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
I(r)&=\int_0^{2\pi} f(z_0+re^{it})ire^{it}dt\\
|
||||
\frac{dI}{dr}&=i\int_0^{2\pi}\frac{\partial}{\partial r}[f(z_0+re^{it})re^{it}]dt
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{\partial}{\partial r}[f(z_0+re^{it})ire^{it}]=if'(z_0+re^{it})e^{it}+if(z_0+re^{it})e^{it}
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{\partial}{\partial t}[f(z_0+re^{it})e^{it}]=f'(z_0+re^{it})ire^{it}+f(z_0+re^{it})ire^{it}
|
||||
$$
|
||||
|
||||
This gives
|
||||
|
||||
$$
|
||||
\frac{\partial}{\partial r}[f(z_0+re^{it})ire^{it}]=\frac{\partial}{\partial t}[f(z_0+re^{it})e^{it}]
|
||||
$$
|
||||
|
||||
So,
|
||||
|
||||
$$
|
||||
\frac{dI}{dr}=i\int_0^{2\pi}\frac{\partial}{\partial r}[f(z_0+re^{it})ire^{it}]dt=i\int_0^{2\pi}\frac{\partial}{\partial t}[f(z_0+re^{it})e^{it}]dt=0
|
||||
$$
|
||||
|
||||
is a integration on a closed curve, so it is $0$.
|
||||
|
||||
So, $I(r)$ is constant.
|
||||
|
||||
QED
|
||||
|
||||
Let $f$ be holomorphic on $A(z_0;R_1,R_2)$. Let $C_r=\{z:|z-z_0|=r\}$, oriented counterclockwise. Let $w\in A(z_0;R_1,R_2)$. Choose $R_1<r_1<|w-z_0|<r_2<R_2$ such that $w\in A(z_0;r_1,r_2)$. Then,
|
||||
|
||||
$$
|
||||
f(w)=\frac{1}{2\pi i}\int_{C_{r_2}} \frac{f(z)}{z-w} dz-\frac{1}{2\pi i}\int_{C_{r_1}} \frac{f(z)}{z-w} dz
|
||||
$$
|
||||
|
||||
Proof:
|
||||
|
||||
Define $g(z)=\begin{cases}
|
||||
\frac{f(z)-f(w)}{z-w}, & z\neq w \\
|
||||
f'(w), & z=w
|
||||
\end{cases}$
|
||||
|
||||
Then $g$ is holomorphic on $A(z_0;r_1,r_2)$ since $f$ is analytic at $w$, $f(z)=\sum_{n=0}^{\infty} \frac{f^{(n)}(w)}{n!}(z-w)^n$
|
||||
|
||||
So,
|
||||
|
||||
$$
|
||||
f(z)-f(w)=f(w)+f'(w)(z-w)+\sum_{n=2}^{\infty} \frac{f^{(n)}(w)}{n!}(z-w)^n-f(w)=f'(w)(z-w)+\sum_{n=2}^{\infty} \frac{f^{(n)}(w)}{n!}(z-w)^n
|
||||
$$
|
||||
|
||||
So,
|
||||
|
||||
$$
|
||||
\frac{f(z)-f(w)}{z-w}=f'(w)+\sum_{n=1}^{\infty} \frac{f^{(n)}(w)}{n!}(z-w)^{n-1}
|
||||
$$
|
||||
|
||||
So,
|
||||
|
||||
$$
|
||||
\lim_{z\to w} \frac{f(z)-f(w)}{z-w}=f'(w)
|
||||
$$
|
||||
|
||||
So $\int_{C_{r_2}} g(z) dz=\int_{C_{r_1}} g(z) dz$,
|
||||
|
||||
$$
|
||||
\int_{C_{r_2}} \frac{f(z)}{z-w} dz-f(w)\int_{C_{r_2}} \frac{1}{z-w} dz=\int_{C_{r_1}} \frac{f(z)}{z-w} dz-f(w)\int_{C_{r_1}} \frac{1}{z-w} dz
|
||||
$$
|
||||
|
||||
Since $\int_{C_{r_2}} \frac{1}{z-w} dz=2\pi i$ and $\int_{C_{r_1}} \frac{1}{z-w} dz=0$, (using Cauchy integral theorem on convex region)
|
||||
|
||||
$$
|
||||
f(w)=\frac{1}{2\pi i}\int_{C_{r_2}} \frac{f(z)}{z-w} dz-\frac{1}{2\pi i}\int_{C_{r_1}} \frac{f(z)}{z-w} dz
|
||||
$$
|
||||
|
||||
QED
|
||||
|
||||
Since $\int_{C_{r_1}} \frac{f(z)}{z-w} dz$ is a Laurent series in negative powers which converges in $\mathbb{C}\setminus \overline{B_{r_1}(z_0)}$, we can conclude that
|
||||
|
||||
$f(z)$ is given by a convergent Laurent series $\sum_{n=-\infty}^{\infty} a_n (z-z_0)^n$ in $\mathbb{C}\setminus \overline{B_{r_1}(z_0)}$ where $a_n=\frac{1}{2\pi i}\int_{C_r} \frac{f(z)}{(z-z_0)^{-1-n}} dz$
|
||||
|
||||
Laurent series converges in $A(z_0;R_1,R_2)$
|
||||
@@ -1,155 +0,0 @@
|
||||
# Math416 Lecture 19
|
||||
|
||||
## Continue on the Laurent series
|
||||
|
||||
### Laurent series
|
||||
|
||||
If $f$ is holomorphic in $A(z_0;R_1,R_2)$ then $f=\sum_{n=-\infty}^{\infty} a_n (z-z_0)^n$ where the Laurent series converges on the annulus $A(z_0;R_1,R_2)$
|
||||
|
||||
$$
|
||||
\int_{C(z_0,r)} f(z)(z-z_0)^{-k-1} dz = \sum_{n=-\infty}^{\infty} a_n \int_{C(z_0,r)} (z-z_0)^{n-k-1} dz=a_k 2\pi i
|
||||
$$
|
||||
|
||||
> $C(z_0,r)$ is a circle centered at $z_0$ with radius $r$
|
||||
|
||||
### Isolated singularities
|
||||
|
||||
A punctured disk at $z_0$ is $A(z_0;0,R)=\{z:0<|z-z_0|<R\}$
|
||||
|
||||
Say a function $f$ has an isolated singularity at $z_0$ if it is holomorphic in a punctured disk $A(z_0;0,R)$
|
||||
|
||||
$f$ has a Laurent series in $A(z_0;0,R)$
|
||||
|
||||
$$
|
||||
f(z) = \sum_{n=-\infty}^{\infty} a_n (z-z_0)^n
|
||||
$$
|
||||
|
||||
that converges in $A(z_0;0,R)$
|
||||
|
||||
#### Principal part of a Laurent series
|
||||
|
||||
The principal part of a Laurent series is the sum of the terms with negative powers of $(z-z_0)$
|
||||
|
||||
$$
|
||||
\sum_{n=-\infty}^{-1} a_n (z-z_0)^n
|
||||
$$
|
||||
|
||||
Say the isolated singularity is
|
||||
|
||||
- removable if $a_n=0$ for all $n<0$
|
||||
- If $f(z)$ has a removable singularity at $z_0$, then extend $f$ to $\mathbb{D}_{z_0,R}$ by defining $f(z_0)=a_0$. This extended $f$ is holomorphic on $\mathbb{D}_{z_0,R}$ and $f(z)=\sum_{n=0}^{\infty} a_n (z-z_0)^n$ for $z\in \mathbb{D}_{z_0,R}$
|
||||
- pole if $a_{-k}\neq 0$ and $a_n=0$ for all $n<-k$
|
||||
- A pole with order $1$ is a simple pole
|
||||
- essential if the cases above are not true
|
||||
|
||||
Example:
|
||||
|
||||
1. $f(z)=\frac{\sin z}{z}$ has a removable singularity at $z=0$.
|
||||
|
||||
the power series is
|
||||
|
||||
$$
|
||||
\sin z = z - \frac{z^3}{3!} + \frac{z^5}{5!} - \cdots
|
||||
$$
|
||||
|
||||
So the Laurent series is
|
||||
|
||||
$$
|
||||
\frac{\sin z}{z} = 1 - \frac{z^2}{3!} + \frac{z^4}{5!} - \cdots
|
||||
$$
|
||||
|
||||
The singularity is removable by defining $f(0)=1$
|
||||
|
||||
2. $f(z)=\frac{z^2-1}{(z-1)(z-3)}=\frac{(z-1)(z+1)}{(z-1)(z-3)}$
|
||||
|
||||
There are two poles at $z=1$ and $z=3$
|
||||
|
||||
the singularity at $z=1$ is removable by defining $f(1)=1$
|
||||
|
||||
the singularity at $z=3$ is a simple pole with order 1 $f(z)=\frac{z+1}{z-3}=\frac{(z-3)+4}{z-3}=4(z-3)^{-1}+1$
|
||||
|
||||
3. $f(z)=\frac{(z+1)^2(z+2)^3}{(z-1)^2(z-5)^6(z-8)}$
|
||||
|
||||
there are three poles at $z=1,5,8$, the order of the poles are 2, 6, 1 respectively.
|
||||
|
||||
#### Corollary: order of poles and zeros
|
||||
|
||||
If $f$ has a pole of order $m$ at $z_0$,
|
||||
|
||||
$$
|
||||
f(z) = \sum_{n=-m}^{\infty} a_n (z-z_0)^n
|
||||
$$
|
||||
|
||||
then $(z-z_0)^m f(z)$ has a removable singularity at $z_0$. Value of holomorphic extension of $(z-z_0)^m f(z)$ at $z_0$ is $a_{-m}$.
|
||||
|
||||
- $f$ is given by a power series in $A(z_0;0,R)$
|
||||
- $f=(z-z_0)^{-m} g(z)$ where $g$ is holomorphic and $g(z_0)\neq 0$, $\frac{1}{f}=(z-z_0)^m \frac{1}{g(z)}$ has a pole of order $m$ at $z_0$. So $f$ has a pole of order $m$ at $z_0$ if and only if $\frac{1}{f}$ has a zero of order $m$ at $z_0$
|
||||
|
||||
> $e^{1/z}=1+\frac{1}{z}+\frac{1}{2!z^2}+\frac{1}{3!z^3}+\cdots$ has an essential singularity at $z=0$ since it has infinitely many terms with negative powers of $z$.
|
||||
|
||||
Suppose $f$ is a holomorphic in a neighborhood of $\infty$: $\exists R>0$ s.t. $f$ is holomorphic on $\{z:|z|>R\}$
|
||||
|
||||
We defined $g(z)=f(1/z)$ where $g$ is holomorphic on punctured disk center $0$ radius $1/R$
|
||||
|
||||
Say $f(z)$ has a zero of order $\infty$ if any only if $g(z)=f(1/z)$ has a zero of order $m$ at $z=0$
|
||||
|
||||
Say $f$ has a pole of order $m$ at $\infty$ if and only if $g(z)=f(1/z)$ has a pole of order $m$ at $z=0$
|
||||
|
||||
Example:
|
||||
|
||||
1. $f(z)=z^2$, $g(z)=f(1/z)=1/z^2$ has a pole of order 2 at $z=0$
|
||||
2. $f(z)=\frac{1}{z^3}$ (vanishes to order 3 at $\infty$), $g(z)=f(1/z)=z^3$ has a zero of order 3 at $z=0$
|
||||
|
||||
We say $f$ has an isolated singularity at $\infty$ if and only if $g(z)=f(1/z)$ has an isolated singularity at $z=0$.
|
||||
|
||||
$f$ has $\begin{cases}
|
||||
\text{removable}\\
|
||||
\text{pole of order } m\\
|
||||
\text{essential}
|
||||
\end{cases}$ singularity at $\infty$ if and only if $g(z)=f(1/z)$ has $\begin{cases}
|
||||
\text{removable}\\
|
||||
\text{pole of order } m\\
|
||||
\text{essential}
|
||||
\end{cases}$ singularity at $z=0$
|
||||
|
||||
#### Theorem: Criterion for a removable singularity (Riemann removable singularity theorem)
|
||||
|
||||
Suppose $f$ has an isolated singularity at $z_0$. Then it is removable if and only if $f$ is bounded on a punctured disk centered at $z_0$.
|
||||
|
||||
Proof:
|
||||
|
||||
($\Leftarrow$) Suppose $z_0$ is a removable singularity. Then $\exists r>0$ such that $B_r(z_0)\setminus\{z_0\}=A(z_0;0,r)$ and $f(z)=\sum_{n=0}^{\infty} a_n (z-z_0)^n$ for $z\in A(z_0;0,r)$. Then $f$ is bounded in $A(z_0;0,r/2)$
|
||||
|
||||
($\Rightarrow$) Suppose $|f(z)|\leq M$ for $z\in A(z_0;0,r/2)$. So $f(z)=\sum_{n=-\infty}^{\infty} a_n (z-z_0)^{n-k-1}=\int_{C_r}f(z)(z-z_0)^{-k-1}dz=a_{k}2\pi i$
|
||||
|
||||
$a_k=\frac{1}{2\pi i}\int_{C_r}f(z)(z-z_0)^{-k-1}dz$
|
||||
|
||||
And $|a_k|\leq \max_{z\in C_r}\left|2\pi|f(z)|z-z_0|^{-k-1}\right|\leq 2\pi M r^{-k-1}2\pi r$
|
||||
|
||||
So $|a_k|\leq (4\pi^2M)r^{-k}$ for all $r<R$
|
||||
|
||||
So if $k<0$, $|a_k|\leq \lim_{r\to 0} (4\pi^2M)r^{-k}=0$
|
||||
|
||||
QED
|
||||
|
||||
Corollary:
|
||||
|
||||
If $f$ is holomorphic at $\infty$, then $f$ is bounded for large $|z|$.
|
||||
|
||||
#### Theorem: Criterion for a pole
|
||||
|
||||
Suppose $f$ has an isolated singularity at $z_0$. Then $z_0$ is a pole of order $m$ if and only if $\lim_{z\to z_0} |f(z)|=\infty$
|
||||
|
||||
Proof:
|
||||
|
||||
($\Rightarrow$) If $z_0$ is a pole of order $m$, then $f(z)=a_{-m}(z-z_0)^{-m}+O((z-z_0)^{-m+1})$
|
||||
|
||||
As $z\to z_0$, $|f(z)|\approx |a_{-m}| |z-z_0|^{-m}\to \infty$
|
||||
|
||||
($\Leftarrow$) Let $g(z)=\frac{1}{f(z)}$ near $z_0$. Then $g$ has a singularity at $z_0$ and $|g(z)|$ is bounded near $z_0$.
|
||||
|
||||
By Riemann removable singularity theorem, $g(z)=(z-z_0)^m h(z)$ for some holomorphic $h$ and $h(z_0)\neq 0$
|
||||
|
||||
So $f(z)=\frac{1}{g(z)}=\frac{1}{(z-z_0)^m h(z)}$ has a pole of order $m$ at $z_0$
|
||||
|
||||
QED
|
||||
@@ -1,243 +0,0 @@
|
||||
# Math416 Lecture 2
|
||||
|
||||
## Review?
|
||||
|
||||
$$
|
||||
z_1=r_1(\cos\theta_1+i\sin\theta_1)=r_1\text{cis}(\theta_1)
|
||||
$$
|
||||
|
||||
$$
|
||||
z_2=r_2(\cos\theta_2+i\sin\theta_2)=r_2\text{cis}(\theta_2)
|
||||
$$
|
||||
|
||||
$$
|
||||
z_1z_2=r_1r_2\text{cis}(\theta_1+\theta_2)
|
||||
$$
|
||||
|
||||
$$
|
||||
\forall n\in \mathbb{Z}, z^n=r^n\text{cis}(n\theta)
|
||||
$$
|
||||
|
||||
### De Moivre's Formula
|
||||
|
||||
$$
|
||||
\forall n\in \mathbb{Z}, z^n=r^n\text{cis}(n\theta)
|
||||
$$
|
||||
|
||||
|
||||
## New Fancy stuff
|
||||
|
||||
Claim:
|
||||
|
||||
$$
|
||||
\forall n\in \mathbb{Z}, z^{\frac{1}{n}}=\sqrt[n]{r}\text{cis}\left(\frac{1}{n}\theta\right)
|
||||
$$
|
||||
|
||||
Proof:
|
||||
|
||||
Take an $n$th power, De Moivre's formula holds $\forall$ rational $k\in \mathbb{Q}$.
|
||||
|
||||
Example:
|
||||
|
||||
we calculate $1^{\frac{1}{3}}$
|
||||
|
||||
$$
|
||||
1=\text{cis}\left(2k\pi\right)
|
||||
$$
|
||||
|
||||
$$
|
||||
1^{\frac{1}{3}}=\text{cis}\left(\frac{2k\pi}{3}\right)
|
||||
$$
|
||||
|
||||
When $k=0$, we get $1$
|
||||
|
||||
When $k=1$, we get $\text{cis}\left(\frac{2\pi}{3}\right)=-\frac{1}{2}+i\frac{\sqrt{3}}{2}$
|
||||
|
||||
When $k=2$, we get $\text{cis}\left(\frac{4\pi}{3}\right)=-\frac{1}{2}-i\frac{\sqrt{3}}{2}$
|
||||
|
||||
Strange example
|
||||
|
||||
Let $p(x)=a_3x^3+a_2x^2+a_1x+a_0$ be a polynomial with real coefficients.
|
||||
|
||||
Without loss of generality, Let $a_3=1$, $x=y-\beta$
|
||||
|
||||
We claim $\beta=\frac{a_2}{3}$
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
p(x)&=(y-\beta)^3+a_2(y-\beta)^2+a_1(y-\beta)+a_0\\
|
||||
&=y^3+\left(a_2-3\beta\right)y^2+\left(a_1-3\beta^2-2a_2\beta\right)y+\left(a_0-3\beta^3-3a_1\beta-a_2\beta^2\right)\\
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
It's sufficient to know how to solve real cubic equations.
|
||||
|
||||
$$
|
||||
q(x)=x^3+ax+b
|
||||
$$
|
||||
|
||||
Let $x=w+\frac{c}{w}$
|
||||
|
||||
Solve
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
(w+\frac{c}{w})^3+a(w+\frac{c}{w})+b=0\\
|
||||
w^3+3w\frac{c}{w}+3\frac{c^2}{w^2}+aw+\frac{ac}{w}+b=0\\
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
We choose $c$ such that $3c+a=0$, $c=-\frac{a}{3}$
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
w^3+3\frac{c^2}{w}+b=0\\
|
||||
w^6+bw^3+c^2=0\\
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Notice that $w^6+bw^3+c^2=0$ is a quadratic equation in $w^3$.
|
||||
|
||||
$$
|
||||
w^3=\frac{-b\pm\sqrt{b^2-4c^3}}{2}
|
||||
$$
|
||||
|
||||
So $w$ is a cube root of $\frac{-b\pm\sqrt{b^2-4c^3}}{2}$
|
||||
|
||||
$x=w+\frac{c}{w}=w-\frac{a}{3w}$
|
||||
|
||||
Example:
|
||||
|
||||
$$
|
||||
p(x)=x^3-3x+1=0
|
||||
$$
|
||||
|
||||
$a=-3$, $b=1$, $c=-\frac{a}{3}=-\frac{-3}{3}=1$
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
w^3&=\frac{-b\pm\sqrt{b^2-4c^3}}{2}\\
|
||||
&=\frac{-1\pm\sqrt{1-4}}{2}\\
|
||||
&=\frac{-1\pm\sqrt{3}i}{2}\\
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
To take cube root of $w$,
|
||||
|
||||
$$
|
||||
w^3=\text{cis}\left(\frac{2\pi}{3}+2k\pi\right)
|
||||
$$
|
||||
|
||||
So
|
||||
|
||||
Case 1:
|
||||
|
||||
$$
|
||||
w=\text{cis}\left(\frac{2\pi}{9}+\frac{2k\pi}{3}\right)
|
||||
$$
|
||||
|
||||
It is sufficient to check $k=0,1,2$ by nth root of unity.
|
||||
|
||||
When $k=0$, $w=\text{cis}\left(\frac{2\pi}{9}\right)$
|
||||
|
||||
When $k=1$, $w=\text{cis}\left(\frac{8\pi}{9}\right)$
|
||||
|
||||
When $k=2$, $w=\text{cis}\left(\frac{14\pi}{9}\right)$
|
||||
|
||||
Case 2:
|
||||
|
||||
$$
|
||||
w=\text{cis}\left(\frac{4\pi}{9}+\frac{2k\pi}{3}\right)
|
||||
$$
|
||||
|
||||
When $k=0$, $w=\text{cis}\left(\frac{4\pi}{9}\right)$
|
||||
|
||||
When $k=1$, $w=\text{cis}\left(\frac{10\pi}{9}\right)$
|
||||
|
||||
When $k=2$, $w=\text{cis}\left(\frac{16\pi}{9}\right)$
|
||||
|
||||
So the final roots are:
|
||||
|
||||
$$
|
||||
w+\frac{c}{w}=w+\frac{1}{w}
|
||||
$$
|
||||
|
||||
$$
|
||||
\text{cis}(\theta)+\frac{1}{\text{cis}(\theta)}=\text{cis}(\theta)+\text{cis}(-\theta)=2\cos(\theta)
|
||||
$$
|
||||
|
||||
So the final roots are:
|
||||
|
||||
$$
|
||||
2\cos\left(\frac{2\pi}{9}\right), 2\cos\left(\frac{8\pi}{9}\right), 2\cos\left(\frac{14\pi}{9}\right), 2\cos\left(\frac{4\pi}{9}\right), 2\cos\left(\frac{10\pi}{9}\right), 2\cos\left(\frac{16\pi}{9}\right)
|
||||
$$
|
||||
|
||||
Remember $\cos(2\pi-\theta)=\cos(\theta)$
|
||||
|
||||
So the final roots are:
|
||||
|
||||
$$
|
||||
2\cos\left(\frac{2\pi}{9}\right), 2\cos\left(\frac{8\pi}{9}\right), 2\cos\left(\frac{14\pi}{9}\right)
|
||||
$$
|
||||
|
||||
### Compact
|
||||
|
||||
A set $K\in \mathbb{R}^n$ is compact if and only if it is closed and bounded. [Compact Theorem in Math 4111](https://notenextra.trance-0.com/Math4111/Math4111_L12#theorem-241)
|
||||
|
||||
If $\{x_n\}\in K$, then there must be some point $w$ such that every disk $D(w,\epsilon)$ contains infinitely many points of $K$. [Infinite Point Theorem about Compact Set in Math 4111](https://notenextra.trance-0.com/Math4111/Math4111_L11#theorem-237)
|
||||
|
||||
Unfortunately, $\mathbb{C}$ is not compact.
|
||||
|
||||
### Riemann Sphere and Complex Projective Space
|
||||
|
||||
Let $\mathbb{C}\sim \mathbb{R}^2\subset \mathbb{R}^3$
|
||||
|
||||
We put a unit sphere on the origin, and project the point on sphere to $\mathbb{R}^2$ by drawing a line through the north pole and the point on the sphere.
|
||||
|
||||
So all the point on the north pole is mapped to outside of the unit circle in $\mathbb{R}^2$.
|
||||
|
||||
all the point on the south pole is mapped to inside of the unit circle in $\mathbb{R}^2$.
|
||||
|
||||
The line through $(0,0,1)$ and $(\xi,\eta,z)$ intersects the unit sphere at $(x,y,0)$
|
||||
|
||||
Line $(tx,ty,1-t)$ intersects $z^2$ at $t^2x^2+t^2y^2+(1-t)^2=1$
|
||||
|
||||
So $t=\frac{2}{1+x^2+y^2}$
|
||||
|
||||
$$
|
||||
z=x+iy\mapsto \frac{1}{1+|z|^2}(2Re(z),2Im(z),|z|^2-1)
|
||||
$$
|
||||
|
||||
$$
|
||||
(\xi,\eta,z)\mapsto \frac{\xi+i\eta}{1-z}
|
||||
$$
|
||||
|
||||
This is a homeomorphism. $\mathbb{C}\setminus\{\infty\}\simeq S^2$
|
||||
|
||||
#### Derivative of a function
|
||||
|
||||
Suppose $\Omega$ is an open subset of $\mathbb{C}$.
|
||||
|
||||
A function $f:\Omega\to \mathbb{C}$'s derivative is defined as
|
||||
|
||||
$$
|
||||
f'(z_0)=\lim_{z\to z_0}\frac{f(z)-f(z_0)}{z-z_0}
|
||||
$$
|
||||
|
||||
$f=u+iv$, $u,v:\Omega\to \mathbb{R}$
|
||||
|
||||
How are $f'$ and derivatives of $u$ and $v$ related?
|
||||
|
||||
1. Differentiation and complex linearity applies to $f$
|
||||
|
||||
Chain rule applies
|
||||
|
||||
$$
|
||||
\frac{d}{dz}(f(g(z)))=f'(g(z))g'(z)
|
||||
$$
|
||||
|
||||
Polynomials
|
||||
|
||||
$$
|
||||
\frac{d}{dz}z^n=nz^{n-1}
|
||||
$$
|
||||
@@ -1,143 +0,0 @@
|
||||
# Math416 Lecture 20
|
||||
|
||||
## Laurent Series and Isolated Singularities
|
||||
|
||||
### Isolated Singularities
|
||||
|
||||
$f$ has an isolated singularity at $z_0$ if $f$ is analytic everywhere in some punctured disk $0 < |z - z_0| < R$ except at $z_0$ itself.
|
||||
|
||||
#### Removable Singularities
|
||||
|
||||
We call $z_0$ a removable singularity if there exists $g\in O(B_r(z_0))$ such that $f(z) = g(z)$ for all $z\in B_r(z_0) \setminus \{z_0\}$.
|
||||
|
||||
#### Poles
|
||||
|
||||
We call $z_0$ a pole if there are finitely many terms with negative powers in the Laurent series expansion of $f$ about $z_0$.
|
||||
|
||||
#### Essential Singularities
|
||||
|
||||
We call $z_0$ an essential singularity if there are infinitely many terms with negative powers in the Laurent series expansion of $f$ about $z_0$.
|
||||
|
||||
#### Theorem: Criterion for a removable singularity (Riemann removable singularity theorem)
|
||||
|
||||
Suppose $f$ has an isolated singularity at $z_0$. Then it is removable if and only if $f$ is bounded on a punctured disk centered at $z_0$.
|
||||
|
||||
#### Theorem 8.10 (Casorati-Weierstrass Theorem)
|
||||
|
||||
If $z_0$ is an essential singularity of $f$, then $\forall r>0$, $\overline{f(B_r(z_0)\setminus\{z_0\})}= \mathbb{C}$.
|
||||
|
||||
Proof:
|
||||
|
||||
Suppose $w\notin$ closure range fo $f$ on $B_r(z_0)\setminus\{z_0\}$, then $\exists \epsilon > 0$ such that $B_\epsilon(w)\cap f(B_r(z_0)\setminus\{z_0\})=\emptyset$.
|
||||
|
||||
$g(z)=1/(f(z)-w)$ and $|g(z)|\leq \frac{1}{\epsilon}$, which is bounded. By Riemann removable singularity theorem, $g$ has a removable singularity. So $f(z)=\frac{1}{g(z)}+w$ is holomorphic on $B_r(z_0)\setminus\{z_0\}$.
|
||||
|
||||
Suppose $g(z_0)\neq 0$, then $f$ has a removable singularity at $z_0$.
|
||||
|
||||
Suppose $g(z_0)=0$, then $f$ has a pole at $z_0$.
|
||||
|
||||
This contradicts the assumption that $z_0$ is an essential singularity.
|
||||
|
||||
QED
|
||||
|
||||
#### Theorem 8.11 (Picard's Theorem)
|
||||
|
||||
If $z_0$ is an essential singularity of $f$, then $\forall r>0$, $f(B_r(z_0)\setminus\{z_0\})$ contains every point in $\mathbb{C}$ except possibly one.
|
||||
|
||||
#### Definition: Residue
|
||||
|
||||
Suppose $f$ has an isolated singularity at $z_0$. The residue of $f$ at $z_0$, write $res_{z_0}(f)$, is the coefficient of $(z-z_0)^{-1}$ in the Laurent series expansion of $f$ about $z_0$.
|
||||
|
||||
> Preview:
|
||||
>
|
||||
> Residue Theorem:
|
||||
>
|
||||
> Suppose $G$ is a simply connected domain, $F$ is a finite set in $G$ $h$ is holomorphic on $G\setminus F$. Let $\gamma$ be a simple closed curve in $G$, containing $\lambda_1, \lambda_2, \cdots, \lambda_N$ from $F$. Then
|
||||
>
|
||||
> $$\int_\gamma h(z) dz = 2\pi i \sum_{j=1}^N res_{\lambda_j}(h)$$
|
||||
|
||||
Special case:
|
||||
|
||||
When $\gamma=\partial B_r(z_0)$, $f(z)=\sum_{n=-\infty}^\infty a_n(z-z_0)^n$ converges on $A(z_0;0,R)$, then
|
||||
|
||||
$$
|
||||
\int_{\gamma} f(z) dz = 2\pi i \sum_{n=-\infty}^\infty a_n \int_{\gamma} (z-z_0)^n dz=2\pi i a_{-1}
|
||||
$$
|
||||
|
||||
Example:
|
||||
|
||||
1. Find residue of $f(z)=\frac{\sin z}{z^4}$ at $z=0$.
|
||||
|
||||
$\sin z = z - \frac{z^3}{3!} + \frac{z^5}{5!} - \cdots$
|
||||
|
||||
$\frac{\sin z}{z^4} = \frac{1}{z^4} - \frac{1}{3!z} + \frac{z}{5!} - \cdots$
|
||||
|
||||
$res_{z=0}(\frac{\sin z}{z^4}) = \frac{1}{3!}$
|
||||
|
||||
2. Find residue of $f(z)=\frac{1}{(z+2)(z-5)}$ at $z=5$ and $z=-2$.
|
||||
|
||||
$res_{z=5}(f(z))=(z-5)^{-1}\cdot\frac{1}{z+2}|_{z=5}=\frac{1}{7}$
|
||||
|
||||
$res_{z=-2}(f(z))=(z+2)^{-1}\cdot\frac{1}{z-5}|_{z=-2}=-\frac{1}{7}$
|
||||
|
||||
#### Corollary of residue
|
||||
|
||||
Suppose $f$ has an simple pole at $z_0$. Then $res_{z_0}(f)=\lim_{z\to z_0}(z-z_0)f(z)$.
|
||||
|
||||
Proof:
|
||||
|
||||
$f(z)=a_{-1}(z-z_0)^{-1}+\sum_{n=0}^\infty a_n(z-z_0)^n$, $(z-z_0)f(z)=a_{-1}+\sum_{n=0}^\infty a_n(z-z_0)^{n+1}$
|
||||
|
||||
$\lim_{z\to z_0}(z-z_0)f(z)=\lim_{z\to z_0}(z-z_0)\cdot a_{-1}+\lim_{z\to z_0}(z-z_0)\cdot\sum_{n=0}^\infty a_n(z-z_0)^n=a_{-1}$
|
||||
|
||||
QED
|
||||
|
||||
#### Find residue for poles with higher order
|
||||
|
||||
Suppose $f$ has a pole of order 2 at $z_0$. Then $f(z)=\frac{a_{-2}}{(z-z_0)^2}+\frac{a_{-1}}{z-z_0}+\sum_{n=0}^\infty a_n(z-z_0)^n$, $(z-z_0)^2f(z)=a_{-2}+(z-z_0)a_{-1}+\sum_{n=0}^\infty a_n(z-z_0)^{n+2}$
|
||||
|
||||
Method 1:
|
||||
|
||||
$res_{z_0}(f)=a_{-1}=\lim_{z\to z_0}\frac{f(z)-\lim_{z\to z_0}(z-z_0)^2f(z)}{(z-z_0)}$
|
||||
|
||||
Method 2:
|
||||
|
||||
$res_{z_0}(f)=\frac{1}{(n-1)!}\frac{d^{n-1}}{dz^{n-1}}(z-z_0)^nf(z)|_{z=z_0}$
|
||||
|
||||
So suppose $f$ has a pole of order $n$ at $z_0$. Then $res_{z_0}(f)=\frac{d^{n-1}}{dz^{n-1}}(z-z_0)^nf(z)|_{z=z_0}$
|
||||
|
||||
Proof:
|
||||
|
||||
$f(z)=\frac{a_{-n}}{(z-z_0)^n}+\frac{a_{-n+1}}{(z-z_0)^{n-1}}+\cdots+\frac{a_{-1}}{z-z_0}+\sum_{m=0}^\infty a_m(z-z_0)^m$
|
||||
|
||||
$(z-z_0)^nf(z)=a_{-n}+(z-z_0)a_{-n+1}+\cdots+(z-z_0)^{n-1}a_{-1}+\sum_{m=0}^\infty a_m(z-z_0)^{m+n}$
|
||||
|
||||
$\frac{d^{n-1}}{dz^{n-1}}(z-z_0)^nf(z)=(n-1)!a_{-1}+\sum_{m=0}^\infty a_m(m+n)(m+n-1)\cdots(m+1)(z-z_0)^{m-1}$
|
||||
|
||||
$\lim_{z\to z_0}\frac{1}{(n-1)!}\frac{d^{n-1}}{dz^{n-1}}(z-z_0)^nf(z)=a_{-1}$
|
||||
|
||||
QED
|
||||
|
||||
## Chapter 9: Generalized Cauchy's Theorem
|
||||
|
||||
### Simple connectedness
|
||||
|
||||
#### Proposition 9.1
|
||||
|
||||
Let $\phi$ be a continuous nowhere vanishing function from $[a,b]\subset\mathbb{R}$ to $\mathbb{C}\setminus\{0\}$. Then there exists a continuous function $\psi:[a,b]\to\mathbb{C}$ such that $e^{\psi(t)}=\phi(t)$ for all $t\in[a,b]$.
|
||||
|
||||
Moreover, $\psi$ is uniquely determined up to an additive integer multiple of $2\pi i \mathbb{Z}$.
|
||||
|
||||
Proof:
|
||||
|
||||
Uniqueness:
|
||||
|
||||
Suppose $\phi_1$ and $\phi_2$ are both continuous functions so that $e^{\phi_1(t)}=\phi(t)=e^{\phi_2(t)}$ for all $t\in[a,b]$.
|
||||
|
||||
Then $e^{\phi_1(t)-\phi_2(t)}=1$ for all $t\in[a,b]$. So $\phi_1(t)-\phi_2(t)=2k\pi i$ for some $k\in\mathbb{Z}$.
|
||||
|
||||
Existence:
|
||||
|
||||
Continue on Thursday.
|
||||
|
||||
QED
|
||||
@@ -1,98 +0,0 @@
|
||||
# Math416 Lecture 21
|
||||
|
||||
## Chapter 9: Generalized Cauchy's Theorem
|
||||
|
||||
### Simple connectedness
|
||||
|
||||
#### Proposition 9.1
|
||||
|
||||
Let $\phi$ be a continuous nowhere vanishing function from $[a,b]\subset\mathbb{R}$ to $\mathbb{C}\setminus\{0\}$. Then there exists a continuous function $\psi:[a,b]\to\mathbb{C}$ such that $e^{\psi(t)}=\phi(t)$ for all $t\in[a,b]$.
|
||||
|
||||
Moreover, $\psi$ is uniquely determined up to an additive integer multiple of $2\pi i \mathbb{Z}$.
|
||||
|
||||
Proof:
|
||||
|
||||
Uniqueness:
|
||||
|
||||
Suppose $\phi_1$ and $\phi_2$ are both continuous functions so that $e^{\phi_1(t)}=\phi(t)=e^{\phi_2(t)}$ for all $t\in[a,b]$.
|
||||
|
||||
Then $e^{\phi_1(t)-\phi_2(t)}=1$ for all $t\in[a,b]$. So $\phi_1(t)-\phi_2(t)=2k\pi i$ for some $k\in\mathbb{Z}$.
|
||||
|
||||
Existence:
|
||||
|
||||
Case 1: Assume $range(\phi)\subset H$ where $H$ is an open half-plane with the origin $0\in \partial H$.
|
||||
|
||||
We know there is a branch $l(z)$ of $\log z$ defined on $H$ with $Log(z)=\log|z|+i\theta(z)$ for some $\arg(z)\in(\alpha,\alpha+\pi)$.
|
||||
|
||||
Let $\psi(t)=l(\phi(t))$.
|
||||
|
||||
Then $e^{\psi(t)}=e^{l(\phi(t))}=\phi(t)$. and $\psi$ is continuous.
|
||||
|
||||
Case 2: By compactness of $[a,b]$, there exists a partition $a=t_0<t_1<\cdots<t_n=b$ such that, for each $0\leq j\leq n-1$, $\phi([t_j,t_{j+1}])$ is contained in some open half plane $H_j$ with the origin $0\in \partial H_j$.
|
||||
|
||||
> Recall:
|
||||
>
|
||||
> Compactness: A set is compact if and only if every open cover has a finite subcover.
|
||||
|
||||
Let $s\in [a,b]$ and there exists $\epsilon(s)>0$ such that $\phi((s-\epsilon(s),s+\epsilon(s)))$ is contained in some open half plane.
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
[a,b]&=\bigcup_{s\in[a,b]}(s-\epsilon(s),s+\epsilon(s))\cup[a,a+\epsilon(a))\cup(b-\epsilon(b),b] \\
|
||||
&=\bigcup_{j=1}^n(s_j-\epsilon(s_j),s_j+\epsilon(s_j))\cup[a,a+\epsilon(a))\cup(b-\epsilon(b),b]
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
We choose $t_j\in[s_j-\epsilon(s_j),s_j+\epsilon(s_j)]\cup[s_{j+1}-\epsilon(s_{j+1}),s_{j+1}+\epsilon(s_{j+1})]$ for each $j=1,\cdots,n-1$.
|
||||
|
||||
On each interval $[t_j,t_{j+1}]$, we can find a $\psi_j(t)$ such that $e^{\psi_j(t)}=\phi(t)$, $\psi_j(t)$ is continuous on $[t_j,t_{j+1}]$. And we can choose $\psi_{j+1}(t_{j+1})=\psi_j(t_{j+1})$.
|
||||
|
||||
Defined $\psi(t)=\{\psi_j(t), t\in[t_j,t_{j+1}]\}$ for $j=1,\cdots,n-1$.
|
||||
|
||||
QED
|
||||
|
||||
### Increment of a log and argument
|
||||
|
||||
If $f\circ\gamma:[a,b]\to\mathbb{C}\setminus\{0\}$ is continuous, then $\exists \psi:[a,b]\to\mathbb{C}$ such that $e^{\psi(t)}=f(\gamma(t))$ for all $t\in[a,b]$.
|
||||
|
||||
We defined the increment in $\log f$ on $\gamma$ as $\Delta(\log f,\gamma)=\psi(b)-\psi(a)$.
|
||||
|
||||
The increment in $\arg f$ on $\gamma$ is defined as $\Delta(\arg f,\gamma)=Im[\psi(b)]-Im[\psi(a)]$.
|
||||
|
||||
If $\gamma$ is a closed curve, then $f\circ\gamma(a)=f\circ\gamma(b)$. Then $\Delta(\log f,\gamma)\in 2\pi i\mathbb{Z}$, $\Delta(\arg f,\gamma)\in 2\pi\mathbb{Z}$.
|
||||
|
||||
Assume $\gamma$ is piecewise continuous and $f$ is continuous and $f(z)\neq 0$ for all $z\in\gamma$.
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\Delta(\log f,\gamma)&=\psi(b)-\psi(a) \\
|
||||
&=\int_a^b\frac{d}{dt}\log f(\gamma(t))dt \\
|
||||
&=\int_a^b\frac{f'(\gamma(t))\gamma'(t)}{f(\gamma(t))}dt \\
|
||||
&=\int_\gamma\frac{f'(z)}{f(z)}dz
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
If $\gamma$ is closed, then $\Delta(\log f,\gamma)=\int_\gamma\frac{f'(z)}{f(z)}dz=0$, $\Delta(\arg f,\gamma)=\frac{1}{i}\int_\gamma\frac{f'(z)}{f(z)}dz=0$.
|
||||
|
||||
Special case:
|
||||
|
||||
When $f(z)=z-z_0$, $z_0\notin range(\gamma)$, then $\Delta(\arg (z-z_0),\gamma)\in 2\pi\mathbb{Z}$.
|
||||
|
||||
The winding number of $\gamma$ around $z_0$ is defined as $n(\gamma,z_0)=\frac{1}{2\pi i}\Delta(\arg (z-z_0),\gamma)$.
|
||||
|
||||
_also the same as the number of times $\gamma$ winds around $z_0$ counterclockwise._
|
||||
|
||||
Winding number is always zero outside the curve.
|
||||
|
||||
### Contour
|
||||
|
||||
A contour is a formed piecewise combination of piecewise continuous closed curves with integer coefficients.
|
||||
|
||||
$$
|
||||
\Gamma=\sum_{j=1}^p n_j\gamma_j
|
||||
$$
|
||||
|
||||
where $\gamma_j$ are piecewise continuous closed curves and $n_j\in\mathbb{Z}$.
|
||||
|
||||
A contour is called a simple if the winding number of $\Gamma$ is zero or one.
|
||||
|
||||
@@ -1,120 +0,0 @@
|
||||
# Math416 Lecture 22
|
||||
|
||||
## Chapter 9: Generalized Cauchy Theorem
|
||||
|
||||
### Winding numbers
|
||||
|
||||
Definition:
|
||||
|
||||
Let $\gamma:[a,b]\to\mathbb{C}$ be a closed curve. The **winding number** of $\gamma$ around $z\in\mathbb{C}$ is defined as
|
||||
|
||||
$$
|
||||
\frac{1}{2\pi i}\Delta(arg(z-z_0),\gamma)
|
||||
$$
|
||||
|
||||
where $\Delta(arg(z-z_0),\gamma)$ is the change in the argument of $z-z_0$ along $\gamma$.
|
||||
|
||||
#### Interior of curve
|
||||
|
||||
The interior of $\gamma$ is the set of points $z\in\mathbb{C}$ such that the winding number of $\gamma$ around $z$ is non-zero.
|
||||
|
||||
$$
|
||||
int_\gamma(z)=\{z\in\mathbb{C}|\frac{1}{2\pi i}\Delta(arg(z-z_0),\gamma)\neq 0\}
|
||||
$$
|
||||
|
||||
#### Contour
|
||||
|
||||
The winding number of a contour $\Gamma$ around $z$ is the sum of the winding numbers of the contours $\gamma_j$ around $z$.
|
||||
|
||||
$$
|
||||
ind_\Gamma(z)=\sum_{j=1}^nn_j ind_{\gamma_j}(z)
|
||||
$$
|
||||
|
||||
A contour is simple if $ind_\gamma(z)=\{0,1\}$ for all $z\in\mathbb{C}\setminus\gamma([a,b])$.
|
||||
|
||||
#### Separation lemma
|
||||
|
||||
Let $\Omega\subseteq \mathbb{C}$ be open, let $K\subset \Omega$ be compact, then $\exists$ a simple contour $\Gamma\subset \Omega\setminus K$ such that
|
||||
|
||||
$$
|
||||
K\subset int_\Gamma(\Gamma)\subset \Omega
|
||||
$$
|
||||
|
||||
Proof:
|
||||
|
||||
First we show that $\exists$ a simple contour $\Gamma\subset \Omega\setminus K$
|
||||
|
||||
Let $0<\delta<dist(K,\partial\Omega)$.
|
||||
|
||||
We draw a grid fo horizontal ad vertical lines each separated from each other by $\delta$.
|
||||
|
||||
Let $S_1,S_2,\dots,S_n$ be the squares that intersect $K$.
|
||||
|
||||
Let $\sigma_j$ be the boundary of $S_j$ traversed in counterclockwise direction.
|
||||
|
||||
Let $\varepsilon$ be the set of edges with exactly one $s_j$ for $j=1,2,\dots,q$.
|
||||
|
||||
Note that $\varepsilon\subseteq \Omega\setminus K$.
|
||||
|
||||
We claim that $\varepsilon$ forms a contour.
|
||||
|
||||
Proof of Claim:
|
||||
|
||||
Say a sequence of edges $E_1,E_2,\dots,E_p$, $E_i\in \varepsilon$. from a chain if terminal points of $E_k$ is the initial point of $E_{k+1}$ for $1\leq k\leq p-1$.
|
||||
|
||||
Say it forms a cycle if inaddition the terminal points of $E_p$ is the initial point of $E_1$.
|
||||
|
||||
Any cycle is a piecewise continuous closed curve.
|
||||
|
||||
We want to show that $\varepsilon$ is a disjoint union of cycles.
|
||||
|
||||
We can prove that every terminal point of an edge in $\varepsilon$ is an initial point of an edge in $\varepsilon$. By case analysis for the state of the four square around the terminal point.
|
||||
|
||||
Let $\gamma=(E_1,E_2,\dots,E_p)$ be a maximal cycle in $\varepsilon$. (Maximal means that we cannot add another edge to it while still having a cycle.)
|
||||
|
||||
Then $\gamma$ is a cycle.
|
||||
|
||||
Look at the terminal point of $E_p$, This is initial point for some edge $E'$, where $E'$ is one of the edges of $\gamma$.
|
||||
|
||||
If $E'$ is not $E_1$, then we can add $E'$ to $\gamma$ to form a larger cycle. Contradiction. (You can do this by case analysis. If there is three edges, then there must be four.)
|
||||
|
||||
Thus $E'=E_1$.
|
||||
|
||||
Thus $\gamma$ is a cycle.
|
||||
|
||||
We can now remove $\gamma$ from $\varepsilon$ to form a new set $\varepsilon'$.
|
||||
|
||||
We can repeat this process to form a disjoint union of cycles using induction.
|
||||
|
||||
Second, we show that $int_\Gamma(\Gamma)\subset \Omega$.
|
||||
|
||||
Let $z_0\in int(S_j)$ for some $1\leq j\leq q$.
|
||||
|
||||
$ind_{S_k}(z_0)=\begin{cases}
|
||||
1 & k=j\\
|
||||
0 & k\neq j
|
||||
\end{cases}$
|
||||
|
||||
Thus
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\sum_{k=1}^q ind_{S_k}(z_0)&=\sum_{k=1}^q \frac{1}{2\pi i}\int_{\partial S_k}\frac{1}{z-z_0}dz\\
|
||||
&=1\\
|
||||
&=ind_\Gamma(z_0)
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
So if $z_0\in int(\bigcup_{j=1}^q S_j)$, then $ind_\Gamma(z_0)=1$.
|
||||
|
||||
And $\bigcup_{j=1}^q S_j\supset K$, so $z_0\in int_\Gamma(K)$.
|
||||
|
||||
Let $z_1\in\mathbb{C}\setminus\left(\bigcup_{j=1}^q S_j\cup\Gamma\right)$.
|
||||
|
||||
Then $ind_{S_k}(z_1)=0$ for all $1\leq k\leq q$.
|
||||
|
||||
Thus $\sum_{k=1}^q ind_{S_k}(z_1)=0=ind_\Gamma(z_1)$.
|
||||
|
||||
QED
|
||||
|
||||
Continue on Generalized Cauchy Theorem next time!!
|
||||
@@ -1,160 +0,0 @@
|
||||
# Math416 Lecture 23
|
||||
|
||||
## Chapter 9: Generalized Cauchy Theorem
|
||||
|
||||
### Separation lemma
|
||||
|
||||
Let $\Omega$ be an open subset in $\mathbb{C}$, let $K\subset \Omega$ be compact. Then There exists a simple contour $\Gamma$ such that
|
||||
|
||||
$$
|
||||
K\subset \text{int}(\Gamma)\subset \Omega
|
||||
$$
|
||||
|
||||
#### Corollary 9.9 for separation lemma
|
||||
|
||||
Let $\Gamma$ be the contour constructed in the separation lemma. Let $f\in O(\Omega)$ be holomorphic on $\Omega$. Then $\forall z_0\in K$ such that
|
||||
|
||||
$$
|
||||
f(z_0)=\frac{1}{2\pi i}\int_{\Gamma}\frac{f(z)}{z-z_0}dz
|
||||
$$
|
||||
|
||||
Proof:
|
||||
|
||||
Suppose $h\in O(G)$, then $\int_{\partial S} h(z)dz=0$, by Cauchy's theorem for square, followed from the triangle case.
|
||||
|
||||
So $\int_{\Gamma} h(z)dz=0=\sum_{j=1}^n \int_{\partial S_j} h(z)dz$
|
||||
|
||||
Fix $z_0\in K$,
|
||||
|
||||
$$
|
||||
g(z_0)=\begin{cases}
|
||||
\frac{f(z)-f(z_0)}{z-z_0} & z\neq z_0 \\
|
||||
f'(z_0) & z=z_0
|
||||
\end{cases}
|
||||
$$
|
||||
|
||||
So $\int_{\Gamma} g(z)dz=0$
|
||||
|
||||
Thus
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\int_{\Gamma}\frac{f(z)}{z-z_0}dz-\int_{\Gamma}\frac{f(z_0)}{z-z_0}dz&=0 \\
|
||||
\int_{\Gamma}\frac{f(z)}{z-z_0}dz&=f(z_0)\int_{\Gamma}\frac{1}{z-z_0}dz \\
|
||||
&=f(z_0)\cdot 2\pi i
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
QED
|
||||
|
||||
#### Theorem 9.10 Cauchy's Theorem
|
||||
|
||||
Let $\Omega$ be an open subset in $\mathbb{C}$, let $\Gamma$ be a contour with $int(\Gamma)\subset \Omega$. Let $f\in O(\Omega)$ be holomorphic on $\Omega$. Then
|
||||
|
||||
$$
|
||||
\int_{\Gamma} f(z)dz=0
|
||||
$$
|
||||
|
||||
Proof:
|
||||
|
||||
Let $K\subset \mathbb{C}\setminus \text{ext}(\Gamma)$.
|
||||
|
||||
By separation lemma, $\exists \Gamma_1$ s.t. $K\subset \text{int}(\Gamma_1)\subset \Omega$.
|
||||
|
||||
Notice that Separation lemma ensured that $w\neq z$ for all $w\in \Gamma_1, z\in \Gamma$.
|
||||
|
||||
By Corollary 9.9, $\forall z\in K, f(z)=\frac{1}{2\pi i}\int_{\Gamma_1}\frac{f(w)}{w-z}dw$
|
||||
|
||||
$$
|
||||
\int_{\Gamma} f(z)dz=\frac{1}{2\pi i}\int_{\Gamma}\left[\int_{\Gamma_1}\frac{f(w)}{w-z}dw\right]dz
|
||||
$$
|
||||
|
||||
By Fubini's theorem (In graduate course for analysis),
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\int_{\Gamma} f(z)dz&=\frac{1}{2\pi i}\int_{\Gamma_1}\left[\int_{\Gamma}\frac{f(w)}{w-z}dz\right]dw \\
|
||||
&=\frac{1}{2\pi i}\int_{\Gamma_1}f(w)\left[\int_{\Gamma}\frac{1}{w-z}dz\right]dw \\
|
||||
&=\frac{1}{2\pi i}\int_{\Gamma_1}f(w)\cdot 2\pi i \ \text{ind}_{\Gamma}(w)dw \\
|
||||
&=0
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Since the winding number for $\Gamma$ on $w\in \Gamma_1$ is 0. ($w$ is outside of $\Gamma$)
|
||||
|
||||
QED
|
||||
|
||||
### Homotopy
|
||||
|
||||
Suppose $\gamma_0, \gamma_1$ are two curves from
|
||||
$[0,1]$ to $\Omega$ with same end points $P,Q$.
|
||||
|
||||
A homotopy is a continuous function of curves $\gamma_t, 0\leq t\leq 1$, deforming $\gamma_0$ to $\gamma_1$, keeping the end points fixed.
|
||||
|
||||
Formally, if $H:[0,1]\times [0,1]\to \Omega$ is a continuous function satsifying
|
||||
|
||||
1. $H(s,0)=\gamma_0(s)$, $\forall s\in [0,1]$
|
||||
2. $H(s,1)=\gamma_1(s)$, $\forall s\in [0,1]$
|
||||
3. $H(0,t)=P$, $\forall t\in [0,1]$
|
||||
4. $H(1,t)=Q$, $\forall t\in [0,1]$
|
||||
|
||||
Then we say $H$ is a homotopy between $\gamma_0$ and $\gamma_1$. (If $\gamma_0$ and $\gamma_1$ are closed curves, $Q=P$)
|
||||
|
||||
#### Lemma 9.12 Technical Lemma
|
||||
|
||||
Let $\phi:[0,1]\times [0,1]\to \mathbb{C}\setminus \{0\}$ is continuous. Then there exists a continuous map $\psi:[0,1]\times [0,1]\to \mathbb{C}$ such that $e^\phi=\psi$. Moreover, $\psi$ is unique up to an additive constant in $2\pi i\mathbb{Z}$.
|
||||
|
||||
Proof:
|
||||
|
||||
Let $\phi_t(s)=\phi(s,t)$, $0\leq t\leq 1$.
|
||||
|
||||
Then $\exists \psi_{00}$ such that $e^{\psi_{00}(s)}=\phi(0,t)$.
|
||||
|
||||
$\exists \psi_{t}(s)$ such that $e^{\psi_{t}(s)}=\phi_t(s)$.
|
||||
|
||||
We want to show $\psi_t(s)$ is continuous in $t$.
|
||||
|
||||
Since $\exists \epsilon>0$ such that $\phi(s,t)$ is at least $\epsilon$ away from $0$ for all $s\in [0,1]$ and $t\in [0,1]$.
|
||||
|
||||
Moreover, $\phi(s,t)$ is uniformly continuous.
|
||||
|
||||
So $\exists \delta>0$ such that $|\phi(s,t)-\phi(s,t_0)|<\epsilon$ if $|t-t_0|<\delta$.
|
||||
|
||||
Therefore,
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\left|\frac{\phi(s,t)}{\phi(s,t_0)}-1\right|&<\frac{\epsilon}{\phi(s,t_0)}
|
||||
&<1
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
So $\text {Re} \frac{\phi(s,t)}{\phi(s,t_0)}>0$.
|
||||
|
||||
Therefore, $\text{Log} \frac{\phi(s,t)}{\phi(s,t_0)}=\chi(s,t)$ is continuous on $s\in [0,1], t\in [t_0-\delta, t_0+\delta]$.
|
||||
|
||||
So $e^{\chi(s,t)}=\frac{\phi(s,t)}{\phi(s,t_0)}$, $\chi(s,t_0)=0,\forall s\in [0,1]$
|
||||
|
||||
Define $\tilde{\psi}(s,t)=\chi(s,t)+\chi(s,t_0)$. So this function is continuous.
|
||||
|
||||
And $e^{\tilde{\psi}(s,t)}=e^{\chi(s,t)+\chi(s,t_0)}=e^{\chi(s,t)}\cdot e^{\chi(s,t_0)}=\phi(s,t)$.
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\tilde{\psi}(0,t_0)&=\chi(0,t_0)+\psi(0,t_0) \\
|
||||
&=0+\psi_{00}(t_0) \\
|
||||
&=\psi_{00}(t_0)
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
$\tilde{\psi}(s,0)$ and $\psi(t,0)$ on $t\in[t_0-\delta, t_0+\delta]$ are both logs of the same function, and agree to each other on $t_0$.
|
||||
|
||||
Therefore, $\tilde{\psi}(s,0)=\psi(s,0)+\text{const}$
|
||||
|
||||
QED
|
||||
|
||||
#### Theorem 9.13 Cauchy's Theorem for Homotopic Curves
|
||||
|
||||
|
||||
|
||||
|
||||
@@ -1,159 +0,0 @@
|
||||
# Math416 Lecture 24
|
||||
|
||||
## Continue on Generalized Cauchy's Theorem
|
||||
|
||||
### Homotopy
|
||||
|
||||
A homotopy between two curves $\gamma_0, \gamma_1 : [0, 1] \to \mathbb{C}$ is a continuous map $H : [0, 1] \times [0, 1] \to \mathbb{C}$ such that $H(z, 0) = \gamma_0(z)$ and $H(z, 1) = \gamma_1(z)$ for all $z \in [0, 1]$.
|
||||
|
||||
#### Lemma:
|
||||
|
||||
Let $\Omega$ be open in $\mathbb{C}$, Let $\gamma_0, \gamma_1$ be closed contour, homotopic in $\Omega$. Then $\operatorname{ind}_{\gamma_0} (z) = \operatorname{ind}_{\gamma_1} (z)$ for all $z \in \Omega$.
|
||||
|
||||
Proof:
|
||||
|
||||
Let $H(s,t)$ be a homotopy between $\gamma_0$ and $\gamma_1$. Let $z_0\in \mathbb{C} \setminus \Omega$.
|
||||
|
||||
Defined $\phi:[0,1]\times[0,1]\to \mathbb{C}\setminus \{0\}$, $\phi(s,t)=H(s,t)-z_0$.
|
||||
|
||||
By [Technical Lemma](https://notenextra.trance-0.com/Math416/Math416_L23#lemma-912-technical-lemma), $\exists$ continuous $\psi:[0,1]\times[0,1]\to \mathbb{C}$ such that $e^{\psi}=\phi$.
|
||||
|
||||
For each $t$, $\gamma_t(s)=H(s,t)$ is a closed curve.
|
||||
|
||||
$\operatorname{ind}_{\gamma_t}(z_0)=\frac{1}{2\pi i}\left[\psi(1,t)-\psi(0,t)\right]$.
|
||||
|
||||
This is continuous (in $t$), integer valued, thus constant.
|
||||
|
||||
QED
|
||||
|
||||
#### Theorem 9.14 Homotopy version of Cauchy's Theorem
|
||||
|
||||
Let $\Omega$ be open, $\gamma_0, \gamma_1$ be two piecewise continuous curves in $\Omega$ that are homotopic.
|
||||
|
||||
Then $\int_{\gamma_0} f(z) \, dz = \int_{\gamma_1} f(z) \, dz$ for all $f\in O(\Omega)$.
|
||||
|
||||
Proof:
|
||||
|
||||
$\Gamma=\gamma_0-\gamma_1$, then $\operatorname{ind}_{\Gamma}(z)=0$ for all $z\in \mathbb{C}\setminus \Omega$.
|
||||
|
||||
QED
|
||||
|
||||
#### Corollary of Theorem 9.14
|
||||
|
||||
If $\gamma_0$ is null-homotopic in $\Omega$ (i.e. $\gamma_0$ is homotopic to a point), then $\int_{\gamma_0} f(z) \, dz = 0$ for all $f\in O(\Omega)$.
|
||||
|
||||
## Chapter 10: Further development of Complex Function Theory
|
||||
|
||||
### Simple connectedness
|
||||
|
||||
#### Definition (non-standard) simply connected
|
||||
|
||||
Let $\Omega$ be a domain in $\mathbb{C}$. We say $\Omega$ is simply connected if $\overline{\mathbb{C}}\setminus \Omega$ is connected. ($\overline{\mathbb{C}}=\mathbb{C}\cup \{\infty\})$
|
||||
|
||||
Example:
|
||||
|
||||
disk is simply connected.
|
||||
|
||||
annulus is not simply connected.
|
||||
|
||||
$\mathbb{C}$ is simply connected.
|
||||
|
||||
Any convex domain is simply connected.
|
||||
|
||||
> Standard definition: $\Omega$ is simply connected if every closed curve in $\Omega$ is null-homotopic in $\Omega$.
|
||||
|
||||
#### Theorem of equivalent definition of simply connected
|
||||
|
||||
For open connected subsets of $\mathbb{C}$, the standard definition and the non-standard definition are equivalent.
|
||||
|
||||
Proved end of book.
|
||||
|
||||
#### Proposition for simply connected domain
|
||||
|
||||
$\Omega$ is simply connected $\iff$ every contour in $\Omega$ has winding number $0$ about every point in $\mathbb{C}\setminus \Omega$.
|
||||
|
||||
Proof:
|
||||
|
||||
If $\Omega$ is simply connected, let $\gamma$ be a curve in $\Omega$, then $\operatorname{ind}_{\gamma}(z)=0$ for all $z$ in the unbounded component of $\overline{\mathbb{C}}\setminus \Omega$. This contains all of $\mathbb{C}\setminus \Omega$.
|
||||
|
||||
Conversely, assume $\Omega$ is not simply connected, then $\exists K\cup L=\overline{\mathbb{C}}\setminus \Omega$, where $K$ and $L$ are disjoint closed, without loss of generality, assume $\infty\in L$.
|
||||
|
||||
Let $H=\Omega\cup K=\mathbb{C}\setminus L$.
|
||||
|
||||
$H$ is open, $K$ is compact subset of $H$, so by [Separation Lemma](https://notenextra.trance-0.com/Math416/Math416_L23#separation-lemma), $\exists \gamma\in H\setminus K=\Omega$ such that $K\subset \operatorname{int}(\gamma)$.
|
||||
|
||||
#### Theorem 10.3 Cauchy's Theorem for simply connected domain
|
||||
|
||||
corollary of Proposition for simply connected domain
|
||||
|
||||
Let $\Omega$ be a simply connected domain, let $\gamma$ be a closed curve in $\Omega$. Then $\int_{\gamma} f(z) \, dz = 0$ for all $f\in O(\Omega)$.
|
||||
|
||||
Proof:
|
||||
|
||||
Know that is true if $\operatorname{ind}_{\gamma}(z)=0$ for all $z\in \mathbb{C}\setminus \Omega$.
|
||||
|
||||
By Proposition, $\Omega$ is simply connected $\iff$ every closed curve in $\Omega$ has winding number $0$ about every point in $\mathbb{C}\setminus \Omega$.
|
||||
|
||||
So the result is true.
|
||||
|
||||
QED
|
||||
|
||||
#### Theorem 10.4-6
|
||||
|
||||
The following condition are equivalent:
|
||||
|
||||
1. $\Omega$ is simply connected.
|
||||
2. every holomorphic function on $\Omega$ has a primitive $g$, i.e. $g'(z)=f(z)$ for all $z\in \Omega$.
|
||||
3. every non-vanishing holomorphic function on $\Omega$ has a holomorphic logarithm.
|
||||
4. every harmonic function on $\Omega$ has a harmonic conjugate.
|
||||
|
||||
Proof:
|
||||
|
||||
$(1)\iff (2)$:
|
||||
|
||||
First we show $(1)\implies (2)$.
|
||||
|
||||
Assume $\Omega$ is simply connected.
|
||||
|
||||
Define $g(z)=\int_{z_0}^{z} f(w) \, dw$ for $z_0\in \Omega$ fixed. Then by Cauchy's Theorem, this definition does not depend on the path.
|
||||
|
||||
$\frac{g(z+h)-g(z)}{h}=\frac{1}{h}\left[\int_{z}^{z+h} f(w) \, dw\right]$
|
||||
|
||||
$\frac{1}{h}\left[\int_{z}^{z+h} f(w) \, dw\right]\to f(z)$ as $h\to 0$.
|
||||
|
||||
So on $[z,z+h]\subset \Omega$, if $|f(w)-f(z)|<\epsilon$, then $|\frac{g(z+h)-g(z)}{h}-hf(z)|<h\epsilon$.
|
||||
|
||||
To show $(2)\implies (1)$, we prove $\neg (1)\implies \neg (2)$.
|
||||
|
||||
|
||||
$(1)\iff (3)$:
|
||||
|
||||
If $\Omega$ is not simply connected, there is some closed curve $\gamma$ and some $z_0\not in \Omega$ such that $\operatorname{ind}_{\gamma}(z_0)\neq 0$.
|
||||
|
||||
SO $\int_{\gamma} \frac{1}{z-z_0} \, dz\neq 0$.
|
||||
|
||||
So $\frac{1}{z-z_0}$ does not have a primitive on $\Omega$. $\frac{1}{z-z_0}$ have no logarithm on $\Omega$.
|
||||
|
||||
This shows $(3)\implies (1)$.
|
||||
|
||||
Suppose $\Omega$ is simply connected.$f\in O(\Omega)$ and $f$ is non-vanishing. We want to show that $f$ has a logarithm on $\Omega$.
|
||||
|
||||
Let $z_0\in \Omega$ be fixed. And $a\in \log f(z_0)$.
|
||||
|
||||
$\frac{f'(z)}{f(z)}=g'$ Since $g\in O(\Omega)$, $we can assume $g(z_0)=a$.
|
||||
|
||||
$g(z)=a+\int_{z_0}^{z} g'(w) \, dw$
|
||||
|
||||
So
|
||||
|
||||
$$
|
||||
(fe^{-g})'=f'e^g+fe^g g'=f(e^g)'=0
|
||||
$$
|
||||
|
||||
So $fe^{-g}=c$ for some $c\in \mathbb{C}$.
|
||||
|
||||
So $f=ce^g$
|
||||
|
||||
QED
|
||||
|
||||
Continue on Residue Theorem on Thursday.
|
||||
@@ -1,148 +0,0 @@
|
||||
# Math416 Lecture 25
|
||||
|
||||
## Continue on Residue Theorem
|
||||
|
||||
### Review the definition of simply connected domain
|
||||
|
||||
A domain $\Omega$ is called simply connected if $\overline{C}\setminus \Omega$ is connected if and only if every closed curve in $\Omega$ is null-homotopic in $\Omega$.
|
||||
|
||||
Proof:
|
||||
|
||||
Last time we proved $\impliedby$ part.
|
||||
|
||||
If every closed curve in $\Omega$ is null-homotopic in $\Omega$, then $\operatorname{ind}_\Gamma(z)=0$ for all $z\in\mathbb{C}\setminus\Omega$ for all contour in $\Omega$.
|
||||
|
||||
$\implies$ $\mathbb{C}\setminus\Omega$ is connected.
|
||||
|
||||
$\impliedby$ part:
|
||||
|
||||
....
|
||||
|
||||
#### Theorem 10.4-6
|
||||
|
||||
The following condition are equivalent:
|
||||
|
||||
1. $\Omega$ is simply connected.
|
||||
2. every holomorphic function on $\Omega$ has a primitive $g$, i.e. $g'(z)=f(z)$ for all $z\in \Omega$.
|
||||
3. every non-vanishing holomorphic function on $\Omega$ has a holomorphic logarithm.
|
||||
4. every harmonic function on $\Omega$ has a harmonic conjugate.
|
||||
|
||||
### Residue Theorem
|
||||
|
||||
#### Theorem 10.8 The Residue Theorem
|
||||
|
||||
Let $\Omega$ be a domain, $\Gamma$ be a contour such that $\Gamma\cup \operatorname{int}(\Gamma)\subset \Omega$
|
||||
|
||||
Let $f$ be holomorphic on $\Omega\setminus \{z_1, z_2, \cdots, z_n\}$ where $z_1, z_2, \cdots, z_n$ are finitely many points in $\Omega$, where $z_1, z_2, \cdots, z_n\notin \Gamma$.
|
||||
|
||||
Then
|
||||
|
||||
$$
|
||||
\int_\Gamma f(z) dz = 2\pi i \sum_{j=1}^n\operatorname{ind}_{\Gamma}(z_j) \operatorname{res}_{z_j}(f)
|
||||
$$
|
||||
|
||||
Proof:
|
||||
|
||||
For each $i\leq j\leq n$, let $C_j$ be a circle centered at $z_j\in \Gamma\setminus \Omega$ such that $\operatorname{int}(C_j)\subset \Omega$, counterclockwise and pairwise disjoint.
|
||||
|
||||
Let $\Gamma_1=\Gamma\setminus\{z_1, z_2, \cdots, z_n\}$, $\Gamma_1=\Gamma-\sum_{j=1}^n \operatorname{ind}_{\Gamma}(z_j)C_j$ (This excludes the singularities outside $\Gamma$)
|
||||
|
||||
$f\in O(\Omega_1)$, $\Gamma_1\in \Omega_1$
|
||||
|
||||
and $\operatorname{ind}_{\Gamma_1}(z)=0$ for all $z\in \mathbb{C}\setminus \Omega_1$, either $z\notin \Gamma$ or $z\in\{z_1, z_2, \cdots, z_n\}$.
|
||||
|
||||
$\operatorname{ind}_{\Gamma_1}(z_j)=\operatorname{ind}_{\Gamma}(z_j)-1\cdot\operatorname{ind}_{C_j}(z_j)=0$ for all $j=1, 2, \cdots, n$.
|
||||
|
||||
By Cauchy's theorem, $\int_{\Gamma_1}f(z)dz=0$.
|
||||
|
||||
So, since $f(z)=\sum_{k=-\infty}^\infty a_k(z-z_0)^k$, and $\gamma(t)=z_k+Re^{it}$ for $t\in[0, 2\pi]$,$\gamma'(t)=iRe^{it}$,
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\int_\Gamma f(z)dz&=\int_{\Gamma_1}f(z)dz+\sum_{j=1}^n\int_{C_j}f(z)dz\\
|
||||
&=0+\sum_{j=1}^n \operatorname{ind}_{\Gamma}(z_j) \int_{C_j}f(z)dz\\
|
||||
&=0+\sum_{j=1}^n \operatorname{ind}_{\Gamma}(z_j) \int_{0}^{2\pi}f(z_j+Re^{it})ie^{i\theta}dt\\
|
||||
&=0+\sum_{j=1}^n \operatorname{ind}_{\Gamma}(z_j) \int_{0}^{2\pi}\left(\sum_{k=-\infty}^\infty a_k (z_j-z_0)^k e^{int}\right) iRe^{i\theta}dt\\
|
||||
&=0+\sum_{j=1}^n \operatorname{ind}_{\Gamma}(z_j) i\sum_{k=-\infty}^\infty a_k R^{k+1}\left(\int_{0}^{2\pi} e^{i(k+1)t}dt\right)\\
|
||||
&=\sum_{j=1}^n 2\pi i \operatorname{ind}_{\Gamma}(z_j) \operatorname{res}_{z_j}(f)\\
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
QED
|
||||
|
||||
#### Corollary 10.9 Cauchy's Integral Formula
|
||||
|
||||
If $\Gamma$ is a simple contour, $z_0\in \operatorname{int}(\Gamma)$, $g\in O(\Omega)$, then
|
||||
|
||||
$$
|
||||
g(z_0)=\frac{1}{2\pi i}\int_\Gamma \frac{g(z)}{z-z_0}dz
|
||||
$$
|
||||
|
||||
Proof:
|
||||
|
||||
The right hand side is the residue of $g(z)/(z-z_0)$ at $z_0$.
|
||||
|
||||
By the residue theorem,
|
||||
|
||||
Notice that $g(z)=a_0+a_1(z-z_0)+a_2(z-z_0)^2+\cdots$, and $\frac{1}{z-z_0}=a_0\sum_{k=0}^\infty (z-z_0)^k$.
|
||||
|
||||
So $a_0=g(z_0)$, and $a_k=\frac{g^{(k)}(z_0)}{k!}$ for $k\geq 1$.
|
||||
|
||||
$$
|
||||
\int_\Gamma \frac{g(z)}{z-z_0}dz=2\pi i \operatorname{res}_{z_0}\left(\frac{g(z)}{z-z_0}\right)=2\pi i g(z_0)
|
||||
$$
|
||||
|
||||
QED
|
||||
|
||||
## Application to evaluating definite integrals
|
||||
|
||||
Idea:
|
||||
|
||||
It is easy to evaluate intervals around closed contours.
|
||||
|
||||
Choose contour so one side (where you want to integrate).
|
||||
|
||||
Handle the other side by:
|
||||
|
||||
- Symmetry
|
||||
- length * supremum of absolute value of integrand
|
||||
- Bound function by another function whose integral goes to zero.
|
||||
|
||||
Example:
|
||||
|
||||
Evaluate $\int_0^\infty \frac{\sin x}{x}dx$.
|
||||
|
||||
On the contour $\gamma(t)$ be the semicircle in the upper half plane removed the origin.
|
||||
|
||||
Then let $f(z)=\frac{e^{iz}}{z}=\frac{\cos z+i\sin z}{z}$, by the Cauchy's theorem,
|
||||
|
||||
$$
|
||||
\int_\gamma f(z)dz=0
|
||||
$$
|
||||
|
||||
So $\frac{\sin z}{z}=0$ on $\gamma$.
|
||||
|
||||
If $x\in \mathbb{R}$, $f(x)=\frac{e^{ix}}{x}=\frac{\cos x+i\sin x}{x}$.
|
||||
|
||||
On the real axis,
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\int_{-R}^{-\epsilon}+\int_\epsilon^R f(x)dx&=\int_{-R}^{-\epsilon}\frac{e^{ix}}{x}dx+\int_\epsilon^R \frac{e^{ix}}{x}dx\\
|
||||
&=\int_{-R}^{-\epsilon}\frac{\cos x+i\sin x}{x}dx+\int_\epsilon^R \frac{\cos x+i\sin x}{x}dx\\
|
||||
&=\int_{-R}^{-\epsilon}\frac{\cos x}{x}dx+i\int_{-R}^{-\epsilon}\frac{\sin x}{x}dx+\int_\epsilon^R \frac{\cos x}{x}dx+i\int_\epsilon^R \frac{\sin x}{x}dx\\
|
||||
&=2i\int_0^\infty \frac{\sin x}{x}dx
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
For the clockwise semi-circle around the origin,
|
||||
|
||||
$$
|
||||
\int_{S_\epsilon} f(z)dz=\int_{S_\epsilon}\frac{e^{iz}}{z}dz
|
||||
$$
|
||||
|
||||
let $\gamma(t)=\epsilon e^{-it}$, $t\in[-\pi,0]$.
|
||||
|
||||
Then $\gamma'(t)=-i\epsilon e^{-it}$,
|
||||
|
||||
CONTINUE NEXT TIME.
|
||||
@@ -1,148 +0,0 @@
|
||||
# Math416 Lecture 26
|
||||
|
||||
## Continue on Application to evaluating definite integrals
|
||||
|
||||
Note: Contour can never go through a singularity.
|
||||
|
||||
Recall the semi annulus contour.
|
||||
|
||||
Know that $\int_\gamma f(z)dz=0$.
|
||||
|
||||
So $\int_A+\int_B+\int_C+\int_D=0$.
|
||||
|
||||
From last lecture, we know that $\int_D=0$ and $\int_A+\int_C=2i\int_0^\infty \frac{\sin x}{x}dx$.
|
||||
|
||||
### Integrating over $B$
|
||||
|
||||
Do $B$, we have $\gamma(t)=\epsilon e^{it}$ for $t\in[0,\pi]$.
|
||||
|
||||
$\int_B=-\int_0^\pi f(\epsilon e^{it})\epsilon i e^{it}dt$.
|
||||
|
||||
$f(z)=\frac{e^{iz}}{z}=\frac{1}{z}(1+iz-\frac{z^2}{2!}+\cdots)$.
|
||||
|
||||
So $z f(z)=1+O(\epsilon)$ and $f(z)=\frac{1}{z}+O(\frac{\epsilon}{z})$.
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\int_B&=-\int_0^\pi (\frac{1}{\epsilon}e^{it}+O(1))\epsilon i e^{it}dt\\
|
||||
&=-i\int_0^\pi 1dt+O(\epsilon)\\
|
||||
&=-i\pi+O(\epsilon)
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
### Integrating over $D$
|
||||
|
||||
#### Method 1: Using estimate
|
||||
|
||||
$z=Re^{it}$ for $t\in[0,\pi]$.
|
||||
|
||||
$f(z)=\frac{e^{iz}}{z}=\frac{e^{iRe^{it}}}{Re^{it}}$.
|
||||
|
||||
$Re^{it}=R(\cos t+i\sin t)$, $iRe^{it}=-R(\sin t-i\cos t)$.
|
||||
|
||||
$e^{iRe^{it}}=e^{-R\sin t}e^{iR\cos t}$.
|
||||
|
||||
$\max|f(z)|=\max\frac{|e^{iR\cos t}|}{|R e^{it}|}=\frac{1}{R}$.
|
||||
|
||||
This only bounds the function $|\int_D|\leq \pi R\frac{1}{R}=\pi$.
|
||||
|
||||
This is not a good estimate.
|
||||
|
||||
#### Method 2: Hard core integration
|
||||
|
||||
$\gamma(t)=Re^{it}$ for $t\in[0,\pi]$.
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\int_D&=\int_0^\pi \frac{e^{iRe^{it}}}{R e^{it}}iR e^{it}dt\\
|
||||
&=i\int_0^\pi e^{iR\cos t}e^{-R\sin t}dt\\
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Notice that we can use $\frac{2}{\pi}t$ to replace $\sin t$.
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\left|\int_D\right|&\leq\int_0^\pi e^{-R\sin t}dt\\
|
||||
&=2\int_0^{\pi/2} e^{-R\sin t}dt\\
|
||||
&\leq 2\int_0^{\pi/2} e^{-2Rt/\pi}dt\\
|
||||
&=-\frac{2\pi}{R}(e^{-\frac{R\pi}{2}t})|_0^{\pi/2}\\
|
||||
&\leq\frac{\pi}{R}
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
As $R\to\infty$, $\left|\int_D\right|\to 0$.
|
||||
|
||||
So $\int_D=0$.
|
||||
|
||||
So we have $\int_A+\int_C=2i\int_0^\infty \frac{\sin x}{x}dx=i\pi$.
|
||||
|
||||
So $\int_0^\infty \frac{\sin x}{x}dx=\frac{\pi}{2}$.
|
||||
|
||||
## Application to evaluate $\int_{-\infty}^\infty \frac{\cos x}{1+x^4}dx$
|
||||
|
||||
$f(z)=\frac{e^{iz}}{1+z^4}=\frac{\cos z+i\sin z}{1+z^4}$.
|
||||
|
||||
Our desired integral can be evaluated by $\int_{-R}^R f(z)dz$
|
||||
|
||||
To evaluate the singularity, $z^4=-1$ has four roots by the De Moivre's theorem.
|
||||
|
||||
$z^4=-1=e^{i\pi+2k\pi i}$ for $k=0,1,2,3$.
|
||||
|
||||
So $z=e^{i\theta}$ for $\theta=\frac{\pi}{4}+\frac{k\pi}{2}$ for $k=0,1,2,3$.
|
||||
|
||||
So the singularities are $z=e^{i\pi/4},e^{i3\pi/4},e^{i5\pi/4},e^{i7\pi/4}$.
|
||||
|
||||
Only $z=e^{i\pi/4},e^{i3\pi/4}$ are in the upper half plane.
|
||||
|
||||
So we can use the semi-circle contour to evaluate the integral. Name the path as $\gamma$.
|
||||
|
||||
$\int_\gamma f(z)dz=2\pi i\left[\operatorname{Res}_{z=e^{i\pi/4}}(f)+\operatorname{Res}_{z=e^{i3\pi/4}}(f)\right]$.
|
||||
|
||||
The two poles are simple poles.
|
||||
|
||||
$\operatorname{Res}_{z_0}(f)=\lim_{z\to z_0}(z-z_0)f(z)$.
|
||||
|
||||
So
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\operatorname{Res}_{z=e^{i\pi/4}}(f)&=\lim_{z\to e^{i\pi/4}}(z-e^{i\pi/4})\frac{e^{iz}}{1+z^4}\\
|
||||
&=\frac{(z-e^{i\pi/4})e^{iz}}{(z-e^{i\pi/4})(z-e^{i3\pi/4})(z-e^{i5\pi/4})(z-e^{i7\pi/4})}\\
|
||||
&=\frac{e^{ie^{i\pi/4}}}{(e^{i\pi/4}-e^{i3\pi/4})(e^{i\pi/4}-e^{i5\pi/4})(e^{i\pi/4}-e^{i7\pi/4})}
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
A short cut goes as follows:
|
||||
|
||||
We know $p(z)=1+z^4$ has four roots $z_1,z_2,z_3,z_4$.
|
||||
|
||||
$$
|
||||
\lim_{z\to z_0}\frac{(z-z_0)}{p(z)}=\frac{1}{p'(z_0)}
|
||||
$$
|
||||
|
||||
So
|
||||
|
||||
$$
|
||||
\operatorname{Res}_{z=e^{i\pi/4}}(f)=\frac{e^{ie^{i\pi/4}}}{4e^{i3\pi/4}}
|
||||
$$
|
||||
|
||||
Similarly,
|
||||
|
||||
$$
|
||||
\operatorname{Res}_{z=e^{i3\pi/4}}(f)=\frac{e^{ie^{i3\pi/4}}}{4e^{i\pi/4}}
|
||||
$$
|
||||
|
||||
So the sum of the residues is
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\operatorname{Res}_{z=e^{i\pi/4}}(f)+\operatorname{Res}_{z=e^{i3\pi/4}}(f)&=\frac{e^{ie^{i\pi/4}}}{4e^{i3\pi/4}}+\frac{e^{ie^{i3\pi/4}}}{4e^{i\pi/4}}\\
|
||||
&=\frac{e^{\frac{i}{\sqrt{2}}} e^{-\frac{1}{\sqrt{2}}}}{4[-\frac{1}{\sqrt{2}}+i\frac{1}{\sqrt{2}}]}+\frac{e^{-\frac{i}{\sqrt{2}}}-e^{-\frac{1}{\sqrt{2}}}}{4[\frac{1}{\sqrt{2}}+i\frac{1}{\sqrt{2}}]}\\
|
||||
&=\frac{\pi\sqrt{2}}{2}e^{-\frac{1}{\sqrt{2}}}(\cos\frac{1}{\sqrt{2}}+\sin\frac{1}{\sqrt{2}})
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
SKIP
|
||||
|
||||
Review on next lecture.
|
||||
@@ -1,195 +0,0 @@
|
||||
# Math416 Lecture 27
|
||||
|
||||
## Continue on Application to evaluate $\int_{-\infty}^\infty \frac{\cos x}{1+x^4}dx$
|
||||
|
||||
Consider the function$f(z)=\frac{e^{iz}}{1+z^4}=\frac{\cos z+i\sin z}{1+z^4}$.
|
||||
|
||||
Our desired integral can be evaluated by $\int_{-R}^R f(z)dz$
|
||||
|
||||
To evaluate the singularity, $z^4=-1$ has four roots by the De Moivre's theorem.
|
||||
|
||||
$z^4=-1=e^{i\pi+2k\pi i}$ for $k=0,1,2,3$.
|
||||
|
||||
So $z=e^{i\theta}$ for $\theta=\frac{\pi}{4}+\frac{k\pi}{2}$ for $k=0,1,2,3$.
|
||||
|
||||
So the singularities are $z=e^{i\pi/4},e^{i3\pi/4},e^{i5\pi/4},e^{i7\pi/4}$.
|
||||
|
||||
Only $z=e^{i\pi/4},e^{i3\pi/4}$ are in the upper half plane.
|
||||
|
||||
So we can use the semi-circle contour to evaluate the integral. Name the path as $\gamma$.
|
||||
|
||||
$\int_\gamma f(z)dz=2\pi i\left[\operatorname{Res}_{z=e^{i\pi/4}}(f)+\operatorname{Res}_{z=e^{i3\pi/4}}(f)\right]$.
|
||||
|
||||
The two poles are simple poles.
|
||||
|
||||
$\operatorname{Res}_{z_0}(f)=\lim_{z\to z_0}(z-z_0)f(z)$.
|
||||
|
||||
So
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\operatorname{Res}_{z=e^{i\pi/4}}(f)&=\lim_{z\to e^{i\pi/4}}(z-e^{i\pi/4})\frac{e^{iz}}{1+z^4}\\
|
||||
&=\frac{(z-e^{i\pi/4})e^{iz}}{(z-e^{i\pi/4})(z-e^{i3\pi/4})(z-e^{i5\pi/4})(z-e^{i7\pi/4})}\\
|
||||
&=\frac{e^{ie^{i\pi/4}}}{(e^{i\pi/4}-e^{i3\pi/4})(e^{i\pi/4}-e^{i5\pi/4})(e^{i\pi/4}-e^{i7\pi/4})}
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
A short cut goes as follows:
|
||||
|
||||
We know $p(z)=1+z^4$ has four roots $z_1,z_2,z_3,z_4$.
|
||||
|
||||
$$
|
||||
\lim_{z\to z_0}\frac{(z-z_0)}{p(z)}=\frac{1}{p'(z_0)}
|
||||
$$
|
||||
|
||||
So
|
||||
|
||||
$$
|
||||
\operatorname{Res}_{z=e^{i\pi/4}}(f)=\frac{e^{ie^{i\pi/4}}}{4e^{i3\pi/4}}
|
||||
$$
|
||||
|
||||
Similarly,
|
||||
|
||||
$$
|
||||
\operatorname{Res}_{z=e^{i3\pi/4}}(f)=\frac{e^{ie^{i3\pi/4}}}{4e^{i\pi/4}}
|
||||
$$
|
||||
|
||||
So the sum of the residues is
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\operatorname{Res}_{z=e^{i\pi/4}}(f)+\operatorname{Res}_{z=e^{i3\pi/4}}(f)&=\frac{e^{ie^{i\pi/4}}}{4e^{i3\pi/4}}+\frac{e^{ie^{i3\pi/4}}}{4e^{i\pi/4}}\\
|
||||
&=\frac{e^{\frac{i}{\sqrt{2}}} e^{-\frac{1}{\sqrt{2}}}}{4[-\frac{1}{\sqrt{2}}+i\frac{1}{\sqrt{2}}]}+\frac{e^{-\frac{i}{\sqrt{2}}}-e^{-\frac{1}{\sqrt{2}}}}{4[\frac{1}{\sqrt{2}}+i\frac{1}{\sqrt{2}}]}\\
|
||||
&=\frac{\pi\sqrt{2}}{2}e^{-\frac{1}{\sqrt{2}}}(\cos\frac{1}{\sqrt{2}}+\sin\frac{1}{\sqrt{2}})
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
For the semicircle part, we can bound our estimate by
|
||||
|
||||
$$
|
||||
\left|\int_{C_R}f(z)dz\right|\leq\pi R\max_{z\in C_R}|f(z)|\leq \pi \frac{1}{R^4}\to 0
|
||||
$$
|
||||
|
||||
as $R\to\infty$.
|
||||
|
||||
So
|
||||
|
||||
$$
|
||||
\int_{-\infty}^\infty\frac{\cos x}{1+x^4}dx=\frac{\pi\sqrt{2}}{2}e^{-\frac{1}{\sqrt{2}}}(\cos\frac{1}{\sqrt{2}}+\sin\frac{1}{\sqrt{2}})
|
||||
$$
|
||||
|
||||
## Big idea of this course
|
||||
|
||||
$f$ is holomorphic $\iff$ $f$ has complex derivative.
|
||||
|
||||
$f$ is holomorphic $\iff$ $f$ satisfies Cauchy-Riemann equations $\frac{\partial u}{\partial x}=\frac{\partial v}{\partial y}$ and $\frac{\partial u}{\partial y}=-\frac{\partial v}{\partial x}$
|
||||
|
||||
$f$ is holomorphic $\iff$ $f$ is analytic (is locally given by power series). The power series is integrable/differentiable term by term in the radius of convergence.
|
||||
|
||||
### Laurent series
|
||||
|
||||
Similar to power series both with annulus of convergence.
|
||||
|
||||
$f(z)=\sum_{n=-\infty}^\infty a_n(z-z_0)^n$ for $z\in A(z_0,r,R)$.
|
||||
|
||||
Identity theorem: If $f$ is holomorphic on a domain $\Omega$, it is uniquely determined by its values on any sets with a limit point in $\Omega$.
|
||||
|
||||
### Cauchy's Theorem
|
||||
|
||||
$$
|
||||
\int_\gamma f(z)dz=0
|
||||
$$
|
||||
|
||||
If $f$ is holomorphic on $\Omega$ and $\gamma$ is a closed path in $\Omega$ and $\gamma\cup \operatorname{int}\gamma\subset \Omega$, then $\int_\gamma f(z)dz=0$.
|
||||
|
||||
### Favorite estimate
|
||||
|
||||
$$
|
||||
\left|\int_\gamma f(z)dz\right|\leq \sup_{z\in\gamma}|f(z)|\cdot \operatorname{length}(\gamma)
|
||||
$$
|
||||
|
||||
### Cauchy's Integral Formula
|
||||
|
||||
$$
|
||||
f(z_0)=\frac{1}{2\pi i}\int_\gamma \frac{f(z)}{z-z_0}dz
|
||||
$$
|
||||
|
||||
where $z_0\in \operatorname{int}\gamma$ and $\gamma$ is a closed path.
|
||||
|
||||
Extension: If $f$ is holomorphic on $\Omega$ and $z_0\in \Omega$, then $f$ is infinitely differentiable and
|
||||
|
||||
$$
|
||||
f^{(n)}(z_0)=\frac{n!}{2\pi i}\int_\gamma \frac{f(z)}{(z-z_0)^{n+1}}dz
|
||||
$$
|
||||
|
||||
### Residue theorem
|
||||
|
||||
If $f$ is holomorphic on $\Omega$ except for a finite number of isolated singularities $z_1,z_2,\dots,z_p$, and $\Gamma$ is a curve inside $\Omega$ that don't pass through any of the singularities ($\Gamma\subset \Omega\setminus \{z_1,z_2,\dots,z_p\}$), then
|
||||
|
||||
$$
|
||||
\int_\Gamma f(z)dz=2\pi i\sum_{z_i}\operatorname{ind}_{\Gamma}(z_i) \operatorname{res}_{z_i}(f)
|
||||
$$
|
||||
|
||||
### Harmonic conjugate
|
||||
|
||||
Locally, always have harmonic conjugates.
|
||||
|
||||
Globally can do this iff domain is simply connected.
|
||||
|
||||
### Schwarz-pick's Lemma:
|
||||
|
||||
If $f$ maps $D$ to $D$ and $f(0)=0$, then $|f(z)|\leq |z|$ for all $z\in D$. and $|f'(0)|\leq 1$.
|
||||
|
||||
For mobius map, $f:D\to D$ holds, $\varphi(f(z),f(w))=\varphi(z,w)$ for all $z,w\in D$.
|
||||
|
||||
$$
|
||||
\varphi(z,w)=\frac{z-w}{1-\overline{w}z}
|
||||
$$
|
||||
|
||||
### Convergence
|
||||
|
||||
#### Types of convergence
|
||||
|
||||
**Converge pointwise** (Not very strong):
|
||||
|
||||
$\forall x\in X, \lim_{n\to\infty}f_n(x)=f(x)$.
|
||||
|
||||
Or, $\forall x\in X, \forall \epsilon>0, \exists N>0, \forall n\geq N \implies |f_n(x)-f(x)|<\epsilon$.
|
||||
|
||||
**Converge uniformly** (Much better):
|
||||
|
||||
$\forall \epsilon>0, \exists N>0, \forall n\geq N \implies \forall x\in X, |f_n(x)-f(x)|<\epsilon$.
|
||||
|
||||
**Converge locally uniformly** (Strong):
|
||||
|
||||
$\forall x\in X$, $\exists$ open $x\in U$, such that $f_n\to f$ uniformly on $U$.
|
||||
|
||||
**Converge uniformly on compact subsets** (Good enough for local properties):
|
||||
|
||||
$\forall$ compact $K\subset X$, $f_n\to f$ uniformly on $K$.
|
||||
|
||||
#### Weierstrass' Theorem
|
||||
|
||||
If $f_n\in O(\Omega)$ and $f_n\to f$ locally uniformly, then $f\in O(\Omega)$.
|
||||
|
||||
#### Cauchy-Hadamard's Theorem
|
||||
|
||||
For a power series, $\sum_{n=0}^\infty a_n(z-z_0)^n$, the radius of convergence is
|
||||
|
||||
$$
|
||||
R=\frac{1}{\limsup_{n\to\infty}|a_n|^{1/n}}
|
||||
$$
|
||||
|
||||
On $B(z_0,R)$, the series converges locally uniformly and absolutely.
|
||||
|
||||
## Argument and Logarithm
|
||||
|
||||
$\arg z$ is any $\theta$ such that $z=re^{i\theta}$.
|
||||
|
||||
$\operatorname{Arg} z$ is the principal value of the argument, $-\pi<\operatorname{Arg} z\leq \pi$.
|
||||
|
||||
$\log z$ is the principal value of the logarithm, $\log z=\ln |z|+i\arg z$.
|
||||
|
||||
$\operatorname{Log} z$ is the set of all logarithms of $z$, $\operatorname{Log} z=\{\log z+2k\pi i: k\in\mathbb{Z}\}$.
|
||||
|
||||
END
|
||||
@@ -1,188 +0,0 @@
|
||||
# Math416 Lecture 3
|
||||
|
||||
## Differentiation of functions in complex variables
|
||||
|
||||
### Differentiability
|
||||
|
||||
#### Definition 2.1 of differentiability in complex variables
|
||||
|
||||
**Suppose $G$ is an open subset of $\mathbb{C}$**. (very important, $f'(z_0)$ cannot be define unless $z_0$ belongs to an open set in which $f$ is defined.)
|
||||
|
||||
A function $f:G\to \mathbb{C}$ is differentiable at $z_0\in G$ if
|
||||
|
||||
$$
|
||||
f'(z_0)=\lim_{z\to z_0}\frac{f(z)-f(z_0)}{z-z_0}
|
||||
$$
|
||||
|
||||
exists.
|
||||
|
||||
Or equivalently,
|
||||
|
||||
We can also express the $f$ as $f=u+iv$, where $u,v:G\to \mathbb{R}$ are real-valued functions.
|
||||
|
||||
Recall that $u:G\to \mathbb{R}$ is differentiable at $z_0\in G$ if and only if there exists a complex number $(x,y)\in \mathbb{C}$ such that a function
|
||||
|
||||
$$
|
||||
R(x,y)=u(x,y)-\left(u(x_0,y_0)+\frac{\partial u}{\partial x}(x_0,y_0)(x-x_0)+\frac{\partial u}{\partial y}(x_0,y_0)(y-y_0)\right)
|
||||
$$
|
||||
|
||||
satisfies
|
||||
|
||||
$$
|
||||
\lim_{(x,y)\to (x_0,y_0)}\frac{|R(x,y)|}{|(x,y)-(x_0,y_0)|}=\lim_{(x,y)\to (x_0,y_0)}\frac{|R(x,y)|}{\sqrt{(x-x_0)^2+(y-y_0)^2}}=0.
|
||||
$$
|
||||
|
||||
_$R(x,y)$ is the immediate result of mean value theorem applied to $u$ at $(x_0,y_0)$_.
|
||||
|
||||
> Theorem from 4111?
|
||||
>
|
||||
> If $u$ is differentiable at $(x_0,y_0)$, then $\frac{\partial u}{\partial x}(x_0,y_0)$ and $\frac{\partial u}{\partial y}(x_0,y_0)$ exist.
|
||||
>
|
||||
> If $\frac{\partial u}{\partial x}(x_0,y_0)$ and $\frac{\partial u}{\partial y}(x_0,y_0)$ exist and one of them is continuous at $(x_0,y_0)$, then $u$ is differentiable at $(x_0,y_0)$.
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\lim_{(x,y)\to (x_0,y_0)}\frac{|R(x,y)|}{|(x,y)-(x_0,y_0)|}&=\lim_{(x,y)\to (x_0,y_0)}\frac{|u(x,y)-u(x_0,y_0)-\frac{\partial u}{\partial x}(x_0,y_0)(x-x_0)-\frac{\partial u}{\partial y}(x_0,y_0)(y-y_0)|}{\sqrt{(x-x_0)^2+(y-y_0)^2}}\\
|
||||
&=\lim_{(x,y)\to (x_0,y_0)}\frac{|u(x,y)-u(x_0,y_0)-\frac{\partial u}{\partial x}(x_0,y_0)(x-x_0)-\frac{\partial u}{\partial y}(x_0,y_0)(y-y_0)|}{\sqrt{(x-x_0)^2+(y-y_0)^2}}\\
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Let $a(x,y)=\frac{\partial u}{\partial x}(x,y)$ and $b(x,y)=\frac{\partial u}{\partial y}(x,y)$.
|
||||
|
||||
We can write $R(x,y)$ as
|
||||
|
||||
$$
|
||||
R(x,y)=u(x,y)-u(x_0,y_0)-a(x,y)(x-x_0)-b(x,y)(y-y_0).
|
||||
$$
|
||||
|
||||
So $\lim_{(x,y)\to (x_0,y_0)}\frac{|R(x,y)|}{\sqrt{(x-x_0)^2+(y-y_0)^2}}=0$ if and only if $\lim_{(x,y)\to (x_0,y_0)}\frac{a(x-x_0)}{\sqrt{(x-x_0)^2+(y-y_0)^2}}=0$ and $\lim_{(x,y)\to (x_0,y_0)}\frac{b(y-y_0)}{\sqrt{(x-x_0)^2+(y-y_0)^2}}=0$.
|
||||
|
||||
On the imaginary part, we proceed similarly. Define
|
||||
$$
|
||||
S(x,y)=v(x,y)-v(x_0,y_0)-\frac{\partial v}{\partial x}(x_0,y_0)(x-x_0)-\frac{\partial v}{\partial y}(x_0,y_0)(y-y_0).
|
||||
$$
|
||||
Then the differentiability of $v$ at $(x_0,y_0)$ guarantees that
|
||||
$$
|
||||
\lim_{(x,y)\to (x_0,y_0)}\frac{|S(x,y)|}{\sqrt{(x-x_0)^2+(y-y_0)^2}}=0.
|
||||
$$
|
||||
Moreover, considering the definition of the complex derivative of $f=u+iv$, if we approach $z_0=x_0+iy_0$ along different directions we obtain
|
||||
$$
|
||||
f'(z_0)=\frac{\partial u}{\partial x}(x_0,y_0)+i\frac{\partial v}{\partial x}(x_0,y_0)
|
||||
=\frac{\partial v}{\partial y}(x_0,y_0)-i\frac{\partial u}{\partial y}(x_0,y_0).
|
||||
$$
|
||||
Equating the real and imaginary parts of these two expressions forces
|
||||
$$
|
||||
\frac{\partial u}{\partial x}(x_0,y_0)=\frac{\partial v}{\partial y}(x_0,y_0),\quad \frac{\partial u}{\partial y}(x_0,y_0)=-\frac{\partial v}{\partial x}(x_0,y_0).
|
||||
$$
|
||||
|
||||
#### Theorem 2.6 (The Cauchy-Riemann equations):
|
||||
|
||||
If $f=u+iv$ is complex differentiable at $z_0\in G$, then $u$ and $v$ are real differentiable at $(x_0,y_0)$ and
|
||||
|
||||
$$
|
||||
\frac{\partial u}{\partial x}(x_0,y_0)=\frac{\partial v}{\partial y}(x_0,y_0),\quad \frac{\partial u}{\partial y}(x_0,y_0)=-\frac{\partial v}{\partial x}(x_0,y_0).
|
||||
$$
|
||||
|
||||
> Some missing details:
|
||||
>
|
||||
> The Cauchy-Riemann equations are necessary and sufficient for the differentiability of $f$ at $z_0$.
|
||||
>
|
||||
> This states that a function $f$ is **complex differentiable** at $z_0$ if and only if $u$ and $v$ are real differentiable at $(x_0,y_0)$ and the Cauchy-Riemann equations hold at $(x_0,y_0)$. That is $f'(z_0)=\frac{\partial u}{\partial x}(x_0,y_0)+i\frac{\partial v}{\partial x}(x_0,y_0)=\frac{\partial v}{\partial y}(x_0,y_0)-i\frac{\partial u}{\partial y}(x_0,y_0)$.
|
||||
|
||||
And $u$ and $v$ have continuous partial derivatives at $(x_0,y_0)$.
|
||||
|
||||
And let $c=\frac{\partial u}{\partial x}(x_0,y_0)$ and $d=\frac{\partial v}{\partial x}(x_0,y_0)$.
|
||||
|
||||
**Then $f'(z_0)=c+id$, is holomorphic at $z_0$.**
|
||||
|
||||
### Holomorphic Functions
|
||||
|
||||
#### Definition 2.8 (Holomorphic functions)
|
||||
|
||||
A function $f:G\to \mathbb{C}$ is holomorphic (or analytic) at $z_0\in G$ if it is complex differentiable at $z_0$.
|
||||
|
||||
> Note that the true definition of analytic function is that can be written as a convergent power series in a neighborhood of each point in its domain. We will prove that these two definitions are equivalent to each other in later sections.
|
||||
|
||||
Example:
|
||||
|
||||
Suppose $f:G\to \mathbb{C}$ where $f=u+iv$ and $\frac{\partial f}{\partial x}=\frac{\partial u}{\partial x}+i\frac{\partial v}{\partial x}$, $\frac{\partial f}{\partial y}=\frac{\partial u}{\partial y}+i\frac{\partial v}{\partial y}$.
|
||||
|
||||
Define $\frac{\partial}{\partial z}=\frac{1}{2}\left(\frac{\partial}{\partial x}-i\frac{\partial}{\partial y}\right)$ and $\frac{\partial}{\partial \bar{z}}=\frac{1}{2}\left(\frac{\partial}{\partial x}+i\frac{\partial}{\partial y}\right)$.
|
||||
|
||||
Suppose $f$ is holomorphic at $\bar{z}_0\in G$ (Cauchy-Riemann equations hold at $\bar{z}_0$).
|
||||
|
||||
Then $\frac{\partial f}{\partial \bar{z}}(\bar{z}_0)=0$.
|
||||
|
||||
Note that $\forall m\in \mathbb{Z}$, $z^m$ is holomorphic on $\mathbb{C}$.
|
||||
|
||||
i.e. $\forall a\in \mathbb{C}$, $\lim_{z\to a}\frac{z^m-a^m}{z-a}=\frac{(z-a)(z^{m-1}+z^{m-2}a+\cdots+a^{m-1})}{z-a}=ma^{m-1}$.
|
||||
|
||||
So polynomials are holomorphic on $\mathbb{C}$.
|
||||
|
||||
So rational functions $p/q$ are holomorphic on $\mathbb{C}\setminus\{z\in \mathbb{C}:q(z)=0\}$.
|
||||
|
||||
#### Definition 2.9 (Complex partial differential operators)
|
||||
|
||||
Let $f:G\to \mathbb{C}$, $f=u+iv$, be a function defined on an open set $G\subset \mathbb{C}$.
|
||||
|
||||
Define:
|
||||
|
||||
$$
|
||||
\frac{\partial}{\partial x}f=\frac{\partial u}{\partial x}+i\frac{\partial v}{\partial x},\quad \frac{\partial}{\partial y}f=\frac{\partial u}{\partial y}+i\frac{\partial v}{\partial y}.
|
||||
$$
|
||||
|
||||
And
|
||||
|
||||
$$
|
||||
\frac{\partial}{\partial z}f=\frac{1}{2}\left(\frac{\partial}{\partial x}-i\frac{\partial}{\partial y}\right)f,\quad \frac{\partial}{\partial \bar{z}}f=\frac{1}{2}\left(\frac{\partial}{\partial x}+i\frac{\partial}{\partial y}\right)f.
|
||||
$$
|
||||
|
||||
This definition of partial differential operators on complex functions is consistent with the definition of partial differential operators on real functions.
|
||||
|
||||
$$
|
||||
\frac{\partial}{\partial x}f=\frac{\partial}{\partial z}f+\frac{\partial}{\partial \bar{z}}f,\quad \frac{\partial}{\partial y}f=i\left(\frac{\partial}{\partial z}f-\frac{\partial}{\partial \bar{z}}f\right).
|
||||
$$
|
||||
|
||||
### Curves in $\mathbb{C}$
|
||||
|
||||
#### Definition 2.11 (Curves in $\mathbb{C}$)
|
||||
|
||||
A curve $\gamma$ in $G\subset \mathbb{C}$ is a continuous map of an interval $I\in \mathbb{R}$ into $G$. We say $\gamma$ is differentiable if $\forall t_0\in I$, $\gamma'(t_0)=\lim_{t\to t_0}\frac{\gamma(t)-\gamma(t_0)}{t-t_0}$ exists.
|
||||
|
||||
If $\gamma'(t_0)$ is a point in $\mathbb{C}$, then $\gamma'(t_0)$ is called the tangent vector to $\gamma$ at $t_0$.
|
||||
|
||||
#### Definition of regular curves in $\mathbb{C}$
|
||||
|
||||
A curve $\gamma$ is regular if $\gamma'(t)\neq 0$ for all $t\in I$.
|
||||
|
||||
#### Definition of angle between two curves
|
||||
|
||||
Let $\gamma_1,\gamma_2$ be two curves in $G\subset \mathbb{C}$ with $\gamma_1(t_0)=\gamma_2(t_0)=z_0$ for some $t_0\in I_1\cap I_2$.
|
||||
|
||||
The angle between $\gamma_1$ and $\gamma_2$ at $z_0$ is the angle between the vectors $\gamma_1'(t_0)$ and $\gamma_2'(t_0)$. Denote as $\arg(\gamma_2'(t_0))-\arg(\gamma_1'(t_0))=\arg(\gamma_2'(t_0)\gamma_1'(t_0))$.
|
||||
|
||||
#### Theorem 2.12 of conformality
|
||||
|
||||
Suppose $f:G\to \mathbb{C}$ is holomorphic function on open set $G\subset \mathbb{C}$ and $\gamma_1,\gamma_2$ are regular curves in $G$ with $\gamma_1(t_0)=\gamma_2(t_0)=z_0$ for some $t_0\in I_1\cap I_2$.
|
||||
|
||||
If $f'(z_0)\neq 0$, then the angle between $\gamma_1$ and $\gamma_2$ at $z_0$ is the same as the angle between the vectors $f'(z_0)\gamma_1'(t_0)$ and $f'(z_0)\gamma_2'(t_0)$.
|
||||
|
||||
#### Lemma of function of a curve and angle
|
||||
|
||||
If $f:G\to \mathbb{C}$ is holomorphic function on open set $G\subset \mathbb{C}$ and $\gamma$ is differentiable curve in $G$ with $\gamma(t_0)=z_0$ for some $t_0\in I$.
|
||||
|
||||
Then,
|
||||
|
||||
$$
|
||||
(f\circ \gamma)'(t_0)=f'(\gamma(t_0))\gamma'(t_0).
|
||||
$$
|
||||
|
||||
If Lemma of function of a curve and angle holds, then the angle between $f\circ \gamma_1$ and $f\circ \gamma_2$ at $z_0$ is
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\arg\left[(f\circ \gamma_2)'(t_2)(f\circ \gamma_1)'(t_1)\right]&=\cdots
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Continue on Thursday. (Applying the chain rules)
|
||||
@@ -1,276 +0,0 @@
|
||||
# Math416 Lecture 4
|
||||
|
||||
## Review
|
||||
|
||||
### Derivative of a complex function
|
||||
|
||||
$$
|
||||
\frac{\partial f}{\partial z}=\frac{1}{2}\left(\frac{\partial f}{\partial x}-\frac{\partial f}{\partial y}\right)
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{\partial f}{\partial \bar{z}}=\frac{1}{2}\left(\frac{\partial f}{\partial x}+\frac{\partial f}{\partial y}\right)
|
||||
$$
|
||||
|
||||
### Angle between two curves
|
||||
|
||||
Let $\gamma_1,\gamma_2$ be two curves in $G\subset \mathbb{C}$ with $\gamma_1(t_0)=\gamma_2(t_0)=z_0$ for some $t_0\in I_1\cap I_2$.
|
||||
|
||||
The angle between $\gamma_1$ and $\gamma_2$ at $z_0$ is the angle between the vectors $\gamma_1'(t_0)$ and $\gamma_2'(t_0)$. Denote as $\arg(\gamma_2'(t_0))-\arg(\gamma_1'(t_0))=\arg(\gamma_2'(t_0)\gamma_1'(t_0))$.
|
||||
|
||||
### Cauchy-Riemann equations
|
||||
|
||||
$$
|
||||
\frac{\partial f}{\partial z}=\frac{1}{2}\left(\frac{\partial f}{\partial x}-\frac{\partial f}{\partial y}\right)
|
||||
$$
|
||||
|
||||
## Continue on last lecture
|
||||
|
||||
### Theorem of conformality
|
||||
|
||||
Suppose $f:G\to \mathbb{C}$ is holomorphic function on open set $G\subset \mathbb{C}$ and $\gamma_1,\gamma_2$ are regular curves in $G$ with $\gamma_1(t_0)=\gamma_2(t_0)=z_0$ for some $t_0\in I_1\cap I_2$.
|
||||
|
||||
If $f'(z_0)\neq 0$, then the angle between $\gamma_1$ and $\gamma_2$ at $z_0$ is the same as the angle between the vectors $f'(z_0)\gamma_1'(t_0)$ and $f'(z_0)\gamma_2'(t_0)$.
|
||||
|
||||
### Lemma of function of a curve and angle
|
||||
|
||||
If $f:G\to \mathbb{C}$ is holomorphic function on open set $G\subset \mathbb{C}$ and $\gamma$ is differentiable curve in $G$ with $\gamma(t_0)=z_0$ for some $t_0\in I$.
|
||||
|
||||
Then,
|
||||
|
||||
$$
|
||||
(f\circ \gamma)'(t_0)=f'(\gamma(t_0))\gamma'(t_0).
|
||||
$$
|
||||
|
||||
> Looks like the chain rule.
|
||||
|
||||
<details>
|
||||
<summary>Proof</summary>
|
||||
|
||||
We want to show that
|
||||
|
||||
$$
|
||||
\lim_{t\to t_0}\frac{(f\circ \gamma)(t)-(f\circ \gamma)(t_0)}{t-t_0}=f'(\gamma(t_0))\gamma'(t_0).
|
||||
$$
|
||||
|
||||
> Notation:
|
||||
>
|
||||
> A function $g(h)$ is $O(h)$ if $\exists C>0$ such that $|g(h)|\leq C|h|$ for all $h$ in a neighborhood of $0$.
|
||||
>
|
||||
> A function $g(h)$ is $o(h)$ if $\lim_{h\to 0}\frac{g(h)}{h}=0$.
|
||||
>
|
||||
> $f$ is differentiable if and only if $f(z+h)=f(z)+f'(z)h+\frac{1}{2}h^2f''(z)+o(h^3)$ as $h\to 0$. (By Taylor expansion)
|
||||
|
||||
Since $f$ is holomorphic at $\gamma(t_0)=z_0$, we have
|
||||
|
||||
$$
|
||||
f(z_0)=f(z_0)+(z-z_0)f'(z_0)+o(z-z_0)
|
||||
$$
|
||||
|
||||
> This result comes from Taylor Expansion of the derivative of the function around the point $z_0$
|
||||
|
||||
and
|
||||
|
||||
$$
|
||||
f(\gamma(t_0))=f(\gamma(t_0))+f'(\gamma(t_0))(\gamma(t)-\gamma(t_0))+o(\gamma(t)-\gamma(t_0))
|
||||
$$
|
||||
|
||||
So,
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\lim_{t\to t_0}\frac{(f\circ \gamma)(t)-(f\circ \gamma)(t_0)}{t-t_0}
|
||||
&=\lim_{t\to t_0}\frac{\left[f(\gamma(t_0))+f'(\gamma(t_0))(\gamma(t)-\gamma(t_0))+o(\gamma(t)-\gamma(t_0))\right]-f(\gamma(t_0))}{t-t_0} \\
|
||||
&=\lim_{t\to t_0}\frac{f'(\gamma(t_0))(\gamma(t)-\gamma(t_0))+o(\gamma(t)-\gamma(t_0))}{t-t_0} \\
|
||||
&=\lim_{t\to t_0}\frac{f'(\gamma(t_0))(\gamma(t)-\gamma(t_0))}{t-t_0} +\lim_{t\to t_0}\frac{o(\gamma(t)-\gamma(t_0))}{t-t_0} \\
|
||||
&=f'(\gamma(t_0))\lim_{t\to t_0}\frac{\gamma(t)-\gamma(t_0)}{t-t_0} +0\\
|
||||
&=f'(\gamma(t_0))\gamma'(t_0)
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
</details>
|
||||
|
||||
#### Definition 2.12 (Conformal function)
|
||||
|
||||
A function $f:G\to \mathbb{C}$ is called conformal if it preserves the angle between two curves.
|
||||
|
||||
#### Theorem 2.13 (Conformal function)
|
||||
|
||||
If $f:G\to \mathbb{C}$ is conformal at $z_0\in G$, then $f$ is holomorphic at $z_0$ and $f'(z_0)\neq 0$.
|
||||
|
||||
Example:
|
||||
|
||||
$$
|
||||
f(z)=z^2
|
||||
$$
|
||||
|
||||
is not conformal at $z=0$ because $f'(0)=0$.
|
||||
|
||||
#### Lemma of conformal function
|
||||
|
||||
Suppose $f$ is real differentiable, let $a=\frac{\partial f}{\partial z}(z_0)$, $b=\frac{\partial f}{\partial \overline{z}}(z_0)$.
|
||||
|
||||
Let $\gamma(t_0)=z_0$. Then $(f\circ \gamma)'(t_0)=a\gamma'(t_0)+b\overline{\gamma'(t_0)}$.
|
||||
|
||||
<details>
|
||||
<summary>Proof</summary>
|
||||
|
||||
$f=u+iv$, $u,v$ are real differentiable.
|
||||
|
||||
$$
|
||||
a=\frac{\partial f}{\partial z}=\frac{1}{2}\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right)+i\frac{1}{2}\left(\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}\right)
|
||||
$$
|
||||
|
||||
$$
|
||||
b=\frac{\partial f}{\partial \overline{z}}=\frac{1}{2}\left(\frac{\partial u}{\partial x}-\frac{\partial v}{\partial y}\right)+i\frac{1}{2}\left(\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}\right)
|
||||
$$
|
||||
|
||||
$$
|
||||
\gamma'(t_0)=\frac{d\alpha}{dt}+i\frac{d\beta}{dt}
|
||||
$$
|
||||
|
||||
$$
|
||||
\overline{\gamma'(t_0)}=\frac{d\beta}{dt}-i\frac{d\alpha}{dt}
|
||||
$$
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
(f\circ \gamma)'(t_0)&=\frac{\partial f}{\partial z}(\gamma(t_0))\gamma'(t_0)+\frac{\partial f}{\partial \overline{z}}(\gamma(t_0))\overline{\gamma'(t_0)} \\
|
||||
&=\left[\frac{1}{2}\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right)+i\frac{1}{2}\left(\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}\right)\right]\left(\frac{d\alpha}{dt}+i\frac{d\beta}{dt}\right)\\
|
||||
&+\left[\frac{1}{2}\left(\frac{\partial u}{\partial x}-\frac{\partial v}{\partial y}\right)+i\frac{1}{2}\left(\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}\right)\right]\left(\frac{d\beta}{dt}-i\frac{d\alpha}{dt}\right) \\
|
||||
&=\left[\frac{1}{2}\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right)\frac{d\alpha}{dt}-\frac{1}{2}\left(\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}\right)\frac{d\beta}{dt}\right]\\
|
||||
&+i\left[\frac{1}{2}\left(\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}\right)\frac{d\alpha}{dt}+\frac{1}{2}\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right)\frac{d\beta}{dt}\right] \\
|
||||
&=\left[a+b\right]\frac{d\alpha}{dt}+i\left[a-b\right]\frac{d\beta}{dt} \\
|
||||
&=\left[u_x+iv_x\right]\frac{d\alpha}{dt}+i\left[v_y-iu_y\right]\frac{d\beta}{dt} \\
|
||||
&=a\gamma'(t_0)+b\overline{\gamma'(t_0)}
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
</details>
|
||||
|
||||
#### Theorem of differentiability
|
||||
|
||||
Let $f:G\to \mathbb{C}$ be a function defined on an open set $G\subset \mathbb{C}$ that is both holomorphic and (real) differentiable, where $f=u+iv$ with $u,v$ real differentiable functions.
|
||||
|
||||
Then, $f$ is conformal at every point $z_0\in G$ if and only if $f$ is holomorphic at $z_0$ and $f'(z_0)\neq 0$.
|
||||
|
||||
<details>
|
||||
<summary>Proof</summary>
|
||||
|
||||
We prove the equivalence in two parts.
|
||||
|
||||
($\implies$) Suppose that $f$ is conformal at $z_0$. By definition, conformality means that $f$ preserves angles (including their orientation) between any two intersecting curves through $z_0$. In the language of real analysis, this requires that the (real) derivative (Jacobian) of $f$ at $z_0$, $Df(z_0)$, acts as a similarity transformation. Any similarity in $\mathbb{R}^2$ can be written as a rotation combined with a scaling; in particular, its matrix representation has the form
|
||||
$$
|
||||
\begin{pmatrix}
|
||||
A & -B \\
|
||||
B & A
|
||||
\end{pmatrix},
|
||||
$$
|
||||
for some real numbers $A$ and $B$. This is exactly the matrix corresponding to multiplication by the complex number $a=A+iB$. Therefore, the Cauchy-Riemann equations must hold at $z_0$, implying that $f$ is holomorphic at $z_0$. Moreover, because the transformation is nondegenerate (preserving angles implies nonzero scaling), we must have $f'(z_0)=a\neq 0$.
|
||||
|
||||
($\impliedby$) Now suppose that $f$ is holomorphic at $z_0$ and $f'(z_0)\neq 0$. Then by the definition of the complex derivative, the first-order (linear) approximation of $f$ near $z_0$ is
|
||||
$$
|
||||
f(z_0+h)=f(z_0)+f'(z_0)h+o(|h|),
|
||||
$$
|
||||
for small $h\in\mathbb{C}$. Multiplication by the nonzero complex number $f'(z_0)$ is exactly a rotation and scaling (i.e., a similarity transformation). Therefore, for any smooth curve $\gamma(t)$ with $\gamma(t_0)=z_0$, we have
|
||||
$$
|
||||
(f\circ\gamma)'(t_0)=f'(z_0)\gamma'(t_0),
|
||||
$$
|
||||
and the angle between any two tangent vectors at $z_0$ is preserved (up to the fixed rotation). Hence, $f$ is conformal at $z_0$.
|
||||
|
||||
For further illustration, consider the special case when $f$ is an affine map.
|
||||
|
||||
Case 1: Suppose
|
||||
$$
|
||||
f(z)=az+b\overline{z}.
|
||||
$$
|
||||
The Wirtinger derivatives of $f$ are
|
||||
$$
|
||||
\frac{\partial f}{\partial z}=a \quad \text{and} \quad \frac{\partial f}{\partial \overline{z}}=b.
|
||||
$$
|
||||
For $f$ to be holomorphic, we require $\frac{\partial f}{\partial \overline{z}}=b=0$. Moreover, to have a nondegenerate (angle-preserving) map, we must have $a\neq 0$. If $b\neq 0$, then the map mixes $z$ and $\overline{z}$, and one can check that the linearization maps the real axis $\mathbb{R}$ into the set $\{(a+b)t\}$, which does not uniformly scale and rotate all directions. Thus, $f$ fails to be conformal when $b\neq 0$.
|
||||
|
||||
Case 2: For a general holomorphic function, the lemma of conformal functions shows that if
|
||||
$$
|
||||
(f\circ \gamma)'(t_0)=f'(z_0)\gamma'(t_0)
|
||||
$$
|
||||
for any differentiable curve $\gamma$ through $z_0$, then the effect of $f$ near $z_0$ is exactly given by multiplication by $f'(z_0)$. Since multiplication by a nonzero complex number is a similarity transformation, $f$ is conformal at $z_0$.
|
||||
|
||||
</details>
|
||||
|
||||
### Harmonic function
|
||||
|
||||
Let $\Omega$ be a domain in $\mathbb{C}$. A function $u:\Omega\to \mathbb{R}$
|
||||
|
||||
> A domain is a connected open set.
|
||||
|
||||
Say $g:\Omega\to \mathbb{R} \text{ or } \mathbb{C}$ is harmonic if it satisfies the Laplace equation
|
||||
|
||||
$$
|
||||
\Delta g=\frac{\partial^2 g}{\partial x^2}+\frac{\partial^2 g}{\partial y^2}=0.
|
||||
$$
|
||||
|
||||
#### Theorem of harmonic conjugate
|
||||
|
||||
Let $f=u+iv$ be holomorphic function on domain $\Omega\subset \mathbb{C}$. Then $u$ and $v$ are harmonic functions on $\Omega$.
|
||||
|
||||
<details>
|
||||
<summary>Proof</summary>
|
||||
|
||||
$$
|
||||
\Delta u=\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}=0.
|
||||
$$
|
||||
|
||||
Using the Cauchy-Riemann equations, we have
|
||||
|
||||
$$
|
||||
\frac{\partial^2 u}{\partial x^2}=\frac{\partial^2 v}{\partial x\partial y}, \quad \frac{\partial^2 u}{\partial y^2}=-\frac{\partial^2 v}{\partial y\partial x}.
|
||||
$$
|
||||
|
||||
So,
|
||||
|
||||
$$
|
||||
\Delta u=\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}=\frac{\partial^2 v}{\partial x\partial y}-\frac{\partial^2 v}{\partial y\partial x}=0.
|
||||
$$
|
||||
|
||||
</details>
|
||||
|
||||
If $v$ is such that $f=u+iv$ is holomorphic on $\Omega$, then $v$ is called harmonic conjugate of $u$ on $\Omega$.
|
||||
|
||||
Example:
|
||||
|
||||
$$
|
||||
u(x,y)=x^2-y^2
|
||||
$$
|
||||
|
||||
is harmonic on $\mathbb{C}$.
|
||||
|
||||
To find a harmonic conjugate of $u$ on $\mathbb{C}$, we need to find a function $v$ such that
|
||||
|
||||
$$
|
||||
\frac{\partial v}{\partial x}=-\frac{\partial u}{\partial y}=2y, \quad \frac{\partial v}{\partial y}=\frac{\partial u}{\partial x}=2x.
|
||||
$$
|
||||
|
||||
Integrating, we get
|
||||
|
||||
$$
|
||||
v(x,y)=2xy+G(y)
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{\partial v}{\partial y}=2x+G'(y)=2x
|
||||
$$
|
||||
|
||||
So,
|
||||
|
||||
$$
|
||||
G'(y)=0 \implies G(y)=C
|
||||
$$
|
||||
|
||||
$$
|
||||
v(x,y)=2xy+C
|
||||
$$
|
||||
|
||||
is a harmonic conjugate of $u$ on $\mathbb{C}$.
|
||||
|
||||
Combine $u$ and $v$ to get $f(x,y)=x^2-y^2+2xyi+C=(x+iy)^2+C=z^2+C$, which is holomorphic on $\mathbb{C}$.
|
||||
@@ -1,239 +0,0 @@
|
||||
# Math416 Lecture 5
|
||||
|
||||
## Review
|
||||
|
||||
Let $f$ be a complex function. that maps $\mathbb{R}^2$ to $\mathbb{R}^2$. $f(x+iy)=u(x,y)+iv(x,y)$.
|
||||
|
||||
$$
|
||||
Df(x+iy)=\begin{pmatrix}
|
||||
\frac{\partial u}{\partial x} & \frac{\partial u}{\partial y}\\
|
||||
\frac{\partial v}{\partial x} & \frac{\partial v}{\partial y}
|
||||
\end{pmatrix}=\begin{pmatrix}
|
||||
\alpha & \beta\\
|
||||
\sigma & \delta
|
||||
\end{pmatrix}
|
||||
$$
|
||||
|
||||
So,
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\frac{\partial f}{\partial z}&=\frac{1}{2}\left(u_x+v_y\right)-i\frac{1}{2}\left(v_x+u_y\right)\\
|
||||
&=\frac{1}{2}\left(\alpha+\delta\right)-i\frac{1}{2}\left(\beta-\sigma\right)\\
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\frac{\partial f}{\partial \overline{z}}&=\frac{1}{2}\left(u_x+v_y\right)+i\frac{1}{2}\left(v_x+u_y\right)\\
|
||||
&=\frac{1}{2}\left(\alpha-\delta\right)+i\frac{1}{2}\left(\beta+\sigma\right)\\
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
When $f$ is conformal,
|
||||
|
||||
$$
|
||||
Df(x+iy)=\begin{pmatrix}
|
||||
\alpha & \beta\\
|
||||
-\beta & \alpha
|
||||
\end{pmatrix}
|
||||
$$
|
||||
|
||||
So,
|
||||
|
||||
$$
|
||||
\frac{\partial f}{\partial z}=\frac{1}{2}(\alpha+\alpha)+i\frac{1}{2}(\beta+\beta)=a
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{\partial f}{\partial \overline{z}}=\frac{1}{2}(\alpha-\alpha)+i\frac{1}{2}(\beta-\beta)=0
|
||||
$$
|
||||
|
||||
> Less pain to represent a complex function using four real numbers.
|
||||
|
||||
## Chapter 3: Linear fractional Transformations
|
||||
|
||||
Let $a,b,c,d$ be complex numbers. such that $ad-bc\neq 0$.
|
||||
|
||||
The linear fractional transformation is defined as
|
||||
|
||||
$$
|
||||
\phi(z)=\frac{az+b}{cz+d}
|
||||
$$
|
||||
|
||||
If we let $\psi(z)=\frac{ez-f}{-gz+h}$ also be a linear fractional transformation, then $\phi\circ\psi$ is also a linear fractional transformation.
|
||||
|
||||
New coefficients can be solved by
|
||||
|
||||
$$
|
||||
\begin{pmatrix}
|
||||
a & b\\
|
||||
c & d
|
||||
\end{pmatrix}
|
||||
\begin{pmatrix}
|
||||
e & f\\
|
||||
g & h
|
||||
\end{pmatrix}
|
||||
=
|
||||
\begin{pmatrix}
|
||||
k&l\\
|
||||
m&n
|
||||
\end{pmatrix}
|
||||
$$
|
||||
|
||||
So $\phi\circ\psi(z)=\frac{kz+l}{mz+n}$
|
||||
|
||||
### Complex projective space
|
||||
|
||||
$\mathbb{R}P^1$ is the set of lines through the origin in $\mathbb{R}^2$.
|
||||
|
||||
We defined $(a,b)\sim(c,d),(a,b),(c,d)\in\mathbb{R}^2\setminus\{(0,0)\}$ if $\exists t\neq 0,t\in\mathbb{R}\setminus\{0\}$ such that $(a,b)=t(c,d)$.
|
||||
|
||||
$R\mathbb{P}^1=S^1\setminus\{\pm x\}\cong S^1$
|
||||
|
||||
Equivalently,
|
||||
|
||||
$\mathbb{C}P^1$ is the set of lines through the origin in $\mathbb{C}$.
|
||||
|
||||
We defined $(a,b)\sim(c,d),(a,b),(c,d)\in\mathbb{C}\setminus\{(0,0)\}$ if $\exists t\neq 0,t\in\mathbb{C}\setminus\{0\}$ such that $(a,b)=(tc,td)$.
|
||||
|
||||
So, $\forall z\in\mathbb{C}\setminus\{0\}$:
|
||||
|
||||
If $a\neq 0$, then $(a,b)\sim(1,\frac{b}{a})$.
|
||||
|
||||
If $a=0$, then $(0,b)\sim(0,-b)$.
|
||||
|
||||
So, $\mathbb{C}P^1$ is the set of lines through the origin in $\mathbb{C}$.
|
||||
|
||||
### Linear fractional transformations
|
||||
|
||||
Let $M=\begin{pmatrix}
|
||||
a & b\\
|
||||
c & d
|
||||
\end{pmatrix}$ be a $2\times 2$ matrix with complex entries. That maps $\mathbb{C}^2$ to $\mathbb{C}^2$.
|
||||
|
||||
Suppose $M$ is non-singular. Then $ad-bc\neq 0$.
|
||||
|
||||
If $M\begin{pmatrix}
|
||||
z_1\\
|
||||
z_2
|
||||
\end{pmatrix}=\begin{pmatrix}
|
||||
\omega_1\\
|
||||
\omega_2
|
||||
\end{pmatrix}$, then $M\begin{pmatrix}
|
||||
tz_1\\
|
||||
tz_2
|
||||
\end{pmatrix}=\begin{pmatrix}
|
||||
t\omega_1\\
|
||||
t\omega_2
|
||||
\end{pmatrix}$.
|
||||
|
||||
So, $M$ induces a map $\phi_M:\mathbb{C}P^1\to\mathbb{C}P^1$ defined by $M\begin{pmatrix}
|
||||
z\\
|
||||
1
|
||||
\end{pmatrix}=\begin{pmatrix}
|
||||
\frac{az+b}{cz+d}\\
|
||||
1
|
||||
\end{pmatrix}$.
|
||||
|
||||
$\phi_M(z)=\frac{az+b}{cz+d}$.
|
||||
|
||||
If we let $M_2=\begin{pmatrix}
|
||||
e &f\\
|
||||
g &h
|
||||
\end{pmatrix}$, where $ad-bc\neq 0$ and $eh-fg\neq 0$, then $\phi_{M_2}(z)=\frac{ez+f}{gz+h}$.
|
||||
|
||||
So, $M_2M_1=\begin{pmatrix}
|
||||
a&b\\
|
||||
c&d
|
||||
\end{pmatrix}\begin{pmatrix}
|
||||
e&f\\
|
||||
g&h
|
||||
\end{pmatrix}=\begin{pmatrix}
|
||||
z\\
|
||||
1
|
||||
\end{pmatrix}$.
|
||||
|
||||
This also gives $\begin{pmatrix}
|
||||
kz+l\\
|
||||
mz+n
|
||||
\end{pmatrix}\sim\begin{pmatrix}
|
||||
\frac{kz+l}{mz+n}\\
|
||||
1
|
||||
\end{pmatrix}$.
|
||||
|
||||
So, if $ab-cd\neq 0$, then $\exists M^{-1}$ such that $M_2M_1=I$.
|
||||
|
||||
So non-constant linear fractional transformations form a group under composition.
|
||||
|
||||
When do two matrices gives the $t_0$ same linear fractional transformation?
|
||||
|
||||
$M_2^{-1}M_1=\alpha I$
|
||||
|
||||
We defined $GL(2,\mathbb{C})$ to be the group of general linear transformations of order 2 over $\mathbb{C}$.
|
||||
|
||||
This is equivalent to the group of invertible $2\times 2$ matrices over $\mathbb{C}$ under matrix multiplication.
|
||||
|
||||
Let $F$ be the function that maps $M$ to $\phi_M$.
|
||||
|
||||
$F:GL(2,\mathbb{C})\to\text{Homeo}(\mathbb{C}P^1)$
|
||||
|
||||
So the kernel of $F$ is the set of matrices that represent the identity transformation. $\ker F=\left\{\alpha I\right\},\alpha\in\mathbb{C}\setminus\{0\}$.
|
||||
|
||||
#### Corollary of conformality
|
||||
|
||||
If $\phi$ is a non-constant linear fractional transformation, then $\phi$ is conformal.
|
||||
|
||||
<details>
|
||||
<summary>Proof</summary>
|
||||
|
||||
Know that $\phi_0\circ\phi(z)=z$,
|
||||
|
||||
Then $\phi(z)=\phi_0^{-1}\circ\phi\circ\phi_0(z)$.
|
||||
|
||||
So $\phi(z)=\frac{az+b}{cz+d}$.
|
||||
|
||||
$\phi:\mathbb{C}\cup\{\infty\}\to\mathbb{C}\cup\{\infty\}$ which gives $\phi(\infty)=\frac{a}{c}$ and $\phi(-\frac{d}{c})=\infty$.
|
||||
|
||||
So, $\phi$ is conformal.
|
||||
|
||||
</details>
|
||||
|
||||
#### Proposition 3.4 of Fixed points
|
||||
|
||||
Any non-constant linear fractional transformation except the identity transformation has 1 or 2 fixed points.
|
||||
|
||||
<details>
|
||||
<summary>Proof</summary>
|
||||
|
||||
Let $\phi(z)=\frac{az+b}{cz+d}$.
|
||||
|
||||
Case 1: $c=0$
|
||||
|
||||
Then $\infty$ is a fixed point.
|
||||
|
||||
Case 2: $c\neq 0$
|
||||
|
||||
Then $\phi(z)=\frac{az+b}{cz+d}$.
|
||||
|
||||
The solution of $\phi(z)=z$ is $cz^2+(d-a)z-b=0$.
|
||||
|
||||
Such solutions are $z=\frac{-(d-a)\pm\sqrt{(d-a)^2+4bc}}{2c}$.
|
||||
|
||||
So, $\phi$ has 1 or 2 fixed points.
|
||||
|
||||
</details>
|
||||
|
||||
#### Proposition 3.5 of triple transitivity
|
||||
|
||||
If $z_1,z_2,z_3\in\mathbb{C}P^1$ are distinct, then there exists a non-constant linear fractional transformation $\phi$ such that $\phi(z_1)=z_2$ and $\phi(z_3)=\infty$.
|
||||
|
||||
Proof as homework.
|
||||
|
||||
#### Theorem 3.8 Preservation of clircles
|
||||
|
||||
We defined clircle to be a circle or a line.
|
||||
|
||||
If $\phi$ is a non-constant linear fractional transformation, then $\phi$ maps clircles to clircles.
|
||||
|
||||
Proof continue on next lecture.
|
||||
@@ -1,246 +0,0 @@
|
||||
# Math416 Lecture 6
|
||||
|
||||
## Review
|
||||
|
||||
### Linear Fractional Transformations
|
||||
|
||||
Transformations of the form $f(z)=\frac{az+b}{cz+d}$,$a,b,c,d\in\mathbb{C}$ and $ad-bc\neq 0$ are called linear fractional transformations.
|
||||
|
||||
#### Theorem 3.8 Preservation of clircles
|
||||
|
||||
We defined clircle to be a circle or a line.
|
||||
|
||||
The circle equation is:
|
||||
|
||||
Let $z=u+iv$ be the center of the circle, $r$ be the radius of the circle.
|
||||
|
||||
$$
|
||||
circle=\{z\in\mathbb{C}:|z-c|=r\}
|
||||
$$
|
||||
|
||||
This is:
|
||||
|
||||
$$
|
||||
|z|^2-c\overline{z}-\overline{c}z+|c|^2-r^2=0
|
||||
$$
|
||||
|
||||
If $\phi$ is a non-constant linear fractional transformation, then $\phi$ maps clircles to clircles.
|
||||
|
||||
We claim that a map is circle preserving if and only if for some $\alpha,\beta,\gamma,\delta\in\mathbb{R}$.
|
||||
|
||||
$$
|
||||
\alpha|z|^2+\beta Re(z)+\gamma Im(z)+\delta=0
|
||||
$$
|
||||
|
||||
when $\alpha=0$, it is a line.
|
||||
|
||||
when $\alpha\neq 0$, it is a circle.
|
||||
|
||||
<details>
|
||||
<summary>Proof</summary>
|
||||
|
||||
Let $w=u+iv=\frac{1}{z}$, so $\frac{1}{w}=\frac{u}{u^2+v^2}-i\frac{v}{u^2+v^2}$.
|
||||
|
||||
Then the original equation becomes:
|
||||
|
||||
$$
|
||||
\alpha\left(\frac{u}{u^2+v^2}\right)^2+\beta\left(\frac{u}{u^2+v^2}\right)+\gamma\left(-\frac{v}{u^2+v^2}\right)+\delta=0
|
||||
$$
|
||||
|
||||
Which is in the form of circle equation.
|
||||
|
||||
</details>
|
||||
|
||||
## Chapter 4 Elementary functions
|
||||
|
||||
> $e^t=\sum_{n=0}^{\infty}\frac{t^n}{n!}$
|
||||
|
||||
So, following the definition of $e^z$, we have:
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
e^{x+iy}&=e^xe^{iy} \\
|
||||
&=e^x\left(\sum_{n=0}^{\infty}\frac{(iy)^n}{n!}\right) \\
|
||||
&=e^x\left(\sum_{n=0}^{\infty}\frac{(-1)^ny^n}{n!}\right) \\
|
||||
&=e^x(\cos y+i\sin y)
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
### $e^z$
|
||||
|
||||
The exponential of $e^z=x+iy$ is defined as:
|
||||
|
||||
$$
|
||||
e^z=exp(z)=e^x(\cos y+i\sin y)
|
||||
$$
|
||||
|
||||
So,
|
||||
|
||||
$$
|
||||
|e^z|=|e^x||\cos y+i\sin y|=e^x
|
||||
$$
|
||||
|
||||
#### Theorem 4.3 $e^z$ is holomorphic
|
||||
|
||||
$e^z$ is holomorphic on $\mathbb{C}$.
|
||||
|
||||
<details>
|
||||
<summary>Proof</summary>
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\frac{\partial}{\partial z}e^z&=\frac{1}{2}\left(\frac{\partial}{\partial x}+\frac{i}{\partial y}\right)e^x(\cos y+i\sin y) \\
|
||||
&=\frac{1}{2}e^x(\cos y+i\sin y)+ie^x(-\sin y+i\cos y) \\
|
||||
&=0
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
</details>
|
||||
|
||||
#### Theorem 4.4 $e^z$ is periodic
|
||||
|
||||
$e^z$ is periodic with period $2\pi i$.
|
||||
|
||||
<details>
|
||||
<summary>Proof</summary>
|
||||
|
||||
$$
|
||||
e^{z+2\pi i}=e^z e^{2\pi i}=e^z\cdot 1=e^z
|
||||
$$
|
||||
|
||||
</details>
|
||||
|
||||
#### Theorem 4.5 $e^z$ as a map
|
||||
|
||||
$e^z$ is a map from $\mathbb{C}$ to $\mathbb{C}$ with period $2\pi i$.
|
||||
|
||||
$$
|
||||
e^{\pi i}+1=0
|
||||
$$
|
||||
|
||||
This is a map from cartesian coordinates to polar coordinates, where $e^x$ is the radius and $y$ is the angle.
|
||||
|
||||
This map attains every value in $\mathbb{C}\setminus\{0\}$.
|
||||
|
||||
#### Definition 4.6-8 $\cos z$ and $\sin z$
|
||||
|
||||
$$
|
||||
\cos z=\frac{1}{2}(e^{iz}+e^{-iz})
|
||||
$$
|
||||
|
||||
$$
|
||||
\sin z=\frac{1}{2i}(e^{iz}-e^{-iz})
|
||||
$$
|
||||
|
||||
$$
|
||||
\cosh z=\frac{1}{2}(e^z+e^{-z})
|
||||
$$
|
||||
|
||||
$$
|
||||
\sinh z=\frac{1}{2}(e^z-e^{-z})
|
||||
$$
|
||||
|
||||
From this definition, we can see that $\cos z$ and $\sin z$ are no longer bounded in the complex plane.
|
||||
|
||||
And this definition is still compatible with the previous definition of $\cos$ and $\sin$ when $z$ is real.
|
||||
|
||||
Moreover,
|
||||
|
||||
$$
|
||||
\cosh(iz)=\cos z
|
||||
$$
|
||||
|
||||
$$
|
||||
\sinh(iz)=i\sin z
|
||||
$$
|
||||
|
||||
### Logarithm
|
||||
|
||||
#### Definition 4.9 Logarithm
|
||||
|
||||
A logarithm of $a$ is any $b$ such that $e^b=a$.
|
||||
|
||||
If $a=0$, then no logarithm exists.
|
||||
|
||||
If $a\neq 0$, then there exists infinitely many logarithms of $a$.
|
||||
|
||||
Let $a=re^{i\theta}$, $b=x+iy$ be a logarithm of $a$.
|
||||
|
||||
Then,
|
||||
|
||||
$$
|
||||
e^{x+iy}=re^{i\theta}
|
||||
$$
|
||||
|
||||
Since logarithm is not unique, we can always add $2k\pi i$ to the angle.
|
||||
|
||||
If $y\in(-\pi,\pi]$, then $\log a=b$ means $e^b=a$ and $Im(b)\in(-\pi,\pi]$.
|
||||
|
||||
If $a=re^{i\theta}$, then $\log a=\log r+i(\theta_0+2k\pi)$.
|
||||
|
||||
#### Definition 4.10 of Branch of $\arg z$ and $\log z$
|
||||
|
||||
Let $G$ be an open connected subset of $\mathbb{C}\setminus\{0\}$.
|
||||
|
||||
A branch of $\arg(z)$ in $G$ is a continuous function $\alpha:G\to G$, such that $\alpha(z)$ is a value of $\arg(z)$.
|
||||
|
||||
A branch of $\log(z)$ in $G$ is a continuous function $\beta$, such that $e^{\beta(z)}=z$.
|
||||
|
||||
Note: $G$ has a branch of $\arg(z)$ if and only if it has a branch of $\log(z)$.
|
||||
|
||||
<details>
|
||||
<summary>Proof</summary>
|
||||
|
||||
Suppose there exists $\alpha(z)$ such that $\forall z\in G$, $\alpha(z)\in G$, then $l(z)=\ln|z|+i\alpha(z)$ is a branch of $\log(z)$.
|
||||
|
||||
Suppose there exists $l(z)$ such that $\forall z\in G$, $l(z)\in G$, then $\alpha(z)=Im(z)$ is a branch of $\arg(z)$.
|
||||
|
||||
</details>
|
||||
|
||||
If $G=\mathbb{C}\setminus\{0\}$, then not branch of $\arg(z)$ exists.
|
||||
|
||||
#### Corollary of 4.10
|
||||
|
||||
Suppose $\alpha_1$ and $\alpha_2$ are two branches of $\arg(z)$ in $G$.
|
||||
|
||||
Then,
|
||||
|
||||
$$
|
||||
\alpha_1(z)-\alpha_2(z)=2k\pi
|
||||
$$
|
||||
|
||||
for some $k\in\mathbb{Z}$.
|
||||
|
||||
|
||||
Suppose $l_1$ and $l_2$ are two branches of $\log(z)$ in $G$.
|
||||
|
||||
Then,
|
||||
|
||||
$$
|
||||
l_1(z)-l_2(z)=2k\pi i
|
||||
$$
|
||||
|
||||
for some $k\in\mathbb{Z}$.
|
||||
|
||||
#### Theorem 4.11
|
||||
|
||||
$\log(z)$ is holomorphic on $\mathbb{C}\setminus\{0\}$.
|
||||
|
||||
<details>
|
||||
<summary>Proof (continue on next lecture)</summary>
|
||||
|
||||
Method 1: Use polar coordinates. (See in homework)
|
||||
|
||||
Method 2: Use the fact that $\log(z)$ is the inverse of $e^z$.
|
||||
|
||||
Suppose $h=s+it$, $e^h=e^s(\cos t+i\sin t)$, $e^h-1=e^s(\cos t-1)+i\sin t$. So
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\frac{e^h-1}{h}&=\frac{(s+it)e^s(\cos t-1)+i\sin t}{s^2+t^2} \\
|
||||
&=\frac{e^s(\cos t-1)}{s^2+t^2}+i\frac{\sin t}{s^2+t^2}
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Continue next time.
|
||||
</details>
|
||||
@@ -1,185 +0,0 @@
|
||||
# Math416 Lecture 7
|
||||
|
||||
## Review
|
||||
|
||||
### Exponential function
|
||||
|
||||
$$
|
||||
e^z=e^{x+iy}=e^x(\cos y+i\sin y)
|
||||
$$
|
||||
|
||||
### Logarithm Reviews
|
||||
|
||||
#### Definition 4.9 Logarithm
|
||||
|
||||
A logarithm of $a$ is any $b$ such that $e^b=a$.
|
||||
|
||||
### Branch of Logarithm
|
||||
|
||||
A branch of logarithm is a continuous function $f$ on a domain $D$ such that $e^{f(z)}=\exp(f(z))=z$ for all $z\in D$.
|
||||
|
||||
## Continue on Chapter 4 Elementary functions
|
||||
|
||||
### Logarithm
|
||||
|
||||
#### Theorem 4.11
|
||||
|
||||
$\log(z)$ is holomorphic on $\mathbb{C}\setminus\{0\}$.
|
||||
|
||||
<details>
|
||||
<summary>Proof</summary>
|
||||
|
||||
We proved that $\frac{\partial}{\partial\overline{z}}e^{z}=0$ on $\mathbb{C}\setminus\{0\}$.
|
||||
|
||||
Then $\frac{d}{dz}e^{z}=\frac{\partial}{\partial x}e^{z}=0$ if we know that $e^{z}$ is holomorphic.
|
||||
|
||||
Since $\frac{d}{dz}e^{z}=e^{z}$, we know that $e^{z}$ is conformal, so any branch of logarithm is also conformal.
|
||||
|
||||
Since $\exp(\log(z))=z$, we know that $\log(z)$ is the inverse of $\exp(z)$, so $\frac{d}{dz}\log(z)=\frac{1}{e^{\log(z)}}=\frac{1}{z}$.
|
||||
|
||||
</details>
|
||||
|
||||
We call $\frac{f'}{f}$ the logarithmic derivative of $f$.
|
||||
|
||||
#### Definition 4.16
|
||||
|
||||
_I don't know if this material is covered or not, so I will add it here to prevent confusion for future readers_
|
||||
|
||||
If $a$ and $c$ are complex numbers, with $a\neq 0$, then by the values of $a^c$ one means the value of $e^{c\log a}$.
|
||||
|
||||
For example, $1^i=e^{i (2\pi n i)}$
|
||||
|
||||
If you accidentally continue on this section and find it interesting, you will find Riemann zeta function
|
||||
|
||||
$$
|
||||
z(s)=\sum_{n=1}^{\infty}\frac{1}{n^s}
|
||||
$$
|
||||
|
||||
And analytic continuation for such function for number less than or equal to $1$.
|
||||
|
||||
And perhaps find trivial zeros for negative integers on real line. It is important to note that the Riemann zeta function has non-trivial zeros, which are located in the critical strip where the real part of $s$ is between 0 and 1. The famous Riemann Hypothesis conjectures that all non-trivial zeros lie on the critical line where the real part of $s$ is $\frac{1}{2}$.
|
||||
|
||||
## Chapter 5. Power series
|
||||
|
||||
### Convergence
|
||||
|
||||
#### Necessary Condition for Convergence
|
||||
|
||||
If $\sum_{n=0}^{\infty}c_n$ converges, then $\lim_{n\to\infty}c_n=0$ exists.
|
||||
|
||||
### Geometric series
|
||||
|
||||
Let $c$ be a complex number
|
||||
|
||||
$$
|
||||
\sum_{n=0}^{N}c^n=\frac{1-c^{N+1}}{1-c}
|
||||
$$
|
||||
|
||||
If $|c|<1$, then $\lim_{N\to\infty}\sum_{n=0}^{N}c^n=\frac{1}{1-c}$.
|
||||
|
||||
otherwise, the series diverges.
|
||||
|
||||
<details>
|
||||
<summary>Proof</summary>
|
||||
|
||||
The geometric series converges if $\frac{c^{N+1}}{1-c}$ converges.
|
||||
|
||||
$$
|
||||
(1-c)(1+c+c^2+\cdots+c^N)=1-c^{N+1}
|
||||
$$
|
||||
|
||||
If $|c|<1$, then $\lim_{N\to\infty}c^{N+1}=0$, so $\lim_{N\to\infty}(1-c)(1+c+c^2+\cdots+c^N)=1$.
|
||||
|
||||
If $|c|\geq 1$, then $c^{N+1}$ does not converge to 0, so the series diverges.
|
||||
|
||||
</details>
|
||||
|
||||
#### Theorem 5.4 (Triangle Inequality for Series)
|
||||
|
||||
If the series $\sum_{n=0}^{\infty}c_n$ converges, then $\left|\sum_{n=0}^\infty c_n\right|\leq \sum_{n=0}^{\infty}|c_n|$.
|
||||
|
||||
#### Definition 5.5
|
||||
|
||||
$$
|
||||
\sum_{n=0}^{\infty}c_n
|
||||
$$
|
||||
|
||||
converges absolutely if $\sum_{n=0}^{\infty}|c_n|$ converges.
|
||||
|
||||
Note: _Some other properties of converging series covered in Math4111, bad, very bad._
|
||||
|
||||
#### Definition 5.6 Convergence of sequence of functions
|
||||
|
||||
A sequence of functions $f_n$ **converges pointwise** to $f$ on a set $G$ if for every $z\in G$, $\forall\epsilon>0$, $\exists N$ such that for all $n\geq N$, $|f_n(z)-f(z)|<\epsilon$.
|
||||
|
||||
(choose $N$ based on $z$)
|
||||
|
||||
A sequence of functions $f_n$ **converges uniformly** to $f$ on a set $G$ if for every $\epsilon>0$, there exists a positive integer $N$ such that for all $n\geq N$ and all $z\in G$, $|f_n(z)-f(z)|<\epsilon$.
|
||||
|
||||
(choose $N$ based on $\epsilon$)
|
||||
|
||||
A sequence of functions $f_n$ **converges locally uniformly** to $f$ on a set $G$ if for every $z\in G$, $\forall\epsilon>0$, $\exists r>0$ such that for all $z\in B(z,r)$, $\forall n\geq N$, $|f_n(z)-f(z)|<\epsilon$.
|
||||
|
||||
(choose $N$ based on $z$ and $\epsilon$)
|
||||
|
||||
A sequence of functions $f_n$ **converges uniformly on compacta** to $f$ on a set $G$ if it converges uniformly on every compact subset of $G$.
|
||||
|
||||
#### Theorem 5.7
|
||||
|
||||
If the subsequence (or partial sum) of a converging sequence of functions converges (a), then the original sequence converges (a).
|
||||
|
||||
The N-th partial sum of the series $\sum_{n=0}^\infty f_n$ is $\sum_{n=0}^{N}f_n$
|
||||
|
||||
You can replace (a) with locally uniform convergence, uniform convergence, pointwise convergence, etc.
|
||||
|
||||
> Corollary from definition of $a^b$ in complex plane
|
||||
>
|
||||
> We defined $a^b=\{e^{b\log a}\}$ if $b$ is real, then $a^b$ is unique, if $b$ is complex, then $a^b=e^{b\log a}\{e^{2k\pi ik b}\},k\in\mathbb{Z}$.
|
||||
|
||||
### Power series
|
||||
|
||||
#### Definition 5.8
|
||||
|
||||
A power series is a series of the form $\sum_{n=0}^{\infty}c_n(z-z_0)^n$.
|
||||
|
||||
#### Definition 5.9 Region of Convergence
|
||||
|
||||
For every power series, there exists a radius of convergence $r$ such that the series converges absolutely and locally uniformly on $B_r(z_0)$.
|
||||
|
||||
And it diverges pointwise outside $B_r(z_0)$.
|
||||
|
||||
<details>
|
||||
<summary>Proof</summary>
|
||||
|
||||
Without loss of generality, we can assume that $z_0=0$.
|
||||
|
||||
Suppose that the power series is $\sum_{n=0}^{\infty}c_n (z)^n$ converges at $z=re^{i\theta}$.
|
||||
|
||||
We want to show that the series converges absolutely and uniformly on $\overline{B_r(0)}$ (_closed disk, I prefer to use this notation, although they use $\mathbb{D}$ for the disk (open disk)_).
|
||||
|
||||
We know $c_n r^ne^{in\theta}\to 0$ as $n\to\infty$.
|
||||
|
||||
So there exists $M\geq|c_n r^ne^{in\theta}|$ for all $n\in\mathbb{N}$.
|
||||
|
||||
So $\forall z\in\overline{B_r(0)}$, $|c_nz^n|\leq |c_n| |z|^n \leq M \left(\frac{|z|}{r}\right)^n$.
|
||||
|
||||
So $\sum_{n=0}^{\infty}|c_nz^n|$ converges absolutely.
|
||||
|
||||
So the series converges absolutely and uniformly on $\overline{B_r(0)}$.
|
||||
|
||||
If $|z| > r$, then $|c_n z^n|$ does not tend to zero, and the series diverges.
|
||||
|
||||
</details>
|
||||
|
||||
We denote this $r$ captialized by te radius of convergence
|
||||
|
||||
#### Possible Cases for the Convergence of Power Series
|
||||
|
||||
1. **Convergence Only at $z = 0$**:
|
||||
- **Proof**: If the power series $\sum_{n=0}^{\infty} c_n (z - z_0)^n$ converges only at $z = 0$, it means that the radius of convergence $R = 0$. This occurs when the terms $c_n (z - z_0)^n$ do not tend to zero for any $z \neq 0$. The series diverges for all $z \neq 0$ because the terms grow without bound.
|
||||
|
||||
2. **Convergence Everywhere**:
|
||||
- **Proof**: If the power series converges for all $z \in \mathbb{C}$, the radius of convergence $R = \infty$. This implies that the terms $c_n (z - z_0)^n$ tend to zero for all $z$. This can happen if the coefficients $c_n$ decrease rapidly enough, such as in the exponential series.
|
||||
|
||||
3. **Convergence Within a Finite Radius**:
|
||||
- **Proof**: For a power series with a finite radius of convergence $R$, the series converges absolutely and uniformly for $|z - z_0| < R$ and diverges for $|z - z_0| > R$. On the boundary $|z - z_0| = R$, the series may converge or diverge depending on the specific series. This is determined by the behavior of the terms on the boundary.
|
||||
@@ -1,184 +0,0 @@
|
||||
# Math416 Lecture 8
|
||||
|
||||
## Review
|
||||
|
||||
### Sequences of Functions
|
||||
|
||||
Let $f_n: G \to \mathbb{C}$ be a sequence of functions.
|
||||
|
||||
#### Convergence Pointwise
|
||||
|
||||
Definition:
|
||||
|
||||
Let $z\in G$, $\forall \epsilon > 0$, $\exists N \in \mathbb{N}$ such that $\forall n \geq N$, $|f_n(z) - f(z)| < \epsilon$.
|
||||
|
||||
#### Convergence Uniformly
|
||||
|
||||
Definition:
|
||||
|
||||
$\forall \epsilon > 0$, $\forall z\in G$, $\exists N \in \mathbb{N}$ such that $\forall n \geq N$, $|f_n(z) - f(z)| < \epsilon$.
|
||||
|
||||
#### Convergence Locally Uniformly
|
||||
|
||||
Definition:
|
||||
|
||||
$\forall \epsilon > 0$, $\forall z\in G$, $\exists N \in \mathbb{N}$ such that $\forall n \geq N$, $|f_n(z) - f(z)| < \epsilon$.
|
||||
|
||||
#### Convergence Uniformly on Compact Sets
|
||||
|
||||
Definition: $\forall C\subset G$ that is compact, $\forall \epsilon > 0, \exists N \in \mathbb{N} \text{ s.t. } \forall n \geq N, \forall z\in C, |f_n(z) - f(z)| < \epsilon$
|
||||
|
||||
#### Power Series
|
||||
|
||||
Definition:
|
||||
|
||||
$$
|
||||
\sum_{n=0}^{\infty} c_n (z - z_0)^n
|
||||
$$
|
||||
|
||||
$z_0$ is the center of the power series.
|
||||
|
||||
#### Theorem of Power Series
|
||||
|
||||
If a power series converges at $z_0$, then it converges absolutely at every point of $\overline{B_r(z_0)}$ that is strictly inside the disk of convergence.
|
||||
|
||||
## Continue on Power Series
|
||||
|
||||
### Review on $\limsup$
|
||||
|
||||
The $\limsup(a_n)$ $a_n\in\mathbb{R}$ is defined as the sup of subsequence of $(a_n)$ as $n$ approaches infinity.
|
||||
|
||||
It has the following properties that is useful for proving the remaining parts for this course.
|
||||
|
||||
Suppose $(a_n)_1^\infty$ is a sequence of real numbers
|
||||
|
||||
1. If $\rho\in \mathbb{R}$ satisfies that $\rho<\limsup_{n\to\infty}a_n$, then $\{a_n : a_n > \rho\}$ is infinite.
|
||||
2. If $\rho\in \mathbb{R}$ satisfies that $\rho>\limsup_{n\to\infty}a_n$, then $\{a_n : a_n > \rho\}$ is finite.
|
||||
|
||||
### Limits of Power Series
|
||||
|
||||
#### Theorem 5.12
|
||||
|
||||
Cauchy-Hadamard Theorem:
|
||||
|
||||
The radius of convergence of the power series is given by $\sum_{n=0}^{\infty} a_n (z - z_0)^n$ is given by
|
||||
|
||||
$$
|
||||
\frac{1}{R} = \limsup_{n\to\infty} |a_n|^{1/n}
|
||||
$$
|
||||
|
||||
<details>
|
||||
<summary>Proof</summary>
|
||||
|
||||
Suppose $(b_n)^{\infty}_{n=0}$ is a sequence of real numbers such that $\lim_{n\to\infty} b_n$ may nor may not exists by $(-1)^n(1-\frac{1}{n})$.
|
||||
|
||||
The limit superior of $(b_n)$ is defined as
|
||||
|
||||
$$
|
||||
s_n = \sup_{k\geq n} b_k
|
||||
$$
|
||||
|
||||
$s_n$ is a decreasing sequence, by completeness of $\mathbb{R}$, every bounded sequence has a limit in $\mathbb{R}$.
|
||||
|
||||
So $s_n$ converges to some limit $s\in\mathbb{R}$.
|
||||
|
||||
Without loss of generality, this also holds for infininum of $s_n$.
|
||||
|
||||
Forward direction:
|
||||
|
||||
We want to show that the radius of convergence of $\sum_{n=0}^{\infty} a_n (z - z_0)^n$ is greater than or equal to $\frac{1}{\limsup_{n\to\infty} |a_n|^{1/n}}$.
|
||||
|
||||
Since $\sum_{n=0}^{\infty} 1z^n=\frac{1}{1-z}$ for $|z|<1$. Assume $\limsup_{n\to\infty} |a_n|^{1/n}$ is finite, then $\sum_{n=0}^{\infty} a_n (z - z_0)^n$ converges absolutely at $z_0$.
|
||||
|
||||
Let $\rho>\limsup_{n\to\infty} |a_n|^{1/n}$, then $\exists N \in \mathbb{N}$ such that $\forall n \geq N$, $|a_n|^{1/n}\leq \rho$. (By property of $\limsup$)
|
||||
|
||||
So $\frac{1}{R}=\limsup_{n\to\infty} |a_n|^{1/n}\leq\rho$
|
||||
|
||||
So $R\geq\frac{1}{\rho}$
|
||||
|
||||
Backward direction:
|
||||
|
||||
Suppose $|z|>R$, then $\exists$ number $|z|$ such that $|z|>\frac{1}{\rho}\geq R$.
|
||||
|
||||
So $\rho<\limsup_{n\to\infty} |a_n|^{1/n}$
|
||||
|
||||
This means that $\exists$ infinitely many $n_j$s such that $|a_{n_j}|^{1/n_j}>\rho$
|
||||
|
||||
So $|a_{n_j}z^{n_j}|>\rho^{n_j}|z|^{n_j}$
|
||||
|
||||
Series $\sum_{n=1}^{\infty} a_nz^n$ diverges, each individual term is not going to $0$.
|
||||
|
||||
So $\sum_{n=0}^{\infty} a_n (z - z_0)^n$ does not converge at $z$ if $|z|> \frac{1}{\rho}\geq R$
|
||||
|
||||
So $R=\frac{1}{\rho}$.
|
||||
|
||||
</details>
|
||||
|
||||
_What if $|z-z_0|=R$?_
|
||||
|
||||
For $\sum_{n=0}^{\infty} z^n$, the radius of convergence is $1$.
|
||||
|
||||
It diverges eventually on the circle of convergence.
|
||||
|
||||
For $\sum_{n=0}^{\infty} \frac{1}{(n+1)^2}z^n$, the radius of convergence is $1$.
|
||||
|
||||
This converges everywhere on the circle of convergence.
|
||||
|
||||
For $\sum_{n=0}^{\infty} \frac{1}{n+1}z^n$, the radius of convergence is $1$.
|
||||
|
||||
This diverges at $z=1$ (harmonic series) and converges at $z=-1$ (alternating harmonic series).
|
||||
|
||||
#### Theorem 5.15
|
||||
|
||||
Differentiation of power series
|
||||
|
||||
Suppose $\sum_{n=0}^{\infty} a_n (z - z_0)^n$ has a positive radius of convergence $R$. Define $f(z)=\sum_{n=0}^{\infty} a_n (z - z_0)^n$, then $f$ is holomorphic on $B_R(0)$ and $f'(z)=\sum_{n=1}^{\infty} n a_n (z - z_0)^{n-1}=\sum_{k=0}^{\infty} (k+1)a_{k+1} (z - z_0)^k$.
|
||||
|
||||
> Here below is the proof on book, which will be covered in next lecture.
|
||||
|
||||
<details>
|
||||
<summary>Proof</summary>
|
||||
|
||||
Without loss of generality, assume $z_0=0$. Let $R$ be the radius of convergence for the two power series: $\sum_{n=0}^{\infty} a_n z^n$ and $\sum_{n=1}^{\infty} n a_n z ^{n-1}$. The two power series have the same radius of convergence $|R|$.
|
||||
|
||||
> For $z,w\in \mathbb{C}, n\in \N$, $$z^n-w^n=(z-w)\sum_{k=0}^{n-1} z^k w^{n-k-1}$$
|
||||
|
||||
Let $z_1\in B_R(0)$, $|z_1|<\rho<R$ for some $\rho\in\mathbb{R}$.
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\frac{f(z)-f(z_1)}{z-z_1}-g(z_1)&=\frac{1}{z-z_1}\left[\sum_{n=0}^\infty a_n z^n -\sum_{n=0}^\infty a_n z_1^n\right]-\sum_{n=1}^{\infty} n a_n z_1 ^{n-1}\\
|
||||
&=\sum_{n=1}^{\infty} a_n \left[\frac{z^n-z_1^n}{z-z_1}-nz_1^{n-1}\right]\\
|
||||
&=\sum_{n=1}^{\infty} a_n \left[\left(\sum_{k=0}^{n-1}z^kz_1^{n-k-1}\right)-nz_1^{n-1}\right]\\
|
||||
&=\sum_{n=2}^{\infty} a_n \left[\sum_{k=1}^{n-1}z_1^{n-k-1}(z^k-z^k_1)\right]
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Using the lemma again we get
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
|z^k-z_1^k|&=|z-z_1|\left|\sum_{j=0}^{k-1}z_jz_1^{k-j-1}\right|\\
|
||||
&\leq |z-z_1| \sum_{j=0}^{k-1}|z_j||z_1^{k-j-1}|\\
|
||||
&\leq k\rho^{k-1}|z-z_1|
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Then,
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\left|\frac{f(z)-f(z_1)}{z-z_1}-g(z_1)\right|&=\left|\sum_{n=2}^{\infty} a_n \left[\sum_{k=1}^{n-1}z_1^{n-k-1}(z^k-z^k_1)\right]\right|\\
|
||||
&\leq \sum_{n=2}^{\infty} |a_n| \left[\sum_{k=1}^{n-1}|z_1|^{n-k-1}|z^k-z_1^k|\right]\\
|
||||
&\leq \sum_{n=2}^{\infty} |a_n| \left[ \sum_{k=1}^{n-1} \rho^{n-k-1} (k\rho^{k-1}|z-z_1|) \right]\\
|
||||
&=|z-z_1|\sum_{n=2}^\infty|a_n|\left[\frac{n(n-1)}{2}\rho^{n-2}\right]
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
One can use ratio test to find that $\sum_{n=2}^\infty|a_n|\left[\frac{n(n-1)}{2}\rho^{n-2}\right]$ converges, we denote the sum using $M$
|
||||
|
||||
So $\left|\frac{f(z)-f(z_1)}{z-z_1}-g(z_1)\right|\leq M|z-z_1|$ for $|z|<\rho$.
|
||||
|
||||
So $\lim_{z\to z_1}\frac{f(z)-f(z_1)}{z-z_1}=g(z_1)$.
|
||||
|
||||
</details>
|
||||
@@ -1,151 +0,0 @@
|
||||
# Math416 Lecture 9
|
||||
|
||||
## Review
|
||||
|
||||
### Power Series
|
||||
|
||||
Let $f(z)=\sum_{n=0}^{\infty}a_n(z-z_0)^n$ be a power series.
|
||||
|
||||
#### Radius of Convergence
|
||||
|
||||
The radius of convergence of a power series is
|
||||
|
||||
$$
|
||||
R=\frac{1}{\limsup_{n\to\infty}|a_n|^{1/n}}.
|
||||
$$
|
||||
|
||||
## New Material on Power Series
|
||||
|
||||
### Derivative of Power Series
|
||||
|
||||
Let $f(z)=\sum_{n=0}^{\infty}a_n(z-z_0)^n$ be a power series.
|
||||
|
||||
Let $g(z)=\sum_{n=0}^{\infty}na_n(z-z_0)^{n-1}$ be another power series.
|
||||
|
||||
Then $g$ is holomorphic on $D(z_0,R)$ and $g'(z)=f(z)$ for all $z\in D(z_0,R)$. and $f'(z)=g(z)$.
|
||||
|
||||
Proof:
|
||||
|
||||
Note radius of convergence of $g$ is also $R$.
|
||||
|
||||
$\limsup_{n\to\infty}|na_n|^{1/(n-1)}=\limsup_{n\to\infty}|a_n|^{1/n}$.
|
||||
|
||||
Let $z\in D(z_0,R)$.
|
||||
|
||||
let $|z-z_0|<\rho<R$.
|
||||
|
||||
Without loss of generality, assume $z_0=0$. Let $|w|<\rho$.
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\frac{f(z)-f(w)}{z-w}-g(z)&=\sum_{n=0}^{\infty}\left[\frac{1}{z-w}\left(a_n(z^n-w^n)\right)-na_nz^{n-1}\right] \\
|
||||
&=\sum_{n=0}^{\infty}a_n\left[\frac{z^n-w^n}{z-w}-nz^{n-1}\right]
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Notice that
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\frac{z^n-w^n}{z-w}&=\sum_{k=0}^{n-1}z^{n-1-k}w^k \\
|
||||
&=z^{n-1}+z^{n-2}w+\cdots+w^{n-1}
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Since
|
||||
|
||||
$$
|
||||
|w^k-z^k|=\left|(w-z)\left(\sum_{j=0}^{k-1}w^{k-1-j}z^j\right)\right|\leq|w-z|k\rho^{k-1}
|
||||
$$
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\frac{z^n-w^n}{z-w}-nz^{n-1}&=(z^{n-1}-z^{n-1})+(z^{n-2}w-z^{n-1})+\cdots+(z w^{n-1}-z^{n-1}) \\
|
||||
&=z^{n-2}(w-z)+z^{n-3}(w^2-z^2)+\cdots+z^0(w^{n-1}-z^{n-1}) \\
|
||||
&=\sum_{k=0}^{n-1}z^{n-1-k}(w^k-z^k)\\
|
||||
&\leq\sum_{k=0}^{n-1}z^{n-1-k}|w-z|k\rho^{k-1} \\
|
||||
&\leq|w-z|\sum_{k=0}^{n-1}k\rho^{k-1} \\
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Apply absolute value,
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\left|\frac{f(z)-f(w)}{z-w}-g(z)\right|&\leq\sum_{n=0}^{\infty}|a_n||w-z|\left[\sum_{k=1}^{n-1}\rho^{n-1-k}k\rho^{k-1}\right] \\
|
||||
&=|w-z|\sum_{n=0}^{\infty}|a_n|\left[\sum_{k=1}^{n-1}\rho^{n-2}k\right] \\
|
||||
&=|w-z|\sum_{n=0}^{\infty}|a_n|\frac{n(n-1)}{2}\rho^{n-2} \\
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Using Cauchy-Hadamard theorem, the radius of convergence of $\sum_{n=0}^{\infty}\frac{ n(n-1)}{2}|a_n|z^{n-2}$ is at least
|
||||
|
||||
$$
|
||||
1/\limsup_{n\to\infty}\left[\frac{n(n-1)}{2}|a_n|\right]^{1/(n-1)}=R.
|
||||
$$
|
||||
|
||||
Therefore,
|
||||
|
||||
$$
|
||||
|w-z|\sum_{n=0}^{\infty}|a_n|\frac{n(n-1)}{2}\rho^{n-2} \leq C|w-z|
|
||||
$$
|
||||
|
||||
where $C$ is dependent on $\rho$.
|
||||
|
||||
So $\lim_{w\to z}\left|\frac{f(z)-f(w)}{z-w}-g(z)\right|=0$. as desired.
|
||||
|
||||
QED
|
||||
|
||||
#### Corollary of power series
|
||||
|
||||
If $f(z)=\sum_{n=0}^{\infty}a_n(z-z_0)^n$ in $D(z_0,R)$, then $a_0=f(z_0), a_1=f'(z_0)/1!, a_2=f''(z_0)/2!$, etc.
|
||||
|
||||
#### Definition (Analytic)
|
||||
|
||||
A function $h$ on an open set $U\subset\mathbb{C}$ is called analytic if for every $z\in U$, $\exists \epsilon>0$ such that on $D(z,\epsilon)\subset U$, $h$ can be represented as a power series $\sum_{n=0}^{\infty}a_n(z-z_0)^n$.
|
||||
|
||||
#### Theorem (Analytic implies holomorphic)
|
||||
|
||||
If $f$ is analytic on $U$, then $f$ is holomorphic on $U$.
|
||||
|
||||
$\sum_{n=0}^{\infty}\frac{1}{n!}f^{(n)}(z)^n$
|
||||
|
||||
Radius of convergence is $\infty$.
|
||||
|
||||
So $f(0)=1=ce^0=c$
|
||||
|
||||
$\sum_{n=0}^{\infty}\frac{1}{n}z^n$
|
||||
|
||||
Radius of convergence is $1$.
|
||||
|
||||
$f'=\sum_{n=1}^{\infty}z^{n-1}=\frac{1}{1-z}$ (Geometric series)
|
||||
|
||||
So $g(z)=c+\log(\frac{1}{1-z})=c+2\pi k i=\log(\frac{1}{1-z})+2\pi k i$
|
||||
|
||||
#### Cauchy Product of power series
|
||||
|
||||
Let $f(z)=\sum_{n=0}^{\infty}a_nz^n$ and $g(z)=\sum_{n=0}^{\infty}b_nz^n$ be two power series.
|
||||
|
||||
Then $f(z)g(z)=\sum_{n=0}^{\infty}=\sum_{n=0}^{\infty}c_nz^n=\sum_{n=0}^{\infty}\sum_{k=0}^{n}a_kb_{n-k}z^n$
|
||||
|
||||
#### Theorem of radius of convergence of Cauchy product
|
||||
|
||||
Let $f(z)=\sum_{n=0}^{\infty}a_nz^n$ and $g(z)=\sum_{n=0}^{\infty}b_nz^n$ be two power series.
|
||||
|
||||
Then the radius of convergence of $f(z)g(z)$ is at least $\min(R_f,R_g)$.
|
||||
|
||||
Without loss of generality, assume $z_0=0$.
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\left(\sum_{j=0}^{N}a_jz^j\right)\left(\sum_{k=0}^{N}b_kz^k\right)-\sum_{l=0}^{N}c_lz^l&=\sum_{j=0}^{N}\sum_{k=N-j}^{N}a_jb_kz^{j+k}\\
|
||||
&\leq\sum_{N/2\leq\max(j,k)\leq N}|a_j||b_k||z^{j+k}|\\
|
||||
&\leq\left(\sum_{j=N/2}^{N}|a_j||z^j|\right)\left(\sum_{k=0}^{\infty}|b_k||z^k|\right)+\left(\sum_{j=0}^{\infty}|a_j||z^j|\right)\left(\sum_{k=N/2}^{\infty}|b_k||z^k|\right)\\
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Since $\sum_{j=0}^{\infty}|a_j||z^j|$ and $\sum_{k=0}^{\infty}|b_k||z^k|$ are convergent, and $\sum_{j=N/2}^{N}|a_j||z^j|$ and $\sum_{k=N/2}^{\infty}|b_k||z^k|$ converges to zero.
|
||||
|
||||
So $\left|\left(\sum_{j=0}^{N}a_jz^j\right)\left(\sum_{k=0}^{N}b_kz^k\right)-\sum_{l=0}^{N}c_lz^l\right|\leq\left(\sum_{j=N/2}^{N}|a_j||z^j|\right)\left(\sum_{k=0}^{\infty}|b_k||z^k|\right)+\left(\sum_{j=0}^{\infty}|a_j||z^j|\right)\left(\sum_{k=N/2}^{\infty}|b_k||z^k|\right)\to 0$ as $N\to\infty$.
|
||||
|
||||
So $\sum_{n=0}^{\infty}c_nz^n$ converges to $f(z)g(z)$ on $D(0,R_fR_g)$.
|
||||
@@ -1,34 +0,0 @@
|
||||
export default {
|
||||
index: "Course Description",
|
||||
"---": {
|
||||
type: 'separator'
|
||||
},
|
||||
Exam_reviews: "Exam reviews",
|
||||
Math416_L1: "Complex Variables (Lecture 1)",
|
||||
Math416_L2: "Complex Variables (Lecture 2)",
|
||||
Math416_L3: "Complex Variables (Lecture 3)",
|
||||
Math416_L4: "Complex Variables (Lecture 4)",
|
||||
Math416_L5: "Complex Variables (Lecture 5)",
|
||||
Math416_L6: "Complex Variables (Lecture 6)",
|
||||
Math416_L7: "Complex Variables (Lecture 7)",
|
||||
Math416_L8: "Complex Variables (Lecture 8)",
|
||||
Math416_L9: "Complex Variables (Lecture 9)",
|
||||
Math416_L10: "Complex Variables (Lecture 10)",
|
||||
Math416_L11: "Complex Variables (Lecture 11)",
|
||||
Math416_L12: "Complex Variables (Lecture 12)",
|
||||
Math416_L13: "Complex Variables (Lecture 13)",
|
||||
Math416_L14: "Complex Variables (Lecture 14)",
|
||||
Math416_L15: "Complex Variables (Lecture 15)",
|
||||
Math416_L16: "Complex Variables (Lecture 16)",
|
||||
Math416_L17: "Complex Variables (Lecture 17)",
|
||||
Math416_L18: "Complex Variables (Lecture 18)",
|
||||
Math416_L19: "Complex Variables (Lecture 19)",
|
||||
Math416_L20: "Complex Variables (Lecture 20)",
|
||||
Math416_L21: "Complex Variables (Lecture 21)",
|
||||
Math416_L22: "Complex Variables (Lecture 22)",
|
||||
Math416_L23: "Complex Variables (Lecture 23)",
|
||||
Math416_L24: "Complex Variables (Lecture 24)",
|
||||
Math416_L25: "Complex Variables (Lecture 25)",
|
||||
Math416_L26: "Complex Variables (Lecture 26)",
|
||||
Math416_L27: "Complex Variables (Lecture 27)",
|
||||
}
|
||||
@@ -1,15 +0,0 @@
|
||||
# Math 416
|
||||
|
||||
Complex variables. This is a course that explores the theory and applications of complex analysis as extension of Real analysis.
|
||||
|
||||
The course is taught by Professor.
|
||||
John E. McCarthy <mailto:mccarthy@math.wustl.edu>
|
||||
|
||||
Some interesting fact is that he cover the lecture terribly quick. At least for me. I need to preview and review the lecture after the course ended. The only thing that I can take granted of is that many theorem in real analysis still holds in the complex. By elegant definition designing, we build a wonderful math with complex variables and extended theorems, which is more helpful when solving questions that cannot be solved in real numbers.
|
||||
|
||||
McCarthy like to write $\zeta$ for $z$ and his writing for $\zeta$ is almost identical with $z$, I decided to use the traditional notation system I've learned to avoid confusion in my notes.
|
||||
|
||||
I will use $B_r(z_0)$ to denote a disk in $\mathbb{C}$ such that $B_r(z_0) = \{ z \in \mathbb{C} : |z - z_0| < r \}$. In the lecture, he use $\mathbb{D}(z_0,r)$ to denote the disk centered at $z_0$ with radius $r$. If $\mathbb{D}$ is used, then it means the unit disk $\mathbb{D}=\{z:|z|<1\}$. You may also see the closure of the disk $\overline{B_r(z_0)}$ and $\overline{\mathbb{D}}$, these are equivalent definition.
|
||||
|
||||
I will use $z$ to replace the strange notation of $\zeta$. If that makes sense.
|
||||
|
||||
Reference in New Issue
Block a user