Update prebuild.sh

.github/workflows/sync-from-gitea-deploy.yml

@@ -0,0 +1,73 @@
+name: Sync from Gitea (distribute→distribute, keep workflow)
+
+on:
+  schedule:
+    # 2 times per day (UTC): 7:00, 11:00
+    - cron: '0 7,11 * * *'
+  workflow_dispatch: {}
+
+permissions:
+  contents: write  # allow pushing with GITHUB_TOKEN
+
+jobs:
+  mirror:
+    runs-on: ubuntu-latest
+
+    steps:
+      - name: Check out GitHub repo
+        uses: actions/checkout@v4
+        with:
+          fetch-depth: 0
+
+      - name: Fetch from Gitea
+        env:
+          GITEA_URL: ${{ secrets.GITEA_URL }}
+          GITEA_USER: ${{ secrets.GITEA_USERNAME }}
+          GITEA_TOKEN: ${{ secrets.GITEA_TOKEN }}
+        run: |
+          # Build authenticated Gitea URL: https://USER:TOKEN@...
+          AUTH_URL="${GITEA_URL/https:\/\//https:\/\/$GITEA_USER:$GITEA_TOKEN@}"
+
+          git remote add gitea "$AUTH_URL"
+          git fetch gitea --prune
+
+      - name: Update distribute from gitea/distribute, keep workflow, and force-push
+        env:
+          GH_TOKEN: ${{ secrets.GITHUB_TOKEN }}
+          GH_REPO: ${{ github.repository }}
+        run: |
+          # Configure identity for commits made by this workflow
+          git config user.name "github-actions[bot]"
+          git config user.email "github-actions[bot]@users.noreply.github.com"
+
+          # Authenticated push URL for GitHub
+          git remote set-url origin "https://x-access-token:${GH_TOKEN}@github.com/${GH_REPO}.git"
+
+          WF_PATH=".github/workflows/sync-from-gitea.yml"
+
+          # If the workflow exists in the current checkout, save a copy
+          if [ -f "$WF_PATH" ]; then
+            mkdir -p /tmp/gh-workflows
+            cp "$WF_PATH" /tmp/gh-workflows/
+          fi
+
+          # Reset local 'distribute' to exactly match gitea/distribute
+          if git show-ref --verify --quiet refs/remotes/gitea/distribute; then
+            git checkout -B distribute gitea/distribute
+          else
+            echo "No gitea/distribute found, nothing to sync."
+            exit 0
+          fi
+
+          # Restore the workflow into the new HEAD and commit if needed
+          if [ -f "/tmp/gh-workflows/sync-from-gitea.yml" ]; then
+            mkdir -p .github/workflows
+            cp /tmp/gh-workflows/sync-from-gitea.yml "$WF_PATH"
+            git add "$WF_PATH"
+            if ! git diff --cached --quiet; then
+              git commit -m "Inject GitHub sync workflow"
+            fi
+          fi
+
+          # Force-push distribute so GitHub mirrors Gitea + workflow
+          git push origin distribute --force

.github/workflows/sync-from-gitea.yml

@@ -3,7 +3,7 @@ name: Sync from Gitea (main→main, keep workflow)
 on:
   schedule:
     # 2 times per day (UTC): 7:00, 11:00
-    - cron: '0 19,23 * * *'
+    - cron: '0 7,11 * * *'
   workflow_dispatch: {}
 
 permissions:

content/CSE332S/_meta.js

@@ -1,23 +1,61 @@
 export default {
-    index: "Course Description",
+    menu: {
-    "---":{
+      title: 'Home',
-        type: 'separator'
+      type: 'menu',
+      items: {
+        index: {
+          title: 'Home',
+          href: '/'
+        },
+        about: {
+          title: 'About',
+          href: '/about'
+        },
+        contact: {
+          title: 'Contact Me',
+          href: '/contact'
+        }
+      },
     },
-    CSE332S_L1: "Object-Oriented Programming Lab (Lecture 1)",
+    Math3200'CSE332S_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE332S_L2: "Object-Oriented Programming Lab (Lecture 2)",
+    Math429'CSE332S_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE332S_L3: "Object-Oriented Programming Lab (Lecture 3)",
+    Math4111'CSE332S_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE332S_L4: "Object-Oriented Programming Lab (Lecture 4)",
+    Math4121'CSE332S_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE332S_L5: "Object-Oriented Programming Lab (Lecture 5)",
+    Math4201'CSE332S_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE332S_L6: "Object-Oriented Programming Lab (Lecture 6)",
+    Math416'CSE332S_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE332S_L7: "Object-Oriented Programming Lab (Lecture 7)",
+    Math401'CSE332S_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE332S_L8: "Object-Oriented Programming Lab (Lecture 8)",
+    CSE332S'CSE332S_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE332S_L9: "Object-Oriented Programming Lab (Lecture 9)",
+    CSE347'CSE332S_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE332S_L10: "Object-Oriented Programming Lab (Lecture 10)",
+    CSE442T'CSE332S_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE332S_L11: "Object-Oriented Programming Lab (Lecture 11)",
+    CSE5313'CSE332S_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE332S_L12: "Object-Oriented Programming Lab (Lecture 12)",
+    CSE510'CSE332S_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE332S_L13: "Object-Oriented Programming Lab (Lecture 13)",
+    CSE559A'CSE332S_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE332S_L14: "Object-Oriented Programming Lab (Lecture 14)",
+    CSE5519'CSE332S_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE332S_L15: "Object-Oriented Programming Lab (Lecture 15)",
+    Swap: {
-    CSE332S_L16: "Object-Oriented Programming Lab (Lecture 16)",
+      display: 'hidden',
-    CSE332S_L17: "Object-Oriented Programming Lab (Lecture 17)"
+      theme:{
-}
+        timestamp: true,
+      }
+    },
+    index: {
+      display: 'hidden',
+      theme:{
+        sidebar: false,
+        timestamp: true,
+      }
+    },
+    about: {
+      display: 'hidden',
+      theme:{
+        sidebar: false,
+        timestamp: true,
+      }
+    },
+    contact: {
+      display: 'hidden',
+      theme:{
+        sidebar: false,
+        timestamp: true,
+      }
+    }
+  }

content/CSE347/_meta.js

@@ -1,18 +1,61 @@
 export default {
-    index: "Course Description",
+    menu: {
-    "---":{
+      title: 'Home',
-        type: 'separator'
+      type: 'menu',
+      items: {
+        index: {
+          title: 'Home',
+          href: '/'
+        },
+        about: {
+          title: 'About',
+          href: '/about'
+        },
+        contact: {
+          title: 'Contact Me',
+          href: '/contact'
+        }
+      },
     },
-    Exam_reviews: "Exam reviews",
+    Math3200'CSE347_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE347_L1: "Analysis of Algorithms (Lecture 1)",
+    Math429'CSE347_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE347_L2: "Analysis of Algorithms (Lecture 2)",
+    Math4111'CSE347_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE347_L3: "Analysis of Algorithms (Lecture 3)",
+    Math4121'CSE347_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE347_L4: "Analysis of Algorithms (Lecture 4)",
+    Math4201'CSE347_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE347_L5: "Analysis of Algorithms (Lecture 5)",
+    Math416'CSE347_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE347_L6: "Analysis of Algorithms (Lecture 6)",
+    Math401'CSE347_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE347_L7: "Analysis of Algorithms (Lecture 7)",
+    CSE332S'CSE347_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE347_L8: "Analysis of Algorithms (Lecture 8)",
+    CSE347'CSE347_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE347_L9: "Analysis of Algorithms (Lecture 9)",
+    CSE442T'CSE347_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE347_L10: "Analysis of Algorithms (Lecture 10)",
+    CSE5313'CSE347_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE347_L11: "Analysis of Algorithms (Lecture 11)"
+    CSE510'CSE347_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-}
+    CSE559A'CSE347_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE5519'CSE347_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Swap: {
+      display: 'hidden',
+      theme:{
+        timestamp: true,
+      }
+    },
+    index: {
+      display: 'hidden',
+      theme:{
+        sidebar: false,
+        timestamp: true,
+      }
+    },
+    about: {
+      display: 'hidden',
+      theme:{
+        sidebar: false,
+        timestamp: true,
+      }
+    },
+    contact: {
+      display: 'hidden',
+      theme:{
+        sidebar: false,
+        timestamp: true,
+      }
+    }
+  }

content/CSE442T/_meta.js

@@ -1,31 +1,61 @@
 export default {
-    index: "Course Description",
+    menu: {
-    "---":{
+      title: 'Home',
-        type: 'separator'
+      type: 'menu',
+      items: {
+        index: {
+          title: 'Home',
+          href: '/'
+        },
+        about: {
+          title: 'About',
+          href: '/about'
+        },
+        contact: {
+          title: 'Contact Me',
+          href: '/contact'
+        }
+      },
     },
-    Exam_reviews: "Exam reviews",
+    Math3200'CSE442T_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE442T_L1: "Introduction to Cryptography (Lecture 1)",
+    Math429'CSE442T_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE442T_L2: "Introduction to Cryptography (Lecture 2)",
+    Math4111'CSE442T_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE442T_L3: "Introduction to Cryptography (Lecture 3)",
+    Math4121'CSE442T_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE442T_L4: "Introduction to Cryptography (Lecture 4)",
+    Math4201'CSE442T_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE442T_L5: "Introduction to Cryptography (Lecture 5)",
+    Math416'CSE442T_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE442T_L6: "Introduction to Cryptography (Lecture 6)",
+    Math401'CSE442T_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE442T_L7: "Introduction to Cryptography (Lecture 7)",
+    CSE332S'CSE442T_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE442T_L8: "Introduction to Cryptography (Lecture 8)",
+    CSE347'CSE442T_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE442T_L9: "Introduction to Cryptography (Lecture 9)",
+    CSE442T'CSE442T_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE442T_L10: "Introduction to Cryptography (Lecture 10)",
+    CSE5313'CSE442T_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE442T_L11: "Introduction to Cryptography (Lecture 11)",
+    CSE510'CSE442T_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE442T_L12: "Introduction to Cryptography (Lecture 12)",
+    CSE559A'CSE442T_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE442T_L13: "Introduction to Cryptography (Lecture 13)",
+    CSE5519'CSE442T_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE442T_L14: "Introduction to Cryptography (Lecture 14)",
+    Swap: {
-    CSE442T_L15: "Introduction to Cryptography (Lecture 15)",
+      display: 'hidden',
-    CSE442T_L16: "Introduction to Cryptography (Lecture 16)",
+      theme:{
-    CSE442T_L17: "Introduction to Cryptography (Lecture 17)",
+        timestamp: true,
-    CSE442T_L18: "Introduction to Cryptography (Lecture 18)",
+      }
-    CSE442T_L19: "Introduction to Cryptography (Lecture 19)",
+    },
-    CSE442T_L20: "Introduction to Cryptography (Lecture 20)",
+    index: {
-    CSE442T_L21: "Introduction to Cryptography (Lecture 21)",
+      display: 'hidden',
-    CSE442T_L22: "Introduction to Cryptography (Lecture 22)",
+      theme:{
-    CSE442T_L23: "Introduction to Cryptography (Lecture 23)",
+        sidebar: false,
-    CSE442T_L24: "Introduction to Cryptography (Lecture 24)"
+        timestamp: true,
-}
+      }
+    },
+    about: {
+      display: 'hidden',
+      theme:{
+        sidebar: false,
+        timestamp: true,
+      }
+    },
+    contact: {
+      display: 'hidden',
+      theme:{
+        sidebar: false,
+        timestamp: true,
+      }
+    }
+  }

content/CSE510/CSE510_L24.md

@@ -90,6 +90,8 @@ Parameter explanations:
 
 IGM makes decentralized execution optimal with respect to the learned factorized value.
 
+## Linear Value Factorization
+
 ### VDN (Value Decomposition Networks)
 
 VDN assumes:

content/CSE510/CSE510_L25.md

@@ -1,101 +0,0 @@
-# CSE510 Deep Reinforcement Learning (Lecture 25)
-
-> Restore human intelligence
-
-## Linear Value Factorization
-
-[link to paper](https://arxiv.org/abs/2006.00587)
-
-### Why Linear Factorization works?
-
-- Multi-agent reinforcement learning are mostly emprical
-- Theoretical Model: Factored Multi-Agent Fitted Q-Iteration (FMA-FQI)
-
-#### Theorem 1
-
-It realize **Counterfactual** credit assignment mechanism.
-
-Agent $i$:
-
-$$
-Q_i^{(t+1)}(s,a_i)=\mathbb{E}_{a_{-i}'}\left[y^{(t)}(s,a_i\oplus a_{-i}')\right]-\frac{n-1}{n}\mathbb{E}_{a'}\left[y^{(t)}(s,a')\right]
-$$
-
-Here $\mathbb{E}_{a_{-i}'}\left[y^{(t)}(s,a_i\oplus a_{-i}')\right]$ is the evaluation of $a_i$.
-
-and $\mathbb{E}_{a'}\left[y^{(t)}(s,a')\right]$ is the baseline
-
-The target $Q$-value: $y^{(t)}(s,a)=r+\gamma\max_{a'}Q_{tot}^{(t)}(s',a')$
-
-#### Theorem 2
-
-it has local convergence with on-policy training
-
-##### Limitations of Linear Factorization
-
-Linear: $Q_{tot}(s,a)=\sum_{i=1}^{n}Q_{i}(s,a_i)$
-
-Limited Representation: Suboptimal (Prisoner's Dilemma)
-
-|a_2\a_2| Action 1 | Action 2 |
-|---|---|---|
-|Action 1| **8** | -12 |
-|Action 2| -12 | 0 |
-
-After linear factorization:
-
-|a_2\a_2| Action 1 | Action 2 |
-|---|---|---|
-|Action 1| -6.5 | -5 |
-|Action 2| -5 | **-3.5** |
-
-#### Theorem 3
-
-it may diverge with off-policy training
-
-### Perfect Alignment: IGM Factorization
-
-- Individual-Global Maximization (IGM) Constraint
-
-$$
-\argmax_{a}Q_{tot}(s,a)=(\argmax_{a_1}Q_1(s,a_1), \dots, \argmax_{a_n}Q_n(s,a_n))
-$$
-
-- IGM Factorization: $Q_{tot} (s,a)=f(Q_1(s,a_1), \dots, Q_n(s,a_n))$
-  - Factorization function $f$ realizes all functions satsisfying IGM.
-
-- FQI-IGM: Fitted Q-Iteration with IGM Factorization
-
-#### Theorem 4
-
-Convergence & optimality. FQI-IGM globally converges to the optimal value function in multi-agent MDPs.
-
-### QPLEX: Multi-Agent Q-Learning with IGM Factorization
-
-[link to paper](https://arxiv.org/pdf/2008.01062)
-
-IGM: $\argmax_a Q_{tot}(s,a)=\begin{pamtrix}
-\argmax_{a_1}Q_1(s,a_1) \\
- \dots \\
-  \argmax_{a_n}Q_n(s,a_n)
-\end{pmatrix}
-$
-
-Core idea:
-
-- Fitting well the values of optimal actions
-- Approximate the values of non-optimal actions
-
-QPLEX Mixing Network:
-
-$$
-Q_{tot}(s,a)=\sum_{i=1}^{n}\max_{a_i'}Q_i(s,a_i')+\sum_{i=1}^{n} \lambda_i(s,a)(Q_i(s,a_i)-\max_{a_i'}Q_i(s,a_i'))
-$$
-
-Here $\sum_{i=1}^{n}\max_{a_i'}Q_i(s,a_i')$ is the baseline $\max_a Q_{tot}(s,a)$
-
-And $Q_i(s,a_i)-\max_{a_i'}Q_i(s,a_i')$ is the "advantage".
-
-Coefficients: $\lambda_i(s,a)>0$, **easily realized and learned with neural networks**
-
-> Continue next time...

content/CSE510/CSE510_L26.md

@@ -1,223 +0,0 @@
-# CSE510 Deep Reinforcement Learning (Lecture 26)
-
-## Continue on Real-World Practical Challenges for RL
-
-### Factored multi-agent RL
-
-- Sample efficiency -> Shared Learning
-- Complexity -> High-Order Factorization
-- Partial Observability -> Communication Learning
-- Sparse reward -> Coordinated Exploration
-
-#### Parameter Sharing vs. Diversity
-
-- Parameter Sharing is critical for deep MARL methods
-- However, agents tend to acquire homogenous behaviors
-- Diversity is essential for exploration and practical tasks
-
-[link to paper: Google Football](https://arxiv.org/pdf/1907.11180)
-
-Schematics of Our Approach: Celebrating Diversity in Shared MARL (CDS)
-
-- In representation, CDS allows MARL to adaptively decide
-when to share learning
-- Encouraging Diversity in Optimization
-
-In optimization, maximizing an information-theoretic objective to achieve identity-aware diversity
-
-$$
-\begin{aligned}
-I^\pi(\tau_T;id)&=H(\tau_t)-H(\tau_T|id)=\mathbbb{E}_{id,\tau_T\sim \pi}\left[\log \frac{p(\tau_T|id)}{p(\tau_T)}\right]\\
-&= \mathbb{E}_{id,\tau}\left[ \log \frac{p(o_0|id)}{p(o_0)}+\sum_{t=0}^{T-1}\log\frac{a_t|\tau_t,id}{p(a_t|\tau_t)}+\log \frac{p(o_{t+1}|\tau_t,a_t,id)}{p(o_{t+1}|\tau_t,a_t)}\right]
-\end{aligned}
-$$
-
-Here: $\sum_{t=0}^{T-1}\log\frac{a_t|\tau_t,id}{p(a_t|\tau_t)}$ represents the action diversity.
-
-$\log \frac{p(o_{t+1}|\tau_t,a_t,id)}{p(o_{t+1}|\tau_t,a_t)}$ represents the observation diversity.
-
-### Summary
-
-- MARL plays a critical role for AI, but is at the early stage
-- Value factorization enables scalable MARL
-  - Linear factorization sometimes is surprising effective
-  - Non-linear factorization shows promise in offline settings
-- Parameter sharing plays an important role for deep MARL
-- Diversity and dynamic parameter sharing can be critical for complex cooperative tasks
-
-## Challenges and open problems in DRL
-
-### Overview for Reinforcement Learning Algorithms
-
-Recall from lecture 2
-
-Better sample efficiency to less sample efficiency:
-
-- Model-based
-- Off-policy/Q-learning
-- Actor-critic
-- On-policy/Policy gradient
-- Evolutionary/Gradient-free
-
-#### Model-Based
-
-- Learn the model of the world, then pan using the model
-- Update model often
-- Re-plan often
-
-#### Value-Based
-
-- Learn the state or state-action value
-- Act by choosing best action in state
-- Exploration is a necessary add-on
-
-#### Policy-based
-
-- Learn the stochastic policy function that maps state to action
-- Act by sampling policy
-- Exploration is baked in
-
-### Where we are?
-
-Deep RL has achieved impressive results in games, robotics, control, and decision systems.
-
-But it is still far from a general, reliable, and efficient learning paradigm.
-
-Today: what limits Deep RL, what's being worked on, and what's still open.
-
-### Outline of challenges
-
-- Offline RL
-- Multi-Agent complexity
-- Sample efficiency & data reuse
-- Stability & reproducibility
-- Generalization & distribution shift
-- Scalable model-based RL
-- Safety
-- Theory gaps & evaluation
-
-### Sample inefficiency
-
-Model-free Deep RL often need million/billion of steps
-
-- Humans with 15-minute learning tend to outperform DDQN with 115 hours
-- OpenAI Five for Dota 2: 180 years playing time per day
-
-Real-world systems can't afford this
-
-Root causes: high-variance gradients, weak priors, poor credit assignment.
-
-Open direction for sample efficiency
-
-- Better data reuse: off-policy learning & replay improvements
-- Self-supervised representation learning for control (learning from interacting with the environment)
-- Hybrid model-based/model-free approaches
-- Transfer & pre-training on large datasets
-  - Knowledge driving-RL: leveraging pre-trained models
-
-#### Knowledge-Driven RL: Motivation
-
-Current LLMs are not good at decision making
-
-Pros: rich knowledge
-
-Cons: Auto-regressive decoding lack of long turn memory
-
-Reinforcement learning in decision making
-
-Pros: Go beyond human intelligence
-
-Cons: sample inefficiency
-
-### Instability & the Deadly triad
-
-Function approximation + boostraping + off-policy learning can diverge
-
-Even stable algorithms (PPO) can be unstable
-
-#### Open direction for Stability
-
-Better optimization landscapes + regularization
-
-Calibration/monitoring tools for RL training
-
-Architectures with built-in inductive biased (e.g., equivariance)
-
-### Reproducibility & Evaluation
-
-Results often depend on random seeds, codebase, and compute budget
-
-Benchmark can be overfit; comparisons apples-to-oranges
-
-Offline evaluation is especially tricky
-
-#### Toward Better Evaluation
-
-- Robustness checks and ablations
-- Out-of-distribution test suites
-- Realistic benchmarks beyond games (e.g., science and healthcare)
-
-### Generalization & Distribution Shift
-
-Policy overfit to training environments and fail under small challenges
-
-Sim-to-real gap, sensor noise, morphology changes, domain drift.
-
-Requires learning invariance and robust decision rules.
-
-#### Open direction for Generalization
-
-- Domain randomization + system identification
-- Robust/ risk-sensitive RL
-- Representation learning for invariance
-- Meta-RL and fast adaptation
-
-### Model-based RL: Promise & Pitfalls
-
-- Learned models enable planning and sample efficiency
-- But distribution mismatch and model exploitation can break policies
-- Long-horizon imagination amplifies errors
-- Model-learning is challenging
-
-### Safety, alignment, and constraints
-
-Reward mis-specification -> unsafe or unintended behavior
-
-Need to respect constraints: energy, collisions, ethics, regulation
-
-Exploration itself may be unsafe
-
-#### Open direction for Safety RL
-
-- Constraint RL (Lagrangians, CBFs, she)
-
-### Theory Gaps & Evaluation
-
-Deep RL lacks strong general guarantees.
-
-We don't fully understand when/why it works
-
-Bridging theory and 
-
-#### Promising theory directoins
-
-Optimization thoery of RL objectives
-
-Generalization and representation learning bounds
-
-Finite-sample analysis s
-
-### Connection to foundation models
-
-- Pre-training on large scale experience
-- World models as sequence predictors
-- RLHF/preference optimization for alignment
-- Open problems: groundign 
-
-### What to expect in the next 3-5 years
-
-Unified model-based offline + safe RL stacks
-
-Large pretrianed decision models
-
-Deployment in high-stake domains

content/CSE510/_meta.js

@@ -1,32 +1,61 @@
 export default {
-    index: "Course Description",
+    menu: {
-    "---":{
+      title: 'Home',
-        type: 'separator'
+      type: 'menu',
+      items: {
+        index: {
+          title: 'Home',
+          href: '/'
+        },
+        about: {
+          title: 'About',
+          href: '/about'
+        },
+        contact: {
+          title: 'Contact Me',
+          href: '/contact'
+        }
+      },
     },
-    CSE510_L1: "CSE510 Deep Reinforcement Learning (Lecture 1)",
+    Math3200'CSE510_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE510_L2: "CSE510 Deep Reinforcement Learning (Lecture 2)",
+    Math429'CSE510_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE510_L3: "CSE510 Deep Reinforcement Learning (Lecture 3)",
+    Math4111'CSE510_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE510_L4: "CSE510 Deep Reinforcement Learning (Lecture 4)",
+    Math4121'CSE510_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE510_L5: "CSE510 Deep Reinforcement Learning (Lecture 5)",
+    Math4201'CSE510_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE510_L6: "CSE510 Deep Reinforcement Learning (Lecture 6)",
+    Math416'CSE510_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE510_L7: "CSE510 Deep Reinforcement Learning (Lecture 7)",
+    Math401'CSE510_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE510_L8: "CSE510 Deep Reinforcement Learning (Lecture 8)",
+    CSE332S'CSE510_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE510_L9: "CSE510 Deep Reinforcement Learning (Lecture 9)",
+    CSE347'CSE510_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE510_L10: "CSE510 Deep Reinforcement Learning (Lecture 10)",
+    CSE442T'CSE510_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE510_L11: "CSE510 Deep Reinforcement Learning (Lecture 11)",
+    CSE5313'CSE510_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE510_L12: "CSE510 Deep Reinforcement Learning (Lecture 12)",
+    CSE510'CSE510_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE510_L13: "CSE510 Deep Reinforcement Learning (Lecture 13)",
+    CSE559A'CSE510_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE510_L14: "CSE510 Deep Reinforcement Learning (Lecture 14)",
+    CSE5519'CSE510_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE510_L15: "CSE510 Deep Reinforcement Learning (Lecture 15)",
+    Swap: {
-    CSE510_L16: "CSE510 Deep Reinforcement Learning (Lecture 16)",
+      display: 'hidden',
-    CSE510_L17: "CSE510 Deep Reinforcement Learning (Lecture 17)",
+      theme:{
-    CSE510_L18: "CSE510 Deep Reinforcement Learning (Lecture 18)",
+        timestamp: true,
-    CSE510_L19: "CSE510 Deep Reinforcement Learning (Lecture 19)",
+      }
-    CSE510_L20: "CSE510 Deep Reinforcement Learning (Lecture 20)",
+    },
-    CSE510_L21: "CSE510 Deep Reinforcement Learning (Lecture 21)",
+    index: {
-    CSE510_L22: "CSE510 Deep Reinforcement Learning (Lecture 22)",
+      display: 'hidden',
-    CSE510_L23: "CSE510 Deep Reinforcement Learning (Lecture 23)",
+      theme:{
-    CSE510_L24: "CSE510 Deep Reinforcement Learning (Lecture 24)",
+        sidebar: false,
-    CSE510_L25: "CSE510 Deep Reinforcement Learning (Lecture 25)",
+        timestamp: true,
-    CSE510_L26: "CSE510 Deep Reinforcement Learning (Lecture 26)",
+      }
-}
+    },
+    about: {
+      display: 'hidden',
+      theme:{
+        sidebar: false,
+        timestamp: true,
+      }
+    },
+    contact: {
+      display: 'hidden',
+      theme:{
+        sidebar: false,
+        timestamp: true,
+      }
+    }
+  }

content/CSE5313/CSE5313_L15.md

@@ -140,7 +140,6 @@ $$
 \begin{aligned} 
 H(Y|X=x)&=-\sum_{y\in \mathcal{Y}} \log_2 \frac{1}{Pr(Y=y|X=x)} \\
 &=-\sum_{y\in \mathcal{Y}} Pr(Y=y|X=x) \log_2 Pr(Y=y|X=x) \\
-\end{aligned}
 $$
 
 The conditional entropy $H(Y|X)$ is defined as:
@@ -151,7 +150,6 @@ H(Y|X)&=\mathbb{E}_{x\sim X}[H(Y|X=x)] \\
 &=-\sum_{x\in \mathcal{X}} Pr(X=x)H(Y|X=x) \\
 &=-\sum_{x\in \mathcal{X}, y\in \mathcal{Y}} Pr(X=x, Y=y) \log_2 Pr(Y=y|X=x) \\
 &=-\sum_{x\in \mathcal{X}, y\in \mathcal{Y}} Pr(x)\sum_{y\in \mathcal{Y}} Pr(Y=y|X=x) \log_2 Pr(Y=y|X=x) \\
-\end{aligned}
 $$
 
 Notes:

content/CSE5313/CSE5313_L18.md

@@ -196,7 +196,7 @@ $\operatorname{Pr}(s_\mathcal{Z}|m_1, \cdots, m_{t-z}) = \operatorname{Pr}(U_1,
 
 Conclude similarly by the law of total probability.
 
-$\operatorname{Pr}(s_\mathcal{Z}|m_1, \cdots, m_{t-z}) = \operatorname{Pr}(s_\mathcal{Z}) \implies I(S_\mathcal{Z}; M_1, \cdots, M_{t-z}) = 0$.
+$\operatorname{Pr}(s_\mathcal{Z}|m_1, \cdots, m_{t-z}) = \operatorname{Pr}(s_\mathcal{Z}) \implies I(S_\mathcal{Z}; M_1, \cdots, M_{t-z}) = 0.
 
 ### Conditional mutual information
 
@@ -246,14 +246,14 @@ A: Fix any $\mathcal{T} = \{i_1, \cdots, i_t\} \subseteq [n]$ of size $t$, and l
 $$
 \begin{aligned}
 H(M) &= I(M; S_\mathcal{T}) + H(M|S_\mathcal{T}) \text{(by def. of mutual information)}\\
-&= I(M; S_\mathcal{T}) \text{(since }S_\mathcal{T}\text{ suffice to decode M)}\\
+&= I(M; S_\mathcal{T}) \text{(since S_\mathcal{T} suffice to decode M)}\\
-&= I(M; S_{i_t}, S_\mathcal{Z}) \text{(since }S_\mathcal{T} = S_\mathcal{Z} ∪ S_{i_t})\\
+&= I(M; S_{i_t}, S_\mathcal{Z}) \text{(since S_\mathcal{T} = S_\mathcal{Z} ∪ S_{i_t})}\\
 &= I(M; S_{i_t}|S_\mathcal{Z}) + I(M; S_\mathcal{Z}) \text{(chain rule)}\\
-&= I(M; S_{i_t}|S_\mathcal{Z}) \text{(since }\mathcal{Z}\leq z \text{, it reveals nothing about M)}\\
+&= I(M; S_{i_t}|S_\mathcal{Z}) \text{(since \mathcal{Z} ≤ z, it reveals nothing about M)}\\
 &= I(S_{i_t}; M|S_\mathcal{Z}) \text{(symmetry of mutual information)}\\
 &= H(S_{i_t}|S_\mathcal{Z}) - H(S_{i_t}|M,S_\mathcal{Z}) \text{(def. of conditional mutual information)}\\
-&\leq H(S_{i_t}|S_\mathcal{Z}) \text{(entropy is non-negative)}\\
+\leq H(S_{i_t}|S_\mathcal{Z}) \text{(entropy is non-negative)}\\
-&\leq H(S_{i_t}|S_\mathcal{Z}) \text{(conditioning reduces entropy)} \\
+\leq H(S_{i_t}|S_\mathcal{Z}) \text{(conditioning reduces entropy). \\
 \end{aligned}
 $$
 

content/CSE5313/CSE5313_L23.md

@@ -160,14 +160,14 @@ Can we trade the recovery threshold $K$ for a smaller $s$?
 
 #### Construction of Short-Dot codes
 
-Choose a super-regular matrix $B\in \mathbb{F}^{P\times K}$, where $P$ is the number of worker nodes.
+Choose a super-regular matrix $B\in \mathbb{F}^{P\time K}$, where $P$ is the number of worker nodes.
 
 - A matrix is supper-regular if every square submatrix is invertible.
 - Lagrange/Cauchy matrix is super-regular (next lecture).
 
 Create matrix $\tilde{A}$ by stacking some $Z\in \mathbb{F}^{(K-M)\times N}$ below matrix $A$.
 
-Let $F=B\cdot \tilde{A}\in \mathbb{F}^{P\times N}$.
+Let $F=B\dot \tilde{A}\in \mathbb{F}^{P\times N}$.
 
 **Short-Dot**: create matrix $F\in \mathbb{F}^{P\times N}$ such that:
 

content/CSE5313/CSE5313_L24.md

@@ -1,395 +0,0 @@
-# CSE5313 Coding and information theory for data science (Lecture 24)
-
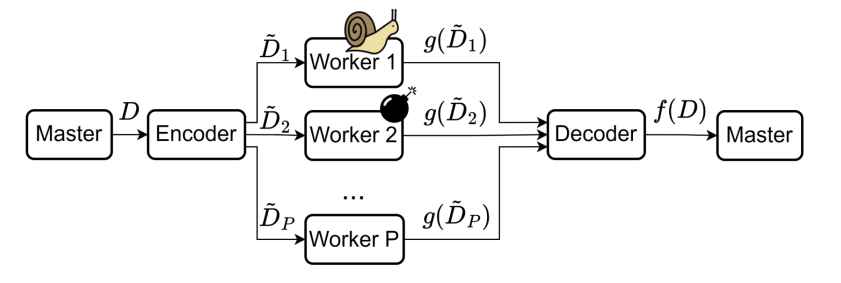
-## Continue on coded computing
-
-![Coded computing scheme](https://notenextra.trance-0.com/CSE5313/Coded_computing_scheme.png)
-
-Matrix-vector multiplication: $y=Ax$, where $A\in \mathbb{F}^{M\times N},x\in \mathbb{F}^N$
-
-- MDS codes.
-  - Recover threshold $K=M$.
-- Short-dot codes.
-  - Recover threshold $K\geq M$.
-  - Every node receives at most $s=\frac{P-K+M}{P}$. $N$ elements of $x$.
-
-### Matrix-matrix multiplication
-
-Problem Formulation:
-
-- $A=[A_0 A_1\ldots A_{M-1}]\in \mathbb{F}^{L\times L}$, $B=[B_0,B_1,\ldots,B_{M-1}]\in \mathbb{F}^{L\times L}$
-- $A_m,B_m$ are submatrices of $A,B$.
-- We want to compute $C=A^\top B$.
-
-Trivial solution:
-
-- Index each worker node by $m,n\in [0,M-1]$.
-- Worker node $(m,n)$ performs matrix multiplication $A_m^\top\cdot B_n$.
-- Need $P=M^2$ nodes.
-- No erasure tolerance.
-
-Can we do better?
-
-#### 1-D MDS Method
-
-Create $[\tilde{A}_0,\tilde{A}_1,\ldots,\tilde{A}_{S-1}]$ by encoding $[A_0,A_1,\ldots,A_{M-1}]$. with some $(S,M)$ MDS code.
-
-Need $P=SM$ worker nodes, and index each one by $s\in [0,S-1], n\in [0,M-1]$.
-
-Worker node $(s,n)$ performs matrix multiplication $\tilde{A}_s^\top\cdot B_n$.
-
-$$
-\begin{bmatrix}
-A_0^\top\\
-A_1^\top\\
-A_0^\top+A_1^\top
-\end{bmatrix}
-\begin{bmatrix}
-B_0 & B_1
-\end{bmatrix}
-$$
-
-Need $S-M$ responses from each column.
-
-The recovery threshold $K=P-S+M$ nodes.
-
-This is trivially parity check code with 1 recovery threshold.
-
-#### 2-D MDS Method
-
-Encode $[A_0,A_1,\ldots,A_{M-1}]$ with some $(S,M)$ MDS code.
-
-Encode $[B_0,B_1,\ldots,B_{M-1}]$ with some $(S,M)$ MDS code.
-
-Need $P=S^2$ nodes.
-
-$$
-\begin{bmatrix}
-A_0^\top\\
-A_1^\top\\
-A_0^\top+A_1^\top
-\end{bmatrix}
-\begin{bmatrix}
-B_0 & B_1 & B_0+B_1
-\end{bmatrix}
-$$
-
-Decodability depends on the pattern.
-
-- Consider an $S\times S$ bipartite graph (rows on left, columns on right).
-- Draw an $(i,j)$ edge if $\tilde{A}_i^\top\cdot \tilde{B}_j$ is missing
-- Row $i$ is decodable if and only if the degree of $i$'th left node $\leq S-M$.
-- Column $j$ is decodable if and only if the degree of $j$'th right node $\leq S-M$.
-
-Peeling algorithm:
-
-- Traverse the graph.
-- If $\exists v$,$\deg v\leq S-M$, remove edges.
-- Repeat.
-
-Corollary:
-
-- A pattern is decodable if and only if the above graph **does not** contain a subgraph with all degree larger than $S-M$.
-
-> [!NOTE]
->
-> 1. $K_{1D-MDS}=P-S+M=\Theta(P)$ (linearly)
-> 2. $K_{2D-MDS}=P-(S-M+1)^2+1$.  
->     - Consider $S\times S$ bipartite graph with $(S-M+1)\times (S-M+1)$ complete subgraph.
->     - There exists subgraph with all degrees larger than $S-M\implies$ not decodable.
->     - On the other hand: Fewer than $(S-M+1)^2$ edges cannot form a subgraph with all degrees $>S-M$.
->     - $K$ scales sub-linearly with $P$.
-> 3. $K_{product}<P-M^2=S^2-M^2=\Theta(\sqrt{P})$
->
-> Our goal is to get rid of $P$.
-
-### Polynomial codes
-
-#### Polynomial representation
-
-Coefficient representation of a polynomial:
-
-- $f(x)=f_dx^d+f_{d-1}x^{d-1}+\cdots+f_1x+f_0$
-- Uniquely defined by coefficients $[f_d,f_{d-1},\ldots,f_0]$.
-
-Value presentation of a polynomial:
-
-- Theorem: A polynomial of degree $d$ is uniquely determined by $d+1$ points.
-- Proof Outline: First create a polynomial of degree $d$ from the $d+1$ points using Lagrange interpolation, and show such polynomial is unique.
-- Uniquely defined by evaluations $[(\alpha_1,f(\alpha_1)),\ldots,(\alpha_{d},f(\alpha_{d}))]$
-
-Why should we want value representation?
-
-- With coefficient representation, polynomial product takes $O(d^2)$ multiplications.
-- With value representation, polynomial product takes $2d+1$ multiplications.
-
-#### Definition of a polynomial code
-
-[link to paper](https://arxiv.org/pdf/1705.10464)
-
-Problem formulation:
-
-$$
-A=[A_0,A_1,\ldots,A_{M-1}]\in \mathbb{F}^{L\times L}, B=[B_0,B_1,\ldots,B_{M-1}]\in \mathbb{F}^{L\times L}
-$$
-
-We want to compute $C=A^\top B$.
-
-Define *matrix* polynomials:
-
-$p_A(x)=\sum_{i=0}^{M-1} A_i x^i$, degree $M-1$
-
-$p_B(x)=\sum_{i=0}^{M-1} B_i x^{iM}$, degree $M(M-1)$
-
-where each $A_i,B_i$ are matrices
-
-We have
-
-$$
-h(x)=p_A(x)p_B(x)=\sum_{i=0}^{M-1}\sum_{j=0}^{M-1} A_i B_j x^{i+jM}
-$$
-
-$\deg h(x)\leq M(M-1)+M-1=M^2-1$
-
-Observe that
-
-$$
-x^{i_1+j_1M}=x^{i_2+j_2M}
-$$
-if and only if $m_1=n_1$ and $m_2=n_2$.
-
-The coefficient of $x^{i+jM}$ is $A_i^\top B_j$.
-
-Computing $C=A^\top B$ is equivalent to find the coefficient representation of $h(x)$.
-
-#### Encoding of polynomial codes
-
-The master choose $\omega_0,\omega_1,\ldots,\omega_{P-1}\in \mathbb{F}$.
-
-- Note that this requires $|\mathbb{F}|\geq P$.
-
-For every node $i\in [0,P-1]$, the master computes $\tilde{A}_i=p_A(\omega_i)$
-
-- Equivalent to multiplying $[A_0^\top,A_1^\top,\ldots,A_{M-1}^\top]$ by Vandermonde matrix over $\omega_0,\omega_1,\ldots,\omega_{P-1}$.
-- Can be speed up using FFT.
-
-Similarly, the master computes $\tilde{B}_i=p_B(\omega_i)$ for every node $i\in [0,P-1]$.
-
-Every node $i\in [0,P-1]$ computes and returns $c_i=p_A(\omega_i)p_B(\omega_i)$ to the master.
-
-$c_i$ is the evaluation of polynomial $h(x)=p_A(x)p_B(x)$ at $\omega_i$.
-
-Recall that $h(x)=\sum_{i=0}^{M-1}\sum_{j=0}^{M-1} A_i^\top B_j x^{i+jM}$.
-
-- Computing $C=A^\top B$ is equivalent to finding the coefficient representation of $h(x)$.
-
-Recall that a polynomial of degree $d$ can be uniquely defined by $d+1$ points.
-
-- With $MN$ evaluations of $h(x)$, we can recover the coefficient representation for polynomial $h(x)$.
-
-The recovery threshold $K=M^2$, independent of $P$, the number of worker nodes.
-
-Done.
-
-### MatDot Codes
-
-[link to paper](https://arxiv.org/pdf/1801.10292)
-
-Problem formulation:
-
-- We want to compute $C=A^\top B$.
-- Unlike polynomial codes, we let $A=\begin{bmatrix}
-A_0\\
-A_1\\
-\vdots\\
-A_{M-1}
-\end{bmatrix}$ and $B=\begin{bmatrix}
-B_0\\
-B_1\\
-\vdots\\
-B_{M-1}
-\end{bmatrix}$. And $A,B\in \mathbb{F}^{L\times L}$.
-
-- In polynomial codes, $A=\begin{bmatrix}
-A_0 A_1\ldots A_{M-1}
-\end{bmatrix}$ and $B=\begin{bmatrix}
-B_0 B_1\ldots B_{M-1}
-\end{bmatrix}$.
-
-Key observation:
-
-$A_m^\top$ is an $L\times \frac{L}{M}$ matrix, and $B_m$ is an $\frac{L}{M}\times L$ matrix. Hence, $A_m^\top B_m$ is an $L\times L$ matrix.
-
-Let $C=A^\top B=\sum_{m=0}^{M-1} A_m^\top B_m$.
-
-Let $p_A(x)=\sum_{m=0}^{M-1} A_m x^m$, degree $M-1$.
-
-Let $p_B(x)=\sum_{m=0}^{M-1} B_m x^m$, degree $M-1$.
-
-Both have degree $M-1$.
-
-And $h(x)=p_A(x)p_B(x)$.
-
-$\deg h(x)\leq M-1+M-1=2M-2$
-
-Key observation:
-
-- The coefficient of the term $x^{M-1}$ in $h(x)$ is $\sum_{m=0}^{M-1} A_m^\top B_m$.
-
-Recall that $C=A^\top B=\sum_{m=0}^{M-1} A_m^\top B_m$.
-
-Finding this coefficient is equivalent to finding the result of $A^\top B$.
-
-> Here we sacrifice the bandwidth of the network for the computational power.
-
-#### General Scheme for MatDot Codes
-
-The master choose $\omega_0,\omega_1,\ldots,\omega_{P-1}\in \mathbb{F}$.
-
-- Note that this requires $|\mathbb{F}|\geq P$.
-
-For every node $i\in [0,P-1]$, the master computes $\tilde{A}_i=p_A(\omega_i)$ and $\tilde{B}_i=p_B(\omega_i)$.
-
-- $p_A(x)=\sum_{m=0}^{M-1} A_m x^m$, degree $M-1$.
-- $p_B(x)=\sum_{m=0}^{M-1} B_m x^m$, degree $M-1$.
-
-The master sends $\tilde{A}_i,\tilde{B}_i$ to node $i$.
-
-Every node $i\in [0,P-1]$ computes and returns $c_i=p_A(\omega_i)p_B(\omega_i)$ to the master.
-
-The master needs $\deg h(x)+1=2M-1$ evaluations to obtain $h(x)$.
-
-- The recovery threshold is $K=2M-1$
-
-### Recap on Matrix-Matrix multiplication
-
-$A,B\in \mathbb{F}^{L\times L}$, we want to compute $C=A^\top B$ with $P$ nodes.
-
-Every node receives $\frac{1}{m}$ of $A$ and $\frac{1}{m}$ of $B$.
-
-|Code| Recovery threshold $K$|
-|:--:|:--:|
-|1D-MDS| $\Theta(P)$ |
-|2D-MDS| $\leq \Theta(\sqrt{P})$ |
-|Polynomial codes| $\Theta(M^2)$ |
-|MatDot codes| $\Theta(M)$ |
-
-## Polynomial Evaluation
-
-Problem formulation:
-
-- We have $K$ datasets $X_1,X_2,\ldots,X_K$.
-- Want to compute some polynomial function $f$ of degree $d$ on each dataset.
-  - Want $f(X_1),f(X_2),\ldots,f(X_K)$.
-- Examples:
-  - $X_1,X_2,\ldots,X_K$ are points in $\mathbb{F}^{M\times M}$, and $f(X)=X^8+3X^2+1$.
-  - $X_k=(X_k^{(1)},X_k^{(2)})$, both in $\mathbb{F}^{M\times M}$, and $f(X)=X_k^{(1)}X_k^{(2)}$.
-  - Gradient computation.
-
-$P$ worker nodes:
-
-- Some are stragglers, i.e., not responsive.
-- Some are adversaries, i.e., return erroneous results.
-- Privacy: We do not want to expose datasets to worker nodes.
-
-### Replication code
-
-Suppose $P=(r+1)\cdot K$.
-
-- Partition the $P$ nodes to $K$ groups of size $r+1$ each.
-- Node in group $i$ computes and returns $f(X_i)$ to the master.
-- Replication tolerates $r$ stragglers, or $\lfloor \frac{r}{2} \rfloor$ adversaries.
-
-### Linear codes
-
-Recall previous linear computations (matrix-vector):
-
-- $[\tilde{A}_1,\tilde{A}_2,\tilde{A}_3]=[A_1,A_2,A_1+A_2]$ is the corresponding codeword of $[A_1,A_2]$.
-- Every worker node $i$ computes $f(\tilde{A}_i)=\tilde{A}_i x$.
-- $[\tilde{A}_1x, \tilde{A}_2x, \tilde{A}_3x]=[A_1x,A_2x,A_1x+A_2x]$ is the corresponding codeword of $[A_1x,A_2x]$.
-  - This enables to decode $[A_1x,A_2x]$ from $[\tilde{A}_1x,\tilde{A}_2x,\tilde{A}_3 x]$.
-
-However, $f$ is a **polynomial of degree $d$**, not a linear transformation unless $d=1$.
-
-- $f(cX)\neq cf(X)$, where $c$ is a constant.
-- $f(X_1+X_2)\neq f(X_1)+f(X_2)$.
-
-> [!CAUTION]
-> 
-> $[f(\tilde{X}_1),f(\tilde{X}_2),\ldots,f(\tilde{X}_K)]$ is not the codeword corresponding to $[f(X_1),f(X_2),\ldots,f(X_K)]$ in any linear code.
-
-Our goal is to create an encoder/decode such that:
-
-- Linear encoding: is the codeword of $[X_1,X_2,\ldots,X_K]$ for some linear code.
-  - i.e., $[\tilde{X}_1,\tilde{X}_2,\ldots,\tilde{X}_K]=[X_1,X_2,\ldots,X_K]G$ for some generator matrix $G$.
-  - Every $\tilde{X}_i$ is some linear combination of $X_1,\ldots,X_K$.
-- The $f(X_i)$ are decodable from some subset of $f(\tilde{X}_i)$'s.
-  - Some of coded results are missing, erroneous.
-- $X_i$'s are kept private.
-
-### Lagrange Coded Computing
-
-Let $\ell(z)$ be a polynomial whose evaluations at $\omega_1,\ldots,\omega_{K}$ are $X_1,\ldots,X_K$.
-
-- That is, $\ell(\omega_i)=X_i$ for every $\omega_i\in \mathbb{F}, i\in [K]$.
-
-Some example constructions:
-
-Given $X_1,\ldots,X_K$ with corresponding $\omega_1,\ldots,\omega_K$
-
-- $\ell(z)=\sum_{i=1}^K X_iL_i(z)$, where $L_i(z)=\prod_{j\in[K],j\neq i} \frac{z-\omega_j}{\omega_i-\omega_j}=\begin{cases} 0 & \text{if } j\neq i \\ 1 & \text{if } j=i \end{cases}$.
-
-Then every $f(X_i)=f(\ell(\omega_i))$ is an evaluation of polynomial $f\circ \ell(z)$ at $\omega_i$.
-
-If the master obtains the composition $h=f\circ \ell$, it can obtain every $f(X_i)=h(\omega_i)$.
-
-Goal: The master wished to obtain the polynomial $h(z)=f(\ell(z))$.
-
-Intuition:
-
-- Encoding is performed by evaluating $\ell(z)$ at $\alpha_1,\ldots,\alpha_P\in \mathbb{F}$, and $P>K$ for redundancy.
-- Nodes apply $f$ on an evaluation of $\ell$ and obtain an evaluation of $h$.
-- The master receives some potentially noisy evaluations, and finds $h$.
-- The master evaluates $h$ at $\omega_1,\ldots,\omega_K$ to obtain $f(X_1),\ldots,f(X_K)$.
-
-### Encoding for Lagrange coded computing
-
-Need polynomial $\ell(z)$ such that:
-
-- $X_k=\ell(\omega_k)$ for every $k\in [K]$.
-
-Having obtained such $\ell$ we let $\tilde{X}_i=\ell(\alpha_i)$ for every $i\in [P]$.
-
-$span{\tilde{X}_1,\tilde{X}_2,\ldots,\tilde{X}_P}=span{\ell_1(x),\ell_2(x),\ldots,\ell_P(x)}$.
-
-Want $X_k=\ell(\omega_k)$ for every $k\in [K]$.
-
-Tool: Lagrange interpolation.
-
-- $\ell_k(z)=\prod_{i\neq k} \frac{z-\omega_j}{\omega_k-\omega_j}$.
-- $\ell_k(\omega_k)=1$ and $\ell_k(\omega_k)=0$ for every $j\neq k$.
-- $\deg \ell_k(z)=K-1$.
-
-Let $\ell(z)=\sum_{k=1}^K X_k\ell_k(z)$.
-
-- $\deg \ell\leq K-1$.
-- $\ell(\omega_k)=X_k$ for every $k\in [K]$.
-
-Let $\tilde{X}_i=\ell(\alpha_i)=\sum_{k=1}^K X_k\ell_k(\alpha_i)$.
-
-Every $\tilde{X}_i$ is a **linear combination** of $X_1,\ldots,X_K$.
-
-$$
-(\tilde{X}_1,\tilde{X}_2,\ldots,\tilde{X}_P)=(X_1,\ldots,X_K)\cdot G=(X_1,\ldots,X_K)\begin{bmatrix}
-\ell_1(\alpha_1) & \ell_1(\alpha_2) & \cdots & \ell_1(\alpha_P) \\
-\ell_2(\alpha_1) & \ell_2(\alpha_2) & \cdots & \ell_2(\alpha_P) \\
-\vdots & \vdots & \ddots & \vdots \\
-\ell_K(\alpha_1) & \ell_K(\alpha_2) & \cdots & \ell_K(\alpha_P)
-\end{bmatrix}
-$$
-
-This $G$ is called a **Lagrange matrix** with respect to 
-
-- $\omega_1,\ldots,\omega_K$. (interpolation points)
-- $\alpha_1,\ldots,\alpha_P$. (evaluation points)
-
-> Continue next lecture

content/CSE5313/CSE5313_L25.md

@@ -1,327 +0,0 @@
-# CSE5313 Coding and information theory for data science (Lecture 25)
-
-## Polynomial Evaluation
-
-Problem formulation:
-
-- We have $K$ datasets $X_1,X_2,\ldots,X_K$.
-- Want to compute some polynomial function $f$ of degree $d$ on each dataset.
-  - Want $f(X_1),f(X_2),\ldots,f(X_K)$.
-- Examples:
-  - $X_1,X_2,\ldots,X_K$ are points in $\mathbb{F}^{M\times M}$, and $f(X)=X^8+3X^2+1$.
-  - $X_k=(X_k^{(1)},X_k^{(2)})$, both in $\mathbb{F}^{M\times M}$, and $f(X)=X_k^{(1)}X_k^{(2)}$.
-  - Gradient computation.
-
-$P$ worker nodes:
-
-- Some are stragglers, i.e., not responsive.
-- Some are adversaries, i.e., return erroneous results.
-- Privacy: We do not want to expose datasets to worker nodes.
-
-### Lagrange Coded Computing
-
-Let $\ell(z)$ be a polynomial whose evaluations at $\omega_1,\ldots,\omega_{K}$ are $X_1,\ldots,X_K$.
-
-- That is, $\ell(\omega_i)=X_i$ for every $\omega_i\in \mathbb{F}, i\in [K]$.
-
-Some example constructions:
-
-Given $X_1,\ldots,X_K$ with corresponding $\omega_1,\ldots,\omega_K$
-
-- $\ell(z)=\sum_{i=1}^K X_i\ell_i(z)$, where $\ell_i(z)=\prod_{j\in[K],j\neq i} \frac{z-\omega_j}{\omega_i-\omega_j}=\begin{cases} 0 & \text{if } j\neq i \\ 1 & \text{if } j=i \end{cases}$.
-
-Then every $f(X_i)=f(\ell(\omega_i))$ is an evaluation of polynomial $f\circ \ell(z)$ at $\omega_i$.
-
-If the master obtains the composition $h=f\circ \ell$, it can obtain every $f(X_i)=h(\omega_i)$.
-
-Goal: The master wished to obtain the polynomial $h(z)=f(\ell(z))$.
-
-Intuition:
-
-- Encoding is performed by evaluating $\ell(z)$ at $\alpha_1,\ldots,\alpha_P\in \mathbb{F}$, and $P>K$ for redundancy.
-- Nodes apply $f$ on an evaluation of $\ell$ and obtain an evaluation of $h$.
-- The master receives some potentially noisy evaluations, and finds $h$.
-- The master evaluates $h$ at $\omega_1,\ldots,\omega_K$ to obtain $f(X_1),\ldots,f(X_K)$.
-
-### Encoding for Lagrange coded computing
-
-Need polynomial $\ell(z)$ such that:
-
-- $X_k=\ell(\omega_k)$ for every $k\in [K]$.
-
-Having obtained such $\ell$ we let $\tilde{X}_i=\ell(\alpha_i)$ for every $i\in [P]$.
-
-$span{\tilde{X}_1,\tilde{X}_2,\ldots,\tilde{X}_P}=span{\ell_1(x),\ell_2(x),\ldots,\ell_P(x)}$.
-
-Want $X_k=\ell(\omega_k)$ for every $k\in [K]$.
-
-Tool: Lagrange interpolation.
-
-- $\ell_k(z)=\prod_{i\neq k} \frac{z-\omega_j}{\omega_k-\omega_j}$.
-- $\ell_k(\omega_k)=1$ and $\ell_k(\omega_k)=0$ for every $j\neq k$.
-- $\deg \ell_k(z)=K-1$.
-
-Let $\ell(z)=\sum_{k=1}^K X_k\ell_k(z)$.
-
-- $\deg \ell\leq K-1$.
-- $\ell(\omega_k)=X_k$ for every $k\in [K]$.
-
-Let $\tilde{X}_i=\ell(\alpha_i)=\sum_{k=1}^K X_k\ell_k(\alpha_i)$.
-
-Every $\tilde{X}_i$ is a **linear combination** of $X_1,\ldots,X_K$.
-
-$$
-(\tilde{X}_1,\tilde{X}_2,\ldots,\tilde{X}_P)=(X_1,\ldots,X_K)\cdot G=(X_1,\ldots,X_K)\begin{bmatrix}
-\ell_1(\alpha_1) & \ell_1(\alpha_2) & \cdots & \ell_1(\alpha_P) \\
-\ell_2(\alpha_1) & \ell_2(\alpha_2) & \cdots & \ell_2(\alpha_P) \\
-\vdots & \vdots & \ddots & \vdots \\
-\ell_K(\alpha_1) & \ell_K(\alpha_2) & \cdots & \ell_K(\alpha_P)
-\end{bmatrix}
-$$
-
-This $G$ is called a **Lagrange matrix** with respect to 
-
-- $\omega_1,\ldots,\omega_K$. (interpolation points, rows)
-- $\alpha_1,\ldots,\alpha_P$. (evaluation points, columns)
-
-> Basically, a modification of Reed-Solomon code.
-
-### Decoding for Lagrange coded computing
-
-Say the system has $S$ stragglers (erasures) and $A$ adversaries (errors).
-
-The master receives $P-S$ computation results $f(\tilde{X}_{i_1}),\ldots,f(\tilde{X}_{i_{P-S}})$.
-
-- By design, therese are evaluations of $h: h(a_{i_1})=f(\ell(a_{i_1})),\ldots,h(a_{i_{P-S}})=f(\ell(a_{i_{P-S}}))$
-- A evaluation are noisy
-- $\deg h=\deg f\cdot \deg \ell=(K-1)\deg f$.
-
-Which process enables to interpolate a polynomial from noisy evaluations?
-
-Ree-Solomon (RS) decoding.
-
-Fact: Reed-Solomon decoding succeeds if and only if the number of erasures + 2 $\times$ the number of errors $\leq d-1$.
-
-Imagine $h$ as the "message" in Reed-Solomon code. $[P,(K-1)\deg f +1,P-(K-1)\deg f]_q$.
-
-- Interpolating $h$ is possible if and only if $S+2A\leq (K-1)\deg f-1$.
-
-Once the master interpolates $h$.
-
-- The evaluations $h(\omega_i)=f(\ell(\omega_i))=f(X_i)$ provides the interpolation results.
-
-#### Theorem of Lagrange coded computing
-
-Lagrange coded computing enables to compute $\{f(X_i)\}_{i=1}^K$ for any $f$ at the presence of at most $S$ stragglers and at most $A$ adversaries if
-
-$$
-(K-1)\deg f+S+2A+1\leq P
-$$
-
-> Interpolation of result does not depend on $P$ (number of worker nodes).
-
-### Privacy for Lagrange coded computing
-
-Currently any size-$K$ group of colluding nodes reveals the entire dataset.
-
-Q: Can an individual node $i$ learn anything about $X_i$?
-
-A: Yes, since $\tilde{X}_i$ is a linear combination of $X_1,\ldots,X_K$ (partial knowledge, a linear combination of private data).
-
-Can we provide **perfect privacy** given that at most $T$ nodes collude?
-
-- That is, $I(X:\tilde{X}_i)=0$ for every $\mathcal{T}\subseteq [P]$ of size at most $T$, where
-  - $X=(X_1,\ldots,X_K)$, and 
-  - $\tilde{X}_\mathcal{T}=(\tilde{X}_{i_1},\ldots,\tilde{X}_{i_{|\mathcal{T}|}})$.
-
-Solution: Slight change of encoding in LLC.
-
-This only applied to $\mathbb{F}=\mathbb{F}_q$ (no perfect privacy over $\mathbb{R},\mathbb{C}$. No uniform distribution can be defined).
-
-The master chooses
-
-- $T$ keys $Z_{K+1},\ldots,Z_{K+T}$ uniformly at random ($|Z_i|=|X_i|$ for all $i$)
-- Interpolation points $\omega_1,\ldots,\omega_{K+T}$.
-
-Find the Lagrange polynomial $\ell(z)$ such that
-
-- $\ell(w_i)=X_i$ for $i\in [K]$
-- $\ell(w_{K+j})=Z_j$ for $j\in [T]$.
-
-Lagrange interpolation:
-
-$$
-\ell(z)=\sum_{i=1}^{K} X_i\ell_i(z)+\sum_{j=1}^{T} X_{K+j}ell_{K+j}(z)
-$$
-
-$$
-(\tilde{X}_1,\ldots,\tilde{X}_P)=(X_1,\ldots,X_K,Z_1,\ldots,Z_T)\cdot G
-$$
-
-where
-
-$$
-G=\begin{bmatrix}
-\ell_1(\alpha_1) & \ell_1(\alpha_2) & \cdots & \ell_1(\alpha_P) \\
-\ell_2(\alpha_1) & \ell_2(\alpha_2) & \cdots & \ell_2(\alpha_P) \\
-\vdots & \vdots & \ddots & \vdots \\
-\ell_K(\alpha_1) & \ell_K(\alpha_2) & \cdots & \ell_K(\alpha_P) \\
-\vdots & \vdots & \ddots & \vdots \\
-\ell_{K+T}(\alpha_1) & \ell_{K+T}(\alpha_2) & \cdots & \ell_{K+T}(\alpha_P)
-\end{bmatrix}
-$$
-
-For analysis, we denote $G=\begin{bmatrix}G^{top}\\G^{bot}\end{bmatrix}$, where $G^{top}\in \mathbb{F}^{K\times P}$ and $G^{bot}\in \mathbb{F}^{T\times P}$.
-
-The proof for privacy is the almost the same as ramp scheme.
-
-<details>
-<summary>Proof</summary>
-
-We have $(\tilde{X}_1,\ldots \tilde{X}_P)=(X_1,\ldots,X_K)\cdot G^{top}+(Z_1,\ldots,Z_T)\cdot G^{bot}$.
-
-Without loss of generality, $\mathcal{T}=[T]$ is the colluding set.
-
-$\mathcal{T}$ hold $(\tilde{X}_1,\ldots \tilde{X}_P)=(X_1,\ldots,X_K)\cdot G^{top}_\mathcal{T}+(Z_1,\ldots,Z_T)\cdot G^{bot}_\mathcal{top}$.
-
-- $G^{top}_\mathcal{T}$, $G^{bot}_\mathcal{T}$ contain the first $T$ columns of $G^{top}$, $G^{bot}$, respectively.
-
-Note that $G^{top}\in \mathbb{F}^{T\times P}_q$ is MDS, and hence $G^{top}_\mathcal{T}$ is a $T\times T$ invertible matrix.
-
-Since $Z=(Z_1,\ldots,Z_T)$ chosen uniformly random, so $Z\cdot G^{bot}_\mathcal{T}$ is a one-time pad.
-
-Same proof for decoding, we only need $K+1$ item to make the interpolation work.
-
-</details>
-
-## Conclusion
-
-- Theorem: Lagrange Coded Computing is resilient against $S$ stragglers, $A$ adversaries, and $T$ colluding nodes if 
-  $$
-  P\geq (K+T-1)\deg f+S+2A+1
-  $$
-  - Privacy (increase with $\deg f$) cost more than the straggler and adversary (increase linearly).
-- Caveat: Requires finite field arithmetic!
-- Some follow-up works analyzed information leakage over the reals
-
-## Side note for Blockchain
-
-Blockchain: A decentralized system for trust management.
-
-Blockchain maintains a chain of blocks.
-
-- A block contains a set of transactions.
-- Transaction = value transfer between clients.
-- The chain is replicated on each node.
-
-Periodically, a new block is proposed and appended to each local chain.
-
-- The block must not contain invalid transactions.
-- Nodes must agree on proposed block.
-
-Existing systems:
-
-- All nodes perform the same set of tasks.
-- Every node must receive every block.
-
-Performance does not scale with number of node
-
-### Improving performance of blockchain
-
-The performance of blockchain is inherently limited by its design.
-
-- All nodes perform the same set of tasks.
-- Every node must receive every block.
-
-Idea: Combine blockchain with distributed computing.
-
-- Node tasks should complement each other.
-
-Sharding (notion from databases):
-
-- Nodes are partitioned into groups of equal size.
-- Each group maintains a local chain.
-- More nodes, more groups, more transactions can be processed.
-- Better performance.
-
-### Security Problem
-
-Biggest problem in blockchains: Adversarial (Byzantine) nodes.
-
-- Malicious actors wish to include invalid transactions.
-
-Solution in traditional blockchains: Consensus mechanisms.
-
-- Algorithms for decentralized agreement.
-- Tolerates up to $1/3$ Byzantine nodes.
-
-Problem: Consensus conflicts with sharding.
-
-- Traditional consensus mechanisms tolerate $\approx 1/3$ Byzantine nodes.
-- If we partition $P$ nodes into $K$ groups, we can tolerate only $P/3K$ node failures.
-  - Down from $P/3$ in non-shared systems.
-
-Goal: Solve the consensus problem in sharded systems.
-
-Tool: Coded computing.
-
-### Problem formulation
-
-At epoch $t$ of a shared blockchain system, we have
-
-- $K$ local chain $Y_1^{t-1},\ldots, Y_K^{t-1}$.
-- $K$ new blocks $X_1(t),\ldots,X_K(t)$.
-- A polynomial verification function $f(X_k(t),Y_k^t)$, which validates $X_k(t)$.
-
-<details>
-<summary>Proof</summary>
-
-Balance check function $f(X_k(t),Y_k^t)=\sum_\tau Y_k(\tau)-X_k(t)$.
-
-More commonly, a (polynomial) hash function. Used to:
-
-- Verify the sender's public key.
-- Verify the ownership of the transferred funds.
-
-</details>
-
-Need: Apply a polynomial functions on $K$ datasets.
-
-Lagrange coded computing!
-
-### Blockchain with Lagrange coded computing
-
-At epoch $t$:
-
-- A leader is elected (using secure election mechanism).
-- The leader receives new blocks $X_1(t),\ldots,X_K(t)$.
-- The leader disperses the encoded blocks $\tilde{X}_1(t),\ldots,\tilde{X}_P(t)$ to nodes.
-  - Needs secure information dispersal mechanisms.
-
-Every node $i\in [P]$:
-
-- Locally stores a coded chain $\tilde{Y}_i^t$ (encoded using LCC).
-- Receives $\tilde{X}_i(t)$.
-- Computes $f(\tilde{X}_i(t),\tilde{Y}_i^t)$ and sends to the leader.
-
-The leader decodes to get $\{f(X_i(t),Y_i^t)\}_{i=1}^K$ and disperse securely to nodes.
-
-Node $i$ appends coded block $\tilde{X}_i(t)$ to coded chain $\tilde{Y}_i^t$ (zeroing invalid transactions).
-
-Guarantees security if $P\geq (K+T-1)\deg f+S+2A+1$.
-
-- $A$ adversaries, degree $d$ verification polynomial.
-
-Sharding without sharding:
-
-- Computations are done on (coded) partial chains/blocks.
-  - Good performance!
-- Since blocks/chains are coded, they are "dispersed" among many nodes.
-  - Security problem in sharding solved!
-- Since the encoding is done (securely) through a leader, no need to send every block to all nodes.
-  - Reduced communication! (main bottleneck).
-
-Novelties:
-
-- First decentralized verification system with less than size of blocks times the number of nodes communication.
-- Coded consensus – Reach consensus on coded data.

content/CSE5313/CSE5313_L26.md

@@ -1,445 +0,0 @@
-# CSE5313 Coding and information theory for data science (Lecture 26)
-
-## Sliced and Broken Information with applications in DNA storage and 3D printing
-
-### Basic info
-
-Deoxyribo-Nucleic Acid.
-
-A double-helix shaped molecule.
-
-Each helix is a string of
-
-- Cytosine,
-- Guanine,
-- Adenine, and
-- Thymine.
-
-Contained inside every living cell.
-
-- Inside the nucleus.
-
-Used to encode proteins.
-
-mRNA carries info to Ribosome as codons of length 3 over GUCA.
-
-- Each codon produces an amino acids.
-- $4^3> 20$, redundancy in nature!
-
-1st Chargaff rule:
-
-- The two strands are complements (A-T and G-C).
-- $#A = #T$ and $#G = #C$ in both strands.
-
-2nd Chargaff rule:
-
-- $#A \approx #T$ and $#G \approx #C$ in each strands.
-- Can be explained via tandem duplications.
-  - $GCAGCATT \implies GCAGCAGCATT$.
-  - Occur naturally during cell mitosis.
-
-### DNA storage
-
-DNA synthesis:
-
-- Artificial creation of DNA from G’s, T’s, A’s, and C’s.
-
-Can be used to store information!
-
-Advantages:
-
-- Density.
-  - 5.5 PB per mm3.
-- Stability.
-  - Half-life 521 years (compare to ≈ 20𝑦 on hard drives).
-- Future proof.
-  - DNA reading and writing will remain relevant "forever."
-
-#### DNA storage prototypes
-
-Some recent attempts:
-
-- 2011, 659kb.
-  - Church, Gao, Kosuri, "Next-generation digital information storage in DNA", Science.
-- 2018, 200MB.
-  - Organick et al., "Random access in large-scale DNA data storage," Nature biotechnology.
-- CatalogDNA (startup):
-  - 2019, 16GB.
-  - 2021, 18 Mbps.
-
-Companies:
-
-- Microsoft, Illumina, Western Digital, many startups.
-
-Challenges:
-
-- Expensive, Slow.
-- Traditional storage media still sufficient and affordable.
-
-#### DNA Storage models
-
-In vivo:
-
-- Implant the synthetic DNA inside a living organism.
-- Need evolution-correcting codes!
-- E.g., coding against tandem-duplications.
-
-In vitro:
-
-- Place the synthetic DNA in test tubes.
-- Challenge: Can only synthesize short sequences ($\approx 1000 bp$).
-- 1 test tube contains millions to billions of short sequences.
-
-How to encode information?
-
-How to achieve noise robustness?
-
-### DNA coding in vitro environment
-
-Traditional data communication:
-
-$$
-m\in\{0,1\}^k\mapsto c\in\{0,1\}^n
-$$
-
-DNA storage:
-
-$$
-m\in\{0,1\}^k\mapsto c\in \binom{\{0,1\}^L}{M}
-$$
-
-where $\binom{\{0,1\}^L}{M}$ is the collection of all $M$-subsets of $\{0,1\}^L$. ($0\leq M\leq 2^L$)
-
-A codeword is a set of $M$ binary strings, each of length $L$.
-
-"Sliced channel":
-
-- The message $m$ is encoded to $c\in \{0,1\}^{ML}, and then sliced to $M$ equal parts.
-- Parts may be noisy (substitutions, deletions, etc.).
-- Also useful in network packet transmission ($M$ packets of length $L$).
-
-#### Sliced channel: Figures of merit
-
-How to quantify the **merit** of a given code $\mathcal{C}$?
-
-- Want resilience to any $K$ substitutions in all $M$ parts.
-
-Redundance:
-
-- Recall in linear codes,
-  - $redundancy=length-dimension=\log (size\ of\ space)-\log (size\ of\ code)$.
-- In sliced channel:
-  - $redundancy=\log (size\ of\ space)-\log (size\ of\ code)=\log \binom{2^L}{M}-\log |\mathcal{C}|$.
-
-Research questions:
-
-- Bounds on redundancy?
-- Code construction?
-- Is more redundancy needed in sliced channel?
-
-#### Sliced channel: Lower bound
-
-Idea: **Sphere packing**
-
-Given $c\in \binom{\{0,1\}^L}{M}$ and $K=1$, how may codewords must we exclude?
-
-<details>
-<summary>Example</summary>
-
-- $L=3,M=2$, and let $c=\{001,011\}$. Ball of radius 1 is sized 5.
-
-all the codeword with distance 1 from $c$ are:
-
-Distance 0:
-
-$$
-\{001,011\}
-$$
-
-Distance 1:
-$$
-\{101,011\}\quad \{011\}\quad \{000,011\}\\
-\{001,111\}\quad \{001\}\quad \{001,010\}
-$$
-
-7 options and 2 of them are not codewords.
-
-So the effective size of the ball is 5.
-
-</details>
-
-Tool: (Fourier analysis of) Boolean functions
-
-Introducing hypercube graph:
-
-- $V=\{0,1\}^L$.
-- $\{x,y\}\in E$ if and only if $d_H(x,y)=1$.
-- What is size of $E$?
-
-Consider $c\in \binom{\{0,1\}^L}{M}$ as a characteristic function: $f_c(x)=\{0,1\}^L\to \{0,1\}$.
-
-Let $\partial f_c$ be its boundary.
-
-- All hypercube edges $\{x,y\}$ such that $f_c(x)\neq f_c(y)$.
-
-#### Lemma of boundary
-
-Size of 1-ball $\geq |\partial f_c|+1$.
-
-<details>
-<summary>Proof</summary>
-
-Every edge on the boundary represents a unique way of flipping one bit in one string in $c$.
-
-</details>
-
-Need to bound $|\partial f_c|$ from below
-
-Tool: Total influence.
-
-#### Definition of total influence.
-
-The **total influence** $I(f)$ of $f:\{0,1\}^L\to \{0,1\}$ is defined as:
-
-$$
-\sum_{i=1}^L\operatorname{Pr}_{x\in \{0,1\}^L}(f(x)\neq f(x^{\oplus i}))
-$$
-
-where $x^{\oplus i}$ equals to $x$ with it's $i$th bit flipped.
-
-#### Theorem: Edge-isoperimetric inequality, no proof)
-
-$I(f)\geq 2\alpha\log\frac{1}{\alpha}$.
-
-where $\alpha=\min\{\text{fraction of 1's},\text{fraction of 0's}\}$.
-
-Notice: Let $\partial_i f$ be the $i$-dimensional edges in $\partial f$.
-
-$$
-\begin{aligned}
-I(f)&=\sum_{i=1}^L\operatorname{Pr}_{x\in \{0,1\}^L}(f(x)\neq f(x^{\oplus i}))\\
-&=\sum_{i=1}^L\frac{|\partial_i f|}{2^{L-1}}\\
-&=\frac{||\partial f||}{2^{L-1}}\\
-\end{aligned}
-$$
-
-Corollary: Let $\epsilon>0$, $L\geq \frac{1}{\epsilon}$ and $M\leq 2^{(1-\epsilon)L}$, and let $c\in \binom{\{0,1\}^L}{M}$. Then,
-
-$$
-|\parital f_c|\geq 2\times 2^{L-1}\frac{M}{2^L}\log \frac{2^L}{M}\geq M\log \frac{2^L}{M}\geq ML\epsilon
-$$
-
-Size of $1$ ball is sliced channel $\geq ML\epsilon$.
-
-this implies that $|\mathcal{C}|leq \frac{\binom{2^L}{M}}{\epsilon ML}$
-
-Corollary:
-
-- Redundancy in sliced channel with $K=1$ with the above parameters $\log ML-O(1)$.
-- Simple generation (not shown) gives $O(K\log ML)$.
-
-### Robust indexing
-
-Idea: Start with $L$ bit string with $\log M$ bits for indexing.
-
-Problem 1: Indices subject to noise.
-
-Problem 2: Indexing bits do not carry information $\implies$ higher redundancy.
-
-[link to paper](https://ieeexplore.ieee.org/document/9174447)
-
-Idea: Robust indexing
-
-Instead of using $1,\ldots, M$ for indexing, use $x_1,\ldots, x_M$ such that
-
-- $\{x_1,\ldots,x_M\}$ are of minimum distance $2K+1$ (solves problem 1) $|x_i|=O(\log M)$.
-- $\{x_1,\ldots,x_M\}$ contain information (solves problem 2).
-
-$\{x_1,\ldots,x_M\}$ depend on the message.
-
-- Consider the message $m=(m_1,m_2)$.
-- Find an encoding function $m_1\mapsto\{\{x_i\}_{i=1}^M|d_H(x_i,x_j)\geq 2K+1\}$ (coding over codes)
-- Assume $e$ is such function (not shown).
-
-...
-
-Additional reading:
-
-Jin Sima, Netanel Raviv, Moshe Schwartz, and Jehoshua Bruck. "Error Correction for DNA Storage." arXiv:2310.01729 (2023).
-
-- Magazine article.
-- Introductory.
-- Broad perspective.
-
-### Information Embedding in 3D printing  
-
-Motivations:
-
-Threats to public safety.
-
-- Ghost guns, forging fingerprints, forging keys, fooling facial recognition.
-
-Solution – Information Embedding.
-
-- Printer ID, user ID, time/location stamp
-
-#### Existing Information Embedding Techniques
-
-Many techniques exist.
-
-Information embedding using variations in layers.
-
-- Width, rotation, etc.
-- Magnetic properties.
-- Radiative materials.
-
-Combating Adversarial Noise
-
-Most techniques are rather accurate.
-
-- I.e., low bit error rate.
-
-Challenge: Adversarial damage after use.
-
-- Scraping.
-- Deformation.
-- **Breaking**.
-
-#### A t-break code
-
-Let $m\in \{0,1\}^k\mapsto c\in \{0,1\}^n$
-
-Adversary breaks $c$ at most $t$ times (security parameter).
-
-Decoder receives a **multi**-st of at most $t+1$ fragments. Assume the following:
-
-- Oriented
-- Unordered
-- Any length
-
-#### Lower bound for t-break code
-
-Claim: A t-break code must have $\Omega(t\log (n/t))$ redundancy.
-
-Lemma: Let $\mathcal{C}$ be a t-break code of length $n$, and for $i\in [n]$ and $\mathcal{C}_i\subseteq\mathcal{C}$ be the subset of $\mathcal{C}$ containing all codewords of Hamming weight $i$. Then $d_H(\mathcal{C}_i)\geq \lceil \frac{t+1}{2}\rceil$.
-
-<details>
-<summary>Proof of Lemma</summary>
-
-Let $x,y\in \mathcal{C}_i$ for some $i$, and let $\ell=d_H(x,y)$.
-
-Write ($\circ$ denotes the concatenation operation):
-
-$x=c_1\circ x_{i_1}\circ c_2\circ x_{i_2}\circ\ldots\circ c_{t+1}\circ x_{i_{t+1}}$
-
-$y=c_1\circ y_{i_1}\circ c_2\circ y_{i_2}\circ\ldots\circ c_{t+1}\circ y_{i_{t+1}}$
-
-Where $x_{i_j}\neq y_{i_j}$ for all $j\in [\ell]$.
-
-Break $x$ and $y$ $2\ell$ times to produce the multi-sets:
-
-$$
-\mathcal{X}=\{\{c_1,c_2,\ldots,c_{t+1},x_{i_1},x_{i_2},\ldots,x_{i_{t+1}}\},\{c_1,c_2,\ldots,c_{t+1},x_{i_1},x_{i_2},\ldots,x_{i_{t+1}}\},\ldots,\{c_1,c_2,\ldots,c_{t+1},x_{i_1},x_{i_2},\ldots,x_{i_{t+1}}\}\}
-$$
-
-$$
-\mathcal{Y}=\{\{c_1,c_2,\ldots,c_{t+1},y_{i_1},y_{i_2},\ldots,y_{i_{t+1}}\},\{c_1,c_2,\ldots,c_{t+1},y_{i_1},y_{i_2},\ldots,y_{i_{t+1}}\},\ldots,\{c_1,c_2,\ldots,c_{t+1},y_{i_1},y_{i_2},\ldots,y_{i_{t+1}}\}\}
-$$
-
-$w_H(x)=w_H(y)=i$, and therefore $\mathcal{X}=\mathcal{Y}$ and $\ell\geq \lceil \frac{t+1}{2}\rceil$.
-
-</details>
-
-<details>
-<summary>Proof of Claim</summary>
-
-Let $j\in \{0,1,\ldots,n\}$ be such that $\mathcal{C}_j$ is the largest among $C_0,C_1,\ldots,C_{n}$.
-
-$\log |\mathcal{C}|=\log(\sum_{i=0}^n|\mathcal{C}_i|)\leq \log \left((n+1)|C_j|\right)\leq \log (n+1)+\log |\mathcal{C}_j|$
-
-By Lemma and ordinary sphere packing bound, for $t'=\lfloor\frac{\lceil \frac{t+1}{2}\rceil-1}{2}\rfloor\approx \frac{t}{4}$,
-
-$$
-|C_j|\leq \frac{2^n}{\sum_{t=0}^{t'}\binom{n}{i}}
-$$
-
-This implies that $n-\log |\mathcal{C}|\geq n-\log(n+1)-\log|\mathcal{C}_j|\geq \dots \geq \Omega(t\log (n/t))$
-
-</details>
-
-Corollary: In the relevant regime $t=O(n^{1-\epsilon})$, we have $\Omega(t\log n)$ redundancy.
-
-### t-break codes: Main ideas.
-
-Encoding:
-
-- Need multiple markers across the codeword.
-- Construct an adjacency matrix 𝐴 of markers to record their order.
-- Append $RS_{2t}(A)$ to the codeword (as in the sliced channel).
-
-Decoding (from $t + 1$ fragments):
-
-- Locate all surviving markers, and locate $RS_{2t}(A)'$.
-- Build an approximate adjacency matrix $A'$ from surviving markers $(d_H(A, A' )\leq  2t)$.
-- Correct $(A',RS_{2t}(A)')\mapsto (A,RS_{2t}(A))$.
-- Order the fragments correctly using $A$.
-
-Tools:
-
-- Random encoding (to have many markers).
-- Mutually uncorrelated codes (so that markers will not overlap).
-
-#### Tool: Mutually uncorrelated codes.
-
-- Want: Markers not to overlap.
-- Solution: Take markers from a Mutually Uncorrelated Codes (existing notion).
-  - A code $\mathcal{M}$ is called mutually uncorrelated if no suffix of any $m_i \in \mathcal{M}$ is if a prefix of another $m_j \in \mathcal{M}$ (including $i=j$).
-- Many constructions exist.
-
-Theorem: For any integer $\ell$ there exists a mutually uncorrelated code $\mathcal{C}_{MU}$ of length $\ell$ and size $|\mathcal{C}_{MU}|\geq \frac{2^\ell}{32\ell}$.
-
-#### Tool: Random encoding.
-
-- Want: Codewords with many markers from $\mathcal{C}_{MU}$, that are not too far apart.
-- Problem: Hard to achieve explicitly.
-- Workaround: Show that a uniformly random string has this property.
-
-Random encoding:
-
-- Choose the message at random.
-- Suitable for embedding, say, printer ID.
-- Not suitable for dynamic information.
-
-Let $m>0$ be a parameter.
-
-Fix a mutually uncorrelated code $\mathcal{C}_{MU}$ of length $\Theta(\log m)$.
-
-Fix $m_1,\ldots, m_t$ from $\mathcal{C}_{MU}$ as "special" markers.
-
-Claim: With probability $1-\frac{1}{\poly(m)}$, in uniformly random string $z\in \{0,1\}^m$.
-
-- Every $O(\log^2(m))$ bits contain a marker from $\mathcal{C}_{MU}$.
-- Every two non-overlapping substrings of length $c\log m$ are distinct.
-- $z$ does not contain any of the special markers $m_1,\ldots, m_t$.
-
-Proof idea:
-
-- Short substring are abundant.
-- Long substring are rare.
-
-#### Sketch of encoding for t-break codes.
-
-Repeatedly sample $z\in \{0,1\}^m$ until it is "good".
-
-Find all markers $m_{i_1},\ldots, m_{i_r}$ in it.
-
-Build a $|\mathcal{C}_{MU}|\times |\mathcal{C}_{MU}|$ matrix $A$ which records order and distances:
-
-- $A_{i,j}=0$ if $m_i,m_j$ are not adjacent.
-- Otherwise, it is the distance between them (in bits).
-
-Append $RS_{2t}(A)$ at the end, and use the special markers $m_1,\ldots, m_t$.
-
-#### Sketch of decoding for t-break codes.
-
-Construct a partial adjacency matrix $A'$ from fragments.

content/CSE5313/CSE5313_L27.md

@@ -1 +0,0 @@
-# CSE5313 Coding and information theory for data science (Lecture 27)

content/CSE5313/Exam_reviews/CSE5313_F1.md

@@ -1,272 +0,0 @@
-# CSE5313 Final Project
-
-## Description
-
-Write a report which presents the paper in detail and criticizes it constructively. Below are some suggestions to guide a proper analysis of the paper:
-
-- What is the problem setting? What is the motivation behind this problem?
-- Which tools are being used? How are these tools related to the topics we have seen in class/HW?
-- Is the paper technically sound, easy to read, and does the problem make sense?
-- Are there any issues with the paper? If so, suggest ways these could be fixed.
-- What is the state of the art in this topic? Were there any major follow-up works? What are major open problems or new directions?
-- Suggest directions for further study and discuss how should those be addressed.
-
-Please typeset your work using a program such as Word or LaTeX, and submit via Gradescope by Dec. 10th (EOD).
-
-Reports will be judged by the depth and breadth of the analysis. Special attention will be given to clarity and organization, including proper abstract, introduction, sections, and citation of previous works.
-
-There is no page limit, but good reports should contain 4-6 single-column pages.
-Please refer to the syllabus for our policy regarding the use of GenAI.
-
-## Paper selection
-
-[Good quantum error-correcting codes exist](https://arxiv.org/pdf/quant-ph/9512032)
-
-> [!TIP]
->
-> I will build the self-contained report that is readable for me 7 months ago, assuming no knowledge in quantum computing and quantum information theory.
->
-> We will use notation defined in class and $[n]=\{1,\cdots,n-1,n\}$, (yes, we use 1 indexed in computer science) each in natural number. And $\mathbb{F}_q$ is the finite field with $q$ elements.
-
-> [!WARNING]
->
-> This notation system is annoying since in mathematics, $A^*$ is the transpose of $A$, but since we are using literatures in physics, we keep the notation of $A^*$. In this report, I will try to make the notation consistent as possible and follows the **physics** convention in this report. So every vector you see will be in $\ket{\psi}$ form. And we will avoid using the $\langle v,w\rangle$ notation for inner product as it used in math, we will use $\langle v|w\rangle$ or $\langle v,w\rangle$ to denote the inner product.
-
-A quantum error-correcting code is defined to be a unitary mapping (encoding) of $k$ qubits (two-state quantum systems) into a subspace of the quantum state space of $n$ qubuits such that if any $t$ of the qubits undergo arbitary decoherence, not necessarily independently, the resulting $n$ qubit state can be used to faithfully reconstruct the original quantum state of the $k$ encoded qubits.
-
-Asymptotic rate $k/n=1-2H_2(2t/n)$, where $H_2$ is the binary entropy function
-
-$$
-H_2=-p\log_2(p)-(1-p)\log_2(1-p)
-$$
-
-### Problem setting and motivation
-
-#### Linear algebra 102
-
-The main vector space we are interested in is $\mathbb{C}^n$, therefore, all the linear operator we defined are from $\mathbb{C}^n$ to $\mathbb{C}^n$.
-
-We denote a vector in vector space as $\ket{\psi}=(z_1,\cdots,z_n)$ (might also be infinite dimensional, and $z_i\in\mathbb{C}$).
-
-A natural inner product space defined on $\mathbb{C}^n$ is given by the Hermitian inner product:
-
-$$
-\langle\psi|\varphi\rangle=\sum_{i=1}^n z_i\bar{z}_i
-$$
-
-This satisfies the following properties:
-1. $\bra{\psi}\sum_i \lambda_i\ket{\varphi}=\sum_i \lambda_i \langle\psi|\varphi\rangle$ (linear on the second argument)
-2. $\langle\varphi|\psi\rangle=(\langle\psi|\varphi\rangle)^*$
-3. $\langle\psi|\psi\rangle\geq 0$ with equality if and only if $\ket{\psi}=0$
-
-Here $\psi$ is just a label for the vector and you don't need to worry about it too much. This is also called the ket, where the counterpart:
-
-- $\langle\psi\rangle$ is called the bra, used to denote the vector dual to $\psi$, such element is a linear functional if you really wants to know what that is.
-- $\langle\psi|\varphi\rangle$ is the inner product between two vectors, and $\bra{\psi} A\ket{\varphi}$ is the inner product between $A\ket{\varphi}$ and $\bra{\psi}$, or equivalently $A^\dagger \bra{\psi}$ and $\ket{\varphi}$.
-- Given a complex matrix $A=\mathbb{C}^{n\times n}$,
-  - $A^*$ is the complex conjugate of $A$.
-    - i.e., $A=\begin{bmatrix}1+i & 2+i & 3+i\\4+i & 5+i & 6+i\\7+i & 8+i & 9+i\end{bmatrix}$, $A^*=\begin{bmatrix}1-i & 2-i & 3-i\\4-i & 5-i & 6-i\\7-i & 8-i & 9-i\end{bmatrix}$
-  - $A^\top$ is the transpose of $A$.
-    - i.e., $A=\begin{bmatrix}1+i & 2+i & 3+i\\4+i & 5+i & 6+i\\7+i & 8+i & 9+i\end{bmatrix}$, $A^\top=\begin{bmatrix}1+i & 4+i & 7+i\\2+i & 5+i & 8+i\\3+i & 6+i & 9+i\end{bmatrix}$
-  - $A^\dagger=(A^*)^\top$ is the complex conjugate transpose, referred to as the adjoint, or Hermitian conjugate of $A$.
-    - i.e., $A=\begin{bmatrix}1+i & 2+i & 3+i\\4+i & 5+i & 6+i\\7+i & 8+i & 9+i\end{bmatrix}$, $A^\dagger=\begin{bmatrix}1-i & 4-i & 7-i\\2-i & 5-i & 8-i\\3-i & 6-i & 9-i\end{bmatrix}$
-  - $A$ is unitary if $A^\dagger A=AA^\dagger=I$.
-  - $A$ is hermitian (self-adjoint in mathematics literatures) if $A^\dagger=A$.
-
-#### Motivation of Tensor product
-
-Recall from the traditional notation of product space of two vector spaces $V$ and $W$, that is, $V\times W$, is the set of all ordered pairs $(\ket{v},\ket{w})$ where $\ket{v}\in V$ and $\ket{w}\in W$.
-
-The space has dimension $\dim V+\dim W$.
-
-We want to define a vector space with notation of multiplication of two vectors from different vector spaces.
-
-That is
-
-$$
-(\ket{v_1}+\ket{v_2})\otimes \ket{w}=(\ket{v_1}\otimes \ket{w})+(\ket{v_2}\otimes \ket{w})
-$$
-$$
-\ket{v}\otimes (\ket{w_1}+\ket{w_2})=(\ket{v}\otimes \ket{w_1})+(\ket{v}\otimes \ket{w_2})
-$$
-
-and enables scalar multiplication by
-
-$$
-\lambda (\ket{v}\otimes \ket{w})=(\lambda \ket{v})\otimes \ket{w}=\ket{v}\otimes (\lambda \ket{w})
-$$
-
-And we wish to build a way associates the basis of $V$ and $W$ to the basis of $V\otimes W$. That makes the tensor product a vector space with dimension $\dim V\times \dim W$.
-
-#### Definition of linear functional
-
-> [!TIP]
->
-> Note the difference between a linear functional and a linear map.
->
-> A generalized linear map is a function $f:V\to W$ satisfying the condition
->
-> 1. $f(\ket{u}+\ket{v})=f(\ket{u})+f(\ket{v})$
-> 2. $f(\lambda \ket{v})=\lambda f(\ket{v})$
-
-A linear functional is a linear map from $V$ to $\mathbb{F}$.
-
-#### Definition of bilinear functional
-
-A bilinear functional is a bilinear function $\beta:V\times W\to \mathbb{F}$ satisfying the condition that $\ket{v}\to \beta(\ket{v},\ket{w})$ is a linear functional for all $\ket{w}\in W$ and $\ket{w}\to \beta(\ket{v},\ket{w})$ is a linear functional for all $\ket{v}\in V$.
-
-The vector space of all bilinear functionals is denoted by $\mathcal{B}(V,W)$.
-
-#### Definition of tensor product
-
-Let $V,W$ be two vector spaces.
-
-Let $V'$ and $W'$ be the dual spaces of $V$ and $W$, respectively, that is $V'=\{\psi:V\to \mathbb{F}\}$ and $W'=\{\phi:W\to \mathbb{F}\}$, $\psi, \phi$ are linear functionals.
-
-The tensor product of vectors $v\in V$ and $w\in W$ is the bilinear functional defined by $\forall (\psi,\phi)\in V'\times W'$ given by the notation
-
-$$
-(v\otimes w)(\psi,\phi)\coloneqq\psi(v)\phi(w)
-$$
-
-The tensor product of two vector spaces $V$ and $W$ is the vector space $\mathcal{B}(V',W')$
-
-Notice that the basis of such vector space is the linear combination of the basis of $V'$ and $W'$, that is, if $\{e_i\}$ is the basis of $V'$ and $\{f_j\}$ is the basis of $W'$, then $\{e_i\otimes f_j\}$ is the basis of $\mathcal{B}(V',W')$.
-
-That is, every element of $\mathcal{B}(V',W')$ can be written as a linear combination of the basis.
-
-Since $\{e_i\}$ and $\{f_j\}$ are bases of $V'$ and $W'$, respectively, then we can always find a set of linear functionals $\{\phi_i\}$ and $\{\psi_j\}$ such that $\phi_i(e_j)=\delta_{ij}$ and $\psi_j(f_i)=\delta_{ij}$.
-
-Here $\delta_{ij}=\begin{cases}
-1 & \text{if } i=j \\
-0 & \text{otherwise}
-\end{cases}$ is the Kronecker delta.
-
-$$
-V\otimes W=\left\{\sum_{i=1}^n \sum_{j=1}^m a_{ij} \phi_i(v)\psi_j(w): \phi_i\in V', \psi_j\in W'\right\}
-$$
-
-Note that $\sum_{i=1}^n \sum_{j=1}^m a_{ij} \phi_i(v)\psi_j(w)$ is a bilinear functional that maps $V'\times W'$ to $\mathbb{F}$.
-
-This enables basis free construction of vector spaces with proper multiplication and scalar multiplication.
-
-This vector space is equipped with the unique inner product $\langle v\otimes w, u\otimes x\rangle_{V\otimes W}$ defined by
-
-$$
-\langle v\otimes w, u\otimes x\rangle=\langle v,u\rangle_V\langle w,x\rangle_W
-$$
-
-In practice, we ignore the subscript of the vector space and just write $\langle v\otimes w, u\otimes x\rangle=\langle v,u\rangle\langle w,x\rangle$.
-
-> [!NOTE]
->
-> All those definitions and proofs can be found in Linear Algebra Done Right by Sheldon Axler.
-
-#### Definition of two-state quantum system
-
-The finite dimensional Hilbert space $\mathcscr{H}
-
-#### Definition of Coherent states from the view of physics
-
-#### Side node: Why quantum error-correcting code is hard
-
-Decoherence process
-
-#### No-cloning theorem
-
-> Reference from P.532 of the book
-
-Suppose we have a quantum system with two slots $A$, and $B$, the data slot, starts out in an unknown but pure quantum state $\ket{\psi}$. This is the state which is to be copied into slot $B$m the target slot. We assume that the target slot starts out in some standard pure state $\ket{s}$. Thus the initial state of the copying machine is $\ket{\psi}\otimes \ket{s}$.
-
-Assume there exists some unitary operator $U$ such that $U(\ket{\psi}\otimes \ket{s})=\ket{\psi}\otimes \ket{\psi}$.
-
-Consider two pure states $\ket{\psi}$ and $\ket{\varphi}$, such that $U(\ket{\psi}\otimes \ket{s})=\ket{\psi}\otimes \ket{\psi}$ and $U(\ket{\varphi}\otimes \ket{s})=\ket{\varphi}\otimes \ket{\varphi}$. The inner product of the two equation yields:
-
-$$
-\langle \psi|\varphi\rangle =(\langle \psi|\varphi\rangle)^2
-$$
-
-This equation has only two solutions, either $\langle \psi|\varphi\rangle=0$ or $\langle \psi|\varphi\rangle=1$.
-
-If $\langle \psi|\varphi\rangle=0$, then $\ket{\psi}=\ket{\varphi}$, no cloning for trivial case.
-
-If $\langle \psi|\varphi\rangle=1$, then $\ket{\psi}$ and $\ket{\varphi}$ are orthogonal.
-
-#### Proposition: Encoding 8 to 9 that correct 1 errors
-
-Recover 1 qubit from a 9 qubit quantum system. (Shor code, 1995)
-
-![Shore code](https://notenextra.trance-0.com/CSE5313/Shore_code.png)
-
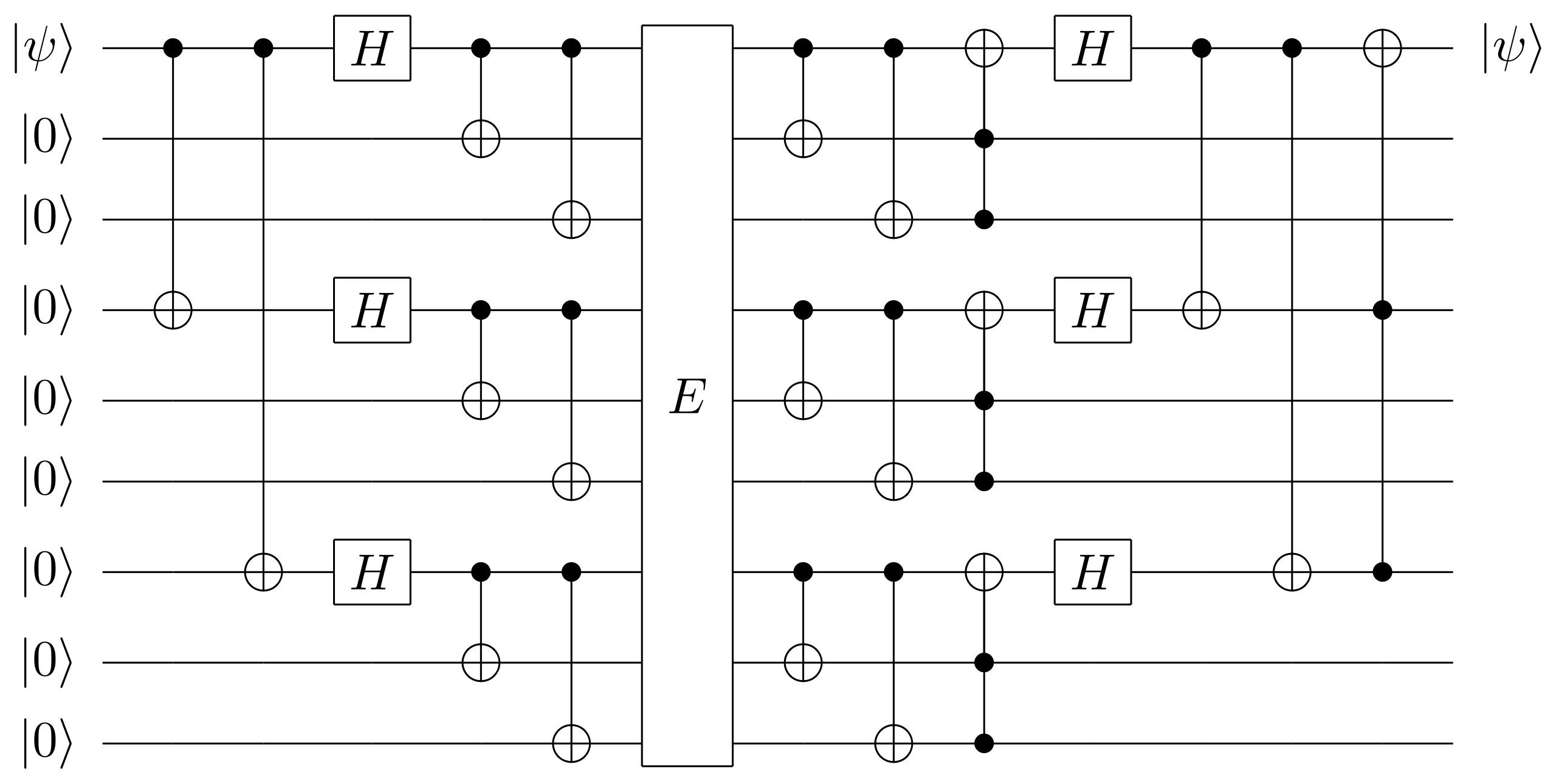
-### Tools and related topics
-
-#### Theoretical upper bound for quantum error-correcting code
-
-From quantum information capacity of a quantum channel
-
-$$
-\min\{1-H_2(2t/3n),H_2(\frac{1}{2}+\sqrt{(1-t/n)t/n})\}
-$$
-
-#### Definition of quantum error-correcting code from binary linear error-correcting code
-
-All the operations will be done in $\mathbb{F}_2=\{0,1\}$.
-
-Consider two binary vectors $v=[v_1,...,v_n],v_i\in\{0,1\}$ and $w=[w_1,...,w_n],w_i\in\{0,1\}$ with size $n$.
-
-Recall from our lecture that
-
-$d$ denotes the Hamming weight of a vector.
-
-$d_H(v,w)=\sum_{i=1}^{n}\begin{cases} 0 & \text{if } v_i=w_i \\ 1 & \text{if } v_i\neq w_i \end{cases}$ denotes the Hamming distance between $v$ and $w$.
-
-$\operatorname{supp}(v)=\{i\in[n]:v_i\neq 0\}$ denotes the support of $v$.
-
-$v|_S$ denotes the projection of $v$ onto the subspace $S$, we usually denote the $S$ by a set of coordinates, that is $S\subseteq[n]$.
-
-When projecting a vector $v$ onto a another vector $w$, we usually write $v|_E\coloneqq v|_{\operatorname{supp} w}$.
-
-When we have two vector we may use $v\leqslant w$ (Note that this is different than $\leq$ sign) to mean $\operatorname{supp}(v)\subseteq \operatorname{supp}(w)$.
-
-<details>
-<summary>Example</summary>
-
-Let $v=[1,0,0,1,1,1,1]$ and $w=[1,0,0,1,0,0,1]$, then $\operatorname{supp}(v)=\{1,4,5,6,7\}$, $\operatorname{supp}(w)=\{1,4,7\}$. Therefore $w\leqslant v$.
-
-$v|_w=[v_1,v_4,v_7]=[1,1,0]$
-</details>
-
-$\mathcal{C}$ denotes the code, a set of arbitrary binary vectors with length $n$.
-
-$d(\mathcal{C})=\{d(v,w)|v,w\in\mathcal{C}\}$ denotes the minimum distance of the code.
-
-If $\mathcal{C}$ is linear then the minimum distance is the minimum Hamming weight of a non-zero codeword.
-
-A $[n,k,d]$ linear code is a linear code of $n$ bits codeword with $k$ message bits that can correct $d$ errors.
-
-$R\coloneqq\frac{\operatorname{dim}\mathcal{C}}{n}$ is the rate of code $\mathcal{C}$.
-
-$\mathcal{C}^{\perp}\coloneqq\{v\in\mathbb{F}_2^n:v\cdot w=0\text{ for all }w\in\mathcal{C}\}$ is the dual code of a code $\mathcal{C}$. From linear algebra, we know that $\dim\mathcal{C}^{\perp}+\dim\mathcal{C}=n$.
-
-<details>
-<summary>Example used in the paper</summary>
-
-Consider the $[7,4,3]$ Hamming code with generator matrix $G$.
-
-</details>
-
-#### Proposition: Encoding $k$ to $n$ that correct $t$ errors
-
-### Evaluation of paper
-
-### Limitation and suggestions
-
-### Further direction and research
-
-#### Toric code, surface code
-
-This is the topic I really want to dig into.
-
-This method gives a [2nm+n+m+1, 1, min(n,m)] error correcting code with only needs local stabilizer checks and really interests me.
-
-### References

content/CSE5313/_meta.js

@@ -1,34 +1,61 @@
 export default {
-    index: "Course Description",
+    menu: {
-    "---":{
+      title: 'Home',
-        type: 'separator'
+      type: 'menu',
+      items: {
+        index: {
+          title: 'Home',
+          href: '/'
+        },
+        about: {
+          title: 'About',
+          href: '/about'
+        },
+        contact: {
+          title: 'Contact Me',
+          href: '/contact'
+        }
+      },
     },
-    Exam_reviews: "Exam reviews and finals",
+    Math3200'CSE5313_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE5313_L1: "CSE5313 Coding and information theory for data science (Lecture 1)",
+    Math429'CSE5313_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE5313_L2: "CSE5313 Coding and information theory for data science (Lecture 2)",
+    Math4111'CSE5313_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE5313_L3: "CSE5313 Coding and information theory for data science (Lecture 3)",
+    Math4121'CSE5313_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE5313_L4: "CSE5313 Coding and information theory for data science (Lecture 4)",
+    Math4201'CSE5313_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE5313_L5: "CSE5313 Coding and information theory for data science (Lecture 5)",
+    Math416'CSE5313_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE5313_L6: "CSE5313 Coding and information theory for data science (Lecture 6)",
+    Math401'CSE5313_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE5313_L7: "CSE5313 Coding and information theory for data science (Lecture 7)",
+    CSE332S'CSE5313_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE5313_L8: "CSE5313 Coding and information theory for data science (Lecture 8)",
+    CSE347'CSE5313_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE5313_L9: "CSE5313 Coding and information theory for data science (Lecture 9)",
+    CSE442T'CSE5313_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE5313_L10: "CSE5313 Coding and information theory for data science (Recitation 10)",
+    CSE5313'CSE5313_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE5313_L11: "CSE5313 Coding and information theory for data science (Recitation 11)",
+    CSE510'CSE5313_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE5313_L12: "CSE5313 Coding and information theory for data science (Lecture 12)",
+    CSE559A'CSE5313_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE5313_L13: "CSE5313 Coding and information theory for data science (Lecture 13)",
+    CSE5519'CSE5313_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE5313_L14: "CSE5313 Coding and information theory for data science (Lecture 14)",
+    Swap: {
-    CSE5313_L15: "CSE5313 Coding and information theory for data science (Lecture 15)",
+      display: 'hidden',
-    CSE5313_L16: "CSE5313 Coding and information theory for data science (Exam Review)",
+      theme:{
-    CSE5313_L17: "CSE5313 Coding and information theory for data science (Lecture 17)",
+        timestamp: true,
-    CSE5313_L18: "CSE5313 Coding and information theory for data science (Lecture 18)",
+      }
-    CSE5313_L19: "CSE5313 Coding and information theory for data science (Lecture 19)",
+    },
-    CSE5313_L20: "CSE5313 Coding and information theory for data science (Lecture 20)",
+    index: {
-    CSE5313_L21: "CSE5313 Coding and information theory for data science (Lecture 21)",
+      display: 'hidden',
-    CSE5313_L22: "CSE5313 Coding and information theory for data science (Lecture 22)",
+      theme:{
-    CSE5313_L23: "CSE5313 Coding and information theory for data science (Lecture 23)",
+        sidebar: false,
-    CSE5313_L24: "CSE5313 Coding and information theory for data science (Lecture 24)",
+        timestamp: true,
-    CSE5313_L25: "CSE5313 Coding and information theory for data science (Lecture 25)",
+      }
-    CSE5313_L26: "CSE5313 Coding and information theory for data science (Lecture 26)",
+    },
-    CSE5313_L27: "CSE5313 Coding and information theory for data science (Lecture 27)",
+    about: {
-}
+      display: 'hidden',
+      theme:{
+        sidebar: false,
+        timestamp: true,
+      }
+    },
+    contact: {
+      display: 'hidden',
+      theme:{
+        sidebar: false,
+        timestamp: true,
+      }
+    }
+  }

content/CSE5519/CSE5519_H5.md

@@ -1,21 +1,2 @@
 # CSE5519 Advances in Computer Vision (Topic H: 2025: Safety, Robustness, and Evaluation of CV Models)
 
-## Incorporating Geo-Diverse Knowledge into Prompting for Increased Geographic Robustness in Object Recognition
-
-Does adding geographical context to CLIP prompts improve recognition across geographies?
-
-Yes, about 1%
-
-Can an LLM provide useful geographic descriptive knowledge to improve recognition?
-
-Yes
-
-How can we optimize soft prompts for CLIP using an accessible data source with consideration of target geographies not represented in the training set?
-
-Where can soft prompts enhanced with geographical knowledge provide the most benefits?
-
-> [!TIP]
->
-> This model proposed an effective way to improve the model performance by self-querying geographical data.
->
-> I wonder what might be the ultimate boundary of the LLM-generated context and performance improvement. Theoretically,  it seems that we can use LLM to generate the majority of possible contexts before making predictions and use the context to improve the performance. However, introducing additional (might be irrelevant) information may generate hallucinations. I wonder if we can find a general approach to let LLM generate a decent context for the task and use the context to improve the performance.

content/CSE5519/CSE5519_J5.md

@@ -1,22 +1,2 @@
 # CSE5519 Advances in Computer Vision (Topic J: 2025: Open-Vocabulary Object Detection)
 
-## DINO-X: A Unified Vision Model for Open-World Object Detection and Understanding
-
-Input:
-
-- Text prompt encoder
-- Visual prompt encoder
-- Customized prompt encoder
-
-Output:
-
-- Box (object selection)
-- Mask (pixel embedding map)
-- Keypoint (object pose, joints estimation)
-- Language (semantic understanding)
-
-> [!TIP]
->
-> This model provides the latest solution for the open-vocabulary object detection task and using Grounding-100M to break the benchmark.
->
-> In some figures they displayed in the paper. I found some interesting differences between human recognition and CV. The fruits with smiling faces. In the object detection task, it seems that the DINO-X is not focusing on the smiling face but the fruit itself. I wonder if they can capture the abstract meaning of this representation and how it is different from human recognition, and why?

content/CSE5519/_meta.js

@@ -1,68 +1,61 @@
 export default {
-    index: "Course Description",
+    menu: {
-    "---":{
+      title: 'Home',
-        type: 'separator'
+      type: 'menu',
+      items: {
+        index: {
+          title: 'Home',
+          href: '/'
+        },
+        about: {
+          title: 'About',
+          href: '/about'
+        },
+        contact: {
+          title: 'Contact Me',
+          href: '/contact'
+        }
+      },
     },
-    CSE5519_L1: "CSE5519 Advances in Computer Vision (Lecture 1)",
+    Math3200'CSE5519_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE5519_L2: "CSE5519 Advances in Computer Vision (Lecture 2)",
+    Math429'CSE5519_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE5519_L3: "CSE5519 Advances in Computer Vision (Lecture 3)",
+    Math4111'CSE5519_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    "---":{
+    Math4121'CSE5519_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-        type: 'separator'
+    Math4201'CSE5519_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Math416'CSE5519_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Math401'CSE5519_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE332S'CSE5519_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE347'CSE5519_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE442T'CSE5519_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE5313'CSE5519_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE510'CSE5519_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE559A'CSE5519_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE5519'CSE5519_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Swap: {
+      display: 'hidden',
+      theme:{
+        timestamp: true,
+      }
     },
-    CSE5519_C1: "CSE5519 Advances in Computer Vision (Topic C: 2021 and before: Neural Rendering)",
+    index: {
-    CSE5519_F1: "CSE5519 Advances in Computer Vision (Topic F: 2021 and before: Representation Learning)",
+      display: 'hidden',
-    CSE5519_B1: "CSE5519 Advances in Computer Vision (Topic B: 2021 and before: Vision-Language Models)",
+      theme:{
-    CSE5519_D1: "CSE5519 Advances in Computer Vision (Topic D: 2021 and before: Image and Video Generation)",
+        sidebar: false,
-    CSE5519_A1: "CSE5519 Advances in Computer Vision (Topic A: 2021 and before: Semantic Segmentation)",
+        timestamp: true,
-    CSE5519_E1: "CSE5519 Advances in Computer Vision (Topic E: 2021 and before: Deep Learning for Geometric Computer Vision)",
+      }
-    CSE5519_I1: "CSE5519 Advances in Computer Vision (Topic I: 2021 and before: Embodied Computer Vision and Robotics)",
-    CSE5519_J1: "CSE5519 Advances in Computer Vision (Topic J: 2021 and before: Open-Vocabulary Object Detection)",
-    "---":{
-        type: 'separator'
     },
-    CSE5519_H2: "CSE5519 Advances in Computer Vision (Topic H: 2022 and before: Safety, Robustness, and Evaluation of CV Models)",
+    about: {
-    CSE5519_G2: "CSE5519 Advances in Computer Vision (Topic G: 2022 and before: Correspondence Estimation and Structure from Motion)",
+      display: 'hidden',
-    CSE5519_A2: "CSE5519 Advances in Computer Vision (Topic A: 2022: Semantic Segmentation)",
+      theme:{
-    CSE5519_E2: "CSE5519 Advances in Computer Vision (Topic E: 2022: Deep Learning for Geometric Computer Vision)",
+        sidebar: false,
-    CSE5519_C2: "CSE5519 Advances in Computer Vision (Topic C: 2022: Neural Rendering)",
+        timestamp: true,
-    CSE5519_F2: "CSE5519 Advances in Computer Vision (Topic F: 2022: Representation Learning)",
+      }
-    CSE5519_B2: "CSE5519 Advances in Computer Vision (Topic B: 2022: Vision-Language Models)",
-    CSE5519_D2: "CSE5519 Advances in Computer Vision (Topic D: 2022: Image and Video Generation)",
-    CSE5519_I2: "CSE5519 Advances in Computer Vision (Topic I: 2022: Embodied Computer Vision and Robotics)",
-    CSE5519_J2: "CSE5519 Advances in Computer Vision (Topic J: 2022: Open-Vocabulary Object Detection)",
-    "---":{
-        type: 'separator'
     },
-    CSE5519_H3: "CSE5519 Advances in Computer Vision (Topic H: 2023: Safety, Robustness, and Evaluation of CV Models)",
+    contact: {
-    CSE5519_B3: "CSE5519 Advances in Computer Vision (Topic B: 2023: Vision-Language Models)",
+      display: 'hidden',
-    CSE5519_G3: "CSE5519 Advances in Computer Vision (Topic G: 2023: Correspondence Estimation and Structure from Motion)",
+      theme:{
-    CSE5519_C3: "CSE5519 Advances in Computer Vision (Topic C: 2023: Neural Rendering)",
+        sidebar: false,
-    CSE5519_D3: "CSE5519 Advances in Computer Vision (Topic D: 2023: Image and Video Generation)",
+        timestamp: true,
-    CSE5519_E3: "CSE5519 Advances in Computer Vision (Topic E: 2023: Deep Learning for Geometric Computer Vision)",
+      }
-    CSE5519_F3: "CSE5519 Advances in Computer Vision (Topic F: 2023: Representation Learning)",
+    }
-    CSE5519_I3: "CSE5519 Advances in Computer Vision (Topic I: 2023 - 2024: Embodied Computer Vision and Robotics)",
+  }
-    CSE5519_J3: "CSE5519 Advances in Computer Vision (Topic J: 2023 - 2024: Open-Vocabulary Object Detection)",
-    CSE5519_A3: "CSE5519 Advances in Computer Vision (Topic A: 2023 - 2024: Semantic Segmentation)",
-    "---":{
-        type: 'separator'
-    },
-    CSE5519_G4: "CSE5519 Advances in Computer Vision (Topic G: 2024: Correspondence Estimation and Structure from Motion)",
-    CSE5519_F4: "CSE5519 Advances in Computer Vision (Topic F: 2024: Representation Learning)",
-    CSE5519_D4: "CSE5519 Advances in Computer Vision (Topic D: 2024: Image and Video Generation)",
-    CSE5519_E4: "CSE5519 Advances in Computer Vision (Topic E: 2024: Deep Learning for Geometric Computer Vision)",
-    CSE5519_B4: "CSE5519 Advances in Computer Vision (Topic B: 2024: Vision-Language Models)",
-    CSE5519_H4: "CSE5519 Advances in Computer Vision (Topic H: 2024: Safety, Robustness, and Evaluation of CV Models)",
-    CSE5519_C4: "CSE5519 Advances in Computer Vision (Topic C: 2024 - 2025: Neural Rendering)",
-    "---":{
-        type: 'separator'
-    },
-    CSE5519_F5: "CSE5519 Advances in Computer Vision (Topic F: 2025: Representation Learning)",
-    CSE5519_B5: "CSE5519 Advances in Computer Vision (Topic B: 2025: Vision-Language Models)",
-    CSE5519_D5: "CSE5519 Advances in Computer Vision (Topic D: 2025: Image and Video Generation)",
-    CSE5519_E5: "CSE5519 Advances in Computer Vision (Topic E: 2025: Deep Learning for Geometric Computer Vision)",
-    CSE5519_A4: "CSE5519 Advances in Computer Vision (Topic A: 2025: Semantic Segmentation)",
-    CSE5519_G5: "CSE5519 Advances in Computer Vision (Topic G: 2025: Correspondence Estimation and Structure from Motion)",
-    CSE5519_I4: "CSE5519 Advances in Computer Vision (Topic I: 2025: Embodied Computer Vision and Robotics)",
-    CSE5519_H5: "CSE5519 Advances in Computer Vision (Topic H: 2025: Safety, Robustness, and Evaluation of CV Models)",
-    CSE5519_J5: "CSE5519 Advances in Computer Vision (Topic J: 2025: Open-Vocabulary Object Detection)",
-}

content/CSE559A/_meta.js

@@ -1,32 +1,61 @@
 export default {
-    index: "Course Description",
+    menu: {
-    "---":{
+      title: 'Home',
-        type: 'separator'
+      type: 'menu',
+      items: {
+        index: {
+          title: 'Home',
+          href: '/'
+        },
+        about: {
+          title: 'About',
+          href: '/about'
+        },
+        contact: {
+          title: 'Contact Me',
+          href: '/contact'
+        }
+      },
     },
-    CSE559A_L1: "Computer Vision (Lecture 1)",
+    Math3200'CSE559A_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE559A_L2: "Computer Vision (Lecture 2)",
+    Math429'CSE559A_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE559A_L3: "Computer Vision (Lecture 3)",
+    Math4111'CSE559A_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE559A_L4: "Computer Vision (Lecture 4)",
+    Math4121'CSE559A_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE559A_L5: "Computer Vision (Lecture 5)",
+    Math4201'CSE559A_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE559A_L6: "Computer Vision (Lecture 6)",
+    Math416'CSE559A_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE559A_L7: "Computer Vision (Lecture 7)",
+    Math401'CSE559A_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE559A_L8: "Computer Vision (Lecture 8)",
+    CSE332S'CSE559A_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE559A_L9: "Computer Vision (Lecture 9)",
+    CSE347'CSE559A_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE559A_L10: "Computer Vision (Lecture 10)",
+    CSE442T'CSE559A_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE559A_L11: "Computer Vision (Lecture 11)",
+    CSE5313'CSE559A_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE559A_L12: "Computer Vision (Lecture 12)",
+    CSE510'CSE559A_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE559A_L13: "Computer Vision (Lecture 13)",
+    CSE559A'CSE559A_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE559A_L14: "Computer Vision (Lecture 14)",
+    CSE5519'CSE559A_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
-    CSE559A_L15: "Computer Vision (Lecture 15)",
+    Swap: {
-    CSE559A_L16: "Computer Vision (Lecture 16)",
+      display: 'hidden',
-    CSE559A_L17: "Computer Vision (Lecture 17)",
+      theme:{
-    CSE559A_L18: "Computer Vision (Lecture 18)",
+        timestamp: true,
-    CSE559A_L19: "Computer Vision (Lecture 19)",
+      }
-    CSE559A_L20: "Computer Vision (Lecture 20)",
+    },
-    CSE559A_L21: "Computer Vision (Lecture 21)",
+    index: {
-    CSE559A_L22: "Computer Vision (Lecture 22)",
+      display: 'hidden',
-    CSE559A_L23: "Computer Vision (Lecture 23)",
+      theme:{
-    CSE559A_L24: "Computer Vision (Lecture 24)",
+        sidebar: false,
-    CSE559A_L25: "Computer Vision (Lecture 25)",
+        timestamp: true,
-    CSE559A_L26: "Computer Vision (Lecture 26)",
+      }
-}
+    },
+    about: {
+      display: 'hidden',
+      theme:{
+        sidebar: false,
+        timestamp: true,
+      }
+    },
+    contact: {
+      display: 'hidden',
+      theme:{
+        sidebar: false,
+        timestamp: true,
+      }
+    }
+  }

content/CSE559A/index.md

@@ -1,167 +1,4 @@
 # CSE 559A: Computer Vision
 
-## Course Overview
+## Course Description
 
-This course introduces computational systems that analyze images and infer physical structure, objects, and scenes. Topics include color, shape, geometry, motion estimation, classification, segmentation, detection, restoration, enhancement, and synthesis. Emphasis is on mathematical foundations, geometric reasoning, and deep-learning approaches.
-
-**Department:** Computer Science & Engineering (559A)
-**Credits:** 3
-**Time:** Tuesday/Thursday 1–2:20pm
-**Location:** Jubel Hall 120
-**Modality:** In-person
-
-**Instructor:** Prof. Nathan Jacobs
-**Email:** [jacobsn@wustl.edu](mailto:jacobsn@wustl.edu) (Piazza preferred)
-**Office:** McKelvey Hall 3032 or Zoom
-**Office Hours:** By appointment
-
-**TAs:** Nia Hodges, Dijkstra Liu, Alex Wollam, David Wang
-Office hours posted on Canvas.
-
-### Textbook
-
-Primary: *Computer Vision: Algorithms and Applications (2nd Ed.)* — [http://szeliski.org/Book/](http://szeliski.org/Book/)
-Secondary: *Computer Vision: Models, Learning, and Inference* — [http://www.computervisionmodels.com/](http://www.computervisionmodels.com/)
-Secondary: *Foundations of Computer Vision* (MIT Press)
-
-## Prerequisites
-
-**Official:** CSE 417T, ESE 417, CSE 514A, or CSE 517A
-**Practical:** Python programming, data structures, and strong background in linear algebra, vector calculus, and probability.
-
-## Learning Outcomes
-
-Students completing the course will be able to:
-
-* Describe the image formation process mathematically.
-* Compare classical and modern approaches to geometry, motion, detection, and semantic tasks.
-* Derive algorithms for vision problems using mathematical tools.
-* Implement geometric and semantic inference systems in Python.
-
-## Course Topics
-
-* **Low-Level Feature Extraction:** classical and modern (CNNs/Transformers)
-* **Semantic Vision:** classification, segmentation, detection
-* **Geometric Vision:** image formation, transformations, motion, metrology, stereo, depth
-* **Extended Topics:** e.g., generative models, multimodal learning (TBD)
-
----
-
-## Grading
-
-### Homework
-
-Homework consists of ~7 programming assignments in Python, focused on implementing core algorithms. Most include auto-graded components. Two late days allowed per assignment; after that, the score is zero. No late submissions for quizzes, paper reviews, or project.
-
-### Exams / Quizzes
-
-There are ~5 quizzes covering lectures and readings. They include both theoretical and applied questions. No late quizzes.
-
-### Paper Reviews
-
-Four short reviews of recent computer vision research papers. Includes an in-class discussion component.
-
-### Project
-
-An individual or small-team project implementing, evaluating, or developing a vision method. Specifications on Canvas.
-
-### Final Grades
-
-| Component         | Weight |
-| ----------------- | ------ |
-| Homework (~7)     | ~60%   |
-| Quizzes (~5)      | ~15%   |
-| Paper Reviews (4) | ~5%    |
-| Project           | ~15%   |
-| Participation     | ~5%    |
-
-### Grading Scale
-
-| Letter | Range         |
-| ------ | ------------- |
-| A      | 94% and above |
-| A-     | <94% to 90%   |
-| B+     | <90% to 87%   |
-| B      | <87% to 84%   |
-| B-     | <84% to 80%   |
-| C+     | <80% to 77%   |
-| C      | <77% to 74%   |
-| C-     | <74% to 70%   |
-| D+     | <70% to 67%   |
-| D      | <67% to 64%   |
-| D-     | <64% to 61%   |
-| F      | <61%          |
-
----
-
-## Schedule
-
-Approximate; see Canvas for updates.
-
-| Week         | Date   | Topic                                  | Notes                                     |
-| ------------ | ------ | -------------------------------------- | ----------------------------------------- |
-| W1           | Jan 14 | Overview                               |                                           |
-|              | Jan 16 | Image Formation & Filtering            |                                           |
-| W2           | Jan 21 | Image Formation & Filtering            | HW0 due                                   |
-|              | Jan 23 | Image Formation & Filtering            |                                           |
-| W3           | Jan 28 | Image Formation & Filtering            | HW1 due                                   |
-|              | Jan 30 | Image Formation & Filtering            | Module Quiz                               |
-| W4           | Feb 4  | Deep Learning for Image Classification | Paper review due                          |
-|              | Feb 6  | Deep Learning for Image Classification |                                           |
-| W5           | Feb 11 | Deep Learning for Image Classification | HW2 due                                   |
-|              | Feb 13 | Deep Learning for Image Classification |                                           |
-| W6           | Feb 18 | Deep Learning for Image Classification | HW3 due; paper review due                 |
-|              | Feb 20 | Deep Learning for Image Classification |                                           |
-| W7           | Feb 25 | Deep Learning for Image Classification | Module Quiz                               |
-|              | Feb 27 | Deep Learning for Image Understanding  |                                           |
-| W8           | Mar 4  | Deep Learning for Image Understanding  | HW4 due; paper review due                 |
-|              | Mar 6  | Deep Learning for Image Understanding  | Module Quiz                               |
-| Spring Break | —      | —                                      |                                           |
-| W9           | Mar 18 | Feature Detection, Matching, Motion    |                                           |
-|              | Mar 20 | Feature Detection, Matching, Motion    |                                           |
-| W10          | Mar 25 | Feature Detection, Matching, Motion    | HW5 due; project launch; paper review due |
-|              | Mar 27 | Feature Detection, Matching, Motion    | Module Quiz                               |
-| W11          | Apr 1  | Multiple Views and Stereo              | HW6 due                                   |
-|              | Apr 3  | Multiple Views and Stereo              |                                           |
-| W12          | Apr 8  | Multiple Views and Stereo              |                                           |
-|              | Apr 10 | Multiple Views and Stereo              | Module Quiz                               |
-| W13          | Apr 15 | Extended Topic                         | HW7 due                                   |
-|              | Apr 17 | Extended Topic                         |                                           |
-| W14          | Apr 22 | Extended Topic                         | Final project due this week               |
-|              | Apr 24 | Final Lecture / Presentations          | No Final Exam                             |
-
----
-
-## Technology Requirements
-
-Assignments may require GPU access (e.g., Google Colab, Academic Jupyter). Students must avoid modifying starter code in ways that break auto-grading.
-
-## Collaboration & Materials Policy
-
-Discussion is allowed, but all submitted work (code, written content, reports) must be individual. Posting assignment solutions publicly is prohibited. Automated plagiarism detection (e.g., Turnitin) may be used.
-
-## Generative AI Policy
-
-* **Homework & Projects:** Allowed with limitations; students must understand all algorithms used.
-* **Quizzes:** May be used for explanation but not direct answering.
-* **Reports:** AI-assisted writing permitted with responsibility for correctness.
-
-More detailed rules are on Canvas.
-
-## University Policies
-
-### Recording Policy
-
-Classroom activities and materials may not be recorded or distributed without explicit authorization.
-
-### COVID-19 Guidelines
-
-Students with symptoms must contact Student Health for testing. Masking policies may change depending on conditions.
-
----
-
-If you'd like, I can also produce:
-
-* a **cleaned, typographically polished** version
-* a **PDF** or **GitHub-ready README.md**
-* a version styled identically to your department’s standard syllabus format

content/Math401/Extending_thesis/Math401_R1.md

@@ -98,7 +98,7 @@ We want to define a vector space with notation of multiplication of two vectors
 That is
 
 $$
-(v_1+v_2)\otimes w=(v_1\otimes w)+(v_2\otimes w)\text{ and } v\otimes (w_1+w_2)=(v\otimes w_1)+(v\otimes w_2)
+(v_1+v_1)\otimes w=(v_1\otimes w)+(v_2\otimes w)\text{ and } v\otimes (w_1+w_2)=(v\otimes w_1)+(v\otimes w_2)
 $$
 
 and enables scalar multiplication by

content/Math401/Extending_thesis/Math401_R4.md

@@ -52,5 +52,3 @@ $$
 ## Quantum error correcting codes
 
 This part is intentionally left blank and may be filled near the end of the semester, by assignments given in CSE5313.
-
-[Link to self-contained report](../../CSE5313/Exam_reviews/CSE5313_F1.md)

content/Math401/Extending_thesis/Math401_S5.md

@@ -1,4 +1,4 @@
-# Math 401, Fall 2025: Thesis notes, S5, Differential Forms
+# Math 401, Fall 2025: Thesis notes, S4, Differential Forms
 
 This note aim to investigate  What is homology and cohomology?
 
@@ -235,7 +235,3 @@ $$
 $$
 
 A tangent vector at $p\in M$ is the 
-
-[2025.12.03]
-
-Goal: Finish the remaining parts of this book

content/Math401/Extending_thesis/Math401_S6.md

@@ -1,11 +0,0 @@
-# Math 401, Fall 2025: Thesis notes, S6, Algebraic Geometry
-
-## Affine algebraic variety
-
-The affine algebraic variety is the common zero set of a collection $\{F_i\}_{i\in I}$ of complex polynomials on complex n-space $\mathbb{C}^n$. We write
-
-$$
-V=\mathbb{V}(\{F_i\}_{i\in I})=\{z\in \mathbb{C}^n\vert F_i(z)=0\text{ for all } i\in I\}
-$$
-
-Note that $I$ may not be countable or finite.

content/Math401/Freiwald_summer/Math401_T6.md

@@ -76,7 +76,7 @@ This is a contradiction, so $|\psi^+\rangle$ is entangled.
 
 #### Density operator
 
-A density operator is a [Hermitian](./Math401_T5#definition-of-hermitian-operator), positive semi-definite operator with trace 1.
+A density operator is a [Hermitian](https://notenextra.trance-0.com/Math401/Math401_T5#definition-of-hermitian-operator), positive semi-definite operator with trace 1.
 
 The density operator of a pure state $|\psi\rangle$ is $\rho=|\psi\rangle\langle\psi|$.
 

content/Math4201/Exam_reviews/Math4201_E3.md

@@ -1,649 +0,0 @@
-# Math 4201 Final Exam Review
-
-> [!NOTE]
->
-> This is a review for definitions we covered in the classes. It may serve as a cheat sheet for the exam if you are allowed to use it.
-
-## Topological space
-
-### Basic definitions
-
-#### Definition for topological space
-
-A topological space is a pair of set $X$ and a collection of subsets of $X$, denoted by $\mathcal{T}$ (imitates the set of "open sets" in $X$), satisfying the following axioms:
-
-1. $\emptyset \in \mathcal{T}$ and $X \in \mathcal{T}$
-2. $\mathcal{T}$ is closed with respect to arbitrary unions. This means, for any collection of open sets $\{U_\alpha\}_{\alpha \in I}$, we have $\bigcup_{\alpha \in I} U_\alpha \in \mathcal{T}$
-3. $\mathcal{T}$ is closed with respect to finite intersections. This means, for any finite collection of open sets $\{U_1, U_2, \ldots, U_n\}$, we have $\bigcap_{i=1}^n U_i \in \mathcal{T}$
-
-#### Definition of open set
-
-$U\subseteq X$ is an open set if $U\in \mathcal{T}$
-
-#### Definition of closed set
-
-$Z\subseteq X$ is a closed set if $X\setminus Z\in \mathcal{T}$
-
-> [!WARNING]
->
-> A set is closed is not the same as its not open.
->
-> In all topologies over non-empty sets, $X, \emptyset$ are both closed and open.
-
-### Basis
-
-#### Definition of topological basis
-
-For a set $X$, a topology basis, denoted by $\mathcal{B}$, is a collection of subsets of $X$, such that the following properties are satisfied:
-
-1. For any $x \in X$, there exists a $B \in \mathcal{B}$ such that $x \in B$ (basis covers the whole space)
-2. If $B_1, B_2 \in \mathcal{B}$ and $x \in B_1 \cap B_2$, then there exists a $B_3 \in \mathcal{B}$ such that $x \in B_3 \subseteq B_1 \cap B_2$ (every non-empty intersection of basis elements are also covered by a basis element)
-
-#### Definition of topology generated by basis
-
-Let $\mathcal{B}$ be a basis for a topology on a set $X$. Then the topology generated by $\mathcal{B}$ is defined by the set as follows:
-
-$$
-\mathcal{T}_{\mathcal{B}} \coloneqq \{ U \subseteq X \mid \forall x\in U, \exists B\in \mathcal{B} \text{ such that } x\in B\subseteq U \}
-$$
-
-> This is basically a closure of $\mathcal{B}$ under arbitrary unions and finite intersections
-
-#### Lemma of topology generated by basis
-
-$U\in \mathcal{T}_{\mathcal{B}}\iff \exists \{B_\alpha\}_{\alpha \in I}\subseteq \mathcal{B}$ such that $U=\bigcup_{\alpha \in I} B_\alpha$
-
-#### Definition of basis generated from a topology
-
-Let $(X, \mathcal{T})$ be a topological space. Then the basis generated from a topology is $\mathcal{C}\subseteq \mathcal{B}$ such that $\forall U\in \mathcal{T}$, $\forall x\in U$, $\exists B\in \mathcal{C}$ such that $x\in B\subseteq U$.
-
-#### Definition of subbasis of topology
-
-A subbasis of a topology is a collection $\mathcal{S}\subseteq \mathcal{T}$ such that $\bigcup_{U\in \mathcal{S}} U=X$.
-
-#### Definition of topology generated by subbasis
-
-Let $\mathcal{S}\subseteq \mathcal{T}$ be a subbasis of a topology on $X$, then the basis generated by such subbasis is the closure of finite intersection of $\mathcal{S}$
-
-$$
-\mathcal{B}_{\mathcal{S}} \coloneqq \{B\mid B\text{ is the intersection of a finite number of elements of }\mathcal{S}\}
-$$
-
-Then the topology generated by $\mathcal{B}_{\mathcal{S}}$ is the subbasis topology denoted by $\mathcal{T}_{\mathcal{S}}$.
-
-Note that all open set with respect to $\mathcal{T}_{\mathcal{S}}$ can be written as a union of finitely intersections of elements of $\mathcal{S}$
-
-### Comparing topologies
-
-#### Definition of finer and coarser topology
-
-Let $(X,\mathcal{T})$ and $(X,\mathcal{T}')$ be topological spaces. Then $\mathcal{T}$ is finer than $\mathcal{T}'$ if $\mathcal{T}'\subseteq \mathcal{T}$. $\mathcal{T}$ is coarser than $\mathcal{T}'$ if $\mathcal{T}\subseteq \mathcal{T}'$.
-
-#### Lemma of comparing basis
-
-Let $(X,\mathcal{T})$ and $(X,\mathcal{T}')$ be topological spaces with basis $\mathcal{B}$ and $\mathcal{B}'$. Then $\mathcal{T}$ is finer than $\mathcal{T}'$ if and only if for any $x\in X$, $x\in B'$, $B'\in \mathcal{B}'$, there exists $B\in \mathcal{B}$, such that $x\in B$ and $x\in B\subseteq B'$.
-
-### Product space
-
-#### Definition of cartesian product
-
-Let $X,Y$ be sets. The cartesian product of $X$ and $Y$ is the set of all ordered pairs $(x,y)$ where $x\in X$ and $y\in Y$, denoted by $X\times Y$.
-
-#### Definition of product topology
-
-Let $(X,\mathcal{T}_X)$ and $(Y,\mathcal{T}_Y)$ be topological spaces. Then the product topology on $X\times Y$ is the topology generated by the basis
-
-$$
-\mathcal{B}_{X\times Y}=\{U\times V, U\in \mathcal{T}_X, V\in \mathcal{T}_Y\}
-$$
-
-or equivalently,
-
-$$
-\mathcal{B}_{X\times Y}'=\{U\times V, U\in \mathcal{B}_X, V\in \mathcal{B}_Y\}
-$$
-
-> Product topology generated from open sets of $X$ and $Y$ is the same as product topology generated from their corresponding basis
-
-### Subspace topology
-
-#### Definition of subspace topology
-
-Let $(X,\mathcal{T})$ be a topological space and $Y\subseteq X$. Then the subspace topology on $Y$ is the topology given by
-
-$$
-\mathcal{T}_Y=\{U\cap Y|U\in \mathcal{T}\}
-$$
-
-or equivalently, let $\mathcal{B}$ be the basis for $(X,\mathcal{T})$. Then the subspace topology on $Y$ is the topology generated by the basis
-
-$$
-\mathcal{B}_Y=\{U\cap Y| U\in \mathcal{B}\}
-$$
-
-#### Lemma of open sets in subspace topology
-
-Let $(X,\mathcal{T})$ be a topological space and $Y\subseteq X$. Then if $U\subseteq Y$, $U$ is open in $(Y,\mathcal{T}_Y)$, then $U$ is open in $(X,\mathcal{T})$.
-
-> This also holds for closed set in closed subspace topology
-
-### Interior and closure
-
-#### Definition of interior
-
-The interior of $A$ is the largest open subset of $A$.
-
-$$
-A^\circ=\bigcup_{U\subseteq A, U\text{ is open in }X} U
-$$
-
-#### Definition of closure
-
-The closure of $A$ is the smallest closed superset of $A$.
-
-$$
-\overline{A}=\bigcap_{U\supseteq A, U\text{ is closed in }X} U
-$$
-
-#### Definition of neighborhood
-
-A neighborhood of a point $x\in X$ is an open set $U\in \mathcal{T}$ such that $x\in U$.
-
-#### Definition of limit points
-
-A point $x\in X$ is a limit point of $A$ if every neighborhood of $x$ contains a point in $A-\{x\}$.
-
-We denote the set of all limits points of $A$ by $A'$.
-
-$\overline{A}=A\cup A'$
-
-### Sequences and continuous functions
-
-#### Definition of convergence
-
-Let $X$ be a topological space. A sequence $(x_n)_{n\in\mathbb{N}_+}$ in $X$ converges to $x\in X$ if for any neighborhood $U$ of $x$, there exists $N\in\mathbb{N}_+$ such that $\forall n\geq N, x_n\in U$.
-
-#### Definition of Hausdoorff space
-
-A topological space $(X,\mathcal{T})$ is Hausdorff if for any two distinct points $x,y\in X$, there exist open neighborhoods $U$ and $V$ of $x$ and $y$ respectively such that $U\cap V=\emptyset$.
-
-#### Uniqueness of convergence in Hausdorff spaces
-
-In a Hausdorff space, if a sequence $(x_n)_{n\in\mathbb{N}_+}$ converges to $x\in X$ and $y\in X$, then $x=y$.
-
-#### Closed singleton in Hausdorff spaces
-
-In a Hausdorff space, if $x\in X$, then $\{x\}$ is a closed set.
-
-#### Definition of continuous function
-
-Let $(X,\mathcal{T}_X)$ and $(Y,\mathcal{T}_Y)$ be topological spaces. A function $f:X\to Y$ is continuous if for any open set $U\subseteq Y$, $f^{-1}(U)$ is open in $X$.
-
-#### Definition of point-wise continuity
-
-Let $(X,\mathcal{T}_X)$ and $(Y,\mathcal{T}_Y)$ be topological spaces. A function $f:X\to Y$ is point-wise continuous at $x\in X$ if for every openset $V\subseteq Y$, $f(x)\in V$ then there exists an open set $U\subseteq X$ such that $x\in U$ and $f(U)\subseteq V$.
-
-#### Lemma of continuous functions
-
-If $f:X\to Y$ is point-wise continuous for all $x\in X$, then $f$ is continuous.
-
-#### Properties of continuous functions
-
-If $f:X\to Y$ is continuous, then
-
-1. $\forall A\subseteq Y$, $f^{-1}(A^c)=X\setminus f^{-1}(A)$ (complements maps to complements)
-2. $\forall A_\alpha\subseteq Y, \alpha\in I$, $f^{-1}(\bigcup_{\alpha\in I} A_\alpha)=\bigcup_{\alpha\in I} f^{-1}(A_\alpha)$
-3. $\forall A_\alpha\subseteq Y, \alpha\in I$, $f^{-1}(\bigcap_{\alpha\in I} A_\alpha)=\bigcap_{\alpha\in I} f^{-1}(A_\alpha)$
-4. $f^{-1}(U)$ is open in $X$ for any open set $U\subseteq Y$.
-5. $f$ is continuous at $x\in X$.
-6. $f^{-1}(V)$ is closed in $X$ for any closed set $V\subseteq Y$.
-7. Assume $\mathcal{B}$ is a basis for $Y$, then $f^{-1}(\mathcal{B})$ is open in $X$ for any $B\in \mathcal{B}$.
-8. $\forall A\subseteq X$, $\overline{f(A)}=f(\overline{A})$
-
-#### Definition of homeomorphism
-
-Let $(X,\mathcal{T}_X)$ and $(Y,\mathcal{T}_Y)$ be topological spaces. A function $f:X\to Y$ is a homeomorphism if $f$ is continuous, bijective and $f^{-1}:Y\to X$ is continuous.
-
-#### Ways to construct continuous functions
-
-1. If $f:X\to Y$ is constant function, $f(x)=y_0$ for all $x\in X$, then $f$ is continuous. (constant functions are continuous)
-2. If $A$ is a subspace of $X$, $f:A\to X$ is the inclusion map $f(x)=x$ for all $x\in A$, then $f$ is continuous. (inclusion maps are continuous)
-3. If $f:X\to Y$ is continuous, $g:Y\to Z$ is continuous, then $g\circ f:X\to Z$ is continuous. (composition of continuous functions is continuous)
-4. If $f:X\to Y$ is continuous, $A$ is a subspace of $X$, then $f|_A:X\to Y$ is continuous. (domain restriction is continuous)
-5. If $f:X\to Y$ is continuous, $Z$ is a subspace of $Y$, then $f:X\to Z$, $g(x)=f(x)\cap Z$ is continuous. If $Y$ is a subspace of $Z$, then $h:X\to Z$, $h(x)=f(x)$ is continuous (composition of $f$ and inclusion map).
-6. If $f:X\to Y$ is continuous, $X$ can be written as a union of open sets $\{U_\alpha\}_{\alpha\in I}$, then $f|_{U_\alpha}:X\to Y$ is continuous.
-7. If $X=Z_1\cup Z_2$, and $Z_1,Z_2$ are closed equipped with subspace topology, let $g_1:Z_1\to Y$ and $g_2:Z_2\to Y$ be continuous, and for all $x\in Z_1\cap Z_2$, $g_1(x)=g_2(x)$, then $f:X\to Y$ by $f(x)\begin{cases}g_1(x), & x\in Z_1 \\ g_2(x), & x\in Z_2\end{cases}$ is continuous. (pasting lemma)
-8. $f:X\to Y$ is continuous, $g:X\to Z$ is continuous if and only if $H:X\to Y\times Z$, where $Y\times Z$ is equipped with the product topology, $H(x)=(f(x),g(x))$ is continuous. (proved in homework)
-
-### Metric spaces
-
-#### Definition of metric
-
-A metric on $X$ is a function $d:X\times X\to \mathbb{R}$ such that $\forall x,y\in X$,
-
-1. $d(x,x)=0$
-2. $d(x,y)\geq 0$
-3. $d(x,y)=d(y,x)$
-4. $d(x,y)+d(y,z)\geq d(x,z)$
-
-#### Definition of metric ball
-
-The metric ball $B_r^{d}(x)$ is the set of all points $y\in X$ such that $d(x,y)\leq r$.
-
-#### Definition of metric topology
-
-Let $X$ be a metric space with metric $d$. Then $X$ is equipped with the metric topology generated by the metric balls $B_r^{d}(x)$ for $r>0$.
-
-#### Definition of metrizable
-
-A topological space $(X,\mathcal{T})$ is metrizable if it is the metric topology for some metric $d$ on $X$.
-
-#### Hausdorff axiom for metric spaces
-
-Every metric space is Hausdorff (take metric balls $B_r(x)$ and $B_r(y)$, $r=\frac{d(x,y)}{2}$).
-
-If a topology isn't Hausdorff, then it isn't metrizable.
-
-Prove by triangle inequality and contradiction.
-
-#### Common metrics in $\mathbb{R}^n$
-
-Euclidean metric
-
-$$
-d(x,y)=\sqrt{\sum_{i=1}^n (x_i-y_i)^2}
-$$
-
-Square metric
-
-$$
-\rho(x,y)=\max_{i=1}^n |x_i-y_i|
-$$
-
-Manhattan metric
-
-$$
-m(x,y)=\sum_{i=1}^n |x_i-y_i|
-$$
-
-These metrics are equivalent.
-
-#### Product topology and metric
-
-If $(X,d),(Y,d')$ are metric spaces, then $X\times Y$ is metric space with metric $d(x,y)=\max\{d(x_1,y_1),d(x_2,y_2)\}$.
-
-#### Uniform metric
-
-Let $\mathbb{R}^\omega$ be the set of all infinite sequences of real numbers. Then $\overline{d(x,y)}=\sup_{i=1}^\omega \min\{1,|x_i-y_i|\}$, the uniform metric on $\mathbb{R}^\omega$ is a metric.
-
-#### Metric space and converging sequences
-
-Let $X$ be a topological space, $A\subseteq X$, $x_n\to x$ such that $x_n\in A$. Then $x\in \overline{A}$.
-
-If $X$ is a **metric space**, $A\subseteq X$, $x\in \overline{A}$, then there exists converging sequence $x_n\to x$ such that $x_n\in A$.
-
-### Metric defined for functions
-
-#### Definition for bounded metric space
-
-A metric space $(Y,d)$ is bounded if there is $M\in \mathbb{R}^{\geq 0}$ such that for all $y_1,y_2\in Y$, $d(y_1,y_2)\leq M$.
-
-#### Definition for metric defined for functions
-
-Let $X$ be a topological space and $Y$ be a bounded metric space, then the set of all maps, denoted by $\operatorname{Map}(X,Y)$, $f:X\to Y\in \operatorname{Map}(X,Y)$ is a metric space with metric $\rho(f,g)=\sup_{x\in X} d(f(x),g(x))$.
-
-#### Space of continuous map is closed
-
-Let $(\operatorname{Map}(X,Y),\rho)$ be a metric space defined above, then every continuous map is a limit point of some sequence of continuous maps.
-
-$$
-Z=\{f\in \operatorname{Map}(X,Y)|f\text{ is continuous}\}
-$$
-
-$Z$ is closed in $(\operatorname{Map}(X,Y),\rho)$.
-
-### Quotient space
-
-#### Quotient map
-
-Let $X$ be a topological space and $X^*$ is a set. $q:X\to X^*$ is a surjective map. Then $q$ is a quotient map.
-
-#### Quotient topology
-
-Let $(X,\mathcal{T})$ be a topological space and $X^*$ be a set, $q:X\to X^*$ is a surjective map. Then
-
-$$
-\mathcal{T}^* \coloneqq \{U\subseteq X^*\mid q^{-1}(U)\in \mathcal{T}\}
-$$
-
-is a topology on $X^*$ called quotient topology.
-
-**That is equivalent to say that $U\subseteq X^*$ is open in $X^*$ if and only if $p^{-1}(U)\subseteq X$ is open in $X$.**
-
-This is also called "strong continuity" since compared with the continuous condition, it requires if $p^{-1}(U)$ is open in $X$, then $U$ is open in $X^*$.
-
-$(X^*,\mathcal{T}^*)$ is called the quotient space of $X$ by $q$.
-
-#### Closed map and open map
-
-$f:X\to Y$ is a open map if for each open set $U$ of $X$, $f(U)$ is open in $Y$; it is a closed map if for each closed set $U$ of $X$, $f(U)$ is closed in $Y$.
-
-> [!WARNING]
->
-> Not all quotient map are closed or open:
->
-> 1. Example of quotient map that is not open nor closed:
->
-> Consider the projection map $f:[0,1]\to S^1$, this map maps open set $[0,0.5)$ in $[0,1]$ to non open map $[0,\pi)$
->
-> 2. Example of open map that is not closed:
->
-> Consider projection map $f:\mathbb{R}\times \mathbb{R}\to \mathbb{R}$ to first coordinate, this map is open but not closed, consider $C\coloneqq\{x\times y\mid xy=1\}$ This set is closed in $\mathbb{R}\times \mathbb{R}$ but $f(C)=\mathbb{R}-\{0\}$ is not closed in $\mathbb{R}$.
->
-> 3. Example of closed map that is not open:
-> 
-> Consider $f:[0,1]\cup[2,3]\to [0,2]$ by taking -1 to elements in $[2,3]$, this map is closed map but not open, since $f([2,3])=[1,2]$ is not open in $[0,2]$ but $[2,3]$ is open in $[0,1]\cup[2,3]$
-
-#### Equivalent classes
-
-$\sim$ is a subset of $X\times X$ with the following properties:
-
-1. $x\sim x$ for all $x\in X$.
-2. If $(x,y)\in \sim$, then $(y,x)\in \sim$.
-3. If $(x,y)\in \sim$ and $(y,z)\in \sim$, then $(x,z)\in \sim$.
-
-The equivalence classes of $x\in X$ is denoted by $[x]=\{y\in X|y\sim x\}$.
-
-We can use equivalent classes to define quotient space.
-
-#### Theorem 22.2
-
-Let $p:X\to Y$ be a quotient map. Let $Z$ be a space and let $g:X\to Z$ be a map that is constant on each set $p^{-1}(\{y\})$, for $y\in Y$. Then $g$ induces a map $f:Y\to Z$ such that $f\circ p=g$. The induced map $f$ is continuous if and only if $g$ is continuous; $f$ is a quotient map if and only if $g$ is a quotient map.
-
-*Prove by setting $f(p(x))=g(x)$, then $g^{-1}(V)=p^{-1}(f^{-1}(V))$ for $V$ open in $Z$.*
-
-## Connectedness and compactness of metric spaces
-
-### Connectedness and separation
-
-#### Definition of separation
-
-Let $X=(X,\mathcal{T})$ be a topological space. A separation of $X$ is a pair of open sets $U,V\in \mathcal{T}$ that:
-
-1. $U\neq \emptyset$ and $V\neq \emptyset$ (that also equivalent to $U\neq X$ and $V\neq X$)
-2. $U\cap V=\emptyset$
-3. $X=U\cup V$ ($\forall x\in X$, $x\in U$ or $x\in V$)
-
-Some interesting corollary:
-
-- Any non-trivial (not $\emptyset$ or $X$) clopen set can create a separation.
-  - Proof: Let $U$ be a non-trivial clopen set. Then $U$ and $U^c$ are disjoint open sets whose union is $X$.
-- For subspace $Y\subset X$, a separation of $Y$ is a pair of open sets $U,V\in \mathcal{T}_Y$ such that:
-  1. $U\neq \emptyset$ and $V\neq \emptyset$ (that also equivalent to $U\neq Y$ and $V\neq Y$)
-  2. $U\cap V=\emptyset$
-  3. $Y=U\cup V$ ($\forall y\in Y$, $y\in U$ or $y\in V$)
-   - If $\overline{A}$ is closure of $A$ in $X$, same for $\overline{B}$, then the closure of $A$ in $Y$ is $\overline{A}\cap Y$ and the closure of $B$ in $Y$ is $\overline{B}\cap Y$. Then for separation $U,V$ of $Y$, $\overline{A}\cap B=A\cap \overline{B}=\emptyset$.
-
-#### Definition of connectedness
-
-A topological space $X$ is connected if there is no separation of $X$.
-
-> [!TIP]
->
-> Connectedness is a local property. (That is, even the big space is connected, the subspace may not be connected. Consider $\mathbb{R}$ with the usual metric. $\mathbb{R}$ is connected, but $\mathbb{R}\setminus\{0\}$ is not connected.)
->
-> Connectedness is a topological property. (That is, if $X$ and $Y$ are homeomorphic, then $X$ is connected if and only if $Y$ is connected. Consider if not, then separation of $X$ gives a separation of $Y$.)
-
-#### Lemma of connected subspace
-
-If $A,B$ is a separation of a topological space $X$, and $Y\subseteq X$ is a **connected** subspace with subspace topology, then $Y$ is either contained in $A$ or $B$.
-
-*Easy to prove by contradiction. Try to construct a separation of $Y$.*
-
-#### Theorem of connectedness of union of connected subsets
-
-Let $\{A_\alpha\}_{\alpha\in I}$ be a collection of connected subsets of a topological space $X$ such that $\bigcap_{\alpha\in I} A_\alpha$ is non-empty. Then $\bigcup_{\alpha\in I} A_\alpha$ is connected.
-
-*Easy to prove by lemma of connected subspace.*
-
-#### Lemma of compressing connectedness
-
-Let $A\subseteq X$ be a connected subspace of a topological space $X$ and $A\subseteq B\subseteq \overline{A}$. Then $B$ is connected.
-
-*Easy to prove by lemma of connected subspace. Suppose $C,D$ is a separation of $B$, then $A$ lies completely in either $C$ or $D$. Without loss of generality, assume $A\subseteq C$. Then $\overline{A}\subseteq\overline{C}$ and $\overline{A}\cap D=\emptyset$ (from $\overline{C}\cap D=\emptyset$ by closure of $A$). (contradiction that $D$ is nonempty) So $D$ is disjoint from $\overline{A}$, and hence from $B$. Therefore, $B$ is connected.*
-
-#### Theorem of connected product space
-
-Any finite cartesian product of connected spaces is connected.
-
-*Prove using the union of connected subsets theorem. Using fiber bundle like structure union with non-empty intersection.*
-
-### Application of connectedness in real numbers
-
-Real numbers are connected.
-
-Using the least upper bound and greatest lower bound property, we can prove that any interval in real numbers is connected.
-
-#### Intermediate Value Theorem
-
-Let $f:[a,b]\to \mathbb{R}$ be continuous. If $c\in\mathbb{R}$ is such that $f(a)<c<f(b)$, then there exists $x\in [a,b]$ such that $f(x)=c$.
-
-*If false, then we can use the disjoint interval with projective map to create a separation of $[a,b]$.*
-
-#### Definition of path-connected space
-
-A topological space $X$ is path-connected if for any two points $x,x'\in X$, there is a continuous map $\gamma:[0,1]\to X$ such that $\gamma(0)=x$ and $\gamma(1)=x'$. Any such continuous map is called a path from $x$ to $x'$.
-
-- Every connected space is path-connected.
-  - The converse may not be true, consider the topologists' sine curve.
-
-### Compactness
-
-#### Definition of compactness via open cover and finite subcover
-
-Let $X=(X,\mathcal{T})$ be a topological space. An open cover of $X$ is $\mathcal{A}\subset \mathcal{T}$ such that $X=\bigcup_{A\in \mathcal{A}} A$. A finite subcover of $\mathcal{A}$ is a finite subset of $\mathcal{A}$ that covers $X$.
-
-$X$ is compact if every open cover of $X$ has a finite subcover (i.e. $X=\bigcup_{A\in \mathcal{A}} A\implies \exists \mathcal{A}'\subset \mathcal{A}$ finite such that $X=\bigcup_{A\in \mathcal{A}'} A$).
-
-#### Definition of compactness via finite intersection property
-
-A collection $\{C_\alpha\}_{\alpha\in I}$ of subsets of a set $X$ has finite intersection property if for every finite subcollection $\{C_{\alpha_1}, ..., C_{\alpha_n}\}$ of $\{C_\alpha\}_{\alpha\in I}$, we have $\bigcap_{i=1}^n C_{\alpha_i}\neq \emptyset$.
-
-Let $X=(X,\mathcal{T})$ be a topological space. $X$ is compact if every collection $\{Z_\alpha\}_{\alpha\in I}$ of closed subsets of $X$ satisfies the finite intersection property has a non-empty intersection (i.e. $\forall \{Z_{\alpha_1}, ..., Z_{\alpha_n}\}\subset \{Z_\alpha\}_{\alpha\in I}, \bigcap_{i=1}^n Z_{\alpha_i} \neq \emptyset\implies \bigcap_{\alpha\in I} Z_\alpha \neq \emptyset$).
-
-#### Compactness is a local property
-
-Let $X$ be a topological space. A subset $Y\subseteq X$ is compact if and only if every open covering of $Y$ (set open in $X$) has a finite subcovering of $Y$.
-
-- A space $X$ is compact but the subspace may not be compact.
-  - Consider $X=[0,1]$ and $Y=[0,1/2)$. $Y$ is not compact because the open cover $\{(0,1/n):n\in \mathbb{N}\}$ does not have a finite subcover.
-- A compact subspace may live in a space that is not compact.
-  - Consider $X=\mathbb{R}$ and $Y=[0,1]$. $Y$ is compact but $X$ is not compact.
-
-#### Closed subspaces of compact spaces
-
-A closed subspace of a compact space is compact.
-
-A compact subspace of Hausdorff space is closed.
-
-*Each point not in the closed set have disjoint open neighborhoods with the closed set in Hausdorff space.*
-
-#### Theorem of compact subspaces with Hausdorff property
-
-If $Y$ is compact subspace of a **Hausdorff space** $X$, $x_0\in X-Y$, then there are disjoint open neighborhoods $U,V\subseteq X$ such that $x_0\in U$ and $Y\subseteq V$.
-
-#### Image of compact space under continuous map is compact
-
-Let $f:X\to Y$ be a continuous map and $X$ is compact. Then $f(X)$ is compact.
-
-#### Tube lemma
-
-Let $X,Y$ be topological spaces and $Y$ is compact. Let $N\subseteq X\times Y$ be an open set contains $X\times \{y_0\}$ for $y_0\in Y$. Then there exists an open set $W\subseteq Y$ is open containing $y_0$ such that $N$ contains $X\times W$.
-
-*Apply the finite intersection property of open sets in $X\times Y$. Projection map is continuous.*
-
-#### Product of compact spaces is compact
-
-Let $X,Y$ be compact spaces, then $X\times Y$ is compact.
-
-Any finite product of compact spaces is compact.
-
-### Compact subspaces of real numbers
-
-#### Every closed and bounded subset of real numbers is compact
-
-$[a,b]$ is compact in $\mathbb{R}$ with standard topology.
-
-#### Good news for real numbers
-
-Any of the three properties is equivalent for subsets of real numbers (product of real numbers):
-
-1. $A\subseteq \mathbb{R}^n$ is closed and bounded (with respect to the standard metric or spherical metric on $\mathbb{R}^n$).
-2. $A\subseteq \mathbb{R}^n$ is compact.
-
-#### Extreme value theorem
-
-If $f:X\to \mathbb{R}$ is continuous map with $X$ being compact. Then $f$ attains its minimum and maximum. (there exists $x_m,x_M\in X$ such that $f(x_m)\leq f(x)\leq f(x_M)$ for all $x\in X$)
-
-#### Lebesgue number lemma
-
-For a compact metric space $(X,d)$ and an open covering $\{U_\alpha\}_{\alpha\in I}$ of $X$. Then there is $\delta>0$ such that for every subset $A\subseteq X$ with diameter less than $\delta$, there is $\alpha\in I$ such that $A\subseteq U_\alpha$.
-
-*Apply the extreme value theorem over the mapping of the averaging function for distance of points to the $X-U_\alpha$. Find minimum radius of balls that have some $U_\alpha$ containing the ball.*
-
-#### Definition for uniform continuous function
-
-$f$ is uniformly continuous if for any $\epsilon > 0$, there exists $\delta > 0$ such that for any $x_1,x_2\in X$, if $d(x_1,x_2)<\delta$, then $d(f(x_1),f(x_2))<\epsilon$.
-
-#### Uniform continuity theorem
-
-Let $f:X\to Y$ be a continuous map between two metric spaces. If $X$ is compact, then $f$ is uniformly continuous.
-
-#### Definition of isolated point
-
-A point $x\in X$ is an isolated point if $\{x\}$ is an open subset of $X$.
-
-#### Theorem of isolated point in compact spaces
-
-Let $X$ be a nonempty compact Hausdorff space. If $X$ has no isolated points, then $X$ is uncountable.
-
-*Proof using infinite nested closed intervals should be nonempty.*
-
-### Variation of compactness
-
-#### Limit point compactness
-
-A topological space $X$ is limit point compact if every infinite subset of $X$ has a limit point in $X$.
-
-- Every compact space is limit point compact.
-
-#### Sequentially compact
-
-A topological space $X$ is sequentially compact if every sequence in $X$ has a convergent subsequence.
-
-- Every compact space is sequentially compact.
-
-#### Equivalence of three in metrizable spaces
-
-If $X$ is a metrizable space, then the following are equivalent:
-
-1. $X$ is compact.
-2. $X$ is limit point compact.
-3. $X$ is sequentially compact.
-
-#### Local compactness
-
-A space $X$ is locally compact if every point $x\in X$, **there is a compact subspace $K$ of $X$ containing a neighborhood $U$ of $x$** $x\in U\subseteq K$ such that $K$ is compact.
-
-#### Theorem of one point compactification
-
-Let $X$ be a locally compact Hausdorff space if and only if there exists a topological space $Y$ satisfying the following properties:
-
-1. $X$ is a subspace of $Y$.
-2. $Y-X$ has one point, usually denoted by $\infty$.
-3. $Y$ is compact and Hausdorff.
-
-The $Y$ is defined as follows:
-
-$U\subseteq Y$ is open if and only if one of the following holds.
-
-1. $U\subseteq X$ and $U$ is open in $X$
-2. $\infty \in U$ and $Y-U\subseteq X$, and $Y-U$ is compact.
-
-## Countability and Separation Axioms
-
-### Countability Axioms
-
-#### First countability axiom
-
-A topological space $(X,\mathcal{T})$ satisfies the first countability axiom if any point $x\in X$, there is a sequence of open neighborhoods of $x$, $\{V_n\}_{n=1}^\infty$ such that any open neighborhood $U$ of $x$ contains one of $V_n$.
-
-Apply the theorem above, we have if $(X,\mathcal{T})$ satisfies the first countability axiom, then:
-
-1. Every convergent sequence converges to a point in the closure of the sequence.
-
-<details>
-<summary>Space that every convergent sequence not converges to a point in the closure of the sequence.</summary>
-
-Consider $\mathbb{R}^\omega$ with the box topology.
-
-And $A=(0,1)\times (0,1)\times \cdots$ and $x=(0,0,\cdots)$.
-
-$x\in \overline{A}$ but no sequence converges to $x$.
-
-Suppose there exists such sequence, $\{x_n=(x_1^n,x_2^n,\cdots)\}_{n=1}^\infty$.
-
-Take $B=(-x_1^1,x_1^1)\times(-x_2^2,x_2^2)\times \cdots$, this is basis containing $x$ but none of $x_n$.
-
-</details>
-
-2. If $f:X\to Y$ such that for any sequence $\{x_n\}_{n=1}^\infty$ in $X$, $f(x_n)\to f(x)$, then $f$ is continuous.
-
-#### Second countability axiom
-
-Let $(X,\mathcal{T})$ be a topological space, then $X$ satisfies the second countability axiom if $X$ has a countable basis.
-
-If $X$ is second countable, then:
-
-1. Any discrete subspace $Y$ of $X$ is countable
-2. There exists a countable subset of $X$ that is dense in $X$.
-3. Every open covering of $X$ has a **countable** subcover (That is if $X=\bigcup_{\alpha\in I} U_\alpha$, then there exists a **countable** subcover $\{U_{\alpha_1}, ..., U_{\alpha_\infty}\}$ of $X$) (*also called Lindelof spaces*)
-
-### Separation Axioms
-
-#### Hausdorff spaces
-
-A topological space $(X,\mathcal{T})$ is Hausdorff if for any two distinct points $x,y\in X$, there are **disjoint open sets** $U,V$ such that $x\in U$ and $y\in V$. (note that $U\cup V$ may not be $X$, compared with definition of separation)
-
-Some corollaries:
-
-1. A subspace of Hausdorff space is Hausdorff, and a product of Hausdorff spaces is Hausdorff.
-
-#### Regular spaces
-
-A topological space $(X,\mathcal{T})$ is regular if for any $x\in X$ and any closed set $A\subseteq X$ such that $x\notin A$, there are **disjoint open sets** $U,V$ such that $x\in U$ and $A\subseteq V$.
-
-Some corollaries:
-
-1. $X$ is regular if and only if given a point $x$ and a open neighborhood $U$ of $x$, there is open neighborhood $V$ of $x$ such that $\overline{V}\subseteq U$.
-2. A subspace of regular space is regular, and a product of regular spaces is regular.
-
-#### Normal spaces
-
-A topological space $(X,\mathcal{T})$ is normal if for any disjoint closed sets $A,B\subseteq X$, there are **disjoint open sets $U,V$** such that $A\subseteq U$ and $B\subseteq V$.
-
-Some corollaries:
-
-1. $X$ is normal if and only if given a closed set $A\subseteq X$, there is open neighborhood $V$ of $A$ such that $\overline{V}\subseteq U$.
-
-> [!CAUTION]
->
-> Product of normal spaces may not be normal (consider Sorgenfrey plane)
-
-#### Regular space with countable basis is normal
-
-Let $X$ be a regular space with countable basis, then $X$ is normal.
-
-*Prove by taking disjoint open neighborhoods by countable cover.*
-
-

content/Math4201/Math4201_L29.md

@@ -51,7 +51,7 @@ Therefore, $X$ is uncountable.
 
 #### Definition of limit point compact
 
-A space $X$ is limit point compact if any infinite subset of $X$ has a [limit point](../Math4201_L8#limit-points) in $X$.
+A space $X$ is limit point compact if any infinite subset of $X$ has a [limit point](./Math4201_L8#limit-points) in $X$.
 
 _That is, $\forall A\subseteq X$ and $A$ is infinite, there exists a point $x\in X$ such that $x\in U$, $\forall U\in \mathcal{T}$ containing $x$, $(U-\{x\})\cap A\neq \emptyset$._
 

content/Math4201/Math4201_L32.md

@@ -30,7 +30,7 @@ First, we prove that $X$ is a subspace of $Y$. (That is, every open set $U\subse
 
 Case 1: $U\subseteq X$ is open in $X$, then $U\cap X=U$ is open in $Y$.
 
-Case 2: $\infty\in U$, then $Y-U$ is a compact subspace of $X$. Since $X$ is Hausdorff, $Y-U$ is a closed subspace of $X$. [Compact subspace of a Hausdorff space is closed](../Math4201_L25#proposition-of-compact-subspaces-with-hausdorff-property)
+Case 2: $\infty\in U$, then $Y-U$ is a compact subspace of $X$, since $X$ is Hausdorff. So $Y-U$ is a closed subspace of $X$.
 
 So $X\cap U=X-(Y-U)$ is open in $X$.
 

content/Math4201/Math4201_L33.md

@@ -131,7 +131,7 @@ $$
 A=\{\underline{x}=(x_1,x_2,x_3,\dots)|x_i\in \{0,1\}\}
 $$
 
-Let $\underline{x}$ and $\underline{x}'$ be two distinct elements of $A$.
+Let $\underline{x} and \underline{x}'$ be two distinct elements of $A$.
 
 $$
 \rho(\underline{x},\underline{x}')=\sup_{i\in \mathbb{N}}\overline{d}(\underline{x}_\alpha,\underline{x}'_\alpha)=1

content/Math4201/Math4201_L34.md

@@ -98,7 +98,7 @@ A $T_0$ space is regular if for any $x\in X$ and any close set $A\subseteq X$ su
 A $T_0$ space is normal if for any disjoint closed sets, $A,B\subseteq X$, there are **disjoint open sets** $U,V$ such that $A\subseteq U$ and $B\subseteq V$.
 
 <details>
-<summary>Finer topology may not be normal</summary>
+<summary></summary>
 
 Let $\mathbb{R}_K$ be the topology on $\mathbb{R}$ generated by the basis:
 
@@ -106,7 +106,7 @@ $$
 \mathcal{B}=\{(a,b)\mid a,b\in \mathbb{R},a<b\}\cup \{(a,b)-K\mid a,b\in \mathbb{R},a<b\}
 $$
 
-where $K\coloneqq \{\frac{1}{n}\mid n\in \mathbb{N}\}$.
+where $K=\coloneqq \{\frac{1}{n}\mid n\in \mathbb{N}\}$.
 
 **This is finer than the standard topology** on $\mathbb{R}$.
 

content/Math4201/Math4201_L35.md

@@ -1,218 +0,0 @@
-# Math4201 Topology I (Lecture 35)
-
-## Countability axioms
-
-### Kolmogorov classification
-
-Consider the topological space $X$.
-
-$X$ is $T_0$ means for every pair of points $x,y\in X$, $x\neq y$, there is one of $x$ and $y$ is in an open set $U$ containing $x$ but not $y$.
-
-$X$ is $T_1$ means for every pair of points $x,y\in X$, $x\neq y$, each of them have a open set $U$ and $V$ such that $x\in U$ and $y\in V$ and $x\notin V$ and $y\notin U$. (singleton sets are closed)
-
-$X$ is $T_2$ means for every pair of points $x,y\in X$, $x\neq y$, there exists disjoint open sets $U$ and $V$ such that $x\in U$ and $y\in V$. (Hausdorff)
-
-$X$ is $T_3$ means that $X$ is regular: for any $x\in X$ and any close set $A\subseteq X$ such that $x\notin A$, there are **disjoint open sets** $U,V$ such that $x\in U$ and $A\subseteq V$.
-
-$X$ is $T_4$ means that $X$ is normal: for any disjoint closed sets, $A,B\subseteq X$, there are **disjoint open sets** $U,V$ such that $A\subseteq U$ and $B\subseteq V$.
-
-<details>
-<summary>Example</summary>
-
-Let $\mathbb{R}_{\ell}$ with lower limit topology.
-
-$\mathbb{R}_{\ell}$ is normal since for any disjoint closed sets, $A,B\subseteq \mathbb{R}_{\ell}$, $x\in A$ and $B$ is closed and doesn't contain $x$. Then there exists $\epsilon_x>0$ such that $[x,x+\epsilon_x)\subseteq A$ and does not intersect $B$.
-
-Therefore, there exists $\delta_y>0$ such that $[y,y+\delta_y)\subseteq B$ and does not intersect $A$.
-
-Let $U=\bigcup_{x\in A}[x,x+\epsilon_x)$ is open and contains $A$.
-
-$V=\bigcup_{y\in B}[y,y+\delta_y)$ is open and contains $B$.
-
-We show that $U$ and $V$ are disjoint.
-
-If $U\cap V\neq \emptyset$, then there exists $x\in A$ and $Y\in B$ such that $[x,x+\epsilon_x)\cap [y,y+\delta_y)\neq \emptyset$.
-
-This is a contradiction since $[x,x+\epsilon_x)\subseteq A$ and $[y,y+\delta_y)\subseteq B$.
-
-</details>
-
-#### Theorem Every metric space is normal
-
-Use the similar proof above.
-
-<details>
-<summary>Proof</summary>
-
-Let $A,B\subseteq X$ be closed.
-
-Since $B$ is closed, for any $x\in A$, there exists $\epsilon_x>0$ such that $B_{\epsilon_x}(x)\subseteq B$.
-
-Since $A$ is closed, for any $y\in B$, there exists $\delta_y>0$ such that $A_{\delta_y}(y)\subseteq A$.
-
-Let $U=\bigcup_{x\in A}B_{\epsilon_x/2}(x)$ and $V=\bigcup_{y\in B}B_{\delta_y/2}(y)$.
-
-We show that $U$ and $V$ are disjoint.
-
-If $U\cap V\neq \emptyset$, then there exists $x\in A$ and $Y\in B$ such that $B_{\epsilon_x/2}(x)\cap B_{\delta_y/2}(y)\neq \emptyset$.
-
-Consider $z\in B_{\epsilon_x/2}(x)\cap B_{\delta_y/2}(y)$. Then $d(x,z)<\epsilon_x/2$ and $d(y,z)<\delta_y/2$. Therefore $d(x,y)\leq d(x,z)+d(z,y)<\epsilon_x/2+\delta_y/2$. 
-
-If $\delta_y<\epsilon_x$, then $d(x,y)<\delta_y/2+\delta_y/2=\delta_y$. Therefore $x\in B_{\delta_y}(y)\subseteq A$. This is a contradiction since $U\cap B=\emptyset$.
-
-If $\epsilon_x<\delta_y$, then $d(x,y)<\epsilon_x/2+\epsilon_x/2=\epsilon_x$. Therefore $y\in B_{\epsilon_x}(x)\subseteq B$. This is a contradiction since $V\cap A=\emptyset$.
-
-Therefore, $U$ and $V$ are disjoint.
-
-</details>
-
-#### Lemma fo regular topological space
-
-$X$ is regular topological space if and only if for any $x\in X$ and any open neighborhood $U$ of $x$, there is open neighborhood $V$ of $x$ such that $\overline{V}\subseteq U$.
-
-#### Lemma of normal topological space
-
-$X$ is a normal topological space if and only if for any $A\subseteq X$ closed and any open neighborhood $U$ of $A$, there is open neighborhood $V$ of $A$ such that $\overline{V}\subseteq U$.
-
-<details>
-<summary>Proof</summary>
-
-$\implies$
-
-Let $A$ and $U$ are given as in the statement.
-
-So $A$ and $(X-U)$ are disjoint closed.
-
-Since $X$ is normal and $A\subseteq V\subseteq X$ and $V\cap W=\emptyset$. $X-U\subseteq W\subseteq X$. where $W$ is open in $X$.
-
-And $\overline{V}\subseteq (X-W)\subseteq U$.
-
-And $A\subseteq V$.
-
-The proof of reverse direction is similar.
-
-Let $A,B$ be disjoint and closed.
-
-Then $A\subseteq U\coloneqq X-B\subseteq X$ and $X-B$ is open in $X$.
-
-Apply the assumption to find $A\subseteq V\subseteq X$ and $V$ is open in $X$ and $\overline{V}\subseteq U\coloneqq X-B$.
-
-</details>
-
-#### Proposition of regular and Hausdorff on subspaces
-
-1. If $X$ is a regular topological space, and $Y$ is a subspace. Then $Y$ with induced topology is regular. (same holds for Hausdorff)
-2. If $\{X_\alpha\}$ is a collection of regular topological spaces, then their product with the product topology is regular. (same holds for Hausdorff)
-
-> [!CAUTION]
->
-> The above does not hold for normal.
-
-Recall that $\mathbb{R}_{\ell}$ with lower limit topology is normal. But $\mathbb{R}_{\ell}\times \mathbb{R}_{\ell}$ with product topology is not normal.
-
-<details>
-<summary>Proof that Sorgenfrey plane is not normal</summary>
-
-The goal of this problem is to show that $\mathbb{R}^2_\ell$ (the Sorgenfrey plane) is not normal. Recall that $\mathbb{R}_\ell$ is the real line with the lower limit topology, and $\mathbb{R}_\ell^2$ is equipped with the product topology. Consider the subset
-
-$$
-L = \{\, (x,-x) \mid x\in \mathbb{R}_\ell \,\} \subset \mathbb{R}^2_\ell.
-$$
-
-Let $A\subset L$ be the set points of the form $(x,-x)$ such that $x$ is rational and $B\subset L$ be the set points of the form $(x,-x)$ such that $x$ is irrational.
-
-1. Show that the subspace topology on $L$ is the discrete topology.  Conclude that $A$ and $B$ are closed subspaces of $\mathbb{R}_\ell^2$
-
-<details>
-<summary>Proof</summary>
-First we show that $L$ is closed.
-
-Consider $x=(a,b)\in\mathbb{R}^2_\ell-L$, by definition $a\neq -b$.
-
-If $a>-b$, then there exists open neighborhood $U_x=[\frac{\min\{a,b\}}{2},a+1)\times[\frac{\min\{a,b\}}{2},b+1)$ that is disjoint from $L$ (no points of form $(x,-x)$ in our rectangle), therefore $x\in U_x$.
-
-If $a<-b$, then there exists open neighborhood $U_x=[a,a+\frac{\min\{a,b\}}{2})\times[b,b+\frac{\min\{a,b\}}{2})$ that is disjoint from $L$, therefore $x\in U_x$.
-
-Therefore, $\mathbb{R}^2_\ell-L=\bigcup_{x\in \mathbb{R}_\ell^2-L} U_x$ is open in $\mathbb{R}^2_\ell$.
-
-So $L$ is closed in $\mathbb{R}^2_\ell$.
-
-To show $L$ with subspace topology on $\mathbb{R}^2_\ell$ is discrete topology, we need to show that every singleton of $L$ is open in $L$.
-
-For each $\{(x,-x)\}\in L$, $[x,x+1)\times [-x,-x+1)$ is open in $\mathbb{R}_\ell^2$ and $\{(x,-x)\}=([x,x+1)\times [-x,-x+1))\cap L$, therefore $\{(x,-x)\}$ is open in $L$.
-
-Since $A,B$ are disjoint and $A\cup B=L$, therefore $A=L-B$ and $B=L-A$, by definition of discrete topology, $A,B$ are both open therefore the complement of $A,B$ are closed. So $A,B$ are closed in $L$.
-
-since $L$ is closed in $\mathbb{R}^2_\ell$, by \textbf{Lemma \ref{closed_set_close_subspace_close}}, $A,B$ is also closed in $\mathbb{R}_\ell^2$. Therefore $A,B$ are closed subspace of $\mathbb{R}_\ell^2$.
-</details>
-
-2. Let $V$ be an open set of $\mathbb{R}^2_\ell$ containing $B$. Let $K_n$ consist of all irrational numbers $x\in [0,1]$ such that $[x, x+1/n) \times [-x, -x+1/n)$ is contained in $V$. Show that $[0,1]$ is the union of the sets $K_n$ and countably many one-point sets.
-
-<details>
-<summary>Proof</summary>
-Since $B$ is open in $L$, for each $b\in B$, by definition of basis in $\mathbb{R}_\ell^2$, and $B$ is open, there exists $b\in ([b,b+\epsilon)\times [-b,-b+\delta))\cap L\subseteq V$ and $0<\epsilon,\delta$, so there exists $n_b$ such that $\frac{1}{n_b}<\min\{\epsilon,\delta\}$ such that $b\in ([b,b+\frac{1}{n_b})\times [-b,-b+\frac{1}{n_b}))\cap L\subseteq V$.
-
-Therefore $\bigcup_{n=1}^\infty K_n$ covers irrational points in $[0,1]$
-
-Note that $B=L-A$ where $A$ is rational points therefore countable.
-
-So $[0,1]$ is the union of the sets $K_n$ and countably many one-point sets.
-</details>
-
-3. Use Problem 5-3 to show that some set $\overline{K_n}$ contains an open interval $(a,b)$ of $\mathbb{R}$. (You don't need to prove Problem 5.3, if it is not your choice of \#5.)
-
-#### Lemma
-
-Let $X$ be a compact Hausdorff space; let $\{A_n\}$ be a countable collection of closed sets of $X$. If each sets $A_n$ has empty interior in $X$, then the union $\bigcup_{n=1}^\infty A_n$ has empty interior in $X$.
-
-<details>
-<summary>Proof</summary>
-We proceed by contradiction, note that $[0,1]$ is a compact Hausdorff space since it's closed and bounded.
-
-And $\{\overline{K_n}\}_{n=0}^\infty$ is a countable collection of closed sets of $[0,1]$.
-
-Suppose for the sake of contradiction, $\overline{K_n}$ has empty interior in $X$ for all $n\in \mathbb{N}$, by \textbf{Lemma \ref{countable_closed_sets_empty_interior}}, then $\bigcup_{n=1}^\infty \overline{K_n}$ has empty interior in $[0,1]$, where $\Q\cap[0,1]$ are countably union of singletons, therefore has empty interior in $[0,1]$.
-
-Therefore $\bigcup_{n=1}^\infty \overline{K_n}$ has empty interior in $[0,1]$, since $\bigcup_{n=1}^\infty K_n\subseteq \bigcup_{n=1}^\infty \overline{K_n}$, $\bigcup_{n=1}^\infty K_n$ also has empty interior in $[0,1]$ by definition of subspace of $[0,1]$, therefore $\bigcup_{n=1}^\infty K_n\cup (\Q\cap[0,1])$ has empty interior in $[0,1]$. This contradicts that $\bigcup_{n=1}^\infty K_n\cup (\Q\cap[0,1])$ covers $[0,1]$ and should at least have interior $(0.1,0.9)$.
-</details>
-
-4. Show that $V$ contains the open parallelogram consisting of all points of the form
-
-$$
-x\times (-x+\epsilon)\quad\text{ for which }\quad a<x<b\text{ and }0<\epsilon<\frac{1}{n}.
-$$
-
-<details>
-<summary>Proof</summary>
-Since $V$ is open, by previous problem we know that there exists $n$ such that $\overline{K_n}$ contains the open interval $(a,b)$.
-
-If $x\in K_n$, $\forall a<x<b$, by definition of $K_n$ $[x,x+\frac{1}{n})\times [-x,-x+\frac{1}{n})\subseteq V$.
-
-If $x$ is a limit point of $K_n$, since $V$ is open, there exists $0<\epsilon<\frac{1}{n}$ such that $[x,x+\epsilon)\times [-x,-x+\epsilon)\subseteq V$.
-
-This gives our desired open parallelogram.
-</details>
-  
-5. Show that if $q$ is a rational number with $a<q<b$, then the point $q\times (-q)$ of $\mathbb{R}_\ell^2$ is a limit point of $V$. Conclude that there are no disjoint open neighborhoods $U$ of $A$ and $V$ of $B$.
-
-<details>
-<summary>Proof</summary>
-Consider all the open neighborhood of $q\times (-q)$ in $\mathbb{R}_\ell^2$, for all $\delta>0$, $[q,q+\delta)\times (-q,-q+\delta)$ will intersect with some $x\times [-x,-x+\epsilon)\subseteq V$ such that $0<\epsilon<\frac{1}{n}<\delta$.
-
-Therefore, any open set containing $q\times (-q)\in A$ will intersect with $V$, it is impossible to build disjoint open neighborhoods $U$ of $A$ and $V$ of $B$.
-</details>
-</details>
-
-This shows that $\mathbb{R}_{\ell}$ is not metrizable. Otherwise $\mathbb{R}_{\ell}\times \mathbb{R}_{\ell}$ would be metrizable. Which could implies that $\mathbb{R}_{\ell}$ is normal.
-
-#### Theorem of metrizability (Urysohn metirzation theorem)
-
-If $X$ is normal and second countable, then $X$ is metrizable.
-
-> [!NOTE]
->
-> - Every metrizable topological space is normal.
-> - Every metrizable space is first countable.
-> - But there are some metrizable space that is not second countable.
->
-> Note that if $X$ is normal and first countable, then it is not necessarily metrizable. (Example $\mathbb{R}_{\ell}$)

content/Math4201/Math4201_L36.md

@@ -1,166 +0,0 @@
-# Math4201 Topology I (Lecture 36)
-
-## Separation Axioms
-
-### Regular spaces
-
-#### Proposition for $T_1$ spaces
-
-If $X$ is a topological space such that all singleton are closed, then then following holds:
-
-- $X$ is regular if and only if for any point $x\in X$ and any open neighborhood $V$ of $X$ such that $\overline{V}\subseteq U$.
-- $X$ is normal if and only if for any closed set $A\subseteq X$, there is an open neighborhood $V$ of $A$ such that $\overline{V}\subseteq U$.
-
-#### Proposition of regular and Hausdorff on subspaces
-
-1. If $X$ is a regular topological space, and $Y$ is a subspace. Then $Y$ with induced topology is regular. (same holds for Hausdorff)
-2. If $\{X_\alpha\}$ is a collection of regular topological spaces, then their product with the product topology is regular. (same holds for Hausdorff)
-
-<details>
-<summary>Proof</summary>
-
-1. If $X$ is regular and $Y\subseteq X$,then we want to show that $Y$ is regular.
-
-We take a point $y\in Y$ and a closed subset $A$ of $Y$ which doesn't contain $y$.
-
-Observe that $A\subseteq Y$ is closed if and only if $A=\overline{A}\cap Y$ where $\overline{A}$ is the closure of $A$ in $X$.
-
-Notice that $y\in Y$ but $y\notin A$, then $y\notin \overline{A}$ (otherwise $y\in A$).
-
-By regularity of $X$, we can find an open neighborhood $y\in U\subseteq X$ and $\overline{A}\subseteq V\subseteq X$ and $U,V$ are open and disjoint.
-
-This implies that $U\cap Y$ and $V\cap Y$ are open neighborhood of $y$ and $A$ and disjoint from each other.
-
-(Proof for Hausdorff is similar)
-
----
-
-2. If $\{X_\alpha\}$ is a collection of regular topological spaces, then their product with the product topology is regular.
-
-We take a collection of regular spaces $\{X_\alpha\}_{\alpha\in I}$.
-
-We want to show that their product with the product topology is regular.
-
-Take $\underline{x}=(x_\alpha)_{\alpha\in I}\in \prod_{\alpha\in I}X_\alpha$, any open neighborhood of $x$ contains a basis element of the form 
-
-$$
-\prod_{\alpha\in I}U_\alpha
-$$
-
-with $x_\alpha\in U_\alpha$ for all $\alpha\in I$, and all but finitely many $U_\alpha$ are equal to $X_\alpha$. (By definition of product topology)
-
-Now for each $\alpha_i$ take an open neighborhood $V_\alpha$ of $x_{\alpha_i}$ such that
-
-1. $\overline{V_\alpha}\subseteq U_\alpha$ (This can be cond by regularity of $X_\alpha$)
-2. $V_\alpha=X_\alpha$ if $U_\alpha=X_\alpha$
-
-The product of $\prod_{\alpha\in I}V_\alpha$ is an open neighborhood of $\underline{x}$ and
-
-$$
-\overline {\prod_{\alpha\in I}V_\alpha}=\prod_{\alpha\in I}\overline{V_\alpha}\subseteq \prod_{\alpha\in I}U_\alpha
-$$
-
-Therefore, $X$ is regular.
-
-(Proof for Hausdorff is similar)
-
-
-If we replace the regularity with Hausdorffness, then we can take two points $\underline{x},\underline{y}$. Then there exists $\alpha_0$ such that $x_{\alpha_0}\neq y_{\alpha_0}$. We can use this to build disjoint open neighborhoods
-
-$$
-x_{\alpha_0}\in U_{\alpha_0}\subseteq X_{\alpha_0},\quad y_{\alpha_0}\in V_{\alpha_0}\subseteq X_{\alpha_0}
-$$
-
-of $x_{\alpha_0}$ and $y_{\alpha_0}$.
-
-Then we take $U_\alpha=\begin{cases} U_{\alpha_0} &\alpha= \alpha_0\\ X_{\alpha_0} & \text{otherwise}\end{cases}$ and $V_\alpha=\begin{cases} V_{\alpha_0} &\alpha= \alpha_0\\ X_{\alpha_0} & \text{otherwise}\end{cases}$.
-
-These two sets are disjoint and $\prod_{\alpha\in I}U_{\alpha}$ and $\prod_{\alpha\in I}V_{\alpha}$ are open neighborhoods of $x$ and $y$.
-
-</details>
-
-Recall that this property does not hold for subspace of normal spaces.
-
-### How we construct new normal spaces from existing one
-
-#### Theorem for constructing normal spaces
-
-1. Any compact Hausdorff space is normal
-2. Any regular second countable space is normal
-
-<details>
-<summary>Proof</summary>
-
-For the first proposition
-
-Earlier we showed that any compact Hausdorff space $X$ is regular, i.e., for any closed subspace $A$ of $X$ and a point $x\in X$ not in $A$. There are open neighborhoods $U_x$ of $A$ and $V_x$ of $x$ such that $U_x\cap V_x=\emptyset$.
-
-Now let $B$ be a closed subset of $X$ disjoint from $A$.
-
-For any $x\in B$, we know that we have a disjoint open neighborhood $U_x$ of $A$ and $V_x$ of $x$.
-
-$\{V_n\}_{n\in \mathbb{B}}$ gives an open covering of $B$, $B$ is closed subset of a compact space, therefore, $B$ is compact.
-
-This implies that $\exists x_1,x_2,\ldots,x_n$ such that $B\subseteq \bigcup_{i=1}^n V_{x_i}$.
-
-$U\coloneqq \bigcup_{i=1}^n U_{x_i}$ is an open covering of $A$.
-
-$U_{x_i}\cap V_{x_i}=\emptyset$ implies that $\bigcup_{i=1}^n U_{x_i}\cap \bigcup_{i=1}^n V_{x_i}=\emptyset$.
-
-In summary, $U$ and $V$ are disjoint open neighborhoods of $A$ and $B$ respectively.
-
----
-
-We want to show that any regular second countable space is normal.
-
-Take $A,B$ be two disjoint closed subsets of $X$. We want to show that we can find disjoint open neighborhoods $U$ of $A$ and $V$ of $B$ such that $U\cap V=\emptyset$.
-
-Step 1:
-
-There is a countable open covering $\{U_i\}_{i\in I}$ of $A$ such that for any $i$, $\overline{U_i}\cap B=\emptyset$.
-
-For any $x\in A$, $X-B$ is an open neighborhood of $x$ and by reformulation of regularity, we can find an open set $U_i'$ such that $\overline{U_i'}\subseteq X-B$.
-
-(We will use the second countability of $X$ to produce countable open coverings)
-
-Let $B$ be a countable basis and let $U_x\in \mathcal{B}$ such that $x\in U_x\subseteq U_x'$.
-
-Note that $\overline{U_x}\subseteq \overline{U_x'}\subseteq X-B$.
-
-and $\{U_x\}_{x\in A}\subseteq \mathcal{B}$ is a countable collection.
-
-So this is a countable open covering of $A$ by relabeling the elements of this open covering we can denote it by $\{U_i\}_{i\in\mathbb{N}}$.
-
-Step 2:
-
-There is a countable open covering $\{V_i\}_{i\in I}$ of $B$ such that for any $i$, $\overline{V_i}\cap A=\emptyset$.
-
-Step 3:
-
-Let's define $\hat{U}_i=U_i-\bigcup_{j=1}^i\overline{V}_j=U_i\cap (X-\bigcup_{j=1}^i \overline{V}_j)$, note that $(X-\bigcup_{j=1}^i \overline{V}_j)$ and $U_i$ is open in $X$, therefore $\hat{U}_i$ is open in $X$.
-
-Since $A\subseteq \bigcup_{i=1}^\infty U_i$ and $\overline{V_j}\cap A=\emptyset$, we have $\bigcup_{i=1}^\infty \hat{U}_i\supseteq A$.
-
-Similarly, we have:
-
-$$
-\hat{V}_i=V_i-\bigcup_{j=1}^i\overline{U}_j=V_i\cap (X-\bigcup_{j=1}^i \overline{U}_j)
-$$
-
-is also open and $\bigcup_{i=1}^\infty \hat{V}_i\supseteq B$.
-
-Then we claim that these two open neighborhoods $U=\bigcup_{i=1}^\infty \hat{U}_i$ and $V=\bigcup_{i=1}^\infty \hat{V}_i$ are disjoint.
-
-To see this, we proceed by contradiction, suppose $x\in \bigcup_{i=1}^\infty \hat{U}_i\cap \bigcup_{i=1}^\infty \hat{V}_i$, $x\in \bigcup_{i=1}^\infty \hat{U}_i$ and $x\in \bigcup_{i=1}^\infty \hat{V}_i$.
-
-$x\in \bigcup_{i=1}^\infty \hat{U}_i$ implies that $\exists k$ such that $x\in \hat{U}_k$ and $\exists l$ such that $x\in \hat{V}_l$.
-
-Suppose without loss of generality that $k\leq l$.
-
-Then $x\in \hat{U}_k\subseteq U_k$, and $x\in \hat{V}$ implies that $\forall j\leq l:x\notin U_j$. This gives $x\notin U_k$.
-
-This is a contradiction.
-
-Therefore, $U$ and $V$ are disjoint.
-
-</details>

content/Math4201/Math4201_L37.md

@@ -1,80 +0,0 @@
-# Math4201 Topology I (Lecture 37)
-
-## Separation Axioms
-
-### Normal spaces
-
-#### Proposition of normal spaces
-
-A topological space $X$ is normal if and only if for all $A\subseteq U$ closed and $U$ is open in $X$, there exists $V$ open such that $A\subseteq V\subseteq \overline{V}\subseteq U$.
-
-#### Urysohn lemma
-
-Let $X$ be a normal space, $A,B$ be two closed and disjoint set in $X$, then there exists continuous function $f:X\to[0,1]$ such that $f(A)=\{0\}$ and $f(B)=\{1\}$.
-
-We say $f$ separates $A$ and $B$.
-
-> [!NOTE]
->
-> We could replace $1,0$ to any $a<b$
-
-<details>
-<summary>Proof</summary>
-
-Step 1:
-
-Consider the rationals in $[0,1]$. Let $P=[0,1]\cap \mathbb{Q}$. This set is countable.
-
-First we want to prove that there exists a set of open sets $\{U_p\}_{p\in P}$ such that if $p<q$, then $\overline{U_p}\subseteq U_q$. ($U_p$ is open in $X$.)
-
-We prove the claim using countable induction.
-
-Define $U_1=X-B$, since $B$ is closed in $A,B$ are disjoint, $A\subseteq U_1$.
-
-Since $X$ is normal, then there exists $U_0$ such that $A\subseteq U_0\subseteq \overline{U_0}\subseteq X$.
-
-By induction step, for each $p\in P$, we have $U_0,U_1,\cdots,U_{p_n}$ such that if $p<q$, then $\overline{U_p}\subseteq U_q$.
-
-Choose $U_{p_{n+1}}$ as follows:
-
-$\exists p,q\in P_n\coloneqq\{1,0,p_3,\ldots,p_n\}$ and $p_{n+1}\in (p,q)$
-
-$\exists U_{p_{n+1}}$ such that $\overline{U_p}\subseteq U_{p_{n+1}}\subseteq \overline{U_{p_{n+1}}}\subseteq U_q$ by normality of $X$.
-
-This constructs the set satisfying the claim.
-
-Step 2:
-
-We can extend from $P$ to any rationals $\mathbb{Q}$.
-
-We set $\forall p<0$, $U_p=\emptyset$ and $\forall p>1$, $U_p=X$.
-
-Otherwise we use the $p$ in $P$.
-
-Step 3:
-
-$\forall x\in X$, set $\mathbb{Q}(x)=\{p\in \mathbb{Q}:x\in U_p\}\subseteq [0,\infty)$.
-
-This function has a lower bound and $f(x)=\inf\mathbb{Q}(x)$.
-
-Observe that $A\subseteq U_p,\forall p$ and $f(A)=\inf(0,\infty)=\{0\}$.
-
-$\forall b\in B$, $b\in U_p$ if and only if $p>1$, so $f(b)=\inf(1,\infty)=1$.
-
-Suppose $x\in \overline{U_r}$, then $x\in U_s,\forall s<r$, this implies that $f(x)\leq r$.
-
-Suppose $x\notin \overline{U_r}$, then $x\notin U_s,\forall s<r$, this implies that $f(x)\geq r$.
-
-If $x\in \overline{U_q}-U_p$, then $f(x)\in [p,q]$, $\exists p<q$.
-
-To show continuity of $f(x)$.
-
-Let $x_0\in X$ of $f(x_0)\in (c,d)$,
-
-our goal is to show that there exists open $U\subseteq X$ a neighborhood of $x_0\in U$ such that $f(U)\in (c,d)$.
-
-Choose $p,q\in \mathbb{Q}$ such that $c<p<f(x_0)<q<d$.
-
-By our construction, $x_0\in \overline{U_q}-U_p$, and $f(\overline{U_q}-U_p)\subseteq [p,q]\subset (c,d)$.
-
-</details>

content/Math4201/Math4201_L38.md

@@ -1,78 +0,0 @@
-# Math4201 Topology I (Lecture 38)
-
-## Countability and separability
-
-### Metrizable spaces
-
-Let $\mathbb{R}^\omega$ be the set of all countable sequences of real numbers.
-
-where the basis is defined
-
-$$
-\mathcal{B}=\{\prod_{i=1}^\infty (a_i,b_i)\text{for all except for finitely many}(a_i,b_i)=\mathbb{R}\}
-$$
-
-#### Lemma $\mathbb{R}^\omega$ is metrizable
-
-Consider the metric define on $\mathbb{R}^\omega$ by $D(\overline{x},\overline{y})=\sup\{\frac{\overline{d}(x_i,y_i)}{i}\}$
-
-where $\overline{x}=(x_1,x_2,x_3,\cdots)$ and $\overline{y}=(y_1,y_2,y_3,\cdots)$, $\overline{d}=\min\{|x_i-y_i|,1\}$.
-
-<details>
-<summary>Sketch of proof</summary>
-
-1. $D$ is a metric. exercise
-
-2. $\forall \overline{x}\in \mathbb{R}^\omega$, $\forall \epsilon >0$, $\exists$ basis open set in product topology $U\subseteq B_D(\overline{x},\epsilon)$ containing $\overline{x}$.
-
-Choose $N\geq \frac{1}{\epsilon}$, then $\forall n\geq N,\frac{\overline{d}(x_n,y_n)}{n}<\frac{1}{N}<\epsilon$
-</details>
-
-We will use the topological space above to prove the following theorem.
-
-#### Urysohn metrization theorem
-
-If $X$ is a normal (regular and second countable) topological space, then $X$ is metrizable.
-
-<details>
-
-<summary>Proof</summary>
-
-We will show that there exists embedding $F:X\to \mathbb{R}^\omega$ such that $F$ is continuous, injective and if $Z=F(X)$, $F:X\to Z$ is a open map.
-
-Recall that [regular and second countable spaces are normal](../Math4201_L36#theorem-for-constructing-normal-spaces)
-
-1. Since $X$ is regular, then 1 point sets in $X$ are closed.
-2. $X$ is regular if and only if $\forall x\in U\subseteq X$, $U$ is open in $X$. There exists $V$ open in $X$ such that $x\in V\subseteq\overline{V}\subseteq U$.
-
-Let $\{B_n\}$ be a countable basis for $X$ (by second countability).
-
-Pass to $(n,m)$ such that $\overline{B_n}\subseteq B_m$.
-
-By [Urysohn lemma](../Math4201_L37#urysohn-lemma), there exists continuous function $g_{m,n}: X\to [0,1]$ such that $g_{m,n}(\overline{B_n})=\{1\}$ and $g_{m,n}(B_m)=\{0\}$.
-
-Therefore, we have $\{g_{m,n}\}$ is a countable set of functions, where $\overline{B_n}\subseteq B_m$.
-
-We claim that $\forall x_0\in U$ such that $U$ is open in $X$, there exists $k\in \mathbb{N}$ such that $f_k(\{x_0\})>0$ and $f_k(X-U)=0$.
-
-Definition of basis implies that $\exists x_0\in B_m\subseteq U$
-
-Note that since $X$ is regular, there exists $x_0\in B_n\subseteq \overline{B_n}\subseteq B_m$.
-
-Choose $f_k=g_{m,n}$, then $f_k(\overline{B_n})=\{1\}$ and $f_k(B_n)=\{0\}$. So $f_k(x_0)=1$ since $x_0\in \overline{B_n}$.
-
-So $F$ is **continuous** since each of the $f_k$ is continuous.
-
-$F$ is **injective** since $x\neq y$ implies that there exists $k$, $f_k=g_{m,n}$ where $x\in \overline{B_n}\subseteq B_m$ such that $f_k(x)\neq f_k(y)$.
-
-If $F(U)$ is open for all $U\subseteq X$, $U$ is open in $X$, then $F:X\to Z$ is homeomorphism.
-
-We want to show that $\forall z_0\in F(U)$, there exists neighborhood $W$ of $z_0$, $z_0\in W\subseteq F(U)$.
-
-We know that $\exists x_0\in F(x_0)$ such that $F(x_0)=z_0$.
-
-We choose $N$ such that $f_N(\{x_0\})>0$ and $f_N(X-U)=0$, ($V\cap Z\subseteq F(U)$).
-
-Let $V=\pi_N^{-1}((0,\infty))$. By construction, $V$ is open in $\mathbb{R}^\omega$. and $V\cap Z$ is open in $Z$ containing $z_0$.
-
-</details>

content/Math4201/Math4201_L39.md

@@ -1,120 +0,0 @@
-# Math4201 Topology I (Lecture 39)
-
-## Separation Axioms
-
-### Embedding manifolds
-
-A $d$ dimensional manifold is the topological space satisfying the following three properties:
-
-1. Haudorff property ($\forall x,y\in X, \exists U,V\in \mathcal{T}_X$ such that $x\in U\cap V$ and $y\notin U\cap V$)
-2. Second countable property ($\exists \mathcal{B}\subseteq \mathcal{T}_X$ such that $\mathcal{B}$ is a basis for $X$ and $\mathcal{B}$ is countable)
-3. Local homeomorphism to $\mathbb{R}^d$ ($\forall x\in M$, there is a neighborhood $U$ of $x$ such that $U$ is homeomorphic to $\mathbb{R}^d$. $\varphi:U\to \mathbb{R}^d$ is bijective, continuous, and open)
-
-<details>
-<summary> Example of manifold</summary>
-
-$\mathbb{R}^d$ is a $d$-dimensional manifold. And any open subspace of $\mathbb{R}^d$ is also a manifold.
-
----
-
-$S^1$ is a $1$-dimensional manifold.
-
----
-
-$T=\mathbb{R}^2/\mathbb{Z}^2$ is a $2$-dimensional manifold.
-
-</details>
-
-Recall the [Urysohn metirzation theorem](../Math4201_L38#urysohn-metirzation-theorem). Any normal and second countable space is metrizable.
-
-In the proof we saw that any such space can be embedded into $\mathbb{R}^\omega$ with the product topology.
-
-Question: What topological space can be embedded into $\mathbb{R}^n$ with the product topology?
-
-#### Theorem for embedding compact manifolds into $\mathbb{R}^n$
-
-Any $d$-dimensional (compact, this assumption makes the proof easier) manifold can be embedded into $\mathbb{R}^n$ with the product topology.
-
-#### Definition for support of function
-
-$\operatorname{supp}(f)=f^{-1}(\mathbb{R}-\{0\})$
-
-#### Definition for partition of unity
-
-Let $\{U_i\}_{i=1}^n$ be an open covering of $X$. A partition of unity for $X$ dominated by $\{U_i\}_{i=1}^n$ is a set of functions $\phi_i:X\to\mathbb{R}$ such that:
-
-1. $\operatorname{supp}(\phi_i)\subseteq U_i$
-2. $\sum_{i=1}^n \phi_i(x)=1$ for all $x\in X$
-
-#### Theorem for existence of partition of unity
-
-Let $X$ be a normal space and $\{U_i\}_{i=1}^n$ is an open covering of $X$. Then there is a partition of unity dominated by $\{U_i\}_{i=1}^n$.
-
-Proof uses Urysohn's lemma.
-
-<details>
-<summary>Proof for embedding compact manifolds</summary>
-
-Let $M$ be a compact manifold.
-
-For any point $x\in M$, there is an open neighborhood $U_x$ of $x$ such that $U_x$ is homeomorphic to $\mathbb{R}^d$.
-
-Let $\{U_x\}_{x\in M}$ be an open cover of $M$.
-
-Since $M$ is compact, $\{U_x\}_{x\in M}$ has a finite subcover.
-
-then $\{U_{x_i}\}_{i=1}^n$ is an open cover of $M$.
-
-Therefore $F_i:U_{x_i}\to \mathbb{R}^d$ is a homeomorphism.
-
-Since $M$ is compact and second countable, $M$ is normal.
-
-Then there sis a partition of unity $\{\phi_i:X\to \mathbb{R}\}_{i=1}^n$ for $M$ with support by $\{U_{x_i}\}_{i=1}^n$ dominated by $\{U_{x_i}\}_{i=1}^n$. Where
-
-- $\sum_{i=1}^n \phi_i(x)=1$
-- $\operatorname{supp}(\phi_i)\subseteq U_{x_i}$
-
-Define $\Psi:X\to \mathbb{R}^d$ as
-
-$$
-\Psi_i(x)=\begin{cases}
-\phi_i(x)F_i(x) & \text{if } x\in U_{x_i} \\
-0 & x\in X-\operatorname{supp}(\phi_i)
-\end{cases}
-$$
-
-Note that $\operatorname{supp}(\phi_i)\subseteq U_{x_i}$, this implies that $(X-\operatorname{supp}(\phi_i))\cup U_{x_i}=X$.
-
-$U_{x_i}\cap (X-\operatorname{supp}(\phi_i))= U_i-\operatorname{supp}(\phi_i)$
-
-In particualr, for any $x$ in the intersection, $\phi_i(x)=0\implies \phi_i(x)F_i(x)=0$.
-
-So on the overlap, $\phi_i(x)F_i(x)=0$ and hence $\Psi_i$ is well defined.
-
-Define $\Phi:X\to \mathbb{R}\times \dots \times \mathbb{R}\times \mathbb{R}^d\times \dots \times \mathbb{R}^d\cong \mathbb{R}^{(1+d)n}$ as
-
-$$
-\Phi(x)=(\phi_1(x),\dots,\phi_n(x),\Psi_1(x),\dots,\Psi_n(x))
-$$
-
-This is continuous because $\phi_i(x)$ and $\Psi_i(x)$ are continuous.
-
-Since $M$ is compact, we just need to show that $\Phi$ is one-to-one to verify that it is an embedding.
-
-Let $\Phi(x)=\Phi(x')$, then $\forall i,\phi_i(x)=\phi_i(x')$, and $\forall i,\Psi_i(x)=\Psi_i(x')$.
-
-Since $\sum_{i=1}^n \phi_i(x)=1$, $\exists i$ such that $\phi_i(x)\neq 0$, therefore $x\in U_{x_i}$.
-
-Since $\phi_i(x)=\phi_i(x')$, then $x'\in U_{x_i}$.
-
-This implies that $\Psi_i(x)=\Psi_i(x')$, $\phi_i(x)F_i(x)=\phi_i(x')F_i(x')$.
-
-So $F_i(x)=F_i(x')$ since $F_i$ is a homeomorphism.
-
-This implies that $x=x'$.
-
-So $\Phi$ is one-to-one, it is injective.
-
-Therefore $\Phi$ is an embedding.
-
-</details>

content/Math4201/_meta.js

@@ -38,9 +38,4 @@ export default {
     Math4201_L32: "Topology I (Lecture 32)",
     Math4201_L33: "Topology I (Lecture 33)",
     Math4201_L34: "Topology I (Lecture 34)",
-    Math4201_L35: "Topology I (Lecture 35)",
-    Math4201_L36: "Topology I (Lecture 36)",
-    Math4201_L37: "Topology I (Lecture 37)",
-    Math4201_L38: "Topology I (Lecture 38)",
-    Math4201_L39: "Topology I (Lecture 39)",
 }

content/Math429/index.md

@@ -1,76 +1 @@
-# Math 429 Linear Algebra
+# Math 429 Linear Algebra
-
-## Course Overview
-
-Welcome to Linear Algebra (Math 429). This course is intended as a proof based introduction to linear algebra. Topics will include: vector spaces, linear maps, eigenvalues, eigenvectors, inner product spaces, and Jordan normal form. Math 310 (or equivalent) is a prerequisite to the course, and a familiarity with proofs and proof techniques will be assumed. The course does not require but assumes a basic familiarity with the contents of Math 309 (Matrix Algebra).
-
-Textbook: Linear Algebra Done Right 4th edition
-
-Instructor: Jay Yang
-
-Office Hours: Tuesday 1-2pm, Wednesday 12-1, (or by appointment)
-
-Office: Cupples I Room 109
-
-Email: jayy@wustl.edu
-
-## Grading
-
-### Homework
-
-Homework will released every Monday, and be due every Wednesday at 11:59pm starting on September 4th. They will in general cover the week's material (Monday-Friday starting with the day the homework is released). All homework is to be submitted via Gradescope. No late homework will be accepted. Your lowest homework score will be dropped. There will be 11 homework assignments.
-
-You may and are encouraged to discuss the homework with your classmates, but the solutions you provide must be your own work. In particular, you are expected to abide by the university policy on academic integrityLinks to an external site..
-
-### Exams
-
-There will be two midterm exams, held in class on Friday February 23th and Friday April 5st. The final exam will be on Tuesday May 7 10:30AM - 12:30PM. No calculators will be permitted on any of the exams. The final exam will be comprehensive.
-
-### Final Grades
-
-The grade will be based on your scores on the homework and exams, split as follows.
-
-|Grade| Weights|
-|---|-----|
-|Homework|	40%|
-|Midterms	|15% each|
-|Final	|30%|
- 
-Your letter grade will be based off the following scale.
-
-Letter Grades
-
-|A	|A-|	B+|	B|	B-|	C+|	C|	C-|	D|
-|---|--|--|---|---|---|---|---|---|
-|90	|85	|80	|75|	70|	65|	60|	55|	50|
- 
-
-Schedule
-This is approximate, and will be updated as we go
-
-|Week|Sections|
-|---|---|
-|Week 1|	1A-1C|
-|Week 2	|1C-2B|
-|Week 3	|2B-3A|
-|Week 4	|3B-3C|
-|Week 5	|3C-3E|
-|Week 6	|3E-3F|
-|Week 7	|3F,5A-5B|
-|Week 8	|5B-5D|
-|Spring Break| |
-|Week 9	|5D,5E,6A|
-|Week 10|6A-6C|
-|Week 11|6C|
-|Week 12|7A-7B|
-|Week 13|7C,8A,8B|
-|Week 14|8B-8D|
- 
-## Resources
-
-LaTeX is a way to type up your assignment. If you decide to type up your assignments, I recommend you use LaTeX. There is a bit of a learning curve though. You may for example consider using OverleafLinks to an external site., or one of many other Tex editors including TeXstudioLinks to an external site.. If you use one of these to typeset your assignment, please submit your homework as a pdf. (Don't submit the .tex files)
-
-The textbook is available open access at [Linear Algebra Done Right](https://link.springer.com/book/10.1007/978-3-031-41026-0) to an external site.. I personally suggest having a physical copy if possible.
-
-If you want other linear algebra textbooks, Hoffmann and Kunze's Linear Algebra is a suggestion.
- 

distribute/next.config.mjs

@@ -20,13 +20,14 @@ const bundleAnalyzer = withBundleAnalyzer({
 })
 
 export default bundleAnalyzer(withNextra({
-  
-  output: 'export',
-  trailingSlash: true,
-  images: {
-    unoptimized: true,
-  },
 
+  // static export start
+  output: 'export',
+  images: {
+    unoptimized: true // mandatory, otherwise won't export
+  },
+  // static export end
+  
   // eslint: {
   //   ignoreDuringBuilds: true,
   // },
@@ -39,7 +40,4 @@ export default bundleAnalyzer(withNextra({
   //   staticGenerationMaxConcurrency: 2,   // try 1–3, default is 8
   //   staticGenerationMinPagesPerWorker: 1 // keep small, default is 25
   // }
-}))
+}))
-
-// If you have other Next.js configurations, you can pass them as the parameter:
-// export default withNextra({ /* other next.js config */ })

distribute/nginx.conf

@@ -1,248 +0,0 @@
-    # Example for conf.d/default.conf
-user www-data;
-worker_processes 1;
-
-error_log /var/log/nginx/error.log;
-pid /var/run/nginx.pid;
-
-events {
-    worker_connections 1024;
-}
-
-http {
-
-    upstream notenextra-math {
-        server notenextra-math:4200;
-    }
-
-    upstream notenextra-cse {
-        server notenextra-cse:4200;
-    }
-
-    # Decide where to send /_pagefind* based on the page that made the request
-    map $http_referer $load_upstream {
-        default                          http://notenextra-cse;
-        ~*://[^/]+/Math(?:/|$)           http://notenextra-math;
-        ~*://[^/]+/CSE(?:/|$)            http://notenextra-cse;
-    }
-
-
-    include       /etc/nginx/mime.types;
-
-    # add extra types
-
-    types {
-        text/javascript mjs;
-    }
-
-    default_type  application/octet-stream;
-
-    log_format  main  '$remote_addr - $remote_user [$time_local] "$request" '
-                      '$status $body_bytes_sent "$http_referer" '
-                      '"$http_user_agent" "$http_x_forwarded_for"';
-
-    access_log  /var/log/nginx/access.log  main;
-
-    server {
-        listen 80;
-        server_name localhost;
-
-        rewrite ^/.well-known/carddav /remote.php/dav/ permanent;
-        rewrite ^/.well-known/caldav /remote.php/dav/ permanent;
-
-        location = /robots.txt {
-            allow all;
-            log_not_found off;
-            access_log off;
-        }
-
-        # Send all next or additional assets (/_pagefind.js and /_pagefind/*) to the chosen app
-        # ^~ /_pagefind matches both "/_pagefind.js" and "/_pagefind/..."
-        location ^~ /_(.*)$ {
-            proxy_pass $load_upstream;   # leaves URI intact (/_pagefind.js, /_pagefind/manifest.json, etc.)
-            proxy_set_header Host $host;
-            proxy_set_header X-Real-IP $remote_addr;
-            proxy_set_header X-Forwarded-For $proxy_add_x_forwarded_for;
-            proxy_set_header X-Forwarded-Proto $scheme;
-        }
-
-        location ~ ^/(build|tests|config|lib|3rdparty|templates|data)/ {
-            deny all;
-        }
-
-        location ~ ^/(?:\.|autotest|occ|issue|indie|db_|console) {
-            deny all;
-        }
-
-        # Course-specific prefix
-        location ^~ /Math3200/ {
-            proxy_pass https://notenextra-math3200.pages.dev;
-            proxy_set_header Host notenextra-math3200.pages.dev;
-
-            proxy_ssl_server_name on;
-            proxy_ssl_name notenextra-math3200.pages.dev;
-
-            proxy_set_header X-Real-IP $remote_addr;
-            proxy_set_header X-Forwarded-For $proxy_add_x_forwarded_for;
-            proxy_set_header X-Forwarded-Proto $scheme;
-        }
-        location ^~ /Math429/ {
-            proxy_pass https://notenextra-math429.pages.dev;
-            proxy_set_header Host notenextra-math429.pages.dev;
-
-            proxy_ssl_server_name on;
-            proxy_ssl_name notenextra-math429.pages.dev;
-
-            proxy_set_header X-Real-IP $remote_addr;
-            proxy_set_header X-Forwarded-For $proxy_add_x_forwarded_for;
-            proxy_set_header X-Forwarded-Proto $scheme;
-        }
-        location ^~ /Math4111/ {
-            proxy_pass https://notenextra-math4111.pages.dev;
-            proxy_set_header Host notenextra-math4111.pages.dev;
-
-            proxy_ssl_server_name on;
-            proxy_ssl_name notenextra-math4111.pages.dev;
-
-            proxy_set_header X-Real-IP $remote_addr;
-            proxy_set_header X-Forwarded-For $proxy_add_x_forwarded_for;
-            proxy_set_header X-Forwarded-Proto $scheme;
-        }
-        location ^~ /Math4121/ {
-            proxy_pass https://notenextra-math4121.pages.dev;
-            proxy_set_header Host notenextra-math4121.pages.dev;
-
-            proxy_ssl_server_name on;
-            proxy_ssl_name notenextra-math4121.pages.dev;
-
-            proxy_set_header X-Real-IP $remote_addr;
-            proxy_set_header X-Forwarded-For $proxy_add_x_forwarded_for;
-            proxy_set_header X-Forwarded-Proto $scheme;
-        }
-        location ^~ /Math4201/ {
-            proxy_pass https://notenextra-math4201.pages.dev;
-            proxy_set_header Host notenextra-math4201.pages.dev;
-
-            proxy_ssl_server_name on;
-            proxy_ssl_name notenextra-math4201.pages.dev;
-
-            proxy_set_header X-Real-IP $remote_addr;
-            proxy_set_header X-Forwarded-For $proxy_add_x_forwarded_for;
-            proxy_set_header X-Forwarded-Proto $scheme;
-        }
-        location ^~ /Math416/ {
-            proxy_pass https://notenextra-math416.pages.dev;
-            proxy_set_header Host notenextra-math416.pages.dev;
-
-            proxy_ssl_server_name on;
-            proxy_ssl_name notenextra-math416.pages.dev;
-
-            proxy_set_header X-Real-IP $remote_addr;
-            proxy_set_header X-Forwarded-For $proxy_add_x_forwarded_for;
-            proxy_set_header X-Forwarded-Proto $scheme;
-        }
-        location ^~ /Math401/ {
-            proxy_pass https://notenextra-math401.pages.dev;
-            proxy_set_header Host notenextra-math401.pages.dev;
-
-            proxy_ssl_server_name on;
-            proxy_ssl_name notenextra-math401.pages.dev;
-
-            proxy_set_header X-Real-IP $remote_addr;
-            proxy_set_header X-Forwarded-For $proxy_add_x_forwarded_for;
-            proxy_set_header X-Forwarded-Proto $scheme;
-        }
-        location ^~ /CSE332S/ {
-            proxy_pass https://notenextra-cse332s.pages.dev;
-            proxy_set_header Host notenextra-cse332s.pages.dev;
-
-            proxy_ssl_server_name on;
-            proxy_ssl_name notenextra-cse332s.pages.dev;
-
-            proxy_set_header X-Real-IP $remote_addr;
-            proxy_set_header X-Forwarded-For $proxy_add_x_forwarded_for;
-            proxy_set_header X-Forwarded-Proto $scheme;
-        }
-        location ^~ /CSE347/ {
-            proxy_pass https://notenextra-cse347.pages.dev;
-            proxy_set_header Host notenextra-cse347.pages.dev;
-
-            proxy_ssl_server_name on;
-            proxy_ssl_name notenextra-cse347.pages.dev;
-
-            proxy_set_header X-Real-IP $remote_addr;
-            proxy_set_header X-Forwarded-For $proxy_add_x_forwarded_for;
-            proxy_set_header X-Forwarded-Proto $scheme;
-        }
-        location ^~ /CSE442T/ {
-            proxy_pass https://notenextra-cse442t.pages.dev;
-            proxy_set_header Host notenextra-cse442t.pages.dev;
-
-            proxy_ssl_server_name on;
-            proxy_ssl_name notenextra-cse442t.pages.dev;
-
-            proxy_set_header X-Real-IP $remote_addr;
-            proxy_set_header X-Forwarded-For $proxy_add_x_forwarded_for;
-            proxy_set_header X-Forwarded-Proto $scheme;
-        }
-        location ^~ /CSE5313/ {
-            proxy_pass https://notenextra-cse5313.pages.dev;
-            proxy_set_header Host notenextra-cse5313.pages.dev;
-
-            proxy_ssl_server_name on;
-            proxy_ssl_name notenextra-cse5313.pages.dev;
-
-            proxy_set_header X-Real-IP $remote_addr;
-            proxy_set_header X-Forwarded-For $proxy_add_x_forwarded_for;
-            proxy_set_header X-Forwarded-Proto $scheme;
-        }
-        location ^~ /CSE510/ {
-            proxy_pass https://notenextra-cse510.pages.dev;
-            proxy_set_header Host notenextra-cse510.pages.dev;
-
-            proxy_ssl_server_name on;
-            proxy_ssl_name notenextra-cse510.pages.dev;
-
-            proxy_set_header X-Real-IP $remote_addr;
-            proxy_set_header X-Forwarded-For $proxy_add_x_forwarded_for;
-            proxy_set_header X-Forwarded-Proto $scheme;
-        }
-        location ^~ /CSE559A/ {
-            proxy_pass https://notenextra-cse559a.pages.dev;
-            proxy_set_header Host notenextra-cse559a.pages.dev;
-
-            proxy_ssl_server_name on;
-            proxy_ssl_name notenextra-cse559a.pages.dev;
-
-            proxy_set_header X-Real-IP $remote_addr;
-            proxy_set_header X-Forwarded-For $proxy_add_x_forwarded_for;
-            proxy_set_header X-Forwarded-Proto $scheme;
-        }
-        location ^~ /CSE5519/ {
-            proxy_pass https://notenextra-cse5519.pages.dev;
-            proxy_set_header Host notenextra-cse5519.pages.dev;
-
-            proxy_ssl_server_name on;
-            proxy_ssl_name notenextra-cse5519.pages.dev;
-
-            proxy_set_header X-Real-IP $remote_addr;
-            proxy_set_header X-Forwarded-For $proxy_add_x_forwarded_for;
-            proxy_set_header X-Forwarded-Proto $scheme;
-        }
-
-        # Everything else
-        location / {
-            proxy_pass https://notenextra-cse332s.pages.dev;
-            proxy_set_header Host notenextra-cse332s.pages.dev;
-
-            proxy_ssl_server_name on;
-            proxy_ssl_name notenextra-cse332s.pages.dev;
-
-            proxy_set_header X-Real-IP $remote_addr;
-            proxy_set_header X-Forwarded-For $proxy_add_x_forwarded_for;
-            proxy_set_header X-Forwarded-Proto $scheme;
-        }
-        access_log  /www/wwwlogs/test.trance-0.com.log;
-        error_log  /www/wwwlogs/test.trance-0.com.error.log;
-    }
-}

distribute/prebuild.sh

@@ -1,10 +1,7 @@
 # This is pre-build script that cleans up resources and compiles for selected pages, then finally you may combine those subdirectories into one via nginx.
 # double check you are using LF instead of CRLF
 
-# please run this script in project root directory
+export KEEP_PAGES="Math3200"
-
-# test environemnt variables, set this in your remote instead
-# export KEEP_PAGES="Math3200"
 
 # check if environment variable is set
 if [ -z "$KEEP_PAGES" ]; then
@@ -24,12 +21,6 @@ for dir in ./content/*/; do
     # strip the leading path and trailing slash
     base_dir="$(basename "${dir%/}")"
 
-    # explicitly ignore Swap
-    if [ "$base_dir" = "Swap" ]; then
-        echo "Ignoring Swap dir: $dir"
-        continue
-    fi
-
     # check if base_dir is in KEEP_PAGES (space-separated list)
     case " $KEEP_PAGES " in
         *" $base_dir "*) 
@@ -46,12 +37,6 @@ done
 for dir in ./public/*/; do
     base_dir="$(basename "${dir%/}")"
 
-    # explicitly ignore Swap
-    if [ "$base_dir" = "Swap" ]; then
-        echo "Ignoring Swap dir: $dir"
-        continue
-    fi
-    
     case " $KEEP_PAGES " in
         *" $base_dir "*) 
             echo "Keeping public dir: $dir"

docker/Jenkinsfile

@@ -1,119 +0,0 @@
-pipeline {
-    environment {
-        registry = "trance0/notenextra"
-        version = "1.2"
-        NODE_OPTIONS = "--max-old-space-size=8192"
-        // NEXT_SEARCH_ALGOLIA_APP_ID = "${NEXT_SEARCH_ALGOLIA_APP_ID}"
-        // NEXT_SEARCH_ALGOLIA_API_KEY = "${NEXT_SEARCH_ALGOLIA_API_KEY}"
-        // NEXT_SEARCH_ALGOLIA_INDEX_NAME = "${NEXT_SEARCH_ALGOLIA_INDEX_NAME}"
-    }
-    
-    agent any
-
-    stages {
-        stage("Cleanup Workspace") {
-            steps {
-                // Using Workspace Cleanup Plugin (if installed and configured)
-                cleanWs()
-            }
-        }
-        stage("Checkout") {
-            steps {
-                checkout([
-                    $class: "GitSCM",
-                    branches: [[ name: "*/main" ]],
-                    userRemoteConfigs: [[
-                        url: "https://github.com/Trance-0/NoteNextra",
-                    ]]
-                ])
-            }
-        }
-        stage('Pre-build script') {
-            steps{
-                script {
-                    echo "Running pre-build script"
-                    sh "./docker/prebuild.sh"
-                }
-            }
-        }
-        stage("Build and test"){
-            parallel {
-                stage("Build Math") {
-                    steps {
-                        script {
-                            echo "Building docker image ${registry}-math:${version}.${env.BUILD_ID}"
-                            def customImage = docker.build("${registry}-math:v${version}.${env.BUILD_ID}","-f ./docker/math/Dockerfile --no-cache --progress=plain .")
-                            echo "Logging in to docker hub"
-                            // docker.withRegistry("https://registry.hub.docker.com", "docker-hub-creds") {
-                            //     echo "Pushing docker image ${registry}:v${version}.${env.BUILD_ID}"
-                            //     customImage.push()
-                            // }
-                            echo "skipping push due to conflicted servers"
-                        }
-                    }
-                }
-                stage("Build CSE") {
-                    steps {
-                        script {
-                            echo "Building docker image ${registry}-cse:${version}.${env.BUILD_ID}"
-                            def customImage = docker.build("${registry}-cse:v${version}.${env.BUILD_ID}","-f ./docker/cse/Dockerfile --no-cache --progress=plain .")
-                            echo "Logging in to docker hub"
-                            // docker.withRegistry("https://registry.hub.docker.com", "docker-hub-creds") {
-                            //     echo "Pushing docker image ${registry}:v${version}.${env.BUILD_ID}"
-                            //     customImage.push()
-                            // }
-                            echo "skipping push due to conflicted servers"
-                        }
-                    }
-                }
-            }
-        }
-        stage("Cleanup Docker tags") {
-            steps {
-                script {
-                    echo "1. Stopping existing container"
-                    sh "docker compose -f ./docker/docker-compose.yaml down"
-                    // Using Workspace Cleanup Plugin (if installed and configured)
-                    echo "2. Removing existing images"
-                    def imageNameMath = "${registry}-math:latest"
-                    def imageNameCSE = "${registry}-cse:latest"
-                    def oldImageIDMath = sh( 
-                                            script: "docker images -qf reference=\${imageNameMath}",
-                                            returnStdout: true
-                                        )
-                    def oldImageIDCSE = sh( 
-                                            script: "docker images -qf reference=\${imageNameCSE}",
-                                            returnStdout: true
-                                        )
-                    if ( "${oldImageIDMath}" != "" ) {
-                        echo "Removing old image ${oldImageIDMath}"
-                        echo "Image Name: " + "${imageNameMath}"
-                        echo "Old Image: ${oldImageIDMath}"
-                        sh "docker rmi ${oldImageIDMath}"
-                    }else{
-                        echo "Warning: ${imageNameMath} does not exist"
-                    }
-                    if ( "${oldImageIDCSE}" != "" ) {
-                        echo "Removing old image ${oldImageIDCSE}"
-                        echo "Image Name: " + "${imageNameCSE}"
-                        echo "Old Image: ${oldImageIDCSE}"
-                        sh "docker rmi ${oldImageIDCSE}"
-                    }else{
-                        echo "Warning: ${imageNameCSE} does not exist"
-                    }
-                    echo "3. Assigned new tags to the images"
-                    sh "docker tag ${registry}-math:v${version}.${env.BUILD_ID} ${registry}-math:latest"
-                    sh "docker tag ${registry}-cse:v${version}.${env.BUILD_ID} ${registry}-cse:latest"
-                }
-            }
-        }
-        stage("Deploy") {
-            steps {
-                script {
-                    echo "Deploying docker image ${registry}-math:${version}.${env.BUILD_ID} and ${registry}-cse:${version}.${env.BUILD_ID} with docker compose"
-                    sh "docker compose -f ./docker/docker-compose.yaml up -d"
-                }
-            }
-        }
-    }
-}

docker/README.md

@@ -1,3 +0,0 @@
-# Notice
-
-To build via docker, run the ./prebuild.sh script before building the docker image, this script will update the meta.json file for parsing scripts in docker.

docker/_meta.js

@@ -1,226 +0,0 @@
-export default {
-  /**
-   * Do not remove the labels "Math Courses Start"
-   * and "Math Courses End" and "CSE Courses Start" and "CSE Courses End"
-   * or the separated builds will not work.
-   * 
-   * WE USE THESE LABELS TO BUILD THE SEPARATED WEBSITES FOR MATH AND CSE COURSES.
-   */
-    menu: {
-      title: 'Home',
-      type: 'menu',
-      items: {
-        index: {
-          title: 'Home',
-          href: '/'
-        },
-        about: {
-          title: 'About',
-          href: '/about'
-        },
-        contact: {
-          title: 'Contact Me',
-          href: '/contact'
-        }
-      },
-    },
-    Math3200_link: {
-      title: 'Math3200',
-      type: 'page',
-      href: '/Math3200'
-    },
-    Math429_link: {
-      title: 'Math429',
-      type: 'page',
-      href: '/Math429'
-    },
-    Math4111_link: {
-      title: 'Math4111',
-      type: 'page',
-      href: '/Math4111'
-    },
-    Math4121_link: {
-      title: 'Math4121',
-      type: 'page',
-      href: '/Math4121'
-    },
-    Math4201_link: {
-      title: 'Math4201',
-      type: 'page',
-      href: '/Math4201'
-    },
-    Math416_link: {
-      title: 'Math416',
-      type: 'page',
-      href: '/Math416'
-    },
-    Math401_link: {
-      title: 'Math401',
-      type: 'page',
-      href: '/Math401'
-    },
-    /* Math Courses Start */
-    Math3200: {
-      title: 'Math3200',
-      type: 'page',
-      theme:{
-        timestamp: true,
-      }
-    },
-    Math429:{
-      title: 'Math429',
-      type: 'page',
-      theme:{
-        timestamp: true,
-      }
-    },
-    Math4111: {
-      title: 'Math4111',
-      type: 'page',
-      theme:{
-        timestamp: true,
-      }
-    },
-    Math4121: {
-      title: 'Math4121',
-      type: 'page',
-      theme:{
-        timestamp: true,
-      }
-    },
-    Math4201: {
-      title: 'Math4201',
-      type: 'page',
-      theme:{
-        timestamp: true,
-      }
-    },
-    Math416: {
-      title: 'Math416',
-      type: 'page',
-      theme:{
-        timestamp: true,
-      }
-    },
-    Math401: {
-      title: 'Math401',
-      type: 'page',
-      theme:{
-        timestamp: true,
-      }
-    },
-    /* Math Courses End */
-    CSE332S_link: {
-      title: 'CSE332S',
-      type: 'page',
-      href: '/CSE332S'
-    },
-    CSE347_link: {
-      title: 'CSE347',
-      type: 'page',
-      href: '/CSE347'
-    },
-    CSE442T_link: {
-      title: 'CSE442T',
-      type: 'page',
-      href: '/CSE442T'
-    },
-    CSE5313_link: {
-      title: 'CSE5313',
-      type: 'page',
-      href: '/CSE5313'
-    },
-    CSE510_link: {
-      title: 'CSE510',
-      type: 'page',
-      href: '/CSE510'
-    },
-    CSE559A_link: {
-      title: 'CSE559A',
-      type: 'page',
-      href: '/CSE559A'
-    },
-    CSE5519_link: {
-      title: 'CSE5519',
-      type: 'page',
-      href: '/CSE5519'
-    },
-    /* CSE Courses Start */
-    CSE332S: {
-      title: 'CSE332S',
-      type: 'page',
-      theme:{
-        timestamp: true,
-      }
-    },
-    CSE347: {
-      title: 'CSE347',
-      type: 'page',
-      theme:{
-        timestamp: true,
-      }
-    },
-    CSE442T: {
-      title: 'CSE442T',
-      type: 'page',
-      theme:{
-        timestamp: true,
-      }
-    },
-    CSE5313: {
-      title: 'CSE5313',
-      type: 'page',
-      theme:{
-        timestamp: true,
-      }
-    },
-    CSE510: {
-      title: 'CSE510',
-      type: 'page',
-      theme:{
-        timestamp: true,
-      }
-    },
-    CSE559A: {
-      title: 'CSE559A',
-      type: 'page',
-      theme:{
-        timestamp: true,
-      }
-    },
-    CSE5519: {
-      title: 'CSE5519',
-      type: 'page',
-      theme:{
-        timestamp: true,
-      }
-    },
-    /* CSE Courses End */
-    Swap: {
-      display: 'hidden',
-      theme:{
-        timestamp: true,
-      }
-    },
-    index: {
-      display: 'hidden',
-      theme:{
-        sidebar: false,
-        timestamp: true,
-      }
-    },
-    about: {
-      display: 'hidden',
-      theme:{
-        sidebar: false,
-        timestamp: true,
-      }
-    },
-    contact: {
-      display: 'hidden',
-      theme:{
-        sidebar: false,
-        timestamp: true,
-      }
-    }
-  }

docker/create_meta.py

@@ -1,168 +0,0 @@
-#!/usr/bin/env python3
-"""
-This code is generate by ChatGPT 5.1, as test automatic script to generate _meta.js file
-
-Generate ./docker/_meta.js with Math/CSE link entries and labeled sections
-from ./content/_meta.js.
-
-This script is intended to be run directly (no arguments) from anywhere.
-"""
-
-from pathlib import Path
-import re
-
-# --------------------------------------------------------------------
-# Configuration
-# --------------------------------------------------------------------
-
-SCRIPT_DIR = Path(__file__).resolve().parent
-SRC_META = SCRIPT_DIR.parent / "content" / "_meta.js"
-DST_META = SCRIPT_DIR / "_meta.js"
-
-COMMENT_BLOCK = [
-    "  /**\n",
-    '   * Do not remove the labels "Math Courses Start"\n',
-    '   * and "Math Courses End" and "CSE Courses Start" and "CSE Courses End"\n',
-    "   * or the separated builds will not work.\n",
-    "   * \n",
-    "   * WE USE THESE LABELS TO BUILD THE SEPARATED WEBSITES FOR MATH AND CSE COURSES.\n",
-    "   */\n",
-]
-
-PROP_RE = re.compile(r"^ {4}(\w+)\s*:")
-
-
-def parse_properties(lines):
-    """
-    Parse top-level properties (indented 4 spaces) of the export default object.
-
-    Returns:
-        header_lines: lines up to and including 'export default {'
-        footer_lines: closing '}' (and anything after)
-        props: dict name -> list of lines for that property
-        order: order of property names as they appeared
-    """
-    export_idx = None
-    for i, line in enumerate(lines):
-        if "export default" in line:
-            export_idx = i
-            break
-    if export_idx is None:
-        raise ValueError("No 'export default' found in source meta file.")
-
-    # find closing brace of the object (typically last non-empty '}' line)
-    closing_idx = None
-    for i in range(len(lines) - 1, -1, -1):
-        if lines[i].strip().startswith("}"):
-            closing_idx = i
-            break
-    if closing_idx is None or closing_idx <= export_idx:
-        raise ValueError("Could not locate closing '}' of export default object.")
-
-    header = lines[: export_idx + 1]
-    footer = lines[closing_idx:]
-    body = lines[export_idx + 1 : closing_idx]
-
-    props = {}
-    order = []
-
-    i = 0
-    n = len(body)
-    while i < n:
-        line = body[i]
-        m = PROP_RE.match(line)
-        if not m:
-            i += 1
-            continue
-
-        key = m.group(1)
-        start = i
-
-        brace_count = line.count("{") - line.count("}")
-        j = i + 1
-        while j < n and brace_count > 0:
-            brace_count += body[j].count("{") - body[j].count("}")
-            j += 1
-
-        block = body[start:j]
-        props[key] = block
-        order.append(key)
-        i = j
-
-    return header, footer, props, order
-
-
-def build_links_block(keys):
-    """Generate *_link blocks for given course keys (Math* or CSE*)."""
-    out = []
-    for k in keys:
-        out.append(f"    {k}_link: {{\n")
-        out.append(f"      title: '{k}',\n")
-        out.append("      type: 'page',\n")
-        out.append(f"      href: '/{k}'\n")
-        out.append("    },\n")
-    return out
-
-
-def generate_new_meta(lines):
-    header, footer, props, order = parse_properties(lines)
-
-    math_keys = [k for k in order if k.startswith("Math")]
-    cse_keys = [k for k in order if k.startswith("CSE")]
-    other_keys = [
-        k for k in order
-        if k not in math_keys + cse_keys + ["menu"]
-    ]
-
-    if "menu" not in props:
-        raise ValueError("Expected a top-level 'menu' property in source meta.")
-
-    out = []
-
-    # header (includes "export default {")
-    out.extend(header)
-    # comment block
-    out.extend(COMMENT_BLOCK)
-    # original menu block
-    out.extend(props["menu"])
-
-    # Math links
-    out.extend(build_links_block(math_keys))
-
-    # Math Courses section
-    out.append("    /* Math Courses Start */\n")
-    for k in math_keys:
-        out.extend(props[k])
-    out.append("    /* Math Courses End */\n")
-
-    # CSE links
-    out.extend(build_links_block(cse_keys))
-
-    # CSE Courses section
-    out.append("    /* CSE Courses Start */\n")
-    for k in cse_keys:
-        out.extend(props[k])
-    out.append("    /* CSE Courses End */\n")
-
-    # other properties (Swap, index, about, contact, etc.) in original order
-    for k in other_keys:
-        out.extend(props[k])
-
-    # footer (closing brace, etc.)
-    out.extend(footer)
-
-    return out
-
-
-# --------------------------------------------------------------------
-# Script execution (no CLI args, no main())
-# --------------------------------------------------------------------
-
-if not SRC_META.exists():
-    raise SystemExit(f"Source meta file not found: {SRC_META}")
-
-src_lines = SRC_META.read_text(encoding="utf-8").splitlines(keepends=True)
-new_lines = generate_new_meta(src_lines)
-DST_META.write_text("".join(new_lines), encoding="utf-8")
-
-print(f"Generated meta file: {DST_META}")

docker/cse/Dockerfile

@@ -1,73 +0,0 @@
-# Dockerfile for Math folders
-
-# Source: https://github.com/vercel/next.js/blob/canary/examples/with-docker-multi-env/docker/production/Dockerfile
-# syntax=docker.io/docker/dockerfile:1
-
-FROM node:20-alpine AS base
-
-ENV NODE_OPTIONS="--max-old-space-size=8192"
-
-# 1. Install dependencies only when needed
-FROM base AS deps
-# Check https://github.com/nodejs/docker-node/tree/b4117f9333da4138b03a546ec926ef50a31506c3#nodealpine to understand why libc6-compat might be needed.
-RUN apk add --no-cache libc6-compat git
-
-WORKDIR /app
-
-# Install dependencies based on the preferred package manager
-COPY package.json yarn.lock* package-lock.json* pnpm-lock.yaml* .npmrc* ./
-RUN \
-  if [ -f yarn.lock ]; then yarn --frozen-lockfile; \
-  elif [ -f package-lock.json ]; then npm ci; \
-  elif [ -f pnpm-lock.yaml ]; then corepack enable pnpm && pnpm i; \
-  else echo "Lockfile not found, use default npm install" && npm i; \
-  fi
-
-# 2. Rebuild the source code only when needed
-FROM base AS builder
-WORKDIR /app
-COPY --from=deps /app/node_modules ./node_modules
-COPY . .
-RUN ls -la
-
-# 2.1 Remove unnecessary files for build with title starting with CSE
-RUN cd ./content && find . -maxdepth 1 -type d -name "Math*" -exec rm -rf {} +
-RUN cd ./public && find . -maxdepth 1 -type d -name "Math*" -exec rm -rf {} +
-
-# 2.1.1 Check the updated folders
-RUN cd ./content && ls -la
-RUN cd ./public && ls -la
-
-# 2.2 Update the _meta.js files in the content folder
-RUN sed -i '/\/\* Math Courses Start \*\//,/\/\* Math Courses End \*\//d' ./content/_meta.js
-
-# 2.2.1 Check the updated _meta.js file
-RUN cat ./content/_meta.js
-
-# This will do the trick, use the corresponding env file for each environment.
-# COPY .env.production.sample .env.production
-RUN npm run build
-
-# 3. Production image, copy all the files and run next
-FROM base AS runner
-WORKDIR /app
-
-ENV NODE_ENV=production
-
-RUN addgroup -g 1001 -S nodejs
-RUN adduser -S nextjs -u 1001
-
-COPY --from=builder /app/public ./public
-
-# Automatically leverage output traces to reduce image size
-# https://nextjs.org/docs/advanced-features/output-file-tracing
-COPY --from=builder --chown=nextjs:nodejs /app/.next/standalone ./
-COPY --from=builder --chown=nextjs:nodejs /app/.next/static ./.next/static
-
-USER nextjs
-
-EXPOSE 4200
-
-ENV PORT=4200
-
-CMD HOSTNAME="0.0.0.0" node server.js

docker/cse/test-build.sh

@@ -1 +0,0 @@
-sudo docker build -t trance-0/notenextra-cse:v1.2.0 -f ./docker/cse/Dockerfile --no-cache --progress=plain .

docker/docker-compose-rebuild.sh

@@ -1 +0,0 @@
-docker compose -f docker/docker-compose.yaml up -d --build notenextra-math notenextra-cse

docker/docker-compose.yaml

@@ -1,33 +0,0 @@
-name: notenextra
-services:
-  # you may need to update relative directories if you move this file
-  # default created directories is /docker/docker-compose.yaml
-  notenextra-math:
-    image: trance0/notenextra-math:latest
-    build:
-      context: ../
-      dockerfile: ./docker/math/Dockerfile
-      tags:
-        - trance0/notenextra-math:latest
-    restart: on-failure:5
-    ports:
-      - 13001:4200
-  notenextra-cse:
-    image: trance0/notenextra-cse:latest
-    build:
-      context: ../
-      dockerfile: ./docker/cse/Dockerfile
-      tags:
-        - trance0/notenextra-cse:latest
-    restart: on-failure:5
-    ports:
-      - 13002:4200
-  nginx:
-    image: nginx:latest
-    ports:
-      - 13000:80
-    volumes:
-      - ./nginx.conf:/etc/nginx/nginx.conf
-    depends_on:
-      - notenextra-math
-      - notenextra-cse

docker/math/Dockerfile

@@ -1,73 +0,0 @@
-# Dockerfile for Math folders
-
-# Source: https://github.com/vercel/next.js/blob/canary/examples/with-docker-multi-env/docker/production/Dockerfile
-# syntax=docker.io/docker/dockerfile:1
-
-FROM node:20-alpine AS base
-
-ENV NODE_OPTIONS="--max-old-space-size=8192"
-
-# 1. Install dependencies only when needed
-FROM base AS deps
-# Check https://github.com/nodejs/docker-node/tree/b4117f9333da4138b03a546ec926ef50a31506c3#nodealpine to understand why libc6-compat might be needed.
-RUN apk add --no-cache libc6-compat git
-
-WORKDIR /app
-
-# Install dependencies based on the preferred package manager
-COPY package.json yarn.lock* package-lock.json* pnpm-lock.yaml* .npmrc* ./
-RUN \
-  if [ -f yarn.lock ]; then yarn --frozen-lockfile; \
-  elif [ -f package-lock.json ]; then npm ci; \
-  elif [ -f pnpm-lock.yaml ]; then corepack enable pnpm && pnpm i; \
-  else echo "Lockfile not found, use default npm install" && npm i; \
-  fi
-
-# 2. Rebuild the source code only when needed
-FROM base AS builder
-WORKDIR /app
-COPY --from=deps /app/node_modules ./node_modules
-COPY . .
-RUN ls -la
-
-# 2.1 Remove unnecessary files for build with title starting with CSE
-RUN cd ./content && find . -maxdepth 1 -type d -name "CSE*" -exec rm -rf {} +
-RUN cd ./public && find . -maxdepth 1 -type d -name "CSE*" -exec rm -rf {} +
-
-# 2.1.1 Check the updated folders
-RUN cd ./content && ls -la
-RUN cd ./public && ls -la
-
-# 2.2 Update the _meta.js files in the content folder
-RUN sed -i '/\/\* CSE Courses Start \*\//,/\/\* CSE Courses End \*\//d' ./content/_meta.js
-
-# 2.2.1 Check the updated _meta.js file
-RUN cat ./content/_meta.js
-
-# This will do the trick, use the corresponding env file for each environment.
-# COPY .env.production.sample .env.production
-RUN npm run build
-
-# 3. Production image, copy all the files and run next
-FROM base AS runner
-WORKDIR /app
-
-ENV NODE_ENV=production
-
-RUN addgroup -g 1001 -S nodejs
-RUN adduser -S nextjs -u 1001
-
-COPY --from=builder /app/public ./public
-
-# Automatically leverage output traces to reduce image size
-# https://nextjs.org/docs/advanced-features/output-file-tracing
-COPY --from=builder --chown=nextjs:nodejs /app/.next/standalone ./
-COPY --from=builder --chown=nextjs:nodejs /app/.next/static ./.next/static
-
-USER nextjs
-
-EXPOSE 4200
-
-ENV PORT=4200
-
-CMD HOSTNAME="0.0.0.0" node server.js

docker/math/test-build.sh

@@ -1 +0,0 @@
-sudo docker build -t trance-0/notenextra-math:v1.2.0 -f ./docker/math/Dockerfile --no-cache --progress=plain .

docker/nginx.conf

@@ -1,102 +0,0 @@
-    # Example for conf.d/default.conf
-user www-data;
-worker_processes 1;
-
-error_log /var/log/nginx/error.log;
-pid /var/run/nginx.pid;
-
-events {
-    worker_connections 1024;
-}
-
-http {
-
-    upstream notenextra-math {
-        server notenextra-math:4200;
-    }
-
-    upstream notenextra-cse {
-        server notenextra-cse:4200;
-    }
-
-    # Decide where to send /_pagefind* based on the page that made the request
-    map $http_referer $load_upstream {
-        default                          http://notenextra-cse;
-        ~*://[^/]+/Math(?:/|$)           http://notenextra-math;
-        ~*://[^/]+/CSE(?:/|$)            http://notenextra-cse;
-    }
-
-
-    include       /etc/nginx/mime.types;
-
-    # add extra types
-
-    types {
-        text/javascript mjs;
-    }
-
-    default_type  application/octet-stream;
-
-    log_format  main  '$remote_addr - $remote_user [$time_local] "$request" '
-                      '$status $body_bytes_sent "$http_referer" '
-                      '"$http_user_agent" "$http_x_forwarded_for"';
-
-    access_log  /var/log/nginx/access.log  main;
-
-    server {
-        listen 80;
-        server_name localhost;
-
-        rewrite ^/.well-known/carddav /remote.php/dav/ permanent;
-        rewrite ^/.well-known/caldav /remote.php/dav/ permanent;
-
-        location = /robots.txt {
-            allow all;
-            log_not_found off;
-            access_log off;
-        }
-
-        # Send all next or additional assets (/_pagefind.js and /_pagefind/*) to the chosen app
-        # ^~ /_pagefind matches both "/_pagefind.js" and "/_pagefind/..."
-        location ^~ /_(.*)$ {
-            proxy_pass $load_upstream;   # leaves URI intact (/_pagefind.js, /_pagefind/manifest.json, etc.)
-            proxy_set_header Host $host;
-            proxy_set_header X-Real-IP $remote_addr;
-            proxy_set_header X-Forwarded-For $proxy_add_x_forwarded_for;
-            proxy_set_header X-Forwarded-Proto $scheme;
-        }
-
-        location ~ ^/(build|tests|config|lib|3rdparty|templates|data)/ {
-            deny all;
-        }
-
-        location ~ ^/(?:\.|autotest|occ|issue|indie|db_|console) {
-            deny all;
-        }
-
-        location ~ ^/Math(.*)$ {
-            proxy_pass http://notenextra-math/Math$1;
-            proxy_set_header Host $host;
-            proxy_set_header X-Real-IP $remote_addr;
-            proxy_set_header X-Forwarded-For $proxy_add_x_forwarded_for;
-            proxy_set_header X-Forwarded-Proto $scheme;
-        }
-
-        location ~ ^/CSE(.*)$ {
-            proxy_pass http://notenextra-cse/CSE$1;
-            proxy_set_header Host $host;
-            proxy_set_header X-Real-IP $remote_addr;
-            proxy_set_header X-Forwarded-For $proxy_add_x_forwarded_for;
-            proxy_set_header X-Forwarded-Proto $scheme;
-        }
-
-        location / {
-            proxy_pass http://notenextra-math;
-            proxy_set_header Host $host;
-            proxy_set_header X-Real-IP $remote_addr;
-            proxy_set_header X-Forwarded-For $proxy_add_x_forwarded_for;
-            proxy_set_header X-Forwarded-Proto $scheme;
-        }
-
-    }
-}

docker/prebuild.sh

@@ -1,10 +0,0 @@
-# This is pre-build script that cleans up resources and compiles for selected pages, then finally you may combine those subdirectories into one via nginx.
-# double check you are using LF instead of CRLF
-
-# please run this script in project root directory
-
-echo "restore docker build _meta.js file"
-
-cp "./docker/_meta.js" "./content/_meta.js"
-
-

next.config.mjs

@@ -20,7 +20,15 @@ const bundleAnalyzer = withBundleAnalyzer({
 })
 
 export default bundleAnalyzer(withNextra({
-  output: 'standalone',
+  // output: 'standalone',
+
+  // static export start
+  output: 'export',
+  images: {
+    unoptimized: true // mandatory, otherwise won't export
+  },
+  basePath: '/',
+  // static export end
   
   // eslint: {
   //   ignoreDuringBuilds: true,

package.json

@@ -1,9 +1,7 @@
 {
   "scripts": {
     "dev": "next --turbopack",
-    "build": "cross-env NODE_OPTIONS='--max-old-space-size=16384' next build",
+    "build": "bash ./distribute/prebuild.sh && cross-env VERCEL_FORCE_NO_BUILD_CACHE=1 NODE_OPTIONS='--max-old-space-size=16384' next build",
-    "build:distribute": "sh ./distribute/prebuild.sh && cross-env NODE_OPTIONS='--max-old-space-size=8192' next build",
-    "build:vercel": "cross-env VERCEL_FORCE_NO_BUILD_CACHE=1 NODE_OPTIONS='--max-old-space-size=16384' next build",
     "build:test": "cross-env ANALYZE=true NODE_OPTIONS='--inspect --max-old-space-size=4096' next build",
     "build:analyze": "cross-env ANALYZE=true NODE_OPTIONS='--max-old-space-size=16384' next build",
     "postbuild": "next-sitemap && pagefind --site .next/server/app --output-path out/_pagefind",

wrangler.toml

@@ -1,4 +1,4 @@
-pages_build_output_dir= "out"
+pages_build_output_dir= ".vercel/output/static"
 
 name = "notenextra"
 compatibility_date = "2025-02-13"