update medias and lecture notes
This commit is contained in:
@@ -135,7 +135,7 @@ $$
|
||||
|
||||
##### Approaches 3: Linear approach
|
||||
|
||||
$x_1\simeq P_1X$ and $x_2\simeq P_2X$
|
||||
$x_1\cong P_1X$ and $x_2\cong P_2X$
|
||||
|
||||
$x_1\times P_1X = 0$ and $x_2\times P_2X = 0$
|
||||
|
||||
|
||||
@@ -1 +1,177 @@
|
||||
# CSE559A Lecture 26
|
||||
|
||||
## Continue on Geometry and Multiple Views
|
||||
|
||||
### The Essential and Fundamental Matrices
|
||||
|
||||
#### Math of the epipolar constraint: Calibrated case
|
||||
|
||||
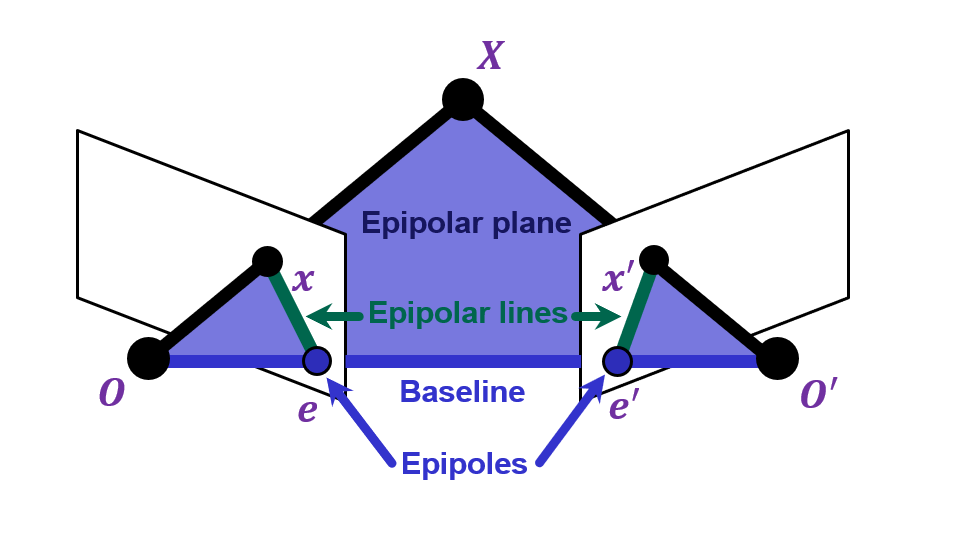
Recall Epipolar Geometry
|
||||
|
||||
|
||||
|
||||
Epipolar constraint:
|
||||
|
||||
If we set the config for the first camera as the world origin and $[I|0]\begin{pmatrix}y\\1\end{pmatrix}=x$, and $[R|t]\begin{pmatrix}y\\1\end{pmatrix}=x'$, then
|
||||
|
||||
Notice that $x'\cdot [t\times (Ry)]=0$
|
||||
|
||||
$$
|
||||
x'^T E x_1 = 0
|
||||
$$
|
||||
|
||||
We denote the constraint defined by the Essential Matrix as $E$.
|
||||
|
||||
$E x$ is the epipolar line associated with $x$ ($l'=Ex$)
|
||||
|
||||
$E^T x'$ is the epipolar line associated with $x'$ ($l=E^T x'$)
|
||||
|
||||
$E e=0$ and $E^T e'=0$ ($x$ and $x'$ don't matter)
|
||||
|
||||
$E$ is singular (rank 2) and have five degrees of freedom.
|
||||
|
||||
#### Epipolar constraint: Uncalibrated case
|
||||
|
||||
If the calibration matrices $K$ and $K'$ are unknown, we can write the epipolar constraint in terms of unknown normalized coordinates:
|
||||
|
||||
$$
|
||||
x'^T_{norm} E x_{norm} = 0
|
||||
$$
|
||||
|
||||
where $x_{norm}=K^{-1} x$, $x'_{norm}=K'^{-1} x'$
|
||||
|
||||
$$
|
||||
x'^T_{norm} E x_{norm} = 0\implies x'^T_{norm} Fx=0
|
||||
$$
|
||||
|
||||
where $F=K'^{-1}EK^{-1}$ is the **Fundamental Matrix**.
|
||||
|
||||
$$
|
||||
(x',y',1)\begin{bmatrix}
|
||||
f_{11} & f_{12} & f_{13} \\
|
||||
f_{21} & f_{22} & f_{23} \\
|
||||
f_{31} & f_{32} & f_{33}
|
||||
\end{bmatrix}\begin{pmatrix}
|
||||
x\\y\\1
|
||||
\end{pmatrix}=0
|
||||
$$
|
||||
|
||||
Properties of $F$:
|
||||
|
||||
$F x$ is the epipolar line associated with $x$ ($l'=F x$)
|
||||
|
||||
$F^T x'$ is the epipolar line associated with $x'$ ($l=F^T x'$)
|
||||
|
||||
$F e=0$ and $F^T e'=0$
|
||||
|
||||
$F$ is singular (rank two) and has seven degrees of freedom
|
||||
|
||||
#### Estimating the fundamental matrix
|
||||
|
||||
Given: correspondences $x=(x,y,1)^T$ and $x'=(x',y',1)^T$
|
||||
|
||||
Constraint: $x'^T F x=0$
|
||||
|
||||
$$
|
||||
(x',y',1)\begin{bmatrix}
|
||||
f_{11} & f_{12} & f_{13} \\
|
||||
f_{21} & f_{22} & f_{23} \\
|
||||
f_{31} & f_{32} & f_{33}
|
||||
\end{bmatrix}\begin{pmatrix}
|
||||
x\\y\\1
|
||||
\end{pmatrix}=0
|
||||
$$
|
||||
|
||||
**Each pair of correspondences gives one equation (one constraint)**
|
||||
|
||||
At least 8 pairs of correspondences are needed to solve for the 9 elements of $F$ (The eight point algorithm)
|
||||
|
||||
We know $F$ needs to be singular/rank 2. How do we force it to be singular?
|
||||
|
||||
Solution: take SVD of the initial estimate and throw out the smallest singular value
|
||||
|
||||
$$
|
||||
F=U\begin{bmatrix}
|
||||
\sigma_1 & 0 \\
|
||||
0 & \sigma_2 \\
|
||||
0 & 0
|
||||
\end{bmatrix}V^T
|
||||
$$
|
||||
|
||||
## Structure from Motion
|
||||
|
||||
Not always uniquely solvable.
|
||||
|
||||
If we scale the entire scene by some factor $k$ and, at the same time, scale the camera matrices by the factor of $1/k$, the projections of the scene points remain exactly the same:
|
||||
$x\cong PX =(1/k P)(kX)$
|
||||
|
||||
Without a reference measurement, it is impossible to recover the absolute scale of the scene!
|
||||
|
||||
In general, if we transform the scene using a transformation $Q$ and apply the inverse transformation to the camera matrices, then the image observations do not change:
|
||||
|
||||
$x\cong PX =(P Q^{-1})(QX)$
|
||||
|
||||
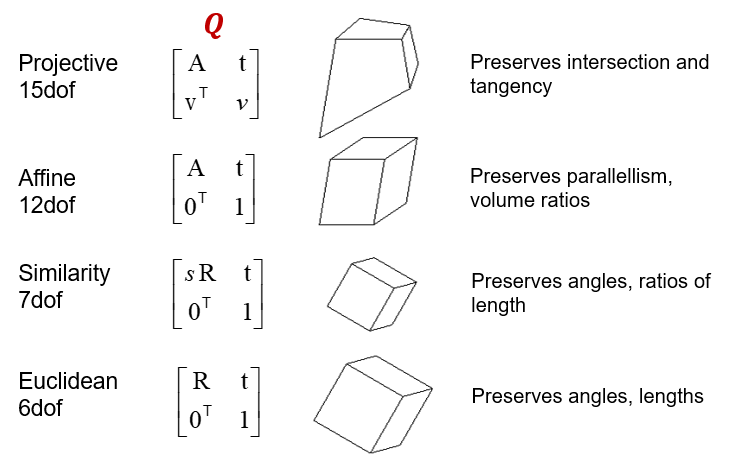
### Types of Ambiguities
|
||||
|
||||
|
||||
|
||||
### Affine projection : more general than orthographic
|
||||
|
||||
A general affine projection is a 3D-to-2D linear mapping plus translation:
|
||||
|
||||
$$
|
||||
P=\begin{bmatrix}
|
||||
a_{11} & a_{12} & a_{13} & t_1 \\
|
||||
a_{21} & a_{22} & a_{23} & t_2 \\
|
||||
0 & 0 & 0 & 1
|
||||
\end{bmatrix}=\begin{bmatrix}
|
||||
A & t \\
|
||||
0^T & 1
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
In non-homogeneous coordinates:
|
||||
|
||||
$$
|
||||
\begin{pmatrix}
|
||||
x\\y\\1
|
||||
\end{pmatrix}=\begin{bmatrix}
|
||||
a_{11} & a_{12} & a_{13} \\
|
||||
a_{21} & a_{22} & a_{23}
|
||||
\end{bmatrix}\begin{pmatrix}
|
||||
X\\Y\\Z
|
||||
\end{pmatrix}+\begin{pmatrix}
|
||||
t_1\\t_2
|
||||
\end{pmatrix}=AX+t
|
||||
$$
|
||||
|
||||
### Affine Structure from Motion
|
||||
|
||||
Given: 𝑚 images of 𝑛 fixed 3D points such that
|
||||
|
||||
$$
|
||||
x_{ij}=A_iX_j+t_i, \quad i=1,\dots,m, \quad j=1,\dots,n
|
||||
$$
|
||||
|
||||
Problem: use the 𝑚𝑛 correspondences $x_{ij}$ to estimate 𝑚 projection matrices $A_i$ and translation vectors $t_i$, and 𝑛 points $X_j$
|
||||
|
||||
The reconstruction is defined up to an arbitrary affine transformation $Q$ (12 degrees of freedom):
|
||||
|
||||
$$
|
||||
\begin{bmatrix}
|
||||
A & t \\
|
||||
0^T & 1
|
||||
\end{bmatrix}\rightarrow\begin{bmatrix}
|
||||
A & t \\
|
||||
0^T & 1
|
||||
\end{bmatrix}Q^{-1}, \quad \begin{pmatrix}X_j\\1\end{pmatrix}\rightarrow Q\begin{pmatrix}X_j\\1\end{pmatrix}
|
||||
$$
|
||||
|
||||
How many constraints and unknowns for $m$ images and $n$ points?
|
||||
|
||||
$2mn$ constraints and $8m + 3n$ unknowns
|
||||
|
||||
To be able to solve this problem, we must have $2mn \geq 8m+3n-12$ (affine ambiguity takes away 12 dof)
|
||||
|
||||
E.g., for two views, we need four point correspondences
|
||||
|
||||
|
||||
BIN
public/CSE559A/Ambiguities_in_projection.png
Normal file
BIN
public/CSE559A/Ambiguities_in_projection.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 35 KiB |
Reference in New Issue
Block a user