Merge branch 'main' of https://github.com/Trance-0/NoteNextra

pages/CSE332S/CSE332S_L13.md

@@ -1 +1,224 @@
 # CSE332S Lecture 13
+
+## Copy control
+
+Copy control consists of 5 distinct operations 
+
+- A `copy constructor` initializes an object by duplicating the const l-value that was passed to it by reference
+- A `copy-assignment operator` (re)sets an object's value by duplicating the const l-value passed to it by reference
+- A `destructor` manages the destruction of an object
+- A `move constructor` initializes an object by transferring the implementation from the r-value reference passed to it (next lecture)
+- A `move-assignment operator` (re)sets an object's value by transferring the implementation from the r-value reference passed to it (next lecture)
+
+Today we'll focus on the first 3 operations and will defer the others (introduced in C++11) until next time
+
+- The others depend on the new C++11 `move semantics`
+
+### Basic copy control operations
+
+A copy constructor or copy-assignment operator takes a reference to a (usually const) instance of the class
+
+- Copy constructor initializes a new object from it
+- Copy-assignment operator sets object's value from it
+- In either case, original the object is left unchanged (which differs from the move versions of these operations)
+- Destructor takes no arguments `~A()` (except implicit `this`)
+
+Copy control operations for built-in types
+
+- Copy construction and copy-assignment copy values
+- Destructor of built-in types does nothing (is a "no-op")
+
+Compiler-synthesized copy control operations
+
+- Just call that same operation on each member of the object
+- Uses defined/synthesized definition of that operation for user-defined types (see above for built-in types)
+
+### Preventing or Allowing Basic Copy Control
+
+Old (C++03) way to prevent compiler from generating a default constructor, copy constructor, destructor, or assignment operator was somewhat awkward
+
+- Declare private, don't define, don't use within class
+- This works, but gives cryptic linker error if operation is used
+
+New (C++11) way to prevent calls to any method
+
+- End the declaration with `= delete` (and don't define)
+- Compiler will then give an intelligible error if a call is made
+
+C++11 allows a constructor to call peer constructors
+
+- Allows re-use of implementation (through delegation)
+- Object is fully constructed once any constructor finishes
+
+C++11 lets you ask compiler to synthesize operations
+
+- Explicitly, but only for basic copy control, default constructor
+- End the declaration with `= default` (and don't define) The compiler will then generate the operation or throw an error if it can't.
+
+## Shallow vs Deep Copy
+
+### Shallow Copy Construction
+
+```cpp
+// just uses the array that's already in the other object
+IntArray::IntArray(const IntArray &a)
+  :size_(a.size_), 
+   values_(a.values_) {
+    // only memory address is copied, not the memory it points to
+}
+
+int main(int argc, char * argv[]){
+   IntArray arr = {0,1,2};
+   IntArray arr2 = arr;
+   return 0;
+}
+```
+
+There are two ways to "copy"
+
+- Shallow: re-aliases existing resources
+  - E.g., by copying the address value from a pointer member variable
+- Deep: makes a complete and separate copy
+  - I.e., by following pointers and deep copying what they alias
+
+Version above shows shallow copy
+
+- Efficient but may be risky (why?) The destructor will delete the memory that the other object is pointing to.
+- Usually want no-op destructor, aliasing via `shared_ptr` or a boolean value to check if the object is the original memory allocator for the resource.
+
+### Deep Copy Construction
+
+```cpp
+IntArray::IntArray(const IntArray &a)
+  :size_(0), values_(nullptr) {
+
+  if (a.size_ > 0) {
+    // new may throw bad_alloc, 
+    // set size_ after it succeeds 
+    values_ = new int[a.size_];
+    size_ = a.size_;
+
+    // could use memcpy instead   
+    for (size_t i = 0; 
+         i < size_; ++i) {
+      values_[i] = a.values_[i];
+    }
+  }
+}
+int main(int argc, char * argv[]){
+   IntArray arr = {0,1,2};
+   IntArray arr2 = arr;
+   return 0;
+}
+
+```
+
+This code shows deep copy
+
+- Safe: no shared aliasing, exception aware initialization
+- But may not be as efficient as shallow copy in many cases
+
+Note trade-offs with arrays
+
+- Allocate memory once
+- More efficient than multiple calls to new (heap search)
+- Constructor and assignment called on each array element
+- Less efficient than block copy
+  - E.g., using `memcpy()`
+- But sometimes necessary
+  - i.e., constructors, destructors establish needed invariants
+
+Each object is responsible for its own resources.
+
+## Swap Trick for Copy-Assignment
+
+The swap trick is a way to implement the copy-assignment operator, given that the `size_` and `values_` members are already defined in constructor.
+
+```cpp
+class Array {
+public:
+    Array(unsigned int) ; // assume constructor allocates memory
+    Array(const Array &); // assume copy constructor makes a deep copy
+    ~Array(); // assume destructor calls delete on values_
+    Array & operator=(const Array &a);
+private:
+    size_t size_;
+    int * values_;
+};
+
+Array & Array::operator=(const Array &a) { // return ref lets us chain
+    if (&a != this) { // note test for self-assignment (safe, efficient)
+        Array temp(a);  // copy constructor makes deep copy of a
+        swap(temp.size_, size_);     // note unqualified calls to swap
+        swap(temp.values_, values_); // (do user-defined or std::swap) 
+    }
+    return *this; // previous *values_ cleaned up by temp's destructor, which is the member variable of the current object
+}
+
+int main(int argc, char * argv[]){
+    IntArray arr = {0,1,2};
+    IntArray arr2 = {3,4,5};
+    arr2 = arr;
+    return 0;
+}
+
+```
+
+## Review: Construction/destruction order with inheritance, copy control with inheritance
+
+### Constructor and Destructor are Inverses
+
+```cpp
+IntArray::IntArray(unsigned int u)
+ : size_(0), values_(nullptr) {
+  // exception safe semantics
+  values_ = new int [u]; 
+  size_ = u;
+}
+
+IntArray::~IntArray() {
+
+  // deallocates heap memory 
+  // that values_ points to,
+  // so it's not leaked:
+  // with deep copy, object
+  // owns the memory
+  delete [] values_;
+
+  // the size_ and values_
+  // member variables are
+  // themselves destroyed
+  // after destructor body
+}
+```
+Constructors initialize
+
+- At the start of each object's lifetime
+- Implicitly called when object is created
+
+Destructors clean up
+
+- Implicitly called when  an object is destroyed
+  - E.g., when stack frame where it was declared goes out of scope
+  - E.g., when its address is passed to delete
+  - E.g., when another object of which it is a member is being destroyed
+
+### More on Initialization and Destruction
+
+Initialization follows a well defined order
+
+- Base class constructor is called
+  - That constructor recursively follows this order, too
+- Member constructors are called
+  - In order members were declared
+  - Good style to list in that order (a good compiler may warn if not)
+- Constructor body is run
+
+Destruction occurs in the reverse order
+
+- Destructor body is run, then member destructors, then base class destructor (which recursively follows reverse order)
+
+**Make destructor virtual if members are virtual**
+
+- Or if class is part of an inheritance hierarchy
+- Avoids “slicing”: ensures destruction starts at the most derived class destructor (not at some higher base class)

pages/Math416/Exam_reviews/Math416_E1.md

@@ -1,3 +1,303 @@
 # Math 416 Midterm 1 Review
 
+So everything we have learned so far is to extend the real line to the complex plane.
+
+## Chapter 1 Complex Numbers
+
+### Definition of complex numbers
+
+An ordered pair of real numbers $(x, y)$ can be represented as a complex number $z = x + yi$, where $i$ is the imaginary unit.
+
+With operations defined as:
+
+$$
+(x_1 + y_1i) + (x_2 + y_2i) = (x_1 + x_2) + (y_1 + y_2)i
+$$
+
+$$
+(x_1 + y_1i) \cdot (x_2 + y_2i) = (x_1x_2 - y_1y_2) + (x_1y_2 + x_2y_1)i
+$$
+
+### De Moivre's Formula
+
+Every complex number $z$ can be written as $z = r(\cos \theta + i \sin \theta)$, where $r$ is the magnitude of $z$ and $\theta$ is the argument of $z$.
+
+$$
+z^n = r^n(\cos n\theta + i \sin n\theta)
+$$
+
+The De Moivre's formula is useful for finding the $n$th roots of a complex number.
+
+$$
+z^n = r^n(\cos n\theta + i \sin n\theta)
+$$
+
+### Roots of complex numbers
+
+Using De Moivre's formula, we can find the $n$th roots of a complex number.
+
+If $z=r(\cos \theta + i \sin \theta)$, then the $n$th roots of $z$ are given by:
+
+$$
+z_k = r^{1/n}(\cos \frac{\theta + 2k\pi}{n} + i \sin \frac{\theta + 2k\pi}{n})
+$$
+
+for $k = 0, 1, 2, \ldots, n-1$.
+
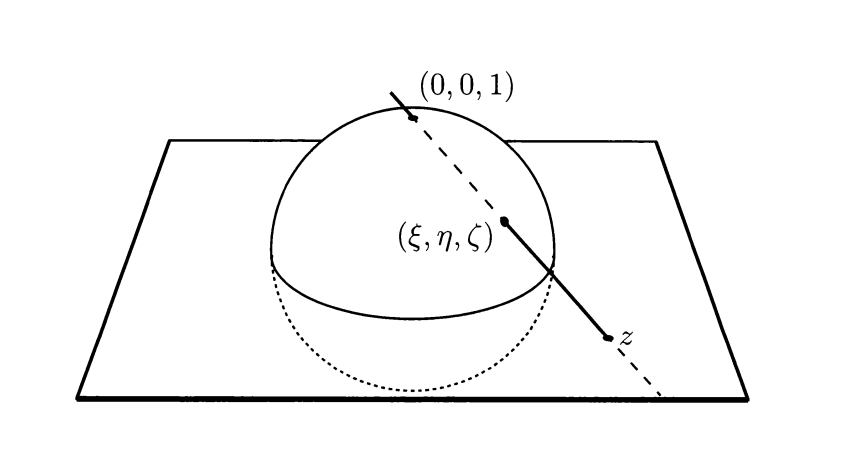
+### Stereographic projection
+
+![Stereographic projection](https://notenextra.trance-0.com/Math416/Stereographic_projection.png)
+
+The stereographic projection is a map from the unit sphere $S^2$ to the complex plane $\mathbb{C}\setminus\{0\}$.
+
+The projection is given by:
+
+$$
+z\mapsto \frac{(2Re(z), 2Im(z), |z|^2-1)}{|z|^2+1}
+$$
+
+The inverse map is given by:
+
+$$
+(\xi,\eta, \zeta)\mapsto \frac{\xi + i\eta}{1 - \zeta}
+$$
+
+## Chapter 2 Complex Differentiation
+
+### Definition of complex differentiation
+
+Let the complex plane $\mathbb{C}$ be defined in an open subset $G$ of $\mathbb{C}$. (Domain)
+
+Then $f$ is said to be differentiable at $z_0\in G$ if the limit
+
+$$
+\lim_{z\to z_0} \frac{f(z)-f(z_0)}{z-z_0}
+$$
+
+exists.
+
+The limit is called the derivative of $f$ at $z_0$ and is denoted by $f'(z_0)$.
+
+To prove that a function is differentiable, we can use the standard delta-epsilon definition of a limit.
+
+$$
+\left|\frac{f(z)-f(z_0)}{z-z_0} - f'(z_0)\right| < \epsilon
+$$
+
+whenever $0 < |z-z_0| < \delta$.
+
+With such definition, all the properties of real differentiation can be extended to complex differentiation.
+
+#### Differentiation of complex functions
+
+1. If $f$ is differentiable at $z_0$, then $f$ is continuous at $z_0$.
+2. If $f,g$ are differentiable at $z_0$, then $f+g, fg$ are differentiable at $z_0$.
+   $$
+   (f+g)'(z_0) = f'(z_0) + g'(z_0)
+   $$
+   $$
+   (fg)'(z_0) = f'(z_0)g(z_0) + f(z_0)g'(z_0)
+   $$
+3. If $f,g$ are differentiable at $z_0$ and $g(z_0)\neq 0$, then $f/g$ is differentiable at $z_0$.
+   $$
+   \left(\frac{f}{g}\right)'(z_0) = \frac{f'(z_0)g(z_0) - f(z_0)g'(z_0)}{g(z_0)^2}
+   $$
+4. If $f$ is differentiable at $z_0$ and $g$ is differentiable at $f(z_0)$, then $g\circ f$ is differentiable at $z_0$.
+   $$
+   (g\circ f)'(z_0) = g'(f(z_0))f'(z_0)
+   $$
+5. If $f(z)=\sum_{k=0}^n c_k(z-z_0)^k$, where $c_k\in\mathbb{C}$, then $f$ is differentiable at $z_0$ and $f'(z_0)=\sum_{k=1}^n kc_k(z_0-z_0)^{k-1}$.
+   $$
+   f'(z_0) = c_1 + 2c_2(z_0-z_0) + 3c_3(z_0-z_0)^2 + \cdots + nc_n(z_0-z_0)^{n-1}
+   $$
+
+### Cauchy-Riemann Equations
+
+Let the function defined on an open subset $G$ of $\mathbb{C}$ be $f(x,y)=u(x,y)+iv(x,y)$, where $u,v$ are real-valued functions.
+
+Then $f$ is differentiable at $z_0=x_0+y_0i$ if and only if the partial derivatives of $u$ and $v$ exist at $(x_0,y_0)$ and satisfy the Cauchy-Riemann equations:
+
+$$
+\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y}, \quad \frac{\partial u}{\partial y} = -\frac{\partial v}{\partial x}
+$$
+
+### Holomorphic functions
+
+A function $f$ is said to be holomorphic on an open subset $G$ of $\mathbb{C}$ if $f$ is differentiable at every point of $G$.
+
+#### Partial differential operators
+
+$$
+\frac{\partial}{\partial z} = \frac{1}{2}\left(\frac{\partial}{\partial x} - i\frac{\partial}{\partial y}\right)
+$$
+
+$$
+\frac{\partial}{\partial \bar{z}} = \frac{1}{2}\left(\frac{\partial}{\partial x} + i\frac{\partial}{\partial y}\right)
+$$
+
+This gives that
+
+$$
+\frac{\partial f}{\partial z} = \frac{1}{2}\left(\frac{\partial f}{\partial x} - i\frac{\partial f}{\partial y}\right)=\frac{1}{2}\left(\frac{\partial u}{\partial x} +\frac{\partial v}{\partial y}\right) + \frac{i}{2}\left(\frac{\partial v}{\partial x} - \frac{\partial u}{\partial y}\right)
+$$
+
+$$
+\frac{\partial f}{\partial \bar{z}} = \frac{1}{2}\left(\frac{\partial f}{\partial x} + i\frac{\partial f}{\partial y}\right)=\frac{1}{2}\left(\frac{\partial u}{\partial x} - \frac{\partial v}{\partial y}\right) + \frac{i}{2}\left(\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}\right)
+$$
+
+If the function $f$ is holomorphic, then by the Cauchy-Riemann equations, we have
+
+$$
+\frac{\partial f}{\partial \bar{z}} = 0
+$$
+
+### Conformal mappings
+
+A holomorphic function $f$ is said to be conformal if it preserves the angles between the curves. More formally, if $f$ is holomorphic on an open subset $G$ of $\mathbb{C}$ and $z_0\in G$, $\gamma_1, \gamma_2$ are two curves passing through $z_0$ ($\gamma_1(t_1)=\gamma_2(t_2)=z_0$) and intersecting at an angle $\theta$, then
+
+$$
+\arg(f\circ\gamma_1)'(t_1) - \arg(f\circ\gamma_2)'(t_2) = \theta
+$$
+
+In other words, the angle between the curves is preserved.
+
+An immediate consequence is that
+
+$$
+\arg(f\cdot \gamma_1)'(t_1) =\arg f'(z_0) + \arg \gamma_1'(t_1)\\
+\arg(f\cdot \gamma_2)'(t_2) =\arg f'(z_0) + \arg \gamma_2'(t_2)
+$$
+
+### Harmonic functions
+
+A real-valued function $u$ is said to be harmonic if it satisfies the Laplace equation:
+
+$$
+\frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = 0
+$$
+
+## Chapter 3 Linear Fractional Transformations
+
+### Definition of linear fractional transformations
+
+A linear fractional transformation is a function of the form
+
+$$
+\phi(z) = \frac{az+b}{cz+d}
+$$
+
+where $a,b,c,d$ are complex numbers and $ad-bc\neq 0$.
+
+### Properties of linear fractional transformations
+
+#### Conformality
+
+A linear fractional transformation is conformal.
+
+$$
+\phi'(z) = \frac{ad-bc}{(cz+d)^2}
+$$
+
+#### Three-fold transitivity
+
+If $z_1,z_2,z_3$ are distinct points in the complex plane, then there exists a unique linear fractional transformation $\phi$ such that $\phi(z_1)=\infty$, $\phi(z_2)=0$, $\phi(z_3)=1$.
+
+The map is given by
+
+$$
+\phi(z) =\begin{cases}
+\frac{(z-z_2)(z_1-z_3)}{(z-z_1)(z_2-z_3)} & \text{if } z_1,z_2,z_3 \text{ are all finite}\\
+\frac{z-z_2}{z_3-z_2} & \text{if } z_1=\infty\\
+\frac{z_3-z_1}{z-z_1} & \text{if } z_2=\infty\\
+\frac{z-z_2}{z-z_1} & \text{if } z_3=\infty\\
+\end{cases}
+$$
+
+So if $z_1,z_2,z_3$, $w_1,w_2,w_3$ are distinct points in the complex plane, then there exists a unique linear fractional transformation $\phi$ such that $\phi(z_i)=w_i$ for $i=1,2,3$.
+
+#### Inversion
+
+
+#### Factorization
+
+#### Clircle
+
+## Chapter 4 Elementary Functions
+
+### Exponential function
+
+### Trigonometric functions
+
+### Logarithmic function
+
+### Power function
+
+### Inverse trigonometric functions
+
+## Chapter 5 Power Series
+
+### Definition of power series
+
+### Properties of power series
+
+### Radius/Region of convergence
+
+### Cauchy-Hadamard Theorem
+
+### Cauchy Product (of power series)
+
+## Chapter 6 Complex Integration
+
+### Definition of Riemann Integral for complex functions
+
+The complex integral of a complex function $\phi$ on the closed subinterval $[a,b]$ of the real line is said to be piecewise continuous if there exists a partition $a=t_0<t_1<\cdots<t_n=b$ such that $\phi$ is continuous on each open interval $(t_{i-1},t_i)$ and has a finite limit at each discontinuity point of the closed interval $[a,b]$.
+
+If $\phi$ is piecewise continuous on $[a,b]$, then the complex integral of $\phi$ on $[a,b]$ is defined as
+
+$$
+\int_a^b \phi(t) dt = \int_a^b \operatorname{Re}\phi(t) dt + i\int_a^b \operatorname{Im}\phi(t) dt
+$$
+
+### Fundamental Theorem of Calculus
+
+If $\phi$ is piecewise continuous on $[a,b]$, then
+
+$$
+\int_a^b \phi'(t) dt = \phi(b)-\phi(a)
+$$
+
+### Triangle inequality
+
+$$
+\left|\int_a^b \phi(t) dt\right| \leq \int_a^b |\phi(t)| dt
+$$
+
+### Integral on curve
+
+Let $\gamma$ be a piecewise smooth curve in the complex plane.
+
+The integral of a complex function $f$ on $\gamma$ is defined as
+
+$$
+\int_\gamma f(z) dz = \int_a^b f(\gamma(t))\gamma'(t) dt
+$$
+
+### Properties of complex integrals
+
+1. Linearity:
+
+
+
+## Chapter 7 Cauchy's Theorem
+
+### Cauchy's Theorem
+
+### Cauchy's Formula for a Circle
+
+### Cauchy's Product
+
+
+
+
+
 

pages/Math416/Math416_L12.md

@@ -99,7 +99,7 @@ $$
 
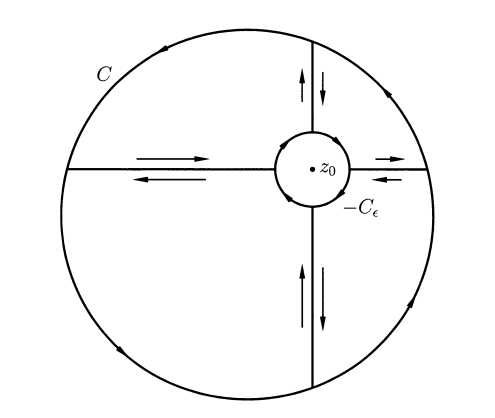
 We divide the integral into four parts:
 
-![Integral on a disk](https://notenextra.trance-0.com/Math416/Cauchy_disk.png)
+![Integral on a disk](https://notenextra.trance-0.com/Math416/Cauchy_theorem_disk.png)
 
 Notice that $\frac{f(\xi)}{\xi-z}$ is holomorphic whenever $f(\xi)\in U$ and $\xi\in \mathbb{C}\setminus\{z\}$.