upgrade structures and migrate to nextra v4

content/CSE559A/CSE559A_L9.md

@@ -0,0 +1,102 @@
+# CSE559A Lecture 9
+
+## Continue on ML for computer vision
+
+### Backpropagation
+
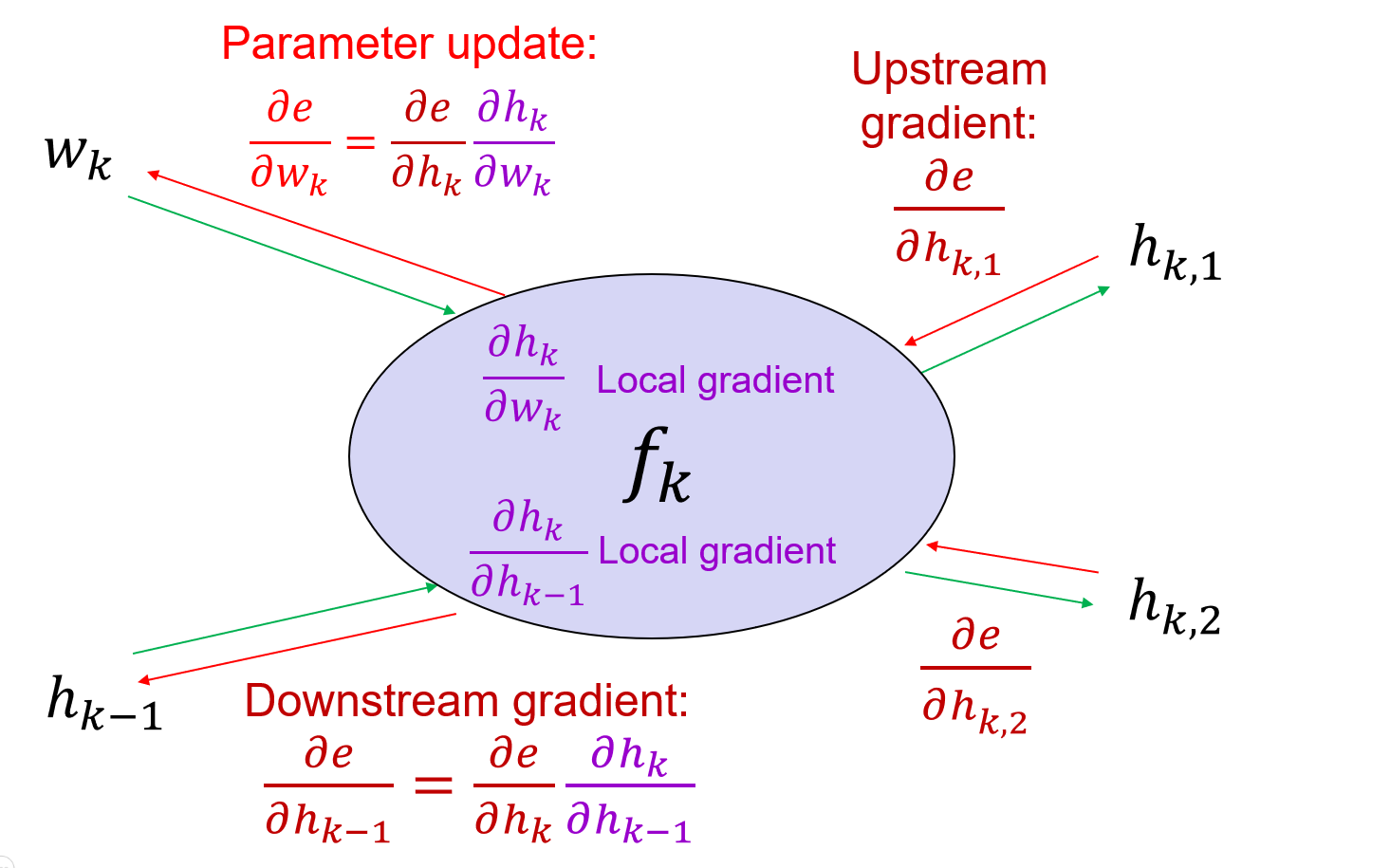
+#### Computation graphs
+
+SGD update for each parameter
+
+$$
+w_k\gets w_k-\eta\frac{\partial e}{\partial w_k}
+$$
+
+$e$ is the error function.
+
+#### Using the chain rule
+
+Suppose $k=1$, $e=l(f_1(x,w_1),y)$
+
+Example: $e=(f_1(x,w_1)-y)^2$
+
+So $h_1=f_1(x,w_1)=w^T_1x$, $e=l(h_1,y)=(y-h_1)^2$
+
+$$
+\frac{\partial e}{\partial w_1}=\frac{\partial e}{\partial h_1}\frac{\partial h_1}{\partial w_1}
+$$
+
+$$
+\frac{\partial e}{\partial h_1}=2(h_1-y)
+$$
+
+$$
+\frac{\partial h_1}{\partial w_1}=x
+$$
+
+$$
+\frac{\partial e}{\partial w_1}=2(h_1-y)x
+$$
+
+For the general cases,
+
+$$
+\frac{\partial e}{\partial w_k}=\frac{\partial e}{\partial h_K}\frac{\partial h_K}{\partial h_{K-1}}\cdots\frac{\partial h_{k+2}}{\partial h_{k+1}}\frac{\partial h_{k+1}}{\partial h_k}\frac{\partial h_k}{\partial w_k}
+$$
+
+Where the upstream gradient $\frac{\partial e}{\partial h_K}$ is known, and the local gradient $\frac{\partial h_k}{\partial w_k}$ is known.
+
+#### General backpropagation algorithm
+
+The adding layer is the gradient distributor layer.
+The multiplying layer is the gradient switcher layer.
+The max operation is the gradient router layer.
+
+![Images of propagation](https://notenextra.trance-0.com/CSE559A/General_computation_graphs_for_MLP.png)
+
+Simple example: Element-wise operation (ReLU)
+
+$f(x)=ReLU(x)=max(0,x)$
+
+$$
+\frac{\partial z}{\partial x}=\begin{pmatrix}
+\frac{\partial z_1}{\partial x_1} & 0 & \cdots & 0 \\
+0 & \frac{\partial z_2}{\partial x_2} & \cdots & 0 \\
+\vdots & \vdots & \ddots & \vdots \\
+0 & 0 & \cdots & \frac{\partial z_n}{\partial x_n}
+\end{pmatrix}
+$$
+
+Where $\frac{\partial z_i}{\partial x_j}=1$ if $i=j$ and $z_i>0$, otherwise $\frac{\partial z_i}{\partial x_j}=0$.
+
+When $\forall x_i<0$ then $\frac{\partial z}{\partial x}=0$ (dead ReLU)
+
+Other examples on ppt.
+
+## Convolutional Neural Networks
+
+### Basic Convolutional layer
+
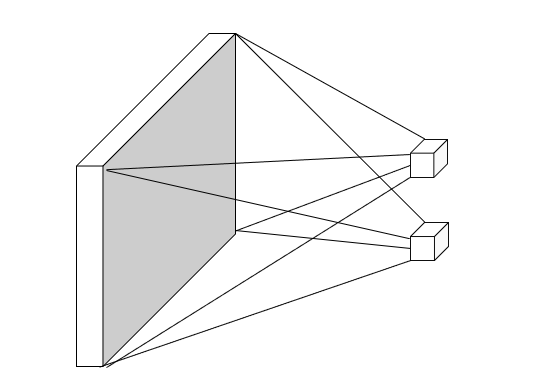
+#### Flatten layer
+
+Fully connected layer, operate on vectorized image.
+
+With the multi-layer perceptron, the neural network trying to fit the templates.
+
+![Flatten layer](https://notenextra.trance-0.com/CSE559A/Flatten_layer.png)
+
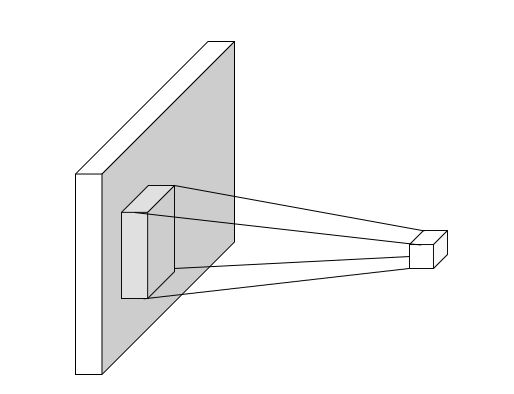
+#### Convolutional layer
+
+Limit the receptive fields of units, tiles them over the input image, and share the weights.
+
+Equivalent to sliding the learned filter over the image , computing dot products at each location.
+
+![Convolutional layer](https://notenextra.trance-0.com/CSE559A/Convolutional_layer.png)
+
+Padding: Add a border of zeros around the image. (higher padding, larger output size)
+
+Stride: The step size of the filter. (higher stride, smaller output size)
+
+### Variants 1x1 convolutions, depthwise convolutions
+
+### Backward pass