update

content/CSE5519/CSE5519_E1.md

@@ -4,6 +4,10 @@
 >
 > This topic is presented by Me. and will be the most detailed one for this course, perhaps.
 
+## Data set of the scene: KITTI
+
+[link to the website](http://www.cvlibs.net/datasets/kitti/)
+
 ## PoseNet
 
 A Convolutional Network for Real-Time 6-DOF Camera Relocalization (ICCV 2015)
@@ -274,11 +278,55 @@ This is a method that estimates both depth and camera pose motion from a single
 
 Jointly training a single-view depth CNN and a camera pose estimation CNN form unlabelled monocular video sequences.
 
+### Assumptions for PoseNet & DepthNet
+
+1. The scene is static and the only motion is the camera motion.
+2. There is no occlusion/disocclusion between the target view and the source view.
+3. The surface is Lambertian.
+
 ![View synthesis as supervision](https://notenextra.trance-0.com/CSE5519/Unsupervised_Learning_DepthNet_PoseNet.png)
 
-### View synthesis as supervision
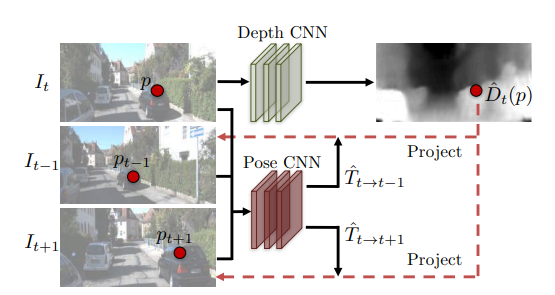
+Let $I_{t-1}, I_{t}, I_{t+1}$ be three consecutive frames in the video.
 
-Notice that in mo
+First, we use the DepthNet to estimate the depth of $I_t$ to obtain $\hat{D}_t$. We use the PoseNet to estimate the camera pose motion between $I_{t-1}$ and $I_{t+1}$ to obtain two transition vector $\hat{T}_{t\to t-1}$ and $\hat{T}_{t\to t+1}$.
+
+Then use the information we have from $\hat{D}_t$ and $\hat{T}_{t\to t-1}, \hat{T}_{t\to t+1}$ with frame $I_{t-1}$ and $I_{t+1}$ to synthesize the image $\hat{I}_s$ from $I_{t-1}$ and $I_{t+1}$.
+
+Note that $\hat{I}_s$ is the synthesized prediction for $I_t$.
+
+### Loss function for PoseNet & DepthNet
+
+Notice that in the training process, we can generate the supervision for PoseNet & DepthNet by using **view synthesis as supervision**.
+
+#### View synthesis as supervision
+
+Let $\mathcal{I}=\{I_1,I_2,I_3,\cdots,I_n\}$ be the video sequence. Note that $I_t(p)$ is the pixel value of $I_t$ at point $p$.
+
+The loss function generated by view synthesis is:
+
+$$
+\mathcal{L}_{vs}=\sum_{I_s\in\mathcal{I}}\sum_{p\in I_s}\left|I_t(p)-\hat{I}_s(p)\right|
+$$
+
+#### Differentiable depth image-based rendering
+
+Assume that the transition and rotation between the frames are smooth and differentiable.
+
+Let $p_t$ denote the pixel coordinates of $I_t$ at time $t$. Let $K$ denote the camera intrinsic matrix. We can always obtain $p_t$'s projected coordinates to our source view $p_s$ by the formula:
+
+$$
+p_s\sim K\hat{T}_{t\to s}\hat{D}_t(p_t)K^{-1}p_t
+$$
+
+The we use spacial transformer network to sample continuous pixel coordinates.
+
+### Compensation for PoseNet & DepthNet
+
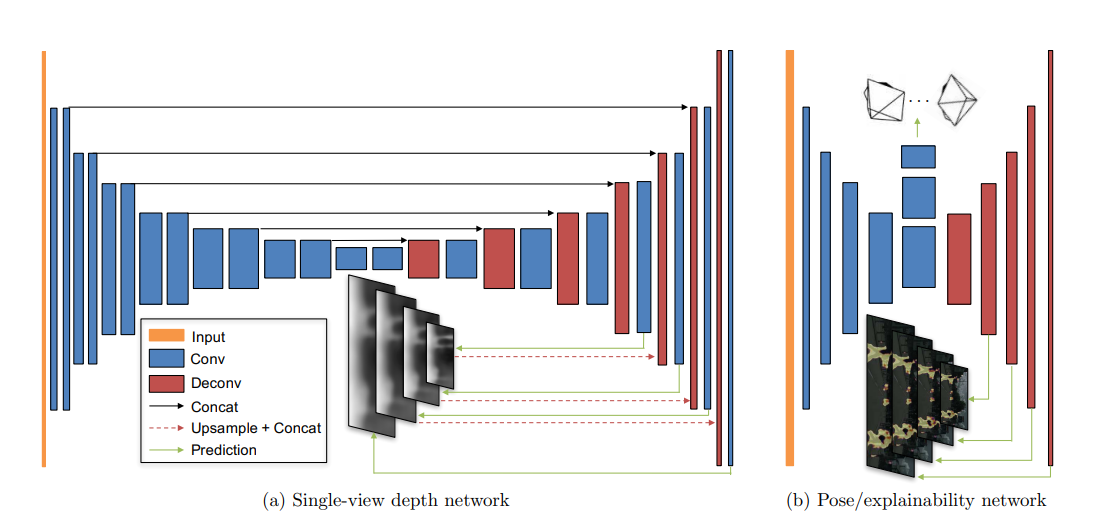
+Since it's inevitable that there are some moving objects or occlusions between the target view and the source view, in pose net we also train a few additional layers to estimate our confidence (explainability mask) of the camera motion.
+
+### Architecture for PoseNet & DepthNet
+
+![Architecture for PoseNet & DepthNet](https://notenextra.trance-0.com/CSE5519/PoseNet_DepthNet.png)
 
 ## Unsupervised Monocular Depth Estimation with Left-Right Consistency
 
@@ -288,6 +336,91 @@ Notice that in mo
 
 This is a method that use pair of images as Left and Right eye to estimate depth. Increased consistency by flipping the right-left relation.
 
+**Intuition:** Given a calibarated pair of binocular cameras, if we cna learn a function that is able to reconstruct one image from the other, then we have learned something about the depth of the scene.
+
+### DispNet and Scene flow
+
+![DispNet and Scene flow](https://notenextra.trance-0.com/CSE5519/DispNet.png)
+
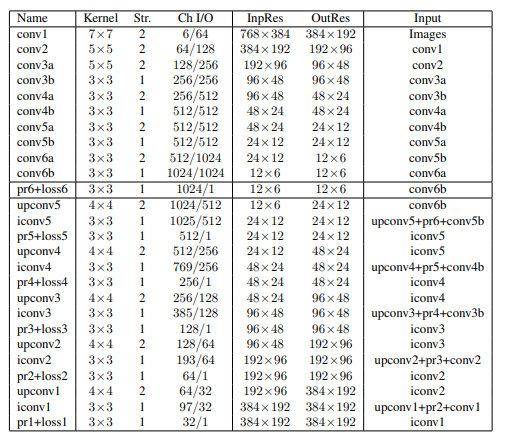
+[link to the paper](https://arxiv.org/pdf/1512.02134)
+
+#### Scene flow
+
+Scene flow is the underlying 3D motion field that can be computed from stereo videos or RGBD videos.
+
+Note, these 3D quantities can be computed only in the case of known camera intrinsics (i.e., $K$ matrix) and extrinsics (i.e., camera pose, translation, etc.).
+
+Scene flow can be reconstructed only for surface points that are visible in both the left and the right frame.
+
+Especially in the context of convolutional networks, it is particularly interesting to estimate also depth and motion in partially occluded areas
+
+#### Disparity
+
+Disparity is the difference in the x-coordinates of the same point in the left and right images.
+
+![SceneFlowNet](https://notenextra.trance-0.com/CSE5519/SceneFlowNet.png)
+
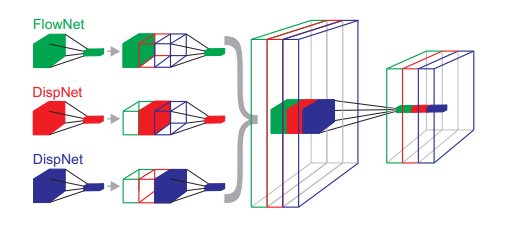
+If there is time difference between the "left" and "right" images, by the difference between the disparity, we can estimate the scene flow, that is, non-rigid motion of the scene.
+
+Object that have the same disparity in both images is "moving along with the camera".
+
+Object that is moving away, or moving toward the camera, will have higher disparity.
+
+### Assumptions for Left-right consistency Network
+
+1. Lambertian surface.
+2. No occlusion/disocclusion between the left and right image (for computing scene flow).
+
+### Loss functions for Left-right consistency Network
+
+$$
+\mathcal{L}=\alpha_{ap}(\mathcal{L}_{ap}^l+\mathcal{L}_{ap}^r)+\alpha_{ds}(\mathcal{L}_{ds}^l+\mathcal{L}_{ds}^r)+\alpha_{lr}(\mathcal{L}_{lr}^l+\mathcal{L}_{lr}^r)
+$$
+
+The loss function consists of three parts:
+
+Let $N$ denote the number of pixels in the image.
+
+#### Appearance matching loss
+
+Let $I^l$ denote the left image, $I^r$ denote the right image, $\hat{L}^l$ denote the left image reconstructed from the right image.
+
+$\hat{I}^l$ denote the left image reconstructed from the right image with the predicted disparity map $d^l$.
+
+The appearance matching loss for left image is:
+
+$$
+\mathcal{L}_{ap}^l=\frac{1}{N}\sum_{p\in I^l}\alpha \frac{1-\operatorname{SSIM}(I^l(p),\hat{I}^l(p))}{2}+(1-\alpha)\left\|I^l(p)-\hat{I}^l(p)\right\|
+$$
+
+Here $\operatorname{SSIM}$ is the structural similarity index.
+
+[link to the paper: structure similarity index](https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=1284395)
+
+$\alpha$ is a hyperparameter that balances the importance of the structural similarity and the pixel-wise difference. In this paper, $\alpha=0.85$.
+
+#### Disparity Smoothness Loss
+
+Let $\partial d$ denote the disparity gradient. $\partial_x d^l_p$ and $\partial_y d^l_p$ are the disparity gradient in the x and y directions respectively on the left image of pixel $p$.
+
+The disparity smoothness loss is:
+
+$$
+\mathcal{L}_{ds}^l=\frac{1}{N}\sum_{p\in I^l}\left|\partial_x d^l_p\right|e^{-\left|\partial_x d^l_p\right|}+\left|\partial_y d^l_p\right|e^{-\left|\partial_y d^l_p\right|}
+$$
+
+#### Left-right disparity consistency loss
+
+Our network produces two disparity maps, $d^l$ and $d^r$. We can use the left-right consistency loss to enforce the consistency between the two disparity maps.
+
+$$
+\mathcal{L}_{lr}^l=\frac{1}{N}\sum_{p\in I^l}\left|d^l_p-d^r_{p+d^l_p}\right|
+$$
+
+### Architecture of Left-right consistency Network
+
+![Architecture of Left-right consistency Network](https://notenextra.trance-0.com/CSE5519/Left-right_consistency_Network.png)
+
 ## GeoNet
 
 Unsupervised Learning of Dense Depth, Optical Flow and Camera Pose (CVPR 2018)
@@ -300,16 +433,80 @@ Depth Estimation from single monocular image.
 
 [link to the repository](https://github.com/yzcjtr/GeoNet)
 
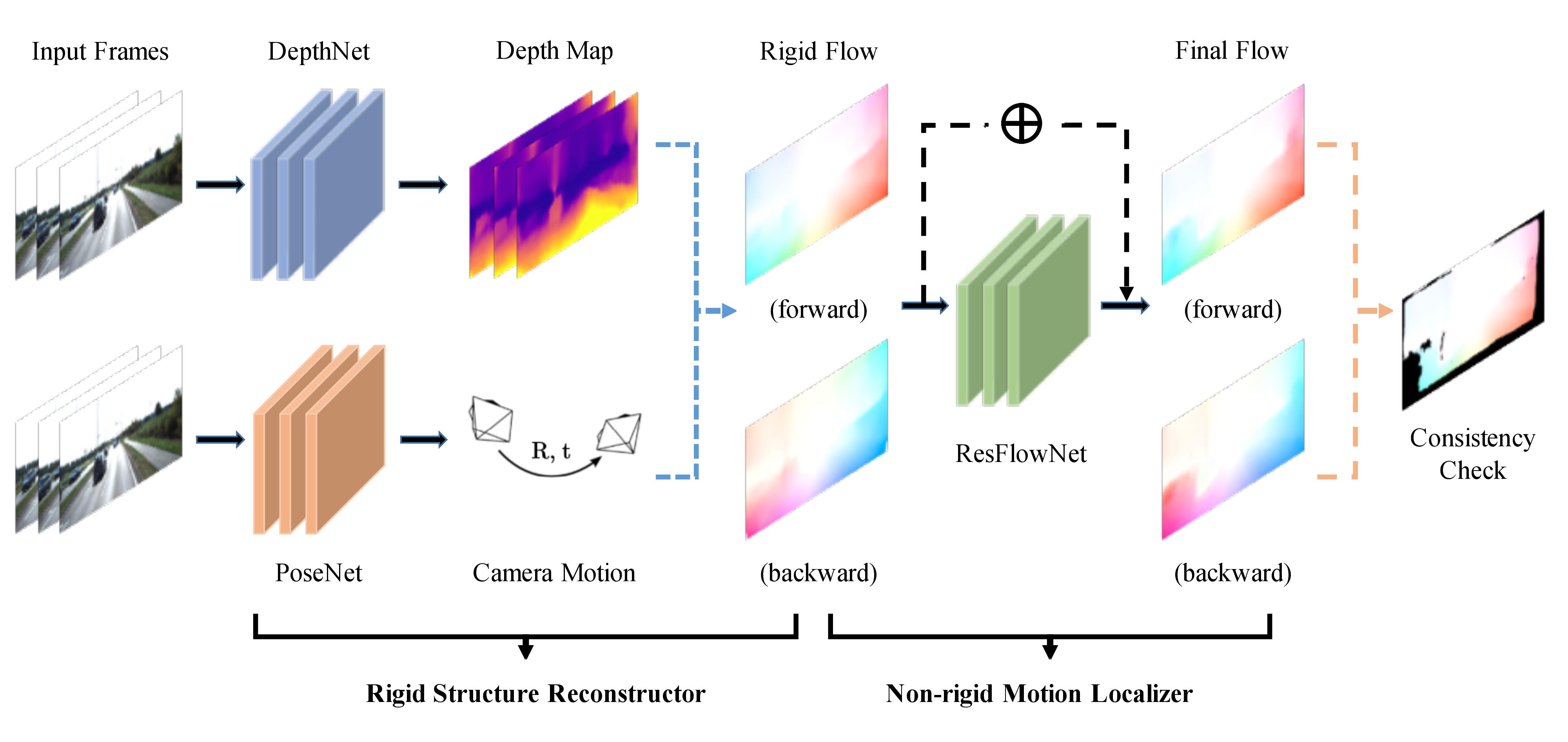
+### Architecture for GeoNet
+
 ![GeoNet](https://notenextra.trance-0.com/CSE5519/GeoNet.jpg)
 
 ### Rigid structure constructor
 
 Combines the DepthNet and PoseNet to estimate the depth and camera pose motion from [Unsupervised Learning of Depth and Ego-Motion From Video](#unsupervised-learning-of-depth-and-ego-motion-from-video).
 
+We denote the output of the Rigid structure constructor from frame $t$ to $s$ as $f^{rig}_{t\to s}$. The function output is a 2D vector showing the shift of the pixel coordinates.
+
+Recall from previous paper,
+
+$$
+\begin{aligned}
+p_t+f^{rig}_{t\to s}(p_t)&=KT_{t\to s}D_t(p_t)K^{-1}p_t\\
+f^{rig}_{t\to s}(p_t)&=K(T_{t\to s}D_t(p_t)+I)K^{-1}p_t-p_t
+\end{aligned}
+$$
+
 ### Non-rigid motion localizer
 
 Use [Left-right consistency](#unsupervised-monocular-depth-estimation-with-left-right-consistency) to estimate the non-rigid motion by training the ResFlowNet.
 
+We denote the output of the Non-rigid motion localizer from frame $t$ to $s$ as $f^{res}_{t\to s}$. SO the final full flow prediction is $f^{full}_{t\to s}=f^{res}_{t\to s}+f^{rig}_{t\to s}$.
+
+Let $\hat{I}^{rig}_s$ denote the inverse wrapped image from frame $s$ to $t$. Note that $\hat{I}^{rig}_s$ is the prediction of $I_t$ from $I_s$, using the rigid structure constructor.
+
+Recall from previous paper, we rename the $\mathcal{L}_{ap}^l$ to $\mathcal{L}_{rw}$.
+
+$$
+\mathcal{L}_{rw}=\frac{1}{N}\sum_{p\in I^l}\alpha \frac{1-\operatorname{SSIM}(I^l(p),\hat{I}^{rig}_s(p))}{2}+(1-\alpha)\left\|I^l(p)-\hat{I}^{rig}_s(p)\right\|_1\tag{1}
+$$
+
+Then we use $\mathcal{L}_{ds}$ to enforce the smoothness of the disparity map.
+
+$$
+\mathcal{L}_{ds}=\sum_{p\in I^l}\left|\partial_x d^l_p\right|e^{-\left|\partial_x d^l_p\right|}+\left|\partial_y d^l_p\right|e^{-\left|\partial_y d^l_p\right|}=\sum_{p_t}|\nabla D(p_t)|\cdot \left(e^{-|\nabla I(p_t)|}\right)^T\tag{2}
+$$
+
+Replacing $\hat{I}^{rig}_s$ with $\hat{I}^{full}_s$, in (1) and (2), we get the $\mathcal{L}_{fw}$ and $\mathcal{L}_{fs}$ for the non-rigid motion localizer.
+
 ### Geometric consistency enforcement
 
 Finally, we use an additional geometric consistency enforcement to handle non-Lambertian surfaces (e.g., metal, plastic, etc.).
+
+This is done by additional term in the loss function.
+
+Let $\Delta f^{full}_{t\to s}(p_t)=f^{full}_{t\to s}(p_t)-f^{full}_{s\to t}(p_t)$.
+
+Let $\delta(p_t)$ denote the function belows for arbitrary $\alpha,\beta>0$:
+
+$$
+\delta(p_t)=\begin{cases}
+1 & \text{if }\|\Delta f^{full}_{t\to s}(p_t)\|_2<\max\{\alpha,\beta\|f^{full}_{t\to s}(p_t)\|_1\} \\
+0 & \text{otherwise}
+\end{cases}
+$$
+
+The geometric consistency enforcement loss is:
+
+$$
+\mathcal{L}_{gc}=\sum_{p_t}\delta(p_t)\|\Delta f^{full}_{t\to s}(p_t)\|_2
+$$
+
+### Loss function for GeoNet
+
+Let $l$ be the set of pyramid image scales. $\langle t,s\rangle$ denote the set of all pairs of frames in the video and their inverse pairs, $t\neq s$.
+
+$$
+\mathcal{L}=\sum_{l}\sum_{\langle t,s\rangle}\mathcal{L}_{rw}+\lambda_{ds}\mathcal{L}_{ds}+\lambda_{fw}\mathcal{L}_{fw}+\lambda_{fs}\mathcal{L}_{fs}+\lambda_{gc}\mathcal{L}_{gc}
+$$
+
+$\lambda_{ds},\lambda_{fw},\lambda_{fs},\lambda_{gc}$ are hyperparameters that balance the importance of the different losses.
+
+### Results for monocular depth estimation
+
+![GeoNet](https://notenextra.trance-0.com/CSE5519/GeoNet_results.png)