Trance-0/NoteNextra-origin
1
0
Fork 0
Code Issues Pull Requests Actions 1 Packages Projects Releases Wiki Activity

bug fixed,

Browse Source 
remaining issues in mobilenavbar need pruning, need rewrite the class.
This commit is contained in:
Trance-0
2025-10-27 15:09:27 -05:00
parent e4995c8118
commit c9c119e991
171 changed files with 27750 additions and 6939 deletions
Download Patch File Download Diff File Expand all files Collapse all files

9
app/layout.tsx
View File

@@ -1,6 +1,6 @@
/* eslint-env node */
import { Footer, Layout} from 'nextra-theme-docs'
import { Banner, Head } from 'nextra/components'
import { Head } from 'nextra/components'
import { getPageMap } from 'nextra/page-map'
import 'nextra-theme-docs/style.css'
import { SpeedInsights } from "@vercel/speed-insights/next"
@@ -32,13 +32,13 @@ export const metadata = {
}
export default async function RootLayout({ children }) {
const pageMap = await getPageMap()
const pageMap = await getPageMap();
const navbar = (
<Navbar
pageMap={pageMap}
logo={
<>
<svg width="32" height="32" viewBox="0 0 16 16">
<svg xmlns="http://www.w3.org/2000/svg" width="32" height="32" fill="currentColor" className="bi bi-braces-asterisk" viewBox="0 0 16 16">
<path fillRule="evenodd" d="M1.114 8.063V7.9c1.005-.102 1.497-.615 1.497-1.6V4.503c0-1.094.39-1.538 1.354-1.538h.273V2h-.376C2.25 2 1.49 2.759 1.49 4.352v1.524c0 1.094-.376 1.456-1.49 1.456v1.299c1.114 0 1.49.362 1.49 1.456v1.524c0 1.593.759 2.352 2.372 2.352h.376v-.964h-.273c-.964 0-1.354-.444-1.354-1.538V9.663c0-.984-.492-1.497-1.497-1.6M14.886 7.9v.164c-1.005.103-1.497.616-1.497 1.6v1.798c0 1.094-.39 1.538-1.354 1.538h-.273v.964h.376c1.613 0 2.372-.759 2.372-2.352v-1.524c0-1.094.376-1.456 1.49-1.456v-1.3c-1.114 0-1.49-.362-1.49-1.456V4.352C14.51 2.759 13.75 2 12.138 2h-.376v.964h.273c.964 0 1.354.444 1.354 1.538V6.3c0 .984.492 1.497 1.497 1.6M7.5 11.5V9.207l-1.621 1.621-.707-.707L6.792 8.5H4.5v-1h2.293L5.172 5.879l.707-.707L7.5 6.792V4.5h1v2.293l1.621-1.621.707.707L9.208 7.5H11.5v1H9.207l1.621 1.621-.707.707L8.5 9.208V11.5z"/>
</svg>
<span style={{ marginLeft: '.4em', fontWeight: 800 }}>
@@ -48,7 +48,6 @@ export default async function RootLayout({ children }) {
}
projectLink="https://github.com/Trance-0/NoteNextra"
/>
// <Navbar pageMap={pageMap}/>
)
return (
<html lang="en" dir="ltr" suppressHydrationWarning>
@@ -85,7 +84,7 @@ export default async function RootLayout({ children }) {
sidebar={{ defaultMenuCollapseLevel: 1 }}
pageMap={pageMap}
// TODO: fix algolia search
// search={<AlgoliaSearch />}
search={<AlgoliaSearch/>}
>
{children}
{/* SpeedInsights in vercel */}

7
components/docsearch.tsx
View File

@@ -2,15 +2,20 @@
// sample code from https://docsearch.algolia.com/docs/docsearch
import { DocSearch } from '@docsearch/react';
import {useTheme} from 'next-themes';
import '@docsearch/css';
function AlgoliaSearch() {
function AlgoliaSearch () {
const {theme} = useTheme();
const darkMode = theme === 'dark';
console.log("darkMode", darkMode);
return (
<DocSearch
appId={process.env.NEXT_SEARCH_ALGOLIA_APP_ID || 'NKGLZZZUBC'}
indexName={process.env.NEXT_SEARCH_ALGOLIA_INDEX_NAME || 'notenextra_trance_0'}
apiKey={process.env.NEXT_SEARCH_ALGOLIA_API_KEY || '727b389a61e862e590dfab9ce9df31a2'}
theme={darkMode===false ? 'light' : 'dark'}
/>
);
}

1
components/navbar.client.tsx
View File

@@ -116,7 +116,6 @@ export const ClientNavbar: FC<{
// const items = topLevelNavbarItems
// use filteredTopLevelNavbarItems to generate items
const items = filteredTopLevelNavbarItems
console.log(filteredTopLevelNavbarItems)
const themeConfig = useThemeConfig()

2
components/navbar.tsx
View File

@@ -4,10 +4,8 @@
'use client'
import { usePathname } from 'next/navigation'
import type { PageMapItem } from 'nextra'
import { Anchor } from 'nextra/components'
import { normalizePages } from 'nextra/normalize-pages'
import type { FC, ReactNode } from 'react'
import cn from 'clsx'

59
content/CSE559A/CSE559A_L1.md
View File

@@ -1,59 +0,0 @@
# CSE559A Lecture 1
## Introducing the syllabus
See the syllabus on Canvas.
## Motivational introduction for computer vision
Computer vision is the study of manipulating images.
Automatic understanding of images and videos
1. vision for measurement (measurement, segmentation)
2. vision for perception, interpretation (labeling)
3. search and organization (retrieval, image or video archives)
### What is image
A 2d array of numbers.
### Vision is hard
connection to graphics.
computer vision need to generate the model from the image.
#### Are A and B the same color?
It depends on the context what you mean by "the same".
todo
#### Chair detector example.
double for loops.
#### Our visual system is not perfect.
Some optical illusion images.
todo, embed images here.
### Ridiculously brief history of computer vision
1960s: interpretation of synthetic worlds
1970s: some progress on interpreting selected images
1980s: ANNs come and go; shift toward geometry and increased mathematical rigor
1990s: face recognition; statistical analysis in vogue
2000s: becoming useful; significant use of machine learning; large annotated datasets available; video processing starts.
2010s: Deep learning with ConvNets
2020s: String synthesis; continued improvement across tasks, vision-language models.
## How computer vision is used now
### OCR, Optical Character Recognition
Technology to convert scanned docs to text.

148
content/CSE559A/CSE559A_L10.md
View File

@@ -1,148 +0,0 @@
# CSE559A Lecture 10
## Convolutional Neural Networks
### Convolutional Layer
Output feature map resolution depends on padding and stride
Padding: add zeros around the input image
Stride: the step of the convolution
Example:
1. Convolutional layer for 5x5 image with 3x3 kernel, padding 1, stride 1 (no skipping pixels)
- Input: 5x5 image
- Output: 3x3 feature map, (5-3+2*1)/1+1=5
2. Convolutional layer for 5x5 image with 3x3 kernel, padding 1, stride 2 (skipping pixels)
- Input: 5x5 image
- Output: 2x2 feature map, (5-3+2*1)/2+1=2
_Learned weights can be thought of as local templates_
```python
import torch
import torch.nn as nn
# suppose input image is HxWx3 (assume RGB image)
conv_layer = nn.Conv2d(in_channels=3, # input channel, input is HxWx3
out_channels=64, # output channel (number of filters), output is HxWx64
kernel_size=3, # kernel size
padding=1, # padding, this ensures that the output feature map has the same resolution as the input image, H_out=H_in, W_out=W_in
stride=1) # stride
```
Usually followed by a ReLU activation function
```python
conv_layer = nn.Conv2d(in_channels=3, out_channels=64, kernel_size=3, padding=1, stride=1)
relu = nn.ReLU()
```
Suppose input image is $H\times W\times K$, the output feature map is $H\times W\times L$ with kernel size $F\times F$, this takes $F^2\times K\times L\times H\times W$ parameters
Each operation $D\times (K^2C)$ matrix with $(K^2C)\times N$ matrix, assume $D$ filters and $C$ output channels.
### Variants 1x1 convolutions, depthwise convolutions
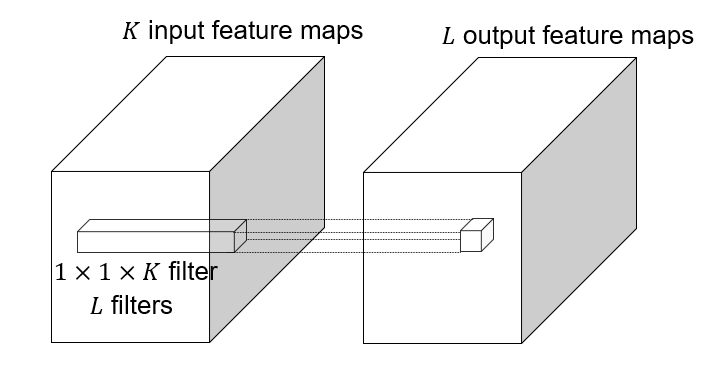
#### 1x1 convolutions
![1x1 convolution](https://notenextra.trance-0.com/CSE559A/1x1_layer.png)
1x1 convolution: $F=1$, this layer do convolution in the pixel level, it is **pixel-wise** convolution for the feature.
Used to save computation, reduce the number of parameters.
Example: 3x3 conv layer with 256 channels at input and output.
Option 1: naive way:
```python
conv_layer = nn.Conv2d(in_channels=256, out_channels=256, kernel_size=3, padding=1, stride=1)
```
This takes $256\times 3 \times 3\times 256=524,288$ parameters.
Option 2: 1x1 convolution:
```python
conv_layer = nn.Conv2d(in_channels=256, out_channels=64, kernel_size=1, padding=0, stride=1)
conv_layer = nn.Conv2d(in_channels=64, out_channels=64, kernel_size=3, padding=1, stride=1)
conv_layer = nn.Conv2d(in_channels=64, out_channels=256, kernel_size=1, padding=0, stride=1)
```
This takes $256\times 1\times 1\times 64 + 64\times 3\times 3\times 64 + 64\times 1\times 1\times 256 = 16,384 + 36,864 + 16,384 = 69,632$ parameters.
This lose some information, but save a lot of parameters.
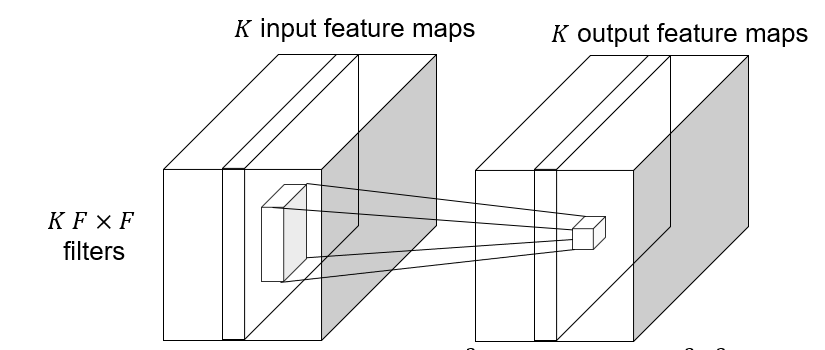
#### Depthwise convolutions
Depthwise convolution: $K\to K$ feature map, save computation, reduce the number of parameters.
![Depthwise convolution](https://notenextra.trance-0.com/CSE559A/Depthwise_layer.png)
#### Grouped convolutions
Self defined convolution on the feature map following the similar manner.
### Backward pass
Vector-matrix form:
$$
\frac{\partial e}{\partial x}=\frac{\partial e}{\partial z}\frac{\partial z}{\partial x}
$$
Suppose the kernel is 3x3, the feature map is $\ldots, x_{i-1}, x_i, x_{i+1}, \ldots$, and $\ldots, z_{i-1}, z_i, z_{i+1}, \ldots$ is the output feature map, then:
The convolution operation can be written as:
$$
z_i = w_1x_{i-1} + w_2x_i + w_3x_{i+1}
$$
The gradient of the kernel is:
$$
\frac{\partial e}{\partial x_i} = \sum_{j=-1}^{1}\frac{\partial e}{\partial z_i}\frac{\partial z_i}{\partial x_i} = \sum_{j=-1}^{1}\frac{\partial e}{\partial z_i}w_j
$$
### Max-pooling
Get max value in the local region.
#### Receptive field
The receptive field of a unit is the region of the input feature map whose values contribute to the response of that unit (either in the previous layer or in the initial image)
## Architecture of CNNs
### AlexNet (2012-2013)
Successor of LeNet-5, but with a few significant changes
- Max pooling, ReLU nonlinearity
- Dropout regularization
- More data and bigger model (7 hidden layers, 650K units, 60M params)
- GPU implementation (50x speedup over CPU)
- Trained on two GPUs for a week
#### Key points
Most floating point operations occur in the convolutional layers.
Most of the memory usage is in the early convolutional layers.
Nearly all parameters are in the fully-connected layers.
### VGGNet (2014)
### GoogLeNet (2014)
### ResNet (2015)
### Beyond ResNet (2016 and onward): Wide ResNet, ResNeXT, DenseNet

141
content/CSE559A/CSE559A_L11.md
View File

@@ -1,141 +0,0 @@
# CSE559A Lecture 11
## Continue on Architecture of CNNs
### AlexNet (2012-2013)
Successor of LeNet-5, but with a few significant changes
- Max pooling, ReLU nonlinearity
- Dropout regularization
- More data and bigger model (7 hidden layers, 650K units, 60M params)
- GPU implementation (50x speedup over CPU)
- Trained on two GPUs for a week
#### Architecture for AlexNet
- Input: 224x224x3
- 11x11 conv, stride 4, 96 filters
- 3x3 max pooling, stride 2
- 5x5 conv, 256 filters, padding 2
- 3x3 max pooling, stride 2
- 3x3 conv, 384 filters, padding 1
- 3x3 conv, 384 filters, padding 1
- 3x3 conv, 256 filters, padding 1
- 3x3 max pooling, stride 2
- 4096-unit FC, ReLU
- 4096-unit FC, ReLU
- 1000-unit FC, softmax
#### Key points for AlexNet
Most floating point operations occur in the convolutional layers.
Most of the memory usage is in the early convolutional layers.
Nearly all parameters are in the fully-connected layers.
#### Further refinement (ZFNet, 2013)
Best paper award at ILSVRC 2013.
Nicely visualizes the feature maps.
### VGGNet (2014)
All the cov layers are 3x3 filters with stride 1 and padding 1. Take advantage of pooling to reduce the spatial dimensionality.
#### Architecture for VGGNet
- Input: 224x224x3
- 3x3 conv, 64 filters, padding 1
- 3x3 conv, 64 filters, padding 1
- 2x2 max pooling, stride 2
- 3x3 conv, 128 filters, padding 1
- 3x3 conv, 128 filters, padding 1
- 2x2 max pooling, stride 2
- 3x3 conv, 256 filters, padding 1
- 3x3 conv, 256 filters, padding 1
- 2x2 max pooling, stride 2
- 3x3 conv, 512 filters, padding 1
- 3x3 conv, 512 filters, padding 1
- 3x3 conv, 512 filters, padding 1
- 2x2 max pooling, stride 2
- 3x3 conv, 512 filters, padding 1
- 3x3 conv, 512 filters, padding 1
- 3x3 conv, 512 filters, padding 1
- 2x2 max pooling, stride 2
- 4096-unit FC, ReLU
- 4096-unit FC, ReLU
- 1000-unit FC, softmax
#### Key points for VGGNet
- Sequence of deeper networks trained progressively
- Large receptive fields replaced by successive layer of 3x3 convs with relu in between
- 7x7 takes $49K^2$ parameters, 3x3 takes $27K^2$ parameters
#### Pretrained models
- Use pretrained-network as feature extractor (removing the last layer and training a new linear layer) (transfer learning)
- Add RNN layers to generate captions
- Fine-tune the model for the new task (finetuning)
- Keep the earlier layers fixed and only train the new prediction layer
### GoogLeNet (2014)
Stem network at the start aggressively downsamples input.
#### Key points for GoogLeNet
- Parallel paths with different receptive field size and operations are means to capture space patterns of correlations in the stack of feature maps
- Use 1x1 convs to reduce dimensionality
- Use Global Average Pooling (GAP) to replace the fully connected layer
- Auxiliary classifiers to improve training
- Training using loss at the end of the network didn't work well: network is too deep, gradient don't provide useful model updates
- As a hack, attach "auxiliary classifiers" at several intermediate points in the network that also try to classify the image and receive loss
- _GooLeNet was before batch normalization, with batch normalization, the auxiliary classifiers were removed._
### ResNet (2015)
152 layers
[ResNet paper](https://arxiv.org/abs/1512.03385)
#### Key points for ResNet
- The residual module
- Introduce `skip` or `shortcut` connections to avoid the degradation problem
- Make it easy for network layers to represent the identity mapping
- Directly performing 3×3 convolutions with 256 feature maps at input and output:
- $256 \times 256 \times 3 \times 3 \approx 600K$ operations
- Using 1×1 convolutions to reduce 256 to 64 feature maps, followed by 3×3 convolutions, followed by 1×1 convolutions to expand back to 256 maps:
- $256 \times 64 \times 1 \times 1 \approx 16K$
- $64 \times 64 \times 3 \times 3 \approx 36K$
- $64 \times 256 \times 1 \times 1 \approx 16K$
- Total $\approx 70K$
_Possibly the first model with top-5 error rate better than human performance._
### Beyond ResNet (2016 and onward): Wide ResNet, ResNeXT, DenseNet
#### Wide ResNet
Reduce number of residual blocks, but increase number of feature maps in each block
- More parallelizable, better feature reuse
- 16-layer WRN outperforms 1000-layer ResNets, though with much larger # of parameters
#### ResNeXt
- Propose “cardinality” as a new factor in network design, apart from depth and width
- Claim that increasing cardinality is a better way to increase capacity than increasing depth or width
#### DenseNet
- Use Dense block between conv layers
- Less parameters than ResNet
Next class:
Transformer architectures

159
content/CSE559A/CSE559A_L12.md
View File

@@ -1,159 +0,0 @@
# CSE559A Lecture 12
## Transformer Architecture
### Outline
**Self-Attention Layers**: An important network module, which often has a global receptive field
**Sequential Input Tokens**: Breaking the restriction to 2d input arrays
**Positional Encodings**: Representing the metadata of each input token
**Exemplar Architecture**: The Vision Transformer (ViT)
**Moving Forward**: What does this new module enable? Who wins in the battle between transformers and CNNs?
### The big picture
CNNs
- Local receptive fields
- Struggles with global content
- Shape of intermediate layers is sometimes a pain
Things we might want:
- Use information from across the image
- More flexible shape handling
- Multiple modalities
Our Hero: MultiheadAttention
Use positional encodings to represent the metadata of each input token
## Self-Attention layers
### Comparing with ways to handling sequential data
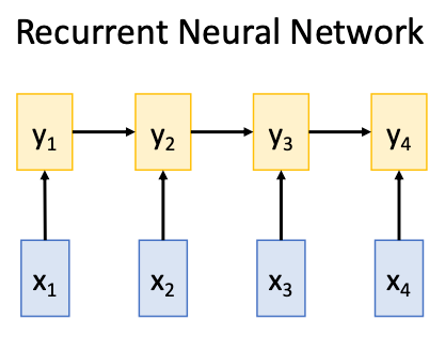
#### RNN
![Image of RNN](https://notenextra.trance-0.com/CSE559A/RNN.png)
Works on **Ordered Sequences**
- Good at long sequences: After one RNN layer $h_r$ sees the whole sequence
- Bad at parallelization: need to compute hidden states sequentially
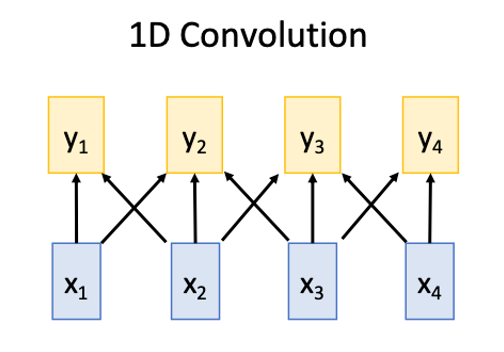
#### 1D conv
![Image of 1D conv](https://notenextra.trance-0.com/CSE559A/1D_Conv.png)
Works on **Multidimensional Grids**
- Bad at long sequences: Need to stack may conv layers or outputs to see the whole sequence
- Good at parallelization: Each output can be computed in parallel
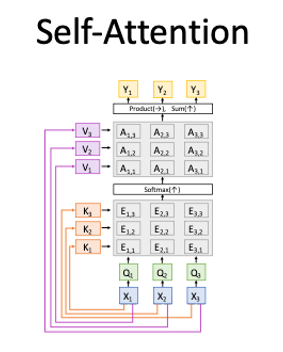
#### Self-Attention
![Image of self-attention](https://notenextra.trance-0.com/CSE559A/Self_Attention.png)
Works on **Set of Vectors**
- Good at Long sequences: Each output can attend to all inputs
- Good at parallelization: Each output can be computed in parallel
- Bad at saving memory: Need to store all inputs in memory
### Encoder-Decoder Architecture
The encoder is constructed by stacking multiple self-attention layers and feed-forward networks.
#### Word Embeddings
Translate tokens to vector space
```python
class Embedder(nn.Module):
def __init__(self, vocab_size, d_model):
super().__init__()
self.embed=nn.Embedding(vocab_size, d_model)
def forward(self, x):
return self.embed(x)
```
#### Positional Embeddings
The positional encodings are a way to represent the position of each token in the sequence.
Combined with the word embeddings, we get the input to the self-attention layer with information about the position of each token in the sequence.
> The reason why we just add the positional encodings to the word embeddings is _perhaps_ that we want the model to self-assign weights to the word-token and positional-token.
#### Query, Key, Value
The query, key, and value are the three components of the self-attention layer.
They are used to compute the attention weights.
```python
class SelfAttention(nn.Module):
def __init__(self, d_model, num_heads):
super().__init__()
self.d_model = d_model
self.d_k = d_k
self.q_linear = nn.Linear(d_model, d_k)
self.k_linear = nn.Linear(d_model, d_k)
self.v_linear = nn.Linear(d_model, d_k)
self.dropout = nn.Dropout(dropout)
self.out = nn.Linear(d_k, d_k)
def forward(self, q, k, v, mask=None):
bs = q.size(0)
k = self.k_linear(k)
q = self.q_linear(q)
v = self.v_linear(v)
# calculate attention weights
outputs = attention(q, k, v, self.d_k, mask, self.dropout)
# apply output linear transformation
outputs = self.out(outputs)
return outputs
```
#### Attention
```python
def attention(q, k, v, d_k, mask=None, dropout=None):
scores = torch.matmul(q, k.transpose(-2, -1)) / math.sqrt(d_k)
if mask is not None:
mask = mask.unsqueeze(1)
scores = scores.masked_fill(mask == 0, -1e9)
scores = F.softmax(scores, dim=-1)
if dropout is not None:
scores = dropout(scores)
outputs = torch.matmul(scores, v)
return outputs
```
The query, key are used to compute the attention map, and the value is used to compute the attention output.
#### Multi-Head self-attention
The multi-head self-attention is a self-attention layer that has multiple heads.
Each head has its own query, key, and value.
### Computing Attention Efficiency
- the standard attention has a complexity of $O(n^2)$
- We can use sparse attention to reduce the complexity to $O(n)$

59
content/CSE559A/CSE559A_L13.md
View File

@@ -1,59 +0,0 @@
# CSE559A Lecture 13
## Positional Encodings
### Fixed Positional Encodings
Set of sinusoids of different frequencies.
$$
f(p,2i)=\sin(\frac{p}{10000^{2i/d}})\quad f(p,2i+1)=\cos(\frac{p}{10000^{2i/d}})
$$
[source](https://kazemnejad.com/blog/transformer_architecture_positional_encoding/)
### Positional Encodings in Reconstruction
MLP is hard to learn high-frequency information from scaler input $(x,y)$.
Example: network mapping from $(x,y)$ to $(r,g,b)$.
### Generalized Positional Encodings
- Dependence on location, scaler, metadata, etc.
- Can just be fully learned (use `nn.Embedding` and optimize based on a categorical input.)
## Vision Transformer (ViT)
### Class Token
In Vision Transformers, a special token called the class token is added to the input sequence to aggregate information for classification tasks.
### Hidden CNN Modules
- PxP convolution with stride P (split the image into patches and use positional encoding)
### ViT + ResNet Hybrid
Build a hybrid model that combines the vision transformer after 50 layer of ResNet.
## Moving Forward
At least for now, CNN and ViT architectures have similar performance at least in ImageNet.
- General Consensus: once the architecture is big enough, and not designed terribly, it can do well.
- Differences remain:
- Computational efficiency
- Ease of use in other tasks and with other input data
- Ease of training
## Wrap up
Self attention as a key building block
Flexible input specification using tokens with positional encodings
A wide variety of architectural styles
Up Next:
Training deep neural networks

73
content/CSE559A/CSE559A_L14.md
View File

@@ -1,73 +0,0 @@
# CSE559A Lecture 14
## Object Detection
AP (Average Precision)
### Benchmarks
#### PASCAL VOC Challenge
20 Challenge classes.
CNN increases the accuracy of object detection.
#### COCO dataset
Common objects in context.
Semantic segmentation. Every pixel is classified to tags.
Instance segmentation. Every pixel is classified and grouped into instances.
### Object detection: outline
Proposal generation
Object recognition
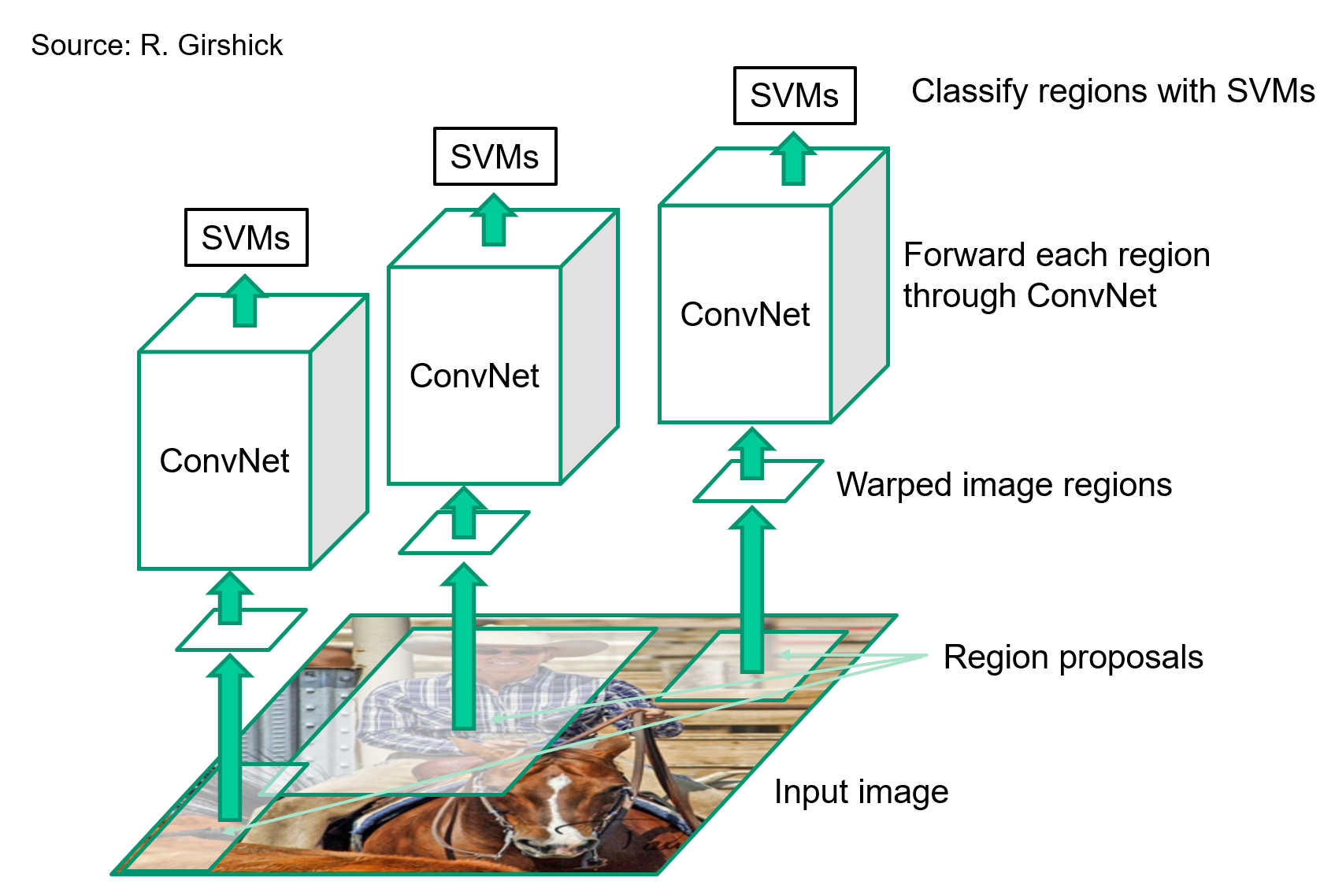
#### R-CNN
Proposal generation
Use CNN to extract features from proposals.
with SVM to classify proposals.
Use selective search to generate proposals.
Use AlexNet finetuned on PASCAL VOC to extract features.
Pros:
- Much more accurate than previous approaches
- Andy deep architecture can immediately be "plugged in"
Cons:
- Not a single end-to-end trainable system
- Fine-tune network with softmax classifier (log loss)
- Train post-hoc linear SVMs (hinge loss)
- Train post-hoc bounding box regressors (least squares)
- Training is slow 2000CNN passes for each image
- Inference (detection) was slow
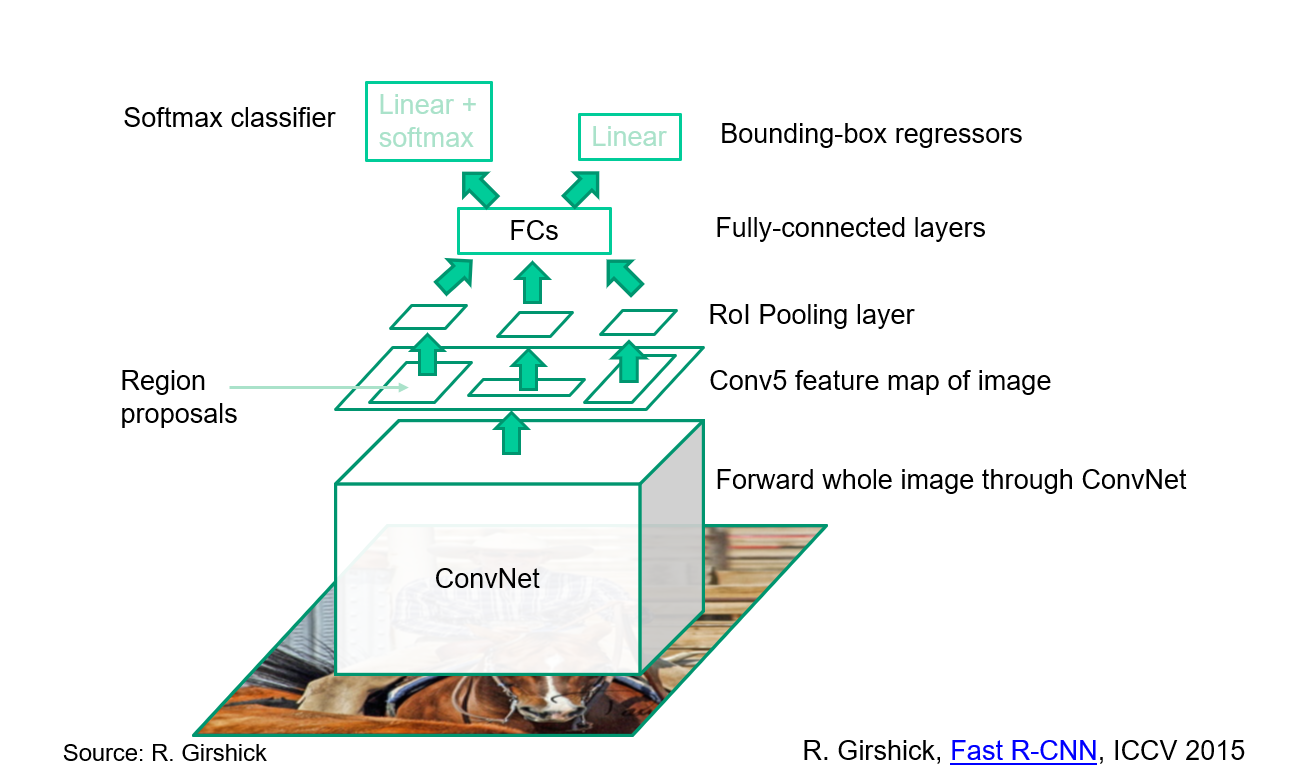
#### Fast R-CNN
Proposal generation
Use CNN to extract features from proposals.
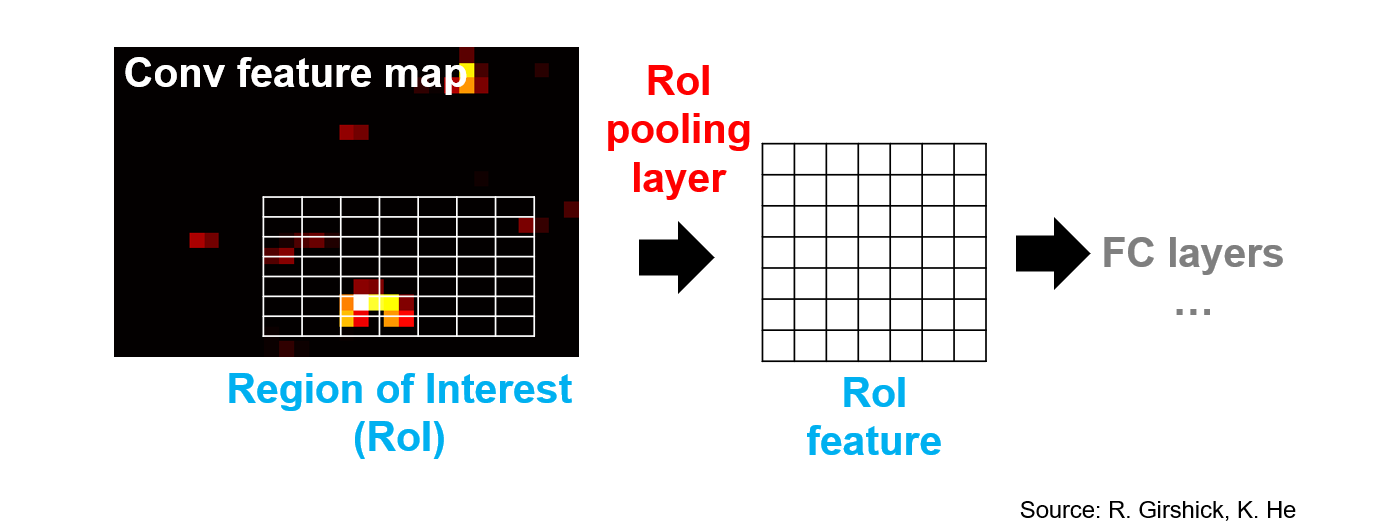
##### ROI pooling and ROI alignment
ROI pooling:
- Pooling is applied to the feature map.
- Pooling is applied to the proposal.
ROI alignment:
- Align the proposal to the feature map.
- Align the proposal to the feature map.
Use bounding box regression to refine the proposal.

131
content/CSE559A/CSE559A_L15.md
View File

@@ -1,131 +0,0 @@
# CSE559A Lecture 15
## Continue on object detection
### Two strategies for object detection
#### R-CNN: Region proposals + CNN features
![R-CNN](https://notenextra.trance-0.com/CSE559A/R-CNN.png)
#### Fast R-CNN: CNN features + RoI pooling
![Fast R-CNN](https://notenextra.trance-0.com/CSE559A/Fast-R-CNN.png)
Use bilinear interpolation to get the features of the proposal.
#### Region of interest pooling
![RoI pooling](https://notenextra.trance-0.com/CSE559A/RoI-pooling.png)
Use backpropagation to get the gradient of the proposal.
### New materials
#### Faster R-CNN
Use one CNN to generate region proposals. And use another CNN to classify the proposals.
##### Region proposal network
Idea: put an "anchor box" of fixed size over each position in the feature map and try to predict whether this box is likely to contain an object.
Introduce anchor boxes at multiple scales and aspect ratios to handle a wider range of object sizes and shapes.
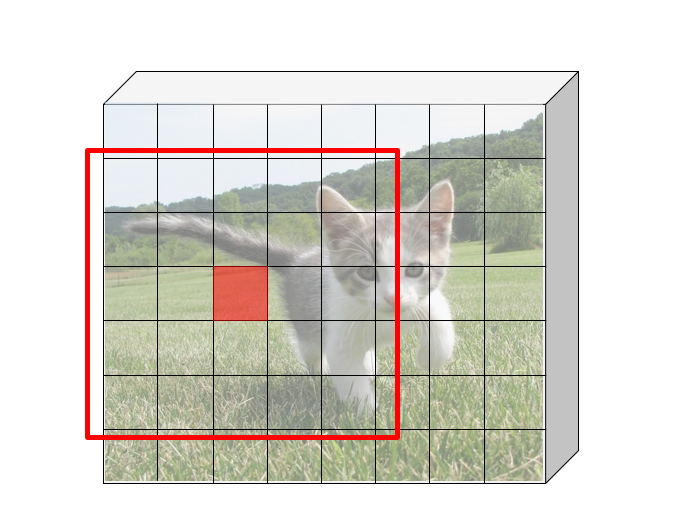
![Anchor boxes](https://notenextra.trance-0.com/CSE559A/Anchor-boxes.png)
### Single-stage and multi-resolution detection
#### YOLO
You only look once (YOLO) is a state-of-the-art, real-time object detection system.
1. Take conv feature maps at 7x7 resolution
2. Add two FC layers to predict, at each location, a score for each class and 2 bboxes with confidences
For PASCAL, output is 7×7×30 (30=20 + 2∗(4+1))
![YOLO](https://notenextra.trance-0.com/CSE559A/YOLO.png)
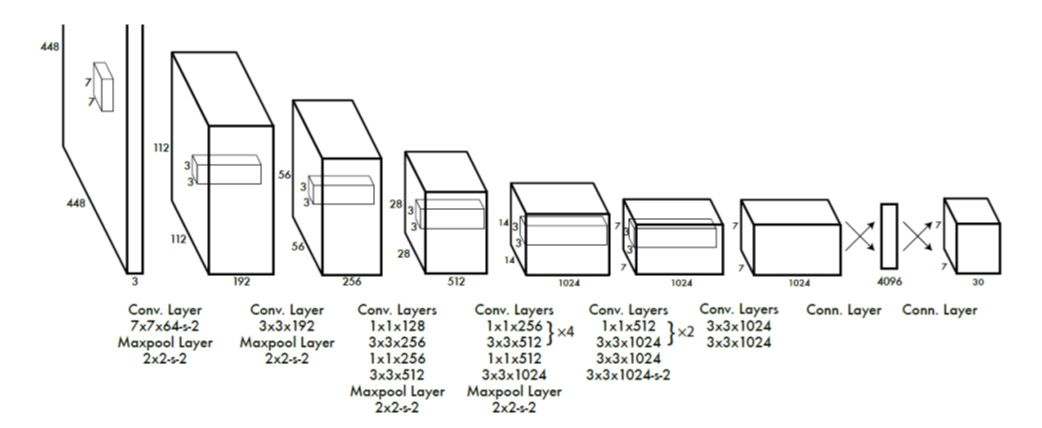
##### YOLO Network Head
```python
model.add(Conv2D(1024, (3, 3), activation='lrelu', kernel_regularizer=l2(0.0005)))
model.add(Conv2D(1024, (3, 3), activation='lrelu', kernel_regularizer=l2(0.0005)))
# use flatten layer for global reasoning
model.add(Flatten())
model.add(Dense(512))
model.add(Dense(1024))
model.add(Dropout(0.5))
model.add(Dense(7 * 7 * 30, activation='sigmoid'))
model.add(YOLO_Reshape(target_shape=(7, 7, 30)))
model.summary()
```
#### YOLO results
1. Each grid cell predicts only two boxes and can only have one class – this limits the number of nearby objects that can be predicted
2. Localization accuracy suffers compared to Fast(er) R-CNN due to coarser features, errors on small boxes
3. 7x speedup over Faster R-CNN (45-155 FPS vs. 7-18 FPS)
#### YOLOv2
1. Remove FC layer, do convolutional prediction with anchor boxes instead
2. Increase resolution of input images and conv feature maps
3. Improve accuracy using batch normalization and other tricks
#### SSD
SSD is a multi-resolution object detection
![SSD](https://notenextra.trance-0.com/CSE559A/SSD.png)
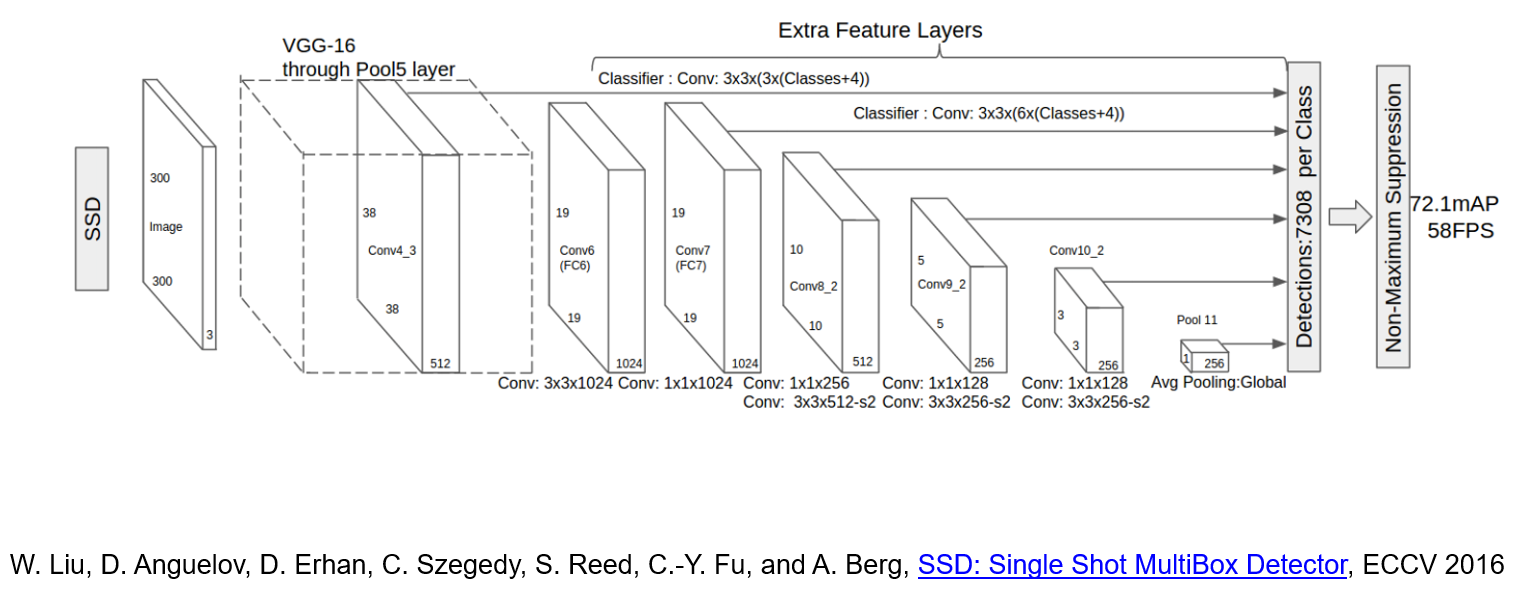
1. Predict boxes of different size from different conv maps
2. Each level of resolution has its own predictor
##### Feature Pyramid Network
- Improve predictive power of lower-level feature maps by adding contextual information from higher-level feature maps
- Predict different sizes of bounding boxes from different levels of the pyramid (but share parameters of predictors)
#### RetinaNet
RetinaNet combine feature pyramid network with focal loss to reduce the standard cross-entropy loss for well-classified examples.
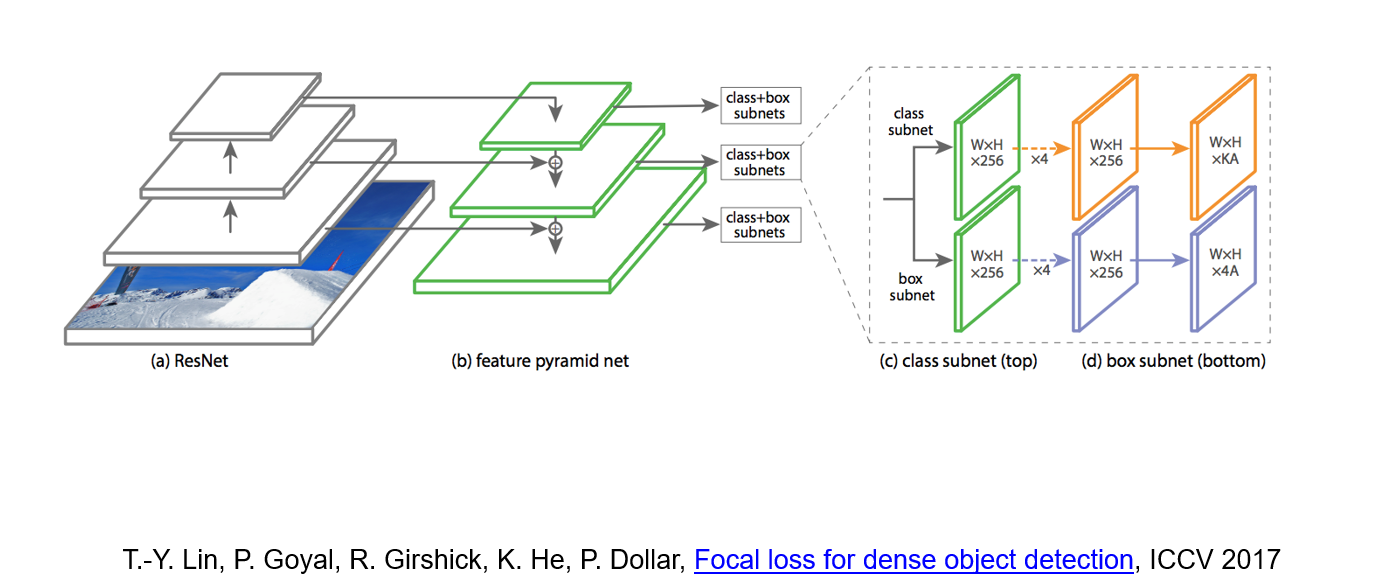
![RetinaNet](https://notenextra.trance-0.com/CSE559A/RetinaNet.png)
> Cross-entropy loss:
> $$CE(p_t) = - \log(p_t)$$
The focal loss is defined as:
$$
FL(p_t) = - (1 - p_t)^{\gamma} \log(p_t)
$$
We can increase $\gamma$ to reduce the loss for well-classified examples.
#### YOLOv3
Minor refinements
### Alternative approaches
#### CornerNet
Use a pair of corners to represent the bounding box.
Use hourglass network to accumulate the information of the corners.
#### CenterNet
Use a center point to represent the bounding box.
#### Detection Transformer
Use transformer architecture to detect the object.
![DETR](https://notenextra.trance-0.com/CSE559A/DETR.png)
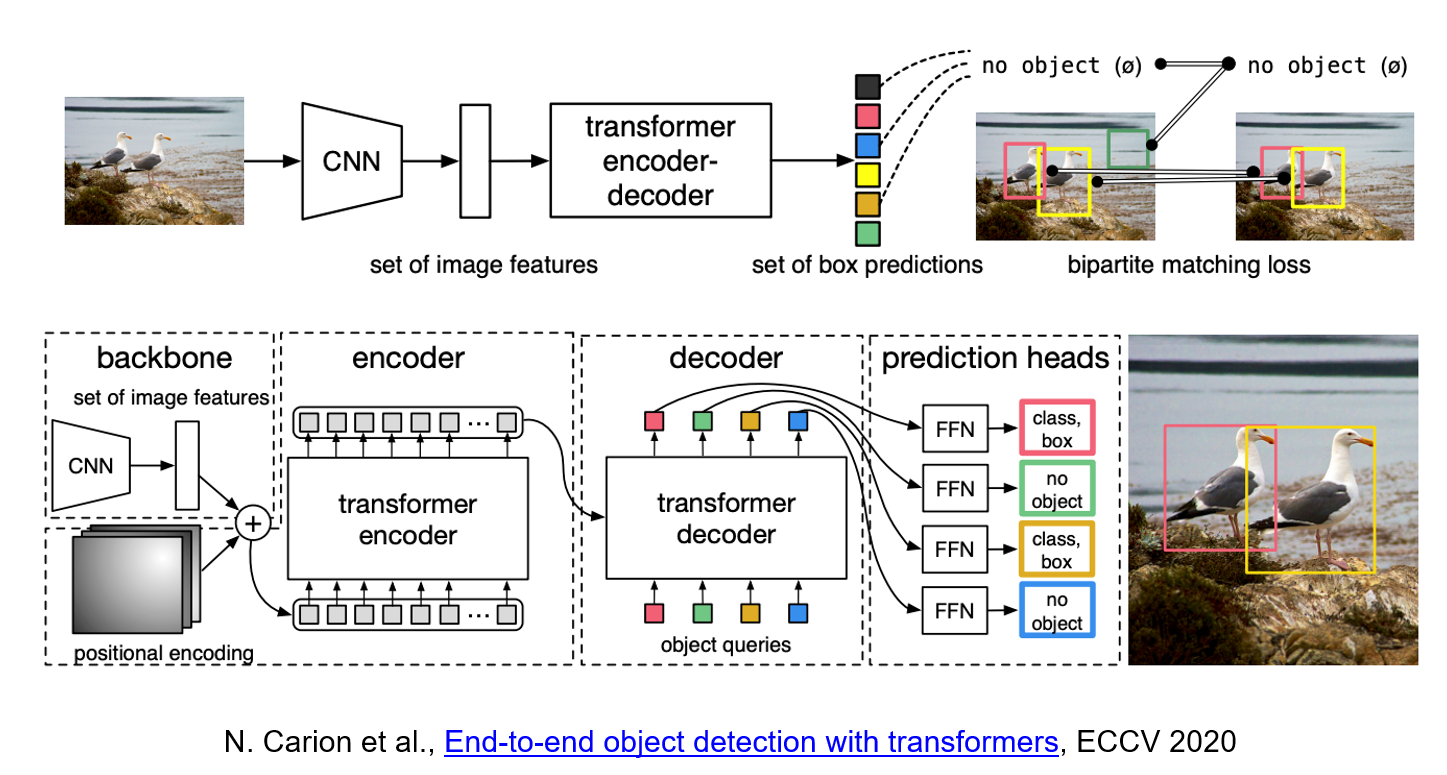
DETR uses a conventional CNN backbone to learn a 2D representation of an input image. The model flattens it and supplements it with a positional encoding before passing it into a transformer encoder. A transformer decoder then takes as input a small fixed number of learned positional embeddings, which we call object queries, and additionally attends to the encoder output. We pass each output embedding of the decoder to a shared feed forward network (FFN) that predicts either a detection (class and bounding box) or a "no object" class.

114
content/CSE559A/CSE559A_L16.md
View File

@@ -1,114 +0,0 @@
# CSE559A Lecture 16
## Dense image labelling
### Semantic segmentation
Use one-hot encoding to represent the class of each pixel.
### General Network design
Design a network with only convolutional layers, make predictions for all pixels at once.
Can the network operate at full image resolution?
Practical solution: first downsample, then upsample
### Outline
- Upgrading a Classification Network to Segmentation
- Operations for dense prediction
- Transposed convolutions, unpooling
- Architectures for dense prediction
- DeconvNet, U-Net, "U-Net"
- Instance segmentation
- Mask R-CNN
- Other dense prediction problems
### Fully Convolutional Networks
"upgrading" a classification network to a dense prediction network
1. Covert "fully connected" layers to 1x1 convolutions
2. Make the input image larger
3. Upsample the output
Start with an existing classification CNN ("an encoder")
Then use bilinear interpolation and transposed convolutions to make full resolution.
### Operations for dense prediction
#### Transposed Convolutions
Use the filter to "paint" in the output: place copies of the filter on the output, multiply by corresponding value in the input, sum where copies of the filter overlap
We can increase the resolution of the output by using a larger stride in the convolution.
- For stride 2, dilate the input by inserting rows and columns of zeros between adjacent entries, convolve with flipped filter
- Sometimes called convolution with fractional input stride 1/2
#### Unpooling
Max unpooling:
- Copy the maximum value in the input region to all locations in the output
- Use the location of the maximum value to know where to put the value in the output
Nearest neighbor unpooling:
- Copy the maximum value in the input region to all locations in the output
- Use the location of the maximum value to know where to put the value in the output
### Architectures for dense prediction
#### DeconvNet
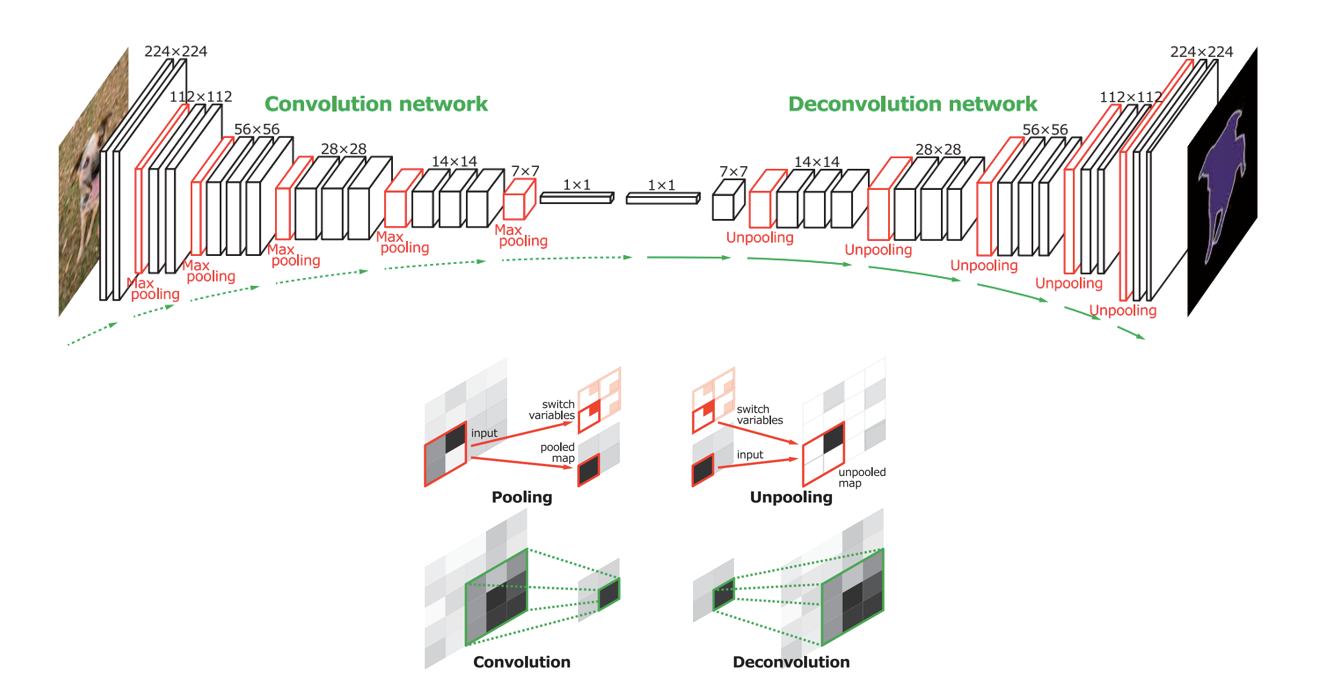
![DeconvNet](https://notenextra.trance-0.com/CSE559A/DeconvNet.png)
_How the information about location is encoded in the network?_
#### U-Net
![U-Net](https://notenextra.trance-0.com/CSE559A/U-Net.png)
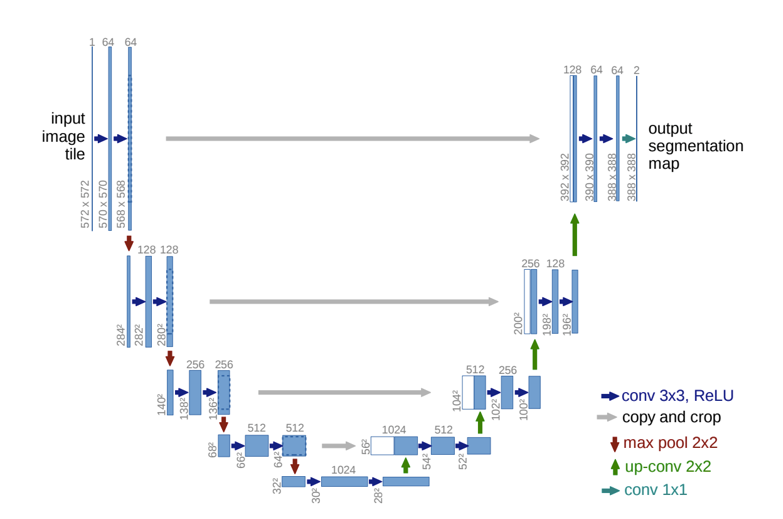
- Like FCN, fuse upsampled higher-level feature maps with higher-res, lower-level feature maps (like residual connections)
- Unlike FCN, fuse by concatenation, predict at the end
#### Extended U-Net Architecture
Many variants of U-Net would replace the "encoder" of the U-Net with other architectures.
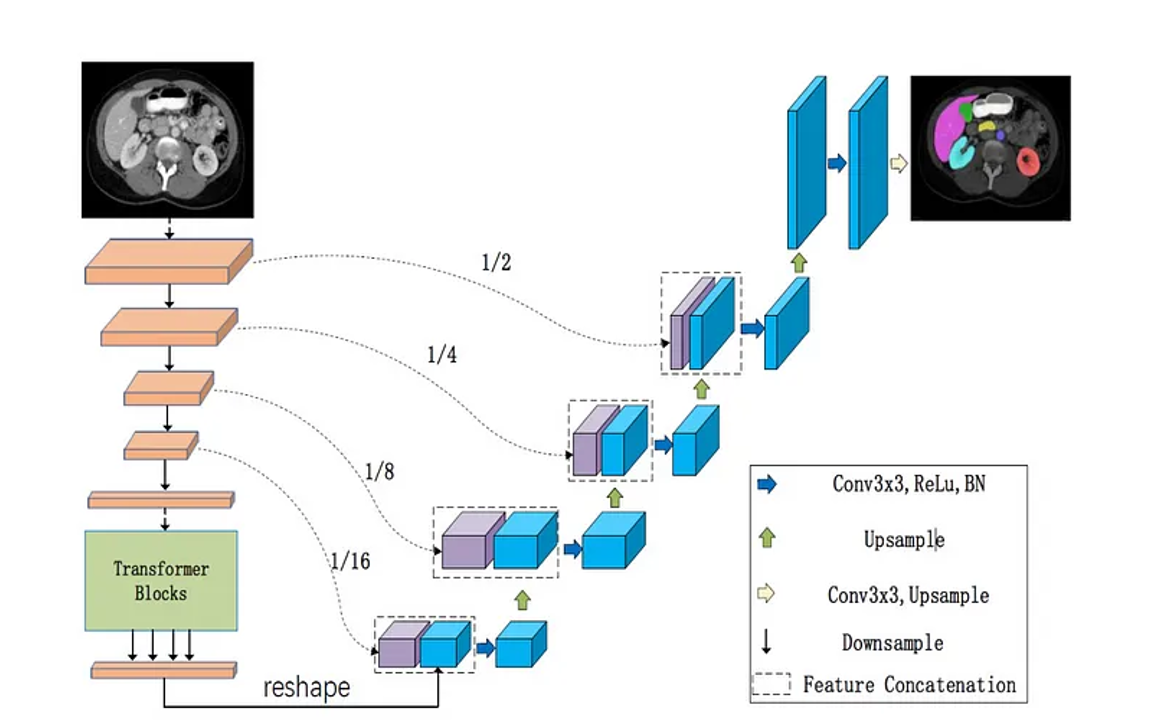
![Extended U-Net Architecture Example](https://notenextra.trance-0.com/CSE559A/ExU-Net.png)
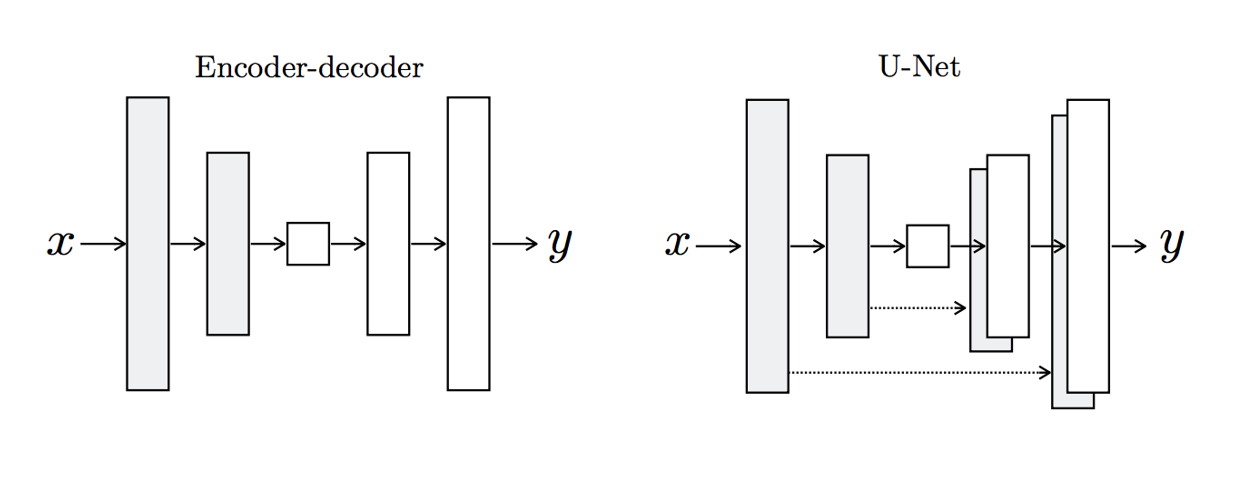
##### Encoder/Decoder v.s. U-Net
![Encoder/Decoder v.s. U-Net](https://notenextra.trance-0.com/CSE559A/EncoderDecoder_vs_U-Net.png)
### Instance Segmentation
#### Mask R-CNN
Mask R-CNN = Faster R-CNN + FCN on Region of Interest
### Extend to keypoint prediction?
- Use a similar architecture to Mask R-CNN
_Continue on Tuesday_
### Other tasks
#### Panoptic feature pyramid network
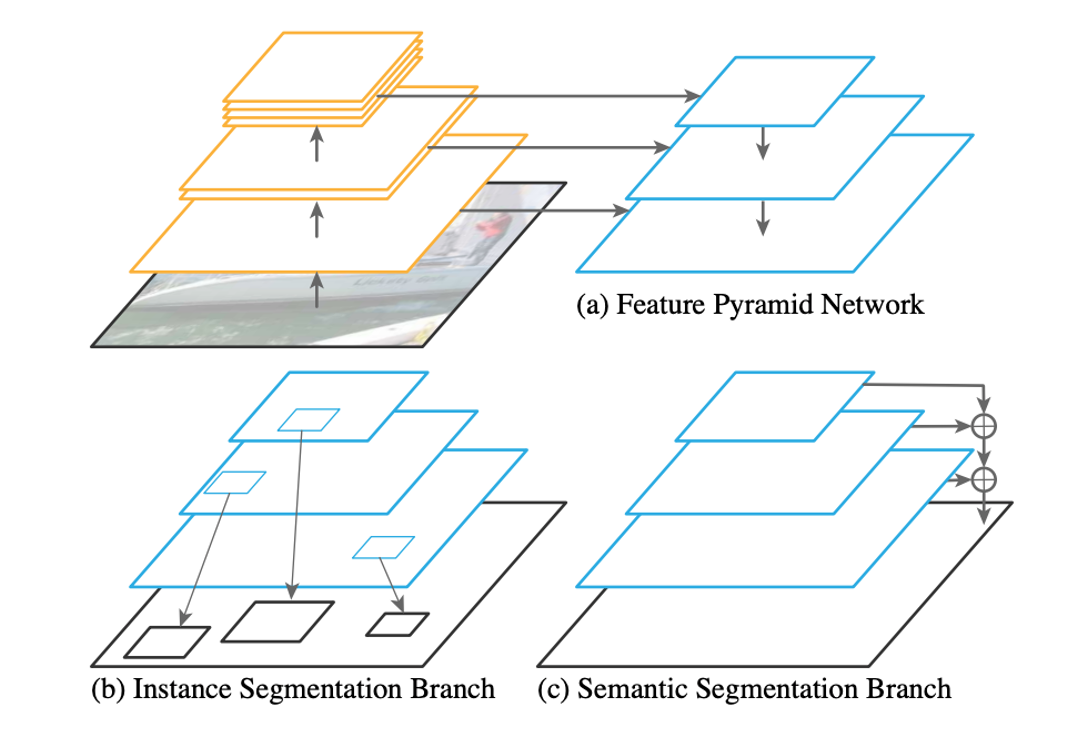
![Panoptic Feature Pyramid Network](https://notenextra.trance-0.com/CSE559A/Panoptic_Feature_Pyramid_Network.png)
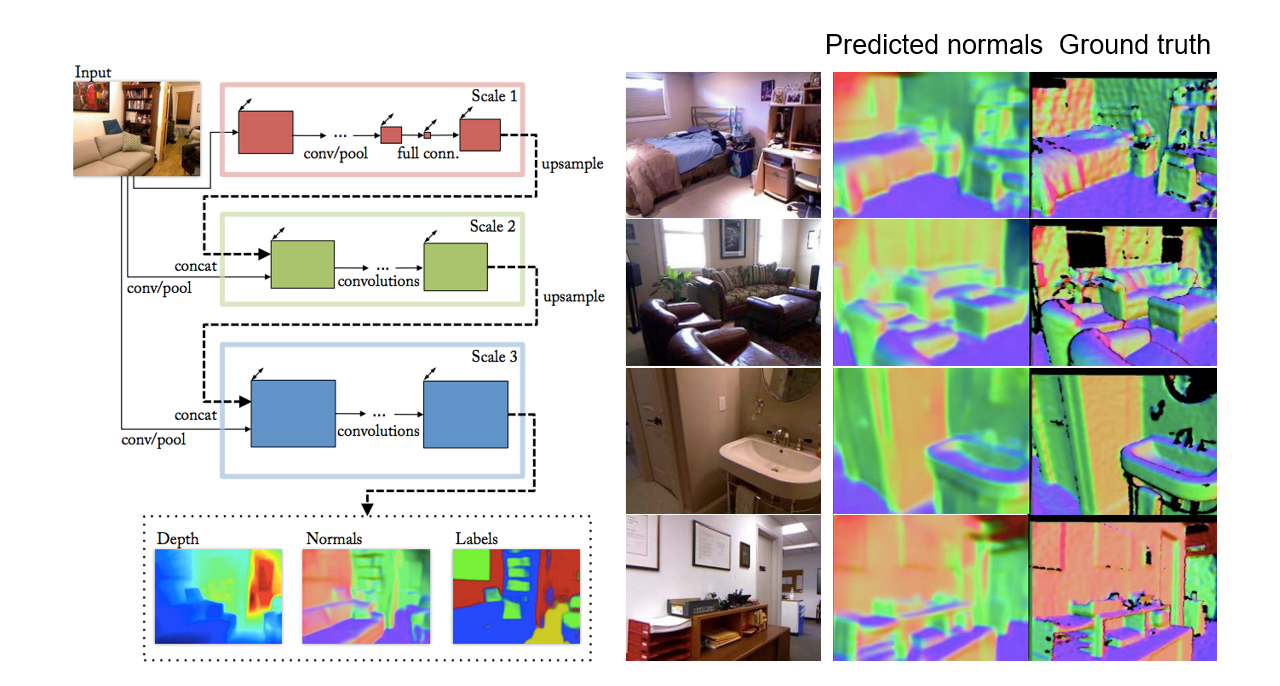
#### Depth and normal estimation
![Depth and Normal Estimation](https://notenextra.trance-0.com/CSE559A/Depth_and_Normal_Estimation.png)
D. Eigen and R. Fergus, Predicting Depth, Surface Normals and Semantic Labels with a Common Multi-Scale Convolutional Architecture, ICCV 2015
#### Colorization
R. Zhang, P. Isola, and A. Efros, Colorful Image Colorization, ECCV 2016

184
content/CSE559A/CSE559A_L17.md
View File

@@ -1,184 +0,0 @@
# CSE559A Lecture 17
## Local Features
### Types of local features
#### Edge
Goal: Identify sudden changes in image intensity
Generate edge map as human artists.
An edge is a place of rapid change in the image intensity function.
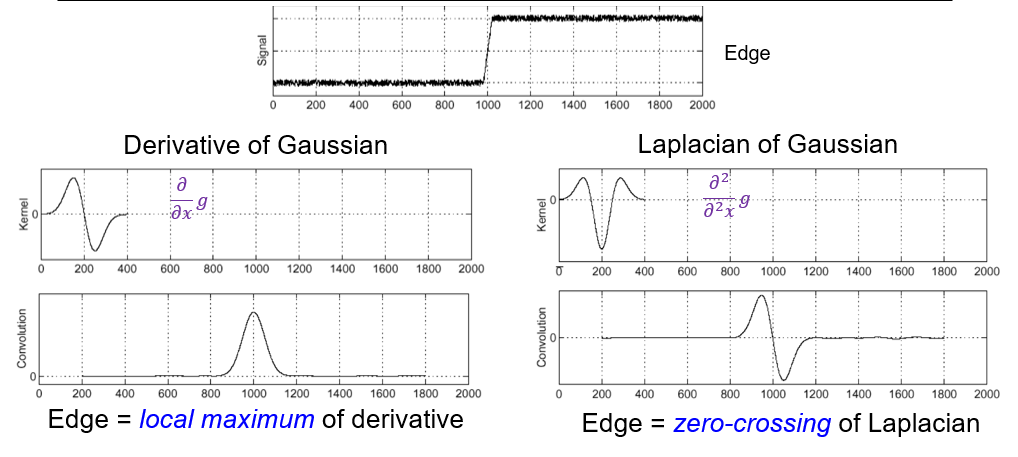
Take the absolute value of the first derivative of the image intensity function.
For 2d functions, $\frac{\partial f}{\partial x}=\lim_{\Delta x\to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}$
For discrete images data, $\frac{\partial f}{\partial x}\approx \frac{f(x+1)-f(x)}{1}$
Run convolution with kernel $[1,0,-1]$ to get the first derivative in the x direction, without shifting. (generic kernel is $[1,-1]$)
Prewitt operator:
$$
M_x=\begin{bmatrix}
1 & 0 & -1 \\
1 & 0 & -1 \\
1 & 0 & -1 \\
\end{bmatrix}
\quad
M_y=\begin{bmatrix}
1 & 1 & 1 \\
0 & 0 & 0 \\
-1 & -1 & -1 \\
\end{bmatrix}
$$
Sobel operator:
$$
M_x=\begin{bmatrix}
1 & 0 & -1 \\
2 & 0 & -2 \\
1 & 0 & -1 \\
\end{bmatrix}
\quad
M_y=\begin{bmatrix}
1 & 2 & 1 \\
0 & 0 & 0 \\
-1 & -2 & -1 \\
\end{bmatrix}
$$
Roberts operator:
$$
M_x=\begin{bmatrix}
1 & 0 \\
0 & -1 \\
\end{bmatrix}
\quad
M_y=\begin{bmatrix}
0 & 1 \\
-1 & 0 \\
\end{bmatrix}
$$
Image gradient:
$$
\nabla f = \left(\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}\right)
$$
Gradient magnitude:
$$
||\nabla f|| = \sqrt{\left(\frac{\partial f}{\partial x}\right)^2 + \left(\frac{\partial f}{\partial y}\right)^2}
$$
Gradient direction:
$$
\theta = \tan^{-1}\left(\frac{\frac{\partial f}{\partial y}}{\frac{\partial f}{\partial x}}\right)
$$
The gradient points in the direction of the most rapid increase in intensity.
> Application: Gradient-domain image editing
>
> Goal: solve for pixel values in the target region to match gradients of the source region while keeping the rest of the image unchanged.
>
> [Poisson Image Editing](http://www.cs.virginia.edu/~connelly/class/2014/comp_photo/proj2/poisson.pdf)
Noisy edge detection:
When the intensity function is very noisy, we can use a Gaussian smoothing filter to reduce the noise before taking the gradient.
Suppose pixels of the true image $f_{i,j}$ are corrupted by Gaussian noise $n_{i,j}$ with mean 0 and variance $\sigma^2$.
Then the noisy image is $g_{i,j}=(f_{i,j}+n_{i,j})-(f_{i,j+1}+n_{i,j+1})\approx N(0,2\sigma^2)$
To find edges, look for peaks in $\frac{d}{dx}(f\circ g)$ where $g$ is the Gaussian smoothing filter.
or we can directly use the Derivative of Gaussian (DoG) filter:
$$
\frac{d}{dx}g(x,\sigma)=\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{x^2}{2\sigma^2}}
$$
##### Separability of Gaussian filter
A Gaussian filter is separable if it can be written as a product of two 1D filters.
$$
\frac{d}{dx}g(x,\sigma)=\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{x^2}{2\sigma^2}}
\quad \frac{d}{dy}g(y,\sigma)=\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{y^2}{2\sigma^2}}
$$
##### Separable Derivative of Gaussian (DoG) filter
$$
\frac{d}{dx}g(x,y)\propto -x\exp\left(-\frac{x^2+y^2}{2\sigma^2}\right)
\quad \frac{d}{dy}g(x,y)\propto -y\exp\left(-\frac{x^2+y^2}{2\sigma^2}\right)
$$
##### Derivative of Gaussian: Scale
Using Gaussian derivatives with different values of 𝜎 finds structures at different scales or frequencies
(Take the hybrid image as an example)
##### Canny edge detector
1. Smooth the image with a Gaussian filter
2. Compute the gradient magnitude and direction of the smoothed image
3. Thresholding gradient magnitude
4. Non-maxima suppression
- For each location `q` above the threshold, check that the gradient magnitude is higher than at adjacent points `p` and `r` in the direction of the gradient
5. Thresholding the non-maxima suppressed gradient magnitude
6. Hysteresis thresholding
- Use two thresholds: high and low
- Start with a seed edge pixel with a gradient magnitude greater than the high threshold
- Follow the gradient direction to find all connected pixels with a gradient magnitude greater than the low threshold
##### Top-down segmentation
Data-driven top-down segmentation:
#### Interest point
Key point matching:
1. Find a set of distinctive keypoints in the image
2. Define a region of interest around each keypoint
3. Compute a local descriptor from the normalized region
4. Match local descriptors between images
Characteristic of good features:
- Repeatability
- The same feature can be found in several images despite geometric and photometric transformations
- Saliency
- Each feature is distinctive
- Compactness and efficiency
- Many fewer features than image pixels
- Locality
- A feature occupies a relatively small area of the image; robust to clutter and occlusion
##### Harris corner detector
### Applications of local features
#### Image alignment
#### 3D reconstruction
#### Motion tracking
#### Robot navigation
#### Indexing and database retrieval
#### Object recognition

68
content/CSE559A/CSE559A_L18.md
View File

@@ -1,68 +0,0 @@
# CSE559A Lecture 18
## Continue on Harris Corner Detector
Goal: Descriptor distinctiveness
- We want to be able to reliably determine which point goes with which.
- Must provide some invariance to geometric and photometric differences.
Harris corner detector:
> Other existing variants:
> - Hessian & Harris: [Beaudet '78], [Harris '88]
> - Laplacian, DoG: [Lindeberg '98], [Lowe 1999]
> - Harris-/Hessian-Laplace: [Mikolajczyk & Schmid '01]
> - Harris-/Hessian-Affine: [Mikolajczyk & Schmid '04]
> - EBR and IBR: [Tuytelaars & Van Gool '04]
> - MSER: [Matas '02]
> - Salient Regions: [Kadir & Brady '01]
> - Others…
### Deriving a corner detection criterion
- Basic idea: we should easily recognize the point by looking through a small window
- Shifting a window in any direction should give a large change in intensity
Corner is the point where the intensity changes in all directions.
Criterion:
Change in appearance of window $W$ for the shift $(u,v)$:
$$
E(u,v) = \sum_{x,y\in W} [I(x+u,y+v) - I(x,y)]^2
$$
First-order Taylor approximation for small shifts $(u,v)$:
$$
I(x+u,y+v) \approx I(x,y) + I_x u + I_y v
$$
plug into $E(u,v)$:
$$
\begin{aligned}
E(u,v) &= \sum_{(x,y)\in W} [I(x+u,y+v) - I(x,y)]^2 \\
&\approx \sum_{(x,y)\in W} [I(x,y) + I_x u + I_y v - I(x,y)]^2 \\
&= \sum_{(x,y)\in W} [I_x u + I_y v]^2 \\
&= \sum_{(x,y)\in W} [I_x^2 u^2 + 2 I_x I_y u v + I_y^2 v^2]
\end{aligned}
$$
Consider the second moment matrix:
$$
M = \begin{bmatrix}
I_x^2 & I_x I_y \\
I_x I_y & I_y^2
\end{bmatrix}=\begin{bmatrix}
a & 0 \\
0 & b
\end{bmatrix}
$$
If either $a$ or $b$ is small, then the window is not a corner.

71
content/CSE559A/CSE559A_L19.md
View File

@@ -1,71 +0,0 @@
# CSE559A Lecture 19
## Feature Detection
### Behavior of corner features with respect to Image Transformations
To be useful for image matching, “the same” corner features need to show up despite geometric and photometric transformations
We need to analyze how the corner response function and the corner locations change in response to various transformations
#### Affine intensity change
Solution:
- Only derivative of intensity are used (invariant to intensity change)
- Intensity scaling
#### Image translation
Solution:
- Derivatives and window function are shift invariant
#### Image rotation
Second moment ellipse rotates but its shape (i.e. eigenvalues) remains the same
#### Scaling
Classify edges instead of corners
## Automatic Scale selection for interest point detection
### Scale space
We want to extract keypoints with characteristic scales that are equivariant (or covariant) with respect to scaling of the image
Approach: compute a scale-invariant response function over neighborhoods centered at each location $(x,y)$ and a range of scales $\sigma$, find scale-space locations $(x,y,\sigma)$ where this function reaches a local maximum
A particularly convenient response function is given by the scale-normalized Laplacian of Gaussian (LoG) filter:
$$
\nabla^2_{norm}=\sigma^2\nabla^2\left(\frac{\partial^2}{\partial x^2}g+\frac{\partial^2}{\partial y^2}g\right)
$$
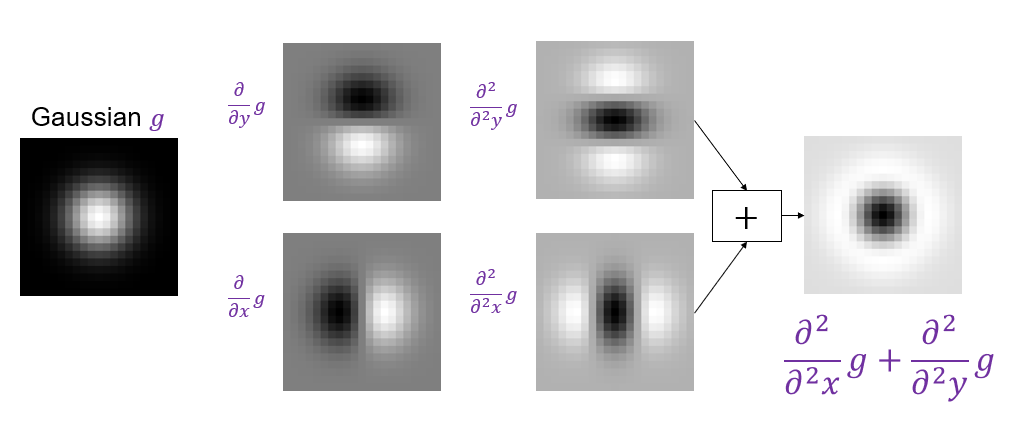
![Visualization of LoG](https://notenextra.trance-0.com/CSE559A/Laplacian_of_Gaussian.png)
#### Edge detection with LoG
![Edge detection with LoG](https://notenextra.trance-0.com/CSE559A/Edge_detection_with_LoG.png)
#### Blob detection with LoG
![Blob detection with LoG](https://notenextra.trance-0.com/CSE559A/Blob_detection_with_LoG.png)
### Difference of Gaussians (DoG)
DoG has a little more flexibility, since you can select the scales of the Gaussians.
### Scale-invariant feature transform (SIFT)
The main goal of SIFT is to enable image matching in the presence of significant transformations
- To recognize the same keypoint in multiple images, we need to match appearance descriptors or "signatures" in their neighborhoods
- Descriptors that are locally invariant w.r.t. scale and rotation can handle a wide range of global transformations
### Maximum stable extremal regions (MSER)
Based on Watershed segmentation algorithm
Select regions that are stable over a large parameter range

165
content/CSE559A/CSE559A_L2.md
View File

@@ -1,165 +0,0 @@
# CSE559A Lecture 2
## The Geometry of Image Formation
Mapping between image and world coordinates.
Today's focus:
$$
x=K[R\ t]X
$$
### Pinhole Camera Model
Add a barrier to block off most of the rays.
- Reduce blurring
- The opening known as the **aperture**
$f$ is the focal length.
$c$ is the center of the aperture.
#### Focal length/ Field of View (FOV)/ Zoom
- Focal length: distance between the aperture and the image plane.
- Field of View (FOV): the angle between the two rays that pass through the aperture and the image plane.
- Zoom: the ratio of the focal length to the image plane.
#### Other types of projection
Beyond the pinhole/perspective camera model, there are other types of projection.
- Radial distortion
- 360-degree camera
- Equirectangular Panoramas
- Random lens
- Rotating sensors
- Photofinishing
- Tiltshift lens
### Perspective Geometry
Length and area are not preserved.
Angle is not preserved.
But straight lines are still straight.
Parallel lines in the world intersect at a **vanishing point** on the image plane.
Vanishing lines: the set of all vanishing points of parallel lines in the world on the same plane in the world.
Vertical vanishing point at infinity.
### Camera/Projection Matrix
Linear projection model.
$$
x=K[R\ t]X
$$
- $x$: image coordinates 2d (homogeneous coordinates)
- $X$: world coordinates 3d (homogeneous coordinates)
- $K$: camera matrix (3x3 and invertible)
- $R$: camera rotation matrix (3x3)
- $t$: camera translation vector (3x1)
#### Homogeneous coordinates
- 2D: $$(x, y)\to\begin{bmatrix}x\\y\\1\end{bmatrix}$$
- 3D: $$(x, y, z)\to\begin{bmatrix}x\\y\\z\\1\end{bmatrix}$$
converting from homogeneous to inhomogeneous coordinates:
- 2D: $$\begin{bmatrix}x\\y\\w\end{bmatrix}\to(x/w, y/w)$$
- 3D: $$\begin{bmatrix}x\\y\\z\\w\end{bmatrix}\to(x/w, y/w, z/w)$$
When $w=0$, the point is at infinity.
Homogeneous coordinates are invariant under scaling (non-zero scalar).
$$
k\begin{bmatrix}x\\y\\w\end{bmatrix}=\begin{bmatrix}kx\\ky\\kw\end{bmatrix}\implies\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}x/k\\y/k\end{bmatrix}
$$
A convenient way to represent a point at infinity is to use a unit vector.
Line equation: $ax+by+c=0$
$$
line_i=\begin{bmatrix}a_i\\b_i\\c_i\end{bmatrix}
$$
Append a 1 to pixel coordinates to get homogeneous coordinates.
$$
pixel_i=\begin{bmatrix}u_i\\v_i\\1\end{bmatrix}
$$
Line given by cross product of two points:
$$
line_i=pixel_1\times pixel_2
$$
Intersection of two lines given by cross product of the lines:
$$
pixel_i=line_1\times line_2
$$
#### Pinhole Camera Projection Matrix
Intrinsic Assumptions:
- Unit aspect ratio
- No skew
- Optical center at (0,0)
Extrinsic Assumptions:
- No rotation
- No translation (camera at world origin)
$$
x=K[I\ 0]X\implies w\begin{bmatrix}u\\v\\1\end{bmatrix}=\begin{bmatrix}f&0&0&0\\0&f&0&0\\0&0&1&0\end{bmatrix}\begin{bmatrix}x\\y\\z\\1\end{bmatrix}
$$
Removing the assumptions:
Intrinsic assumptions:
- Unit aspect ratio
- No skew
Extrinsic assumptions:
- No rotation
- No translation
$$
x=K[I\ 0]X\implies w\begin{bmatrix}u\\v\\1\end{bmatrix}=\begin{bmatrix}\alpha&0&u_0&0\\0&\beta&v_0&0\\0&0&1&0\end{bmatrix}\begin{bmatrix}x\\y\\z\\1\end{bmatrix}
$$
Adding skew:
$$
x=K[I\ 0]X\implies w\begin{bmatrix}u\\v\\1\end{bmatrix}=\begin{bmatrix}\alpha&s&u_0&0\\0&\beta&v_0&0\\0&0&1&0\end{bmatrix}\begin{bmatrix}x\\y\\z\\1\end{bmatrix}
$$
Finally, adding camera rotation and translation:
$$
x=K[I\ t]X\implies w\begin{bmatrix}u\\v\\1\end{bmatrix}=\begin{bmatrix}\alpha&s&u_0\\0&\beta&v_0\\0&0&1\end{bmatrix}\begin{bmatrix}r_{11}&r_{12}&r_{13}&t_x\\r_{21}&r_{22}&r_{23}&t_y\\r_{31}&r_{32}&r_{33}&t_z\end{bmatrix}\begin{bmatrix}x\\y\\z\\1\end{bmatrix}
$$
What is the degrees of freedom of the camera matrix?
- rotation: 3
- translation: 3
- camera matrix: 5
Total: 11

145
content/CSE559A/CSE559A_L20.md
View File

@@ -1,145 +0,0 @@
# CSE559A Lecture 20
## Local feature descriptors
Detection: Identify the interest points
Description: Extract vector feature descriptor surrounding each interest point.
Matching: Determine correspondence between descriptors in two views
### Image representation
Histogram of oriented gradients (HOG)
- Quantization
- Grids: fast but applicable only with few dimensions
- Clustering: slower but can quantize data in higher dimensions
- Matching
- Histogram intersection or Euclidean may be faster
- Chi-squared often works better
- Earth mover’s distance is good for when nearby bins represent similar values
#### SIFT vector formation
Computed on rotated and scaled version of window according to computed orientation & scale
- resample the window
Based on gradients weighted by a Gaussian of variance half the window (for smooth falloff)
4x4 array of gradient orientation histogram weighted by magnitude
8 orientations x 4x4 array = 128 dimensions
Motivation: some sensitivity to spatial layout, but not too much.
For matching:
- Extraordinarily robust detection and description technique
- Can handle changes in viewpoint
- Up to about 60 degree out-of-plane rotation
- Can handle significant changes in illumination
- Sometimes even day vs. night
- Fast and efficient—can run in real time
- Lots of code available
#### SURF
- Fast approximation of SIFT idea
- Efficient computation by 2D box filters & integral images
- 6 times faster than SIFT
- Equivalent quality for object identification
#### Shape context
![Shape context descriptor](https://notenextra.trance-0.com/CSE559A/Shape_context_descriptor.png)
#### Self-similarity Descriptor
![Self-similarity descriptor](https://notenextra.trance-0.com/CSE559A/Self-similarity_descriptor.png)
## Local feature matching
### Matching
Simplest approach: Pick the nearest neighbor. Threshold on absolute distance
Problem: Lots of self similarity in many photos
Solution: Nearest neighbor with low ratio test
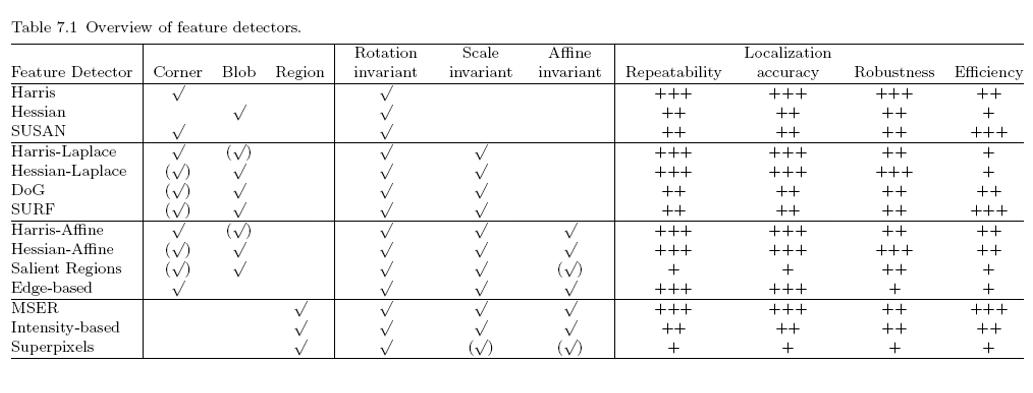
![Comparison of keypoint detectors](https://notenextra.trance-0.com/CSE559A/Comparison_of_keypoint_detectors.png)
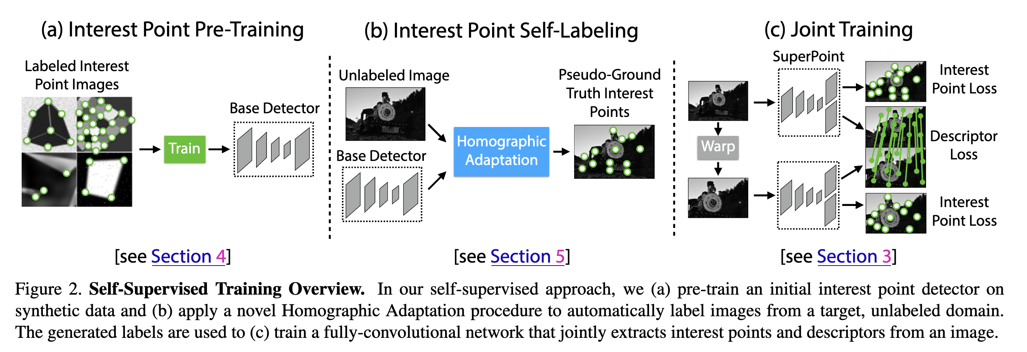
## Deep Learning for Correspondence Estimation
![Deep learning for correspondence estimation](https://notenextra.trance-0.com/CSE559A/Deep_learning_for_correspondence_estimation.png)
## Optical Flow
### Field
Motion field: the projection of the 3D scene motion into the image
Magnitude of vectors is determined by metric motion
Only caused by motion
Optical flow: the apparent motion of brightness patterns in the image
Magnitude of vectors is measured in pixels
Can be caused by lightning
### Brightness constancy constraint, aperture problem
Machine Learning Approach
- Collect examples of inputs and outputs
- Design a prediction model suitable for the task
- Invariances, Equivariances; Complexity; Input and Output shapes and semantics
- Specify loss functions and train model
- Limitations: Requires training the model; Requires a sufficiently complete training dataset; Must re-learn known facts; Higher computational complexity
Optimization Approach
- Define properties we expect to hold for a correct solution
- Translate properties into a cost function
- Derive an algorithm to solve for the cost function
- Limitations: Often requires making overly simple assumptions on properties; Some tasks can’t be easily defined
Given frames at times $t-1$ and $t$, estimate the apparent motion field $u(x,y)$ and $v(x,y)$ between them
Brightness constancy constraint: projection of the same point looks the same in every frame
$$
I(x,y,t-1) = I(x+u(x,y),y+v(x,y),t)
$$
Additional assumptions:
- Small motion: points do not move very far
- Spatial coherence: points move like their neighbors
Trick for solving:
Brightness constancy constraint:
$$
I(x,y,t-1) = I(x+u(x,y),y+v(x,y),t)
$$
Linearize the right-hand side using Taylor expansion:
$$
I(x,y,t-1) \approx I(x,y,t) + I_x u(x,y) + I_y v(x,y)
$$
$$
I_x u(x,y) + I_y v(x,y) + I(x,y,t) - I(x,y,t-1) = 0
$$
Hence,
$$
I_x u(x,y) + I_y v(x,y) + I_t = 0
$$

215
content/CSE559A/CSE559A_L21.md
View File

@@ -1,215 +0,0 @@
# CSE559A Lecture 21
## Continue on optical flow
### The brightness constancy constraint
$$
I_x u(x,y) + I_y v(x,y) + I_t = 0
$$
Given the gradients $I_x, I_y$ and $I_t$, can we uniquely recover the motion $(u,v)$?
- Suppose $(u, v)$ satisfies the constraint: $\nabla I \cdot (u,v) + I_t = 0$
- Then $\nabla I \cdot (u+u', v+v') + I_t = 0$ for any $(u', v')$ s.t. $\nabla I \cdot (u', v') = 0$
- Interpretation: the component of the flow perpendicular to the gradient (i.e., parallel to the edge) cannot be recovered!
#### Aperture problem
- The brightness constancy constraint is only valid for a small patch in the image
- For a large motion, the patch may look very different
Consider the barber pole illusion
### Estimating optical flow (Lucas-Kanade method)
- Consider a small patch in the image
- Assume the motion is constant within the patch
- Then we can solve for the motion $(u, v)$ by minimizing the error:
$$
I_x u(x,y) + I_y v(x,y) + I_t = 0
$$
How to get more equations for a pixel?
Spatial coherence constraint: assume the pixel’s neighbors have the same (𝑢,𝑣)
If we have 𝑛 pixels in the neighborhood, then we can set up a linear least squares system:
$$
\begin{bmatrix}
I_x(x_1, y_1) & I_y(x_1, y_1) \\
\vdots & \vdots \\
I_x(x_n, y_n) & I_y(x_n, y_n)
\end{bmatrix}
\begin{bmatrix}
u \\ v
\end{bmatrix} = -\begin{bmatrix}
I_t(x_1, y_1) \\ \vdots \\ I_t(x_n, y_n)
\end{bmatrix}
$$
#### Lucas-Kanade flow
Let $A=
\begin{bmatrix}
I_x(x_1, y_1) & I_y(x_1, y_1) \\
\vdots & \vdots \\
I_x(x_n, y_n) & I_y(x_n, y_n)
\end{bmatrix}$
$b = \begin{bmatrix}
I_t(x_1, y_1) \\ \vdots \\ I_t(x_n, y_n)
\end{bmatrix}$
$d = \begin{bmatrix}
u \\ v
\end{bmatrix}$
The solution is $d=(A^T A)^{-1} A^T b$
Lucas-Kanade flow:
- Find $(u,v)$ minimizing $\sum_{i} (I(x_i+u,y_i+v,t)-I(x_i,y_i,t-1))^2$
- use Taylor approximation of $I(x_i+u,y_i+v,t)$ for small shifts $(u,v)$ to obtain closed-form solution
### Refinement for Lucas-Kanade
In some cases, the Lucas-Kanade method may not work well:
- The motion is large (larger than a pixel)
- A point does not move like its neighbors
- Brightness constancy does not hold
#### Iterative refinement (for large motion)
Iterative Lukas-Kanade Algorithm
1. Estimate velocity at each pixel by solving Lucas-Kanade equations
2. Warp It towards It+1 using the estimated flow field
- use image warping techniques
3. Repeat until convergence
Iterative refinement is limited due to Aliasing
#### Coarse-to-fine refinement (for large motion)
- Estimate flow at a coarse level
- Refine the flow at a finer level
- Use the refined flow to warp the image
- Repeat until convergence
![Lucas Kanade coarse-to-fine refinement](https://notenextra.trance-0.com/CSE559A/Lucas_Kanade_coarse-to-fine_refinement.png)
#### Representing moving images with layers (for a point may not move like its neighbors)
- The image can be decomposed into a moving layer and a stationary layer
- The moving layer is the layer that moves
- The stationary layer is the layer that does not move
![Lucas Kanade refinement with layers](https://notenextra.trance-0.com/CSE559A/Lucas_Kanade_refinement_with_layers.png)
### SOTA models
#### 2009
Start with something similar to Lucas-Kanade
- gradient constancy
- energy minimization with smoothing term
- region matching
- keypoint matching (long-range)
#### 2015
Deep neural networks
- Use a deep neural network to represent the flow field
- Use synthetic data to train the network (floating chairs)
#### 2023
GMFlow
use Transformer to model the flow field
## Robust Fitting of parametric models
Challenges:
- Noise in the measured feature locations
- Extraneous data: clutter (outliers), multiple lines
- Missing data: occlusions
### Least squares fitting
Normal least squares fitting
$y=mx+b$ is not a good model for the data since there might be vertical lines
Instead we use total least squares
Line parametrization: $ax+by=d$
$(a,b)$ is the unit normal to the line (i.e., $a^2+b^2=1$)
$d$ is the distance between the line and the origin
Perpendicular distance between point $(x_i, y_i)$ and line $ax+by=d$ (assuming $a^2+b^2=1$):
$$
|ax_i + by_i - d|
$$
Objective function:
$$
E = \sum_{i=1}^n (ax_i + by_i - d)^2
$$
Solve for $d$ first: $d =a\bar{x}+b\bar{y}$
Plugging back in:
$$
E = \sum_{i=1}^n (a(x_i-\bar{x})+b(y_i-\bar{y}))^2 = \left\|\begin{bmatrix}x_1-\bar{x}&y_1-\bar{y}\\\vdots&\vdots\\x_n-\bar{x}&y_n-\bar{y}\end{bmatrix}\begin{pmatrix}a\\b\end{pmatrix}\right\|^2
$$
We want to find $N$ that minimizes $\|UN\|^2$ subject to $\|N\|^2= 1$
Solution is given by the eigenvector of $U^T U$ associated with the smallest eigenvalue
Drawbacks:
- Sensitive to outliers
### Robust fitting
General approach: find model parameters 𝜃 that minimize
$$
\sum_{i} \rho_{\sigma}(r(x_i;\theta))
$$
$r(x_i;\theta)$: residual of $x_i$ w.r.t. model parameters $\theta$
$\rho_{\sigma}$: robust function with scale parameter $\sigma$, e.g., $\rho_{\sigma}(u)=\frac{u^2}{\sigma^2+u^2}$
Nonlinear optimization problem that must be solved iteratively
- Least squares solution can be used for initialization
- Scale of robust function should be chosen carefully
Drawbacks:
- Need to manually choose the robust function and scale parameter
### RANSAC
Voting schemes
Random sample consensus: very general framework for model fitting in the presence of outliers
Outline:
- Randomly choose a small initial subset of points
- Fit a model to that subset
- Find all inlier points that are "close" to the model and reject the rest as outliers
- Do this many times and choose the model with the most inliers
### Hough transform

260
content/CSE559A/CSE559A_L22.md
View File

@@ -1,260 +0,0 @@
# CSE559A Lecture 22
## Continue on Robust Fitting of parametric models
### RANSAC
#### Definition: RANdom SAmple Consensus
RANSAC is a method to fit a model to a set of data points.
It is a non-deterministic algorithm that can be used to fit a model to a set of data points.
Pros:
- Simple and general
- Applicable to many different problems
- Often works well in practice
Cons:
- Lots of parameters to set
- Number of iterations grows exponentially as outlier ratio increases
- Can't always get a good initialization of the model based on the minimum number of samples.
### Hough Transform
Use point-line duality to find lines.
In practice, we don't use (m,b) parameterization.
Instead, we use polar parameterization:
$$
\rho = x \cos \theta + y \sin \theta
$$
Algorithm outline:
- Initialize accumulator $H$ to all zeros
- For each feature point $(x,y)$
- For $\theta = 0$ to $180$
- $\rho = x \cos \theta + y \sin \theta$
- $H(\theta, \rho) += 1$
- Find the value(s) of $(\theta, \rho)$ where $H(\theta, \rho)$ is a local maximum (perform NMS on the accumulator array)
- The detected line in the image is given by $\rho = x \cos \theta + y \sin \theta$
#### Effect of noise
![Hough transform with noise](https://notenextra.trance-0.com/CSE559A/Hough_transform_noise.png)
Noise makes the peak fuzzy.
#### Effect of outliers
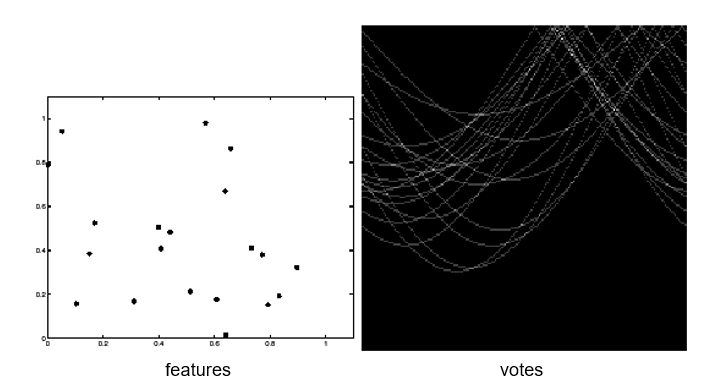
![Hough transform with outliers](https://notenextra.trance-0.com/CSE559A/Hough_transform_outliers.png)
Outliers can break the peak.
#### Pros and Cons
Pros:
- Can deal with non-locality and occlusion
- Can detect multiple instances of a model
- Some robustness to noise: noise points unlikely to contribute consistently to any single bin
- Leads to a surprisingly general strategy for shape localization (more on this next)
Cons:
- Complexity increases exponentially with the number of model parameters
- In practice, not used beyond three or four dimensions
- Non-target shapes can produce spurious peaks in parameter space
- It's hard to pick a good grid size
### Generalize Hough Transform
Template representation: for each type of landmark point, store all possible displacement vectors towards the center
Detecting the template:
For each feature in a new image, look up that feature type in the model and vote for the possible center locations associated with that type in the model
#### Implicit shape models
Training:
- Build codebook of patches around extracted interest points using clustering
- Map the patch around each interest point to closest codebook entry
- For each codebook entry, store all positions it was found, relative to object center
Testing:
- Given test image, extract patches, match to codebook entry
- Cast votes for possible positions of object center
- Search for maxima in voting space
- Extract weighted segmentation mask based on stored masks for the codebook occurrences
## Image alignment
### Affine transformation
Simple fitting procedure: linear least squares
Approximates viewpoint changes for roughly planar objects and roughly orthographic cameras
Can be used to initialize fitting for more complex models
Fitting an affine transformation:
$$
\begin{bmatrix}
&&&\cdots\\
x_i & y_i & 0&0&1&0\\
0&0&x_i&y_i&0&1\\
&&&\cdots\\
\end{bmatrix}
\begin{bmatrix}
m_1\\
m_2\\
m_3\\
m_4\\
t_1\\
t_2\\
\end{bmatrix}
=
\begin{bmatrix}
\cdots\\
\end{bmatrix}
$$
Only need 3 points to solve for 6 parameters.
### Homography
Recall that
$$
x' = \frac{a x + b y + c}{g x + h y + i}, \quad y' = \frac{d x + e y + f}{g x + h y + i}
$$
Use 2D homogeneous coordinates:
$(x,y) \rightarrow \begin{pmatrix}x \\ y \\ 1\end{pmatrix}$
$\begin{pmatrix}x\\y\\w\end{pmatrix} \rightarrow (x/w,y/w)$
Reminder: all homogeneous coordinate vectors that are (non-zero) scalar multiples of each other represent the same point
Equation for homography in homogeneous coordinates:
$$
\begin{pmatrix}
x' \\
y' \\
1
\end{pmatrix}
\cong
\begin{pmatrix}
h_{11} & h_{12} & h_{13} \\
h_{21} & h_{22} & h_{23} \\
h_{31} & h_{32} & h_{33}
\end{pmatrix}
\begin{pmatrix}
x \\
y \\
1
\end{pmatrix}
$$
Constraint from a match $(x_i,x_i')$, $x_i'\cong Hx_i$
How can we get rid of the scale ambiguity?
Cross product trick:$x_i' × Hx_i=0$
The cross product is defined as:
$$
\begin{pmatrix}a\\b\\c\end{pmatrix} \times \begin{pmatrix}a'\\b'\\c'\end{pmatrix} = \begin{pmatrix}bc'-b'c\\ca'-c'a\\ab'-a'b\end{pmatrix}
$$
Let $h_1^T, h_2^T, h_3^T$ be the rows of $H$. Then
$$
x_i' × Hx_i=\begin{pmatrix}
x_i' \\
y_i' \\
1
\end{pmatrix} \times \begin{pmatrix}
h_1^T x_i \\
h_2^T x_i \\
h_3^T x_i
\end{pmatrix}
=
\begin{pmatrix}
y_i' h_3^T x_i−h_2^T x_i \\
h_1^T x_i−x_i' h_3^T x_i \\
x_i' h_2^T x_i−y_i' h_1^T x_i
\end{pmatrix}
$$
Constraint from a match $(x_i,x_i')$:
$$
x_i' × Hx_i=\begin{pmatrix}
x_i' \\
y_i' \\
1
\end{pmatrix} \times \begin{pmatrix}
h_1^T x_i \\
h_2^T x_i \\
h_3^T x_i
\end{pmatrix}
=
\begin{pmatrix}
y_i' h_3^T x_i−h_2^T x_i \\
h_1^T x_i−x_i' h_3^T x_i \\
x_i' h_2^T x_i−y_i' h_1^T x_i
\end{pmatrix}
$$
Rearranging the terms:
$$
\begin{bmatrix}
0^T &-x_i^T &y_i' x_i^T \\
x_i^T &0^T &-x_i' x_i^T \\
y_i' x_i^T &x_i' x_i^T &0^T
\end{bmatrix}
\begin{bmatrix}
h_1 \\
h_2 \\
h_3
\end{bmatrix} = 0
$$
These equations aren't independent! So, we only need two.
### Robust alignment
#### Descriptor-based feature matching
Extract features
Compute putative matches
Loop:
- Hypothesize transformation $T$
- Verify transformation (search for other matches consistent with $T$)
#### RANSAC
Even after filtering out ambiguous matches, the set of putative matches still contains a very high percentage of outliers
RANSAC loop:
- Randomly select a seed group of matches
- Compute transformation from seed group
- Find inliers to this transformation
- If the number of inliers is sufficiently large, re-compute least-squares estimate of transformation on all of the inliers
At the end, keep the transformation with the largest number of inliers

15
content/CSE559A/CSE559A_L23.md
View File

@@ -1,15 +0,0 @@
# CSE559A Lecture 23
## DUSt3r
Dense and Unconstrained Stereo 3D Reconstruction of arbitrary image collections.
[Github DUST3R](https://github.com/naver/dust3r)

1
content/CSE559A/CSE559A_L24.md
View File

@@ -1 +0,0 @@

217
content/CSE559A/CSE559A_L25.md
View File

@@ -1,217 +0,0 @@
# CSE559A Lecture 25
## Geometry and Multiple Views
### Cues for estimating Depth
#### Multiple Views (the strongest depth cue)
Two common settings:
**Stereo vision**: a pair of cameras, usually with some constraints on the relative position of the two cameras.
**Structure from (camera) motion**: cameras observing a scene from different viewpoints
Structure and depth are inherently ambiguous from single views.
Other hints for depth:
- Occlusion
- Perspective effects
- Texture
- Object motion
- Shading
- Focus/Defocus
#### Focus on Stereo and Multiple Views
Stereo correspondence: Given a point in one of the images, where could its corresponding points be in the other images?
Structure: Given projections of the same 3D point in two or more images, compute the 3D coordinates of that point
Motion: Given a set of corresponding points in two or more images, compute the camera parameters
#### A simple example of estimating depth with stereo:
Stereo: shape from "motion" between two views
We'll need to consider:
- Info on camera pose ("calibration")
- Image point correspondences
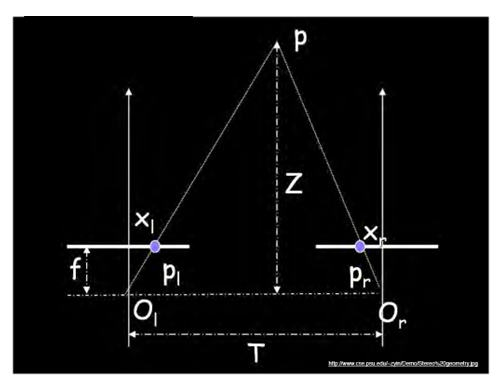
![Simple stereo system](https://notenextra.trance-0.com/CSE559A/Simple_stereo_system.png)
Assume parallel optical axes, known camera parameters (i.e., calibrated cameras). What is expression for Z?
Similar triangles $(p_l, P, p_r)$ and $(O_l, P, O_r)$:
$$
\frac{T-x_l+x_r}{Z-f}=\frac{T}{Z}
$$
$$
Z = \frac{f \cdot T}{x_l-x_r}
$$
### Camera Calibration
Use an scene with known geometry
- Correspond image points to 3d points
- Get least squares solution (or non-linear solution)
Solving unknown camera parameters:
$$
\begin{bmatrix}
su\\
sv\\
s
\end{bmatrix}
= \begin{bmatrix}
m_{11} & m_{12} & m_{13} & m_{14}\\
m_{21} & m_{22} & m_{23} & m_{24}\\
m_{31} & m_{32} & m_{33} & m_{34}
\end{bmatrix}
\begin{bmatrix}
X\\
Y\\
Z\\
1
\end{bmatrix}
$$
Method 1: Homogenous linear system. Solve for m's entries using least squares.
$$
\begin{bmatrix}
X_1 & Y_1 & Z_1 & 1 & 0 & 0 & 0 & 0 & -u_1X_1 & -u_1Y_1 & -u_1Z_1 & -u_1 \\
0 & 0 & 0 & 0 & X_1 & Y_1 & Z_1 & 1 & -v_1X_1 & -v_1Y_1 & -v_1Z_1 & -v_1 \\
\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots\\
X_n & Y_n & Z_n & 1 & 0 & 0 & 0 & 0 & -u_nX_n & -u_nY_n & -u_nZ_n & -u_n \\
0 & 0 & 0 & 0 & X_n & Y_n & Z_n & 1 & -v_nX_n & -v_nY_n & -v_nZ_n & -v_n
\end{bmatrix}
\begin{bmatrix} m_{11} \\ m_{12} \\ m_{13} \\ m_{14} \\ m_{21} \\ m_{22} \\ m_{23} \\ m_{24} \\ m_{31} \\ m_{32} \\ m_{33} \\ m_{34} \end{bmatrix} = 0
$$
Method 2: Non-homogenous linear system. Solve for m's entries using least squares.
**Advantages**
- Easy to formulate and solve
- Provides initialization for non-linear methods
**Disadvantages**
- Doesn't directly give you camera parameters
- Doesn't model radial distortion
- Can't impose constraints, such as known focal length
**Non-linear methods are preferred**
- Define error as difference between projected points and measured points
- Minimize error using Newton's method or other non-linear optimization
#### Triangulation
Given projections of a 3D point in two or more images (with known camera matrices), find the coordinates of the point
##### Approaches 1: Geometric approach
Find shortest segment connecting the two viewing rays and let $X$ be the midpoint of that segment
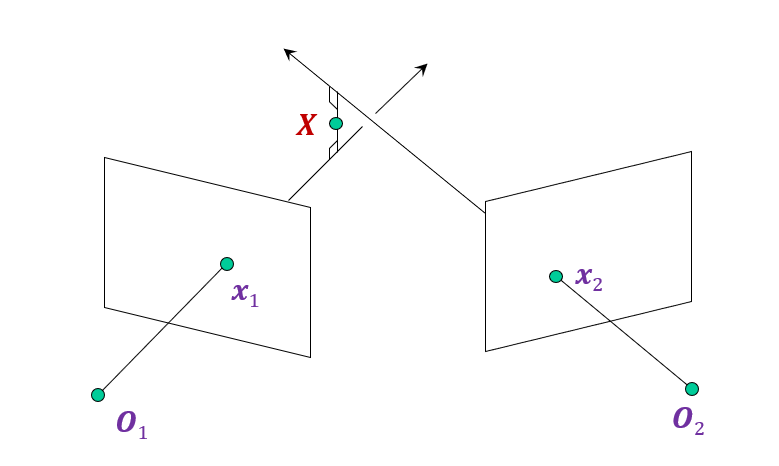
![Triangulation geometric approach](https://notenextra.trance-0.com/CSE559A/Triangulation_geometric_approach.png)
##### Approaches 2: Non-linear optimization
Minimize error between projected point and measured point
$$
||\operatorname{proj}(P_1 X) - x_1||_2^2 + ||\operatorname{proj}(P_2 X) - x_2||_2^2
$$
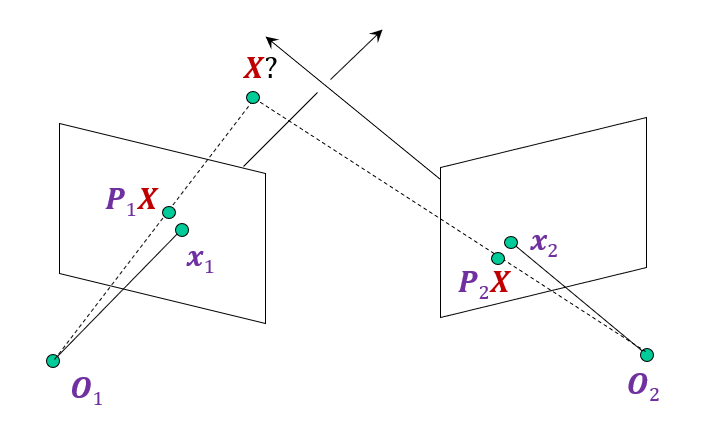
![Triangulation non-linear optimization](https://notenextra.trance-0.com/CSE559A/Triangulation_non_linear_optimization.png)
##### Approaches 3: Linear approach
$x_1\cong P_1X$ and $x_2\cong P_2X$
$x_1\times P_1X = 0$ and $x_2\times P_2X = 0$
$[x_{1_{\times}}]P_1X = 0$ and $[x_{2_{\times}}]P_2X = 0$
Rewrite as:
$$
a\times b=\begin{bmatrix}
0 & -a_3 & a_2\\
a_3 & 0 & -a_1\\
-a_2 & a_1 & 0
\end{bmatrix}
\begin{bmatrix}
b_1\\
b_2\\
b_3
\end{bmatrix}
=[a_{\times}]b
$$
Using **singular value decomposition**, we can solve for $X$
### Epipolar Geometry
What constraints must hold between two projections of the same 3D point?
Given a 2D point in one view, where can we find the corresponding point in the other view?
Given only 2D correspondences, how can we calibrate the two cameras, i.e., estimate their relative position and orientation and the intrinsic parameters?
Key ideas:
- We can answer all these questions without knowledge of the 3D scene geometry
- Important to think about projections of camera centers and visual rays into the other view
#### Epipolar Geometry Setup
![Epipolar geometry setup](https://notenextra.trance-0.com/CSE559A/Epipolar_geometry_setup.png)
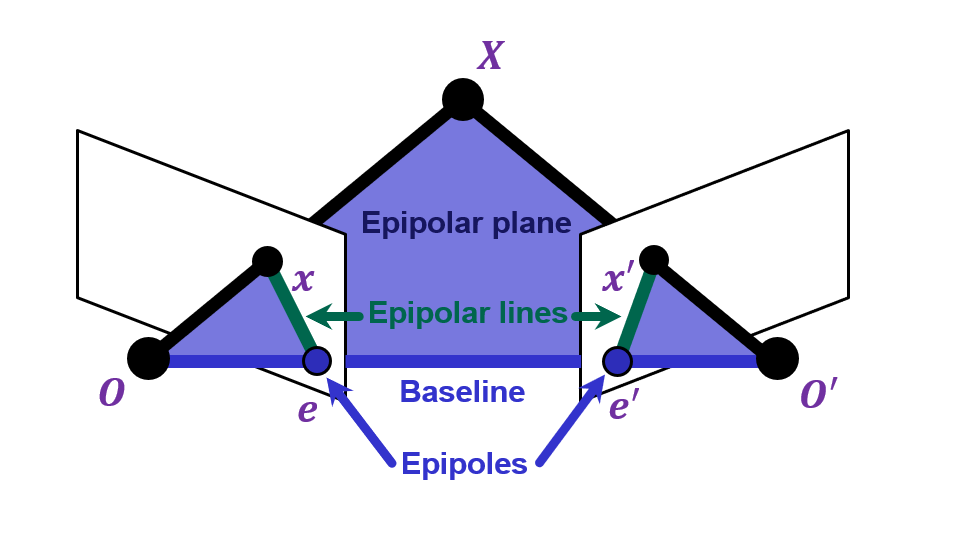
Suppose we have two cameras with centers $O,O'$
The baseline is the line connecting the origins
Epipoles $e,e'$ are where the baseline intersects the image planes, or projections of the other camera in each view
Consider a point $X$, which projects to $x$ and $x'$
The plane formed by $X,O,O'$ is called an epipolar plane
There is a family of planes passing through $O$ and $O'$
Epipolar lines are projections of the baseline into the image planes
**Epipolar lines** connect the epipoles to the projections of $X$
Equivalently, they are intersections of the epipolar plane with the image planes – thus, they come in matching pairs.
**Application**: This constraint can be used to find correspondences between points in two camera. by the epipolar line in one image, we can find the corresponding feature in the other image.
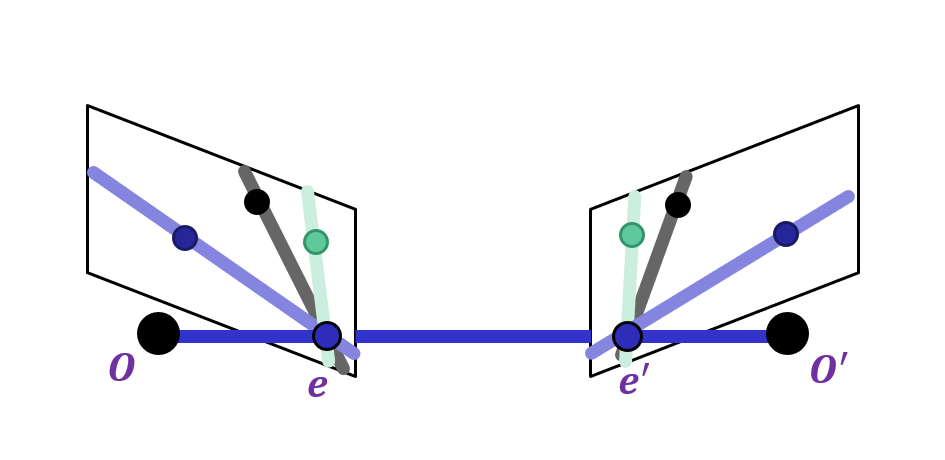
![Epipolar line for converging cameras](https://notenextra.trance-0.com/CSE559A/Epipolar_line_for_converging_cameras.png)
Epipoles are finite and may be visible in the image.
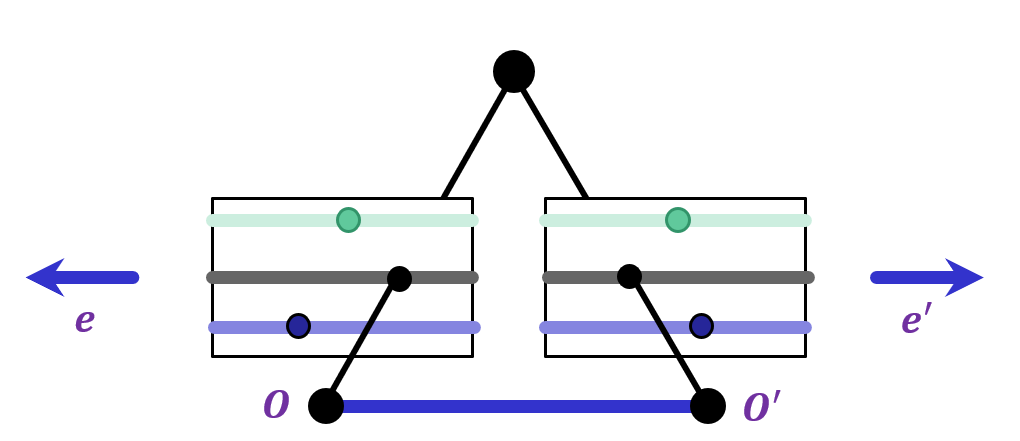
![Epipolar line for parallel cameras](https://notenextra.trance-0.com/CSE559A/Epipolar_line_for_parallel_cameras.png)
Epipoles are infinite, epipolar lines parallel.
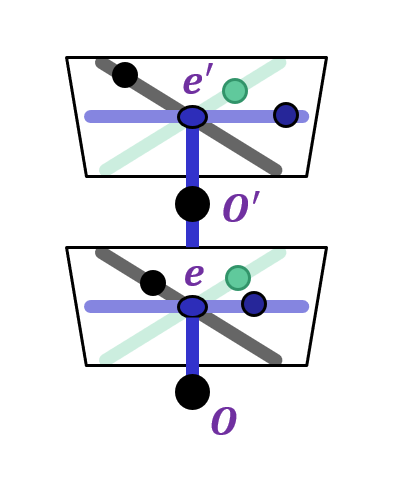
![Epipolar line for perpendicular cameras](https://notenextra.trance-0.com/CSE559A/Epipolar_line_for_perpendicular_cameras.png)
Epipole is "focus of expansion" and coincides with the principal point of the camera
Epipolar lines go out from principal point
Next class:
### The Essential and Fundamental Matrices
### Dense Stereo Matching

177
content/CSE559A/CSE559A_L26.md
View File

@@ -1,177 +0,0 @@
# CSE559A Lecture 26
## Continue on Geometry and Multiple Views
### The Essential and Fundamental Matrices
#### Math of the epipolar constraint: Calibrated case
Recall Epipolar Geometry
![Epipolar Geometry Configuration](https://notenextra.trance-0.com/CSE559A/Epipolar_geometry_setup.png)
Epipolar constraint:
If we set the config for the first camera as the world origin and $[I|0]\begin{pmatrix}y\\1\end{pmatrix}=x$, and $[R|t]\begin{pmatrix}y\\1\end{pmatrix}=x'$, then
Notice that $x'\cdot [t\times (Ry)]=0$
$$
x'^T E x_1 = 0
$$
We denote the constraint defined by the Essential Matrix as $E$.
$E x$ is the epipolar line associated with $x$ ($l'=Ex$)
$E^T x'$ is the epipolar line associated with $x'$ ($l=E^T x'$)
$E e=0$ and $E^T e'=0$ ($x$ and $x'$ don't matter)
$E$ is singular (rank 2) and have five degrees of freedom.
#### Epipolar constraint: Uncalibrated case
If the calibration matrices $K$ and $K'$ are unknown, we can write the epipolar constraint in terms of unknown normalized coordinates:
$$
x'^T_{norm} E x_{norm} = 0
$$
where $x_{norm}=K^{-1} x$, $x'_{norm}=K'^{-1} x'$
$$
x'^T_{norm} E x_{norm} = 0\implies x'^T_{norm} Fx=0
$$
where $F=K'^{-1}EK^{-1}$ is the **Fundamental Matrix**.
$$
(x',y',1)\begin{bmatrix}
f_{11} & f_{12} & f_{13} \\
f_{21} & f_{22} & f_{23} \\
f_{31} & f_{32} & f_{33}
\end{bmatrix}\begin{pmatrix}
x\\y\\1
\end{pmatrix}=0
$$
Properties of $F$:
$F x$ is the epipolar line associated with $x$ ($l'=F x$)
$F^T x'$ is the epipolar line associated with $x'$ ($l=F^T x'$)
$F e=0$ and $F^T e'=0$
$F$ is singular (rank two) and has seven degrees of freedom
#### Estimating the fundamental matrix
Given: correspondences $x=(x,y,1)^T$ and $x'=(x',y',1)^T$
Constraint: $x'^T F x=0$
$$
(x',y',1)\begin{bmatrix}
f_{11} & f_{12} & f_{13} \\
f_{21} & f_{22} & f_{23} \\
f_{31} & f_{32} & f_{33}
\end{bmatrix}\begin{pmatrix}
x\\y\\1
\end{pmatrix}=0
$$
**Each pair of correspondences gives one equation (one constraint)**
At least 8 pairs of correspondences are needed to solve for the 9 elements of $F$ (The eight point algorithm)
We know $F$ needs to be singular/rank 2. How do we force it to be singular?
Solution: take SVD of the initial estimate and throw out the smallest singular value
$$
F=U\begin{bmatrix}
\sigma_1 & 0 \\
0 & \sigma_2 \\
0 & 0
\end{bmatrix}V^T
$$
## Structure from Motion
Not always uniquely solvable.
If we scale the entire scene by some factor $k$ and, at the same time, scale the camera matrices by the factor of $1/k$, the projections of the scene points remain exactly the same:
$x\cong PX =(1/k P)(kX)$
Without a reference measurement, it is impossible to recover the absolute scale of the scene!
In general, if we transform the scene using a transformation $Q$ and apply the inverse transformation to the camera matrices, then the image observations do not change:
$x\cong PX =(P Q^{-1})(QX)$
### Types of Ambiguities
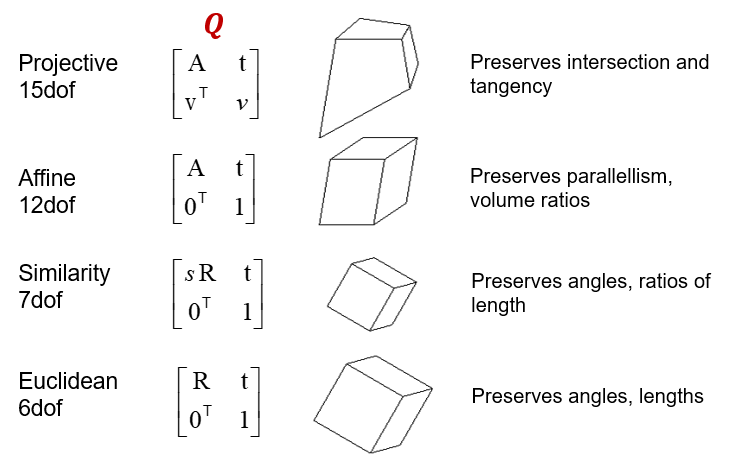
![Ambiguities in projection](https://notenextra.trance-0.com/CSE559A/Ambiguities_in_projection.png)
### Affine projection : more general than orthographic
A general affine projection is a 3D-to-2D linear mapping plus translation:
$$
P=\begin{bmatrix}
a_{11} & a_{12} & a_{13} & t_1 \\
a_{21} & a_{22} & a_{23} & t_2 \\
0 & 0 & 0 & 1
\end{bmatrix}=\begin{bmatrix}
A & t \\
0^T & 1
\end{bmatrix}
$$
In non-homogeneous coordinates:
$$
\begin{pmatrix}
x\\y\\1
\end{pmatrix}=\begin{bmatrix}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23}
\end{bmatrix}\begin{pmatrix}
X\\Y\\Z
\end{pmatrix}+\begin{pmatrix}
t_1\\t_2
\end{pmatrix}=AX+t
$$
### Affine Structure from Motion
Given: 𝑚 images of 𝑛 fixed 3D points such that
$$
x_{ij}=A_iX_j+t_i, \quad i=1,\dots,m, \quad j=1,\dots,n
$$
Problem: use the 𝑚𝑛 correspondences $x_{ij}$ to estimate 𝑚 projection matrices $A_i$ and translation vectors $t_i$, and 𝑛 points $X_j$
The reconstruction is defined up to an arbitrary affine transformation $Q$ (12 degrees of freedom):
$$
\begin{bmatrix}
A & t \\
0^T & 1
\end{bmatrix}\rightarrow\begin{bmatrix}
A & t \\
0^T & 1
\end{bmatrix}Q^{-1}, \quad \begin{pmatrix}X_j\\1\end{pmatrix}\rightarrow Q\begin{pmatrix}X_j\\1\end{pmatrix}
$$
How many constraints and unknowns for $m$ images and $n$ points?
$2mn$ constraints and $8m + 3n$ unknowns
To be able to solve this problem, we must have $2mn \geq 8m+3n-12$ (affine ambiguity takes away 12 dof)
E.g., for two views, we need four point correspondences

357
content/CSE559A/CSE559A_L3.md
View File

@@ -1,357 +0,0 @@
# CSE559A Lecture 3
## Image formation
### Degrees of Freedom
$$
x=K[R|t]X
$$
$$
w\begin{bmatrix}
x\\
y\\
1
\end{bmatrix}
=
\begin{bmatrix}
\alpha & s & u_0 \\
0 & \beta & v_0 \\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
r_{11} & r_{12} & r_{13} &t_x\\
r_{21} & r_{22} & r_{23} &t_y\\
r_{31} & r_{32} & r_{33} &t_z\\
\end{bmatrix}
\begin{bmatrix}
x\\
y\\
z\\
1
\end{bmatrix}
$$
### Impact of translation of camera
$$
p=K[R|t]\begin{bmatrix}
x\\
y\\
z\\
0
\end{bmatrix}=K[R]\begin{bmatrix}
x\\
y\\
z\\
\end{bmatrix}
$$
Projection of a vanishing point or projection of a point at infinity is invariant to translation.
### Recover world coordinates from pixel coordinates
$$
\begin{bmatrix}
u\\
v\\
1
\end{bmatrix}=K[R|t]^{-1}X
$$
Key issue: where is the world origin $w$? Suppose $w=1/s$
$$
\begin{aligned}
\begin{bmatrix}
u\\
v\\
1
\end{bmatrix}
&=sK[R|t]X\\
K^{-1}\begin{bmatrix}
u\\
v\\
1
\end{bmatrix}
&=s[R|t]X\\
R^{-1}K^{-1}\begin{bmatrix}
u\\
v\\
1
\end{bmatrix}&=s[I|R^{-1}t]X\\
R^{-1}K^{-1}\begin{bmatrix}
u\\
v\\
1
\end{bmatrix}&=[I|R^{-1}t]sX\\
R^{-1}K^{-1}\begin{bmatrix}
u\\
v\\
1
\end{bmatrix}&=sX+sR^{-1}t\\
\frac{1}{s}R^{-1}K^{-1}\begin{bmatrix}
u\\
v\\
1
\end{bmatrix}-R^{-1}t&=X\\
\end{aligned}
$$
## Projective Geometry
### Orthographic Projection
Special case of perspective projection when $f\to\infty$
- Distance for the center of projection is infinite
- Also called parallel projection
- Projection matrix is
$$
w\begin{bmatrix}
u\\
v\\
1
\end{bmatrix}=
\begin{bmatrix}
f & 0 & 0 & 0\\
0 & f & 0 & 0\\
0 & 0 & 0 & s\\
\end{bmatrix}
\begin{bmatrix}
x\\
y\\
z\\
1
\end{bmatrix}
$$
Continue in later part of the course
## Image processing foundations
### Motivation for image processing
Representational Motivation:
- We need more than raw pixel values
Computational Motivation:
- Many image processing operations must be run across many locations in a image
- A loop in python is slow
- High-level libraries reduce errors, developer time, and algorithm runtime
- Two common libraries:
- Torch+Torchvision: Focus on deep learning
- scikit-image: Focus on classical image processing algorithms
### Operations on images
#### Point operations
Operations that are applied to one pixel at a time
Negative image
$$
I_{neg}(x,y)=L-1-I(x,y)
$$
Power law transformation:
$$
I_{out}(x,y)=cI(x,y)^{\gamma}
$$
- $c$ is a constant
- $\gamma$ is the gamma value
Contrast stretching
use function to stretch the range of pixel values
$$
I_{out}(x,y)=f(I(x,y))
$$
- $f$ is a function that stretches the range of pixel values
Image histogram
- Histogram of an image is a plot of the frequency of each pixel value
Limitations:
- No spatial information
- No information about the relationship between pixels
#### Linear filtering in spatial domain
Operations that are applied to a neighborhood at each position
Used to:
- Enhance image features
- Denoise, sharpen, resize
- Extract information about image structure
- Edge detection, corner detection, blob detection
- Detect image patterns
- Template matching
- Convolutional Neural Networks
Image filtering
Do dot product of the image with a kernel
$$
h[m,n]=\sum_{k=0}^{m-i}\sum_{l=0}^{n-i}g[k,l]f[m+k,n+l]
$$
```python
def filter2d(image, kernel):
"""
Apply a 2D filter to an image, do not use this in practice
"""
for i in range(image.shape[0]):
for j in range(image.shape[1]):
image[i, j] = np.dot(kernel, image[i-1:i+2, j-1:j+2])
return image
```
Computational cost: $k^2mn$, assume $k$ is the size of the kernel and $m$ and $n$ are the dimensions of the image
Do not use this in practice, use built-in functions instead.
**Box filter**
$$
\frac{1}{9}\begin{bmatrix}
1 & 1 & 1\\
1 & 1 & 1\\
1 & 1 & 1
\end{bmatrix}
$$
Smooths the image
**Identity filter**
$$
\begin{bmatrix}
0 & 0 & 0\\
0 & 1 & 0\\
0 & 0 & 0
\end{bmatrix}
$$
Does not change the image
**Sharpening filter**
$$
\begin{bmatrix}
0 & 0 & 0 \\
0 & 2 & 0 \\
0 & 0 & 0
\end{bmatrix}-
\begin{bmatrix}
1 & 1 & 1 \\
1 & 1 & 1 \\
1 & 1 & 1
\end{bmatrix}
$$
Enhances the image edges
**Vertical edge detection**
$$
\begin{bmatrix}
1 & 0 & -1 \\
2 & 0 & -2 \\
1 & 0 & -1
\end{bmatrix}
$$
Detects vertical edges
**Horizontal edge detection**
$$
\begin{bmatrix}
1 & 2 & 1 \\
0 & 0 & 0 \\
-1 & -2 & -1
\end{bmatrix}
$$
Detects horizontal edges
Key property:
- Linear:
- `filter(I,f_1+f_2)=filter(I,f_1)+filter(I,f_2)`
- Scale invariant:
- `filter(I,af)=a*filter(I,f)`
- Shift invariant:
- `filter(I,shift(f))=shift(filter(I,f))`
- Commutative:
- `filter(I,f_1)*filter(I,f_2)=filter(I,f_2)*filter(I,f_1)`
- Associative:
- `filter(I,f_1)*(filter(I,f_2)*filter(I,f_3))=(filter(I,f_1)*filter(I,f_2))*filter(I,f_3)`
- Distributive:
- `filter(I,f_1+f_2)=filter(I,f_1)+filter(I,f_2)`
- Identity:
- `filter(I,f_0)=I`
Important filter:
**Gaussian filter**
$$
G(x,y)=\frac{1}{2\pi\sigma^2}e^{-\frac{x^2+y^2}{2\sigma^2}}
$$
Smooths the image (Gaussian blur)
Common mistake: Make filter too large, visualize the filter before applying it (make the value on the edge $3\sigma$)
Properties of Gaussian filter:
- Remove high frequency components
- Convolution with self is another Gaussian filter
- Separable kernel:
- `G(x,y)=G(x)G(y)` (factorable into the product of two 1D Gaussian filters)
##### Filter Separability
- Separable filter:
- `f(x,y)=f(x)f(y)`
Example:
$$
\begin{bmatrix}
1 & 2 & 1 \\
2 & 4 & 2 \\
1 & 2 & 1
\end{bmatrix}=
\begin{bmatrix}
1 \\
2 \\
1
\end{bmatrix}\times
\begin{bmatrix}
1 & 2 & 1
\end{bmatrix}
$$
Gaussian filter is separable
$$
G(x,y)=\frac{1}{2\pi\sigma^2}e^{-\frac{x^2+y^2}{2\sigma^2}}=G(x)G(y)
$$
This reduces the computational cost of the filter from $k^2mn$ to $2kmn$

196
content/CSE559A/CSE559A_L4.md
View File

@@ -1,196 +0,0 @@
# CSE559A Lecture 4
## Practical issues with filtering
$$
h[m,n]=\sum_{k=0}^{m-i}\sum_{l=0}^{n-i}g[k,l]f[m+k,n+l]
$$
Loss of information on edges of image
- The filter window falls off the edge of the image
- Need to extrapolate
- Methods:
- clip filter
- wrap around (extend the image periodically)
- copy edge (extend the image by copying the edge pixels)
- reflect across edge (extend the image by reflecting the edge pixels)
## Convolution vs Correlation
- Convolution:
- The filter is flipped and convolved with the image
$$
h[m,n]=\sum_{k=i}^{m}\sum_{l=i}^{n}g[k,l]f[m-k,n-l]
$$
- Correlation:
- The filter is not flipped and convolved with the image
$$
h[m,n]=\sum_{k=0}^{m-i}\sum_{l=0}^{n-i}g[k,l]f[m+k,n+l]
$$
does not matter for deep learning
```python
scipy.signal.convolve2d(image, kernel, mode='same')
scipy.signal.correlate2d(image, kernel, mode='same')
```
but pytorch uses correlation for convolution, the convolution in pytorch is actually a correlation in scipy.
## Frequency domain representation of linear image filters
TL;DR: It can be helpful to think about linear spatial filters in terms fro their frequency domain representation
- Fourier transform and frequency domain
- The convolution theorem
Hybrid image: More in homework 2
Human eye is sensitive to low frequencies in far field, high frequencies in near field
### Change of basis from an image perspective
For vectors:
- Vector -> Invertible matrix multiplication -> New vector
- Normally we think of the standard/natural basis, with unit vectors in the direction of the axes
For images:
- Image -> Vector -> Invertible matrix multiplication -> New vector -> New image
- Standard basis is just a collection of one-hot images
Use `im.flatten()` to convert an image to a vector
$$
Image(M^{-1}GMVec(I))
$$
- M is the change of basis matrix, $M^{-1}M=I$
- G is the operation we want to perform
- Vec(I) is the vectorized image
#### Lossy image compression (JPEG)
- JPEG is a lossy compression algorithm
- It uses the DCT (Discrete Cosine Transform) to transform the image to the frequency domain
- The DCT is a linear operation, so it can be represented as a matrix multiplication
- The JPEG algorithm then quantizes the coefficients and entropy codes them (use Huffman coding)
## Thinking in frequency domain
### Fourier transform
Any univariate function can be represented as a weighted sum of sine and cosine functions
$$
X[k]=\sum_{n=N-1}^{0}x[n]e^{-2\pi ikn/N}=\sum_{n=0}^{N-1}x[n]\left[\sin\left(\frac{2\pi}{N}kn\right)+i\cos\left(\frac{2\pi}{N}kn\right)\right]
$$
- $X[k]$ is the Fourier transform of $x[n]$
- $e^{-2\pi ikn/N}$ is the basis function
- $x[n]$ is the original function
Real part:
$$
\text{Re}(X[k])=\sum_{n=0}^{N-1}x[n]\cos\left(\frac{2\pi}{N}kn\right)
$$
Imaginary part:
$$
\text{Im}(X[k])=\sum_{n=0}^{N-1}x[n]\sin\left(\frac{2\pi}{N}kn\right)
$$
Fourier transform stores the magnitude and phase of the sine and cosine function at each frequency
- Amplitude: encodes how much signal there is at a particular frequency
- Phase: encodes the spacial information (indirectly)
- For mathematical convenience, this is often written as a complex number
Amplitude: $A=\pm\sqrt{\text{Re}(\omega)^2+\text{Im}(\omega)^2}$
Phase: $\phi=\tan^{-1}\left(\frac{\text{Im}(\omega)}{\text{Re}(\omega)}\right)$
So use $A\sin(\omega+\phi)$ to represent the signal
Example:
$g(t)=\sin(2\pi ft)+\frac{1}{3}\sin(2\pi (3f)t)$
### Fourier analysis of images
Intensity image and Fourier image
Signals can be composed.
![jpeg basis](https://notenextra.trance-0.com/CSE559A/8x8_DCT_basis.png)
Note: frequency domain is often visualized using a log of the absolute value of the Fourier transform
Blurring the image is to delete the high frequency components (removing the center of the frequency domain)
## Convolution theorem
The Fourier transform of the convolution of two functions is the product of their Fourier transforms
$$
F[f*g]=F[f]F[g]
$$
- $F$ is the Fourier transform
- $*$ is the convolution
Convolution in spatial domain is equivalent to multiplication in frequency domain
$$
g*h=F^{-1}[F[g]F[h]]
$$
- $F^{-1}$ is the inverse Fourier transform
### Is convolution invertible?
- Redo the convolution in the image domain is division in the frequency domain
$$
g*h=F^{-1}\left[\frac{F[g]}{F[h]}\right]
$$
- This is not always possible, because $F[h]$ may be zero and we may not know the filter
Small perturbations in the frequency domain can cause large perturbations in the spatial domain and vice versa
Deconvolution is hard and a active area of research
- Even if you know the filter, it is not always possible to invert the convolution, requires strong regularization
- If you don't know the filter, it is even harder
## 2D image transformations
### Array slicing and image wrapping
Fast operation for extracting a subimage
- cropped image `image[10:20, 10:20]`
- flipped image `image[::-1, ::-1]`
Image wrapping allows more flexible operations
#### Upsampling an image
- Upsampling an image is the process of increasing the resolution of the image
Bilinear interpolation:
- Use the average of the 4 nearest pixels to determine the value of the new pixel
Other interpolation methods:
- Bicubic interpolation: Use the average of the 16 nearest pixels to determine the value of the new pixel
- Nearest neighbor interpolation: Use the value of the nearest pixel to determine the value of the new pixel

222
content/CSE559A/CSE559A_L5.md
View File

@@ -1,222 +0,0 @@
# CSE559A Lecture 5
## Continue on linear interpolation
- In linear interpolation, extreme values are at the boundary.
- In bicubic interpolation, extreme values may be inside.
`scipy.interpolate.RegularGridInterpolator`
### Image transformations
Image warping is a process of applying transformation $T$ to an image.
Parametric (global) warping: $T(x,y)=(x',y')$
Geometric transformation: $T(x,y)=(x',y')$ This applies to each pixel in the same way. (global)
#### Translation
$T(x,y)=(x+a,y+b)$
matrix form:
$$
\begin{pmatrix}
x'\\y'
\end{pmatrix}
=
\begin{pmatrix}
1&0\\0&1
\end{pmatrix}
\begin{pmatrix}
x\\y
\end{pmatrix}
+
\begin{pmatrix}
a\\b
\end{pmatrix}
$$
#### Scaling
$T(x,y)=(s_xx,s_yy)$ matrix form:
$$
\begin{pmatrix}
x'\\y'
\end{pmatrix}
=
\begin{pmatrix}
s_x&0\\0&s_y
\end{pmatrix}
\begin{pmatrix}
x\\y
\end{pmatrix}
$$
#### Rotation
$T(x,y)=(x\cos\theta-y\sin\theta,x\sin\theta+y\cos\theta)$
matrix form:
$$
\begin{pmatrix}
x'\\y'
\end{pmatrix}
=
\begin{pmatrix}
\cos\theta&-\sin\theta\\\sin\theta&\cos\theta
\end{pmatrix}
\begin{pmatrix}
x\\y
\end{pmatrix}
$$
To undo the rotation, we need to rotate the image by $-\theta$. This is equivalent to apply $R^T$ to the image.
#### Affine transformation
$T(x,y)=(a_1x+a_2y+a_3,b_1x+b_2y+b_3)$
matrix form:
$$
\begin{pmatrix}
x'\\y'
\end{pmatrix}
=
\begin{pmatrix}
a_1&a_2&a_3\\b_1&b_2&b_3
\end{pmatrix}
\begin{pmatrix}
x\\y\\1
\end{pmatrix}
$$
Taking all the transformations together.
#### Projective homography
$T(x,y)=(\frac{ax+by+c}{gx+hy+i},\frac{dx+ey+f}{gx+hy+i})$
$$
\begin{pmatrix}
x'\\y'\\1
\end{pmatrix}
=
\begin{pmatrix}
a&b&c\\d&e&f\\g&h&i
\end{pmatrix}
\begin{pmatrix}
x\\y\\1
\end{pmatrix}
$$
### Image warping
#### Forward warping
Send each pixel to its new position and do the matching.
- May cause gaps where the pixel is not mapped to any pixel.
#### Inverse warping
Send each new position to its original position and do the matching.
- Some mapping may not be invertible.
#### Which one is better?
- Inverse warping is better because it usually more efficient, doesn't have a problem with holes.
- However, it may not always be possible to find the inverse mapping.
## Sampling and Aliasing
### Naive sampling
- Remove half of the rows and columns in the image.
Example:
When sampling a sine wave, the result may interpret as different wave.
#### Nyquist-Shannon sampling theorem
- A bandlimited signal can be uniquely determined by its samples if the sampling rate is greater than twice the maximum frequency of the signal.
- If the sampling rate is less than twice the maximum frequency of the signal, the signal will be aliased.
#### Anti-aliasing
- Sample more frequently. (not always possible)
- Get rid of all frequencies that are greater than half of the new sampling frequency.
- Use a low-pass filter to get rid of all frequencies that are greater than half of the new sampling frequency. (eg, Gaussian filter)
```python
import scipy.ndimage as ndimage
def down_sample(height, width, image):
# Apply Gaussian blur to the image
im_blur = ndimage.gaussian_filter(image, sigma=1)
# Down sample the image by taking every second pixel
return im_blur[::2, ::2]
```
## Nonlinear filtering
### Median filter
Replace the value of a pixel with the median value of its neighbors.
- Good for removing salt and pepper noise. (black and white dot noise)
### Morphological operations
Binary image: image with only 0 and 1.
Let $B$ be a structuring element and $A$ be the original image (binary image).
- Erosion: $A\ominus B = \{p\mid B_p\subseteq A\}$, this is the set of all points that are completely covered by $B$.
- Dilation: $A\oplus B = \{p\mid B_p\cap A\neq\emptyset\}$, this is the set of all points that are at least partially covered by $B$.
- Opening: $A\circ B = (A\ominus B)\oplus B$, this is the set of all points that are at least partially covered by $B$ after erosion.
- Closing: $A\bullet B = (A\oplus B)\ominus B$, this is the set of all points that are completely covered by $B$ after dilation.
Boundary extraction: use XOR operation on eroded image and original image.
Connected component labeling: label the connected components in the image. _use prebuild function in scipy.ndimage_
## Light,Camera/Eyes, and Color
### Principles of grouping and Gestalt Laws
- Proximity: objects that are close to each other are more likely to be grouped together.
- Similarity: objects that are similar are more likely to be grouped together.
- Closure: objects that form a closed path are more likely to be grouped together.
- Continuity: objects that form a continuous path are more likely to be grouped together.
### Light and surface interactions
A photon's life choices:
- Absorption
- Diffuse reflection (nice to model) (lambertian surface)
- Specular reflection (mirror-like) (perfect mirror)
- Transparency
- Refraction
- Fluorescence (returns different color)
- Subsurface scattering (candles)
- Photosphorescence
- Interreflection
#### BRDF (Bidirectional Reflectance Distribution Function)
$$
\rho(\theta_i,\phi_i,\theta_o,\phi_o)
$$
- $\theta_i$ is the angle of incidence.
- $\phi_i$ is the azimuthal angle of incidence.
- $\theta_o$ is the angle of reflection.
- $\phi_o$ is the azimuthal angle of reflection.

213
content/CSE559A/CSE559A_L6.md
View File

@@ -1,213 +0,0 @@
# CSE559A Lecture 6
## Continue on Light, eye/camera, and color
### BRDF (Bidirectional Reflectance Distribution Function)
$$
\rho(\theta_i,\phi_i,\theta_o,\phi_o)
$$
#### Diffuse Reflection
- Dull, matte surface like chalk or latex paint
- Most often used in computer vision
- Brightness _does_ depend on direction of illumination
Diffuse reflection governed by Lambert's law: $I_d = k_d N\cdot L I_i$
- $N$: surface normal
- $L$: light direction
- $I_i$: incident light intensity
- $k_d$: albedo
$$
\rho(\theta_i,\phi_i,\theta_o,\phi_o)=k_d \cos\theta_i
$$
#### Photometric Stereo
Suppose there are three light sources, $L_1, L_2, L_3$, and we have the following measurements:
$$
I_1 = k_d N\cdot L_1
$$
$$
I_2 = k_d N\cdot L_2
$$
$$
I_3 = k_d N\cdot L_3
$$
We can solve for $N$ by taking the dot product of $N$ and each light direction and then solving the system of equations.
Will not do this in the lecture.
#### Specular Reflection
- Mirror-like surface
$$
I_e=\begin{cases}
I_i & \text{if } V=R \\
0 & \text{if } V\neq R
\end{cases}
$$
- $V$: view direction
- $R$: reflection direction
- $\theta_i$: angle between the incident light and the surface normal
Near-perfect mirror have a high light around $R$.
common model:
$$
I_e=k_s (V\cdot R)^{n_s}I_i
$$
- $k_s$: specular reflection coefficient
- $n_s$: shininess (imperfection of the surface)
- $I_i$: incident light intensity
#### Phong illumination model
- Phong approximation of surface reflectance
- Assume reflectance is modeled by three compoents
- Diffuse reflection
- Specular reflection
- Ambient reflection
$$
I_e=k_a I_a + I_i \left[k_d (N\cdot L) + k_s (V\cdot R)^{n_s}\right]
$$
- $k_a$: ambient reflection coefficient
- $I_a$: ambient light intensity
- $k_d$: diffuse reflection coefficient
- $k_s$: specular reflection coefficient
- $n_s$: shininess
- $I_i$: incident light intensity
Many other models.
#### Measuring BRDF
Use Gonioreflectometer.
- Device for measuring the reflectance of a surface as a function of the incident and reflected angles.
- Can be used to measure the BRDF of a surface.
BRDF dataset:
- MERL dataset
- CURET dataset
### Camera/Eye
#### DSLR Camera
- Pinhole camera model
- Lens
- Aperture (the pinhole)
- Sensor
- ...
#### Digital Camera block diagram
![Digital Camera block diagram](https://notenextra.trance-0.com/CSE559A/DigitalCameraBlockDiagram.png)
Scanning protocols:
- Global shutter: all pixels are exposed at the same time
- Interlaced: odd and even lines are exposed at different times
- Rolling shutter: each line is exposed as it is read out
#### Eye
- Pupil
- Iris
- Retina
- Rods and cones
- ...
#### Eye Movements
- Saccade
- Can be consciously controlled. Related to perceptual attention.
- 200ms to initiation, 20 to 200ms to carry out. Large amplitude.
- Smooth pursuit
- Tracking an object
- Difficult w/o an object to track!
- Microsaccade and Ocular microtremor (OMT)
- Involuntary. Smaller amplitude. Especially evident during prolonged
fixation.
#### Contrast Sensitivity
- Uniform contrast image content, with increasing frequency
- Why not uniform across the top?
- Low frequencies: harder to see because of slower intensity changes
- Higher frequencies: harder to see because of ability of our visual system to resolve fine features
### Color Perception
Visible light spectrum: 380 to 780 nm
- 400 to 500 nm: blue
- 500 to 600 nm: green
- 600 to 700 nm: red
#### HSV model
We use Gaussian functions to model the sensitivity of the human eye to different wavelengths.
- Hue: color (the wavelength of the highest peak of the sensitivity curve)
- Saturation: color purity (the variance of the sensitivity curve)
- Value: color brightness (the highest peak of the sensitivity curve)
#### Color Sensing in Camera (RGB)
- 3-chip vs. 1-chip: quality vs. cost
Bayer filter:
- Why more green?
- Human eye is more sensitive to green light.
#### Color spaces
Images in python:
As matrix.
```python
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from skimage import io
def plot_rgb_3d(image_path):
image = io.imread(image_path)
r, g, b = image[:,:,0], image[:,:,1], image[:,:,2]
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(r.flatten(), g.flatten(), b.flatten(), c=image.reshape(-1, 3)/255.0, marker='.')
ax.set_xlabel('Red')
ax.set_ylabel('Green')
ax.set_zlabel('Blue')
plt.show()
plot_rgb_3d('image.jpg')
```
Other color spaces:
- YCbCr (fast to compute, usually used in TV)
- HSV
- L\*a\*b\* (CIELAB, perceptually uniform color space)
Most information is in the intensity channel.

228
content/CSE559A/CSE559A_L7.md
View File

@@ -1,228 +0,0 @@
# CSE559A Lecture 7
## Computer Vision (In Artificial Neural Networks for Image Understanding)
Early example of image understanding using Neural Networks: [Back propagation for zip code recognition]
Central idea; representation change, on each layer of feature.
Plan for next few weeks:
1. How do we train such models?
2. What are those building blocks
3. How should we combine those building blocks?
## How do we train such models?
CV is finally useful...
1. Image classification
2. Image segmentation
3. Object detection
ImageNet Large Scale Visual Recognition Challenge (ILSVRC)
- 1000 classes
- 1.2 million images
- 10000 test images
### Deep Learning (Just neural networks)
Bigger datasets, larger models, faster computers, lots of incremental improvements.
```python
import torch
import torch.nn as nn
import torch.nn.functional as F
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(1, 6, 5)
self.conv2 = nn.Conv2d(6, 16, 5)
self.fc1 = nn.Linear(16 * 5 * 5, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
x = F.max_pool2d(F.relu(self.conv2(x)), 2)
x = x.view(-1, self.num_flat_features(x))
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
def num_flat_features(self, x):
size = x.size()[1:]
num_features = 1
for s in size:
num_features *= s
return num_features
# create pytorch dataset and dataloader
dataset = torch.utils.data.TensorDataset(torch.randn(1000, 1, 28, 28), torch.randint(10, (1000,)))
dataloader = torch.utils.data.DataLoader(dataset, batch_size=4, shuffle=True, num_workers=2)
# training process
net = Net()
optimizer = optim.Adam(net.parameters(), lr=0.001)
criterion = nn.CrossEntropyLoss()
# loop over the dataset multiple times
for epoch in range(2):
for i, data in enumerate(dataloader, 0):
inputs, labels = data
optimizer.zero_grad()
outputs = net(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
print(f"Finished Training")
```
Some generated code above.
### Supervised Learning
Training: given a dataset, learn a mapping from input to output.
Testing: given a new input, predict the output.
Example: Linear classification models
Find a linear function that separates the data.
$$
f(x) = w^T x + b
$$
[Linear classification models](http://cs231n.github.io/linear-classify/)
Simple representation of a linear classifier.
### Empirical loss minimization framework
Given a training set, find a model that minimizes the loss function.
Assume iid samples.
Example of loss function:
l1 loss:
$$
\ell(f(x; w), y) = |f(x; w) - y|
$$
l2 loss:
$$
\ell(f(x; w), y) = (f(x; w) - y)^2
$$
### Linear classification models
$$
\hat{L}(w) = \frac{1}{n} \sum_{i=1}^n \ell(f(x_i; w), y_i)
$$
hard to find the global minimum.
#### Linear regression
However, if we use l2 loss, we can find the global minimum.
$$
\hat{L}(w) = \frac{1}{n} \sum_{i=1}^n (f(x_i; w) - y_i)^2
$$
This is a convex function, so we can find the global minimum.
The gradient is:
$$
\nabla_w||Xw-Y||^2 = 2X^T(Xw-Y)
$$
Set the gradient to 0, we get:
$$
w = (X^T X)^{-1} X^T Y
$$
From the maximum likelihood perspective, we can also derive the same result.
#### Logistic regression
Sigmoid function:
$$
\sigma(x) = \frac{1}{1 + e^{-x}}
$$
The loss of logistic regression is not convex, so we cannot find the global minimum using normal equations.
#### Gradient Descent
Full batch gradient descent:
$$
w \leftarrow w - \eta \nabla_w \hat{L}(w)
$$
Stochastic gradient descent:
$$
w \leftarrow w - \eta \nabla_w \hat{L}(w; x_i, y_i)
$$
Mini-batch gradient descent:
$$
w \leftarrow w - \eta \nabla_w \hat{L}(w; x_i, y_i)
$$
Mini-batch Gradient Descent:
$$
w \leftarrow w - \eta \nabla_w \hat{L}(w; x_i, y_i)
$$
at each step, we update the weights using the average gradient of the mini-batch.
the mini-batch is selected randomly from the training set.
#### Multi-class classification
Use softmax function to convert the output to a probability distribution.
## Neural Networks
From linear to non-linear.
- Shadow approach:
- Use feature transformation to make the data linearly separable.
- Deep approach:
- Stack multiple layers of linear models.
Common non-linear functions:
- ReLU:
- $$
\text{ReLU}(x) = \max(0, x)
$$
- Sigmoid:
- $$
\text{Sigmoid}(x) = \frac{1}{1 + e^{-x}}
$$
- Tanh:
- $$
\text{Tanh}(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}
$$
### Backpropagation

80
content/CSE559A/CSE559A_L8.md
View File

@@ -1,80 +0,0 @@
# CSE559A Lecture 8
Paper review sharing.
## Recap: Three ways to think about linear classifiers
Geometric view: Hyperplanes in the feature space
Algebraic view: Linear functions of the features
Visual view: One template per class
## Continue on linear classification models
Two layer networks as combination of templates.
Interpretability is lost during the depth increase.
A two layer network is a **universal approximator** (we can approximate any continuous function to arbitrary accuracy). But the hidden layer may need to be huge.
[Multi-layer networks demo](https://playground.tensorflow.org)
### Supervised learning outline
1. Collect training data
2. Specify model (select hyper-parameters)
3. Train model
#### Hyper-parameters selection
- Number of layers, number of units per layer, learning rate, etc.
- Type of non-linearity, regularization, etc.
- Type of loss function, etc.
- SGD settings: batch size, number of epochs, etc.
#### Hyper-parameter searching
Use validation set to evaluate the performance of the model.
Never peek the test set.
Use the training set to do K-fold cross validation.
### Backpropagation
#### Computation graphs
SGD update for each parameter
$$
w_k\gets w_k-\eta\frac{\partial e}{\partial w_k}
$$
$e$ is the error function.
#### Using the chain rule
Suppose $k=1$, $e=l(f_1(x,w_1),y)$
Example: $e=(f_1(x,w_1)-y)^2$
So $h_1=f_1(x,w_1)=w^T_1x$, $e=l(h_1,y)=(y-h_1)^2$
$$
\frac{\partial e}{\partial w_1}=\frac{\partial e}{\partial h_1}\frac{\partial h_1}{\partial w_1}
$$
$$
\frac{\partial e}{\partial h_1}=2(h_1-y)
$$
$$
\frac{\partial h_1}{\partial w_1}=x
$$
$$
\frac{\partial e}{\partial w_1}=2(h_1-y)x
$$
#### General backpropagation algorithm

102
content/CSE559A/CSE559A_L9.md
View File

@@ -1,102 +0,0 @@
# CSE559A Lecture 9
## Continue on ML for computer vision
### Backpropagation
#### Computation graphs
SGD update for each parameter
$$
w_k\gets w_k-\eta\frac{\partial e}{\partial w_k}
$$
$e$ is the error function.
#### Using the chain rule
Suppose $k=1$, $e=l(f_1(x,w_1),y)$
Example: $e=(f_1(x,w_1)-y)^2$
So $h_1=f_1(x,w_1)=w^T_1x$, $e=l(h_1,y)=(y-h_1)^2$
$$
\frac{\partial e}{\partial w_1}=\frac{\partial e}{\partial h_1}\frac{\partial h_1}{\partial w_1}
$$
$$
\frac{\partial e}{\partial h_1}=2(h_1-y)
$$
$$
\frac{\partial h_1}{\partial w_1}=x
$$
$$
\frac{\partial e}{\partial w_1}=2(h_1-y)x
$$
For the general cases,
$$
\frac{\partial e}{\partial w_k}=\frac{\partial e}{\partial h_K}\frac{\partial h_K}{\partial h_{K-1}}\cdots\frac{\partial h_{k+2}}{\partial h_{k+1}}\frac{\partial h_{k+1}}{\partial h_k}\frac{\partial h_k}{\partial w_k}
$$
Where the upstream gradient $\frac{\partial e}{\partial h_K}$ is known, and the local gradient $\frac{\partial h_k}{\partial w_k}$ is known.
#### General backpropagation algorithm
The adding layer is the gradient distributor layer.
The multiplying layer is the gradient switcher layer.
The max operation is the gradient router layer.
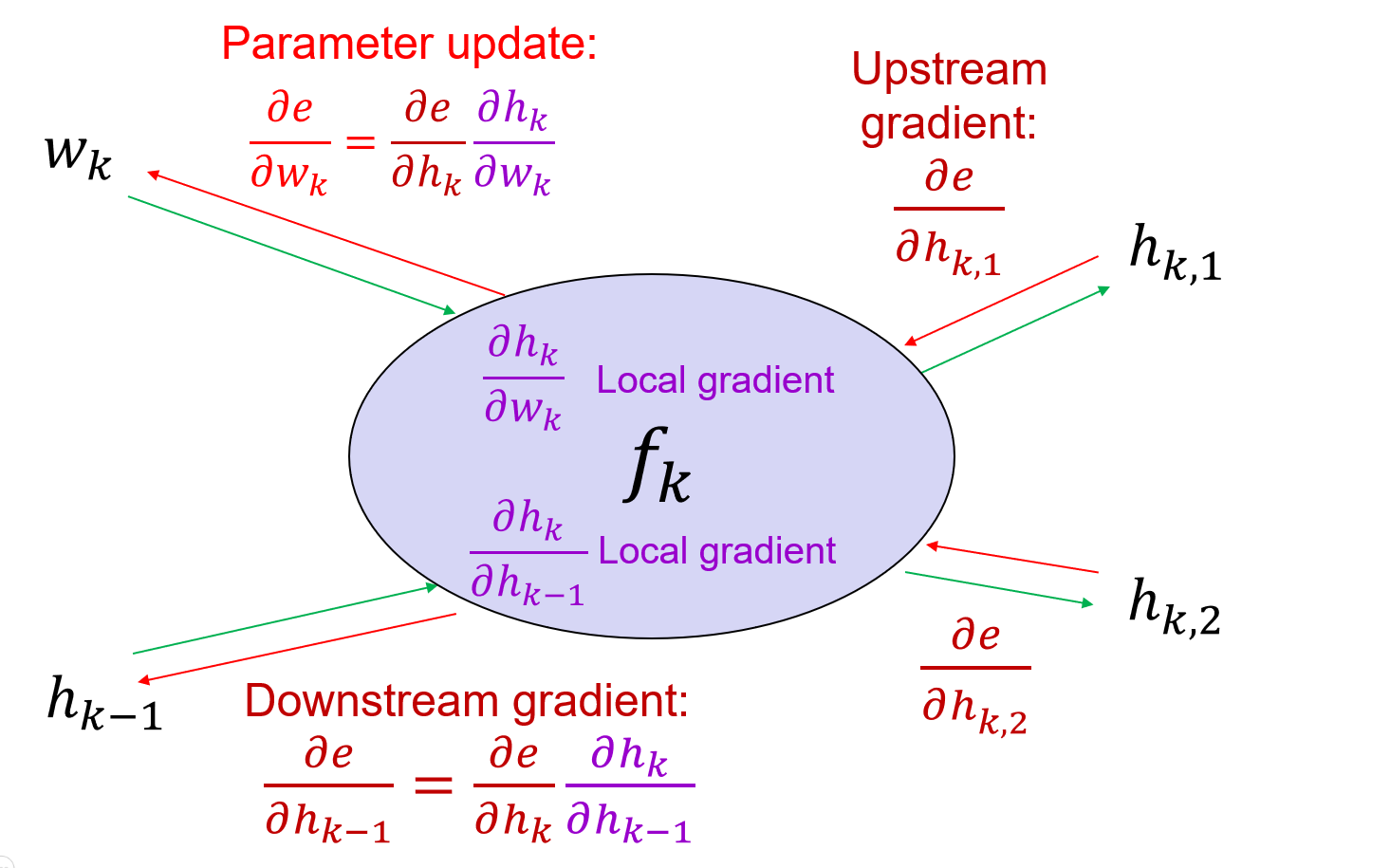
![Images of propagation](https://notenextra.trance-0.com/CSE559A/General_computation_graphs_for_MLP.png)
Simple example: Element-wise operation (ReLU)
$f(x)=ReLU(x)=max(0,x)$
$$
\frac{\partial z}{\partial x}=\begin{pmatrix}
\frac{\partial z_1}{\partial x_1} & 0 & \cdots & 0 \\
0 & \frac{\partial z_2}{\partial x_2} & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & \frac{\partial z_n}{\partial x_n}
\end{pmatrix}
$$
Where $\frac{\partial z_i}{\partial x_j}=1$ if $i=j$ and $z_i>0$, otherwise $\frac{\partial z_i}{\partial x_j}=0$.
When $\forall x_i<0$ then $\frac{\partial z}{\partial x}=0$ (dead ReLU)
Other examples on ppt.
## Convolutional Neural Networks
### Basic Convolutional layer
#### Flatten layer
Fully connected layer, operate on vectorized image.
With the multi-layer perceptron, the neural network trying to fit the templates.
![Flatten layer](https://notenextra.trance-0.com/CSE559A/Flatten_layer.png)
#### Convolutional layer
Limit the receptive fields of units, tiles them over the input image, and share the weights.
Equivalent to sliding the learned filter over the image , computing dot products at each location.
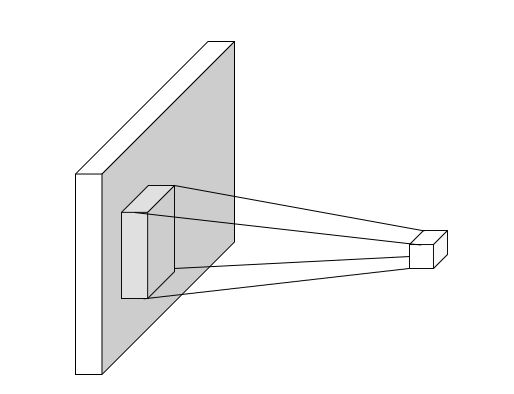
![Convolutional layer](https://notenextra.trance-0.com/CSE559A/Convolutional_layer.png)
Padding: Add a border of zeros around the image. (higher padding, larger output size)
Stride: The step size of the filter. (higher stride, smaller output size)
### Variants 1x1 convolutions, depthwise convolutions
### Backward pass

32
content/CSE559A/_meta.js
View File

@@ -1,32 +0,0 @@
export default {
index: "Course Description",
"---":{
type: 'separator'
},
CSE559A_L1: "Computer Vision (Lecture 1)",
CSE559A_L2: "Computer Vision (Lecture 2)",
CSE559A_L3: "Computer Vision (Lecture 3)",
CSE559A_L4: "Computer Vision (Lecture 4)",
CSE559A_L5: "Computer Vision (Lecture 5)",
CSE559A_L6: "Computer Vision (Lecture 6)",
CSE559A_L7: "Computer Vision (Lecture 7)",
CSE559A_L8: "Computer Vision (Lecture 8)",
CSE559A_L9: "Computer Vision (Lecture 9)",
CSE559A_L10: "Computer Vision (Lecture 10)",
CSE559A_L11: "Computer Vision (Lecture 11)",
CSE559A_L12: "Computer Vision (Lecture 12)",
CSE559A_L13: "Computer Vision (Lecture 13)",
CSE559A_L14: "Computer Vision (Lecture 14)",
CSE559A_L15: "Computer Vision (Lecture 15)",
CSE559A_L16: "Computer Vision (Lecture 16)",
CSE559A_L17: "Computer Vision (Lecture 17)",
CSE559A_L18: "Computer Vision (Lecture 18)",
CSE559A_L19: "Computer Vision (Lecture 19)",
CSE559A_L20: "Computer Vision (Lecture 20)",
CSE559A_L21: "Computer Vision (Lecture 21)",
CSE559A_L22: "Computer Vision (Lecture 22)",
CSE559A_L23: "Computer Vision (Lecture 23)",
CSE559A_L24: "Computer Vision (Lecture 24)",
CSE559A_L25: "Computer Vision (Lecture 25)",
CSE559A_L26: "Computer Vision (Lecture 26)",
}

4
content/CSE559A/index.md
View File

@@ -1,4 +0,0 @@
# CSE 559A: Computer Vision
## Course Description

1
content/Math3200/Lecture_1.mdx Normal file
View File

@@ -0,0 +1 @@
<div style={{ width: '100%', height: '25px'}}></div><iframe src="https://notenextra.trance-0.com/Math3200/Lecture_1.html" title="Math 3200 Lecture 1" style={{ width: '100%', height: '100vh', border: 'none' }}/>

11
content/Math3200/index.md Normal file
View File

@@ -0,0 +1,11 @@
# Math 3200 Elementary Statistics and Data Analysis
## Course Description
This course is designed to provide students with a comprehensive understanding of the fundamental concepts and techniques in statistics and data analysis. It covers the basic principles of statistics, including descriptive statistics, probability theory, and statistical inference. Students will learn how to collect, analyze, and interpret data using various statistical methods and tools. The course will also introduce students to the principles of data visualization and the use of statistical software for data analysis.
## Notes for Developers
This site is generated using html files rendered by RMarkdown. Some search functionality may not work.
Source code is available [here](https://nextcloud.trance-0.com/index.php/s/NZJ9ynCdmTqqeGo).

69
content/Math401/index.md Normal file
View File

@@ -0,0 +1,69 @@
# Math 401
This is a course about symmetrical group and bunch of applications in other fields of math.
Prof. Renado Fere is teaching this course.
The course is split into two parts:
1. Symmetrical group
2. Summer research project
## Symmetrical group (Spring 2025 Course)
Notes from N1-N3.
Basically are overview of some interesting topics related to symmetrical group or other related math topics.
I don't record them carefully, but I will try to update them if they are necessary for my future reference.
## Summer research project
### Schedule
Presentation starts next week
Start with examples, do exploratory work, it's just a summer.
Final work: Find certain topic you are interested in, and do a expository paper.
Find the motivation, background, definition, theorem, example, application for the theory you are interested in.
At least 3 presentations is required.
Collect the papers you interested in as you go the research, it is not linear.
Symposium on November.
Lightning talk (3 minutes) on end of July.
### Topic of interest
I am interested in the following topics:
1. Quantum error correction
2. Von Neumann algebra and other operator algebras which are related to quantum algorithms
### Notes
T1-T7 should be the notes for the spring course Math 444. Taught by Prof. Renado Fere on Spring 2025 but I don't know that and they are helpful for understanding the material for the book that might contains my subject of interest.
[The Functional Analysis of Quantum Information Theory](https://arxiv.org/abs/1410.7188)
The original lecture notes, by Prof. Renado Fere, are here, may move to other places. Last updated on 2025-06-14.
[Math 444 Spring 2025 Notes, Lecture 1](https://www.math.wustl.edu/~feres/Math444Spring25/Math444Spring25Notes01.pdf)
[Math 444 Spring 2025 Notes, Lecture 2](https://www.math.wustl.edu/~feres/Math444Spring25/Math444Spring25Notes02.pdf)
[Math 444 Spring 2025 Notes, Lecture 3](https://www.math.wustl.edu/~feres/Math444Spring25/Math444Spring25Notes03.pdf)
[Math 444 Spring 2025 Notes, Lecture 4](https://www.math.wustl.edu/~feres/Math444Spring25/Math444Spring25Notes04.pdf)
[Math 444 Spring 2025 Notes, Lecture 5](https://www.math.wustl.edu/~feres/Math444Spring25/Math444Spring25Notes05.pdf)
[Math 444 Spring 2025 Notes, Lecture 6](https://www.math.wustl.edu/~feres/Math444Spring25/Math444Spring25Notes06.pdf)
[Math 444 Spring 2025 Notes, Lecture 7](https://www.math.wustl.edu/~feres/Math444Spring25/Math444Spring25Notes07.pdf)
[Math 444 Spring 2025 Notes, Lecture 9](https://www.math.wustl.edu/~feres/Math444Spring25/Math444Spring25Notes09.pdf)

89
content/Math4111/Exam_reviews/Math4111_E2.md Normal file
View File

@@ -0,0 +1,89 @@
# Math 4111 Exam 2 review
$E$ is open if $\forall x\in E$, $x\in E^\circ$ ($E\subset E^\circ$)
$E$ is closed if $E\supset E'$
Then $E$ closed $\iff E^c$ open $\iff \forall x\in E^\circ, \exists r>0$ such that $B_r(x)\subset E^c$
$\forall x\in E^c$, $\forall x\notin E$
$B_r(x)\subset E^c\iff B_r(x)\cap E=\phi$
## Past exam questions
$S,T$ is compact $\implies S\cup T$ is compact
Proof:
Suppose $S$ and $T$ are compact, let $\{G_\alpha\}_{\alpha\in A}$ be an open cover of $S\cup T$
(NOT) $\{G_\alpha\}$ is an open cover of $S$, $\{H_\beta\}$ is an open cover of $T$.
...
QED
## K-cells are compact
We'll prove the case $k=1$ and $I=[0,1]$ (This is to simplify notation. This same ideas are used in the general case)
Proof:
That $[0,1]$ is compact.
(Key idea, divide and conquer)
Suppose for contradiction that $\exists$ open cover $\{G_a\}_{\alpha\in A}$ of $[0,1]$ with no finite subcovers of $[0,1]$
**Step1.** Divide $[0,1]$ in half. $[0,\frac{1}{2}]$ and $[\frac{1}{2},1]$ and at least one of the subintervals cannot be covered by a finite subcollection of $\{G_\alpha\}_{\alpha\in A}$
(If both of them could be, combine the two finite subcollections to get a finite subcover of $[0,1]$)
Let $I_1$ be a subinterval without a finite subcover.
**Step2.** Divide $I_1$ in half. Let $I_2$ be one of these two subintervals of $I_1$ without a finite subcover.
**Step3.** etc.
We obtain a seg of intervals $I_1\subset I_2\subset \dots$ such that
(a) $[0,1]\supset I_1\supset I_2\supset \dots$
(b) $\forall n\in \mathbb{N}$, $I_n$ is not covered by a finite subcollection of $\{G_\alpha\}_{\alpha\in A}$
(c) The length of $I_n$ is $\frac{1}{2^n}$
By (a) and **Theorem 2.38**, $\exists x^*\in \bigcap^{\infty}_{n=1} I_n$.
Since $x^*\in [0,1]$, $\exists \alpha_0$ such that $x^*\in G_{\alpha_0}$
Since $G_{\alpha_0}$ is open, $\exist r>0$ such that $B_r(x^*)\subset G_{\alpha_0}$
Let $n\in \mathbb{N}$ be such that $\frac{1}{2^n}<r$. Then by $(c)$, $I(n)\subset B_r(x^*)\subset G_{\alpha_0}$
Then $\{G_{\alpha_0}\}$ is a cover of $I_n$ which contradicts with (b)
QED
## Redundant subcover question
$M$ is compact and $\{G_\alpha\}_{\alpha\in A}$ is a "redundant" subcover of $M$.
$\exists \{G_{\alpha_i}\}_{i=1}^n$ is a finite subcover of $M$.
We define $S$ be the $x\in M$ that is only being covered once.
$$
S=M\backslash\left(\bigcup_{i\neq j,i,j\in A} G_{\alpha_i}\cap G_{\alpha_j}\right)
$$
We claim $S$ is a closed set.
$G_{\alpha_i}\cap G_{\alpha_j}$ is open.
$\left(\bigcup_{i\neq j,i,j\in A} G_{\alpha_i}\cap G_{\alpha_j}\right)$ is closed
$S=M\backslash\left(\bigcup_{i\neq j,i,j\in A} G_{\alpha_i}\cap G_{\alpha_j}\right)$ is closed.
So $S$ is compact, we found another finite subcover yeah!

174
content/Math4111/Exam_reviews/Math4111_E3.md Normal file
View File

@@ -0,0 +1,174 @@
# Math 4111 Exam 3 review
## Relations between series and topology (compactness, closure, etc.)
Limit points $E'=\{x\in\mathbb{R}:\forall r>0, B_r(x)\backslash\{x\}\cap E\neq\phi\}$
Closure $\overline{E}=E\cup E'=\{x\in\mathbb{R}:\forall r>0, B_r(x)\cap E\neq\phi\}$
$p_n\to p\implies \forall \epsilon>0, \exists N$ such that $\forall n\geq N, p_n\in B_\epsilon(p)$
### Some interesting results
#### Lemma
$p\in \overline{E}\iff \exists (p_n)\subseteq E$ such that $p_n\to p$
$p\in E'\iff \exists (p_n)\subseteq E\backslash\{p\}$ such that $p_n\to p$ (you cannot choose $p$ in the sequence)
#### Bolzano-Weierstrass Theorem
Let $E$ be a compact set and $(p_n)$ be a sequence in $E$. Then $\exists (p_{n_k})\subseteq (p_n)$ such that $p_{n_k}\to p\in E$.
Rudin Proof:
Rudin's proof uses a fact from Chapter 2.
If $E$ is compact, and $S\subseteq E$ is infinite, then $S$ has a limit point in $E$ ($S'\cap E\neq\phi$).
## Examples of Cauchy sequence that does not converge
> Cauchy sequence in $(X,d),\forall \epsilon>0, \exists N$ such that $\forall m,n\geq N, d(p_m,p_n)<\epsilon$
Let $X=\mathbb{Q}$ and $(p_q)=\{1,1.4,1.41,1.414,1.4142,1.41421,\dots\}$ The sequence is Cauchy but does not converge in $\mathbb{Q}$.
This does not hold in $\mathbb{R}$ because compact metric spaces are complete.
Fact: Every Cauchy sequence is bounded.
## Proof that $e$ is irrational
> $e=\sum_{n=0}^\infty \frac{1}{n!}$
Let $s_n=\sum_{k=0}^n \frac{1}{k!}$
So $e-s_n=\left(\sum_{k=n+1}^\infty \frac{1}{k!}\right)<\frac{1}{n!n}$
If $e$ is rational, then $\exists p,q\in\mathbb{Z}$ such that $e=\frac{q}{p}$ and $q!s_q\in\mathbb{Z}$, $q!e=q!\frac{p}{q}\in \mathbb{Z}$, so $q!(e-s_q)\in\mathbb{Z}$
$0<q!(e-s_q)<\frac{1}{n!n}$ leads to contradiction.
## $\limsup$ and $\liminf$
Let $(a_n)=(-1)^n$
$\limsup a_n=1$ and $\liminf a_n=-1$
Let $(a_n)\to a$
$\limsup a_n=\liminf a_n=a$
### Facts about $\limsup$ and $\liminf$
#### Convergence of subsequence
_$\limsup$ is the largest value that subsequence of $a_n$ can approach to._
_$\liminf$ is the smallest value that subsequence of $a_n$ can approach to._
#### Elements of sequence
$\forall x>s^*,\{n:a_n>x\}$ is finite. $\exists N$ such that $\forall n\geq N, a_n\leq x$
$\forall x<s^*,\{n:a_n>x\}$ is infinite.
One example is $(a_n)=(-1)^n\frac{n}{n+1}$
$\limsup a_n=1$ and $\liminf a_n=-1$
So the size of set of elements of $a_n$ that are greater than any $x<1$ is infinite. and the size of set of elements of $a_n$ that are greater than any $x>1$ is finite.
#### $\limsup(a_n+b_n)\leq \limsup a_n+\limsup b_n$
One example for smaller than is $(a_n)=(-1)^n$ and $(b_n)=(-1)^{n+1}$
$\limsup(a_n+b_n)=0$ and $\limsup a_n+\limsup b_n=2$
## ($\forall n,s_n\leq t_n$) $\implies \limsup s_n\leq \limsup t_n$
One example of using this theorem is $(s_n)=\left(\sum_{k=1}^n\frac{1}{k!}\right)$ and $(t_n)=\left(\frac{1}{n}+1\right)^n$
## Rearrangement of series
Will not be tested.
_infinite sum is not similar to finite sum. For infinite sum, the order of terms matters. But for finite sum, the order of terms does not matter, you can rearrange the terms as you want._
## Ways to prove convergence of series
### n-th term test (divergence test)
If $\lim_{n\to\infty}a_n\neq 0$, then $\sum a_n$ diverges.
### Definition of convergence of series (convergence and divergence test)
If $\sum a_n$ converges, then $\lim_{n\to\infty}\sum_{k=1}^n a_k=0$.
Example: Telescoping series and geometric series.
### Comparison test (convergence and divergence test (absolute convergence))
Let $(a_n)$ be a sequence in $\mathbb{C}$ and $(c_n)$ be a non-negative sequence in $\mathbb{R}$. Suppose $\forall n, |a_n|\leq c_n$.
(a) If the series $\sum_{n=1}^{\infty}c_n$ converges, then the series $\sum_{n=1}^{\infty}a_n$ converges.
(b) If the series $\sum_{n=1}^{\infty}a_n$ diverges, then the series $\sum_{n=1}^{\infty}c_n$ diverges.
### Ratio test (convergence and divergence test (absolute convergence))
> $$ \left|\frac{a_{n+1}}{a_n}\right| \leq \alpha \implies |a_n|\leq \alpha^n$$
Given a series $\sum_{n=0}^{\infty} a_n$, $a_n\in\mathbb{C}\backslash\{0\}$.
Then
(a) If $\limsup_{n\to\infty} \left|\frac{a_{n+1}}{a_n}\right| < 1$, then $\sum_{n=0}^{\infty} a_n$ converges.
(b) If $\left|\frac{a_{n+1}}{a_n}\right| \geq 1$ for all $n\geq n_0$ for some $n_0\in\mathbb{N}$, then $\sum_{n=0}^{\infty} a_n$ diverges.
### Root test (convergence and divergence test (absolute convergence))
> $$ \sqrt[n]{|a_n|} \leq \alpha \implies |a_n|\leq \alpha^n$$
Given a series $\sum_{n=0}^{\infty} a_n$, put $\alpha = \limsup_{n\to\infty} \sqrt[n]{|a_n|}$.
Then
(a) If $\alpha < 1$, then $\sum_{n=0}^{\infty} a_n$ converges.
(b) If $\alpha > 1$, then $\sum_{n=0}^{\infty} a_n$ diverges.
(c) If $\alpha = 1$, the test gives no information
### Cauchy criterion
### Geometric series
### P-series
(a) $\sum_{n=0}^{\infty}\frac{1}{n}$ diverges.
(b) $\sum_{n=0}^{\infty}\frac{1}{n^2}$ converges.
### Cauchy condensation test (convergence test)
Suppose $(a_n)$ is a non-negative sequence. The series $\sum_{n=1}^{\infty}a_n$ converges if and only if the series $\sum_{k=0}^{\infty}2^ka_{2^k}$ converges.
### Dirichlet test (convergence test)
Suppose
(a) the partial sum $A_n$ of $\sum a_n$ form a bounded sequence.
(b) $b_0\geq b_1\geq b_2\geq \cdots$ (non-increasing)
(c) $\lim_{n\to\infty}b_n=0$.
Then $\sum a_nb_n$ converges.
Example: $\sum_{n=1}^\infty \frac{(-1)^{n+1}}{n}$ converges.
### Abel's test (convergence test)
Let $(b_n)^\infty_{n=0}$ be a sequence such that:
(a) $b_0\geq b_1\geq b_2\geq \cdots$ (non-increasing)
(b) $\lim_{n\to\infty}b_n=0$
Then if $|z|=1$ and $z\neq 1$, $\sum_{n=0}^\infty b_nz^n$ converges.

164
content/Math4111/Exam_reviews/Math4111_Final.md Normal file
View File

@@ -0,0 +1,164 @@
# Math 4111 Final Review
## Weierstrass M-test
Let $\sum_{n=1}^{\infty} f_n(x)$ be a series of functions.
The weierstrass M-test goes as follows:
1. $\exists M_n \geq 0$ such that $\forall x\in E, |f_n(x)| \leq M_n$.
2. $\sum M_n$ converges.
Then $\sum_{n=1}^{\infty} f_n(x)$ converges uniformly.
Example:
### Ver.0
$\forall x\in [-1,1)$,
$$
\sum_{n=1}^{\infty} \frac{x^n}{n}
$$
converges. (point-wise convergence on $[-1,1)$)
$\forall x\in [-1,1)$,
$$
\left| \frac{x^n}{n} \right| \leq \frac{1}{n}
$$
Since $\sum_{n=1}^{\infty} \frac{1}{n}$ diverges, we don't know if the series converges uniformly or not using the weierstrass M-test.
### Ver.1
However, if we consider the series on $[-1,1]$,
$$
\sum_{n=1}^{\infty} \frac{x^n}{n^2}
$$
converges uniformly. Let $M_n = \frac{1}{n^2}$. This satisfies the weierstrass M-test. And this series converges uniformly on $[-1,1]$.
### Ver.2
$\forall x\in [-\frac{1}{2},\frac{1}{2}]$,
$$
\sum_{n=1}^{\infty} \frac{x^n}{n}
$$
converges uniformly. Since $\left| \frac{x^n}{n} \right|=\frac{|x|^n}{n}\leq \frac{(1/2)^n}{n}\leq \frac{1}{2^n}=M_n$, by geometric series test, $\sum_{n=1}^{\infty} M_n$ converges.
M-test still not applicable here.
$$
\sum_{n=1}^{\infty} \frac{x^n}{n}
$$
converges uniformly on $[-\frac{1}{2},\frac{1}{2}]$.
> Comparison test:
>
> For a series $\sum_{n=1}^{\infty} a_n$, if
>
> 1. $\exists M_n$ such that $|a_n|\leq M_n$
> 2. $\sum_{n=1}^{\infty} M_n$ converges
>
> Then $\sum_{n=1}^{\infty} a_n$ converges.
## Proving continuity of a function
If $f:E\to Y$ is continuous at $p\in E$, then for any $\epsilon>0$, there exists $\delta>0$ such that for any $x\in E$, if $|x-p|<\delta$, then $|f(x)-f(p)|<\epsilon$.
Example:
Let $f(x)=2x+1$. For $p=1$, prove that $f$ is continuous at $p$.
Let $\epsilon>0$ be given. Let $\delta=\frac{\epsilon}{2}$. Then for any $x\in \mathbb{R}$, if $|x-1|<\delta$, then
$$
|f(x)-f(1)|=|2x+1-3|=|2x-2|=2|x-1|<2\delta=\epsilon.
$$
Therefore, $f$ is continuous at $p=1$.
_You can also use smaller $\delta$ and we don't need to find the "optimal" $\delta$._
## Play of open covers
Example of non compact set:
$\mathbb{Q}$ is not compact, we can construct an open cover $G_n=(-\infty,\sqrt{2})\cup (\sqrt{2}+\frac{1}{n},\infty)$.
Every unbounded set is not compact, we construct an open cover $G_n=(-n,n)$.
Every k-cell is compact.
Every finite set is compact.
Let $p\in A$ and $A$ is compact. Then $A\backslash \{p\}$ is not compact, we can construct an open cover $G_n=(\inf(A)-1,p)\cup (p+\frac{1}{n},\sup(A)+1)$.
If $K$ is closed in $X$ and $X$ is compact, then $K$ is compact.
Proof:
Let $\{G_\alpha\}_{\alpha\in A}$ be an open cover of $K$.
> $A$ is open in $X$, if and only if $X\backslash A$ is closed in $X$.
Since $X\backslash K$ is opened in $X$, $\{G_\alpha\}_{\alpha\in A}\cup \{X\backslash K\}$ is an open cover of $X$.
Since $X$ is compact, there exists a finite subcover $\{G_{\alpha_1},\cdots,G_{\alpha_n},X\backslash K\}$ of $X$.
Since $X\backslash K$ is not in the subcover, $\{G_{\alpha_1},\cdots,G_{\alpha_n}\}$ is a finite subcover of $K$.
Therefore, $K$ is compact.
## Cauchy criterion
### In sequences
Def: A sequence $\{a_n\}$ is Cauchy if for any $\epsilon>0$, there exists $N$ such that for any $m,n\geq N$, $|a_m-a_n|<\epsilon$.
Theorem: In $\mathbb{R}$, every sequence is Cauchy if and only if it is convergent.
### In series
Let $s_n=\sum_{k=1}^{n} a_k$.
Def: A series $\sum_{n=1}^{\infty} a_n$ converges if the sequence of partial sums $\{s_n\}$ converges.
$\forall \epsilon>0$, there exists $N$ such that for any $m>n\geq N$,
$$
|s_m-s_n|=\left|\sum_{k=n+1}^{m} a_k\right|<\epsilon.
$$
## Comparison test
If $|a_n|\leq b_n$ and $\sum_{n=1}^{\infty} b_n$ converges, then $\sum_{n=1}^{\infty} a_n$ converges.
Proof:
Since $\sum_{n=1}^{\infty} b_n$ converges, $\forall \epsilon>0$, there exists $N$ such that for any $m>n\geq N$,
$$
\left|\sum_{k=n+1}^{m} b_k\right|<\epsilon.
$$
By triangle inequality,
$$
\left|\sum_{k=n}^{m}a_k\right|\leq \sum_{k=n+1}^{m} |a_k|\leq \sum_{k=n+1}^{m} b_k<\epsilon.
$$
Therefore, $\forall \epsilon>0$, there exists $N$ such that for any $m>n\geq N$,
$$
|s_m-s_n|=\left|\sum_{k=n+1}^{m} a_k\right|<\epsilon.
$$
Therefore, $\{s_n\}$ is Cauchy, and $\sum_{n=1}^{\infty} a_n$ converges.

98
content/Math4111/Math4111_L1.md Normal file
View File

@@ -0,0 +1,98 @@
# Lecture 1
## Introduction
Reading is not recommended before class, it's hard.
## Chapter 1: The real number and complex number systems
* Natural numbers: $\mathbb{N}=\{1,2,3,4....\}$ note by some conventions, $0$ is also a natural number
* IntegersL $\mathbb{Z}=\{...,-2,-1,0,1,2,...\}$
* Rational numbers: $\mathbb{Q}=\{\frac{m}{n}:m,n\in\mathbb{Z}\ and\ n\neq 0\}$
* Real numbers: $\mathbb{R}$ the topic of chapter
* Complex numbers: $\mathbb{C}=\{a+bi:a,b\in \mathbb{R}\}$
### Theorem ($\sqrt{2}$ is irrational)
$\exist p\in \mathbb{Q},p^2=2$ is false.
$\equiv\cancel{\exist} p\in \mathbb{Q}, p^2=2$
$\equiv p\in \mathbb{Q},p^2\neq 2$
<details>
<summary>Proof</summary>
Suppose for contradiction, $\exist p\in \mathbb{Q}$ such that $p^2=\mathbb{Q}$.
Let $p=\frac{m}{n}$, where $m,n \in \mathbb{Z}$ are not both even. (reduced form)
$p^2=2$ and $p=\frac{m}{n}$, so $m^2=2n^2$, so $m^2$ is even, $m$ is even.
So $m^2$ is divisible by 4, $2n^2$ is divisible by 4.
So $n^2$ is even. but they are not both even.
</details>
### Theorem (No closest rational for a irrational number)
Let $A=\{p\in \mathbb{q}, p>0\ and\ p^2\leq 2\}$, Then $A$ does not have a largest element.
i.e. $\exist p\in A$ such that $\forall q\in A, q\leq p$ is false.
> Remark: The book give a very slick proof trying to lean from these kinds of proofs takes some effort. (It is perfectly fine to write that solution this way...)
#### Thought process
Let $p\in A,p\in \mathbb{Q}$, $p>0, p^2<2$.
We want a $\delta\in\mathbb{Q}$ such that $\delta>0$ and $(p+\delta)^2<2$.
$$
\begin{aligned}
(p+\delta)^2&<2\\
p^2+2p\delta+\delta^2&<2\\
\delta(2p+\delta)&< 2-p^2\\
\delta&<\frac{2-p^2}{2p-\delta}
\end{aligned}
$$
From $(p+\delta)^2<2$, we know $\delta<2$ (this is a crude bound, $\delta<\sqrt{2}$).
So one choice can be $\delta=\frac{2-p^2}{2p+2}$
#### Proof
$\forall p\in A$, we can find a $\delta=\frac{2-p^2}{2p+2}$ which is greater than zero ($p^2<2,2-p^2>0,2p+2>0,\delta>0$) and construct a new number $(p+\delta)^2$ such that $p^2<(p+\delta)^2<2$.
_Here we construct a formula for approximate $\sqrt{2}=\lim_{i\to \infty}p_0=1,p_{i+1}=p_i+\frac{2-p_i^2}{2p_i+2}$_
Interesting...
We can also further optimize the formula by changing the bound of $\delta$ to $\delta< 2-p$, since $(p+\delta)^2<2,p+\delta<2$
```python
def sqrt_2(acc):
if acc==0: return 1
c=sqrt_2(n-1)
return c+((2-c**2)/(2*c+2))
```
### Definition and notations for sets
Some set notation
$\Pi\in \mathbb{R}$
use $\subset,\subsetneq$ in this class.
* $A\subset B$, $\forall x\in A, x\in B$
* $A=B$, $A\subset B$ and $B\subset A$
* $A\subsetneq$ means $A\subset B$ and $A\neq B$

62
content/Math4111/index.md Normal file
View File

@@ -0,0 +1,62 @@
# Math 4111
This is a course about real analysis.
Topics include:
1. Number Theory
2. Basic topology and set theory
3. Sequences and Series
4. Convergence of Series and Sequences
5. Limits and Continuity
The course is taught by [Alan Chang](https://math.wustl.edu/pQEDle/alan-chang).
<!--
It is easy in my semester perhaps, it is the first course I got 3 perfect scores in exams. (Unfortunately, I did not get the extra credit for the third midterm exam.)
## Midterms stats
Our semester is way more easier than the previous ones. The previous ones got median scores of 25.
Stats for first midterm:
| |out of|avg|stddev|25th|50th|75th|
|--|--|--|--|--|--|--|
|total|50|40.7|9.9|37.0|45.0|48.0|
|1a|10|9.3|2.0|10.0|10.0|10.0|
|1b|10|8.3|2.4|6.8|9.0|10.0|
|2a|10|7.5|3.1|6.0|8.0|10.0|
|2b|10|6.9|3.4|4.0|8.0|10.0|
|3|10|8.8|2.4|9.0|10.0|10.0|
I skipped the last half hour, still get 50. I can't believe how easy it is compared to homework assignments.
Stats for second midterm:
| |out of|avg|stddev|25th|50th|75th|
|--|--|--|--|--|--|--|
|total|50.0|37.3|12.4|30.5|41.0|47.5|
|1|10|7.6|3.2|4.0|10.0|10.0|
|2|10|8.9|2.7|10.0|10.0|10.0|
|3|10|6.6|3.4|4.0|8.0|10.0|
|4a|10|6.6|4.1|2.0|9.0|10.0|
|4b|10|7.7|3.5|8.0|10.0|10.0|
I skipped the last half hour again, still get 50. But I felt this time is more challenging than the first one. Much like what Math is.
Stats for third midterm:
| |out of|avg|stddev|25th|50th|75th|
|--|--|--|--|--|--|--|
|total|50.0|37.2|10.1|31.0|40.0|44.8|
|1|10|8.2|3.1|7.0|10.0|10.0|
|2|10|8.2|2.5|7.0|10.0|10.0|
|3|10|7.1|3.0|6.0|6.0|10.0|
|4a|10|5.6|4.2|0.0|6.5|9.8|
|4b|10|8.1|3.4|6.5|10.0|10.0|
|5|0|0.0|0.1|0.0|0.0|0.0|
I got 50 and just barely made it. The third midterm is the hardest one. The extra credit question is way too hard and I only got few minutes to solve it.-->

264
content/Math4121/Exam_reviews/Math4121_E1.md Normal file
View File

@@ -0,0 +1,264 @@
# Math4121 Exam 1 Review
Range: Chapter 5 and 6 of Rudin. We skipped (and so you will not be tested on)
- Differentiation of Vector Valued Functions (pp. 111-113)
- Integration of Vector-Valued Function and Rectifiable Curves (pp.135-137)
You will also not be tested on Uniform Convergence and Integration, which we cover in class on Monday 2/10.
## Chapter 5: Differentiation
### Definition of the Derivative
Let $f$ be a real function defined on an closed interval $[a,b]$. We say that $f$ is differentiable at a point $x \in [a,b]$ if the following limit exists:
$$
f'(x) = \lim_{t\to x} \frac{f(t) - f(x)}{t - x}
$$
If the limit exists, we call it the derivative of $f$ at $x$ and denote it by $f'(x)$.
#### Theorem 5.2
Every differentiable function is [continuous](https://notenextra.trance-0.com/Math4111/Math4111_L22#definition-45).
The converse is not true, consider $f(x) = |x|$.
#### Theorem 5.3
If $f,g$ are differentiable at $x$, then
1. $(f+g)'(x) = f'(x) + g'(x)$
2. $(fg)'(x) = f'(x)g(x) + f(x)g'(x)$
3. If $g(x) \neq 0$, then $(f/g)'(x) = (f'(x)g(x) - f(x)g'(x))/g(x)^2$
#### Theorem 5.4
Constant function is differentiable and its derivative is $0$.
#### Theorem 5.5
Chain rule: If $f$ is differentiable at $x$ and $g$ is differentiable at $f(x)$, then the composite function $g\circ f$ is differentiable at $x$ and
$$
(g\circ f)'(x) = g'(f(x))f'(x)
$$
#### Theorem 5.8
The derivative of local extremum ($\exists \delta > 0$ s.t. $f(x)\geq f(y)$ or $f(x)\leq f(y)$ for all $y\in (x-\delta,x+\delta)$) is $0$.
#### Theorem 5.9
Generalized mean value theorem: If $f,g$ are differentiable on $(a,b)$, then there exists a point $x\in (a,b)$ such that
$$
(f(b)-f(a))g'(x) = (g(b)-g(a))f'(x)
$$
If we put $g(x) = x$, we get the mean value theorem.
$$
f(b)-f(a) = f'(x)(b-a)
$$
for some $x\in (a,b)$.
#### Theorem 5.12
Intermediate value theorem:
If $f$ is differentiable on $[a,b]$, for all $\lambda$ between $f'(a)$ and $f'(b)$, there exists a $c\in (a,b)$ such that $f'(x) = \lambda$.
#### Theorem 5.13
L'Hôpital's rule: If $f,g$ are differentiable in $(a,b)$ and $g'(x) \neq 0$ for all $x\in (a,b)$, where $-\infty \leq a < b \leq \infty$,
Suppose
$$
\frac{f'(x)}{g'(x)} \to A \text{ as } x\to a
$$
If
$$
f(x) \to 0, g(x) \to 0 \text{ as } x\to a
$$
or if
$$
g(x) \to \infty \text{ as } x\to a
$$
then
$$
\lim_{x\to a} \frac{f(x)}{g(x)} = A
$$
#### Theorem 5.15
Taylor's theorem: If $f$ is $n$ times differentiable on $[a,b]$, $f^{(n-1)}$ is continuous on $[a,b]$, and $f^{(n)}$ exists on $(a,b)$, for any distinct points $\alpha, \beta \in [a,b]$, there exists a point $x\in (\alpha, \beta)$ such that
$$
f(\beta) =\left(\sum_{k=0}^{n-1} \frac{f^{(k)}(\alpha)}{k!}(\beta-\alpha)^k\right) + \frac{f^{(n)}(x)}{n!}(\beta-\alpha)^n
$$
## Chapter 6: Riemann-Stieltjes Integration
### Definition of the Integral
Let $\alpha$ be a monotonically increasing function on $[a,b]$.
A partition of $[a,b]$ is a set of points $P = \{x_0, x_1, \cdots, x_n\}$ such that
$$
a = x_0 < x_1 < \cdots < x_n = b
$$
Let $\Delta \alpha_i = \alpha(x_{i}) - \alpha(x_{i-1})$ for $i = 1, \cdots, n$.
Let $m_i = \inf \{f(x) : x_{i-1} \leq x \leq x_{i}\}$ and $M_i = \sup \{f(x) : x_{i-1} \leq x \leq x_{i}\}$ for $i = 1, \cdots, n$.
The lower sum of $f$ with respect to $\alpha$ is
$$L(f,P,\alpha) = \sum_{i=1}^{n} m_i \Delta \alpha_i$$
The upper sum of $f$ with respect to $\alpha$ is
$$U(f,P,\alpha) = \sum_{i=1}^{n} M_i \Delta \alpha_i$$
Let $\overline{\int_a^b} f(x) d\alpha(x)=\sup_P L(f,P,\alpha)$ and $\underline{\int_a^b} f(x) d\alpha(x)=\inf_P U(f,P,\alpha)$.
If $\overline{\int_a^b} f(x) d\alpha(x) = \underline{\int_a^b} f(x) d\alpha(x)$, we say that $f$ is Riemann-Stieltjes integrable with respect to $\alpha$ on $[a,b]$ and we write
$$
\int_a^b f(x) d\alpha(x) = \overline{\int_a^b} f(x) d\alpha(x) = \underline{\int_a^b} f(x) d\alpha(x)
$$
#### Theorem 6.4
Refinement of partition will never make the lower sum smaller or the upper sum larger.
$$
L(f,P,\alpha) \leq L(f,P^*,\alpha) \leq U(f,P^*,\alpha) \leq U(f,P,\alpha)
$$
#### Theorem 6.5
$\underline{\int_a^b} f(x) d\alpha(x) \leq \overline{\int_a^b} f(x) d\alpha(x)$
#### Theorem 6.6
$f\in \mathscr{R}(\alpha)$ on $[a,b]$ if and only if for every $\epsilon > 0$, there exists a partition $P$ of $[a,b]$ such that
$$
U(f,P,\alpha) - L(f,P,\alpha) < \epsilon
$$
#### Theorem 6.8
Every continuous function on a closed interval is Riemann-Stieltjes integrable with respect to any monotonically increasing function.
#### Theorem 6.9
If $f$ is monotonically increasing on $[a,b]$ and **$\alpha$ is continuous on $[a,b]$**, then $f\in \mathscr{R}(\alpha)$ on $[a,b]$.
Key: We can repartition the interval $[a,b]$ using $f$.
#### Theorem 6.10
If $f$ is bounded on $[a,b]$ and has only **finitely many discontinuities** on $[a,b]$, then $f\in \mathscr{R}(\alpha)$ on $[a,b]$.
Key: We can use the bound and partition around the points of discontinuity to make the error arbitrary small.
#### Theorem 6.11
If $f\in \mathscr{R}(\alpha)$ on $[a,b]$, and $m\leq f(x) \leq M$ for all $x\in [a,b]$, and $\phi$ is a continuous function on $[m,M]$, then $\phi\circ f\in \mathscr{R}(\alpha)$ on $[a,b]$.
_Composition of bounded integrable functions and continuous functions is integrable._
#### Theorem 6.12
Properties of the integral:
Let $f,g\in \mathscr{R}(\alpha)$ on $[a,b]$, and $c$ be a constant. Then
1. $f+g\in \mathscr{R}(\alpha)$ on $[a,b]$ and $\int_a^b (f(x) + g(x)) d\alpha(x) = \int_a^b f(x) d\alpha(x) + \int_a^b g(x) d\alpha(x)$
2. $cf\in \mathscr{R}(\alpha)$ on $[a,b]$ and $\int_a^b cf(x) d\alpha(x) = c\int_a^b f(x) d\alpha(x)$
3. $f\in \mathscr{R}(\alpha)$ on $[a,b]$ and $c\in [a,b]$, then $\int_a^b f(x) d\alpha(x) = \int_a^c f(x) d\alpha(x) + \int_c^b f(x) d\alpha(x)$.
4. **Favorite Estimate**: If $|f(x)| \leq M$ for all $x\in [a,b]$, then $\left|\int_a^b f(x) d\alpha(x)\right| \leq M(\alpha(b)-\alpha(a))$.
5. If $f\in \mathscr{R}(\beta)$ on $[a,b]$, then $\int_a^b f(x) d(\alpha+\beta) = \int_a^b f(x) d\alpha + \int_a^b f(x) d\beta$.
#### Theorem 6.13
If $f,g\in \mathscr{R}(\alpha)$ on $[a,b]$, then
1. $fg\in \mathscr{R}(\alpha)$ on $[a,b]$
2. $|f|\in \mathscr{R}(\alpha)$ on $[a,b]$ and $\left|\int_a^b f(x) d\alpha(x)\right| \leq \int_a^b |f(x)| d\alpha(x)$
Key: (1), use Theorem 6.12, 6.11 to build up $fg$ from $(f+g)^2-f^2-g^2$. (2), take $\phi(x) = |x|$ in Theorem 6.11.
#### Theorem 6.14
Integration over indicator functions:
If $a<s<b$, $f$ is bounded on $[a,b]$, and $f$ is continuous at $s$, and $\alpha(x)=I(x-s)$, then
$$
\int_a^b f(x) d\alpha(x) = f(s)
$$
Key: Note the max difference can be made only occurs at $s$.
#### Theorem 6.15
Integration over step functions:
If $\alpha(x) = \sum_{i=1}^{n} c_i I(x-x_i)$ for $x\in [a,b]$, then
$$
\int_a^b f(x) d\alpha(x) = \sum_{i=1}^{n} c_i f(x_i)
$$
#### Theorem 6.21
Fundamental theorem of calculus:
Let $f\in \mathscr{R}(\alpha)$ on $[a,b]$, and $F(x) = \int_a^x f(t) d\alpha(t)$. Then
1. $F$ is continuous on $[a,b]$
2. If $f$ is continuous at $x\in [a,b]$, then $F$ is differentiable at $x$ and $F'(x) = f(x)$
## Chapter 7: Sequence and Series of Functions
### Example of non-Riemann integrable function
$\lim_{m\to \infty} \lim_{n\to \infty} (\cos(m!\pi x))^{2n}=\begin{cases} 1 & x\in \mathbb{Q} \\ 0 & x\notin \mathbb{Q} \end{cases}$
This function is everywhere discontinuous and not Riemann integrable.
### Uniform Convergence
#### Definition 7.7
A sequence of functions $\{f_n\}$ converges uniformly to $f$ on $E$ if for every $\epsilon > 0$, there exists a positive integer $N$ such that
$$
|f_n(x) - f(x)| < \epsilon \text{ for all } x\in E \text{ and } n\geq N
$$
If $E$ is a point, then that's the common definition of convergence.
If we have uniform convergence, then we can swap the order of limits.
#### Theorem 7.16
If $\{f_n\}\in \mathscr{R}(\alpha)$ on $[a,b]$, and $\{f_n\}$ converges uniformly to $f$ on $[a,b]$, then
$$
\int_a^b f(x) d\alpha(x) = \lim_{n\to \infty} \int_a^b f_n(x) d\alpha(x)
$$
Key: Use the definition of uniform convergence to bound the difference between the integral of the limit and the limit of the integral. $\int_a^b (f-f_n)d\alpha \leq |f-f_n| \int_a^b d\alpha = |f-f_n| (\alpha(b)-\alpha(a))$.

279
content/Math4121/Exam_reviews/Math4121_E2.md Normal file
View File

@@ -0,0 +1,279 @@
# Math4121 Exam 2 Review
Range: Chapter 2-4 of Bressoud's A Radical Approach to Lebesgue's Theory of Integration
## Chapter 2
### The Riemann-Stieltjes Integral
#### Definition of the Riemann-Stieltjes Integral
Let $f$ be a bounded function on $[a,b]$ and $\alpha$ be a bounded function on $[a,b]$.
We say that $f$ is Riemann-Stieltjes integrable with respect to $\alpha$ on $[a,b]$ if there exists a number $I$ such that for every $\epsilon > 0$, there exists a $\delta > 0$ such that for every partition $P = \{a = x_0, x_1, \ldots, x_n = b\}$ of $[a,b]$ with $||P|| < \delta$, we have
$$
\left| \int_a^b f \, d\alpha - I \right| < \epsilon
$$
If $f$ is Riemann-Stieltjes integrable with respect to $\alpha$ on $[a,b]$, we write
$$
\int_a^b f \, d\alpha = I
$$
#### Darboux Sums
Let $P = \{a = x_0, x_1, \ldots, x_n = b\}$ be a partition of $[a,b]$.
The upper Darboux sum of $f$ with respect to $\alpha$ is
$$
U(f, \alpha, P) = \sum_{i=1}^n M_i (x_i - x_{i-1})
$$
where $M_i = \sup_{x \in [x_{i-1}, x_i]} f(x)$ and $\alpha_i = \sup_{x \in [x_{i-1}, x_i]} \alpha(x)$.
The lower Darboux sum of $f$ with respect to $\alpha$ is
$$
L(f, \alpha, P) = \sum_{i=1}^n m_i (x_i - x_{i-1})
$$
where $m_i = \inf_{x \in [x_{i-1}, x_i]} f(x)$ and $\alpha_i = \inf_{x \in [x_{i-1}, x_i]} \alpha(x)$.
### Fail of Riemann-Stieltjes Integration
Consider the function
$$
((x)) = \begin{cases}
x-\lfloor x \rfloor & x \in [\lfloor x \rfloor, \lfloor x \rfloor + \frac{1}{2}) \\
0 & x=\lfloor x \rfloor + \frac{1}{2}\\
x-\lfloor x \rfloor - 1 & x \in (\lfloor x \rfloor + \frac{1}{2}, \lfloor x \rfloor + 1] \end{cases}
$$
![Graph of y=((x))](https://notenextra.trance-0.com/Math4121/y=((x)).png)
We define
$$
f(x) = \sum_{n=1}^{\infty} \frac{((nx))}{n^2}=\lim_{N\to\infty}\sum_{n=1}^{N} \frac{((nx))}{n^2}
$$
![Graph of y=f(x)](https://notenextra.trance-0.com/Math4121/sum_y=((x)).png)
(i) The series converges uniformly over $x\in[0,1]$.
$$
\left|f(x)-\sum_{n=1}^{N} \frac{((nx))}{n^2}\right|\leq \sum_{n=N+1}^{\infty}\frac{|((nx))|}{n^2}\leq \sum_{n=N+1}^{\infty} \frac{1}{n^2}<\epsilon
$$
As a consequence, $f(x)\in \mathscr{R}$.
(ii) $f$ has a discontinuity at every rational number with even denominator.
$$
\begin{aligned}
\lim_{h\to 0^+}f(\frac{a}{2b}+h)-f(\frac{a}{2b})&=\lim_{h\to 0^+}\sum_{n=1}^{\infty}\frac{((\frac{na}{2b}+h))}{n^2}-\sum_{n=1}^{\infty}\frac{((\frac{na}{2b}))}{n^2}\\
&=\lim_{h\to 0^+}\sum_{n=1}^{\infty}\frac{((\frac{na}{2b}+h))-((\frac{na}{2b}))}{n^2}\\
&=\sum_{n=1}^{\infty}\lim_{h\to 0^+}\frac{((\frac{na}{2b}+h))-((\frac{na}{2b}))}{n^2}\\
&>0
\end{aligned}
$$
#### Some integrable functions are not differentiable (violates the fundamental theorem of calculus)
Solve:
Define the oscilation of $f$ on $[x_{i-1}, x_i]$ as
$$
\omega(f, [x_{i-1}, x_i]) = \sup_{x,y \in [x_{i-1}, x_i]} |f(x) - f(y)|-\inf_{x,y \in [x_{i-1}, x_i]} |f(x) - f(y)|
$$
And define continuous functions as those functions that have oscilation 0 on every subinterval of their domain.
that is, the function $f$ is continuous at $c$ if $\omega(f,c) = 0$.
And we claim that the function is integrable on $[a,b]$ if and only if the outer measure of the set of discontinuities of $f$ is 0.
> Finite cover:
>
> Given a set $S$, an **finite cover** of $S$ is a **finite** collection of open/ or closed/ or half-open intervals $\{I_1, I_2, \ldots, I_n\}$ such that $S \subseteq \bigcup_{i=1}^n I_i$. The set of all finite covers of $S$ is denoted by $\mathcal{C}_S$.
> Length of a cover:
>
> The **length** of a cover $\ell(C)$ is the sum of the lengths of the intervals in the cover. (open/closed/half-open doesn't matter.)
> Outer content:
>
> The **outer content** of a set $S$ is the infimum of the lengths of all **finite covers** of $S$. $c_e(S) = \inf_{C\in \mathcal{C}_S}\ell(C)$. (e denotes "exterior")
Homework question: You cannot cover an interval $[a,b]$ with length $k$ with a finite cover of length strictly less than $k$.
Proceed by counting the intervals $I_i = [l_i, r_i]$ in the cover, and $r_n-l_0$ is less than or equal to $c_e(S)$ and $l_0\leq a$ and $r_n\leq b$.
#### Theorem 2.5
Given a bounded function $f$ defined on the interval $[a,b]$, let $S_\sigma$ be the points in $[a,b]$ with oscilation greater than $\sigma$.
The function $f$ is Riemann-Stieltjes integrable over $[a,b]$ if and only if $\lim_{\sigma \to 0} |S_\sigma| = 0$. That is, for every $\sigma > 0$, the outer content of $S_\sigma$ is 0.
Extra terminology:
> Dense:
>
> A set $S$ is **dense** in the interval $I$ is every open subinterval of $I$ contains a point of $S$.
>
> This is equivalent to saying that $S$ is dense in $I$ if every point of $I$ is a limit point of $S$ or a point of $S$. (proved in homework)
> Totally discontinuous:
>
> A discontinuous function is **totally discontinuous** in an interval if the set of points of continuity is not dense in that interval.
>
> In other words, there exists an open interval $I$ such that the set of points of continuity of $f$ in $I$ is empty.
> Pointwise discontinuity:
>
> A discontinuous function is **pointwise discontinuous** if the set of points of discontinuity is dense in the domain of $f$.
> Accumulation point (limit point):
>
> A point $p$ is an **accumulation point** of a set $S$ if every neighborhood of $p$ contains a point of $S$ other than $p$ itself. (That is, there exists a convergent sequence $\{p_n\}_{n=1}^\infty$ in $S$ such that $\lim_{n\to\infty} p_n = p$ and $p_n \neq p$ for all $n \in \mathbb{N}$. Proved in Rudin)
> Derived set:
>
> The **derived set** of a set $S$ is the set of all accumulation points of $S$. $S' = \{p \in \mathbb{R} \mid \forall \epsilon > 0, \exists x \in S \text{ s.t. } 0 < |x-p| < \epsilon\}$.
> Type 1 set:
>
> A set $S$ is a **type 1 set** if $S'\neq \emptyset$ and $S''=\emptyset$.
> Type $n$ set:
>
> A set $S$ is a **type $n$ set** if $S'$ is a type $n-1$ set.
> First species:
>
> A set $S$ is of **first species** if it is type $n$ for some $n\geq 0$, otherwise it is of **second species**.
$\mathbb{Q}$ is not first species since it is dense in $\mathbb{R}$ and $\mathbb{Q}' = \mathbb{R}$.
$\mathbb{R}$ is not first species.
## Chapter 3
### Topology of $\mathbb{R}$
> Open set:
>
> A set $S$ is **open** if for every $x \in S$, there exists an $\epsilon > 0$ such that $B_\epsilon(x) \subseteq S$.
> Closed set:
>
> A set $S$ is **closed** if its complement is open.
>
> Equivalently, a set $S$ is closed if it contains all of its limit points. That is $S' \subseteq S$.
> Interior of a set:
>
> The **interior** of a set $S$ is the set of all points in $S$ such that there exists an $\epsilon > 0$ such that $B_\epsilon(x) \subseteq S$. $S^\circ = \{x \in S \mid \exists \epsilon > 0 \text{ s.t. } B_\epsilon(x) \subseteq S\}$. (It is also the union of all open sets contained in $S$.)
> Closure of a set:
>
> The **closure** of a set $S$ is the set of all points that for every $\epsilon > 0$, $B_\epsilon(x) \cap S \neq \emptyset$. $\overline{S} = \{x \in \mathbb{R} \mid \forall \epsilon > 0, B_\epsilon(x) \cap S \neq \emptyset\}$.
> Boundary of a set:
>
> The **boundary** of a set $S$ is the set of all points in $S$ that are not in the interior of $S$. $\partial S = \overline{S} \setminus S^\circ$.
#### Theorem 3.4
Bolzano-Weierstrass Theorem:
Every bounded infinite set has an accumulation point.
Proof:
Let $S$ be a bounded infinite set. Cut the interval $[a,b]$ into two halves, and let $I_1$ be one with infinitely many points of $S$. (such set exists since $S$ is infinite.)
Let $I_2$ be the one half with infinitely many points of $I_1$.
By induction, we can cut the interval into two halves, and let $I_{n+1}$ be the one half with infinitely many points of $I_n$.
By the nested interval property, there exists a point $c$ that is in all $I_n$.
$c$ is an accumulation point of $S$.
QED
#### Theorem 3.6 (Heine-Borel Theorem)
For any open cover of a compact set, there exists a finite subcover.
> Compact set:
>
> A set $S$ is **compact** if every open cover of $S$ has a finite subcover. In $\mathbb{R}$, this is equivalent to being closed and bounded.
> Cardinality:
>
> The **cardinality** of $\mathbb{R}$ is $\mathfrak{c}$.
>
> The **cardinality** of $\mathbb{N}$, $\mathbb{Z}$, and $\mathbb{Q}$ is $\aleph_0$.
## Chapter 4
### Nowhere Dense set
A set $S$ is **nowhere dense** if there are no open intervals in which $S$ is dense.
That is equivalent to **$S'$ contains no open intervals**.
Note: If $S$ is nowhere dense, then $S^c$ is dense. But if $S$ is dense, $S^c$ is not necessarily nowhere dense. (Consider $\mathbb{Q}$)
### Perfect Set
A set $S$ is **perfect** if $S'=S$.
Example: open intervals, Cantor set.
#### Cantor set
The Cantor set ($SVC(3)$) is the set of all real numbers in $[0,1]$ that can be represented in base 3 using only the digits 0 and 2.
The outer content of the Cantor set is 0.
#### Generalized Cantor set (SVC(n))
The outer content of $SVC(n)$ is $\frac{n-3}{n-2}$.
#### Lemma 4.4
Osgood's Lemma:
Let $G$ be a closed, bounded set and Let $G_1\subseteq G_2\subseteq \ldots$ and $G=\bigcup_{n=1}^{\infty} G_n$. Then $\lim_{n\to\infty} c_e(G_n)=c_e(G)$.
Key: Using Heine-Borel Theorem.
#### Theorem 4.5
Arzela-Osgood Theorem:
Let $\{f_n\}_{n=1}^{\infty}$ be a sequence of continuous, uniformly bounded functions on $[0,1]$ that converges pointwise to $0$. It follows that
$$
\lim_{n\to\infty}\int_0^1 f_n(x) \, dx = \int_0^1 \lim_{n\to\infty} f_n(x) \, dx=0
$$
Key: Using Osgood's Lemma and do case analysis on bounded and unbounded parts of the Riemann-Stieltjes integral.
#### Theorem 4.7
Baire Category Theorem:
An open interval cannot be covered by a countable union of nowhere dense sets.

370
content/Math4121/Exam_reviews/Math4121_Final.md Normal file
View File

@@ -0,0 +1,370 @@
# Math4121 Final Review
## Guidelines
There is one question from Exam 2 material.
3 T/F from Exam 1 material.
The remaining questions cover the material since Exam 2 (Chapters 5 and 6 of Bressoud and my lecture notes for the final week).
The format of the exam is quite similar to Exam 2, maybe a tad longer (but not twice as long, don't worry).
## Chapter 5: Measure Theory
### Jordan Measure
> Content
>
> Let $\mathcal{C}_S^e$ be the set of all finite covers of $S$ by closed intervals ($S\subset C$, where $C$ is a finite union of closed intervals).
>
> Let $\mathcal{C}_S^i$ be the set of disjoint intervals that contained in $S$ ($\bigcup_{i=1}^n I_i\subset S$, where $I_i$ are disjoint intervals).
>
> Let $c_e(S)=\sup_{C\in\mathcal{C}_S^e} \sum_{i=1}^n |I_i|$ be the outer content of $S$.
>
> Let $c_i(S)=\inf_{I\in\mathcal{C}_S^i} \sum_{i=1}^n |I_i|$ be the inner content of $S$.
>
> _Here we use $|I|$ to denote the length of the interval $I$, in book we use volume but that's not important here._
>
> The content of $S$ is defined if $c(S)=c_e(S)=c_i(S)$
Note that from this definition, **for any pairwise disjoint collection of sets** $S_1, S_2, \cdots, S_N$, we have
$$
\sum_{i=1}^N c_i(S_i)\leq c_i(\bigcup_{i=1}^N S_i)\leq c_e(\bigcup_{i=1}^N S_i)\leq \sum_{i=1}^N c_e(S_i)
$$
by $\sup$ and $\inf$ in the definition of $c_e(S)$ and $c_i(S)$.
#### Proposition 5.1
$$
c_e(S)=c_i(S)+c_e(\partial S)
$$
Note the boundary of $S$ is defined as $\partial S=\overline{S}\setminus S^\circ$ (corrected by Nathan Zhou).
> Some common notations for sets:
>
> $S^\circ$ is the interior of $S$. $S^\circ=\{x\in S| \exists \epsilon>0, B(x,\epsilon)\subset S\}$ (largest open set contained in $S$)
>
> $S'$ is the set of limit points of $S$ (derived set of $S$). $S'=\{x\in \mathbb{R}^n|\forall \epsilon>0, B(x,\epsilon)\setminus \{x\}\cap S\neq \emptyset\}$ (Topological definition of limit point).
>
> $\overline{S}$ is the closure of $S$. $\overline{S}=S\cup S'$ (smallest closed set containing $S$)
Equivalently, $\forall x\in \partial S$, $\forall \epsilon>0$, $\exists p\notin S$ and $q\notin S$ s.t. $d(x,p)<\epsilon$ and $d(x,q)<\epsilon$.
So the content of $S$ is defined if and only if $c_e(\partial S)=0$.
> Jordan Measurable
>
> A set $S$ is Jordan measurable if and only if $c_e(\partial S)=0$, ($c(S)=c_e(S)=c_i(S)$)
#### Proposition 5.2
Finite additivity of content:
Let $S_1, S_2, \cdots, S_N$ be a finite collection of pairwise disjoint Jordan measurable sets.
$$
c(\bigcup_{i=1}^N S_i)=\sum_{i=1}^N c(S_i)
$$
Example for Jordan measure of sets
| Set | Inner Content | Outer Content | Content |
| --- | --- | --- | --- |
| $\emptyset$ | 0 | 0 | 0 |
| $\{q\},q\in \mathbb{R}$ | 0 | 0 | 0 |
| $\{\frac{1}{n}\}_{n=1}^\infty$ | 0 | 0 | 0 |
| $\{[n,n+\frac{1}{2^n}]\}_{n=1}^\infty$ | 1 | 1 | 1 |
| $SVC(3)$ | 0 | 1 | Undefined |
| $SVC(4)$ | 0 | $\frac{1}{2}$ | Undefined |
| $Q\cap [0,1]$ | 0 | 1 | Undefined |
| $[0,1]\setminus Q$ | 0 | 1 | Undefined |
| $[a,b], a<b\in \mathbb{R}$ | $b-a$ | $b-a$ | $b-a$ |
| $[a,b),a<b\in \mathbb{R}$ | $b-a$ | $b-a$ | $b-a$ |
| $(a,b],a<b\in \mathbb{R}$ | $b-a$ | $b-a$ | $b-a$ |
| $(a,b),a<b\in \mathbb{R}$ | $b-a$ | $b-a$ | $b-a$ |
### Borel Measure
Our desired property of measures:
1. Measure of interval is the length of the interval. $m([a,b])=m((a,b))=m([a,b))=m((a,b])=b-a$
2. Countable additivity: If $S_1, S_2, \cdots, S_N$ are pairwise disjoint Borel measurable sets, then $m(\bigcup_{i=1}^N S_i)=\sum_{i=1}^N m(S_i)$
3. Closure under set minus: If $S$ is Borel measurable and $T$ is Borel measurable, then $S\setminus T$ is Borel measurable with $m(S\setminus T)=m(S)-m(T)$
#### Borel Measurable Sets
$\mathcal{B}$ is the smallest $\sigma$-algebra that contains all closed intervals.
> Sigma algebra: A $\sigma$-algebra is a collection of sets that is closed under **countable** union, intersection, and complement.
>
> That is:
>
> 1. $\emptyset\in \mathcal{B}$
> 2. If $A\in \mathcal{B}$, then $A^c\in \mathcal{B}$
> 3. If $A_1, A_2, \cdots, A_N\in \mathcal{B}$, then $\bigcup_{i=1}^N A_i\in \mathcal{B}$
#### Proposition 5.3
Borel measurable sets does not contain all Jordan measurable sets.
Proof by cardinality of sets.
Example for Borel measure of sets
| Set | Borel Measure |
| --- | --- |
| $\emptyset$ | 0 |
| $\{q\},q\in \mathbb{R}$ | 0 |
| $\{\frac{1}{n}\}_{n=1}^\infty$ | 0 |
| $\{[n,n+\frac{1}{2^n}]\}_{n=1}^\infty$ | 1 |
| $SVC(3)$ | 0 |
| $SVC(4)$ | 0 |
| $Q\cap [0,1]$ | 0 |
| $[0,1]\setminus Q$ | 1 |
| $[a,b], a<b\in \mathbb{R}$ | $b-a$ |
| $[a,b),a<b\in \mathbb{R}$ | $b-a$ |
| $(a,b],a<b\in \mathbb{R}$ | $b-a$ |
| $(a,b),a<b\in \mathbb{R}$ | $b-a$ |
### Lebesgue Measure
> Lebesgue measure
>
> Let $\mathcal{C}$ be the set of all countable covers of $S$.
>
> The Lebesgue outer measure of $S$ is defined as:
>
> $$m_e(S)=\inf_{C\in\mathcal{C}} \sum_{i=1}^\infty |I_i|$$
>
> If $S\subset[a,b]$, then the inner measure of $S$ is defined as:
>
> $$m_i(S)=(b-a)-m_e([a,b]\setminus S)$$
>
> If $m_i(S)=m_e(S)$, then $S$ is Lebesgue measurable.
#### Proposition 5.4
Subadditivity of Lebesgue outer measure:
For any collection of sets $S_1, S_2, \cdots, S_N$,
$$m_e(\bigcup_{i=1}^N S_i)\leq \sum_{i=1}^N m_e(S_i)$$
#### Theorem 5.5
If $S$ is bounded, then any of the following conditions imply that $S$ is Lebesgue measurable:
1. $m_e(S)=0$
2. $S$ is countable (measure of countable set is 0)
3. $S$ is an interval
> Alternative definition of Lebesgue measure
>
> The outer measure of $S$ is defined as the infimum of all the open sets that contain $S$.
>
> The inner measure of $S$ is defined as the supremum of all the closed sets that are contained in $S$.
#### Theorem 5.6
Caratheodory's criterion:
A set $S$ is Lebesgue measurable if and only if for any set $X$ with finite outer measure,
$$m_e(X-S)=m_e(X)-m_e(X\cap S)$$
#### Lemma 5.7
Local additivity of Lebesgue outer measure:
If $I_1, I_2, \cdots, I_N$ are any countable collection of **pairwise disjoint intervals** and $S$ is a bounded set, then
$$
m_e\left(S\cup \bigcup_{i=1}^N I_i\right)=\sum_{i=1}^N m_e(S\cap I_i)
$$
#### Theorem 5.8
Countable additivity of Lebesgue outer measure:
If $S_1, S_2, \cdots, S_N$ are any countable collection of pairwise disjoint Lebesgue measurable sets, **whose union has a finite outer measure,** then
$$
m_e\left(\bigcup_{i=1}^N S_i\right)=\sum_{i=1}^N m_e(S_i)
$$
#### Theorem 5.9
Any finite union or intersection of Lebesgue measurable sets is Lebesgue measurable.
#### Theorem 5.10
Any countable union or intersection of Lebesgue measurable sets is Lebesgue measurable.
#### Corollary 5.12
Limit of a monotone sequence of Lebesgue measurable sets is Lebesgue measurable.
If $S_1\subseteq S_2\subseteq S_3\subseteq \cdots$ are Lebesgue measurable sets, then $\bigcup_{i=1}^\infty S_i$ is Lebesgue measurable. And $m(\bigcup_{i=1}^\infty S_i)=\lim_{i\to\infty} m(S_i)$
If $S_1\supseteq S_2\supseteq S_3\supseteq \cdots$ are Lebesgue measurable sets, **and $S_1$ has finite measure**, then $\bigcap_{i=1}^\infty S_i$ is Lebesgue measurable. And $m(\bigcap_{i=1}^\infty S_i)=\lim_{i\to\infty} m(S_i)$
#### Theorem 5.13
Non-measurable sets (under axiom of choice)
Note that $(0,1)\subseteq \bigcup_{q\in \mathbb{Q}\cap (-1,1)}(\mathcal{N}+q)\subseteq (-1,2)$
$$
\bigcup_{q\in \mathbb{Q}\cap (-1,1)}(\mathcal{N}+q)
$$
is not Lebesgue measurable.
## Chapter 6: Lebesgue Integration
### Lebesgue Integral
Let the partition on y-axis be $l=l_0<l_1<\cdots<l_n=L$, and $S_i=\{x|l_i<f(x)<l_{i+1}\}$
The Lebesgue integral of $f$ over $[a,b]$ is bounded by:
$$
\sum_{i=0}^{n-1} l_i m(S_i)\leq \int_a^b f(x) \, dx\leq \sum_{i=0}^{n-1} l_{i+1} m(S_i)
$$
> Definition of measurable function:
>
> A function $f$ is measurable if for all $c\in \mathbb{R}$, the set $\{x\in [a,b]|f(x)>c\}$ is Lebesgue measurable.
>
> Equivalently, a function $f$ is measurable if any of the following conditions hold:
>
> 1. For all $c\in \mathbb{R}$, the set $\{x\in [a,b]|f(x)>c\}$ is Lebesgue measurable.
> 2. For all $c\in \mathbb{R}$, the set $\{x\in [a,b]|f(x)\geq c\}$ is Lebesgue measurable.
> 3. For all $c\in \mathbb{R}$, the set $\{x\in [a,b]|f(x)<c\}$ is Lebesgue measurable.
> 4. For all $c\in \mathbb{R}$, the set $\{x\in [a,b]|f(x)\leq c\}$ is Lebesgue measurable.
> 5. For all $c<d\in \mathbb{R}$, the set $\{x\in [a,b]|c\leq f(x)<d\}$ is Lebesgue measurable.
>
> Prove by using the fact$\{x\in [a,b]|f(x)\geq c\}=\bigcap_{n=1}^\infty \{x\in [a,b]|f(x)>c-\frac{1}{n}\}$
#### Proposition 6.3
If $f,g$ is a measurable function, and $k\in \mathbb{R}$, then $f+g,kf,f^2,fg,|f|$ is measurable.
> Definition of almost everywhere:
>
> A property holds almost everywhere if it holds everywhere except for a set of Lebesgue measure 0.
#### Proposition 6.4
If $f_n$ is a sequence of measurable functions, then $\limsup_{n\to\infty} f_n, \liminf_{n\to\infty} f_n$ is measurable.
#### Theorem 6.5
Limit of measurable functions is measurable.
> Definition of simple function:
>
> A simple function is a linear combination of indicator functions of Lebesgue measurable sets.
#### Theorem 6.6
Measurable function as limit of simple functions.
$f$ is a measurable function if and only if ffthere exists a sequence of simple functions $f_n$ s.t. $f_n\to f$ almost everywhere.
### Integration
#### Proposition 6.10
Let $\phi,\psi$ be simple functions, $c\in \mathbb{R}$ and $E=E_1\cup E_2$ where $E_1\cap E_2=\emptyset$.
Then
1. $\int_E \phi(x) \, dx=\int_{E_1} \phi(x) \, dx+\int_{E_2} \phi(x) \, dx$
2. $\int_E (c\phi)(x) \, dx=c\int_E \phi(x) \, dx$
3. $\int_E (\phi+\psi)(x) \, dx=\int_E \phi(x) \, dx+\int_E \psi(x) \, dx$
4. If $\phi\leq \psi$ for all $x\in E$, then $\int_E \phi(x) \, dx\leq \int_E \psi(x) \, dx$
> Definition of Lebesgue integral of simple function:
>
> Let $\phi$ be a simple function, $\phi=\sum_{i=1}^n l_i \chi_{S_i}$
>
> $$\int_E \phi(x) \, dx=\sum_{i=1}^n l_i m(S_i\cap E)$$
> Definition of Lebesgue integral of measurable function:
>
> Let $f$ be a nonnegative measurable function, then
>
> $$\int_E f(x) \, dx=\sup_{\phi\leq f} \int_E \phi(x) \, dx$$
>
> If $f$ is not nonnegative, then
>
> $$\int_E f(x) \, dx=\int_E f^+(x) \, dx-\int_E f^-(x) \, dx$$
>
> where $f^+(x)=\max(f(x),0)$ and $f^-(x)=\max(-f(x),0)$
#### Proposition 6.12
Integral over a set of measure 0 is 0.
#### Theorem 6.13
If a nonnegative measurable function $f$ has integral 0 on a set $E$, then $f(x)=0$ almost everywhere on $E$.
#### Theorem 6.14
Monotone convergence theorem:
If $f_n$ is a sequence of monotone increasing measurable functions and $f_n\to f$ almost everywhere, and $\exists A>0$ s.t. $|\int_E f_n(x) \, dx|\leq A$ for all $n$, then $f(x)=\lim_{n\to\infty} f_n(x)$ exists almost everywhere and it's integrable on $E$ with
$$
\int_E f(x) \, dx=\lim_{n\to\infty} \int_E f_n(x) \, dx
$$
#### Theorem 6.19
Dominated convergence theorem:
If $f_n$ is a sequence of integrable functions and $f_n\to f$ almost everywhere, and there exists a nonnegative integrable function $g$ s.t. $|f_n(x)|\leq g(x)$ for all $x\in E$ and all $n$, then $f(x)=\lim_{n\to\infty} f_n(x)$ exists almost everywhere and it's integrable on $E$ with
$$
\int_E f(x) \, dx=\lim_{n\to\infty} \int_E f_n(x) \, dx
$$
#### Theorem 6.20
Fatou's lemma:
If $f_n$ is a sequence of nonnegative integrable functions, then
$$
\int_E \liminf_{n\to\infty} f_n(x) \, dx\leq \liminf_{n\to\infty} \int_E f_n(x) \, dx
$$
> Definition of Hardy-Littlewood maximal function
>
> Given integrable $f$m and an interval $I$, look at the averaging operator $A_I f(x)=\frac{\chi_I(x)}{m(I)}\int_I f(y)dy$.
>
> The maximal function is defined as
>
> $$f^*(x)=\sup_{I \text{ is an open interval}} A_I f(x)$$
### Lebesgue's Fundamental theorem of calculus
If $f$ is Lebesgue integrable on $[a,b]$, then $F(x) = \int_a^x f(t)dt$ is differentiable **almost everywhere** and $F'(x) = f(x)$ **almost everywhere**.
Outline:
Let $\lambda,\epsilon > 0$. Find $g$ continuous such that $\int_{\mathbb{R}}|f-g|dm < \frac{\lambda \epsilon}{5}$.
To control $A_I f(x)-f(x)=(A_I(f-g)(x))+(A_I g(x)-g(x))+(g(x)-f(x))$, we need to estimate the three terms separately.
Our goal is to show that $\lim_{r\to 0^+}\sup_{I\text{ is open interval}, m(I)<r, x\in I}|A_I f(x)-f(x)|=0$. For $x$ almost every $x\in[a,b]$.

111
content/Math4121/Math4121_L1.md Normal file
View File

@@ -0,0 +1,111 @@
# Math4121 Lecture 1
## Chapter 5: Differentiation
### The derivative of a real function
#### Definition 5.1
Let $f$ be a real-valued function on an interval $[a,b]$ ($f: [a,b] \to \mathbb{R}$).
We say that $f$ is _differentiable_ at a point $x\in [a,b]$ if the limit
$$
\lim_{t\to x} \frac{f(t)-f(x)}{t-x}
$$
exists.
Then we defined the derivative of $f$, $f'$, a function whose domain is the set of all $x\in [a,b]$ at which $f$ is differentiable, by
$$
f'(x) = \lim_{t\to x} \frac{f(t)-f(x)}{t-x}
$$
#### Theorem 5.2
Let $f:[a,b]\to \mathbb{R}$. If $f$ is differentiable at $x\in [a,b]$, then $f$ is continuous at $x$.
Proof:
> Recall [Definition 4.5](https://notenextra.trance-0.com/Math4111/Math4111_L22#definition-45)
>
> $f$ is continuous at $x$ if $\forall \epsilon > 0, \exists \delta > 0$ such that if $|t-x| < \delta$, then $|f(t)-f(x)| < \epsilon$.
>
> Whenever you see a limit, you should think of this definition.
We need to show that $\lim_{t\to x} f(t) = f(x)$.
Equivalently, we need to show that
$$
\lim_{t\to x} (f(t)-f(x)) = 0
$$
So for $t\ne x$, since $f$ is differentiable at $x$, we have
$$
\begin{aligned}
\lim_{t\to x} (f(t)-f(x)) &= \lim_{t\to x} \left(\frac{f(t)-f(x)}{t-x}\right)(t-x) \\
&= \lim_{t\to x} \left(\frac{f(t)-f(x)}{t-x}\right) \lim_{t\to x} (t-x) \\
&= f'(x) \cdot 0 \\
&= 0
\end{aligned}
$$
Therefore, differentiable is a stronger condition than continuous.
> There exists some function that is continuous but not differentiable.
>
> For example, $f(x) = |x|$ is continuous at $x=0$, but not differentiable at $x=0$.
>
> We can see that the left-hand limit and the right-hand limit are not the same.
>
> $$ \lim_{t\to 0^-} \frac{|t|-|0|}{t-0} = -1 \quad \text{and} \quad \lim_{t\to 0^+} \frac{|t|-|0|}{t-0} = 1 $$
>
> Therefore, the limit does not exist. for $f(x) = |x|$ at $x=0$.
#### Theorem 5.3
Suppose $f$ is differentiable at $x\in [a,b]$ and $g$ is differentiable at a point $x\in [a,b]$. Then $f+g$, $fg$ and $f/g$ are differentiable at $x$, and
(a) $(f+g)'(x) = f'(x) + g'(x)$
(b) $(fg)'(x) = f'(x)g(x) + f(x)g'(x)$
(c) $\left(\frac{f}{g}\right)'(x) = \frac{f'(x)g(x) - f(x)g'(x)}{g(x)^2}$, provided $g(x)\ne 0$
Proof:
Since the limit of product is the product of the limits, we can use the definition of the derivative to prove the theorem.
(a)
$$
\begin{aligned}
(f+g)'(x) &= \lim_{t\to x} \frac{(f+g)(t)-(f+g)(x)}{t-x} \\
&= \lim_{t\to x} \frac{f(t)-f(x)}{t-x} + \lim_{t\to x} \frac{g(t)-g(x)}{t-x} \\
&= f'(x) + g'(x)
\end{aligned}
$$
(b)
Since $f$ is differentiable at $x$, we have $\lim_{t\to x} f(t) = f(x)$.
$$
\begin{aligned}
(fg)'(x) &= \lim_{t\to x} \left(\frac{f(t)g(t)-f(x)g(x)}{t-x}\right) \\
&= \lim_{t\to x} \left(f(t)\frac{g(t)-g(x)}{t-x} + g(x)\frac{f(t)-f(x)}{t-x}\right) \\
&= f(t) \lim_{t\to x} \frac{g(t)-g(x)}{t-x} + g(x) \lim_{t\to x} \frac{f(t)-f(x)}{t-x} \\
&= f(x)g'(x) + g(x)f'(x)
\end{aligned}
$$
(c)
$$
\begin{aligned}
\left(\frac{f}{g}\right)'(x) &= \lim_{t\to x}\left(\frac{f(t)g(x)}{g(t)g(x)} - \frac{f(x)g(x)}{g(t)g(x)}\right) \\
&= \frac{1}{g(t)g(x)}\left(\lim_{t\to x} (f(t)g(x)-f(x)g(t))\right) \\
\end{aligned}
$$

30
content/Math4121/index.md Normal file
View File

@@ -0,0 +1,30 @@
# Math4121
Riemann integration; measurable functions; Measures; the Lebesgue integral; integrable functions; $L^p$ spaces.
## Textbook
Principles of Mathematical Analysis by Walter Rudin
A radical Approach to Lebesgue's Theory of Integration by David
## Grade
| item | percentage |
| --- | --- |
| Homework | 40% |
| Midterm 1 | 15% |
| Midterm 2 | 15% |
| Final | 30% |
## Homework
Due every Monday.
## Office Hour
Monday 1pm-2pm
Wednesday 12pm-1pm
Friday 11:30am-12:30pm

840
content/Math416/Exam_reviews/Math416_E1.md Normal file
View File

@@ -0,0 +1,840 @@
# Math 416 Midterm 1 Review
So everything we have learned so far is to extend the real line to the complex plane.
## Chapter 0 Calculus on Real values
### Differentiation
Let $f,g$ be function on real line and $c$ be a real number.
$$
\frac{d}{dx}(f+g)=f'+g'
$$
$$
\frac{d}{dx}(cf)=cf'
$$
$$
\frac{d}{dx}(fg)=f'g+fg'
$$
$$
\frac{d}{dx}(f/g)=(f'g-fg')/g^2
$$
$$
\frac{d}{dx}(f\circ g)=(f'\circ g)\frac{d}{dx}g
$$
$$
\frac{d}{dx}x^n=nx^{n-1}
$$
$$
\frac{d}{dx}e^x=e^x
$$
$$
\frac{d}{dx}\ln x=\frac{1}{x}
$$
$$
\frac{d}{dx}\sin x=\cos x
$$
$$
\frac{d}{dx}\cos x=-\sin x
$$
$$
\frac{d}{dx}\tan x=\sec^2 x
$$
$$
\frac{d}{dx}\sec x=\sec x\tan x
$$
$$
\frac{d}{dx}\csc x=-\csc x\cot x
$$
$$
\frac{d}{dx}\sinh x=\cosh x
$$
$$
\frac{d}{dx}\cosh x=\sinh x
$$
$$
\frac{d}{dx}\tanh x=\operatorname{sech}^2 x
$$
$$
\frac{d}{dx}\operatorname{sech} x=-\operatorname{sech}x\tanh x
$$
$$
\frac{d}{dx}\operatorname{csch} x=-\operatorname{csch}x\coth x
$$
$$
\frac{d}{dx}\coth x=-\operatorname{csch}^2 x
$$
$$
\frac{d}{dx}\arcsin x=\frac{1}{\sqrt{1-x^2}}
$$
$$
\frac{d}{dx}\arccos x=-\frac{1}{\sqrt{1-x^2}}
$$
$$
\frac{d}{dx}\arctan x=\frac{1}{1+x^2}
$$
$$
\frac{d}{dx}\operatorname{arccot} x=-\frac{1}{1+x^2}
$$
$$
\frac{d}{dx}\operatorname{arcsec} x=\frac{1}{x\sqrt{x^2-1}}
$$
$$
\frac{d}{dx}\operatorname{arccsc} x=-\frac{1}{x\sqrt{x^2-1}}
$$
### Integration
Let $f,g$ be function on real line and $c$ be a real number.
$$
\int (f+g)dx=\int fdx+\int gdx
$$
$$
\int cfdx=c\int fdx
$$
$$
\int e^x dx=e^x
$$
$$
\int \ln x dx=x\ln x-x
$$
$$
\int \frac{1}{x} dx=\ln|x|
$$
$$
\int \sin x dx=-\cos x
$$
$$
\int \cos x dx=\sin x
$$
$$
\int \tan x dx=-\ln|\cos x|
$$
$$
\int \cot x dx=\ln|\sin x|
$$
$$
\int \sec x dx=\ln|\sec x+\tan x|
$$
$$
\int \csc x dx=\ln|\csc x-\cot x|
$$
$$
\int \sinh x dx=\cosh x
$$
$$
\int \cosh x dx=\sinh x
$$
$$
\int \tanh x dx=\ln|\cosh x|
$$
$$
\int \coth x dx=\ln|\sinh x|
$$
$$
\int \operatorname{sech} x dx=2\arctan(\tanh(x/2))
$$
$$
\int \operatorname{csch} x dx=\ln|\coth x-\operatorname{csch} x|
$$
$$
\int \operatorname{sech}^2 x dx=\tanh x
$$
$$
\int \operatorname{csch}^2 x dx=-\coth x
$$
$$
\int \frac{1}{1+x^2} dx=\arctan x
$$
$$
\int \frac{1}{x^2+1} dx=\arctan x
$$
$$
\int \frac{1}{x^2-1} dx=\frac{1}{2}\ln|\frac{x-1}{x+1}|
$$
$$
\int \frac{1}{x^2-a^2} dx=\frac{1}{2a}\ln|\frac{x-a}{x+a}|
$$
$$
\int \frac{1}{x^2+a^2} dx=\frac{1}{a}\arctan(\frac{x}{a})
$$
$$
\int \frac{1}{\sqrt{x^2-a^2}} dx=\ln|x+\sqrt{x^2-a^2}|
$$
$$
\int \frac{1}{\sqrt{x^2+a^2}} dx=\ln|x+\sqrt{x^2+a^2}|
$$
## Chapter 1 Complex Numbers
### Definition of complex numbers
An ordered pair of real numbers $(x, y)$ can be represented as a complex number $z = x + yi$, where $i$ is the imaginary unit.
With operations defined as:
$$
(x_1 + y_1i) + (x_2 + y_2i) = (x_1 + x_2) + (y_1 + y_2)i
$$
$$
(x_1 + y_1i) \cdot (x_2 + y_2i) = (x_1x_2 - y_1y_2) + (x_1y_2 + x_2y_1)i
$$
#### Modulus
The modulus of a complex number $z = x + yi$ is defined as
$$
|z| = \sqrt{x^2 + y^2}=|z\overline{z}|
$$
### De Moivre's Formula
Every complex number $z$ can be written as $z = r(\cos \theta + i \sin \theta)$, where $r$ is the magnitude of $z$ and $\theta$ is the argument of $z$.
$$
z^n = r^n(\cos n\theta + i \sin n\theta)
$$
The De Moivre's formula is useful for finding the $n$th roots of a complex number.
$$
z^n = r^n(\cos n\theta + i \sin n\theta)
$$
### Roots of complex numbers
Using De Moivre's formula, we can find the $n$th roots of a complex number.
If $z=r(\cos \theta + i \sin \theta)$, then the $n$th roots of $z$ are given by:
$$
z_k = r^{1/n}(\cos \frac{\theta + 2k\pi}{n} + i \sin \frac{\theta + 2k\pi}{n})
$$
for $k = 0, 1, 2, \ldots, n-1$.
### Stereographic projection
![Stereographic projection](https://notenextra.trance-0.com/Math416/Stereographic_projection.png)
The stereographic projection is a map from the unit sphere $S^2$ to the complex plane $\mathbb{C}\setminus\{0\}$.
The projection is given by:
$$
z\mapsto \frac{(2Re(z), 2Im(z), |z|^2-1)}{|z|^2+1}
$$
The inverse map is given by:
$$
(\xi,\eta, \zeta)\mapsto \frac{\xi + i\eta}{1 - \zeta}
$$
## Chapter 2 Complex Differentiation
### Definition of complex differentiation
Let the complex plane $\mathbb{C}$ be defined in an open subset $G$ of $\mathbb{C}$. (Domain)
Then $f$ is said to be differentiable at $z_0\in G$ if the limit
$$
\lim_{z\to z_0} \frac{f(z)-f(z_0)}{z-z_0}
$$
exists.
The limit is called the derivative of $f$ at $z_0$ and is denoted by $f'(z_0)$.
To prove that a function is differentiable, we can use the standard delta-epsilon definition of a limit.
$$
\left|\frac{f(z)-f(z_0)}{z-z_0} - f'(z_0)\right| < \epsilon
$$
whenever $0 < |z-z_0| < \delta$.
With such definition, all the properties of real differentiation can be extended to complex differentiation.
#### Differentiation of complex functions
1. If $f$ is differentiable at $z_0$, then $f$ is continuous at $z_0$.
2. If $f,g$ are differentiable at $z_0$, then $f+g, fg$ are differentiable at $z_0$.
$$
(f+g)'(z_0) = f'(z_0) + g'(z_0)
$$
$$
(fg)'(z_0) = f'(z_0)g(z_0) + f(z_0)g'(z_0)
$$
3. If $f,g$ are differentiable at $z_0$ and $g(z_0)\neq 0$, then $f/g$ is differentiable at $z_0$.
$$
\left(\frac{f}{g}\right)'(z_0) = \frac{f'(z_0)g(z_0) - f(z_0)g'(z_0)}{g(z_0)^2}
$$
4. If $f$ is differentiable at $z_0$ and $g$ is differentiable at $f(z_0)$, then $g\circ f$ is differentiable at $z_0$.
$$
(g\circ f)'(z_0) = g'(f(z_0))f'(z_0)
$$
5. If $f(z)=\sum_{k=0}^n c_k(z-z_0)^k$, where $c_k\in\mathbb{C}$, then $f$ is differentiable at $z_0$ and $f'(z_0)=\sum_{k=1}^n kc_k(z_0-z_0)^{k-1}$.
$$
f'(z_0) = c_1 + 2c_2(z_0-z_0) + 3c_3(z_0-z_0)^2 + \cdots + nc_n(z_0-z_0)^{n-1}
$$
### Cauchy-Riemann Equations
Let the function defined on an open subset $G$ of $\mathbb{C}$ be $f(x,y)=u(x,y)+iv(x,y)$, where $u,v$ are real-valued functions.
Then $f$ is differentiable at $z_0=x_0+y_0i$ if and only if the partial derivatives of $u$ and $v$ exist at $(x_0,y_0)$ and satisfy the Cauchy-Riemann equations:
$$
\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y}, \quad \frac{\partial u}{\partial y} = -\frac{\partial v}{\partial x}
$$
On the polar form, the Cauchy-Riemann equations are
$$
r\frac{\partial u}{\partial r} = \frac{\partial v}{\partial \theta}, \quad \frac{\partial u}{\partial \theta} = -r\frac{\partial v}{\partial r}
$$
### Holomorphic functions
A function $f$ is said to be holomorphic on an open subset $G$ of $\mathbb{C}$ if $f$ is differentiable at every point of $G$.
#### Partial differential operators
$$
\frac{\partial}{\partial z} = \frac{1}{2}\left(\frac{\partial}{\partial x} - i\frac{\partial}{\partial y}\right)
$$
$$
\frac{\partial}{\partial \bar{z}} = \frac{1}{2}\left(\frac{\partial}{\partial x} + i\frac{\partial}{\partial y}\right)
$$
This gives that
$$
\frac{\partial f}{\partial z} = \frac{1}{2}\left(\frac{\partial f}{\partial x} - i\frac{\partial f}{\partial y}\right)=\frac{1}{2}\left(\frac{\partial u}{\partial x} +\frac{\partial v}{\partial y}\right) + \frac{i}{2}\left(\frac{\partial v}{\partial x} - \frac{\partial u}{\partial y}\right)
$$
$$
\frac{\partial f}{\partial \bar{z}} = \frac{1}{2}\left(\frac{\partial f}{\partial x} + i\frac{\partial f}{\partial y}\right)=\frac{1}{2}\left(\frac{\partial u}{\partial x} - \frac{\partial v}{\partial y}\right) + \frac{i}{2}\left(\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}\right)
$$
If the function $f$ is holomorphic, then by the Cauchy-Riemann equations, we have
$$
\frac{\partial f}{\partial \bar{z}} = 0
$$
### Conformal mappings
A holomorphic function $f$ is said to be conformal if it preserves the angles between the curves. More formally, if $f$ is holomorphic on an open subset $G$ of $\mathbb{C}$ and $z_0\in G$, $\gamma_1, \gamma_2$ are two curves passing through $z_0$ ($\gamma_1(t_1)=\gamma_2(t_2)=z_0$) and intersecting at an angle $\theta$, then
$$
\arg(f\circ\gamma_1)'(t_1) - \arg(f\circ\gamma_2)'(t_2) = \theta
$$
In other words, the angle between the curves is preserved.
An immediate consequence is that
$$
\arg(f\cdot \gamma_1)'(t_1) =\arg f'(z_0) + \arg \gamma_1'(t_1)\\
\arg(f\cdot \gamma_2)'(t_2) =\arg f'(z_0) + \arg \gamma_2'(t_2)
$$
### Harmonic functions
A real-valued function $u$ is said to be harmonic if it satisfies the Laplace equation:
$$
\frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = 0
$$
## Chapter 3 Linear Fractional Transformations
### Definition of linear fractional transformations
A linear fractional transformation is a function of the form
$$
\phi(z) = \frac{az+b}{cz+d}
$$
where $a,b,c,d$ are complex numbers and $ad-bc\neq 0$.
### Properties of linear fractional transformations
#### Matrix form
A linear fractional transformation can be written as a matrix multiplication:
$$
\phi(z) = \begin{bmatrix}
a & b\\
c & d\\
\end{bmatrix}
\begin{bmatrix}
z\\
1\\
\end{bmatrix}
$$
#### Conformality
A linear fractional transformation is conformal.
$$
\phi'(z) = \frac{ad-bc}{(cz+d)^2}
$$
#### Three-fold transitivity
If $z_1,z_2,z_3$ are distinct points in the complex plane, then there exists a unique linear fractional transformation $\phi$ such that $\phi(z_1)=\infty$, $\phi(z_2)=0$, $\phi(z_3)=1$.
The map is given by
$$
\phi(z) =\begin{cases}
\frac{(z-z_2)(z_1-z_3)}{(z-z_1)(z_2-z_3)} & \text{if } z_1,z_2,z_3 \text{ are all finite}\\
\frac{z-z_2}{z_3-z_2} & \text{if } z_1=\infty\\
\frac{z_3-z_1}{z-z_1} & \text{if } z_2=\infty\\
\frac{z-z_2}{z-z_1} & \text{if } z_3=\infty\\
\end{cases}
$$
So if $z_1,z_2,z_3$, $w_1,w_2,w_3$ are distinct points in the complex plane, then there exists a unique linear fractional transformation $\phi$ such that $\phi(z_i)=w_i$ for $i=1,2,3$.
#### Factorization
Every linear fractional transformation can be written as a composition of homothetic mappings, translations, inversions, and multiplications.
If $\phi(z)=\frac{az+b}{cz+d}$, then
$$
\phi(z) = \frac{b-ad/c}{cz+d}+\frac{a}{c}
$$
#### Clircle
A linear-fractional transformation maps circles and lines to circles and lines.
## Chapter 4 Elementary Functions
### Exponential function
The exponential function is defined as
$$
e^z = \sum_{n=0}^\infty \frac{z^n}{n!}
$$
Let $z=x+iy$, then
$$
\begin{aligned}
e^z &= e^{x+iy}\\
&= e^x e^{iy}\\
&= e^x\sum_{n=0}^\infty \frac{(iy)^n}{n!}\\
&= e^x\sum_{n=0}^\infty \frac{(-1)^n y^{2n}}{(2n)!} + i \sum_{n=0}^\infty \frac{(-1)^n y^{2n+1}}{(2n+1)!}\\
&= e^x(\cos y + i\sin y)\\
\end{aligned}
$$
So we can rewrite the polar form of a complex number as
$$
z = r(\cos \theta + i\sin \theta) = re^{i\theta}
$$
#### $e^x$ is holomorphic
Let $f(z)=e^z$, then $u(x,y)=e^x\cos y$, $v(x,y)=e^x\sin y$.
$$
\frac{\partial u}{\partial x} = e^x\cos y = \frac{\partial v}{\partial y}\\
\frac{\partial u}{\partial y} = -e^x\sin y = -\frac{\partial v}{\partial x}
$$
### Trigonometric functions
$$
\sin z = \frac{e^{iz}-e^{-iz}}{2i}, \quad \cos z = \frac{e^{iz}+e^{-iz}}{2}, \quad \tan z = \frac{\sin z}{\cos z}
$$
$$
\sec z = \frac{1}{\cos z}, \quad \csc z = \frac{1}{\sin z}, \quad \cot z = \frac{1}{\tan z}
$$
#### Hyperbolic functions
$$
\sinh z = \frac{e^z-e^{-z}}{2}, \quad \cosh z = \frac{e^z+e^{-z}}{2}, \quad \tanh z = \frac{\sinh z}{\cosh z}
$$
$$
\operatorname{sech} z = \frac{1}{\cosh z}, \quad \operatorname{csch} z = \frac{1}{\sinh z}, \quad \operatorname{coth} z = \frac{1}{\tanh z}
$$
### Logarithmic function
The logarithmic function is defined as
$$
\ln z=\{w\in\mathbb{C}: e^w=z\}
$$
#### Properties of the logarithmic function
Let $z=x+iy$, then
$$
|e^z|=\sqrt{e^x(\cos y)^2+(\sin y)^2}=e^x
$$
So we have
$$
\log z = \ln |z| + i\arg z
$$
### Power function
For any two complex numbers $a,b$, we can define the power function as
$$
a^b = e^{b\log a}
$$
> Example:
>
> $$i^i=e^{i\ln i}=e^{i(\ln 1+i\frac{\pi}{2})}=e^{-\frac{\pi}{2}} $$
>
> $$e^{i\pi}=-1$$
## Chapter 5 Power Series
### Definition of power series
A power series is a series of the form
$$
\sum_{n=0}^\infty a_n (z-z_0)^n
$$
### Properties of power series
#### Geometric series
$$
\sum_{n=0}^\infty z^n = \frac{1}{1-z}, \quad |z|<1
$$
### Radius/Region of convergence
The radius of convergence of a power series is the largest number $R$ such that the series converges for all $z$ with $|z-z_0|<R$.
The region of convergence of a power series is the set of all points $z$ such that the series converges.
### Cauchy-Hadamard Theorem
The radius of convergence of a power series is given by
$$
R=\frac{1}{\limsup_{n\to\infty} |a_n|^{1/n}}
$$
### Derivative of power series
The derivative of a power series is given by
$$
f'(z)=\sum_{n=1}^\infty n a_n (z-z_0)^{n-1}
$$
### Cauchy Product (of power series)
Let $\sum_{n=0}^\infty a_n (z-z_0)^n$ and $\sum_{n=0}^\infty b_n (z-z_0)^n$ be two power series with radius of convergence $R_1$ and $R_2$ respectively.
Then the Cauchy product of the two series is given by
$$
\sum_{n=0}^\infty c_n (z-z_0)^n
$$
where
$$
c_n = \sum_{k=0}^n a_k b_{n-k}
$$
The radius of convergence of the Cauchy product is at least $\min(R_1,R_2)$.
## Chapter 6 Complex Integration
### Definition of Riemann Integral for complex functions
The complex integral of a complex function $\phi$ on the closed subinterval $[a,b]$ of the real line is said to be piecewise continuous if there exists a partition $a=t_0<t_1<\cdots<t_n=b$ such that $\phi$ is continuous on each open interval $(t_{i-1},t_i)$ and has a finite limit at each discontinuity point of the closed interval $[a,b]$.
If $\phi$ is piecewise continuous on $[a,b]$, then the complex integral of $\phi$ on $[a,b]$ is defined as
$$
\int_a^b \phi(t) dt = \int_a^b \operatorname{Re}\phi(t) dt + i\int_a^b \operatorname{Im}\phi(t) dt
$$
### Fundamental Theorem of Calculus
If $\phi$ is piecewise continuous on $[a,b]$, then
$$
\int_a^b \phi'(t) dt = \phi(b)-\phi(a)
$$
### Triangle inequality
$$
\left|\int_a^b \phi(t) dt\right| \leq \int_a^b |\phi(t)| dt
$$
### Integral on curve
Let $\gamma$ be a piecewise smooth curve in the complex plane.
The integral of a complex function $f$ on $\gamma$ is defined as
$$
\int_\gamma f(z) dz = \int_a^b f(\gamma(t))\gamma'(t) dt
$$
### Favorite estimate
Let $\gamma:[a,b]\to\mathbb{C}$ be a piecewise smooth curve, and let $f:[a,b]\to\mathbb{C}$ be a continuous complex-valued function. Let $M$ be a real number such that $|f(z)|\leq M$ for all $z\in\gamma$. Then
$$
\left|\int_\gamma f(z) dz\right| \leq M\ell(\gamma)
$$
where $\ell(\gamma)$ is the length of the curve $\gamma$.
## Chapter 7 Cauchy's Theorem
### Cauchy's Theorem
Let $\gamma$ be a closed curve in $\mathbb{C}$ and $U$ be a simply connected open subset of $\mathbb{C}$ containing $\gamma$ and its interior. Let $f$ be a holomorphic function on $U$. Then
$$
\int_\gamma f(z) dz = 0
$$
### Cauchy's Formula for a Circle
Let $C$ be a counterclockwise oriented circle and let $f$ be holomorphic function defined in an open set containing $C$ and its interior. Then for any $z$ in the interior of $C$,
$$
f(z)=\frac{1}{2\pi i}\int_C \frac{f(\zeta)}{\zeta-z} d\zeta
$$
### Mean Value Property
Let the function $f$ be holomorphic on a disk $|z-z_0|<R$. Then for any $0<r<R$, let $C_r$ denote the circle with center $z_0$ and radius $r$. Then
$$
f(z_0)=\frac{1}{2\pi}\int_0^{2\pi} f(z_0+re^{i\theta}) d\theta
$$
The value of the function at the center of the disk is the average of the values of the function on the boundary of the disk.
### Cauchy Integrals
Let $\gamma$ be a piecewise smooth curve in $\mathbb{C}$ and let $\phi$ be a continuous complex-valued function on $\gamma$. Then the Cauchy integral of $\phi$ on $\gamma$ is the function $f$ defined in $C\setminus\gamma$ by
$$
f(z)=\int_\gamma \frac{\phi(\zeta)}{\zeta-z} d\zeta
$$
Cauchy Integral Formula for circle $C_r$:
$$
f(z)=\frac{1}{2\pi i}\int_{C_r} \frac{f(\zeta)}{\zeta-z} d\zeta
$$
> Example:
>
> Evaluate $$\int_{|z|=2} \frac{z}{z-1} dz$$
>
> Note that if we let $f(\zeta)=\zeta$ and $z=1$ is inside the circle, then we can use Cauchy Integral Formula for circle $C_r$ to evaluate the integral.
>
> So we have
>
> $$\int_{|z|=2} \frac{z}{z-1} dz = 2\pi i f(1) = 2\pi i$$
General Cauchy Integral Formula for circle $C_r$:
$$
f^{(n)}(z)=\frac{n!}{2\pi i}\int_{C_r} \frac{f(\zeta)}{(\zeta-z)^{n+1}} d\zeta
$$
> Example:
>
> Evaluate $$\int_{C}\frac{\sin z}{z^{38}}dz$$
>
> Note that if we let $f(\zeta)=\sin \zeta$ and $z=0$ is inside the circle, then we can use General Cauchy Integral Formula for circle $C_r$ to evaluate the integral.
>
> So we have
>
> $$\int_{C}\frac{\sin z}{z^{38}}dz = \frac{2\pi i}{37!} f^{(37)}(0) = \frac{2\pi i}{37!} \sin ^{(37)}(0)$$
>
> Note that $\sin ^{(n)}(0)=\begin{cases} 0,& n\equiv 0 \pmod{4}\\
1,& n\equiv 1 \pmod{4}\\
0,& n\equiv 2 \pmod{4}\\
-1,& n\equiv 3 \pmod{4}
\end{cases}$
>
> So we have
>
> $$\int_{C}\frac{\sin z}{z^{38}}dz = \frac{2\pi i}{37!} \sin ^{(37)}(0) = \frac{2\pi i}{37!} \cdot 1 = \frac{2\pi i}{37!}$$
_Cauchy integral is a easier way to evaluate the integral._
### Liouville's Theorem
If a function $f$ is entire (holomorphic on $\mathbb{C}$) and bounded, then $f$ is constant.
### Finding power series of holomorphic functions
If $f$ is holomorphic on a disk $|z-z_0|<R$, then $f$ can be represented as a power series on the disk.
where $a_n=\frac{f^{(n)}(z_0)}{n!}$
> Example:
>
> If $q(z)=(z-1)(z-2)(z-3)$, find the power series of $q(z)$ centered at $z=0$.
>
> Note that $q(z)$ is holomorphic on $\mathbb{C}$ and $q(z)=0$ at $z=1,2,3$.
>
> So we can use the power series of $q(z)$ centered at $z=1$.
>
> To solve this, we can simply expand $q(z)=(z-1)(z-2)(z-3)$ and get $q(z)=z^3-6z^2+11z-6$.
>
> So we have $a_0=q(1)=-6$, $a_1=q'(1)=3z^2-12z+11=11$, $a_2=\frac{q''(1)}{2!}=\frac{6z-12}{2}=-3$, $a_3=\frac{q'''(1)}{3!}=\frac{6}{6}=1$.
>
> So the power series of $q(z)$ centered at $z=1$ is
>
> $$q(z)=-6+11(z-1)-3(z-1)^2+(z-1)^3$$
### Fundamental Theorem of Algebra
Every non-constant polynomial with complex coefficients has a root in $\mathbb{C}$.
Can be factored into linear factors:
$$
p(z)=a_n(z-z_1)(z-z_2)\cdots(z-z_n)
$$
We can treat holomorphic functions as polynomials.
$f$ has zero of order $m$ at $z_0$ if and only if $f(z)=(z-z_0)^m g(z)$ for some holomorphic $g(z)$ and $g(z_0)\neq 0$.
### Zeros of holomorphic functions
If $f$ is holomorphic on a disk $|z-z_0|<R$ and $f$ has a zero of order $m$ at $z_0$, then $f(z_0)=0$, $f'(z_0)=0$, $f''(z_0)=0$, $\cdots$, $f^{(m-1)}(z_0)=0$ and $f^{(m)}(z_0)\neq 0$.
And there exists a holomorphic function $g$ on the disk such that $f(z)=(z-z_0)^m g(z)$ and $g(z_0)\neq 0$.
> Example:
>
> Find zeros of $f(z)=\cos(z\frac{\pi}{2})$
>
> Note that $f(z)=0$ if and only if $z\frac{\pi}{2}=(2k+1)\frac{\pi}{2}$ for some integer $k$.
>
> So the zeros of $f(z)$ are $z=(2k+1)$ for some integer $k$.
>
> The order of the zero is $1$ since $f'(z)=-\frac{\pi}{2}\sin(z\frac{\pi}{2})$ and $f'(z)\neq 0$ for all $z=(2k+1)$.
If $f$ vanishes to infinite order at $z_0$ (that is, $f(z_0)=f'(z_0)=f''(z_0)=\cdots=0$), then $f(z)\equiv 0$ on the connected open set $U$ containing $z_0$.
### Identity Theorem
If $f$ and $g$ are holomorphic on a connected open set $U\subset\mathbb{C}$ and $f(z)=g(z)$ for all $z$ in a subset of $U$ that has a limit point in $U$, then $f(z)=g(z)$ for all $z\in U$.
Key: consider $h(z)=f(z)-g(z)$, prove $h(z)\equiv 0$ on $U$ by applying the zero of holomorphic function.
### Weierstrass Theorem
Limit of a sequence of holomorphic functions is holomorphic.
Let $f_n$ be a sequence of holomorphic functions on a domain $D\subset\mathbb{C}$ that converges uniformly to $f$ on every compact subset of $D$. Then $f$ is holomorphic on $D$.
### Maximum Modulus Principle
If $f$ is a non-constant holomorphic function on a domain $D\subset\mathbb{C}$, then $|f|$ does not attain a maximum value in $D$.
#### Corollary: Minimum Modulus Principle
If $f$ is a non-constant holomorphic function on a domain $D\subset\mathbb{C}$, then $\frac{1}{f}$ does not attain a minimum value in $D$.
### Schwarz Lemma
If $f$ is a holomorphic function on the unit disk $|z|<1$ and $|f(z)|\leq |z|$, then $|f'(0)|\leq 1$.

279
content/Math416/Exam_reviews/Math416_Final.md Normal file
View File

@@ -0,0 +1,279 @@
# Math 416 Final Review
Story after Cauchy's theorem
## Chapter 7: Cauchy's Theorem
### Existence of harmonic conjugate
Suppose $f=u+iv$ is holomorphic on a domain $U\subset\mathbb{C}$. Then $u=\Re f$ is harmonic on $U$. That is $\Delta u=\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}=0$.
Moreover, there exists $g\in O(U)$ such that $g$ is unique up to an additive imaginary constant.
> Example:
>
> Find a harmonic conjugate of $u(x,y)=\log|\frac{z}{z-1}|$
>
> Note that $\log(\frac{z}{z-1})=\log \left|\frac{z}{z-1}\right|+i(\arg(z)-\arg(z-1))$ is harmonic on $\mathbb{C}\setminus\{1\}$.
>
> So the harmonic conjugate of $u(x,y)=\log|\frac{z}{z-1}|$ is $v(x,y)=\arg(z)-\arg(z-1)+C$ where $C$ is a constant.
>
> Note that the harmonic conjugate may exist locally but not globally. (e.g. $u(x,y)=\log|z(z-1)|$ has a local harmonic conjugate $i(\arg(z)+\arg(z-1)+C)$ but this is not a well defined function since $\arg(z)+\arg(z-1)$ is not single-valued.)
### Corollary for harmonic functions
#### Theorem 7.19
Harmonic function are infinitely differentiable.
#### Theorem 7.20
Mean value property of harmonic functions.
Let $u$ be harmonic on an open set of $\Omega$, then
$$u(z_0)=\frac{1}{2\pi}\int_0^{2\pi} u(z_0+re^{i\theta}) d\theta$$
for any $z_0\in\Omega$ and $r>0$ such that $D(z_0,r)\subset\Omega$.
#### Theorem 7.21
Identity theorem for harmonic functions.
Let $u$ be harmonic on a domain $\Omega$. If $u=0$ on some open set $G\subset\Omega$, then $u\equiv 0$ on $\Omega$.
#### Theorem 7.22
Maximum principle for harmonic functions.
Let $u$ be a non-constant real-valued harmonic function on a domain $\Omega$. Then $|u|$ does not attain a maximum value in $\Omega$.
## Chapter 8: Laurent Series and Isolated Singularities
### Laurent Series
Laurent series is a generalization of Taylor series.
Laurent series is a power series of the form
$$f(z)=\sum_{n=-\infty}^{\infty} a_n (z-z_0)^n$$
where
$$
a_k=\frac{1}{2\pi i}\int_{C_r}\frac{f(z)}{(z-z_0)^{k+1}}dz
$$
The series converges on an annulus $R_1<|z-z_0|<R_2$.
where $R_1=\limsup_{n\to\infty} |a_{-n}|^{1/n}$ and $R_2=\frac{1}{\limsup_{n\to\infty} |a_n|^{1/n}}$.
### Cauchy's Formula for an Annulus
Let $f$ be holomorphic on an annulus $R_1<r_1<|z-z_0|<r_2<R_2$. And $w\in A(z_0;R_1,R_2)$. Find the Annulus $w\in A(z_0;r_1,r_2)$
Then
$$
f(w)=\frac{1}{2\pi i}\int_{C_{r_1}}\frac{f(z)}{z-w}dz-\frac{1}{2\pi i}\int_{C_{r_2}}\frac{f(z)}{z-w}dz
$$
### Isolated singularities
Let $f$ be holomorphic on $0<|z-z_0|<R$ (The punctured disk of radius $R$ centered at $z_0$). If there exists a Laurent series of $f$ convergent on $0<|z-z_0|<R$, then $z_0$ is called an isolated singularity of $f$.
The series $f(z)=\sum_{n=-\infty}^{-1}a_n(z-z_0)^n$ is called the principle part of Laurent series of $f$ at $z_0$.
#### Removable singularities
If the principle part of Laurent series of $f$ at $z_0$ is zero, then $z_0$ is called a removable singularity of $f$.
Criterion for a removable singularity:
If $f$ is bounded on $0<|z-z_0|<R$, then $z_0$ is a removable singularity.
> Example:
>
> $f(z)=\frac{1}{e^z-1}$ has a removable singularity at $z=0$.
>
> The Laurent series of $f$ at $z=0$ is
>
> $$f(z)=\frac{1}{z}+\sum_{n=0}^{\infty}\frac{z^n}{n!}$$
>
> The principle part is zero, so $z=0$ is a removable singularity.
#### Poles
If the principle part of Laurent series of $f$ at $z_0$ is a finite sum, then $z_0$ is called a pole of $f$.
Criterion for a pole:
If $f$ has an isolated singularity at $z_0$, and $\lim_{z\to z_0}|f(z)|=\infty$, then $z_0$ is a pole of $f$.
> Example:
>
> $f(z)=\frac{1}{z^2}$ has a pole at $z=0$.
>
> The Laurent series of $f$ at $z=0$ is
>
> $$f(z)=\frac{1}{z^2}$$
>
> The principle part is $\frac{1}{z^2}$, so $z=0$ is a pole.
#### Essential singularities
If $f$ has an isolated singularity at $z_0$, and it is neither a removable singularity nor a pole, then $z_0$ is called an essential singularity of $f$.
"Criterion" for an essential singularity:
If the principle part of Laurent series of $f$ at $z_0$ has infinitely many non-zero coefficients corresponding to negative powers of $z-z_0$, then $z_0$ is called an essential singularity of $f$.
> Example:
>
> $f(z)=\sin(\frac{1}{z})$ has an essential singularity at $z=0$.
>
> The Laurent series of $f$ at $z=0$ is
>
> $$f(z)=\frac{1}{z}-\frac{1}{6z^3}+\frac{1}{120z^5}-\cdots$$
>
> Since there are infinitely many non-zero coefficients corresponding to negative powers of $z$, $z=0$ is an essential singularity.
#### Singularities at infinity
We say $f$ has a singularity (removable, pole, or essential) at infinity if $f(1/z)$ has an isolated singularity (removable, pole, or essential) at $z=0$.
> Example:
>
> $f(z)=\frac{z^4}{(z-1)(z-3)}$ has a pole of order 2 at infinity.
>
> Plug in $z=1/w$, we get $f(1/w)=\frac{1}{w^2}\frac{1}{(1/w-1)(1/w-3)}=\frac{1}{w^2}\frac{1}{(1-w)(1-3w)}=\frac{1}{w^2}(1+O(w))$, which has pole of order 2 at $w=0$.
#### Residue
The residue of $f$ at $z_0$ is the coefficient of the term $(z-z_0)^{-1}$ in the Laurent series of $f$ at $z_0$.
> Example:
>
> $f(z)=\frac{1}{z^2}$ has a residue of 0 at $z=0$.
>
> $f(z)=\frac{z^3}{z-1}$ has a residue of 1 at $z=1$.
Residue for pole with higher order:
If $f$ has a pole of order $n$ at $z_0$, then the residue of $f$ at $z_0$ is
$$
\operatorname{res}(f,z_0)=\frac{1}{(n-1)!}\lim_{z\to z_0}\frac{d^{n-1}}{dz^{n-1}}((z-z_0)^nf(z))
$$
## Chapter 9: Generalized Cauchy's Theorem
### Winding number
The winding number of a closed curve $C$ with respect to a point $z_0$ is
$$
\operatorname{ind}_C(z_0)=\frac{1}{2\pi i}\int_C\frac{1}{z-z_0}dz
$$
_the winding number is the number of times the curve $C$ winds around the point $z_0$ counterclockwise. (May be negative)_
### Contour integrals
A contour is a piecewise continuous curve $\gamma:[a,b]\to\mathbb{C}$ with integer coefficients.
$$
\Gamma=\sum_{i=1}^p n_j\gamma_j
$$
where $\gamma_j:[a_j,b_j]\to\mathbb{C}$ is continuous closed curve and $n_j\in\mathbb{Z}$.
### Interior of a curve
The interior of a curve is the set of points $z\in\mathbb{C}$ such that $\operatorname{ind}_{\Gamma}(z)\neq 0$.
The winding number of contour $\Gamma$ is the sum of the winding numbers of the components of $\Gamma$ around $z_0$.
$$
\operatorname{ind}_{\Gamma}(z)=\sum_{j=1}^p n_j\operatorname{ind}_{\gamma_j}(z)
$$
### Separation lemma
Let $\Omega\subseteq\mathbb{C}$ be a domain and $K\subset \Omega$ be compact. Then there exists a simple contour $\Gamma\subset \Omega\setminus K$ such that $K\subset \operatorname{int}_{\Gamma}(\Gamma)\subset \Omega$.
Key idea:
Let $0<\delta<d(K,\partial \Omega)$, then draw the grid lines and trace the contour.
### Residue theorem
Let $\Omega$ be a domain, $\Gamma$ be a contour such that $\Gamma\cap \operatorname{int}(\Gamma)\subset \Omega$. Let $f$ be holomorphic on $\Omega\setminus \{z_1,z_2,\cdots,z_p\}$ and $z_1,z_2,\cdots,z_p$ are finitely many points in $\Omega$, where $z_1,z_2,\cdots,z_p\notin \Gamma$. Then
$$
\int_{\Gamma}f(z)dz=2\pi i\sum_{j=1}^p \operatorname{res}(f,z_j)
$$
Key: Prove by circle around each singularity and connect them using two way paths.
### Homotopy*
Suppose $\gamma_0, \gamma_1$ are two curves from
$[0,1]$ to $\Omega$ with same end points $P,Q$.
A homotopy is a continuous function of curves $\gamma_t, 0\leq t\leq 1$, deforming $\gamma_0$ to $\gamma_1$, keeping the end points fixed.
Formally, if $H:[0,1]\times [0,1]\to \Omega$ is a continuous function satsifying
1. $H(s,0)=\gamma_0(s)$, $\forall s\in [0,1]$
2. $H(s,1)=\gamma_1(s)$, $\forall s\in [0,1]$
3. $H(0,t)=P$, $\forall t\in [0,1]$
4. $H(1,t)=Q$, $\forall t\in [0,1]$
Then we say $H$ is a homotopy between $\gamma_0$ and $\gamma_1$. (If $\gamma_0$ and $\gamma_1$ are closed curves, $Q=P$)
#### Lemma 9.12 Technical Lemma
Let $\phi:[0,1]\times [0,1]\to \mathbb{C}\setminus \{0\}$ is continuous. Then there exists a continuous map $\psi:[0,1]\times [0,1]\to \mathbb{C}$ such that $e^\phi=\psi$. Moreover, $\psi$ is unique up to an additive constant in $2\pi i\mathbb{Z}$.
### General approach to evaluate definite integrals
Choose a contour so that one side is the desired integral.
Handle the other sides using:
- Symmetry
- Favorite estimate
- Bound function by another function whose integral goes to 0

167
content/Math416/Math416_L1.md Normal file
View File

@@ -0,0 +1,167 @@
# Math416 Lecture 1
## Chapter 1: Complex Numbers
### Preface
I don't know what happened to the first class. I will try to rewrite the notes from my classmates here.
#### Rigidity
Integral is preserved for any closed path.
#### Group
A set with a multiplication operator. $(G,\cdot)$ such that: for all $a,b,c\in G$:
1. $a\cdot b\in G$
2. $a\cdot (b\cdot c)=(a\cdot b)\cdot c$
3. $a\cdot 1=a$
4. $a\cdot a^{-1}=1$
#### Ring
A group with two operations: addition and multiplication. $(R,+,\cdot)$ such that: for all $a,b,c\in R$:
1. Commutative under addition: $a+b=b+a$
2. Associative under multiplication: $(a\cdot b)\cdot c=a\cdot (b\cdot c)$
3. Distributive under addition: $a\cdot (b+c)=a\cdot b+a\cdot c$
Example:
$\{a+\sqrt{6}b\mid a,b\in \mathbb{Z}\}$ is a ring
#### Definition 1.1
the complex number is defined to be the set $\mathbb{C}$ of ordered pairs $(x,y)$ with $x,y\in \mathbb{R}$ and the operations:
- Addition: $(x_1,y_1)+(x_2,y_2)=(x_1+x_2,y_1+y_2)$
- Multiplication: $(x_1,y_1)(x_2,y_2)=(x_1x_2-y_1y_2,x_1y_2+x_2y_1)$
#### Axiom 1.2
The operation of addition and multiplication on $\mathbb{C}$ satisfies the following conditions (The field axioms):
For all $z_1,z_2,z_3\in \mathbb{C}$:
1. $z_1+z_2=z_2+z_1$ (commutative law of addition)
2. $(z_1+z_2)+z_3=z_1+(z_2+z_3)$ (associative law of addition)
3. $z_1\cdot z_2=z_2\cdot z_1$ (commutative law of multiplication)
4. $(z_1\cdot z_2)\cdot z_3=z_1\cdot (z_2\cdot z_3)$ (associative law of multiplication)
5. $z_1\cdot (z_2+z_3)=z_1\cdot z_2+z_1\cdot z_3$ (distributive law)
6. There exists an additive identity element $0=(0,0)$ such that $z+0=z$ for all $z\in \mathbb{C}$.
7. There exists a multiplicative identity element $1=(1,0)$ such that $z\cdot 1=z$ for all $z\in \mathbb{C}$.
8. There exists an additive inverse $-z=(-x,-y)$ for all $z=(x,y)\in \mathbb{C}$ such that $z+(-z)=0$.
9. There exists a multiplicative inverse $z^{-1}=\left(\frac{x}{x^2+y^2},-\frac{y}{x^2+y^2}\right)$ for all $z=(x,y)\in \mathbb{C}$ such that $z\cdot z^{-1}=1$.
$$
(a,b)^{-1}=\left(\frac{a}{a^2+b^2},-\frac{b}{a^2+b^2}\right)
$$
#### Embedding of $\mathbb{R}$ in $\mathbb{C}$ 1.3
Let $z=x+iy\in \mathbb{C}$ where $a,b\in \mathbb{R}$.
- $x$ is called the real part of $z$ and
- $y$ is called the imaginary part of $z$.
- $|z|=\sqrt{x^2+y^2}$ is called the absolute value or modulus of $z$.
- The angle between the positive real axis and the line segment from $0$ to $z$ is called the argument of $z$ and is denoted by $\theta$ (argument of $z$).
- $\overline{z}=x-iy$ is called the conjugate of $z$. ($z\cdot \overline{z}=|z|^2$)
- $z_1+z_2=(x_1+x_2,y_1+y_2)$ (vector addition)
#### Lemma 1.3
$$
|z_1z_2|=|z_1||z_2|
$$
#### Theorem 1.5 (Triangle Inequality)
$$
|z_1+z_2|\leq |z_1|+|z_2|
$$
<details>
<summary>Proof</summary>
Geometrically, the triangle inequality states that the sum of the lengths of any two sides of a triangle is greater than the length of the third side.
Algebraically,
$$
\begin{aligned}
(|z_1+z_2|)^2-|z_1+z_2|^2&=|z_1+z_2|^2-2|z_1+z_2|-(z_1+z_2)(\overline{z_1}+\overline{z_2})\\
&=|z_1|^2+|z_2|^2+2|z_1||z_2|-(|z_1|^2+|z_2|^2+\overline{z_1}z_2+\overline{z_2}z_1)\\
&=2|z_1||z_2|-2Re(\overline{z_1}z_2)\\
&=2(|z_1||z_2|-|z_1z_2|)\\
&\geq 0
\end{aligned}
$$
</details>
Suppose $2(|z_1||z_2|-|z_1z_2|)=0$, and $\overline{z_1}z_2$ is a non-negative real number $c$, then $|z_1||z_2|=|z_1z_2|$...
> What is the use of this?
Let $\arg(z)=\theta\in (-\pi,\pi]$, $z_1=r_1(\cos\theta_1+i\sin\theta_1)$, $z_2=r_2(\cos\theta_2+i\sin\theta_2)$.
$$
z_1z_2=r_1r_2[cos(\theta_1+\theta_2)+i\sin(\theta_1+\theta_2)]
$$
(Define $\text{cis}(\theta)=\cos\theta+i\sin\theta$)
#### Theorem 1.6 Parallelogram Equality
The sum of the squares of the lengths of the diagonals of a parallelogram equals the sum of the squares of the lengths of the sides.
<details>
<summary>Proof</summary>
Let $z_1,z_2$ be two complex numbers representing the two sides of the parallelogram, then the sum of the squares of the lengths of the diagonals of the parallelogram is $|z_1-z_2|^2+|z_1+z_2|^2$, and the sum of the squares of the lengths of the sides is $2|z_1|^2+2|z_2|^2$.
$$
\begin{aligned}
|z_1-z_2|^2+|z_1+z_2|^2 &= (x_1-x_2)^2+(y_1-y_2)^2+(x_1+x_2)^2+(y_1+y_2)^2 \\
&= 2x_1^2+2x_2^2+2y_1^2+2y_2^2 \\
&= 2(|z_1|^2+|z_2|^2)
\end{aligned}
$$
</details>
#### Definition 1.9
The argument of a complex number $z$ is defined as the angle $\theta$ between the positive real axis and the ray from the origin through $z$.
### De Moivre's Formula
#### Theorem 1.10 De Moivre's Formula
Let $z=r\text{cis}(\theta)$, then
$\forall n\in \mathbb{Z}$:
$$
z^n=r^n\text{cis}(n\theta)
$$
<details>
<summary>Proof</summary>
For $n=0$, $z^0=1=1\text{cis}(0)$.
For $n=-1$, $z^{-1}=\frac{1}{z}=\frac{1}{r}\text{cis}(-\theta)=\frac{1}{r}(cos(-\theta)+i\sin(-\theta))$.
</details>
Application:
$$
\begin{aligned}
(\text{cis}(\theta))^3&=\text{cis}(3\theta)\\
&=\cos(3\theta)+i\sin(3\theta)\\
&=cos^3(\theta)-3cos(\theta)sin^2(\theta)+i(3cos^2(\theta)sin(\theta)-sin^3(\theta))\\
\end{aligned}
$$

15
content/Math416/index.md Normal file
View File

@@ -0,0 +1,15 @@
# Math 416
Complex variables. This is a course that explores the theory and applications of complex analysis as extension of Real analysis.
The course is taught by Professor.
John E. McCarthy <mailto:mccarthy@math.wustl.edu>
Some interesting fact is that he cover the lecture terribly quick. At least for me. I need to preview and review the lecture after the course ended. The only thing that I can take granted of is that many theorem in real analysis still holds in the complex. By elegant definition designing, we build a wonderful math with complex variables and extended theorems, which is more helpful when solving questions that cannot be solved in real numbers.
McCarthy like to write $\zeta$ for $z$ and his writing for $\zeta$ is almost identical with $z$, I decided to use the traditional notation system I've learned to avoid confusion in my notes.
I will use $B_r(z_0)$ to denote a disk in $\mathbb{C}$ such that $B_r(z_0) = \{ z \in \mathbb{C} : |z - z_0| < r \}$. In the lecture, he use $\mathbb{D}(z_0,r)$ to denote the disk centered at $z_0$ with radius $r$. If $\mathbb{D}$ is used, then it means the unit disk $\mathbb{D}=\{z:|z|<1\}$. You may also see the closure of the disk $\overline{B_r(z_0)}$ and $\overline{\mathbb{D}}$, these are equivalent definition.
I will use $z$ to replace the strange notation of $\zeta$. If that makes sense.

123
content/Math4201/Math4201_L10.md
View File

@@ -1,123 +0,0 @@
# Math4201 Topology I (Lecture 10)
## Continuity
### Continuous functions
Let $X,Y$ be topological spaces and $f:X\to Y$. For any $x\in X$ and any open neighborhood $V$ of $f(x)$ in $Y$, $f^{-1}(V)$ contains an open neighborhood of $x$ in $X$.
#### Lemma for continuous functions
Let $f:X\to Y$ be a function, then:
1. $A\subseteq Y$: $f^{-1}(A^c) = (f^{-1}(A))^c$.
2. $\{A_\alpha\}_{\alpha\in I}\subseteq Y$: $f^{-1}(\bigcup_{\alpha\in I} A_\alpha) = \bigcup_{\alpha\in I} f^{-1}(A_\alpha)$.
3. $\{A_\alpha\}_{\alpha\in I}\subseteq Y$: $f^{-1}(\bigcap_{\alpha\in I} A_\alpha) = \bigcap_{\alpha\in I} f^{-1}(A_\alpha)$.
<details>
<summary>Proof</summary>
1. By definition of continuous functions, $\forall V$ open in $Y$, $f^{-1}(V)$ is open in $X$.
2. It is sufficient to shoa that $x\in f^{-1}(\bigcup_{\alpha\in I} A_\alpha)$ if and only if $x\in \bigcup_{\alpha\in I} f^{-1}(A_\alpha)$.
This condition holds if and only if $\exists \alpha\in I$ such that $f(x)\in A_\alpha$.
Which is equivalent to $\exists \alpha\in I$ such that $x\in f^{-1}(A_\alpha)$.
So $x\in f^{-1}(\bigcup_{\alpha\in I} A_\alpha)$
In particular, $f^{-1}(\bigcup_{\alpha\in I} A_\alpha) = \bigcup_{\alpha\in I} f^{-1}(A_\alpha)$.
3. Similar to 2 but use forall.
</details>
#### Properties of continuous functions
A function $f:X\to Y$ is continuous if and only if:
1. $f^{-1}(V)$ is open in $X$ for any open set $V\subset Y$.
2. $f$ is continuous at any point $x\in X$.
3. $f^{-1}(C)$ is closed in $X$ for any closed set $C\subset Y$.
4. Assume $\mathcal{B}$ is a basis for $Y$, then $f^{-1}(\mathcal{B})$ is open in $X$ for any $B\in \mathcal{B}$.
5. For any $A\subseteq X$, $f(\overline{A})\subseteq \overline{f(A)}$.
<details>
<summary>Proof</summary>
**Showing $1\iff 3$**:
> Use the lemma for continuous functions (1)
**Showing $1\iff 4$**:
$1 \implies 4$:
Because any $B\in \mathcal{B}$ is open in $Y$, so $f^{-1}(B)$ is open in $X$.
$4 \implies 1$:
Let $V\subset Y$ be an open set. Then there are basis elements $\{B_\alpha\}_{\alpha\in I}$ such that $V=\bigcup_{\alpha\in I} B_\alpha$.
So $f^{-1}(V) = f^{-1}(\bigcup_{\alpha\in I} B_\alpha) = \bigcup_{\alpha\in I} f^{-1}(B_\alpha)$ (by lemma (2)) is a union of open sets, so $f^{-1}(V)$ is open in $X$.
**Showing $1\implies 5$**:
Take $A\subseteq X$ and $x\in \overline{A}$. It suffices to show $f(x)$ is an element of the closure of $f(A)$. This is equivalent to say that any open neighborhood $V$ of $f(x)$ intersects $f(A)$ has a non-trivial intersection with $f(A)$.
For any such $V$, 1 implies that $f^{-1}(V)$ is open in $X$. Moreover, $x\in f^{-1}(V)$ because $f(x)\in V$.
This means that $f^{-1}(V)$ is an open neighborhood of $x$. Since $x\in \overline{A}$, we have $f^{-1}(V)\cap A\neq \emptyset$ and contains a point $x'\in X$.
So $x'\in f^{-1}(V)\cap A$, this implies that $f(x')\in V$ and $f(x')\in f(A)$, so $f(x')\in V\cap f(A)$.
> [!NOTE]
>
> This verifies our claim. Proof of $5\implies 1$ is similar and left as an exercise.
</details>
<details>
<summary>Example of property 5</summary>
Let $X=(0,1)\cup (1,2)$ and $Y=\mathbb{R}$ equipped with the subspace topology induced by the standard topology on $\mathbb{R}$.
Let $f:X\to Y$ be the inclusion map, $f(x)=x$ for all $x\in X$. This is continuous.
Let $A=(0,1)\cup (1,2)$. Then $\overline{A}=A$. So $f(\overline{A})=f(A)=(0,1)\cup (1,2)$.
However, $\overline{f(A)}=\overline{(0,1)\cup (1,2)}=[0,2]$.
So $f(\overline{A})\subsetneq \overline{f(A)}$.
</details>
#### Definition of homeomorphism
A **homeomorphism** $f:X\to Y$ is a continuous map of topological spaces that is a bijection and $f^{-1}:Y\to X$ is also continuous.
<details>
<summary>Example of homeomorphism</summary>
Let $X=\mathbb{R}$ and $Y=\mathbb{R}+$ with standard topology.
$f:\mathbb{R}\to \mathbb{R}^+$ be defined by $f(x)=e^x$ is continuous and bijective.
$f^{-1}:\mathbb{R}^+\to \mathbb{R}$ be defined by $f^{-1}(y)=\ln(y)$ is continuous and homeomorphism.
</details>
### Epsilon delta definition of continuity
Let $f:\mathbb{R}\to \mathbb{R}$ be a continuous function where we use the standard topology on $\mathbb{R}$.
Then [property 4](#properties-of-continuous-functions) implies that for any open interval $(a,b)\in \mathbb{R}$, $f^{-1}((a,b))$ is open in $\mathbb{R}$.
Now take an arbitrary $x\in \mathbb{R}$ and $\epsilon > 0$. In particular $f^{-1}((f(x)-\epsilon, f(x)+\epsilon))$ is an open set containing $x$.
In particular, there is an open interval (by the standard topology on $\mathbb{R}$) $(c,d)$ such that $x\in (c,d)\subseteq f^{-1}((f(x)-\epsilon, f(x)+\epsilon))$.
Let $\delta = \min\{x-c, d-x\}$. Then $(x-\delta, x+\delta)\subseteq (c,d)\subseteq f^{-1}((f(x)-\epsilon, f(x)+\epsilon))$.
This says that if $|y-x| < \delta$, then $|f(y)-f(x)| < \epsilon$.

113
content/Math4201/Math4201_L11.md
View File

@@ -1,113 +0,0 @@
# Math4201 Topology I (Lecture 11)
> [!NOTE]
>
> Q: Let $f:X\to Y$ be a continuous bijection. Is it true that $f^{-1}$ is continuous?
>
> A: No. Consider $X=[0,2\pi)$ and $Y=\mathbb{S}^1$ with standard topology in $\mathbb{R}^2$.
>
> Let $f\coloneqq \theta\in [0,2\pi)\to (\cos \theta, \sin \theta)\in \mathbb{S}^1$ is a continuous bijection. ($\forall f^{-1}(V)$ is open in $X$)
>
> But $f^{-1}$ is not continuous, consider the open set in $X, U=[0,\pi)$. Then $f^{-1}(U)=[0,\pi)$ is not open in $Y$.
## Continuous functions
### Constructing continuous functions
#### Theorem composition of continuous functions is continuous
Let $X,Y,Z$ be topological spaces, $f:X\to Y$ is continuous, and $g:Y\to Z$ is continuous. Then $f\circ g:X\to Z$ is continuous.
<details>
<summary>Proof</summary>
Let $U\subseteq Z$ be open. Then $g^{-1}(U)$ is open in $Y$. Since $f$ is continuous, $f^{-1}(g^{-1}(U))$ is open in $X$.
</details>
#### Pasting lemma
Let $X$ be a topological space and $X=Z_1\cup Z_2$ with $Z_1,Z_2$ closed in $X$ equipped with the subspace topology. (may be not disjoint)
Let $g_1:Z_1\to Y$ and $g_2:Z_2\to Y$ be two continuous maps and $\forall x\in Z_1\cap Z_2$, $g_1(x)=g_2(x)$.
Define $f:X\to Y$ by $f(x)\begin{cases}g_1(x), & x\in Z_1 \\ g_2(x), & x\in Z_2\end{cases}$ is continuous.
<details>
<summary>Proof</summary>
Let $U\subseteq Y$ be open. Then $f^{-1}(U)=g_1^{-1}(U)\cup g_2^{-1}(U)$.
$g_1^{-1}(U)$ and $g_2^{-1}(U)$ are open in $Z_1$ and $Z_2$ respectively.
> It's a bit annoying to show that $g_1^{-1}(U)$ and $g_2^{-1}(U)$ are open in $X$.
Different way. Consider the definition of continuous functions using closed sets.
If $W\subseteq X$ is closed, then $W=Z_1\cap Z_2$ is closed in $X$.
So $f^{-1}(W)=g_1^{-1}(W)\cup g_2^{-1}(W)$ is closed in $Z_1$ and $Z_2$ respectively.
Note that $Z_1$ and $Z_2$ are closed in $X$, so $g_1^{-1}(W)$ and $g_2^{-1}(W)$ are closed in $X$. [closed in closed subspace lemma](https://notenextra.trance-0.com/Math4201/Math4201_L7#lemma-of-closed-in-closed-subspace)
So $f^{-1}(W)$ is closed in $X$.
</details>
Let $X$ be a topological space and $X=U_1\cup U_2$ with $U_1,U_2$ open in $X$ equipped with the subspace topology.
With $g_1:U_1\to Y$ and $g_2:U_2\to Y$ be two continuous maps and $\forall x\in U_1\cap U_2$, $g_1(x)=g_2(x)$.
Then $f:X\to Y$ by $f(x)\begin{cases}g_1(x), & x\in U_1 \\ g_2(x), & x\in U_2\end{cases}$ is continuous.
<details>
<summary>Proof</summary>
Let $U\subseteq Y$ be open. Then $f^{-1}(U)=g_1^{-1}(U)\cup g_2^{-1}(U)$.
$g_1^{-1}(U)$ and $g_2^{-1}(U)$ are open in $U_1$ and $U_2$ respectively.
Apply the [open in open subspace lemma](https://notenextra.trance-0.com/Math4201/Math4201_L6#lemma-of-open-set-in-subspace-topology)
So $f^{-1}(U)$ is open in $X$.
</details>
The open set version holds more generally.
Let $X$ be a topological space and $X=\bigcup_{\alpha\in I} U_\alpha$ with $U_\alpha$ open in $X$ equipped with the subspace topology.
Let $g_\alpha:U_\alpha\to Y$ be two continuous maps and $\forall x\in U_\alpha\cap U_\beta$, $g_\alpha(x)=g_\beta(x)$.
Then $f:X\to Y$ by $f(x)=g_\alpha(x), \text{if } x\in U_\alpha$ is continuous.
#### Continuous functions on different codomains
Let $f:X\to Y$ and $g:X\to Z$ be two continuous maps of topological spaces.
Let $H:X\to Y\times Z$, where $Y\times Z$ is equipped with the product topology, be defined by $H(x)=(f(x),g(x))$. Then $H$ is continuous.
> A stronger version of this theorem is that $f:X\to Y$ and $g:X\to Z$ are continuous maps of topological spaces if and only if $H:X\to Y\times Z$ is continuous.
<details>
<summary>Proof</summary>
It is sufficient to check the basis elements of the topology on $Y\times Z$.
The basis for the topology on $Y\times Z$ is $U\times V\subseteq Y\times Z$, where $U\subseteq Y$ and $V\subseteq Z$ are open. This form a basis for the topology on $Y\times Z$.
We only need to show that $H^{-1}(U\times V)$ is open in $X$.
Let $H^{-1}(U\times V)=\{x\in X | (f(x),g(x))\in U\times V\}$.
So $H^{-1}(U\times V)=f^{-1}(U)\cap g^{-1}(V)$.
Since $f$ and $g$ are continuous, $f^{-1}(U)$ and $g^{-1}(V)$ are open in $X$.
So $H^{-1}(U\times V)$ is open in $X$.
</details>
Exercise: Prove the stronger version of the theorem,
If $H:X\to Y\times Z$ is continuous, then $f:X\to Y$ and $g:X\to Z$ are continuous.

180
content/Math4201/Math4201_L12.md
View File

@@ -1,180 +0,0 @@
# Math4201 Topology I (Lecture 12)
## Metric spaces
### Basic properties and definitions
#### Definition of metric space
A metric space is a set $X$ with a function $d:X\times X\to \mathbb{R}$ that satisfies the following properties:
1. $\forall x,y\in X, d(x,y)\geq 0$ and $d(x,y)=0$ if and only if $x=y$. (positivity)
2. $\forall x,y\in X, d(x,y)=d(y,x)$. (symmetry)
3. $\forall x,y,z\in X, d(x,z)\leq d(x,y)+d(y,z)$. (triangle inequality)
<details>
<summary>Example of metric space</summary>
Let $X=\mathbb{R}$ and $d(x,y)=|x-y|$.
Check definition of metric space:
1. Positivity: $d(x,y)=|x-y|\geq 0$ and $d(x,y)=0$ if and only if $x=y$.
2. Symmetry: $d(x,y)=|x-y|=|y-x|=d(y,x)$.
3. Triangle inequality: $d(x,z)=|x-z|\leq |x-y|+|y-z|=d(x,y)+d(y,z)$ since $|a+b|\leq |a|+|b|$ for all $a,b\in \mathbb{R}$.
---
Let $X$ be arbitrary. The trivial metric is $d(x,y)=\begin{cases}
0 & \text{if } x=y \\
1 & \text{if } x\neq y
\end{cases}$
Check definition of metric space:
1. Positivity: $d(x,y)=\begin{cases}
0 & \text{if } x=y \\
1 & \text{if } x\neq y
\end{cases}\geq 0$ and $d(x,y)=0$ if and only if $x=y$.
1. Symmetry: $d(x,y)=\begin{cases}
0 & \text{if } x=y \\
1 & \text{if } x\neq y
\end{cases}=d(y,x)$.
1. Triangle inequality use case by case analysis.
</details>
#### Balls of a metric space forms a basis for a topology
Let $(X,d)$ be a metric space. $x\in X$ and $r>0, r\in \mathbb{R}$. We define the ball of radius $r$ centered at $x$ as $B_r(x)=\{y\in X:d(x,y)<r\}$.
Goal: Show that the balls of a metric space forms a basis for a topology.
$$
\{B_r(x)|x\in X,r>0,r\in \mathbb{R}\}\text{ is a basis for a topology on }X
$$
<details>
<summary>Example of balls of a metric space</summary>
Let $X=\mathbb{R}$ and $d(x,y)=\begin{cases}
0 & \text{if } x=y \\
1 & \text{if } x\neq y
\end{cases}$
The balls of this metric space are:
$$
B_r(x)=\begin{cases}
\{x\} & \text{if } r<1 \\
X & \text{if } r\geq 1
\end{cases}
$$
> [!NOTE]
>
> This basis generate the discrete topology of $X$.
---
Let $X=\mathbb{R}$ and $d(x,y)=|x-y|$.
The balls of this metric space are:
$$
B_r(x)=\{(x-r,x+r)\}
$$
This basis is the set of all open sets in $\mathbb{R}$, which generates the standard topology of $\mathbb{R}$.
</details>
<details>
<summary>Proof</summary>
Let's check the two properties of basis:
1. $\forall x\in X$, $\exists B_r(x)\in \{B_r(x)|x\in X,r>0,r\in \mathbb{R}\}$ such that $x\in B_r(x)$. (Trivial by definition of non-zero radius ball)
2. $\forall B_r(x),B_r(y)\in \{B_r(x)|x\in X,r>0,r\in \mathbb{R}\}$, $\forall z\in B_r(x)\cap B_r(y)$, $\exists B_r(z)\in \{B_r(x)|x\in X,r>0,r\in \mathbb{R}\}$ such that $z\in B_r(z)\subseteq B_r(x)\cap B_r(y)$.
Observe that for any $z\in B_r(x)$, then there exists $\delta>0$ such that $B_\delta(z)\subseteq B_r(x)$.
Let $\delta=r-d(x,z)$, then $B_\delta(z)\subseteq B_r(x)$ (by triangle inequality)
Similarly, there exists $\delta'>0$ such that $B_\delta'(z)\subseteq B_r(y)$.
Take $\lambda=min\{\delta,\delta'\}$, then $B_\lambda(z)\subseteq B_r(x)\cap B_r(y)$.
</details>
#### Definition of Metric topology
For any metric space $(X,d)$, the topology generated by the balls of the metric space is called metric topology.
#### Definition of metrizable
A topological space $(X,\mathcal{T})$ is metrizable if it is the metric topology for some metric $d$ on $X$.
> Q: When is a topological space metrizable?
#### Lemma: Every metric topology is Hausdorff
If a topology isn't Hausdorff, then it isn't metrizable.
<details>
<summary>Example of non-metrizable space</summary>
Trivial topology **with at least two points** is not Hausdorff, so it isn't metrizable.
---
Finite complement topology on infinite set is not Hausdorff.
Suppose there exists $x,y\in X$ such that $x\neq y$ and $x\in U\subseteq X$ and $y\in V\subseteq X$ such that $X-U$ and $X-V$ are finite.
Since $U\cap V=\emptyset$, we have $V\subseteq X-U$, which is finite. So $X-V$ is infinite. (contradiction that $X-V$ is finite)
So $X$ with finite complement topology is not Hausdorff, so it isn't metrizable.
</details>
<details>
<summary>Proof</summary>
Let $x,y\in (X,d)$ and $x\neq y$. To show that $X$ is Hausdorff, it is suffices to show that there exists $r,r'>0$ such that $B_r(x)\cap B_r'(y)=\emptyset$.
Take $r=r'=\frac{1}{2}d(x,y)$, then $B_r(x)\cap B_r'(y)=\emptyset$. (by triangle inequality)
We prove this by contradiction.
Suppose $\exists z\in B_r(x)\cap B_r'(y)$, then $d(x,z)<r$ and $d(y,z)<r'$.
Then $d(x,y)\leq d(x,z)+d(z,y)<r+r'=\frac{1}{2}d(x,y)+\frac{1}{2}d(x,y)=d(x,y)$. (contradiction $d(x,y)<d(x,y)$)
Therefore, $X$ is Hausdorff.
</details>
### Other metrics on $\mathbb{R}^n$
Let $\mathbb{R}^n$ be the set of all $n$-tuples of real numbers with standard topology.
Let $d: \mathbb{R}^n\times \mathbb{R}^n\to \mathbb{R}$ be defined by (the Euclidean distance)
$$
d(u,v)=\sqrt{\sum_{i=1}^n (u_i-v_i)^2}
$$
In $\mathbb{R}^2$ the ball is a circle.
Let $\rho(u,v)=\max_{i=1}^n |u_i-v_i|$. (Square metric)
In $\mathbb{R}^2$ the ball is a square.
Let $m(u,v)=\sum_{i=1}^n |u_i-v_i|$. (Manhattan metric)
In $\mathbb{R}^2$ the ball is a diamond.
#### Lemma: Square metric, Manhattan metric, and Euclidean metric are well defined metrics on $\mathbb{R}^n$
Proof ignored. Hard part is to show the triangle inequality. May use Cauchy-Schwarz inequality.

159
content/Math4201/Math4201_L13.md
View File

@@ -1,159 +0,0 @@
# Math4201 Topology I (Lecture 13)
## Metic spaces
### Three different metrics on $\mathbb{R}^n$
Euclidean metric:
$$
d(x,y)=\sqrt{\sum_{i=1}^n (x_i-y_i)^2}
$$
Square metric:
$$
d(x,y)=\max_{i=1}^n |x_i-y_i|
$$
Manhattan metric:
$$
d(x,y)=\sum_{i=1}^n |x_i-y_i|
$$
So to prove our proposition, we need to show that any pair of metrics $d$ and $d'$ with basis generated by balls defined
$$
\mathcal{B}=\{B_r^{(d)}(x)|x\in X,r>0,r\in \mathbb{R}\}
$$
and
$$
\mathcal{B}'=\{B_r^{(d')}(x)|x\in X,r>0,r\in \mathbb{R}\}
$$
are equivalent.
#### Proposition: The metrics induce the same topology on $\mathbb{R}^n$
The three metrics induce the same topology on $\mathbb{R}^n$, and it's the standard topology.
#### Lemma of equivalent topologies
If $\mathcal{T}$ and $\mathcal{T}'$ are two topologies on $X$, we say $\mathcal{T}$ and $\mathcal{T}'$ are equivalent to each other if and only if the following two conditions are satisfied:
1. $\forall B_1\in \mathcal{T}, \exists B_2\in \mathcal{T}'$ such that $\forall x\in B_1, \exists x\in B_2\subseteq B_1$.
2. $\forall B_2\in \mathcal{T}', \exists B_1\in \mathcal{T}$ such that $\forall x\in B_2, \exists x\in B_1\subseteq B_2$.
#### Lemma of equivalent metrics
Let $d$ and $d'$ be two metrics on $X$. If the following holds, then the metric topology associated to $d$ and $d'$ are equivalent.
1. $\forall x\in X, \forall \delta>0, \exists \epsilon>0$ such that $B_\delta(x)\subseteq B_\epsilon(x)$
2. $\forall x\in X, \forall \epsilon>0, \exists \delta>0$ such that $B_\epsilon(x)\subseteq B_\delta(x)$
<details>
<summary>Proof</summary>
To apply the lemma, we try to compute the three metrics on $\mathbb{R}^n$.
$u=(u_1,u_2,\dots,u_n), v=(v_1,v_2,\dots,v_n)\in \mathbb{R}^n$
For Euclidean metric:
$$
d(u,v)=\sqrt{\sum_{i=1}^n (u_i-v_i)^2}
$$
For square metric:
$$
\rho(u,v)=\max_{i=1}^n |u_i-v_i|
$$
For Manhattan metric:
$$
m(u,v)=\sum_{i=1}^n |u_i-v_i|
$$
**First** we will show that $d$ and $\rho$ are equivalent.
Note that
$$
\max_{i=1}^n |u_i-v_i|\leq \sqrt{\sum_{i=1}^n (u_i-v_i)^2}
$$
So $\forall u\in B_r^{(d)}(x), d(u,v)<r\implies \rho(u,v)<r$
So $u\in B_r^{(\rho)}(x)$.
$$
B_r^{(d)}(u)\subseteq B_r^{(\rho)}(u)
$$
Note that
$$
\sqrt{\sum_{i=1}^n (u_i-v_i)^2}\leq \sqrt{\sum_{i=1}^n max\{|u_i-v_i|\}^2}=\sqrt{n}\times max\{|u_i-v_i|\}
$$
So $\forall u\in B_{r/\sqrt{n}}^{(\rho)}(x), \rho(u,v)<r/\sqrt{n}\implies d(u,v)<r$
So $u\in B_r^{(d)}(x)$.
So $B_{r/\sqrt{n}}^{(\rho)}(x)\subseteq B_r^{(d)}(x)$.
> imagine two square capped circle inside
**Then we will show** that $\rho$ and $m$ are equivalent.
Observing that
$$
\max_{i=1}^n |u_i-v_i|\leq \sum_{i=1}^n |u_i-v_i|\leq n\times \max_{i=1}^n |u_i-v_i|
$$
Then we have
$$
B_{r/n}^{(\rho)}(x)\subseteq B_r^{(m)}(x)\subseteq B_n^{(\rho)}(x)
$$
> imagine two square capped a diamonds inside
**Finally**, we will show that the topology generated by the square metric is the same as the product topology on $\mathbb{R}^n$.
Recall the basis for the product topology on $\mathbb{R}^n$ with standard topology.
$$
\mathcal{B}=\{(a_1,b_1)\times (a_2,b_2)\times \cdots \times (a_n,b_n)|a_i,b_i\in \mathbb{R},a_i<b_i\}
$$
Let $x=(x_1,x_2,\dots,x_n)\in (a_1,b_1)\times (a_2,b_2)\times \cdots \times (a_n,b_n)$.
Let $\delta=\min_{i=1}^n \{|x_i-a_i|,|x_i-b_i|\}$.
Then $x\in B_\delta^{(\rho)}(x)\subseteq (a_1,b_1)\times (a_2,b_2)\times \cdots \times (a_n,b_n)$.
In the other direction, let $x\in B_r^{(\rho)}(x)$, $x=(x_1,x_2,\dots,x_n)$.
Then $B_r^{(\rho)}(x)\subseteq (x_1-r,x_1+r)\times (x_2-r,x_2+r)\times \cdots \times (x_n-r,x_n+r)$.
This is an element of $\mathcal{B}$, by combining the two directions, we have the standard topology is the same as the topology generated by the square metric.
</details>
#### Proposition of metric induced product topology
Let $(X,d),(Y,d')$ be two metric spaces with metric topology $\mathcal{T},\mathcal{T}'$. On $X\times Y$, we can define a metric $\rho$ by $\rho((x,y),(x',y'))\coloneqq \max\{d(x,x'),d'(y,y')\}$, $(x,y),(x',y')\in X\times Y$.
Then this metric topology on $X\times Y$ is the same as the product topology on $X\times Y$.
> [!NOTE]
>
> Product of metrizable topological spaces is metrizable.

113
content/Math4201/Math4201_L14.md
View File

@@ -1,113 +0,0 @@
# Math4201 Topology I (Lecture 14)
## Metric topology
### Product topology and metric topology
If $X$ and $Y$ are metrizable spaces, then the product space $X\times Y$ is metrizable.
If $X$ is metrizable, then the subspace $A\subset X$ equipped with subspace topology is metrizable.
<details>
<summary>Proof</summary>
Let $d$ be a metric on $X$. Then define $d'$ be the restriction of $d$ to $A$:
$$
d':A\times A\to \mathbb{R}+
$$
$$
d'(x,y)=d(x,y)
$$
$x,y\in A\subseteq X$
$d'$ is a metric on $A$. Since the metric topology on $A$ associated to $d'$ is the same as the subspace topology.
Note that for any $x\in A$ and $r>0$
$$
B_r^{d}(x)\cap A=B_r^{d'}(x)\tag{*}
$$
A basis for metric topology on $A$ is given by:
$$
\mathcal{B}=\{B_r^{d'}(x)|x\in A,r>0,r\in \mathbb{R}\}
$$
A basis for the subspace topology on $A$ is given by:
$$
\mathcal{B}'=\{B_r^{d}(x)\cap A|x\in A,r>0,r\in \mathbb{R}\}
$$
Since (*) holds, $\mathcal{B}\subseteq \mathcal{B}'$.
This shows that subspace topology on $A$ is finer than the metric topology on $A$.
We need to show that for any $B_r^{d}(x)$ with $x\in X$ and $y\in B_r^{d}(x)\cap A$, we have $r'>0$ such that $y\in B_r^{d'}(y)\subseteq B_r^{d}(x)\cap A$.
Use triangle inequality, we have $r'=r-d(x,y)>0$ such that $y\in B_r^{d'}(y)\subseteq B_r^{d}(x)\cap A$.
</details>
#### Proposition on sequence and closure
Let $X$ be a topological space and $A\subseteq X$. Then the following holds:
If there is a sequence $\{x_n\}_{n=1}^\infty$ such that $x_n\in A$ and $x_n\to x$, then $x\in \overline{A}$. ($x$ may not be in $A$)
The reverse holds if $X$ is a metric space. That is, if $X$ is a metric space and $x\in \overline{A}$, then there is a sequence $\{x_n\}_{n=1}^\infty$ such that $x_n\in A$ and $x_n\to x$.
<details>
<summary>Example of non-metrizable space</summary>
For the second part of the claim
Let $X=\mathbb{R}\times \mathbb{R}\times \mathbb{R}\times \cdots$ with the product topology over infinite product.
$X=\text{Map}(\mathbb{N},\mathbb{R})=\{(x_1,x_2,x_3,\cdots)|x_i\in \mathbb{R},i\in \mathbb{N}\}$.
The box topology on $X$ is the topology generated by:
$$
\mathcal{B}=\{(a_1,b_1)\times (a_2,b_2)\times (a_3,b_3)\times \cdots|a_i,b_i\in \mathbb{R},i\in \mathbb{N}\}
$$
It is easy to check that this is a basis.
Take $A=\mathbb{R}^{> 0}\times \mathbb{R}^{> 0}\times \mathbb{R}^{> 0}\times \cdots=\{(x_1,x_2,x_3,\cdots)|x_i> 0\}$.
$\overline{A}=\mathbb{R}^{\geq 0}\times \mathbb{R}^{\geq 0}\times \mathbb{R}^{\geq 0}\times \cdots=\{(x_1,x_2,x_3,\cdots)|x_i\geq 0\}$.
In particular, $(0,0,0,\cdots)\in \overline{A}$
Take a basis element $B=(a_1,b_1)\times (a_2,b_2)\times (a_3,b_3)\times \cdots\in \mathcal{B}$ containing $(0,0,0,\cdots)$. This means that $a_i<0<b_i$ Then $(\frac {b_1}{2},\frac {b_2}{2},\frac {b_3}{2},\cdots)\in B\cap A$.
This shows that $(0,0,0,\cdots)\in \overline{A}$.
We claim that there is no sequence $\{x_n\}_{n=1}^\infty$ such that $x_n\in A$ and $x_n\to (0,0,0,\cdots)$.
We proceed by contradiction and suppose that there is such a sequence $\{x_n\}_{n=1}^\infty$ such that $x_n\in A$ and $x_n\to (0,0,0,\cdots)$.
Since $x_n\in A$, we have $v_n=(a_1^n,a_2^n,a_3^n,\cdots)$ with $a_i^n>0$ for all $i\in \mathbb{N}$.
Consider the following open set around $(0,0,0,\cdots)$:
$C=(-\frac{a_1^1}{2},\frac{a_1^1}{2})\times (-\frac{a_2^1}{2},\frac{a_2^1}{2})\times (-\frac{a_3^1}{2},\frac{a_3^1}{2})\times \cdots$
We claim that $v_n\notin C$. Otherwise, we should have $-\frac{a_i^j}{2}<a_j^n<\frac{a_j^j}{2}$ for all $i\in \mathbb{N}$.
But this doesn't hold for $j=n$. This shows that $v_n\cancel{\to} (0,0,0,\cdots)$. Which is a contradiction.
---
For the first part of the claim. Let $\{x_n\}_{n=1}^\infty\subset A$ converge to $x$. Then for any open set $U$ of $x$, we have $N$ such that $x_n\in U$ for $n\geq N$.
In particular, $U\cap A$ is non-empty because it has $x_n$ for large enough $n$.
So $x\in \overline{A}$.
</details>

132
content/Math4201/Math4201_L15.md
View File

@@ -1,132 +0,0 @@
# Math4201 Topology I (Lecture 15)
## Continue on convergence of sequences
### Closure and convergence
#### Proposition in metric space, every convergent sequence converges to a point in the closure
If $X$ is a metric space, $A\subset X$, and $x\in \overline{A}$, then there is a sequence $\{x_n\}_{n=1}^\infty\subseteq A$ such that $x_n\to x$.
<details>
<summary>Proof</summary>
Let $U_n=B_{\frac{1}{n}}(x)$ be a sequence of open neighborhoods of $x$.
Since $x\in \overline{A}$ and $U_n$ is an open neighborhood of $x$, then $U_n\cap A\neq \emptyset$. Take $x_n\in U_n\cap A$, we claim that $\{x_n\}_{n=1}^\infty\subseteq A$ that $x_n\to x$.
Take an open neighborhood $U$ of $x$. Then by the definition of metric topology, there is $r>0$ such that $B_r(x)\subseteq U$.
let $N$ be such that $\frac{1}{N}<r$. Then for an $n\geq N$, we have $\frac{1}{n}\leq \frac{1}{N}<r$. This implies that $B_{\frac{1}{n}}(x)\subseteq B_r(x)\subseteq U$.
So $x_n\in B_{\frac{1}{n}}(x)\subseteq U$ for all $n\geq N$.
</details>
#### Corollary $\mathbb{R}^\omega$ with the box topology is not metrizable
$\mathbb{R}^\omega$ is $\text{Map}(\mathbb{N},\mathbb{R})=\mathbb{R}\times \mathbb{R}\times \mathbb{R}\times \cdots$.
> Note that $\mathbb{R}^\omega$ is Hausdorff. So not all Hausdorff spaces are metrizable.
<details>
<summary>Proof</summary>
Otherwise, the last proposition holds for $\mathbb{R}^\omega$ with the box topology.
Last time we showed that this is not the case.
</details>
#### Definition of first countability axiom
A topological space $(X,\mathcal{T})$ satisfies the **first countability axiom** if for any point $x\in X$, there is a sequence of open neighborhoods of $x$, $\{V_n\}_{n=1}^\infty$ such that any open neighborhood $U$ of $x$ contains one of $V_n$.
Note that if we take $U_n=V_1\cap V_2\cap \cdots \cap V_n$, then any open neighborhood $U$ that contains $V_N$, then it also contains $U_n$ for all $n\geq N$.
> As the previous prof, for metric space, it is natural to try $V_n=B_{\frac{1}{n}}(x)$ for some $x\in X$.
#### Proposition on first countability axiom
Rewrite the [Proposition of metric space, every convergent sequence converges to a point in the closure](#proposition-in-metric-space-every-convergent-sequence-converges-to-a-point-in-the-closure)
We can have the following:
If $(X,\mathcal{T})$ satisfies the first countability axiom, then every convergent sequence converges to a point in the closure.
We can easily prove this by takeing the sequence of open neighborhoods $\{V_n\}_{n=1}^\infty$ instead of $U_n=B_{\frac{1}{n}}(x)$.
#### Proposition of continuous functions
Let $f:X\to Y$ be a map between two topological spaces.
1. If $f$ is continuous, then for any convergent sequence $\{x_n\}_{n=1}^\infty$ in $X$ converging to $x$, the sequence $\{f(x_n)\}_{n=1}^\infty$ converges to $f(x)$.
2. If $X$ is equipped with the metric topology and for any convergent sequence $\{x_n\}_{n=1}^\infty\to x$ in $X$, the sequence $\{f(x_n)\}_{n=1}^\infty\to f(x)$ in $Y$, then $f$ is continuous.
<details>
<summary>Exercise</summary>
Find an example of a function $f:X\to Y$ which is not continuous but for any convergent sequence in $X$, $\{x_n\}_{n=1}^\infty\to x$, the sequence $\{f(x_n)\}_{n=1}^\infty\to f(x)$.
</details>
<details>
<summary>Solution</summary>
Consider $X=\mathbb{R}$ with complement finite topology and $Y=\mathbb{R}$ with the standard topology.
Take identity function $f(x)=x$.
This function is not continuous by trivially taking $(0,1)\subseteq \mathbb{R}$ and the complement of $(0,1)$ is not a finite set, so the function is not continuous.
However, for every convergent sequence in $X$, $\{x_n\}_{n=1}^\infty\to x$, the sequence $\{f(x_n)\}_{n=1}^\infty\to f(x)$ trivially.
</details>
<details>
<summary>Proof</summary>
Part 1:
Let $f:X\to Y$ be a continuous map and
$$
\{x_n\}_{n=1}^\infty\subseteq X
$$
converges to $x$.
Want to show that $\{f(x_n)\}_{n=1}^\infty$ converges to $f(x)$.
i.e. for any open neighborhood $U$ of $f(x)$, we want to show $f(x_n)$ is eventually in $U$. Take $f^{-1}(U)$. This is an open neighborhood of $x$ since $x_n\to x$.
There is $N$ such that $\forall n\geq N$, we have $x_n\in f^{-1}(U)$, $f(x_n)\in U$.
This implies that $\{f(x_n)\}_{n=1}^\infty$ converges to $f(x)$.
Part 2:
Let $f:X\to Y$ be a map between two topological spaces with $X$ being metric such that for any convergent sequence in $X$, $\{x_n\}_{n=1}^\infty\to x$ in $X$, we have $f(x_n)\to f(x)$ in $Y$.
Want to show that $f$ is continuous.
Recall that it suffice to show that for any $A\subseteq X$, $f(\overline{A})\subseteq \overline{f(A)}$.
Take $y\in f(\overline{A})$. Then $y=f(x)$ with $x\in \overline{A}$. By the previous proposition, there is a sequence $\{x_n\}_{n=1}^\infty\subseteq A$ (since $X$ is a metric space) such that $x_n\to x$.
By our assumption,
$$
\{f(x_n)\}_{n=1}^\infty\to f(x) \tag{*}
$$
Note that $\{f(x_n)\}_{n=1}^\infty$ is a sequence in $f(A)$ and ($*$) implies that $y=f(x)\in f(A)$ (by the first part of the proposition). This gives us the claim.
</details>
> [!NOTE]
>
> The second part of the proposition is also true when $X$ is not a metric space but satisfies the first countability axiom.
#### Equivalent formulation of continuity
If $(X,d)$ and $(Y,d')$ are metric spaces and $f:X\to Y$ is a map, then $f$ is continuous if and only if for any $x_0\in X$ and any $\epsilon > 0$, there exists $\delta > 0$ such that if $\forall n\in X, d(x_n,x_0)<\delta$, then $d'(f(x_n),f(x_0))<\epsilon$.
Proof similar to the $X=Y=\mathbb{R}$ case.

159
content/Math4201/Math4201_L16.md
View File

@@ -1,159 +0,0 @@
# Math4201 Lecture 16 (Topology I)
## Continuous maps
The following maps are continuous:
$$
F_+:\mathbb{R}\times \mathbb{R}\to \mathbb{R}, (x,y)\to x+y
$$
$$
F_-:\mathbb{R}\times \mathbb{R}\to \mathbb{R}, (x,y)\to x-y
$$
$$
F_\times:\mathbb{R}\times \mathbb{R}\to \mathbb{R}, (x,y)\to x\times y
$$
$$
F_\div:\mathbb{R}\times (\mathbb{R}\setminus \{0\})\to \mathbb{R}, (x,y)\to \frac{x}{y}
$$
### Composition of continuous functions is continuous
Let $f,g:X\to \mathbb{R}$ be continuous functions. $X$ is topological space.
Then the following functions are continuous:
$$
H:X\to \mathbb{R}\times \mathbb{R}, x\to (f(x),g(x))
$$
Since the composition of continuous functions is continuous, we have
$$
F_+\circ H:X\to \mathbb{R}, x\to f(x)+g(x)
$$
$$
F_-\circ H:X\to \mathbb{R}, x\to f(x)-g(x)
$$
$$
F_\times\circ H:X\to \mathbb{R}, x\to f(x)\times g(x)
$$
are all continuous.
More over, if $g(x)\neq 0$ for all $x\in X$, then
$$
F_\div\circ H:X\to \mathbb{R}, x\to \frac{f(x)}{g(x)}
$$
is continuous following the similar argument.
### Defining metric for functions
#### Definition of bounded metric space
A metric space $(Y,d)$ is **bounded** if there is $M\in\mathbb{R}^{\geq 0}$ such that
$$
\forall y,y'\in Y, d(y,y')<M
$$
<details>
<summary>Example of bounded metric space</summary>
If $(Y,d)$ is a bounded metric space, let $M$ be a positive constant, then $\overline{d}=\min\{M,d\}$ is a bounded metric space.
In fact, the metric topology by $d$ and $\overline{d}$ are the same. (proved in homeworks)
</details>
Let $X$ be a topological space. and $(Y,d)$ be a **bounded** metric space.
$$
\operatorname{Map}(X,Y)\coloneqq \{f:X\to Y|f \text{ is a map}\}
$$
Define $\rho:\operatorname{Map}(X,Y)\times \operatorname{Map}(X,Y)\to \mathbb{R}$ by
$$
\rho(f,g)=\sup_{x\in X} d(f(x),g(x))
$$
#### Lemma space of map with metric defined is a metric space
$(\operatorname{Map}(X,Y),\rho)$ is a metric space.
<details>
<summary>Proof</summary>
Proof is similar to showing that the square metric is a metric on $\mathbb{R}^n$.
$\rho(f,g)=0\implies \sup_{x\in X}(d(f(x),g(x)))=0$
Since $d(f(x),g(x))\geq 0$, this implies that $d(f(x),g(x))=0$ for all $x\in X$.
The triangle inequality of being metric for $\rho$ follows from the similar properties for $d$.
</details>
#### Lemma continuous maps form a closed subset of the space of maps
Let $(\operatorname{Map}(X,Y),\rho)$ be a metric space defined before.
and
$$
Z=\{f:X\to Y|f \text{ is a continuous map}\}
$$
Then $Z$ is a closed subset of $(\operatorname{Map}(X,Y),\rho)$.
<details>
<summary>Proof</summary>
We need to show that $\overline{Z}=Z$.
Since $\operatorname{Map}(X,Y)$ is a metric space, this is equivalent to showing that: Let $f_n:X\to Y\in Z$ be a sequence of continuous maps,
Which is to prove the uniform convergence,
$$
f_n \to f \in \operatorname{Map}(X,Y)
$$
Then we want to show that $f$ is also continuous.
It is to show that for any open subspace $V$ of $Y$, $f^{-1}(V)$ is open in $X$.
Take $x_0\in f^{-1}(V)$, we'd like to show that there is an open neighborhood $U$ of $x_0$ such that $U\subseteq f^{-1}(V)$.
Since $x_0\in f^{-1}(V)$, then $f(x_0)\in V$. By metric definition, there is $r>0$ such that $B_r(f(x_0))\subseteq V$.
Take $N$ to be large enough such $\rho(f_N(x), f(x)) < \frac{r}{3}$
So $\forall x\in X$, $d(f(x),f_N(x))<\frac{r}{3}$
Since $f_N$ is continuous, $f_N^{-1}(B_{r/3}(f(x_0)))$ is an open set $U\subseteq X$ containing $x_0$.
Take $x\in U$, $d(f(x),f(x_0))<d(f(x),f_N(x_0))+d(f_N(x),f_N(x_0))+d(f_N(x_0),f(x_0))$ using triangle inequality.
Note that,
$d(f(x),f_N(x))<\frac{r}{3}$ (using $N$ large enough),
$d(f_N(x),f_N(x_0))<\frac{r}{3}$ (using $x\in U$, then $f_N(x)\in B_{r/3}(f_N(x_0))$, so $d(f_N(x),f_N(x_0))<\frac{r}{3}$),
$d(f_N(x_0),f(x_0))<\frac{r}{3}$ (using $N$ large enough),
So $d(f(x),f(x_0))<\frac{r}{3}+\frac{r}{3}+\frac{r}{3}=r$.
So $f(x)\in B_r(f(x_0))\implies x\in f^{-1}(B_r(f(x_0)))\implies x\in f^{-1}(V)\implies U\subseteq f^{-1}(V)$.
So $f^{-1}(V)$ is open in $X$.
</details>

86
content/Math4201/Math4201_L17.md
View File

@@ -1,86 +0,0 @@
# Math4201 Topology I (Lecture 17)
## Quotient topology
How can we define topologies on the space obtained points in a topological space?
### Quotient map
Let $(X,\mathcal{T})$ be a topological space. $X^*$ is a set and $q:X\to X^*$ is a surjective map.
The quotient topology on $X^*$ is defined as follows:
$$
\mathcal{T}^* = \{U\subseteq X^*\mid q^{-1}(U)\in \mathcal{T}\}
$$
$U\subseteq X^*$ is open if and only if $q^{-1}(U)$ is open in $X$.
In particular, $q$ is continuous map.
#### Definition of quotient map
$q:X\to X^*$ defined above is called a **quotient map**.
#### Definition of quotient space
$(X^*,\mathcal{T}^*)$ is called the **quotient space** of $X$ by $q$.
### Typical way of constructing a surjective map
#### Equivalence relation
$\sim$ is a subset of $X\times X$ satisfying:
- reflexive: $\forall x\in X, x\sim x$
- symmetric: $\forall x,y\in X, x\sim y\implies y\sim x$
- transitive: $\forall x,y,z\in X, x\sim y\text{ and } y\sim z\implies x\sim z$
#### Equivalence classes
Check equivalence relation.
For $x\in X$, the equivalence class of $x$ is denoted as $[x]\coloneqq \{y\in X\mid y\sim x\}$.
$X^*$ is the set of all equivalence classes on $X$.
$q:X\to X^*$ is defined as $q(x)=[x]$ will be a surjective map.
<details>
<summary>Example of surjective maps and their quotient spaces</summary>
Let $X=\mathbb{R}^2$ and $(s,t)\sim (s',t')$ if and only if $s-s'$ and $t-t'$ are both integers.
This space as a topological space is homeomorphic to the torus.
---
Let $X=\{(s,t)\in \mathbb{R}^2\mid s^2+t^2\leq 1\}$ and $(s,t)\sim (s',t')$ if and only if $s^2+t^2$ and $s'^2+t'^2$. with subspace topology as a subspace of $\mathbb{R}^2$.
This space as a topological space is homeomorphic to the spherical shell $S^2$.
</details>
We will show that the quotient topology is a topology on $X^*$.
<details>
<summary>Proof</summary>
We need to show that the quotient topology is a topology on $X^*$.
1. $\emptyset, X^*$ are open in $X^*$.
$\emptyset, X^*$ are open in $X^*$ because $q^{-1}(\emptyset)=q^{-1}(X^*)=\emptyset$ and $q^{-1}(X^*)=X$ are open in $X$.
2. $\mathcal{T}^*$ is closed with respect to arbitrary unions.
$$
q^{-1}(\bigcup_{\alpha \in I} U_\alpha)=\bigcup_{\alpha \in I} q^{-1}(U_\alpha)
$$
3. $\mathcal{T}^*$ is closed with respect to finite intersections.
$$
q^{-1}(\bigcap_{\alpha \in I} U_\alpha)=\bigcap_{\alpha \in I} q^{-1}(U_\alpha)
$$
</details>

115
content/Math4201/Math4201_L18.md
View File

@@ -1,115 +0,0 @@
# Math4201 Topology I (Lecture 18)
## Quotient topology
Let $(X,\mathcal{T})$ be a topological space and $X^*$ be a set, $q:X\to X^*$ is a surjective map. The quotient topology on $X^*$:
$U\subseteq X^*$ is open $\iff q^{-1}(U)$ is open in $X$.
Equivalently,
$Z\subseteq X^*$ is closed $\iff q^{-1}(Z)$ is closed in $X$.
### Open maps
Let $(X,\mathcal{T})$ and $(Y,\mathcal{T}')$ be two topological spaces
Let $f:X\to Y$ is a quotient map if and only if $f$ is surjective and
$U\subseteq Y$ is open $\iff f^{-1}(U)$ is open
or equivalently
$Z\subseteq Y$ is closed $\iff f^{-1}(Z)$ is closed.
#### Definition of open map
Let $X\to Y$ be **continuous**. We say $f$ is open if for any $V\subseteq X$ be open, $f(V)$ is open in $Y$.
Let $X\to Y$ be **continuous**. We say $f$ is closed if for any $V\subseteq X$ be closed, $f(V)$ is closed in $Y$.
$$
ff^{-1}(U)=U\text{ if }f \text{ is surjective}=U\cap f(X)
$$
<details>
<summary>Examples of open maps</summary>
Let $X,Y$ be topological spaces. Define the projection map $\pi_X:X\times Y\to X$, $\pi_X(x,y)=x$.
This is a surjective continuous map $(Y\neq \phi)$
This map is open. If $U\subseteq X$ is open and $V\subseteq Y$ is open, then $U\times V$ is open in $X\times Y$ and such open sets form a basis.
$\pi_X(U\times V)=\begin{cases}
U&\text{ if }V\neq \emptyset\\
\emptyset &\text{ if }V=\emptyset
\end{cases}$
In particular, image of any such open set is open. Since any open $W\subseteq X\times Y$ is a union of such open sets.
$W=\bigcup_{\alpha\in I}U_\alpha\times V\alpha$
$\pi_X(W)=\pi_X(\bigcup_{\alpha\in I}U_\alpha\times V_\alpha)=\bigcup_{\alpha\in I}\pi_X(U_\alpha\times V_\alpha)=\bigcup_{\alpha\in I}U_\alpha$
is open in $X$.
However, $\pi_X$ is not necessarily a closed map.
Let $X=Y=\mathbb{R}$ and $X\times Y=\mathbb{R}^2$
$Z\subseteq \mathbb{R}^2=\{(x,y)\in\mathbb{R}^2|x\neq 0, y=\frac{1}{x}\}$ is a closed set in $\mathbb{R}^2$
$\pi_X(Z)=\mathbb{R}\setminus \{0\}$ is not closed.
---
Let $X=[0,1]\cup [2,3]$, $Y=[0,2]$ with subspace topology on $\mathbb{R}$
Let $f:X\to Y$ be defined as:
$$
f(x)=\begin{cases}
x& \text{ if } x\in [0,1]\\
x-1& \text{ if }x\in [2,3]
\end{cases}
$$
$f$ is continuous and surjective, $f$ is closed $Z\subseteq [0,1]\cup [2,3]=Z_1\cup Z_2$, $Z_1\subseteq [0,1],Z_2\subseteq [2,3]$ is closed, $f(Z)=f(Z_1)\cup f(Z_2)$ is closed in $X$.
But $f$ is not open. Take $U=[0,1]\subseteq X$, $f=[0,1]\subseteq [0,2]$ is not open because of the point $1$.
> In general, and closed surjective map is a quotient map. In particular, this is an example of a closed surjective quotient map which is not open.
</details>
Let $f$ be a surjective open map. Then $f$ is a quotient map:
$U\subseteq Y$ is open and $f$ is continuous, $\implies f^{-1}(U)\subseteq X$ is open
$f^{-1}(U)\subseteq X$ is open and $f$ is surjective and open, $\implies f(f^{-1}(U))=U$ is open.
#### Proposition of continuous and open maps
If $f$ is a continuous bijection, then $f$ is open. if and only if $f^{-1}$ is continuous.
<details>
<summary>Proof</summary>
To show $f^{-1}$ is continuous, we have to show for $U\subseteq X$ open. $(f^{-1})^{-1}(U)=f(U)\subseteq Y$ is open.
This is the same thing as saying that $f$ is open.
</details>
Let $f$ be a quotient map $f: X \to Y$, and $g$ be a continuous map $g:X\to Z$.
We want to find $\hat{g}$ such that $g=\hat{g}\circ f$.
If $x_1,x_2\in X$, such that $f(x_1)=f(x_2)$ and $g(x_1)\neq g(x_2)$, then we cannot find $\hat{g}$.
#### Proposition for continuous and quotient maps
Let $f$ and $g$ be as above. Moreover, for any $y\in Y$, all the points in $f^{-1}(y)$ are mapped to a single point by $g$. Then there is a unique continuous map $\hat{g}$ such that $g=\hat{g}\circ f$.
Continue next week.

84
content/Math4201/Math4201_L19.md
View File

@@ -1,84 +0,0 @@
# Math4201 Topology I (Lecture 19)
## Quotient topology
### More propositions
#### Proposition for continuous and quotient maps
Let $X,Y,Z$ be topological spaces. $p$ is a quotient map from $X$ to $Y$ and $g$ is a continuous map from $X$ to $Z$.
Moreover, if for any $y\in Y$, the map $g$ is constant on $p^{-1}(y)$, then there is a continuous map $f: Y\to Z$ satisfying $f\circ p=g$.
<details>
<summary>Proof</summary>
For any $y\in Y$, take $x\in X$ such that $p(x)=y$ (since $p$ is surjective).
Define $f(y)\coloneqq g(x)$.
Note that this is well-defined and it doesn't depend on the specific choice of $x$ that $p(x)=y$ because $g$ is constant on $p^{-1}(y)$.
Then we check that $f$ is continuous.
Let $U\subseteq Z$ be open. Then we want to show that $f^{-1}(U)\subseteq Y$ is open.
Since $p$ is a quotient map, this is equivalent to showing that $p^{-1}(f^{-1}(U))\subseteq X$ is open. Note that $p^{-1}(f^{-1}(U))=g^{-1}(U)$.
Since $g$ is continuous, $g^{-1}(U)$ is open in $X$.
Since $g^{-1}(U)$ is open in $X$, $p^{-1}(g^{-1}(U))$ is open in $Y$.
</details>
> In general, $p^{-1}(y)$ is called the **fiber** of $p$ over $y$. The $g$ must be constant on the fiber.
>
> We may define $p^{-1}(y)$ as the equivalence class of $y$ if $p$ is defined using the equivalence relation. By definition $p^{-1}([x])$ is the element of $x$ that are $\sim x$.
#### Additional to the proposition
Note that $f$ is unique.
It is not hard to see that $f$ is a quotient map if and only if $g$ is a quotient map. (check book for detailed proofs)
#### Definition of saturated map
Let $p:X\to Y$ be a quotient map. We say $A\subseteq X$ is **saturated** by $p$ if $A=p^{-1}(B)$ for some $B\subseteq Y$.
Equivalently, if $x\in A$, then $p^{-1}(p(x))\subseteq A$.
#### Proposition for quotient maps from saturated sets
Let $p:X\to Y$ be a quotient map and $q$ be given by restriction of $p$ to $A\subseteq X$. $q:A\to p(A)$, $q(x)=p(x),x\in A$.
Assume that $A$ is saturated by $p$.
1. If $A$ is closed or open, then $q$ is a quotient map.
2. If $p$ is closed or open, then $q$ is a quotient map.
<details>
<summary>Proof</summary>
We prove 1 and assume that $A$ is open, (the closed case is similar).
clearly, $q:A\to p(A)$ is surjective.
In general, restricting the domain and the range of a continuous map is continuous.
Since $A$ is saturated by $p$, then $p^{-1}(p(A))=A$ is open, so $p(A)$ is open because $p$ is a quotient map. Let $V\subseteq p(A)$ and $q^{-1}(V)\subseteq A$ is open. Then $q^{-1}(V)=p^{-1}(V)$.
(i) $q^{-1}(V)\subseteq p^{-1}(V)$: $x\in q^{-1}(V)\implies q(x)\in V$. Then $p(x)=q(x)\in V$
(ii) $p^{-1}(V)\subseteq q^{-1}(V)$: $x\in p^{-1}(V)\implies p(x)\in V\subseteq p(A)$. This implies that $x\in p^{-1}(p(A))=A$ since $A$ is saturated by $p$. Therefore $x\in q^{-1}(V)$.
Since $A$ is open in $X$, any open subspace of $A$ is open in $X$. In particular, $q^{-1}(V)=p^{-1}(V)$ is open in $X$.
Since $p$ is a quotient map, and $p^{-1}(V)$ is open in $X$, $V$ is open in $Y$. So $V\subseteq p(A)$ is open in $Y$.
This shows $q$ is a quotient map.
---
We prove 2 next time...
</details>

110
content/Math4201/Math4201_L2.md
View File

@@ -1,110 +0,0 @@
# Math4201 Topology I (Lecture 2)
## Topology
Distance in $\mathbb{R}$, or more generally in $\mathbb{R}^n$. ([metric space](https://notenextra.trance-0.com/Math4111/Math4111_L9#metric-space))
Intervals in $\mathbb{R}$, or more generally open balls in $\mathbb{R}^n$. (topological space)
### Topological Spaces
#### Definition of Topological Space
A topological space is a pair of set $X$ and a collection of subsets of $X$, denoted by $\mathcal{T}$ (imitates the set of "open sets" in $X$), satisfying the following axioms:
1. $\emptyset \in \mathcal{T}$ and $X \in \mathcal{T}$
2. $\mathcal{T}$ is closed with respect to arbitrary unions. This means, for any collection of open sets $\{U_\alpha\}_{\alpha \in I}$, we have $\bigcup_{\alpha \in I} U_\alpha \in \mathcal{T}$
3. $\mathcal{T}$ is closed with respect to finite intersections. This means, for any finite collection of open sets $\{U_1, U_2, \ldots, U_n\}$, we have $\bigcap_{i=1}^n U_i \in \mathcal{T}$
The elements of $\mathcal{T}$ are called **open sets**.
The topological space is denoted by $(X, \mathcal{T})$.
<details>
<summary>Examples of topological spaces</summary>
Trivial topology: Let $X$ be arbitrary. The trivial topology is $\mathcal{T}_0 = \{\emptyset, X\}$
Discrete topology: Let $X$ be arbitrary. The discrete topology is $\mathcal{T}_1 = \mathcal{P}(X)=\{U \subseteq X\}$
Understanding all possible topologies on a set.
Let's say $X=\{a,b\}$
The trivial topology is $\mathcal{T}_0 = \{\emptyset, \{a,b\}\}$
The discrete topology is $\mathcal{T}_1 = \{\emptyset, \{a\}, \{b\}, \{a,b\}\}$
Other topologies:
$\mathcal{T}_2 = \{\emptyset, \{a\}, \{a,b\}\}$
$\mathcal{T}_3 = \{\emptyset, \{b\}, \{a,b\}\}$
</details>
<details>
<summary>Non-example of topological space</summary>
Let $X=\{a,b,c\}$
The set $\mathcal{T}_1=\{\emptyset, \{a\}, \{b\}, \{a,b,c\}\}$ is not a topology because it is not closed under union $\{a\} \cup \{b\} = \{a,b\} \notin \mathcal{T}_1$
</details>
#### Definition of Complement finite topology
Let $X$ be arbitrary. The complement finite topology is $\mathcal{T}\coloneqq \{U\subseteq X|X\setminus U \text{ is finite}\}\cup \{\emptyset\}$
The topology is valid because:
<details>
<summary>Proof</summary>
1. $\emptyset \in \mathcal{T}$ because $X\setminus \emptyset = X$ is finite.
2. Let $\{U_\alpha\}_{\alpha \in I}$ be an arbitrary collection such that $X\setminus U_\alpha$ is finite for each $\alpha \in I$.
Without loss of generality, we can assume that $U_\alpha \neq \emptyset$ for each $\alpha \in I$, since the union of arbitrary set with $\emptyset$ is the set itself.
If all of them are empty, then the union is empty, which complement is $X\subset \mathcal{T}$.
Otherwise,
$$
X\setminus \bigcup_{\alpha \in I} U_\alpha = \bigcap_{\alpha \in I} (X\setminus U_\alpha)
$$
is finite because each $X\setminus U_\alpha$ is finite. Therefore, $\bigcup_{\alpha \in I} U_\alpha \in \mathcal{T}$.
3. Let $\{U_1, U_2, \ldots, U_n\}$ be a finite collection such that $X\setminus U_i$ is finite for each $i=1,2,\ldots,n$.
Without loss of generality, we can assume that $U_i \neq \emptyset$ for each $i=1,2,\ldots,n$, since the intersection of arbitrary set with $\emptyset$ is $\emptyset$.
If all of them are empty, then the intersection is $X\subset \mathcal{T}$.
Otherwise,
$$
X\setminus \bigcap_{i=1}^n U_i = \bigcup_{i=1}^n (X\setminus U_i)
$$
is finite because each $X\setminus U_i$ is finite. Therefore, $\bigcap_{i=1}^n U_i \in \mathcal{T}$.
</details>
Another non-example is $\mathcal{T} = \{U\subseteq X|U \text{ is finite}\}\cup \{X\}$
The topology is invalid because an arbitrary union of points is not a finite set.
Consider $X=\mathbb{Z}$ but take $U_1=\{1\}, U_2=\{2\}, U_3=\{3\}, \ldots$
Then $\bigcup_{i=1}^\infty U_i = \mathbb{Z}^+$ is not a finite set and is not $\{X\}$.
> [!NOTE]
>
> If $X$ is finite, then finite complement topology is the same as the discrete topology.
#### Definition of Topology basis
For a set $X$, a topology basis, denoted by $\mathcal{B}$, is a collection of subsets of $X$, such that the following properties are satisfied:
1. For any $x \in X$, there exists a $B \in \mathcal{B}$ such that $x \in B$
2. If $B_1, B_2 \in \mathcal{B}$ and $x \in B_1 \cap B_2$, then there exists a $B_3 \in \mathcal{B}$ such that $x \in B_3 \subseteq B_1 \cap B_2$

121
content/Math4201/Math4201_L20.md
View File

@@ -1,121 +0,0 @@
# Math4201 Topology I (Lecture 20)
## Quotient topology
### More propositions
#### Proposition for quotient maps in restrictions
Let $X,Y$ be topological spaces and $p:X\to Y$ is surjective and open/closed. Let $A\subseteq X$ be saturated by $p$, ($p^{-1}(p(A))=A$).
Then $q: A\to p(A)$ given by the restriction of $p$ is open/closed surjective map (In particular, it's a quotient map).
<details>
<summary>Proof</summary>
$q$ is surjective and continuous. Now assume $p$ is open and we will show that $q$ is also open. Any open subspace of $A$ is given as $U\cap A$ where $U$ is open in $X$. By definition, $q(U\cap A)=p(U\cap A)=p(U)\cap p(A)$
To see the second identity:
1. $p(U\cap A)\subseteq p(U)\cap p(A)$
$\forall y\in p(U\cap A)$, $y=p(x)$ with $x\in U\cap A$, since $x\in A$ and $x\in U$, $y=p(x)\in p(U)\cap p(A)$
2. $p(U)\cap p(A)\subseteq p(U\cap A)$
$\forall y\in p(U)\cap p(A)$, $y=p(x_1)$ with $x_1\in U$ and $y=p(x_2)$ with $x_2\in A$, since $x_1\in U$ and $x_2\in A$, $y=p(x_1)=p(x_2)\in p(U\cap A)$
So $x_1=x_2\in U\cap A$, $y=p(x_1)=p(x_2)\in p(U)\cap p(A)$, $y\in p(U\cap A)$.
Note that $p(U)\subseteq X$ is open by $p$ is an open map.
So $p(U)\cap p(A)$ is open in $p(A)$.
$q(U\cap A)=p(U\cap A)=p(U)\cap p(A)$ is open.
So $q$ is open in $p(A)$.
</details>
### Simplicial complexes (extra chapter)
#### Definition for simplicial complexes
Simplicial complexes are topological space with simplices ($n$ dimensional triangles) as their building blocks.
#### Definition for n dimensional simplex
Let $v_0,\dots,v_n$ be points in $\mathbb{R}^m$ such that $v_n-v_0$, $v_{n-1}-v_0$, $\cdots$, and $v_1-v_0$ are linearly independent in $\mathbb{R}^m$. (in particular $n\leq m$).
The $n$-dimensional simplex determined by $\{v_0,\dots,v_n\}$ is given as:
$$
\Delta^n\coloneqq [v_0,\dots,v_n]=\{t_0v_0+t_1v_1+\cdots+t_nv_n\vert t_i\geq 0, \sum_{i=0}^n t_i=1\}
$$
The coefficients $t_0,\dots,t_n$ are called barycentric coordinates.
<details>
<summary>Example of simplicial complex</summary>
$n=0$,
$\Delta^0=\{v_0\}$
$n=1$,
$\Delta^1=\{t_0v_0+t_1v_1\vert t_0+t_1=1\}$, this is the line segment between $v_0$ and $v_1$.
$n=2$,
$\Delta^2=\{t_0v_0+t_1v_1+t_2v_2\vert t_0+t_1+t_2=1\}$, this is the triangle with vertices $v_0,v_1,v_2$.
</details>
> [!NOTE]
>
> Every non-empty subset $\{v_{i_0},\dots,v_{i_k}\}$ of $\{v_0,\dots,v_n\}$ determines a $k$ dimensional simplex $[v_{i_0},\dots,v_{i_k}]\subseteq \Delta^n=[v_0,\dots,v_n]$. Inside the $n$ dimensional simplex $t_{i_0}v_{i_0}+\cdots+t_{i_n}v_{i_k}\in \Delta^n$. Where the coefficient $t_j$ of $v_j\notin \{v_{i_0},\dots,v_{i_n}\}$ is $0$.
Any such $k$ dimensional simplex is called a face of the simplex $[v_{i_0},\dots,v_{i_n}]$.
<details>
<summary>Example of faces for simplicial complex</summary>\
For a triangle $[v_0,v_1,v_2]$, the faces are $[v_0,v_1]$, $[v_0,v_2]$, and $[v_1,v_2]$ (the edges of the triangle).
</details>
#### Definition for abstract simplicial complex
Let $V$ be a finite or countable set, an abstract simplicial complex on $V$ is a collection of **finite non-empty subset** of $V$, denoted by $K$. And the two conditions are satisfied:
1. If $\sigma\in K$ and $\tau\subseteq \sigma$, then $\tau\in K$.
2. For any $v\in V$, $\{v\}\in K$.
<details>
<summary>Example of abstract simplicial complex</summary>
Let $V=\{a,b,c,d\}$.
If we want to include $\{a,b,c\}$, then we need to include $\{a,b\}$ and $\{b,c\}$, so we have $K=\{\{a,b,c\},\{a,b\},\{b,c\},\{a\},\{b\},\{c\},\{d\}\}$ is an abstract simplicial complex.
</details>
#### Topological realization of abstract simplicial complex
Let $\bigsqcup_{\sigma\in K}\Delta^{|\sigma|-1}$ be the disjoint union of all $|\sigma|-1$ dimensional simplices in $K$.
$$
\tilde{X_k}=\bigsqcup_{\sigma\in K}\Delta^{|\sigma|-1}
$$
We use subspace topology to define a topology on $\Delta^n$ and the union of such topology for each $\Delta^{|\sigma|-1}$ defines a topology on $\tilde{X_k}$.
We define the equivalence relation $x\in \Delta_{\sigma}^{|\sigma|-1}\sim x'\in \Delta_{\sigma'}^{|\sigma'|-1}$ if $x\in \Delta_{\sigma'\cap \sigma}^{|\sigma'\cap \sigma|-1}\subseteq \Delta_{\sigma}^{|\sigma|-1}$. and $x'\in \Delta_{\sigma'\cap \sigma}^{|\sigma'\cap \sigma|-1}\subseteq \Delta_{\sigma'}^{|\sigma'|-1}$.
are the sample points of $\Delta_{\sigma\cap \sigma'}^{|\sigma\cap \sigma'|-1}$.
$X_K$ is the quotient space of $\tilde{X_k}$ by the equivalence relation.
Continue next time.

98
content/Math4201/Math4201_L21.md
View File

@@ -1,98 +0,0 @@
# Math4201 Topology I (Lecture 21)
## Simplicial complexes
### Recall from last lecture
Let $\sigma=\{a_0,a_1,\dots,a_n\}$ be a finite set. The $n$-dimensional simplex determined by $\tau$ is given as:
$$
\Delta^n(a_0,a_1,\dots,a_n)=\left\{t_0a_0+t_1a_1+\cdots+t_na_n\mid t_i\geq 0, \sum_{i=0}^n t_i=1\right\}
$$
If we have vertices $\tau=\{a_0,a_1,\dots,a_k\}$, $\tau\subseteq \sigma$, the face of $\Delta^n$ is determined by $\tau$ with dimension $|\tau|-1$.
$\Delta^n$ is the topologized by the subspace topology inherited by the standard topology on Euclidean space $\mathbb{R}^n$.
Note that there are different ways to of embedding and all give the same topological space.
### Abstract simplicial complexes
#### Definition for abstract simplicial complex
Let $V=\{v_0,v_1,\dots,v_n\}$ be a finite set (set of vertices of a simplicial complex). $K$ be the collection of subspaces of $V$.
1. $\sigma\in K$ and $\tau\subseteq \sigma$, then $\tau\in K$.
2. For any $v\in V$, $\{v\}\in K$.
Then $\tilde{X_k}=\bigsqcup_{\sigma\in K}\Delta_\sigma$.
$\Delta_\sigma$ is a simplex of dimension $|\sigma|-1$.
$X_K$ is the topological realization of $K$.
Define an equivalence relation on $\tilde{X_k}$ as follows:
$x\in \Delta_\sigma\sim x'\in \Delta_{\sigma'}$ if and only if $x\in \Delta_{\sigma'\cap \sigma}^{|\sigma'\cap \sigma|-1}\subseteq \Delta_\sigma$ and $x'\in \Delta_{\sigma'\cap \sigma}^{|\sigma'\cap \sigma|-1}\subseteq \Delta_{\sigma'}$.
This just means that the two points have the same barycentric coordinates in the simplex.
#### Definition of barycentric coordinates
Let $\sigma=\{a_0,a_1,\dots,a_n\}$ be a simplex. The barycentric coordinates of a point $x\in \Delta_\sigma$ are the coefficients $t_0,t_1,\dots,t_n$ such that:
$$
x=t_0a_0+t_1a_1+\cdots+t_na_n
$$
and $t_i\geq 0$ and $\sum_{i=0}^n t_i=1$.
The point $x$ is in the simplex $\Delta_\sigma$ if and only if $t_i\geq 0$ for all $i$.
<details>
<summary>Example of abstract simplicial complex</summary>
Let $V=\{v_1,v_2,v_3,v_4,v_5\}$.
If we want to enclose $K=\{\{v_1,v_2,v_3,v_4\},\{v_3,v_4,v_5\}\}$, we need to fill all the singletons $\{v_1\},\{v_2\},\{v_3\},\{v_4\},\{v_5\}$, all the pairs in $K$, $\{v_1,v_2\},\{v_1,v_3\},\{v_1,v_4\},\{v_2,v_3\},\{v_2,v_4\},\{v_3,v_4\},\{v_3,v_5\},\{v_4,v_5\}$, and the triangle $\{v_1,v_2,v_3\}, \{v_1,v_2,v_4\}, \{v_1,v_3,v_4\}, \{v_2,v_3,v_5\}$.
The final simplicial complex is $\tilde{X_k}=\bigsqcup_{\sigma\in K}\Delta(v_1,v_2,v_3,v_4)\sqcup \Delta(v_3,v_4,v_5)\sqcup \{v_1,v_2,v_3,v_4,v_5\}$.
We use $\Delta(v_1,v_2,v_3,v_4)$ to denote the simplex with vertices $v_1,v_2,v_3,v_4$.
</details>
#### Defining maps on abstract simplicial complexes
Let $K$ be an abstract simplicial complex. $V=\{v_1,v_2,\dots,v_m\}$
A map $\pi:\tilde{X_k}\to X_K$ is a quotient map
$X_K$ is equipped with the quotient topology.
Let $f:V\to \mathbb{R}^m$, then $u_i=f(v_i)$.
$\tilde{X_k}=\bigsqcup_{\sigma\in K}\Delta_\sigma$ is the disjoint union of all simplices in $K$.
For $\sigma=\{v_{i_0},\dots,v_{i_k}\}$, we have a map $\Delta_\sigma\to \mathbb{R}^\ell$ given by $[t_{i_0}u_0+t_{i_1}u_1+\cdots+t_{i_k}u_k\mid t_j\geq 0, \sum_{j=0}^k t_j=1]$.
This is well-defined because the coefficients $t_j$ are uniquely determined by the vertices $v_{i_0},\dots,v_{i_k}$.
This induces $F:\tilde{X_k}\to \mathbb{R}^\ell$. This map is continuous because $F\vert_{\Delta_\sigma}$ is continuous for all $\sigma\in K$.
Recall that if for any $x\in X_K$, the map $F$ restricted to $\pi^{-1}(x)$ is constant, then there is a unique continuous map $g$ satisfying $F=g\circ \pi$.
In fact, this condition is satisfied and there is such a map $G$.
<details>
<summary>Example of map on abstract simplicial complexes</summary>
Consider the previous example of abstract simplicial complex.
Let $f:V\to \mathbb{R}$ by $f(v_i)=i$.
Then $f(\Delta_{\{v_1,v_2,v_3,v_4\}})=[1,4]$
Then $f(\Delta_{\{v_1,v_3\}})=[1,3]$
</details>

162
content/Math4201/Math4201_L22.md
View File

@@ -1,162 +0,0 @@
# Math4201 Topology I (Lecture 22)
## Connectedness of topological spaces
### Connectedness
#### Definition of separation
A separate of a topological space $X$ is a pair of disjoint nonempty open subsets $U,V\subset X$ such that $X=U\cup V$. A space is connected if there is no separation.
Otherwise, it is disconnected.
<details>
<summary>Example of separation</summary>
Let $X$ be an arbitrary set with trivial topology. (The only open sets are $\emptyset$ and $X$.)
This space is connected.
---
Let $X=\{a,b\}$ with discrete topology. Then $X$ is disconnected.
A separation is given by $U=\{a\}$ and $V=\{b\}$.
</details>
#### Theorem of separation and clopen sets
Note that $U,V$ give a separation of $X$ if and only if $U=V^c$ and $V$ is open, then $U$ is closed and open.
So if $X$ is connected, then there is a non-empty proper (not the same as $X$) closed and open set.
The reverse is also true. (If the only clopen sets are $\emptyset$ and $X$, then $X$ is connected.)
<details>
<summary>Example of connected and disconnected space in real numbers</summary>
Let $X=[a,b]$ with subspace topology inherited from $\mathbb{R}$ is connected.
Then other connected subspace of $\mathbb{R}$ are $(a,b)$, $[a,b)$, $(a,b]$, $(-\infty,b)$, $(-\infty,b]$, $(a,\infty)$, $[a,\infty)$, and $\mathbb{R}$.
---
If $X\subseteq \mathbb{R}$ with the subspace topology such that there are $a<b<c$ with $a,c\in X, b\notin X$, then $X$ is disconnected.
Note that $X=((-\infy,b)\cap X)\cup ((b,\infty)\cap X)$ are two disjoint open sets whose union is $X$.
$U$ is not empty because $a\in U$.
$V$ is not empty because $c\in V$.
$U\cap V=\phi$ because $b\notin U\cap V$, is a valid separation of $X$.
So $X$ is disconnected.
</details>
#### Definition of totally disconnected space
Any topological space that any subset of it with at least two elements is disconnected is called a totally disconnected space.
<details>
<summary>Example of totally disconnected space</summary>
In $\mathbb{R}$, any subset of rational numbers with at least two elements is disconnected.
Because there is a irrational number between any two rational numbers.
</details>
<details>
<summary>Example of disconnected space</summary>
Let $X\subseteq \mathbb{R}^2$ and $X=U\cap V$, where $U=\{(x,y)\in \mathbb{R}^2\mid y=1/x\}$ and $V=\{(x,y)\in \mathbb{R}^2\mid x=0\}$.
Then $X$ is disconnected since $U, V$ gives a separation of $X$ (In this case, $U$ and $V$ are closed sets in $\mathbb{R}^2$).
</details>
#### Lemma of separated subsets
Let $U,V$ give a separation of a topological space $X$. Let $Y\subseteq X$ with the subspace topology is connected. Then $Y$ is either contained in $U$ or $V$.
<details>
<summary>Proof</summary>
Consider $U'=U\cap Y$ and $V'=V\cap Y$. Then $U'$ and $V'$ are disjoint nonempty open subsets of $Y$. and $Y=U'\cup V'$.
Since $Y$ is connected, then $U'$ or $V'$ are not a separation, so $U'$ or $V'$ is empty.
</details>
#### Theorem of connectedness of union of connected subsets
Let $X=\bigcup_{\alpha\in I} X_\alpha$ such that $\bigcap_{\alpha\in I} X_\alpha$ is non-empty. And $X_\alpha$ are connected. Then $X$ is also connected.
<details>
<summary>Proof</summary>
Let $x\in \bigcap_{\alpha\in I} X_\alpha$. By contradiction, suppose $U,V$ give a separation of $X$. Assume $x\in U$ and $x\notin V$, Applying the lemma to $Y=X_\alpha$ for each $\alpha\in I$, we have $X_\alpha\subseteq U$ or $X_\alpha\subseteq V$.
Since $x\in X_\alpha$ is an element of $u$, the fist possibility holds, so $\bigcap_{\alpha\in I} X_\alpha\subseteq U$ implies $X\subseteq U$, then $U=x$, $V=\emptyset$, which is a contradiction.
</details>
<details>
<summary>Example</summary>
Let $X=S^1\subseteq \mathbb{R}^2$ with the subspace topology. Let $X_0=S^1\cap \{(x,y)\mid x\leq 0\}$ and $X_1=S^1\cap \{(x,y)\mid x\geq 0\}$.
Then $X_0\cap X_1=\{(0,1), (0,-1)\}$.
Note that both of them are homeomorphic to $[0,1]\subseteq \mathbb{R}$, which are known to be connected.
</details>
#### Proposition of connectedness and homeomorphism
Connectedness is a topological property (preserve under homeomorphism).
i.e. If $X$ and $Y$ are homeomorphic, then $X$ is connected if and only if $Y$ is connected.
<details>
<summary>Proof</summary>
By contradiction, $U,V$ give a separation of $X$ let $\phi:X\to Y$ be a homeomorphism. Then $\phi(U)$ and $\phi(V)$ are disjoint nonempty open subsets of $Y$ whose union is $Y$.
So $Y$ is disconnected.
This contradicts the assumption that $Y$ is connected.
Therefore, $X$ is connected.
The reverse direction is similar.
</details>
> [!NOTE]
>
> The connectedness of two topological spaces can be preserved under weaker conditions than homeomorphism.
#### Proposition of connectedness and continuous map
If $X$ is connected and $f:X\to Y$ is a continuous map, then $f(X)\subseteq Y$ with subspace topology is connected.
<details>
<summary>Proof</summary>
By contradiction, suppose $f(X)$ is disconnected. Then there are disjoint nonempty open subsets $U,V$ of $f(X)$ such that $f(X)=U\cup V$.
Since $f$ is continuous, $f^{-1}(U)$ and $f^{-1}(V)$ are open in $X$ and $X=f^{-1}(U)\cup f^{-1}(V)$.
Since $X$ is connected, then $f^{-1}(U)$ and $f^{-1}(V)$ are not a separation, so $f^{-1}(U)$ or $f^{-1}(V)$ is empty.
This contradicts the assumption that $X$ is connected.
Therefore, $f(X)$ is connected.
</details>

133
content/Math4201/Math4201_L23.md
View File

@@ -1,133 +0,0 @@
# Math4201 Topology I (Lecture 23)
## Connectedness of topological spaces
### Connected space
#### Definition of connected space
Let $X$ be a topological space. $X$ is separated if there exist two disjoint nonempty open subsets $U,V\subset X$ such that $X=U\cup V$.
If $X$ is not separated, then $X$ is connected.
#### Any interval in $\mathbb{R}$ with standard topology is connected
Let $I=[a,b]$ be an interval in $\mathbb{R}$ with standard topology. Then $I$ is connected.
<details>
<summary>Proof</summary>
By contradiction, we assume that $U,V$ give a separation of $\mathbb{R}$. In particular, $\exists a\in U, b\in V$.
Let $a_0\coloneqq \sup\{x\in U\cap [a,b]\}$. Note that $a\in U\cap [a,b]$, so $a_0\geq a$. Since any element of $U\cap [a,b]$ is less than or equal to $b$, $a_0\leq b$.
**Case 1**: $a_0=a$
Since $U$ is open, there is $\epsilon>0$ such that $[a,a+\epsilon)\subset U\cap [a,b]$. So $a_0\geq a+\epsilon>a$, which contradicts the definition of $a_0$.
**Case 2**: $a_0=b$.
Since $V$ is open, there is $\epsilon>0$ such that $(b-\epsilon,b]\subseteq V\cap [a,b]$. This implies that $b-\epsilon$ is also an upper bound of $U\cap [a,b]$, so $a_0\leq b-\epsilon<b$, which contradicts the definition of $a_0$.
**Case 3**: $a<a_0<b$.
**Subcase I**: $a_0\in U$.
There is an $\epsilon>0$ such that $(a_0-\epsilon,a_0+\epsilon)\subset U\cap [a,b]$ because $U$ is open.
In particular, $a_0$ is greater than any element of $(a_0-\epsilon,a_0+\epsilon)$, which contradicts the definition of $a_0$.
**Subcase II**: $a_0\in V$.
There is an $\epsilon>0$ such that $(a_0-\epsilon,a_0+\epsilon)\subset V\cap [a,b]$ because $V$ is open.
In particular, $a_0$ is less than any element of $(a_0-\epsilon,a_0+\epsilon)$. Since $a_0$ is an upper bound of $U\cap [a,b]$, any point $>a_0$ is not in $U\cap [a,b]$.
So, $U\cap [a,b]\subseteq [a,a_0-\epsilon)$. This shows that $a_0-\epsilon$ is an upper bound of $U\cap [a,b]$, which contradicts the definition of $a_0$.
</details>
_Intuitively, since both sets in $\mathbb{R}$ are open, you cannot set a clear boundary between the two sets by least upper bound argument._
#### Corollary as Intermediate Value Theorem
If $f:[a,b]\to \mathbb{R}$ is continuous, and $c\in\mathbb{R}$ is such that $f(a)<c<f(b)$, then there exists $x\in [a,b]$ such that $f(x)=c$.
<details>
<summary>Proof</summary>
Since $[a,b]$ is connected, since $f$ is continuous, $f([a,b])$ is connected.
By contradiction, if $c\notin f([a,b])$, then $f([a,b])$ has two points $f(a),f(b)$ and $c$ is a point between that isn't in $f([a,b])$. This contradicts the connectedness of $f([a,b])$.
So $f(a)<c<f(b)$ or $f(b)<c<f(a)$ must hold.
</details>
#### Definition of path-connected space
A topological space $X$ is path-connected if for any two points $x,x'\in X$, there is a continuous map $\gamma:[0,1]\to X$ such that $\gamma(0)=x$ and $\gamma(1)=x'$. Any such continuous map is called a path from $x$ to $x'$.
> [!NOTE]
>
> Path-connectedness is a stronger condition than connectedness.
#### Theorem of path-connectedness and connectedness
Any path-connected space is connected.
<details>
<summary>Proof</summary>
By contradiction, let $U,V$ be a separation of $X$. In particular, $\exists x\in U, x'\in V$.
Since $X$ is path-connected, $\exists \gamma:[0,1]\to X$ such that $\gamma(0)=x$ and $\gamma(1)=x'$.
Then since $\gamma$ is continuous, $\gamma^{-1}(U)$ and $\gamma^{-1}(V)$ are open in $[0,1]$ and $[0,1]=\gamma^{-1}(U)\cup \gamma^{-1}(V)$. We want to show that this gives a separation of $[0,1]$.
Since $U\cap V=\emptyset$, $\gamma^{-1}(U)$ and $\gamma^{-1}(V)$ are disjoint.
$U\cup V=X$ so $\gamma^{-1}(U)\cup \gamma^{-1}(V)=[0,1]$.
Each of $\gamma^{-1}(U)$ and $\gamma^{-1}(V)$ is non-empty because $x\in U\implies 0\in \gamma^{-1}(U)$ and $x'\in V\implies 1\in \gamma^{-1}(V)$.
This contradicts the assumption that $[0,1]$ is connected.
</details>
<details>
<summary>Example of path-connected space</summary>
A subspace $X$ of $\mathbb{R}^n$ is convex if for any two points $x,x'\in X$, the line segment connecting $x$ and $x'$ is contained in $X$.
In particular $B_R(x)$ is convex. So $X$ is path-connected.
---
Let $X=\mathbb{R}^n\setminus\{0\}$. with $n\geq 2$. Then $X$ is path-connected. (simply walk around the origin)
</details>
#### Theorem for invariant property of connectedness
If $f:X\to Y$ is a continuous and surjective map, and $X$ is connected, then $Y$ is connected.
<details>
<summary>Proof</summary>
Take $y,y'\in Y$, since $f$ is surjective, $\exists x,x'\in X$ such that $f(x)=y$ and $f(x')=y'$. Let $\gamma:[0,1]\to X$ be a path from $x$ to $x'$.
Then $f\circ \gamma:[0,1]\to Y$ is a continuous map. and $f\circ \gamma(0)=y$ and $f\circ \gamma(1)=y'$.
</details>
<details>
<summary>Example of connected but not path-connected space</summary>
Let $A=\{(x,y)\in \mathbb{R}^2\mid y=\sin(1/x), x>0\}$. Then $A$ is connected, and also path-connected.
However, take $\overline{A}=A\cup \{0\}\times [-1,1]$. Then $\overline{A}$ is not path-connected but connected.
_Show next time_
</details>

110
content/Math4201/Math4201_L24.md
View File

@@ -1,110 +0,0 @@
# Math4201 Topology I (Lecture 24)
## Connected and compact spaces
### Connectedness
Recall from example last lecture, there exists a connected space but not path-connected space.
#### Lemma on connectedness
Let $X$ be a topological space and $A\subseteq X$ is a connected subspace. If $B\subseteq X$ satisfies $A\subseteq B\subseteq \overline{A}$, then $B$ is connected. In particular, $\overline{A}$ is connected.
<details>
<summary>Proof</summary>
Assume that $B$ is not connected. In particular, there are open subspaces $U$ and $V$ of $X$ such that $U\cap B, V\cap B$ is a separation of $B$.
Take $U\cap A, V\cap A$, we show that this gives a separation of $A$.
(i) Since $U,V$ are open, $U\cap A, V\cap A$ are open in $A$.
(ii) Since $(U\cap B)\cap (V\cap B)=\emptyset$, $(U\cap A)\cap (V\cap A)=\emptyset$.
(iii) Since $(U\cap B)\cup (V\cap B)=B$, any point in $B$ is in either $U\cap B$ or $V\cap B$.
Since $A\subseteq B$, $(U\cap A)\cup (V\cap A)=A$.
(iv) $U\cap A$ and $V\cap A$ is nonempty by assumption $U\cap B$ is nonempty and contains $x\in B\cap U\subseteq \overline{A}$. So any open neighborhood of $x$ have non-empty intersection $x'\in A$, so $x'\in U\cap A$ and $U\cap A$ is nonempty. Similarly, $V\cap A$ is nonempty.
So $U\cap A$ and $V\cap A$ is a separation of $A$, which contradicts the assumption that $A$ is connected.
Therefore, $B$ is connected.
</details>
#### Topologists' sine curve
Let $A=\{(x,y)\in \mathbb{R}^2\mid y=\sin(1/x), x>0\}$. Then $A$ is connected, and also path-connected.
$$
\gamma(t) = (t, \sin(1/t)) \text{ for } t\in (0,1]
$$
However, take $\overline{A}=A\cup \{0\}\times [-1,1]$. Then $\overline{A}$ is not path-connected but connected.
<details>
<summary>Proof that topologists' sine curve is not path-connected</summary>
We want to show $X=\overline{A}$ has no continuous path
$$
\gamma:([0,1])\to X
$$
such that $\gamma(0)=(0,0)$ and $\gamma(1)=(1,\sin(1))$.
If there exists such a path, let $t_0\in [0,1]$ be defined as
$$
t_0=\sup\{t\in [0,1]\mid \gamma(t)=(0,x), x\in [0,1]\}
$$
By the assumption on $t_0$, we can find a sequence $\{t_n\}_{n\in\mathbb{N}_+}\subseteq A$ such that $t_n\to t$.
By continuity of $\gamma$, we have $\gamma(t_n)\to \gamma(t_0)$, $(0,y_n)\to (0,y_0)$.
Now focus on the restriction of $\gamma$ to $[t_0,1]$, $\gamma:[t_0,1]\to X$, $\gamma(t_0)=(0,y_0)$, $\gamma(1)=(1,\sin(1))$.
$t\in (t_0,1]$, then $\gamma(t)\in$ graph of $y=\sin(1/x)$.
Consider $\pi$ be the projection map to $x$-axis, $\pi\circ \gamma:[t_0,1]\to \mathbb{R}$, $\pi\circ \gamma(t_0)=0$ and $\pi\circ \gamma(1)=1$.
In particular, there is a sequence $s_n\in [t_0,1]$ such that $s_n\to t_0$ and $\pi\circ \gamma(s_n)=\frac{1}{n\pi+\frac{\pi}{2}}$. (using intermediate value theorem)
Then $\gamma(s_n)=(\frac{1}{n\pi},\sin(n\pi+\frac{\pi}{2}))=(\frac{1}{n\pi},(-1)^n)$.
Since as $s_n\to t_0$, and $\gamma$ is continuous, then we get a contradiction that the sequence $\gamma(s_n)$ should converge to $(0,t_0)$ where it is not.
</details>
### Compactness
Motivation: in real numbers.
#### Extreme value theorem
Let $f:[a,b]\to \mathbb{R}$ be continuous. Then there are $x_m,x_M\in [a,b]$ such that $f(x_m)\leq f(x)\leq f(x_M)$ for all $x\in [a,b]$.
#### Definition of cover
Let $X$ be a topological space. A covering of $X$ is a collection of subsets of $X$ that covers $X$.
$$
\{U_\alpha\}_{\alpha\in I}
$$
such that $X=\bigcup_{\alpha\in I} U_\alpha$.
An open cover of $X$ is a covering of $X$ such that each $U_\alpha$ is open.
#### Definition of compact space
A topological space $X$ is compact if for any open covering $\{U_\alpha\}_{\alpha\in I}$ of $X$, there exists a finite subcovering $\{U_{\alpha_i}\}_{i=1}^n$ such that $X=\bigcup_{i=1}^n U_{\alpha_i}$.
<details>
<summary>Example of non-compact space</summary>
Consider the interval $(0,1]$, the open covering $(\frac{1}{n},1]$ open in $(0,1]$, $\{(\frac{1}{n},1]\}_{n\in \mathbb{N}_+}$ has no finite subcovering.
</details>

164
content/Math4201/Math4201_L3.md
View File

@@ -1,164 +0,0 @@
# Math4201 Topology I (Lecture 3)
## Recall form last lecture
### Topological Spaces
#### Basis for a topology
Let $X$ be a set. A basis for a topology on $X$ is a collection $\mathcal{B}$ (elements of $\mathcal{B}$ are called basis elements) of subsets of $X$ such that:
1. $\forall x\in X$, $\exists B\in \mathcal{B}$ such that $x\in B$
2. $\forall B_1,B_2\in \mathcal{B}$, $\forall x\in B_1\cap B_2$, $\exists B_3\in \mathcal{B}$ such that $x\in B_3\subseteq B_1\cap B_2$
<details>
<summary>Example of standard basis in real numbers</summary>
Let $X=\mathbb{R}$ and $\mathcal{B}=\{(a,b)|a,b\in \mathbb{R},a<b\}$ (collection of all open intervals).
Check properties 1:
for any $x\in \mathbb{R}$, $\exists (x-1,x+1)\in \mathcal{B}$ such that $x\in (x-1,x+1)$
Check properties 2:
let $B_1=(a,b)$ and $B_2=(c,d)$ be two basis elements, and $x\in B_1\cap B_2=(\max(a,c),\min(b,d))\in \mathcal{B}$.
</details>
<details>
<summary>Example of lower limit basis in real numbers</summary>
Let $X=\mathbb{R}$ and $\mathcal{B}_{LL}=\{[a,b)|a,b\in \mathbb{R},a<b\}$ (collection of all open intervals).
Check properties 1:
for any $x\in \mathbb{R}$, $\exists [x,x+1)\in \mathcal{B}_{LL}$ such that $x\in [x,x+1)$
Check properties 2:
let $B_1=[a,b)$ and $B_2=[c,d)$ be two basis elements, and $x\in B_1\cap B_2=[max(a,c),min(b,d))\in \mathcal{B}_{LL}$.
</details>
Extend this to $\mathbb{R}^2$.
#### Definition for cartesian product
Let $X$ and $Y$ be sets. The cartesian product of $X$ and $Y$ is the set $X\times Y=\{(x,y)|x\in X,y\in Y\}$.
<details>
<summary>Example of open rectangles basis for real plane</summary>
Let $X=\mathbb{R}^2$ and $\mathcal{B}$ be the collection of rectangle of the form $(a,b)\times (c,d)$ where $a,b,c,d\in \mathbb{R}$ and $a<b,c<d$. (boundary is not included)
Check properties 1:
for any $(x,y)\in \mathbb{R}^2$, $\exists (x,y)\in \mathcal{B}$ such that $(x,y)\in (x,y)$
Check properties 2:
let $B_1=(a,b)\times (c,d)$ and $B_2=(e,f)\times (g,h)$ be two basis elements, and $(x,y)\in B_1\cap B_2=(max(a,e),min(b,f))\times (max(c,g),min(d,h))\in \mathcal{B}$.
</details>
<details>
<summary>Example of open disks basis for real plane</summary>
Let $X=\mathbb{R}^2$ and $\mathcal{B}$ be the collection of open disks.
Check properties 1:
for any $x\in \mathbb{R}^2$, $\exists B_1(x)\in \mathcal{B}$ such that $x\in B_1(x)$.
Check properties 2:
let $B_{r_1}(x)$ and $B_{r_2}(y)$ be two basis elements, for every $z\in B_{r_1}(x)\cap B_{r_2}(y)$, $\exists B_{r_3}(z)\in \mathcal{B}$ such that $z\in B_{r_3}(z)\subseteq B_{r_1}(x)\cap B_{r_2}(y)$.
(even $B_{r_1}(x)\cap B_{r_2}(y)\notin \mathcal{B}$)
</details>
#### Topology generated by a basis
Let $\mathcal{B}$ be a basis for a topology on $X$. The topology generated by $\mathcal{B}$, denoted by $\mathcal{T}_{\mathcal{B}}$.
$U\in \mathcal{T}_{\mathcal{B}}\iff \forall x\in U, \exists B\in \mathcal{B}$ such that $x\in B\subseteq U$
<details>
<summary>Proof</summary>
$\mathcal{T}_{\mathcal{B}}$ is a topology on $X$ because:
1. $\emptyset \in \mathcal{T}_{\mathcal{B}}$ because $\emptyset \in \mathcal{B}$. $X\in \mathcal{T}_{\mathcal{B}}$ because $\forall x\in X, \exists B\in \mathcal{B}$ such that $x\in B\subseteq X$ (by definition of basis (property 1)))
2. $\mathcal{T}_{\mathcal{B}}$ is closed under arbitrary unions.
Want to show $\{U_\alpha | U_\alpha\in \mathcal{T}_{\mathcal{B}}\}_{\alpha \in I}\implies \bigcup_{\alpha \in I} U_\alpha\in \mathcal{T}_{\mathcal{B}}$.
Because $\forall x\in \bigcup_{\alpha \in I} U_\alpha$, $\exists \alpha_0$ such that $x\in U_{\alpha_0}$. Since $U_{\alpha_0}\in \mathcal{T}_{\mathcal{B}}$, $\exists B\in \mathcal{B}$ such that $x\in B\subseteq U_{\alpha_0}\subseteq \bigcup_{\alpha \in I} U_\alpha$.
3. $\mathcal{T}_{\mathcal{B}}$ is closed under finite intersections.
Want to show $U_1,U_2,\ldots,U_n\in \mathcal{T}_{\mathcal{B}}\implies \bigcap_{i=1}^n U_i\in \mathcal{T}_{\mathcal{B}}$.
If $n=2$, since $\forall x\in U_1\cap U_2$, $x\in U_1$ and $x\in U_2$, $\exists B_1\in \mathcal{B}$ such that $x\in B_1\subseteq U_1$ and $\exists B_2\in \mathcal{B}$.
Applying the second property of basis, $\exists B_3\in \mathcal{B}$ such that $x\in B_3\subseteq B_1\cap B_2\subseteq U_1\cap U_2$.
By induction, we can show that $\bigcap_{i=1}^n U_i\in \mathcal{T}_{\mathcal{B}}$.
</details>
<details>
<summary>Example of topology generated by a basis</summary>
Let $X$ be arbitrary.
Let $\mathcal{B}=\{x|x\in X\}$ (collection of all singleton subsets of $X$).
Then $\mathcal{T}$ is the discrete topology.
</details>
#### Properties of basis in generated topology
**Observation 1**: Any $B\in \mathcal{B}$ is an open set in $\mathcal{T}_{\mathcal{B}}$.
By the defining property of basis, $\forall x\in B$, $\exists x\in B\subseteq B$.
**Observation 2**: For any collection $\{B_\alpha\}_{\alpha \in I}$, $\bigcup_{\alpha \in I} B_\alpha\in \mathcal{T}_{\mathcal{B}}$.
By observation 1, each $B_\alpha\in \mathcal{T}_{\mathcal{B}}$. Since $\mathcal{T}_{\mathcal{B}}$ is a topology, $\bigcup_{\alpha \in I} B_\alpha\in \mathcal{T}_{\mathcal{B}}$.
#### Lemma
Let $\mathcal{B}$ and $\mathcal{T}_{\mathcal{B}}$ be a basis and the topology generated by $\mathcal{B}$ on $X$. Then,
$U\in \mathcal{T}_{\mathcal{B}}\iff$ there are basis elements $\{B_\alpha\}_{\alpha \in I}$ such that $U=\bigcup_{\alpha \in I} B_\alpha$.
<details>
<summary>Proof</summary>
$(\Rightarrow)$
If $U\in \mathcal{T}_{\mathcal{B}}$, we want to show that $U$ is a union of basis elements.
For any $x\in U$, by the definition of $\mathcal{T}_{\mathcal{B}}$, there is a basis element $B_x$ such that $x\in B_x\subseteq U$.
So, $U\subseteq \bigcup_{x\in U} B_x$.
Since $\forall B_x\in \{B_x\}_{\alpha \in I}$, $B_x\subseteq U$, we have $U\supseteq\bigcup_{x\in U} B_x$.
So, $U=\bigcup_{x\in U} B_x$.
$(\Leftarrow)$
Applies observation 2.
</details>
> [!NOTE]
>
> A basis for a topology is like a basis for a vector space in the sense that any open set/vector can be represented in terms of basis elements.
>
> But unlike linear algebra, it's not true that any open set can be written as a union of basis element in a **unique** way.

151
content/Math4201/Math4201_L4.md
View File

@@ -1,151 +0,0 @@
# Math4201 Topology I (Lecture 4)
## Recall from last lecture
Assignment due next Thursday. 10PM
Let $\mathcal{B}$ be a basis for a topology. Then the topology ($\mathcal{T}_{\mathcal{B}}$) **generated** by $\mathcal{B}$ is $\{U\in \mathcal{T}_{\mathcal{B}} \mid \forall x\in U, \exists B\in \mathcal{B} \text{ such that } x\in B\subseteq U\}$.
## New materials
### Topology basis
Given a topology on a set $X$, When is a given collection of subsets of $X$ a basis for a topology?
Suppose $U\in\mathcal{T}$ is an open set in $X$. If an arbitrary set $\mathcal{C}$ is a basis for $\mathcal{T}$, then by the definition of a topology generated by a basis, we should have the following:
$$
\exists C\in \mathcal{C} \text{ such that } x\in C\subseteq U
$$
#### Theorem of basis of topology
> [!CAUTION]
>
> In this course, we use lowercase letters to denote element of a set, and uppercase letters to denote sets. We use $\mathcal{X}$ to denote set of subsets of $X$.
Let $(X,\mathcal{T})$ be a topological space. Let $\mathcal{C}\subseteq \mathcal{T}$ be a collection of subsets of $X$ satisfying the following property:
$$
\forall U\in \mathcal{T}, \exists C\in \mathcal{C} \text{ such that } U\subseteq C
$$
Then $\mathcal{C}$ is a basis and the topology generated by $\mathcal{C}$ is $\mathcal{T}$.
<details>
<summary>Proof</summary>
We want to show that $\mathcal{C}$ is a basis.
> Recall the definition of a basis:
>
> 1. $\forall x\in X$, there is $B\in \mathcal{B}$ such that $x\in B$
> 2. $\forall B_1,B_2\in \mathcal{B}$, $\forall x\in B_1\cap B_2$, there is $B_3\in \mathcal{B}$ such that $x\in B_3\subseteq B_1\cap B_2$
First, we want to show that $\mathcal{C}$ satisfies the first property.
Take $x\in X$. Since $X\in \mathcal{T}$, we can apply the given condition ($
\forall U\in \mathcal{T}, \exists C\in \mathcal{C} \text{ such that } U\subseteq C
$) to get $C\in \mathcal{C}$ such that $x\in C\subseteq X$.
Next, we want to show that $\mathcal{C}$ satisfies the second property.
Let $C_1,C_2\in \mathcal{C}$ and $x\in C_1\cap C_2$. Since $C_1,C_2\in \mathcal{T}$, by the definition of $\mathcal{T}$, we have $U=C_1\cap C_2\in \mathcal{T}$.
We can apply the given condition to get $C_3\in \mathcal{C}$ such that $x\in C_3\subseteq U=C_1\cap C_2$.
---
Then we want to show that the topology generated by $\mathcal{C}$ is $\mathcal{T}$.
> Recall the definition of the topology generated by a basis:
>
> To prove this, we need to show that $\forall U\in \mathcal{T}\implies U\in \mathcal{T}_{\mathcal{C}}$ and $\forall U\in \mathcal{T}_{\mathcal{C}}\implies U\in \mathcal{T}$.
>
> Moreover, from last lecture, we have $U\in \mathcal{T}_{\mathcal{B}}\iff U=\bigcup_{\alpha \in I} B_\alpha$ for some $\{B_\alpha\}_{\alpha \in I}\subseteq \mathcal{B}$.
First, we want to show that $\forall U\in \mathcal{T}_{\mathcal{C}}\implies U\in \mathcal{T}$.
Let $U=\bigcup_{\alpha \in I} C_\alpha$ for some $\{C_\alpha\}_{\alpha \in I}\subseteq \mathcal{C}$. Then since $C_\alpha\in \mathcal{T}$, by the definition of $\mathcal{T}$, we have $U\in \mathcal{T}$.
Next, we want to show that $\forall U\in \mathcal{T}\implies U\in \mathcal{T}_{\mathcal{C}}$.
Let $U\in \mathcal{T}$. Then $\forall x\in U$ by the given condition, we have $C\in \mathcal{C}$ such that $x\in C\subseteq U$.
So, $U=\bigcup_{\alpha \in I} C_\alpha\in \mathcal{T}_{\mathcal{C}}$. (using the [same trick last time](https://notenextra.trance-0.com/Math4201/Math4201_L3#lemma))
</details>
Let $\mathcal{T}$ be the topology on $X$. Then $\mathcal{T}$ itself satisfies the basis condition.
#### Definition of subbasis of topology
A subbasis of a topology on a set $X$ is a collection $\mathcal{S}\subseteq \mathcal{T}$ of subsets of $X$ such that their union is $X$.
$$
\mathcal{S}=\{S_{\alpha}\mid S_\alpha\subseteq X\}_{\alpha \in I}\text{ and }\bigcup_{\alpha \in I} S_\alpha=X
$$
#### Definition of topology generated by a subbasis
If we consider the basis generated by the subbasis $\mathcal{S}$ by the following:
$$
\mathcal{B}=\{B\mid B\text{ is the intersection of a finite number of elements of }\mathcal{S}\}
$$
Then $\mathcal{B}$ is a basis.
<details>
<summary>Proof</summary>
First, $\forall x\in X$, there is $S_\alpha\in \mathcal{S}$ such that $x\in S_\alpha$. In particular, $x\in \mathcal{B}$.
Second, let $B_1,B_2\in \mathcal{B}$. Since $B_1$ is the intersection of a finite number of elements of $\mathcal{S}$, we have $B_1=\bigcap_{i=1}^n S_{i_1}, B_2=\bigcap_{i=1}^n S_{i_2}$ for some $S_{i_1},S_{i_2}\in \mathcal{S}$.
So $B_1\cap B_2$ is the intersection of finitely many elements of $\mathcal{S}$.
So $B_1\cap B_2\in \mathcal{B}$.
</details>
We call the topology generated by $\mathcal{B}$ the topology generated by the subbasis $\mathcal{S}$. Denote it by $\mathcal{T}_{\mathcal{S}}$.
An open set with respect to $\mathcal{T}_{\mathcal{S}}$ is a subset of $X$ such that it can be written as a union of finitely intersections of elements of $\mathcal{S}$.
<details>
<summary>Example (standard topology on real numbers)</summary>
Let $X=\mathbb{R}$. Take $\mathcal{S}=\{(-\infty, a)|a\in \mathbb{R}\}\cup \{(a,+\infty)|a\in \mathbb{R}\}$.
We claim this is a subbasis of the standard topology on $\mathbb{R}$.
The basis $\mathcal{B}$ associated with $\mathcal{S}$ is the collection of all open intervals.
$$
\mathcal{B}=\{(a,b)=(-\infty, b)\cap (a,+\infty)\}
$$
So, $\mathcal{B}=\mathcal{B}_{st}$ (the standard basis).
This topology on $\mathbb{R}$ is the same as the standard topology on $\mathbb{R}$.
</details>
<details>
<summary>Example (finite complement topology)</summary>
Let $X$ be an arbitrary set. Let $\mathcal{S}$ defined as follows:
$$
\mathcal{S}=\{S\subseteq X\mid S=X\setminus \{x\} \text{ for some } x\in X\}
$$
Let $x,y\in X$ and $x\neq y$. Then $S_x=X\setminus \{x\}$ and $S_y=X\setminus \{y\}$ are two elements of $\mathcal{S}$. Since $x\neq y$, we have $S_x\cup S_y=X\setminus \{x\}\cup X\setminus \{y\}=X$. So $\mathcal{S}$ is a subbasis of $X$.
So, the basis associated with $\mathcal{S}$, $\mathcal{B}$, is the collection of subsets of $X$ with finite complement.
This is in fact a topology, which is the **finite complement topology** on $X$.
</details>

106
content/Math4201/Math4201_L5.md
View File

@@ -1,106 +0,0 @@
# Math4201 Topology I (Lecture 5 Bonus)
## Comparison of two types of topologies
Let $X=\mathbb{R}^2$ and the two types of topologies are:
The "circular topology":
$$
\mathcal{T}_c=\{B_r(p)\mid p\in \mathbb{R}^2,r>0\}
$$
The "rectangle topology":
$$
\mathcal{T}_r=\{(a,b)\times (c,d)\mid a,b,c,d\in \mathbb{R},a<b,c<d\}
$$
> Are these two topologies the same?
### Comparison of two topologies
#### Definition of finer and coarser
Let $\mathcal{T}$ and $\mathcal{T}'$ be two topologies on $X$. We say $\mathcal{T}$ is finer than $\mathcal{T}'$ if $\mathcal{T}'\subseteq \mathcal{T}$. We say $\mathcal{T}$ is coarser than $\mathcal{T}'$ if $\mathcal{T}\subseteq \mathcal{T}'$. We say $\mathcal{T}$ and $\mathcal{T}'$ are equivalent if $\mathcal{T}=\mathcal{T}'$.
$\mathcal{T}$ is strictly finer than $\mathcal{T}'$ if $\mathcal{T}'\subsetneq \mathcal{T}$. (that is, $\mathcal{T}'$ is finer and not equivalent to $\mathcal{T}$)
$\mathcal{T}$ is strictly coarser than $\mathcal{T}'$ if $\mathcal{T}\subsetneq \mathcal{T}'$. (that is, $\mathcal{T}$ is coarser and not equivalent to $\mathcal{T}'$)
<details>
<summary>Example (discrete topology is finer than the trivial topology)</summary>
Let $X$ be an arbitrary set. The discrete topology is $\mathcal{T}_1 = \mathcal{P}(X)=\{U \subseteq X\}$
The trivial topology is $\mathcal{T}_0 = \{\emptyset, X\}$
Clearly, $\mathcal{T}_1 \subseteq \mathcal{T}_0$.
So the discrete topology is finer than the trivial topology.
</details>
#### Lemma
> [!TIP]
>
> Motivating condition:
>
> We want $U$ be an open set in $\mathcal{T}'$, then $U$ has to be open with respect to $\mathcal{T}$. In other words, $\forall x\in U, \exists$ some $B\in \mathcal{B}$ such that $x\in B\subseteq U$.
Let $\mathcal{T}$ and $\mathcal{T}'$ be topologies on $X$ associated with bases $\mathcal{B}$ and $\mathcal{B}'$. Then
$$
\mathcal{T}\text{ is finer than } \mathcal{T}'\iff \text{ for any } x\in X, x\in B'\in \mathcal{B}', \exists B\in \mathcal{B} \text{ such that } x\in B\subseteq B'
$$
<details>
<summary>Proof</summary>
$(\Rightarrow)$
Let $B'\in \mathcal{B}'$. If $x\in B'$, then $B'\in \mathcal{T}'$ and $T$ is finer than $T'$, so $B'\in \mathcal{T}$.
Take $T=\mathcal{T}_{\mathcal{B}}$. $\exists B\in \mathcal{B}$ such that $x\in B\subseteq B'$.
$(\Leftarrow)$
Let $U\in \mathcal{T}$. Then $U=\bigcup_{\alpha \in I} B_\alpha'$ for some $\{B_\alpha'\}_{\alpha \in I}\subseteq \mathcal{B}'$.
For any $B_\alpha'$ and any $x\in \mathcal{B}_\alpha'$, $\exists B_\alpha\in \mathcal{B}$ such that $x\in B_\alpha\subseteq B_\alpha'$.
Then $B_\alpha'$ is open set in $\mathcal{T}$.
So $U$ is open in $\mathcal{T}$.
$T$ is finer than $T'$.
</details>
Back to the example:
For every point in open circle, we can find a rectangle that contains it.
For every point in open rectangle, we can find a circle that contains it.
So these two topologies are equivalent.
#### Standard topology in $\mathbb{R}^2$
The standard topology in $\mathbb{R}^2$ is the topology generated by the basis $\mathcal{B}_{st}=\{(a,b)\times (c,d)\mid a,b,c,d\in \mathbb{R},a<b,c<d\}$. This is equivalent to the topology generated by the basis $\mathcal{B}_{disk}=\{(x,y)\in \mathbb{R}^2|d((x,y),(a,b))<r\}$.
<details>
<summary>Example (lower limit topology is strictly finer than the standard topology)</summary>
The lower limit topology is the topology generated by the basis $\mathcal{B}_{ll}=\{[a,b)\mid a,b\in \mathbb{R},a<b\}$.
This is finer than the standard topology.
Since $(a,b)\in \mathcal{B}_{st}$, we have $\forall x\in (a,b), \exists B=[x,b)\in \mathcal{B}_{ll}$ such that $x\in B\subsetneq (a,b)$.
So the lower limit topology is strictly finer than the standard topology.
$[0,1)$ is not open in the standard topology. but it is open in the lower limit topology.
</details>

144
content/Math4201/Math4201_L6.md
View File

@@ -1,144 +0,0 @@
# Math4201 Topology I (Lecture 6)
## Product topology
### Define topological spaces on cartesian product of two topological spaces
Let $(X,\mathcal{T}_X)$ and $(Y,\mathcal{T}_Y)$ be two topological spaces.
$$
X\times Y=\{(x,y)|x\in X,y\in Y\}
$$
Goal: Define a topology on $X\times Y$.
One way is to take $\mathcal{B}_{X\times Y}=\{(U\times V)|U\in \mathcal{T}_X,V\in \mathcal{T}_Y\}$ is a basis for the topology on $X\times Y$.
> There are two ways to define the topology on $\mathbb{R}^2$: By rectangles ($\mathcal{B}_{rect}=\{(a,b)\times (c,d)|a,b,c,d\in \mathbb{R},a<b,c<d\}$) or by open disks ($\mathcal{B}_{disk}=\{(x,y)\in \mathbb{R}^2|d((x,y),(a,b))<r\}$). (check bonus video)
<details>
<summary>Proof</summary>
Take $U=X,V=Y$, then $(x,y)\in (U\times V)=X\times Y$.
So the first property of basis is satisfied.
Check the second property of basis:
Let $B_1=U_1\times V_1,B_2=U_2\times V_2$ be two basis elements, and $(x,y)\in B_1\cap B_2$.
$$
B_1\cap B_2=(U_1\times V_1)\cap (U_2\times V_2)=(U_1\cap U_2)\times (V_1\cap V_2)
$$
Since $U_1\cap U_2\in \mathcal{T}_X$ and $V_1\cap V_2\in \mathcal{T}_Y$, we have $(U_1\cap U_2)\times (V_1\cap V_2)\in \mathcal{B}_{X\times Y}$.
Take $B_3=(U_1\cap U_2)\times (V_1\cap V_2)$, then $(x,y)\in B_3=B_1\cap B_2$.
</details>
> [!CAUTION]
>
> $\mathcal{B}_{X\times Y}$ is not a topology on $X\times Y$.
>
> $\mathcal{B}_{X\times Y}$ is not closed with respect to arbitrary unions.
#### Definition of product topology
Let $(X,\mathcal{T}_X)$ and $(Y,\mathcal{T}_Y)$ be two topological spaces.
$$
\mathcal{B}_{X\times Y}=\{(U\times V)|U\in \mathcal{T}_X,V\in \mathcal{T}_Y\}
$$
The product topology or $X\times Y$ is the topology generated by $\mathcal{B}_{X\times Y}$.
Let $\mathcal{B}_X$ be a basis for $\mathcal{T}_X$ and $\mathcal{B}_Y$ be a basis for $\mathcal{T}_Y$.
If we define
$$
\mathcal{B}'_{X\times Y}=\{(U\times V)|U\in \mathcal{B}_X,V\in \mathcal{B}_Y\}
$$
#### Proposition
$\mathcal{B}'_{X\times Y}$ is a basis for the product topology on $X\times Y$.
> [!NOTE]
>
> This basis is smaller than $\mathcal{B}_{X\times Y}$.
>
> Consider $X=Y=\mathbb{R}$ and $U=(a,b)\cap (c,d)$ and $V=(e,f)\cap (g,h)$. (Assume $a<b,c<d,e<f,g<h$) The union of $U$ and $V$ is four rectangles, which is not in $\mathcal{B}'_{X\times Y}$. but it is in $\mathcal{B}_{X\times Y}$.
<details>
<summary>Proof</summary>
Using the [lemma](https://notenextra.trance-0.com/Math4201/Math4201_L4#theorem-of-basis-of-topology) from Friday. it suffices to show that:
Let $W\in X\times Y$ and $(x,y)\in W$, we need to show that there are $B\in \mathcal{B}_X, B'\in \mathcal{B}_Y$ such that $(x,y)\in (B\times B')\subseteq W$.
Since $W$ is open with respect to the topology generated by $\mathcal{B}_{X\times Y}$, in particular, there is $U\times V$ such that $(x,y)\in U\times V\subseteq W$. And $x\in U$ and $y\in V$.
Since $U\in \mathcal{B}_X$ and $V\in \mathcal{B}_Y$, by property of basis $\mathcal{B}_X$ and $\mathcal{B}_Y$, $\forall x\in U$, $\exists B\in \mathcal{B}_X$ such that $x\in B\subseteq U$ and $\forall y\in V$, $\exists B'\in \mathcal{B}_Y$ such that $y\in B'\subseteq V$.
So $(x,y)\in (B\times B')\subseteq U\times V\subseteq W$.
</details>
#### Definition of standard topology on $\mathbb{R}^n$
The standard topology on $\mathbb{R}^n$ is defined as the product topology on $\mathbb{R}^{n-1}\times \mathbb{R}$.
## Subspace topology
Let $(X,\mathcal{T})$ be a topological space and $Y\subseteq X$.
Want to define a topology on $Y$.
$$
\mathcal{T}_Y=\{U\cap Y|U\in \mathcal{T}\}
$$
We claim that $\mathcal{T}_Y$ is a topology on $Y$, called as the subspace topology on $Y$.
<details>
<summary>Proof</summary>
First, $\emptyset \cap Y=\emptyset \in \mathcal{T}_Y$ and $Y=X\cap Y\in \mathcal{T}_Y$.
Second, let $\{U_\alpha\cap Y\}_{\alpha \in I}$ be collection of open sets in $\mathcal{T}_Y$. Note that $U_\alpha\in \mathcal{T}$ for all $\alpha \in I$.
So, $\bigcup_{\alpha \in I} U_\alpha\cap Y=\left(\bigcup_{\alpha \in I} U_\alpha\right)\cap Y\in \mathcal{T}_Y$ because $\bigcup_{\alpha \in I} U_\alpha\in \mathcal{T}$.
Third, let $\{U_i\cap Y\}_{i=1}^n$ be a finite collection of open sets in $\mathcal{T}_Y$. Note that $U_i\in \mathcal{T}$ for all $i=1,2,\ldots,n$.
So, $\bigcap_{i=1}^n U_i\cap Y=\left(\bigcap_{i=1}^n U_i\right)\cap Y\in \mathcal{T}_Y$ because $\bigcap_{i=1}^n U_i\in \mathcal{T}$.
</details>
### Generate basis for subspace topology
Let $\mathcal{B}$ is a basis for $(X,\mathcal{T})$. We'd like to use $\mathcal{B}$ to define a basis for $(Y,\mathcal{T}_Y)$.
$$
\mathcal{B}_Y=\{B\cap Y|B\in \mathcal{B}\}
$$
#### Proposition for basis of subspace topology
$\mathcal{B}_Y$ is a basis for a topology on $Y$ that generates the subspace topology on $Y$.
Proof as exercise. (same as the proof for the basis of product topology)
<details>
<summary>Example: not every open set in subspace topology is open in the original space</summary>
Let $X=\mathbb{R}$ with standard topology and $Y=[0,1]\cup [2,3]$. equipped with subspace topology generated by the standard basis for $\mathbb{R}$.
so $[0,1]=(-1,\frac{3}{2})\cap Y$ In particular, $[0,1]$ is open set in $Y$, but not an open set in $\mathbb{R}$.
</details>
#### Lemma of open set in subspace topology
Let $(X,\mathcal{T})$ be a topological space and $Y\subseteq X$ is open. $Z\subseteq Y$ is open subset with respect to the subspace topology on $Y$. Then $Z$ is open in $X$.

163
content/Math4201/Math4201_L7.md
View File

@@ -1,163 +0,0 @@
# Math 4201 Topology I (Lecture 7)
## Review from last lecture
Not every open set in subspace topology is open in the original space
Let $X=\mathbb{R}$ with standard topology and $Y=[0,1]\cup [2,3]$. equipped with subspace topology generated by the standard basis for $\mathbb{R}$.
so $[0,1]=(-1,\frac{3}{2})\cap Y$ In particular, $[0,1]$ is open set in $Y$, but not an open set in $\mathbb{R}$.
## New materials
### Closed sets in topological space
#### Proposition of open set in subspace topology
If $X$ is a topological space, then $Y\subseteq X$ is open and is with the subspace topology. If $Z\subset Y$ is open subspace of $Y$, then $Z$ is also an open subspace of $X$.
<details>
<summary>Proof</summary>
Since $Z\subset Y$ is open in the subspace topology, there is an open $U\subset Y$ such that $Z=U\cap Y$.
SInce $Z$ is the intersection of open sets in $X$, then $Z$ is open in $X$.
</details>
#### Definition of closed set
For any topology $\mathcal{T}$ on a set $X$, a subset $Z\subseteq X$ is said to be **closed** if its complement $Z^c$ is an open set (in $X$).
> Note the complement is defined $Z=X\setminus Z$.
<details>
<summary>Example of closed set in standard topology of real numbers</summary>
For example, $[a,b]$ is a closed set in the standard topology of real numbers. since $\mathbb{R}-[a,b]=(-\infty,a)\cup (b,\infty)$ is an open set.
</details>
<details>
<summary>Example of closed set in trivial topology</summary>
For any set $X$, the trivial topology is $\mathcal{T}_0=\{\emptyset, X\}$.
Since $X^c=\emptyset$ is an open set, $X$ is a closed set.
Since $\emptyset^c=X$ is an open set, $\emptyset$ is a closed set.
</details>
<details>
<summary>Example of closed set in finite complement topology</summary>
For any set $X$, the finite complement topology is $\mathcal{T}_1=\{U\subseteq X\mid X\setminus U\text{ is finite}\}$.
Then the set of all finite subsets of $X$ is a closed set.
</details>
For general, if $\mathcal{T}$ is a topology on $X$, then:
1. $\emptyset, X$ are closed sets.
2. $\mathcal{T}$ is closed with respect to arbitrary unions.
Let $\{Z_\alpha\}_{\alpha \in I}$ be an arbitrary collection of closed sets in $X$. Then $X-Z_\alpha$ is open for each $\alpha \in I$. So $\forall \alpha \in I$. $\bigcup_{\alpha \in I} (X-Z_\alpha)=X-\bigcap_{\alpha \in I} Z_\alpha$ is open. So $\bigcap_{\alpha \in I} Z_\alpha$ is closed.
So the corollary is: an arbitrary intersection of closed sets is closed.
3. $\mathcal{T}$ is closed with respect to finite intersections. This also implies that a finite union of closed sets is closed.
If $\{Z_1, Z_2, \ldots, Z_n\}$ is a closed subset of $X$, then $X-Z_i$ is open for each $i=1,2,\ldots,n$. So $\forall i=1,2,\ldots,n$. $\bigcap_{i=1}^n (X-Z_i)=X-\bigcup_{i=1}^n Z_i$ is open. So $\bigcup_{i=1}^n Z_i$ is closed.
> [!NOTE]
>
> We can also define the topology using the closed sets instead of the open sets.
>
> 1. $\emptyset, X$ are closed sets.
> 2. $\mathcal{T}$ is closed with respect to arbitrary intersections.
> 3. $\mathcal{T}$ is closed with respect to finite unions.
>
> This yields the same topology.
#### Theorem of closed set in subspace topology
Let $X$ is a topological space and $Y\subseteq X$ equipped with the subspace topology.
A subset $Z\subseteq Y$ is closed in $Y$ if and only if $Z$ is the intersection of a closed $W\subseteq X$ and $Y$. That is $Z=W\cap Y$.
<details>
<summary>Proof</summary>
$\Rightarrow$
If $Z$ is closed in $Y$, then $Y-Z$ is open in $Y$.
Then, there is open set $U\subseteq X$ such that $Y-Z=U\cap Y$.
So $Z=(X-U)\cap Y$, $X-U$ is closed in $X$ because $U$ is open in $X$.
Take $W=X-U$.
$\Leftarrow$
If $Z=W\cap Y$ for some closed $W\subseteq X$, then $Y-Z=Y-(W\cap Y)=(Y-W)\cap Y$ is open in $Y$.
So $Z$ is closed in $Y$.
</details>
#### Lemma of closed in closed subspace
Let $X$ is a topological space and $Y\subseteq X$ is closed and is equipped with the subspace topology. Then any closed subset of $Y$ is also closed in $X$.
> [!WARNING]
>
> Not any subset of a topological space $X$ is either open or closed.
<details>
<summary>Example of open and closed subset</summary>
Let $X=\mathbb{R}$ with standard topology.
$(a,b)$ is open, but not closed.
$[a,b]$ is closed, but not open.
$[a,b)$ is neither open nor closed.
$\emptyset,\mathbb{R}$ is both open and closed.
</details>
<details>
<summary>Example of open and closed subset in other topologies</summary>
Let $X=[0,1]\cup (2,3)$ induced by the standard topology of $\mathbb{R}$.
$Z=[0,1]$ is an open subset of $X$.
$Z=[0,1]$ is also closed subset of $X$ since $Z=[0,1]\cap X$ is open in $\mathbb{R}$.
</details>
We can associate an open and a closed to any subset $A$ of a topological space $X$.
#### Interior and closure of a set
The interior of a set $A$ is defined as follows:
$$
\operatorname{Int}(A)=\bigcup_{U\subseteq A, U\text{ is open in }X} U
$$
Also denoted as $A^\circ$.
The interior of a set $A$ is the largest open subset of $A$.
That is $\forall U\subseteq A, U\text{ is open in }X$, then $U\subseteq \operatorname{Int}(A)$. (by definition that $U$ must be in collection of open sets that is a subset of $A$)
#### Closure of a set
The closure of a set $A$ is the smallest closed subset of $X$ that contains $A$.
> Note that if we change the definition as the intersection of all closed subsets of $X$ that **contained in $A$**, we will get the empty set.
$$
\overline{A}=\bigcap_{A\subseteq C, C\text{ is closed in }X} C
$$
The closure of a set $A$ is the smallest closed subset of $X$ that contains $A$. (follows the same logic as the previous definition)

142
content/Math4201/Math4201_L8.md
View File

@@ -1,142 +0,0 @@
# Math4201 Topology I (Lecture 8)
Recall from real analysis, a set is closed if and only if it has limit points.
## New materials
### Limit points
Let $(X,\mathcal{T})$ be a topological space. $A$ is a subset of $X$, then we say $x\in X$ is a limit point of $A$ if any open set $U\subset X$ containing $x$ has another point $y\in A-\{x\}$.
<details>
<summary>Example of limit points</summary>
Let $X=\mathbb{R}$ with standard topology.
Let $A=(0,1)$, then set of limit points of $A$ is $[0,1]$.
Let $A=\left\{\frac{1}{n}\right\}_{n\in \mathbb{N}}$, then set of limit points of $A$ is $\{0\}$.
Let $A=\{0\}\cup (1,2)$, then set of limit points of $A$ is $[1,2]$
Let $A=\mathbb{Z}$, then set of limit points of $A$ is $\emptyset$.
</details>
#### Proposition of limit points and closed sets
A set is close if and only if it has limit points.
Theorem: For any subset $A$ of a topological space $X$, the closure of $A$ is $\overline{A}=A\cup A'$.
<details>
<summary>Proof</summary>
First we want to prove the theorem implies the proposition,
$\Rightarrow$
Let $A$ be a close set in $X$, then $\overline{A}=A$ because $A$ in the intersection of all closed subsets $Z\subseteq A$ in $X$ that contains $A$.
So $Z=A$ is such a closed subset of $X$ that contains $A$.
By the theorem, $\overline{A}=A\cup A'$. Combining this with the fact that $A$ is closed, we have $A=A\cup A'$.
So $A'\subseteq A$.
$\Leftarrow$
Suppose $A\subseteq X$ is a set that includes all its limit points, then $A'\subseteq A$.Then $A'\cup A=A$.
By the theorem, $\overline{A}=A\cup A'=A$.
Since $\overline{A}$ is the smallest closed subset of $X$ that contains $A$, we have $A$ is closed.
</details>
#### Definition of neighborhood
Let $(X,\mathcal{T})$ be a topological space. A neighborhood of a point $x\in X$ is an open set $U\in \mathcal{T}$ such that $x\in U$.
#### Lemma of intersection of neighborhoods for closure of a set
$x\in \overline{A}$ if and only if any neighborhood of $U$ of $x$ non-trivial intersects $A$. ($A\cap U\neq \emptyset$)
<details>
<summary>Proof of Lemma</summary>
$\Leftarrow$
We proceed by contradiction.
Suppose $A\notin \overline{A}$, then $x\notin \overline{A}$.
Then $\overline{A}=\bigcap_{A\subseteq Z, Z\text{ is closed}} Z$
So, there is $A\subseteq Z\subset X$ and $Z$ is closed.
So this implies that $x\in X-Z\coloneq U$ and $U$ is open since it a complement of a closed set $Z$.
Since $A\subseteq Z$, we have $A\cap U= \emptyset$. (disjoint)
So $U$ and $A$ are disjoint. So $U$ is an open neighborhood of $x$ that is disjoint from $A$.
This contradicts the assumption that $x\in \overline{A}$.
$\Rightarrow$
Let $x\in \overline{A}$, and we want to show that any neighborhood of $U$ of $x$ non-trivial intersects $A$. ($A\cap U\neq \emptyset$)
By contradiction, suppose that there is an open neighborhood of $x$ that is disjoint from $A$. Then $Z\coloneq X-U$ is closed and $A\subseteq Z$ because $U\cap A= \emptyset$.
Also $x\notin Z$.
By the definition of closure, $\overline{A}=\subset Z$.
Since $x\notin Z$, we have $x\notin \overline{A}$.
This contradicts the assumption that $x\in \overline{A}$.
</details>
#### Proof of theorem
For any subset $A$ of a topological space $X$, the closure of $A$ is $\overline{A}=A\cup A'$.
<details>
<summary>Proof</summary>
First we show $A\subseteq \overline{A}$.
If $x\in A'$, then any open neighborhood $U$ of $x$ has a non-trivial intersection with $A$ by the lemma.
So $x\in \overline{A}$.
We already know $A\subseteq \overline{A}$.
Therese two inductions implies $A\cup A'\subseteq \overline{A}$.
Next we show that $\overline{A}\subseteq A\cup A'$.
If $x\in \overline{A}$, then by the lemma, any open neighborhood $U$ of $x$ has a non-trivial intersection with $A$.
If $x\in A$, then $x\in A\cup A'$.
If $x\notin A$, then the intersection of any open neighborhood $U$ of $x$ with $A$ does not contain $x$.
This implies that this intersection has to include a point $y$ that is not $x$.
Since this holds for any open neighborhood $U$ of $x$, we have $x\in A'$. ($x$ is a limit point of $A$)
So $x\in A'$.
Therese two inductions implies $\overline{A}\subseteq A\cup A'$.
</details>
> [!TIP]
>
> Now the three definition of closure are equivalent.
>
> 1. The smallest closed subset of $X$ that contains $A$.
> 2. $A\cup A'$.

172
content/Math4201/Math4201_L9.md
View File

@@ -1,172 +0,0 @@
# Math4201 Topology I (Lecture 9)
## Convergence of sequences
Let $(X,\mathcal{T})$ be a topological space and $\{x_n\}_{n\in\mathbb{N}_+}$ be a sequence of points in $X$. We say $x_n\to x$ as $n\to \infty$ ($x_n$ converges to $x$ as $n\to \infty$)
if for any open neighborhood $U$ of $x$, there exists $N\in\mathbb{N}_+$ such that $\forall n\geq N, x_n\in U$.
<details>
<summary>Example of convergence of sequences</summary>
Let $X=\{a,b,c\}$ with the topology $\mathcal{T}=\{\emptyset, \{b\}, \{a,b\}, \{b,c\}, \{a,b,c\}\}$
Let $x_n=b$ for all $n\in\mathbb{N}_+$. Then $x_n\to b$ as $n\to \infty$.
Moreover, $x_n\to a$ as $n\to \infty$ since any open neighborhood of $a$ ($\{a,b\}$,$\{a,b,c\}$) contains $b$.
Without loss of generality, $x_n\to c$ as $n\to \infty$ since any open neighborhood of $c$ ($\{b,c\}$,$\{a,b,c\}$) contains $b$.
> You may find convergence of sequences in more than one point.
Let $x_n=a$ for all $n\in\mathbb{N}_+$. Then $x_n\to a$ as $n\to \infty$ (take $U=\{a,b\}$)
A non-example of convergence of sequences:
Let $x_n=\begin{cases}a, & n\text{ is even} \\ c, & n\text{ is odd}\end{cases}$. Then $x_n$ does not converge to any point in $X$. So this sequence does not have a limit in $(X,\mathcal{T})$.
</details>
### More special topologies
#### Hausdorff space
A topological space $(X,\mathcal{T})$ is a Hausdorff space if for any two distinct points $x,y\in X$, there exist open neighborhoods $U$ and $V$ of $x$ and $y$ respectively such that $U\cap V=\emptyset$.
<details>
<summary>Non-example of Hausdorff space</summary>
Let $X=\{a,b,c\}$ with the topology $\mathcal{T}=\{\emptyset, \{b\}, \{a,b\}, \{b,c\}, \{a,b,c\}\}$
Let $x=a,y=b$. Then they don't have disjoint open neighborhoods.
This topology is not a Hausdorff space.
</details>
If a topological space is a Hausdorff space, then every sequence has a unique limit point or have no limit point.
#### Properties of Hausdorff space
Let $(X,\mathcal{T})$ be a Hausdorff space. Then every sequence $\{x_n\}_{n\in\mathbb{N}_+}$ converges to $x$ and $y$, then $x=y$.
> [!TIP]
>
> We want to show if $x\neq y$, then there exists an open neighborhood $U$ of $x$ and $V$ of $y$ such that $U\cap V=\emptyset$.
<details>
<summary>Proof</summary>
We proceed by contradiction.
Suppose $x\neq y$, then by definition of Hausdorff space, there exists an open neighborhood $U$ of $x$ and $V$ of $y$ such that $U\cap V=\emptyset$.
If $x_n$ converges to $x$, then for any open neighborhood $U_x$ of $x$, there exists $N_x\in\mathbb{N}_+$ such that $\forall n\geq N_x, x_n\in U_x$. Similarly, for any open neighborhood $U_y$ of $y$, there exists $N_y\in\mathbb{N}_+$ such that $\forall n\geq N_y, x_n\in U_y$.
Then we can find $N=max\{N_x,N_y\}$ such that $x_n\in U_x\cap U_y$ for all $n\geq N$. This contradicts the assumption that $U\cap V=\emptyset$.
Therefore, $x=y$.
</details>
#### Properties of closed singleton
Let $(X,\mathcal{T})$ be a Hausdorff topological space. Then $\forall x\in X$, $\{x\}$ is a closed set.
<details>
<summary>Non-example of closed singleton</summary>
Let $X=\{a,b,c\}$ with the topology $\mathcal{T}=\{\emptyset, \{b\}, \{a,b\}, \{b,c\}, \{a,b,c\}\}$
Then $\{b\}$ is not a closed set, since $X\setminus \{b\}=\{a,c\}$ is not an open set.
</details>
<details>
<summary>Proof</summary>
We need to show that $A=X\setminus \{x\}$ is an open set.
Take $y\in A$, then by the assumption, $x$ and $y$ have disjoint open neighborhoods $U_x$ and $V_y$ respectively. $x\in U_x$ and $y\in V_y$ and $U_x\cap V_y=\emptyset$.
So $x\notin V_y$, $y\in V_y$. So $A\subseteq\bigcup_{y\in A,y\neq x} V_y$.
Since $\forall V_y,x\notin V_y$, So $A\subseteq\bigcup_{y\in A,y\neq x} V_y$.
So $A=\bigcup_{y\in A,y\neq x} V_y$ is an arbitrary union of open sets, so $A$ is an open set.
Therefore, $\{x\}$ is a closed set.
</details>
## Continuous
### Continuous functions
#### Definition for continuous functions
Let $(X,\mathcal{T})$ and $(Y,\mathcal{T}')$ be topological spaces and $f:X\to Y$. We say that $f$ is continuous if for every open set $V\in Y$, $f^{-1}(V)\coloneqq\{x\in X: f(x)\in V\}$ is open in $X$.
That is, $\forall V\in \mathcal{T}', f^{-1}(V)\in \mathcal{T}$.
#### Definition for point-wise continuity
Let $(X,\mathcal{T})$ and $(Y,\mathcal{T}')$ be topological spaces and $f:X\to Y$. We say that $f$ is continuous at $x\in X$ if for every open set $V\in \mathcal{T}'$ such that $f(x)\in V$, there exists an open set $U\in \mathcal{T}$ such that $x\in U$ and $f(U)\subseteq V$. ($f^{-1}(V)$ contains an open neighborhood of $x$)
#### Lemma for continuous functions
$f:X\to Y$ is continuous if and only if $\forall x\in X$, $f$ is continuous at $x$.
<details>
<summary>Proof</summary>
$\Rightarrow$:
Trivial
$\Leftarrow$:
Take an open set $V\in \mathcal{T}'$. Then for any point $x\in f^{-1}(V)$, we have $f(x)\in V$.
In particular, by definition of continuity at $x$, there exists an open set $U_x$ of $x$ such that $U_x\subseteq f^{-1}(V)$.
Then $f^{-1}(V)=\bigcup_{x\in f^{-1}(V)} U_x$ is an arbitrary union of open sets, so $f^{-1}(V)$ is open in $X$.
</details>
<details>
<summary>Example of continuous functions</summary>
Let $X$ be any set and $\mathcal{T}$ be the discrete topology on $X$, $\mathcal{T}'$ be the trivial topology on $X$.
Let $f:(X,\mathcal{T})\to (X,\mathcal{T}')$ be the identity function. Then $f$ is continuous.
Since forall $V\in \mathcal{T}'$, $V$ is open in $X$, we can find $f^{-1}(V)$ is open in $X$. (only neet to test $X,\emptyset$)
In general, if $T$ is a finer than $T'$, then $f:(X,\mathcal{T})\to (X,\mathcal{T}')$ be the identity map is continuous.
However, if we let $f:(X,\mathcal{T}')\to (X,\mathcal{T})$ be the identity function, then $f$ is not continuous unless $X$ is a singleton.
</details>
#### Definition for constant maps
Let $X,Y$ be topological spaces and $y_0\in Y$, $f:X\to Y$ is defined by $f(x)=y_0$ for all $x\in X$. Then $f$ is continuous.
<details>
<summary>Proof</summary>
Take an open set $V\in \mathcal{T}'$. $f^{-1}(V)=\begin{cases}X, & y_0\in V \\ \emptyset, & y_0\notin V\end{cases}$ is open in $X$. (by definition of topology, $X,\emptyset$ are open in $X$)
</details>
<details>
<summary>Example of inclusion maps</summary>
Let $X$ be a topological space and $A\subseteq X$ equipped with the subspace topology.
Let $f:A\to X$ be the inclusion map $f(x)=x$ for all $x\in A$.
Then take $V\subseteq X$ be an open set. $f^{-1}(V)=V\cap A\subseteq A$ is open in $A$ (by subspace topology).
</details>

31
content/Math4201/_meta.js
View File

@@ -1,31 +0,0 @@
export default {
index: "Course Description",
"---":{
type: 'separator'
},
Exam_reviews: "Exam reviews",
Math4201_L1: "Topology I (Lecture 1)",
Math4201_L2: "Topology I (Lecture 2)",
Math4201_L3: "Topology I (Lecture 3)",
Math4201_L4: "Topology I (Lecture 4)",
Math4201_L5: "Topology I (Lecture 5) Bonus",
Math4201_L6: "Topology I (Lecture 6)",
Math4201_L7: "Topology I (Lecture 7)",
Math4201_L8: "Topology I (Lecture 8)",
Math4201_L9: "Topology I (Lecture 9)",
Math4201_L10: "Topology I (Lecture 10)",
Math4201_L11: "Topology I (Lecture 11)",
Math4201_L12: "Topology I (Lecture 12)",
Math4201_L13: "Topology I (Lecture 13)",
Math4201_L14: "Topology I (Lecture 14)",
Math4201_L15: "Topology I (Lecture 15)",
Math4201_L16: "Topology I (Lecture 16)",
Math4201_L17: "Topology I (Lecture 17)",
Math4201_L18: "Topology I (Lecture 18)",
Math4201_L19: "Topology I (Lecture 19)",
Math4201_L20: "Topology I (Lecture 20)",
Math4201_L21: "Topology I (Lecture 21)",
Math4201_L22: "Topology I (Lecture 22)",
Math4201_L23: "Topology I (Lecture 23)",
Math4201_L24: "Topology I (Lecture 24)",
}

0
content/Math429/index.md Normal file
View File

132
content/_meta.js
View File

@@ -24,40 +24,128 @@ export default {
}
},
},
Math4201_link: {
title: 'Math 4201',
/* Load link with relative path */
Math3200_link: {
title: 'Math3200',
type: 'page',
href: '/Math4201',
href: '/Math3200'
},
Math429_link: {
title: 'Math429',
type: 'page',
href: '/Math429'
},
Math4111_link: {
title: 'Math 4111',
title: 'Math4111',
type: 'page',
href: '/Math4111',
href: '/Math4111'
},
CSE559A_link: {
title: 'CSE 559A',
Math4121_link: {
title: 'Math4121',
type: 'page',
href: '/CSE559A',
href: '/Math4121'
},
Math4201_link: {
title: 'Math4201',
type: 'page',
href: '/Math4201'
},
Math416_link: {
title: 'Math416',
type: 'page',
href: '/Math416'
},
Math401_link: {
title: 'Math401',
type: 'page',
href: '/Math401'
},
/* Math Courses Start */
Math3200: {
title: 'Math3200',
type: 'page',
theme:{
timestamp: true,
}
},
Math429:{
title: 'Math429',
type: 'page',
theme:{
timestamp: true,
}
},
Math4111: {
title: 'Math4111',
type: 'page',
theme:{
timestamp: true,
}
},
Math4121: {
title: 'Math4121',
type: 'page',
theme:{
timestamp: true,
}
},
Math4201: {
title: 'Math4201',
type: 'page',
theme:{
timestamp: true,
}
},
Math416: {
title: 'Math416',
type: 'page',
theme:{
timestamp: true,
}
},
Math401: {
title: 'Math401',
type: 'page',
theme:{
timestamp: true,
}
},
/* Math Courses End */
Math4201: {
title: 'Math 4201',
CSE332S_link: {
title: 'CSE332S',
type: 'page',
theme:{
// sidebar: false,
timestamp: true,
}
href: '/CSE332S'
},
/* CSE Courses Start */
CSE559A: {
title: 'CSE 559A',
CSE347_link: {
title: 'CSE347',
type: 'page',
theme:{
// sidebar: false,
timestamp: true,
}
href: '/CSE347'
},
CSE442T_link: {
title: 'CSE442T',
type: 'page',
href: '/CSE442T'
},
CSE5313_link: {
title: 'CSE5313',
type: 'page',
href: '/CSE5313'
},
CSE510_link: {
title: 'CSE510',
type: 'page',
href: '/CSE510'
},
CSE559A_link: {
title: 'CSE559A',
type: 'page',
href: '/CSE559A'
},
CSE5519_link: {
title: 'CSE5519',
type: 'page',
href: '/CSE5519'
},
/* CSE Courses End */
Swap: {
display: 'hidden',
theme:{

1
next-env.d.ts vendored
View File

@@ -1,6 +1,5 @@
/// <reference types="next" />
/// <reference types="next/image-types/global" />
/// <reference path="./.next/types/routes.d.ts" />
// NOTE: This file should not be edited
// see https://nextjs.org/docs/app/api-reference/config/typescript for more information.

BIN
public/CSE559A/1D_Conv.png
View File

Binary file not shown.
Side by Side

Before

Width:  |  Height:  |  Size: 34 KiB

BIN
public/CSE559A/1x1_layer.png
View File

Binary file not shown.
Side by Side

Before

Width:  |  Height:  |  Size: 14 KiB

BIN
public/CSE559A/8x8_DCT_basis.png
View File

Binary file not shown.
Side by Side

Before

Width:  |  Height:  |  Size: 6.9 KiB

BIN
public/CSE559A/Ambiguities_in_projection.png
View File

Binary file not shown.
Side by Side

Before

Width:  |  Height:  |  Size: 35 KiB

BIN
public/CSE559A/Anchor-boxes.png
View File

Binary file not shown.
Side by Side

Before

Width:  |  Height:  |  Size: 298 KiB

BIN
public/CSE559A/Blob_detection_with_LoG.png
View File

Binary file not shown.
Side by Side

Before

Width:  |  Height:  |  Size: 20 KiB

BIN
public/CSE559A/Comparison_of_keypoint_detectors.png
View File

Binary file not shown.
Side by Side

Before

Width:  |  Height:  |  Size: 105 KiB

BIN
public/CSE559A/Convolutional_layer.png
View File

Binary file not shown.
Side by Side

Before

Width:  |  Height:  |  Size: 6.5 KiB

BIN
public/CSE559A/DETR.png
View File

Binary file not shown.
Side by Side

Before

Width:  |  Height:  |  Size: 642 KiB

BIN
public/CSE559A/DeconvNet.png
View File

Binary file not shown.
Side by Side

Before

Width:  |  Height:  |  Size: 268 KiB

BIN
public/CSE559A/Deep_learning_for_correspondence_estimation.png
View File

Binary file not shown.
Side by Side

Before

Width:  |  Height:  |  Size: 232 KiB

BIN
public/CSE559A/Depth_and_Normal_Estimation.png
View File

Binary file not shown.
Side by Side

Before

Width:  |  Height:  |  Size: 818 KiB

BIN
public/CSE559A/Depthwise_layer.png
View File

Binary file not shown.
Side by Side

Before

Width:  |  Height:  |  Size: 22 KiB

BIN
public/CSE559A/DigitalCameraBlockDiagram.png
View File

Binary file not shown.
Side by Side

Before

Width:  |  Height:  |  Size: 59 KiB

BIN
public/CSE559A/Edge_detection_with_LoG.png
View File

Binary file not shown.
Side by Side

Before

Width:  |  Height:  |  Size: 128 KiB

BIN
public/CSE559A/EncoderDecoder_vs_U-Net.png
View File

Binary file not shown.
Side by Side

Before

Width:  |  Height:  |  Size: 40 KiB

BIN
public/CSE559A/Epipolar_geometry_setup.png
View File

Binary file not shown.
Side by Side

Before

Width:  |  Height:  |  Size: 35 KiB

BIN
public/CSE559A/Epipolar_line_for_converging_cameras.png
View File

Binary file not shown.
Side by Side

Before

Width:  |  Height:  |  Size: 29 KiB

BIN
public/CSE559A/Epipolar_line_for_parallel_cameras.png
View File

Binary file not shown.
Side by Side

Before

Width:  |  Height:  |  Size: 17 KiB

BIN
public/CSE559A/Epipolar_line_for_perpendicular_cameras.png
View File

Binary file not shown.
Side by Side

Before

Width:  |  Height:  |  Size: 17 KiB

BIN
public/CSE559A/ExU-Net.png
View File

Binary file not shown.
Side by Side

Before

Width:  |  Height:  |  Size: 359 KiB

BIN
public/CSE559A/Fast-R-CNN.png
View File

Binary file not shown.
Side by Side

Before

Width:  |  Height:  |  Size: 198 KiB

BIN
public/CSE559A/Flatten_layer.png
View File

Binary file not shown.
Side by Side

Before

Width:  |  Height:  |  Size: 15 KiB

BIN
public/CSE559A/General_computation_graphs_for_MLP.png
View File

Binary file not shown.
Side by Side

Before

Width:  |  Height:  |  Size: 114 KiB

Some files were not shown because too many files have changed in this diff Show More