bug fixed,
remaining issues in mobilenavbar need pruning, need rewrite the class.
This commit is contained in:
840
content/Math416/Exam_reviews/Math416_E1.md
Normal file
840
content/Math416/Exam_reviews/Math416_E1.md
Normal file
@@ -0,0 +1,840 @@
|
||||
# Math 416 Midterm 1 Review
|
||||
|
||||
So everything we have learned so far is to extend the real line to the complex plane.
|
||||
|
||||
## Chapter 0 Calculus on Real values
|
||||
|
||||
### Differentiation
|
||||
|
||||
Let $f,g$ be function on real line and $c$ be a real number.
|
||||
|
||||
$$
|
||||
\frac{d}{dx}(f+g)=f'+g'
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}(cf)=cf'
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}(fg)=f'g+fg'
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}(f/g)=(f'g-fg')/g^2
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}(f\circ g)=(f'\circ g)\frac{d}{dx}g
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}x^n=nx^{n-1}
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}e^x=e^x
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}\ln x=\frac{1}{x}
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}\sin x=\cos x
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}\cos x=-\sin x
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}\tan x=\sec^2 x
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}\sec x=\sec x\tan x
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}\csc x=-\csc x\cot x
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}\sinh x=\cosh x
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}\cosh x=\sinh x
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}\tanh x=\operatorname{sech}^2 x
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}\operatorname{sech} x=-\operatorname{sech}x\tanh x
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}\operatorname{csch} x=-\operatorname{csch}x\coth x
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}\coth x=-\operatorname{csch}^2 x
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}\arcsin x=\frac{1}{\sqrt{1-x^2}}
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}\arccos x=-\frac{1}{\sqrt{1-x^2}}
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}\arctan x=\frac{1}{1+x^2}
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}\operatorname{arccot} x=-\frac{1}{1+x^2}
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}\operatorname{arcsec} x=\frac{1}{x\sqrt{x^2-1}}
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{d}{dx}\operatorname{arccsc} x=-\frac{1}{x\sqrt{x^2-1}}
|
||||
$$
|
||||
|
||||
### Integration
|
||||
|
||||
Let $f,g$ be function on real line and $c$ be a real number.
|
||||
|
||||
$$
|
||||
\int (f+g)dx=\int fdx+\int gdx
|
||||
$$
|
||||
|
||||
$$
|
||||
\int cfdx=c\int fdx
|
||||
$$
|
||||
|
||||
$$
|
||||
\int e^x dx=e^x
|
||||
$$
|
||||
|
||||
$$
|
||||
\int \ln x dx=x\ln x-x
|
||||
$$
|
||||
|
||||
$$
|
||||
\int \frac{1}{x} dx=\ln|x|
|
||||
$$
|
||||
|
||||
$$
|
||||
\int \sin x dx=-\cos x
|
||||
$$
|
||||
|
||||
$$
|
||||
\int \cos x dx=\sin x
|
||||
$$
|
||||
|
||||
$$
|
||||
\int \tan x dx=-\ln|\cos x|
|
||||
$$
|
||||
|
||||
$$
|
||||
\int \cot x dx=\ln|\sin x|
|
||||
$$
|
||||
|
||||
$$
|
||||
\int \sec x dx=\ln|\sec x+\tan x|
|
||||
$$
|
||||
|
||||
$$
|
||||
\int \csc x dx=\ln|\csc x-\cot x|
|
||||
$$
|
||||
|
||||
$$
|
||||
\int \sinh x dx=\cosh x
|
||||
$$
|
||||
|
||||
$$
|
||||
\int \cosh x dx=\sinh x
|
||||
$$
|
||||
|
||||
$$
|
||||
\int \tanh x dx=\ln|\cosh x|
|
||||
$$
|
||||
|
||||
$$
|
||||
\int \coth x dx=\ln|\sinh x|
|
||||
$$
|
||||
|
||||
$$
|
||||
\int \operatorname{sech} x dx=2\arctan(\tanh(x/2))
|
||||
$$
|
||||
|
||||
$$
|
||||
\int \operatorname{csch} x dx=\ln|\coth x-\operatorname{csch} x|
|
||||
$$
|
||||
|
||||
$$
|
||||
\int \operatorname{sech}^2 x dx=\tanh x
|
||||
$$
|
||||
|
||||
$$
|
||||
\int \operatorname{csch}^2 x dx=-\coth x
|
||||
$$
|
||||
|
||||
$$
|
||||
\int \frac{1}{1+x^2} dx=\arctan x
|
||||
$$
|
||||
|
||||
$$
|
||||
\int \frac{1}{x^2+1} dx=\arctan x
|
||||
$$
|
||||
|
||||
$$
|
||||
\int \frac{1}{x^2-1} dx=\frac{1}{2}\ln|\frac{x-1}{x+1}|
|
||||
$$
|
||||
|
||||
$$
|
||||
\int \frac{1}{x^2-a^2} dx=\frac{1}{2a}\ln|\frac{x-a}{x+a}|
|
||||
$$
|
||||
|
||||
$$
|
||||
\int \frac{1}{x^2+a^2} dx=\frac{1}{a}\arctan(\frac{x}{a})
|
||||
$$
|
||||
|
||||
$$
|
||||
\int \frac{1}{\sqrt{x^2-a^2}} dx=\ln|x+\sqrt{x^2-a^2}|
|
||||
$$
|
||||
|
||||
$$
|
||||
\int \frac{1}{\sqrt{x^2+a^2}} dx=\ln|x+\sqrt{x^2+a^2}|
|
||||
$$
|
||||
|
||||
## Chapter 1 Complex Numbers
|
||||
|
||||
### Definition of complex numbers
|
||||
|
||||
An ordered pair of real numbers $(x, y)$ can be represented as a complex number $z = x + yi$, where $i$ is the imaginary unit.
|
||||
|
||||
With operations defined as:
|
||||
|
||||
$$
|
||||
(x_1 + y_1i) + (x_2 + y_2i) = (x_1 + x_2) + (y_1 + y_2)i
|
||||
$$
|
||||
|
||||
$$
|
||||
(x_1 + y_1i) \cdot (x_2 + y_2i) = (x_1x_2 - y_1y_2) + (x_1y_2 + x_2y_1)i
|
||||
$$
|
||||
|
||||
#### Modulus
|
||||
|
||||
The modulus of a complex number $z = x + yi$ is defined as
|
||||
|
||||
$$
|
||||
|z| = \sqrt{x^2 + y^2}=|z\overline{z}|
|
||||
$$
|
||||
|
||||
### De Moivre's Formula
|
||||
|
||||
Every complex number $z$ can be written as $z = r(\cos \theta + i \sin \theta)$, where $r$ is the magnitude of $z$ and $\theta$ is the argument of $z$.
|
||||
|
||||
$$
|
||||
z^n = r^n(\cos n\theta + i \sin n\theta)
|
||||
$$
|
||||
|
||||
The De Moivre's formula is useful for finding the $n$th roots of a complex number.
|
||||
|
||||
$$
|
||||
z^n = r^n(\cos n\theta + i \sin n\theta)
|
||||
$$
|
||||
|
||||
### Roots of complex numbers
|
||||
|
||||
Using De Moivre's formula, we can find the $n$th roots of a complex number.
|
||||
|
||||
If $z=r(\cos \theta + i \sin \theta)$, then the $n$th roots of $z$ are given by:
|
||||
|
||||
$$
|
||||
z_k = r^{1/n}(\cos \frac{\theta + 2k\pi}{n} + i \sin \frac{\theta + 2k\pi}{n})
|
||||
$$
|
||||
|
||||
for $k = 0, 1, 2, \ldots, n-1$.
|
||||
|
||||
### Stereographic projection
|
||||
|
||||
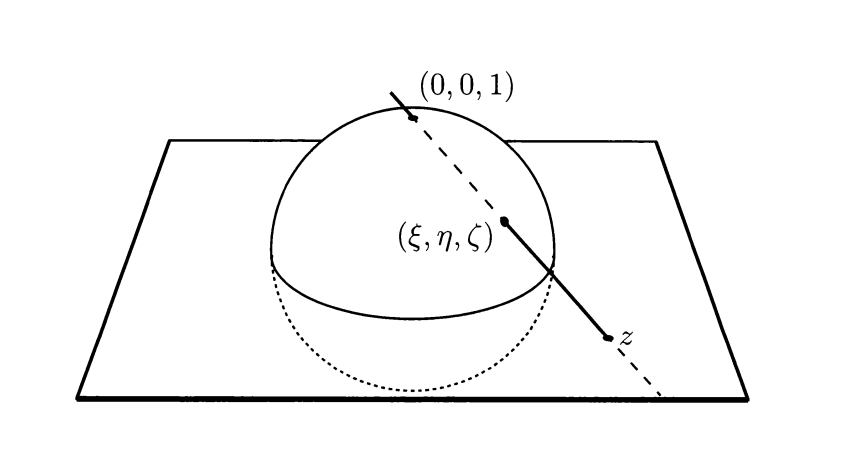
|
||||
|
||||
The stereographic projection is a map from the unit sphere $S^2$ to the complex plane $\mathbb{C}\setminus\{0\}$.
|
||||
|
||||
The projection is given by:
|
||||
|
||||
$$
|
||||
z\mapsto \frac{(2Re(z), 2Im(z), |z|^2-1)}{|z|^2+1}
|
||||
$$
|
||||
|
||||
The inverse map is given by:
|
||||
|
||||
$$
|
||||
(\xi,\eta, \zeta)\mapsto \frac{\xi + i\eta}{1 - \zeta}
|
||||
$$
|
||||
|
||||
## Chapter 2 Complex Differentiation
|
||||
|
||||
### Definition of complex differentiation
|
||||
|
||||
Let the complex plane $\mathbb{C}$ be defined in an open subset $G$ of $\mathbb{C}$. (Domain)
|
||||
|
||||
Then $f$ is said to be differentiable at $z_0\in G$ if the limit
|
||||
|
||||
$$
|
||||
\lim_{z\to z_0} \frac{f(z)-f(z_0)}{z-z_0}
|
||||
$$
|
||||
|
||||
exists.
|
||||
|
||||
The limit is called the derivative of $f$ at $z_0$ and is denoted by $f'(z_0)$.
|
||||
|
||||
To prove that a function is differentiable, we can use the standard delta-epsilon definition of a limit.
|
||||
|
||||
$$
|
||||
\left|\frac{f(z)-f(z_0)}{z-z_0} - f'(z_0)\right| < \epsilon
|
||||
$$
|
||||
|
||||
whenever $0 < |z-z_0| < \delta$.
|
||||
|
||||
With such definition, all the properties of real differentiation can be extended to complex differentiation.
|
||||
|
||||
#### Differentiation of complex functions
|
||||
|
||||
1. If $f$ is differentiable at $z_0$, then $f$ is continuous at $z_0$.
|
||||
2. If $f,g$ are differentiable at $z_0$, then $f+g, fg$ are differentiable at $z_0$.
|
||||
$$
|
||||
(f+g)'(z_0) = f'(z_0) + g'(z_0)
|
||||
$$
|
||||
$$
|
||||
(fg)'(z_0) = f'(z_0)g(z_0) + f(z_0)g'(z_0)
|
||||
$$
|
||||
3. If $f,g$ are differentiable at $z_0$ and $g(z_0)\neq 0$, then $f/g$ is differentiable at $z_0$.
|
||||
$$
|
||||
\left(\frac{f}{g}\right)'(z_0) = \frac{f'(z_0)g(z_0) - f(z_0)g'(z_0)}{g(z_0)^2}
|
||||
$$
|
||||
4. If $f$ is differentiable at $z_0$ and $g$ is differentiable at $f(z_0)$, then $g\circ f$ is differentiable at $z_0$.
|
||||
$$
|
||||
(g\circ f)'(z_0) = g'(f(z_0))f'(z_0)
|
||||
$$
|
||||
5. If $f(z)=\sum_{k=0}^n c_k(z-z_0)^k$, where $c_k\in\mathbb{C}$, then $f$ is differentiable at $z_0$ and $f'(z_0)=\sum_{k=1}^n kc_k(z_0-z_0)^{k-1}$.
|
||||
$$
|
||||
f'(z_0) = c_1 + 2c_2(z_0-z_0) + 3c_3(z_0-z_0)^2 + \cdots + nc_n(z_0-z_0)^{n-1}
|
||||
$$
|
||||
|
||||
### Cauchy-Riemann Equations
|
||||
|
||||
Let the function defined on an open subset $G$ of $\mathbb{C}$ be $f(x,y)=u(x,y)+iv(x,y)$, where $u,v$ are real-valued functions.
|
||||
|
||||
Then $f$ is differentiable at $z_0=x_0+y_0i$ if and only if the partial derivatives of $u$ and $v$ exist at $(x_0,y_0)$ and satisfy the Cauchy-Riemann equations:
|
||||
|
||||
$$
|
||||
\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y}, \quad \frac{\partial u}{\partial y} = -\frac{\partial v}{\partial x}
|
||||
$$
|
||||
|
||||
On the polar form, the Cauchy-Riemann equations are
|
||||
|
||||
$$
|
||||
r\frac{\partial u}{\partial r} = \frac{\partial v}{\partial \theta}, \quad \frac{\partial u}{\partial \theta} = -r\frac{\partial v}{\partial r}
|
||||
$$
|
||||
|
||||
### Holomorphic functions
|
||||
|
||||
A function $f$ is said to be holomorphic on an open subset $G$ of $\mathbb{C}$ if $f$ is differentiable at every point of $G$.
|
||||
|
||||
#### Partial differential operators
|
||||
|
||||
$$
|
||||
\frac{\partial}{\partial z} = \frac{1}{2}\left(\frac{\partial}{\partial x} - i\frac{\partial}{\partial y}\right)
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{\partial}{\partial \bar{z}} = \frac{1}{2}\left(\frac{\partial}{\partial x} + i\frac{\partial}{\partial y}\right)
|
||||
$$
|
||||
|
||||
This gives that
|
||||
|
||||
$$
|
||||
\frac{\partial f}{\partial z} = \frac{1}{2}\left(\frac{\partial f}{\partial x} - i\frac{\partial f}{\partial y}\right)=\frac{1}{2}\left(\frac{\partial u}{\partial x} +\frac{\partial v}{\partial y}\right) + \frac{i}{2}\left(\frac{\partial v}{\partial x} - \frac{\partial u}{\partial y}\right)
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{\partial f}{\partial \bar{z}} = \frac{1}{2}\left(\frac{\partial f}{\partial x} + i\frac{\partial f}{\partial y}\right)=\frac{1}{2}\left(\frac{\partial u}{\partial x} - \frac{\partial v}{\partial y}\right) + \frac{i}{2}\left(\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}\right)
|
||||
$$
|
||||
|
||||
If the function $f$ is holomorphic, then by the Cauchy-Riemann equations, we have
|
||||
|
||||
$$
|
||||
\frac{\partial f}{\partial \bar{z}} = 0
|
||||
$$
|
||||
|
||||
### Conformal mappings
|
||||
|
||||
A holomorphic function $f$ is said to be conformal if it preserves the angles between the curves. More formally, if $f$ is holomorphic on an open subset $G$ of $\mathbb{C}$ and $z_0\in G$, $\gamma_1, \gamma_2$ are two curves passing through $z_0$ ($\gamma_1(t_1)=\gamma_2(t_2)=z_0$) and intersecting at an angle $\theta$, then
|
||||
|
||||
$$
|
||||
\arg(f\circ\gamma_1)'(t_1) - \arg(f\circ\gamma_2)'(t_2) = \theta
|
||||
$$
|
||||
|
||||
In other words, the angle between the curves is preserved.
|
||||
|
||||
An immediate consequence is that
|
||||
|
||||
$$
|
||||
\arg(f\cdot \gamma_1)'(t_1) =\arg f'(z_0) + \arg \gamma_1'(t_1)\\
|
||||
\arg(f\cdot \gamma_2)'(t_2) =\arg f'(z_0) + \arg \gamma_2'(t_2)
|
||||
$$
|
||||
|
||||
### Harmonic functions
|
||||
|
||||
A real-valued function $u$ is said to be harmonic if it satisfies the Laplace equation:
|
||||
|
||||
$$
|
||||
\frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = 0
|
||||
$$
|
||||
|
||||
## Chapter 3 Linear Fractional Transformations
|
||||
|
||||
### Definition of linear fractional transformations
|
||||
|
||||
A linear fractional transformation is a function of the form
|
||||
|
||||
$$
|
||||
\phi(z) = \frac{az+b}{cz+d}
|
||||
$$
|
||||
|
||||
where $a,b,c,d$ are complex numbers and $ad-bc\neq 0$.
|
||||
|
||||
### Properties of linear fractional transformations
|
||||
|
||||
#### Matrix form
|
||||
|
||||
A linear fractional transformation can be written as a matrix multiplication:
|
||||
|
||||
$$
|
||||
\phi(z) = \begin{bmatrix}
|
||||
a & b\\
|
||||
c & d\\
|
||||
\end{bmatrix}
|
||||
\begin{bmatrix}
|
||||
z\\
|
||||
1\\
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
#### Conformality
|
||||
|
||||
A linear fractional transformation is conformal.
|
||||
|
||||
$$
|
||||
\phi'(z) = \frac{ad-bc}{(cz+d)^2}
|
||||
$$
|
||||
|
||||
#### Three-fold transitivity
|
||||
|
||||
If $z_1,z_2,z_3$ are distinct points in the complex plane, then there exists a unique linear fractional transformation $\phi$ such that $\phi(z_1)=\infty$, $\phi(z_2)=0$, $\phi(z_3)=1$.
|
||||
|
||||
The map is given by
|
||||
|
||||
$$
|
||||
\phi(z) =\begin{cases}
|
||||
\frac{(z-z_2)(z_1-z_3)}{(z-z_1)(z_2-z_3)} & \text{if } z_1,z_2,z_3 \text{ are all finite}\\
|
||||
\frac{z-z_2}{z_3-z_2} & \text{if } z_1=\infty\\
|
||||
\frac{z_3-z_1}{z-z_1} & \text{if } z_2=\infty\\
|
||||
\frac{z-z_2}{z-z_1} & \text{if } z_3=\infty\\
|
||||
\end{cases}
|
||||
$$
|
||||
|
||||
So if $z_1,z_2,z_3$, $w_1,w_2,w_3$ are distinct points in the complex plane, then there exists a unique linear fractional transformation $\phi$ such that $\phi(z_i)=w_i$ for $i=1,2,3$.
|
||||
|
||||
#### Factorization
|
||||
|
||||
Every linear fractional transformation can be written as a composition of homothetic mappings, translations, inversions, and multiplications.
|
||||
|
||||
If $\phi(z)=\frac{az+b}{cz+d}$, then
|
||||
|
||||
$$
|
||||
\phi(z) = \frac{b-ad/c}{cz+d}+\frac{a}{c}
|
||||
$$
|
||||
|
||||
#### Clircle
|
||||
|
||||
A linear-fractional transformation maps circles and lines to circles and lines.
|
||||
|
||||
## Chapter 4 Elementary Functions
|
||||
|
||||
### Exponential function
|
||||
|
||||
The exponential function is defined as
|
||||
|
||||
$$
|
||||
e^z = \sum_{n=0}^\infty \frac{z^n}{n!}
|
||||
$$
|
||||
|
||||
Let $z=x+iy$, then
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
e^z &= e^{x+iy}\\
|
||||
&= e^x e^{iy}\\
|
||||
&= e^x\sum_{n=0}^\infty \frac{(iy)^n}{n!}\\
|
||||
&= e^x\sum_{n=0}^\infty \frac{(-1)^n y^{2n}}{(2n)!} + i \sum_{n=0}^\infty \frac{(-1)^n y^{2n+1}}{(2n+1)!}\\
|
||||
&= e^x(\cos y + i\sin y)\\
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
So we can rewrite the polar form of a complex number as
|
||||
|
||||
$$
|
||||
z = r(\cos \theta + i\sin \theta) = re^{i\theta}
|
||||
$$
|
||||
|
||||
#### $e^x$ is holomorphic
|
||||
|
||||
Let $f(z)=e^z$, then $u(x,y)=e^x\cos y$, $v(x,y)=e^x\sin y$.
|
||||
|
||||
$$
|
||||
\frac{\partial u}{\partial x} = e^x\cos y = \frac{\partial v}{\partial y}\\
|
||||
\frac{\partial u}{\partial y} = -e^x\sin y = -\frac{\partial v}{\partial x}
|
||||
$$
|
||||
|
||||
### Trigonometric functions
|
||||
|
||||
$$
|
||||
\sin z = \frac{e^{iz}-e^{-iz}}{2i}, \quad \cos z = \frac{e^{iz}+e^{-iz}}{2}, \quad \tan z = \frac{\sin z}{\cos z}
|
||||
$$
|
||||
|
||||
$$
|
||||
\sec z = \frac{1}{\cos z}, \quad \csc z = \frac{1}{\sin z}, \quad \cot z = \frac{1}{\tan z}
|
||||
$$
|
||||
|
||||
#### Hyperbolic functions
|
||||
|
||||
$$
|
||||
\sinh z = \frac{e^z-e^{-z}}{2}, \quad \cosh z = \frac{e^z+e^{-z}}{2}, \quad \tanh z = \frac{\sinh z}{\cosh z}
|
||||
$$
|
||||
|
||||
$$
|
||||
\operatorname{sech} z = \frac{1}{\cosh z}, \quad \operatorname{csch} z = \frac{1}{\sinh z}, \quad \operatorname{coth} z = \frac{1}{\tanh z}
|
||||
$$
|
||||
|
||||
### Logarithmic function
|
||||
|
||||
The logarithmic function is defined as
|
||||
|
||||
$$
|
||||
\ln z=\{w\in\mathbb{C}: e^w=z\}
|
||||
$$
|
||||
|
||||
#### Properties of the logarithmic function
|
||||
|
||||
Let $z=x+iy$, then
|
||||
|
||||
$$
|
||||
|e^z|=\sqrt{e^x(\cos y)^2+(\sin y)^2}=e^x
|
||||
$$
|
||||
|
||||
So we have
|
||||
|
||||
$$
|
||||
\log z = \ln |z| + i\arg z
|
||||
$$
|
||||
|
||||
### Power function
|
||||
|
||||
For any two complex numbers $a,b$, we can define the power function as
|
||||
|
||||
$$
|
||||
a^b = e^{b\log a}
|
||||
$$
|
||||
|
||||
> Example:
|
||||
>
|
||||
> $$i^i=e^{i\ln i}=e^{i(\ln 1+i\frac{\pi}{2})}=e^{-\frac{\pi}{2}} $$
|
||||
>
|
||||
> $$e^{i\pi}=-1$$
|
||||
|
||||
|
||||
## Chapter 5 Power Series
|
||||
|
||||
### Definition of power series
|
||||
|
||||
A power series is a series of the form
|
||||
|
||||
$$
|
||||
\sum_{n=0}^\infty a_n (z-z_0)^n
|
||||
$$
|
||||
|
||||
### Properties of power series
|
||||
|
||||
#### Geometric series
|
||||
|
||||
$$
|
||||
\sum_{n=0}^\infty z^n = \frac{1}{1-z}, \quad |z|<1
|
||||
$$
|
||||
|
||||
### Radius/Region of convergence
|
||||
|
||||
The radius of convergence of a power series is the largest number $R$ such that the series converges for all $z$ with $|z-z_0|<R$.
|
||||
|
||||
The region of convergence of a power series is the set of all points $z$ such that the series converges.
|
||||
|
||||
### Cauchy-Hadamard Theorem
|
||||
|
||||
The radius of convergence of a power series is given by
|
||||
|
||||
$$
|
||||
R=\frac{1}{\limsup_{n\to\infty} |a_n|^{1/n}}
|
||||
$$
|
||||
|
||||
### Derivative of power series
|
||||
|
||||
The derivative of a power series is given by
|
||||
|
||||
$$
|
||||
f'(z)=\sum_{n=1}^\infty n a_n (z-z_0)^{n-1}
|
||||
$$
|
||||
|
||||
### Cauchy Product (of power series)
|
||||
|
||||
Let $\sum_{n=0}^\infty a_n (z-z_0)^n$ and $\sum_{n=0}^\infty b_n (z-z_0)^n$ be two power series with radius of convergence $R_1$ and $R_2$ respectively.
|
||||
|
||||
Then the Cauchy product of the two series is given by
|
||||
|
||||
$$
|
||||
\sum_{n=0}^\infty c_n (z-z_0)^n
|
||||
$$
|
||||
|
||||
where
|
||||
|
||||
$$
|
||||
c_n = \sum_{k=0}^n a_k b_{n-k}
|
||||
$$
|
||||
|
||||
The radius of convergence of the Cauchy product is at least $\min(R_1,R_2)$.
|
||||
|
||||
## Chapter 6 Complex Integration
|
||||
|
||||
### Definition of Riemann Integral for complex functions
|
||||
|
||||
The complex integral of a complex function $\phi$ on the closed subinterval $[a,b]$ of the real line is said to be piecewise continuous if there exists a partition $a=t_0<t_1<\cdots<t_n=b$ such that $\phi$ is continuous on each open interval $(t_{i-1},t_i)$ and has a finite limit at each discontinuity point of the closed interval $[a,b]$.
|
||||
|
||||
If $\phi$ is piecewise continuous on $[a,b]$, then the complex integral of $\phi$ on $[a,b]$ is defined as
|
||||
|
||||
$$
|
||||
\int_a^b \phi(t) dt = \int_a^b \operatorname{Re}\phi(t) dt + i\int_a^b \operatorname{Im}\phi(t) dt
|
||||
$$
|
||||
|
||||
### Fundamental Theorem of Calculus
|
||||
|
||||
If $\phi$ is piecewise continuous on $[a,b]$, then
|
||||
|
||||
$$
|
||||
\int_a^b \phi'(t) dt = \phi(b)-\phi(a)
|
||||
$$
|
||||
|
||||
### Triangle inequality
|
||||
|
||||
$$
|
||||
\left|\int_a^b \phi(t) dt\right| \leq \int_a^b |\phi(t)| dt
|
||||
$$
|
||||
|
||||
### Integral on curve
|
||||
|
||||
Let $\gamma$ be a piecewise smooth curve in the complex plane.
|
||||
|
||||
The integral of a complex function $f$ on $\gamma$ is defined as
|
||||
|
||||
$$
|
||||
\int_\gamma f(z) dz = \int_a^b f(\gamma(t))\gamma'(t) dt
|
||||
$$
|
||||
|
||||
### Favorite estimate
|
||||
|
||||
Let $\gamma:[a,b]\to\mathbb{C}$ be a piecewise smooth curve, and let $f:[a,b]\to\mathbb{C}$ be a continuous complex-valued function. Let $M$ be a real number such that $|f(z)|\leq M$ for all $z\in\gamma$. Then
|
||||
|
||||
$$
|
||||
\left|\int_\gamma f(z) dz\right| \leq M\ell(\gamma)
|
||||
$$
|
||||
|
||||
where $\ell(\gamma)$ is the length of the curve $\gamma$.
|
||||
|
||||
## Chapter 7 Cauchy's Theorem
|
||||
|
||||
### Cauchy's Theorem
|
||||
|
||||
Let $\gamma$ be a closed curve in $\mathbb{C}$ and $U$ be a simply connected open subset of $\mathbb{C}$ containing $\gamma$ and its interior. Let $f$ be a holomorphic function on $U$. Then
|
||||
|
||||
$$
|
||||
\int_\gamma f(z) dz = 0
|
||||
$$
|
||||
|
||||
### Cauchy's Formula for a Circle
|
||||
|
||||
Let $C$ be a counterclockwise oriented circle and let $f$ be holomorphic function defined in an open set containing $C$ and its interior. Then for any $z$ in the interior of $C$,
|
||||
|
||||
$$
|
||||
f(z)=\frac{1}{2\pi i}\int_C \frac{f(\zeta)}{\zeta-z} d\zeta
|
||||
$$
|
||||
|
||||
### Mean Value Property
|
||||
|
||||
Let the function $f$ be holomorphic on a disk $|z-z_0|<R$. Then for any $0<r<R$, let $C_r$ denote the circle with center $z_0$ and radius $r$. Then
|
||||
|
||||
$$
|
||||
f(z_0)=\frac{1}{2\pi}\int_0^{2\pi} f(z_0+re^{i\theta}) d\theta
|
||||
$$
|
||||
|
||||
The value of the function at the center of the disk is the average of the values of the function on the boundary of the disk.
|
||||
|
||||
### Cauchy Integrals
|
||||
|
||||
Let $\gamma$ be a piecewise smooth curve in $\mathbb{C}$ and let $\phi$ be a continuous complex-valued function on $\gamma$. Then the Cauchy integral of $\phi$ on $\gamma$ is the function $f$ defined in $C\setminus\gamma$ by
|
||||
|
||||
$$
|
||||
f(z)=\int_\gamma \frac{\phi(\zeta)}{\zeta-z} d\zeta
|
||||
$$
|
||||
|
||||
Cauchy Integral Formula for circle $C_r$:
|
||||
|
||||
$$
|
||||
f(z)=\frac{1}{2\pi i}\int_{C_r} \frac{f(\zeta)}{\zeta-z} d\zeta
|
||||
$$
|
||||
|
||||
> Example:
|
||||
>
|
||||
> Evaluate $$\int_{|z|=2} \frac{z}{z-1} dz$$
|
||||
>
|
||||
> Note that if we let $f(\zeta)=\zeta$ and $z=1$ is inside the circle, then we can use Cauchy Integral Formula for circle $C_r$ to evaluate the integral.
|
||||
>
|
||||
> So we have
|
||||
>
|
||||
> $$\int_{|z|=2} \frac{z}{z-1} dz = 2\pi i f(1) = 2\pi i$$
|
||||
|
||||
General Cauchy Integral Formula for circle $C_r$:
|
||||
|
||||
$$
|
||||
f^{(n)}(z)=\frac{n!}{2\pi i}\int_{C_r} \frac{f(\zeta)}{(\zeta-z)^{n+1}} d\zeta
|
||||
$$
|
||||
|
||||
> Example:
|
||||
>
|
||||
> Evaluate $$\int_{C}\frac{\sin z}{z^{38}}dz$$
|
||||
>
|
||||
> Note that if we let $f(\zeta)=\sin \zeta$ and $z=0$ is inside the circle, then we can use General Cauchy Integral Formula for circle $C_r$ to evaluate the integral.
|
||||
>
|
||||
> So we have
|
||||
>
|
||||
> $$\int_{C}\frac{\sin z}{z^{38}}dz = \frac{2\pi i}{37!} f^{(37)}(0) = \frac{2\pi i}{37!} \sin ^{(37)}(0)$$
|
||||
>
|
||||
> Note that $\sin ^{(n)}(0)=\begin{cases} 0,& n\equiv 0 \pmod{4}\\
|
||||
1,& n\equiv 1 \pmod{4}\\
|
||||
0,& n\equiv 2 \pmod{4}\\
|
||||
-1,& n\equiv 3 \pmod{4}
|
||||
\end{cases}$
|
||||
>
|
||||
> So we have
|
||||
>
|
||||
> $$\int_{C}\frac{\sin z}{z^{38}}dz = \frac{2\pi i}{37!} \sin ^{(37)}(0) = \frac{2\pi i}{37!} \cdot 1 = \frac{2\pi i}{37!}$$
|
||||
|
||||
_Cauchy integral is a easier way to evaluate the integral._
|
||||
|
||||
### Liouville's Theorem
|
||||
|
||||
If a function $f$ is entire (holomorphic on $\mathbb{C}$) and bounded, then $f$ is constant.
|
||||
|
||||
### Finding power series of holomorphic functions
|
||||
|
||||
If $f$ is holomorphic on a disk $|z-z_0|<R$, then $f$ can be represented as a power series on the disk.
|
||||
|
||||
where $a_n=\frac{f^{(n)}(z_0)}{n!}$
|
||||
|
||||
> Example:
|
||||
>
|
||||
> If $q(z)=(z-1)(z-2)(z-3)$, find the power series of $q(z)$ centered at $z=0$.
|
||||
>
|
||||
> Note that $q(z)$ is holomorphic on $\mathbb{C}$ and $q(z)=0$ at $z=1,2,3$.
|
||||
>
|
||||
> So we can use the power series of $q(z)$ centered at $z=1$.
|
||||
>
|
||||
> To solve this, we can simply expand $q(z)=(z-1)(z-2)(z-3)$ and get $q(z)=z^3-6z^2+11z-6$.
|
||||
>
|
||||
> So we have $a_0=q(1)=-6$, $a_1=q'(1)=3z^2-12z+11=11$, $a_2=\frac{q''(1)}{2!}=\frac{6z-12}{2}=-3$, $a_3=\frac{q'''(1)}{3!}=\frac{6}{6}=1$.
|
||||
>
|
||||
> So the power series of $q(z)$ centered at $z=1$ is
|
||||
>
|
||||
> $$q(z)=-6+11(z-1)-3(z-1)^2+(z-1)^3$$
|
||||
|
||||
### Fundamental Theorem of Algebra
|
||||
|
||||
Every non-constant polynomial with complex coefficients has a root in $\mathbb{C}$.
|
||||
|
||||
Can be factored into linear factors:
|
||||
|
||||
$$
|
||||
p(z)=a_n(z-z_1)(z-z_2)\cdots(z-z_n)
|
||||
$$
|
||||
|
||||
We can treat holomorphic functions as polynomials.
|
||||
|
||||
$f$ has zero of order $m$ at $z_0$ if and only if $f(z)=(z-z_0)^m g(z)$ for some holomorphic $g(z)$ and $g(z_0)\neq 0$.
|
||||
|
||||
### Zeros of holomorphic functions
|
||||
|
||||
If $f$ is holomorphic on a disk $|z-z_0|<R$ and $f$ has a zero of order $m$ at $z_0$, then $f(z_0)=0$, $f'(z_0)=0$, $f''(z_0)=0$, $\cdots$, $f^{(m-1)}(z_0)=0$ and $f^{(m)}(z_0)\neq 0$.
|
||||
|
||||
And there exists a holomorphic function $g$ on the disk such that $f(z)=(z-z_0)^m g(z)$ and $g(z_0)\neq 0$.
|
||||
|
||||
> Example:
|
||||
>
|
||||
> Find zeros of $f(z)=\cos(z\frac{\pi}{2})$
|
||||
>
|
||||
> Note that $f(z)=0$ if and only if $z\frac{\pi}{2}=(2k+1)\frac{\pi}{2}$ for some integer $k$.
|
||||
>
|
||||
> So the zeros of $f(z)$ are $z=(2k+1)$ for some integer $k$.
|
||||
>
|
||||
> The order of the zero is $1$ since $f'(z)=-\frac{\pi}{2}\sin(z\frac{\pi}{2})$ and $f'(z)\neq 0$ for all $z=(2k+1)$.
|
||||
|
||||
If $f$ vanishes to infinite order at $z_0$ (that is, $f(z_0)=f'(z_0)=f''(z_0)=\cdots=0$), then $f(z)\equiv 0$ on the connected open set $U$ containing $z_0$.
|
||||
|
||||
### Identity Theorem
|
||||
|
||||
If $f$ and $g$ are holomorphic on a connected open set $U\subset\mathbb{C}$ and $f(z)=g(z)$ for all $z$ in a subset of $U$ that has a limit point in $U$, then $f(z)=g(z)$ for all $z\in U$.
|
||||
|
||||
Key: consider $h(z)=f(z)-g(z)$, prove $h(z)\equiv 0$ on $U$ by applying the zero of holomorphic function.
|
||||
|
||||
### Weierstrass Theorem
|
||||
|
||||
Limit of a sequence of holomorphic functions is holomorphic.
|
||||
|
||||
Let $f_n$ be a sequence of holomorphic functions on a domain $D\subset\mathbb{C}$ that converges uniformly to $f$ on every compact subset of $D$. Then $f$ is holomorphic on $D$.
|
||||
|
||||
### Maximum Modulus Principle
|
||||
|
||||
If $f$ is a non-constant holomorphic function on a domain $D\subset\mathbb{C}$, then $|f|$ does not attain a maximum value in $D$.
|
||||
|
||||
#### Corollary: Minimum Modulus Principle
|
||||
|
||||
If $f$ is a non-constant holomorphic function on a domain $D\subset\mathbb{C}$, then $\frac{1}{f}$ does not attain a minimum value in $D$.
|
||||
|
||||
### Schwarz Lemma
|
||||
|
||||
If $f$ is a holomorphic function on the unit disk $|z|<1$ and $|f(z)|\leq |z|$, then $|f'(0)|\leq 1$.
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
279
content/Math416/Exam_reviews/Math416_Final.md
Normal file
279
content/Math416/Exam_reviews/Math416_Final.md
Normal file
@@ -0,0 +1,279 @@
|
||||
# Math 416 Final Review
|
||||
|
||||
Story after Cauchy's theorem
|
||||
|
||||
## Chapter 7: Cauchy's Theorem
|
||||
|
||||
### Existence of harmonic conjugate
|
||||
|
||||
Suppose $f=u+iv$ is holomorphic on a domain $U\subset\mathbb{C}$. Then $u=\Re f$ is harmonic on $U$. That is $\Delta u=\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}=0$.
|
||||
|
||||
Moreover, there exists $g\in O(U)$ such that $g$ is unique up to an additive imaginary constant.
|
||||
|
||||
> Example:
|
||||
>
|
||||
> Find a harmonic conjugate of $u(x,y)=\log|\frac{z}{z-1}|$
|
||||
>
|
||||
> Note that $\log(\frac{z}{z-1})=\log \left|\frac{z}{z-1}\right|+i(\arg(z)-\arg(z-1))$ is harmonic on $\mathbb{C}\setminus\{1\}$.
|
||||
>
|
||||
> So the harmonic conjugate of $u(x,y)=\log|\frac{z}{z-1}|$ is $v(x,y)=\arg(z)-\arg(z-1)+C$ where $C$ is a constant.
|
||||
>
|
||||
> Note that the harmonic conjugate may exist locally but not globally. (e.g. $u(x,y)=\log|z(z-1)|$ has a local harmonic conjugate $i(\arg(z)+\arg(z-1)+C)$ but this is not a well defined function since $\arg(z)+\arg(z-1)$ is not single-valued.)
|
||||
|
||||
### Corollary for harmonic functions
|
||||
|
||||
#### Theorem 7.19
|
||||
|
||||
Harmonic function are infinitely differentiable.
|
||||
|
||||
#### Theorem 7.20
|
||||
|
||||
Mean value property of harmonic functions.
|
||||
|
||||
Let $u$ be harmonic on an open set of $\Omega$, then
|
||||
|
||||
$$u(z_0)=\frac{1}{2\pi}\int_0^{2\pi} u(z_0+re^{i\theta}) d\theta$$
|
||||
|
||||
for any $z_0\in\Omega$ and $r>0$ such that $D(z_0,r)\subset\Omega$.
|
||||
|
||||
#### Theorem 7.21
|
||||
|
||||
Identity theorem for harmonic functions.
|
||||
|
||||
Let $u$ be harmonic on a domain $\Omega$. If $u=0$ on some open set $G\subset\Omega$, then $u\equiv 0$ on $\Omega$.
|
||||
|
||||
#### Theorem 7.22
|
||||
|
||||
Maximum principle for harmonic functions.
|
||||
|
||||
Let $u$ be a non-constant real-valued harmonic function on a domain $\Omega$. Then $|u|$ does not attain a maximum value in $\Omega$.
|
||||
|
||||
## Chapter 8: Laurent Series and Isolated Singularities
|
||||
|
||||
### Laurent Series
|
||||
|
||||
Laurent series is a generalization of Taylor series.
|
||||
|
||||
Laurent series is a power series of the form
|
||||
|
||||
$$f(z)=\sum_{n=-\infty}^{\infty} a_n (z-z_0)^n$$
|
||||
|
||||
where
|
||||
|
||||
$$
|
||||
a_k=\frac{1}{2\pi i}\int_{C_r}\frac{f(z)}{(z-z_0)^{k+1}}dz
|
||||
$$
|
||||
|
||||
The series converges on an annulus $R_1<|z-z_0|<R_2$.
|
||||
|
||||
where $R_1=\limsup_{n\to\infty} |a_{-n}|^{1/n}$ and $R_2=\frac{1}{\limsup_{n\to\infty} |a_n|^{1/n}}$.
|
||||
|
||||
### Cauchy's Formula for an Annulus
|
||||
|
||||
Let $f$ be holomorphic on an annulus $R_1<r_1<|z-z_0|<r_2<R_2$. And $w\in A(z_0;R_1,R_2)$. Find the Annulus $w\in A(z_0;r_1,r_2)$
|
||||
|
||||
Then
|
||||
|
||||
$$
|
||||
f(w)=\frac{1}{2\pi i}\int_{C_{r_1}}\frac{f(z)}{z-w}dz-\frac{1}{2\pi i}\int_{C_{r_2}}\frac{f(z)}{z-w}dz
|
||||
$$
|
||||
|
||||
### Isolated singularities
|
||||
|
||||
Let $f$ be holomorphic on $0<|z-z_0|<R$ (The punctured disk of radius $R$ centered at $z_0$). If there exists a Laurent series of $f$ convergent on $0<|z-z_0|<R$, then $z_0$ is called an isolated singularity of $f$.
|
||||
|
||||
The series $f(z)=\sum_{n=-\infty}^{-1}a_n(z-z_0)^n$ is called the principle part of Laurent series of $f$ at $z_0$.
|
||||
|
||||
#### Removable singularities
|
||||
|
||||
If the principle part of Laurent series of $f$ at $z_0$ is zero, then $z_0$ is called a removable singularity of $f$.
|
||||
|
||||
Criterion for a removable singularity:
|
||||
|
||||
If $f$ is bounded on $0<|z-z_0|<R$, then $z_0$ is a removable singularity.
|
||||
|
||||
> Example:
|
||||
>
|
||||
> $f(z)=\frac{1}{e^z-1}$ has a removable singularity at $z=0$.
|
||||
>
|
||||
> The Laurent series of $f$ at $z=0$ is
|
||||
>
|
||||
> $$f(z)=\frac{1}{z}+\sum_{n=0}^{\infty}\frac{z^n}{n!}$$
|
||||
>
|
||||
> The principle part is zero, so $z=0$ is a removable singularity.
|
||||
|
||||
#### Poles
|
||||
|
||||
If the principle part of Laurent series of $f$ at $z_0$ is a finite sum, then $z_0$ is called a pole of $f$.
|
||||
|
||||
Criterion for a pole:
|
||||
|
||||
If $f$ has an isolated singularity at $z_0$, and $\lim_{z\to z_0}|f(z)|=\infty$, then $z_0$ is a pole of $f$.
|
||||
|
||||
> Example:
|
||||
>
|
||||
> $f(z)=\frac{1}{z^2}$ has a pole at $z=0$.
|
||||
>
|
||||
> The Laurent series of $f$ at $z=0$ is
|
||||
>
|
||||
> $$f(z)=\frac{1}{z^2}$$
|
||||
>
|
||||
> The principle part is $\frac{1}{z^2}$, so $z=0$ is a pole.
|
||||
|
||||
#### Essential singularities
|
||||
|
||||
If $f$ has an isolated singularity at $z_0$, and it is neither a removable singularity nor a pole, then $z_0$ is called an essential singularity of $f$.
|
||||
|
||||
"Criterion" for an essential singularity:
|
||||
|
||||
If the principle part of Laurent series of $f$ at $z_0$ has infinitely many non-zero coefficients corresponding to negative powers of $z-z_0$, then $z_0$ is called an essential singularity of $f$.
|
||||
|
||||
> Example:
|
||||
>
|
||||
> $f(z)=\sin(\frac{1}{z})$ has an essential singularity at $z=0$.
|
||||
>
|
||||
> The Laurent series of $f$ at $z=0$ is
|
||||
>
|
||||
> $$f(z)=\frac{1}{z}-\frac{1}{6z^3}+\frac{1}{120z^5}-\cdots$$
|
||||
>
|
||||
> Since there are infinitely many non-zero coefficients corresponding to negative powers of $z$, $z=0$ is an essential singularity.
|
||||
|
||||
#### Singularities at infinity
|
||||
|
||||
We say $f$ has a singularity (removable, pole, or essential) at infinity if $f(1/z)$ has an isolated singularity (removable, pole, or essential) at $z=0$.
|
||||
|
||||
> Example:
|
||||
>
|
||||
> $f(z)=\frac{z^4}{(z-1)(z-3)}$ has a pole of order 2 at infinity.
|
||||
>
|
||||
> Plug in $z=1/w$, we get $f(1/w)=\frac{1}{w^2}\frac{1}{(1/w-1)(1/w-3)}=\frac{1}{w^2}\frac{1}{(1-w)(1-3w)}=\frac{1}{w^2}(1+O(w))$, which has pole of order 2 at $w=0$.
|
||||
|
||||
#### Residue
|
||||
|
||||
The residue of $f$ at $z_0$ is the coefficient of the term $(z-z_0)^{-1}$ in the Laurent series of $f$ at $z_0$.
|
||||
|
||||
> Example:
|
||||
>
|
||||
> $f(z)=\frac{1}{z^2}$ has a residue of 0 at $z=0$.
|
||||
>
|
||||
> $f(z)=\frac{z^3}{z-1}$ has a residue of 1 at $z=1$.
|
||||
|
||||
Residue for pole with higher order:
|
||||
|
||||
If $f$ has a pole of order $n$ at $z_0$, then the residue of $f$ at $z_0$ is
|
||||
|
||||
$$
|
||||
\operatorname{res}(f,z_0)=\frac{1}{(n-1)!}\lim_{z\to z_0}\frac{d^{n-1}}{dz^{n-1}}((z-z_0)^nf(z))
|
||||
$$
|
||||
|
||||
## Chapter 9: Generalized Cauchy's Theorem
|
||||
|
||||
### Winding number
|
||||
|
||||
The winding number of a closed curve $C$ with respect to a point $z_0$ is
|
||||
|
||||
$$
|
||||
\operatorname{ind}_C(z_0)=\frac{1}{2\pi i}\int_C\frac{1}{z-z_0}dz
|
||||
$$
|
||||
|
||||
_the winding number is the number of times the curve $C$ winds around the point $z_0$ counterclockwise. (May be negative)_
|
||||
|
||||
### Contour integrals
|
||||
|
||||
A contour is a piecewise continuous curve $\gamma:[a,b]\to\mathbb{C}$ with integer coefficients.
|
||||
|
||||
$$
|
||||
\Gamma=\sum_{i=1}^p n_j\gamma_j
|
||||
$$
|
||||
|
||||
where $\gamma_j:[a_j,b_j]\to\mathbb{C}$ is continuous closed curve and $n_j\in\mathbb{Z}$.
|
||||
|
||||
### Interior of a curve
|
||||
|
||||
The interior of a curve is the set of points $z\in\mathbb{C}$ such that $\operatorname{ind}_{\Gamma}(z)\neq 0$.
|
||||
|
||||
The winding number of contour $\Gamma$ is the sum of the winding numbers of the components of $\Gamma$ around $z_0$.
|
||||
|
||||
$$
|
||||
\operatorname{ind}_{\Gamma}(z)=\sum_{j=1}^p n_j\operatorname{ind}_{\gamma_j}(z)
|
||||
$$
|
||||
|
||||
### Separation lemma
|
||||
|
||||
Let $\Omega\subseteq\mathbb{C}$ be a domain and $K\subset \Omega$ be compact. Then there exists a simple contour $\Gamma\subset \Omega\setminus K$ such that $K\subset \operatorname{int}_{\Gamma}(\Gamma)\subset \Omega$.
|
||||
|
||||
Key idea:
|
||||
|
||||
Let $0<\delta<d(K,\partial \Omega)$, then draw the grid lines and trace the contour.
|
||||
|
||||
### Residue theorem
|
||||
|
||||
Let $\Omega$ be a domain, $\Gamma$ be a contour such that $\Gamma\cap \operatorname{int}(\Gamma)\subset \Omega$. Let $f$ be holomorphic on $\Omega\setminus \{z_1,z_2,\cdots,z_p\}$ and $z_1,z_2,\cdots,z_p$ are finitely many points in $\Omega$, where $z_1,z_2,\cdots,z_p\notin \Gamma$. Then
|
||||
|
||||
$$
|
||||
\int_{\Gamma}f(z)dz=2\pi i\sum_{j=1}^p \operatorname{res}(f,z_j)
|
||||
$$
|
||||
|
||||
Key: Prove by circle around each singularity and connect them using two way paths.
|
||||
|
||||
|
||||
### Homotopy*
|
||||
|
||||
Suppose $\gamma_0, \gamma_1$ are two curves from
|
||||
$[0,1]$ to $\Omega$ with same end points $P,Q$.
|
||||
|
||||
A homotopy is a continuous function of curves $\gamma_t, 0\leq t\leq 1$, deforming $\gamma_0$ to $\gamma_1$, keeping the end points fixed.
|
||||
|
||||
Formally, if $H:[0,1]\times [0,1]\to \Omega$ is a continuous function satsifying
|
||||
|
||||
1. $H(s,0)=\gamma_0(s)$, $\forall s\in [0,1]$
|
||||
2. $H(s,1)=\gamma_1(s)$, $\forall s\in [0,1]$
|
||||
3. $H(0,t)=P$, $\forall t\in [0,1]$
|
||||
4. $H(1,t)=Q$, $\forall t\in [0,1]$
|
||||
|
||||
Then we say $H$ is a homotopy between $\gamma_0$ and $\gamma_1$. (If $\gamma_0$ and $\gamma_1$ are closed curves, $Q=P$)
|
||||
|
||||
#### Lemma 9.12 Technical Lemma
|
||||
|
||||
Let $\phi:[0,1]\times [0,1]\to \mathbb{C}\setminus \{0\}$ is continuous. Then there exists a continuous map $\psi:[0,1]\times [0,1]\to \mathbb{C}$ such that $e^\phi=\psi$. Moreover, $\psi$ is unique up to an additive constant in $2\pi i\mathbb{Z}$.
|
||||
|
||||
|
||||
### General approach to evaluate definite integrals
|
||||
|
||||
Choose a contour so that one side is the desired integral.
|
||||
|
||||
Handle the other sides using:
|
||||
|
||||
- Symmetry
|
||||
- Favorite estimate
|
||||
- Bound function by another function whose integral goes to 0
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
167
content/Math416/Math416_L1.md
Normal file
167
content/Math416/Math416_L1.md
Normal file
@@ -0,0 +1,167 @@
|
||||
# Math416 Lecture 1
|
||||
|
||||
## Chapter 1: Complex Numbers
|
||||
|
||||
### Preface
|
||||
|
||||
I don't know what happened to the first class. I will try to rewrite the notes from my classmates here.
|
||||
|
||||
#### Rigidity
|
||||
|
||||
Integral is preserved for any closed path.
|
||||
|
||||
#### Group
|
||||
|
||||
A set with a multiplication operator. $(G,\cdot)$ such that: for all $a,b,c\in G$:
|
||||
|
||||
1. $a\cdot b\in G$
|
||||
2. $a\cdot (b\cdot c)=(a\cdot b)\cdot c$
|
||||
3. $a\cdot 1=a$
|
||||
4. $a\cdot a^{-1}=1$
|
||||
|
||||
#### Ring
|
||||
|
||||
A group with two operations: addition and multiplication. $(R,+,\cdot)$ such that: for all $a,b,c\in R$:
|
||||
|
||||
1. Commutative under addition: $a+b=b+a$
|
||||
2. Associative under multiplication: $(a\cdot b)\cdot c=a\cdot (b\cdot c)$
|
||||
3. Distributive under addition: $a\cdot (b+c)=a\cdot b+a\cdot c$
|
||||
|
||||
Example:
|
||||
|
||||
$\{a+\sqrt{6}b\mid a,b\in \mathbb{Z}\}$ is a ring
|
||||
|
||||
#### Definition 1.1
|
||||
|
||||
the complex number is defined to be the set $\mathbb{C}$ of ordered pairs $(x,y)$ with $x,y\in \mathbb{R}$ and the operations:
|
||||
|
||||
- Addition: $(x_1,y_1)+(x_2,y_2)=(x_1+x_2,y_1+y_2)$
|
||||
- Multiplication: $(x_1,y_1)(x_2,y_2)=(x_1x_2-y_1y_2,x_1y_2+x_2y_1)$
|
||||
|
||||
#### Axiom 1.2
|
||||
|
||||
The operation of addition and multiplication on $\mathbb{C}$ satisfies the following conditions (The field axioms):
|
||||
|
||||
For all $z_1,z_2,z_3\in \mathbb{C}$:
|
||||
|
||||
1. $z_1+z_2=z_2+z_1$ (commutative law of addition)
|
||||
2. $(z_1+z_2)+z_3=z_1+(z_2+z_3)$ (associative law of addition)
|
||||
3. $z_1\cdot z_2=z_2\cdot z_1$ (commutative law of multiplication)
|
||||
4. $(z_1\cdot z_2)\cdot z_3=z_1\cdot (z_2\cdot z_3)$ (associative law of multiplication)
|
||||
5. $z_1\cdot (z_2+z_3)=z_1\cdot z_2+z_1\cdot z_3$ (distributive law)
|
||||
6. There exists an additive identity element $0=(0,0)$ such that $z+0=z$ for all $z\in \mathbb{C}$.
|
||||
7. There exists a multiplicative identity element $1=(1,0)$ such that $z\cdot 1=z$ for all $z\in \mathbb{C}$.
|
||||
8. There exists an additive inverse $-z=(-x,-y)$ for all $z=(x,y)\in \mathbb{C}$ such that $z+(-z)=0$.
|
||||
9. There exists a multiplicative inverse $z^{-1}=\left(\frac{x}{x^2+y^2},-\frac{y}{x^2+y^2}\right)$ for all $z=(x,y)\in \mathbb{C}$ such that $z\cdot z^{-1}=1$.
|
||||
|
||||
$$
|
||||
(a,b)^{-1}=\left(\frac{a}{a^2+b^2},-\frac{b}{a^2+b^2}\right)
|
||||
$$
|
||||
|
||||
#### Embedding of $\mathbb{R}$ in $\mathbb{C}$ 1.3
|
||||
|
||||
Let $z=x+iy\in \mathbb{C}$ where $a,b\in \mathbb{R}$.
|
||||
|
||||
- $x$ is called the real part of $z$ and
|
||||
- $y$ is called the imaginary part of $z$.
|
||||
- $|z|=\sqrt{x^2+y^2}$ is called the absolute value or modulus of $z$.
|
||||
- The angle between the positive real axis and the line segment from $0$ to $z$ is called the argument of $z$ and is denoted by $\theta$ (argument of $z$).
|
||||
- $\overline{z}=x-iy$ is called the conjugate of $z$. ($z\cdot \overline{z}=|z|^2$)
|
||||
- $z_1+z_2=(x_1+x_2,y_1+y_2)$ (vector addition)
|
||||
|
||||
#### Lemma 1.3
|
||||
|
||||
$$
|
||||
|z_1z_2|=|z_1||z_2|
|
||||
$$
|
||||
|
||||
#### Theorem 1.5 (Triangle Inequality)
|
||||
|
||||
$$
|
||||
|z_1+z_2|\leq |z_1|+|z_2|
|
||||
$$
|
||||
|
||||
<details>
|
||||
<summary>Proof</summary>
|
||||
|
||||
Geometrically, the triangle inequality states that the sum of the lengths of any two sides of a triangle is greater than the length of the third side.
|
||||
|
||||
Algebraically,
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
(|z_1+z_2|)^2-|z_1+z_2|^2&=|z_1+z_2|^2-2|z_1+z_2|-(z_1+z_2)(\overline{z_1}+\overline{z_2})\\
|
||||
&=|z_1|^2+|z_2|^2+2|z_1||z_2|-(|z_1|^2+|z_2|^2+\overline{z_1}z_2+\overline{z_2}z_1)\\
|
||||
&=2|z_1||z_2|-2Re(\overline{z_1}z_2)\\
|
||||
&=2(|z_1||z_2|-|z_1z_2|)\\
|
||||
&\geq 0
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
</details>
|
||||
|
||||
Suppose $2(|z_1||z_2|-|z_1z_2|)=0$, and $\overline{z_1}z_2$ is a non-negative real number $c$, then $|z_1||z_2|=|z_1z_2|$...
|
||||
|
||||
> What is the use of this?
|
||||
|
||||
Let $\arg(z)=\theta\in (-\pi,\pi]$, $z_1=r_1(\cos\theta_1+i\sin\theta_1)$, $z_2=r_2(\cos\theta_2+i\sin\theta_2)$.
|
||||
|
||||
$$
|
||||
z_1z_2=r_1r_2[cos(\theta_1+\theta_2)+i\sin(\theta_1+\theta_2)]
|
||||
$$
|
||||
|
||||
(Define $\text{cis}(\theta)=\cos\theta+i\sin\theta$)
|
||||
|
||||
#### Theorem 1.6 Parallelogram Equality
|
||||
|
||||
The sum of the squares of the lengths of the diagonals of a parallelogram equals the sum of the squares of the lengths of the sides.
|
||||
|
||||
<details>
|
||||
<summary>Proof</summary>
|
||||
|
||||
Let $z_1,z_2$ be two complex numbers representing the two sides of the parallelogram, then the sum of the squares of the lengths of the diagonals of the parallelogram is $|z_1-z_2|^2+|z_1+z_2|^2$, and the sum of the squares of the lengths of the sides is $2|z_1|^2+2|z_2|^2$.
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
|z_1-z_2|^2+|z_1+z_2|^2 &= (x_1-x_2)^2+(y_1-y_2)^2+(x_1+x_2)^2+(y_1+y_2)^2 \\
|
||||
&= 2x_1^2+2x_2^2+2y_1^2+2y_2^2 \\
|
||||
&= 2(|z_1|^2+|z_2|^2)
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
</details>
|
||||
|
||||
#### Definition 1.9
|
||||
|
||||
The argument of a complex number $z$ is defined as the angle $\theta$ between the positive real axis and the ray from the origin through $z$.
|
||||
|
||||
### De Moivre's Formula
|
||||
|
||||
#### Theorem 1.10 De Moivre's Formula
|
||||
|
||||
Let $z=r\text{cis}(\theta)$, then
|
||||
|
||||
$\forall n\in \mathbb{Z}$:
|
||||
|
||||
$$
|
||||
z^n=r^n\text{cis}(n\theta)
|
||||
$$
|
||||
|
||||
<details>
|
||||
<summary>Proof</summary>
|
||||
|
||||
For $n=0$, $z^0=1=1\text{cis}(0)$.
|
||||
|
||||
For $n=-1$, $z^{-1}=\frac{1}{z}=\frac{1}{r}\text{cis}(-\theta)=\frac{1}{r}(cos(-\theta)+i\sin(-\theta))$.
|
||||
|
||||
</details>
|
||||
|
||||
Application:
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
(\text{cis}(\theta))^3&=\text{cis}(3\theta)\\
|
||||
&=\cos(3\theta)+i\sin(3\theta)\\
|
||||
&=cos^3(\theta)-3cos(\theta)sin^2(\theta)+i(3cos^2(\theta)sin(\theta)-sin^3(\theta))\\
|
||||
\end{aligned}
|
||||
$$
|
||||
15
content/Math416/index.md
Normal file
15
content/Math416/index.md
Normal file
@@ -0,0 +1,15 @@
|
||||
# Math 416
|
||||
|
||||
Complex variables. This is a course that explores the theory and applications of complex analysis as extension of Real analysis.
|
||||
|
||||
The course is taught by Professor.
|
||||
John E. McCarthy <mailto:mccarthy@math.wustl.edu>
|
||||
|
||||
Some interesting fact is that he cover the lecture terribly quick. At least for me. I need to preview and review the lecture after the course ended. The only thing that I can take granted of is that many theorem in real analysis still holds in the complex. By elegant definition designing, we build a wonderful math with complex variables and extended theorems, which is more helpful when solving questions that cannot be solved in real numbers.
|
||||
|
||||
McCarthy like to write $\zeta$ for $z$ and his writing for $\zeta$ is almost identical with $z$, I decided to use the traditional notation system I've learned to avoid confusion in my notes.
|
||||
|
||||
I will use $B_r(z_0)$ to denote a disk in $\mathbb{C}$ such that $B_r(z_0) = \{ z \in \mathbb{C} : |z - z_0| < r \}$. In the lecture, he use $\mathbb{D}(z_0,r)$ to denote the disk centered at $z_0$ with radius $r$. If $\mathbb{D}$ is used, then it means the unit disk $\mathbb{D}=\{z:|z|<1\}$. You may also see the closure of the disk $\overline{B_r(z_0)}$ and $\overline{\mathbb{D}}$, these are equivalent definition.
|
||||
|
||||
I will use $z$ to replace the strange notation of $\zeta$. If that makes sense.
|
||||
|
||||
Reference in New Issue
Block a user