Update prebuild.sh

Another issue solved by AI?

.github/workflows/sync-from-gitea-deploy.yml

@@ -0,0 +1,73 @@
+name: Sync from Gitea (distribute→distribute, keep workflow)
+
+on:
+  schedule:
+    # 2 times per day (UTC): 7:00, 11:00
+    - cron: '0 7,11 * * *'
+  workflow_dispatch: {}
+
+permissions:
+  contents: write  # allow pushing with GITHUB_TOKEN
+
+jobs:
+  mirror:
+    runs-on: ubuntu-latest
+
+    steps:
+      - name: Check out GitHub repo
+        uses: actions/checkout@v4
+        with:
+          fetch-depth: 0
+
+      - name: Fetch from Gitea
+        env:
+          GITEA_URL: ${{ secrets.GITEA_URL }}
+          GITEA_USER: ${{ secrets.GITEA_USERNAME }}
+          GITEA_TOKEN: ${{ secrets.GITEA_TOKEN }}
+        run: |
+          # Build authenticated Gitea URL: https://USER:TOKEN@...
+          AUTH_URL="${GITEA_URL/https:\/\//https:\/\/$GITEA_USER:$GITEA_TOKEN@}"
+
+          git remote add gitea "$AUTH_URL"
+          git fetch gitea --prune
+
+      - name: Update distribute from gitea/distribute, keep workflow, and force-push
+        env:
+          GH_TOKEN: ${{ secrets.GITHUB_TOKEN }}
+          GH_REPO: ${{ github.repository }}
+        run: |
+          # Configure identity for commits made by this workflow
+          git config user.name "github-actions[bot]"
+          git config user.email "github-actions[bot]@users.noreply.github.com"
+
+          # Authenticated push URL for GitHub
+          git remote set-url origin "https://x-access-token:${GH_TOKEN}@github.com/${GH_REPO}.git"
+
+          WF_PATH=".github/workflows/sync-from-gitea.yml"
+
+          # If the workflow exists in the current checkout, save a copy
+          if [ -f "$WF_PATH" ]; then
+            mkdir -p /tmp/gh-workflows
+            cp "$WF_PATH" /tmp/gh-workflows/
+          fi
+
+          # Reset local 'distribute' to exactly match gitea/distribute
+          if git show-ref --verify --quiet refs/remotes/gitea/distribute; then
+            git checkout -B distribute gitea/distribute
+          else
+            echo "No gitea/distribute found, nothing to sync."
+            exit 0
+          fi
+
+          # Restore the workflow into the new HEAD and commit if needed
+          if [ -f "/tmp/gh-workflows/sync-from-gitea.yml" ]; then
+            mkdir -p .github/workflows
+            cp /tmp/gh-workflows/sync-from-gitea.yml "$WF_PATH"
+            git add "$WF_PATH"
+            if ! git diff --cached --quiet; then
+              git commit -m "Inject GitHub sync workflow"
+            fi
+          fi
+
+          # Force-push distribute so GitHub mirrors Gitea + workflow
+          git push origin distribute --force

.github/workflows/sync-from-gitea.yml

@@ -0,0 +1,73 @@
+name: Sync from Gitea (main→main, keep workflow)
+
+on:
+  schedule:
+    # 2 times per day (UTC): 7:00, 11:00
+    - cron: '0 7,11 * * *'
+  workflow_dispatch: {}
+
+permissions:
+  contents: write  # allow pushing with GITHUB_TOKEN
+
+jobs:
+  mirror:
+    runs-on: ubuntu-latest
+
+    steps:
+      - name: Check out GitHub repo
+        uses: actions/checkout@v4
+        with:
+          fetch-depth: 0
+
+      - name: Fetch from Gitea
+        env:
+          GITEA_URL: ${{ secrets.GITEA_URL }}
+          GITEA_USER: ${{ secrets.GITEA_USERNAME }}
+          GITEA_TOKEN: ${{ secrets.GITEA_TOKEN }}
+        run: |
+          # Build authenticated Gitea URL: https://USER:TOKEN@...
+          AUTH_URL="${GITEA_URL/https:\/\//https:\/\/$GITEA_USER:$GITEA_TOKEN@}"
+
+          git remote add gitea "$AUTH_URL"
+          git fetch gitea --prune
+
+      - name: Update main from gitea/main, keep workflow, and force-push
+        env:
+          GH_TOKEN: ${{ secrets.GITHUB_TOKEN }}
+          GH_REPO: ${{ github.repository }}
+        run: |
+          # Configure identity for commits made by this workflow
+          git config user.name "github-actions[bot]"
+          git config user.email "github-actions[bot]@users.noreply.github.com"
+
+          # Authenticated push URL for GitHub
+          git remote set-url origin "https://x-access-token:${GH_TOKEN}@github.com/${GH_REPO}.git"
+
+          WF_PATH=".github/workflows/sync-from-gitea.yml"
+
+          # If the workflow exists in the current checkout, save a copy
+          if [ -f "$WF_PATH" ]; then
+            mkdir -p /tmp/gh-workflows
+            cp "$WF_PATH" /tmp/gh-workflows/
+          fi
+
+          # Reset local 'main' to exactly match gitea/main
+          if git show-ref --verify --quiet refs/remotes/gitea/main; then
+            git checkout -B main gitea/main
+          else
+            echo "No gitea/main found, nothing to sync."
+            exit 0
+          fi
+
+          # Restore the workflow into the new HEAD and commit if needed
+          if [ -f "/tmp/gh-workflows/sync-from-gitea.yml" ]; then
+            mkdir -p .github/workflows
+            cp /tmp/gh-workflows/sync-from-gitea.yml "$WF_PATH"
+            git add "$WF_PATH"
+            if ! git diff --cached --quiet; then
+              git commit -m "Inject GitHub sync workflow"
+            fi
+          fi
+
+          # Force-push main so GitHub mirrors Gitea + workflow
+          git push origin main --force

.gitignore

@@ -143,6 +143,7 @@ analyze/
 
 # pagefind postbuild
 public/_pagefind/
+public/sitemap.xml
 
 # npm package lock file for different platforms
 package-lock.json

Dockerfile

@@ -1,7 +1,7 @@
 # Source: https://github.com/vercel/next.js/blob/canary/examples/with-docker-multi-env/docker/production/Dockerfile
 # syntax=docker.io/docker/dockerfile:1
 
-FROM node:18-alpine AS base
+FROM node:20-alpine AS base
 
 ENV NODE_OPTIONS="--max-old-space-size=8192"
 

README.md

@@ -28,3 +28,11 @@ Considering the memory usage for this project, it is better to deploy it as sepa
 ```bash
 docker-compose up -d -f docker/docker-compose.yaml
 ```
+
+### Snippets
+
+Update dependencies
+
+```bash
+npx npm-check-updates -u
+```

app/layout.tsx

@@ -1,12 +1,13 @@
 /* eslint-env node */
-import { Footer, Layout, Navbar } from 'nextra-theme-docs'
-import { Banner, Head } from 'nextra/components'
+import { Footer, Layout} from 'nextra-theme-docs'
+import { Head } from 'nextra/components'
 import { getPageMap } from 'nextra/page-map'
 import 'nextra-theme-docs/style.css'
 import { SpeedInsights } from "@vercel/speed-insights/next"
 import { Analytics } from "@vercel/analytics/react"
 import 'katex/dist/katex.min.css'
 import AlgoliaSearch from '../components/docsearch'
+import { Navbar } from '../components/navbar'
 
 export const metadata = {
   metadataBase: new URL('https://notenextra.trance-0.com'),
@@ -31,11 +32,13 @@ export const metadata = {
 }
 
 export default async function RootLayout({ children }) {
+  const pageMap = await getPageMap();
   const navbar = (
     <Navbar
+      pageMap={pageMap}
       logo={
         <>
-          <svg width="32" height="32" viewBox="0 0 16 16">
+          <svg xmlns="http://www.w3.org/2000/svg" width="32" height="32" fill="currentColor" className="bi bi-braces-asterisk" viewBox="0 0 16 16">
             <path fillRule="evenodd" d="M1.114 8.063V7.9c1.005-.102 1.497-.615 1.497-1.6V4.503c0-1.094.39-1.538 1.354-1.538h.273V2h-.376C2.25 2 1.49 2.759 1.49 4.352v1.524c0 1.094-.376 1.456-1.49 1.456v1.299c1.114 0 1.49.362 1.49 1.456v1.524c0 1.593.759 2.352 2.372 2.352h.376v-.964h-.273c-.964 0-1.354-.444-1.354-1.538V9.663c0-.984-.492-1.497-1.497-1.6M14.886 7.9v.164c-1.005.103-1.497.616-1.497 1.6v1.798c0 1.094-.39 1.538-1.354 1.538h-.273v.964h.376c1.613 0 2.372-.759 2.372-2.352v-1.524c0-1.094.376-1.456 1.49-1.456v-1.3c-1.114 0-1.49-.362-1.49-1.456V4.352C14.51 2.759 13.75 2 12.138 2h-.376v.964h.273c.964 0 1.354.444 1.354 1.538V6.3c0 .984.492 1.497 1.497 1.6M7.5 11.5V9.207l-1.621 1.621-.707-.707L6.792 8.5H4.5v-1h2.293L5.172 5.879l.707-.707L7.5 6.792V4.5h1v2.293l1.621-1.621.707.707L9.208 7.5H11.5v1H9.207l1.621 1.621-.707.707L8.5 9.208V11.5z"/>
           </svg>
           <span style={{ marginLeft: '.4em', fontWeight: 800 }}>
@@ -46,7 +49,6 @@ export default async function RootLayout({ children }) {
       projectLink="https://github.com/Trance-0/NoteNextra"
     />
   )
-  const pageMap = await getPageMap()
   return (
     <html lang="en" dir="ltr" suppressHydrationWarning>
       <Head color={{
@@ -81,8 +83,8 @@ export default async function RootLayout({ children }) {
           docsRepositoryBase="https://github.com/Trance-0/NoteNextra/tree/main"
           sidebar={{ defaultMenuCollapseLevel: 1 }}
           pageMap={pageMap}
-          // TODO: fix algolia search
-          // search={<AlgoliaSearch />}
+          // TODO: fix local search with distributed search index over containers
+          search={<AlgoliaSearch/>}
         >
           {children}
           {/* SpeedInsights in vercel */}

components/docsearch.tsx

@@ -2,15 +2,36 @@
 // sample code from https://docsearch.algolia.com/docs/docsearch
 
 import { DocSearch } from '@docsearch/react';
+import {useTheme} from 'next-themes';
 
 import '@docsearch/css';
 
-function AlgoliaSearch() {
+function AlgoliaSearch () {
+  const {theme, systemTheme} = useTheme();
+  const darkMode = theme === 'dark' || (theme === 'system' && systemTheme === 'dark');
+  // console.log("darkMode", darkMode);
   return (
     <DocSearch
       appId={process.env.NEXT_SEARCH_ALGOLIA_APP_ID || 'NKGLZZZUBC'}
       indexName={process.env.NEXT_SEARCH_ALGOLIA_INDEX_NAME || 'notenextra_trance_0'}
       apiKey={process.env.NEXT_SEARCH_ALGOLIA_API_KEY || '727b389a61e862e590dfab9ce9df31a2'}
+      theme={darkMode===false ? 'light' : 'dark'}
+      // this is the first time that AI is solving some problem that I have no idea how to solve
+      // BEGIN OF CODE GENERATED BY AI
+      transformItems={(items) =>
+        // DocSearch lets you sanitize results before render. Filter out hits that don’t have a URL and give lvl0 a safe fallback.
+        items
+          .filter((i) => typeof i.url === 'string' && i.url) // drop records with null/empty url
+          .map((i) => ({
+            ...i,
+            hierarchy: {
+              ...i.hierarchy,
+              // ensure strings for all places DocSearch prints text
+              lvl0: i.hierarchy?.lvl0 ?? i.hierarchy?.lvl1 ?? 'Documentation',
+            },
+          }))
+      }
+      // END OF CODE GENERATED BY AI
     />
   );
 }

components/navbar.client.tsx

@@ -0,0 +1,187 @@
+'use client'
+
+import {
+  MenuItem as _MenuItem,
+  Menu,
+  MenuButton,
+  MenuItems
+} from '@headlessui/react'
+import cn from 'clsx'
+import { Anchor, Button } from 'nextra/components'
+import { useFSRoute } from 'nextra/hooks'
+import { ArrowRightIcon, MenuIcon } from 'nextra/icons'
+import type { MenuItem } from 'nextra/normalize-pages'
+import type { FC, ReactNode } from 'react'
+import { setMenu, useConfig, useMenu, useThemeConfig } from 'nextra-theme-docs'
+import { usePathname } from 'next/navigation'
+import { normalizePages } from 'nextra/normalize-pages'
+import { PageMapItem } from 'nextra'
+
+const classes = {
+  link: cn(
+    'x:text-sm x:contrast-more:text-gray-700 x:contrast-more:dark:text-gray-100 x:whitespace-nowrap',
+    'x:text-gray-600 x:hover:text-black x:dark:text-gray-400 x:dark:hover:text-gray-200',
+    'x:ring-inset x:transition-colors'
+  )
+}
+
+const NavbarMenu: FC<{
+  menu: MenuItem
+  children: ReactNode
+}> = ({ menu, children }) => {
+  const routes = Object.fromEntries(
+    (menu.children || []).map(route => [route.name, route])
+  )
+  return (
+    <Menu>
+      <MenuButton
+        className={({ focus }) =>
+          cn(
+            classes.link,
+            'x:items-center x:flex x:gap-1.5 x:cursor-pointer',
+            focus && 'x:nextra-focus'
+          )
+        }
+      >
+        {children}
+        <ArrowRightIcon
+          height="14"
+          className="x:*:origin-center x:*:transition-transform x:*:rotate-90"
+        />
+      </MenuButton>
+      <MenuItems
+        transition
+        className={cn(
+          'x:focus-visible:nextra-focus',
+          'nextra-scrollbar x:motion-reduce:transition-none',
+          // From https://headlessui.com/react/menu#adding-transitions
+          'x:origin-top x:transition x:duration-200 x:ease-out x:data-closed:scale-95 x:data-closed:opacity-0',
+          'x:border x:border-black/5 x:dark:border-white/20',
+          'x:z-30 x:rounded-md x:py-1 x:text-sm x:shadow-lg',
+          'x:backdrop-blur-md x:bg-nextra-bg/70',
+          // headlessui adds max-height as style, use !important to override
+          'x:max-h-[min(calc(100vh-5rem),256px)]!'
+        )}
+        anchor={{ to: 'bottom', gap: 10, padding: 16 }}
+      >
+        {Object.entries(
+          // eslint-disable-next-line @typescript-eslint/no-unnecessary-condition -- fixme
+          (menu.items as Record<string, { title: string; href?: string }>) || {}
+        ).map(([key, item]) => (
+          <_MenuItem
+            key={key}
+            as={Anchor}
+            href={item.href || routes[key]?.route}
+            className={({ focus }) =>
+              cn(
+                'x:block x:py-1.5 x:transition-colors x:ps-3 x:pe-9',
+                focus
+                  ? 'x:text-gray-900 x:dark:text-gray-100'
+                  : 'x:text-gray-600 x:dark:text-gray-400'
+              )
+            }
+          >
+            {item.title}
+          </_MenuItem>
+        ))}
+      </MenuItems>
+    </Menu>
+  )
+}
+
+const isMenu = (page: any): page is MenuItem => page.type === 'menu'
+
+export const ClientNavbar: FC<{
+  pageMap: PageMapItem[]
+  children: ReactNode
+  className?: string
+}> = ({ pageMap, children, className }) => {
+
+  const { topLevelNavbarItems } = normalizePages({
+      list: pageMap,
+      route: usePathname()
+  })
+
+  // filter out titles for elements in topLevelNavbarItems with non empty route
+  const existingCourseNames = new Set(
+      topLevelNavbarItems.filter(
+          item => !('href' in item)
+      ).map(item => item.title)
+  )
+  // console.log(existingCourseNames)
+
+  // filter out elements in topLevelNavbarItems with url but have title in existingCourseNames
+  const filteredTopLevelNavbarItems = topLevelNavbarItems.filter(item => !('href' in item && existingCourseNames.has(item.title)))
+
+  // const items = topLevelNavbarItems
+  // use filteredTopLevelNavbarItems to generate items
+  const items = filteredTopLevelNavbarItems
+
+  // console.log(filteredTopLevelNavbarItems)
+  const themeConfig = useThemeConfig()
+
+  const pathname = useFSRoute()
+  const menu = useMenu()
+
+  return (
+    <>
+      <div
+        className={cn(
+          'x:flex x:gap-4 x:overflow-x-auto nextra-scrollbar x:py-1.5 x:max-md:hidden',
+          className
+        )}
+      >
+        {items.map((page, _index, arr) => {
+          if ('display' in page && page.display === 'hidden') return
+          if (isMenu(page)) {
+            return (
+              <NavbarMenu key={page.name} menu={page}>
+                {page.title}
+              </NavbarMenu>
+            )
+          }
+          const href =
+            // If it's a directory
+            ('frontMatter' in page ? page.route : page.firstChildRoute) ||
+            page.href ||
+            page.route
+
+          const isCurrentPage =
+            href === pathname ||
+            (pathname.startsWith(page.route + '/') &&
+              arr.every(item => !('href' in item) || item.href !== pathname)) ||
+            undefined
+
+          return (
+            <Anchor
+              href={href}
+              key={page.name}
+              className={cn(
+                classes.link,
+                'x:aria-[current]:font-medium x:aria-[current]:subpixel-antialiased x:aria-[current]:text-current'
+              )}
+              aria-current={isCurrentPage}
+            >
+              {page.title}
+            </Anchor>
+          )
+        })}
+      </div>
+      {themeConfig.search && (
+        <div className="x:max-md:hidden">{themeConfig.search}</div>
+      )}
+
+      {children}
+
+      <Button
+        aria-label="Menu"
+        className={({ active }) =>
+          cn('nextra-hamburger x:md:hidden', active && 'x:bg-gray-400/20')
+        }
+        onClick={() => setMenu(prev => !prev)}
+      >
+        <MenuIcon height="24" className={cn({ open: menu })} />
+      </Button>
+    </>
+  )
+}

components/navbar.tsx

@@ -0,0 +1,168 @@
+// customized navbar component, modified from https://github.com/shuding/nextra/blob/c8238813e1ba425cdd72783d57707b0ff3ca52ea/examples/custom-theme/app/_components/navbar.tsx#L9
+
+// Rebuild from source code https://github.com/shuding/nextra/tree/c8238813e1ba425cdd72783d57707b0ff3ca52ea/packages/nextra-theme-docs/src/components/navbar
+
+'use client'
+
+import type { PageMapItem } from 'nextra'
+import { Anchor } from 'nextra/components'
+import type { FC, ReactNode } from 'react'
+
+import cn from 'clsx'
+// eslint-disable-next-line no-restricted-imports -- since we don't need `newWindow` prop
+import NextLink from 'next/link'
+import { DiscordIcon, GitHubIcon } from 'nextra/icons'
+import { ClientNavbar } from './navbar.client'
+
+// export const Navbar: FC<{ pageMap: PageMapItem[] }> = ({ pageMap }) => {
+//     const pathname = usePathname()
+//     const { topLevelNavbarItems } = normalizePages({
+//         list: pageMap,
+//         route: pathname
+//     })
+//     return (
+//         <ul
+//             style={{
+//                 display: 'flex',
+//                 listStyleType: 'none',
+//                 padding: 20,
+//                 gap: 20,
+//                 background: 'lightcoral',
+//                 margin: 0
+//             }}
+//         >
+//             {filteredTopLevelNavbarItems.map(item => {
+
+//                 const route = item.route || ('href' in item ? item.href! : '')
+//                 return (
+//                     <li key={route}>
+//                         <Anchor href={route} style={{ textDecoration: 'none' }}>
+//                             {item.title}
+//                         </Anchor>
+//                     </li>
+//                 )
+//             })}
+//         </ul>
+//     )
+// }
+
+
+/* TODO: eslint typescript-sort-keys/interface: error */
+
+interface NavbarProps {
+  /**
+   * Page map.
+   */
+  pageMap: PageMapItem[]
+  /**
+   * Extra content after the last icon.
+   */
+  children?: ReactNode
+  /**
+   * Specifies whether the logo should have a link or provides the URL for the logo's link.
+   * @default true
+   */
+  logoLink?: string | boolean
+  /**
+   * Logo of the website.
+   */
+  logo: ReactNode
+  /**
+   * URL of the project homepage.
+   */
+  projectLink?: string
+  /**
+   * Icon of the project link.
+   * @default <GitHubIcon />
+   */
+  projectIcon?: ReactNode
+  /**
+   * URL of the chat link.
+   */
+  chatLink?: string
+  /**
+   * Icon of the chat link.
+   * @default <DiscordIcon />
+   */
+  chatIcon?: ReactNode
+  /**
+   * CSS class name.
+   */
+  className?: string
+  /**
+   * Aligns navigation links to the specified side.
+   * @default 'right'
+   */
+  align?: 'left' | 'right'
+}
+
+// Fix compiler error
+// Expression type `JSXElement` cannot be safely reordered
+const defaultGitHubIcon = (
+  <GitHubIcon height="24" aria-label="Project repository" />
+)
+const defaultChatIcon = <DiscordIcon width="24" />
+
+export const Navbar: FC<NavbarProps> = ({
+  pageMap,
+  children,
+  logoLink = true,
+  logo,
+  projectLink,
+  projectIcon = defaultGitHubIcon,
+  chatLink,
+  chatIcon = defaultChatIcon,
+  className,
+  align = 'right'
+}) => {
+  const logoClass = cn(
+    'x:flex x:items-center',
+    align === 'left' ? 'x:max-md:me-auto' : 'x:me-auto'
+  )
+  return (
+    <header
+      className={cn(
+        'nextra-navbar x:sticky x:top-0 x:z-30 x:w-full x:bg-transparent x:print:hidden',
+        'x:max-md:[.nextra-banner:not([class$=hidden])~&]:top-(--nextra-banner-height)'
+      )}
+    >
+      <div
+        className={cn(
+          'nextra-navbar-blur',
+          'x:absolute x:-z-1 x:size-full',
+          'nextra-border x:border-b',
+          'x:backdrop-blur-md x:bg-nextra-bg/70'
+        )}
+      />
+      <nav
+        style={{ height: 'var(--nextra-navbar-height)' }}
+        className={cn(
+          'x:mx-auto x:flex x:max-w-(--nextra-content-width) x:items-center x:gap-4 x:pl-[max(env(safe-area-inset-left),1.5rem)] x:pr-[max(env(safe-area-inset-right),1.5rem)]',
+          'x:justify-end',
+          className
+        )}
+      >
+        {logoLink ? (
+          <NextLink
+            href={typeof logoLink === 'string' ? logoLink : '/'}
+            className={cn(
+              logoClass,
+              'x:transition-opacity x:focus-visible:nextra-focus x:hover:opacity-75'
+            )}
+            aria-label="Home page"
+          >
+            {logo}
+          </NextLink>
+        ) : (
+          <div className={logoClass}>{logo}</div>
+        )}
+        <ClientNavbar pageMap={pageMap} 
+        className={align === 'left' ? 'x:me-auto' : ''}>
+          {projectLink && <Anchor href={projectLink}>{projectIcon}</Anchor>}
+          {chatLink && <Anchor href={chatLink}>{chatIcon}</Anchor>}
+          {children}
+        </ClientNavbar>
+      </nav>
+    </header>
+  )
+}

content/CSE332S/_meta.js

@@ -1,23 +1,61 @@
 export default {
-    index: "Course Description",
-    "---":{
-        type: 'separator'
+    menu: {
+      title: 'Home',
+      type: 'menu',
+      items: {
+        index: {
+          title: 'Home',
+          href: '/'
         },
-    CSE332S_L1: "Object-Oriented Programming Lab (Lecture 1)",
-    CSE332S_L2: "Object-Oriented Programming Lab (Lecture 2)",
-    CSE332S_L3: "Object-Oriented Programming Lab (Lecture 3)",
-    CSE332S_L4: "Object-Oriented Programming Lab (Lecture 4)",
-    CSE332S_L5: "Object-Oriented Programming Lab (Lecture 5)",
-    CSE332S_L6: "Object-Oriented Programming Lab (Lecture 6)",
-    CSE332S_L7: "Object-Oriented Programming Lab (Lecture 7)",
-    CSE332S_L8: "Object-Oriented Programming Lab (Lecture 8)",
-    CSE332S_L9: "Object-Oriented Programming Lab (Lecture 9)",
-    CSE332S_L10: "Object-Oriented Programming Lab (Lecture 10)",
-    CSE332S_L11: "Object-Oriented Programming Lab (Lecture 11)",
-    CSE332S_L12: "Object-Oriented Programming Lab (Lecture 12)",
-    CSE332S_L13: "Object-Oriented Programming Lab (Lecture 13)",
-    CSE332S_L14: "Object-Oriented Programming Lab (Lecture 14)",
-    CSE332S_L15: "Object-Oriented Programming Lab (Lecture 15)",
-    CSE332S_L16: "Object-Oriented Programming Lab (Lecture 16)",
-    CSE332S_L17: "Object-Oriented Programming Lab (Lecture 17)"
-}
+        about: {
+          title: 'About',
+          href: '/about'
+        },
+        contact: {
+          title: 'Contact Me',
+          href: '/contact'
+        }
+      },
+    },
+    Math3200'CSE332S_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Math429'CSE332S_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Math4111'CSE332S_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Math4121'CSE332S_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Math4201'CSE332S_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Math416'CSE332S_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Math401'CSE332S_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE332S'CSE332S_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE347'CSE332S_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE442T'CSE332S_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE5313'CSE332S_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE510'CSE332S_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE559A'CSE332S_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE5519'CSE332S_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Swap: {
+      display: 'hidden',
+      theme:{
+        timestamp: true,
+      }
+    },
+    index: {
+      display: 'hidden',
+      theme:{
+        sidebar: false,
+        timestamp: true,
+      }
+    },
+    about: {
+      display: 'hidden',
+      theme:{
+        sidebar: false,
+        timestamp: true,
+      }
+    },
+    contact: {
+      display: 'hidden',
+      theme:{
+        sidebar: false,
+        timestamp: true,
+      }
+    }
+  }

content/CSE347/_meta.js

@@ -1,18 +1,61 @@
 export default {
-    index: "Course Description",
-    "---":{
-        type: 'separator'
+    menu: {
+      title: 'Home',
+      type: 'menu',
+      items: {
+        index: {
+          title: 'Home',
+          href: '/'
         },
-    Exam_reviews: "Exam reviews",
-    CSE347_L1: "Analysis of Algorithms (Lecture 1)",
-    CSE347_L2: "Analysis of Algorithms (Lecture 2)",
-    CSE347_L3: "Analysis of Algorithms (Lecture 3)",
-    CSE347_L4: "Analysis of Algorithms (Lecture 4)",
-    CSE347_L5: "Analysis of Algorithms (Lecture 5)",
-    CSE347_L6: "Analysis of Algorithms (Lecture 6)",
-    CSE347_L7: "Analysis of Algorithms (Lecture 7)",
-    CSE347_L8: "Analysis of Algorithms (Lecture 8)",
-    CSE347_L9: "Analysis of Algorithms (Lecture 9)",
-    CSE347_L10: "Analysis of Algorithms (Lecture 10)",
-    CSE347_L11: "Analysis of Algorithms (Lecture 11)"
-}
+        about: {
+          title: 'About',
+          href: '/about'
+        },
+        contact: {
+          title: 'Contact Me',
+          href: '/contact'
+        }
+      },
+    },
+    Math3200'CSE347_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Math429'CSE347_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Math4111'CSE347_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Math4121'CSE347_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Math4201'CSE347_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Math416'CSE347_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Math401'CSE347_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE332S'CSE347_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE347'CSE347_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE442T'CSE347_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE5313'CSE347_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE510'CSE347_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE559A'CSE347_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE5519'CSE347_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Swap: {
+      display: 'hidden',
+      theme:{
+        timestamp: true,
+      }
+    },
+    index: {
+      display: 'hidden',
+      theme:{
+        sidebar: false,
+        timestamp: true,
+      }
+    },
+    about: {
+      display: 'hidden',
+      theme:{
+        sidebar: false,
+        timestamp: true,
+      }
+    },
+    contact: {
+      display: 'hidden',
+      theme:{
+        sidebar: false,
+        timestamp: true,
+      }
+    }
+  }

content/CSE442T/CSE442T_L16.md

@@ -13,7 +13,8 @@ Ouput $(r,m\oplus f_i(r))$
 
 $Dec_i(r,c):$ Output $c\oplus f_i(r)$
 
-Proof of security:
+<details>
+<summary>Proof of security</summary>
 
 Suppose $D$ distinguishes, for infinitly many $n$.
 
@@ -35,7 +36,7 @@ $(r_1,F(r_1)),\ldots, (r_q,F(r_q))$
 
 So $D$ distinguishing output of $r_1,\ldots, r_q$ of PRF from the RF, this contradicts with definition of PRF.
 
-QED
+</details>
 
 Noe we have 
 

content/CSE442T/CSE442T_L17.md

@@ -32,7 +32,8 @@ Proof of the validity of the decryption: Exercise.
 
 The encryption scheme is secure under this construction (Trapdoor permutation (TDP), Hardcore bit (HCB)).
 
-Proof:
+<details>
+<summary>Proof</summary>
 
 We proceed by contradiction. (Constructing contradiction with definition of hardcore bit.)
 
@@ -76,7 +77,7 @@ $$
 
 This contradicts the definition of hardcore bit.
 
-QED
+</details>
 
 ### Public key encryption scheme (multi-bit)
 
@@ -144,7 +145,8 @@ Output: $m$
 
 #### Security of El-Gamal encryption scheme
 
-Proof:
+<details>
+<summary>Proof</summary>
 
 If not secure, then there exists a distinguisher $\mathcal{D}$ that can distinguish the encryption of $m_1,m_2\in G_q$ with non-negligible probability $\mu(n)$.
 
@@ -155,5 +157,5 @@ $$
 
 And proceed by contradiction. This contradicts the DDH assumption.
 
-QED
+</details>
 

content/CSE442T/CSE442T_L20.md

@@ -26,7 +26,8 @@ Under the discrete log assumption, $H$ is a CRHF.
 - It is easy to compute
 - Compressing by 1 bit
 
-Proof:
+<details>
+<summary>Proof</summary>
 
 The hash function $h$ is a CRHF
 
@@ -72,7 +73,7 @@ So $\mathcal{B}$ can break the discrete log assumption with non-negligible proba
 
 So $h$ is a CRHF.
 
-QED
+</details>
 
 To compress by more, say $h_k:{0,1}^n\to \{0,1\}^{n-k},k\geq 1$, then we can use $h: \{0,1\}^{n+1}\to \{0,1\}^n$ multiple times.
 
@@ -106,7 +107,8 @@ One-time secure:
 
 Then ($Gen',Sign',Ver'$) is one-time secure.
 
-Ideas of Proof:
+<details>
+<summary>Ideas of Proof</summary>
 
 If the digital signature scheme ($Gen',Sign',Ver'$) is not one-time secure, then there exists an adversary $\mathcal{A}$ which can ask oracle for one signature on $m_1$ and receive $\sigma_1=Sign'_{sk'}(m_1)=Sign_{sk}(h_i(m_1))$.
 
@@ -119,7 +121,7 @@ Case 1: $h_i(m_1)=h_i(m_2)$, Then $\mathcal{A}$ finds a collision of $h$.
 
 Case 2: $h_i(m_1)\neq h_i(m_2)$, Then $\mathcal{A}$ produced valid signature on $h_i(m_2)$ after only seeing $Sign'_{sk'}(m_1)\neq Sign'_{sk'}(m_2)$. This contradicts the one-time secure of ($Gen,Sign,Ver$).
 
-QED
+</details>
 
 ### Many-time Secure Digital Signature
 

content/CSE442T/_meta.js

@@ -1,31 +1,61 @@
 export default {
-    index: "Course Description",
-    "---":{
-        type: 'separator'
+    menu: {
+      title: 'Home',
+      type: 'menu',
+      items: {
+        index: {
+          title: 'Home',
+          href: '/'
         },
-    Exam_reviews: "Exam reviews",
-    CSE442T_L1: "Introduction to Cryptography (Lecture 1)",
-    CSE442T_L2: "Introduction to Cryptography (Lecture 2)",
-    CSE442T_L3: "Introduction to Cryptography (Lecture 3)",
-    CSE442T_L4: "Introduction to Cryptography (Lecture 4)",
-    CSE442T_L5: "Introduction to Cryptography (Lecture 5)",
-    CSE442T_L6: "Introduction to Cryptography (Lecture 6)",
-    CSE442T_L7: "Introduction to Cryptography (Lecture 7)",
-    CSE442T_L8: "Introduction to Cryptography (Lecture 8)",
-    CSE442T_L9: "Introduction to Cryptography (Lecture 9)",
-    CSE442T_L10: "Introduction to Cryptography (Lecture 10)",
-    CSE442T_L11: "Introduction to Cryptography (Lecture 11)",
-    CSE442T_L12: "Introduction to Cryptography (Lecture 12)",
-    CSE442T_L13: "Introduction to Cryptography (Lecture 13)",
-    CSE442T_L14: "Introduction to Cryptography (Lecture 14)",
-    CSE442T_L15: "Introduction to Cryptography (Lecture 15)",
-    CSE442T_L16: "Introduction to Cryptography (Lecture 16)",
-    CSE442T_L17: "Introduction to Cryptography (Lecture 17)",
-    CSE442T_L18: "Introduction to Cryptography (Lecture 18)",
-    CSE442T_L19: "Introduction to Cryptography (Lecture 19)",
-    CSE442T_L20: "Introduction to Cryptography (Lecture 20)",
-    CSE442T_L21: "Introduction to Cryptography (Lecture 21)",
-    CSE442T_L22: "Introduction to Cryptography (Lecture 22)",
-    CSE442T_L23: "Introduction to Cryptography (Lecture 23)",
-    CSE442T_L24: "Introduction to Cryptography (Lecture 24)"
-}
+        about: {
+          title: 'About',
+          href: '/about'
+        },
+        contact: {
+          title: 'Contact Me',
+          href: '/contact'
+        }
+      },
+    },
+    Math3200'CSE442T_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Math429'CSE442T_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Math4111'CSE442T_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Math4121'CSE442T_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Math4201'CSE442T_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Math416'CSE442T_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Math401'CSE442T_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE332S'CSE442T_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE347'CSE442T_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE442T'CSE442T_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE5313'CSE442T_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE510'CSE442T_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE559A'CSE442T_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE5519'CSE442T_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Swap: {
+      display: 'hidden',
+      theme:{
+        timestamp: true,
+      }
+    },
+    index: {
+      display: 'hidden',
+      theme:{
+        sidebar: false,
+        timestamp: true,
+      }
+    },
+    about: {
+      display: 'hidden',
+      theme:{
+        sidebar: false,
+        timestamp: true,
+      }
+    },
+    contact: {
+      display: 'hidden',
+      theme:{
+        sidebar: false,
+        timestamp: true,
+      }
+    }
+  }

content/CSE442T/index.md

@@ -8,7 +8,7 @@ One-way functions, Pseudorandomness, Private-key cryptography, Public-key crypto
 
 ### Instructor
 
-[Brian Garnett](bcgarnett@wustl.edu)
+Brian Garnett (bcgarnett@wustl.edu)
 
 Math Phd… Great!
 

content/CSE510/CSE510_L11.md

@@ -198,20 +198,20 @@ $$
 
 Take the softmax policy as example:
 
-Weight actions using the linear combination of features $\phi(s,a)^T\theta$:
+Weight actions using the linear combination of features $\phi(s,a)^\top\theta$:
 
 Probability of action is proportional to the exponentiated weights:
 
 $$
-\pi_\theta(s,a) \propto \exp(\phi(s,a)^T\theta)
+\pi_\theta(s,a) \propto \exp(\phi(s,a)^\top\theta)
 $$
 
 The score function is
 
 $$
 \begin{aligned}
-\nabla_\theta \ln\left[\frac{\exp(\phi(s,a)^T\theta)}{\sum_{a'\in A}\exp(\phi(s,a')^T\theta)}\right] &= \nabla_\theta(\ln \exp(\phi(s,a)^T\theta) - (\ln \sum_{a'\in A}\exp(\phi(s,a')^T\theta))) \\
-&= \nabla_\theta\left(\phi(s,a)^T\theta -\frac{\phi(s,a)\sum_{a'\in A}\exp(\phi(s,a')^T\theta)}{\sum_{a'\in A}\exp(\phi(s,a')^T\theta)}\right) \\
+\nabla_\theta \ln\left[\frac{\exp(\phi(s,a)^\top\theta)}{\sum_{a'\in A}\exp(\phi(s,a')^\top\theta)}\right] &= \nabla_\theta(\ln \exp(\phi(s,a)^\top\theta) - (\ln \sum_{a'\in A}\exp(\phi(s,a')^\top\theta))) \\
+&= \nabla_\theta\left(\phi(s,a)^\top\theta -\frac{\phi(s,a)\sum_{a'\in A}\exp(\phi(s,a')^\top\theta)}{\sum_{a'\in A}\exp(\phi(s,a')^\top\theta)}\right) \\
 &=\phi(s,a) - \sum_{a'\in A} \prod_\theta(s,a') \phi(s,a')
 &= \phi(s,a) - \mathbb{E}_{a'\sim \pi_\theta(s,a')}[\phi(s,a')]
 \end{aligned}
@@ -221,7 +221,7 @@ $$
 
 In continuous action spaces, a Gaussian policy is natural
 
-Mean is a linear combination of state features $\mu(s) = \phi(s)^T\theta$
+Mean is a linear combination of state features $\mu(s) = \phi(s)^\top\theta$
 
 Variance may be fixed $\sigma^2$, or can also parametrized
 

content/CSE510/CSE510_L12.md

@@ -53,7 +53,7 @@ $$
 Action-Value Actor-Critic
 
 - Simple actor-critic algorithm based on action-value critic
-- Using linear value function approximation $Q_w(s,a)=\phi(s,a)^T w$
+- Using linear value function approximation $Q_w(s,a)=\phi(s,a)^\top w$
 
 Critic: updates $w$ by linear $TD(0)$
 Actor: updates $\theta$ by policy gradient

content/CSE510/CSE510_L13.md

@@ -193,7 +193,7 @@ $$
 
 Make linear approximation to $L_{\pi_{\theta_{old}}}$ and quadratic approximation to KL term.
 
-Maximize $g\cdot(\theta-\theta_{old})-\frac{\beta}{2}(\theta-\theta_{old})^T F(\theta-\theta_{old})$
+Maximize $g\cdot(\theta-\theta_{old})-\frac{\beta}{2}(\theta-\theta_{old})^\top F(\theta-\theta_{old})$
 
 where $g=\frac{\partial}{\partial \theta}L_{\pi_{\theta_{old}}}(\pi_{\theta})\vert_{\theta=\theta_{old}}$ and $F=\frac{\partial^2}{\partial \theta^2}\overline{KL}_{\pi_{\theta_{old}}}(\pi_{\theta})\vert_{\theta=\theta_{old}}$
 
@@ -201,7 +201,7 @@ where $g=\frac{\partial}{\partial \theta}L_{\pi_{\theta_{old}}}(\pi_{\theta})\ve
 <summary>Taylor Expansion of KL Term</summary>
 
 $$
-D_{KL}(\pi_{\theta_{old}}|\pi_{\theta})\approx D_{KL}(\pi_{\theta_{old}}|\pi_{\theta_{old}})+d^T \nabla_\theta D_{KL}(\pi_{\theta_{old}}|\pi_{\theta})\vert_{\theta=\theta_{old}}+\frac{1}{2}d^T \nabla_\theta^2 D_{KL}(\pi_{\theta_{old}}|\pi_{\theta})\vert_{\theta=\theta_{old}}d
+D_{KL}(\pi_{\theta_{old}}|\pi_{\theta})\approx D_{KL}(\pi_{\theta_{old}}|\pi_{\theta_{old}})+d^\top \nabla_\theta D_{KL}(\pi_{\theta_{old}}|\pi_{\theta})\vert_{\theta=\theta_{old}}+\frac{1}{2}d^\top \nabla_\theta^2 D_{KL}(\pi_{\theta_{old}}|\pi_{\theta})\vert_{\theta=\theta_{old}}d
 $$
 
 $$
@@ -220,9 +220,9 @@ $$
 \begin{aligned}
 \nabla_\theta^2 D_{KL}(\pi_{\theta_{old}}|\pi_{\theta})\vert_{\theta=\theta_{old}}&=-\mathbb{E}_{x\sim \pi_{\theta_{old}}}\nabla_\theta^2 \log P_\theta(x)\vert_{\theta=\theta_{old}}\\
 &=-\mathbb{E}_{x\sim \pi_{\theta_{old}}}\nabla_\theta \left(\frac{\nabla_\theta P_\theta(x)}{P_\theta(x)}\right)\vert_{\theta=\theta_{old}}\\
-&=-\mathbb{E}_{x\sim \pi_{\theta_{old}}}\left(\frac{\nabla_\theta^2 P_\theta(x)-\nabla_\theta P_\theta(x)\nabla_\theta P_\theta(x)^T}{P_\theta(x)^2}\right)\vert_{\theta=\theta_{old}}\\
-&=-\mathbb{E}_{x\sim \pi_{\theta_{old}}}\left(\frac{\nabla_\theta^2 P_\theta(x)\vert_{\theta=\theta_{old}}}P_{\theta_{old}}(x)\right)+\mathbb{E}_{x\sim \pi_{\theta_{old}}}\left(\nabla_\theta \log P_\theta(x)\nabla_\theta \log P_\theta(x)^T\right)\vert_{\theta=\theta_{old}}\\
-&=\mathbb{E}_{x\sim \pi_{\theta_{old}}}\nabla_\theta\log P_\theta(x)\nabla_\theta\log P_\theta(x)^T\vert_{\theta=\theta_{old}}\\
+&=-\mathbb{E}_{x\sim \pi_{\theta_{old}}}\left(\frac{\nabla_\theta^2 P_\theta(x)-\nabla_\theta P_\theta(x)\nabla_\theta P_\theta(x)^\top}{P_\theta(x)^2}\right)\vert_{\theta=\theta_{old}}\\
+&=-\mathbb{E}_{x\sim \pi_{\theta_{old}}}\left(\frac{\nabla_\theta^2 P_\theta(x)\vert_{\theta=\theta_{old}}}P_{\theta_{old}}(x)\right)+\mathbb{E}_{x\sim \pi_{\theta_{old}}}\left(\nabla_\theta \log P_\theta(x)\nabla_\theta \log P_\theta(x)^\top\right)\vert_{\theta=\theta_{old}}\\
+&=\mathbb{E}_{x\sim \pi_{\theta_{old}}}\nabla_\theta\log P_\theta(x)\nabla_\theta\log P_\theta(x)^\top\vert_{\theta=\theta_{old}}\\
 \end{aligned}
 $$
 

content/CSE510/CSE510_L14.md

@@ -27,7 +27,7 @@ $\theta_{new}=\theta_{old}+d$
 First order Taylor expansion for the loss and second order for the KL:
 
 $$
-\approx \arg\max_{d} J(\theta_{old})+\nabla_\theta J(\theta)\mid_{\theta=\theta_{old}}d-\frac{1}{2}\lambda(d^T\nabla_\theta^2 D_{KL}\left[\pi_{\theta_{old}}||\pi_{\theta}\right]\mid_{\theta=\theta_{old}}d)+\lambda \delta
+\approx \arg\max_{d} J(\theta_{old})+\nabla_\theta J(\theta)\mid_{\theta=\theta_{old}}d-\frac{1}{2}\lambda(d^\top\nabla_\theta^2 D_{KL}\left[\pi_{\theta_{old}}||\pi_{\theta}\right]\mid_{\theta=\theta_{old}}d)+\lambda \delta
 $$
 
 If you are really interested, try to fill the solving the KL Constrained Problem section.
@@ -38,7 +38,7 @@ Setting the gradient to zero:
 
 $$
 \begin{aligned}
-0&=\frac{\partial}{\partial d}\left(-\nabla_\theta J(\theta)\mid_{\theta=\theta_{old}}d+\frac{1}{2}\lambda(d^T F(\theta_{old})d\right)\\
+0&=\frac{\partial}{\partial d}\left(-\nabla_\theta J(\theta)\mid_{\theta=\theta_{old}}d+\frac{1}{2}\lambda(d^\top F(\theta_{old})d\right)\\
 &=-\nabla_\theta J(\theta)\mid_{\theta=\theta_{old}}+\frac{1}{2}\lambda F(\theta_{old})d
 \end{aligned}
 $$
@@ -58,15 +58,15 @@ $$
 $$
 
 $$
-D_{KL}(\pi_{\theta_{old}}||\pi_{\theta})\approx \frac{1}{2}(\theta-\theta_{old})^T F(\theta_{old})(\theta-\theta_{old})
+D_{KL}(\pi_{\theta_{old}}||\pi_{\theta})\approx \frac{1}{2}(\theta-\theta_{old})^\top F(\theta_{old})(\theta-\theta_{old})
 $$
 
 $$
-\frac{1}{2}(\alpha g_N)^T F(\alpha g_N)=\delta
+\frac{1}{2}(\alpha g_N)^\top F(\alpha g_N)=\delta
 $$
 
 $$
-\alpha=\sqrt{\frac{2\delta}{g_N^T F g_N}}
+\alpha=\sqrt{\frac{2\delta}{g_N^\top F g_N}}
 $$
 
 However, due to the quadratic approximation, the KL constrains may be violated.

content/CSE510/CSE510_L17.md

@@ -1,14 +1,47 @@
 # CSE510 Deep Reinforcement Learning (Lecture 17)
 
-## Model-based RL
-
-### Model-based RL vs. Model-free RL
+## Why Model-Based RL?
 
 - Sample efficiency
 - Generalization and transferability
 - Support efficient exploration in large-scale RL problems
 - Explainability
 - Super-human performance in practice
+  - Video games, Go, Algorithm discovery, etc.
+
+> [!NOTE]
+>
+> Model is anything the agent can use to predict how the environment will respond to its actions, concretely, the state transition $T(s'| s, a)$ and reward $R(s, a)$.
+
+For ADP-based (model-based) RL
+
+1. Start with initial model
+2. Solve for optimal policy given current model 
+   - (using value or policy iteration)
+3. Take action according to an exploration/exploitation policy
+   - Explores more early on and gradually uses policy from 2
+4. Update estimated model based on observed transition
+5. Goto 2
+
+### Problems in Large Scale Model-Based RL
+
+- New planning methods for given a model
+  - Model is large and not perfect
+- Model learning
+  - Requiring generalization
+- Exploration/exploitation strategy
+  - Requiring generalization and attention
+
+### Large Scale Model-Based RL
+
+- New optimal planning methods (Today)
+  - Model is large and not perfect
+- Model learning (Next Lecture)
+  - Requiring generalization
+- Exploration/exploitation strategy (Next week)
+  - Requiring generalization and attention
+
+## Model-based RL
 
 ### Deterministic Environment: Cross-Entropy Method
 
@@ -29,12 +62,14 @@ Simplest method: guess and check: "random shooting method"
 - pick $A_1, A_2, ..., A_n$ from some distribution (e.g. uniform)
 - Choose $A_i$ based on $\argmax_i J(A_i)$
 
-#### Cross-Entropy Method with continuous-valued inputs
+#### Cross-Entropy Method (CEM) with continuous-valued inputs
 
-1. sample $A_1, A_2, ..., A_n$ from some distribution $p(A)$
-2. evaluate $J(A_1), J(A_2), ..., J(A_n)$
-3. pick the _elites_ $A_1, A_2, ..., A_m$ with the highest $J(A_i)$, where $m<n$
-4. update the distribution $p(A)$ to be more likely to choose the elites
+Cross-entropy method with continuous-valued inputs:s
+
+1. Sample $A_1, A_2, ..., A_n$ from some distribution $p(A)$
+2. Evaluate $J(A_1), J(A_2), ..., J(A_n)$
+3. Pick the _elites_ $A_1, A_2, ..., A_m$ with the highest $J(A_i)$, where $m<n$
+4. Update the distribution $p(A)$ to be more likely to choose the elites
 
 Pros:
 
@@ -68,15 +103,70 @@ Use model as simulator to evaluate actions.
 
 Tree policy:
 
-Decision policy:
+- Select/create leaf node
+- Selection and Expansion
+- Bandit problem!
+
+Default policy/rollout policy
+
+- Play the game till end
+- Simulation
+
+Decision policy
+
+- Selecting the final action
+
+#### Upper Confidence Bound on Trees (UCT)
+
+Selecting Child Node - Multi-Arm Bandit Problem
+
+UCB1 applied for each child selection
+
+$$
+UCT=\overline{X_j}+2C_p\sqrt{\frac{2\ln n_j}{n_j}}
+$$
+
+- where $\overline{X_j}$ is the mean reward of selecting this position
+  - $[0,1]$
+- $n$ is the number of times current(parent) node has been visited
+- $n_j$ is the number of times child node $j$ has been visited
+  - Guaranteed we explore each child node at least once
+- $C_p$ is some constant $>0$
+
+Each child has non-zero probability of being selected
+
+We can adjust $C_p$ to change exploration vs. exploitation trade-off
+
+#### Decision Policy: Final Action Selection
+
+Selecting the best child
 
 - Max (highest weight)
 - Robust (most visits)
 - Max-Robust (max of the two)
 
-#### Upper Confidence Bound on Trees (UCT)
+#### Advantages and disadvantages of MCTS
 
+Advantages:
 
+- Proved MCTS converges to minimax solution
+  - Domain-independent
+  - Anytime algorithm
+  - Achieving better with a large branch factor
+
+Disadvantages:
+
+- Basic version converges very slowly
+- Leading to small-probability failures
+
+### Example usage of MCTS
+
+AlphaGo vs Lee Sedol, Game 4
+
+- White 78 (Lee): unexpected move (even other professional players didn't see coming) - needle in the haystack
+- AlphaGo failed to explore this in MCTS
+
+Imitation learning from MCTS:
 
 #### Continuous Case: Trajectory Optimization
 

content/CSE510/CSE510_L18.md

@@ -0,0 +1,65 @@
+# CSE510 Deep Reinforcement Learning (Lecture 18)
+
+## Model-based RL framework
+
+Model Learning with High-Dimensional Observations
+
+- Learning model in a latent space with observation reconstruction
+- Learning model in a latent space without observation reconstruction
+- Learning model in the observation space (i.e., videos)
+
+### Naive approach:
+
+If we knew $f(s_t,a_t)=s_{t+1}$, we could use the tools from last week. (or $p(s_{t+1}| s_t, a_t)$ in the stochastic case)
+
+So we can learn $f(s_t,a_t)$ from data, and _then_ plan through it.
+
+Model-based reinforcement learning version **0.5**:
+
+1. Run base polity $\pi_0$ (e.g. random policy) to collect $\mathcal{D} = \{(s_t, a_t, s_{t+1})\}_{t=0}^\top$
+2. Learn dynamics model $f(s_t,a_t)$ to minimize $\sum_{i}\|f(s_i,a_i)-s_{i+1}\|^2$
+3. Plan through $f(s_t,a_t)$ to choose action $a_t$
+
+Sometime, it does work!
+
+- Essentially how system identification works in classical robotics
+- Some care should be taken to design a good base policy
+- Particularly effective if we can hand-engineer a dynamics representation using our knowledge of physics, and fit just a few parameters
+
+However, Distribution mismatch problem becomes worse as we use more
+expressive model classes.
+
+Version 0.5: collect random samples, train dynamics, plan
+
+- Pro: simple, no iterative procedure
+- Con: distribution mismatch problem
+
+Version 1.0: iteratively collect data, replan, collect data
+
+- Pro: simple, solves distribution mismatch
+- Con: open loop plan might perform poorly, esp. in stochastic domains
+
+Version 1.5: iteratively collect data using MPC (replan at each step)
+
+- Pro: robust to small model errors
+- Con: computationally expensive, but have a planning algorithm available
+
+Version 2.0: backpropagate directly into policy
+
+- Pro: computationally cheap at runtime
+- Con: can be numerically unstable, especially in stochastic domains
+- Solution: model-free RL + model-based RL
+
+Final version:
+
+1. Run base polity $\pi_0$ (e.g. random policy) to collect $\mathcal{D} = \{(s_t, a_t, s_{t+1})\}_{t=0}^\top$
+2. Learn dynamics model $f(s_t,a_t)$ to minimize $\sum_{i}\|f(s_i,a_i)-s_{i+1}\|^2$
+3. Backpropagate through $f(s_t,a_t)$ into the policy to optimized $\pi_\theta(s_t,a_t)$
+4. Run the policy $\pi_\theta(s_t,a_t)$ to collect $\mathcal{D} = \{(s_t, a_t, s_{t+1})\}_{t=0}^\top$
+5. Goto 2
+
+## Model Learning with High-Dimensional Observations
+
+- Learning model in a latent space with observation reconstruction
+- Learning model in a latent space without observation reconstruction
+

content/CSE510/CSE510_L19.md

@@ -0,0 +1,100 @@
+# CSE510 Deep Reinforcement Learning (Lecture 19)
+
+## Model learning with high-dimensional observations
+
+- Learning model in a latent space with observation reconstruction
+- Learning model in a latent space without reconstruction
+
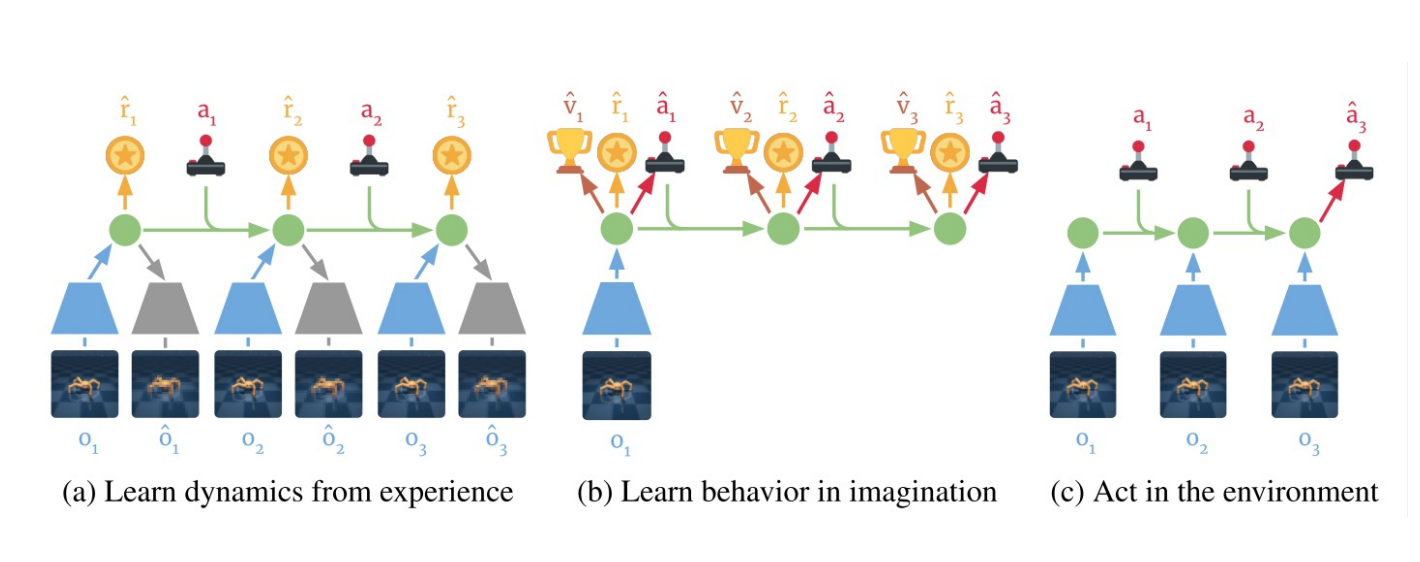
+### Learn in Latent Space: Dreamer
+
+Learning embedding of images & dynamics model (jointly)
+
+![Dreamer](https://notenextra.trance-0.com/CSE510/Dreamer.png)
+
+Representation model: $p_\theta(s_t|s_{t-1}, a_{t-1}, o_t)$
+
+Observation model: $q_\theta(o_t|s_t)$
+
+Reward model: $q_\theta(r_t|s_t)$
+
+Transition model: $q_\theta(s_t| s_{t-1}, a_{t-1})$.
+
+Variational evidence lower bound (ELBO) objective:
+
+$$
+\mathcal{J}_{REC}\doteq \mathbb{E}_{p}\left(\sum_t(\mathcal{J}_O^t+\mathcal{J}_R^t+\mathcal{J}_D^t)\right)
+$$
+
+where
+
+$$
+\mathcal{J}_O^t\doteq \ln q(o_t|s_t)
+$$
+
+$$
+\mathcal{J}_R^t\doteq \ln q(r_t|s_t)
+$$
+
+$$
+\mathcal{J}_D^t\doteq -\beta \operatorname{KL}(p(s_t|s_{t-1}, a_{t-1}, o_t)||q(s_t|s_{t-1}, a_{t-1}))
+$$
+
+#### More versions for Dreamer
+
+Latest is V3, [link to the paper](https://arxiv.org/pdf/2301.04104)
+
+### Learn in Latent Space
+
+- Pros
+  - Learn visual skill efficiently (using relative simple networks)
+- Cons
+  - Using autoencoder might not recover the right representation
+  - Not necessarily suitable for model-based methods
+  - Embedding is often not a good state representation without using history observations
+
+### Planning with Value Prediction Network (VPN)
+
+Idea: generating trajectories by following $\epsilon$-greedy policy based on the planning method
+
+Q-value calculated from $d$-step planning is defined as:
+
+$$
+Q_\theta^d(s,o)=r+\gamma V_\theta^{d}(s')
+$$
+
+$$
+V_\theta^{d}(s)=\begin{cases}
+V_\theta(s) & \text{if } d=1\\
+\frac{1}{d}V_\theta(s)+\frac{d-1}{d}\max_{o} Q_\theta^{d-1}(s,o)& \text{if } d>1
+\end{cases}
+$$
+
+![VPN](https://notenextra.trance-0.com/CSE510/VPN.png)
+
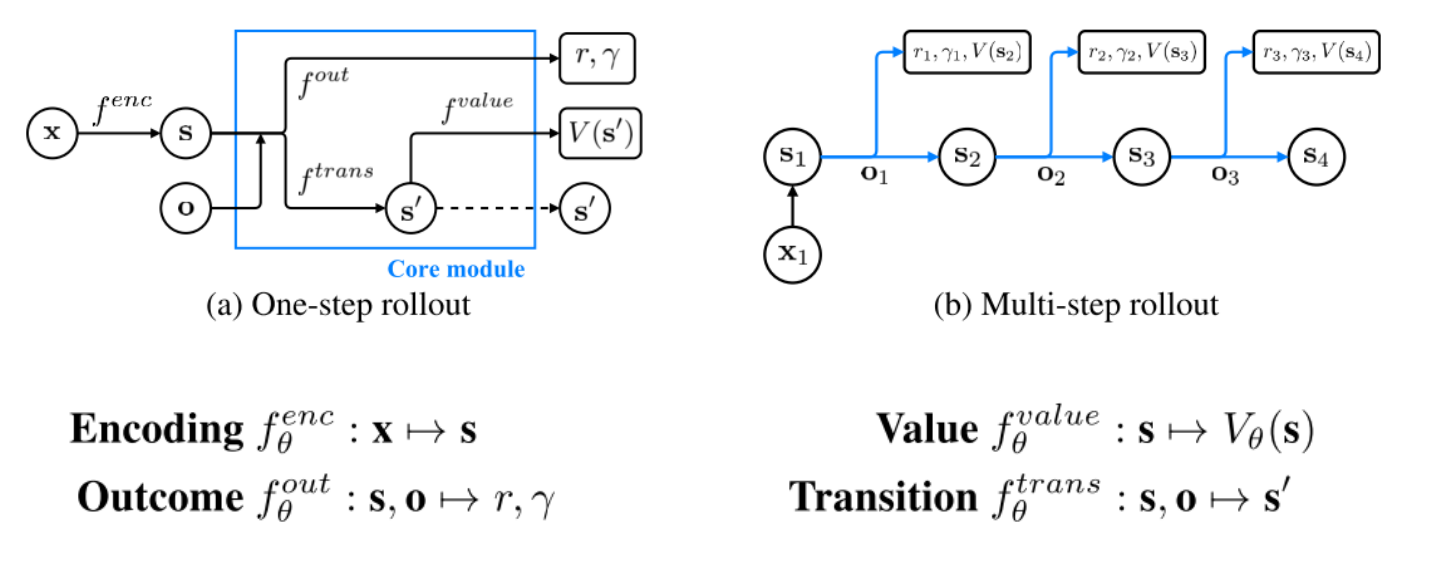
+Given an n-step trajectory $x_1, o_1, r_1, \gamma_1, x_2, o_2, r_2, \gamma_2, ..., x_{n+1}$ generated by the $\epsilon$-greedy policy, k-step predictions are defined as follows:
+
+$$
+s_t^k=\begin{cases}
+f^{enc}_\theta(x_t) & \text{if } k=0\\
+f^{trans}_\theta(s_{t-1}^{k-1},o_{t-1}) & \text{if } k>0
+\end{cases}
+$$
+
+$$
+v_t^k=f^{value}_\theta(s_t^k)
+$$
+
+$$
+r_t^k,\gamma_t^k=f^{out}_\theta(s_t^{k-1},o_t)
+$$
+
+$$
+\mathcal{L}_t=\sum_{l=1}^k(R_t-v_t^l)^2+(r_t-r_t^l)^2+(\gamma_t-\gamma_t^l)^2\text{ where } R_t=\begin{cases}
+r_t+\gamma_t R_{t+1} & \text{if } t\leq n\\
+\max_{o} Q_{\theta-}^d(s_{n+1},o)& \text{if } t=n+1
+\end{cases}
+$$
+
+### MuZero
+
+beats AlphaZero

content/CSE510/CSE510_L20.md

@@ -0,0 +1,143 @@
+# CSE510 Deep Reinforcement Learning (Lecture 20)
+
+## Exploration in RL
+
+### Motivations
+
+#### Exploration vs. Exploitation Dilemma
+
+Online decision-making involves a fundamental choice:
+
+- Exploration: trying out new things (new behaviors), with the hope of discovering higher rewards
+- Exploitation: doing what you know will yield the highest reward
+
+The best long-term strategy may involve short-term sacrifices
+
+Gather enough knowledge early to make the best long-term decisions
+
+<details>
+<summary>Example</summary>
+Restaurant Selection
+
+- Exploitation: Go to your favorite restaurant
+- Exploration: Try a new restaurant
+
+Oil Drilling
+
+- Exploitation: Drill at the best known location
+- Exploration: Drill at a new location
+
+Game Playing
+
+- Exploitation: Play the move you believe is best
+- Exploration: Play an experimental move
+
+</details>
+
+#### Breakout vs. Montezuma's Revenge
+
+| Property | Breakout | Montezuma's Revenge |
+|----------|----------|--------------------|
+| **Reward frequency** | Dense (every brick hit gives points) | Extremely sparse (only after collecting key or treasure) |
+| **State space** | Simple (ball, paddle, bricks) | Complex (many rooms, objects, ladders, timing) |
+| **Action relevance** | Almost any action affects reward soon | Most actions have no immediate feedback |
+| **Exploration depth** | Shallow (few steps to reward) | Deep (dozens/hundreds of steps before reward) |
+| **Determinism** | Mostly deterministic dynamics | Deterministic but requires long sequences of precise actions |
+| **Credit assignment** | Easy — short time gap | Very hard — long delay from cause to effect |
+
+#### Motivation
+
+- Motivation: "Forces" that energize an organism to act and that direct its activity
+- Extrinsic Motivation: being motivated to do something because of some external reward ($, a prize, food, water, etc.)
+- Intrinsic Motivation: being motivated to do something because it is inherently enjoyable (curiosity, exploration, novelty, surprise, incongruity, complexity…)
+
+### Intuitive Exploration Strategy
+
+- Intrinsic motivation drives the exploration for unknowns
+- Intuitively, we explore efficiently once we know what we do not know, and target our exploration efforts to the unknown part of the space.
+- All non-naive exploration methods consider some form of uncertainty estimation, regarding state (or state-action) I have visited, transition dynamics, or Q-functions.
+
+- Optimal methods in smaller settings don't work, but can inspire for larger settings
+- May use some hacks
+
+### Classes of Exploration Methods in Deep RL
+
+- Optimistic exploration
+  - Uncertainty about states
+  - Visiting novel states (state visitation counting)
+- Information state search
+  - Uncertainty about state transitions or dynamics
+  - Dynamics prediction error or Information gain for dynamics learning
+- Posterior sampling
+  - Uncertainty about Q-value functions or policies
+  - Selecting actions according to the probability they are best
+
+### Optimistic Exploration
+
+#### Count-Based Exploration in Small MDPs
+
+Book-keep state visitation counts $N(s)$
+Add exploration reward bonuses that encourage policies that visit states with fewer counts.
+
+$$
+R(s,a,s') = r(s,a,s') + \mathcal{B}(N(s))
+$$
+
+where $\mathcal{B}(N(s))$ is the intrinsic exploration reward bonus.
+
+- UCB: $\mathcal{B}(N(s)) = \sqrt{\frac{2\ln n}{N(s)}}$ (more aggressive exploration)
+- MBIE-EB (Strehl & Littman): $\mathcal{B}(N(s)) = \sqrt{\frac{1}{N(s)}}$
+- BEB (Kolter & Ng): $\mathcal{B}(N(s)) = \frac{1}{N(s)}$
+
+- We want to come up with something that rewards states that we have not visited often.
+- But in large MDPs, we rarely visit a state twice!
+- We need to capture a notion of state similarity, and reward states that are most dissimilar to what we have seen so far
+  - as opposed to different (as they will always be different).   
+
+#### Fitting Generative Models
+
+Idea: fit a density model $p_\theta(s)$ (or $p_\theta(s,a)$)
+
+$p_\theta(s)$ might be high even for a new $s$.
+
+If $s$ is similar to perviously seen states, can we use $p_\theta(s)$ to get a "pseudo-count" for $s$?
+
+If we have small MDPs, the true probability is
+
+$$
+P(s)=\frac{N(s)}{n}
+$$
+
+where $N(s)$ is the number of times $s$ has been visited and $n$ is the total states visited.
+
+after we visit $s$, then
+
+$$
+P'(s)=\frac{N(s)+1}{n+1}
+$$
+
+1. fit model $p_\theta(s)$ to all states $\mathcal{D}$ so far.
+2. take a step $i$ and observe $s_i$.
+3. fit new model $p_\theta'(s)$ to all states $\mathcal{D} \cup {s_i}$.
+4. use $p_\theta(s_i)$ and $p_\theta'(s_i)$ to estimate the "pseudo-count" for $\hat{N}(s_i)$.
+5. set $r_i^+=r_i+\mathcal{B}(\hat{N}(s_i))$
+6. go to 1
+
+How to get $\hat{N}(s_i)$? use the equations
+
+$$
+p_\theta(s_i)=\frac{\hat{N}(s_i)}{\hat{n}}\quad p_\theta'(s_i)=\frac{\hat{N}(s_i)+1}{\hat{n}+1}
+$$
+
+[link to the paper](https://arxiv.org/pdf/1606.01868)
+
+#### Density models
+
+[link to the paper](https://arxiv.org/pdf/1703.01310)
+
+#### State Counting with DeepHashing
+
+- We still count states (images) but not in pixel space, but in latent compressed space.
+- Compress $s$ into a latent code, then count occurrences of the code.
+- How do we get the image encoding? e.g., using autoencoders.
+- There is no guarantee such reconstruction loss will capture the important things that make two states to be similar

content/CSE510/CSE510_L21.md

@@ -0,0 +1,242 @@
+# CSE510 Deep Reinforcement Learning (Lecture 21)
+
+> Due to lack of my attention, this lecture note is generated by ChatGPT to create continuations of the previous lecture note.
+
+## Exploration in RL: Information-Based Exploration (Intrinsic Curiosity)
+
+### Computational Curiosity
+
+- "The direct goal of curiosity and boredom is to improve the world model."
+- Curiosity encourages agents to seek experiences that better predict or explain the environment.
+- A "curiosity unit" gives reward based on the mismatch between current model predictions and actual outcomes.
+- Intrinsic reward is high when the agent's prediction fails, that is, when it encounters surprising outcomes.
+- This yields positive intrinsic reinforcement when the internal predictive model errs, causing the agent to repeat actions that lead to prediction errors.
+- The agent is effectively motivated to create situations where its model fails.
+
+### Model Prediction Error as Intrinsic Reward
+
+We augment the reward with an intrinsic bonus based on model prediction error:
+
+$R(s, a, s') = r(s, a, s') + B(|T(s, a; \theta) - s'|)$
+
+Parameter explanations:
+
+- $s$: current state of the agent.
+- $a$: action taken by the agent in state $s$.
+- $s'$: next state resulting from executing action $a$ in state $s$.
+- $r(s, a, s')$: extrinsic environment reward for transition $(s, a, s')$.
+- $T(s, a; \theta)$: learned dynamics model with parameters $\theta$ that predicts the next state.
+- $\theta$: parameter vector of the predictive dynamics model $T$.
+- $|T(s, a; \theta) - s'|$: prediction error magnitude between predicted next state and actual next state.
+- $B(\cdot)$: function converting prediction error magnitude into an intrinsic reward bonus.
+- $R(s, a, s')$: total reward, sum of extrinsic reward and intrinsic curiosity bonus.
+
+Key ideas:
+
+- The agent receives an intrinsic reward $B(|T(s, a; \theta) - s'|)$ when the actual outcome differs from what its world model predicts.
+- Initially many transitions are surprising, encouraging broad exploration.
+- As the model improves, familiar transitions yield smaller error and smaller intrinsic reward.
+- Exploration becomes focused on less-known parts of the state space.
+- Intrinsic motivation is non-stationary: as the agent learns, previously novel states lose their intrinsic reward.
+
+#### Avoiding Trivial Curiosity Traps
+
+[link to paper](https://ar5iv.labs.arxiv.org/html/1705.05363#:~:text=reward%20signal%20based%20on%20how,this%20feature%20space%20using%20self)
+
+Naively defining $B(s, a, s')$ directly in raw observation space can lead to trivial curiosity traps.
+
+Examples:
+
+- The agent may purposely cause chaotic or noisy observations (like flickering pixels) that are impossible to predict.
+- The model cannot reduce prediction error on pure noise, so the agent is rewarded for meaningless randomness.
+- This yields high intrinsic reward without meaningful learning or progress toward task goals.
+
+To prevent this, we restrict prediction to a more informative feature space:
+
+$B(s, a, s') = |T(E(s; \phi), a; \theta) - E(s'; \phi)|$
+
+Parameter explanations:
+
+- $E(s; \phi)$: learned encoder mapping raw state $s$ into a feature vector.
+- $\phi$: parameter vector of the encoder $E$.
+- $T(E(s; \phi), a; \theta)$: forward model predicting next feature representation from encoded state and action.
+- $E(s'; \phi)$: encoded feature representation of the next state $s'$.
+- $B(s, a, s')$: intrinsic reward based on prediction error in feature space.
+
+Key ideas:
+
+- The encoder $E(s; \phi)$ is trained so that features capture aspects of the state that are controllable by the agent.
+- One approach is to train $E$ via an inverse dynamics model that predicts $a$ from $(s, s')$.
+- This encourages $E$ to keep only information necessary to infer actions, discarding irrelevant noise.
+- Measuring prediction error in feature space ignores unpredictable environmental noise.
+- Intrinsic reward focuses on errors due to lack of knowledge about controllable dynamics.
+- The agent's curiosity is directed toward aspects of the environment it can influence and learn.
+
+A practical implementation is the Intrinsic Curiosity Module (ICM) by Pathak et al. (2017):
+
+- The encoder $E$ and forward model $T$ are trained jointly.
+- The loss includes both forward prediction error and inverse dynamics error.
+- Intrinsic reward is set to the forward prediction error in feature space.
+- This drives exploration of states where the agent cannot yet predict the effect of its actions.
+
+#### Random Network Distillation (RND)
+
+Random Network Distillation (RND) provides a simpler curiosity bonus without learning a dynamics model.
+
+Basic idea:
+
+- Use a fixed random neural network $f_{\text{target}}$ that maps states to feature vectors.
+- Train a predictor network $f_{\text{pred}}$ to approximate $f_{\text{target}}$ on visited states.
+- The intrinsic reward is the prediction error between $f_{\text{pred}}(s)$ and $f_{\text{target}}(s)$.
+
+Typical form of the intrinsic reward:
+
+$r^{\text{int}}(s) = |f_{\text{pred}}(s; \psi) - f_{\text{target}}(s)|^{2}$
+
+Parameter explanations:
+
+- $f_{\text{target}}$: fixed random neural network generating target features for each state.
+- $f_{\text{pred}}(s; \psi)$: trainable predictor network with parameters $\psi$.
+- $\psi$: parameter vector for the predictor network.
+- $s$: state input to both networks.
+- $|f_{\text{pred}}(s; \psi) - f_{\text{target}}(s)|^{2}$: squared error between predictor and target features.
+- $r^{\text{int}}(s)$: intrinsic reward based on prediction error in random feature space.
+
+Key properties:
+
+- For novel or rarely visited states, $f_{\text{pred}}$ has not yet learned to match $f_{\text{target}}$, so error is high.
+- For frequently visited states, prediction error becomes small, and intrinsic reward decays.
+- The target network is random and fixed, so it does not adapt to the policy.
+- This provides a stable novelty signal without explicit dynamics learning.
+- RND achieves strong exploration performance in challenging environments, such as hard-exploration Atari games.
+
+### Efficacy of Curiosity-Driven Exploration
+
+Empirical observations:
+
+- Curiosity-driven intrinsic rewards often lead to significantly higher extrinsic returns in sparse-reward environments compared to agents trained only on extrinsic rewards.
+- Intrinsic rewards act as a proxy objective that guides the agent toward interesting or informative regions of the state space.
+- In some experiments, agents trained with only intrinsic rewards (no extrinsic reward during training) still learn behaviors that later achieve high task scores when extrinsic rewards are measured.
+- Using random features for curiosity (as in RND) can perform nearly as well as using learned features in many domains.
+- Simple surprise signals are often sufficient to drive effective exploration.
+- Learned feature spaces may generalize better to truly novel scenarios but are not always necessary.
+
+Historical context:
+
+- The concept of learning from intrinsic rewards alone is not new.
+- Itti and Baldi (2005) studied "Bayesian surprise" as a driver of human attention.
+- Schmidhuber (1991, 2010) formalized curiosity, creativity, and fun as intrinsic motivations in learning agents.
+- Singh et al. (2004) proposed intrinsically motivated reinforcement learning frameworks.
+- These early works laid the conceptual foundation for modern curiosity-driven deep RL methods.
+
+For further reading on intrinsic curiosity methods:
+
+- Pathak et al., "Curiosity-driven Exploration by Self-supervised Prediction", 2017.
+- Burda et al., "Exploration by Random Network Distillation", 2018.
+- Schmidhuber, "Formal Theory of Creativity, Fun, and Intrinsic Motivation", 2010.
+
+## Exploration via Posterior Sampling
+
+While optimistic and curiosity bonus methods modify the reward function, posterior sampling approaches handle exploration by maintaining uncertainty over models or value functions and sampling from this uncertainty.
+
+These methods are rooted in Thompson Sampling and naturally balance exploration and exploitation.
+
+### Posterior Sampling in Multi-Armed Bandits (Thompson Sampling)
+
+In a multi-armed bandit problem (no state transitions), Thompson Sampling works as follows:
+
+1. Maintain a prior and posterior distribution over the reward parameters for each arm.
+2. At each time step, sample reward parameters for all arms from their current posterior.
+3. Select the arm with the highest sampled mean reward.
+4. Observe the reward, update the posterior, and repeat.
+
+Intuition:
+
+- Each action is selected with probability equal to the posterior probability that it is optimal.
+- Arms with high uncertainty are more likely to be sampled as optimal in some posterior draws.
+- Exploration arises naturally from uncertainty, without explicit epsilon-greedy noise or bonus terms.
+- Over time, the posterior concentrates on the true reward means, and the algorithm shifts toward exploitation.
+
+Theoretical properties:
+
+- Thompson Sampling attains near-optimal regret bounds in many bandit settings.
+- It often performs as well as or better than upper confidence bound algorithms in practice.
+
+### Posterior Sampling for Reinforcement Learning (PSRL)
+
+In reinforcement learning with states and transitions, posterior sampling generalizes to sampling entire MDP models.
+
+Posterior Sampling for Reinforcement Learning (PSRL) operates as follows:
+
+1. Maintain a posterior distribution over environment dynamics and rewards, based on observed transitions.
+2. At the beginning of an episode, sample an MDP model from this posterior.
+3. Compute the optimal policy for the sampled MDP (for example, by value iteration).
+4. Execute this policy in the real environment for the whole episode.
+5. Use the observed transitions to update the posterior, then repeat.
+
+Key advantages:
+
+- The agent commits to a sampled model's policy for an extended duration, which induces deep exploration.
+- If a sampled model is optimistic in unexplored regions, the corresponding policy will deliberately visit those regions.
+- Exploration is coherent across time within an episode, unlike per-step randomization in epsilon-greedy.
+- The method does not require ad hoc exploration bonuses; exploration is an emergent property of the posterior.
+
+Challenges:
+
+- Maintaining an exact posterior over high-dimensional MDPs is usually intractable.
+- Practical implementations use approximations.
+
+### Approximate Posterior Sampling with Ensembles (Bootstrapped DQN)
+
+A common approximate posterior method in deep RL is Bootstrapped DQN.
+
+Basic idea:
+
+- Train an ensemble of $K$ Q-networks (heads), $Q^{(1)}, \dots, Q^{(K)}$.
+- Each head is trained on a different bootstrap sample or masked subset of experience.
+- At the start of each episode, sample a head index $k$ uniformly from ${1, \dots, K}$.
+- For the entire episode, act greedily with respect to $Q^{(k)}$.
+
+Parameter definitions for the ensemble:
+
+- $K$: number of Q-network heads in the ensemble.
+- $Q^{(k)}(s, a)$: Q-value estimate for head $k$ at state-action pair $(s, a)$.
+- $k$: index of the sampled head used for the current episode.
+- $(s, a)$: state and action arguments to Q-value functions.
+
+Implementation details:
+
+- A shared feature backbone network processes state inputs, feeding into all heads.
+- Each head has its own final layers, allowing diverse value estimates.
+- Masking or bootstrapping assigns different subsets of transitions to different heads during training.
+
+Benefits:
+
+- Each head approximates a different plausible Q-function, analogous to a sample from a posterior.
+- When a head is optimistic about certain under-explored actions, its greedy policy will explore them deeply.
+- Exploration behavior is temporally consistent within an episode.
+- No modification of the reward function is required; exploration arises from policy randomization via multiple heads.
+
+Comparison to epsilon-greedy:
+
+- Epsilon-greedy adds per-step random actions, which can be inefficient for long-horizon exploration.
+- Bootstrapped DQN commits to a strategy for an episode, enabling the agent to execute complete exploratory plans.
+- This can dramatically increase the probability of discovering long sequences needed to reach sparse rewards.
+
+Other approximate posterior approaches:
+
+- Bayesian neural networks for Q-functions (explicit parameter distributions).
+- Using Monte Carlo dropout at inference to sample Q-functions.
+- Randomized prior functions added to Q-networks to maintain exploration.
+
+Theoretical insights:
+
+- Posterior sampling methods can enjoy strong regret bounds in some RL settings.
+- They can have better asymptotic constants than optimism-based methods in certain problems.
+- Coherent, temporally extended exploration is essential in environments with delayed rewards and complex goals.
+
+For further reading:
+
+- Osband et al., "Deep Exploration via Bootstrapped DQN", 2016.
+- Osband and Van Roy, "Why Is Posterior Sampling Better Than Optimism for Reinforcement Learning?", 2017.
+- Chapelle and Li, "An Empirical Evaluation of Thompson Sampling", 2011.

content/CSE510/CSE510_L22.md

@@ -0,0 +1,296 @@
+# CSE510 Deep Reinforcement Learning (Lecture 22)
+
+> Due to lack of my attention, this lecture note is generated by ChatGPT to create continuations of the previous lecture note.
+
+## Offline Reinforcement Learning: Introduction and Challenges
+
+Offline reinforcement learning (offline RL), also called batch RL, aims to learn an optimal policy -without- interacting with the environment. Instead, the agent is given a fixed dataset of transitions collected by an unknown behavior policy.
+
+### The Offline RL Dataset
+
+We are given a static dataset:
+
+$$
+D = { (s_i, a_i, s'-i, r_i ) }-{i=1}^N
+$$
+
+Parameter explanations:
+
+- $s_i$: state sampled from behavior policy state distribution.
+- $a_i$: action selected by the behavior policy $\pi_beta$.
+- $s'_i$: next state sampled from environment dynamics $p(s'|s,a)$.
+- $r_i$: reward observed for transition $(s_i,a_i)$.
+- $N$: total number of transitions in the dataset.
+- $D$: full offline dataset used for training.
+
+The goal is to learn a new policy $\pi$ maximizing expected discounted return using only $D$:
+
+$$
+\max_{\pi} ; \mathbb{E}\Big[\sum_{t=0}^T \gamma^t r(s_t, a_t)\Big]
+$$
+
+Parameter explanations:
+
+- $\pi$: policy we want to learn.
+- $r(s,a)$: reward received for state-action pair.
+- $\gamma$: discount factor controlling weight of future rewards.
+- $T$: horizon or trajectory length.
+
+### Why Offline RL Is Difficult
+
+Offline RL is fundamentally harder than online RL because:
+
+- The agent cannot try new actions to fix wrong value estimates.
+- The policy may choose out-of-distribution actions not present in $D$.
+- Q-value estimates for unseen actions can be arbitrarily incorrect.
+- Bootstrapping on wrong Q-values can cause divergence.
+
+This leads to two major failure modes:
+
+1. --Distribution shift--: new policy actions differ from dataset actions.
+2. --Extrapolation error--: the Q-function guesses values for unseen actions.
+
+### Extrapolation Error Problem
+
+In standard Q-learning, the Bellman backup is:
+
+$$
+Q(s,a) \leftarrow r + \gamma \max_{a'} Q(s', a')
+$$
+
+Parameter explanations:
+
+- $Q(s,a)$: estimated value of taking action $a$ in state $s$.
+- $\max_{a'}$: maximum over possible next actions.
+- $a'$: candidate next action for evaluation in backup step.
+
+If $a'$ was rarely or never taken in the dataset, $Q(s',a')$ is poorly estimated, so Q-learning boots off invalid values, causing instability.
+
+### Behavior Cloning (BC): The Safest Baseline
+
+The simplest offline method is to imitate the behavior policy:
+
+$$
+\max_{\phi} ; \mathbb{E}_{(s,a) \sim D}[\log \pi_{\phi}(a|s)]
+$$
+
+Parameter explanations:
+
+- $\phi$: neural network parameters of the cloned policy.
+- $\pi_{\phi}$: learned policy approximating behavior policy.
+- $\log \pi_{\phi}(a|s)$: negative log-likelihood loss.
+
+Pros:
+
+- Does not suffer from extrapolation error.
+- Extremely stable.
+
+Cons:
+
+- Cannot outperform the behavior policy.
+- Ignores reward information entirely.
+
+### Naive Offline Q-Learning Fails
+
+Directly applying off-policy Q-learning on $D$ generally leads to:
+
+- Overestimation of unseen actions.
+- Divergence due to extrapolation error.
+- Policies worse than behavior cloning.
+
+## Strategies for Safe Offline RL
+
+There are two primary families of solutions:
+
+1. --Policy constraint methods--
+2. --Conservative value estimation methods--
+
+## 1. Policy Constraint Methods
+
+These methods restrict the learned policy to stay close to the behavior policy so it does not take unsupported actions.
+
+### Advantage Weighted Regression (AWR / AWAC)
+
+Policy update:
+
+$$
+\pi(a|s) \propto \pi_{beta}(a|s)\exp\left(\frac{1}{\lambda}A(s,a)\right)
+$$
+
+Parameter explanations:
+
+- $\pi_{beta}$: behavior policy used to collect dataset.
+- $A(s,a)$: advantage function derived from Q or V estimates.
+- $\lambda$: temperature controlling strength of advantage weighting.
+- $\exp(\cdot)$: positive weighting on high-advantage actions.
+
+Properties:
+
+- Uses advantages to filter good and bad actions.
+- Improves beyond behavior policy while staying safe.
+
+### Batch-Constrained Q-learning (BCQ)
+
+BCQ constrains the policy using a generative model:
+
+1. Train a VAE $G_{\omega}$ to model $a$ given $s$.
+2. Train a small perturbation model $\xi$.
+3. Limit the policy to $a = G_{\omega}(s) + \xi(s)$.
+
+Parameter explanations:
+
+- $G_{\omega}(s)$: VAE-generated action similar to data actions.
+- $\omega$: VAE parameters.
+- $\xi(s)$: small correction to generated actions.
+- $a$: final policy action constrained near dataset distribution.
+
+BCQ avoids selecting unseen actions and strongly reduces extrapolation.
+
+### BEAR (Bootstrapping Error Accumulation Reduction)
+
+BEAR adds explicit constraints:
+
+$$
+D_{MMD}\left(\pi(a|s), \pi_{beta}(a|s)\right) < \epsilon
+$$
+
+Parameter explanations:
+
+- $D_{MMD}$: Maximum Mean Discrepancy distance between action distributions.
+- $\epsilon$: threshold restricting policy deviation from behavior policy.
+
+BEAR controls distribution shift more tightly than BCQ.
+
+## 2. Conservative Value Function Methods
+
+These methods modify Q-learning so Q-values of unseen actions are -underestimated-, preventing the policy from exploiting overestimated values.
+
+### Conservative Q-Learning (CQL)
+
+One formulation is:
+
+$$
+J(Q) = J_{TD}(Q) + \alpha\big(\mathbb{E}_{a\sim\pi(\cdot|s)}Q(s,a) - \mathbb{E}_{a\sim D}Q(s,a)\big)
+$$
+
+Parameter explanations:
+
+- $J_{TD}$: standard Bellman TD loss.
+- $\alpha$: weight of conservatism penalty.
+- $\mathbb{E}_{a\sim\pi(\cdot|s)}$: expectation over policy-chosen actions.
+- $\mathbb{E}_{a\sim D}$: expectation over dataset actions.
+
+Effect:
+
+- Increases Q-values of dataset actions.
+- Decreases Q-values of out-of-distribution actions.
+
+### Implicit Q-Learning (IQL)
+
+IQL avoids constraints entirely by using expectile regression:
+
+Value regression:
+
+$$
+V(s) = \arg\min_{v} ; \mathbb{E}\big[\rho_{\tau}(Q(s,a) - v)\big]
+$$
+
+Parameter explanations:
+
+- $v$: scalar value estimate for state $s$.
+- $\rho_{\tau}(x)$: expectile regression loss.
+- $\tau$: expectile parameter controlling conservatism.
+- $Q(s,a)$: Q-value estimate.
+
+Key idea:
+
+- For $\tau < 1$, IQL reduces sensitivity to large (possibly incorrect) Q-values.
+- Implicitly conservative without special constraints.
+
+IQL often achieves state-of-the-art performance due to simplicity and stability.
+
+## Model-Based Offline RL
+
+### Forward Model-Based RL
+
+Train a dynamics model:
+
+$$
+p_{\theta}(s'|s,a)
+$$
+
+Parameter explanations:
+
+- $p_{\theta}$: learned transition model.
+- $\theta$: parameters of transition model.
+
+We can generate synthetic transitions using $p_{\theta}$, but model error accumulates.
+
+### Penalty-Based Model Approaches (MOPO, MOReL)
+
+Add uncertainty penalty:
+
+$$
+r_{model}(s,a) = r(s,a) - \beta , u(s,a)
+$$
+
+Parameter explanations:
+
+- $r_{model}$: penalized reward for model rollouts.
+- $u(s,a)$: model uncertainty estimate.
+- $\beta$: penalty coefficient.
+
+These methods limit exploration into unknown model regions.
+
+## Reverse Model-Based Imagination (ROMI)
+
+ROMI generates new training data by -backward- imagination.
+
+### Reverse Dynamics Model
+
+ROMI learns:
+
+$$
+p_{\psi}(s_{t} \mid s_{t+1}, a_{t})
+$$
+
+Parameter explanations:
+
+- $\psi$: parameters of reverse dynamics model.
+- $s_{t+1}$: later state.
+- $a_{t}$: action taken leading to $s_{t+1}$.
+- $s_{t}$: predicted predecessor state.
+
+ROMI also learns a reverse policy for sampling likely predecessor actions.
+
+### Reverse Imagination Process
+
+Given a goal state $s_{g}$:
+
+1. Sample $a_{t}$ from reverse policy.
+2. Predict $s_{t}$ from reverse dynamics.
+3. Form imagined transition $(s_{t}, a_{t}, s_{t+1})$.
+4. Repeat to build longer imagined trajectories.
+
+Benefits:
+
+- Imagined transitions end in real states, ensuring grounding.
+- Completes missing parts of dataset.
+- Helps propagate reward backward reliably.
+
+ROMI combined with conservative RL often outperforms standard offline methods.
+
+# Summary of Lecture 22
+
+Offline RL requires balancing:
+
+- Improvement beyond dataset behavior.
+- Avoiding unsafe extrapolation to unseen actions.
+
+Three major families of solutions:
+
+1. Policy constraints (BCQ, BEAR, AWR)
+2. Conservative Q-learning (CQL, IQL)
+3. Model-based conservatism and imagination (MOPO, MOReL, ROMI)
+
+Offline RL is becoming practical for real-world domains such as healthcare, robotics, autonomous driving, and recommender systems.

content/CSE510/CSE510_L23.md

@@ -0,0 +1,162 @@
+# CSE510 Deep Reinforcement Learning (Lecture 23)
+
+> Due to lack of my attention, this lecture note is generated by ChatGPT to create continuations of the previous lecture note.
+
+## Offline Reinforcement Learning Part II: Advanced Approaches
+
+Lecture 23 continues with advanced topics in offline RL, expanding on model-based imagination methods and credit assignment structures relevant for offline multi-agent and single-agent settings.
+
+## Reverse Model-Based Imagination (ROMI)
+
+ROMI is a method for augmenting an offline dataset with additional transitions generated by imagining trajectories -backwards- from desirable states. Unlike forward model rollouts, backward imagination stays grounded in real data because imagined transitions always terminate in dataset states.
+
+### Reverse Dynamics Model
+
+ROMI learns a reverse dynamics model:
+
+$$
+p_{\psi}(s_{t} \mid s_{t+1}, a_{t})
+$$
+
+Parameter explanations:
+
+- $p_{\psi}$: learned reverse transition model.
+- $\psi$: parameter vector for the reverse model.
+- $s_{t+1}$: next state (from dataset).
+- $a_{t}$: action that hypothetically leads into $s_{t+1}$.
+- $s_{t}$: predicted predecessor state.
+
+ROMI also learns a reverse policy to sample actions that likely lead into known states:
+
+$$
+\pi_{rev}(a_{t} \mid s_{t+1})
+$$
+
+Parameter explanations:
+
+- $\pi_{rev}$: reverse policy distribution.
+- $a_{t}$: action sampled for backward trajectory generation.
+- $s_{t+1}$: state whose predecessors are being imagined.
+
+### Reverse Imagination Process
+
+To generate imagined transitions:
+
+1. Select a goal or high-value state $s_{g}$ from the offline dataset.
+2. Sample $a_{t}$ from $\pi_{rev}(a_{t} \mid s_{g})$.
+3. Predict $s_{t}$ from $p_{\psi}(s_{t} \mid s_{g}, a_{t})$.
+4. Form an imagined transition $(s_{t}, a_{t}, s_{g})$.
+5. Repeat backward to obtain a longer imagined trajectory.
+
+Benefits:
+
+- Imagined states remain grounded by terminating in real dataset states.
+- Helps propagate reward signals backward through states not originally visited.
+- Avoids runaway model error that occurs in forward model rollouts.
+
+ROMI effectively fills in missing gaps in the state-action graph, improving training stability and performance when paired with conservative offline RL algorithms.
+
+## Implicit Credit Assignment via Value Factorization Structures
+
+Although initially studied for multi-agent systems, insights from value factorization also improve offline RL by providing structured credit assignment signals.
+
+### Counterfactual Credit Assignment Insight
+
+A factored value function structure of the form:
+
+$$
+Q_{tot}(s, a_{1}, \dots, a_{n}) = f(Q_{1}(s, a_{1}), \dots, Q_{n}(s, a_{n}))
+$$
+
+can implicitly implement counterfactual credit assignment.
+
+Parameter explanations:
+
+- $Q_{tot}$: global value function.
+- $Q_{i}(s,a_{i})$: individual component value for agent or subsystem $i$.
+- $f(\cdot)$: mixing function combining components.
+- $s$: environment state.
+- $a_{i}$: action taken by entity $i$.
+
+In architectures designed for IGM (Individual-Global-Max) consistency, gradients backpropagated through $f$ isolate the marginal effect of each component. This implicitly gives each agent or subsystem a counterfactual advantage signal.
+
+Even in single-agent structured RL, similar factorization structures allow credit flowing into components representing skills, modes, or action groups, enabling better temporal and structural decomposition.
+
+## Model-Based vs Model-Free Offline RL
+
+Lecture 23 contrasts model-based imagination (ROMI) with conservative model-free methods such as IQL and CQL.
+
+### Forward Model-Based Rollouts
+
+Forward imagination using a learned model:
+
+$$
+p_{\theta}(s'|s,a)
+$$
+
+Parameter explanations:
+
+- $p_{\theta}$: learned forward dynamics model.
+- $\theta$: parameters of the forward model.
+- $s'$: predicted next state.
+- $s$: current state.
+- $a$: action taken in current state.
+
+Problems:
+
+- Forward rollouts drift away from dataset support.
+- Model error compounds with each step.
+- Leads to training instability if used without penalties.
+
+### Penalty Methods (MOPO, MOReL)
+
+Augmented reward:
+
+$$
+r_{model}(s,a) = r(s,a) - \beta u(s,a)
+$$
+
+Parameter explanations:
+
+- $r_{model}(s,a)$: penalized reward for model-generated steps.
+- $u(s,a)$: uncertainty score of model for state-action pair.
+- $\beta$: penalty coefficient.
+- $r(s,a)$: original reward.
+
+These methods limit exploration into uncertain model regions.
+
+### ROMI vs Forward Rollouts
+
+- Forward methods expand state space beyond dataset.
+- ROMI expands -backward-, staying consistent with known good future states.
+- ROMI reduces error accumulation because future anchors are real.
+
+## Combining ROMI With Conservative Offline RL
+
+ROMI is typically combined with:
+
+- CQL (Conservative Q-Learning)
+- IQL (Implicit Q-Learning)
+- BCQ and BEAR (policy constraint methods)
+
+Workflow:
+
+1. Generate imagined transitions via ROMI.
+2. Add them to dataset.
+3. Train Q-function or policy using conservative losses.
+
+Benefits:
+
+- Better coverage of reward-relevant states.
+- Increased policy improvement over dataset.
+- More stable Q-learning backups.
+
+## Summary of Lecture 23
+
+Key points:
+
+- Offline RL can be improved via structured imagination.
+- ROMI creates safe imagined transitions by reversing dynamics.
+- Reverse imagination avoids pitfalls of forward model error.
+- Factored value structures provide implicit counterfactual credit assignment.
+- Combining ROMI with conservative learners yields state-of-the-art performance.

content/CSE510/CSE510_L24.md

@@ -0,0 +1,244 @@
+# CSE510 Deep Reinforcement Learning (Lecture 24)
+
+## Cooperative Multi-Agent Reinforcement Learning (MARL)
+
+This lecture introduces cooperative multi-agent reinforcement learning, focusing on formal models, value factorization, and modern algorithms such as QMIX and QPLEX.
+
+## Multi-Agent Coordination Under Uncertainty
+
+In cooperative MARL, multiple agents aim to maximize a shared team reward. The environment can be modeled using a Markov game or a Decentralized Partially Observable MDP (Dec-POMDP).
+
+A transition is defined as:
+
+$$
+P(s' \mid s, a_{1}, \dots, a_{n})
+$$
+
+Parameter explanations:
+
+- $s$: current global state.
+- $s'$: next global state.
+- $a_{i}$: action taken by agent $i$.
+- $P(\cdot)$: environment transition function.
+
+The shared return is:
+
+$$
+\mathbb{E}\left[\sum_{t=0}^{T} \gamma^{t} r_{t}\right]
+$$
+
+Parameter explanations:
+
+- $\gamma$: discount factor.
+- $T$: horizon length.
+- $r_{t}$: shared team reward at time $t$.
+
+### CTDE: Centralized Training, Decentralized Execution
+
+Training uses global information (centralized), but execution uses local agent observations. This is critical for real-world deployment.
+
+## Joint vs Factored Q-Learning
+
+### Joint Q-Learning
+
+In joint-action learning, one learns a full joint Q-function:
+
+$$
+Q_{tot}(s, a_{1}, \dots, a_{n})
+$$
+
+Parameter explanations:
+
+- $Q_{tot}$: joint value for the entire team.
+- $(a_{1}, \dots, a_{n})$: joint action vector across agents.
+
+Problem:
+
+- The joint action space grows exponentially in $n$.
+- Learning is not scalable.
+
+### Value Factorization
+
+Instead of learning $Q_{tot}$ directly, we factorize it into individual utility functions:
+
+$$
+Q_{tot}(s, \mathbf{a}) = f(Q_{1}(s,a_{1}), \dots, Q_{n}(s,a_{n}))
+$$
+
+Parameter explanations:
+
+- $\mathbf{a}$: joint action vector.
+- $f(\cdot)$: mixing network combining individual Q-values.
+
+The goal is to enable decentralized greedy action selection.
+
+## Individual-Global-Max (IGM) Condition
+
+The IGM condition enables decentralized optimal action selection:
+
+$$
+\arg\max_{\mathbf{a}} Q_{tot}(s,\mathbf{a})=
+
+\big(\arg\max_{a_{1}} Q_{1}(s,a_{1}), \dots, \arg\max_{a_{n}} Q_{n}(s,a_{n})\big)
+$$
+
+Parameter explanations:
+
+- $\arg\max_{\mathbf{a}}$: search for best joint action.
+- $\arg\max_{a_{i}}$: best local action for agent $i$.
+- $Q_{i}(s,a_{i})$: individual utility for agent $i$.
+
+IGM makes decentralized execution optimal with respect to the learned factorized value.
+
+## Linear Value Factorization
+
+### VDN (Value Decomposition Networks)
+
+VDN assumes:
+
+$$
+Q_{tot}(s,\mathbf{a}) = \sum_{i=1}^{n} Q_{i}(s,a_{i})
+$$
+
+Parameter explanations:
+
+- $Q_{i}(s,a_{i})$: value of agent $i$'s action.
+- $\sum_{i=1}^{n}$: linear sum over agents.
+
+Pros:
+
+- Very simple, satisfies IGM.
+- Fully decentralized execution.
+
+Cons:
+
+- Limited representation capacity.
+- Cannot model non-linear teamwork interactions.
+
+## QMIX: Monotonic Value Factorization
+
+QMIX uses a state-conditioned mixing network enforcing monotonicity:
+
+$$
+\frac{\partial Q_{tot}}{\partial Q_{i}} \ge 0
+$$
+
+Parameter explanations:
+
+- $\partial Q_{tot} / \partial Q_{i}$: gradient of global Q w.r.t. individual Q.
+- $\ge 0$: ensures monotonicity required for IGM.
+
+The mixing function is:
+
+$$
+Q_{tot}(s,\mathbf{a}) = f_{mix}(Q_{1}, \dots, Q_{n}; s)
+$$
+
+Parameter explanations:
+
+- $f_{mix}$: neural network with non-negative weights.
+- $s$: global state conditioning the mixing process.
+
+Benefits:
+
+- More expressive than VDN.
+- Supports CTDE while keeping decentralized greedy execution.
+
+## Theoretical Issues With Linear and Monotonic Factorization
+
+Limitations:
+
+- Linear models (VDN) cannot represent complex coordination.
+- QMIX monotonicity limits representation power for tasks requiring non-monotonic interactions.
+- Off-policy training can diverge in some factorizations.
+
+## QPLEX: Duplex Dueling Multi-Agent Q-Learning
+
+QPLEX introduces a dueling architecture that satisfies IGM while providing full representation capacity within the IGM class.
+
+### QPLEX Advantage Factorization
+
+QPLEX factorizes:
+
+$$
+Q_{tot}(s,\mathbf{a}) = \sum_{i=1}^{n} \lambda_{i}(s,\mathbf{a})\big(Q_{i}(s,a_{i}) - \max_{a'-{i}} Q_{i}(s,a'-{i})\big)
+
+- \max_{\mathbf{a}} \sum_{i=1}^{n} Q_{i}(s,a_{i})
+  $$
+
+Parameter explanations:
+
+- $\lambda_{i}(s,\mathbf{a})$: positive mixing coefficients.
+- $Q_{i}(s,a_{i})$: individual utility.
+- $\max_{a'-{i}} Q_{i}(s,a'-{i})$: per-agent baseline value.
+- $\max_{\mathbf{a}}$: maximization over joint actions.
+
+QPLEX Properties:
+
+- Fully satisfies IGM.
+- Has full representation capacity for all IGM-consistent Q-functions.
+- Enables stable off-policy training.
+
+## QPLEX Training Objective
+
+QPLEX minimizes a TD loss over $Q_{tot}$:
+
+$$
+L = \mathbb{E}\Big[(r + \gamma \max_{\mathbf{a'}} Q_{tot}(s',\mathbf{a'}) - Q_{tot}(s,\mathbf{a}))^{2}\Big]
+$$
+
+Parameter explanations:
+
+- $r$: shared team reward.
+- $\gamma$: discount factor.
+- $s'$: next state.
+- $\mathbf{a'}$: next joint action evaluated by TD target.
+- $Q_{tot}$: QPLEX global value estimate.
+
+## Role of Credit Assignment
+
+Credit assignment addresses: "Which agent contributed what to the team reward?"
+
+Value factorization supports implicit credit assignment:
+
+- Gradients into each $Q_{i}$ act as counterfactual signals.
+- Dueling architectures allow each agent to learn its influence.
+- QPLEX provides clean marginal contributions implicitly.
+
+## Performance on SMAC Benchmarks
+
+QPLEX outperforms:
+
+- QTRAN
+- QMIX
+- VDN
+- Other CTDE baselines
+
+Key reasons:
+
+- Effective realization of IGM.
+- Strong representational capacity.
+- Off-policy stability.
+
+## Extensions: Diversity and Shared Parameter Learning
+
+Parameter sharing encourages sample efficiency, but can cause homogeneous agent behavior.
+
+Approaches such as CDS (Celebrating Diversity in Shared MARL) introduce:
+
+- Identity-aware diversity.
+- Information-based intrinsic rewards for agent differentiation.
+- Balanced sharing vs agent specialization.
+
+These techniques improve exploration and cooperation in complex multi-agent tasks.
+
+## Summary of Lecture 24
+
+Key points:
+
+- Cooperative MARL requires scalable value decomposition.
+- IGM enables decentralized action selection from centralized training.
+- QMIX introduces monotonic non-linear factorization.
+- QPLEX achieves full IGM representational capacity.
+- Implicit credit assignment arises naturally from factorization.
+- Diversity methods allow richer multi-agent coordination strategies.

content/CSE510/_meta.js

@@ -1,23 +1,61 @@
 export default {
-    index: "Course Description",
-    "---":{
-        type: 'separator'
+    menu: {
+      title: 'Home',
+      type: 'menu',
+      items: {
+        index: {
+          title: 'Home',
+          href: '/'
         },
-    CSE510_L1: "CSE510 Deep Reinforcement Learning (Lecture 1)",
-    CSE510_L2: "CSE510 Deep Reinforcement Learning (Lecture 2)",
-    CSE510_L3: "CSE510 Deep Reinforcement Learning (Lecture 3)",
-    CSE510_L4: "CSE510 Deep Reinforcement Learning (Lecture 4)",
-    CSE510_L5: "CSE510 Deep Reinforcement Learning (Lecture 5)",
-    CSE510_L6: "CSE510 Deep Reinforcement Learning (Lecture 6)",
-    CSE510_L7: "CSE510 Deep Reinforcement Learning (Lecture 7)",
-    CSE510_L8: "CSE510 Deep Reinforcement Learning (Lecture 8)",
-    CSE510_L9: "CSE510 Deep Reinforcement Learning (Lecture 9)",
-    CSE510_L10: "CSE510 Deep Reinforcement Learning (Lecture 10)",
-    CSE510_L11: "CSE510 Deep Reinforcement Learning (Lecture 11)",
-    CSE510_L12: "CSE510 Deep Reinforcement Learning (Lecture 12)",
-    CSE510_L13: "CSE510 Deep Reinforcement Learning (Lecture 13)",
-    CSE510_L14: "CSE510 Deep Reinforcement Learning (Lecture 14)",
-    CSE510_L15: "CSE510 Deep Reinforcement Learning (Lecture 15)",
-    CSE510_L16: "CSE510 Deep Reinforcement Learning (Lecture 16)",
-    CSE510_L17: "CSE510 Deep Reinforcement Learning (Lecture 17)",
-}
+        about: {
+          title: 'About',
+          href: '/about'
+        },
+        contact: {
+          title: 'Contact Me',
+          href: '/contact'
+        }
+      },
+    },
+    Math3200'CSE510_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Math429'CSE510_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Math4111'CSE510_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Math4121'CSE510_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Math4201'CSE510_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Math416'CSE510_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Math401'CSE510_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE332S'CSE510_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE347'CSE510_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE442T'CSE510_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE5313'CSE510_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE510'CSE510_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE559A'CSE510_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE5519'CSE510_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Swap: {
+      display: 'hidden',
+      theme:{
+        timestamp: true,
+      }
+    },
+    index: {
+      display: 'hidden',
+      theme:{
+        sidebar: false,
+        timestamp: true,
+      }
+    },
+    about: {
+      display: 'hidden',
+      theme:{
+        sidebar: false,
+        timestamp: true,
+      }
+    },
+    contact: {
+      display: 'hidden',
+      theme:{
+        sidebar: false,
+        timestamp: true,
+      }
+    }
+  }

content/CSE510/index.md

@@ -7,14 +7,17 @@ CSE 5100
 **Fall 2025**
 
 ## Instructor Information
+
 **Chongjie Zhang**  
 Office: McKelvey Hall 2010D  
 Email: chongjie@wustl.edu
 
 ### Instructor's Office Hours:
+
 Chongjie Zhang's Office Hours: Wednesdays 11:00 -12:00 am in Mckelvey Hall 2010D Or you may email me to make an appointment.
 
 ### TAs:
+
 - Jianing Ye: jianing.y@wustl.edu
 - Kefei Duan: d.kefei@wustl.edu
 - Xiu Yuan: xiu@wustl.edu
@@ -22,6 +25,7 @@ Chongjie Zhang's Office Hours: Wednesdays 11:00 -12:00 am in Mckelvey Hall 2010D
 **Office Hours:** Thursday 4:00pm -5:00pm in Mckelvey Hall 1030 (tentative) Or you may email TAs to make an appointment.
 
 ## Course Description
+
 Deep Reinforcement Learning (RL) is a cutting-edge field at the intersection of artificial intelligence and decision-making. This course provides an in-depth exploration of the fundamental principles, algorithms, and applications of deep reinforcement learning. We start from the Markov Decision Process (MDP) framework and cover basic RL algorithms—value-based, policy-based, actor–critic, and model-based methods—then move to advanced topics including offline RL and multi-agent RL. By combining deep learning with reinforcement learning, students will gain the skills to build intelligent systems that learn from experience and make near-optimal decisions in complex environments.
 
 The course caters to graduate and advanced undergraduate students. Student performance evaluation will revolve around written and programming assignments and the course project. 
@@ -39,6 +43,7 @@ By the end of this course, students should be able to:
 - Execute an end-to-end DRL project: problem selection, environment design, algorithm selection, experimental protocol, ablations, and reproducibility.
 
 ## Prerequisites
+
 If you are unsure about any of these, please speak to the instructor.
 
 - Proficiency in Python programming.
@@ -51,11 +56,13 @@ One of the following:
 - b) a Machine Learning course (CSE 417T or ESE 417).
 
 ## Textbook
+
 **Primary text** (optional but recommended): Sutton & Barto, Reinforcement Learning: An Introduction (2nd ed., online). We will not cover all of the chapters and, from time to time, cover topics not contained in the book.
 
 **Additional references:** Russell & Norvig, Artificial Intelligence: A Modern Approach (4th ed.); OpenAI Spinning Up in Deep RL tutorial.
 
 ## Homeworks
+
 There will be a total of three homework assignments distributed throughout the semester. Each assignment will be accessible on Canvas, allowing you approximately two weeks to finish and submit it before the designated deadline. 
 
 Late work will not be accepted. If you have a documented medical or emergency reason, contact the TAs as soon as possible.
@@ -65,21 +72,25 @@ Late work will not be accepted. If you have a documented medical or emergency re
 **Academic Integrity:** Do not copy from peers or online sources. Violations will be referred per university policy.
 
 ## Final Project
+
 A research‑level project of your choice that demonstrates mastery of DRL concepts and empirical methodology. Possible directions include: (a) improving an existing approach, (b) tackling an unsolved task/benchmark, (c) reproducing and extending a recent paper, or (d) creating a new task/problem relevant to RL.
 
 **Team size:** 1–2 students by default (contact instructor/TAs for approval if proposing a larger team).
 
 ### Milestones:
+
 - **Proposal:** ≤ 2 pages outlining problem, related work, methodology, evaluation plan, and risks.
 - **Progress report with short survey:** ≤ 4 pages with preliminary results or diagnostics.
 - **Presentation/Poster session:** brief talk or poster demo.
 - **Final report:** 7–10 pages (NeurIPS format) with clear experiments, ablations, and reproducibility details.
 
 ## Evaluation
+
 **Homework / Problem Sets (3) — 45%**  
 Each problem set combines written questions (derivations/short answers) and programming components (implementations and experiments).
 
 **Final Course Project — 50% total**
+
 - Proposal (max 2 pages) — 5% of project
 - Progress report with brief survey (max 4 pages) — 10% of project
 - Presentation/Poster session — 10% of project
@@ -91,7 +102,9 @@ Contributions in class and on the course discussion forum, especially in the pro
 **Course evaluations** (mid-semester and final course evaluations): extra credit up to 2%
 
 ## Grading Scale
+
 The intended grading scale is as follows. The instructor reserves the right to adjust the grading scale.
+
 - A's (A-,A,A+): >= 90%
 - B's (B-,B,B+): >= 80%
 - C's (C-,C,C+): >= 70%

content/CSE5313/CSE5313_L10.md

@@ -40,20 +40,20 @@ Let $G$ and $H$ be the generator and parity-check matrices of (any) linear code
 #### Lemma 1
 
 $$
-H G^T = 0
+H G^\top = 0
 $$
 
 <details>
 <summary>Proof</summary>
 
-By definition of generator matrix and parity-check matrix, $forall e_i\in H$, $e_iG^T=0$.
+By definition of generator matrix and parity-check matrix, $forall e_i\in H$, $e_iG^\top=0$.
 
-So $H G^T = 0$.
+So $H G^\top = 0$.
 </details>
 
 #### Lemma 2
 
-Any matrix $M\in \mathbb{F}_q^{(n-k)\times n}$ such that $\operatorname{rank}(M) = n - k$ and $M G^T = 0$ is a parity-check matrix for $C$ (i.e. $C = \ker M$).
+Any matrix $M\in \mathbb{F}_q^{(n-k)\times n}$ such that $\operatorname{rank}(M) = n - k$ and $M G^\top = 0$ is a parity-check matrix for $C$ (i.e. $C = \ker M$).
 
 <details>
 <summary>Proof</summary>
@@ -62,7 +62,7 @@ It is sufficient to show that the two statements
 
 1. $\forall c\in C, c=uG, u\in \mathbb{F}^k$
 
-$M c^T = M(uG)^T = M(G^T u^T) = 0$ since $M G^T = 0$.
+$M c^\top = M(uG)^\top = M(G^\top u^\top) = 0$ since $M G^\top = 0$.
 
 Thus $C \subseteq \ker M$.
 
@@ -84,15 +84,15 @@ We proceed by applying the lemma 2.
 
 1. $\operatorname{rank}(H) = n - k$ since $H$ is a Vandermonde matrix times a diagonal matrix with no zero entries, so $H$ is invertible.
 
-2. $H G^T = 0$.
+2. $H G^\top = 0$.
 
-note that $\forall$ row $i$ of $H$, $0\leq i\leq n-k-1$, $\forall$ column $j$ of $G^T$, $0\leq j\leq k-1$
+note that $\forall$ row $i$ of $H$, $0\leq i\leq n-k-1$, $\forall$ column $j$ of $G^\top$, $0\leq j\leq k-1$
 
 So
 
 $$
 \begin{aligned}
-H G^T &= \begin{bmatrix}
+H G^\top &= \begin{bmatrix}
 1 & 1 & \cdots & 1\\
 \alpha_1 & \alpha_2 & \cdots & \alpha_n\\
 \alpha_1^2 & \alpha_2^2 & \cdots & \alpha_n^2\\

content/CSE5313/CSE5313_L11.md

@@ -101,7 +101,7 @@ $$
 
 Let $\mathcal{C}=[n,k,d]_q$.
 
-The dual code of $\mathcal{C}$ is $\mathcal{C}^\perp=\{x\in \mathbb{F}^n_q|xc^T=0\text{ for all }c\in \mathcal{C}\}$.
+The dual code of $\mathcal{C}$ is $\mathcal{C}^\perp=\{x\in \mathbb{F}^n_q|xc^\top=0\text{ for all }c\in \mathcal{C}\}$.
 
 <details>
 <summary>Example</summary>
@@ -151,7 +151,7 @@ So $\langle f,h\rangle=0$.
 <details>
 <summary>Proof for the theorem</summary>
 
-Recall that the dual code of $\operatorname{RM}(r,m)^\perp=\{x\in \mathbb{F}_2^m|xc^T=0\text{ for all }c\in \operatorname{RM}(r,m)\}$.
+Recall that the dual code of $\operatorname{RM}(r,m)^\perp=\{x\in \mathbb{F}_2^m|xc^\top=0\text{ for all }c\in \operatorname{RM}(r,m)\}$.
 
 So $\operatorname{RM}(m-r-1,m)\subseteq \operatorname{RM}(r,m)^\perp$.
 

content/CSE5313/CSE5313_L14.md

@@ -230,7 +230,7 @@ Step 1: Arrange the $B=\binom{k+1}{2}+k(d-k)$ symbols in a matrix $M$ follows:
 $$
 M=\begin{pmatrix}
 S & T\\
-T^T & 0
+T^\top & 0
 \end{pmatrix}\in \mathbb{F}_q^{d\times d}
 $$
 
@@ -267,15 +267,15 @@ Repair from (any) nodes $H = \{h_1, \ldots, h_d\}$.
 
 Newcomer contacts each $h_j$: “My name is $i$, and I’m lost.”
 
-Node $h_j$ sends $c_{h_j}M c_i^T$ (inner product).
+Node $h_j$ sends $c_{h_j}M c_i^\top$ (inner product).
 
-Newcomer assembles $C_H Mc_i^T$.
+Newcomer assembles $C_H Mc_i^\top$.
 
 $CH$ invertible by construction!
 
-- Recover $Mc_i^T$.
+- Recover $Mc_i^\top$.
 
-- Recover $c_i^TM$ ($M$ is symmetric)
+- Recover $c_i^\topM$ ($M$ is symmetric)
 
 #### Reconstruction on Product-Matrix MBR codes
 
@@ -292,9 +292,9 @@ DC assembles $C_D M$.
 
 $\Psi_D$ invertible by construction.
 
-- DC computes $\Psi_D^{-1}C_DM = (S+\Psi_D^{-1}\Delta_D^T, T)$
+- DC computes $\Psi_D^{-1}C_DM = (S+\Psi_D^{-1}\Delta_D^\top, T)$
 - DC obtains $T$.
-- Subtracts $\Psi_D^{-1}\Delta_D T^T$ from $S+\Psi_D^{-1}\Delta_D T^T$ to obtain $S$.
+- Subtracts $\Psi_D^{-1}\Delta_D T^\top$ from $S+\Psi_D^{-1}\Delta_D T^\top$ to obtain $S$.
 
 <details>
 <summary>Fill an example here please.</summary>

content/CSE5313/CSE5313_L17.md

@@ -0,0 +1,354 @@
+# CSE5313 Coding and information theory for data science (Lecture 17)
+
+## Shannon's coding Theorem
+
+**Shannon’s coding theorem**: For a discrete memoryless channel with capacity $C$,
+every rate $R < C = \max_{x\in \mathcal{X}} I(X; Y)$ is achievable.
+
+### Computing Channel Capacity
+
+$X$: channel input (per 1 channel use), $Y$: channel output (per 1 channel use).
+
+Let the rate of the code be $\frac{\log_F |C|}{n}$ (or $\frac{k}{n}$ if it is linear).
+
+The Binary Erasure Channel (BEC): analog of BSC, but the bits are lost (not corrupted).
+
+Let $\alpha$ be the fraction of erased bits.
+
+### Corollary: The capacity of the BEC is $C = 1 - \alpha$.
+
+<details>
+
+<summary>Proof</summary>
+
+$$
+\begin{aligned}
+C&=\max_{x\in \mathcal{X}} I(X;Y)\\
+&=\max_{x\in \mathcal{X}} (H(Y)-H(Y|X))\\
+&=H(Y)-H(\alpha)
+\end{aligned}
+$$
+
+Suppose we denote $Pr(X=1)\coloneqq p$.
+
+$Pr(Y=0)=Pr(X=0)Pr(no erasure)=(1-p)(1-\alpha)$
+
+$Pr(Y=1)=Pr(X=1)Pr(no erasure)=p(1-\alpha)$
+
+$Pr(Y=*)=\alpha$
+
+So,
+
+$$
+\begin{aligned}
+H(Y)&=H((1-p)(1-\alpha),p(1-\alpha),\alpha)\\
+&=(1-p)(1-\alpha)\log_2 ((1-p)(1-\alpha))+p(1-\alpha)\log_2 (p(1-\alpha))+\alpha\log_2 (\alpha)\\
+&=H(\alpha)+(1-\alpha)H(p)
+\end{aligned}
+$$
+
+So $I(X;Y)=H(Y)-H(Y|X)=H(\alpha)+(1-\alpha)H(p)-H(\alpha)=(1-\alpha)H(p)$
+
+So $C=\max_{x\in \mathcal{X}} I(X;Y)=\max_{p\in [0,1]} (1-\alpha)H(p)=(1-\alpha)$
+
+So the capacity of the BEC is $C = 1 - \alpha$.
+
+</details>
+
+### General interpretation of capacity
+
+Recall $I(X;Y)=H(Y)-H(Y|X)$.
+
+Edge case:
+
+- If $H(X|Y)=0$, then output $Y$ reveals all information about input $X$.
+  - rate of $R=I(X;Y)=H(Y)$ is possible. (same as information compression)
+- If $H(Y|X)=H(X)$, then $Y$ reveals no information about $X$.
+  - rate of $R=I(X;Y)=0$ no information is transferred.
+
+> [!NOTE]
+>
+> Compression is transmission without noise.
+
+## Side notes for Cryptography
+
+Goal: Quantify the amount of information that is leaked to the eavesdropper.
+
+- Let:
+  - $M$ be the message distribution.
+  - Let $Z$ be the cyphertext distribution.
+- How much information is leaked about $m$ to the eavesdropper (who sees $operatorname{Enc}(m)$)?
+- Idea: One-time pad.
+
+### One-time pad
+
+$M=\mathcal{M}=\{0,1\}^n$
+
+Suppose the Sender and Receiver agree on $k\sim U=\operatorname{Uniform}\{0,1\}^n$
+
+Let $operatorname{Enc}(m)=m\oplus k$
+
+Measure the information leaked to the eavesdropper (who sees $operatorname{Enc}(m)$).
+
+That is to compute $I(M;Z)=H(Z)-H(Z|M)$.
+
+<details>
+<summary>Proof</summary>
+
+Recall that $Z=M\oplus U$.
+
+So
+
+$$
+\begin{aligned}
+Pr(Z=z)&=\operatorname{Pr}(M\oplus U=z)\\
+&=\sum_{m\in \mathcal{M}} \operatorname{Pr}(M\oplus U=z|M=m) \text{by the law of total probability}\\
+&=\sum_{m\in \mathcal{M}} \operatorname{Pr}(M=m) \operatorname{Pr}(U=m\oplus z)\\
+&=\frac{1}{2^n} \sum_{m\in \mathcal{M}} \operatorname{Pr}(M=m)\text{message is uniformly distributed}\\
+&=\frac{1}{2^n}
+\end{aligned}
+$$
+
+$Z$ is uniformly distributed over $\{0,1\}^n$.
+
+So $H(Z)=\log_2 2^n=n$.
+
+$H(Z|M)=H(U)=n$ because $U$ is uniformly distributed over $\{0,1\}^n$.
+
+- Notice $m\oplus\{0,1\}^n=\{0,1\}^n$ for every $m\in \mathcal{M}$. (since $(\{0,1\}^n,\oplus)$ is a group)
+- For every $z\in \{0,1\}^n$, $Pr(m\oplus U=z)=Pr(U=z\oplus m)=2^{-n}$
+
+So $I(M;Z)=H(Z)-H(Z|M)=n-n=0$.
+
+</details>
+
+### Discussion of information theoretical privacy
+
+What does $I(Z;M)=0$ mean?
+
+- No information is leaked to the eavesdropper.
+- Regardless of the value of $M$ and $U$.
+- Regardless of any computational power.
+
+Information Theoretic privacy:
+
+- Guarantees given in terms of mutual information.
+- Remains private in the face of any computational power.
+- Remains private forever.
+
+Very strong form of privacy
+
+> [!NOTE]
+>
+> The mutual information is an average metric for privacy, no guarantee for any individual message.
+>
+> The one-time pad is so-far, the only known perfect privacy scheme.
+
+## The asymptotic equipartition property (AEP) and data compression
+
+> [!NOTE]
+>
+> This section will help us understand the limits of data compression.
+
+### The asymptotic equipartition property
+
+Idea: consider the space of all possible sequences produced by a random source, and focus on the "typical" ones.
+
+- Asymptotic in the sense that many of the results focus on the regime of large source sequences.
+- Fundamental to the concept of typical sets used in data compression.
+- The analog of the law of large numbers (LLN) in information theory.
+  - Direct consequence of the weak law.
+
+#### The law of large numbers
+
+The average of outcomes obtained from a large number of trials is close to the expected value of the random variable.
+
+For independent and identically distributed (i.i.d.) random variables $X_1,X_2,\cdots,X_n$, with expected value $\mathbb{E}[X_i]=\mu$, the sample average
+
+$$
+\overline{X}_n=\frac{1}{n}\sum_{i=1}^n X_i
+$$
+
+converges to the expected value $\mu$ as $n$ goes to infinity.
+
+#### The weak law of large numbers
+
+converges in probability to the expected value $\mu$
+
+$$
+\overline{X}_n^p\to \mu\text{ as }n\to\infty
+$$
+
+That is,
+
+$$
+\lim_{n\to\infty} P\left(|\overline{X}_n<\epsilon)=1
+$$
+
+for any positive $\epsilon$.
+
+> Intuitively, for any nonzero margin $\epsilon$, no matter how small, with a sufficiently large sample there will be a very high probability that the average of the observations will be close to the expected value (within the margin)
+
+#### The AEP
+
+Let $X$ be an i.i.d source that takes values in alphabet $\mathcal{X}$ and produces a sequence of i.i.d. random variables $X_1, \cdots, X_n$.
+
+Let $p(X_1, \cdots, X_n)$ be the probability of observing the sequence $X_1, \cdots, X_n$.
+
+Theorem (AEP):
+
+$$
+-\frac{1}{n} \log p(X_1, \cdots, X_n) \xrightarrow{p} H(X)\text{ as }n\to \infty
+$$
+
+<details>
+<summary>Proof</summary>
+
+$\frac{1}{n} \log p(X_1, \cdots, X_n) = \frac{1}{n} \sum_{i=1}^n \log p(X_i)$
+
+The $\log p(X_i)$ terms are also i.i.d. random variables.
+
+So by the weak law of large numbers,
+
+$$
+\frac{1}{n} \sum_{i=1}^n \log p(X_i) \xrightarrow{p} \mathbb{E}[\log p(X_i)]=H(X)
+$$
+
+$$
+-\mathbb{E}[\log p(X_i)]=\mathbb{E}[\log \frac{1}{p(X_i)}]=H(X)
+$$
+
+</details>
+
+### Typical sets
+
+#### Definition of typical set
+
+The typical set (denoted by $A_\epsilon^{(n)}$) with respect to $p(x)$ is the set of sequence $(x_1, \cdots, x_n)\in \mathcal{X}^n$ that satisfies
+
+$$
+2^{-n(H(X)-\epsilon)}\leq p(x_1, \cdots, x_n)\leq 2^{-n(H(X)+\epsilon)}
+$$
+
+In other words, the typical set contains all $n$-length sequences with probability close to $2^{-nH(X)}$.
+
+- This notion of typicality only concerns the probability of a sequence and not the actual sequence itself.
+- It has great use in compression theory.
+
+#### Properties of the typical set
+
+- If $(x_1, \cdots, x_n)\in A_\epsilon^{(n)}$, then $H(X)-\epsilon\leq -\frac{1}{n} \log p(x_1, \cdots, x_n)\leq H(X)+\epsilon$.
+- $\operatorname{Pr}(A_\epsilon^{(n)})\geq 1-\epsilon$. for sufficiently large $n$.
+
+<details>
+<summary>Sketch of proof</summary>
+
+Use the AEP to show that $\operatorname{Pr}(A_\epsilon^{(n)})\geq 1-\epsilon$. for sufficiently large $n$.
+
+For any $\delta>0$, there exists $n_0$ such that for all $n\geq n_0$,
+$$
+\operatorname{Pr}(A_\epsilon^{(n)})\geq 1-\delta
+$$
+</details>
+
+- $|A_\epsilon^{(n)}|\leq 2^{n(H(X)+\epsilon)}$.
+- $|A_\epsilon^{(n)}|\geq (1-\epsilon)2^{n(H(X)-\epsilon)}$. for sufficiently large $n$.
+
+#### Smallest probable set
+
+The typical set $A_\epsilon^{(n)}$ is a fairly small set with most of the probability.
+
+Q: Is it the smallest such set?
+
+A: Not quite, but pretty close.
+
+Notation: Let $X_1, \cdots, X_n$ be i.i.d. random variables drawn from $p(x)$. For some $\delta < \frac{1}{2}$,
+we denote $B_\delta^{(n)}\subset \mathcal{X}^n$ as the smallest set such that $\operatorname{Pr}(B_\delta^{(n)})\geq 1-\delta$.
+
+Notation: We write $a_n \doteq b_n$ if
+
+$$
+\lim_{n\to\infty} \frac{a_n}{b_n}=1
+$$
+
+Theorem: $|B_\delta^{(n)}|\doteq |A_\epsilon^{(n)}|\doteq 2^{nH(X)}$.
+
+Check book for detailed proof.
+
+What is the difference between $B_\delta^{(n)}$ and $A_\epsilon^{(n)}$?
+
+Consider a Bernoulli sequence $X_1, \cdots, X_n$ with $p = 0.9$.
+
+The typical sequences are those in which the proportion of 1's is close to 0.9.
+
+- However, they do not include the most likely sequence, i.e., the sequence of all 1's!
+- $H(X) = 0.469$.
+- $-\frac{1}{n} \log p(1, \cdots, 1) = -\frac{1}{n} \log 0.9^n = 0.152$. Its average logarithmic probability cannot come close to the entropy of $X$ no matter how large $n$ can be.
+- The set $B_\delta^{(n)}$ contains all the most probable sequences… and includes the sequence of all 1's.
+
+### Consequences of the AEP: data compression schemes
+
+
+Let $X_1, \cdots, X_n$ be i.i.d. random variables drawn from $p(x)$.
+
+We want to find the shortest description of the sequence $X_1, \cdots, X_n$.
+
+First, divide all sequences in $\mathcal{X}^n$
+into two sets, namely the typical set $A_\epsilon^{(n)}$ and its complement $A_\epsilon^{(n)c}$.
+
+- $A_\epsilon^{(n)}$ contains most of the probability while $A_\epsilon^{(n)c}$ contains most elements.
+- The typical set has probability close to 1 and contains approximately $2^{nH(X)}$ elements.
+
+Order the sequences in each set in lexicographic order.
+
+- This means we can represent each sequence of $A_\epsilon^{(n)}$ by giving its index in the set.
+- There are at most $2^{n(H(X)+\epsilon)}$ sequences in $A_\epsilon^{(n)}$.
+- Indexing requires no more than $nH(X)+\epsilon+1$ bits.
+- Prefix all of these by a "0" bit ⇒ at most $nH(X)+\epsilon+2$ bits to represent each.
+- Similarly, index each sequence in $A_\epsilon^{(n)c}$ with no more than $n\log |\mathcal{X}|+1$ bits.
+- Prefix it by "1" ⇒ at most $n\log |\mathcal{X}|+2$ bits to represent each.
+- Voilà! We have a code for all sequences in $\mathcal{X}^n$.
+- The typical sequences have short descriptions of length $\approx nH(X)$ bits. 
+
+#### Algorithm for data compression
+
+1. Divide all $n$-length sequences in $\mathcal{X}^n$ into the typical set $A_\epsilon^{(n)}$ and its complement $A_\epsilon^{(n)c}$.
+2. Order the sequences in each set in lexicographic order.
+3. Index each sequence in $A_\epsilon^{(n)}$ using $\leq nH(X)+\epsilon+1$ bits and each sequence in $A_\epsilon^{(n)c}$ using $\leq n\log |\mathcal{X}|+1$ bits.
+4. Prefix the sequence by "0" if it is in $A_\epsilon^{(n)}$ and "1" if it is in $A_\epsilon^{(n)c}$.
+
+Notes:
+
+- The code is one-to-one and can be decoded easily. The initial bit acts as a "flag".
+- The number of elements in $A_\epsilon^{(n)c}$ is less than the number of elements in $\mathcal{X}^n$, but it turns out this does not matter.
+
+#### Expected length of codewords
+
+Use $x_n$ to denote a sequence $x_1, \cdots, x_n$ and $\ell_{x_n}$ to denote the length of the corresponding codeword.
+
+Suppose $n$ is sufficiently large.
+
+This means $\operatorname{Pr}(A_\epsilon^{(n)})\geq 1-\epsilon$.
+
+Lemma: The expected length of the codeword $\mathbb{E}[\ell_{x_n}]$ is upper bounded by
+$nH(X)+\epsilon'$, where $\epsilon'=\epsilon+\epsilon\log |\mathcal{X}|+\frac{2}{n}$.
+
+$\epsilon'$ can be made arbitrarily small by choosing $\epsilon$ and $n$ appropriately.
+
+#### Efficient data compression guarantee
+
+The expected length of the codeword $\mathbb{E}[\ell_{x_n}]$ is upper bounded by $nH(X)+\epsilon'$, where $\epsilon'=\epsilon+\epsilon\log |\mathcal{X}|+\frac{2}{n}$.
+
+Theorem: Let $X_n\triangleq X_1, \cdots, X_n$ be i.i.d. with $p(x)$ and $\epsilon > 0$. Then there exists a code that maps sequences $x_n$ to binary strings (codewords) such that the mapping is one-to-one and
+$\mathbb{E}[\ell_{x_n}] \leq n(H(X)+\epsilon)$ for $n$ sufficiently large.
+
+- Thus, we can represent sequences $X_n$ using $\approx nH(X)$ bits on average
+
+## Shannon's source coding theorem
+
+There exists an algorithm that can compress $n$ i.i.d. random variables $X_1, \cdots, X_n$, each with entropy $H(X)$, into slightly more than $nH(X)$ bits with negligible risk of information loss. Conversely, if they are compressed into fewer than $nH(X)$ bits, the risk of information loss is very high.
+
+- We have essentially proved the first half!
+
+
+Proof of converse: Show that any set of size smaller than that of $A_\epsilon^{(n)}$ covers a set of probability bounded away from 1

content/CSE5313/CSE5313_L18.md

@@ -0,0 +1,270 @@
+# CSE5313 Coding and information theory for data science (Lecture 18)
+
+## Secret sharing
+
+The president and the vice president must both consent to a nuclear missile launch.
+
+We would like to share the nuclear code such that:
+
+- $Share1, Share2 \mapsto Nuclear Code$
+- $Share1 \not\mapsto Nuclear Code$
+- $Share2 \not\mapsto Nuclear Code$
+- $Share1 \not\mapsto Share2$
+- $Share2 \not\mapsto Share1$
+
+In other words:
+
+- The two shares are everything.
+- One share is nothing.
+
+<details>
+<summary>Solution</summary>
+
+Scheme:
+
+- The nuclear code is a field element $m \in \mathbb{F}_q$, chosen at random $m \sim M$ (M arbitrary).
+- Let $p(x) = m + rx \in \mathbb{F}_q[x]$.
+  - $r \sim U$, where $U = Uniform \mathbb{F}_q$, i.e., $Pr(\alpha = 1/q)$ for every $\alpha \in \mathbb{F}_q$.
+- Fix $\alpha_1, \alpha_2 \in \mathbb{F}_q$ (not random).
+- $s_1 = p(\alpha_1) = m + r\alpha_1, s_1 \sim S_1$.
+- $s_2 = p(\alpha_2) = m + r\alpha_2, s_2 \sim S_2$.
+
+And then:
+
+- One share reveals nothing about $m$.
+- I.e., $I(S_i; M) = 0$ (gradient could be anything)
+- Two shares reveal $p \Rightarrow reveal p(0) = m$.
+- I.e., $H(M|S_1, S_2) = 0$ (two points determine a line).
+
+</details>
+
+### Formalize the notion of secret sharing
+
+#### Problem setting
+
+A dealer is given a secret $m$ chosen from an arbitrary distribution $M$.
+
+The dealer creates $n$ shares $s_1, s_2, \cdots, s_n$ and send to $n$ parties.
+
+Two privacy parameters: $t,z\in \mathbb{N}$ $z<t$.
+
+**Requirements**:
+
+For $\mathcal{A}\subseteq[n]$ denote $S_\mathcal{A} = \{s_i:i\in \mathcal{A}\}$.
+
+- Decodability: Any set of $t$ shares can reconstruct the secret.
+  - $H(M|S_\mathcal{T}) = 0$ for all $\mathcal{T}\subseteq[n]$ with $|\mathcal{T}|\geq t$.
+- Security: Any set of $z$ shares reveals no information about the secret.
+  - $I(M;S_\mathcal{Z}) = 0$ for all $\mathcal{Z}\subseteq[n]$ with $|\mathcal{Z}|\leq z$.
+
+This is called $(n,z,t)$-secret sharing scheme.
+
+#### Interpretation
+
+- $\mathcal{Z} \subseteq [n]$, $|\mathcal{Z}| \leq z$ is a corrupted set of parties.
+- An adversary which corrupts at most $z$ parties cannot infer anything about the secret.
+
+#### Applications
+
+- Secure distributed storage.
+  - Any $\leq z$ hacked servers reveal nothing about the data.
+- Secure distributed computing with a central server (e.g., federated learning).
+  - Any $\leq z$ corrupted computation nodes know nothing about the data.
+- Secure multiparty computing (decentralized).
+  - Any $\leq z$ corrupted parties cannot know the inputs of other parties.
+
+### Scheme 1: Shamir secret sharing scheme
+
+Parameters $n,t$, and $z=t-1$.
+
+Fix $\mathbb{F}_q$, $q>n$ and distinct points $\alpha_1, \alpha_2, \cdots, \alpha_n \in \mathbb{F}_q\setminus \{0\}$. (public, known to all).
+
+Given $m\sim M$ the dealer:
+
+- Choose $r_1, r_2, \cdots, r_z \sim U_1, U_2, \cdots, U_z$ (uniformly random from $\mathbb{F}_q$).
+- Defines $p\in \mathbb{F}_q[x]$ by $p(x) = m + r_1x + r_2x^2 + \cdots + r_zx^z$.
+- Send share $s_i = p(\alpha_i)$ to party $i$.
+
+#### Theorem valid encoding scheme
+
+This is an $(n,t-1,t)$-secret sharing scheme.
+
+Decodability:
+
+- $\deg p=t-1$, any $t$ shares can reconstruct $p$ by Lagrange interpolation.
+
+<details>
+<summary>Proof</summary>
+
+Specifically, any $t$ parties $\mathcal{T}\subseteq[n]$ can define the interpolation polynomial $h(x)=\sum_{i\in \mathcal{T}} s_i \delta_{i}(x)$, where $\delta_{i}(x)=\prod_{j\in \mathcal{T}\setminus \{i\}} \frac{x-\alpha_j}{\alpha_i-\alpha_j}$. ($\delta_{i}(\alpha_i)=1$, $\delta_{i}(\alpha_j)=0$ for $j\neq i$).
+
+$\deg h=\deg p=t-1$, so $h(x)=p(x)$ for all $x\in \mathcal{T}$.
+
+Therefore, $h(0)=p(0)=m$.
+</details>
+
+Privacy:
+
+Need to show that $I(M;S_\mathcal{Z})=0$ for all $\mathcal{Z}\subseteq[n]$ with $|\mathcal{Z}|=z$.
+
+> that is equivalent to show that $M$ and $s_\mathcal{Z}$ are independent for all $\mathcal{Z}\subseteq[n]$ with $|\mathcal{Z}|=z$.
+
+<details>
+<summary>Proof</summary>
+
+We will show that $\operatorname{Pr}(s_\mathcal{Z}|M=m)=\operatorname{Pr}(M=m)$, for all $s_\mathcal{Z}\in S_\mathcal{Z}$ and $m\in M$.
+
+Let $m,\mathcal{Z}=(i_1,i_2,\cdots,i_z)$, and $s_\mathcal{Z}$.
+
+$$
+\begin{bmatrix}
+m & U_1 & U_2 & \cdots & U_z
+\end{bmatrix} = \begin{bmatrix}
+1 & 1 & 1 & \cdots & 1 \\
+\alpha_{i_1} & \alpha_{i_2} & \alpha_{i_3} & \cdots & \alpha_{i_n} \\
+\alpha_{i_1}^2 & \alpha_{i_2}^2 & \alpha_{i_3}^2 & \cdots & \alpha_{i_n}^2 \\
+\vdots & \vdots & \vdots & \ddots & \vdots \\
+\alpha_{i_1}^{z} & \alpha_{i_2}^{z} & \alpha_{i_3}^{z} & \cdots & \alpha_{i_n}^{z}
+\end{bmatrix}=s_\mathcal{Z}=\begin{bmatrix}
+s_{i_1} \\ s_{i_2} \\ \vdots \\ s_{i_z}
+\end{bmatrix}
+$$
+
+So,
+
+$$
+\begin{bmatrix}
+U_1 & U_2 & \cdots & U_z
+\end{bmatrix} = (s_\mathcal{Z}-\begin{bmatrix}
+m & m & m & \cdots & m
+\end{bmatrix})
+\begin{bmatrix}
+\alpha_{i_1}^{-1} & \alpha_{i_2}^{-1} & \alpha_{i_3}^{-1} & \cdots & \alpha_{i_n}^{-1} \\
+\end{bmatrix}
+
+\begin{bmatrix}
+1 & 1 & 1 & \cdots & 1 \\
+\alpha_1 & \alpha_2 & \alpha_3 & \cdots & \alpha_n \\
+\alpha_1^2 & \alpha_2^2 & \alpha_3^2 & \cdots & \alpha_n^2 \\
+\vdots & \vdots & \vdots & \ddots & \vdots \\
+\alpha_1^{z-1} & \alpha_2^{z-1} & \alpha_3^{z-1} & \cdots & \alpha_n^{z-1}
+\end{bmatrix}^{-1}
+$$
+
+So exactly one solution for $U_1, U_2, \cdots, U_z$ is possible.
+
+So $\operatorname{Pr}(U_1, U_2, \cdots, U_z|M=m)=\frac{1}{q^z}$ for all $m\in M$.
+
+Recall the law of total probability:
+
+$$
+\operatorname{Pr}(s_\mathcal{Z})=\sum_{m'\in M} \operatorname{Pr}(s_\mathcal{Z}|M=m') \operatorname{Pr}(M=m')=\frac{1}{q^z}\sum_{m'\in M} \operatorname{Pr}(M=m')=\frac{1}{q^z}
+$$
+
+So $\operatorname{Pr}(s_\mathcal{Z}|M=m)=\operatorname{Pr}(M=m)\implies I(M;S_\mathcal{Z})=0$.
+
+</details>
+
+### Scheme 2: Ramp secret sharing scheme (McEliece-Sarwate scheme)
+
+- Any $z$ know nothing
+- Any $t$ knows everything
+- Partial knowledge for $z<s<t$
+
+Parameters $n,t$, and $z<t$.
+
+Fix $\mathbb{F}_q$, $q>n$ and distinct points $\alpha_1, \alpha_2, \cdots, \alpha_n \in \mathbb{F}_q\setminus \{0\}$. (public, known to all)
+
+Given $m_1, m_2, \cdots, m_n \sim M$, the dealer:
+
+- Choose $r_1, r_2, \cdots, r_z \sim U_1, U_2, \cdots, U_z$ (uniformly random from $\mathbb{F}_q$).
+- Defines $p(x) = m_1+m_2x + \cdots + m_{t-z}x^{t-z-1} + r_1x^{t-z} + r_2x^{t-z+1} + \cdots + r_zx^{t-1}$.
+- Send share $s_i = p(\alpha_i)$ to party $i$.
+
+Decodability
+
+Similar to Shamir scheme, any $t$ shares can reconstruct $p$ by Lagrange interpolation.
+
+Privacy
+
+Similar to the proof of Shamir, exactly one value of $U_1, \cdots, U_z$
+is possible!
+
+$\operatorname{Pr}(s_\mathcal{Z}|m_1, \cdots, m_{t-z}) = \operatorname{Pr}(U_1, \cdots, U_z) = the above = 1/q^z$
+
+($U_i$'s are uniform and independent).
+
+Conclude similarly by the law of total probability.
+
+$\operatorname{Pr}(s_\mathcal{Z}|m_1, \cdots, m_{t-z}) = \operatorname{Pr}(s_\mathcal{Z}) \implies I(S_\mathcal{Z}; M_1, \cdots, M_{t-z}) = 0.
+
+### Conditional mutual information
+
+The dealer needs to communicate the shares to the parties.
+
+Assumed: There exists a noiseless communication channel between the dealer and every party.
+
+From previous lecture:
+
+- The optimal number of bits for communicating $s_i$ (i'th share) to the i'th party is $H(s_i)$.
+- Q: What is $H(s_i|M)$?
+
+Tools:
+- Conditional mutual information.
+- Chain rule for mutual information.
+
+#### Definition of conditional mutual information
+
+The conditional mutual information $I(X;Y|Z)$ of $X$ and $Y$ given $Z$ is defined as:
+
+$$
+\begin{aligned}
+I(X;Y|Z)&=H(X|Z)-H(X|Y,Z)\\
+&=H(X|Z)+H(X)-H(X)-H(X|Y,Z)\\
+&=(H(X)-H(X|Y,Z))-(H(X)-H(X|Z))\\
+&=I(X; Y,Z)- I(X; Z)
+\end{aligned}
+$$
+
+where $H(X|Y,Z)$ is the conditional entropy of $X$ given $Y$ and $Z$.
+
+#### The chain rule of mutual information
+
+$$
+I(X;Y,Z)=I(X;Y|Z)+I(X;Z)
+$$
+
+Conditioning reduces entropy.
+
+#### Lower bound for communicating secret
+
+Consider the Shamir scheme ($z = t - 1$, one message).
+
+Q: What is $H(s_i)$ with respect to $H(M)$ ?
+A: Fix any $\mathcal{T} = \{i_1, \cdots, i_t\} \subseteq [n]$ of size $t$, and let $\mathcal{Z} = \{i_1, \cdots, i_{t-1}\}$.
+
+$$
+\begin{aligned}
+H(M) &= I(M; S_\mathcal{T}) + H(M|S_\mathcal{T}) \text{(by def. of mutual information)}\\
+&= I(M; S_\mathcal{T}) \text{(since S_\mathcal{T} suffice to decode M)}\\
+&= I(M; S_{i_t}, S_\mathcal{Z}) \text{(since S_\mathcal{T} = S_\mathcal{Z} ∪ S_{i_t})}\\
+&= I(M; S_{i_t}|S_\mathcal{Z}) + I(M; S_\mathcal{Z}) \text{(chain rule)}\\
+&= I(M; S_{i_t}|S_\mathcal{Z}) \text{(since \mathcal{Z} ≤ z, it reveals nothing about M)}\\
+&= I(S_{i_t}; M|S_\mathcal{Z}) \text{(symmetry of mutual information)}\\
+&= H(S_{i_t}|S_\mathcal{Z}) - H(S_{i_t}|M,S_\mathcal{Z}) \text{(def. of conditional mutual information)}\\
+\leq H(S_{i_t}|S_\mathcal{Z}) \text{(entropy is non-negative)}\\
+\leq H(S_{i_t}|S_\mathcal{Z}) \text{(conditioning reduces entropy). \\
+\end{aligned}
+$$
+
+So the bits used for sharing the secret is at least the bits of actual secret.
+
+In Shamir we saw: $H(s_i) \geq H(M)$.
+
+- If $M$ is uniform (standard assumption), then Shamir achieves this bound with equality.
+- In ramp secret sharing we have $H(s_i) \geq \frac{1}{t-z}H(M_1, \cdots, M_{t-z})$ (similar proof).
+- Also optimal if $M$ is uniform.
+
+#### Downloading file with lower bandwidth from more servers
+
+[link to paper](https://arxiv.org/abs/1505.07515)

content/CSE5313/CSE5313_L19.md

@@ -0,0 +1,233 @@
+# CSE5313 Coding and information theory for data science (Lecture 19)
+
+## Private information retrieval
+
+### Problem setup
+
+Premise:
+
+- Database $X = \{x_1, \ldots, x_m\}$, each $x_i \in \mathbb{F}_q^k$ is a "file" (e.g., medical record).
+- $X$ is coded $X \mapsto \{y_1, \ldots, y_n\}$, $y_j$ stored at server $j$.
+- The user (physician) wants $x_i$.
+- The user sends a query $q_j \sim Q_j$ to server $j$.
+- Server $j$ responds with $a_j \sim A_j$.
+
+Decodability:
+
+- The user can retrieve the file: $H(X_i | A_1, \ldots, A_n) = 0$.
+
+Privacy:
+
+- $i$ is seen as $i \sim U = U_{m}$, reflecting server's lack of knowledge.
+- $i$ must be kept private: $I(Q_j; U) = 0$ for all $j \in n$.
+
+> In short, we want to retrieve $x_i$ from the servers without revealing $i$ to the servers.
+
+### Private information retrieval from Replicated Databases
+
+#### Simple case, one server
+
+Say $n = 1, y_1 = X$.
+
+- All data is stored in one server.
+- Simple solution:
+- $q_1 =$ "send everything".
+- $a_1 = y_1 = X$.
+
+Theorem: Information Theoretic PIR with $n = 1$ can only be achieved by downloading the entire database.
+
+- Can we do better if $n > 1$?
+
+#### Collusion parameter
+
+Key question for $n > 1$: Can servers collude?
+
+- I.e., does server $j$ see any $Q_\ell$, $\ell \neq j$?
+- Key assumption:
+  - Privacy parameter $z$.
+  - At most $z$ servers can collude.
+  - $z = 1\implies$ No collusion.
+- Requirement for $z = 1$: $I(Q_j; U) = 0$ for all $j \in n$.
+- Requirement for a general $z$:
+  - $I(Q_\mathcal{T}; U) = 0$ for all $\mathcal{T} \in n$, $|\mathcal{T}| \leq z$, where $Q_\mathcal{T} = Q_\ell$ for all $\ell \in \mathcal{T}$.
+- Motivation:
+  - Interception of communication links.
+  - Data breaches.
+
+Other assumptions:
+
+- Computational Private information retrieval (even all the servers are hacked, still cannot get the information -> solve np-hard problem):
+- Non-zero MI
+
+#### Private information retrieval from 2-replicated databases
+
+First PIR protocol: Chor et al. FOCS ‘95.
+
+- The data $X = \{x_1, \ldots, x_m\}$ is replicated on two servers.
+  - $z = 1$, i.e., no collusion.
+- Protocol: User has $i \sim U_{m}$.
+  - User generates $r \sim U_{\mathbb{F}_q^m}$.
+  - $q_1 = r, q_2 = r + e_i$ ($e_i \in \mathbb{F}_q^m$ is the $i$-th unit vector, $q_2$ is equivalent to one-time pad encryption of $x_i$ with key $r$).
+  - $a_j = q_j X^\top = \sum_{\ell \in m} q_j, \ell x_\ell$
+  - Linear combination of the files according to the query vector $q_j$.
+- Decoding?
+  - $a_2 - a_1 = q_2 - q_1 X^\top = e_i X^\top = x_i$.
+- Download?
+  - $a_j =$ size of file $\implies$ downloading **twice** the size of the file.
+- Privacy?
+  - Since $z = 1$, need to show $I(U; Q_i) = 0$.
+    - $I(U; Q_1) = I(e_U; F) = 0$ since $U$ and $F$ are independent.
+    - $I(U; Q_2) = I(e_U; F + e_U) = 0$ since this is one-time pad!
+
+##### Parameters and notations in PIR
+
+Parameters of the system:
+
+- $n =$ # servers (as in storage).
+- $m =$ # files.
+- $k =$ size of each file (as in storage).
+- $z =$ max. collusion (as in secret sharing).
+- $t =$ # of answers required to obtain $x_i$ (as in secret sharing).
+  - $n - t$ servers are “stragglers”, i.e., might not respond.
+
+Figures of merit:
+
+- PIR-rate = $\#$ desired symbols / $\#$ downloaded symbols
+- PIR-capacity = largest possible rate.
+
+Notaional conventions:
+
+-The dataset $X = \{x_j\}_{j \in m} = \{x_{j, \ell}\}_{(j, \ell) \in [m] \times [k]}$ is seen as a vector in $\mathbb{F}_q^{mk}$.
+
+- Index $\mathbb{F}_q^{mk}$ using $[m] \times [k]$, i.e., $x_{j, \ell}$ is the $\ell$-th symbol of the $j$-th file.
+
+#### Private information retrieval from 4-replicated databases
+
+Consider $n = 4$ replicated servers, file size $k = 2$, collusion $z = 1$.
+
+Protocol: User has $i \sim U_{m}$.
+
+- Fix distinct nonzero $\alpha_1, \ldots, \alpha_4 \in \mathbb{F}_q$.
+- Choose $r \sim U_{\mathbb{F}_q^{2m}}$.
+- User sends $q_j = e_{i, 1} + \alpha_j e_{i, 2} + \alpha_j^2 r$ to each server $j$.
+- Server $j$ responds with
+  $$
+  a_j = q_j X^\top = e_{i, 1} X^\top + \alpha_j e_{i, 2} X^\top + \alpha_j^2 r X^\top
+  $$
+  - This is an evaluation at $\alpha_j$ of the polynomial $f_i(w) = x_{i, 1} + x_{i, 2} \cdot w + r \cdot w^2$.
+  - Where $r$ is some random combination of the entries of $X$.
+- Decoding?
+  - Any 3 responses suffice to interpolate $f_i$ and obtain $x_i = x_{i, 1}, x_{i, 2}$.
+  - $\implies t = 3$, (one straggler is allowed)
+- Privacy?
+  - Does $q_j = e_{i, 1} + \alpha_j e_{i, 2} + \alpha_j^2 r$ look familiar?
+  - This is a share in [ramp scheme](CSE5313_L18.md#scheme-2-ramp-secret-sharing-scheme-mceliece-sarwate-scheme) with vector messages $m_1 = e_{i, 1}, m_2 = e_{i, 2}, m_i \in \mathbb{F}_q^{2m}$.
+  - This is equivalent to $2m$ "parallel" ramp scheme over $\mathbb{F}_q$.
+  - Each one reveals nothing to any $z = 1$ shareholders $\implies$ Private!
+
+### Private information retrieval from general replicated databases
+
+$n$ servers, $m$ files, file size $k$, $X \in \mathbb{F}_q^{mk}$.
+
+Server decodes $x_i$ from any $t$ responses.
+
+Any $\leq z$ servers might collude to infer $i$ ($z < t$).
+
+Protocol: User has $i \sim U_{m}$.
+
+- User chooses $r_1, \ldots, r_z \sim U_{\mathbb{F}_q^{mk}}$.
+- User sends $q_j = \sum_{\ell=1}^k e_{i, \ell} \alpha_j^{\ell-1} + \sum_{\ell=1}^z r_\ell \alpha_j^{k+\ell-1}$ to each server $j$.
+- Server $j$ responds with $a_j = q_j X^\top = f_i(\alpha_j)$.
+  - $f_i(w) = \sum_{\ell=1}^k e_{i, \ell} X^\top w^{\ell-1} + \sum_{\ell=1}^z r_\ell X^\top w^{k+\ell-1}$ (random combinations of $X$).
+  - Caveat: must have $t = k + z$.
+  - $\implies \deg f_i = k + z - 1 = t - 1$.
+- Decoding?
+  - Interpolation from any $t$ evaluations of $f_i$.
+- Privacy?
+  - Against any $z = t - k$ colluding servers, immediate from the proof of the ramp scheme.
+
+PIR-rate?
+
+- Each $a_j$ is a single field element.
+- Download $t = k + z$ elements in $\mathbb{F}_q$ in order to obtain $x_i \in \mathbb{F}_q^k$.
+- $\implies$ PIR-rate = $\frac{k}{k+z} = \frac{k}{t}$.
+
+#### Theorem: PIR-capacity for general replicated databases
+
+The PIR-capacity for $n$ replicated databases with $z$ colluding servers, $n - t$ unresponsive servers, and $m$ files is $C = \frac{1-\frac{z}{t}}{1-(\frac{z}{t})^m}$.
+
+- When $m \to \infty$, $C \to 1 - \frac{z}{t} = \frac{t-z}{t} = \frac{k}{t}$.
+- The above scheme achieves PIR-capacity as $m \to \infty$
+
+### Private information retrieval from coded databases
+
+#### Problem setup:
+
+Example:
+
+- $n = 3$ servers, $m$ files $x_j$, $x_j = x_{j, 1}, x_{j, 2}$, $k = 2$, and $q = 2$.
+- Code each file with a parity code: $x_{j, 1}, x_{j, 2} \mapsto x_{j, 1}, x_{j, 2}, x_{j, 1} + x_{j, 2}$.
+- Server $j \in 3$ stores all $j$-th symbols of all coded files.
+
+Queries, answers, decoding, and privacy must be tailored for the code at hand.
+
+With respect to a code $C$ and parameters $n, k, t, z$, such scheme is called coded-PIR.
+
+- The content for server $j$ is denoted by $c_j = c_{j, 1}, \ldots, c_{j, m}$.
+- $C$ is usually an MDS code.
+
+#### Private information retrieval from parity-check codes
+
+Example:
+
+ Say $z = 1$ (no collusion).
+
+- Protocol: User has $i \sim U_{m}$.
+- User chooses $r_1, r_2 \sim U_{\mathbb{F}_2^m}$.
+- Two queries to each server:
+  - $q_{1, 1} = r_1 + e_i$, $q_{1, 2} = r_2$.
+  - $q_{2, 1} = r_1$, $q_{2, 2} = r_2 + e_i$.
+  - $q_{3, 1} = r_1$, $q_{3, 2} = r_2$.
+- Server $j$ responds with $q_{j, 1} c_j^\top$ and $q_{j, 2} c_j^\top$.
+- Decoding?
+  - $q_{1, 1} c_1^\top + q_{2, 1} c_2^\top + q_{3, 1} c_3^\top = r_1 c_1 + c_2 + c_3 + e_i c_1^\top = r_1 \cdot 0^\top + x_{i, 1} = x_{i, 1}$.
+  - $q_{1, 1} c_1^\top + q_{2, 1} c_2^\top + q_{3, 1} c_3^\top = r_1 \cdot 0^\top + x_{i, 1} = x_{i, 1}$.
+  - $q_{1, 2} c_1^\top + q_{2, 2} c_2^\top + q_{3, 2} c_3^\top = r_2 c_1 + c_2 + c_3^\top + e_i c_2^\top = x_{i, 2}$.
+- Privacy?
+  - Every server sees two uniformly random vectors in $\mathbb{F}_2^m$.
+
+<details>
+<summary>Proof from coding-theoretic interpretation</summary>
+
+Let $G = g_1^\top, g_2^\top, g_3^\top$ be the generator matrix. 
+
+- For every file $x_j = x_{j, 1}, x_{j, 2}$ we encode $x_j G = (x_{j, 1} g_1^\top, x_{j, 2} g_2^\top, x_{j, 1} g_3^\top) = (c_{j, 1}, c_{j, 2}, c_{j, 3})$.
+- Server $j$ stores $X g_j^\top = (x_1^\top, \ldots, x_m^\top)^\top g_j^\top = (c_{j, 1}, \ldots, c_{j, m})^\top$.
+
+- By multiplying by $r_1$, the servers together store a codeword in $C$:
+  - $r_1 X g_1^\top, r_1 X g_2^\top, r_1 X g_3^\top = r_1 X G$.
+- By replacing one of the $r_1$’s by $r_1 + e_i$, we introduce an error in that entry:
+  - $\left((r_1 + e_i) X g_1^\top, r_1 X g_2^\top, r_1 X g_3^\top\right) = r_1 X G + (e_i X g_1^\top, 0,0)$.
+- Downloading this “erroneous” word from the servers and multiply by $H = h_1^\top, h_2^\top, h_3^\top$ be the parity-check matrix.
+
+$$
+\begin{aligned}
+\left((r_1 + e_i) X g_1^\top, r_1 X g_2^\top, r_1 X g_3^\top\right) H^\top &= \left(r_1 X G + (e_i X g_1^\top, 0,0)\right) H^\top \\
+&= r_1 X G H^\top + (e_i X g_1^\top, 0,0) H^\top \\
+&= 0 + x_{i, 1} g_1^\top \\
+&= x_{i, 1}.
+\end{aligned}
+$$
+
+> In homework we will show tha this work with any MDS code ($z=1$).
+
+- Say we obtained $x_{i, 1} g_1^\top, \ldots, x_{i, k} g_k^\top$ (𝑑 − 1 at a time, how?).
+- $x_{i, 1} g_1^\top, \ldots, x_{i, k} g_k^\top = x_{i, B}$, where $B$ is a $k \times k$ submatrix of $G$.
+- $B$ is a $k \times k$ submatrix of $G$ $\implies$ invertible! $\implies$ Obtain $x_{i}$.
+
+</details>
+
+> [!TIP]
+>
+> error + known location $\implies$ erasure. $d = 2 \implies$ 1 erasure is correctable.
+

content/CSE5313/CSE5313_L2.md

@@ -267,11 +267,9 @@ Hamming distance is a metric.
 
 ### Level of error handling
 
-error detection
-
-erasure correction
-
-error correction
+- error detection
+- erasure correction
+- error correction
 
 Erasure: replacement of an entry by $*\not\in F$.
 
@@ -283,11 +281,27 @@ Example: If $d_H(\mathcal{C})=d$.
 
 Theorem: If $d_H(\mathcal{C})=d$, then there exists $f:F^n\to \mathcal{C}\cap \{\text{"error detected"}\}$. that detects every patter of $\leq d-1$ errors correctly.
 
-\* track lost *\
+- That is, we can identify if the channel introduced at most $d-1$ errors.
+- No decoding is needed.
 
 Idea:
 
-Since $d_H(\mathcal{C})=d$, one needs $\geq d$ errors to cause "confusion$.
+Since $d_H(\mathcal{C})=d$, one needs $\geq d$ errors to cause "confusion".
+
+<details>
+<summary>Proof</summary>
+
+The function
+$$
+f(y)=\begin{cases}
+y\text{  if }y\in \mathcal{C}\\
+\text{"error detected"} & \text{otherwise}
+\end{cases}
+$$
+
+will only fails if there are $\geq d$ errors.
+
+</details>
 
 #### Erasure correction
 
@@ -295,7 +309,11 @@ Theorem: If $d_H(\mathcal{C})=d$, then there exists $f:\{F^n\cup \{*\}\}\to \mat
 
 Idea:
 
-\* track lost *\
+Suppose $d=4$.
+
+If $4$ erasures occurred, there might be two possible codewords $c,c'\in \mathcal{C}$.
+
+If $\leq 3$ erasures occurred, there is only one possible codeword $c\in \mathcal{C}$.
 
 #### Error correction
 

content/CSE5313/CSE5313_L20.md

@@ -0,0 +1,252 @@
+# CSE5313 Coding and information theory for data science (Lecture 20)
+
+## Review for Private Information Retrieval
+
+### PIR from replicated databases
+
+For 2 replicated databases, we have the following protocol:
+
+- User has $i \sim U_{m}$.
+- User chooses $r_1, r_2 \sim U_{\mathbb{F}_2^m}$.
+- Two queries to each server:
+  - $q_{1, 1} = r_1 + e_i$, $q_{1, 2} = r_2$.
+  - $q_{2, 1} = r_1$, $q_{2, 2} = r_2 + e_i$.
+- Server $j$ responds with $q_{j, 1} c_j^\top$ and $q_{j, 2} c_j^\top$.
+- Decoding?
+  - $q_{1, 1} c_1^\top + q_{2, 1} c_2^\top = r_1 c_1 + c_2 + e_i c_1^\top = r_1 \cdot 0^\top + x_{i, 1} = x_{i, 1}$.
+  - $q_{1, 2} c_1^\top + q_{2, 2} c_2^\top = r_2 c_1 + c_2 + e_i c_2^\top = x_{i, 2}$.
+
+PIR-rate is $\frac{k}{2k} = \frac{1}{2}$.
+
+### PIR from coded parity-check databases
+
+For 3 coded parity-check databases, we have the following protocol:
+
+- User has $i \sim U_{m}$.
+- User chooses $r_1, r_2, r_3 \sim U_{\mathbb{F}_2^m}$.
+- Three queries to each server:
+  - $q_{1, 1} = r_1 + e_i$, $q_{1, 2} = r_2$, $q_{1, 3} = r_3$.
+  - $q_{2, 1} = r_1$, $q_{2, 2} = r_2 + e_i$, $q_{2, 3} = r_3$.
+  - $q_{3, 1} = r_1$, $q_{3, 2} = r_2$, $q_{3, 3} = r_3 + e_i$.
+- Server $j$ responds with $q_{j, 1} c_j^\top, q_{j, 2} c_j^\top, q_{j, 3} c_j^\top$.
+- Decoding?
+  - $q_{1, 1} c_1^\top + q_{2, 1} c_2^\top + q_{3, 1} c_3^\top = r_1 c_1 + c_2 + c_3 + e_i c_1^\top = r_1 \cdot 0^\top + x_{i, 1} = x_{i, 1}$.
+  - $q_{1, 2} c_1^\top + q_{2, 2} c_2^\top + q_{3, 2} c_3^\top = r_2 c_1 + c_2 + c_3 + e_i c_2^\top = x_{i, 2}$.
+  - $q_{1, 3} c_1^\top + q_{2, 3} c_2^\top + q_{3, 3} c_3^\top = r_3 c_1 + c_2 + c_3 + e_i c_3^\top = x_{i, 3}$.
+
+PIR-rate is $\frac{k}{3k} = \frac{1}{3}$.
+
+## Beyond z=1
+
+### Star-product theme
+
+Given $x=(x_1, \ldots, x_j)_{j\in [n]}, y=(y_1, \ldots, y_j)_{j\in [n]}$, over $\mathbb{F}_q$, the star-product is defined as:
+
+$$
+x \star y = (x_1 y_1, \ldots, x_n y_n)
+$$
+
+Given two linear codes, $C,D\subseteq \mathbb{F}_q^n$, the star-product code is defined as:
+
+$$
+C \star D = span_{\mathbb{F}_q} \{x \star y | x \in C, y \in D\}
+$$
+
+Singleton bound for star-product:
+
+$$
+d_{C \star D} \leq n-\dim C-\dim D+2
+$$
+
+### PIR form a database coded with any MDS code and z>1
+
+To generalize the previous scheme to $z > 1$ need to encode multiple $r$'s together.
+
+- As in the ramp scheme.
+
+> Recall from the ramp scheme, we use $r_1, \ldots, r_z \sim U_{\mathbb{F}_q^k}$ as our key vector to avoid occlusion of the servers.
+
+In the star-product scheme:
+
+- Files are coded with an MDS code $C$.
+- The multiple $r$'s are coded with an MDS code $D$.
+- The scheme is based on the minimum distance of $C \star D$.
+
+To code the data:
+
+- Let $C \subseteq \mathbb{F}_q^n$ be an MDS code of dimension $k$.
+- For all $j \in m$, encode file $x_j = x_{j, 1}, \ldots, x_{j, k}$ using $G_C$:
+
+$$
+\begin{pmatrix}
+x_{1, 1} & x_{1, 2} & \cdots & x_{1, k}\\
+x_{2, 1} & x_{2, 2} & \cdots & x_{2, k}\\
+\vdots & \vdots & \ddots & \vdots\\
+x_{m, 1} & x_{m, 2} & \cdots & x_{m, k}
+\end{pmatrix} \cdot G_C = \begin{pmatrix}
+c_{1, 1} & c_{1, 2} & \cdots & c_{1, n}\\
+c_{2, 1} & c_{2, 2} & \cdots & c_{2, n}\\
+\vdots & \vdots & \ddots & \vdots\\
+c_{m, 1} & c_{m, 2} & \cdots & c_{m, n}
+\end{pmatrix}
+$$
+
+- For all $j \in n$, store $c_j = c_{1, j}, c_{2, j}, \ldots, c_{m, j}$ (a column of the above matrix) in server $j$.
+
+Let $r_1, \ldots, r_z \sim U_{\mathbb{F}_q^k}$.
+
+To code the queries:
+
+- Let $D \subseteq \mathbb{F}_q^k$ be an MDS code of dimension $z$.
+- Encode the $r_j$'s using $G_D=[g_1^\top, \ldots, g_z^\top]$.
+
+$$
+(r_1^\top, \ldots, r_z^\top) \cdot G_D = \begin{pmatrix}
+r_{1, 1} & r_{2, 1} & \cdots & r_{z, 1}\\
+r_{1, 2} & r_{2, 2} & \cdots & r_{z, 2}\\
+\vdots & \vdots & \ddots & \vdots\\
+r_{1, m} & r_{2, m} & \cdots & r_{z, m}
+\end{pmatrix}
+\cdot G_D=\left((r_1^\top,\ldots, r_z^\top)g_1^\top,\ldots, (r_1^\top,\ldots, r_z^\top)g_n^\top \right)
+$$
+
+To introduce the "errors in known locations" to the encoded $r_j$'s:
+
+- Let $W \in \{0, 1\}^{m \times n}$ with some $d_{C \star D} - 1$ entries in its $i$-th row equal to 1.
+- These are the entries we will retrieve.
+
+For every server $j \in [n]$ send $q_j = r_1^\top, \ldots, r_z^\top g_j^\top + w_j$, where $w_j$ is the $i$-th column of $W$.
+
+- This is similar to ramp scheme, where $w_j$ is the "message".
+- Privacy against collusion of $z$ servers.
+
+Response from server: $a_j = q_j c_j^\top$.
+
+Decoding? Let $Q \in \mathbb{F}_q^{m \times n}$ be a matrix whose columns are the $q_j$'s.
+$$
+Q = \begin{pmatrix}
+r_1^\top & \cdots & r_z^\top
+\end{pmatrix} \cdot G_D + W
+$$
+
+- The user has
+
+$$
+\begin{aligned}
+q_1 c_1^\top, \ldots, q_n c_n^\top &= \left(\sum_{j \in m} q_{1, j} c_{j, 1}, \ldots, \sum_{j \in m} q_{n, j} c_{j, n}\right) \\
+&=\sum_{j \in m} (q_{1,j}c_{j, 1}, \ldots, q_{n,j}c_{j, n}) \\
+&=\sum_{j \in m} q^j \star c^j
+$$
+
+where $q^j$ is a row of $Q$ and $c^j$ is a codeword in $C$ (an $n, k$ $q$ MDS code).
+
+We have:
+
+- $Q=(r_1^\top, \ldots, r_z^\top) \cdot G_D + W$
+- $W\in \{0, 1\}^{m \times n}$ with some $d_{C \star D} - 1$ entries in its $i$-th row equal to 1.
+- $(q^j \star c^j)=sum_{j \in m} q^j \star c^j$
+- Each $q^j$ is a row of $Q$
+  - For $j \neq i$, $q^j$ is a codeword in $D$
+  - $q^i = d^i + w^i$
+- Therefore:
+
+$$
+\begin{aligned}
+\sum_{j \in [m]} q^j \star c^j &= \sum_{j \neq i} (d^j \star c^j) + ((d^i + w^i) \star c^i) \\
+&= \sum_{j \neq i} (d^j \star c^j) + w^i \star c^i
+&= (\text{codeword in } C \star D )+( \text{noise of Hamming weight } \leq d_{C \star D} - 1)
+\end{aligned}
+$$
+
+Multiply by $H_{C \star D}$ and get $d_{C \star D} - 1$ elements of $c^i$.
+
+- Recall that $c^i = x_i \cdot G_C$
+- Repeat $k^{d_{C \star D} - 1}$ times to obtain $k$ elements of $c^i$.
+  - Suffices to obtain $x_i$, since $C$ is $n, k$ $q$ MDS code.
+
+PIR-rate:
+
+- = $\frac{k}{# \text{ downloaded elements}} = \frac{k}{\frac{k}{d_{C \star D} - 1} \cdot n} = \frac{d_{C \star D} - 1}{n}$
+- Singleton bound for star-product: $d_{C \star D} \leq n - \dim C - \dim D + 2$.
+- Achieved with equality if $C$ and $D$ are Reed-Solomon codes.
+- PIR-rate = $\frac{n - \dim C - \dim D + 1}{n} = \frac{n - k - z + 1}{n}$.
+- Intuition:
+  - "paying" $k$ for "reconstruction from any $k$".
+  - "paying" $z$ for "protection against colluding sets of size $z$".
+- Capacity unknown! (as of 2022).
+  - Known for special cases, e.g., $k = 1, z = 1$, certain types of schemes, etc.
+
+### PIR over graphs
+
+Graph-based replication:
+
+- Every file is replicated twice on two separate servers.
+- Every two servers have at most one file in common.
+- "file" = "granularity" of data, i.e., the smallest information unit shared by any two servers.
+
+A server that stores $(x_{i, j})_{j=1}^d$ receives $(q_{i, j})_{j=1}^d$, and replies with $\sum_{j=1}^d q_{i, j} \cdot x_{i, j}$.
+
+The idea:
+
+- Consider a 2-server replicated PIR and "split" the queries between the servers.
+- Sum the responses, unwanted files "cancel out", while $x_i$ does not.
+
+Problem: Collusion.
+
+Solution: Add per server randomness.
+
+Good for any graph, and any $q \geq 3$ (for simplicity assume $2 | q$).
+
+The protocol:
+
+- Choose random $\gamma \in \mathbb{F}_q^n$, $\nu \in \mathbb{F}_q^m$, and $h \in \mathbb{F} \setminus \{0, 1\}$.
+- Queries:
+  - If node $j$ is incident with edge $\ell$, send $q_{j, \ell} = \gamma_j \cdot \nu_\ell$ to node $j$.
+  - I.e., if server $j$ stores file $\ell$.
+- Except one node $j_0$ that stores $x_i$, which gets $q_{j_0, i} = h \cdot \gamma_{j_0} \cdot \nu_i$.
+- Server $j$ responds with $a_j = \sum_{j=1}^d q_{j, \ell} \cdot x_{i, \ell}$.
+  - Where $x_{i, 1}, \ldots, $x_{i, d}$ are the files adjacent with it.
+
+<details>
+<summary>Example</summary>
+
+- Consider the following graph.
+- $n = 5, m = 7, and i = 3$.
+- $q_3 = \gamma_3 \cdot v_2, v_3, v_6$ and $a_3 = x_2 \cdot \gamma_3 v_2 + x_3 \cdot \gamma_3 v_3 + x_6 \cdot \gamma_3 v_6$.
+- $q_2 = \gamma_2 \cdot v_1, h v_3, v_4$ and $a_2 = x_1 \cdot \gamma_2 v_1 + x_3 \cdot h \gamma_2 v_3 + x_4 \cdot \gamma_2 v_4$.
+
+![Example of PIR over graphs](https://notenextra.trance-0.com/CSE5313/PIR_over_graphs.png)
+
+</details>
+
+Correctness:
+
+- $\sum_{j=1}^5 \gamma_j^{-1} a_j =( h + 1 )v_3 x_3$
+- $h \neq 1, v_3 \neq 0 \implies$ find $x_3$.
+
+Parameters:
+
+- Storage overhead 2 (for any graph).
+- Download $n \cdot k$.
+- PIR rate 1/n.
+
+Collusion resistance:
+
+1-privacy: Each node sees an entirely random vector.
+
+2-privacy:
+
+- If no edge – as for 1-privacy.
+- If edge exists – E.g.,
+  - $\gamma_3 v_6$ and $\gamma_4 v_6$ are independent.
+  - $\gamma_3 v_3$ and $h \cdot \gamma_2 v_3$ are independent.
+
+S-privacy: 
+
+- Let $S \subseteq n$ (e.g., $S = 2,3,5$), and consider the query matrix of their mutual files: 
+
+$$
+Q_S = diag(\gamma_3, \gamma_2, \gamma_5) \begin{pmatrix} 1 &\\ h & 1 \\ & 1\end{pmatrix} diag(v_3, v_4)
+$$
+
+- It can be shown that $Pr(Q_S)=\frac{1}{(q-1)^4}$, regardless of $i \implies$ perfect privacy.

content/CSE5313/CSE5313_L21.md

@@ -0,0 +1,316 @@
+# CSE5313 Coding and information theory for data science (Lecture 21)
+
+## Gradient coding
+
+### Intro to Statistical Machine Learning
+
+Given by the learning problem:
+
+**Unknown** target function $f:X\to Y$.
+
+Training data $\mathcal{D}=\{(x_i,y_i)\}_{i=1}^n$.
+
+Learning algorithm: $\mathbb{A}$ and Hypothesis set $\mathcal{H}$.
+
+Goal is to find $g\approx f$,
+
+Common hypothesis sets:
+
+- Linear classifiers:
+
+$$
+f(x)=sign (wx^\top)
+$$
+
+- Linear regressors:
+
+$$
+f(x)=wx^\top
+$$
+
+- Neural networks:
+  - Concatenated linear classifiers (or differentiable approximation thereof).
+
+The dataset $\mathcal{D}$ is taken from unknown distribution $D$.
+
+#### Common approach – Empirical Risk Minimization
+
+- Q: How to quantify $f\approx g$ ?
+- A: Use a loss function.
+  - A function which measures the deviation between $g$'s output and $f$'s output.
+- Using the chosen loss function, define two measures:
+  - True risk: $\mathbb{E}_{D}[\mathbb{L}(f,g)]$
+  - Empirical risk: $\frac{1}{n}\sum_{i=1}^n \ell(g(x_i),y_i)$
+
+Machine learning is over $\mathbb{R}$.
+
+### Gradient Descent (Motivation)
+
+Parameterize $g$ using some real vector $\vec{w}$, we want to minimize $ER(\vec{w})$.
+
+Algorithm:
+
+- Initialize $\vec{w}_0$.
+- For $t=1,2,\cdots,T$:
+  - Computer $\nabla_{\vec{w}} ER(\vec{w})$.
+  - $\vec{w}\gets \vec{w}-\eta\nabla_{\vec{w}} ER(\vec{w})$
+  - Terminate if some stop condition are met.
+
+Bottleneck: Calculating $\nabla_{\vec{w}} ER(\vec{w})=\frac{1}{n}\sum_{i=1}^n \nabla_{\vec{w}} \ell(g(x_i),y_i)$.
+
+Potentially, $O(PN)$ where $N$ is number of points, dimension of feature space.
+
+Solution: Parallelize.
+
+#### Distributed Gradient Descent
+
+Idea: use a distributed system with **master** and **workers**.
+
+Problem: Stragglers (slow servers, 5-6 slower than average time).
+
+Potential Solutions:
+
+- Wait for all servers:
+  - Accurate, but slow
+- Sum results without the slowest ones
+  - Less accurate, but faster
+- Introduce redundancy
+  - Send each $\mathcal{D}_i$ to more than one server.
+  - Each server receives more than one $\mathcal{D}_i$.
+  - Each server sends a linear combination of the partials gradient to its $\mathcal{D}_i$.
+  - The master decodes the sum of partial gradients from the linear combination.
+
+### Problem setups
+
+System setup: 1 master $M$, $n$ workers $W_1,\cdots,W_n$.
+
+A dataset $\mathcal{D}=\{(x_i,y_i)\}_{i=1}^n$.
+
+Each server $j$:
+
+- Receives some $d$ data points $\mathcal{D}_j=\{(x_{j,i},y_{j,i})\}_{i=1}^d$. where $d$ is the replication factor.
+- Computes a certain vector $v_i$ from each $(x_{j,i},y_{j,i})$.
+- Returns a linear combination $u_i=\sum_{j=1}^n \alpha_j v_j$. to the master.
+
+The master:
+
+- Waits for the first $n-s$ $u_i$'s to arrive ($s$ is the straggler tolerance factor).
+- Linear combines the $u_i$'s to get the final gradient.
+
+Goal: Retrieve $\sum_i v_i$ regardless of which $n-s$ workers responded.
+
+- Computation of the full gradient that tolerates any $s$ straggler.
+
+The $\alpha_{i,j}$'s are fixed (do not depend on data). These form a **gradient coding matrix** $B\in\mathbb{C}^{n\times n}$.
+
+Row $i$ has $d$ non-zero entries $\alpha_{i,j}$. at some positions.
+
+The $\lambda_i$'s:
+
+- Might depend on the identity of the $n-s$ responses.
+- Nevertheless must exists in any case.
+
+Recall:
+
+- The master must be able to recover $\sum_i v_i$ form any $n-s$ responses.
+
+Let $\mathcal{K}$ be the indices of the responses.
+
+Let $B_\mathcal{K}$ be the submatrix of $B$ indexed by $\mathcal{K}$.
+
+Must have:
+
+- For every $\mathcal{K}$ of size $n-s$ there exists coefficients $\lambda_1,\cdots,\lambda_{n-s}$ such that:
+
+$$
+(\lambda_1,\cdots,\lambda_{n-s})B_\mathcal{K}=(1,1,1,1,\cdots,1)=\mathbb{I}
+$$
+
+Then if $\mathcal{K}=\{i_1,\cdots,i_{n-s}\}$ responded,
+
+$$
+(\lambda_1 v_{i_1},\cdots,\lambda_{n-s} v_{i_{n-s}})\begin{pmatrix}
+u_{i_1}\\
+u_{i_2}\\
+\vdots\\
+u_{i_{n-s}}
+\end{pmatrix}=\sum_i v_i
+$$
+
+#### Definition of gradient coding matrix.
+
+For replication factor $d$ and straggler tolerance factor $s$: $B\in\mathbb{C}^{n\times n}$ is a gradient coding matrix if:
+
+- $\mathbb{I}$ is in th span of any $n-s$ rows.
+- Every row of $B$ contains at most $d$ nonzero elements.
+
+Grading coding matrix implies gradient coding algorithm:
+
+- The master sends $S_i$ to worker $i$. where $i=1,\cdots,n$ are the nonzero indices of row $i$.
+- Worker $i$:
+  - Computes $\mathcal{D}_{i,\ell}\to v_{i,\ell}$ for $\ell=1,\cdots,d$.
+  - Sends $u_i=\sum_{j=1}^d \alpha_{i,j}v_{i,j}$ to the master.
+- Let $\mathcal{K}=\{i_1,\cdots,i_{n-s}\}$ be the indices of the first $n-s$ responses.
+- Since $\mathbb{I}$ is in the span of any $n-s$ rows of $B$, there exists $\lambda_1,\cdots,\lambda_{n-s}$ such that $(\lambda_1,\cdots,\lambda_{n-s})((u_{i_1},\cdots,u_{i_{n-s}}))=\sum_i v_i$.
+
+#### Construction of Gradient Coding Matrices
+
+Goal:
+
+- For a given straggler tolerance parameter $s$, we wish to construct a gradient coding matrix $B$ with the smallest possible $d$.
+
+- Tools:
+
+I. Cyclic Reed-Solomon codes over the complex numbers.
+II. Definition of $\mathcal{C}^\perp$ (dual of $\mathcal {C}$) and $\mathcal{C}^R$ (reverse of $\mathcal{C}$).
+III. A simple lemma about MDS codes.
+
+Recall: An $n,k$ Reed-Solomon code over a field $\mathcal{F}$ is as follows.
+
+- Fix distinct $\alpha_1,\cdots,\alpha_n-1\in\mathcal{F}$.
+- $\mathcal{C}=\{f(\alpha_1),f(\alpha_2),\cdots,f(\alpha_n-1)\}$.
+- Dimension $k$ and minimum distance $n-k+1$ follow from $\mathcal{F}$ being a field.
+- Also works for $\mathcal {F}=\mathbb{C}$.
+
+### I. Cyclic Reed-Solomon codes over the complex numbers.
+
+The following Reed-Solomon code over the complex numbers is called a cyclic code.
+
+- Let $i=\sqrt{-1}$.
+- For $j\in \{0,\cdots,n-1\}$, choose $a_j=e^{2\pi i j/n}$. The $a_j$'s are roots of unity of order $n$.
+- Use these $a_j$'s to define a Reed-Solomon code as usual.
+
+This code is cyclic:
+
+- Let $c=(f_c(a_0),f_c(a_1),\cdots,f_c(a_{n-1}))$ for some $f_c(x)\in \mathbb{C}[x]$.
+- Need to show that $c'=f_c(a_j)$ for all $j\in \{0,\cdots,n-1\}$.
+
+$$
+c'=(f_c(a_1),f_c(a_2),\cdots,f_c(a_{n-1}),f_c(a_0))=(f_c(a_0),f_c(a_1),\cdots,f_c(a_{n-1}))
+$$
+
+### II. Dual and Reversed Codes
+
+- Let $\mathcal{C}=[n,k,d]_{\mathbb{F}}$ be an MDS code.
+
+#### Definition for dual code of $\mathcal{C}$
+
+The dual code of $\mathcal{C}$ is
+
+$$
+\mathcal{C}^\perp=\{c'\in \mathbb{F}^n|c'c^\top=0\text{ for all }c\in \mathcal{C}\}
+$$
+
+Claim: $\mathcal{C}^\perp$ is an $[n,n-k,k+1]_{\mathbb{F}}$ code.
+
+#### Definition for reversed code of $\mathcal{C}$
+
+The reversed code of $\mathcal{C}$ is
+
+$$
+\mathcal{C}^R=\{(c_{n-1},\cdots,c_0)|(c_0,\cdots,c_{n-1})\in \mathcal{C}\}
+$$
+
+We claim that if $\mathcal{C}$ is cyclic, then $\mathcal{C}^R$ is cyclic.
+
+### III. Lemma about MDS codes
+
+Let $\mathcal{C}=[n,k,n-k+1]_{\mathbb{F}}$ be an MDS code.
+
+#### Lemma
+
+For any subset $\mathcal{K}\subset \{0,\cdots,n-1\}$, of size $n-k+1$ there exists $c\in \mathcal{C}$ whose support (set of nonzero indices) is $\mathcal{K}$.
+
+<details>
+<summary>Proof</summary>
+
+Let $G\in \mathbb{F}^{k\times n}$ be a generator matrix, and let $G_{\mathcal{K}^c}\in \mathbb{F}^{k\times (k-1)}$ be its restriction to columns not indexed by $\mathcal{K}$.
+
+$G_{\mathcal{K}^c}$ has more rows than columns, so there exists $v\in \mathbb{F}^{k}$ such that $vG_{\mathcal{K}^c}=0$.
+
+So $c=vG$ has at least $|\mathcal{K}^c|=k-1$ zeros inn entires indexed by $\mathcal{K}^c$.
+
+The remaining $n-(k-1)=d$ entries of $c$, indexed by $\mathcal{K}$, must be nonzero.
+
+Thus the suppose of $c$ is $\mathcal{K}$.
+
+</details>
+
+### Construct gradient coding matrix
+
+Consider nay $n$ workers and $s$ stragglers.
+
+Let $d=s+1$
+
+Let $\mathcal{C}=[n,n-s]_{\mathbb{C}}$ be the cyclic RS code build by I.
+
+Then by III, there exists $c\in \mathcal{c}$ whose support is the $n-(n-s)+1=s+1$ first entires.
+
+Denote $c=(\beta_1,\cdots,\beta_{s+1},0,0,\cdots,0)$. for some nonzero $\beta_1,\cdots,\beta_{s+1}$.
+
+Build:
+
+$B\in \mathbb{C}^{n\times n}$ whose columns are all cyclic shifts of $c$.
+
+We claim that $B$ is a gradient coding matrix.
+
+$$
+\begin{pmatrix}
+\beta_1     & 0           &        & 0          & \beta_{s+1} & \beta_s& \cdots & \beta_2 \\
+\vdots      & \beta_1     &        & \vdots     & 0           & \beta_{s+1} &  & \vdots \\
+\beta_{s+1} & \vdots      &        &            & \vdots      & 0 &  & \beta_{s+1}\\
+0           & \beta_{s+1} & \ddots & 0          &             &\vdots & \dots & 0\\
+\vdots      & 0           & \ddots & \beta_1     & & & & &\\
+            & \vdots      & \ddots & \vdots     & & & &0\\
+0           & 0           &        & \beta_{s+1}& \beta_s& \beta_{s-1}& \cdots & \beta_1\\
+\end{pmatrix}
+$$
+
+<details>
+<summary>Proof</summary>
+
+Every row is a codeword in $\mathcal{C}^R$.
+
+- Specifically, a shift of $(0,\cdots,0,\beta_{s+1},\cdots,\beta_1)$.
+- Then every row contains $\leq d=s+1$ nonzeros.
+
+$\mathcal{I}$ is in the span of any $n-s$ rows of $B$.
+
+- Observe that $\mathcal{I}\in \mathcal{C}$, (evaluate the polynomial $f(x)=1$ at $\alpha_1,\cdots,\alpha_n$).
+- Then $\mathcal{I}\in \mathcal{C}^R$.
+- Therefore, it suffices to show that any $n-s$ span $\mathcal{C}^R$.
+- Since $\dim \mathcal{C}=\dim \mathcal{C}^R=n-s$, it suffices to show that any $n-s$ rows are independent.
+
+Observe: The left most $n-s$ columns are linearly independent, and therefore span $\mathcal{C}$.
+
+Assume for contradiction there exists $n-s$ dependent rows.
+
+Then $\exists v\in \mathbb{C}^{n}$ such that $vB=0$.
+
+$v$ is orthogonal to the basis of $\mathcal{C}$.
+
+So $v\in \mathcal{C}^\perp$.
+
+From II, $\mathcal{C}^\perp$ is an $[n,s]$ MDS code, and hence every $v\in \mathcal{C}^\perp$ is of Hamming weight $\geq n-s+1$.
+
+This is a contradiction.
+
+</details>
+
+### Bound for gradient coding
+
+We want $s$ to be large and $d$ to be small.
+
+How small can $d$ with respect to $s$?
+
+- A: Build a bipartite graph.
+  - Left side: $n$ workers $W_1,\cdots,W_n$.
+  - Right side: $n$ partial datasets $D_1,\cdots,D_n$.
+  - Connect $W_i$ to $D_i$ if worker $i$ contains $D_i$.
+    - Equivalently if $B_{i,i}\neq 0$.
+  - $\deg (W_i) = d$ by definition.
+  - $\deg (\mathcal{D}_j)\geq s+1$.
+  - Sum degree on left $nd$ and right $\geq n(s+1)$.
+  - So $d\geq s+1$.
+
+We can break the lower bound using approximate computation.

content/CSE5313/CSE5313_L22.md

@@ -0,0 +1,247 @@
+# CSE5313 Coding and information theory for data science (Lecture 22)
+
+## Approximate Gradient Coding
+
+### Exact gradient computation and approximate gradient computation
+
+In the previous formulation, the gradient $\sum_i v_i$
+is computed exactly.
+
+- Accurate
+- Requires $d \geq s + 1$ (high replication factor). 
+- Need to know $s$ in advance!
+
+However:
+
+- Approximate gradient computation are very common!
+  - E.g., stochastic gradient descent.
+- Machine learning is inherently inaccurate.
+  - Relies on biased data, unverified assumptions about model, etc.
+
+Idea: If we relax the exact computation requirement, can have $d < s + 1$?
+
+- No fixed $s$ anymore.
+
+Approximate computation:
+
+- Exact computation: $\nabla \triangleq v = \sum_i v_i = (1, \cdots, 1) v_1, \cdots, v_n^\top$.
+⊤.
+- Approximate computation: $\nabla \triangleq v = \sum_i v_i \approx u v_1, \cdots, v_n^\top$,
+  - Where $d_2(u, \mathbb{I})$ is "small" ($d_2(u, v) =\sqrt{ \sum_i (u_i - v_i)^2}$).
+  - Why?
+- Lemma: Let $v_u = u (v_1, \cdots, v_n)^\top$. If $d_2(u, \mathbb{I}) \leq \epsilon$ then $d_2(v, v_u) \leq \epsilon \cdot \ell_{spec}(V)$.
+  - $V$ is the matrix whose rows are the $v_i$'s.
+  - $\ell_{spec}$ is the spectral norm (positive sqrt of maximum eigenvalue of $V^\top V$).
+- Idea: Distribute $S_1, \cdots, S_n$ as before, and
+  - as the master gets more and more responses,
+  - it can reconstruct $u v_1, \cdots, v_n^\top$,
+  - such that $d_2(u, \ell)$ gets smaller and smaller.
+
+> [!NOTE]
+> $d \geq s + 1$ no longer holds.
+> $s$ no longer a parameter of the system, but $s = n - \#responses$ at any given time.
+
+### Trivial Scheme
+
+Off the bat, the "do nothing" approach:
+
+- Send $S_i$ to worker $i$, i.e., $d = 1$.
+- Worker $i$ replies with the $i$'th partial gradient $v_i$.
+- The master averages up all the responses.
+
+How good is that?
+
+- For $u = \frac{n}{n-s} \cdot \mathbb{I}$, the factor $\frac{n}{n-s}$ corrects the $\frac{1}{n}$ in $v_i = \frac{1}{n} \cdot \nabla \text{ on } S_i$.
+- Is this $\approx \sum_i v_i$? In other words, what is $d_2(\frac{n}{n-s} \cdot \mathbb{I}, \mathbb{I})$?
+
+Trivial scheme: $\frac{n}{n-s} \cdot \mathbb{I}$ approximation.
+
+Must do better than that!
+
+### Roadmap
+
+- Quick reminder from linear algebra.
+  - Eigenvectors and orthogonality.
+- Quick reminder from graph theory.
+  - Adjacency matrix of a graph.
+- Graph theoretic concept: expander graphs.
+  - "Well connected" graphs.
+  - Extensively studied.
+- An approximate gradient coding scheme from expander graphs.
+
+### Linear algebra - Reminder
+
+- Let $A \in \mathbb{R}^{n \times n}$.
+- If $A v = \lambda v$ then $\lambda$ is an eigenvalue and $v$ is an eigenvector.
+- $v_1, \cdots, v_n \in \mathbb{R}^n$ are orthonormal:
+  - $\|v_i\|_2 = 1$ for all $i$.
+  - $v_i \cdot v_j^\top = 0$ for all $i \neq j$.
+- Nice property: $\| \alpha_1 v_1 + \cdots + \alpha_n v_n \|_2^2 = \sqrt{\sum_i \alpha_i^2}$.
+- $A$ is called symmetric if $A = A^\top$.
+- Theorem: A **real and symmetric** matrix has an orthonormal basis of eigenvectors.
+  - That is, there exists an orthonormal basis $v_1, \cdots, v_n$ such that $A v_i = \lambda_i v_i$ for some $\lambda_i$'s.
+
+### Graph theory - Reminder
+
+- Undirected graph $G = V, E$.
+- $V$ is a vertex set, usually $n = 1,2, \cdots, n$.
+- $E \subseteq \binom{V}{2}$ is an edge set (i.e., $E$ is a collection of subsets of $V$ of size two).
+- Each edge $e \in E$ is of the form $e = (a, b)$ for some distinct $a, b \in V$.
+- Spectral graph theory:
+  - Analyze properties of graphs (combinatorial object) using matrices (algebraic object).
+  - Specifically, for a graph $G$ let $A_G \in \{0,1\}^{n \times n}$ be the adjacency matrix of $G$.
+  - $A_{i,j} = 1$ if and only if $\{i,j\} \in E$ (otherwise 0).
+  - $A$ is real and symmetric.
+  - Therefore, has an orthonormal basis of eigenvectors.
+
+#### Some nice properties of adjacency matrices
+
+- Let $G = (V, E)$ be $d$-regular, with adjacency matrix $A_G$ whose (real) eigenvalues $\lambda_1 \geq \cdots \geq \lambda_n$.
+- Some theorems:
+  - $\lambda_1 = d$.
+  - $\lambda_n \geq -d$, equality if and only if $G$ is bipartite.
+  - $A_G \mathbb{I}^\top = \lambda_1 \mathbb{I}^\top = d \mathbb{I}^\top$ (easy to show!).
+    - Does that ring a bell? ;)
+  - If $\lambda_1 = \lambda_2$ then $G$ is not connected.
+
+#### Expander graphs - Intuition.
+
+- An important family of graphs.
+- Multiple applications in:
+  - Algorithms, complexity theory, error correcting codes, etc.
+- Intuition: A graph is called an expander if there are no "lonely small sets" of nodes.
+- Every set of at most $n/2$ nodes is "well connected" to the remaining nodes in the graph.
+- A bit more formally:
+  - An infinite family of graphs $G_n$ $n=1$ $\infty$ (where $G_n$ has $n$ nodes) is called an **expander family**, if the "minimal connectedness" of small sets in $G_n$ does not go to zero with $n$.
+
+#### Expander graphs - Definitions.
+
+- All graphs in this lecture are $d$-regular, i.e., all nodes have the same degree $d$.
+- For sets of nodes $S, T \subseteq V$, let $E(S, T)$ be the set of edges between $S$ and $T$. I.e., $E(S, T) = \{(i,j) \in E | i \in S \text{ and } j \in T\}$.
+- For a set of nodes $S$ let:
+  - $S^c = n \setminus S$ be its complement.
+  - Let $\partial S = E(S, S^c)$ be the boundary of $S$.
+  - I.e., the set of edges between $S$ and its complement $S^c$.
+- The expansion parameter $h_G$ of $G$ is:
+  - I.e., how many edges leave $S$, relative to its size.
+  - How "well connected" $S$ is to the remaining nodes.
+
+> [!NOTE]
+> $h_G = \min_{S \subseteq V, |S| \leq n/2} \frac{\partial S}{|S|}$.
+
+- An infinite family of $d$-regular graphs $(G_n)_{n=1}^\infty$ (where $G_n$ has $n$ nodes) is called an **expander family** if $h(G_n) \geq \epsilon$ for all $n$.
+  - Same $d$ and same $\epsilon$ for all $n$.
+- Expander families with large $\epsilon$ are hard to build explicitly.
+- Example: (Lubotsky, Philips and Sarnak '88)
+  - $V = \mathbb{Z}_p$ (prime).
+  - Connect $x$ to $x + 1, x - 1, x^{-1}$.
+  - $d = 3$, very small $\epsilon$.
+- However, **random** graphs are expanders with high probability.
+
+#### Expander graphs - Eigenvalues
+
+- There is a strong connection between the expansion parameter of a graph and the eigenvalues $\lambda_1 \geq \cdots \geq \lambda_n$ of its adjacency matrix.
+- Some theorems (no proof):
+  - $\frac{d-\lambda_2}{2} \leq h_G \leq \sqrt{2d (d - \lambda_2)}$.
+  - $d - \lambda_2$ is called the **spectral gap** of $G$.
+    - If the spectral gap is large, $G$ is a good expander.
+    - How large can it be?
+  - Let $\lambda = \max \{|\lambda_2|, |\lambda_n|\}$. Then $\lambda \geq 2 d - 1 - o_n(1)$. (Alon-Boppana Theorem).
+  - Graphs which achieve the Alon-Boppana bound (i.e., $\lambda \leq 2 d - 1$) are called **Ramanujan graphs**.
+    - The "best" expanders.
+    - Some construction are known.
+    - Efficient construction of Ramanujan graphs for all parameters is very recent (2016).
+
+#### Approximate GC from Expander Graphs
+
+Back to approximate gradient coding.
+
+- Let $d$ be any replication parameter.
+- Let $G$ be an expander graph (i.e., taken from an infinite expander family $(G_n)_{n=1}^\infty$)
+  - With eigenvalues $\lambda_1 \geq \cdots \geq \lambda_n$, and respective eigenvectors $w_1, \cdots, w_n$
+  - Assume $\|w_1\|_2 =\| w_2\|_2 = \cdots = \|w_n\|_2 = 1$, and $w_i w_j^\top = 0$ for all $i \neq j$.
+- Let the gradient coding matrix $B=\frac{1}{d} A_G$.
+  - The eigenvalues of $B$ are $\mu_1 = 1\geq \mu_2 \geq \cdots \geq \mu_n$. where $\mu_i = \frac{\lambda_i}{d}$.
+  - Let $\mu = \max \{|\mu_2|, |\mu_n|\}$.
+  - $d$ nonzero entries in each row $\Rightarrow$ Replication factor $d$.
+- Claim: For any number of stragglers $s$, we can get close to $\mathbb{I}$.
+  - Much better than the trivial scheme.
+  - Proximity is a function of $d$ and $\lambda$.
+- For every $s$ and any set $\mathcal{K}$ of $n - s$ responses, we build an "decoding vector".
+  - A function of $s$ and of the identities of the responding workers.
+  - Will be used to linearly combine the $n - s$ responses to get the approximate gradient.
+- Let $w_{\mathcal{K}} \in \mathbb{R}^n$ such that $(w_{\mathcal{K}})_i = \begin{cases} -1 & \text{if } i \notin \mathcal{K} \\ \frac{s}{n-s} & \text{if } i \in \mathcal{K} \end{cases}$.
+
+Lemma 1: $w_{\mathcal{K}}$ is spanned by $w_2, \cdots, w_n$, the $n - 1$ last eigenvectors of $A_G$.
+
+<details>
+<summary>Proof</summary>
+
+$w_2, \cdots, w_n$ are independent, and all orthogonal to $w_1 = \mathbb{I}$.
+
+$\Rightarrow$ The span of $w_2, \cdots, w_n$ is exactly all vectors whose sum of entries is zero.
+
+Sum of entries of $w_{\mathcal{K}}$ is zero $\Rightarrow$ $w_{\mathcal{K}}$ is in their span.
+
+Corollary: $w_{\mathcal{K}} = \alpha_2 w_2 + \cdots + \alpha_n w_n$ for some $\alpha_i$'s in $\mathbb{R}$.
+</details>
+
+Lemma 2: From direct computation, the norm of $w_{\mathcal{K}} = \alpha_2 w_2 + \cdots + \alpha_n w_n$ is $\frac{ns}{n-s}$.
+
+Corollary: $w_{\mathcal{K}}^2 = \sum_{i=2}^n \alpha_i^2 = \frac{ns}{n-s}$ (from Lemma 2 + orthonormality of $w_2, \cdots, w_n$).
+
+The scheme:
+
+- If the set of responses is $\mathcal{K}$, the decoding vector is $w_{\mathcal{K}} + \ell_2$.
+- Notice that $\operatorname{supp}(w_{\mathcal{K}} + \ell_2) = \mathcal{K}$.
+- The responses the master receives are the rows of $B v_1, \cdots, v_n^\top$ indexed by $\mathcal{K}$.
+- $\Rightarrow$ The master can compute $w_{\mathcal{K}} + \ell_2 B v_1, \cdots, v_n^\top$.
+
+Left to show: How close is $w_{\mathcal{K}} + \ell_2 B$ to $\ell_2$?
+
+<details>
+<summary>Proof</summary>
+
+Recall that:
+
+1. $w_{\mathcal{K}} = \alpha_2 w_2 + \cdots + \alpha_n w_n$.
+2. $w_i$'s are eigenvectors of $A_G$ (with eigenvalues $\lambda_i$) and of $B = \frac{1}{d} A_G$ (with eigenvalues $\mu_i = \frac{\lambda_i}{d}$).
+
+$d_2 (w_{\mathcal{K}} + \mathbb{I} B, \mathbb{I}) = d_2 (\mathbb{I} + \alpha_2 w_2 + \cdots + \alpha_n w_n B, \mathbb{I})$ (from 1.)
+
+$d_2 (w_{\mathcal{K}} + \mathbb{I} B, \mathbb{I}) = d_2 (\mathbb{I} + \alpha_2 \mu_2 w_2 + \cdots + \alpha_n \mu_n w_n, \mathbb{I})$ (eigenvalues of $B$, and $\mu_1 = 1$)
+
+$d_2 (w_{\mathcal{K}} + \mathbb{I} B, \mathbb{I}) = d_2 (\mathbb{I} + \alpha_2 \mu_2 w_2 + \cdots + \alpha_n \mu_n w_n , \mathbb{I})$ (by def.).
+
+$d_2 (w_{\mathcal{K}} + \mathbb{I} B, \mathbb{I}) = \|\sum_{i=2}^n \alpha_i \mu_i w_i\|_2$
+
+$d_2 (w_{\mathcal{K}} + \mathbb{I} B, \mathbb{I}) = \|\sum_{i=2}^n \alpha_i \mu_i w_i\|_2$ (w_i's are orthonormal).
+
+$d_2 (w_{\mathcal{K}} + \mathbb{I} B, \mathbb{I}) = \sqrt{\sum_{i=2}^n \alpha_i^2 \mu_i^2}$ (w_i's are orthonormal).
+
+</details>
+
+#### Improvement factor
+
+Corollary: If $B = \frac{1}{d} A_G$ for a (d-regular) Ramanujan graph $G$,
+
+- $\Rightarrow$ improvement factor $\approx \frac{2}{d}$.
+- Some explicit constructions of Ramanujan graphs (Lubotsky, Philips and Sarnak '88)
+  - with 2 $\frac{2}{d}$ $\approx$ 0.5!
+
+### Recap
+
+- Expander graph: A $d$-regular graph with no lonely small subsets of nodes.
+  - Every subset with $\leq n/2$ has a large ratio $\partial S / S$ (not $\rightarrow 0$ with $n$).
+  - Many constructions exist, random graph is expander w.h.p.
+  - The expansion factor is determined by the spectral gap $d - \lambda_2$,
+  - Where $\lambda = \max \{\lambda_2, \lambda_n\}$, and $\lambda_1 = d \geq \lambda_2 \geq \cdots \geq \lambda_n$ are the eigenvalues of $A_G$.
+  - "Best" expander = Ramanujan graph = has $\lambda \leq 2 d - 1$.
+- "Do nothing" approach: approximation $\frac{ns}{n-s}$.
+- Approximate gradient coding:
+  - Send $d$ subsets $S_{j1}, \cdots, S_{jd}$ to each node $i$, which returns a linear combination according to a coefficient matrix $B$.
+  - Let $B = \frac{1}{d} A_G$, for $G$ a Ramanujan graph: approximation $\frac{\lambda}{d} \frac{ns}{n-s}$.
+  - Up to 50% closer than "do nothing", at the price of higher computation load
+
+>[!NOTE]
+> Faster = more computation load.

content/CSE5313/CSE5313_L23.md

@@ -0,0 +1,242 @@
+# CSE5313 Coding and information theory for data science (Lecture 23)
+
+## Coded Computing
+
+### Motivation
+
+Some facts:
+
+- Moore's law is saturating.
+  - Improving CPU performance is hard.
+- Modern datasets are growing remarkably large.
+  - E.g., TikTok, YouTube.
+- Learning tasks are computationally heavy.
+  - E.g., training neural networks.
+
+Solution: Distributed Computing for Scalability
+
+- Offloading computation tasks to multiple computation nodes.
+- Gather and accumulate computation results.
+- E.g., Apache Hadoop, Apache Spark, MapReduce.
+
+### General Framework
+
+- The system involves 1 master node and $P$ worker nodes.
+- The master has a dataset $D$ and wants $f(D)$, where $f$ is some function.
+- The master partitions $D=(D_1,\cdots,D_P)$, and sends $D_i$ to node $i$.
+- Every node $i$ computes $g(D_i)$, where $g$ is somem function.
+- Finally, the master collects $g(D_1),\cdots,g(D_P)$ and computes $f(D)=h(g(D_1),\cdots,g(D_P))$, where $h$ is some function.
+
+#### Challenges
+
+Stragglers
+
+- Nodes that are significantly slower than the others.
+
+Adversaries
+
+- Nodes that return errounous results.
+  - Computation/communication errors.
+  - Adversarial attacks.
+
+Privary
+
+- Nodes may be curious about the dataset.
+
+### Resemblance to communication channel
+
+Suppose $f,g=\operatorname{id}$, and let $D=(D_1,\cdots,D_P)\in \mathbb{F}^p$ a message.
+
+- $D_i$ is a field element
+- $\mathbb{F}$ could be $\mathbb{R}$ or $\mathbb{C}$, $\mathbb{F}^q$.
+
+Observation: This is a distributed storage system.
+
+- An erasure - node that does not respond.
+- An error - node that returns errounous results.
+
+Solution:
+
+- Add redundancy to the message
+- Error-correcting codes.
+
+### Coded Distributed Computing
+
+- The master partitions $D$ and encodes it before sending to $P$ workers.
+- Workers perform computations on coded data $\tilde{D}$ and generate coded results $g(\tilde{D})$.
+- The master decode the coded results and obtain $f(D)=h(g(\tilde{D}))$.
+
+### Outline
+
+Matrix-Vector Multiplication
+
+- MDS codes.
+- Short-Dot codes.
+
+Matrix-Matrix Multiplication
+
+- Polynomial codes.
+- MatDot codes.
+
+Polynomial Evaluation
+
+- Lagrange codes.
+- Application to BLockchain.
+
+### Trivial solution - replication
+
+Why no straggler tolerance?
+
+- We employ an individual worker node $i$ to compute $y_i=(a_i,\ldots,a_{iN})\cdot (x_1,\ldots,x_N)^T$.
+
+Replicate the computation?
+
+- Let $r+1$ nodes compute every $y_i$.
+
+We need $P=rM+M$ worker nodes to tolerate $r$ erasures and $\lfloor \frac{r}{2}\rfloor$ adversaries.
+
+### Use of MDS codes
+
+Let $2|M$ and $P=3$.
+
+Let $A_1,A_2$ be submatrices of $A$ such that $A=[A_1^\top|A_2^\top]^\top$.
+
+- Worker node 1 conputes $A_1\cdot x$.
+- Worker node 2 conputes $A_2\cdot x$.
+- Worker node 3 conputes $(A_1+A_2)\cdot x$.
+
+Observation: the results can be obtained from any two worker nodes.
+
+Let $G\in \mathbb{F}^{M\times P}$ be the generator matrix of an $(P,M)$ MDS code.
+
+The master node computes $F=G^\top A\in \mathbb{F}^{P\times N}$.
+
+Every worker node $i$ computers $F_i\cdot x$.
+
+- $F_i=(G^\top A)_i$ is the i-th row of $G^\top A$.
+
+Notice that $Fx=G^\top A\cdot x=G^\top y$ is the codeword of $y$.
+
+Node $i$ computes an entry in this codeword.
+
+$1$ response = $1$ entyr of the codeword.
+
+The master does **not** need all workers to respond to obtain $y$.
+
+- The MDS property allows decoding from any $M$ $y_i$'s
+- This scheme tolerates $P-M$ erasures, and the recovery threshold $K=M$.
+- We need $P=r+M$ worker nodes to tolerate $r$ stragglers or $\frac{r}{2}$ adversaries.
+  - With replication, we need $P=rM+M$ worker nodes.
+
+#### Potential improvements for MDS codes
+
+- The matrix $A$ is usually a (trained) model, and $x$ is the data (feature vector).
+- $x$ is transmitted frequently, while the row of $A$ (or $G^\top A$) is communicated in advance.
+- Every worker needs to receive the entire $x$ and compute the dot product.
+- Communication-heavy
+- Can we design a scheme that allows every node only receive only a part of $x$?
+
+### Short-Dot codes
+
+[link to paper](https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=8758338)
+
+We want to create a matrix $F\in \mathbb{F}^{P\times M}$ from $A$ such that:
+
+- Every node computes $F_i\cdot x$.
+- Every $K$ rows linearly span the row space of $A$.
+- Each row of $F$ contains at most $s$ non-zero entries.
+
+In the MDS method, $F=G^\top A$.
+
+- The recovery threshold $K=M$.
+- Every worker node needs to receive $s=N$ symbols (the entire x)
+
+No free lunch
+
+Can we trade the recovery threshold $K$ for a smaller $s$?
+
+- Every worker node receives less than $N$ symbols.
+- The master will need more than $M$ responses to recover the computation result.
+
+#### Construction of Short-Dot codes
+
+Choose a super-regular matrix $B\in \mathbb{F}^{P\time K}$, where $P$ is the number of worker nodes.
+
+- A matrix is supper-regular if every square submatrix is invertible.
+- Lagrange/Cauchy matrix is super-regular (next lecture).
+
+Create matrix $\tilde{A}$ by stacking some $Z\in \mathbb{F}^{(K-M)\times N}$ below matrix $A$.
+
+Let $F=B\dot \tilde{A}\in \mathbb{F}^{P\times N}$.
+
+**Short-Dot**: create matrix $F\in \mathbb{F}^{P\times N}$ such that:
+
+- Every $K$ rows linearly span the row space of $A$.
+- Each row of $F$ contains at most $s=\frac{P-K+M}{P}$. $N$ non-zero entries (sparse).
+
+#### Recovery of Short-Dot codes
+
+Claim: Every $K$ rows of $F$ linearly span the row space of $A$.
+
+<details>
+<summary>Proof</summary>
+
+Since $B$ is supper-regular, it is also MDS, i.e., every $K\times K$ submatrix of $B$ is invertible.
+
+Hence, every row of $A$ can be represented as a linear combination of any $K$ rows of $F$.
+
+That is, for every $\mathcal{X}\subseteq[P],|\mathcal{X}|=K$, we can have $\tilde{A}=(B^{\mathcal{X}})^{-1}F^{\mathcal{X}}$.
+
+</details>
+
+What about the sparsity of $F$?
+
+- Want each row of $F$ to be sparse.
+
+#### Sparsity of Short-Dot codes
+
+Build $P\times P$ square matrix whose each row/column contains $P-K+M$ non-zero entries.
+
+Concatenate $\frac{N}{P}$ such matrices and obtain 
+
+[Missing slides 18]
+
+We now investigate what 𝑍 should look like to construct such a matrix 𝐹.
+• Recall that each column of 𝐹 must contains 𝐾 − 𝑀 zeros.
+– They are indexed by the set 𝒰 ∈ 𝑃 , where |𝒰| = 𝐾 − 𝑀.
+– Let 𝐵
+𝒰 ∈ 𝔽
+𝐾−𝑀 ×𝐾 be a submatrix of 𝐵 containing rows indexed by 𝒰.
+• Since 𝐹 = 𝐵𝐴ሚ , it follows that 𝐹𝑗 = 𝐵𝐴ሚ
+𝑗
+, where 𝐹𝑗 and 𝐴ሚ
+𝑗 are the 𝑗-th column of 𝐹 and 𝐴ሚ.
+• Next, we have 𝐵
+𝒰𝐴ሚ
+𝑗 = 0 (𝐾−𝑀)×1.
+• Split 𝐵
+𝒰 = [𝐵 1,𝑀
+𝒰
+,𝐵[𝑀+1,𝐾]
+𝒰 ], 𝐴ሚ
+𝑗 = 𝐴𝑗
+𝑇
+, 𝑍𝑗
+𝑇
+𝑇
+.
+• 𝐵
+𝒰𝐴ሚ
+𝑗 = 𝐵 1,𝑀
+𝒰 𝐴𝑗 + 𝐵[𝑀+1,𝐾]
+𝒰 𝑍𝑗 = 0 (𝐾−𝑀)×1.
+• 𝑍𝑗= −(𝐵 𝑀+1,𝐾
+𝒰
+)
+−1 𝐵 1,𝑀
+𝒰 𝐴𝑗
+.
+• Note that 𝐵 𝑀+1,𝐾
+𝒰 ∈ 𝔽
+𝐾−𝑀 × 𝐾−𝑀 is invertible.
+– Since 𝐵 is super-regular. 

content/CSE5313/CSE5313_L6.md

@@ -92,10 +92,10 @@ Two equivalent ways to constructing a linear code:
 
 - A **parity check** matrix $H\in \mathbb{F}^{(n-k)\times n}$ with $(n-k)$ rows and $n$ columns.
   $$
-  \mathcal{C}=\{c\in \mathbb{F}^n:Hc^T=0\}
+  \mathcal{C}=\{c\in \mathbb{F}^n:Hc^\top=0\}
   $$
   - The right kernel of $H$ is $\mathcal{C}$.
-  - Multiplying $c^T$ by $H$ "checks" if $c\in \mathcal{C}$.
+  - Multiplying $c^\top$ by $H$ "checks" if $c\in \mathcal{C}$.
 
 ### Encoding of linear codes
 
@@ -144,7 +144,7 @@ Decoding: $(y+e)\to x$, $y=xG$.
 Use **syndrome** to identify which coset $\mathcal{C}_i$ that the noisy-code to $\mathcal{C}_i+e$ belongs to.
 
 $$
-H(y+e)^T=H(y+e)=Hx+He=He
+H(y+e)^\top=H(y+e)=Hx+He=He
 $$
 
 ### Syndrome decoding
@@ -215,7 +215,7 @@ Fourth row is $\mathcal{C}+(00100)$.
 
 Any two elements in a row are of the form $y_1'=y_1+e$ and $y_2'=y_2+e$ for some $e\in \mathbb{F}^n$.
 
-Same syndrome if $H(y_1'+e)^T=H(y_2'+e)^T$.
+Same syndrome if $H(y_1'+e)^\top=H(y_2'+e)^\top$.
 
 Entries in different rows have different syndrome.
 
@@ -233,9 +233,10 @@ Compare with exhaustive search: Time: $O(|F|^n)$.
 
 #### Syndrome decoding - Intuition
 
-Given 𝒚′, we identify the set 𝐶 + 𝒆 to which 𝒚′ belongs by computing the syndrome.
-• We identify 𝒆 as the coset leader (leftmost entry) of the row 𝐶 + 𝒆.
-• We output the codeword in 𝐶 which is closest (𝒄3) by subtracting 𝒆 from 𝒚′.
+Given $y'$, we identify the set $\mathcal{C} + e$ to which $y'$ belongs by computing the syndrome.
+
+- We identify $e$ as the coset leader (leftmost entry) of the row $\mathcal{C} + e$.
+- We output the codeword in $\mathcal{C}$ which is closest ($c'$) by subtracting $e$ from $y'$.
 
 #### Syndrome decoding - Formal
 
@@ -243,4 +244,4 @@ Given $y'\in \mathbb{F}^n$, we identify the set $\mathcal{C}+e$ to which $y'$ be
 
 We identify $e$ as the coset leader (leftmost entry) of the row $\mathcal{C}+e$.
 
-We output the codeword in $\mathcal{C}$ which is closest ($c_3$) by subtracting $e$ from $y'$.
+We output the codeword in $\mathcal{C}$ which is closest (example $c_3$) by subtracting $e$ from $y'$.

content/CSE5313/CSE5313_L7.md

@@ -7,7 +7,7 @@ Let $\mathcal{C}= [n,k,d]_{\mathbb{F}}$ be a linear code.
 There are two equivalent ways to describe a linear code:
 
 1. A generator matrix $G\in \mathbb{F}^{k\times n}_q$ with $k$ rows and $n$ columns, entry taken from $\mathbb{F}_q$. $\mathcal{C}=\{xG|x\in \mathbb{F}^k\}$
-2. A parity check matrix $H\in \mathbb{F}^{(n-k)\times n}_q$ with $(n-k)$ rows and $n$ columns, entry taken from $\mathbb{F}_q$. $\mathcal{C}=\{c\in \mathbb{F}^n:Hc^T=0\}$
+2. A parity check matrix $H\in \mathbb{F}^{(n-k)\times n}_q$ with $(n-k)$ rows and $n$ columns, entry taken from $\mathbb{F}_q$. $\mathcal{C}=\{c\in \mathbb{F}^n:Hc^\top=0\}$
 
 ### Dual code
 
@@ -21,7 +21,7 @@ $$
 
 Also, the alternative definition is:
 
-1. $C^{\perp}=\{x\in \mathbb{F}^n:Gx^T=0\}$ (only need to check basis of $C$)
+1. $C^{\perp}=\{x\in \mathbb{F}^n:Gx^\top=0\}$ (only need to check basis of $C$)
 2. $C^{\perp}=\{xH|x\in \mathbb{F}^{n-k}\}$
 
 By rank-nullity theorem, $dim(C^{\perp})=n-dim(C)=n-k$.
@@ -87,7 +87,7 @@ Assume minimum distance is $d$. Show that every $d-1$ columns of $H$ are indepen
 
 - Fact: In linear codes minimum distance is the minimum weight ($d_H(x,y)=w_H(x-y)$).
 
-Indeed, if there exists a $d-1$ columns of $H$ that are linearly dependent, then we have $Hc^T=0$ for some $c\in \mathcal{C}$ with $w_H(c)<d$.
+Indeed, if there exists a $d-1$ columns of $H$ that are linearly dependent, then we have $Hc^\top=0$ for some $c\in \mathcal{C}$ with $w_H(c)<d$.
 
 Reverse are similar.
 
@@ -130,7 +130,7 @@ $k=2^m-m-1$.
 
 Define the code by encoding function:
 
-$E(x): \mathbb{F}_2^m\to \mathbb{F}_2^{2^m}=(xy_1^T,\cdots,xy_{2^m}^T)$ ($y\in \mathbb{F}_2^m$)
+$E(x): \mathbb{F}_2^m\to \mathbb{F}_2^{2^m}=(xy_1^\top,\cdots,xy_{2^m}^\top)$ ($y\in \mathbb{F}_2^m$)
 
 Space of codewords is image of $E$.
 

content/CSE5313/CSE5313_L8.md

@@ -258,7 +258,7 @@ Algorithm:
 - Begin with $(n-k)\times (n-k)$ identity matrix.
 - Assume we choose columns $h_1,h_2,\ldots,h_\ell$ (each $h_i$ is in $\mathbb{F}^n_q$)
 - Then next column $h_{\ell}$ must not be in the space of any previous $d-2$ columns.
-  - $h_{\ell}$ cannot be written as $[h_1,h_2,\ldots,h_{\ell-1}]x^T$ for $x$ of Hamming weight at most $d-2$.
+  - $h_{\ell}$ cannot be written as $[h_1,h_2,\ldots,h_{\ell-1}]x^\top$ for $x$ of Hamming weight at most $d-2$.
   - So the ineligible candidates for $h_{\ell}$ is:
     - $B_{\ell-1}(0,d-2)=\{x\in \mathbb{F}^{\ell-1}_q: d_H(0,x)\leq d-2\}$.
     - $|B_{\ell-1}(0,d-2)|=\sum_{i=0}^{d-2}\binom{\ell-1}{i}(q-1)^i$, denoted by $V_q(\ell-1, d-2)$.

content/CSE5313/CSE5313_L9.md

@@ -148,15 +148,15 @@ The generator matrix for Reed-Solomon code is a Vandermonde matrix $V(a_1,a_2,\l
 
 Fact: $V(a_1,a_2,\ldots,a_n)$ is invertible if and only if $a_1,a_2,\ldots,a_n$ are distinct. (that's how we choose $a_1,a_2,\ldots,a_n$)
 
-The parity check matrix for Reed-Solomon code is also a Vandermonde matrix $V(a_1,a_2,\ldots,a_n)^T$ with scalar multiples of the columns.
+The parity check matrix for Reed-Solomon code is also a Vandermonde matrix $V(a_1,a_2,\ldots,a_n)^\top$ with scalar multiples of the columns.
 
 Some technical lemmas:
 
 Let $G$ and $H$ be the generator and parity-check matrices of (any) linear code
 $C = [n, k, d]_{\mathbb{F}_q}$. Then:
 
-I. Then $H G^T = 0$.
-II. Any matrix $M \in \mathbb{F}_q^{n-k \times k}$ such that $\rank(M) = n - k$ and $M G^T = 0$ is a parity-check matrix for $C$ (i.e. $C = \ker M$).
+I. Then $H G^\top = 0$.
+II. Any matrix $M \in \mathbb{F}_q^{n-k \times k}$ such that $\rank(M) = n - k$ and $M G^\top = 0$ is a parity-check matrix for $C$ (i.e. $C = \ker M$).
 
 ## Reed-Muller code
 

content/CSE5313/Exam_reviews/CSE5313_E1.md

@@ -0,0 +1,359 @@
+# CSE 5313 Exam 1 review
+
+## Basic math
+
+```python
+class PrimeField:
+    def __init__(self, p: int, value: int = 0):
+        if not utils.prime(p):
+            raise ValueError("p must be a prime number")
+        if value >= p or value < 0:
+            raise ValueError("value must be integers in the range [0, p)")
+        self.p = p
+        self.value = value
+
+    def field_check(func):
+        def wrapper(self: 'PrimeField', other: 'PrimeField') -> 'PrimeField':
+            if self.p != other.p:
+                raise ValueError("Fields must have the same prime modulus")
+            return func(self, other)
+        return wrapper
+
+    def additive_inverse(self) -> 'PrimeField':
+        return PrimeField(self.p, self.p - self.value)
+
+    def multiplicative_inverse(self) -> 'PrimeField':
+        # done by Fermat's little theorem
+        return PrimeField(self.p, pow(self.value, self.p - 2, self.p))
+
+    def next_value(self) -> 'PrimeField':
+        return self + PrimeField(self.p, 1)
+
+    @field_check
+    def __add__(self, other: 'PrimeField') -> 'PrimeField':
+        return PrimeField(self.p, (self.value + other.value) % self.p)
+
+    @field_check
+    def __sub__(self, other: 'PrimeField') -> 'PrimeField':
+        return PrimeField(self.p, (self.value - other.value) % self.p)
+
+    @field_check
+    def __mul__(self, other: 'PrimeField') -> 'PrimeField':
+        return PrimeField(self.p, (self.value * other.value) % self.p)
+
+    @field_check
+    def __truediv__(self, other: 'PrimeField') -> 'PrimeField':
+        return PrimeField(self.p, (self.value * other.multiplicative_inverse().value)%self.p)
+
+    def __pow__(self, other: int) -> 'PrimeField':
+        # no field check for power operation
+        return PrimeField(self.p, pow(self.value, other, self.p))
+    
+    @field_check
+    def __eq__(self, other: 'PrimeField') -> bool:
+        return self.value == other.value
+
+    @field_check
+    def __ne__(self, other: 'PrimeField') -> bool:
+        return self.value != other.value
+
+    @field_check
+    def __lt__(self, other: 'PrimeField') -> bool:
+        return self.value < other.value
+    
+    @field_check
+    def __le__(self, other: 'PrimeField') -> bool:
+        return self.value <= other.value
+    
+    @field_check
+    def __gt__(self, other: 'PrimeField') -> bool:
+        return self.value > other.value
+    
+    @field_check
+    def __ge__(self, other: 'PrimeField') -> bool:
+        return self.value >= other.value
+    
+    def __str__(self) -> str:
+        return f"PrimeField({self.p}, {self.value})"
+```
+
+For field extension.
+
+```python
+class Polynomial():
+    # strict constructor
+    def __init__(self, p: int, coefficients: list[PrimeField]=[]):
+        if len(coefficients) == 0:
+            # no empty list is allowed
+            coefficients = [PrimeField(p, 0)]
+        if not utils.prime(p):
+            raise ValueError("p must be a prime number")
+        self.p = p
+        for coefficient in coefficients:
+            if not isinstance(coefficient, PrimeField) or coefficient.p != p:
+                raise ValueError("coefficients must be in the same field")
+        self.coefficients = coefficients
+        self.remove_leading_zero_coefficients()
+
+    # lazy constructor
+    @classmethod
+    def from_integers(cls, p: int, coefficients: list[int]) -> 'Polynomial':
+        # coefficients test
+        for coefficient in coefficients:
+            if 0 > coefficient or coefficient >= p:
+                raise ValueError("coefficients must be integers in the range [0, p)")
+        return cls(p, [PrimeField(p, coefficient) for coefficient in coefficients])
+
+    def __len__(self) -> int:
+        return len(self.coefficients)
+
+    def degree(self) -> int:
+        return len(self.coefficients) - 1
+
+    def evaluate(self, x: PrimeField) -> PrimeField:
+        if x.p != self.p:
+            raise ValueError("x must be in the same field as the polynomial")
+        return sum([(x ** i) * coefficient for i, coefficient in enumerate(self.coefficients)], PrimeField(self.p, 0))
+
+    def padding_coefficients(self, degree: int) -> None:
+        if degree < self.degree():
+            raise ValueError("degree must be greater than or equal to the current degree")
+        self.coefficients += [PrimeField(self.p, 0) for _ in range(degree - self.degree())]
+
+    def remove_leading_zero_coefficients(self) -> None:
+        while self.degree() > 0 and self.coefficients[self.degree()].value == 0:
+            self.coefficients.pop()
+
+    def field_check(func):
+        def wrapper(self: 'Polynomial', other: 'Polynomial') -> 'Polynomial':
+            if self.p != other.p:
+                raise ValueError("Fields must have the same prime modulus")
+            return func(self, other)
+        return wrapper
+
+    def is_constant(self) -> bool:
+        return self.degree() == 0
+
+    def next_value(self) -> 'Polynomial':
+        # function enumerate all possible polynomials, degree may increase by 1
+        new_coefficients = self.coefficients.copy()
+        # do list addition
+        pt=0
+        new_coefficients[pt] = new_coefficients[pt].next_value()
+        while pt < self.degree() and new_coefficients[pt] == PrimeField(self.p, 0):
+            pt += 1
+            new_coefficients[pt] = new_coefficients[pt].next_value()
+        if pt == self.degree():
+            new_coefficients.append(PrimeField(self.p, 1))
+        return Polynomial(self.p, new_coefficients)
+
+    def is_irreducible(self) -> bool:
+        # brute force check all possible divisors
+        if self.is_constant():
+            return False
+        # start from first non-constant coefficient
+        divisor = self.from_integers(self.p, [0,1])
+        while divisor.degree() < self.degree():
+            # debug
+            # print(f"{self}, enumerate divisor: {divisor.as_integers()}")
+            if self % divisor == self.from_integers(self.p, [0]):
+                # debug
+                # print(f"divisor: {divisor}, self: {self}")
+                return False
+            divisor = divisor.next_value()
+        return True
+
+    @field_check
+    def __add__(self, other: 'Polynomial') -> 'Polynomial':
+        padding_degree = max(self.degree(), other.degree())
+        self.padding_coefficients(padding_degree)
+        other.padding_coefficients(padding_degree)
+        new_coefficients = [self.coefficients[i] + other.coefficients[i] for i in range(padding_degree + 1)]
+        return Polynomial(self.p, new_coefficients)
+
+    @field_check
+    def __sub__(self, other: 'Polynomial') -> 'Polynomial':
+        padding_degree = max(self.degree(), other.degree())
+        self.padding_coefficients(padding_degree)
+        other.padding_coefficients(padding_degree)
+        new_coefficients = [self.coefficients[i] - other.coefficients[i] for i in range(padding_degree + 1)]
+        return Polynomial(self.p, new_coefficients)
+
+    @field_check
+    def __mul__(self, other: 'Polynomial') -> 'Polynomial':
+        new_coefficients = [PrimeField(self.p, 0) for _ in range(self.degree() + other.degree() + 1)]
+        for i in range(self.degree() + 1):
+            for j in range(other.degree() + 1):
+                new_coefficients[i + j] += self.coefficients[i] * other.coefficients[j]
+        return Polynomial(self.p, new_coefficients)
+
+    def __long_division__(self, other: 'Polynomial') -> 'Polynomial':
+        if self.degree() < other.degree():
+            return self.from_integers(self.p, [0]), self
+        quotient = self.from_integers(self.p, [0])
+        remainder = self
+        while remainder.degree() != 0 and remainder.degree() >= other.degree():
+            # debug
+            # print(f"remainder: {remainder}, remainder degree: {remainder.degree()}, other: {other}, other degree: {other.degree()}")
+            # reduce to primitive operation
+            division_result = (remainder.coefficients[remainder.degree()] / other.coefficients[other.degree()]).value
+            division_polynomial = self.from_integers(self.p,[0]* (remainder.degree() - other.degree()) + [division_result])
+            quotient += division_polynomial
+            # degree automatically adjusted
+            remainder = remainder - (division_polynomial * other)
+        return quotient, remainder
+
+    @field_check
+    def __truediv__(self, other: 'Polynomial') -> 'Polynomial':
+        return Polynomial(self.p, self.__long_division__(other)[0].coefficients)
+    
+    @field_check
+    def __mod__(self, other: 'Polynomial') -> 'Polynomial':
+        return Polynomial(self.p, self.__long_division__(other)[1].coefficients)
+
+    def __pow__(self, other: int) -> 'Polynomial':
+        # you many need better algorithm to speed up this operation
+        if other == 0:
+            return Polynomial(self.p, [PrimeField(self.p, 1)])
+        if other == 1:
+            return self
+        # fast exponentiation
+        if other % 2 == 0:
+            return (self * self) ** (other // 2)
+        return self * (self * self) ** ((other - 1) // 2)
+    
+    @field_check
+    def __eq__(self, other: 'Polynomial') -> bool:
+        return self.degree() == other.degree() and all(self.coefficients[i] == other.coefficients[i] for i in range(self.degree() + 1))
+    
+    @field_check
+    def __ne__(self, other: 'Polynomial') -> bool:
+        return self.degree() != other.degree() or any(self.coefficients[i] != other.coefficients[i] for i in range(self.degree() + 1))
+    
+    def __str__(self) -> str:
+        string_arr = [f"{coefficient.value}x^{i}" for i, coefficient in enumerate(self.coefficients) if coefficient.value != 0]
+        return f"Polynomial over GF({self.p}): {' + '.join(string_arr)}"
+
+    def as_integers(self) -> list[int]:
+        return [coefficient.value for coefficient in self.coefficients]
+
+    def as_number(self) -> int:
+        return sum([coefficient.value * self.p ** i for i, coefficient in enumerate(self.coefficients)])
+```
+
+### Finite fields
+
+```python
+class FiniteField():
+    def __init__(self, p: int, n: int = 1, value: Polynomial = None, irreducible_polynomial: Polynomial = None):
+        # set default value to zero polynomial
+        if value is None:
+            value = Polynomial.from_integers(p, [0])
+        if value.degree() >= n:
+            raise ValueError("Value must be a polynomial of degree less than n")
+        if not utils.prime(p):
+            raise ValueError("p must be a prime number")
+        if n<1:
+            raise ValueError("n must be non-negative")
+        # auto set irreducible polynomial
+        if irreducible_polynomial is not None:
+            if not irreducible_polynomial.is_irreducible():
+                raise ValueError("Irreducible polynomial is not irreducible")
+        else:
+            irreducible_polynomial = Polynomial.from_integers(p, [0]*(n) + [1])
+            while not irreducible_polynomial.is_irreducible():
+                irreducible_polynomial = irreducible_polynomial.next_value()
+        self.p = p
+        self.n = n
+        self.value = value
+        self.irreducible_polynomial = irreducible_polynomial
+
+    @classmethod
+    def from_integers(cls, p: int, n: int, coefficients: list[int], irreducible_polynomial: Polynomial = None) -> 'FiniteField':
+        return cls(p, n, Polynomial.from_integers(p, coefficients), irreducible_polynomial)
+
+    def additive_inverse(self) -> 'FiniteField':
+        coefficients = [-coefficient for coefficient in self.value.coefficients]
+        return FiniteField(self.p, self.n, Polynomial(self.p, coefficients), self.irreducible_polynomial)
+
+    def multiplicative_inverse(self) -> 'FiniteField':
+        # via Fermat's little theorem
+        return FiniteField(self.p, self.n, self.value ** ((self.p**self.n) - 2) % self.irreducible_polynomial, self.irreducible_polynomial)
+
+    def get_subfield(self) -> list['FiniteField']:
+        subfield = [
+            FiniteField(self.p, self.n, Polynomial.from_integers(self.p, [0]), self.irreducible_polynomial),
+            FiniteField(self.p, self.n, Polynomial.from_integers(self.p, [1]), self.irreducible_polynomial)
+        ]
+        current_element = self
+        for _ in range(0, (self.p**self.n) - 1):
+            if current_element in subfield:
+                break
+            subfield.append(current_element)
+            current_element = current_element * self
+        return subfield
+
+    def is_primitive(self) -> bool:
+        # check if the element is a primitive element from definition
+        subfield = self.get_subfield()
+        return len(subfield) == (self.p**self.n)
+
+    def next_value(self) -> 'FiniteField':
+        new_value = self.value.next_value()
+        # do modulo over n
+        while new_value.degree() >= self.n:
+            new_value = new_value % self.irreducible_polynomial
+        return FiniteField(self.p, self.n, new_value, self.irreducible_polynomial)
+
+    def field_property_check(func):
+        def wrapper(self: 'FiniteField', other: 'FiniteField') -> 'FiniteField':
+            if self.n != other.n:
+                raise ValueError("Fields must have the same degree")
+            if self.p != other.p:
+                raise ValueError("Fields must have the same prime modulus")
+            if self.irreducible_polynomial != other.irreducible_polynomial:
+                raise ValueError("Irreducible polynomials must be the same")
+            return func(self, other)
+        return wrapper
+
+    @field_property_check
+    def __add__(self, other: 'FiniteField') -> 'FiniteField':
+        return FiniteField(self.p, self.n, (self.value + other.value)%self.irreducible_polynomial, self.irreducible_polynomial)
+
+    @field_property_check
+    def __sub__(self, other: 'FiniteField') -> 'FiniteField':
+        return FiniteField(self.p, self.n, (self.value + other.additive_inverse()).value%self.irreducible_polynomial, self.irreducible_polynomial)
+
+    @field_property_check
+    def __mul__(self, other: 'FiniteField') -> 'FiniteField':
+        return FiniteField(self.p, self.n, (self.value * other.value)%self.irreducible_polynomial, self.irreducible_polynomial)
+
+    @field_property_check
+    def __truediv__(self, other: 'FiniteField') -> 'FiniteField':
+        return FiniteField(self.p, self.n, (self.value * other.multiplicative_inverse()).value%self.irreducible_polynomial, self.irreducible_polynomial)
+
+    @field_property_check
+    def __eq__(self, other: 'FiniteField') -> bool:
+        return self.value == other.value
+
+    @field_property_check
+    def __ne__(self, other: 'FiniteField') -> bool:
+        return self.value != other.value
+
+    def __str__(self) -> str:
+        return f"FiniteField over GF({self.p}) of degree {self.n}: {self.value}"
+
+    def as_vector(self) -> list[int]:
+        return [coefficient.value for coefficient in self.value.coefficients]
+
+    def as_number(self) -> int:
+        return self.value.as_number()
+
+    def as_polynomial(self) -> Polynomial:
+        return self.value
+
+```
+
+## Linear codes
+
+## Local recoverable codes

content/CSE5313/_meta.js

@@ -1,22 +1,61 @@
 export default {
-    index: "Course Description",
-    "---":{
-        type: 'separator'
+    menu: {
+      title: 'Home',
+      type: 'menu',
+      items: {
+        index: {
+          title: 'Home',
+          href: '/'
         },
-    CSE5313_L1: "CSE5313 Coding and information theory for data science (Lecture 1)",
-    CSE5313_L2: "CSE5313 Coding and information theory for data science (Lecture 2)",
-    CSE5313_L3: "CSE5313 Coding and information theory for data science (Lecture 3)",
-    CSE5313_L4: "CSE5313 Coding and information theory for data science (Lecture 4)",
-    CSE5313_L5: "CSE5313 Coding and information theory for data science (Lecture 5)",
-    CSE5313_L6: "CSE5313 Coding and information theory for data science (Lecture 6)",
-    CSE5313_L7: "CSE5313 Coding and information theory for data science (Lecture 7)",
-    CSE5313_L8: "CSE5313 Coding and information theory for data science (Lecture 8)",
-    CSE5313_L9: "CSE5313 Coding and information theory for data science (Lecture 9)",
-    CSE5313_L10: "CSE5313 Coding and information theory for data science (Recitation 10)",
-    CSE5313_L11: "CSE5313 Coding and information theory for data science (Recitation 11)",
-    CSE5313_L12: "CSE5313 Coding and information theory for data science (Lecture 12)",
-    CSE5313_L13: "CSE5313 Coding and information theory for data science (Lecture 13)",
-    CSE5313_L14: "CSE5313 Coding and information theory for data science (Lecture 14)",
-    CSE5313_L15: "CSE5313 Coding and information theory for data science (Lecture 15)",
-    CSE5313_L16: "CSE5313 Coding and information theory for data science (Exam Review)",
-}
+        about: {
+          title: 'About',
+          href: '/about'
+        },
+        contact: {
+          title: 'Contact Me',
+          href: '/contact'
+        }
+      },
+    },
+    Math3200'CSE5313_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Math429'CSE5313_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Math4111'CSE5313_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Math4121'CSE5313_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Math4201'CSE5313_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Math416'CSE5313_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Math401'CSE5313_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE332S'CSE5313_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE347'CSE5313_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE442T'CSE5313_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE5313'CSE5313_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE510'CSE5313_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE559A'CSE5313_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE5519'CSE5313_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Swap: {
+      display: 'hidden',
+      theme:{
+        timestamp: true,
+      }
+    },
+    index: {
+      display: 'hidden',
+      theme:{
+        sidebar: false,
+        timestamp: true,
+      }
+    },
+    about: {
+      display: 'hidden',
+      theme:{
+        sidebar: false,
+        timestamp: true,
+      }
+    },
+    contact: {
+      display: 'hidden',
+      theme:{
+        sidebar: false,
+        timestamp: true,
+      }
+    }
+  }

content/CSE5313/index.md

@@ -1,2 +1,151 @@
-# CSE5313 Coding and information theory for data science
+# CSE5313: Coding and Information Theory for Data Science
 
+**Instructor:** Netanel Raviv ([netanel.raviv@wustl.edu](mailto:netanel.raviv@wustl.edu))  
+**TA in Charge:** Junsheng Liu ([junsheng@wustl.edu](mailto:junsheng@wustl.edu))  
+**Time/Location:** Tuesdays & Thursdays, 11:30am–12:50pm, Whitaker 218  
+**Course Website:** [wustl.instructure.com/courses/155103](https://wustl.instructure.com/courses/155103)  
+**Piazza:** [piazza.com/wustl/fall2025/fall2025cse531301](https://piazza.com/wustl/fall2025/fall2025cse531301)
+
+---
+
+## Overview
+
+Coding/information theory emerged in the mid-20th century as a mathematical theory of communication with noise. In recent decades, it has become a vast topic encompassing most aspects of handling large datasets. The course will begin with the classical mathematical theory and its basic communication applications, then continue to contemporary applications in storage, computation, privacy, machine learning, and emerging technologies such as networks, blockchains, and DNA storage.
+
+---
+
+## Prerequisites
+
+Prior knowledge in:
+
+- Algebra (such as Math 309 or ESE 318)
+- Discrete math (such as CSE 240 or Math 310)
+- Probability (such as Math 2200 or ESE 326)
+- Some mathematical maturity is assumed
+
+---
+
+## Format
+
+### Lectures
+
+- Tuesdays and Thursdays at 11:30am in Whitaker 218
+- Lectures will **not** be recorded or streamed online
+- Attendance and participation are highly encouraged
+
+### Exams
+
+- **Midterm:** October 27th, 2025, 6:30–8:30pm, Louderman 458
+- The midterm will contain written response questions.  
+- **IMPORTANT:** At the end of the exam, you must scan and upload your exam to Gradescope using your phone. Specific instructions will be given before the exam. Feedback will be provided only electronically; the hard-copy will not be returned.
+
+### Office Hours
+
+- The instructor will hold a weekly office hour: Tuesdays, 1–2pm in McKelvey 3035.
+- Students are encouraged to attend.
+
+### Homework Assignments
+
+- 3–5 homework assignments submitted via Gradescope, with written-response questions
+- A separate final assignment involving a research paper
+- Students are encouraged to contact the instructor to discuss the choice of research paper; otherwise, a paper will be assigned
+
+---
+
+## Preliminary List of Topics
+
+- **Mathematical background**
+    - Channel coding, finite fields, linear codes, bounds
+- **Coding for distributed storage**
+    - Locally recoverable codes, regenerating codes, bounds
+- **Introduction to Information Theory**
+    - Information entropy, mutual information, asymptotic equipartition property, data compression
+- **Coding and privacy**
+    - Information-theoretic privacy, secret sharing, multiparty computing, private information retrieval
+- **Coded computation**
+    - Vector-matrix and matrix-matrix multiplication, Lagrange codes, gradient coding, blockchains
+- **Emerging and advanced topics**
+    - Coding for DNA storage and forensic 3D fingerprinting
+
+---
+
+## Textbooks
+
+There are no formal reading assignments, but students are encouraged to use the following:
+
+- *Introduction to Coding Theory*, R. M. Roth
+- *Elements of Information Theory*, T. M. Cover and J. A. Thomas
+
+Slides for every lecture will be made available online.
+
+---
+
+## Announcements
+
+All course announcements will be made in class or posted on the course website.
+
+---
+
+## Course Grade
+
+The final grade (0–100) will be determined as follows:
+
+- Homework assignments: **50%**
+- Midterm: **25%**
+- Final assignment: **25%**
+
+Letter grades will be assigned according to the following table:
+
+|  Letter  |    Range    |  Letter  |    Range    |  Letter  |    Range     |  Letter  |    Range      |
+|:--------:|:-----------:|:--------:|:-----------:|:--------:|:------------:|:--------:|:-------------:|
+|    A     | [94, 100]   |   B−     | [80, 84)    |   D+     | [67, 70)     |    D     | [64, 67)      |
+|   A−     | [90, 94)    |   C+     | [77, 80)    |    D−    | [61, 64)     |    F     | (−∞, 61)      |
+|   B+     | [87, 90)    |    C     | [74, 77)    |          |              |          |               |
+|    B     | [84, 87)    |   C−     | [70, 74)    |          |              |          |               |
+
+### Appeals
+
+- Appeals must be submitted through Gradescope within 7 days of work being returned
+- Provide a detailed explanation supporting your appeal
+
+---
+
+## Late Days
+
+- Each student has a budget of **five late days** for homework submissions
+- Assignments are due by **8:59pm CDT** on the due date
+- Any part of a late day counts as a full late day
+- No more than two late days can be used for any one homework
+- You are responsible for tracking your late-day usage
+- After using all late days, homework can only be late for medical or family emergencies
+
+---
+
+## Collaboration and Academic Integrity
+
+- Discuss problems with peers, but write your solutions **on your own**
+- List all students you discussed each problem with and any significant external sources used in your submission
+- Lack of necessary citations is a violation of policy
+- **You may not use any solution keys, guides, or solutions** from previous classes, similar courses, or textbooks, however obtained
+- No collaboration is allowed during exams
+- Violations may result in failing the class and formal academic integrity proceedings
+
+---
+
+### Clarification Regarding Generative AI Tools
+
+- The use of generative artificial intelligence tools (GenAI) is permitted **with restrictions**
+    - Do **not** ask GenAI for complete solutions
+    - Permitted uses: 
+        - Light document editing (grammar, typos, etc.)
+        - Understanding background information
+        - Seeking alternative explanations for course material
+    - **Submission of AI-generated text is prohibited**
+    - Beyond light editing, all submitted text must be written by the student
+
+**IMPORTANT:**
+- Every submitted assignment/project must include a "Use Of GenAI" paragraph summarizing any GenAI usage
+- Failure to include this paragraph or including untruthful statements will be considered a violation of academic integrity
+- The course staff reserves the right to summon any student for an oral exam regarding any submitted work, and adjust the grade accordingly.  
+    - The oral exam will focus on explaining your reasoning (no memorization required)
+    - Students may be selected at random, not necessarily due to suspicion

content/CSE5519/CSE5519_A4.md

@@ -1,2 +1,15 @@
 # CSE5519 Advances in Computer Vision (Topic A: 2025: Semantic Segmentation)
 
+## Dual Semantic Guidance for Open Vocabulary Sematic segmentation
+
+[link to the paper](https://openaccess.thecvf.com/content/CVPR2025/papers/Wang_Dual_Semantic_Guidance_for_Open_Vocabulary_Semantic_Segmentation_CVPR_2025_paper.pdf)
+
+## Novelty in Dual Semantic Guidance
+
+Use dual semantic guidance for semantic segmentation. For each mask, deploy clip like object detection to align the mask with text description.
+
+> [!TIP]
+>
+> This paper proposed a generalizable semantic segmentation model with a CLIP-like image-text encoder to refine the mask prediction.
+> 
+> However, I wonder how this model generalized to segment different faces of geometry and create a clear boundary between different objects and the background. In most cases, CLIP may not need complete image information to predict the object and can make a decision based on partial objects. If we have some novel objects containing features of two that might be out of CLIP's codebook, will the CLIP-alignment still work?

content/CSE5519/CSE5519_B4.md

@@ -1,2 +1,17 @@
 # CSE5519 Advances in Computer Vision (Topic B: 2024: Vision-Language Models)
 
+## Improved Baselines with Visual Instruction Tuning (LLaVA-1.5)
+
+[link to the paper](https://openaccess.thecvf.com/content/CVPR2024/papers/Liu_Improved_Baselines_with_Visual_Instruction_Tuning_CVPR_2024_paper.pdf)
+
+This paper shows that the visual instruction tuning can improve the performance of the vision-language model.
+
+### Novelty in LLaVA-1.5
+
+1. Scaling to high resolution images by dividing images into grids and maintaining the data efficiency.
+2. Compositional ability, (use long-form language reasoning together with shorter visual reasoning can improve the model's writing ability)
+3. Random downsampling will not degrade the performance.
+
+>[!TIP] 
+>
+> This paper shows that LLaVA-1.5 obeys the scaling law and splitting the high resolution images into grids to maintain the data efficiency. I wonder why this method is not applicable to multi-image understanding tasks? Why we cannot assign index embeddings to each image and push the image sets to the model for better understanding? What are the technical challenges to implement this idea?

content/CSE5519/CSE5519_B5.md

@@ -1,2 +1,21 @@
 # CSE5519 Advances in Computer Vision (Topic B: 2025: Vision-Language Models)
 
+## Molmo and PixMo:
+
+[link to paper](https://openaccess.thecvf.com/content/CVPR2025/papers/Deitke_Molmo_and_PixMo_Open_Weights_and_Open_Data_for_State-of-the-Art_CVPR_2025_paper.pdf)
+
+## Novelty in Molmo and PixMo
+
+PixMo dataset (712k images with long 200+ words description)
+
+- Simplified two-stage training pipline
+  - Standard ViT architecture with tokenizer and image encoder (CLIP) and pooling the embeddings to the decoder only LLM.
+- overlapping multi-crop policy
+  - Add overlapping region and image cropping to truncate the large image.
+- training over multiple annotations
+  - Text-only residual dropout
+- optimizer setups
+
+> [!TIP]
+>
+> This paper provides an interesting dataset and a refined training pipeline that is comparable to current closed-source SOTA performance. What is the contribution of the paper from the algorithm perspective? It seems that it is just a test for a new dataset with a slightly altered training pipeline.

content/CSE5519/CSE5519_C4.md

@@ -1,2 +1,13 @@
 # CSE5519 Advances in Computer Vision (Topic C: 2024 - 2025: Neural Rendering)
 
+## COLMAP-Free 3D Gaussian SplattingLinks to an external site
+
+[link to the paper](https://arxiv.org/pdf/2312.07504)
+
+We propose a novel 3D Gaussian Splatting (3DGS) framework that eliminates the need for COLMAP for camera pose estimation and bundle adjustment.
+
+> [!TIP]
+>
+> This paper presents a novel 3D Gaussian Splatting framework that eliminates the need for COLMAP for camera pose estimation and bundle adjustment.
+> 
+> Inspired by point map construction, the author uses Gaussian splatting to reconstruct the 3D scene. I wonder how this method might contribute to higher resolution reconstruction or improvements. Can we use the original COLMAP on traditional NeRF methods for comparable results?

content/CSE5519/CSE5519_D4.md

@@ -1,2 +1,21 @@
 # CSE5519 Advances in Computer Vision (Topic D: 2024: Image and Video Generation)
 
+## Autoregressive Model Beats Diffusion: Llama for Scalable Image Generation
+
+[link to the paper](https://arxiv.org/pdf/2406.06525)
+
+This paper shows that the autoregressive model can outperform the diffusion model in terms of image generation.
+
+### Novelty in the autoregressive model
+
+Use Llama 3.1 as the autoregressive model.
+
+Use code book and downsampling to reduce the memory footprint.
+
+> [!TIP]
+>
+> This paper shows that the autoregressive model can outperform the diffusion model in terms of image generation.
+>
+> And in later works, we showed that usually the image can be represented by a few code words; for example, 32 tokens may be enough to represent most of the images (that most humans need to annotate). However, I doubt the result if it can be generalized to more complex image generation tasks, for example, the image generation with a human face, since I found it difficult to describe people around me distinctively without calling their name.
+> 
+> For more real-life videos, to ensure contextual consistency, we may need to use more code words. Is such a method scalable to video generation to produce realistic results? Or will there be an exponential memory cost for the video generation?

content/CSE5519/CSE5519_E1.md

@@ -469,7 +469,7 @@ $$
 Then we use $\mathcal{L}_{ds}$ to enforce the smoothness of the disparity map.
 
 $$
-\mathcal{L}_{ds}=\sum_{p\in I^l}\left|\partial_x d^l_p\right|e^{-\left|\partial_x d^l_p\right|}+\left|\partial_y d^l_p\right|e^{-\left|\partial_y d^l_p\right|}=\sum_{p_t}|\nabla D(p_t)|\cdot \left(e^{-|\nabla I(p_t)|}\right)^T\tag{2}
+\mathcal{L}_{ds}=\sum_{p\in I^l}\left|\partial_x d^l_p\right|e^{-\left|\partial_x d^l_p\right|}+\left|\partial_y d^l_p\right|e^{-\left|\partial_y d^l_p\right|}=\sum_{p_t}|\nabla D(p_t)|\cdot \left(e^{-|\nabla I(p_t)|}\right)^\top\tag{2}
 $$
 
 Replacing $\hat{I}^{rig}_s$ with $\hat{I}^{full}_s$, in (1) and (2), we get the $\mathcal{L}_{fw}$ and $\mathcal{L}_{fs}$ for the non-rigid motion localizer.

content/CSE5519/CSE5519_E4.md

@@ -1,2 +1,19 @@
 # CSE5519 Advances in Computer Vision (Topic E: 2024: Deep Learning for Geometric Computer Vision)
 
+## DUSt3R: Geometric 3D Vision Made Easy.Links to an external site.
+
+[link to paper](https://arxiv.org/pdf/2312.14132)
+
+### Novelty in DUSt3R
+
+Use point map to represent the 3D scene, combining with the camera intrinsics to estimate the 3D scene.
+
+Direct-RGB to 3D scene.
+
+Use ViT to encode the image, and then use two Transformer decoder (with information sharing between them) to decode the two representation of the same scene $F_1$ and $F_2$. Direct regression from RGB to point map and confidence map.
+
+>[!TIP]
+>
+> Compared with previous works, this paper directly regresses the point map and confidence map from RGB, producing a more accurate and efficient 3D scene representation.
+> 
+> However, I'm not sure how the information across the two representations is shared in the Transformer decoder. If for a multiview image, there are two pairs of images that don't have any overlapping region, how can the model correctly reconstruct the 3D scene?

content/CSE5519/CSE5519_E5.md

@@ -1,2 +1,15 @@
 # CSE5519 Advances in Computer Vision (Topic E: 2025: Deep Learning for Geometric Computer Vision)
 
+## VGGT: Visual Geometry Grounded Transformer
+
+[link to paper](https://arxiv.org/pdf/2503.11651)
+
+### Novelty in VGGT
+
+Use alternating attention to encode the image.
+
+> [!TIP]
+>
+>  VGGT uses a feed-forward neural network that directly infers all key 3D attributes of a scene using alternating attention and is robust to some non-rigid deformations.
+> 
+> I wonder how this model adapts to different light settings for the same image, how the non-Lambertian reflectance is captured, and how this framework can be extended to recover the true color of the objects and evaluate the surface properties of the objects.

content/CSE5519/CSE5519_F4.md

@@ -1,2 +1,35 @@
 # CSE5519 Advances in Computer Vision (Topic F: 2024: Representation Learning)
 
+## Long-CLIP: Unlocking the long-text capability of CLIP
+
+[link to the paper](https://arxiv.org/pdf/2403.15378)
+
+### Novelty in Long-CLIP
+
+1. a **knowledge-preserving** stretching of positional embeddings
+2. a **primary component matching** of CLIP features.
+
+### Knowledge-preserving stretching of positional embeddings
+
+Retain the embedding of the top 20 positions, as for remaining 57 positions (training text is lower than 77 tokens), use the large ratio for linear interpolation.
+
+$$
+\operatorname{PE}^*(pos)=\begin{cases}
+\operatorname{PE}(pos) & \text{if } pos \leq 20 \\
+\operatorname{PE}(1-\alpha)\times \operatorname{PE}(\lfloor \frac{pos}{\lambda_2}\rfloor) + \alpha \times \operatorname{PE}(\lceil \frac{pos}{\lambda_2}\rceil) & \text{if } pos > 20
+\end{cases}
+$$
+
+where $\alpha=\frac{pos\%\lambda_2}{\lambda_2}$.
+
+#### Primary component matching of CLIP features
+
+Do not train with long text, (may decrease the performance of CLIP for short text)
+
+Use fine-grained and coarse-grained components to match the CLIP features.
+
+> [!TIP]
+>
+> This paper shows an interesting approach to increasing the long-text capability of CLIP. The authors use a knowledge-preserving stretching of positional embeddings and a primary component matching of CLIP features to achieve this.
+> 
+> However, the primary component matching is not a very satisfying solution, as it may not capture the novelty in high-frequency components, for example, the texture of clothes in the main character in the image, suppose multiple texture exists in the image. How does the model solve this problem and align the feature to the correct object of description? Or simply assumes that the bigger objects in the image are more important for the captioning task?

content/CSE5519/CSE5519_F5.md

@@ -1,2 +1,17 @@
 # CSE5519 Advances in Computer Vision (Topic F: 2025: Representation Learning)
 
+## Can Generative Models Improve Self-Supervised Representation Learning?
+
+[link to the paper](https://arxiv.org/pdf/2403.05966)
+
+### Novelty in SSL with Generative Models
+
+- Use generative models to generate synthetic data to train self-supervised representation learning models.
+- Use generative augmentation to generate new data from the original data using a generative model. (with gaussian noise, or other data augmentation techniques)
+- Using standard augmentation techniques like flipping, cropping, and color jittering with generative techniques can further improve the performance of the self-supervised representation learning models.
+
+> [!TIP]
+>
+> This paper shows that using generative models to generate synthetic data can improve the performance of self-supervised representation learning models. The key seems to be the use of generative augmentation to generate new data from the original data using a generative model.
+> 
+> However, both representation learning and generative modeling have some hallucinations. I wonder will these kinds of hallucinations would be reinforced, and the bias in the generation model would propagate to the representation learning model in the process of generative augmentation?

content/CSE5519/CSE5519_G4.md

@@ -1,2 +1,25 @@
 # CSE5519 Advances in Computer Vision (Topic G: 2024: Correspondence Estimation and Structure from Motion)
 
+## Global Structure from Motion Revisited
+
+[link to paper](https://arxiv.org/pdf/2407.20219v1)
+
+### Novelty in Global Structure from Motion Revisited
+
+1. Start with Quality matches
+   - Use only geometrically verified
+2. Match verification strategy
+   - Homography
+   - Essential Matrix
+   - Fundamental Matrix
+3. Filtering Bad Matches
+   - Cheirality test: Remove points behind the camera
+   - Epipolar proximity: Remove the matches near the epipole (unstable)
+   - Triangulation angle: Remove matches with small viewing angles (pool estimation for depth)
+4. Track Assembly
+   - Concatenate remaining matches across all image pairs
+   - Form continuous tracks of the same 3D point visible in multiple views
+
+> [!TIP]
+>
+> Compared with the COLMAP, the Global Structure from Motion Revisited is more robust to the noise and the outliers but less robust to repeated patterns. I wonder how this problem is resolved in normal COLMAP pipeline.

content/CSE5519/CSE5519_G5.md

@@ -1,2 +1,14 @@
 # CSE5519 Advances in Computer Vision (Topic G: 2025: Correspondence Estimation and Structure from Motion)
 
+## MegaSaM: Accurate, Fast, and Robust Structure and Motion from Casual Dynamic Videos
+
+[link to paper](https://arxiv.org/pdf/2412.04463)
+
+- vanilla Droid-SLAM
+- mono-depth initialization
+- objective movement map prediction
+- two-stage training scheme
+
+> [!TIP]
+>
+> How does the two-stage training scheme help with the robustness of the model? For me, it seems that this paper is just the integration of GeoNet (separated pose and depth) with full regression.

content/CSE5519/CSE5519_H4.md

@@ -1,2 +1,20 @@
 # CSE5519 Advances in Computer Vision (Topic H: 2024: Safety, Robustness, and Evaluation of CV Models)
 
+## Efficient Bias Mitigation Without Privileged Information
+
+[link to the paper](https://arxiv.org/pdf/2409.17691)
+
+TAB: Targeted Augmentation for Bias mitigation
+
+1. Loss history embedding construction (use Helper model to generate loss history for training dataset)
+2. Loss aware partitioning (partition the training dataset into groups based on the loss history, reweight the loss of each group to balance the dataset)
+3. Group-balanced dataset generation (generate a new dataset by sampling from the groups based on the reweighting)
+4. Robust model training (train the model on the new dataset)
+
+> [!TIP]
+>
+> This paper is a good example of how to mitigate bias in a dataset without using privileged information.
+>
+> However, the mitigation is heavy relied on the loss history, which might be different for each model architecture. Thus, the produced dataset may not be generalizable to other models.
+>
+> How to evaluate the bias mitigation effect across different models and different datasets?

content/CSE5519/CSE5519_I4.md

@@ -1,2 +1,16 @@
 # CSE5519 Advances in Computer Vision (Topic I: 2025: Embodied Computer Vision and Robotics)
 
+## Navigation World Models
+
+[link to paper](https://arxiv.org/pdf/2412.03572)
+
+### Novelty in NWM
+
+- Conditional Diffusion Transformer
+- Use time and action to conditioning the diffusion process
+
+> [!TIP]
+>
+> This paper provides a new way to train navigation world models. Via conditioned diffusion, the model can generate an imagined trajectory in an unknown environment and perform navigation tasks.
+> 
+> However, the model collapses frequently when using out-of-distribution data, resulting in poor navigation performance. I wonder how we can further condition on the novelty of the environment and integrate exploration strategies to train the model online to fix the collapse issue. What might be the challenges of doing so in the Conditioned Diffusion Transformer?

content/CSE5519/_meta.js

@@ -1,68 +1,61 @@
 export default {
-    index: "Course Description",
-    "---":{
-        type: 'separator'
+    menu: {
+      title: 'Home',
+      type: 'menu',
+      items: {
+        index: {
+          title: 'Home',
+          href: '/'
         },
-    CSE5519_L1: "CSE5519 Advances in Computer Vision (Lecture 1)",
-    CSE5519_L2: "CSE5519 Advances in Computer Vision (Lecture 2)",
-    CSE5519_L3: "CSE5519 Advances in Computer Vision (Lecture 3)",
-    "---":{
-        type: 'separator'
+        about: {
+          title: 'About',
+          href: '/about'
         },
-    CSE5519_C1: "CSE5519 Advances in Computer Vision (Topic C: 2021 and before: Neural Rendering)",
-    CSE5519_F1: "CSE5519 Advances in Computer Vision (Topic F: 2021 and before: Representation Learning)",
-    CSE5519_B1: "CSE5519 Advances in Computer Vision (Topic B: 2021 and before: Vision-Language Models)",
-    CSE5519_D1: "CSE5519 Advances in Computer Vision (Topic D: 2021 and before: Image and Video Generation)",
-    CSE5519_A1: "CSE5519 Advances in Computer Vision (Topic A: 2021 and before: Semantic Segmentation)",
-    CSE5519_E1: "CSE5519 Advances in Computer Vision (Topic E: 2021 and before: Deep Learning for Geometric Computer Vision)",
-    CSE5519_I1: "CSE5519 Advances in Computer Vision (Topic I: 2021 and before: Embodied Computer Vision and Robotics)",
-    CSE5519_J1: "CSE5519 Advances in Computer Vision (Topic J: 2021 and before: Open-Vocabulary Object Detection)",
-    "---":{
-        type: 'separator'
+        contact: {
+          title: 'Contact Me',
+          href: '/contact'
+        }
       },
-    CSE5519_H2: "CSE5519 Advances in Computer Vision (Topic H: 2022 and before: Safety, Robustness, and Evaluation of CV Models)",
-    CSE5519_G2: "CSE5519 Advances in Computer Vision (Topic G: 2022 and before: Correspondence Estimation and Structure from Motion)",
-    CSE5519_A2: "CSE5519 Advances in Computer Vision (Topic A: 2022: Semantic Segmentation)",
-    CSE5519_E2: "CSE5519 Advances in Computer Vision (Topic E: 2022: Deep Learning for Geometric Computer Vision)",
-    CSE5519_C2: "CSE5519 Advances in Computer Vision (Topic C: 2022: Neural Rendering)",
-    CSE5519_F2: "CSE5519 Advances in Computer Vision (Topic F: 2022: Representation Learning)",
-    CSE5519_B2: "CSE5519 Advances in Computer Vision (Topic B: 2022: Vision-Language Models)",
-    CSE5519_D2: "CSE5519 Advances in Computer Vision (Topic D: 2022: Image and Video Generation)",
-    CSE5519_I2: "CSE5519 Advances in Computer Vision (Topic I: 2022: Embodied Computer Vision and Robotics)",
-    CSE5519_J2: "CSE5519 Advances in Computer Vision (Topic J: 2022: Open-Vocabulary Object Detection)",
-    "---":{
-        type: 'separator'
     },
-    CSE5519_H3: "CSE5519 Advances in Computer Vision (Topic H: 2023: Safety, Robustness, and Evaluation of CV Models)",
-    CSE5519_B3: "CSE5519 Advances in Computer Vision (Topic B: 2023: Vision-Language Models)",
-    CSE5519_G3: "CSE5519 Advances in Computer Vision (Topic G: 2023: Correspondence Estimation and Structure from Motion)",
-    CSE5519_C3: "CSE5519 Advances in Computer Vision (Topic C: 2023: Neural Rendering)",
-    CSE5519_D3: "CSE5519 Advances in Computer Vision (Topic D: 2023: Image and Video Generation)",
-    CSE5519_E3: "CSE5519 Advances in Computer Vision (Topic E: 2023: Deep Learning for Geometric Computer Vision)",
-    CSE5519_F3: "CSE5519 Advances in Computer Vision (Topic F: 2023: Representation Learning)",
-    CSE5519_I3: "CSE5519 Advances in Computer Vision (Topic I: 2023 - 2024: Embodied Computer Vision and Robotics)",
-    CSE5519_J3: "CSE5519 Advances in Computer Vision (Topic J: 2023 - 2024: Open-Vocabulary Object Detection)",
-    CSE5519_A3: "CSE5519 Advances in Computer Vision (Topic A: 2023 - 2024: Semantic Segmentation)",
-    "---":{
-        type: 'separator'
+    Math3200'CSE5519_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Math429'CSE5519_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Math4111'CSE5519_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Math4121'CSE5519_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Math4201'CSE5519_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Math416'CSE5519_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Math401'CSE5519_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE332S'CSE5519_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE347'CSE5519_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE442T'CSE5519_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE5313'CSE5519_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE510'CSE5519_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE559A'CSE5519_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE5519'CSE5519_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Swap: {
+      display: 'hidden',
+      theme:{
+        timestamp: true,
+      }
     },
-    CSE5519_G4: "CSE5519 Advances in Computer Vision (Topic G: 2024: Correspondence Estimation and Structure from Motion)",
-    CSE5519_F4: "CSE5519 Advances in Computer Vision (Topic F: 2024: Representation Learning)",
-    CSE5519_D4: "CSE5519 Advances in Computer Vision (Topic D: 2024: Image and Video Generation)",
-    CSE5519_E4: "CSE5519 Advances in Computer Vision (Topic E: 2024: Deep Learning for Geometric Computer Vision)",
-    CSE5519_B4: "CSE5519 Advances in Computer Vision (Topic B: 2024: Vision-Language Models)",
-    CSE5519_H4: "CSE5519 Advances in Computer Vision (Topic H: 2024: Safety, Robustness, and Evaluation of CV Models)",
-    CSE5519_C4: "CSE5519 Advances in Computer Vision (Topic C: 2024 - 2025: Neural Rendering)",
-    "---":{
-        type: 'separator'
+    index: {
+      display: 'hidden',
+      theme:{
+        sidebar: false,
+        timestamp: true,
+      }
     },
-    CSE5519_F5: "CSE5519 Advances in Computer Vision (Topic F: 2025: Representation Learning)",
-    CSE5519_B5: "CSE5519 Advances in Computer Vision (Topic B: 2025: Vision-Language Models)",
-    CSE5519_D5: "CSE5519 Advances in Computer Vision (Topic D: 2025: Image and Video Generation)",
-    CSE5519_E5: "CSE5519 Advances in Computer Vision (Topic E: 2025: Deep Learning for Geometric Computer Vision)",
-    CSE5519_A4: "CSE5519 Advances in Computer Vision (Topic A: 2025: Semantic Segmentation)",
-    CSE5519_G5: "CSE5519 Advances in Computer Vision (Topic G: 2025: Correspondence Estimation and Structure from Motion)",
-    CSE5519_I4: "CSE5519 Advances in Computer Vision (Topic I: 2025: Embodied Computer Vision and Robotics)",
-    CSE5519_H5: "CSE5519 Advances in Computer Vision (Topic H: 2025: Safety, Robustness, and Evaluation of CV Models)",
-    CSE5519_J5: "CSE5519 Advances in Computer Vision (Topic J: 2025: Open-Vocabulary Object Detection)",
-}
+    about: {
+      display: 'hidden',
+      theme:{
+        sidebar: false,
+        timestamp: true,
+      }
+    },
+    contact: {
+      display: 'hidden',
+      theme:{
+        sidebar: false,
+        timestamp: true,
+      }
+    }
+  }

content/CSE559A/CSE559A_L21.md

@@ -64,7 +64,7 @@ $d = \begin{bmatrix}
 u \\ v
 \end{bmatrix}$
 
-The solution is $d=(A^T A)^{-1} A^T b$
+The solution is $d=(A^\top A)^{-1} A^\top b$
 
 Lucas-Kanade flow: 
 
@@ -170,7 +170,7 @@ E = \sum_{i=1}^n (a(x_i-\bar{x})+b(y_i-\bar{y}))^2 = \left\|\begin{bmatrix}x_1-\
 $$
 
 We want to find $N$ that minimizes $\|UN\|^2$ subject to $\|N\|^2= 1$
-Solution is given by the eigenvector of $U^T U$ associated with the smallest eigenvalue
+Solution is given by the eigenvector of $U^\top U$ associated with the smallest eigenvalue
 
 Drawbacks:
 

content/CSE559A/CSE559A_L22.md

@@ -178,7 +178,7 @@ $$
 \begin{pmatrix}a\\b\\c\end{pmatrix} \times \begin{pmatrix}a'\\b'\\c'\end{pmatrix} = \begin{pmatrix}bc'-b'c\\ca'-c'a\\ab'-a'b\end{pmatrix}
 $$
 
-Let $h_1^T, h_2^T, h_3^T$ be the rows of $H$. Then
+Let $h_1^\top, h_2^\top, h_3^\top$ be the rows of $H$. Then
 
 $$
 x_i' × Hx_i=\begin{pmatrix}
@@ -186,15 +186,15 @@ x_i' × Hx_i=\begin{pmatrix}
     y_i' \\
     1
 \end{pmatrix} \times \begin{pmatrix}
-    h_1^T x_i \\
-    h_2^T x_i \\
-    h_3^T x_i
+    h_1^\top x_i \\
+    h_2^\top x_i \\
+    h_3^\top x_i
 \end{pmatrix}
 =
 \begin{pmatrix}
-    y_i' h_3^T x_i−h_2^T x_i \\
-    h_1^T x_i−x_i' h_3^T x_i \\
-    x_i' h_2^T x_i−y_i' h_1^T x_i
+    y_i' h_3^\top x_i−h_2^\top x_i \\
+    h_1^\top x_i−x_i' h_3^\top x_i \\
+    x_i' h_2^\top x_i−y_i' h_1^\top x_i
 \end{pmatrix}
 $$
 
@@ -206,15 +206,15 @@ x_i' × Hx_i=\begin{pmatrix}
     y_i' \\
     1
 \end{pmatrix} \times \begin{pmatrix}
-    h_1^T x_i \\
-    h_2^T x_i \\
-    h_3^T x_i
+    h_1^\top x_i \\
+    h_2^\top x_i \\
+    h_3^\top x_i
 \end{pmatrix}
 =
 \begin{pmatrix}
-    y_i' h_3^T x_i−h_2^T x_i \\
-    h_1^T x_i−x_i' h_3^T x_i \\
-    x_i' h_2^T x_i−y_i' h_1^T x_i
+    y_i' h_3^\top x_i−h_2^\top x_i \\
+    h_1^\top x_i−x_i' h_3^\top x_i \\
+    x_i' h_2^\top x_i−y_i' h_1^\top x_i
 \end{pmatrix}
 $$
 
@@ -222,9 +222,9 @@ Rearranging the terms:
 
 $$
 \begin{bmatrix}
-    0^T &-x_i^T &y_i' x_i^T \\
-    x_i^T &0^T &-x_i' x_i^T \\
-    y_i' x_i^T &x_i' x_i^T &0^T
+    0^\top &-x_i^\top &y_i' x_i^\top \\
+    x_i^\top &0^\top &-x_i' x_i^\top \\
+    y_i' x_i^\top &x_i' x_i^\top &0^\top
 \end{bmatrix}
 \begin{bmatrix}
     h_1 \\

content/CSE559A/CSE559A_L26.md

@@ -17,16 +17,16 @@ If we set the config for the first camera as the world origin and $[I|0]\begin{p
 Notice that $x'\cdot [t\times (Ry)]=0$
 
 $$
-x'^T E x_1 = 0
+x'^\top E x_1 = 0
 $$
 
 We denote the constraint defined by the Essential Matrix as $E$.
 
 $E x$ is the epipolar line associated with $x$ ($l'=Ex$)
 
-$E^T x'$ is the epipolar line associated with $x'$ ($l=E^T x'$)
+$E^\top x'$ is the epipolar line associated with $x'$ ($l=E^\top x'$)
 
-$E e=0$ and $E^T e'=0$ ($x$ and $x'$ don't matter)
+$E e=0$ and $E^\top e'=0$ ($x$ and $x'$ don't matter)
 
 $E$ is singular (rank 2) and have five degrees of freedom.
 
@@ -35,13 +35,13 @@ $E$ is singular (rank 2) and have five degrees of freedom.
 If the calibration matrices $K$ and $K'$ are unknown, we can write the epipolar constraint in terms of unknown normalized coordinates:
 
 $$
-x'^T_{norm} E x_{norm} = 0
+x'^\top_{norm} E x_{norm} = 0
 $$
 
 where $x_{norm}=K^{-1} x$, $x'_{norm}=K'^{-1} x'$
 
 $$
-x'^T_{norm} E x_{norm} = 0\implies x'^T_{norm} Fx=0
+x'^\top_{norm} E x_{norm} = 0\implies x'^\top_{norm} Fx=0
 $$
 
 where $F=K'^{-1}EK^{-1}$ is the **Fundamental Matrix**.
@@ -60,17 +60,17 @@ Properties of $F$:
 
 $F x$ is the epipolar line associated with $x$ ($l'=F x$)
 
-$F^T x'$ is the epipolar line associated with $x'$ ($l=F^T x'$)
+$F^\top x'$ is the epipolar line associated with $x'$ ($l=F^\top x'$)
 
-$F e=0$ and $F^T e'=0$
+$F e=0$ and $F^\top e'=0$
 
 $F$ is singular (rank two) and has seven degrees of freedom
 
 #### Estimating the fundamental matrix
 
-Given: correspondences $x=(x,y,1)^T$ and $x'=(x',y',1)^T$
+Given: correspondences $x=(x,y,1)^\top$ and $x'=(x',y',1)^\top$
 
-Constraint: $x'^T F x=0$
+Constraint: $x'^\top F x=0$
 
 $$
 (x',y',1)\begin{bmatrix}
@@ -95,7 +95,7 @@ F=U\begin{bmatrix}
 \sigma_1 & 0 \\
 0 & \sigma_2 \\
 0 & 0
-\end{bmatrix}V^T
+\end{bmatrix}V^\top
 $$
 
 ## Structure from Motion
@@ -126,7 +126,7 @@ a_{21} & a_{22} & a_{23} & t_2 \\
 0 & 0 & 0 & 1
 \end{bmatrix}=\begin{bmatrix}
 A & t \\
-0^T & 1
+0^\top & 1
 \end{bmatrix}
 $$
 
@@ -160,10 +160,10 @@ The reconstruction is defined up to an arbitrary affine transformation $Q$ (12 d
 $$
 \begin{bmatrix}
 A & t \\
-0^T & 1
+0^\top & 1
 \end{bmatrix}\rightarrow\begin{bmatrix}
 A & t \\
-0^T & 1
+0^\top & 1
 \end{bmatrix}Q^{-1}, \quad \begin{pmatrix}X_j\\1\end{pmatrix}\rightarrow Q\begin{pmatrix}X_j\\1\end{pmatrix}
 $$
 

content/CSE559A/CSE559A_L5.md

@@ -74,7 +74,7 @@ x\\y
 \end{pmatrix}
 $$
 
-To undo the rotation, we need to rotate the image by $-\theta$. This is equivalent to apply $R^T$ to the image.
+To undo the rotation, we need to rotate the image by $-\theta$. This is equivalent to apply $R^\top$ to the image.
 
 #### Affine transformation
 

content/CSE559A/CSE559A_L7.md

@@ -96,7 +96,7 @@ Example: Linear classification models
 Find a linear function that separates the data.
 
 $$
-f(x) = w^T x + b
+f(x) = w^\top x + b
 $$
 
 [Linear classification models](http://cs231n.github.io/linear-classify/)
@@ -144,13 +144,13 @@ This is a convex function, so we can find the global minimum.
 The gradient is:
 
 $$
-\nabla_w||Xw-Y||^2 = 2X^T(Xw-Y)
+\nabla_w||Xw-Y||^2 = 2X^\top(Xw-Y)
 $$
 
 Set the gradient to 0, we get:
 
 $$
-w = (X^T X)^{-1} X^T Y
+w = (X^\top X)^{-1} X^\top Y
 $$
 
 From the maximum likelihood perspective, we can also derive the same result.

content/CSE559A/CSE559A_L8.md

@@ -59,7 +59,7 @@ Suppose $k=1$, $e=l(f_1(x,w_1),y)$
 
 Example: $e=(f_1(x,w_1)-y)^2$
 
-So $h_1=f_1(x,w_1)=w^T_1x$, $e=l(h_1,y)=(y-h_1)^2$
+So $h_1=f_1(x,w_1)=w^\top_1x$, $e=l(h_1,y)=(y-h_1)^2$
 
 $$
 \frac{\partial e}{\partial w_1}=\frac{\partial e}{\partial h_1}\frac{\partial h_1}{\partial w_1}

content/CSE559A/CSE559A_L9.md

@@ -20,7 +20,7 @@ Suppose $k=1$, $e=l(f_1(x,w_1),y)$
 
 Example: $e=(f_1(x,w_1)-y)^2$
 
-So $h_1=f_1(x,w_1)=w^T_1x$, $e=l(h_1,y)=(y-h_1)^2$
+So $h_1=f_1(x,w_1)=w^\top_1x$, $e=l(h_1,y)=(y-h_1)^2$
 
 $$
 \frac{\partial e}{\partial w_1}=\frac{\partial e}{\partial h_1}\frac{\partial h_1}{\partial w_1}

content/CSE559A/_meta.js

@@ -1,32 +1,61 @@
 export default {
-    index: "Course Description",
-    "---":{
-        type: 'separator'
+    menu: {
+      title: 'Home',
+      type: 'menu',
+      items: {
+        index: {
+          title: 'Home',
+          href: '/'
         },
-    CSE559A_L1: "Computer Vision (Lecture 1)",
-    CSE559A_L2: "Computer Vision (Lecture 2)",
-    CSE559A_L3: "Computer Vision (Lecture 3)",
-    CSE559A_L4: "Computer Vision (Lecture 4)",
-    CSE559A_L5: "Computer Vision (Lecture 5)",
-    CSE559A_L6: "Computer Vision (Lecture 6)",
-    CSE559A_L7: "Computer Vision (Lecture 7)",
-    CSE559A_L8: "Computer Vision (Lecture 8)",
-    CSE559A_L9: "Computer Vision (Lecture 9)",
-    CSE559A_L10: "Computer Vision (Lecture 10)",
-    CSE559A_L11: "Computer Vision (Lecture 11)",
-    CSE559A_L12: "Computer Vision (Lecture 12)",
-    CSE559A_L13: "Computer Vision (Lecture 13)",
-    CSE559A_L14: "Computer Vision (Lecture 14)",
-    CSE559A_L15: "Computer Vision (Lecture 15)",
-    CSE559A_L16: "Computer Vision (Lecture 16)",
-    CSE559A_L17: "Computer Vision (Lecture 17)",
-    CSE559A_L18: "Computer Vision (Lecture 18)",
-    CSE559A_L19: "Computer Vision (Lecture 19)",
-    CSE559A_L20: "Computer Vision (Lecture 20)",
-    CSE559A_L21: "Computer Vision (Lecture 21)",
-    CSE559A_L22: "Computer Vision (Lecture 22)",
-    CSE559A_L23: "Computer Vision (Lecture 23)",
-    CSE559A_L24: "Computer Vision (Lecture 24)",
-    CSE559A_L25: "Computer Vision (Lecture 25)",
-    CSE559A_L26: "Computer Vision (Lecture 26)",
-}
+        about: {
+          title: 'About',
+          href: '/about'
+        },
+        contact: {
+          title: 'Contact Me',
+          href: '/contact'
+        }
+      },
+    },
+    Math3200'CSE559A_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Math429'CSE559A_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Math4111'CSE559A_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Math4121'CSE559A_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Math4201'CSE559A_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Math416'CSE559A_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Math401'CSE559A_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE332S'CSE559A_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE347'CSE559A_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE442T'CSE559A_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE5313'CSE559A_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE510'CSE559A_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE559A'CSE559A_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    CSE5519'CSE559A_link\s*:\s*(\{\s+.+\s+.+)\s+.+\s+.+\s+.+\s+(\},)'
+    Swap: {
+      display: 'hidden',
+      theme:{
+        timestamp: true,
+      }
+    },
+    index: {
+      display: 'hidden',
+      theme:{
+        sidebar: false,
+        timestamp: true,
+      }
+    },
+    about: {
+      display: 'hidden',
+      theme:{
+        sidebar: false,
+        timestamp: true,
+      }
+    },
+    contact: {
+      display: 'hidden',
+      theme:{
+        sidebar: false,
+        timestamp: true,
+      }
+    }
+  }

content/Math401/Extending_thesis/Math401_R1.md

@@ -234,7 +234,7 @@ Then the measurable space $(\Omega, \mathscr{B}(\mathbb{C}), \lambda)$ is a meas
 
 If $\Omega=\mathbb{R}$, then we denote such measurable space as $L^2(\mathbb{R}, \lambda)$.
 
-<details>
+</details>
 
 #### Probability space
 
@@ -262,10 +262,10 @@ Basic definitions
 
 The special orthogonal group $SO(n)$ is the set of all **distance preserving** linear transformations on $\mathbb{R}^n$.
 
-It is the group of all $n\times n$ orthogonal matrices ($A^T A=I_n$) on $\mathbb{R}^n$ with determinant $1$.
+It is the group of all $n\times n$ orthogonal matrices ($A^\top A=I_n$) on $\mathbb{R}^n$ with determinant $1$.
 
 $$
-SO(n)=\{A\in \mathbb{R}^{n\times n}: A^T A=I_n, \det(A)=1\}
+SO(n)=\{A\in \mathbb{R}^{n\times n}: A^\top A=I_n, \det(A)=1\}
 $$
 
 <details>
@@ -276,7 +276,7 @@ In [The random Matrix Theory of the Classical Compact groups](https://case.edu/a
 $O(n)$ (the group of all $n\times n$ **orthogonal matrices** over $\mathbb{R}$),
 
 $$
-O(n)=\{A\in \mathbb{R}^{n\times n}: AA^T=A^T A=I_n\}
+O(n)=\{A\in \mathbb{R}^{n\times n}: AA^\top=A^\top A=I_n\}
 $$
 
 $U(n)$ (the group of all $n\times n$ **unitary matrices** over $\mathbb{C}$), 
@@ -296,7 +296,7 @@ $$
 $Sp(2n)$ (the group of all $2n\times 2n$ symplectic matrices over $\mathbb{C}$),
 
 $$
-Sp(2n)=\{U\in U(2n): U^T J U=UJU^T=J\}
+Sp(2n)=\{U\in U(2n): U^\top J U=UJU^\top=J\}
 $$
 
 where $J=\begin{pmatrix}
@@ -426,7 +426,7 @@ is a pure state.
 
 </details>
 
-## Drawing the connection between the space $S^{2n+1}$, $CP^n$, and $\mathbb{R}$
+## Drawing the connection between the space $S^{2n+1}$, $\mathbb{C}P^n$, and $\mathbb{R}$
 
 A pure quantum state of size $N$ can be identified with a **Hopf circle** on the sphere $S^{2N-1}$.
 

content/Math401/Extending_thesis/Math401_R2.md

@@ -202,8 +202,6 @@ $$
 \end{aligned}
 $$
 
-QED
-
 </details>
 
 #### Proof of the Levy's concentration theorem via the Maxwell-Boltzmann distribution law

content/Math401/Extending_thesis/Math401_R4.md

@@ -4,14 +4,51 @@
 
 This part may not be a part of "mathematical" research. But that's what I initially begin with.
 
-## Superdense coding
-
 > [!TIP]
 >
 > A helpful resource is [The Functional Analysis of Quantum Information Theory](https://arxiv.org/pdf/1410.7188) Section 2.2
 >
 > Or another way in quantum computing [Quantum Computing and Quantum Information](https://www.cambridge.org/highereducation/books/quantum-computation-and-quantum-information/01E10196D0A682A6AEFFEA52D53BE9AE#overview) Section 2.3
 
+## References to begin with
+
+### Quantum computing and quantum information
+
+Every quantum bit is composed of two orthogonal states, denoted by $|0\rangle$ and $|1\rangle$.
+
+Each state
+
+$$
+\varphi=\alpha|0\rangle+\beta|1\rangle
+$$
+
+where $\alpha$ and $\beta$ are complex numbers, and $|\alpha|^2+|\beta|^2=1$.
+
+### Logic gates
+
+All the logic gates are unitary operators in $\mathbb{C}^{2\times 2}$.
+
+Example: the NOT gate is represented by the following matrix:
+
+$$
+NOT=\begin{pmatrix}
+0 & 1 \\
+1 & 0
+\end{pmatrix}
+$$
+
+Hadamard gate is represented by the following matrix:
+
+$$
+H=\frac{1}{\sqrt{2}}\begin{pmatrix}
+1 & 1 \\
+1 & -1
+\end{pmatrix}
+$$
+
+## Superdense coding
+
+
 ## Quantum error correcting codes
 
 This part is intentionally left blank and may be filled near the end of the semester, by assignments given in CSE5313.

content/Math401/Extending_thesis/Math401_S3.md

@@ -1,2 +1,276 @@
 # Math 401, Fall 2025: Thesis notes, S3, Coherent states and POVMs
 
+> This section should extends on the reading for
+>
+> [Holomorphic methods in analysis and mathematical physics]()
+
+
+## Bargmann space (original)
+
+Also known as Segal-Bargmann space or Bargmann-Fock space.
+
+It is the space of [holomorphic functions](../../Math416/Math416_L3#definition-28-holomorphic-functions) that is square-integrable over the complex plane.
+
+> Section belows use [Remarks on a Hilbert Space of Analytic Functions](https://www.jstor.org/stable/71180) as the reference.
+
+A family of Hilbert spaces, $\mathfrak{F}_n(n=1,2,3,\cdots)$, is defined as follows:
+
+The element of $\mathfrak{F}_n$ are [entire](../../Math416/Math416_L13#definition-711) [analytic functions](../../Math416/Math416_L9#definition-analytic) in complex Euclidean space $\mathbb{C}^n$. $f:\mathbb{C}^n\to \mathbb{C}\in \mathfrak{F}_n$
+
+Let $f,g\in \mathfrak{F}_n$. The inner product is defined by
+
+$$
+\langle f,g\rangle=\int_{\mathbb{C}^n} \overline{f(z)}g(z) d\mu_n(z)
+$$
+
+Let $z_k=x_k+iy_k$ be the complex coordinates of $z\in \mathbb{C}^n$.
+
+The measure $\mu_n$ is the defined by
+
+$$
+d\mu_n(z)=\pi^{-n}\exp(-\sum_{i=1}^n |z_i|^2)\prod_{k=1}^n dx_k dy_k
+$$
+
+<details>
+<summary>Example</summary>
+
+For $n=2$,
+
+$$
+\mathfrak{F}_2=\text{ space of entire analytic functions on } \mathbb{C}^2\to \mathbb{C}
+$$
+
+$$
+\langle f,g\rangle=\int_{\mathbb{C}^2} \overline{f(z)}g(z) d\mu(z),z=(z_1,z_2)
+$$
+
+$$
+d\mu_2(z)=\frac{1}{\pi^2}\exp(-|z|^2)dx_1 dy_1 dx_2 dy_2
+$$
+
+</details>
+
+so that $f$ belongs to $\mathfrak{F}_n$ if and only if $\langle f,f\rangle<\infty$.
+
+This is absolutely terrible early texts, we will try to formulate it in a more modern way.
+
+> The section belows are from the lecture notes [Holomorphic method in analysis and mathematical physics](https://arxiv.org/pdf/quant-ph/9912054)
+
+## Complex function spaces
+
+### Holomorphic spaces
+
+Let $U$ be a non-empty open set in $\mathbb{C}^d$. Let $\mathcal{H}(U)$ be the space of holomorphic (or analytic) functions on $U$.
+
+Let $f\in \mathcal{H}(U)$, note that by definition of holomorphic on several complex variables, $f$ is continuous and holomorphic in each variable with the other variables fixed.
+
+Let $\alpha$ be a continuous, strictly positive function on $U$.
+
+$$
+\mathcal{H}L^2(U,\alpha)=\left\{F\in \mathcal{H}(U): \int_U |F(z)|^2 \alpha(z) d\mu(z)<\infty\right\},
+$$
+
+where $\mu$ is the Lebesgue measure on $\mathbb{C}^d=\mathbb{R}^{2d}$.
+
+#### Theorem of holomorphic spaces
+
+1. For all $z\in U$, there exists a constant $c_z$ such that
+    $$
+    |F(z)|^2\le c_z \|F\|^2_{L^2(U,\alpha)}
+    $$
+    for all $F\in \mathcal{H}L^2(U,\alpha)$.
+2. $\mathcal{H}L^2(U,\alpha)$ is a closed subspace of $L^2(U,\alpha)$, and therefore a Hilbert space.
+
+<details>
+<summary>Proof</summary>
+
+First we check part 1.
+
+Let $z=(z_1,z_2,\cdots,z_d)\in U, z_k\in \mathbb{C}$. Let $P_s(z)$ be the "polydisk"of radius $s$ centered at $z$ defined as
+
+$$
+P_s(z)=\{v\in \mathbb{C}^d: |v_k-z_k|<s, k=1,2,\cdots,d\}
+$$
+
+If $z\in U$, we cha choose $s$ small enough such that $\overline{P_s(z)}\subset U$ so that we can claim that $F(z)=(\pi s^2)^{-d}\int_{P_s(z)}F(v)d\mu(v)$ is well-defined.
+
+If $d=1$. Then by Taylor series at $v=z$, since $F$ is analytic in $U$ we have
+
+$$
+F(v)=F(z)+\sum_{k=1}^{\infty}a_n(v-z)^n
+$$
+
+Since the series converges uniformly to $F$ on the compact set $\overline{P_s(z)}$, we can interchange the integral and the sum.
+
+Using polar coordinates with origin at $z$, $(v-z)^n=r^n e^{in\theta}$ where $r=|v-z|, \theta=\arg(v-z)$.
+
+For $n\geq 1$, the integral over $P_s(z)$ (open disk) is zero (by Cauchy's theorem).
+
+So,
+
+$$
+\begin{aligned}
+F(z)&=(\pi s^2)^{-1}\int_{P_s(z)}F(z)+\sum_{k=1}^{\infty}a_n(v-z)^n d\mu(v)\\
+&=(\pi s^2)^{-1}F(z)+(\pi s^2)^{-1}\sum_{k=1}^{\infty}a_n\int_{P_s(z)}r^n e^{in\theta} d\mu(v)\\
+&=(\pi s^2)^{-1}F(z)
+\end{aligned}
+$$
+
+For $d>1$, we can use the same argument to show that
+
+Let $\mathbb{I}_{P_s(z)}(v)=\begin{cases}1 & v\in P_s(z) \\0 & v\notin P_s(z)\end{cases}$ be the indicator function of $P_s(z)$.
+
+$$
+\begin{aligned}
+F(z)&=(\pi s^2)^{-d}\int_{U}\mathbb{I}_{P_s(z)}(v)\frac{1}{\alpha(v)}F(v)\alpha(v) d\mu(v)\\
+&=(\pi s^2)^{-d}\langle \mathbb{I}_{P_s(z)}\frac{1}{\alpha},F\rangle_{L^2(U,\alpha)}
+\end{aligned}
+$$
+
+By definition of inner product.
+
+So $\|F(z)\|^2\leq (\pi s^2)^{-2d}\|\mathbb{I}_{P_s(z)}\frac{1}{\alpha}\|^2_{L^2(U,\alpha)} \|F\|^2_{L^2(U,\alpha)}$.
+
+All the terms are bounded and finite.
+
+For part 2, we need to show that $\forall z\in U$, we can find a neighborhood $V$ of $z$ and a constant $d_z$ such that
+
+$$
+|F(z)|^2\leq d_z \|F\|^2_{L^2(U,\alpha)}
+$$
+
+Suppose we have a sequence $F_n\in \mathcal{H}L^2(U,\alpha)$ such that $F_n\to F$, $F\in L^2(U,\alpha)$.
+
+Then $F_n$ is a cauchy sequence in $L^2(U,\alpha)$. So,
+
+$$
+\sup_{v\in V}|F_n(v)-F_m(v)|\leq \sqrt{d_z}\|F_n-F_m\|_{L^2(U,\alpha)}\to 0\text{ as }n,m\to \infty
+$$
+
+So the sequence $F_m$ converges locally uniformly to some limit function which must be $F$ ($\mathbb{C}^d$ is Hausdorff, unique limit point).
+
+Locally uniform limit of holomorphic functions is holomorphic. (Use Morera's Theorem to show that the limit is still holomorphic in each variable.) So the limit function $F$ is actually in $\mathcal{H}L^2(U,\alpha)$, which shows that $\mathcal{H}L^2(U,\alpha)$ is closed.
+
+which shows that $\mathcal{H}L^2(U,\alpha)$ is closed.
+
+</details>
+
+> [!TIP]
+>
+> [1.] states that point-wise evaluation of $F$ on $U$ is continuous. That is, for each $z\in U$, the map $\varphi: \mathcal{H}L^2(U,\alpha)\to \mathbb{C}$ that takes $F\in \mathcal{H}L^2(U,\alpha)$ to $F(z)$ is a continuous linear functional on $\mathcal{H}L^2(U,\alpha)$. This is false for ordinary non-holomorphic functions, e.g. $L^2$ spaces.
+
+#### Reproducing kernel
+
+Let $\mathcal{H}L^2(U,\alpha)$ be a holomorphic space. The reproducing kernel of $\mathcal{H}L^2(U,\alpha)$ is a function $K:U\times U\to \mathbb{C}$, $K(z,w),z,w\in U$ with the following properties:
+
+1. $K(z,w)$ is holomorphic in $z$ and anti-holomorphic in $w$.
+   $$
+   K(w,z)=\overline{K(z,w)}
+   $$
+
+2. For each fixed $z\in U$, $K(z,w)$ is a square integrable $d\alpha(w)$. For all $F\in \mathcal{H}L^2(U,\alpha)$,
+   $$
+   F(z)=\int_U K(z,w)F(w) \alpha(w) dw
+   $$
+
+3. If $F\in L^2(U,\alpha)$, let $PF$ denote the orthogonal projection of $F$ onto closed subspace $\mathcal{H}L^2(U,\alpha)$. Then
+   $$
+   PF(z)=\int_U K(z,w)F(w) \alpha(w) dw
+   $$
+
+4. For all $z,u\in U$,
+   $$
+   \int_U K(z,w)K(w,u) \alpha(w) dw=K(z,u)
+   $$
+
+5. For all $z\in U$,
+   $$
+   |F(z)|^2\leq K(z,z) \|F\|^2_{L^2(U,\alpha)}
+   $$
+
+<details>
+<summary>Proof</summary>
+
+For part 1, By [Riesz Theorem](../../Math429/Math429_L27#theorem-642-riesz-representation-theorem), the linear functional evaluation at $z\in U$ on $\mathcal{H}L^2(U,\alpha)$ can be represented uniquely as inner product with some $\phi_z\in \mathcal{H}L^2(U,\alpha)$.
+
+$$
+F(z)=\langle F,\phi_z\rangle_{L^2(U,\alpha)}=\int_U F(w)\overline{\phi_z(w)} \alpha(w) dw
+$$
+
+And assume part 2 is true, then we have
+
+$K(z,w)=\overline{\phi_z(w)}$
+
+So part 1 is true.
+
+For part 2, we can use the same argument
+
+$$
+\phi_z(w)=\langle \phi_z,\phi_w\rangle_{L^2(U,\alpha)}=\overline{\langle \phi_w,\phi_z\rangle_{L^2(U,\alpha)}}=\overline{\phi_w(z)}
+$$
+
+... continue if needed.
+
+</details>
+
+#### Construction of reproducing kernel
+
+Let $\{e_j\}$ be any orthonormal basis of $\mathcal{H}L^2(U,\alpha)$. Then for all $z,w\in U$,
+
+$$
+\sum_{j=1}^{\infty} |e_j(z)\overline{e_j(w)}|<\infty
+$$
+
+and
+
+$$
+K(z,w)=\sum_{j=1}^{\infty} e_j(z)\overline{e_j(w)}
+$$
+
+### Bargmann space
+
+The Bargmann spaces are the holomorphic spaces 
+
+$$
+\mathcal{H}L^2(\mathbb{C}^d,\mu_t)
+$$
+
+where
+
+$$
+\mu_t(z)=(\pi t)^{-d}\exp(-|z|^2/t)
+$$
+
+> For this research, we can tentatively set $t=1$ and $d=2$ for simplicity so that you can continue to read the next section.
+
+#### Reproducing kernel for Bargmann space
+
+For all $d\geq 1$, the reproducing kernel of the space $\mathcal{H}L^2(\mathbb{C}^d,\mu_t)$ is given by
+
+$$
+K(z,w)=\exp(z\cdot \overline{w}/t)
+$$
+
+where $z\cdot \overline{w}=\sum_{k=1}^d z_k\overline{w_k}$.
+
+This gives the pointwise bounds
+
+$$
+|F(z)|^2\leq \exp(\|z\|^2/t) \|F\|^2_{L^2(\mathbb{C}^d,\mu_t)}
+$$
+
+For all $F\in \mathcal{H}L^2(\mathbb{C}^d,\mu_t)$, and $z\in \mathbb{C}^d$.
+
+> Proofs are intentionally skipped, you can refer to the lecture notes for details.
+
+#### Lie bracket of vector fields
+
+Let $X,Y$ be two vector fields on a smooth manifold $M$. The Lie bracket of $X$ and $Y$ is an operator $[X,Y]:C^\infty(M)\to C^\infty(M)$ defined by
+
+$$
+[X,Y](f)=X(Y(f))-Y(X(f))
+$$
+
+This operator is a vector field.
+
+> Continue here for quantization of Coherent states and POVMs

content/Math401/Extending_thesis/Math401_S4.md

@@ -1,272 +1,4 @@
-# Math 401, Fall 2025: Thesis notes, S4, Bargmann space
-
-## Bargmann space (original)
-
-Also known as Segal-Bargmann space or Bargmann-Fock space.
-
-It is the space of [holomorphic functions](../../Math416/Math416_L3#definition-28-holomorphic-functions) that is square-integrable over the complex plane.
-
-> Section belows use [Remarks on a Hilbert Space of Analytic Functions](https://www.jstor.org/stable/71180) as the reference.
-
-A family of Hilbert spaces, $\mathfrak{F}_n(n=1,2,3,\cdots)$, is defined as follows:
-
-The element of $\mathfrak{F}_n$ are [entire](../../Math416/Math416_L13#definition-711) [analytic functions](../../Math416/Math416_L9#definition-analytic) in complex Euclidean space $\mathbb{C}^n$. $f:\mathbb{C}^n\to \mathbb{C}\in \mathfrak{F}_n$
-
-Let $f,g\in \mathfrak{F}_n$. The inner product is defined by
-
-$$
-\langle f,g\rangle=\int_{\mathbb{C}^n} \overline{f(z)}g(z) d\mu_n(z)
-$$
-
-Let $z_k=x_k+iy_k$ be the complex coordinates of $z\in \mathbb{C}^n$.
-
-The measure $\mu_n$ is the defined by
-
-$$
-d\mu_n(z)=\pi^{-n}\exp(-\sum_{i=1}^n |z_i|^2)\prod_{k=1}^n dx_k dy_k
-$$
-
-<details>
-<summary>Example</summary>
-
-For $n=2$,
-
-$$
-\mathfrak{F}_2=\text{ space of entire analytic functions on } \mathbb{C}^2\to \mathbb{C}
-$$
-
-$$
-\langle f,g\rangle=\int_{\mathbb{C}^2} \overline{f(z)}g(z) d\mu(z),z=(z_1,z_2)
-$$
-
-$$
-d\mu_2(z)=\frac{1}{\pi^2}\exp(-|z|^2)dx_1 dy_1 dx_2 dy_2
-$$
-
-</details>
-
-so that $f$ belongs to $\mathfrak{F}_n$ if and only if $\langle f,f\rangle<\infty$.
-
-This is absolutely terrible early texts, we will try to formulate it in a more modern way.
-
-> The section belows are from the lecture notes [Holomorphic method in analysis and mathematical physics](https://arxiv.org/pdf/quant-ph/9912054)
-
-## Complex function spaces
-
-### Holomorphic spaces
-
-Let $U$ be a non-empty open set in $\mathbb{C}^d$. Let $\mathcal{H}(U)$ be the space of holomorphic (or analytic) functions on $U$.
-
-Let $f\in \mathcal{H}(U)$, note that by definition of holomorphic on several complex variables, $f$ is continuous and holomorphic in each variable with the other variables fixed.
-
-Let $\alpha$ be a continuous, strictly positive function on $U$.
-
-$$
-\mathcal{H}L^2(U,\alpha)=\left\{F\in \mathcal{H}(U): \int_U |F(z)|^2 \alpha(z) d\mu(z)<\infty\right\},
-$$
-
-where $\mu$ is the Lebesgue measure on $\mathbb{C}^d=\mathbb{R}^{2d}$.
-
-#### Theorem of holomorphic spaces
-
-1. For all $z\in U$, there exists a constant $c_z$ such that
-    $$
-    |F(z)|^2\le c_z \|F\|^2_{L^2(U,\alpha)}
-    $$
-    for all $F\in \mathcal{H}L^2(U,\alpha)$.
-2. $\mathcal{H}L^2(U,\alpha)$ is a closed subspace of $L^2(U,\alpha)$, and therefore a Hilbert space.
-
-<details>
-<summary>Proof</summary>
-
-First we check part 1.
-
-Let $z=(z_1,z_2,\cdots,z_d)\in U, z_k\in \mathbb{C}$. Let $P_s(z)$ be the "polydisk"of radius $s$ centered at $z$ defined as
-
-$$
-P_s(z)=\{v\in \mathbb{C}^d: |v_k-z_k|<s, k=1,2,\cdots,d\}
-$$
-
-If $z\in U$, we cha choose $s$ small enough such that $\overline{P_s(z)}\subset U$ so that we can claim that $F(z)=(\pi s^2)^{-d}\int_{P_s(z)}F(v)d\mu(v)$ is well-defined.
-
-If $d=1$. Then by Taylor series at $v=z$, since $F$ is analytic in $U$ we have
-
-$$
-F(v)=F(z)+\sum_{k=1}^{\infty}a_n(v-z)^n
-$$
-
-Since the series converges uniformly to $F$ on the compact set $\overline{P_s(z)}$, we can interchange the integral and the sum.
-
-Using polar coordinates with origin at $z$, $(v-z)^n=r^n e^{in\theta}$ where $r=|v-z|, \theta=\arg(v-z)$.
-
-For $n\geq 1$, the integral over $P_s(z)$ (open disk) is zero (by Cauchy's theorem).
-
-So,
-
-$$
-\begin{aligned}
-F(z)&=(\pi s^2)^{-1}\int_{P_s(z)}F(z)+\sum_{k=1}^{\infty}a_n(v-z)^n d\mu(v)\\
-&=(\pi s^2)^{-1}F(z)+(\pi s^2)^{-1}\sum_{k=1}^{\infty}a_n\int_{P_s(z)}r^n e^{in\theta} d\mu(v)\\
-&=(\pi s^2)^{-1}F(z)
-\end{aligned}
-$$
-
-For $d>1$, we can use the same argument to show that
-
-Let $\mathbb{I}_{P_s(z)}(v)=\begin{cases}1 & v\in P_s(z) \\0 & v\notin P_s(z)\end{cases}$ be the indicator function of $P_s(z)$.
-
-$$
-\begin{aligned}
-F(z)&=(\pi s^2)^{-d}\int_{U}\mathbb{I}_{P_s(z)}(v)\frac{1}{\alpha(v)}F(v)\alpha(v) d\mu(v)\\
-&=(\pi s^2)^{-d}\langle \mathbb{I}_{P_s(z)}\frac{1}{\alpha},F\rangle_{L^2(U,\alpha)}
-\end{aligned}
-$$
-
-By definition of inner product.
-
-So $\|F(z)\|^2\leq (\pi s^2)^{-2d}\|\mathbb{I}_{P_s(z)}\frac{1}{\alpha}\|^2_{L^2(U,\alpha)} \|F\|^2_{L^2(U,\alpha)}$.
-
-All the terms are bounded and finite.
-
-For part 2, we need to show that $\forall z\in U$, we can find a neighborhood $V$ of $z$ and a constant $d_z$ such that
-
-$$
-|F(z)|^2\leq d_z \|F\|^2_{L^2(U,\alpha)}
-$$
-
-Suppose we have a sequence $F_n\in \mathcal{H}L^2(U,\alpha)$ such that $F_n\to F$, $F\in L^2(U,\alpha)$.
-
-Then $F_n$ is a cauchy sequence in $L^2(U,\alpha)$. So,
-
-$$
-\sup_{v\in V}|F_n(v)-F_m(v)|\leq \sqrt{d_z}\|F_n-F_m\|_{L^2(U,\alpha)}\to 0\text{ as }n,m\to \infty
-$$
-
-So the sequence $F_m$ converges locally uniformly to some limit function which must be $F$ ($\mathbb{C}^d$ is Hausdorff, unique limit point).
-
-Locally uniform limit of holomorphic functions is holomorphic. (Use Morera's Theorem to show that the limit is still holomorphic in each variable.) So the limit function $F$ is actually in $\mathcal{H}L^2(U,\alpha)$, which shows that $\mathcal{H}L^2(U,\alpha)$ is closed.
-
-which shows that $\mathcal{H}L^2(U,\alpha)$ is closed.
-
-</details>
-
-> [!TIP]
->
-> [1.] states that point-wise evaluation of $F$ on $U$ is continuous. That is, for each $z\in U$, the map $\varphi: \mathcal{H}L^2(U,\alpha)\to \mathbb{C}$ that takes $F\in \mathcal{H}L^2(U,\alpha)$ to $F(z)$ is a continuous linear functional on $\mathcal{H}L^2(U,\alpha)$. This is false for ordinary non-holomorphic functions, e.g. $L^2$ spaces.
-
-#### Reproducing kernel
-
-Let $\mathcal{H}L^2(U,\alpha)$ be a holomorphic space. The reproducing kernel of $\mathcal{H}L^2(U,\alpha)$ is a function $K:U\times U\to \mathbb{C}$, $K(z,w),z,w\in U$ with the following properties:
-
-1. $K(z,w)$ is holomorphic in $z$ and anti-holomorphic in $w$.
-   $$
-   K(w,z)=\overline{K(z,w)}
-   $$
-
-2. For each fixed $z\in U$, $K(z,w)$ is a square integrable $d\alpha(w)$. For all $F\in \mathcal{H}L^2(U,\alpha)$,
-   $$
-   F(z)=\int_U K(z,w)F(w) \alpha(w) dw
-   $$
-
-3. If $F\in L^2(U,\alpha)$, let $PF$ denote the orthogonal projection of $F$ onto closed subspace $\mathcal{H}L^2(U,\alpha)$. Then
-   $$
-   PF(z)=\int_U K(z,w)F(w) \alpha(w) dw
-   $$
-
-4. For all $z,u\in U$,
-   $$
-   \int_U K(z,w)K(w,u) \alpha(w) dw=K(z,u)
-   $$
-
-5. For all $z\in U$,
-   $$
-   |F(z)|^2\leq K(z,z) \|F\|^2_{L^2(U,\alpha)}
-   $$
-
-<details>
-<summary>Proof</summary>
-
-For part 1, By [Riesz Theorem](../../Math429/Math429_L27#theorem-642-riesz-representation-theorem), the linear functional evaluation at $z\in U$ on $\mathcal{H}L^2(U,\alpha)$ can be represented uniquely as inner product with some $\phi_z\in \mathcal{H}L^2(U,\alpha)$.
-
-$$
-F(z)=\langle F,\phi_z\rangle_{L^2(U,\alpha)}=\int_U F(w)\overline{\phi_z(w)} \alpha(w) dw
-$$
-
-And assume part 2 is true, then we have
-
-$K(z,w)=\overline{\phi_z(w)}$
-
-So part 1 is true.
-
-For part 2, we can use the same argument
-
-$$
-\phi_z(w)=\langle \phi_z,\phi_w\rangle_{L^2(U,\alpha)}=\overline{\langle \phi_w,\phi_z\rangle_{L^2(U,\alpha)}}=\overline{\phi_w(z)}
-$$
-
-... continue if needed.
-
-</details>
-
-#### Construction of reproducing kernel
-
-Let $\{e_j\}$ be any orthonormal basis of $\mathcal{H}L^2(U,\alpha)$. Then for all $z,w\in U$,
-
-$$
-\sum_{j=1}^{\infty} |e_j(z)\overline{e_j(w)}|<\infty
-$$
-
-and
-
-$$
-K(z,w)=\sum_{j=1}^{\infty} e_j(z)\overline{e_j(w)}
-$$
-
-### Bargmann space
-
-The Bargmann spaces are the holomorphic spaces 
-
-$$
-\mathcal{H}L^2(\mathbb{C}^d,\mu_t)
-$$
-
-where
-
-$$
-\mu_t(z)=(\pi t)^{-d}\exp(-|z|^2/t)
-$$
-
-> For this research, we can tentatively set $t=1$ and $d=2$ for simplicity so that you can continue to read the next section.
-
-#### Reproducing kernel for Bargmann space
-
-For all $d\geq 1$, the reproducing kernel of the space $\mathcal{H}L^2(\mathbb{C}^d,\mu_t)$ is given by
-
-$$
-K(z,w)=\exp(z\cdot \overline{w}/t)
-$$
-
-where $z\cdot \overline{w}=\sum_{k=1}^d z_k\overline{w_k}$.
-
-This gives the pointwise bounds
-
-$$
-|F(z)|^2\leq \exp(\|z\|^2/t) \|F\|^2_{L^2(\mathbb{C}^d,\mu_t)}
-$$
-
-For all $F\in \mathcal{H}L^2(\mathbb{C}^d,\mu_t)$, and $z\in \mathbb{C}^d$.
-
-> Proofs are intentionally skipped, you can refer to the lecture notes for details.
-
-#### Lie bracket of vector fields
-
-Let $X,Y$ be two vector fields on a smooth manifold $M$. The Lie bracket of $X$ and $Y$ is an operator $[X,Y]:C^\infty(M)\to C^\infty(M)$ defined by
-
-$$
-[X,Y](f)=X(Y(f))-Y(X(f))
-$$
-
-This operator is a vector field.
+# Math 401, Fall 2025: Thesis notes, S4, Complex manifolds
 
 ## Complex Manifolds
 
@@ -278,6 +10,74 @@ This operator is a vector field.
 >
 > - [Introduction to Complex Manifolds](https://bookstore.ams.org/gsm-244)
 
+### Holomorphic vector bundles
+
+#### Definition of real vector bundle
+
+Let $M$ be a topological space, A **real vector bundle** over $M$ is a topological space $E$ together with a surjective continuous map $\pi:E\to M$ such that:
+
+1. For each $p\in M$, the fiber $E_p=\pi^{-1}(p)$ over $p$ is endowed with the structure of a $k$-dimensional real vector space.
+2. For each $p\in M$, there exists an open neighborhood $U$ of $p$ and a homeomorphism $\Phi: \pi^{-1}(U)\to U\times \mathbb{R}^k$ called a **local trivialization** such that:
+    - $\pi^{-1}(U)=\pi$(where $\pi_U:U\times \mathbb{R}^k\to \pi^{-1}(U)$ is the projection map)
+    - For each $q\in U$, the map $\Phi_q: E_q\to \mathbb{R}^k$ is isomorphism from $E_q$ to $\{q\}\times \mathbb{R}^k\cong \mathbb{R}^k$.
+
+#### Definition of complex vector bundle
+
+Let $M$ be a topological space, A **complex vector bundle** over $M$ is a real vector bundle $E$ together with a complex structure on each fiber $E_p$ that is compatible with the complex vector space structure.
+
+1. For each $p\in M$, the fiber $E_p=\pi^{-1}(p)$ over $p$ is endowed with the structure of a $k$-dimensional complex vector space.
+2. For each $p\in M$, there exists an open neighborhood $U$ of $p$ and a homeomorphism $\Phi: \pi^{-1}(U)\to U\times \mathbb{C}^k$ called a **local trivialization** such that:
+    - $\pi^{-1}(U)=\pi$(where $\pi_U:U\times \mathbb{C}^k\to \pi^{-1}(U)$ is the projection map)
+    - For each $q\in U$, the map $\Phi_q: E_q\to \mathbb{C}^k$ is isomorphism from $E_q$ to $\{q\}\times \mathbb{C}^k\cong \mathbb{C}^k$.
+
+#### Definition of smooth complex vector bundle
+
+If above $M$ and $E$ are smooth manifolds, $\pi$ is a smooth map, and the local trivializations can be chosen to be diffeomorphisms (smooth bijections with smooth inverses), then the vector bundle is called a **smooth complex vector bundle**.
+
+#### Definition of holomorphic vector bundle
+
+If above $M$ and $E$ are complex manifolds, $\pi$ is a holomorphic map, and the local trivializations can be chosen to be biholomorphic maps (holomorphic bijections with holomorphic inverses), then the vector bundle is called a **holomorphic vector bundle**.
+
+### Holomorphic line bundles
+
+A **holomorphic line bundle** is a holomorphic vector bundle with rank 1.
+
+> Intuitively, a holomorphic line bundle is a complex vector bundle with a complex structure on each fiber.
+
+### Simplicial, Sheafs, Cohomology and homology
+
+What is homology and cohomology?
+
+> This section is based on extension for conversation with Professor Feres on [11/05/2025].
+
+#### Definition of meromorphic function
+
+Let $Y$ be an open subset of $X$. A function $f$ is called meromorphic function on $Y$, if there exists a non-empty open subset $Y'\subset Y$ such that
+
+1. $f:Y'\to \mathbb{C}$ is a holomorphic function.
+2. $A=Y\setminus Y'$ is a set of isolated points (called the set of poles)
+3. $\lim_{x\to p}|f(x)|=+\infty$ for all $p\in A$
+
+> Basically, a local holomorphic function on $Y$.
+
+#### De Rham Theorem
+
+This is analogous to the Stoke's Theorem on chains, $\int_c d\omega=\int_{\partial c} \omega$.
+
+$$
+H_k(X)\cong H^k(X)
+$$
+
+Where $H_k(X)$ is the $k$-th homology of $X$, and $H^k(X)$ is the $k$-th cohomology of $X$.
+
+#### Simplicial Cohomology
+
+Riemann surfaces admit triangulations. The triangle are 2 simplices. The edges are 1 simplices. the vertices are 0 simplices.
+
+Our goal is to build global description of Riemann surfaces using local description on each triangulation.
+
+#### Singular Cohomology
+
 ### Riemann-Roch Theorem (Theorem 9.64)
 
 Suppose $M$ is a connected compact Riemann surface of genus $g$, and $L\to M$ is a holomorphic line bundle. Then

content/Math401/Extending_thesis/Math401_S5.md

@@ -0,0 +1,237 @@
+# Math 401, Fall 2025: Thesis notes, S4, Differential Forms
+
+This note aim to investigate  What is homology and cohomology?
+
+To answer this question, it's natural to revisit some concepts we have in Calc III. Particularly, Stoke's Theorem and De Rham Theorem.
+
+Recall that the Stock's theorem states that:
+
+$$
+\int_c d\omega=\int_{\partial c} \omega
+$$
+
+Where $\partial c$ is a closed curve and $\omega$ is a 1-form.
+
+What is form means here?
+
+> This section is based on extension for conversation with Professor Feres on [11/12/2025].
+
+## Differential Forms and applications
+
+> Main reference: [Differential Forms and its applications](https://link.springer.com/book/10.1007/978-3-642-57951-6)
+
+### Differential Forms in our sweet home, $\mathbb{R}^n$
+
+> [!NOTE]
+>
+> I'm a bit deviated form the notation we used in the book, in the actual text, they use $\mathbb{R}^n_p$ to represent the tangent space of $\mathbb{R}^n$ at $p$. But to help you link those concepts as we see in smooth manifolds, $T_pM$, we will use $T_p\mathbb{R}^n$ to represent the tangent space of $\mathbb{R}^n$ at $p$.
+
+Let $p$ be a point in $\mathbb{R}^n$. The tangent space of $\mathbb{R}^n$ at $p$ is denoted by $T_p\mathbb{R}^n$, is the set of all vectors in $\mathbb{R}^n$ that use $p$ as origin.
+
+#### Definition of a vector field
+
+A vector field is a map that associates to each point $p$ in $\mathbb{R}^n$ a vector $v(p)$ in $T_p\mathbb{R}^n$.
+
+That is
+
+$$
+v(p)=a_1(p)e_1+...+a_n(p)e_n
+$$
+
+where $e_1,...,e_n$ is the standard basis of $\mathbb{R}^n$, (in fact could be anything you like)
+
+And $a_i(p)$ is a function that maps $\mathbb{R}^n$ to $\mathbb{R}$.
+
+$v$ is differentiable at $p$ if the function $a_i$ is differentiable at $p$.
+
+This gives a vector field $v$ on $\mathbb{R}^n$.
+
+#### Definition of dual space of tangent space
+
+To each tangent space $T_p\mathbb{R}^n$ we can associate the dual space $(T_p\mathbb{R}^n)^*$, the set of all linear maps from $T_p\mathbb{R}^n$ to $\mathbb{R}$. ($\varphi:T_p\mathbb{R}^n\to \mathbb{R}$)
+
+The basis for $(T_p\mathbb{R}^n)^*$ is obtained by taking $(dx_i)_p$ for $i=1,...,n$.
+
+This is the dual basis for $\{(e_i)_p\}$ since.
+
+$$
+(dx_i)_p(e_j)=\frac{\partial x_i}{\partial x_j}=\begin{cases}0 \text{ if } i\neq j\\
+1 \text{ if } i=j
+\end{cases}
+$$
+
+#### Definition of a 1-form
+
+A 1-form is a linear map from $(T_p\mathbb{R}^n)^*$ to $\mathbb{R}$.
+
+$$
+\omega(p)=a_1(p)(dx_1)_p+...+a_n(p)(dx_n)_p
+$$
+
+where $a_i(p)$ is a function that maps $\mathbb{R}^n$ to $\mathbb{R}$.
+
+Generalization of 1-form is $k$-form defined as follows:
+
+#### Definition of a $k$-form
+
+We can define the set of linear map $\Lambda^2(\mathbb{R}^n_p)^*$ where $\varphi$ maps from $(T_p\mathbb{R}^n)^*\times ... \times (T_p\mathbb{R}^n)^*$ to $\mathbb{R}$, that are bilinear and alternate ($\varphi(v_1,v_2)=-\varphi(v_2,v_1$).
+
+when $\varphi_1$ and $\varphi_2$ are linear maps from $(T_p\mathbb{R}^n)^*$ to $\mathbb{R}$, then $\varphi_1\wedge \varphi_2$ is a bilinear map from $(T_p\mathbb{R}^n)^*\times (T_p\mathbb{R}^n)^*$ to $\mathbb{R}$ by setting
+
+$$
+(\varphi_1\wedge \varphi_2)(v_1,v_2)=\varphi_1(v_1)\varphi_2(v_2)-\varphi_1(v_2)\varphi_2(v_1)=\det(\varphi_i(v_j))
+$$
+
+where $i,j=1,\ldots,k$, $k$ is the degree of the exterior form
+
+More generally, $(\varphi_1\wedge \varphi_2\wedge\dots \wedge \varphi_k)(v_1,v_2,\dots,v_k)=\det(\varphi_i(v_j))$.
+
+And $\{(dx_i\wedge dx_j)_p,i<j\}$ forms a basis for $\Lambda^2(\mathbb{R}^n_p)^*$.
+
+- $(dx_i\wedge dx_j)_p=-(dx_j\wedge dx_i)_p$
+- $(dx_i\wedge dx_i)_p=0$
+
+An exterior fom of degree 2 in $\mathbb{R}^n$ is a correspondence $\omega$ that associates to each point $p$ in $\mathbb{R}^n$ an element $\omega(p)\in \Lambda^2(\mathbb{R}^n_p)^*$.
+
+That is
+
+$$
+\omega(p)=a_{12}(p)(dx_1\wedge dx_2)_p+a_{13}(p)(dx_1\wedge dx_3)_p+a_{23}(p)(dx_2\wedge dx_3)_p
+$$
+
+In the case of $\mathbb{R}^3$.
+
+<details>
+<summary>Example for real space 4 product</summary>
+
+0-forms: functino in $\mathbb{R}^4$
+
+1-forms: $a_1(p)(dx_1)_p+a_2(p)(dx_2)_p+a_3(p)(dx_3)_p+a_4(p)(dx_4)_p$
+
+2-forms: $a_{12}(p)(dx_1\wedge dx_2)_p+a_{13}(p)(dx_1\wedge dx_3)_p+a_{14}(p)(dx_1\wedge dx_4)_p+a_{23}(p)(dx_2\wedge dx_3)_p+a_{24}(p)(dx_2\wedge dx_4)_p+a_{34}(p)(dx_3\wedge dx_4)_p$
+
+3-forms: $a_{123}(p)(dx_1\wedge dx_2\wedge dx_3)_p+a_{124}(p)(dx_1\wedge dx_2\wedge dx_4)_p+a_{134}(p)(dx_1\wedge dx_3\wedge dx_4)_p+a_{234}(p)(dx_2\wedge dx_3\wedge dx_4)_p$
+
+4-forms: $a_{1234}(p)(dx_1\wedge dx_2\wedge dx_3\wedge dx_4)_p$
+</details>
+
+#### Exterior product of forms
+
+Let $\omega=\sum a_{I}dx_I$ be a k form where $I=(i_1,i_2,\ldots,i_k)$ and $i_1<i_2<\cdots<i_k$.
+
+$\varphi\wedge \omega=\sum b_jdx_j$ be a s form where $j=(j_1,j_2,\ldots,j_s)$ and $j_1<j_2<\cdots<j_s$.
+
+The exterior product is defined as
+
+$$
+(\varphi\wedge \omega)(v_1,\ldots,v_k)=\sum_{IJ}a_I b_J dx_I\wedge dx_J
+$$
+
+<details>
+<summary>Example for exterior product of forms</summary>
+
+Let $\omega=x_1dx_1+x_2dx_2+x_3dx_3$ be a 1-form in $\mathbb{R}^3$ and $\varphi=x_1dx_1\wedge dx_1\wedge dx_3$ be a 2-form in $\mathbb{R}^3$.
+
+Then
+
+$$
+\begin{aligned}
+\omega\wedge \varphi&=x_2 dx_2\wedge dx_1\wedge dx_3+x_3x_1 dx_3\wedge dx_1\wedge dx_2\\
+&=(x_1x_3-x_2)dx_1\wedge dx_2\wedge dx_3
+\end{aligned}
+$$
+
+Note $dx_1\wedge dx_1=0$ therefore $dx_1\wedge dx_1\wedge dx_3=0$
+</details>
+
+#### Additional properties of exterior product
+
+Let $\omega$ be a $k$ form, $\varphi$ be a $s$ form, and $\theta$ be an $r$ form.
+
+- $(\omega\wedge\varphi)\wedge\theta=\omega\wedge(\varphi\wedge\theta)$
+- $(\omega\wedge\varphi)=(-1)^{k+s}(\varphi\wedge\omega)$
+- $\omega\wedge(\varphi+\theta)=\omega\wedge\varphi+\omega\wedge\theta$
+
+#### Important implications with differential maps
+
+Let $f:\mathbb{R}^n\to \mathbb{R}^m$ be a differentiable map. Then $f$ induces a map $f^*$ from k-forms in $\mathbb{R}^n$ to k-forms in $\mathbb{R}^m$.
+
+That is
+
+$$
+(f^*\omega)(p)(v_1,\ldots,v_k)=\omega(f(p))(df(p)_1v_1,\ldots,df(p)_kv_k)
+$$
+
+Here $p\in \mathbb{R}^n$, $v_1,\ldots,v_k\in T_p\mathbb{R}^n$, and $df(p):T_p\mathbb{R}^n\to T_{f(p)}\mathbb{R}^m$.
+
+If $g$ is a 0-form, we have
+
+$f^*(g)=g\circ f$
+
+#### Additional properties for differential maps
+
+Let $f:\mathbb{R}^n\to \mathbb{R}^m$ be a differentiable map, $\omega,\varphi$ be k-forms on $\mathbb{R}^m$ and $g:\mathbb{R}^m\to \mathbb{R}$ be a 0-form on $\mathbb{R}^m$. Then:
+
+- $f^*(\omega+\varphi)=f^*\omega+f^*\varphi$
+- $f^*(g\omega)=f^*(g)f^*\omega$
+- If $\varphi_1,\dots,\varphi_k$ are 1-forms in $\mathbb{R}^m$, $f^*(\varphi_1\wedge\cdots\wedge\varphi_k)=f^*\varphi_1\wedge\cdots\wedge f^*\varphi_k$
+
+If $g:\mathbb{R}^p\to \mathbb{R}^n$ is a differential map and $\varphi,\omega$ are any two-forms in $\mathbb{R}^m$.
+
+- $f^*(\omega\wedge\varphi)=f^*\omega\wedge f^*\varphi$
+- $(f\circ g)^*omega=g^*(f^*\omega)$
+
+#### Exterior Differential
+
+Let $\omega=\sum a_{I}dx_I$ be a k form in $mathbb{R}^n$. The exterior differential $d\omega$ of $\omega$ is defined by
+
+$$
+d\omega=\sum da_{I}\wedge dx_I
+$$
+
+#### Additional properties of exterior differential
+
+- $d(\omega_1+\omega_2)=d\omega_1+d\omega_2$ where $\omega_1,\omega_2$ are k-forms
+- $d(\omega\wedge\varphi)=d\omega\wedge\varphi+(-1)^kw\wedge d\varphi$ where $\omega$ is a k-form and $\varphi$ is a s-form
+- $d(d\omega)=d^2\omega=0$
+- $d(f^*\omega)=f^*d\omega$ where $f$ is a differentiable map and $\omega$ is a k-form
+
+## Differentiable manifolds
+
+### A different flavor of differential manifolds
+
+#### Definition of differentiable manifold
+
+An $n$-dimensional differentiable manifold is a set $M$ together with a family of of injective maps $f_\alpha:U_\alpha\subseteq \mathbb{R}^n\to M$ of open sets $U_\alpha$ in $\mathbb{R}^n$ in to $M$ such that:
+
+- $\bigcup_\alpha f_\alpha(U_\alpha)=M$
+- For each pair $\alpha,\beta$, with $f_\alpha(U_\alpha)\cap f_\beta(U_\beta)=W\neq \emptyset$, the sets $f_\alpha^{-1}(W)$ and $f_\beta^{-1}(W)$ are open sets in $\mathbb{R}^n$ and the maps $f_\beta^{-1}\circ f_\alpha$ and $f_\alpha^{-1}\circ f_\beta$ are differentiable.
+- The family $\{(U_\alpha,f_\alpha)\}$ is the maximal relative to the two properties above.
+
+> This condition is weaker than smooth manifold, in smooth manifold, we require the function to be class of $C^\infty$ (continuous differentiable of all order), now we only needs it to be differentiable.
+
+#### Definition of differentiable map between differentiable manifolds
+
+Let $M_1^n$ and $M_2^M$ be differentiable manifolds. A map $\varphi:M_1\to M_2$ is a differentiable at a point $p\in M_1$ if given a parameterization $g:V\subset \mathbb{R}^m\to M_2$ around $\varphi(p)$, there exists a parameterization $f:U\subseteq \mathbb{R}^n\to M_1$ around $p$ such that:
+
+$\varphi(f(U))\subset g(V)$ and the map
+
+$$
+g^{-1}\circ \varphi\circ f: U\subset \mathbb{R}^n\to \mathbb{R}^m
+$$
+
+is differentiable at $f^{-1}(p)$.
+
+It is differentiable in an open set of $M_1$ if it is differentiable at all points in such set.
+
+The map $g^{-1}\circ \varphi\circ f$ is the expression of parameterization of $f$ and $g$. (Since the change of parameterization is differentiable, the property that $f$ is differentiable does not depends on the choice of parameterization.)
+
+#### Tangent vector over differentiable curve
+
+Let $\alpha: I\to M$ be a differentiable curve on a differentiable manifold $M$, with $\alpha(0)=p\in M$, and let $D$ be the set of functions of $M$ which are differentiable at $p$. then tangent vector to the curve $\alpha$ at $p$ is the map $\alpha'(0):D\to \mathbb{R}$ given by
+
+$$
+\alpha'(0)\varphi=\frac{d}{dt}(\varphi\cdot \alpha(t))|_{t=0}
+$$
+
+A tangent vector at $p\in M$ is the 

content/Math401/Extending_thesis/_meta.js

@@ -1,3 +1,4 @@
 export default {
     index: "Math 401, Fall 2025: Overview of thesis",
+    
 }

content/Math401/Freiwald_summer/Math401_P1_1.md

@@ -140,7 +140,6 @@ $$
 
 is a pure state.
 
-QED
 </details>
 
 ## Drawing the connection between the space $S^{2n+1}$, $CP^n$, and $\mathbb{R}$

content/Math401/Freiwald_summer/Math401_P1_2.md

@@ -8,10 +8,10 @@ The page's lemma is a fundamental result in quantum information theory that prov
 
 The special orthogonal group $SO(n)$ is the set of all **distance preserving** linear transformations on $\mathbb{R}^n$.
 
-It is the group of all $n\times n$ orthogonal matrices ($A^T A=I_n$) on $\mathbb{R}^n$ with determinant $1$.
+It is the group of all $n\times n$ orthogonal matrices ($A^\top A=I_n$) on $\mathbb{R}^n$ with determinant $1$.
 
 $$
-SO(n)=\{A\in \mathbb{R}^{n\times n}: A^T A=I_n, \det(A)=1\}
+SO(n)=\{A\in \mathbb{R}^{n\times n}: A^\top A=I_n, \det(A)=1\}
 $$
 
 <details>
@@ -22,7 +22,7 @@ In [The random Matrix Theory of the Classical Compact groups](https://case.edu/a
 $O(n)$ (the group of all $n\times n$ **orthogonal matrices** over $\mathbb{R}$),
 
 $$
-O(n)=\{A\in \mathbb{R}^{n\times n}: AA^T=A^T A=I_n\}
+O(n)=\{A\in \mathbb{R}^{n\times n}: AA^\top=A^\top A=I_n\}
 $$
 
 $U(n)$ (the group of all $n\times n$ **unitary matrices** over $\mathbb{C}$), 
@@ -42,7 +42,7 @@ $$
 $Sp(2n)$ (the group of all $2n\times 2n$ symplectic matrices over $\mathbb{C}$),
 
 $$
-Sp(2n)=\{U\in U(2n): U^T J U=UJU^T=J\}
+Sp(2n)=\{U\in U(2n): U^\top J U=UJU^\top=J\}
 $$
 
 where $J=\begin{pmatrix}

content/Math401/Freiwald_summer/Math401_P1_3.md

@@ -205,8 +205,6 @@ $$
 \end{aligned}
 $$
 
-QED
-
 </details>
 
 #### Proof of the Levy's concentration theorem via the Maxwell-Boltzmann distribution law

content/Math401/Freiwald_summer/Math401_T2.md

@@ -74,7 +74,7 @@ $c\in \mathbb{C}$.
 The matrix transpose is defined by
 
 $$
-u^T=(a_1,a_2,\cdots,a_n)^T=\begin{pmatrix}
+u^\top=(a_1,a_2,\cdots,a_n)^\top=\begin{pmatrix}
 a_1 \\
 a_2 \\
 \vdots \\
@@ -508,8 +508,6 @@ $$
 f(x_j)=\sum_{a\in X_j} f(a)\epsilon_{a}^{(j)}(x_j)=f(x_j)
 $$
 
-QED.
-
 </details>
 
 Now, let $a=(a_1,a_2,\cdots,a_n)$ be a vector in $X$, and $x=(x_1,x_2,\cdots,x_n)$ be a vector in $X$. Note that $a_j,x_j\in X_j$ for $j=1,2,\cdots,n$.
@@ -540,8 +538,6 @@ $$
 f(x)=\sum_{a\in X} f(a)\epsilon_a(x)=f(x)
 $$
 
-QED.
-
 </details>
 
 #### Definition of tensor product of basis elements
@@ -613,7 +609,6 @@ If $\sum_{i=1}^n a_i u_i\otimes v_i=\sum_{j=1}^m b_j u_j\otimes v_j$, then $a_i=
 
 Then $\sum_{i=1}^n a_i T_1(u_i)\otimes T_2(v_i)=\sum_{j=1}^m b_j T_1(u_j)\otimes T_2(v_j)$.
 
-QED
 </details>
 
 An example of 
@@ -699,7 +694,7 @@ $$
 
 The unitary group $U(n)$ is the group of all $n\times n$ unitary matrices.
 
-Such that $A^*=A$, where $A^*$ is the complex conjugate transpose of $A$. $A^*=(\overline{A})^T$.
+Such that $A^*=A$, where $A^*$ is the complex conjugate transpose of $A$. $A^*=(\overline{A})^\top$.
 
 #### Cyclic group $\mathbb{Z}_n$
 

content/Math401/Freiwald_summer/Math401_T4.md

@@ -171,7 +171,6 @@ $$
 
 This is a contradiction, so Bell's inequality is violated.
 
-QED
 </details>
 
 Other revised experiments (eg. Aspect's experiment, Calcium entangled photon experiment) are also conducted and the inequality is still violated.

content/Math401/Math401_N3.md

@@ -187,7 +187,8 @@ $$
 
 where $L(\mu)$ is the minimum mean code word length of all uniquely decipherable codes for $(A,\mu)$.
 
-Proof:
+<details>
+<summary>Proof</summary>
 
 First, we show that
 
@@ -278,7 +279,7 @@ $$
 \end{aligned}
 $$
 
-QED
+</details>
 
 ### Entropy
 
@@ -387,13 +388,9 @@ n−1 symbols.
 By the inductive hypothesis, the code on $A'$ is optimal.
   is optimal.
 
-By Step 2 above, assigning the two merged symbols $a$ and $b$ codewords $w_0$ and $w_1$ (based on 
-1       
-$w_1$ (based on $c$'s codeword $w$) results in the optimal solution for $A$.
+By Step 2 above, assigning the two merged symbols $a$ and $b$ codewords $w_0$ and $w_1$ (based on 1.1.4) results in the optimal solution for $A$.
 
 Therefore, by induction, Huffman’s algorithm gives an optimal prefix code for any $n$.
-
-QED
-
+</details>
 
 

content/Math4111/Math4111_L1.md

@@ -24,7 +24,8 @@ $\equiv\cancel{\exist} p\in \mathbb{Q}, p^2=2$
 
 $\equiv p\in \mathbb{Q},p^2\neq 2$
 
-#### Proof
+<details>
+<summary>Proof</summary>
 
 Suppose for contradiction, $\exist p\in \mathbb{Q}$ such that $p^2=\mathbb{Q}$.
 
@@ -36,7 +37,7 @@ So $m^2$ is divisible by 4, $2n^2$ is divisible by 4.
 
 So $n^2$ is even. but they are not both even.
 
-QED
+</details>
 
 ### Theorem (No closest rational for a irrational number)
 

content/Math4111/Math4111_L2.md

@@ -47,19 +47,18 @@ Let $S$ be an ordered set and $E\subset S$. We say $\alpha\in S$ is the LUB of $
 1. $\alpha$ is the UB of $E$. ($\forall x\in E,x\leq \alpha$)
 2. if $\gamma<\alpha$, then $\gamma$ is not UB of $E$. ($\forall \gamma <\alpha, \exist x\in E$ such that $x>\gamma$ )
 
-#### Lemma 
-
-Uniqueness of upper bounds.
+#### Lemma (Uniqueness of upper bounds)
 
 If $\alpha$ and $\beta$ are LUBs of $E$, then $\alpha=\beta$.
 
-Proof:
+<details>
+<summary>Proof</summary>
 
 Suppose for contradiction $\alpha$ and $\beta$ are both LUB of $E$, then $\alpha\neq\beta$
 
 WLOG $\alpha>\beta$ and $\beta>\alpha$.
 
-QED
+</details>
 
 We write $\sup E$ to denote the LUB of $E$.
 

content/Math4111/Math4111_L3.md

@@ -26,7 +26,8 @@ Let $S=\mathbb{Z}$.
 
 Proof that $LUBP\implies GLBP$.
 
-Proof:
+<details>
+<summary>Proof</summary>
 
 Let $S$ be an ordered set with LUBP. Let $B<S$ be non-empty and bounded below.
 
@@ -57,7 +58,7 @@ Let's say $\alpha=sup\ L$. We claim that $\alpha=inf\ B$. We need to show $2$ th
 
 Thus $\alpha=inf\ B$
 
-QED
+</details>
 
 ### Field
 

content/Math4111/Math4111_L4.md

@@ -27,7 +27,8 @@
 
 (Archimedean property) If $x,y\in \mathbb{R}$ and $x>0$, then $\exists n\in \mathbb{N}$ such that $nx>y$.
 
-Proof
+<details>
+<summary>Proof</summary>
 
 Suppose the property is false, then $\exist x,y\in \mathbb{R}$ with $x>0$ such that $\forall v\in \mathbb{N}$, nx\leq y$
 
@@ -39,7 +40,7 @@ This implies $(m+1)x>\alpha$
 
 Since $(m+1)x\in \alpha$, this contradicts the fact that $\alpha$ is an upper bound of $A$.
 
-QED
+</details>
 
 ### $\mathbb{Q}$ is dense in $\mathbb{R}$
 
@@ -51,7 +52,8 @@ $$
 x<\frac{m}{n}<y\iff nx<m<ny
 $$
 
-Proof:
+<details>
+<summary>Proof</summary>
 
 Let $x,y\in\mathbb{R}$, with $x<y$. We'll find $n\in \mathbb{N},\mathbb{m}\in \mathbb{Z}$ such that $nx<m<ny$.
 
@@ -59,7 +61,7 @@ By Archimedean property, $\exist n\in \mathbb{N}$ such that $n(y-x)>1$, and $\ex
 
 So $-m_2<nx<m_1$. Thus $\exist m\in \mathbb{Z}$ such that $m-1\leq nx<m$ (Here we use a property of $\mathbb{Z}$) We have $ny>1+nx\geq 1+(m-1)=m$
 
-QED
+</details>
 
 ### $\sqrt{2}\in \mathbb{R}$, $(\sqrt[n]{x}\in\mathbb{R})$
 

content/Math4111/Math4111_L5.md

@@ -30,7 +30,8 @@ $\forall x\in \mathbb{R}_{>0},\forall n\in \mathbb{N},\exist$ unique $y\in \math
 
 (Because of this Theorem we can define $x^{1/x}=y$ and $\sqrt{x}=y$)
 
-Proof:
+<details>
+<summary>Proof</summary>
 
 We cna assume $n\geq 2$ (For $n=1,y=x$)
 
@@ -94,7 +95,7 @@ So want $k\leq \frac{y^n-x}{ny^{n-1}}$
 
 [For actual proof, see the text.]
 
-QED
+</details>
 
 ### Complex numbers
 
@@ -151,7 +152,8 @@ $$
 (\sum a_j b_j)^2=(\sum a_j^2)(\sum b_j^2)
 $$
 
-Proof:
+<details>
+<summary>Proof</summary>
 
 For real numbers:
 
@@ -169,7 +171,7 @@ let $t=C/B$ to get $0\leq A-2(C/B)C+(C/B)^2B=A-\frac{C^2}{B}$
 
 to generalize this to $\mathbb{C}$, $A=\sum |a_j|^2,B=\sum |b_j|^2,C=\sum |a_j \bar{b_j}|$.
 
-QED
+</details>
 
 ### Euclidean spaces
 

content/Math4111/Math4111_L6.md

@@ -126,7 +126,8 @@ $A$ is countable, $n\in \mathbb{N}$,
 
 $\implies A^n=\{(a_{1},...,a_{n}):a_1\in A, a_n\in A\}$, is countable.
 
-Proof:
+<details>
+<summary>Proof</summary>
 
 Induct on $n$,
 
@@ -138,13 +139,14 @@ Induction step: suppose $A^{n-1}$ is countable. Note $A^n=\{(b,a):b\in A^{n-1},a
 
 Since $b$ is fixed, so this is in 1-1 correspondence with $A$, so it's countable by Theorem 2.12.
 
-QED
+</details>
 
 #### Theorem 2.14
 
 Let $A$ be the set of all sequences for 0s and 1s. Then $A$ is uncountable.
 
-Proof:
+<details>
+<summary>Proof</summary>
 
 Let $E\subset A$ be a countable subset. We'll show $A\backslash E\neq \phi$ (i.e.$\exists t\in A$ such that $t\notin E$)
 
@@ -154,4 +156,4 @@ Then we define a new sequence $t$ which differs from $S_1$'s first bit and $S_2$
 
 This is called Cantor's diagonal argument.
 
-QED
+</details>

content/Math4111/Math4111_L7.md

@@ -80,7 +80,8 @@ Let $(X,d)$ be  a metric space, $\forall p\in X,\forall r>0$, $B_r(p)$ is an ope
 
 *every ball is an open set*
 
-Proof:
+<details>
+<summary>Proof</summary>
 
 Let $q\in B_r(p)$.
 
@@ -88,7 +89,7 @@ Let $h=r-d(p,q)$.
 
 Since $q\in B_r(p),h>0$. We claim that $B_h(q)$. Then $d(q,s)<h$, so $d(p,s)\leq d(p,q)+d(q,s)<d(p,q)+h=r$. (using triangle inequality) So $S\in B_r(p)$.
 
-QED
+</details>
 
 ### Closed sets
 

content/Math4111/Math4111_L8.md

@@ -24,7 +24,8 @@ It should be empty. Proof any point cannot be in two balls at the same time. (By
 
 $p\in E'\implies \forall r>0,B_r(p)\cap E$ is infinite.
 
-Proof:
+<details>
+<summary>Proof</summary>
 
 We will prove the contrapositive.
 
@@ -41,7 +42,7 @@ let $B_s(p)\cap E)\backslash \{p\}={q_1,...,q_n}$
 
 Then $(B_s(p)\cap E)\backslash \{p\}=\phi$, so $p\notin E$
 
-QED
+</details>
 
 #### Theorem 2.22 De Morgan's law
 
@@ -68,7 +69,8 @@ $E$ is open $\iff$ $E^c$ is closed.
 >$\phi$, $\R$ is both open and closed. "clopen set"  
 >$[0,1)$ is not open and not closed. bad...
 
-Proof:
+<details>
+<summary>Proof</summary>
 
 $\impliedby$ Suppose $E^c$ is closed. Let $x\in E$, so $x\notin E^c$
 
@@ -95,21 +97,23 @@ $$
 
 So $(E^c)'\subset E^c$
 
-QED
+</details>
 
 #### Theorem 2.24
 
 ##### An arbitrary union of open sets is open
 
-Proof:
+<details>
+<summary>Proof</summary>
 
 Suppose $\forall \alpha, G_\alpha$ is open. Let $x\in \bigcup _{\alpha} G_\alpha$. Then $\exists \alpha_0$ such that $x\in G_{\alpha_0}$. Since $G_{\alpha_0}$ is open, $\exists r>0$ such that $B_r(x)\subset G_{\alpha_0}$ Then $B_r(x)\subset G_{\alpha_0}\subset \bigcup_{\alpha} G_\alpha$
 
-QED
+</details>
 
 ##### A finite intersection of open set is open
 
-Proof:
+<details>
+<summary>Proof</summary>
 
 Suppose $\forall i\in \{1,...,n\}$, $G_i$ is open.
 
@@ -117,7 +121,7 @@ Let $x\in \bigcap^n_{i=1}G_i$, then $\forall i\in \{1,..,n\}$ and $G_i$ is open,
 
 Let $r=min\{r_1,...,r_n\}$. Then $\forall i\in \{1,...,n\}$. $B_r(x)\subset B_{r_i}(x)\subset G_i$. So $B_r(x)\subset \bigcup_{i=1}^n G_i$
 
-QED
+</details>
 
 The other two can be proved by **Theorem 2.22,2.23**
 
@@ -131,7 +135,8 @@ Remark: Using the definition of $E'$, we have, $\bar{E}=\{p\in X,\forall r>0,B_r
 
 $\bar {E}$ is closed.
 
-Proof:
+<details>
+<summary>Proof</summary>
 
 We will show $\bar{E}^c$ is open.
 
@@ -147,4 +152,4 @@ This proves (b)
 
 So $\bar{E}^c$ is open
 
-QED
+</details>

content/Math4201/Exam_reviews/Math4201_E1.md

@@ -1,4 +1,4 @@
-# Math 4201 Exam 1 review
+# Math 4201 Exam 1 Review
 
 > [!NOTE]
 >
@@ -343,5 +343,3 @@ $\sim$ is a subset of $X\times X$ with the following properties:
 3. If $(x,y)\in \sim$ and $(y,z)\in \sim$, then $(x,z)\in \sim$.
 
 The equivalence classes of $x\in X$ is denoted by $[x]=\{y\in X|y\sim x\}$.
-
-

content/Math4201/Exam_reviews/Math4201_E2.md

@@ -0,0 +1,194 @@
+# Math 4201 Exam 2 Review
+
+> [!NOTE]
+>
+> This is a review for definitions we covered in the classes. It may serve as a cheat sheet for the exam if you are allowed to use it.
+
+## Connectedness and compactness of metric spaces
+
+### Connectedness and separation
+
+#### Definition of separation
+
+Let $X=(X,\mathcal{T})$ be a topological space. A separation of $X$ is a pair of open sets $U,V\in \mathcal{T}$ that:
+
+1. $U\neq \emptyset$ and $V\neq \emptyset$ (that also equivalent to $U\neq X$ and $V\neq X$)
+2. $U\cap V=\emptyset$
+3. $X=U\cup V$ ($\forall x\in X$, $x\in U$ or $x\in V$)
+
+Some interesting corollary:
+
+- Any non-trivial (not $\emptyset$ or $X$) clopen set can create a separation.
+  - Proof: Let $U$ be a non-trivial clopen set. Then $U$ and $U^c$ are disjoint open sets whose union is $X$.
+- For subspace $Y\subset X$, a separation of $Y$ is a pair of open sets $U,V\in \mathcal{T}_Y$ such that:
+  1. $U\neq \emptyset$ and $V\neq \emptyset$ (that also equivalent to $U\neq Y$ and $V\neq Y$)
+  2. $U\cap V=\emptyset$
+  3. $Y=U\cup V$ ($\forall y\in Y$, $y\in U$ or $y\in V$)
+   - If $\overline{A}$ is closure of $A$ in $X$, same for $\overline{B}$, then the closure of $A$ in $Y$ is $\overline{A}\cap Y$ and the closure of $B$ in $Y$ is $\overline{B}\cap Y$. Then for separation $U,V$ of $Y$, $\overline{A}\cap B=A\cap \overline{B}=\emptyset$.
+
+#### Definition of connectedness
+
+A topological space $X$ is connected if there is no separation of $X$.
+
+> [!TIP]
+>
+> Connectedness is a local property. (That is, even the big space is connected, the subspace may not be connected. Consider $\mathbb{R}$ with the usual metric. $\mathbb{R}$ is connected, but $\mathbb{R}\setminus\{0\}$ is not connected.)
+>
+> Connectedness is a topological property. (That is, if $X$ and $Y$ are homeomorphic, then $X$ is connected if and only if $Y$ is connected. Consider if not, then separation of $X$ gives a separation of $Y$.)
+
+#### Lemma of connected subspace
+
+If $A,B$ is a separation of a topological space $X$, and $Y\subseteq X$ is a **connected** subspace with subspace topology, then $Y$ is either contained in $A$ or $B$.
+
+_Easy to prove by contradiction. Try to construct a separation of $Y$._
+
+#### Theorem of connectedness of union of connected subsets
+
+Let $\{A_\alpha\}_{\alpha\in I}$ be a collection of connected subsets of a topological space $X$ such that $\bigcap_{\alpha\in I} A_\alpha$ is non-empty. Then $\bigcup_{\alpha\in I} A_\alpha$ is connected.
+
+_Easy to prove by lemma of connected subspace._
+
+#### Lemma of compressing connectedness
+
+Let $A\subseteq X$ be a connected subspace of a topological space $X$ and $A\subseteq B\subseteq \overline{A}$. Then $B$ is connected.
+
+_Easy to prove by lemma of connected subspace. Suppose $C,D$ is a separation of $B$, then $A$ lies completely in either $C$ or $D$. Without loss of generality, assume $A\subseteq C$. Then $\overline{A}\subseteq\overline{C}$ and $\overline{A}\cap D=\emptyset$ (from $\overline{C}\cap D=\emptyset$ by closure of $A$). (contradiction that $D$ is nonempty) So $D$ is disjoint from $\overline{A}$, and hence from $B$. Therefore, $B$ is connected._
+
+#### Theorem of connected product space
+
+Any finite cartesian product of connected spaces is connected.
+
+_Prove using the union of connected subsets theorem. Using fiber bundle like structure union with non-empty intersection._
+
+### Application of connectedness in real numbers
+
+Real numbers are connected.
+
+Using the least upper bound and greatest lower bound property, we can prove that any interval in real numbers is connected.
+
+#### Intermediate Value Theorem
+
+Let $f:[a,b]\to \mathbb{R}$ be continuous. If $c\in\mathbb{R}$ is such that $f(a)<c<f(b)$, then there exists $x\in [a,b]$ such that $f(x)=c$.
+
+_If false, then we can use the disjoint interval with projective map to create a separation of $[a,b]$._
+
+#### Definition of path-connected space
+
+A topological space $X$ is path-connected if for any two points $x,x'\in X$, there is a continuous map $\gamma:[0,1]\to X$ such that $\gamma(0)=x$ and $\gamma(1)=x'$. Any such continuous map is called a path from $x$ to $x'$.
+
+- Every connected space is path-connected.
+  - The converse may not be true, consider the topologists' sine curve.
+
+### Compactness
+
+#### Definition of compactness via open cover and finite subcover
+
+Let $X=(X,\mathcal{T})$ be a topological space. An open cover of $X$ is $\mathcal{A}\subset \mathcal{T}$ such that $X=\bigcup_{A\in \mathcal{A}} A$. A finite subcover of $\mathcal{A}$ is a finite subset of $\mathcal{A}$ that covers $X$.
+
+$X$ is compact if every open cover of $X$ has a finite subcover (i.e. $X=\bigcup_{A\in \mathcal{A}} A\implies \exists \mathcal{A}'\subset \mathcal{A}$ finite such that $X=\bigcup_{A\in \mathcal{A}'} A$).
+
+#### Definition of compactness via finite intersection property
+
+A collection $\{C_\alpha\}_{\alpha\in I}$ of subsets of a set $X$ has finite intersection property if for every finite subcollection $\{C_{\alpha_1}, ..., C_{\alpha_n}\}$ of $\{C_\alpha\}_{\alpha\in I}$, we have $\bigcap_{i=1}^n C_{\alpha_i}\neq \emptyset$.
+
+Let $X=(X,\mathcal{T})$ be a topological space. $X$ is compact if every collection $\{Z_\alpha\}_{\alpha\in I}$ of closed subsets of $X$ satisfies the finite intersection property has a non-empty intersection (i.e. $\forall \{Z_{\alpha_1}, ..., Z_{\alpha_n}\}\subset \{Z_\alpha\}_{\alpha\in I}, \bigcap_{i=1}^n Z_{\alpha_i} \neq \emptyset\implies \bigcap_{\alpha\in I} Z_\alpha \neq \emptyset$).
+
+#### Compactness is a local property
+
+Let $X$ be a topological space. A subset $Y\subseteq X$ is compact if and only if every open covering of $Y$ (set open in $X$) has a finite subcovering of $Y$.
+
+- A space $X$ is compact but the subspace may not be compact.
+  - Consider $X=[0,1]$ and $Y=[0,1/2)$. $Y$ is not compact because the open cover $\{(0,1/n):n\in \mathbb{N}\}$ does not have a finite subcover.
+- A compact subspace may live in a space that is not compact.
+  - Consider $X=\mathbb{R}$ and $Y=[0,1]$. $Y$ is compact but $X$ is not compact.
+
+#### Closed subspaces of compact spaces
+
+A closed subspace of a compact space is compact.
+
+A compact subspace of Hausdorff space is closed.
+
+_Each point not in the closed set have disjoint open neighborhoods with the closed set in Hausdorff space._
+
+#### Theorem of compact subspaces with Hausdorff property
+
+If $Y$ is compact subspace of a **Hausdorff space** $X$, $x_0\in X-Y$, then there are disjoint open neighborhoods $U,V\subseteq X$ such that $x_0\in U$ and $Y\subseteq V$.
+
+#### Image of compact space under continuous map is compact
+
+Let $f:X\to Y$ be a continuous map and $X$ is compact. Then $f(X)$ is compact.
+
+#### Tube lemma
+
+Let $X,Y$ be topological spaces and $Y$ is compact. Let $N\subseteq X\times Y$ be an open set contains $X\times \{y_0\}$ for $y_0\in Y$. Then there exists an open set $W\subseteq Y$ is open containing $y_0$ such that $N$ contains $X\times W$.
+
+_Apply the finite intersection property of open sets in $X\times Y$. Projection map is continuous._
+
+#### Product of compact spaces is compact
+
+Let $X,Y$ be compact spaces, then $X\times Y$ is compact.
+
+Any finite product of compact spaces is compact.
+
+### Compact subspaces of real numbers
+
+#### Every closed and bounded subset of real numbers is compact
+
+$[a,b]$ is compact in $\mathbb{R}$ with standard topology.
+
+#### Good news for real numbers
+
+Any of the three properties is equivalent for subsets of real numbers (product of real numbers):
+
+1. $A\subseteq \mathbb{R}^n$ is closed and bounded (with respect to the standard metric or spherical metric on $\mathbb{R}^n$).
+2. $A\subseteq \mathbb{R}^n$ is compact.
+
+#### Extreme value theorem
+
+If $f:X\to \mathbb{R}$ is continuous map with $X$ being compact. Then $f$ attains its minimum and maximum. (there exists $x_m,x_M\in X$ such that $f(x_m)\leq f(x)\leq f(x_M)$ for all $x\in X$)
+
+#### Lebesgue number lemma
+
+For a compact metric space $(X,d)$ and an open covering $\{U_\alpha\}_{\alpha\in I}$ of $X$. Then there is $\delta>0$ such that for every subset $A\subseteq X$ with diameter less than $\delta$, there is $\alpha\in I$ such that $A\subseteq U_\alpha$.
+
+_Apply the extreme value theorem over the mapping of the averaging function for distance of points to the $X-U_\alpha$. Find minimum radius of balls that have some $U_\alpha$ containing the ball._
+
+#### Definition for uniform continuous function
+
+$f$ is uniformly continuous if for any $\epsilon > 0$, there exists $\delta > 0$ such that for any $x_1,x_2\in X$, if $d(x_1,x_2)<\delta$, then $d(f(x_1),f(x_2))<\epsilon$.
+
+#### Theorem of uniform continuous function
+
+Let $f:X\to Y$ be a continuous map between two metric spaces. If $X$ is compact, then $f$ is uniformly continuous.
+
+#### Definition of isolated point
+
+A point $x\in X$ is an isolated point if $\{x\}$ is an open subset of $X$.
+
+#### Theorem of isolated point in compact spaces
+
+Let $X$ be a nonempty compact Hausdorff space. If $X$ has no isolated points, then $X$ is uncountable.
+
+_Proof using infinite nested closed intervals should be nonempty._
+
+### Variation of compactness
+
+#### Limit point compactness
+
+A topological space $X$ is limit point compact if every infinite subset of $X$ has a limit point in $X$.
+
+- Every compact space is limit point compact.
+
+#### Sequentially compact
+
+A topological space $X$ is sequentially compact if every sequence in $X$ has a convergent subsequence.
+
+- Every compact space is sequentially compact.
+
+#### Equivalence of three in metrizable spaces
+
+If $X$ is a metrizable space, then the following are equivalent:
+
+1. $X$ is compact.
+2. $X$ is limit point compact.
+3. $X$ is sequentially compact.

content/Math4201/Math4201_L25.md

@@ -0,0 +1,166 @@
+# Math4201 Topology I (Lecture 25)
+
+## Continue on compact spaces
+
+### Compact spaces
+
+#### Definition of compact spaces
+
+A compact space $X$ is a topological space such that any open covering of $X$ has a finite subcovering.
+
+$$
+X=\bigcup_{\alpha\in A} U_\alpha\implies \exists \alpha_1, ..., \alpha_n\in A \text{ such that } X=\bigcup_{i=1}^n U_{\alpha_i}
+$$
+
+<details>
+<summary>Example of compact spaces</summary>
+
+$(0,1)$ is not compact, consider the open cover $\{(0,1/n):n\in \mathbb{N}\}$ which does not have a finite subcover.
+
+---
+
+$\mathbb{R}$ is not compact, consider the open cover $\{(-n,n):n\in \mathbb{N}\}$ which does not have a finite subcover.
+
+---
+
+Later we will see that $[0,1]$ is compact. (more generally, any closed and bounded interval is compact)
+
+</details>
+
+> [!TIP]
+>
+> A property (or definition) is good for topologists if it is preserved by homeomorphism, or even better, by continuous maps.
+
+#### Proposition of compact spaces preserved by continuous maps
+
+Let $X$ be a compact space and $f:X\to Y$ be a continuous map. Then $f(X)$ is compact.
+
+<details>
+<summary>Proof</summary>
+
+Consider an open covering of $f(X)$, So, there are open sets $\{f(x)\cap U_{\alpha}\}_{x\in X}$ such that $f(X)=\bigcup_{\alpha\in I} (f(x)\cap U_{\alpha})$.
+
+This implies that $\{f^{-1}(f(x)\cap U_{\alpha})\}_{x\in X, \alpha\in I}$ consists of:
+
+1. $f^{-1}(U_{\alpha})$ is open because $f$ is continuous.
+2. $f^{-1}(f(x)\cap U_{\alpha})$ covers $X$ because $\forall x\in X, f(x)\in f(X)\subseteq \bigcup_{\alpha\in I} (f(x)\cap U_{\alpha})$ so $x\in f^{-1}( U_{\alpha})$.
+
+Since $X$ is compact, there are finitely many $x_1, ..., x_n\in X$ such that $X=\bigcup_{i=1}^n f^{-1}(U_{\alpha_i})$.
+
+So, $f(X)=\bigcup_{i=1}^n f(f^{-1}(U_{\alpha_i}))=\bigcup_{i=1}^n U_{\alpha_i}$.
+
+This implies that $f(X)$ is compact.
+
+</details>
+
+#### Corollary of compact spaces preserved by homeomorphism
+
+If $f:X\to Y$ is homeomorphism and $X$ is compact, then $Y$ is compact.
+
+#### Lemma of compact subspaces
+
+Let $X$ be a topological space and $Y\subseteq X$ be a subspace with subspace topology from $X$.
+
+Then $Y$ is compact if and only if for any open cover $\{U_\alpha\}_{\alpha\in I}$ of $Y$, there exists a finite subcover $\{U_{\alpha_1}, ..., U_{\alpha_n}\}$ of $Y$.
+
+#### Proposition of closed compact sets
+
+Every closed subspace $Y$ of a compact space $Y\subseteq X$ is compact.
+
+<details>
+<summary>Proof</summary>
+
+Let $\{U_\alpha\}_{\alpha\in I}$ be an open cover of $Y$. Since $Y$ is closed, $X-Y$ is open. So, $(X-Y)\cup \bigcup_{\alpha\in I} U_\alpha$ is an open cover of $X$.
+
+Since $X$ is compact, there are finitely many $\alpha_1, ..., \alpha_n\in I$ such that $X=\bigcup_{i=1}^n U_{\alpha_i}$ and possibly $X-Y\subseteq U_{\alpha_m}$.
+
+So, $Y=\bigcup_{i=1}^n (U_{\alpha_i}\cap Y)=\bigcup_{i=1}^n U_{\alpha_i}$.
+
+This implies that $Y$ is compact.
+
+</details>
+
+> [!WARNING]
+>
+> The converse of the proposition is almost true.
+
+#### Proposition of compact subspaces with Hausdorff property
+
+If $Y$ is compact subspace of a **Hausdorff space** $X$, then $Y$ is closed in $X$.
+
+<details>
+<summary>Proof</summary>
+
+To show the claim, we need to show $x$ outside $y$, there is an open neighborhood of $x$ that is disjoint from $Y$.
+
+For any $y\in Y$, there are disjoint open neighborhoods $U_y$ and $V_y$ of $x$ and $y$ respectively (by the Hausdorff property of $X$).
+
+So $\bigcup_{y\in Y} V_y\supseteq Y$ and $Y$ is a compact subspace of $X$, so there are finitely many $y_1, ..., y_n\in Y$ such that $Y\subseteq \bigcup_{i=1}^n V_{y_i}$.
+
+Since for each $y_i\in V_{y_i}$, there exists an open neighborhood $U_{y_i}$ of $x$ such that $U_{y_i}\cap V_{y_i}=\emptyset$, we have $U_{y_i}\cap Y=\emptyset$.
+
+So $\bigcap_{i=1}^n U_{y_i}$ is disjoint from $\bigcup_{i=1}^n V_{y_i}\supseteq Y$, so disjoint from $Y$.
+
+Furthermore, $x\in \bigcap_{i=1}^n U_{y_i}$, so $\bigcap_{i=1}^n U_{y_i}$ is open in $X$ because it is an finite intersection of open sets.
+
+This holds for any $x\in X-Y$, so $X-Y$ is open in $X$, so $Y$ is closed in $X$.
+
+</details>
+
+This the course of proving this proposition, we showed the following:
+
+#### Proposition
+
+If $X$ is Hausdorff and $Y\subseteq X$ is compact, and $x\in X-Y$, then there are disjoint open neighborhoods $U,V\subseteq X$ such that $x\in U$ and $Y\subseteq V$.
+
+<details>
+<summary>Proof</summary>
+
+Use the proof from last proposition, take $U=\bigcap_{i=1}^n U_{y_i}$ and $V=\bigcup_{i=1}^n V_{y_i}$.
+
+</details>
+
+#### Theorem of closed maps from compact and Hausdorff spaces
+
+If $f:X\to Y$ is continuous and $X$ is compact, $Y$ is Hausdorff, then $f$ is a closed map.
+
+In particular, if $f:X\to Y$ is continuous and bijection with $X$ compact and $Y$ Hausdorff, then $f$ is a homeomorphism.
+
+<details>
+<summary>Example distinguishing these two properties</summary>
+
+Consider the map $f:[0,2\pi)\to \mathbb{S}^1$ defined by $f(x)=(\cos x, \sin x)$. This is a continuous bijection.
+
+$f$ is continuous bijection and $Y$ is Hausdorff, But $X$ is not compact.
+
+Then $f$ is not a homeomorphism because $f^{-1}$ is not continuous.
+
+</details>
+
+<details>
+<summary>Proof</summary>
+
+Consider $Z\subseteq X$ is closed and $X$ is compact, so $Z$ is compact.
+
+So $f(Z)$ is compact since $f$ is continuous. Note that $f(Z)\subseteq Y$ is Hausdorff, so $f(Z)$ is closed in $Y$.
+
+So $f$ is a closed map.
+
+</details>
+
+#### Theorem of products of compact spaces
+
+If $X,Y$ are compact spaces, then $X\times Y$ is compact. (More generalized version: Tychonoff's theorem)
+
+<details>
+<summary>Incomplete Proof</summary>
+
+Let $\{U_\alpha\}_{\alpha\in I}$ be an open cover of $X\times Y$.
+
+Step 1: For any $x\in X$, there are finitely many $\alpha_1, ..., \alpha_n\in I$ and open neighborhoods $x\in V\subseteq X$ such that $V\times Y\subseteq \bigcup_{i=1}^n U_{\alpha_i}\times Y$.
+
+For any $y\in Y$, there is $U_\alpha$ and $x\in U_y\subseteq X$ and $y\in V_y\subseteq Y$ such that $(x,y)\in U_y\times V_y\subseteq U_\alpha$.
+
+Continue next time...
+
+</details>

content/Math4201/Math4201_L26.md

@@ -0,0 +1,116 @@
+# Math4201 Topology I (Lecture 26)
+
+## Continue on compact spaces
+
+### Compact spaces
+
+#### Tube lemma
+
+Let $X$ be a compact topological space and $y$ be a topological space. Let $N\subseteq X\times Y$ be an open set contains $X\times \{y_0\}$ for $y_0\in Y$. Then there exists an open set $W\subseteq Y$ is open containing $y_0$ such that $N$ contains $X\times W$.
+
+<details>
+<summary>Proof</summary>
+
+For any $x\in X$, there are open sets $x\in U_x\subseteq X$ and $y_0\in V_x\subseteq Y$ such that $U_x\times V_x\subseteq N$.
+
+In particular, $\{U_x\}_{x\in X}$ is an open cover of $X$. Since $\forall x\in X$, $x\in U_x$, so there exists a finite subcover $\bigcup_{i=1}^k U_{x_i}=X$.
+
+Take $W=\bigcap_{i=1}^k V_{x_i}$. This is intersection of finitely many open sets, so it is open.
+
+$y_0\in V_{x_i}$ for all $x_i\in X$, so $y_0\in W$.
+
+So $U_{x_i}\times W\subseteq U_{x_i}\times V_{x_i}\subseteq N$ for all $i=1, ..., k$.
+
+So $\bigcup_{i=1}^k U_{x_i}\times W\subseteq N$.
+
+</details>
+
+#### Product of compact space is compact
+
+Let $X$ and $Y$ be compact spaces, then $X\times Y$ is compact.
+
+<details>
+<summary>Proof</summary>
+
+Let $\{N_\alpha\}_{\alpha\in I}$ be an open covering of $X\times Y$.
+
+For any $y_0\in Y$, $X\times \{y_0\}$ is a compact subspace of $X\times Y$.
+
+So there are finitely many $N_\alpha$'s whose union $M_{y_0}$ is open containing $X\times \{y_0\}$.
+
+Using the tube lemma, $M_{y_0}$ contains $X\times W_{y_0}$ for some open neighborhood $W_{y_0}\subseteq Y$ of $y_0$.
+
+Now note that $\{W_{y_0}\}_{y_0\in Y}$ is an open cover of $Y$.
+
+In particular, there are finitely many $y_1, ..., y_n\in Y$ such that $Y=\bigcup_{i=1}^n W_{y_i}$ by compactness of $Y$.
+
+So $\forall i$, $X\times W_{y_i}\subseteq M_{y_i}$.
+
+This is a union of finitely many $N_\alpha$'s, so it is open.
+
+This implies that taking the union of all such $N_\alpha$'s, for all $1\leq i\leq k$, which is finite, covers $\bigcup_{i=1}^k X\times W_{y_i}=X\times Y$.
+
+</details>
+
+#### Closed intervals in real numbers are compact
+
+$[a,b]$ is compact in $\mathbb{R}$.
+
+<details>
+<summary>Proof</summary>
+
+Let $\{U_\alpha\}_{\alpha\in I}$ be an open cover of $[a,b]$.
+
+Define:
+
+$$
+C=\{c\in [a,b]\mid [a,c]\text{ is covered by finitely many } U_\alpha's\}
+$$
+
+Our goal is to show that $b\in C$.
+
+Clearly $a$ is covered by one $U_\alpha$, so $[a,a]\in C$.
+
+Take $y=\sup C\in [a,b]$.
+
+Since $y\in [a,b]$, there is $U_\alpha$ such that $y\in U_\alpha$.
+
+Since $U_\alpha$ is open, there exists an open interval $(y-\epsilon, y+\epsilon)\subseteq U_\alpha$. So there is some $z\in C$ such that $z\in (y-\epsilon, y+\epsilon)$. Otherwise $y-\epsilon$ is an upper bound of $C$, which contradicts the definition of $y$.
+
+So $[a,z]$ can be covered by finitely many $U_\alpha$'s. $U_{\alpha_1}, ..., U_{\alpha_k}$ and $\bigcup_{i=1}^k U_{\alpha_i}\supseteq [a,z]$.
+
+So $\bigcup_{i=1}^k U_{\alpha_i}\supseteq [a,z]\cup (y-\epsilon, y+\epsilon)=[a,y+\epsilon]$.
+
+If $y\neq b$, then there is an element $c\in [a,b]$ that belongs to $(y,y+\epsilon)$ and $[a,c]\subseteq [a,y+\epsilon)$ can be covered by finitely many $U_\alpha$'s, so $c\in C$. This contradicts the definition of $y$. $y<c\in C$.
+
+</details>
+
+#### Heine-Borel theorem
+
+A subset $K\subseteq \mathbb{R}^n$ is compact if and only if it is closed and bounded with respect to the standard metric on $\mathbb{R}^n$.
+
+#### Definition of bounded
+
+$A\subseteq \mathbb{R}^n$ is bounded if there exists $c\in \mathbb{R}^{>0}$ such that $d(x,y)<c$ for all $x,y\in A$.
+
+<details>
+<summary>Proof for Heine-Borel theorem</summary>
+
+Suppose $k\subseteq \mathbb{R}^n$ is compact.
+
+Since $\mathbb{R}^n$ is Hausdorff, $K\subseteq \mathbb{R}^n$ is compact, so $K$ is closed subspace of $\mathbb{R}^n$. by Proposition of compact subspaces with Hausdorff property.
+
+To show that $K$ is bounded, consider the open cover with the following balls:
+$$
+B_1(0), B_2(0), ..., B_n(0), ...
+$$
+
+Since $K$ is compact, there are $n_1, ..., n_k\in \mathbb{N}$ such that $K\subseteq \bigcup_{i=1}^k B_{n_i}(0)$. Note that $B_{n_i}(0)$ is bounded, so $K$ is bounded. $\forall x,y\in B_{n_i}(0)$, $d(x,y)<2n_i$. So $K$ is bounded.
+
+---
+
+Suppose $K\subseteq \mathbb{R}^n$ is closed and bounded.
+
+Continue next time.
+
+</details>

content/Math4201/Math4201_L27.md

@@ -0,0 +1,135 @@
+# Math4201 Topology I (Lecture 27)
+
+## Continue on compact spaces
+
+### Compact spaces
+
+
+#### Heine-Borel theorem
+
+A subset $K\subseteq \mathbb{R}^n$ is compact if and only if it is closed and bounded with respect to the standard metric on $\mathbb{R}^n$.
+
+#### Definition of bounded
+
+$A\subseteq \mathbb{R}^n$ is bounded if there exists $c\in \mathbb{R}^{>0}$ such that $d(x,y)<c$ for all $x,y\in A$.
+
+<details>
+<summary>Proof for Heine-Borel theorem</summary>
+
+Suppose $k\subseteq \mathbb{R}^n$ is compact.
+
+Since $\mathbb{R}^n$ is Hausdorff, $K\subseteq \mathbb{R}^n$ is compact, so $K$ is closed subspace of $\mathbb{R}^n$. by Proposition of compact subspaces with Hausdorff property.
+
+To show that $K$ is bounded, consider the open cover with the following balls:
+$$
+B_1(0), B_2(0), ..., B_n(0), ...
+$$
+
+Since $K$ is compact, there are $n_1, ..., n_k\in \mathbb{N}$ such that $K\subseteq \bigcup_{i=1}^k B_{n_i}(0)$. Note that $B_{n_i}(0)$ is bounded, so $K$ is bounded. $\forall x,y\in B_{n_i}(0)$, $d(x,y)<2n_i$. So $K$ is bounded.
+
+---
+
+Suppose $K\subseteq \mathbb{R}^n$ is closed and bounded.
+
+First let $M=[a_1,b_1]\times [a_2,b_2]\times \cdots \times [a_n,b_n]$.
+
+This is compact because it is a product of compact spaces.
+
+Since $K$ is bounded, we can find $[a_i,b_i]$s such that $K\subseteq M$.
+
+Since $K$ is closed subspace of $\mathbb{R}^n$, $K$ is closed in $M$.
+
+Since any closed subspace of a compact space is compact, $K$ is compact.
+
+</details>
+
+> [!WARNING]
+>
+> This theorem is not true for general topological spaces.
+>
+> For example, take $X=B_1(0)$ with the standard topology on $\mathbb{R}^n$.
+>
+> Take $K=B_1(0)$, this is not compact because it is not closed in $\mathbb{R}^n$.
+
+#### Extreme Value Theorem
+
+If $f:X\to \mathbb{R}$ is continuous map with $X$ being compact. Then $f$ attains its minimum and maximum.
+
+<details>
+<summary>Proof</summary>
+
+Let $M=\sup\{f(x)\mid x\in X\}$ and $m=\inf\{f(x)\mid x\in X\}$.
+
+We want to show that there are $x_m,x_M\in X$ such that $f(x_m)=m$ and $f(x_M)=M$.
+
+Consider the open covering of $X$ given as
+
+$$
+\{U_\alpha\coloneqq f^{-1}((-\infty, \alpha))\}_{\alpha\in \mathbb{R}}
+$$
+
+If $X$ doesn't attain its maximum, then this is an open covering of $X$:
+
+1. $U_\alpha$ is open because $f$ is continuous and $(-\infty, \alpha)$ is open in $\mathbb{R}$.
+2. $\bigcup_{\alpha\in \mathbb{R}} U_\alpha = X$ because for any $x\in X$, by the assumption there is $x'\in X$ with $f(x)<f(x')$ (otherwise $f(x)$ is the maximum value). Then $x\in U_{f(x')}$.
+
+So there is an open covering of $X$ and hence it's got a finite subcover $\{U_{\alpha_i}\}_{i=1}^n$.
+
+$$
+X=\bigcup_{i=1}^n U_{\alpha_i}=\bigcup_{i=1}^n f^{-1}((-\infty, \alpha_i))=f^{-1}(-\infty, \alpha_k)
+$$
+
+and $\alpha_1\leq \alpha_2\leq \cdots \leq \alpha_n$. There is $x_i$ such that $\alpha_i=f(x_i)$.
+
+Note that $x_k\notin U_{\alpha_k}$ because $f(x_k)>\alpha_k$. So $x_k\notin X$. This contradicts the assumption that $X$ doesn't attain its maximum.
+
+</details>
+
+#### Theorem of uniform continuity
+
+Let $f:(X,d)\to (X',d')$ be a continuous map between two metric spaces. **Let $X$ be compact**, then for any $\epsilon > 0$, there exists $\delta > 0$ such that for any $x_1,x_2\in X$, if $d(x_1,x_2)<\delta$, then $d'(f(x_1),f(x_2))<\epsilon$.
+
+#### Definition of uniform continuous function
+
+$f$ is uniformly continuous if for any $\epsilon > 0$, there exists $\delta > 0$ such that for any $x_1,x_2\in X$, if $d(x_1,x_2)<\delta$, then $d'(f(x_1),f(x_2))<\epsilon$.
+
+<details>
+<summary>Example of uniform continuous function</summary>
+
+Let $f(x)=x^2$ on $\mathbb{R}$.
+
+This is not uniformly continuous because for fixed $\epsilon > 0$, the interval $\delta$ will converge to zero as $x_1,x_2$ goes to infinity.
+
+---
+
+However, if we take $f\mid_{[0,1]}$, this is uniformly continuous because for fixed $\epsilon > 0$, we can choose $\delta = \epsilon$.
+
+</details>
+
+#### Lebesgue number lemma
+
+Let $X$ be a compact metric space and $\{U_\alpha\}_{\alpha\in I}$ be an open cover of $X$. Then there is $\delta>0$ such that for any two points $x_1,x_2\in X$ with $d(x_1,x_2)<\delta$, there is $\alpha\in I$ such that $x_1,x_2\in U_\alpha$.
+
+<details>
+<summary>Proof of uniform continuity theorem</summary>
+
+Let $\epsilon > 0$. be given and consider
+
+$$
+\{f^{-1}(B_{\epsilon/2}^{d'}((x'))\}_{x'\in X'}
+$$
+
+We claim that there is an open covering of $X$.
+
+1. $f^{-1}(B_{\epsilon/2}^{d'}((x')))$ is open because $f$ is continuous and $B_{\epsilon/2}^{d'}((x'))$ is open in $X'$.
+2. $X=\bigcup_{x'\in X'} f^{-1}(B_{\epsilon/2}^{d'}((x')))$ because for any $x\in X$, $x\in f^{-1}(B_{\epsilon/2}^{d'}((f(x)))$.
+
+Since $X$ is compact, there is a finite subcover $\{f^{-1}(B_{\epsilon/2}^{d'}((x')))\}_{i=1}^n$.
+
+By Lebesgue number lemma, there is $\delta>0$ such that for any two points $x_1,x_2\in X$ with $d(x_1,x_2)<\delta$, there is $x'\in X'$ such that $x_1,x_2\in f^{-1}(B_{\epsilon/2}^{d'}((x')))$.
+
+So $f(x_1),f(x_2)\in B_{\epsilon/2}^{d'}((x'))$.
+
+Apply the triangle inequality with $d'(x_1,x')$ and $d'(x_2,x')$, we have $d'(f(x_1),f(x_2))<2\epsilon/2=\epsilon$.
+
+</details>

content/Math4201/Math4201_L28.md

@@ -0,0 +1,144 @@
+# Math4201 Topology I (Lecture 28)
+
+## Compact spaces
+
+### Extreme value theorem
+
+#### Definition of diameter
+
+Let $(X,d)$ be a metric space and $A\subseteq X$. The diameter of $A$ is defined as
+$$
+\operatorname{diam}(A) = \sup\{d(x,y):x,y\in A\}
+$$
+
+#### Lebesgue number lemma
+
+Let $X$ be a compact metric space and $\{U_\alpha\}_{\alpha\in I}$ be an open cover of $X$. Then there is $\delta>0$ such that for every subset $A\subseteq X$ with diameter less than $\delta$, there is $\alpha\in I$ such that $A\subseteq U_\alpha$.
+
+<details>
+<summary>Proof</summary>
+
+Consider $x\in X$, there is an element $U_\alpha$ in the open covering such that $x\in U_\alpha$.
+
+In particular, there is $r_x$ such that $B_{r_x}(x)\subseteq U_\alpha$.
+
+Then the collection $\{B_{\frac{r_x}{2}}(x)\}_{x\in X}$ is an open covering of $X$. (each $x\in X$ is contained in some $B_{\frac{r_x}{2}}(x)$)
+
+Since $X$ is compact, there is a finite subcover $\{B_{\frac{r_{x_i}}{2}}(x_i)\}_{i=1}^n$ of $X$. Such that $\bigcup_{i=1}^n B_{\frac{r_{x_i}}{2}}(x_i)=X$.
+
+Let $\delta = \min\{r_{\frac{r_{x_1}}{2}}, ..., r_{\frac{r_{x_n}}{2}}\}>0$.
+
+Let $A\subseteq X$ be a subset with diameter less than $\delta$.
+
+Take $y\in A$, then $A\subseteq B_\delta(y)$.
+
+Take $x_i$ such that $y\in B_{\frac{r_{x_i}}{2}}(x_i)$. (such cover exists by definition of the subcover)
+
+And then $\alpha$ such that $B_{\frac{r_{x_i}}{2}}(x_i)\subseteq U_\alpha$.
+
+We claim that $B_\delta(y)\subseteq U_\alpha$, which would imply that $A\subseteq U_\alpha$.
+
+$y\in B_{\frac{r_{x_i}}{2}}(x_i)$, and we know that $B_{r_{x_i}}(x_i)\subseteq U_\alpha$.
+
+Since $\delta < \frac{r_{x_i}}{2}$, it suffices to show that $B_{\frac{r_{x_i}}{2}}(y)\subseteq U_\alpha$.
+
+For any $z\in B_{\frac{r_{x_i}}{2}}(y)$, we have $d(z,y)<\frac{r_{x_i}}{2}$, and $d(y,x_i)<\frac{r_{x_i}}{2}$.
+
+So $d(z,x_i)\leq d(z,y)+d(y,x_i)<\frac{r_{x_i}}{2}+\frac{r_{x_i}}{2}=r_{x_i}$, so $z\in B_{r_{x_i}}(x_i)\subseteq U_\alpha$.
+
+So $B_{\frac{r_{x_i}}{2}}(y)\subseteq U_\alpha$.
+
+</details>
+
+#### Definition of finite intersection property
+
+A collection $\{C_\alpha\}_{\alpha\in I}$ of subsets of a set $X$ has finite intersection property if for every finite subcollection $\{C_{\alpha_1}, ..., C_{\alpha_n}\}$ of $\{C_\alpha\}_{\alpha\in I}$, we have $\bigcap_{i=1}^n C_{\alpha_i}\neq \emptyset$.
+
+#### Theorem 
+
+A space $X$ is compact if and only if every collection $\{Z_\alpha\}_{\alpha\in I}$ of closed subsets of $X$ satisfies the **finite** intersection property has a non-empty intersection.
+
+$$
+\bigcap_{\alpha\in I} Z_\alpha \neq \emptyset
+$$
+
+<details>
+<summary>Non-example</summary>
+
+Consider $X=(0,1)$ is not compact with the standard topology.
+
+Consider $Z_n=(0,\frac{1}{n}]$, each interval is closed in $X$. This satisfies the finite intersection property because $\bigcap_{i=1}^k Z_{n_i}\neq \emptyset$ for any finite subcollection $\{Z_{n_1}, ..., Z_{n_k}\}$. _We can find a smaller for any finite subcollection to get a non-empty intersection._
+
+But $\bigcap_{n=1}^\infty Z_n = \emptyset$.
+
+</details>
+
+<details>
+<summary>Proof</summary>
+
+$\implies$
+
+Let $U_\alpha=X-Z_\alpha$ is open for each $\alpha\in I$. By contradiction, suppose that $\bigcap_{\alpha\in I} Z_\alpha = \emptyset$.
+
+So $X-\bigcap_{\alpha\in I} Z_\alpha = X=\bigcup_{\alpha\in I} U_\alpha = \bigcup_{\alpha\in I} (X-Z_\alpha)=X$.
+
+So $\{U_\alpha\}_{\alpha\in I}$ is an open cover of $X$. Since $X$ is compact, there is a finite subcover $\{U_{\alpha_1}, ..., U_{\alpha_n}\}$.
+
+So $\bigcap_{i=1}^n U_{\alpha_i} = X-\bigcup_{i=1}^n Z_{\alpha_i} = X$, $\bigcap_{i=1}^n Z_{\alpha_i} = \emptyset$. This contradicts the finite intersection property.
+
+$\impliedby$
+
+Proof is similar.
+
+</details>
+
+#### Definition of isolated point
+
+A point $x\in X$ is an isolated point if $\{x\}$ is an open subset of $X$.
+
+<details>
+<summary>Example of isolated point</summary>
+
+$X=[0,1]\cup \{2\}$ with subspace topology from $\mathbb{R}$.
+
+Then $\{2\}$ is an isolated point $\{2\}=X\cap (2-\frac{1}{2}, 2+\frac{1}{2})$.
+
+</details>
+
+#### Theorem of compact Hausdorff spaces without isolated points
+
+Any non-empty compact Hausdorff space without an isolated point is uncountable.
+
+<details>
+<summary>Proof</summary>
+
+Proof by contradiction.
+
+Let $X=\{x_n\}_{n\in\mathbb{N}}$ be a countable set.
+
+Since $x_1$ is not an isolated point, so there exists $y_1\in X$ such that $y_1\neq x_1$. Apply the Hausdorff property, there exists disjoint open neighborhoods $U_1$ and $V_1$ such that $x_1\in U_1$ and $y_1\in V_1$.
+
+In particular $\overline{V_1}$ does not contain $x_1$, but it contains $y_1$. (Follows from disjoint open neighborhoods)
+
+Since $x_2$ is not an isolated point, so there exists $y_2\in X$ such that $y_2\neq x_2$. Apply the Hausdorff property, there exists disjoint open neighborhoods $U_2$ and $V_2$ such that $x_2\in U_2$ and $y_2\in V_2$.
+
+If $x_2\notin V_1$, then we define $V_2$ as $V_1$.
+
+If $x_2\in V_1$, then by the assumption, there is another point $y_2$ in $V_1$ which isn't the same as $x_2$.
+
+CONTINUE NEXT TIME.
+
+</details>
+
+#### Theorem real numbers is uncountable
+
+$\mathbb{R}$ is uncountable, and any interval in $\mathbb{R}$ is uncountable.
+
+<details>
+<summary>Proof</summary>
+
+It suffices to prove this for a closed interval $[a,b]$ with $a<b$. Because any interval contains such a closed interval.
+
+The claim for a closed interval $[a,b]$ follows from the following theorem because $[a,b]$ is a non-empty compact Hausdorff space without an isolated point.
+
+</details>

content/Math4201/Math4201_L29.md

@@ -0,0 +1,143 @@
+# Math4201 Topology I (Lecture 29)
+
+## Compact and connected spaces
+
+### Compact spaces
+
+#### Theorem of uncountable compact Hausdorff spaces without isolated points
+
+Any non-empty compact Hausdorff space $X$ without any isolated points is uncountable.
+
+<details>
+<summary>Proof</summary>
+
+By contradiction, let $X=\{x_n\}_{n\in\mathbb{N}}$ be a countable set.
+
+We construct inductively a sequence of open non-empty subspaces $\{V_i\}$ of $X$ such that
+
+$$
+\overline{V_1}\supseteq \overline{V_2}\supseteq \overline{V_3}\supseteq \dots
+$$
+
+where $x_i$ not in $\overline{V_i}$.
+
+This could imply that for any $j\leq i$, $x_j$ is not in $\overline{V_j}$ but $\overline{V_j}\supseteq \overline{V_i}$. This contradicts the fact that $x_j$ not in $\overline{V_i}$, that is $x_1, ..., x_i$ are not in $\overline{V_i}$.
+
+This is a contradiction because $\{\overline{V_i}\}$ satisfies the finite intersection property.
+
+$$
+\bigcap_{i=1}^\infty \overline{V_i} \neq \emptyset
+$$
+
+But in this case, $\bigcap_{i=1}^\infty \overline{V_i} = \emptyset$ because $x_i$ not in $\overline{V_i}$.
+
+To construct such $\{V_i\}$, we can start with $V_1,\dots, V_{k-1}$ are constructed, then there is a point $y_k$ in $V_{k-1}$ which isn't same as $x_k$.
+
+So $x_k$ not in $\overline{V_k}$ because $U_k$ is an open neighborhood of $x_k$ that don't intersect with $V_k$.
+
+Since $X$ is Hausdorff, there exists an open neighborhood $U_k$ of $x_k$ and $U_y$ of $y_k$ such that $U_k\cap U_y=\emptyset$.
+
+Let $x_k\in U_k$ and $y_k\in W_k\subseteq X$ that is open, and $U_k\cap W_k=\emptyset$.
+
+Let $V_k=W_k\cap V_{k-1}$. Then this is open and is contained in $V_{k-1}$ since $\overline{V_k}\subseteq \overline{V_{k-1}}$.
+
+Case 1: $x_k\notin V_{k-1}$. There is such $y_k$ because $V_{k-1}$ is not empty.
+
+Case 2: $x_k\in V_{k-1}$. Since $x_k$ is not isolated points, any open neighborhood of $x_k$ including $V_{k-1}$ contains another point.
+
+Therefore, $X$ is uncountable.
+
+</details>
+
+#### Definition of limit point compact
+
+A space $X$ is limit point compact if any infinite subset of $X$ has a [limit point](./Math4201_L8#limit-points) in $X$.
+
+_That is, $\forall A\subseteq X$ and $A$ is infinite, there exists a point $x\in X$ such that $x\in U$, $\forall U\in \mathcal{T}$ containing $x$, $(U-\{x\})\cap A\neq \emptyset$._
+
+_This property also holds for finite sets, for example, any finite set with discrete topology is limit point compact. (since you cannot find a infinite subset of a finite set that has a limit point)_
+
+#### Definition of sequentially compact
+
+A space $X$ is sequentially compact if any sequence has a convergent subsequence. i.e. If $\{x_n\}_{n\in\mathbb{N}}$ is a sequence in $X$, then there are $n_1<n_2<\dots<n_k<\dots$ such that $\{y_i=x_{n_i}\}_{i\in\mathbb{N}}$ is convergent.
+
+#### Theorem of limit point compact spaces
+
+If $(X,d)$ is a **metric space**, then the following are equivalent:
+
+1. $X$ is compact.
+2. $X$ is limit point compact.
+3. $X$ is sequentially compact.
+
+<details>
+<summary>Example of limit point compact spaces but not compact</summary>
+
+Let $X'=\{a,b\}$ with trivial topology, and $X=\mathbb{N}\times X'$ with the product topology where we use the discrete topology on $\mathbb{N}$.
+
+$X$ isn't compact because $\{\{i\}\times X':i\in\mathbb{N}\}$ is an open cover of $X$ that doesn't have a finite subcover.
+
+because these open sets are disjoint, $X$ is limit point compact.
+
+Let $A\subseteq X$ be an infinite subset of $X$. In particular, it contains a point of the form $(i,a)$ or $(i,b)$ for $i\in\mathbb{N}$. Let $(i,a)\in A$. Then $(i,b)$ is a limit point of $A$, since any open neighborhood ($\{i\}\times X'$) of $(i,b)$ contains a point of the form $(i,a)$ or $(i,b)$.
+
+$X$ is not sequentially compact because the sequence $\{(n,a)\}_{n\in\mathbb{N}}$ has no convergent subsequence.
+
+</details>
+
+<details>
+<summary>Proof</summary>
+
+First, we show that 1. implies 2.
+
+We proceed by contradiction.
+
+Let $X$ be compact and $A\subseteq X$ be an infinite subset of $X$ that doesn't have any limit points.
+
+Then $X-A$ is open because any $x\in X-A$ isn't in the closure of $A$ otherwise it would be a limit point for $A$, and hence $x$ has an open neighborhood contained in the complement of $A$.
+
+Next, let $x\in A$. Since $x$ isn't a limit point of $A$, there is an open neighborhood $U_x$ of $x$ in $X$ that $U_x\cap A=\{x\}$. Now consider the open covering of $X$ given as
+
+$$
+\{X-A\}\cup \{U_x:x\in A\}
+$$
+
+This is an open cover because either $x\in X-A$ or $x\in A$ and in the latter case, $x\in U_x$ since $X$ is compact, this should have a finite subcover. Any such subcover should contain $U_x$ for any $x$ because $U_x$ is the element in the subcover for $x$.
+
+This implies that our finite cover contains infinite open sets, which is a contradiction.
+
+---
+
+Continue with the proof that 2. implies 3. next time.
+</details>
+
+#### Corollary of compact spaces
+
+1. If $X$ is a compact topological space, then it is limit point compact.
+2. If $X$ is a sequentially compact topological space, then it is limit point compact.
+
+<details>
+<summary>Proof</summary>
+
+Proof of 1. follows from the theorem of limit point compact spaces.
+
+</details>
+
+That means, sequentially compact is a stronger property than limit point compact, and compact is the stronger property than limit point compact.
+
+> [!WARNING]
+>
+> Hope you will not use it soon for your exams but here are some interesting examples.
+>
+> **There exists spaces that are sequentially compact but not compact.**
+>
+> [link to spaces](https://topology.pi-base.org/spaces?q=Sequentially%20Compact%2B%7ECompact)
+>
+> [S000035](https://topology.pi-base.org/spaces/S000035)
+>
+> **There exists spaces that are compact but not sequentially compact.**
+>
+> [link to spaces](https://topology.pi-base.org/spaces?q=Compact%2B%7ESequentially%20Compact)
+> 
+> Consider the space of functions $f:[0,1]\to [0,1]$ with the topology of pointwise convergence. This space is compact $I^I$ but not sequentially compact (You can always find a sequence of functions that does not converge to any function in the space, when there is uncountable many functions in the space).
+>
+> [S000103](https://topology.pi-base.org/spaces/S000103)

content/Math4201/Math4201_L30.md

@@ -0,0 +1,128 @@
+# Math4201 Topology I (Lecture 30)
+
+## Compactness
+
+### Compactness in Metric Spaces
+
+#### Limit point compactness
+
+A topological space $X$ is limit point compact if every infinite subset of $X$ has a limit point in $X$.
+
+- Every compact space is limit point compact.
+
+#### Sequentially compact
+
+A topological space $X$ is sequentially compact if every sequence in $X$ has a convergent subsequence.
+
+#### Theorem of equivalence of compactness in metrizable spaces
+
+If $(X,d)$ is a metric space then the following are equivalent:
+
+1. $X$ is compact.
+2. $X$ is limit point compact.
+3. $X$ is sequentially compact.
+
+<details>
+<summary>Proof</summary>
+
+(1) $\implies$ (2):
+
+We proceed by contradiction,
+
+Let $X$ be compact and $A\subseteq X$ be an infinite subset of $X$ that doesn't have any limit points.
+
+Then $X-A$ is open because any $x\in X-A$ isn't in the closure of $A$ otherwise it would be a limit point for $A$, and hence $x$ has an open neighborhood contained in the complement of $A$.
+
+Next, let $x\in A$. Since $x$ isn't a limit point of $A$, there is an open neighborhood $U_x$ of $x$ in $X$ that $U_x\cap A=\{x\}$. Now consider the open covering of $X$ given as
+
+$$
+\{X-A\}\cup \{U_x:x\in A\}
+$$
+
+This is an open cover because either $x\in X-A$ or $x\in A$ and in the latter case, $x\in U_x$ since $X$ is compact, this should have a finite subcover. Any such subcover should contain $U_x$ for any $x$ because $U_x$ is the element in the subcover for $x$.
+
+This implies that our finite cover contains infinite open sets, which is a contradiction.
+
+---
+
+(2) $\implies$ (3):
+
+Let $\{x_n\}_{n\in\mathbb{N}}$ be an arbitrary sequence in $X$.
+
+Since $d(z,x_{n_k})\leq \frac{1}{k}$ the subsequence $(x_{n_k})$ converges to $z$.
+
+This completes the proof.
+
+except possibly $z$.
+
+Now we consider
+
+$$
+B_{r_k}(z)\text { with } r_k=\min \left(\frac{1}{k}, d_k\right)
+$$
+
+This ball has a point $x_{n_k}$ from $\{x_n\}$ which isn't equal to $z$.
+
+$r_k\leq d_k\implies n_k\geq n_{k-1}$.
+
+Since $z$ is a limit point of $\{x_n\}$, there exists $x_{n_k}$ such that $d(z,x_{n_k})<\frac{1}{k}$. So $x_{n_k}\in B_{r_k}(z)$.
+
+So, we have a convergent subsequence $(x_{n_k})$.
+
+---
+
+(3) $\implies$ (1):
+
+First wee prove the analogue of Lebesgue number lemma for a sequentially compact space $(X,d)$.
+
+Let $\{U_\alpha\}_{\alpha\in I}$ be an open covering of $X$. **By contradiction**, assume that for any $\delta>0$, there are two points $x,x'$ with $d(x,x')<\delta$ don't belong to the same open set in the covering.
+
+Take $\delta=\frac{1}{n}$, and let $x_n,x_n'$ be the points as above, then $d(x_n,x_n')<\frac{1}{n}$.
+
+$x_n,x_n'$ don't belong to the same open set in $\{U_\alpha\}_{\alpha\in I}$.
+
+By assumption $\{x_n\}$ is convergent after passing to a subsequence
+
+$$
+\{x_{n_k}\}_i
+$$
+
+Let $y$ be the limit of this subsequence and $U_\alpha$ be an element of the open covering containing $y$. There is $\epsilon>0$ such that $B_\epsilon(y)\subseteq U_\alpha$.
+
+If $k$ is large enough, then $x_{n_k}\in B_{\epsilon/2}(y)$ and $d(x_{n_k},x_{n_k}')<\epsilon/2$. (take $k$ such that $\frac{1}{n_k}<\epsilon/2$)
+
+Then $d(x_{n_k}',y)<\epsilon/2$ this implies that $x_{n_k}'\in U_\alpha$.
+
+Thus, $d(x_{n_k}',y)\leq d(x_{n_k}',x_{n_k})+d(x_{n_k},y)<\epsilon/2+\epsilon/2=\epsilon$.
+
+So, $x_{n_k}'\in B_\epsilon(y)\subseteq U_\alpha$.
+
+This is a contradiction.
+
+Next we show that for any $\epsilon$, there are
+
+$$
+y_1,y_2,\cdots,y_k
+$$
+
+such that $X=\bigcup_{i=1}^k B_{\epsilon}(y_i)$.
+
+Let's assume that it's not true and construct a sequence of points inductively in the following way:
+
+- Pick $y_1$ be arbitrary point in $X$.
+- In the $k$-th step, if $X\neq B_{\epsilon}(y_1)\cup \cdots \cup B_{\epsilon}(y_k)$, then pick $y_{k+1}\notin B_{\epsilon}(y_1)\cup \cdots \cup B_{\epsilon}(y_k)$.
+- In particular, $d(y_{k+1},y_j)\geq \epsilon$ for all $j<k$.
+
+By iteration, this process we obtain a sequence such such that the distance between any two elements is at most $\epsilon$.
+
+This sequence cannot have a converging subsequence which is a contradiction.
+
+To prove the compactness of $X$, take an open covering $\{U_\alpha\}_{\alpha\in I}$ of $X$ and let be $\delta>0$ such that any set with diameter at least $\delta$ is one of the $U_\alpha$'s. Let also $y_1,y_2,\cdots,y_k\in X$ be chosen such that $B_{\frac{\delta}{2}}(y_1)\cup \cdots \cup B_{\frac{\delta}{2}}(y_k)=X$.
+
+Since diameter of $B_{\frac{\delta}{2}}(y_i)$ is less than $\delta$, it belongs to $U_\alpha$ for some $\alpha\in I$.
+
+Then $\{U_{\alpha_i}\}_{i=1}^k$ is a finite subcover of $X$.
+
+This completes the proof.
+
+</details>