121 lines
3.3 KiB
Markdown
121 lines
3.3 KiB
Markdown
# Math4121 Lecture 29
|
|
|
|
## Continue on Measure Theory
|
|
|
|
### Lebesgue Measure
|
|
|
|
Caratheodory's criterion:
|
|
|
|
$S$ is Lebesgue measurable if for all $A\subset S$,
|
|
|
|
$$
|
|
m_e(X) = m_e(X\cap S) + m_e(X\cap S^c)
|
|
$$
|
|
|
|
Let $\mathfrak{M}$ be the collection of all Lebesgue measurable sets.
|
|
|
|
1. $\phi\in\mathfrak{M}$
|
|
2. $\mathfrak{M}$ is closed under countable unions (proved last lecture)
|
|
3. $\mathfrak{M}$ is closed under complementation ($\mathfrak{M}$ is a $\sigma$-algebra) (goal today)
|
|
|
|
> Desired properties of a measure:
|
|
>
|
|
> 1. $m(I)=\ell(I)$ for all intervals $I$
|
|
> 2. If $\{S_n\}_{n=1}^{\infty}$ is a set of pairwise disjoint Lebesgue measurable sets, then
|
|
>
|
|
> $$ m\left(\bigcup_{n=1}^{\infty}S_n\right) = \sum_{n=1}^{\infty}m(S_n)$$
|
|
> 3. If $R\subset S$, then $m(S\setminus R) = m(S) - m(R)$
|
|
|
|
Recall the Borel $\sigma$-algebra $\mathcal{B}$ was the smallest $\sigma$-algebra containing closed intervals. Therefore $\mathcal{B}\subset\mathfrak{M}$.
|
|
|
|
Towards proving $\mathfrak{M}$ is closed under countable unions:
|
|
|
|
#### Theorem 5.9 (Finite union/intersection of Lebesgue measurable sets is Lebesgue measurable)
|
|
|
|
Any finite union/intersection of Lebesgue measurable sets is Lebesgue measurable.
|
|
|
|
<details>
|
|
<summary>Proof</summary>
|
|
|
|
Suppose $S_1, S_2$ is a measurable, and we need to show that $S_1\cup S_2$ is measurable. Given $X$, need to show that
|
|
|
|
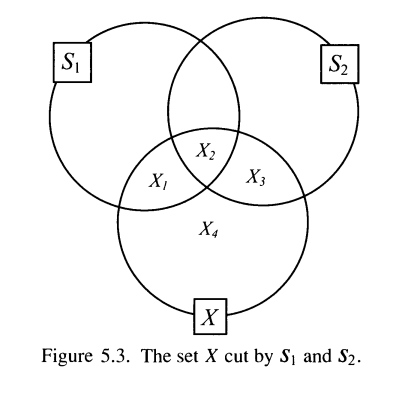
|
|
|
|
$$
|
|
m_e(X) = m_e(X_1\cup X_2\cup X_3)+ m_e(X_4)
|
|
$$
|
|
|
|
Since $S_1$ measurable, $m_e(X_1\cup X_2\cup X_3)=m_e(X_3)+m_e(X_1\cup X_2)$.
|
|
|
|
Since $S_2$ measurable, $m_e(X_3\cup X_4)=m_e(X_3)+m_e(X_4)$.
|
|
|
|
Therefore,
|
|
|
|
$$
|
|
\begin{aligned}
|
|
m_e(X) &= m_e(X_1\cup X_2\cup X_3) + m_e(X_4) \\
|
|
&= m_e(X_1\cup X_2) + m_e(X_3)+m_e(X_4) \\
|
|
&= m_e(X_1\cup X_2) + m_e(X_3\cup X_4) \\
|
|
&= m_e(X)
|
|
\end{aligned}
|
|
$$
|
|
|
|
by measurability of $S_1$ again.
|
|
|
|
</details>
|
|
|
|
#### Theorem 5.10 (Countable union/intersection of Lebesgue measurable sets is Lebesgue measurable)
|
|
|
|
Any countable union/intersection of Lebesgue measurable sets is Lebesgue measurable.
|
|
|
|
<details>
|
|
<summary>Proof</summary>
|
|
|
|
Let $\{S_j\}_{j=1}^{\infty}\subset\mathfrak{M}$. Definte $T_j=\bigcup_{k=1}^{j}S_k$ such that $T_{j-1}\subset T_j$ for all $j$.
|
|
|
|
And $U_1=T_1$, $U_j=T_j\setminus T_{j-1}$ for $j\geq 2$.
|
|
|
|
Then $\bigcup_{j=1}^{\infty}S_j=\bigcup_{j=1}^{\infty}T_j=\bigcup_{j=1}^{\infty}U_j$. Notice that $\{U_j\}_{j=1}^{\infty}$ are pairwise disjoint, and $\{T_j\}_{j=1}^{\infty}$ are monotone.
|
|
|
|
Let $X$ have finite outer measure. Since $U_n$ is measurable,
|
|
|
|
$$
|
|
\begin{aligned}
|
|
m_e(X\cap T_n) &= m_e(X\cap T_n\cap U_n)+ m_e(X\cap T_n\cap U_n^c) \\
|
|
&= m_e(X\cap U_n)+ m_e(X\cap T_{n-1}) \\
|
|
&= \sum_{j=1}^{n}m_e(X\cap U_j)
|
|
\end{aligned}
|
|
$$
|
|
|
|
Since $T_n$ is measurable and $T_n\subset S$, $S^c\subset T_n^c$. $m_e(X\cap T_n^c)\geq m_e(X\cap S^c)$.
|
|
|
|
Therefore,
|
|
|
|
$$
|
|
m_e(X)=m_e(X\cap T_n)+m_e(X\cap T_n^c)\\
|
|
\geq \sum_{j=1}^{n}m_e(X\cap U_j)+m_e(X\cap S^c)
|
|
$$
|
|
|
|
Take the limit as $n\to\infty$,
|
|
|
|
$$
|
|
\begin{aligned}
|
|
m_e(X) &\geq \sum_{j=1}^{\infty}m_e(X\cap U_j)+m_e(X\cap S^c) \\
|
|
&= m_e(\bigcup_{j=1}^{\infty}(X\cap U_j))+m_e(X\cap S^c) \\
|
|
&= m_e(X\cap S)+m_e(X\cap S^c) \\
|
|
&\geq m_e(X)
|
|
\end{aligned}
|
|
$$
|
|
|
|
Therefore, $m_e(X\cap S)=m_e(X)$.
|
|
|
|
Therefore, $S$ is measurable.
|
|
|
|
</details>
|
|
|
|
#### Corollary from the proof
|
|
|
|
Every open or closed set is Lebesgue measurable.
|
|
|
|
(Every open set is a countable union of disjoint open intervals)
|