NoteNextra-origin/content/Math416/Exam_reviews/Math416_E1.md

Math 416 Midterm 1 Review

So everything we have learned so far is to extend the real line to the complex plane.

Chapter 0 Calculus on Real values

Differentiation

Let f,g be function on real line and c be a real number.

\frac{d}{dx}(f+g)=f'+g'

\frac{d}{dx}(cf)=cf'

\frac{d}{dx}(fg)=f'g+fg'

\frac{d}{dx}(f/g)=(f'g-fg')/g^2

\frac{d}{dx}(f\circ g)=(f'\circ g)\frac{d}{dx}g

\frac{d}{dx}x^n=nx^{n-1}

\frac{d}{dx}e^x=e^x

\frac{d}{dx}\ln x=\frac{1}{x}

\frac{d}{dx}\sin x=\cos x

\frac{d}{dx}\cos x=-\sin x

\frac{d}{dx}\tan x=\sec^2 x

\frac{d}{dx}\sec x=\sec x\tan x

\frac{d}{dx}\csc x=-\csc x\cot x

\frac{d}{dx}\sinh x=\cosh x

\frac{d}{dx}\cosh x=\sinh x

\frac{d}{dx}\tanh x=\operatorname{sech}^2 x

\frac{d}{dx}\operatorname{sech} x=-\operatorname{sech}x\tanh x

\frac{d}{dx}\operatorname{csch} x=-\operatorname{csch}x\coth x

\frac{d}{dx}\coth x=-\operatorname{csch}^2 x

\frac{d}{dx}\arcsin x=\frac{1}{\sqrt{1-x^2}}

\frac{d}{dx}\arccos x=-\frac{1}{\sqrt{1-x^2}}

\frac{d}{dx}\arctan x=\frac{1}{1+x^2}

\frac{d}{dx}\operatorname{arccot} x=-\frac{1}{1+x^2}

\frac{d}{dx}\operatorname{arcsec} x=\frac{1}{x\sqrt{x^2-1}}

\frac{d}{dx}\operatorname{arccsc} x=-\frac{1}{x\sqrt{x^2-1}}

Integration

Let f,g be function on real line and c be a real number.

\int (f+g)dx=\int fdx+\int gdx

\int cfdx=c\int fdx

\int e^x dx=e^x

\int \ln x dx=x\ln x-x

\int \frac{1}{x} dx=\ln|x|

\int \sin x dx=-\cos x

\int \cos x dx=\sin x

\int \tan x dx=-\ln|\cos x|

\int \cot x dx=\ln|\sin x|

\int \sec x dx=\ln|\sec x+\tan x|

\int \csc x dx=\ln|\csc x-\cot x|

\int \sinh x dx=\cosh x

\int \cosh x dx=\sinh x

\int \tanh x dx=\ln|\cosh x|

\int \coth x dx=\ln|\sinh x|

\int \operatorname{sech} x dx=2\arctan(\tanh(x/2))

\int \operatorname{csch} x dx=\ln|\coth x-\operatorname{csch} x|

\int \operatorname{sech}^2 x dx=\tanh x

\int \operatorname{csch}^2 x dx=-\coth x

\int \frac{1}{1+x^2} dx=\arctan x

\int \frac{1}{x^2+1} dx=\arctan x

\int \frac{1}{x^2-1} dx=\frac{1}{2}\ln|\frac{x-1}{x+1}|

\int \frac{1}{x^2-a^2} dx=\frac{1}{2a}\ln|\frac{x-a}{x+a}|

\int \frac{1}{x^2+a^2} dx=\frac{1}{a}\arctan(\frac{x}{a})

\int \frac{1}{\sqrt{x^2-a^2}} dx=\ln|x+\sqrt{x^2-a^2}|

\int \frac{1}{\sqrt{x^2+a^2}} dx=\ln|x+\sqrt{x^2+a^2}|

Chapter 1 Complex Numbers

Definition of complex numbers

An ordered pair of real numbers (x, y) can be represented as a complex number z = x + yi, where i is the imaginary unit.

With operations defined as:

(x_1 + y_1i) + (x_2 + y_2i) = (x_1 + x_2) + (y_1 + y_2)i

(x_1 + y_1i) \cdot (x_2 + y_2i) = (x_1x_2 - y_1y_2) + (x_1y_2 + x_2y_1)i

Modulus

The modulus of a complex number z = x + yi is defined as

|z| = \sqrt{x^2 + y^2}=|z\overline{z}|

De Moivre's Formula

Every complex number z can be written as z = r(\cos \theta + i \sin \theta), where r is the magnitude of z and \theta is the argument of z.

z^n = r^n(\cos n\theta + i \sin n\theta)

The De Moivre's formula is useful for finding the $n$th roots of a complex number.

z^n = r^n(\cos n\theta + i \sin n\theta)

Roots of complex numbers

Using De Moivre's formula, we can find the $n$th roots of a complex number.

If z=r(\cos \theta + i \sin \theta), then the $n$th roots of z are given by:

z_k = r^{1/n}(\cos \frac{\theta + 2k\pi}{n} + i \sin \frac{\theta + 2k\pi}{n})

for k = 0, 1, 2, \ldots, n-1.

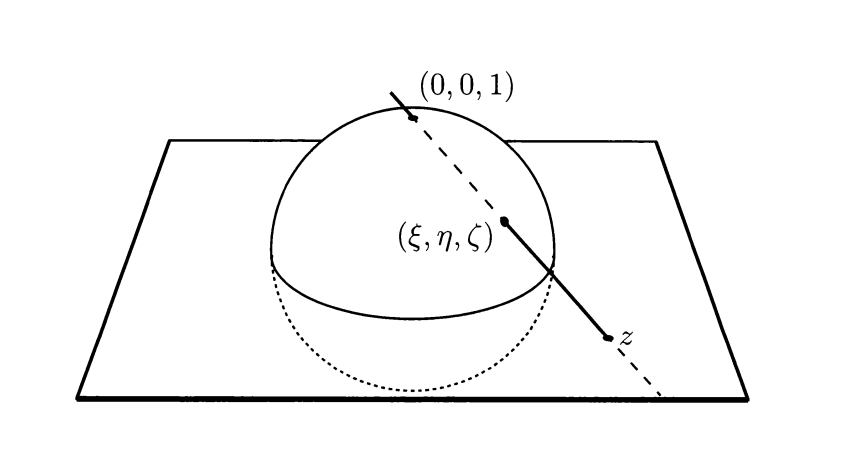
Stereographic projection

The stereographic projection is a map from the unit sphere S^2 to the complex plane \mathbb{C}\setminus\{0\}.

The projection is given by:

z\mapsto \frac{(2Re(z), 2Im(z), |z|^2-1)}{|z|^2+1}

The inverse map is given by:

(\xi,\eta, \zeta)\mapsto \frac{\xi + i\eta}{1 - \zeta}

Chapter 2 Complex Differentiation

Definition of complex differentiation

Let the complex plane \mathbb{C} be defined in an open subset G of \mathbb{C}. (Domain)

Then f is said to be differentiable at z_0\in G if the limit

\lim_{z\to z_0} \frac{f(z)-f(z_0)}{z-z_0}

exists.

The limit is called the derivative of f at z_0 and is denoted by f'(z_0).

To prove that a function is differentiable, we can use the standard delta-epsilon definition of a limit.

\left|\frac{f(z)-f(z_0)}{z-z_0} - f'(z_0)\right| < \epsilon

whenever 0 < |z-z_0| < \delta.

With such definition, all the properties of real differentiation can be extended to complex differentiation.

Differentiation of complex functions

1. If f is differentiable at z_0, then f is continuous at z_0.
2. If f,g are differentiable at z_0, then f+g, fg are differentiable at z_0.

   
   (f+g)'(z_0) = f'(z_0) + g'(z_0)
   

   
   (fg)'(z_0) = f'(z_0)g(z_0) + f(z_0)g'(z_0)
   

3. If f,g are differentiable at z_0 and g(z_0)\neq 0, then f/g is differentiable at z_0.

   
   \left(\frac{f}{g}\right)'(z_0) = \frac{f'(z_0)g(z_0) - f(z_0)g'(z_0)}{g(z_0)^2}
   

4. If f is differentiable at z_0 and g is differentiable at f(z_0), then g\circ f is differentiable at z_0.

   
   (g\circ f)'(z_0) = g'(f(z_0))f'(z_0)
   

5. If f(z)=\sum_{k=0}^n c_k(z-z_0)^k, where c_k\in\mathbb{C}, then f is differentiable at z_0 and f'(z_0)=\sum_{k=1}^n kc_k(z_0-z_0)^{k-1}.

   
   f'(z_0) = c_1 + 2c_2(z_0-z_0) + 3c_3(z_0-z_0)^2 + \cdots + nc_n(z_0-z_0)^{n-1}
   

Cauchy-Riemann Equations

Let the function defined on an open subset G of \mathbb{C} be f(x,y)=u(x,y)+iv(x,y), where u,v are real-valued functions.

Then f is differentiable at z_0=x_0+y_0i if and only if the partial derivatives of u and v exist at (x_0,y_0) and satisfy the Cauchy-Riemann equations:

\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y}, \quad \frac{\partial u}{\partial y} = -\frac{\partial v}{\partial x}

On the polar form, the Cauchy-Riemann equations are

r\frac{\partial u}{\partial r} = \frac{\partial v}{\partial \theta}, \quad \frac{\partial u}{\partial \theta} = -r\frac{\partial v}{\partial r}

Holomorphic functions

A function f is said to be holomorphic on an open subset G of \mathbb{C} if f is differentiable at every point of G.

Partial differential operators

\frac{\partial}{\partial z} = \frac{1}{2}\left(\frac{\partial}{\partial x} - i\frac{\partial}{\partial y}\right)

\frac{\partial}{\partial \bar{z}} = \frac{1}{2}\left(\frac{\partial}{\partial x} + i\frac{\partial}{\partial y}\right)

This gives that

\frac{\partial f}{\partial z} = \frac{1}{2}\left(\frac{\partial f}{\partial x} - i\frac{\partial f}{\partial y}\right)=\frac{1}{2}\left(\frac{\partial u}{\partial x} +\frac{\partial v}{\partial y}\right) + \frac{i}{2}\left(\frac{\partial v}{\partial x} - \frac{\partial u}{\partial y}\right)

\frac{\partial f}{\partial \bar{z}} = \frac{1}{2}\left(\frac{\partial f}{\partial x} + i\frac{\partial f}{\partial y}\right)=\frac{1}{2}\left(\frac{\partial u}{\partial x} - \frac{\partial v}{\partial y}\right) + \frac{i}{2}\left(\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}\right)

If the function f is holomorphic, then by the Cauchy-Riemann equations, we have

\frac{\partial f}{\partial \bar{z}} = 0

Conformal mappings

A holomorphic function f is said to be conformal if it preserves the angles between the curves. More formally, if f is holomorphic on an open subset G of \mathbb{C} and z_0\in G, \gamma_1, \gamma_2 are two curves passing through z_0 (\gamma_1(t_1)=\gamma_2(t_2)=z_0) and intersecting at an angle \theta, then

\arg(f\circ\gamma_1)'(t_1) - \arg(f\circ\gamma_2)'(t_2) = \theta

In other words, the angle between the curves is preserved.

An immediate consequence is that

\arg(f\cdot \gamma_1)'(t_1) =\arg f'(z_0) + \arg \gamma_1'(t_1)\\
\arg(f\cdot \gamma_2)'(t_2) =\arg f'(z_0) + \arg \gamma_2'(t_2)

Harmonic functions

A real-valued function u is said to be harmonic if it satisfies the Laplace equation:

\frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = 0

Chapter 3 Linear Fractional Transformations

Definition of linear fractional transformations

A linear fractional transformation is a function of the form

\phi(z) = \frac{az+b}{cz+d}

where a,b,c,d are complex numbers and ad-bc\neq 0.

Properties of linear fractional transformations

Matrix form

A linear fractional transformation can be written as a matrix multiplication:

\phi(z) = \begin{bmatrix}
a & b\\
c & d\\
\end{bmatrix}
\begin{bmatrix}
z\\
1\\
\end{bmatrix}

Conformality

A linear fractional transformation is conformal.

\phi'(z) = \frac{ad-bc}{(cz+d)^2}

Three-fold transitivity

If z_1,z_2,z_3 are distinct points in the complex plane, then there exists a unique linear fractional transformation \phi such that \phi(z_1)=\infty, \phi(z_2)=0, \phi(z_3)=1.

The map is given by

\phi(z) =\begin{cases}
\frac{(z-z_2)(z_1-z_3)}{(z-z_1)(z_2-z_3)} & \text{if } z_1,z_2,z_3 \text{ are all finite}\\
\frac{z-z_2}{z_3-z_2} & \text{if } z_1=\infty\\
\frac{z_3-z_1}{z-z_1} & \text{if } z_2=\infty\\
\frac{z-z_2}{z-z_1} & \text{if } z_3=\infty\\
\end{cases}

So if z_1,z_2,z_3, w_1,w_2,w_3 are distinct points in the complex plane, then there exists a unique linear fractional transformation \phi such that \phi(z_i)=w_i for i=1,2,3.

Factorization

Every linear fractional transformation can be written as a composition of homothetic mappings, translations, inversions, and multiplications.

If \phi(z)=\frac{az+b}{cz+d}, then

\phi(z) = \frac{b-ad/c}{cz+d}+\frac{a}{c}

Clircle

A linear-fractional transformation maps circles and lines to circles and lines.

Chapter 4 Elementary Functions

Exponential function

The exponential function is defined as

e^z = \sum_{n=0}^\infty \frac{z^n}{n!}

Let z=x+iy, then

\begin{aligned}
e^z &= e^{x+iy}\\
&= e^x e^{iy}\\
&= e^x\sum_{n=0}^\infty \frac{(iy)^n}{n!}\\
&= e^x\sum_{n=0}^\infty \frac{(-1)^n y^{2n}}{(2n)!} + i \sum_{n=0}^\infty \frac{(-1)^n y^{2n+1}}{(2n+1)!}\\
&= e^x(\cos y + i\sin y)\\
\end{aligned}

So we can rewrite the polar form of a complex number as

z = r(\cos \theta + i\sin \theta) = re^{i\theta}

e^x is holomorphic

Let f(z)=e^z, then u(x,y)=e^x\cos y, v(x,y)=e^x\sin y.

\frac{\partial u}{\partial x} = e^x\cos y = \frac{\partial v}{\partial y}\\
\frac{\partial u}{\partial y} = -e^x\sin y = -\frac{\partial v}{\partial x}

Trigonometric functions

\sin z = \frac{e^{iz}-e^{-iz}}{2i}, \quad \cos z = \frac{e^{iz}+e^{-iz}}{2}, \quad \tan z = \frac{\sin z}{\cos z}

\sec z = \frac{1}{\cos z}, \quad \csc z = \frac{1}{\sin z}, \quad \cot z = \frac{1}{\tan z}

Hyperbolic functions

\sinh z = \frac{e^z-e^{-z}}{2}, \quad \cosh z = \frac{e^z+e^{-z}}{2}, \quad \tanh z = \frac{\sinh z}{\cosh z}

\operatorname{sech} z = \frac{1}{\cosh z}, \quad \operatorname{csch} z = \frac{1}{\sinh z}, \quad \operatorname{coth} z = \frac{1}{\tanh z}

Logarithmic function

The logarithmic function is defined as

\ln z=\{w\in\mathbb{C}: e^w=z\}

Properties of the logarithmic function

Let z=x+iy, then

|e^z|=\sqrt{e^x(\cos y)^2+(\sin y)^2}=e^x

So we have

\log z = \ln |z| + i\arg z

Power function

For any two complex numbers a,b, we can define the power function as

a^b = e^{b\log a}

Example:

i^i=e^{i\ln i}=e^{i(\ln 1+i\frac{\pi}{2})}=e^{-\frac{\pi}{2}} e^{i\pi}=-1

Chapter 5 Power Series

Definition of power series

A power series is a series of the form

\sum_{n=0}^\infty a_n (z-z_0)^n

Properties of power series

Geometric series

\sum_{n=0}^\infty z^n = \frac{1}{1-z}, \quad |z|<1

Radius/Region of convergence

The radius of convergence of a power series is the largest number R such that the series converges for all z with |z-z_0|<R.

The region of convergence of a power series is the set of all points z such that the series converges.

Cauchy-Hadamard Theorem

The radius of convergence of a power series is given by

R=\frac{1}{\limsup_{n\to\infty} |a_n|^{1/n}}

Derivative of power series

The derivative of a power series is given by

f'(z)=\sum_{n=1}^\infty n a_n (z-z_0)^{n-1}

Cauchy Product (of power series)

Let \sum_{n=0}^\infty a_n (z-z_0)^n and \sum_{n=0}^\infty b_n (z-z_0)^n be two power series with radius of convergence R_1 and R_2 respectively.

Then the Cauchy product of the two series is given by

\sum_{n=0}^\infty c_n (z-z_0)^n

where

c_n = \sum_{k=0}^n a_k b_{n-k}

The radius of convergence of the Cauchy product is at least \min(R_1,R_2).

Chapter 6 Complex Integration

Definition of Riemann Integral for complex functions

The complex integral of a complex function \phi on the closed subinterval [a,b] of the real line is said to be piecewise continuous if there exists a partition a=t_0<t_1<\cdots<t_n=b such that \phi is continuous on each open interval (t_{i-1},t_i) and has a finite limit at each discontinuity point of the closed interval [a,b].

If \phi is piecewise continuous on [a,b], then the complex integral of \phi on [a,b] is defined as

\int_a^b \phi(t) dt = \int_a^b \operatorname{Re}\phi(t) dt + i\int_a^b \operatorname{Im}\phi(t) dt

Fundamental Theorem of Calculus

If \phi is piecewise continuous on [a,b], then

\int_a^b \phi'(t) dt = \phi(b)-\phi(a)

Triangle inequality

\left|\int_a^b \phi(t) dt\right| \leq \int_a^b |\phi(t)| dt

Integral on curve

Let \gamma be a piecewise smooth curve in the complex plane.

The integral of a complex function f on \gamma is defined as

\int_\gamma f(z) dz = \int_a^b f(\gamma(t))\gamma'(t) dt

Favorite estimate

Let \gamma:[a,b]\to\mathbb{C} be a piecewise smooth curve, and let f:[a,b]\to\mathbb{C} be a continuous complex-valued function. Let M be a real number such that |f(z)|\leq M for all z\in\gamma. Then

\left|\int_\gamma f(z) dz\right| \leq M\ell(\gamma)

where \ell(\gamma) is the length of the curve \gamma.

Chapter 7 Cauchy's Theorem

Cauchy's Theorem

Let \gamma be a closed curve in \mathbb{C} and U be a simply connected open subset of \mathbb{C} containing \gamma and its interior. Let f be a holomorphic function on U. Then

\int_\gamma f(z) dz = 0

Cauchy's Formula for a Circle

Let C be a counterclockwise oriented circle and let f be holomorphic function defined in an open set containing C and its interior. Then for any z in the interior of C,

f(z)=\frac{1}{2\pi i}\int_C \frac{f(\zeta)}{\zeta-z} d\zeta

Mean Value Property

Let the function f be holomorphic on a disk |z-z_0|<R. Then for any 0<r<R, let C_r denote the circle with center z_0 and radius r. Then

f(z_0)=\frac{1}{2\pi}\int_0^{2\pi} f(z_0+re^{i\theta}) d\theta

The value of the function at the center of the disk is the average of the values of the function on the boundary of the disk.

Cauchy Integrals

Let \gamma be a piecewise smooth curve in \mathbb{C} and let \phi be a continuous complex-valued function on \gamma. Then the Cauchy integral of \phi on \gamma is the function f defined in C\setminus\gamma by

f(z)=\int_\gamma \frac{\phi(\zeta)}{\zeta-z} d\zeta

Cauchy Integral Formula for circle C_r:

f(z)=\frac{1}{2\pi i}\int_{C_r} \frac{f(\zeta)}{\zeta-z} d\zeta

Example:

Evaluate \int_{|z|=2} \frac{z}{z-1} dz

Note that if we let f(\zeta)=\zeta and z=1 is inside the circle, then we can use Cauchy Integral Formula for circle C_r to evaluate the integral.

So we have

\int_{|z|=2} \frac{z}{z-1} dz = 2\pi i f(1) = 2\pi i

General Cauchy Integral Formula for circle C_r:

f^{(n)}(z)=\frac{n!}{2\pi i}\int_{C_r} \frac{f(\zeta)}{(\zeta-z)^{n+1}} d\zeta

Example:

Evaluate \int_{C}\frac{\sin z}{z^{38}}dz

Note that if we let f(\zeta)=\sin \zeta and z=0 is inside the circle, then we can use General Cauchy Integral Formula for circle C_r to evaluate the integral.

So we have

\int_{C}\frac{\sin z}{z^{38}}dz = \frac{2\pi i}{37!} f^{(37)}(0) = \frac{2\pi i}{37!} \sin ^{(37)}(0)

Note that $\sin ^{(n)}(0)=\begin{cases} 0,& n\equiv 0 \pmod{4}\ 1,& n\equiv 1 \pmod{4}\ 0,& n\equiv 2 \pmod{4}\ -1,& n\equiv 3 \pmod{4} \end{cases}$

So we have

\int_{C}\frac{\sin z}{z^{38}}dz = \frac{2\pi i}{37!} \sin ^{(37)}(0) = \frac{2\pi i}{37!} \cdot 1 = \frac{2\pi i}{37!}

Cauchy integral is a easier way to evaluate the integral.

Liouville's Theorem

If a function f is entire (holomorphic on \mathbb{C}) and bounded, then f is constant.

Finding power series of holomorphic functions

If f is holomorphic on a disk |z-z_0|<R, then f can be represented as a power series on the disk.

where a_n=\frac{f^{(n)}(z_0)}{n!}

Example:

If q(z)=(z-1)(z-2)(z-3), find the power series of q(z) centered at z=0.

Note that q(z) is holomorphic on \mathbb{C} and q(z)=0 at z=1,2,3.

So we can use the power series of q(z) centered at z=1.

To solve this, we can simply expand q(z)=(z-1)(z-2)(z-3) and get q(z)=z^3-6z^2+11z-6.

So we have a_0=q(1)=-6, a_1=q'(1)=3z^2-12z+11=11, a_2=\frac{q''(1)}{2!}=\frac{6z-12}{2}=-3, a_3=\frac{q'''(1)}{3!}=\frac{6}{6}=1.

So the power series of q(z) centered at z=1 is

q(z)=-6+11(z-1)-3(z-1)^2+(z-1)^3

Fundamental Theorem of Algebra

Every non-constant polynomial with complex coefficients has a root in \mathbb{C}.

Can be factored into linear factors:

p(z)=a_n(z-z_1)(z-z_2)\cdots(z-z_n)

We can treat holomorphic functions as polynomials.

f has zero of order m at z_0 if and only if f(z)=(z-z_0)^m g(z) for some holomorphic g(z) and g(z_0)\neq 0.

Zeros of holomorphic functions

If f is holomorphic on a disk |z-z_0|<R and f has a zero of order m at z_0, then f(z_0)=0, f'(z_0)=0, f''(z_0)=0, \cdots, f^{(m-1)}(z_0)=0 and f^{(m)}(z_0)\neq 0.

And there exists a holomorphic function g on the disk such that f(z)=(z-z_0)^m g(z) and g(z_0)\neq 0.

Example:

Find zeros of f(z)=\cos(z\frac{\pi}{2})

Note that f(z)=0 if and only if z\frac{\pi}{2}=(2k+1)\frac{\pi}{2} for some integer k.

So the zeros of f(z) are z=(2k+1) for some integer k.

The order of the zero is 1 since f'(z)=-\frac{\pi}{2}\sin(z\frac{\pi}{2}) and f'(z)\neq 0 for all z=(2k+1).

If f vanishes to infinite order at z_0 (that is, f(z_0)=f'(z_0)=f''(z_0)=\cdots=0), then f(z)\equiv 0 on the connected open set U containing z_0.

Identity Theorem

If f and g are holomorphic on a connected open set U\subset\mathbb{C} and f(z)=g(z) for all z in a subset of U that has a limit point in U, then f(z)=g(z) for all z\in U.

Key: consider h(z)=f(z)-g(z), prove h(z)\equiv 0 on U by applying the zero of holomorphic function.

Weierstrass Theorem

Limit of a sequence of holomorphic functions is holomorphic.

Let f_n be a sequence of holomorphic functions on a domain D\subset\mathbb{C} that converges uniformly to f on every compact subset of D. Then f is holomorphic on D.

Maximum Modulus Principle

If f is a non-constant holomorphic function on a domain D\subset\mathbb{C}, then |f| does not attain a maximum value in D.

Corollary: Minimum Modulus Principle

If f is a non-constant holomorphic function on a domain D\subset\mathbb{C}, then \frac{1}{f} does not attain a minimum value in D.

Schwarz Lemma

If f is a holomorphic function on the unit disk |z|<1 and |f(z)|\leq |z|, then |f'(0)|\leq 1.