170 lines
5.0 KiB
Markdown
170 lines
5.0 KiB
Markdown
# Math416 Lecture 11
|
|
|
|
## Continue on integration over complex plane
|
|
|
|
### Continue on last example
|
|
|
|
Last lecture we have:Let $R$ be a rectangular start from the $-a$ to $a$, $a+ib$ to $-a+ib$, $\int_{R} e^{-z^2}dz=0$, however, the integral consists of four parts:
|
|
|
|
Path 1: $-a\to a$
|
|
|
|
$\int_{I_1}e^{-z^2}dz=\int_{-a}^{a}e^{-z^2}dz=\int_{-a}^{a}e^{-x^2}dx$
|
|
|
|
Path 2: $a+ib\to -a+ib$
|
|
|
|
$\int_{I_2}e^{-z^2}dz=\int_{a+ib}^{-a+ib}e^{-z^2}dz=\int_{0}^{b}e^{-(a+iy)^2}dy$
|
|
|
|
Path 3: $-a+ib\to -a-ib$
|
|
|
|
$-\int_{I_3}e^{-z^2}dz=-\int_{-a+ib}^{-a-ib}e^{-z^2}dz=-\int_{a}^{-a}e^{-(x-ib)^2}dx$
|
|
|
|
Path 4: $-a-ib\to a-ib$
|
|
|
|
$-\int_{I_4}e^{-z^2}dz=-\int_{-a-ib}^{a-ib}e^{-z^2}dz=-\int_{b}^{0}e^{-(-a+iy)^2}dy$
|
|
|
|
> #### The reverse of a curve 6.9
|
|
>
|
|
> If $\gamma:[a,b]\to\mathbb{C}$ is a curve, then the rever of $\gamma$ is the curve $-\gamma:[-b,-a]\to\mathbb{C}$ defined by $(-\gamma)(t)=\gamma(a+b-t)$. It is the curve one obtains from $\gamma$ by traversing it in the opposite direction.
|
|
>
|
|
> - If $\gamma$ is piecewise in $C^1$, then $-\gamma$ is piecewise in $C^1$.
|
|
> - $\int_{-\gamma}f(z)dz=-\int_{\gamma}f(z)dz$ for any function $f$ that is continuous on $\gamma([a,b])$.
|
|
|
|
If we keep $b$ fixed, and let $a\to\infty$, then
|
|
|
|
> #### Definition 6.10 (Estimate of the integral)
|
|
>
|
|
> Let $\gamma:[a,b]\to\mathbb{C}$ be a piecewise $C^1$ curve, and let $f:[a,b]\to\mathbb{C}$ be a continuous complex-valued function. Let $M$ be the maximum of $|f|$ on $\gamma([a,b])$. ($M=\max\{|f(t)|:t\in[a,b]\}$)
|
|
>
|
|
> Then
|
|
>
|
|
> $$\left|\int_{\gamma}f(z)dz\right|\leq L(\gamma)M$$
|
|
|
|
_Continue on previous example, we have:_
|
|
|
|
$$
|
|
\left|\int_{\gamma}f(z)dz\right|\leq L(\gamma)\max_{z\in\gamma}|f(z)|\to 0
|
|
$$
|
|
|
|
Since,
|
|
|
|
$$
|
|
\int_{-\infty}^{\infty}e^{-x^2}dx-\int_{-\infty}^{\infty}e^{-x^2+b^2}(\cos 2bx+i\sin 2bx)dx=0
|
|
$$
|
|
|
|
Since $\sin 2bx$ is odd, and $\cos 2bx$ is even, we have
|
|
|
|
$$
|
|
\int_{-\infty}^{\infty}e^{-x^2}dx=\int_{-\infty}^{\infty}e^{-x^2+b^2}\cos 2bxdx=\sqrt{\pi}e^{-b^2}
|
|
$$
|
|
|
|
##### Proof for the last step:
|
|
|
|
$$
|
|
\int_{-\infty}^{\infty}e^{-x^2}dx=\sqrt{\pi}
|
|
$$
|
|
|
|
Proof:
|
|
|
|
Let $J=\int_{-\infty}^{\infty}e^{-x^2}dx$
|
|
|
|
Then
|
|
|
|
$$J^2=\int_{-\infty}^{\infty}e^{-x^2}dx\int_{-\infty}^{\infty}e^{-y^2}dy=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}e^{-(x^2+y^2)}dxdy$$
|
|
|
|
We can evaluate the integral on the right-hand side by converting to polar coordinates. $x=r\cos\theta$, $y=r\sin\theta,dxdy=rdrd\theta$
|
|
|
|
$$
|
|
J^2=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}e^{-(x^2+y^2)}dxdy=\int_{0}^{2\pi}\int_{0}^{\infty}e^{-r^2}rdrd\theta
|
|
$$
|
|
|
|
$$
|
|
J^2=\int_{0}^{2\pi}\int_{0}^{\infty}e^{-r^2}rdrd\theta=\int_{0}^{2\pi}\left[-\frac{1}{2}e^{-r^2}\right]_{0}^{\infty}d\theta
|
|
$$
|
|
|
|
$$
|
|
J^2=\int_{0}^{2\pi}\frac{1}{2}d\theta=\pi
|
|
$$
|
|
|
|
$$
|
|
J=\sqrt{\pi}
|
|
$$
|
|
|
|
QED
|
|
|
|
## Chapter 7 Cauchy's theorem
|
|
|
|
### Cauchy's theorem (Fundamental theorem of complex function theory)
|
|
|
|
Let $\gamma$ be a closed curve in $\mathbb{C}$ and let $u$ be an open set _containing $\gamma^*$_. Let $f$ be a holomorphic function on $u$. Then
|
|
|
|
$$
|
|
\int_{\gamma}f(z)dz=0
|
|
$$
|
|
|
|
Note: What "containing $\gamma^*$" means? (Rabbit hole for topologists)
|
|
|
|
#### Lemma 7.1 (Goursat's lemma)
|
|
|
|
Cauchy's theorem is true if $\gamma$ is a triangle.
|
|
|
|
Proof:
|
|
|
|
We plan to keep shrinking the triangle until $f(z+h)=f(z)+hf'(z)+\epsilon(h)$ where $\epsilon(h)$ is a function of $h$ that goes to $0$ as $h\to 0$.
|
|
|
|
Let's start with a triangle $T$ with vertices $z_1,z_2,z_3$.
|
|
|
|
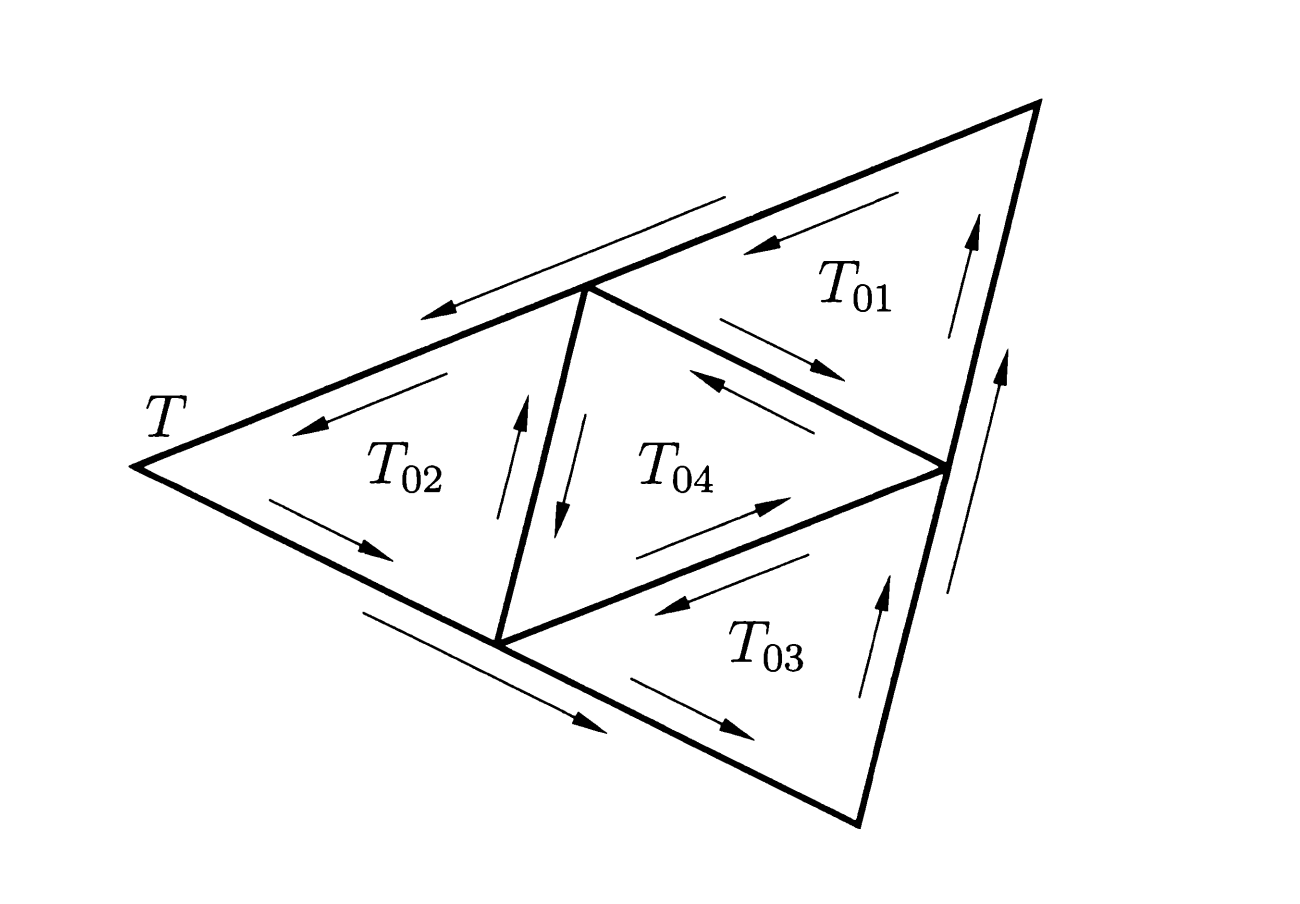
|
|
|
|
We divide $T$ into four smaller triangles by drawing lines from the midpoints of the sides to the opposite vertices.
|
|
|
|
Let $R_1,\ldots,R_4$ be the four smaller triangles.
|
|
|
|
For one $R_j$, $\left|\int_{R_j}f(z)dz\right|\geq\frac{1}{4}|I|$, we choose it then call it $T_1$.
|
|
|
|
There exists $T_1$ such that $\left|\int_{T_1}f(z)dz\right|\geq\frac{1}{4}|I|$.
|
|
|
|
Since $L(T_1)=\frac{1}{2}L(T)$, we iterate after $n$ steps, get a triangle $T_n$ such that $L(T_n)=\frac{L(T)}{2^n}$ and $\left|\int_{T_n}f(z)dz\right|\geq\frac{1}{4^n}|I|$.
|
|
|
|
Since $K_n=T_n\cup \text{interior}(T_n)$ is compact, we can find $K_n+1\subset K_n$ and $diam(K_n+1)<\frac{1}{2}diam(K_n)$. $diam(K_n)\to 0$ as $n\to\infty$. (Using completeness theorem)
|
|
|
|
Since $f$ is holomorphic on $u$, $\lim_{z\to z_0}\frac{f(z)-f(z_0)}{z-z_0}=f'(z_0)$ exists.
|
|
|
|
So $f(z)=f(z_0)+f'(z_0)(z-z_0)+R(z)$, we have
|
|
|
|
$$
|
|
\int_{T_n}f(z)dz=\int_{T_n}f(z_0)dz+\int_{T_n}f'(z_0)(z-z_0)dz+\int_{T_n}R(z)dz
|
|
$$
|
|
|
|
since $f(z_0)dz+\int_{T_n}f'(z_0)(z-z_0)$ is in form of Cauchy integral formula, we have
|
|
|
|
$$
|
|
\int_{T_n}f(z_0)dz+\int_{T_n}f'(z_0)(z-z_0)dz=0
|
|
$$
|
|
|
|
Let $e_n=\max\{\frac{R(z)}{z-z_0}:z_0\in T_n\}$
|
|
|
|
Since $diam(K_n)\to 0$ as $n\to\infty$, we have $e_n\to 0$ as $n\to\infty$.
|
|
|
|
So
|
|
|
|
$$
|
|
\begin{aligned}
|
|
|I|&\leq 4^n\left|\int_{T_n}f(z)dz\right|\\
|
|
&\leq 4^n\left|\int_{T_n}R_n(z)dz\right|\\
|
|
&\leq 4^n\cdot L(T_n)\cdot \max_{z\in T_n}|R_n(z)|\\
|
|
&\leq 4^n\cdot \frac{L(T_0)}{2^n}\cdot e_n L(T_n)\\
|
|
&\leq 4^n\cdot \frac{L(T_0)}{2^n}\cdot e_n\cdot \frac{L(T_0)}{2^n}\\
|
|
&\leq e_n\cdot L(T_0)^2
|
|
\end{aligned}
|
|
$$
|
|
|
|
Since $e_n\to 0$ as $n\to\infty$, we have $I\to 0$ as $n\to\infty$.
|
|
|
|
So
|
|
|
|
$$
|
|
\int_{T_n}f(z)dz\to 0
|
|
$$
|
|
|
|
QED
|