NoteNextra-origin/content/CSE510/CSE510_L10.md

# CSE510 Deep Reinforcement Learning (Lecture 10)

## Deep Q-network (DQN)

Network input = Observation history

- Window of previous screen shots in Atari

Network output = One output node per action (returns Q-value)

### Stability issues of DQN

Naïve Q-learning oscillates or diverges with neural nets

Data is sequential and successive samples are correlated (time-correlated)

- Correlations present in the sequence of observations
- Correlations between the estimated value and the target values
- Forget previous experiences and overfit similar correlated samples

Policy changes rapidly with slight changes to Q-values

- Policy may oscillate
- Distribution of data can swing from one extreme to another

Scale of rewards and Q-values is unknown

- Gradients can be unstable when back-propagated

### Deadly Triad in Reinforcement Learning

Off-policy learning

- (learning the expected reward changes of policy change instead of the optimal policy)

Function approximation

- (usually with supervised learning)
- $Q(s,a)\gets f_\theta(s,a)$

Bootstrapping

- (self-reference, update new function from itself)
- $Q(s,a)\gets r(s,a)+\gamma \max_{a'\in A} Q(s',a')$

### Stable Solutions for DQN

DQN provides a stable solution to deep value-based RL

1. Experience replay
2. Freeze target Q-network
3. Clip rewards to sensible range

#### Experience replay

To remove correlations, build dataset from agent's experience

- Take action $a_t$
- Store transition $(s_t, a_t, r_t, s_{t+1})$ in replay memory $D$
- Sample random mini-batch of transitions $(s,a,r,s')$ from replay memory $D$
- Optimize Mean Squared Error between Q-network and Q-learning target

$$
L_i(\theta_i) = \mathbb{E}_{(s,a,r,s') \sim U(D)} \left[ \left( r+\gamma \max_{a'\in A} Q(s',a';\theta_i^-)-Q(s,a;\theta_i) \right)^2 \right]
$$

Here $U(D)$ is the uniform distribution over the replay memory $D$.

#### Fixed Target Q-Network

To avoid oscillations, fix parameters used in Q- learning target

- Compute Q-learning target w.r.t old, fixed parameters
- Optimize MSE between Q-learning targets and Q-network
- Periodically update target Q-network parameters

#### Reward/Value Range

- To limit impact of any one update, control the reward / value range
- DQN clips the rewards to $[-1, +1]$
  - Prevents too large Q-values
  - Ensures gradients are well-conditioned

### DQN Implementation

#### Preprocessing

- Raw images: $210\times 160$ pixel images with 128-color palette
- Rescaled images: $84\times 84$
- Input: $84\times 84\times 4$ (4 most recent frames)

#### Training

DQN source code:
sites.google.com/a/deepmind.com/

- 49 Atari 2600 games
- Use RMSProp algorithms with minibatches 32
- Use 50 million frames (38 days)
- Replay memory contains 1 million recent frames
- Agent select actions on every 4th frames 

#### Evaluation

- Agent plays each games 30 times for 5 min with random initial conditions
- Human plays the games in the same scenarios
- Random agent play in the same scenarios to obtain baseline performance 

### DeepMind Atari

Beat human players in 49 out of 49 games

Strengths:

- Quick-moving, short-horizon games
- Pinball (2539%)

Weakness:

- Long-horizon games that do not converge
- Walk-around games
- Montezuma’s revenge

### DQN Summary

- Deep Q-network agent can learn successful policies directly from high-dimensional input using end-to-end reinforcement learning

- The algorithm achieve a level surpassing professional human games tester across 49 games

## Extensions of DQN

- Double Q-learning for fighting maximization bias
- Prioritized experience replay
- Dueling Q networks
- Multistep returns
- Distributed DQN

### Double Q-learning for fighting maximization bias

#### Maximization Bias for Q-learning

![Maximization Bias of Q-learning](https://notenextra.trance-0.com/CSE510/Maximization_bias_of_Q-learning.png)

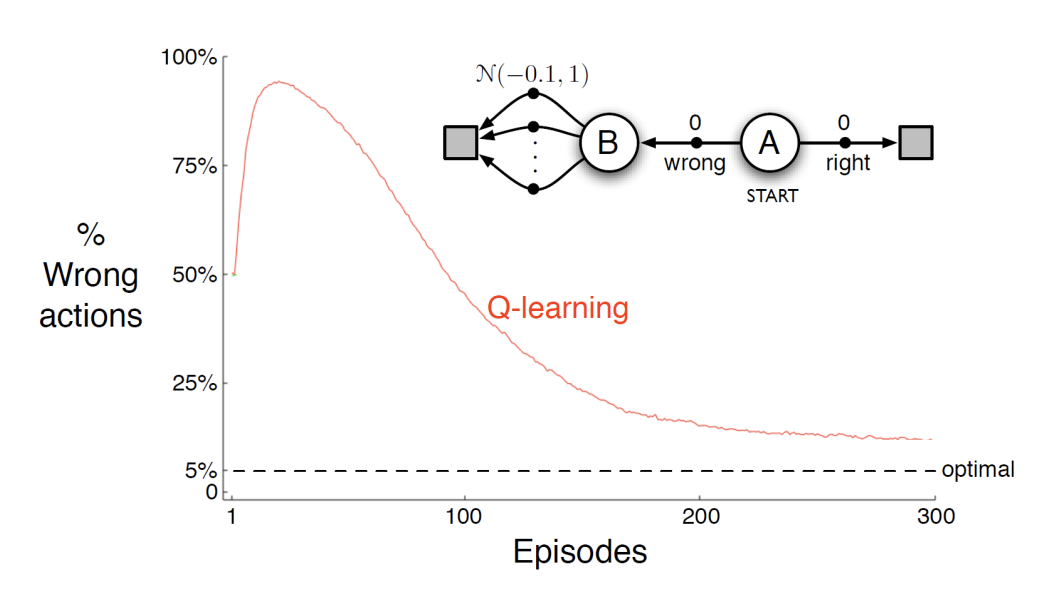
False signals from $\mathcal{N}(0.1,1)$, may have few positive results from random noise. (However, in the long run, it will converge to the expected negative value.)

#### Double Q-learning

(Hado van Hasselt 2010)

Train 2 action-value functions, Q1 and Q2

Do Q-learning on both, but

- never on the same time steps (Q1 and Q2 are indep.)
- pick Q1 or Q2 at random to be updated on each step

If updating Q1, use Q2 for the value of the next state:

$$
Q_1(S_t,A_t) \gets Q_1(S_t,A_t) + \alpha (R_{t+1} + \gamma Q_2(S_{t+1}, \arg\max_{a'\in A} Q_1(S_{t+1},a')) - Q_1(S_t,A_t))
$$

Action selections are (say) $\epsilon$-greedy with respect to the sum of Q1 and Q2. (unbiased estimation and same convergence as Q-learning)

Drawbacks:

- More computationally expensive (only one function is trained at a time)

```pseudocode
Initialize Q1 and Q2
For each episode:
    Initialize state
    For each step:
        Choose $A$ from $S$ using policy derived from Q1 and Q2
        Take action $A$, observe $R$ and $S'$
        With probability $0.5$, update Q1:
            $Q1(S,A) \gets Q1(S,A) + \alpha (R + \gamma Q2(S', \arg\max_{a'\in A} Q1(S',a')) - Q1(S,A))$
        Otherwise, update Q2:
            $Q2(S,A) \gets Q2(S,A) + \alpha (R + \gamma Q1(S', \arg\max_{a'\in A} Q2(S',a')) - Q2(S,A))$
        $S \gets S'$
    End for
End for
```

#### Double DQN

(van Hasselt, Guez, Silver, 2015)

A better implementation of Double Q-learning.

- Dealing with maximization bias of Q-Learning
- Current Q-network $w$ is used to select actions
- Older Q-network $w^-$ is used to evaluate actions 

$$
l=\left(r+\gamma Q(s', \arg\max_{a'\in A} Q(s',a';w);w^-) - Q(s,a;w)\right)^2
$$

Here $\arg\max_{a'\in A} Q(s',a';w)$ is the action selected by the current Q-network $w$.

$Q(s', \arg\max_{a'\in A} Q(s',a';w);w^-)$ is the action evaluation by the older Q-network $w^-$.

### Prioritized Experience Replay

(Schaul, Quan, Antonoglou, Silver, ICLR 2016)

Weight experience according to "surprise" (or error)

- Store experience in priority queue according to DQN error
  $$
  \left|r+\gamma \arg\max_{a'\in A} Q(s',a',w^-)-Q(s,a,w)\right|
  $$

- Stochastic Prioritization
  $$
  P(i)=\frac{p_i^\alpha}{\sum_k p_k^\alpha}
  $$
  - $p_i$ is proportional to the DQN error

- $\alpha$ determines how much prioritization is used, with $\alpha = 0$ corresponding to the uniform case.

### Dueling Q networks

(Wang et.al., ICML, 2016)

- Split Q-network into two channels

  - Action-independent value function $V(s; w)$: measures how good is the state $s$

  - Action-dependent advantage function $A(s, a; w)$: measure how much better is action $a$ than the average action in state $s$
    $$
    Q(s,a; w) = V(s; w) + A(s, a; w)
    $$

- Advantage function is defined as:
  $$
  A^\pi(s, a) = Q^\pi(s, a) - V^\pi(s)
  $$

The value stream learns to pay attention to the road

**The advantage stream**: pay attention only when there are cars immediately in front, so as to avoid collisions

### Multistep returns

Truncated n-step return from a state $s_t$

$$
R^{n}_t = \sum_{i=0}^{n-1} \gamma^{(k)}_t R_{t+k+1}
$$

Multistep Q-learning update rule:

$$
I=\left(R^{n}_t + \gamma^{(n)}_t \max_{a'\in A} Q(s_{t+n},a';w)-Q(s,a,w)\right)^2
$$

Singlestep Q-learning update rule:

$$
I=\left(r+\gamma \max_{a'\in A} Q(s',a';w)-Q(s,a,w)\right)^2
$$

### Distributed DQN

- Separating Learning from Acting
- Distributing hundreds of actors over CPUs
- Advantages: better harnessing computation, local priority evaluation, better exploration

#### Distributed DQN with Recurrent Experience Replay (R2D2)

Providing an LSTM layer after the convolutional stack

- To deal with partial observability

Other tricks:

- prioritized distributed replay
- n-step double Q-learning (with n = 5)
- generating experience by a large number of actors (typically 256)
- learning from batches of replayed experience by a single learner

#### Agent 57

[link to paper](https://deepmind.google/discover/blog/agent57-outperforming-the-human-atari-benchmark/)