NoteNextra-origin/pages/Math416/Exam_reviews/Math416_E1.md

Math 416 Midterm 1 Review

So everything we have learned so far is to extend the real line to the complex plane.

Chapter 1 Complex Numbers

Definition of complex numbers

An ordered pair of real numbers (x, y) can be represented as a complex number z = x + yi, where i is the imaginary unit.

With operations defined as:

(x_1 + y_1i) + (x_2 + y_2i) = (x_1 + x_2) + (y_1 + y_2)i

(x_1 + y_1i) \cdot (x_2 + y_2i) = (x_1x_2 - y_1y_2) + (x_1y_2 + x_2y_1)i

De Moivre's Formula

Every complex number z can be written as z = r(\cos \theta + i \sin \theta), where r is the magnitude of z and \theta is the argument of z.

z^n = r^n(\cos n\theta + i \sin n\theta)

The De Moivre's formula is useful for finding the $n$th roots of a complex number.

z^n = r^n(\cos n\theta + i \sin n\theta)

Roots of complex numbers

Using De Moivre's formula, we can find the $n$th roots of a complex number.

If z=r(\cos \theta + i \sin \theta), then the $n$th roots of z are given by:

z_k = r^{1/n}(\cos \frac{\theta + 2k\pi}{n} + i \sin \frac{\theta + 2k\pi}{n})

for k = 0, 1, 2, \ldots, n-1.

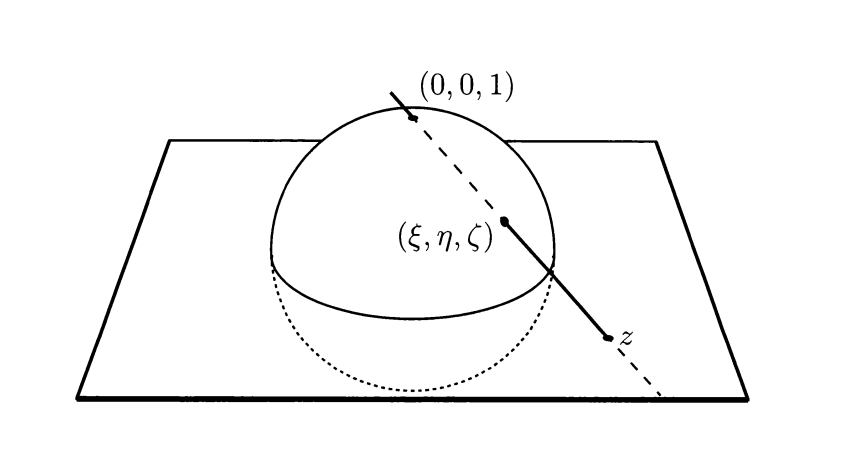
Stereographic projection

The stereographic projection is a map from the unit sphere S^2 to the complex plane \mathbb{C}\setminus\{0\}.

The projection is given by:

z\mapsto \frac{(2Re(z), 2Im(z), |z|^2-1)}{|z|^2+1}

The inverse map is given by:

(\xi,\eta, \zeta)\mapsto \frac{\xi + i\eta}{1 - \zeta}

Chapter 2 Complex Differentiation

Definition of complex differentiation

Let the complex plane \mathbb{C} be defined in an open subset G of \mathbb{C}. (Domain)

Then f is said to be differentiable at z_0\in G if the limit

\lim_{z\to z_0} \frac{f(z)-f(z_0)}{z-z_0}

exists.

The limit is called the derivative of f at z_0 and is denoted by f'(z_0).

To prove that a function is differentiable, we can use the standard delta-epsilon definition of a limit.

\left|\frac{f(z)-f(z_0)}{z-z_0} - f'(z_0)\right| < \epsilon

whenever 0 < |z-z_0| < \delta.

With such definition, all the properties of real differentiation can be extended to complex differentiation.

Differentiation of complex functions

1. If f is differentiable at z_0, then f is continuous at z_0.
2. If f,g are differentiable at z_0, then f+g, fg are differentiable at z_0.

   
   (f+g)'(z_0) = f'(z_0) + g'(z_0)
   

   
   (fg)'(z_0) = f'(z_0)g(z_0) + f(z_0)g'(z_0)
   

3. If f,g are differentiable at z_0 and g(z_0)\neq 0, then f/g is differentiable at z_0.

   
   \left(\frac{f}{g}\right)'(z_0) = \frac{f'(z_0)g(z_0) - f(z_0)g'(z_0)}{g(z_0)^2}
   

4. If f is differentiable at z_0 and g is differentiable at f(z_0), then g\circ f is differentiable at z_0.

   
   (g\circ f)'(z_0) = g'(f(z_0))f'(z_0)
   

5. If f(z)=\sum_{k=0}^n c_k(z-z_0)^k, where c_k\in\mathbb{C}, then f is differentiable at z_0 and f'(z_0)=\sum_{k=1}^n kc_k(z_0-z_0)^{k-1}.

   
   f'(z_0) = c_1 + 2c_2(z_0-z_0) + 3c_3(z_0-z_0)^2 + \cdots + nc_n(z_0-z_0)^{n-1}
   

Cauchy-Riemann Equations

Let the function defined on an open subset G of \mathbb{C} be f(x,y)=u(x,y)+iv(x,y), where u,v are real-valued functions.

Then f is differentiable at z_0=x_0+y_0i if and only if the partial derivatives of u and v exist at (x_0,y_0) and satisfy the Cauchy-Riemann equations:

\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y}, \quad \frac{\partial u}{\partial y} = -\frac{\partial v}{\partial x}

Holomorphic functions

A function f is said to be holomorphic on an open subset G of \mathbb{C} if f is differentiable at every point of G.

Partial differential operators

\frac{\partial}{\partial z} = \frac{1}{2}\left(\frac{\partial}{\partial x} - i\frac{\partial}{\partial y}\right)

\frac{\partial}{\partial \bar{z}} = \frac{1}{2}\left(\frac{\partial}{\partial x} + i\frac{\partial}{\partial y}\right)

This gives that

\frac{\partial f}{\partial z} = \frac{1}{2}\left(\frac{\partial f}{\partial x} - i\frac{\partial f}{\partial y}\right)=\frac{1}{2}\left(\frac{\partial u}{\partial x} +\frac{\partial v}{\partial y}\right) + \frac{i}{2}\left(\frac{\partial v}{\partial x} - \frac{\partial u}{\partial y}\right)

\frac{\partial f}{\partial \bar{z}} = \frac{1}{2}\left(\frac{\partial f}{\partial x} + i\frac{\partial f}{\partial y}\right)=\frac{1}{2}\left(\frac{\partial u}{\partial x} - \frac{\partial v}{\partial y}\right) + \frac{i}{2}\left(\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}\right)

If the function f is holomorphic, then by the Cauchy-Riemann equations, we have

\frac{\partial f}{\partial \bar{z}} = 0

Conformal mappings

A holomorphic function f is said to be conformal if it preserves the angles between the curves. More formally, if f is holomorphic on an open subset G of \mathbb{C} and z_0\in G, \gamma_1, \gamma_2 are two curves passing through z_0 (\gamma_1(t_1)=\gamma_2(t_2)=z_0) and intersecting at an angle \theta, then

\arg(f\circ\gamma_1)'(t_1) - \arg(f\circ\gamma_2)'(t_2) = \theta

In other words, the angle between the curves is preserved.

An immediate consequence is that

\arg(f\cdot \gamma_1)'(t_1) =\arg f'(z_0) + \arg \gamma_1'(t_1)\\
\arg(f\cdot \gamma_2)'(t_2) =\arg f'(z_0) + \arg \gamma_2'(t_2)

Harmonic functions

A real-valued function u is said to be harmonic if it satisfies the Laplace equation:

\frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = 0

Chapter 3 Linear Fractional Transformations

Definition of linear fractional transformations

A linear fractional transformation is a function of the form

\phi(z) = \frac{az+b}{cz+d}

where a,b,c,d are complex numbers and ad-bc\neq 0.

Properties of linear fractional transformations

Conformality

A linear fractional transformation is conformal.

\phi'(z) = \frac{ad-bc}{(cz+d)^2}

Three-fold transitivity

If z_1,z_2,z_3 are distinct points in the complex plane, then there exists a unique linear fractional transformation \phi such that \phi(z_1)=\infty, \phi(z_2)=0, \phi(z_3)=1.

The map is given by

\phi(z) =\begin{cases}
\frac{(z-z_2)(z_1-z_3)}{(z-z_1)(z_2-z_3)} & \text{if } z_1,z_2,z_3 \text{ are all finite}\\
\frac{z-z_2}{z_3-z_2} & \text{if } z_1=\infty\\
\frac{z_3-z_1}{z-z_1} & \text{if } z_2=\infty\\
\frac{z-z_2}{z-z_1} & \text{if } z_3=\infty\\
\end{cases}

So if z_1,z_2,z_3, w_1,w_2,w_3 are distinct points in the complex plane, then there exists a unique linear fractional transformation \phi such that \phi(z_i)=w_i for i=1,2,3.

Inversion

Factorization

Clircle

Chapter 4 Elementary Functions

Exponential function

Trigonometric functions

Logarithmic function

Power function

Inverse trigonometric functions

Chapter 5 Power Series

Definition of power series

Properties of power series

Radius/Region of convergence

Cauchy-Hadamard Theorem

Cauchy Product (of power series)

Chapter 6 Complex Integration

Definition of Riemann Integral for complex functions

The complex integral of a complex function \phi on the closed subinterval [a,b] of the real line is said to be piecewise continuous if there exists a partition a=t_0<t_1<\cdots<t_n=b such that \phi is continuous on each open interval (t_{i-1},t_i) and has a finite limit at each discontinuity point of the closed interval [a,b].

If \phi is piecewise continuous on [a,b], then the complex integral of \phi on [a,b] is defined as

\int_a^b \phi(t) dt = \int_a^b \operatorname{Re}\phi(t) dt + i\int_a^b \operatorname{Im}\phi(t) dt

Fundamental Theorem of Calculus

If \phi is piecewise continuous on [a,b], then

\int_a^b \phi'(t) dt = \phi(b)-\phi(a)

Triangle inequality

\left|\int_a^b \phi(t) dt\right| \leq \int_a^b |\phi(t)| dt

Integral on curve

Let \gamma be a piecewise smooth curve in the complex plane.

The integral of a complex function f on \gamma is defined as

\int_\gamma f(z) dz = \int_a^b f(\gamma(t))\gamma'(t) dt

Properties of complex integrals

1. Linearity:

Chapter 7 Cauchy's Theorem

Cauchy's Theorem

Cauchy's Formula for a Circle

Cauchy's Product