121 lines
3.3 KiB
Markdown
121 lines
3.3 KiB
Markdown
# Math 416 Lecture 12
|
|
|
|
## Continue on last class
|
|
|
|
### Cauchy's Theorem on triangles
|
|
|
|
Let $T$ be a triangle in $\mathbb{C}$ and $f$ be holomorphic on $T$. Then
|
|
|
|
$$
|
|
\int_T f(z) dz = 0
|
|
$$
|
|
|
|
### Cauchy's Theorem for Convex Sets
|
|
|
|
Let's start with a simple case: $f(z)=1$.
|
|
|
|
For any closed curve $\gamma$ in $U$, we have
|
|
|
|
$$
|
|
\int_\gamma f(z) dz = \int_a^b f(\gamma(t)) \gamma'(t) dt \approx \sum_{i=1}^n f(\gamma(t_i)) \gamma'(t_i) \Delta t_i
|
|
$$
|
|
|
|
#### Definition of a convex set
|
|
|
|
A set $U$ is convex if for any two points $z_1, z_2 \in U$, the line segment $[z_1, z_2] \subset U$.
|
|
|
|
Let $O(U)$ be the set of all holomorphic functions on $U$.
|
|
|
|
#### Definition of primitive
|
|
|
|
Say $f$ has a primitive on $U$. If there exists a holomorphic function $g$ on $U$ such that $g'(z)=f(z)$ for all $z \in U$, then $g$ is called a primitive of $f$ on $U$.
|
|
|
|
#### Cauchy's Theorem for a Convex region
|
|
|
|
Cauchy's Theorem holds if $f$ has a primitive on a convex region $U$.
|
|
|
|
$$
|
|
\int_\gamma f(z) dz = \int_\gamma \left[\frac{d}{dz}g(z)\right] dz = g(z_1)-g(z_2)
|
|
$$
|
|
|
|
Since the curve is closed, $z_1=z_2$, so $\int_\gamma f(z) dz = 0$.
|
|
|
|
Proof:
|
|
|
|
It is sufficient to prove that if $U$ is convex, $f$ is holomorphic on $U$, then $f=g'$ for some $g$ holomorphic on $U$.
|
|
|
|
We pick a point $z_0\in U$ and define $g(z)=\int_{[z_0,z]}f(\xi)d\xi$.
|
|
|
|
We claim $g\in O(U)$ and $g'=f$.
|
|
|
|
Let $z_1$ close to $z$, since $f$ is holomorphic on $U$, using the Goursat's theorem, we can find a triangle $T$ with $\xi\in T$ and $z\in T$ and $T\subset U$.
|
|
|
|
$$
|
|
\begin{aligned}
|
|
0&=\int_{z_0}^{z}f(\xi)d\xi+\int_{z}^{z_1}f(\xi)d\xi\\
|
|
&=g(z)-g(z_1)+\int_{z}^{z_1}f(\xi)d\xi+\int_{z_1}^{z_0}f(\xi)d\xi\\
|
|
\frac{g(z)-g(z_1)}{z-z_1}&=-\frac{1}{z-z_1}\left(\int_{z}^{z_1}f(\xi)d\xi\right)\\
|
|
\frac{g(z_1)-g(z_0)}{z_1-z_0}-f(z_1)&=-\frac{1}{z_1-z_0}\left(\int_{z}^{z_1}f(\xi)d\xi\right)-f(z_1)\\
|
|
&=-\frac{1}{z_1-z_0}\left(\int_{z}^{z_1}f(\xi)-f(z_1)d\xi\right)\\
|
|
&=I
|
|
\end{aligned}
|
|
$$
|
|
|
|
Use the fact that $f$ is holomorphic on $U$, then $f$ is continuous on $U$, so $\lim_{z\to z_1}f(z)=f(z_1)$.
|
|
|
|
There exists a $\delta>0$ such that $|z-z_1|<\delta$ implies $|f(z)-f(z_1)|<\epsilon$.
|
|
|
|
So
|
|
|
|
$$
|
|
|I|\leq\frac{1}{z_1-z_0}\int_{z}^{z_1}|f(\xi)-f(z_1)|d\xi<\frac{\epsilon}{z_1-z_0}\int_{z}^{z_1}d\xi=\epsilon
|
|
$$
|
|
|
|
So $I\to 0$ as $z_1\to z$.
|
|
|
|
Therefore, $g'(z_1)=f(z_1)$ for all $z_1\in U$.
|
|
|
|
QED
|
|
|
|
### Cauchy's Theorem for a disk
|
|
|
|
Let $U$ be the open set, $f\in O(U)$. Let $C$ be a circle inside $U$ and $z$ be a point inside $C$.
|
|
|
|
Then
|
|
|
|
$$
|
|
f(z)=\frac{1}{2\pi i}\int_C\frac{f(\xi)d\xi}{\xi-z} d\xi
|
|
$$
|
|
|
|
Proof:
|
|
|
|
Let $C_\epsilon$ be a circle with center $z$ and radius $\epsilon$ inside $C$.
|
|
|
|
Claim:
|
|
|
|
$$
|
|
\int_{C_\epsilon}\frac{f(\xi)d\xi}{\xi-z}=\int_{C}\frac{f(\xi)d\xi}{\xi-z}
|
|
$$
|
|
|
|
We divide the integral into four parts:
|
|
|
|
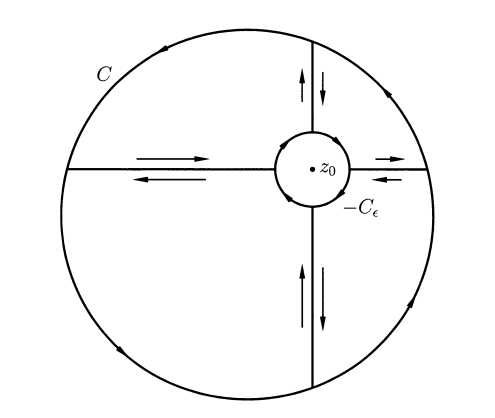
|
|
|
|
Notice that $\frac{f(\xi)}{\xi-z}$ is holomorphic whenever $f(\xi)\in U$ and $\xi\in \mathbb{C}\setminus\{z\}$.
|
|
|
|
So we can apply Cauchy's theorem to the integral on the inside square.
|
|
|
|
$$
|
|
\int_{C_\epsilon}\frac{f(\xi)d\xi}{\xi-z}=0
|
|
$$
|
|
|
|
Since $\frac{1}{2\pi i}\int_{C_\epsilon}\frac{1}{\xi-z}d\xi=1$, $\sigma=\epsilon e^{it}+z_0$ and $\sigma'=\epsilon e^{it}$, we have
|
|
|
|
/* TRACK LOST*/
|
|
|
|
$$
|
|
\int_{C_\epsilon}\frac{f(\xi)d\xi}{\xi-z}=\int_0^{2\pi}\frac{f(\sigma)d\sigma}{\sigma-z}=2\pi i f(z)
|
|
$$
|
|
|
|
QED
|