160 lines
4.3 KiB
Markdown
160 lines
4.3 KiB
Markdown
# CSE559A Lecture 12
|
|
|
|
## Transformer Architecture
|
|
|
|
### Outline
|
|
|
|
**Self-Attention Layers**: An important network module, which often has a global receptive field
|
|
|
|
**Sequential Input Tokens**: Breaking the restriction to 2d input arrays
|
|
|
|
**Positional Encodings**: Representing the metadata of each input token
|
|
|
|
**Exemplar Architecture**: The Vision Transformer (ViT)
|
|
|
|
**Moving Forward**: What does this new module enable? Who wins in the battle between transformers and CNNs?
|
|
|
|
### The big picture
|
|
|
|
CNNs
|
|
|
|
- Local receptive fields
|
|
- Struggles with global content
|
|
- Shape of intermediate layers is sometimes a pain
|
|
|
|
Things we might want:
|
|
|
|
- Use information from across the image
|
|
- More flexible shape handling
|
|
- Multiple modalities
|
|
|
|
Our Hero: MultiheadAttention
|
|
|
|
Use positional encodings to represent the metadata of each input token
|
|
|
|
## Self-Attention layers
|
|
|
|
### Comparing with ways to handling sequential data
|
|
|
|
#### RNN
|
|
|
|
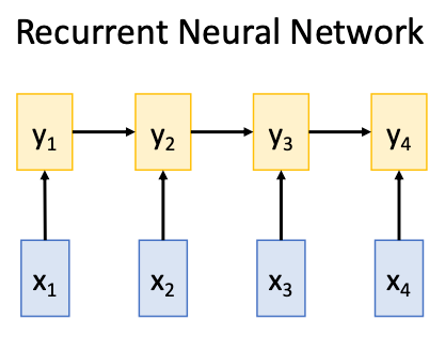
|
|
|
|
Works on **Ordered Sequences**
|
|
|
|
- Good at long sequences: After one RNN layer $h_r$ sees the whole sequence
|
|
- Bad at parallelization: need to compute hidden states sequentially
|
|
|
|
#### 1D conv
|
|
|
|
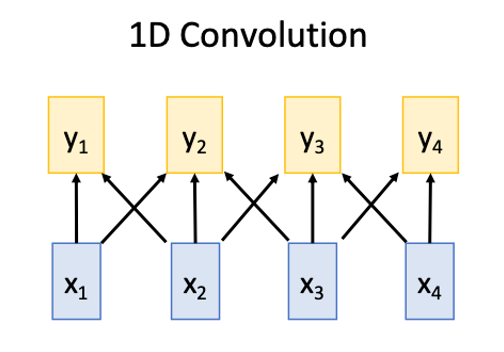
|
|
|
|
Works on **Multidimensional Grids**
|
|
|
|
- Bad at long sequences: Need to stack may conv layers or outputs to see the whole sequence
|
|
- Good at parallelization: Each output can be computed in parallel
|
|
|
|
#### Self-Attention
|
|
|
|
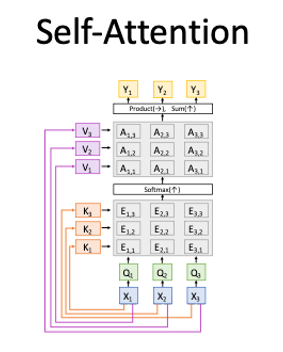
|
|
|
|
Works on **Set of Vectors**
|
|
|
|
- Good at Long sequences: Each output can attend to all inputs
|
|
- Good at parallelization: Each output can be computed in parallel
|
|
- Bad at saving memory: Need to store all inputs in memory
|
|
|
|
### Encoder-Decoder Architecture
|
|
|
|
The encoder is constructed by stacking multiple self-attention layers and feed-forward networks.
|
|
|
|
#### Word Embeddings
|
|
|
|
Translate tokens to vector space
|
|
|
|
```python
|
|
class Embedder(nn.Module):
|
|
def __init__(self, vocab_size, d_model):
|
|
super().__init__()
|
|
self.embed=nn.Embedding(vocab_size, d_model)
|
|
|
|
def forward(self, x):
|
|
return self.embed(x)
|
|
```
|
|
|
|
#### Positional Embeddings
|
|
|
|
The positional encodings are a way to represent the position of each token in the sequence.
|
|
|
|
Combined with the word embeddings, we get the input to the self-attention layer with information about the position of each token in the sequence.
|
|
|
|
> The reason why we just add the positional encodings to the word embeddings is _perhaps_ that we want the model to self-assign weights to the word-token and positional-token.
|
|
|
|
#### Query, Key, Value
|
|
|
|
The query, key, and value are the three components of the self-attention layer.
|
|
|
|
They are used to compute the attention weights.
|
|
|
|
```python
|
|
class SelfAttention(nn.Module):
|
|
def __init__(self, d_model, num_heads):
|
|
super().__init__()
|
|
self.d_model = d_model
|
|
self.d_k = d_k
|
|
self.q_linear = nn.Linear(d_model, d_k)
|
|
self.k_linear = nn.Linear(d_model, d_k)
|
|
self.v_linear = nn.Linear(d_model, d_k)
|
|
self.dropout = nn.Dropout(dropout)
|
|
self.out = nn.Linear(d_k, d_k)
|
|
|
|
def forward(self, q, k, v, mask=None):
|
|
|
|
bs = q.size(0)
|
|
|
|
k = self.k_linear(k)
|
|
q = self.q_linear(q)
|
|
v = self.v_linear(v)
|
|
|
|
# calculate attention weights
|
|
outputs = attention(q, k, v, self.d_k, mask, self.dropout)
|
|
|
|
# apply output linear transformation
|
|
outputs = self.out(outputs)
|
|
|
|
return outputs
|
|
```
|
|
|
|
#### Attention
|
|
|
|
```python
|
|
def attention(q, k, v, d_k, mask=None, dropout=None):
|
|
scores = torch.matmul(q, k.transpose(-2, -1)) / math.sqrt(d_k)
|
|
|
|
if mask is not None:
|
|
mask = mask.unsqueeze(1)
|
|
scores = scores.masked_fill(mask == 0, -1e9)
|
|
|
|
scores = F.softmax(scores, dim=-1)
|
|
|
|
if dropout is not None:
|
|
scores = dropout(scores)
|
|
|
|
outputs = torch.matmul(scores, v)
|
|
|
|
return outputs
|
|
```
|
|
|
|
The query, key are used to compute the attention map, and the value is used to compute the attention output.
|
|
|
|
#### Multi-Head self-attention
|
|
|
|
The multi-head self-attention is a self-attention layer that has multiple heads.
|
|
|
|
Each head has its own query, key, and value.
|
|
|
|
### Computing Attention Efficiency
|
|
|
|
- the standard attention has a complexity of $O(n^2)$
|
|
- We can use sparse attention to reduce the complexity to $O(n)$
|