72 lines
2.4 KiB
Markdown
72 lines
2.4 KiB
Markdown
# CSE559A Lecture 19
|
|
|
|
## Feature Detection
|
|
|
|
### Behavior of corner features with respect to Image Transformations
|
|
|
|
To be useful for image matching, “the same” corner features need to show up despite geometric and photometric transformations
|
|
|
|
We need to analyze how the corner response function and the corner locations change in response to various transformations
|
|
|
|
#### Affine intensity change
|
|
|
|
Solution:
|
|
|
|
- Only derivative of intensity are used (invariant to intensity change)
|
|
- Intensity scaling
|
|
|
|
#### Image translation
|
|
|
|
Solution:
|
|
|
|
- Derivatives and window function are shift invariant
|
|
|
|
#### Image rotation
|
|
|
|
Second moment ellipse rotates but its shape (i.e. eigenvalues) remains the same
|
|
|
|
#### Scaling
|
|
|
|
Classify edges instead of corners
|
|
|
|
## Automatic Scale selection for interest point detection
|
|
|
|
### Scale space
|
|
|
|
We want to extract keypoints with characteristic scales that are equivariant (or covariant) with respect to scaling of the image
|
|
|
|
Approach: compute a scale-invariant response function over neighborhoods centered at each location $(x,y)$ and a range of scales $\sigma$, find scale-space locations $(x,y,\sigma)$ where this function reaches a local maximum
|
|
|
|
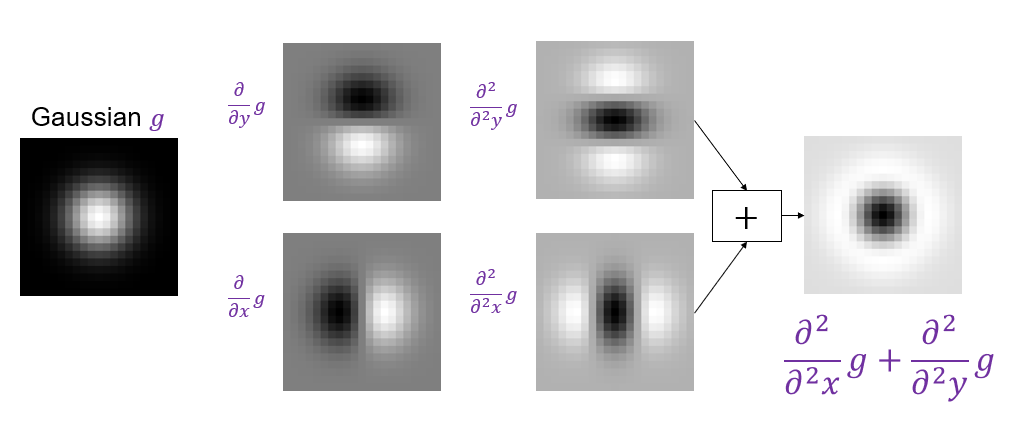
A particularly convenient response function is given by the scale-normalized Laplacian of Gaussian (LoG) filter:
|
|
|
|
$$
|
|
\nabla^2_{norm}=\sigma^2\nabla^2\left(\frac{\partial^2}{\partial x^2}g+\frac{\partial^2}{\partial y^2}g\right)
|
|
$$
|
|
|
|
|
|
|
|
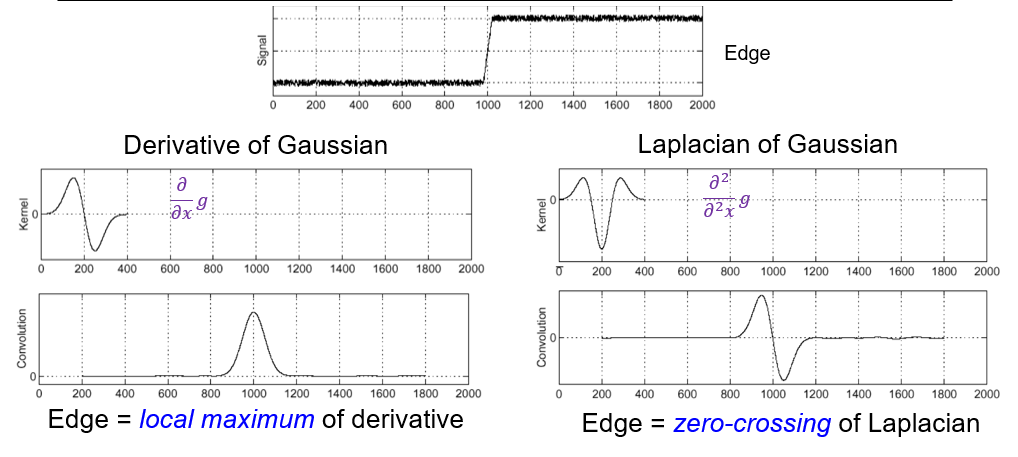
#### Edge detection with LoG
|
|
|
|
|
|
|
|
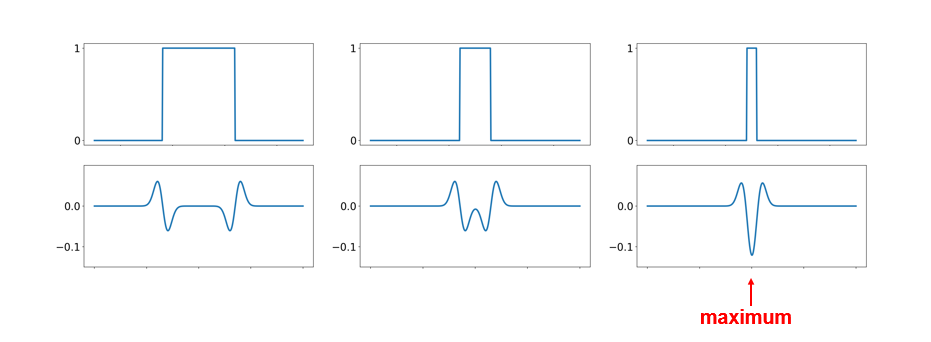
#### Blob detection with LoG
|
|
|
|
|
|
|
|
### Difference of Gaussians (DoG)
|
|
|
|
DoG has a little more flexibility, since you can select the scales of the Gaussians.
|
|
|
|
### Scale-invariant feature transform (SIFT)
|
|
|
|
The main goal of SIFT is to enable image matching in the presence of significant transformations
|
|
|
|
- To recognize the same keypoint in multiple images, we need to match appearance descriptors or "signatures" in their neighborhoods
|
|
- Descriptors that are locally invariant w.r.t. scale and rotation can handle a wide range of global transformations
|
|
|
|
### Maximum stable extremal regions (MSER)
|
|
|
|
Based on Watershed segmentation algorithm
|
|
|
|
Select regions that are stable over a large parameter range
|