NoteNextra-origin/content/CSE559A/CSE559A_L22.md

CSE559A Lecture 22

Continue on Robust Fitting of parametric models

RANSAC

Definition: RANdom SAmple Consensus

RANSAC is a method to fit a model to a set of data points.

It is a non-deterministic algorithm that can be used to fit a model to a set of data points.

Pros:

• Simple and general
• Applicable to many different problems
• Often works well in practice

Cons:

• Lots of parameters to set
• Number of iterations grows exponentially as outlier ratio increases
• Can't always get a good initialization of the model based on the minimum number of samples.

Hough Transform

Use point-line duality to find lines.

In practice, we don't use (m,b) parameterization.

Instead, we use polar parameterization:

\rho = x \cos \theta + y \sin \theta

Algorithm outline:

• Initialize accumulator H to all zeros
  • For each feature point (x,y)
    • For \theta = 0 to 180
    • \rho = x \cos \theta + y \sin \theta
    • H(\theta, \rho) += 1
• Find the value(s) of (\theta, \rho) where H(\theta, \rho) is a local maximum (perform NMS on the accumulator array)
  • The detected line in the image is given by \rho = x \cos \theta + y \sin \theta

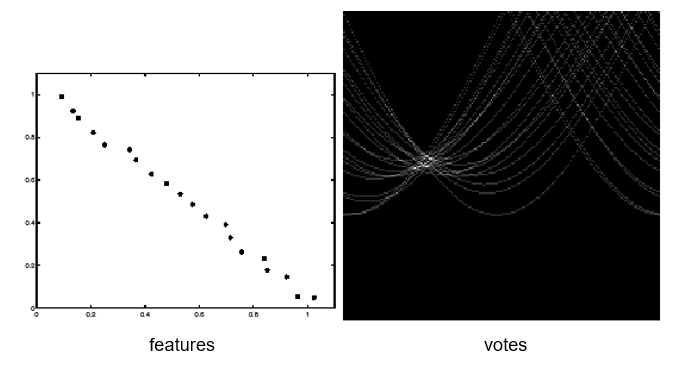
Effect of noise

Noise makes the peak fuzzy.

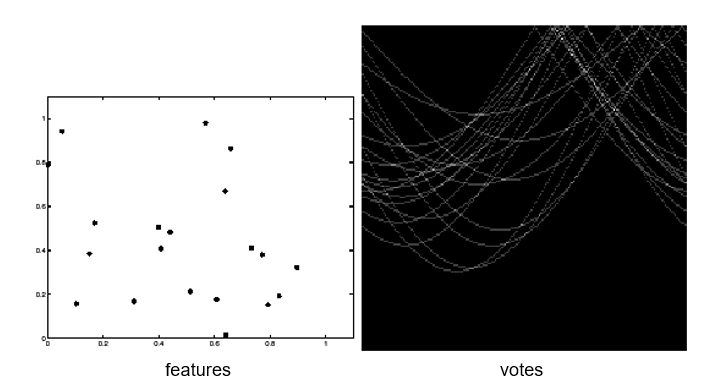
Effect of outliers

Outliers can break the peak.

Pros and Cons

Pros:

• Can deal with non-locality and occlusion
• Can detect multiple instances of a model
• Some robustness to noise: noise points unlikely to contribute consistently to any single bin
• Leads to a surprisingly general strategy for shape localization (more on this next)

Cons:

• Complexity increases exponentially with the number of model parameters
  • In practice, not used beyond three or four dimensions
• Non-target shapes can produce spurious peaks in parameter space
• It's hard to pick a good grid size

Generalize Hough Transform

Template representation: for each type of landmark point, store all possible displacement vectors towards the center

Detecting the template:

For each feature in a new image, look up that feature type in the model and vote for the possible center locations associated with that type in the model

Implicit shape models

Training:

• Build codebook of patches around extracted interest points using clustering
• Map the patch around each interest point to closest codebook entry
• For each codebook entry, store all positions it was found, relative to object center

Testing:

• Given test image, extract patches, match to codebook entry
• Cast votes for possible positions of object center
• Search for maxima in voting space
• Extract weighted segmentation mask based on stored masks for the codebook occurrences

Image alignment

Affine transformation

Simple fitting procedure: linear least squares Approximates viewpoint changes for roughly planar objects and roughly orthographic cameras Can be used to initialize fitting for more complex models

Fitting an affine transformation:

\begin{bmatrix}
&&&\cdots\\
x_i & y_i & 0&0&1&0\\
0&0&x_i&y_i&0&1\\
&&&\cdots\\
\end{bmatrix}
\begin{bmatrix}
m_1\\
m_2\\
m_3\\
m_4\\
t_1\\
t_2\\
\end{bmatrix}
=
\begin{bmatrix}
\cdots\\
\end{bmatrix}

Only need 3 points to solve for 6 parameters.

Homography

Recall that

x' = \frac{a x + b y + c}{g x + h y + i}, \quad y' = \frac{d x + e y + f}{g x + h y + i}

Use 2D homogeneous coordinates:

(x,y) \rightarrow \begin{pmatrix}x \\ y \\ 1\end{pmatrix}

\begin{pmatrix}x\\y\\w\end{pmatrix} \rightarrow (x/w,y/w)

Reminder: all homogeneous coordinate vectors that are (non-zero) scalar multiples of each other represent the same point

Equation for homography in homogeneous coordinates:

\begin{pmatrix}
x' \\
y' \\
1
\end{pmatrix}
\cong
\begin{pmatrix}
h_{11} & h_{12} & h_{13} \\
h_{21} & h_{22} & h_{23} \\
h_{31} & h_{32} & h_{33}
\end{pmatrix}
\begin{pmatrix}
x \\
y \\
1
\end{pmatrix}

Constraint from a match (x_i,x_i'), x_i'\cong Hx_i

How can we get rid of the scale ambiguity?

Cross product trick:$x_i' × Hx_i=0$

The cross product is defined as:

\begin{pmatrix}a\\b\\c\end{pmatrix} \times \begin{pmatrix}a'\\b'\\c'\end{pmatrix} = \begin{pmatrix}bc'-b'c\\ca'-c'a\\ab'-a'b\end{pmatrix}

Let h_1^T, h_2^T, h_3^T be the rows of H. Then

x_i' × Hx_i=\begin{pmatrix}
    x_i' \\
    y_i' \\
    1
\end{pmatrix} \times \begin{pmatrix}
    h_1^T x_i \\
    h_2^T x_i \\
    h_3^T x_i
\end{pmatrix}
=
\begin{pmatrix}
    y_i' h_3^T x_i−h_2^T x_i \\
    h_1^T x_i−x_i' h_3^T x_i \\
    x_i' h_2^T x_i−y_i' h_1^T x_i
\end{pmatrix}

Constraint from a match (x_i,x_i'):

x_i' × Hx_i=\begin{pmatrix}
    x_i' \\
    y_i' \\
    1
\end{pmatrix} \times \begin{pmatrix}
    h_1^T x_i \\
    h_2^T x_i \\
    h_3^T x_i
\end{pmatrix}
=
\begin{pmatrix}
    y_i' h_3^T x_i−h_2^T x_i \\
    h_1^T x_i−x_i' h_3^T x_i \\
    x_i' h_2^T x_i−y_i' h_1^T x_i
\end{pmatrix}

Rearranging the terms:

\begin{bmatrix}
    0^T &-x_i^T &y_i' x_i^T \\
    x_i^T &0^T &-x_i' x_i^T \\
    y_i' x_i^T &x_i' x_i^T &0^T
\end{bmatrix}
\begin{bmatrix}
    h_1 \\
    h_2 \\
    h_3
\end{bmatrix} = 0

These equations aren't independent! So, we only need two.

Robust alignment

Descriptor-based feature matching

Extract features Compute putative matches Loop:

• Hypothesize transformation T
• Verify transformation (search for other matches consistent with T)

RANSAC

Even after filtering out ambiguous matches, the set of putative matches still contains a very high percentage of outliers

RANSAC loop:

• Randomly select a seed group of matches
• Compute transformation from seed group
• Find inliers to this transformation
• If the number of inliers is sufficiently large, re-compute least-squares estimate of transformation on all of the inliers

At the end, keep the transformation with the largest number of inliers