Trance-0/NoteNextra-origin

Fork 0

Files

Trance-0 6d4b8f8ca4 Update Math416_E1.md

2025-03-12 20:40:18 -05:00

13 KiB

Raw Blame History

Math 416 Midterm 1 Review

So everything we have learned so far is to extend the real line to the complex plane.

Chapter 0 Calculus on Real values

Differentiation

Let f,g be function on real line and c be a real number.


\frac{d}{dx}(f+g)=f'+g'


\frac{d}{dx}(cf)=cf'


\frac{d}{dx}(fg)=f'g+fg'


\frac{d}{dx}(f/g)=(f'g-fg')/g^2


\frac{d}{dx}(f\circ g)=(f'\circ g)\frac{d}{dx}g


\frac{d}{dx}x^n=nx^{n-1}


\frac{d}{dx}e^x=e^x


\frac{d}{dx}\ln x=\frac{1}{x}


\frac{d}{dx}\sin x=\cos x


\frac{d}{dx}\cos x=-\sin x


\frac{d}{dx}\tan x=\sec^2 x


\frac{d}{dx}\sec x=\sec x\tan x


\frac{d}{dx}\csc x=-\csc x\cot x


\frac{d}{dx}\sinh x=\cosh x


\frac{d}{dx}\cosh x=\sinh x


\frac{d}{dx}\tanh x=\operatorname{sech}^2 x


\frac{d}{dx}\operatorname{sech} x=-\operatorname{sech}x\tanh x


\frac{d}{dx}\operatorname{csch} x=-\operatorname{csch}x\coth x


\frac{d}{dx}\coth x=-\operatorname{csch}^2 x


\frac{d}{dx}\arcsin x=\frac{1}{\sqrt{1-x^2}}


\frac{d}{dx}\arccos x=-\frac{1}{\sqrt{1-x^2}}


\frac{d}{dx}\arctan x=\frac{1}{1+x^2}


\frac{d}{dx}\operatorname{arccot} x=-\frac{1}{1+x^2}


\frac{d}{dx}\operatorname{arcsec} x=\frac{1}{x\sqrt{x^2-1}}


\frac{d}{dx}\operatorname{arccsc} x=-\frac{1}{x\sqrt{x^2-1}}

Integration

Let f,g be function on real line and c be a real number.


\int (f+g)dx=\int fdx+\int gdx


\int cfdx=c\int fdx


\int e^x dx=e^x


\int \ln x dx=x\ln x-x


\int \frac{1}{x} dx=\ln|x|


\int \sin x dx=-\cos x


\int \cos x dx=\sin x


\int \tan x dx=-\ln|\cos x|


\int \cot x dx=\ln|\sin x|


\int \sec x dx=\ln|\sec x+\tan x|


\int \csc x dx=\ln|\csc x-\cot x|


\int \sinh x dx=\cosh x


\int \cosh x dx=\sinh x


\int \tanh x dx=\ln|\cosh x|


\int \coth x dx=\ln|\sinh x|


\int \operatorname{sech} x dx=2\arctan(\tanh(x/2))


\int \operatorname{csch} x dx=\ln|\coth x-\operatorname{csch} x|


\int \operatorname{sech}^2 x dx=\tanh x


\int \operatorname{csch}^2 x dx=-\coth x


\int \frac{1}{1+x^2} dx=\arctan x


\int \frac{1}{x^2+1} dx=\arctan x


\int \frac{1}{x^2-1} dx=\frac{1}{2}\ln|\frac{x-1}{x+1}|


\int \frac{1}{x^2-a^2} dx=\frac{1}{2a}\ln|\frac{x-a}{x+a}|


\int \frac{1}{x^2+a^2} dx=\frac{1}{a}\arctan(\frac{x}{a})

Chapter 1 Complex Numbers

Definition of complex numbers

An ordered pair of real numbers (x, y) can be represented as a complex number z = x + yi, where i is the imaginary unit.

With operations defined as:


(x_1 + y_1i) + (x_2 + y_2i) = (x_1 + x_2) + (y_1 + y_2)i


(x_1 + y_1i) \cdot (x_2 + y_2i) = (x_1x_2 - y_1y_2) + (x_1y_2 + x_2y_1)i

Modulus

The modulus of a complex number z = x + yi is defined as


|z| = \sqrt{x^2 + y^2}=|z\overline{z}|

De Moivre's Formula

Every complex number z can be written as z = r(\cos \theta + i \sin \theta), where r is the magnitude of z and \theta is the argument of z.


z^n = r^n(\cos n\theta + i \sin n\theta)

The De Moivre's formula is useful for finding the $n$th roots of a complex number.


z^n = r^n(\cos n\theta + i \sin n\theta)

Roots of complex numbers

Using De Moivre's formula, we can find the $n$th roots of a complex number.

If z=r(\cos \theta + i \sin \theta), then the $n$th roots of z are given by:


z_k = r^{1/n}(\cos \frac{\theta + 2k\pi}{n} + i \sin \frac{\theta + 2k\pi}{n})

for k = 0, 1, 2, \ldots, n-1.

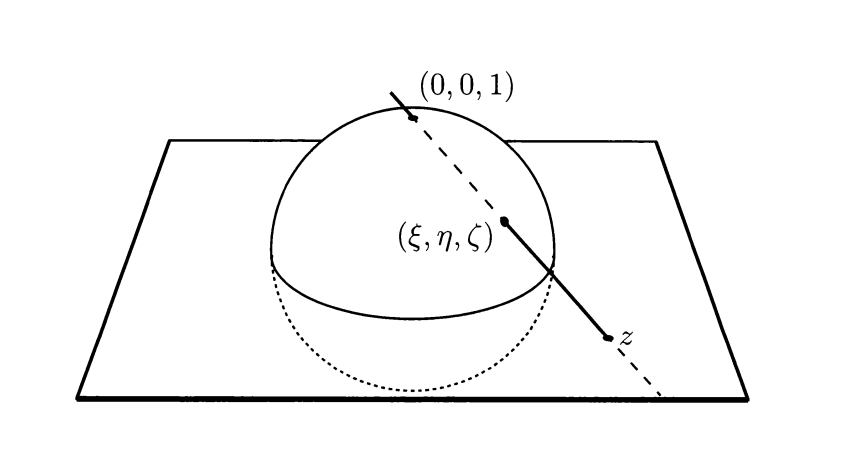
Stereographic projection

The stereographic projection is a map from the unit sphere S^2 to the complex plane \mathbb{C}\setminus\{0\}.

The projection is given by:


z\mapsto \frac{(2Re(z), 2Im(z), |z|^2-1)}{|z|^2+1}

The inverse map is given by:


(\xi,\eta, \zeta)\mapsto \frac{\xi + i\eta}{1 - \zeta}

Chapter 2 Complex Differentiation

Definition of complex differentiation

Let the complex plane \mathbb{C} be defined in an open subset G of \mathbb{C}. (Domain)

Then f is said to be differentiable at z_0\in G if the limit


\lim_{z\to z_0} \frac{f(z)-f(z_0)}{z-z_0}

exists.

The limit is called the derivative of f at z_0 and is denoted by f'(z_0).

To prove that a function is differentiable, we can use the standard delta-epsilon definition of a limit.


\left|\frac{f(z)-f(z_0)}{z-z_0} - f'(z_0)\right| < \epsilon

whenever 0 < |z-z_0| < \delta.

With such definition, all the properties of real differentiation can be extended to complex differentiation.

Differentiation of complex functions

If f is differentiable at z_0, then f is continuous at z_0.

If f,g are differentiable at z_0, then f+g, fg are differentiable at z_0.


(f+g)'(z_0) = f'(z_0) + g'(z_0)


(fg)'(z_0) = f'(z_0)g(z_0) + f(z_0)g'(z_0)

If f,g are differentiable at z_0 and g(z_0)\neq 0, then f/g is differentiable at z_0.


\left(\frac{f}{g}\right)'(z_0) = \frac{f'(z_0)g(z_0) - f(z_0)g'(z_0)}{g(z_0)^2}

If f is differentiable at z_0 and g is differentiable at f(z_0), then g\circ f is differentiable at z_0.
```
(g\circ f)'(z_0) = g'(f(z_0))f'(z_0)
```
If f(z)=\sum_{k=0}^n c_k(z-z_0)^k, where c_k\in\mathbb{C}, then f is differentiable at z_0 and f'(z_0)=\sum_{k=1}^n kc_k(z_0-z_0)^{k-1}.
```
f'(z_0) = c_1 + 2c_2(z_0-z_0) + 3c_3(z_0-z_0)^2 + \cdots + nc_n(z_0-z_0)^{n-1}
```

Cauchy-Riemann Equations

Let the function defined on an open subset G of \mathbb{C} be f(x,y)=u(x,y)+iv(x,y), where u,v are real-valued functions.

Then f is differentiable at z_0=x_0+y_0i if and only if the partial derivatives of u and v exist at (x_0,y_0) and satisfy the Cauchy-Riemann equations:


\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y}, \quad \frac{\partial u}{\partial y} = -\frac{\partial v}{\partial x}

On the polar form, the Cauchy-Riemann equations are


r\frac{\partial u}{\partial r} = \frac{\partial v}{\partial \theta}, \quad \frac{\partial u}{\partial \theta} = -r\frac{\partial v}{\partial r}

Holomorphic functions

A function f is said to be holomorphic on an open subset G of \mathbb{C} if f is differentiable at every point of G.

Partial differential operators


\frac{\partial}{\partial z} = \frac{1}{2}\left(\frac{\partial}{\partial x} - i\frac{\partial}{\partial y}\right)


\frac{\partial}{\partial \bar{z}} = \frac{1}{2}\left(\frac{\partial}{\partial x} + i\frac{\partial}{\partial y}\right)

This gives that


\frac{\partial f}{\partial z} = \frac{1}{2}\left(\frac{\partial f}{\partial x} - i\frac{\partial f}{\partial y}\right)=\frac{1}{2}\left(\frac{\partial u}{\partial x} +\frac{\partial v}{\partial y}\right) + \frac{i}{2}\left(\frac{\partial v}{\partial x} - \frac{\partial u}{\partial y}\right)


\frac{\partial f}{\partial \bar{z}} = \frac{1}{2}\left(\frac{\partial f}{\partial x} + i\frac{\partial f}{\partial y}\right)=\frac{1}{2}\left(\frac{\partial u}{\partial x} - \frac{\partial v}{\partial y}\right) + \frac{i}{2}\left(\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}\right)

If the function f is holomorphic, then by the Cauchy-Riemann equations, we have


\frac{\partial f}{\partial \bar{z}} = 0

Conformal mappings

A holomorphic function f is said to be conformal if it preserves the angles between the curves. More formally, if f is holomorphic on an open subset G of \mathbb{C} and z_0\in G, \gamma_1, \gamma_2 are two curves passing through z_0 (\gamma_1(t_1)=\gamma_2(t_2)=z_0) and intersecting at an angle \theta, then


\arg(f\circ\gamma_1)'(t_1) - \arg(f\circ\gamma_2)'(t_2) = \theta

In other words, the angle between the curves is preserved.

An immediate consequence is that


\arg(f\cdot \gamma_1)'(t_1) =\arg f'(z_0) + \arg \gamma_1'(t_1)\\
\arg(f\cdot \gamma_2)'(t_2) =\arg f'(z_0) + \arg \gamma_2'(t_2)

Harmonic functions

A real-valued function u is said to be harmonic if it satisfies the Laplace equation:


\frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = 0

Chapter 3 Linear Fractional Transformations

Definition of linear fractional transformations

A linear fractional transformation is a function of the form


\phi(z) = \frac{az+b}{cz+d}

where a,b,c,d are complex numbers and ad-bc\neq 0.

Properties of linear fractional transformations

Matrix form

A linear fractional transformation can be written as a matrix multiplication:


\phi(z) = \begin{bmatrix}
a & b\\
c & d\\
\end{bmatrix}
\begin{bmatrix}
z\\
1\\
\end{bmatrix}

Conformality

A linear fractional transformation is conformal.


\phi'(z) = \frac{ad-bc}{(cz+d)^2}

Three-fold transitivity

If z_1,z_2,z_3 are distinct points in the complex plane, then there exists a unique linear fractional transformation \phi such that \phi(z_1)=\infty, \phi(z_2)=0, \phi(z_3)=1.

The map is given by


\phi(z) =\begin{cases}
\frac{(z-z_2)(z_1-z_3)}{(z-z_1)(z_2-z_3)} & \text{if } z_1,z_2,z_3 \text{ are all finite}\\
\frac{z-z_2}{z_3-z_2} & \text{if } z_1=\infty\\
\frac{z_3-z_1}{z-z_1} & \text{if } z_2=\infty\\
\frac{z-z_2}{z-z_1} & \text{if } z_3=\infty\\
\end{cases}

So if z_1,z_2,z_3, w_1,w_2,w_3 are distinct points in the complex plane, then there exists a unique linear fractional transformation \phi such that \phi(z_i)=w_i for i=1,2,3.

Factorization

Every linear fractional transformation can be written as a composition of homothetic mappings, translations, inversions, and multiplications.

If \phi(z)=\frac{az+b}{cz+d}, then


\phi(z) = \frac{b-ad/c}{cz+d}+\frac{a}{c}

Clircle

A linear-fractional transformation maps circles and lines to circles and lines.

Chapter 4 Elementary Functions

Exponential function

The exponential function is defined as


e^z = \sum_{n=0}^\infty \frac{z^n}{n!}

Let z=x+iy, then


\begin{aligned}
e^z &= e^{x+iy}\\
&= e^x e^{iy}\\
&= e^x\sum_{n=0}^\infty \frac{(iy)^n}{n!}\\
&= e^x\sum_{n=0}^\infty \frac{(-1)^n y^{2n}}{(2n)!} + i \sum_{n=0}^\infty \frac{(-1)^n y^{2n+1}}{(2n+1)!}\\
&= e^x(\cos y + i\sin y)\\
\end{aligned}

So we can rewrite the polar form of a complex number as


z = r(\cos \theta + i\sin \theta) = re^{i\theta}

`e^x` is holomorphic

Let f(z)=e^z, then u(x,y)=e^x\cos y, v(x,y)=e^x\sin y.


\frac{\partial u}{\partial x} = e^x\cos y = \frac{\partial v}{\partial y}\\
\frac{\partial u}{\partial y} = -e^x\sin y = -\frac{\partial v}{\partial x}

Trigonometric functions


\sin z = \frac{e^{iz}-e^{-iz}}{2i}, \quad \cos z = \frac{e^{iz}+e^{-iz}}{2}, \quad \tan z = \frac{\sin z}{\cos z}


\sec z = \frac{1}{\cos z}, \quad \csc z = \frac{1}{\sin z}, \quad \cot z = \frac{1}{\tan z}

Hyperbolic functions


\sinh z = \frac{e^z-e^{-z}}{2}, \quad \cosh z = \frac{e^z+e^{-z}}{2}, \quad \tanh z = \frac{\sinh z}{\cosh z}


\operatorname{sech} z = \frac{1}{\cosh z}, \quad \operatorname{csch} z = \frac{1}{\sinh z}, \quad \operatorname{coth} z = \frac{1}{\tanh z}

Logarithmic function

The logarithmic function is defined as


\ln z=\{w\in\mathbb{C}: e^w=z\}

Properties of the logarithmic function

Let z=x+iy, then


|e^z|=\sqrt{e^x(\cos y)^2+(\sin y)^2}=e^x

So we have


\log z = \ln |z| + i\arg z

Power function

Inverse trigonometric functions

Chapter 5 Power Series

Definition of power series

A power series is a series of the form


\sum_{n=0}^\infty a_n (z-z_0)^n

Properties of power series

Geometric series


\sum_{n=0}^\infty z^n = \frac{1}{1-z}, \quad |z|<1

Radius/Region of convergence

Cauchy-Hadamard Theorem

Cauchy Product (of power series)

Chapter 6 Complex Integration

Definition of Riemann Integral for complex functions

The complex integral of a complex function \phi on the closed subinterval [a,b] of the real line is said to be piecewise continuous if there exists a partition a=t_0<t_1<\cdots<t_n=b such that \phi is continuous on each open interval (t_{i-1},t_i) and has a finite limit at each discontinuity point of the closed interval [a,b].

If \phi is piecewise continuous on [a,b], then the complex integral of \phi on [a,b] is defined as


\int_a^b \phi(t) dt = \int_a^b \operatorname{Re}\phi(t) dt + i\int_a^b \operatorname{Im}\phi(t) dt

Fundamental Theorem of Calculus

If \phi is piecewise continuous on [a,b], then


\int_a^b \phi'(t) dt = \phi(b)-\phi(a)

Triangle inequality


\left|\int_a^b \phi(t) dt\right| \leq \int_a^b |\phi(t)| dt

Integral on curve

Let \gamma be a piecewise smooth curve in the complex plane.

The integral of a complex function f on \gamma is defined as


\int_\gamma f(z) dz = \int_a^b f(\gamma(t))\gamma'(t) dt

13 KiB Raw Blame History