update

pages/CSE559A/CSE559A_L14.md

@@ -72,6 +72,4 @@ ROI alignment:
 - Align the proposal to the feature map.
 - Align the proposal to the feature map.
 
-Use bounding box regression to refine the proposal.
-
-
+Use bounding box regression to refine the proposal.

pages/CSE559A/CSE559A_L15.md

@@ -0,0 +1,31 @@
+# CSE559A Lecture 15
+
+## Continue on object detection
+
+### Two strategies for object detection
+
+#### R-CNN: Region proposals + CNN features
+
+![R-CNN](https://notenextra.trance-0.com/CSE559A/R-CNN.png)
+
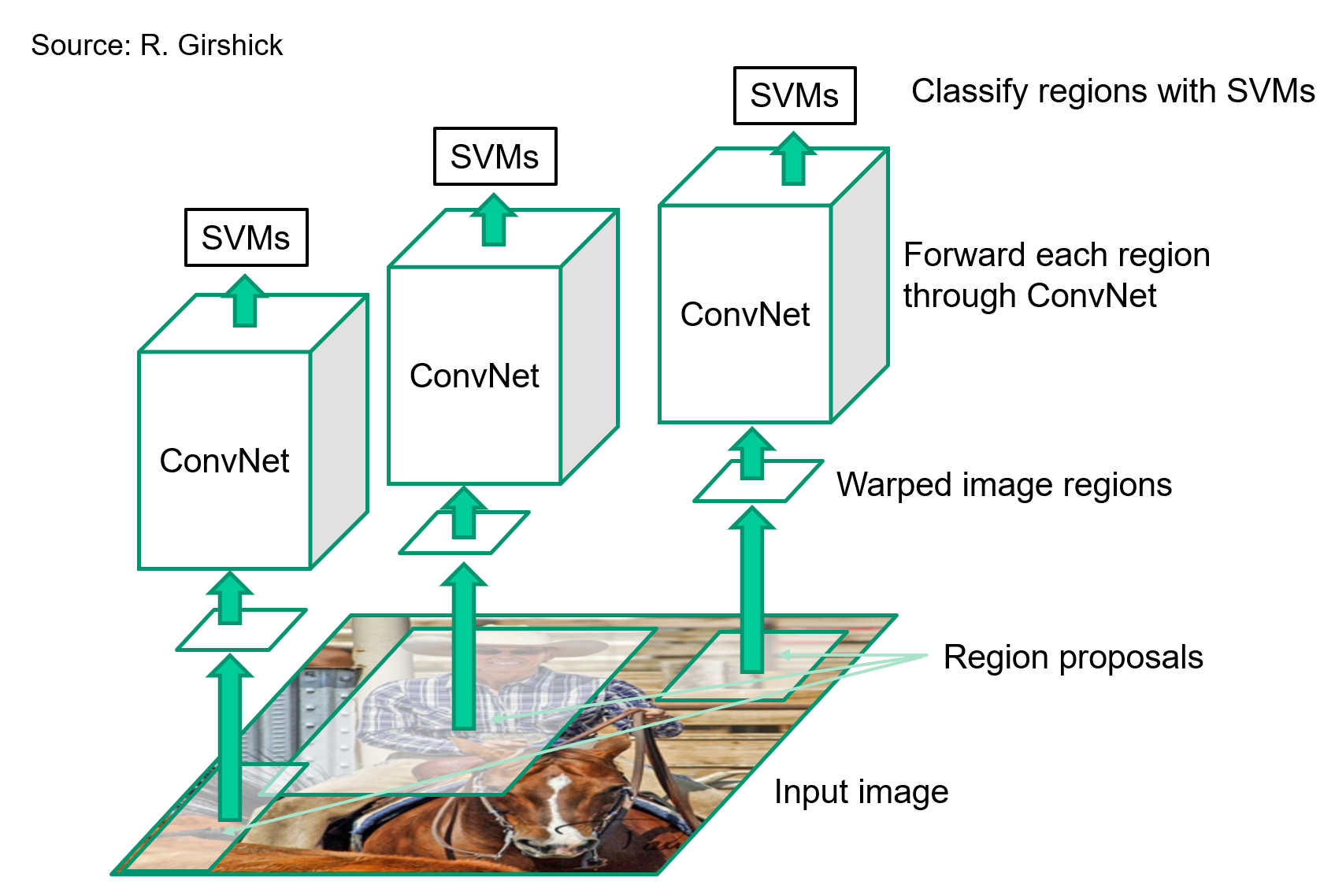
+#### Fast R-CNN: CNN features + RoI pooling
+
+![Fast R-CNN](https://notenextra.trance-0.com/CSE559A/Fast-R-CNN.png)
+
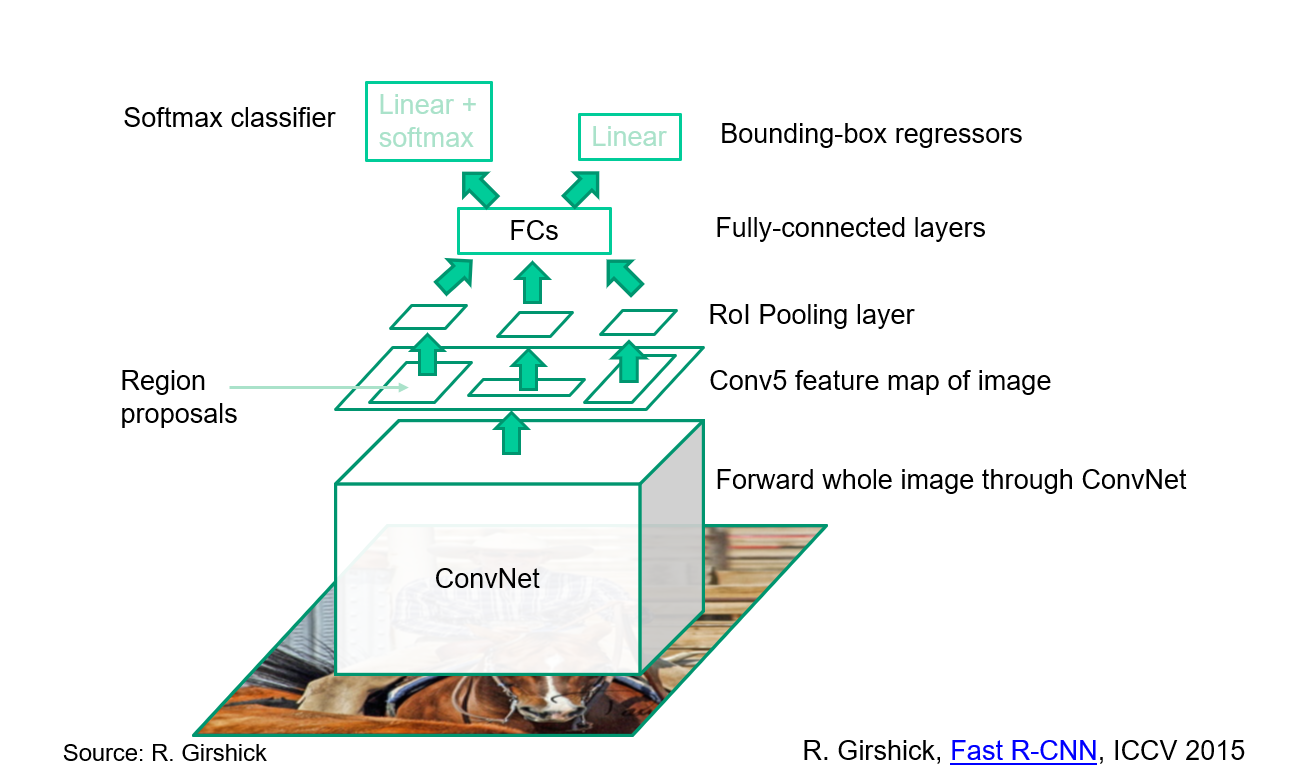
+Use bilinear interpolation to get the features of the proposal.
+
+#### Region of interest pooling
+
+![RoI pooling](https://notenextra.trance-0.com/CSE559A/RoI-pooling.png)
+
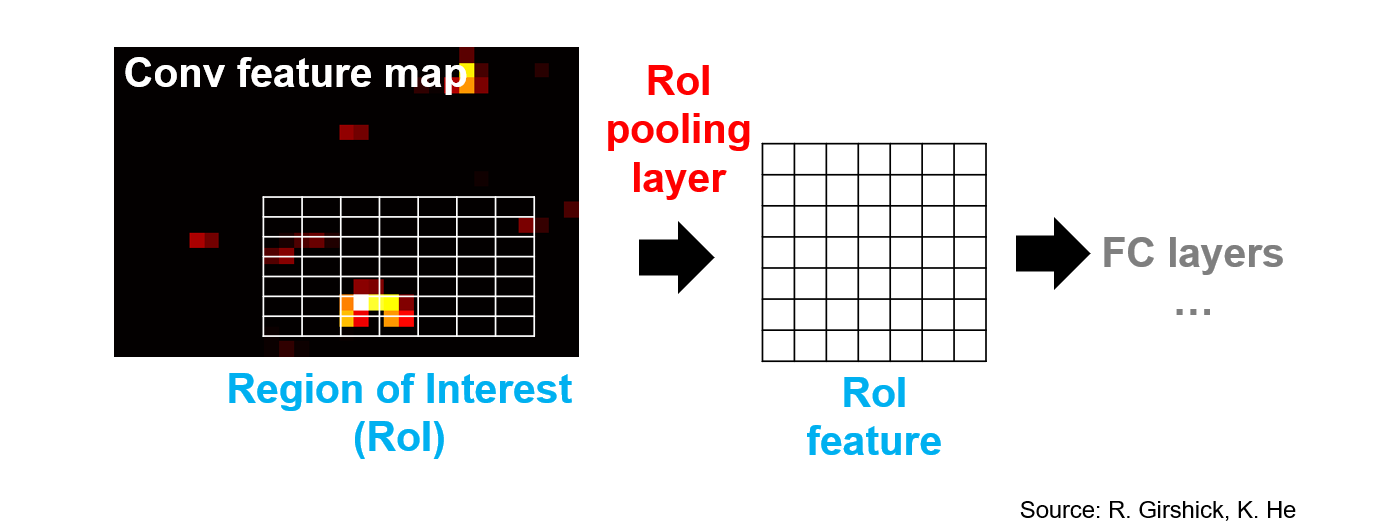
+Use backpropagation to get the gradient of the proposal.
+
+### New materials
+
+#### Faster R-CNN
+
+Use one CNN to generate region proposals. And use another CNN to classify the proposals.
+
+
+
+

pages/CSE559A/_meta.js

@@ -17,4 +17,5 @@ export default {
     CSE559A_L12: "Computer Vision (Lecture 12)",
     CSE559A_L13: "Computer Vision (Lecture 13)",
     CSE559A_L14: "Computer Vision (Lecture 14)",
+    CSE559A_L15: "Computer Vision (Lecture 15)",
 }

pages/Math4121/Math4121_L22.md

@@ -2,8 +2,6 @@
 
 ## Continue on Arzela-Osgood Theorem
 
-
-
 Proof:
 
 Part 2: Control the integral on $\mathcal{U}$
@@ -100,7 +98,7 @@ Part 2: If $f$ is pointwise discontinuous, then $\mathcal{D}$ is of first catego
 
 Let $P_k=\{x\in [a,b]: w(f;x)\geq \frac{1}{k}\}$, $\mathcal{D}=\bigcup_{k=1}^\infty P_k$.
 
-Need to show that each $P_k$ is nowhere dense. (under the assumption that $\mathcal{C)$ is dense).
+Need to show that each $P_k$ is nowhere dense. (under the assumption that $\mathcal{C}$ is dense).
 
 Let $I\subseteq [a,b]$ so $\exists c\in \mathcal{C}\cap I$. So by definition of $w(f;c)$, $\exists J\subseteq I$ and $c\in J$ such that $w(f;J)\leq \frac{1}{k}$ so for all $x\in J$, $w(f;x)\leq \frac{1}{k}$. so $J\subseteq P_k=\emptyset$.
 

pages/Math4121/Math4121_L23.md

@@ -1 +1,139 @@
-# Lecture 23
+# Math 4121 Lecture 23
+
+## Chapter 5 Measure Theory
+
+### Weierstrass idea
+
+Define
+
+$$
+S_f(x) = \{(x,y)\in \mathbb{R}^2: 0\leq y\leq f(x)\}
+$$
+
+We take the outer content in $\mathbb{R}^2$ of $S_f(x)$ to be the area of the largest rectangle that can be inscribed in $S_f(x)$.
+
+$$
+(w)\int_a^b f(x) dx = c_e(S_f(x))
+$$
+
+We can generalize this to higher dimensions.
+
+#### Definition volume of rectangle
+
+Let $R=I_1\times I_2\times \cdots \times I_n\in \mathbb{R}^n$ be a rectangle.
+
+The volume of $R$ is defined as
+
+$$
+\text{vol}(R) = \prod_{i=1}^n \ell(I_i)
+$$
+
+#### Definition of outer content
+
+For $S\subseteq \mathbb{R}^n$, we define the outer content of $S$ as
+
+$$
+c_e(S) = \inf_{\{R_j\}_{j=1}^N} \sum_{j=1}^N \text{vol}(R_j)
+$$
+
+where $S\subseteq \bigcup_{j=1}^N R_j$ and $R_j$ are rectangles.
+
+Note: $\overline{\int}f(x) dx=c_e(S_f(x))$
+
+#### Definition of inner content
+
+For $S\subseteq \mathbb{R}^n$, we define the inner content of $S$ as
+
+$$
+c_i(S) = \sup_{\{R_j\}_{j=1}^N} \sum_{j=1}^N \text{vol}(R_j)
+$$
+
+where $R_j$ are disjoint rectangles $\in \mathbb{R}^n$ and $\bigcup_{j=1}^N R_j\subseteq S$.
+
+Note: $\underline{\int}f(x) dx=c_i(S_f(x))$
+
+#### Definition of Jordan measurable set
+
+A set $S\subseteq \mathbb{R}^n$ is said to be _Jordan measurable_ if $c_e(S)=c_i(S)$.
+
+and we denote the common value **content** as $c_e(S)=c_i(S)=c(S)$.
+
+#### Definition of interior of a set
+
+The interior of a set $S\subseteq \mathbb{R}^n$ is defined as
+
+$$
+S^\circ = \{x\in \mathbb{R}^n: B_\delta(x)\subseteq S \text{ for some } \delta > 0\}
+$$
+
+_It is the largest open set contained in $S$._
+
+#### Definition of closure of a set
+
+The closure of a set $S\subseteq \mathbb{R}^n$ is defined as
+
+$$
+\overline{S} = S\cup S'
+$$
+
+or equivalently,
+
+$$
+\overline{S} = \{x\in \mathbb{R}^n: B_\delta(x)\cap S\neq \emptyset \text{ for all } \delta > 0\}
+$$
+
+where $S'$ is the set of all limit points of $S$.
+
+_It is the smallest closed set containing $S$._
+
+Homework problem: Complement of the closure of $S$ is the interior of the complement of $S$, i.e.,
+
+$$
+(\overline{S})^c = (S^c)^\circ
+$$
+
+#### Definition of boundary of a set
+
+The boundary of a set $S\subseteq \mathbb{R}^n$ is defined as
+
+$$
+\partial S = \overline{S}\setminus S^\circ
+$$
+
+#### Proposition 5.1 (Criterion for Jordan measurability)
+
+Let $S\subseteq \mathbb{R}^n$ be a bounded set. Then
+
+$$
+c_e(S) = c_i(S)+c_e(\partial S)
+$$
+
+So $S$ is Jordan measurable if and only if $c_e(\partial S)=0$.
+
+Proof:
+
+Let $\epsilon > 0$, and $\{R_j\}_{j=1}^N$ be an open cover of $\partial S$. such that $\sum_{j=1}^N \text{vol}(R_j) < c_e(\partial S)+\frac{\epsilon}{2}$.
+
+We slightly enlarge each $R_j$ to $Q_j$ such that $R_j\subseteq Q_j$ and $\text{vol}(Q_j)\leq \text{vol}(R_j)+\frac{\epsilon}{2N}$.
+
+and $dis(R_j,Q_j^c)>\delta > 0$
+
+If we could construct such $\{Q_j\}_{j=N+1}^M$ disjoint and
+
+$$
+\bigcup_{j=N+1}^M Q_j\subseteq S\subseteq \bigcup_{j=1}^M Q_j
+$$
+
+then we have
+
+$$
+c_e(S)\leq \sum_{j=1}^M \text{vol}(\partial S)+\epsilon +c_i(S)
+$$
+
+We can do this by constructing a set of square with side length $\eta$. We claim:
+
+If $\eta$ is small enough (depends on $\delta$), then $\mathcal{C}_\eta=\{Q\in K_\eta:Q\subset S\}$, $\mathcal{C}_\eta\cup \left(\bigcup_{j=1}^N Q_j\right)$ is a cover of $S$.
+
+Suppose $\exists x\in S$ but not in $\mathcal{C}_\eta$. Then $x$ is closed to $\partial S$ so in some $Q_j$. (This proof is not rigorous, but you get the idea. Also not clear in book actually.)
+
+EOP

pages/Math416/Math416_L15.md

@@ -34,7 +34,7 @@ Proof:
 
 Let $z_0\in G$. There exists a neighborhood $\overline{B_r(z_0)}\subset G$ of $z_0$ such that $\left(f_n\right)_{n\in\mathbb{N}}$ converges uniformly on $\overline{B_r(z_0)}$.
 
-Let $C_r=partial B_r(z_0)$.
+Let $C_r=\partial B_r(z_0)$.
 
 By Cauchy integral formula, we have
 
@@ -42,7 +42,7 @@ $$
 f_n(z_0) = \frac{1}{2\pi i}\int_{C_r}\frac{f_n(\zeta)}{\zeta-z_0}d\zeta
 $$
 
-$\forall z\in B_r(z_0)$, we have $\frac{f_n(w)}{w-\zeta}$ converges uniformly on $C_r$.
+$\forall z\in B_r(z_0)$, we have $\frac{f(w)}{w-\zeta}$ converges uniformly on $C_r$.
 
 So $\lim_{n\to\infty}f_n(z_0) = f(z_0) = \frac{1}{2\pi i}\int_{C_r}\frac{f(w)}{w-z_0}dw$
 

pages/Math416/Math416_L16.md

@@ -0,0 +1,163 @@
+# Math416 Lecture 16
+
+## Answer checking for exam
+
+### Q1
+
+Cauchy riemann equations:
+
+$$
+\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y}\quad\text{and}\quad\frac{\partial u}{\partial y} = -\frac{\partial v}{\partial x}
+$$
+
+Liouville's Theorem:
+
+Any non-constant entire function is unbounded.
+
+So $\cos(z)$ is unbounded in $\mathbb{C}$.
+
+$$
+\text{Log}(-e^2) = \ln|-e^2| + i\arg(-e^2) = -2 + \pi i
+$$
+
+At any point $z_0\in \mathbb{C}\setminus\{0\}$, there is an open set $z_0\in U\subset \mathbb{C}$ and a branch of logarithm defined on $U$.
+
+### Q2
+
+Power series expansion
+
+### Q3
+
+limit superior
+
+### Q4
+
+Bound integral
+
+### Q5
+
+$f_n$ converges pointwise to $f$ on $U$ if $\forall z\in U$, $\forall \epsilon > 0$, $\exists N$ s.t. $\forall n\geq N$, $|f_n(z)-f(z)| < \epsilon$.
+
+$f_n$ converges uniformly to $f$ on $U$ if $\forall \epsilon > 0$, $\exists N$ s.t. $\forall n\geq N$, $\forall z\in U$, $|f_n(z)-f(z)| < \epsilon$.
+
+Show for $|z|<1$, $f_n(z)=z^n$ converges pointwise to $0$ but not uniformly to $0$.
+
+(a) pointwise convergence:
+
+$|z^n| = |z|^n < \epsilon$ if $n > \frac{\ln\epsilon}{\ln|z|}$.
+
+(b) uniform convergence:
+
+No matter how small $\epsilon$ is, there is always a $z$ s.t. $|z^n| > \epsilon$ for all $n$.
+
+## Continue from last lecture
+
+### Schwarz's Lemma
+
+Let $f$ be an holomorphic function that maps the unit disk $D(0,1)$ to itself and $f(0)=0$. Then $|f(z)|\leq |z|$ for all $z\in D(0,1)$
+
+#### Schwarz-Pick's Lemma
+
+(see exercise 7.17.2)
+
+Let $f$ be an holomorphic function that maps the unit disk $D(0,1)$ to itself. Then $\forall z,w\in D(0,1)$,
+
+$$
+\left|\frac{f(z)-f(w)}{1-\overline{f(w)}f(z)}\right|\leq \left|\frac{z-w}{1-\overline{w}z}\right|
+$$
+
+> Recall the Möbius map
+>
+> $$\phi_\alpha(z) = \frac{z-\alpha}{1-\overline{\alpha}z}$$
+>
+> is a homeomorphism of the unit disk.
+> 
+> So we can use the Möbius to restate the Schwarz-Pick's Lemma as:
+>
+> $$|\phi_{f(w)}(f(z))|\leq |\phi_w(z)|$$
+
+Suppose we defined $g=\phi_{f(w)}\circ f\circ \phi_{-w}$, then $g$ is a holomorphic function that maps the unit disk to itself and $g(0)=0$.
+
+By Schwarz's Lemma, let $z\in D(0,1)$, $|g(z)|\leq |z|$.
+
+$$
+|\phi_{f(w)}(f(\phi_{-w}(z)))|\leq |z|
+$$
+
+Let $\zeta=\phi_{-w}(z)$, then $\zeta=\frac{z+w}{1+\overline{w}z}\in D(0,1)$, so $|\zeta|=\phi_w(z)$.
+
+#### Extension of Schwarz-Pick's Lemma in hyperbolic metric
+
+Suppose we defined the distance on $\mathbb{C}$ as $d(z,w)=|\frac{z-w}{1-\overline{w}z}|$.
+
+We claim that this is a metric on $\mathbb{C}$. $\forall z,w,v\in \mathbb{C}$:
+
+(a) $d(z,w)=0$ if and only if $z=w$ and $d(z,w)> 0$ otherwise.
+
+(b) $d(z,w)=d(w,z)$.
+
+(c) $d(z,w)\leq d(z,v)+d(v,w)$.
+
+We call this metric the Pseudo hyperbolic metric.
+
+> Hyperbolic metric:
+>
+> $$ \text{Hypdist}(z,w)=\tanh^{-1}(d(z,w))$$
+> 
+> Where $d(z,w)=|\frac{z-w}{1-\overline{w}z}|$
+
+So we can restate the Schwarz-Pick's Lemma as:
+
+$$
+d(f(z),f(w))\leq d(z,w)
+$$
+
+And in hyperbolic metric, it becomes:
+
+$$
+\text{Hypdist}(f(z),f(w))\leq \text{Hypdist}(z,w)
+$$
+
+Suppose the equality holds for Schwarz-Pick's Lemma, then $|g(z)|=\tau z$ where $|\tau|=1$.
+
+Computation ignored here.
+
+Then $f$ is a Möbius map that is automorphism of the unit disk.
+
+### Existence of harmonic conjugate
+
+Suppose $f=u+iv$ is holomorphic on a domain $U\subset \mathbb{C}$. Then $u=\text{Re}(f)$ is harmonic on $U$. That is $\Delta u=\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}=0$.
+
+#### Theorem 7.18
+
+Let $u$ be a real harmonic function on a convex domain $G\subset \mathbb{C}$. Then there exists $g\in O(G)$ such that $\text{Re}(g)=u$. Moreover, $g$ is unique up to an additive imaginary constant.
+
+Proof:
+
+Existence next time.
+
+Uniqueness:
+
+Suppose $g,h\in O(G)$ s.t. $\text{Re}(g)=\text{Re}(h)=u$.
+
+$\text{Re}g=u=\text{Re}h$ on $G$.
+
+If we can show that $(g-h)'=0$ on $G$, then we win.
+
+Let $g=u+iv$, $h=u+iw$.
+
+By the Cauchy-Riemann equations,
+
+$$
+\begin{aligned}
+\frac{\partial}{\partial x}(g-h)&=\frac{\partial}{\partial x}i(v-w)\\
+&=i\left(\frac{\partial u}{\partial y}-\frac{\partial u}{\partial y}\right)\\
+&=0
+\end{aligned}
+$$
+
+Suppose $G=\mathbb{C}\setminus\{0\}$, then $u=\ln|z|=\frac{1}{2}\ln(x^2+y^2)$, which is harmonic.
+
+Continue next time.
+
+

pages/Math416/_meta.js

@@ -19,4 +19,5 @@ export default {
     Math416_L13: "Complex Variables (Lecture 13)",
     Math416_L14: "Complex Variables (Lecture 14)",
     Math416_L15: "Complex Variables (Lecture 15)",
+    Math416_L16: "Complex Variables (Lecture 16)",
 }