214 lines
4.6 KiB
Markdown
214 lines
4.6 KiB
Markdown
# CSE559A Lecture 6
|
|
|
|
## Continue on Light, eye/camera, and color
|
|
|
|
### BRDF (Bidirectional Reflectance Distribution Function)
|
|
|
|
$$
|
|
\rho(\theta_i,\phi_i,\theta_o,\phi_o)
|
|
$$
|
|
|
|
#### Diffuse Reflection
|
|
|
|
- Dull, matte surface like chalk or latex paint
|
|
|
|
- Most often used in computer vision
|
|
- Brightness _does_ depend on direction of illumination
|
|
|
|
Diffuse reflection governed by Lambert's law: $I_d = k_d N\cdot L I_i$
|
|
|
|
- $N$: surface normal
|
|
- $L$: light direction
|
|
- $I_i$: incident light intensity
|
|
- $k_d$: albedo
|
|
|
|
$$
|
|
\rho(\theta_i,\phi_i,\theta_o,\phi_o)=k_d \cos\theta_i
|
|
$$
|
|
|
|
#### Photometric Stereo
|
|
|
|
Suppose there are three light sources, $L_1, L_2, L_3$, and we have the following measurements:
|
|
|
|
$$
|
|
I_1 = k_d N\cdot L_1
|
|
$$
|
|
|
|
$$
|
|
I_2 = k_d N\cdot L_2
|
|
$$
|
|
|
|
$$
|
|
I_3 = k_d N\cdot L_3
|
|
$$
|
|
|
|
We can solve for $N$ by taking the dot product of $N$ and each light direction and then solving the system of equations.
|
|
|
|
Will not do this in the lecture.
|
|
|
|
#### Specular Reflection
|
|
|
|
- Mirror-like surface
|
|
|
|
$$
|
|
I_e=\begin{cases}
|
|
I_i & \text{if } V=R \\
|
|
0 & \text{if } V\neq R
|
|
\end{cases}
|
|
$$
|
|
|
|
- $V$: view direction
|
|
- $R$: reflection direction
|
|
- $\theta_i$: angle between the incident light and the surface normal
|
|
|
|
Near-perfect mirror have a high light around $R$.
|
|
|
|
common model:
|
|
|
|
$$
|
|
I_e=k_s (V\cdot R)^{n_s}I_i
|
|
$$
|
|
|
|
- $k_s$: specular reflection coefficient
|
|
- $n_s$: shininess (imperfection of the surface)
|
|
- $I_i$: incident light intensity
|
|
|
|
#### Phong illumination model
|
|
|
|
- Phong approximation of surface reflectance
|
|
- Assume reflectance is modeled by three compoents
|
|
- Diffuse reflection
|
|
- Specular reflection
|
|
- Ambient reflection
|
|
|
|
$$
|
|
I_e=k_a I_a + I_i \left[k_d (N\cdot L) + k_s (V\cdot R)^{n_s}\right]
|
|
$$
|
|
|
|
- $k_a$: ambient reflection coefficient
|
|
- $I_a$: ambient light intensity
|
|
- $k_d$: diffuse reflection coefficient
|
|
- $k_s$: specular reflection coefficient
|
|
- $n_s$: shininess
|
|
- $I_i$: incident light intensity
|
|
|
|
Many other models.
|
|
|
|
#### Measuring BRDF
|
|
|
|
Use Gonioreflectometer.
|
|
|
|
- Device for measuring the reflectance of a surface as a function of the incident and reflected angles.
|
|
- Can be used to measure the BRDF of a surface.
|
|
|
|
BRDF dataset:
|
|
|
|
- MERL dataset
|
|
- CURET dataset
|
|
|
|
### Camera/Eye
|
|
|
|
#### DSLR Camera
|
|
|
|
- Pinhole camera model
|
|
- Lens
|
|
- Aperture (the pinhole)
|
|
- Sensor
|
|
- ...
|
|
|
|
#### Digital Camera block diagram
|
|
|
|
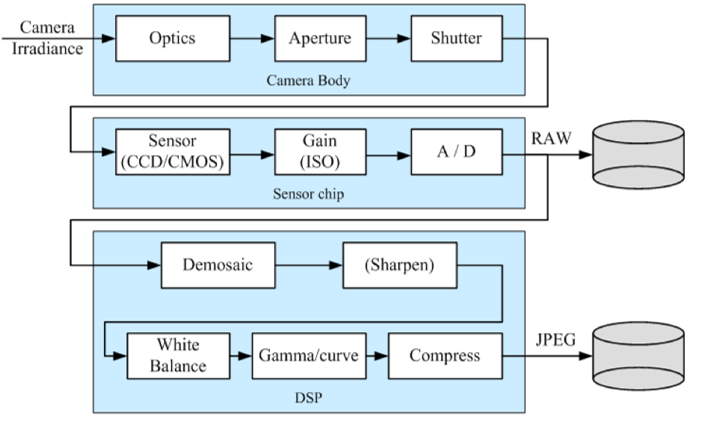
|
|
|
|
Scanning protocols:
|
|
|
|
- Global shutter: all pixels are exposed at the same time
|
|
- Interlaced: odd and even lines are exposed at different times
|
|
- Rolling shutter: each line is exposed as it is read out
|
|
|
|
#### Eye
|
|
|
|
- Pupil
|
|
- Iris
|
|
- Retina
|
|
- Rods and cones
|
|
- ...
|
|
|
|
#### Eye Movements
|
|
|
|
- Saccade
|
|
- Can be consciously controlled. Related to perceptual attention.
|
|
- 200ms to initiation, 20 to 200ms to carry out. Large amplitude.
|
|
- Smooth pursuit
|
|
- Tracking an object
|
|
- Difficult w/o an object to track!
|
|
- Microsaccade and Ocular microtremor (OMT)
|
|
- Involuntary. Smaller amplitude. Especially evident during prolonged
|
|
fixation.
|
|
|
|
#### Contrast Sensitivity
|
|
|
|
- Uniform contrast image content, with increasing frequency
|
|
- Why not uniform across the top?
|
|
- Low frequencies: harder to see because of slower intensity changes
|
|
- Higher frequencies: harder to see because of ability of our visual system to resolve fine features
|
|
|
|
### Color Perception
|
|
|
|
Visible light spectrum: 380 to 780 nm
|
|
|
|
- 400 to 500 nm: blue
|
|
- 500 to 600 nm: green
|
|
- 600 to 700 nm: red
|
|
|
|
#### HSV model
|
|
|
|
We use Gaussian functions to model the sensitivity of the human eye to different wavelengths.
|
|
|
|
- Hue: color (the wavelength of the highest peak of the sensitivity curve)
|
|
- Saturation: color purity (the variance of the sensitivity curve)
|
|
- Value: color brightness (the highest peak of the sensitivity curve)
|
|
|
|
#### Color Sensing in Camera (RGB)
|
|
|
|
- 3-chip vs. 1-chip: quality vs. cost
|
|
|
|
Bayer filter:
|
|
|
|
- Why more green?
|
|
- Human eye is more sensitive to green light.
|
|
|
|
#### Color spaces
|
|
|
|
Images in python:
|
|
|
|
As matrix.
|
|
|
|
```python
|
|
import matplotlib.pyplot as plt
|
|
|
|
from mpl_toolkits.mplot3d import Axes3D
|
|
from skimage import io
|
|
|
|
def plot_rgb_3d(image_path):
|
|
image = io.imread(image_path)
|
|
r, g, b = image[:,:,0], image[:,:,1], image[:,:,2]
|
|
fig = plt.figure()
|
|
ax = fig.add_subplot(111, projection='3d')
|
|
ax.scatter(r.flatten(), g.flatten(), b.flatten(), c=image.reshape(-1, 3)/255.0, marker='.')
|
|
ax.set_xlabel('Red')
|
|
ax.set_ylabel('Green')
|
|
ax.set_zlabel('Blue')
|
|
plt.show()
|
|
|
|
plot_rgb_3d('image.jpg')
|
|
```
|
|
|
|
Other color spaces:
|
|
|
|
- YCbCr (fast to compute, usually used in TV)
|
|
- HSV
|
|
- L\*a\*b\* (CIELAB, perceptually uniform color space)
|
|
|
|
Most information is in the intensity channel.
|