841 lines
20 KiB
Markdown
841 lines
20 KiB
Markdown
# Math 416 Midterm 1 Review
|
|
|
|
So everything we have learned so far is to extend the real line to the complex plane.
|
|
|
|
## Chapter 0 Calculus on Real values
|
|
|
|
### Differentiation
|
|
|
|
Let $f,g$ be function on real line and $c$ be a real number.
|
|
|
|
$$
|
|
\frac{d}{dx}(f+g)=f'+g'
|
|
$$
|
|
|
|
$$
|
|
\frac{d}{dx}(cf)=cf'
|
|
$$
|
|
|
|
$$
|
|
\frac{d}{dx}(fg)=f'g+fg'
|
|
$$
|
|
|
|
$$
|
|
\frac{d}{dx}(f/g)=(f'g-fg')/g^2
|
|
$$
|
|
|
|
$$
|
|
\frac{d}{dx}(f\circ g)=(f'\circ g)\frac{d}{dx}g
|
|
$$
|
|
|
|
$$
|
|
\frac{d}{dx}x^n=nx^{n-1}
|
|
$$
|
|
|
|
$$
|
|
\frac{d}{dx}e^x=e^x
|
|
$$
|
|
|
|
$$
|
|
\frac{d}{dx}\ln x=\frac{1}{x}
|
|
$$
|
|
|
|
$$
|
|
\frac{d}{dx}\sin x=\cos x
|
|
$$
|
|
|
|
$$
|
|
\frac{d}{dx}\cos x=-\sin x
|
|
$$
|
|
|
|
$$
|
|
\frac{d}{dx}\tan x=\sec^2 x
|
|
$$
|
|
|
|
$$
|
|
\frac{d}{dx}\sec x=\sec x\tan x
|
|
$$
|
|
|
|
$$
|
|
\frac{d}{dx}\csc x=-\csc x\cot x
|
|
$$
|
|
|
|
$$
|
|
\frac{d}{dx}\sinh x=\cosh x
|
|
$$
|
|
|
|
$$
|
|
\frac{d}{dx}\cosh x=\sinh x
|
|
$$
|
|
|
|
$$
|
|
\frac{d}{dx}\tanh x=\operatorname{sech}^2 x
|
|
$$
|
|
|
|
$$
|
|
\frac{d}{dx}\operatorname{sech} x=-\operatorname{sech}x\tanh x
|
|
$$
|
|
|
|
$$
|
|
\frac{d}{dx}\operatorname{csch} x=-\operatorname{csch}x\coth x
|
|
$$
|
|
|
|
$$
|
|
\frac{d}{dx}\coth x=-\operatorname{csch}^2 x
|
|
$$
|
|
|
|
$$
|
|
\frac{d}{dx}\arcsin x=\frac{1}{\sqrt{1-x^2}}
|
|
$$
|
|
|
|
$$
|
|
\frac{d}{dx}\arccos x=-\frac{1}{\sqrt{1-x^2}}
|
|
$$
|
|
|
|
$$
|
|
\frac{d}{dx}\arctan x=\frac{1}{1+x^2}
|
|
$$
|
|
|
|
$$
|
|
\frac{d}{dx}\operatorname{arccot} x=-\frac{1}{1+x^2}
|
|
$$
|
|
|
|
$$
|
|
\frac{d}{dx}\operatorname{arcsec} x=\frac{1}{x\sqrt{x^2-1}}
|
|
$$
|
|
|
|
$$
|
|
\frac{d}{dx}\operatorname{arccsc} x=-\frac{1}{x\sqrt{x^2-1}}
|
|
$$
|
|
|
|
### Integration
|
|
|
|
Let $f,g$ be function on real line and $c$ be a real number.
|
|
|
|
$$
|
|
\int (f+g)dx=\int fdx+\int gdx
|
|
$$
|
|
|
|
$$
|
|
\int cfdx=c\int fdx
|
|
$$
|
|
|
|
$$
|
|
\int e^x dx=e^x
|
|
$$
|
|
|
|
$$
|
|
\int \ln x dx=x\ln x-x
|
|
$$
|
|
|
|
$$
|
|
\int \frac{1}{x} dx=\ln|x|
|
|
$$
|
|
|
|
$$
|
|
\int \sin x dx=-\cos x
|
|
$$
|
|
|
|
$$
|
|
\int \cos x dx=\sin x
|
|
$$
|
|
|
|
$$
|
|
\int \tan x dx=-\ln|\cos x|
|
|
$$
|
|
|
|
$$
|
|
\int \cot x dx=\ln|\sin x|
|
|
$$
|
|
|
|
$$
|
|
\int \sec x dx=\ln|\sec x+\tan x|
|
|
$$
|
|
|
|
$$
|
|
\int \csc x dx=\ln|\csc x-\cot x|
|
|
$$
|
|
|
|
$$
|
|
\int \sinh x dx=\cosh x
|
|
$$
|
|
|
|
$$
|
|
\int \cosh x dx=\sinh x
|
|
$$
|
|
|
|
$$
|
|
\int \tanh x dx=\ln|\cosh x|
|
|
$$
|
|
|
|
$$
|
|
\int \coth x dx=\ln|\sinh x|
|
|
$$
|
|
|
|
$$
|
|
\int \operatorname{sech} x dx=2\arctan(\tanh(x/2))
|
|
$$
|
|
|
|
$$
|
|
\int \operatorname{csch} x dx=\ln|\coth x-\operatorname{csch} x|
|
|
$$
|
|
|
|
$$
|
|
\int \operatorname{sech}^2 x dx=\tanh x
|
|
$$
|
|
|
|
$$
|
|
\int \operatorname{csch}^2 x dx=-\coth x
|
|
$$
|
|
|
|
$$
|
|
\int \frac{1}{1+x^2} dx=\arctan x
|
|
$$
|
|
|
|
$$
|
|
\int \frac{1}{x^2+1} dx=\arctan x
|
|
$$
|
|
|
|
$$
|
|
\int \frac{1}{x^2-1} dx=\frac{1}{2}\ln|\frac{x-1}{x+1}|
|
|
$$
|
|
|
|
$$
|
|
\int \frac{1}{x^2-a^2} dx=\frac{1}{2a}\ln|\frac{x-a}{x+a}|
|
|
$$
|
|
|
|
$$
|
|
\int \frac{1}{x^2+a^2} dx=\frac{1}{a}\arctan(\frac{x}{a})
|
|
$$
|
|
|
|
$$
|
|
\int \frac{1}{\sqrt{x^2-a^2}} dx=\ln|x+\sqrt{x^2-a^2}|
|
|
$$
|
|
|
|
$$
|
|
\int \frac{1}{\sqrt{x^2+a^2}} dx=\ln|x+\sqrt{x^2+a^2}|
|
|
$$
|
|
|
|
## Chapter 1 Complex Numbers
|
|
|
|
### Definition of complex numbers
|
|
|
|
An ordered pair of real numbers $(x, y)$ can be represented as a complex number $z = x + yi$, where $i$ is the imaginary unit.
|
|
|
|
With operations defined as:
|
|
|
|
$$
|
|
(x_1 + y_1i) + (x_2 + y_2i) = (x_1 + x_2) + (y_1 + y_2)i
|
|
$$
|
|
|
|
$$
|
|
(x_1 + y_1i) \cdot (x_2 + y_2i) = (x_1x_2 - y_1y_2) + (x_1y_2 + x_2y_1)i
|
|
$$
|
|
|
|
#### Modulus
|
|
|
|
The modulus of a complex number $z = x + yi$ is defined as
|
|
|
|
$$
|
|
|z| = \sqrt{x^2 + y^2}=|z\overline{z}|
|
|
$$
|
|
|
|
### De Moivre's Formula
|
|
|
|
Every complex number $z$ can be written as $z = r(\cos \theta + i \sin \theta)$, where $r$ is the magnitude of $z$ and $\theta$ is the argument of $z$.
|
|
|
|
$$
|
|
z^n = r^n(\cos n\theta + i \sin n\theta)
|
|
$$
|
|
|
|
The De Moivre's formula is useful for finding the $n$th roots of a complex number.
|
|
|
|
$$
|
|
z^n = r^n(\cos n\theta + i \sin n\theta)
|
|
$$
|
|
|
|
### Roots of complex numbers
|
|
|
|
Using De Moivre's formula, we can find the $n$th roots of a complex number.
|
|
|
|
If $z=r(\cos \theta + i \sin \theta)$, then the $n$th roots of $z$ are given by:
|
|
|
|
$$
|
|
z_k = r^{1/n}(\cos \frac{\theta + 2k\pi}{n} + i \sin \frac{\theta + 2k\pi}{n})
|
|
$$
|
|
|
|
for $k = 0, 1, 2, \ldots, n-1$.
|
|
|
|
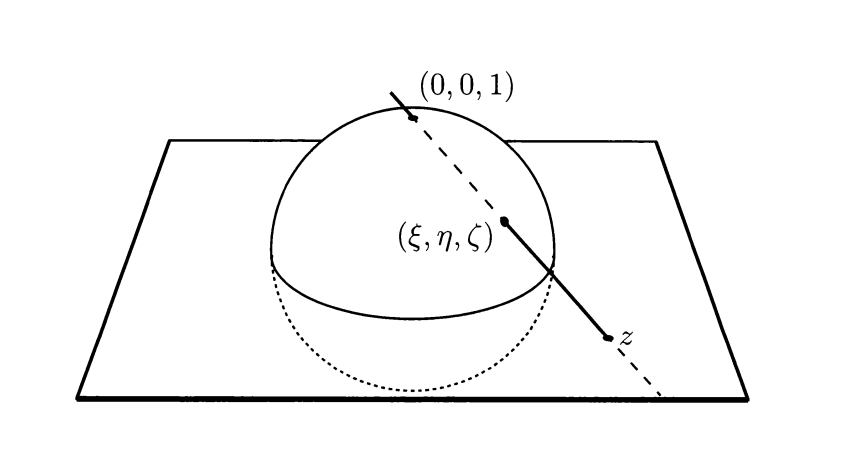
### Stereographic projection
|
|
|
|
|
|
|
|
The stereographic projection is a map from the unit sphere $S^2$ to the complex plane $\mathbb{C}\setminus\{0\}$.
|
|
|
|
The projection is given by:
|
|
|
|
$$
|
|
z\mapsto \frac{(2Re(z), 2Im(z), |z|^2-1)}{|z|^2+1}
|
|
$$
|
|
|
|
The inverse map is given by:
|
|
|
|
$$
|
|
(\xi,\eta, \zeta)\mapsto \frac{\xi + i\eta}{1 - \zeta}
|
|
$$
|
|
|
|
## Chapter 2 Complex Differentiation
|
|
|
|
### Definition of complex differentiation
|
|
|
|
Let the complex plane $\mathbb{C}$ be defined in an open subset $G$ of $\mathbb{C}$. (Domain)
|
|
|
|
Then $f$ is said to be differentiable at $z_0\in G$ if the limit
|
|
|
|
$$
|
|
\lim_{z\to z_0} \frac{f(z)-f(z_0)}{z-z_0}
|
|
$$
|
|
|
|
exists.
|
|
|
|
The limit is called the derivative of $f$ at $z_0$ and is denoted by $f'(z_0)$.
|
|
|
|
To prove that a function is differentiable, we can use the standard delta-epsilon definition of a limit.
|
|
|
|
$$
|
|
\left|\frac{f(z)-f(z_0)}{z-z_0} - f'(z_0)\right| < \epsilon
|
|
$$
|
|
|
|
whenever $0 < |z-z_0| < \delta$.
|
|
|
|
With such definition, all the properties of real differentiation can be extended to complex differentiation.
|
|
|
|
#### Differentiation of complex functions
|
|
|
|
1. If $f$ is differentiable at $z_0$, then $f$ is continuous at $z_0$.
|
|
2. If $f,g$ are differentiable at $z_0$, then $f+g, fg$ are differentiable at $z_0$.
|
|
$$
|
|
(f+g)'(z_0) = f'(z_0) + g'(z_0)
|
|
$$
|
|
$$
|
|
(fg)'(z_0) = f'(z_0)g(z_0) + f(z_0)g'(z_0)
|
|
$$
|
|
3. If $f,g$ are differentiable at $z_0$ and $g(z_0)\neq 0$, then $f/g$ is differentiable at $z_0$.
|
|
$$
|
|
\left(\frac{f}{g}\right)'(z_0) = \frac{f'(z_0)g(z_0) - f(z_0)g'(z_0)}{g(z_0)^2}
|
|
$$
|
|
4. If $f$ is differentiable at $z_0$ and $g$ is differentiable at $f(z_0)$, then $g\circ f$ is differentiable at $z_0$.
|
|
$$
|
|
(g\circ f)'(z_0) = g'(f(z_0))f'(z_0)
|
|
$$
|
|
5. If $f(z)=\sum_{k=0}^n c_k(z-z_0)^k$, where $c_k\in\mathbb{C}$, then $f$ is differentiable at $z_0$ and $f'(z_0)=\sum_{k=1}^n kc_k(z_0-z_0)^{k-1}$.
|
|
$$
|
|
f'(z_0) = c_1 + 2c_2(z_0-z_0) + 3c_3(z_0-z_0)^2 + \cdots + nc_n(z_0-z_0)^{n-1}
|
|
$$
|
|
|
|
### Cauchy-Riemann Equations
|
|
|
|
Let the function defined on an open subset $G$ of $\mathbb{C}$ be $f(x,y)=u(x,y)+iv(x,y)$, where $u,v$ are real-valued functions.
|
|
|
|
Then $f$ is differentiable at $z_0=x_0+y_0i$ if and only if the partial derivatives of $u$ and $v$ exist at $(x_0,y_0)$ and satisfy the Cauchy-Riemann equations:
|
|
|
|
$$
|
|
\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y}, \quad \frac{\partial u}{\partial y} = -\frac{\partial v}{\partial x}
|
|
$$
|
|
|
|
On the polar form, the Cauchy-Riemann equations are
|
|
|
|
$$
|
|
r\frac{\partial u}{\partial r} = \frac{\partial v}{\partial \theta}, \quad \frac{\partial u}{\partial \theta} = -r\frac{\partial v}{\partial r}
|
|
$$
|
|
|
|
### Holomorphic functions
|
|
|
|
A function $f$ is said to be holomorphic on an open subset $G$ of $\mathbb{C}$ if $f$ is differentiable at every point of $G$.
|
|
|
|
#### Partial differential operators
|
|
|
|
$$
|
|
\frac{\partial}{\partial z} = \frac{1}{2}\left(\frac{\partial}{\partial x} - i\frac{\partial}{\partial y}\right)
|
|
$$
|
|
|
|
$$
|
|
\frac{\partial}{\partial \bar{z}} = \frac{1}{2}\left(\frac{\partial}{\partial x} + i\frac{\partial}{\partial y}\right)
|
|
$$
|
|
|
|
This gives that
|
|
|
|
$$
|
|
\frac{\partial f}{\partial z} = \frac{1}{2}\left(\frac{\partial f}{\partial x} - i\frac{\partial f}{\partial y}\right)=\frac{1}{2}\left(\frac{\partial u}{\partial x} +\frac{\partial v}{\partial y}\right) + \frac{i}{2}\left(\frac{\partial v}{\partial x} - \frac{\partial u}{\partial y}\right)
|
|
$$
|
|
|
|
$$
|
|
\frac{\partial f}{\partial \bar{z}} = \frac{1}{2}\left(\frac{\partial f}{\partial x} + i\frac{\partial f}{\partial y}\right)=\frac{1}{2}\left(\frac{\partial u}{\partial x} - \frac{\partial v}{\partial y}\right) + \frac{i}{2}\left(\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}\right)
|
|
$$
|
|
|
|
If the function $f$ is holomorphic, then by the Cauchy-Riemann equations, we have
|
|
|
|
$$
|
|
\frac{\partial f}{\partial \bar{z}} = 0
|
|
$$
|
|
|
|
### Conformal mappings
|
|
|
|
A holomorphic function $f$ is said to be conformal if it preserves the angles between the curves. More formally, if $f$ is holomorphic on an open subset $G$ of $\mathbb{C}$ and $z_0\in G$, $\gamma_1, \gamma_2$ are two curves passing through $z_0$ ($\gamma_1(t_1)=\gamma_2(t_2)=z_0$) and intersecting at an angle $\theta$, then
|
|
|
|
$$
|
|
\arg(f\circ\gamma_1)'(t_1) - \arg(f\circ\gamma_2)'(t_2) = \theta
|
|
$$
|
|
|
|
In other words, the angle between the curves is preserved.
|
|
|
|
An immediate consequence is that
|
|
|
|
$$
|
|
\arg(f\cdot \gamma_1)'(t_1) =\arg f'(z_0) + \arg \gamma_1'(t_1)\\
|
|
\arg(f\cdot \gamma_2)'(t_2) =\arg f'(z_0) + \arg \gamma_2'(t_2)
|
|
$$
|
|
|
|
### Harmonic functions
|
|
|
|
A real-valued function $u$ is said to be harmonic if it satisfies the Laplace equation:
|
|
|
|
$$
|
|
\frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = 0
|
|
$$
|
|
|
|
## Chapter 3 Linear Fractional Transformations
|
|
|
|
### Definition of linear fractional transformations
|
|
|
|
A linear fractional transformation is a function of the form
|
|
|
|
$$
|
|
\phi(z) = \frac{az+b}{cz+d}
|
|
$$
|
|
|
|
where $a,b,c,d$ are complex numbers and $ad-bc\neq 0$.
|
|
|
|
### Properties of linear fractional transformations
|
|
|
|
#### Matrix form
|
|
|
|
A linear fractional transformation can be written as a matrix multiplication:
|
|
|
|
$$
|
|
\phi(z) = \begin{bmatrix}
|
|
a & b\\
|
|
c & d\\
|
|
\end{bmatrix}
|
|
\begin{bmatrix}
|
|
z\\
|
|
1\\
|
|
\end{bmatrix}
|
|
$$
|
|
|
|
#### Conformality
|
|
|
|
A linear fractional transformation is conformal.
|
|
|
|
$$
|
|
\phi'(z) = \frac{ad-bc}{(cz+d)^2}
|
|
$$
|
|
|
|
#### Three-fold transitivity
|
|
|
|
If $z_1,z_2,z_3$ are distinct points in the complex plane, then there exists a unique linear fractional transformation $\phi$ such that $\phi(z_1)=\infty$, $\phi(z_2)=0$, $\phi(z_3)=1$.
|
|
|
|
The map is given by
|
|
|
|
$$
|
|
\phi(z) =\begin{cases}
|
|
\frac{(z-z_2)(z_1-z_3)}{(z-z_1)(z_2-z_3)} & \text{if } z_1,z_2,z_3 \text{ are all finite}\\
|
|
\frac{z-z_2}{z_3-z_2} & \text{if } z_1=\infty\\
|
|
\frac{z_3-z_1}{z-z_1} & \text{if } z_2=\infty\\
|
|
\frac{z-z_2}{z-z_1} & \text{if } z_3=\infty\\
|
|
\end{cases}
|
|
$$
|
|
|
|
So if $z_1,z_2,z_3$, $w_1,w_2,w_3$ are distinct points in the complex plane, then there exists a unique linear fractional transformation $\phi$ such that $\phi(z_i)=w_i$ for $i=1,2,3$.
|
|
|
|
#### Factorization
|
|
|
|
Every linear fractional transformation can be written as a composition of homothetic mappings, translations, inversions, and multiplications.
|
|
|
|
If $\phi(z)=\frac{az+b}{cz+d}$, then
|
|
|
|
$$
|
|
\phi(z) = \frac{b-ad/c}{cz+d}+\frac{a}{c}
|
|
$$
|
|
|
|
#### Clircle
|
|
|
|
A linear-fractional transformation maps circles and lines to circles and lines.
|
|
|
|
## Chapter 4 Elementary Functions
|
|
|
|
### Exponential function
|
|
|
|
The exponential function is defined as
|
|
|
|
$$
|
|
e^z = \sum_{n=0}^\infty \frac{z^n}{n!}
|
|
$$
|
|
|
|
Let $z=x+iy$, then
|
|
|
|
$$
|
|
\begin{aligned}
|
|
e^z &= e^{x+iy}\\
|
|
&= e^x e^{iy}\\
|
|
&= e^x\sum_{n=0}^\infty \frac{(iy)^n}{n!}\\
|
|
&= e^x\sum_{n=0}^\infty \frac{(-1)^n y^{2n}}{(2n)!} + i \sum_{n=0}^\infty \frac{(-1)^n y^{2n+1}}{(2n+1)!}\\
|
|
&= e^x(\cos y + i\sin y)\\
|
|
\end{aligned}
|
|
$$
|
|
|
|
So we can rewrite the polar form of a complex number as
|
|
|
|
$$
|
|
z = r(\cos \theta + i\sin \theta) = re^{i\theta}
|
|
$$
|
|
|
|
#### $e^x$ is holomorphic
|
|
|
|
Let $f(z)=e^z$, then $u(x,y)=e^x\cos y$, $v(x,y)=e^x\sin y$.
|
|
|
|
$$
|
|
\frac{\partial u}{\partial x} = e^x\cos y = \frac{\partial v}{\partial y}\\
|
|
\frac{\partial u}{\partial y} = -e^x\sin y = -\frac{\partial v}{\partial x}
|
|
$$
|
|
|
|
### Trigonometric functions
|
|
|
|
$$
|
|
\sin z = \frac{e^{iz}-e^{-iz}}{2i}, \quad \cos z = \frac{e^{iz}+e^{-iz}}{2}, \quad \tan z = \frac{\sin z}{\cos z}
|
|
$$
|
|
|
|
$$
|
|
\sec z = \frac{1}{\cos z}, \quad \csc z = \frac{1}{\sin z}, \quad \cot z = \frac{1}{\tan z}
|
|
$$
|
|
|
|
#### Hyperbolic functions
|
|
|
|
$$
|
|
\sinh z = \frac{e^z-e^{-z}}{2}, \quad \cosh z = \frac{e^z+e^{-z}}{2}, \quad \tanh z = \frac{\sinh z}{\cosh z}
|
|
$$
|
|
|
|
$$
|
|
\operatorname{sech} z = \frac{1}{\cosh z}, \quad \operatorname{csch} z = \frac{1}{\sinh z}, \quad \operatorname{coth} z = \frac{1}{\tanh z}
|
|
$$
|
|
|
|
### Logarithmic function
|
|
|
|
The logarithmic function is defined as
|
|
|
|
$$
|
|
\ln z=\{w\in\mathbb{C}: e^w=z\}
|
|
$$
|
|
|
|
#### Properties of the logarithmic function
|
|
|
|
Let $z=x+iy$, then
|
|
|
|
$$
|
|
|e^z|=\sqrt{e^x(\cos y)^2+(\sin y)^2}=e^x
|
|
$$
|
|
|
|
So we have
|
|
|
|
$$
|
|
\log z = \ln |z| + i\arg z
|
|
$$
|
|
|
|
### Power function
|
|
|
|
For any two complex numbers $a,b$, we can define the power function as
|
|
|
|
$$
|
|
a^b = e^{b\log a}
|
|
$$
|
|
|
|
> Example:
|
|
>
|
|
> $$i^i=e^{i\ln i}=e^{i(\ln 1+i\frac{\pi}{2})}=e^{-\frac{\pi}{2}} $$
|
|
>
|
|
> $$e^{i\pi}=-1$$
|
|
|
|
|
|
## Chapter 5 Power Series
|
|
|
|
### Definition of power series
|
|
|
|
A power series is a series of the form
|
|
|
|
$$
|
|
\sum_{n=0}^\infty a_n (z-z_0)^n
|
|
$$
|
|
|
|
### Properties of power series
|
|
|
|
#### Geometric series
|
|
|
|
$$
|
|
\sum_{n=0}^\infty z^n = \frac{1}{1-z}, \quad |z|<1
|
|
$$
|
|
|
|
### Radius/Region of convergence
|
|
|
|
The radius of convergence of a power series is the largest number $R$ such that the series converges for all $z$ with $|z-z_0|<R$.
|
|
|
|
The region of convergence of a power series is the set of all points $z$ such that the series converges.
|
|
|
|
### Cauchy-Hadamard Theorem
|
|
|
|
The radius of convergence of a power series is given by
|
|
|
|
$$
|
|
R=\frac{1}{\limsup_{n\to\infty} |a_n|^{1/n}}
|
|
$$
|
|
|
|
### Derivative of power series
|
|
|
|
The derivative of a power series is given by
|
|
|
|
$$
|
|
f'(z)=\sum_{n=1}^\infty n a_n (z-z_0)^{n-1}
|
|
$$
|
|
|
|
### Cauchy Product (of power series)
|
|
|
|
Let $\sum_{n=0}^\infty a_n (z-z_0)^n$ and $\sum_{n=0}^\infty b_n (z-z_0)^n$ be two power series with radius of convergence $R_1$ and $R_2$ respectively.
|
|
|
|
Then the Cauchy product of the two series is given by
|
|
|
|
$$
|
|
\sum_{n=0}^\infty c_n (z-z_0)^n
|
|
$$
|
|
|
|
where
|
|
|
|
$$
|
|
c_n = \sum_{k=0}^n a_k b_{n-k}
|
|
$$
|
|
|
|
The radius of convergence of the Cauchy product is at least $\min(R_1,R_2)$.
|
|
|
|
## Chapter 6 Complex Integration
|
|
|
|
### Definition of Riemann Integral for complex functions
|
|
|
|
The complex integral of a complex function $\phi$ on the closed subinterval $[a,b]$ of the real line is said to be piecewise continuous if there exists a partition $a=t_0<t_1<\cdots<t_n=b$ such that $\phi$ is continuous on each open interval $(t_{i-1},t_i)$ and has a finite limit at each discontinuity point of the closed interval $[a,b]$.
|
|
|
|
If $\phi$ is piecewise continuous on $[a,b]$, then the complex integral of $\phi$ on $[a,b]$ is defined as
|
|
|
|
$$
|
|
\int_a^b \phi(t) dt = \int_a^b \operatorname{Re}\phi(t) dt + i\int_a^b \operatorname{Im}\phi(t) dt
|
|
$$
|
|
|
|
### Fundamental Theorem of Calculus
|
|
|
|
If $\phi$ is piecewise continuous on $[a,b]$, then
|
|
|
|
$$
|
|
\int_a^b \phi'(t) dt = \phi(b)-\phi(a)
|
|
$$
|
|
|
|
### Triangle inequality
|
|
|
|
$$
|
|
\left|\int_a^b \phi(t) dt\right| \leq \int_a^b |\phi(t)| dt
|
|
$$
|
|
|
|
### Integral on curve
|
|
|
|
Let $\gamma$ be a piecewise smooth curve in the complex plane.
|
|
|
|
The integral of a complex function $f$ on $\gamma$ is defined as
|
|
|
|
$$
|
|
\int_\gamma f(z) dz = \int_a^b f(\gamma(t))\gamma'(t) dt
|
|
$$
|
|
|
|
### Favorite estimate
|
|
|
|
Let $\gamma:[a,b]\to\mathbb{C}$ be a piecewise smooth curve, and let $f:[a,b]\to\mathbb{C}$ be a continuous complex-valued function. Let $M$ be a real number such that $|f(z)|\leq M$ for all $z\in\gamma$. Then
|
|
|
|
$$
|
|
\left|\int_\gamma f(z) dz\right| \leq M\ell(\gamma)
|
|
$$
|
|
|
|
where $\ell(\gamma)$ is the length of the curve $\gamma$.
|
|
|
|
## Chapter 7 Cauchy's Theorem
|
|
|
|
### Cauchy's Theorem
|
|
|
|
Let $\gamma$ be a closed curve in $\mathbb{C}$ and $U$ be a simply connected open subset of $\mathbb{C}$ containing $\gamma$ and its interior. Let $f$ be a holomorphic function on $U$. Then
|
|
|
|
$$
|
|
\int_\gamma f(z) dz = 0
|
|
$$
|
|
|
|
### Cauchy's Formula for a Circle
|
|
|
|
Let $C$ be a counterclockwise oriented circle and let $f$ be holomorphic function defined in an open set containing $C$ and its interior. Then for any $z$ in the interior of $C$,
|
|
|
|
$$
|
|
f(z)=\frac{1}{2\pi i}\int_C \frac{f(\zeta)}{\zeta-z} d\zeta
|
|
$$
|
|
|
|
### Mean Value Property
|
|
|
|
Let the function $f$ be holomorphic on a disk $|z-z_0|<R$. Then for any $0<r<R$, let $C_r$ denote the circle with center $z_0$ and radius $r$. Then
|
|
|
|
$$
|
|
f(z_0)=\frac{1}{2\pi}\int_0^{2\pi} f(z_0+re^{i\theta}) d\theta
|
|
$$
|
|
|
|
The value of the function at the center of the disk is the average of the values of the function on the boundary of the disk.
|
|
|
|
### Cauchy Integrals
|
|
|
|
Let $\gamma$ be a piecewise smooth curve in $\mathbb{C}$ and let $\phi$ be a continuous complex-valued function on $\gamma$. Then the Cauchy integral of $\phi$ on $\gamma$ is the function $f$ defined in $C\setminus\gamma$ by
|
|
|
|
$$
|
|
f(z)=\int_\gamma \frac{\phi(\zeta)}{\zeta-z} d\zeta
|
|
$$
|
|
|
|
Cauchy Integral Formula for circle $C_r$:
|
|
|
|
$$
|
|
f(z)=\frac{1}{2\pi i}\int_{C_r} \frac{f(\zeta)}{\zeta-z} d\zeta
|
|
$$
|
|
|
|
> Example:
|
|
>
|
|
> Evaluate $$\int_{|z|=2} \frac{z}{z-1} dz$$
|
|
>
|
|
> Note that if we let $f(\zeta)=\zeta$ and $z=1$ is inside the circle, then we can use Cauchy Integral Formula for circle $C_r$ to evaluate the integral.
|
|
>
|
|
> So we have
|
|
>
|
|
> $$\int_{|z|=2} \frac{z}{z-1} dz = 2\pi i f(1) = 2\pi i$$
|
|
|
|
General Cauchy Integral Formula for circle $C_r$:
|
|
|
|
$$
|
|
f^{(n)}(z)=\frac{n!}{2\pi i}\int_{C_r} \frac{f(\zeta)}{(\zeta-z)^{n+1}} d\zeta
|
|
$$
|
|
|
|
> Example:
|
|
>
|
|
> Evaluate $$\int_{C}\frac{\sin z}{z^{38}}dz$$
|
|
>
|
|
> Note that if we let $f(\zeta)=\sin \zeta$ and $z=0$ is inside the circle, then we can use General Cauchy Integral Formula for circle $C_r$ to evaluate the integral.
|
|
>
|
|
> So we have
|
|
>
|
|
> $$\int_{C}\frac{\sin z}{z^{38}}dz = \frac{2\pi i}{37!} f^{(37)}(0) = \frac{2\pi i}{37!} \sin ^{(37)}(0)$$
|
|
>
|
|
> Note that $\sin ^{(n)}(0)=\begin{cases} 0,& n\equiv 0 \pmod{4}\\
|
|
1,& n\equiv 1 \pmod{4}\\
|
|
0,& n\equiv 2 \pmod{4}\\
|
|
-1,& n\equiv 3 \pmod{4}
|
|
\end{cases}$
|
|
>
|
|
> So we have
|
|
>
|
|
> $$\int_{C}\frac{\sin z}{z^{38}}dz = \frac{2\pi i}{37!} \sin ^{(37)}(0) = \frac{2\pi i}{37!} \cdot 1 = \frac{2\pi i}{37!}$$
|
|
|
|
_Cauchy integral is a easier way to evaluate the integral._
|
|
|
|
### Liouville's Theorem
|
|
|
|
If a function $f$ is entire (holomorphic on $\mathbb{C}$) and bounded, then $f$ is constant.
|
|
|
|
### Finding power series of holomorphic functions
|
|
|
|
If $f$ is holomorphic on a disk $|z-z_0|<R$, then $f$ can be represented as a power series on the disk.
|
|
|
|
where $a_n=\frac{f^{(n)}(z_0)}{n!}$
|
|
|
|
> Example:
|
|
>
|
|
> If $q(z)=(z-1)(z-2)(z-3)$, find the power series of $q(z)$ centered at $z=0$.
|
|
>
|
|
> Note that $q(z)$ is holomorphic on $\mathbb{C}$ and $q(z)=0$ at $z=1,2,3$.
|
|
>
|
|
> So we can use the power series of $q(z)$ centered at $z=1$.
|
|
>
|
|
> To solve this, we can simply expand $q(z)=(z-1)(z-2)(z-3)$ and get $q(z)=z^3-6z^2+11z-6$.
|
|
>
|
|
> So we have $a_0=q(1)=-6$, $a_1=q'(1)=3z^2-12z+11=11$, $a_2=\frac{q''(1)}{2!}=\frac{6z-12}{2}=-3$, $a_3=\frac{q'''(1)}{3!}=\frac{6}{6}=1$.
|
|
>
|
|
> So the power series of $q(z)$ centered at $z=1$ is
|
|
>
|
|
> $$q(z)=-6+11(z-1)-3(z-1)^2+(z-1)^3$$
|
|
|
|
### Fundamental Theorem of Algebra
|
|
|
|
Every non-constant polynomial with complex coefficients has a root in $\mathbb{C}$.
|
|
|
|
Can be factored into linear factors:
|
|
|
|
$$
|
|
p(z)=a_n(z-z_1)(z-z_2)\cdots(z-z_n)
|
|
$$
|
|
|
|
We can treat holomorphic functions as polynomials.
|
|
|
|
$f$ has zero of order $m$ at $z_0$ if and only if $f(z)=(z-z_0)^m g(z)$ for some holomorphic $g(z)$ and $g(z_0)\neq 0$.
|
|
|
|
### Zeros of holomorphic functions
|
|
|
|
If $f$ is holomorphic on a disk $|z-z_0|<R$ and $f$ has a zero of order $m$ at $z_0$, then $f(z_0)=0$, $f'(z_0)=0$, $f''(z_0)=0$, $\cdots$, $f^{(m-1)}(z_0)=0$ and $f^{(m)}(z_0)\neq 0$.
|
|
|
|
And there exists a holomorphic function $g$ on the disk such that $f(z)=(z-z_0)^m g(z)$ and $g(z_0)\neq 0$.
|
|
|
|
> Example:
|
|
>
|
|
> Find zeros of $f(z)=\cos(z\frac{\pi}{2})$
|
|
>
|
|
> Note that $f(z)=0$ if and only if $z\frac{\pi}{2}=(2k+1)\frac{\pi}{2}$ for some integer $k$.
|
|
>
|
|
> So the zeros of $f(z)$ are $z=(2k+1)$ for some integer $k$.
|
|
>
|
|
> The order of the zero is $1$ since $f'(z)=-\frac{\pi}{2}\sin(z\frac{\pi}{2})$ and $f'(z)\neq 0$ for all $z=(2k+1)$.
|
|
|
|
If $f$ vanishes to infinite order at $z_0$ (that is, $f(z_0)=f'(z_0)=f''(z_0)=\cdots=0$), then $f(z)\equiv 0$ on the connected open set $U$ containing $z_0$.
|
|
|
|
### Identity Theorem
|
|
|
|
If $f$ and $g$ are holomorphic on a connected open set $U\subset\mathbb{C}$ and $f(z)=g(z)$ for all $z$ in a subset of $U$ that has a limit point in $U$, then $f(z)=g(z)$ for all $z\in U$.
|
|
|
|
Key: consider $h(z)=f(z)-g(z)$, prove $h(z)\equiv 0$ on $U$ by applying the zero of holomorphic function.
|
|
|
|
### Weierstrass Theorem
|
|
|
|
Limit of a sequence of holomorphic functions is holomorphic.
|
|
|
|
Let $f_n$ be a sequence of holomorphic functions on a domain $D\subset\mathbb{C}$ that converges uniformly to $f$ on every compact subset of $D$. Then $f$ is holomorphic on $D$.
|
|
|
|
### Maximum Modulus Principle
|
|
|
|
If $f$ is a non-constant holomorphic function on a domain $D\subset\mathbb{C}$, then $|f|$ does not attain a maximum value in $D$.
|
|
|
|
#### Corollary: Minimum Modulus Principle
|
|
|
|
If $f$ is a non-constant holomorphic function on a domain $D\subset\mathbb{C}$, then $\frac{1}{f}$ does not attain a minimum value in $D$.
|
|
|
|
### Schwarz Lemma
|
|
|
|
If $f$ is a holomorphic function on the unit disk $|z|<1$ and $|f(z)|\leq |z|$, then $|f'(0)|\leq 1$.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|