upgrade structures and migrate to nextra v4
This commit is contained in:
59
content/CSE559A/CSE559A_L1.md
Normal file
59
content/CSE559A/CSE559A_L1.md
Normal file
@@ -0,0 +1,59 @@
|
||||
# CSE559A Lecture 1
|
||||
|
||||
## Introducing the syllabus
|
||||
|
||||
See the syllabus on Canvas.
|
||||
|
||||
## Motivational introduction for computer vision
|
||||
|
||||
Computer vision is the study of manipulating images.
|
||||
|
||||
Automatic understanding of images and videos
|
||||
|
||||
1. vision for measurement (measurement, segmentation)
|
||||
2. vision for perception, interpretation (labeling)
|
||||
3. search and organization (retrieval, image or video archives)
|
||||
|
||||
### What is image
|
||||
|
||||
A 2d array of numbers.
|
||||
|
||||
### Vision is hard
|
||||
|
||||
connection to graphics.
|
||||
|
||||
computer vision need to generate the model from the image.
|
||||
|
||||
#### Are A and B the same color?
|
||||
|
||||
It depends on the context what you mean by "the same".
|
||||
|
||||
todo
|
||||
|
||||
#### Chair detector example.
|
||||
|
||||
double for loops.
|
||||
|
||||
#### Our visual system is not perfect.
|
||||
|
||||
Some optical illusion images.
|
||||
|
||||
todo, embed images here.
|
||||
|
||||
### Ridiculously brief history of computer vision
|
||||
|
||||
1960s: interpretation of synthetic worlds
|
||||
1970s: some progress on interpreting selected images
|
||||
1980s: ANNs come and go; shift toward geometry and increased mathematical rigor
|
||||
1990s: face recognition; statistical analysis in vogue
|
||||
2000s: becoming useful; significant use of machine learning; large annotated datasets available; video processing starts.
|
||||
2010s: Deep learning with ConvNets
|
||||
2020s: String synthesis; continued improvement across tasks, vision-language models.
|
||||
|
||||
## How computer vision is used now
|
||||
|
||||
### OCR, Optical Character Recognition
|
||||
|
||||
Technology to convert scanned docs to text.
|
||||
|
||||
|
||||
148
content/CSE559A/CSE559A_L10.md
Normal file
148
content/CSE559A/CSE559A_L10.md
Normal file
@@ -0,0 +1,148 @@
|
||||
# CSE559A Lecture 10
|
||||
|
||||
## Convolutional Neural Networks
|
||||
|
||||
### Convolutional Layer
|
||||
|
||||
Output feature map resolution depends on padding and stride
|
||||
|
||||
Padding: add zeros around the input image
|
||||
|
||||
Stride: the step of the convolution
|
||||
|
||||
Example:
|
||||
|
||||
1. Convolutional layer for 5x5 image with 3x3 kernel, padding 1, stride 1 (no skipping pixels)
|
||||
- Input: 5x5 image
|
||||
- Output: 3x3 feature map, (5-3+2*1)/1+1=5
|
||||
2. Convolutional layer for 5x5 image with 3x3 kernel, padding 1, stride 2 (skipping pixels)
|
||||
- Input: 5x5 image
|
||||
- Output: 2x2 feature map, (5-3+2*1)/2+1=2
|
||||
|
||||
_Learned weights can be thought of as local templates_
|
||||
|
||||
```python
|
||||
import torch
|
||||
import torch.nn as nn
|
||||
|
||||
# suppose input image is HxWx3 (assume RGB image)
|
||||
|
||||
conv_layer = nn.Conv2d(in_channels=3, # input channel, input is HxWx3
|
||||
out_channels=64, # output channel (number of filters), output is HxWx64
|
||||
kernel_size=3, # kernel size
|
||||
padding=1, # padding, this ensures that the output feature map has the same resolution as the input image, H_out=H_in, W_out=W_in
|
||||
stride=1) # stride
|
||||
```
|
||||
|
||||
Usually followed by a ReLU activation function
|
||||
|
||||
```python
|
||||
conv_layer = nn.Conv2d(in_channels=3, out_channels=64, kernel_size=3, padding=1, stride=1)
|
||||
relu = nn.ReLU()
|
||||
```
|
||||
|
||||
Suppose input image is $H\times W\times K$, the output feature map is $H\times W\times L$ with kernel size $F\times F$, this takes $F^2\times K\times L\times H\times W$ parameters
|
||||
|
||||
Each operation $D\times (K^2C)$ matrix with $(K^2C)\times N$ matrix, assume $D$ filters and $C$ output channels.
|
||||
|
||||
### Variants 1x1 convolutions, depthwise convolutions
|
||||
|
||||
#### 1x1 convolutions
|
||||
|
||||
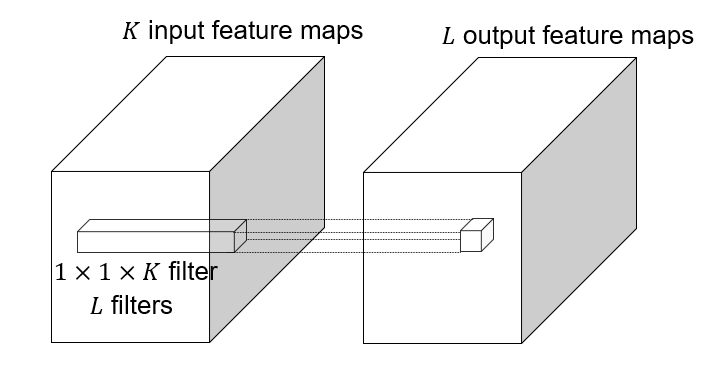
|
||||
|
||||
1x1 convolution: $F=1$, this layer do convolution in the pixel level, it is **pixel-wise** convolution for the feature.
|
||||
|
||||
Used to save computation, reduce the number of parameters.
|
||||
|
||||
Example: 3x3 conv layer with 256 channels at input and output.
|
||||
|
||||
Option 1: naive way:
|
||||
|
||||
```python
|
||||
conv_layer = nn.Conv2d(in_channels=256, out_channels=256, kernel_size=3, padding=1, stride=1)
|
||||
```
|
||||
|
||||
This takes $256\times 3 \times 3\times 256=524,288$ parameters.
|
||||
|
||||
Option 2: 1x1 convolution:
|
||||
|
||||
```python
|
||||
conv_layer = nn.Conv2d(in_channels=256, out_channels=64, kernel_size=1, padding=0, stride=1)
|
||||
conv_layer = nn.Conv2d(in_channels=64, out_channels=64, kernel_size=3, padding=1, stride=1)
|
||||
conv_layer = nn.Conv2d(in_channels=64, out_channels=256, kernel_size=1, padding=0, stride=1)
|
||||
```
|
||||
|
||||
This takes $256\times 1\times 1\times 64 + 64\times 3\times 3\times 64 + 64\times 1\times 1\times 256 = 16,384 + 36,864 + 16,384 = 69,632$ parameters.
|
||||
|
||||
This lose some information, but save a lot of parameters.
|
||||
|
||||
#### Depthwise convolutions
|
||||
|
||||
Depthwise convolution: $K\to K$ feature map, save computation, reduce the number of parameters.
|
||||
|
||||
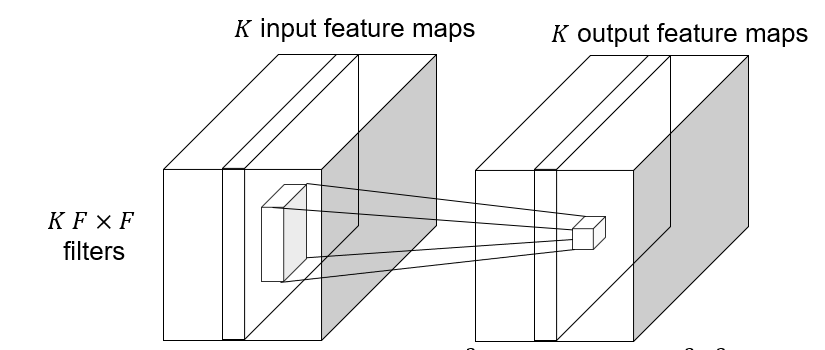
|
||||
|
||||
#### Grouped convolutions
|
||||
|
||||
Self defined convolution on the feature map following the similar manner.
|
||||
|
||||
### Backward pass
|
||||
|
||||
Vector-matrix form:
|
||||
|
||||
$$
|
||||
\frac{\partial e}{\partial x}=\frac{\partial e}{\partial z}\frac{\partial z}{\partial x}
|
||||
$$
|
||||
|
||||
Suppose the kernel is 3x3, the feature map is $\ldots, x_{i-1}, x_i, x_{i+1}, \ldots$, and $\ldots, z_{i-1}, z_i, z_{i+1}, \ldots$ is the output feature map, then:
|
||||
|
||||
The convolution operation can be written as:
|
||||
|
||||
$$
|
||||
z_i = w_1x_{i-1} + w_2x_i + w_3x_{i+1}
|
||||
$$
|
||||
|
||||
The gradient of the kernel is:
|
||||
|
||||
$$
|
||||
\frac{\partial e}{\partial x_i} = \sum_{j=-1}^{1}\frac{\partial e}{\partial z_i}\frac{\partial z_i}{\partial x_i} = \sum_{j=-1}^{1}\frac{\partial e}{\partial z_i}w_j
|
||||
$$
|
||||
|
||||
### Max-pooling
|
||||
|
||||
Get max value in the local region.
|
||||
|
||||
#### Receptive field
|
||||
|
||||
The receptive field of a unit is the region of the input feature map whose values contribute to the response of that unit (either in the previous layer or in the initial image)
|
||||
|
||||
## Architecture of CNNs
|
||||
|
||||
### AlexNet (2012-2013)
|
||||
|
||||
Successor of LeNet-5, but with a few significant changes
|
||||
|
||||
- Max pooling, ReLU nonlinearity
|
||||
- Dropout regularization
|
||||
- More data and bigger model (7 hidden layers, 650K units, 60M params)
|
||||
- GPU implementation (50x speedup over CPU)
|
||||
- Trained on two GPUs for a week
|
||||
|
||||
#### Key points
|
||||
|
||||
Most floating point operations occur in the convolutional layers.
|
||||
|
||||
Most of the memory usage is in the early convolutional layers.
|
||||
|
||||
Nearly all parameters are in the fully-connected layers.
|
||||
|
||||
### VGGNet (2014)
|
||||
|
||||
### GoogLeNet (2014)
|
||||
|
||||
### ResNet (2015)
|
||||
|
||||
### Beyond ResNet (2016 and onward): Wide ResNet, ResNeXT, DenseNet
|
||||
|
||||
|
||||
141
content/CSE559A/CSE559A_L11.md
Normal file
141
content/CSE559A/CSE559A_L11.md
Normal file
@@ -0,0 +1,141 @@
|
||||
# CSE559A Lecture 11
|
||||
|
||||
## Continue on Architecture of CNNs
|
||||
|
||||
### AlexNet (2012-2013)
|
||||
|
||||
Successor of LeNet-5, but with a few significant changes
|
||||
|
||||
- Max pooling, ReLU nonlinearity
|
||||
- Dropout regularization
|
||||
- More data and bigger model (7 hidden layers, 650K units, 60M params)
|
||||
- GPU implementation (50x speedup over CPU)
|
||||
- Trained on two GPUs for a week
|
||||
|
||||
#### Architecture for AlexNet
|
||||
|
||||
- Input: 224x224x3
|
||||
- 11x11 conv, stride 4, 96 filters
|
||||
- 3x3 max pooling, stride 2
|
||||
- 5x5 conv, 256 filters, padding 2
|
||||
- 3x3 max pooling, stride 2
|
||||
- 3x3 conv, 384 filters, padding 1
|
||||
- 3x3 conv, 384 filters, padding 1
|
||||
- 3x3 conv, 256 filters, padding 1
|
||||
- 3x3 max pooling, stride 2
|
||||
- 4096-unit FC, ReLU
|
||||
- 4096-unit FC, ReLU
|
||||
- 1000-unit FC, softmax
|
||||
|
||||
#### Key points for AlexNet
|
||||
|
||||
Most floating point operations occur in the convolutional layers.
|
||||
|
||||
Most of the memory usage is in the early convolutional layers.
|
||||
|
||||
Nearly all parameters are in the fully-connected layers.
|
||||
|
||||
#### Further refinement (ZFNet, 2013)
|
||||
|
||||
Best paper award at ILSVRC 2013.
|
||||
|
||||
Nicely visualizes the feature maps.
|
||||
|
||||
### VGGNet (2014)
|
||||
|
||||
All the cov layers are 3x3 filters with stride 1 and padding 1. Take advantage of pooling to reduce the spatial dimensionality.
|
||||
|
||||
#### Architecture for VGGNet
|
||||
|
||||
- Input: 224x224x3
|
||||
- 3x3 conv, 64 filters, padding 1
|
||||
- 3x3 conv, 64 filters, padding 1
|
||||
- 2x2 max pooling, stride 2
|
||||
- 3x3 conv, 128 filters, padding 1
|
||||
- 3x3 conv, 128 filters, padding 1
|
||||
- 2x2 max pooling, stride 2
|
||||
- 3x3 conv, 256 filters, padding 1
|
||||
- 3x3 conv, 256 filters, padding 1
|
||||
- 2x2 max pooling, stride 2
|
||||
- 3x3 conv, 512 filters, padding 1
|
||||
- 3x3 conv, 512 filters, padding 1
|
||||
- 3x3 conv, 512 filters, padding 1
|
||||
- 2x2 max pooling, stride 2
|
||||
- 3x3 conv, 512 filters, padding 1
|
||||
- 3x3 conv, 512 filters, padding 1
|
||||
- 3x3 conv, 512 filters, padding 1
|
||||
- 2x2 max pooling, stride 2
|
||||
- 4096-unit FC, ReLU
|
||||
- 4096-unit FC, ReLU
|
||||
- 1000-unit FC, softmax
|
||||
|
||||
#### Key points for VGGNet
|
||||
|
||||
- Sequence of deeper networks trained progressively
|
||||
- Large receptive fields replaced by successive layer of 3x3 convs with relu in between
|
||||
- 7x7 takes $49K^2$ parameters, 3x3 takes $27K^2$ parameters
|
||||
|
||||
#### Pretrained models
|
||||
|
||||
- Use pretrained-network as feature extractor (removing the last layer and training a new linear layer) (transfer learning)
|
||||
- Add RNN layers to generate captions
|
||||
- Fine-tune the model for the new task (finetuning)
|
||||
- Keep the earlier layers fixed and only train the new prediction layer
|
||||
|
||||
### GoogLeNet (2014)
|
||||
|
||||
Stem network at the start aggressively downsamples input.
|
||||
|
||||
#### Key points for GoogLeNet
|
||||
|
||||
- Parallel paths with different receptive field size and operations are means to capture space patterns of correlations in the stack of feature maps
|
||||
- Use 1x1 convs to reduce dimensionality
|
||||
- Use Global Average Pooling (GAP) to replace the fully connected layer
|
||||
- Auxiliary classifiers to improve training
|
||||
- Training using loss at the end of the network didn't work well: network is too deep, gradient don't provide useful model updates
|
||||
- As a hack, attach "auxiliary classifiers" at several intermediate points in the network that also try to classify the image and receive loss
|
||||
- _GooLeNet was before batch normalization, with batch normalization, the auxiliary classifiers were removed._
|
||||
|
||||
### ResNet (2015)
|
||||
|
||||
152 layers
|
||||
|
||||
[ResNet paper](https://arxiv.org/abs/1512.03385)
|
||||
|
||||
#### Key points for ResNet
|
||||
|
||||
- The residual module
|
||||
- Introduce `skip` or `shortcut` connections to avoid the degradation problem
|
||||
- Make it easy for network layers to represent the identity mapping
|
||||
- Directly performing 3×3 convolutions with 256 feature maps at input and output:
|
||||
- $256 \times 256 \times 3 \times 3 \approx 600K$ operations
|
||||
- Using 1×1 convolutions to reduce 256 to 64 feature maps, followed by 3×3 convolutions, followed by 1×1 convolutions to expand back to 256 maps:
|
||||
- $256 \times 64 \times 1 \times 1 \approx 16K$
|
||||
- $64 \times 64 \times 3 \times 3 \approx 36K$
|
||||
- $64 \times 256 \times 1 \times 1 \approx 16K$
|
||||
- Total $\approx 70K$
|
||||
|
||||
_Possibly the first model with top-5 error rate better than human performance._
|
||||
|
||||
### Beyond ResNet (2016 and onward): Wide ResNet, ResNeXT, DenseNet
|
||||
|
||||
#### Wide ResNet
|
||||
|
||||
Reduce number of residual blocks, but increase number of feature maps in each block
|
||||
|
||||
- More parallelizable, better feature reuse
|
||||
- 16-layer WRN outperforms 1000-layer ResNets, though with much larger # of parameters
|
||||
|
||||
#### ResNeXt
|
||||
|
||||
- Propose “cardinality” as a new factor in network design, apart from depth and width
|
||||
- Claim that increasing cardinality is a better way to increase capacity than increasing depth or width
|
||||
|
||||
#### DenseNet
|
||||
|
||||
- Use Dense block between conv layers
|
||||
- Less parameters than ResNet
|
||||
|
||||
Next class:
|
||||
|
||||
Transformer architectures
|
||||
159
content/CSE559A/CSE559A_L12.md
Normal file
159
content/CSE559A/CSE559A_L12.md
Normal file
@@ -0,0 +1,159 @@
|
||||
# CSE559A Lecture 12
|
||||
|
||||
## Transformer Architecture
|
||||
|
||||
### Outline
|
||||
|
||||
**Self-Attention Layers**: An important network module, which often has a global receptive field
|
||||
|
||||
**Sequential Input Tokens**: Breaking the restriction to 2d input arrays
|
||||
|
||||
**Positional Encodings**: Representing the metadata of each input token
|
||||
|
||||
**Exemplar Architecture**: The Vision Transformer (ViT)
|
||||
|
||||
**Moving Forward**: What does this new module enable? Who wins in the battle between transformers and CNNs?
|
||||
|
||||
### The big picture
|
||||
|
||||
CNNs
|
||||
|
||||
- Local receptive fields
|
||||
- Struggles with global content
|
||||
- Shape of intermediate layers is sometimes a pain
|
||||
|
||||
Things we might want:
|
||||
|
||||
- Use information from across the image
|
||||
- More flexible shape handling
|
||||
- Multiple modalities
|
||||
|
||||
Our Hero: MultiheadAttention
|
||||
|
||||
Use positional encodings to represent the metadata of each input token
|
||||
|
||||
## Self-Attention layers
|
||||
|
||||
### Comparing with ways to handling sequential data
|
||||
|
||||
#### RNN
|
||||
|
||||
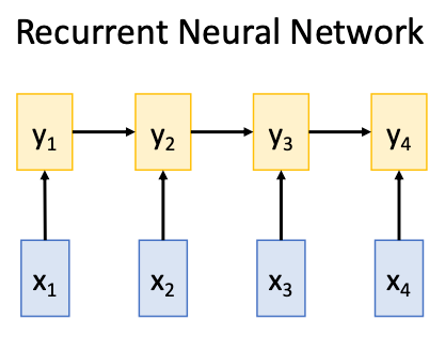
|
||||
|
||||
Works on **Ordered Sequences**
|
||||
|
||||
- Good at long sequences: After one RNN layer $h_r$ sees the whole sequence
|
||||
- Bad at parallelization: need to compute hidden states sequentially
|
||||
|
||||
#### 1D conv
|
||||
|
||||
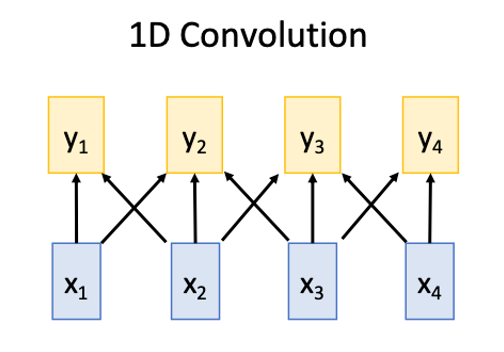
|
||||
|
||||
Works on **Multidimensional Grids**
|
||||
|
||||
- Bad at long sequences: Need to stack may conv layers or outputs to see the whole sequence
|
||||
- Good at parallelization: Each output can be computed in parallel
|
||||
|
||||
#### Self-Attention
|
||||
|
||||
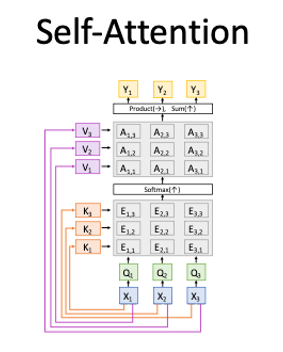
|
||||
|
||||
Works on **Set of Vectors**
|
||||
|
||||
- Good at Long sequences: Each output can attend to all inputs
|
||||
- Good at parallelization: Each output can be computed in parallel
|
||||
- Bad at saving memory: Need to store all inputs in memory
|
||||
|
||||
### Encoder-Decoder Architecture
|
||||
|
||||
The encoder is constructed by stacking multiple self-attention layers and feed-forward networks.
|
||||
|
||||
#### Word Embeddings
|
||||
|
||||
Translate tokens to vector space
|
||||
|
||||
```python
|
||||
class Embedder(nn.Module):
|
||||
def __init__(self, vocab_size, d_model):
|
||||
super().__init__()
|
||||
self.embed=nn.Embedding(vocab_size, d_model)
|
||||
|
||||
def forward(self, x):
|
||||
return self.embed(x)
|
||||
```
|
||||
|
||||
#### Positional Embeddings
|
||||
|
||||
The positional encodings are a way to represent the position of each token in the sequence.
|
||||
|
||||
Combined with the word embeddings, we get the input to the self-attention layer with information about the position of each token in the sequence.
|
||||
|
||||
> The reason why we just add the positional encodings to the word embeddings is _perhaps_ that we want the model to self-assign weights to the word-token and positional-token.
|
||||
|
||||
#### Query, Key, Value
|
||||
|
||||
The query, key, and value are the three components of the self-attention layer.
|
||||
|
||||
They are used to compute the attention weights.
|
||||
|
||||
```python
|
||||
class SelfAttention(nn.Module):
|
||||
def __init__(self, d_model, num_heads):
|
||||
super().__init__()
|
||||
self.d_model = d_model
|
||||
self.d_k = d_k
|
||||
self.q_linear = nn.Linear(d_model, d_k)
|
||||
self.k_linear = nn.Linear(d_model, d_k)
|
||||
self.v_linear = nn.Linear(d_model, d_k)
|
||||
self.dropout = nn.Dropout(dropout)
|
||||
self.out = nn.Linear(d_k, d_k)
|
||||
|
||||
def forward(self, q, k, v, mask=None):
|
||||
|
||||
bs = q.size(0)
|
||||
|
||||
k = self.k_linear(k)
|
||||
q = self.q_linear(q)
|
||||
v = self.v_linear(v)
|
||||
|
||||
# calculate attention weights
|
||||
outputs = attention(q, k, v, self.d_k, mask, self.dropout)
|
||||
|
||||
# apply output linear transformation
|
||||
outputs = self.out(outputs)
|
||||
|
||||
return outputs
|
||||
```
|
||||
|
||||
#### Attention
|
||||
|
||||
```python
|
||||
def attention(q, k, v, d_k, mask=None, dropout=None):
|
||||
scores = torch.matmul(q, k.transpose(-2, -1)) / math.sqrt(d_k)
|
||||
|
||||
if mask is not None:
|
||||
mask = mask.unsqueeze(1)
|
||||
scores = scores.masked_fill(mask == 0, -1e9)
|
||||
|
||||
scores = F.softmax(scores, dim=-1)
|
||||
|
||||
if dropout is not None:
|
||||
scores = dropout(scores)
|
||||
|
||||
outputs = torch.matmul(scores, v)
|
||||
|
||||
return outputs
|
||||
```
|
||||
|
||||
The query, key are used to compute the attention map, and the value is used to compute the attention output.
|
||||
|
||||
#### Multi-Head self-attention
|
||||
|
||||
The multi-head self-attention is a self-attention layer that has multiple heads.
|
||||
|
||||
Each head has its own query, key, and value.
|
||||
|
||||
### Computing Attention Efficiency
|
||||
|
||||
- the standard attention has a complexity of $O(n^2)$
|
||||
- We can use sparse attention to reduce the complexity to $O(n)$
|
||||
59
content/CSE559A/CSE559A_L13.md
Normal file
59
content/CSE559A/CSE559A_L13.md
Normal file
@@ -0,0 +1,59 @@
|
||||
# CSE559A Lecture 13
|
||||
|
||||
## Positional Encodings
|
||||
|
||||
### Fixed Positional Encodings
|
||||
|
||||
Set of sinusoids of different frequencies.
|
||||
|
||||
$$
|
||||
f(p,2i)=\sin(\frac{p}{10000^{2i/d}})\quad f(p,2i+1)=\cos(\frac{p}{10000^{2i/d}})
|
||||
$$
|
||||
|
||||
[source](https://kazemnejad.com/blog/transformer_architecture_positional_encoding/)
|
||||
|
||||
### Positional Encodings in Reconstruction
|
||||
|
||||
MLP is hard to learn high-frequency information from scaler input $(x,y)$.
|
||||
|
||||
Example: network mapping from $(x,y)$ to $(r,g,b)$.
|
||||
|
||||
### Generalized Positional Encodings
|
||||
|
||||
- Dependence on location, scaler, metadata, etc.
|
||||
- Can just be fully learned (use `nn.Embedding` and optimize based on a categorical input.)
|
||||
|
||||
## Vision Transformer (ViT)
|
||||
|
||||
### Class Token
|
||||
|
||||
In Vision Transformers, a special token called the class token is added to the input sequence to aggregate information for classification tasks.
|
||||
|
||||
### Hidden CNN Modules
|
||||
|
||||
- PxP convolution with stride P (split the image into patches and use positional encoding)
|
||||
|
||||
### ViT + ResNet Hybrid
|
||||
|
||||
Build a hybrid model that combines the vision transformer after 50 layer of ResNet.
|
||||
|
||||
## Moving Forward
|
||||
|
||||
At least for now, CNN and ViT architectures have similar performance at least in ImageNet.
|
||||
|
||||
- General Consensus: once the architecture is big enough, and not designed terribly, it can do well.
|
||||
- Differences remain:
|
||||
- Computational efficiency
|
||||
- Ease of use in other tasks and with other input data
|
||||
- Ease of training
|
||||
|
||||
## Wrap up
|
||||
|
||||
Self attention as a key building block
|
||||
|
||||
Flexible input specification using tokens with positional encodings
|
||||
|
||||
A wide variety of architectural styles
|
||||
|
||||
Up Next:
|
||||
Training deep neural networks
|
||||
73
content/CSE559A/CSE559A_L14.md
Normal file
73
content/CSE559A/CSE559A_L14.md
Normal file
@@ -0,0 +1,73 @@
|
||||
# CSE559A Lecture 14
|
||||
|
||||
## Object Detection
|
||||
|
||||
AP (Average Precision)
|
||||
|
||||
### Benchmarks
|
||||
|
||||
#### PASCAL VOC Challenge
|
||||
|
||||
20 Challenge classes.
|
||||
|
||||
CNN increases the accuracy of object detection.
|
||||
|
||||
#### COCO dataset
|
||||
|
||||
Common objects in context.
|
||||
|
||||
Semantic segmentation. Every pixel is classified to tags.
|
||||
|
||||
Instance segmentation. Every pixel is classified and grouped into instances.
|
||||
|
||||
### Object detection: outline
|
||||
|
||||
Proposal generation
|
||||
|
||||
Object recognition
|
||||
|
||||
#### R-CNN
|
||||
|
||||
Proposal generation
|
||||
|
||||
Use CNN to extract features from proposals.
|
||||
|
||||
with SVM to classify proposals.
|
||||
|
||||
Use selective search to generate proposals.
|
||||
|
||||
Use AlexNet finetuned on PASCAL VOC to extract features.
|
||||
|
||||
Pros:
|
||||
|
||||
- Much more accurate than previous approaches
|
||||
- Andy deep architecture can immediately be "plugged in"
|
||||
|
||||
Cons:
|
||||
|
||||
- Not a single end-to-end trainable system
|
||||
- Fine-tune network with softmax classifier (log loss)
|
||||
- Train post-hoc linear SVMs (hinge loss)
|
||||
- Train post-hoc bounding box regressors (least squares)
|
||||
- Training is slow 2000CNN passes for each image
|
||||
- Inference (detection) was slow
|
||||
|
||||
#### Fast R-CNN
|
||||
|
||||
Proposal generation
|
||||
|
||||
Use CNN to extract features from proposals.
|
||||
|
||||
##### ROI pooling and ROI alignment
|
||||
|
||||
ROI pooling:
|
||||
|
||||
- Pooling is applied to the feature map.
|
||||
- Pooling is applied to the proposal.
|
||||
|
||||
ROI alignment:
|
||||
|
||||
- Align the proposal to the feature map.
|
||||
- Align the proposal to the feature map.
|
||||
|
||||
Use bounding box regression to refine the proposal.
|
||||
131
content/CSE559A/CSE559A_L15.md
Normal file
131
content/CSE559A/CSE559A_L15.md
Normal file
@@ -0,0 +1,131 @@
|
||||
# CSE559A Lecture 15
|
||||
|
||||
## Continue on object detection
|
||||
|
||||
### Two strategies for object detection
|
||||
|
||||
#### R-CNN: Region proposals + CNN features
|
||||
|
||||
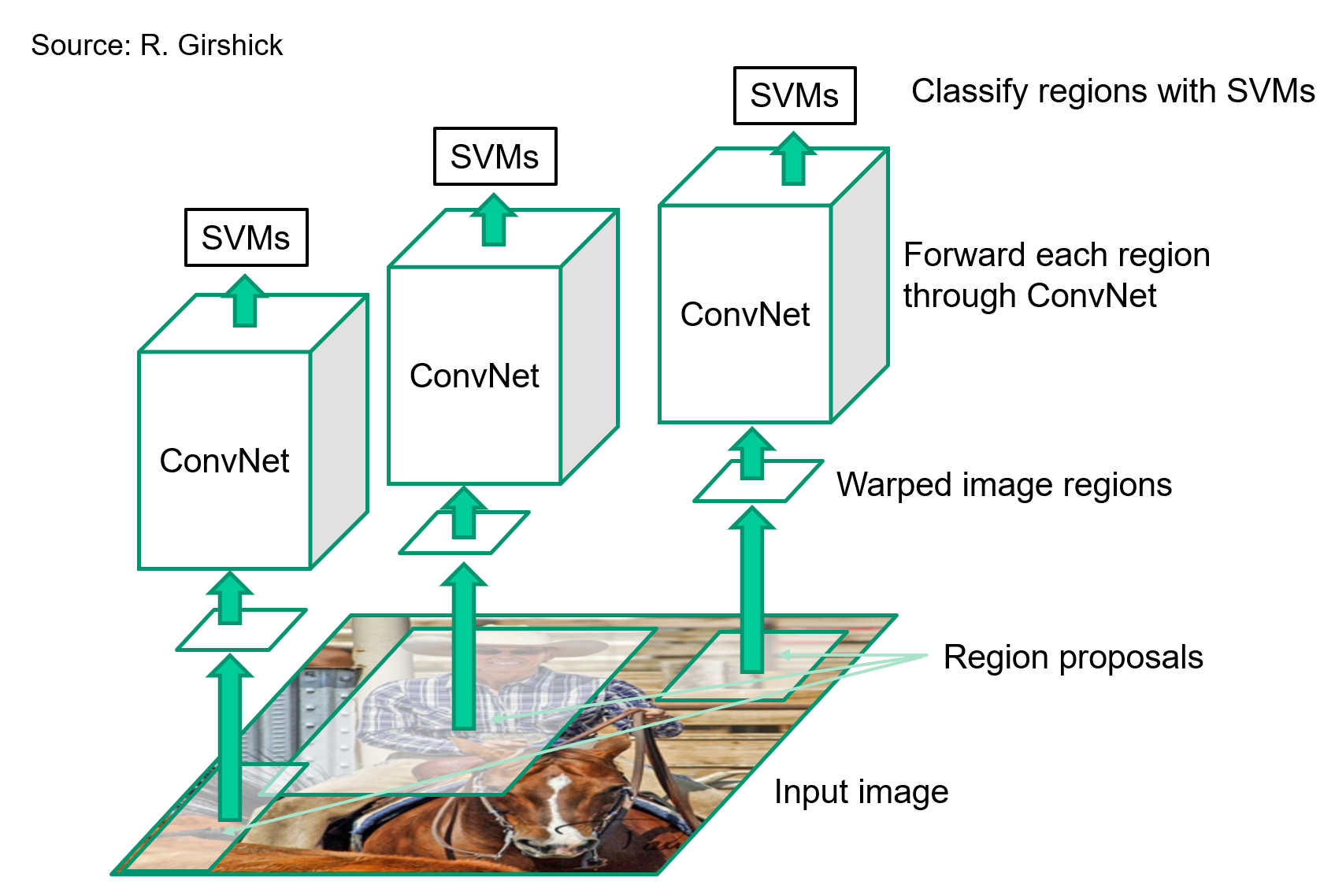
|
||||
|
||||
#### Fast R-CNN: CNN features + RoI pooling
|
||||
|
||||
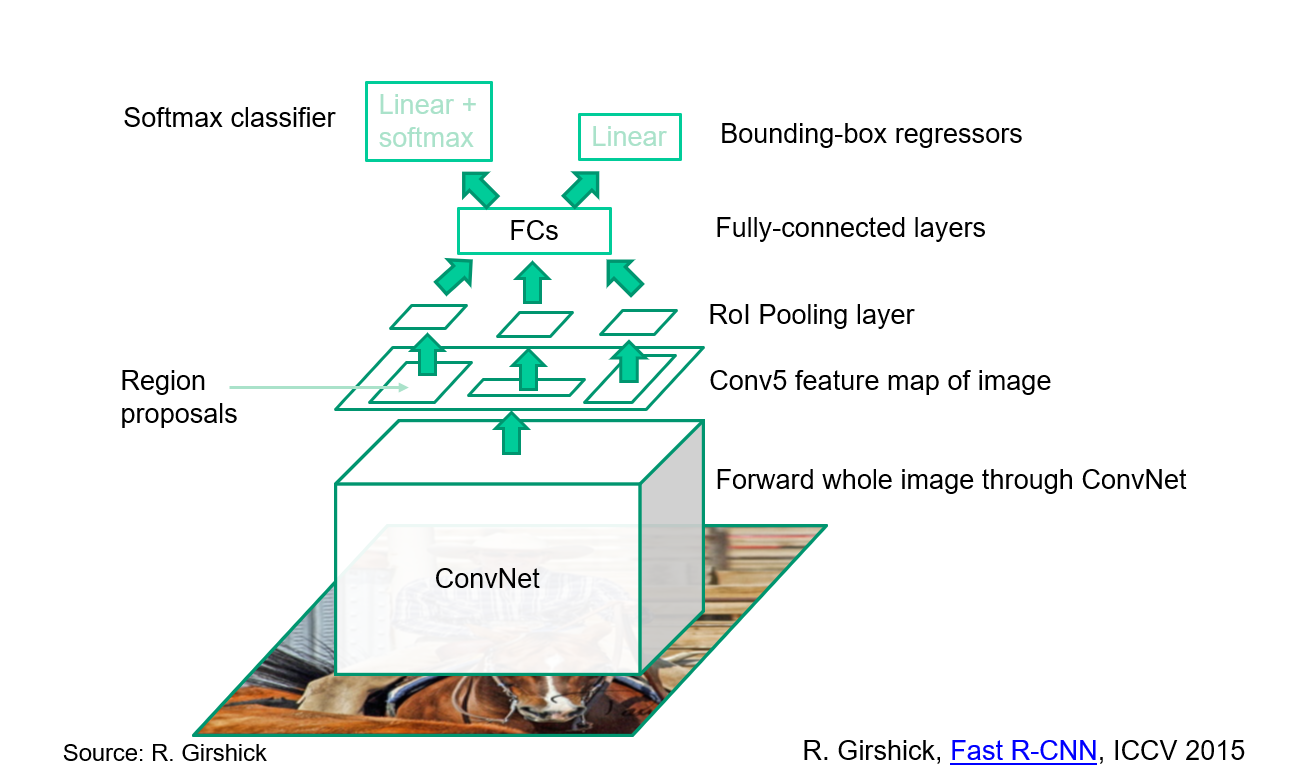
|
||||
|
||||
Use bilinear interpolation to get the features of the proposal.
|
||||
|
||||
#### Region of interest pooling
|
||||
|
||||
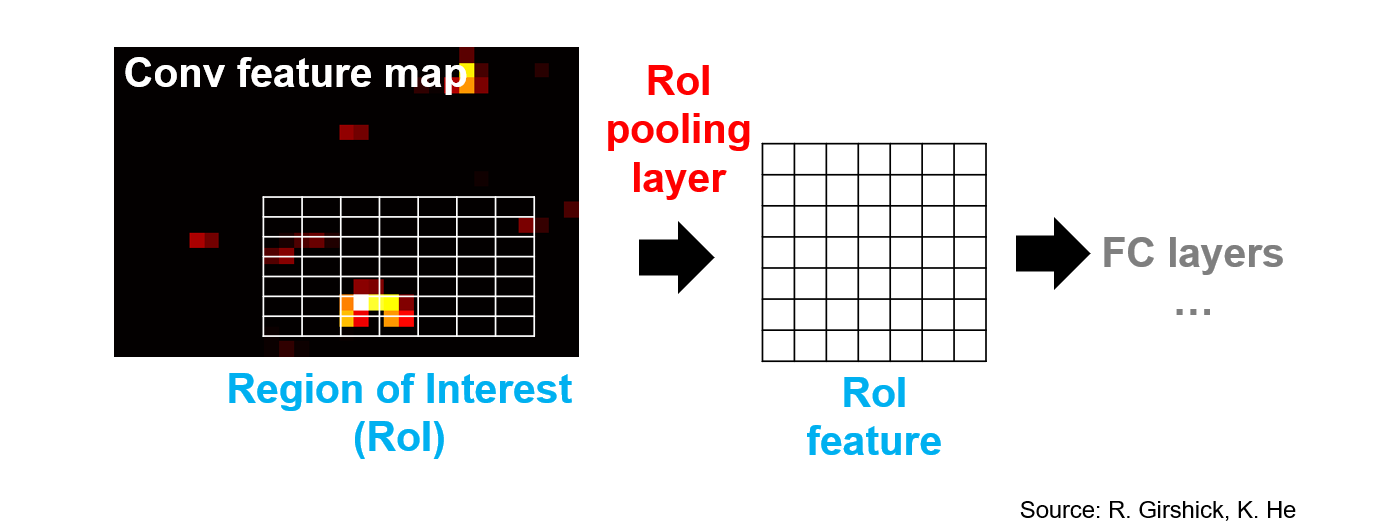
|
||||
|
||||
Use backpropagation to get the gradient of the proposal.
|
||||
|
||||
### New materials
|
||||
|
||||
#### Faster R-CNN
|
||||
|
||||
Use one CNN to generate region proposals. And use another CNN to classify the proposals.
|
||||
|
||||
##### Region proposal network
|
||||
|
||||
Idea: put an "anchor box" of fixed size over each position in the feature map and try to predict whether this box is likely to contain an object.
|
||||
|
||||
Introduce anchor boxes at multiple scales and aspect ratios to handle a wider range of object sizes and shapes.
|
||||
|
||||
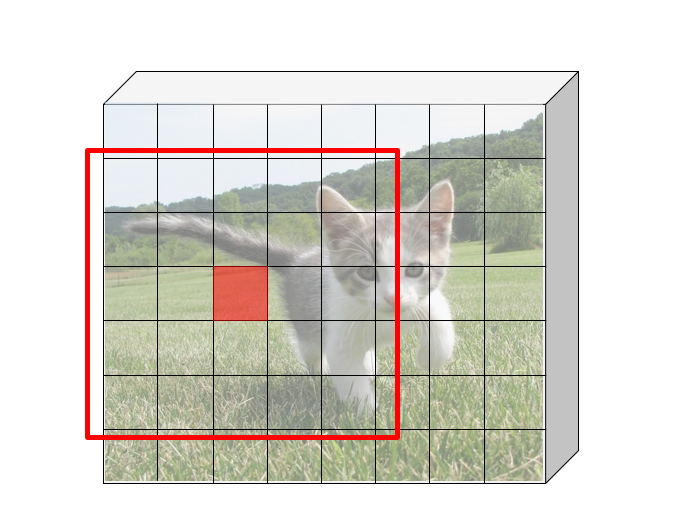
|
||||
|
||||
### Single-stage and multi-resolution detection
|
||||
|
||||
#### YOLO
|
||||
|
||||
You only look once (YOLO) is a state-of-the-art, real-time object detection system.
|
||||
|
||||
1. Take conv feature maps at 7x7 resolution
|
||||
2. Add two FC layers to predict, at each location, a score for each class and 2 bboxes with confidences
|
||||
|
||||
For PASCAL, output is 7×7×30 (30=20 + 2∗(4+1))
|
||||
|
||||
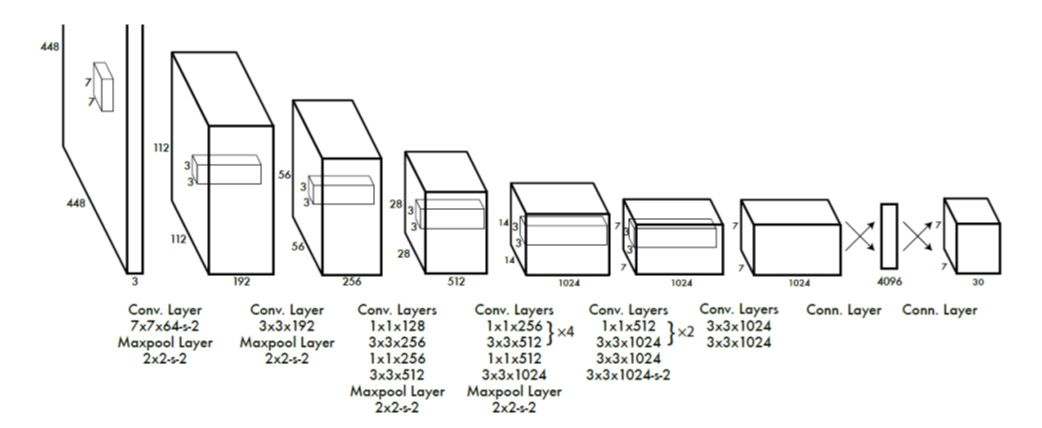
|
||||
|
||||
##### YOLO Network Head
|
||||
|
||||
```python
|
||||
model.add(Conv2D(1024, (3, 3), activation='lrelu', kernel_regularizer=l2(0.0005)))
|
||||
model.add(Conv2D(1024, (3, 3), activation='lrelu', kernel_regularizer=l2(0.0005)))
|
||||
# use flatten layer for global reasoning
|
||||
model.add(Flatten())
|
||||
model.add(Dense(512))
|
||||
model.add(Dense(1024))
|
||||
model.add(Dropout(0.5))
|
||||
model.add(Dense(7 * 7 * 30, activation='sigmoid'))
|
||||
model.add(YOLO_Reshape(target_shape=(7, 7, 30)))
|
||||
model.summary()
|
||||
```
|
||||
|
||||
#### YOLO results
|
||||
|
||||
1. Each grid cell predicts only two boxes and can only have one class – this limits the number of nearby objects that can be predicted
|
||||
2. Localization accuracy suffers compared to Fast(er) R-CNN due to coarser features, errors on small boxes
|
||||
3. 7x speedup over Faster R-CNN (45-155 FPS vs. 7-18 FPS)
|
||||
|
||||
#### YOLOv2
|
||||
|
||||
1. Remove FC layer, do convolutional prediction with anchor boxes instead
|
||||
2. Increase resolution of input images and conv feature maps
|
||||
3. Improve accuracy using batch normalization and other tricks
|
||||
|
||||
#### SSD
|
||||
|
||||
SSD is a multi-resolution object detection
|
||||
|
||||
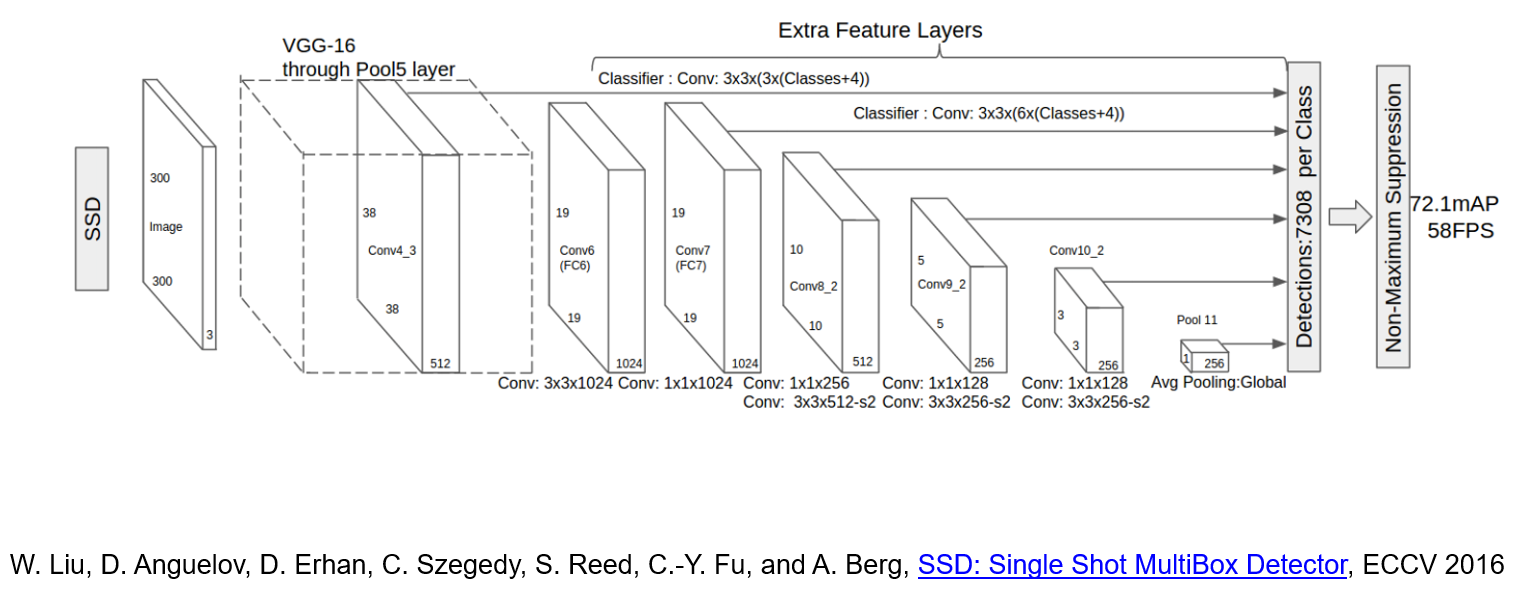
|
||||
|
||||
1. Predict boxes of different size from different conv maps
|
||||
2. Each level of resolution has its own predictor
|
||||
|
||||
##### Feature Pyramid Network
|
||||
|
||||
- Improve predictive power of lower-level feature maps by adding contextual information from higher-level feature maps
|
||||
- Predict different sizes of bounding boxes from different levels of the pyramid (but share parameters of predictors)
|
||||
|
||||
#### RetinaNet
|
||||
|
||||
RetinaNet combine feature pyramid network with focal loss to reduce the standard cross-entropy loss for well-classified examples.
|
||||
|
||||
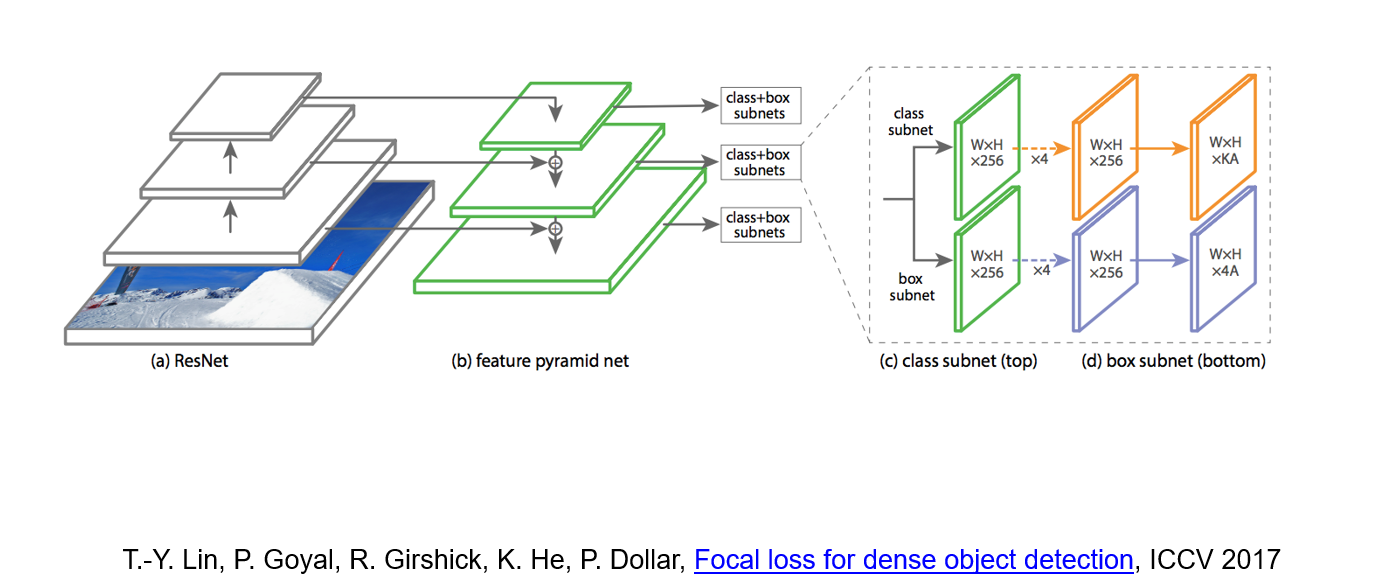
|
||||
|
||||
> Cross-entropy loss:
|
||||
> $$CE(p_t) = - \log(p_t)$$
|
||||
|
||||
The focal loss is defined as:
|
||||
|
||||
$$
|
||||
FL(p_t) = - (1 - p_t)^{\gamma} \log(p_t)
|
||||
$$
|
||||
|
||||
We can increase $\gamma$ to reduce the loss for well-classified examples.
|
||||
|
||||
#### YOLOv3
|
||||
|
||||
Minor refinements
|
||||
|
||||
### Alternative approaches
|
||||
|
||||
#### CornerNet
|
||||
|
||||
Use a pair of corners to represent the bounding box.
|
||||
|
||||
Use hourglass network to accumulate the information of the corners.
|
||||
|
||||
#### CenterNet
|
||||
|
||||
Use a center point to represent the bounding box.
|
||||
|
||||
#### Detection Transformer
|
||||
|
||||
Use transformer architecture to detect the object.
|
||||
|
||||
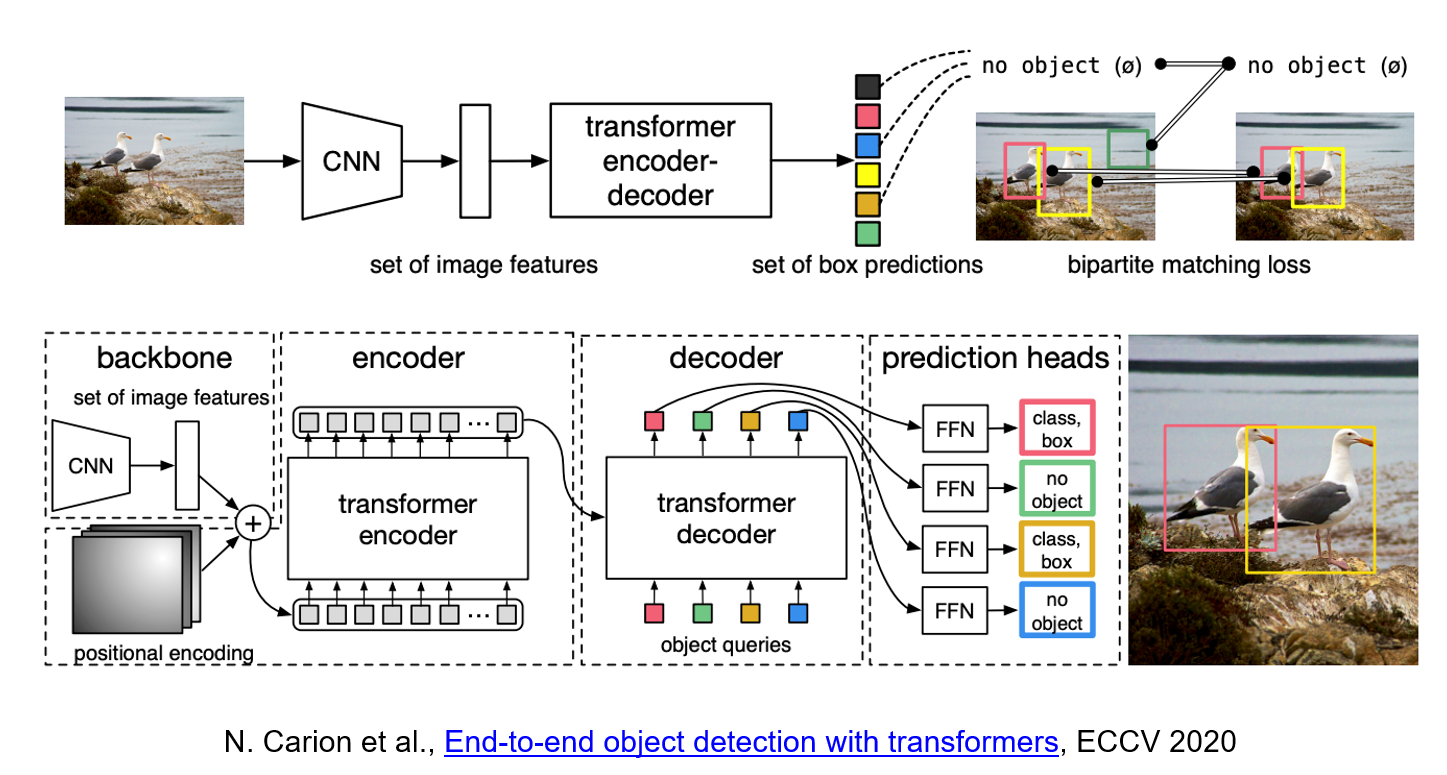
|
||||
|
||||
DETR uses a conventional CNN backbone to learn a 2D representation of an input image. The model flattens it and supplements it with a positional encoding before passing it into a transformer encoder. A transformer decoder then takes as input a small fixed number of learned positional embeddings, which we call object queries, and additionally attends to the encoder output. We pass each output embedding of the decoder to a shared feed forward network (FFN) that predicts either a detection (class and bounding box) or a "no object" class.
|
||||
|
||||
114
content/CSE559A/CSE559A_L16.md
Normal file
114
content/CSE559A/CSE559A_L16.md
Normal file
@@ -0,0 +1,114 @@
|
||||
# CSE559A Lecture 16
|
||||
|
||||
## Dense image labelling
|
||||
|
||||
### Semantic segmentation
|
||||
|
||||
Use one-hot encoding to represent the class of each pixel.
|
||||
|
||||
### General Network design
|
||||
|
||||
Design a network with only convolutional layers, make predictions for all pixels at once.
|
||||
|
||||
Can the network operate at full image resolution?
|
||||
|
||||
Practical solution: first downsample, then upsample
|
||||
|
||||
### Outline
|
||||
|
||||
- Upgrading a Classification Network to Segmentation
|
||||
- Operations for dense prediction
|
||||
- Transposed convolutions, unpooling
|
||||
- Architectures for dense prediction
|
||||
- DeconvNet, U-Net, "U-Net"
|
||||
- Instance segmentation
|
||||
- Mask R-CNN
|
||||
- Other dense prediction problems
|
||||
|
||||
### Fully Convolutional Networks
|
||||
|
||||
"upgrading" a classification network to a dense prediction network
|
||||
|
||||
1. Covert "fully connected" layers to 1x1 convolutions
|
||||
2. Make the input image larger
|
||||
3. Upsample the output
|
||||
|
||||
Start with an existing classification CNN ("an encoder")
|
||||
|
||||
Then use bilinear interpolation and transposed convolutions to make full resolution.
|
||||
|
||||
### Operations for dense prediction
|
||||
|
||||
#### Transposed Convolutions
|
||||
|
||||
Use the filter to "paint" in the output: place copies of the filter on the output, multiply by corresponding value in the input, sum where copies of the filter overlap
|
||||
|
||||
We can increase the resolution of the output by using a larger stride in the convolution.
|
||||
|
||||
- For stride 2, dilate the input by inserting rows and columns of zeros between adjacent entries, convolve with flipped filter
|
||||
- Sometimes called convolution with fractional input stride 1/2
|
||||
|
||||
#### Unpooling
|
||||
|
||||
Max unpooling:
|
||||
|
||||
- Copy the maximum value in the input region to all locations in the output
|
||||
- Use the location of the maximum value to know where to put the value in the output
|
||||
|
||||
Nearest neighbor unpooling:
|
||||
|
||||
- Copy the maximum value in the input region to all locations in the output
|
||||
- Use the location of the maximum value to know where to put the value in the output
|
||||
|
||||
### Architectures for dense prediction
|
||||
|
||||
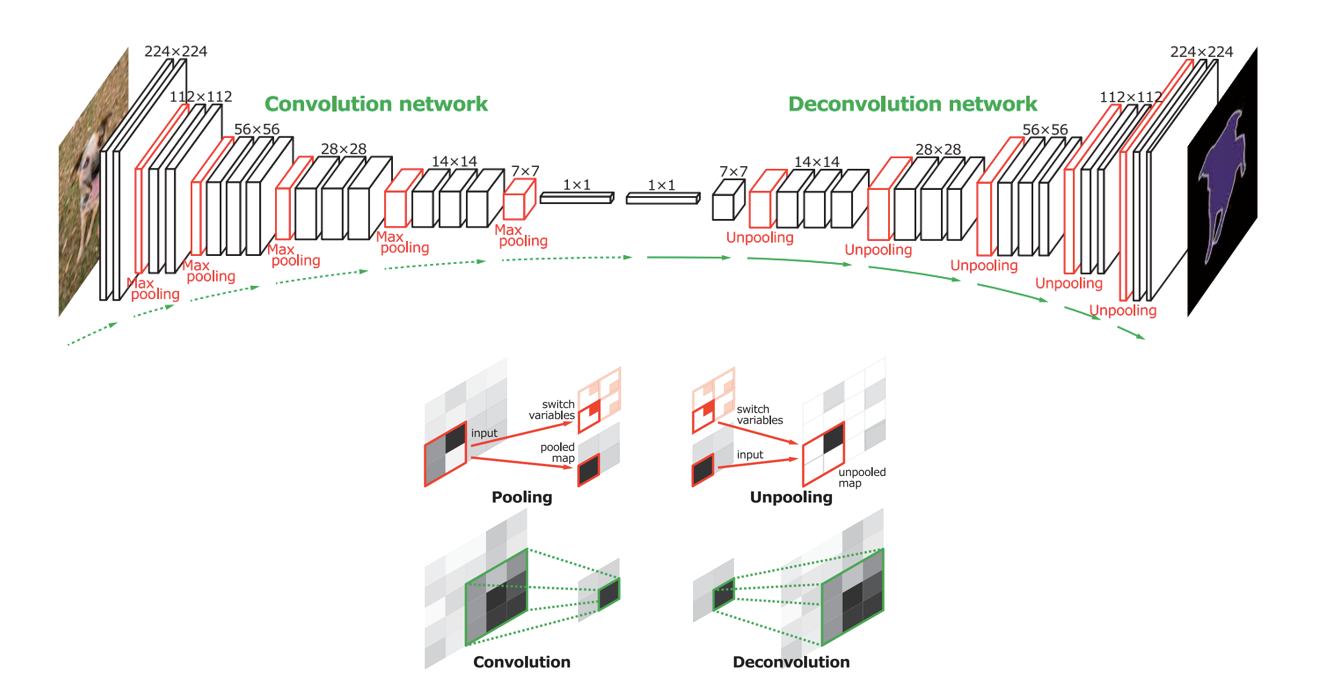
#### DeconvNet
|
||||
|
||||
|
||||
|
||||
_How the information about location is encoded in the network?_
|
||||
|
||||
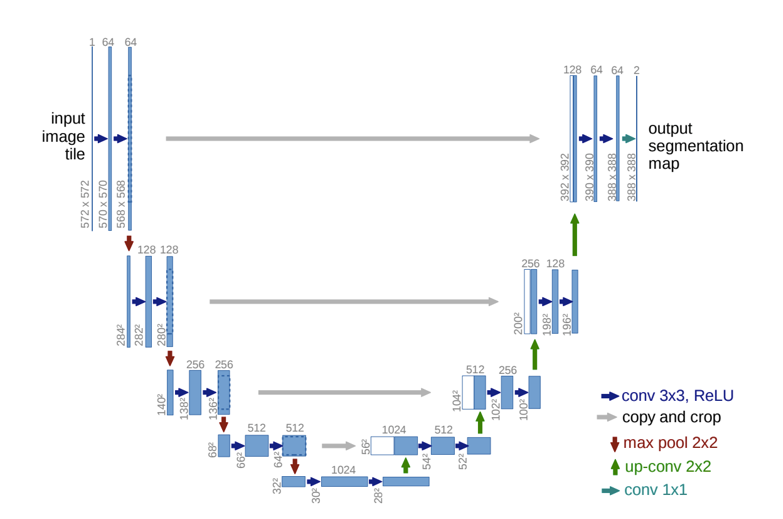
#### U-Net
|
||||
|
||||
|
||||
|
||||
- Like FCN, fuse upsampled higher-level feature maps with higher-res, lower-level feature maps (like residual connections)
|
||||
- Unlike FCN, fuse by concatenation, predict at the end
|
||||
|
||||
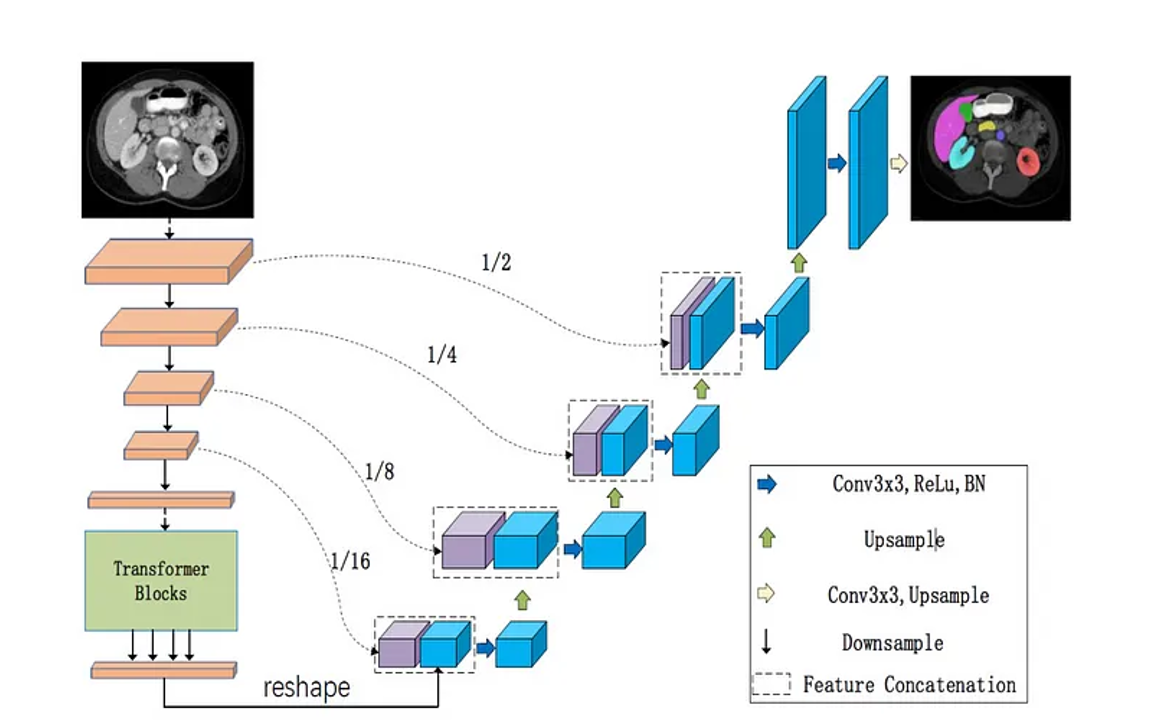
#### Extended U-Net Architecture
|
||||
|
||||
Many variants of U-Net would replace the "encoder" of the U-Net with other architectures.
|
||||
|
||||
|
||||
|
||||
##### Encoder/Decoder v.s. U-Net
|
||||
|
||||
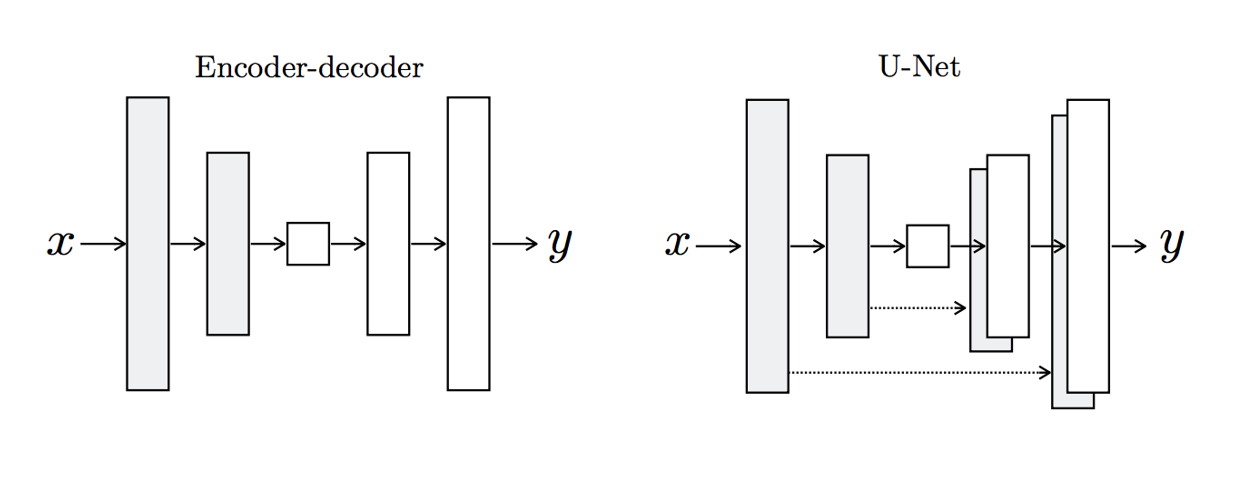
|
||||
|
||||
### Instance Segmentation
|
||||
|
||||
#### Mask R-CNN
|
||||
|
||||
Mask R-CNN = Faster R-CNN + FCN on Region of Interest
|
||||
|
||||
### Extend to keypoint prediction?
|
||||
|
||||
- Use a similar architecture to Mask R-CNN
|
||||
|
||||
_Continue on Tuesday_
|
||||
|
||||
### Other tasks
|
||||
|
||||
#### Panoptic feature pyramid network
|
||||
|
||||
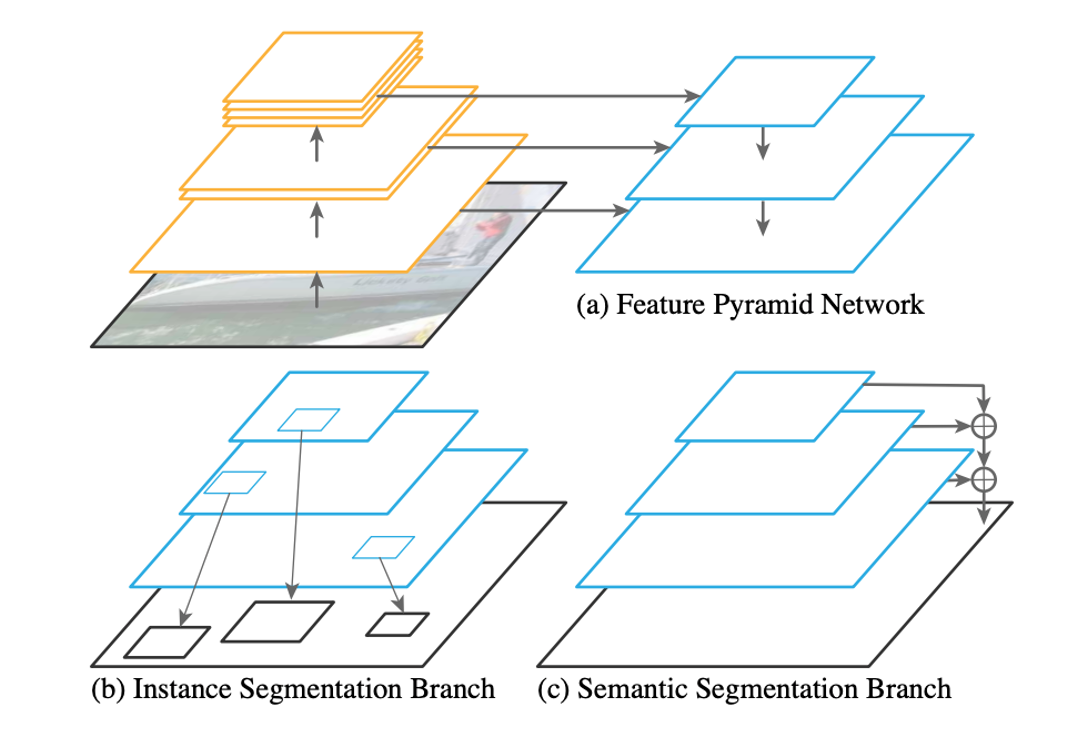
|
||||
|
||||
#### Depth and normal estimation
|
||||
|
||||
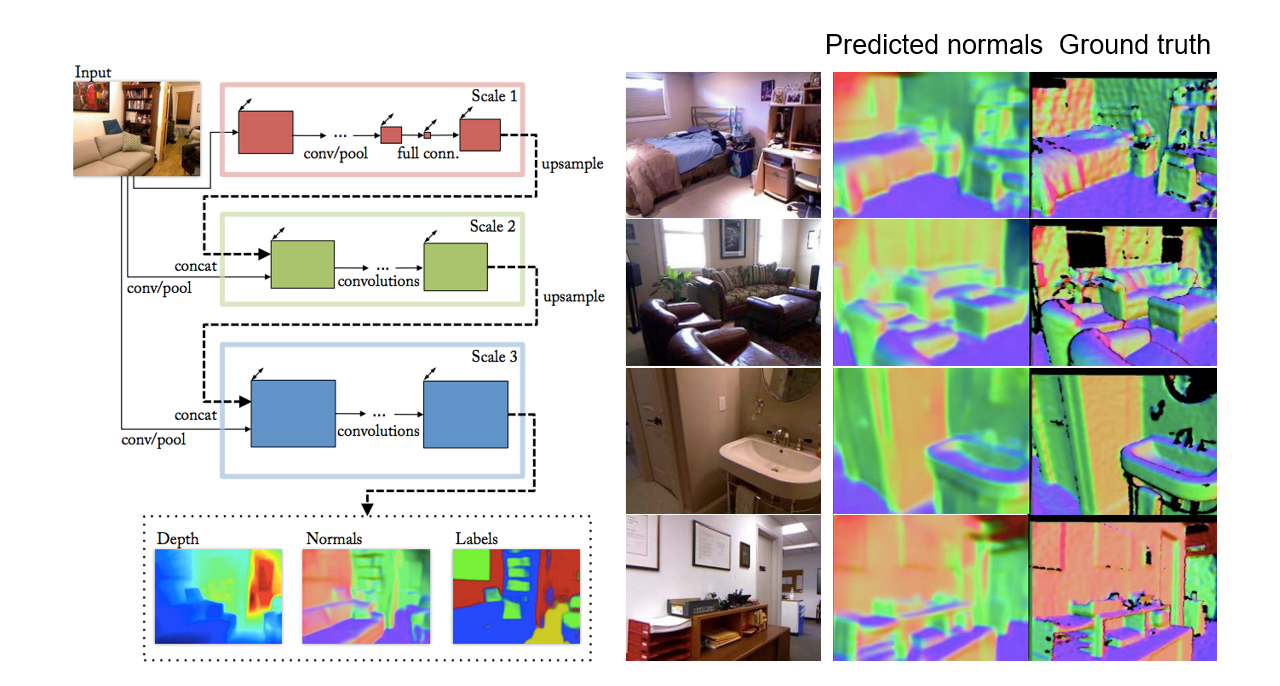
|
||||
|
||||
D. Eigen and R. Fergus, Predicting Depth, Surface Normals and Semantic Labels with a Common Multi-Scale Convolutional Architecture, ICCV 2015
|
||||
|
||||
#### Colorization
|
||||
|
||||
R. Zhang, P. Isola, and A. Efros, Colorful Image Colorization, ECCV 2016
|
||||
184
content/CSE559A/CSE559A_L17.md
Normal file
184
content/CSE559A/CSE559A_L17.md
Normal file
@@ -0,0 +1,184 @@
|
||||
# CSE559A Lecture 17
|
||||
|
||||
## Local Features
|
||||
|
||||
### Types of local features
|
||||
|
||||
#### Edge
|
||||
|
||||
Goal: Identify sudden changes in image intensity
|
||||
|
||||
Generate edge map as human artists.
|
||||
|
||||
An edge is a place of rapid change in the image intensity function.
|
||||
|
||||
Take the absolute value of the first derivative of the image intensity function.
|
||||
|
||||
For 2d functions, $\frac{\partial f}{\partial x}=\lim_{\Delta x\to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}$
|
||||
|
||||
For discrete images data, $\frac{\partial f}{\partial x}\approx \frac{f(x+1)-f(x)}{1}$
|
||||
|
||||
Run convolution with kernel $[1,0,-1]$ to get the first derivative in the x direction, without shifting. (generic kernel is $[1,-1]$)
|
||||
|
||||
Prewitt operator:
|
||||
|
||||
$$
|
||||
M_x=\begin{bmatrix}
|
||||
1 & 0 & -1 \\
|
||||
1 & 0 & -1 \\
|
||||
1 & 0 & -1 \\
|
||||
\end{bmatrix}
|
||||
\quad
|
||||
M_y=\begin{bmatrix}
|
||||
1 & 1 & 1 \\
|
||||
0 & 0 & 0 \\
|
||||
-1 & -1 & -1 \\
|
||||
\end{bmatrix}
|
||||
$$
|
||||
Sobel operator:
|
||||
|
||||
$$
|
||||
M_x=\begin{bmatrix}
|
||||
1 & 0 & -1 \\
|
||||
2 & 0 & -2 \\
|
||||
1 & 0 & -1 \\
|
||||
\end{bmatrix}
|
||||
\quad
|
||||
M_y=\begin{bmatrix}
|
||||
1 & 2 & 1 \\
|
||||
0 & 0 & 0 \\
|
||||
-1 & -2 & -1 \\
|
||||
\end{bmatrix}
|
||||
$$
|
||||
Roberts operator:
|
||||
|
||||
$$
|
||||
M_x=\begin{bmatrix}
|
||||
1 & 0 \\
|
||||
0 & -1 \\
|
||||
\end{bmatrix}
|
||||
\quad
|
||||
M_y=\begin{bmatrix}
|
||||
0 & 1 \\
|
||||
-1 & 0 \\
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
Image gradient:
|
||||
|
||||
$$
|
||||
\nabla f = \left(\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}\right)
|
||||
$$
|
||||
|
||||
Gradient magnitude:
|
||||
|
||||
$$
|
||||
||\nabla f|| = \sqrt{\left(\frac{\partial f}{\partial x}\right)^2 + \left(\frac{\partial f}{\partial y}\right)^2}
|
||||
$$
|
||||
|
||||
Gradient direction:
|
||||
|
||||
$$
|
||||
\theta = \tan^{-1}\left(\frac{\frac{\partial f}{\partial y}}{\frac{\partial f}{\partial x}}\right)
|
||||
$$
|
||||
|
||||
The gradient points in the direction of the most rapid increase in intensity.
|
||||
|
||||
> Application: Gradient-domain image editing
|
||||
>
|
||||
> Goal: solve for pixel values in the target region to match gradients of the source region while keeping the rest of the image unchanged.
|
||||
>
|
||||
> [Poisson Image Editing](http://www.cs.virginia.edu/~connelly/class/2014/comp_photo/proj2/poisson.pdf)
|
||||
|
||||
Noisy edge detection:
|
||||
|
||||
When the intensity function is very noisy, we can use a Gaussian smoothing filter to reduce the noise before taking the gradient.
|
||||
|
||||
Suppose pixels of the true image $f_{i,j}$ are corrupted by Gaussian noise $n_{i,j}$ with mean 0 and variance $\sigma^2$.
|
||||
Then the noisy image is $g_{i,j}=(f_{i,j}+n_{i,j})-(f_{i,j+1}+n_{i,j+1})\approx N(0,2\sigma^2)$
|
||||
|
||||
To find edges, look for peaks in $\frac{d}{dx}(f\circ g)$ where $g$ is the Gaussian smoothing filter.
|
||||
|
||||
or we can directly use the Derivative of Gaussian (DoG) filter:
|
||||
|
||||
$$
|
||||
\frac{d}{dx}g(x,\sigma)=\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{x^2}{2\sigma^2}}
|
||||
$$
|
||||
|
||||
##### Separability of Gaussian filter
|
||||
|
||||
A Gaussian filter is separable if it can be written as a product of two 1D filters.
|
||||
|
||||
$$
|
||||
\frac{d}{dx}g(x,\sigma)=\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{x^2}{2\sigma^2}}
|
||||
\quad \frac{d}{dy}g(y,\sigma)=\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{y^2}{2\sigma^2}}
|
||||
$$
|
||||
|
||||
##### Separable Derivative of Gaussian (DoG) filter
|
||||
|
||||
$$
|
||||
\frac{d}{dx}g(x,y)\propto -x\exp\left(-\frac{x^2+y^2}{2\sigma^2}\right)
|
||||
\quad \frac{d}{dy}g(x,y)\propto -y\exp\left(-\frac{x^2+y^2}{2\sigma^2}\right)
|
||||
$$
|
||||
|
||||
##### Derivative of Gaussian: Scale
|
||||
|
||||
Using Gaussian derivatives with different values of 𝜎 finds structures at different scales or frequencies
|
||||
|
||||
(Take the hybrid image as an example)
|
||||
|
||||
##### Canny edge detector
|
||||
|
||||
1. Smooth the image with a Gaussian filter
|
||||
2. Compute the gradient magnitude and direction of the smoothed image
|
||||
3. Thresholding gradient magnitude
|
||||
4. Non-maxima suppression
|
||||
- For each location `q` above the threshold, check that the gradient magnitude is higher than at adjacent points `p` and `r` in the direction of the gradient
|
||||
5. Thresholding the non-maxima suppressed gradient magnitude
|
||||
6. Hysteresis thresholding
|
||||
- Use two thresholds: high and low
|
||||
- Start with a seed edge pixel with a gradient magnitude greater than the high threshold
|
||||
- Follow the gradient direction to find all connected pixels with a gradient magnitude greater than the low threshold
|
||||
|
||||
##### Top-down segmentation
|
||||
|
||||
Data-driven top-down segmentation:
|
||||
|
||||
#### Interest point
|
||||
|
||||
Key point matching:
|
||||
|
||||
1. Find a set of distinctive keypoints in the image
|
||||
2. Define a region of interest around each keypoint
|
||||
3. Compute a local descriptor from the normalized region
|
||||
4. Match local descriptors between images
|
||||
|
||||
Characteristic of good features:
|
||||
|
||||
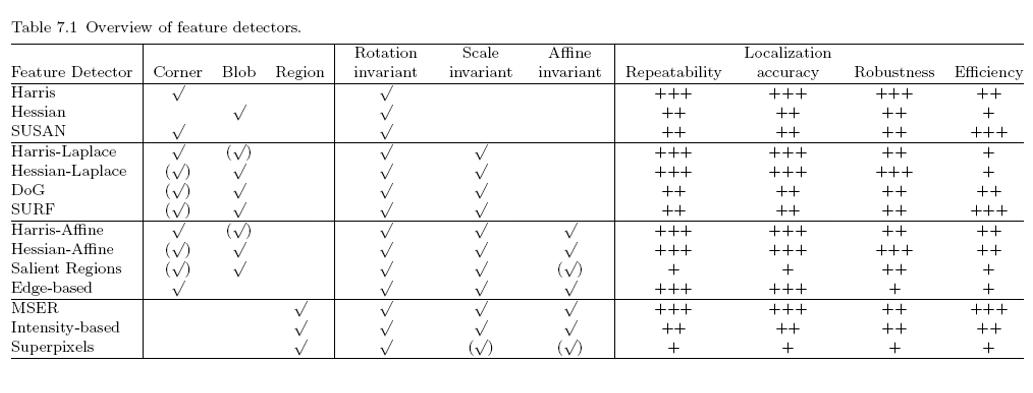
- Repeatability
|
||||
- The same feature can be found in several images despite geometric and photometric transformations
|
||||
- Saliency
|
||||
- Each feature is distinctive
|
||||
- Compactness and efficiency
|
||||
- Many fewer features than image pixels
|
||||
- Locality
|
||||
- A feature occupies a relatively small area of the image; robust to clutter and occlusion
|
||||
|
||||
##### Harris corner detector
|
||||
|
||||
### Applications of local features
|
||||
|
||||
#### Image alignment
|
||||
|
||||
#### 3D reconstruction
|
||||
|
||||
#### Motion tracking
|
||||
|
||||
#### Robot navigation
|
||||
|
||||
#### Indexing and database retrieval
|
||||
|
||||
#### Object recognition
|
||||
|
||||
|
||||
|
||||
68
content/CSE559A/CSE559A_L18.md
Normal file
68
content/CSE559A/CSE559A_L18.md
Normal file
@@ -0,0 +1,68 @@
|
||||
# CSE559A Lecture 18
|
||||
|
||||
## Continue on Harris Corner Detector
|
||||
|
||||
Goal: Descriptor distinctiveness
|
||||
|
||||
- We want to be able to reliably determine which point goes with which.
|
||||
- Must provide some invariance to geometric and photometric differences.
|
||||
|
||||
Harris corner detector:
|
||||
|
||||
> Other existing variants:
|
||||
> - Hessian & Harris: [Beaudet '78], [Harris '88]
|
||||
> - Laplacian, DoG: [Lindeberg '98], [Lowe 1999]
|
||||
> - Harris-/Hessian-Laplace: [Mikolajczyk & Schmid '01]
|
||||
> - Harris-/Hessian-Affine: [Mikolajczyk & Schmid '04]
|
||||
> - EBR and IBR: [Tuytelaars & Van Gool '04]
|
||||
> - MSER: [Matas '02]
|
||||
> - Salient Regions: [Kadir & Brady '01]
|
||||
> - Others…
|
||||
|
||||
### Deriving a corner detection criterion
|
||||
|
||||
- Basic idea: we should easily recognize the point by looking through a small window
|
||||
- Shifting a window in any direction should give a large change in intensity
|
||||
|
||||
Corner is the point where the intensity changes in all directions.
|
||||
|
||||
Criterion:
|
||||
|
||||
Change in appearance of window $W$ for the shift $(u,v)$:
|
||||
|
||||
$$
|
||||
E(u,v) = \sum_{x,y\in W} [I(x+u,y+v) - I(x,y)]^2
|
||||
$$
|
||||
|
||||
First-order Taylor approximation for small shifts $(u,v)$:
|
||||
|
||||
$$
|
||||
I(x+u,y+v) \approx I(x,y) + I_x u + I_y v
|
||||
$$
|
||||
|
||||
plug into $E(u,v)$:
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
E(u,v) &= \sum_{(x,y)\in W} [I(x+u,y+v) - I(x,y)]^2 \\
|
||||
&\approx \sum_{(x,y)\in W} [I(x,y) + I_x u + I_y v - I(x,y)]^2 \\
|
||||
&= \sum_{(x,y)\in W} [I_x u + I_y v]^2 \\
|
||||
&= \sum_{(x,y)\in W} [I_x^2 u^2 + 2 I_x I_y u v + I_y^2 v^2]
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Consider the second moment matrix:
|
||||
|
||||
$$
|
||||
M = \begin{bmatrix}
|
||||
I_x^2 & I_x I_y \\
|
||||
I_x I_y & I_y^2
|
||||
\end{bmatrix}=\begin{bmatrix}
|
||||
a & 0 \\
|
||||
0 & b
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
If either $a$ or $b$ is small, then the window is not a corner.
|
||||
|
||||
|
||||
71
content/CSE559A/CSE559A_L19.md
Normal file
71
content/CSE559A/CSE559A_L19.md
Normal file
@@ -0,0 +1,71 @@
|
||||
# CSE559A Lecture 19
|
||||
|
||||
## Feature Detection
|
||||
|
||||
### Behavior of corner features with respect to Image Transformations
|
||||
|
||||
To be useful for image matching, “the same” corner features need to show up despite geometric and photometric transformations
|
||||
|
||||
We need to analyze how the corner response function and the corner locations change in response to various transformations
|
||||
|
||||
#### Affine intensity change
|
||||
|
||||
Solution:
|
||||
|
||||
- Only derivative of intensity are used (invariant to intensity change)
|
||||
- Intensity scaling
|
||||
|
||||
#### Image translation
|
||||
|
||||
Solution:
|
||||
|
||||
- Derivatives and window function are shift invariant
|
||||
|
||||
#### Image rotation
|
||||
|
||||
Second moment ellipse rotates but its shape (i.e. eigenvalues) remains the same
|
||||
|
||||
#### Scaling
|
||||
|
||||
Classify edges instead of corners
|
||||
|
||||
## Automatic Scale selection for interest point detection
|
||||
|
||||
### Scale space
|
||||
|
||||
We want to extract keypoints with characteristic scales that are equivariant (or covariant) with respect to scaling of the image
|
||||
|
||||
Approach: compute a scale-invariant response function over neighborhoods centered at each location $(x,y)$ and a range of scales $\sigma$, find scale-space locations $(x,y,\sigma)$ where this function reaches a local maximum
|
||||
|
||||
A particularly convenient response function is given by the scale-normalized Laplacian of Gaussian (LoG) filter:
|
||||
|
||||
$$
|
||||
\nabla^2_{norm}=\sigma^2\nabla^2\left(\frac{\partial^2}{\partial x^2}g+\frac{\partial^2}{\partial y^2}g\right)
|
||||
$$
|
||||
|
||||
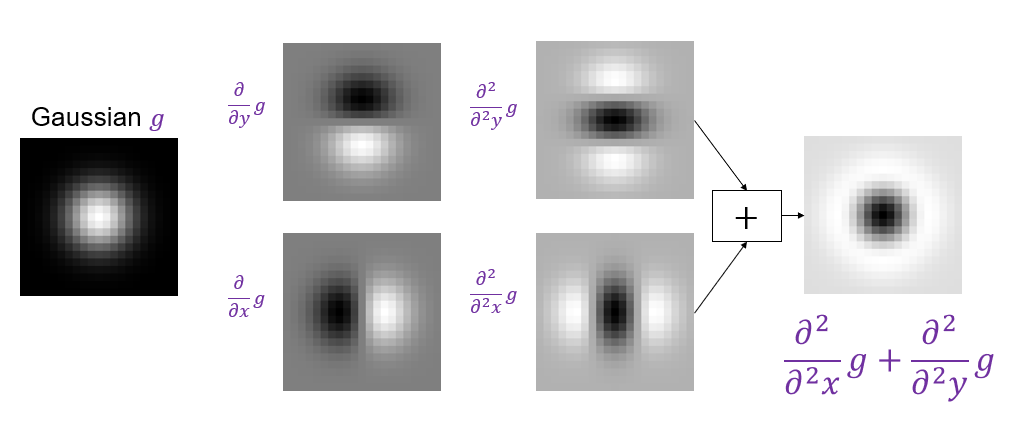
|
||||
|
||||
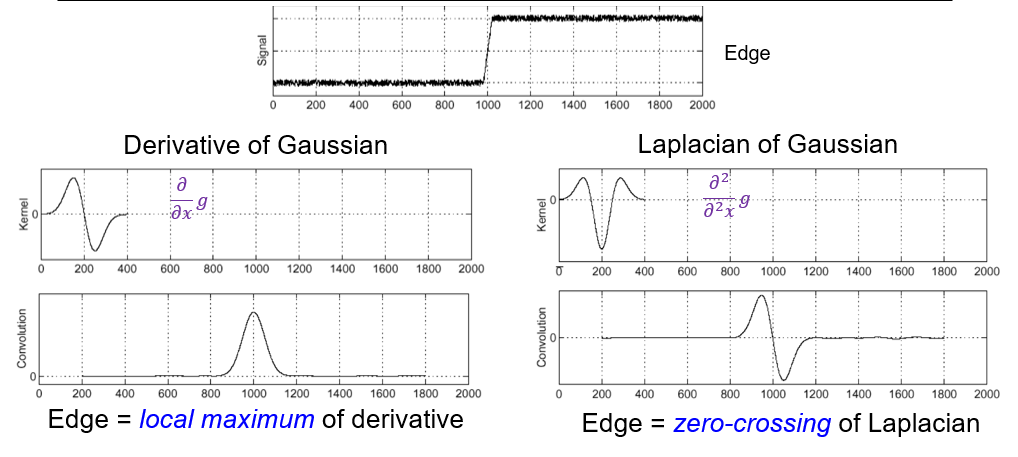
#### Edge detection with LoG
|
||||
|
||||
|
||||
|
||||
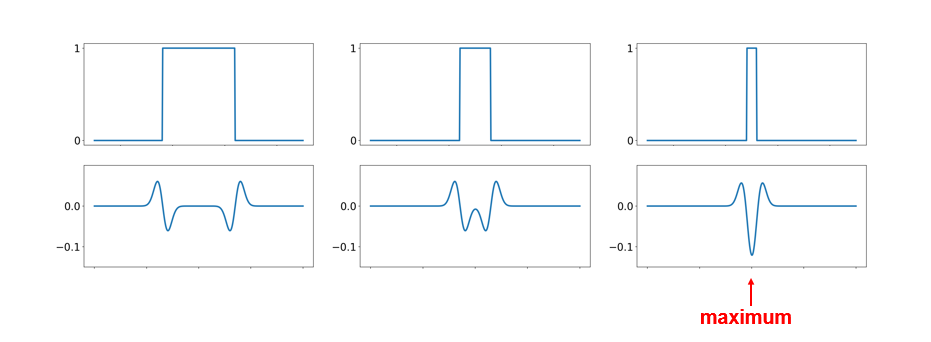
#### Blob detection with LoG
|
||||
|
||||
|
||||
|
||||
### Difference of Gaussians (DoG)
|
||||
|
||||
DoG has a little more flexibility, since you can select the scales of the Gaussians.
|
||||
|
||||
### Scale-invariant feature transform (SIFT)
|
||||
|
||||
The main goal of SIFT is to enable image matching in the presence of significant transformations
|
||||
|
||||
- To recognize the same keypoint in multiple images, we need to match appearance descriptors or "signatures" in their neighborhoods
|
||||
- Descriptors that are locally invariant w.r.t. scale and rotation can handle a wide range of global transformations
|
||||
|
||||
### Maximum stable extremal regions (MSER)
|
||||
|
||||
Based on Watershed segmentation algorithm
|
||||
|
||||
Select regions that are stable over a large parameter range
|
||||
165
content/CSE559A/CSE559A_L2.md
Normal file
165
content/CSE559A/CSE559A_L2.md
Normal file
@@ -0,0 +1,165 @@
|
||||
# CSE559A Lecture 2
|
||||
|
||||
## The Geometry of Image Formation
|
||||
|
||||
Mapping between image and world coordinates.
|
||||
|
||||
Today's focus:
|
||||
|
||||
$$
|
||||
x=K[R\ t]X
|
||||
$$
|
||||
|
||||
### Pinhole Camera Model
|
||||
|
||||
Add a barrier to block off most of the rays.
|
||||
|
||||
- Reduce blurring
|
||||
- The opening known as the **aperture**
|
||||
|
||||
$f$ is the focal length.
|
||||
$c$ is the center of the aperture.
|
||||
|
||||
#### Focal length/ Field of View (FOV)/ Zoom
|
||||
|
||||
- Focal length: distance between the aperture and the image plane.
|
||||
- Field of View (FOV): the angle between the two rays that pass through the aperture and the image plane.
|
||||
- Zoom: the ratio of the focal length to the image plane.
|
||||
|
||||
#### Other types of projection
|
||||
|
||||
Beyond the pinhole/perspective camera model, there are other types of projection.
|
||||
|
||||
- Radial distortion
|
||||
- 360-degree camera
|
||||
- Equirectangular Panoramas
|
||||
- Random lens
|
||||
- Rotating sensors
|
||||
- Photofinishing
|
||||
- Tiltshift lens
|
||||
|
||||
### Perspective Geometry
|
||||
|
||||
Length and area are not preserved.
|
||||
|
||||
Angle is not preserved.
|
||||
|
||||
But straight lines are still straight.
|
||||
|
||||
Parallel lines in the world intersect at a **vanishing point** on the image plane.
|
||||
|
||||
Vanishing lines: the set of all vanishing points of parallel lines in the world on the same plane in the world.
|
||||
|
||||
Vertical vanishing point at infinity.
|
||||
|
||||
### Camera/Projection Matrix
|
||||
|
||||
Linear projection model.
|
||||
|
||||
$$
|
||||
x=K[R\ t]X
|
||||
$$
|
||||
|
||||
- $x$: image coordinates 2d (homogeneous coordinates)
|
||||
- $X$: world coordinates 3d (homogeneous coordinates)
|
||||
- $K$: camera matrix (3x3 and invertible)
|
||||
- $R$: camera rotation matrix (3x3)
|
||||
- $t$: camera translation vector (3x1)
|
||||
|
||||
#### Homogeneous coordinates
|
||||
|
||||
- 2D: $$(x, y)\to\begin{bmatrix}x\\y\\1\end{bmatrix}$$
|
||||
- 3D: $$(x, y, z)\to\begin{bmatrix}x\\y\\z\\1\end{bmatrix}$$
|
||||
|
||||
converting from homogeneous to inhomogeneous coordinates:
|
||||
|
||||
- 2D: $$\begin{bmatrix}x\\y\\w\end{bmatrix}\to(x/w, y/w)$$
|
||||
- 3D: $$\begin{bmatrix}x\\y\\z\\w\end{bmatrix}\to(x/w, y/w, z/w)$$
|
||||
|
||||
When $w=0$, the point is at infinity.
|
||||
|
||||
Homogeneous coordinates are invariant under scaling (non-zero scalar).
|
||||
|
||||
$$
|
||||
k\begin{bmatrix}x\\y\\w\end{bmatrix}=\begin{bmatrix}kx\\ky\\kw\end{bmatrix}\implies\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}x/k\\y/k\end{bmatrix}
|
||||
$$
|
||||
|
||||
A convenient way to represent a point at infinity is to use a unit vector.
|
||||
|
||||
Line equation: $ax+by+c=0$
|
||||
|
||||
$$
|
||||
line_i=\begin{bmatrix}a_i\\b_i\\c_i\end{bmatrix}
|
||||
$$
|
||||
|
||||
|
||||
Append a 1 to pixel coordinates to get homogeneous coordinates.
|
||||
|
||||
$$
|
||||
pixel_i=\begin{bmatrix}u_i\\v_i\\1\end{bmatrix}
|
||||
$$
|
||||
|
||||
Line given by cross product of two points:
|
||||
|
||||
$$
|
||||
line_i=pixel_1\times pixel_2
|
||||
$$
|
||||
|
||||
Intersection of two lines given by cross product of the lines:
|
||||
|
||||
$$
|
||||
pixel_i=line_1\times line_2
|
||||
$$
|
||||
|
||||
#### Pinhole Camera Projection Matrix
|
||||
|
||||
Intrinsic Assumptions:
|
||||
|
||||
- Unit aspect ratio
|
||||
- No skew
|
||||
- Optical center at (0,0)
|
||||
|
||||
Extrinsic Assumptions:
|
||||
|
||||
- No rotation
|
||||
- No translation (camera at world origin)
|
||||
|
||||
$$
|
||||
x=K[I\ 0]X\implies w\begin{bmatrix}u\\v\\1\end{bmatrix}=\begin{bmatrix}f&0&0&0\\0&f&0&0\\0&0&1&0\end{bmatrix}\begin{bmatrix}x\\y\\z\\1\end{bmatrix}
|
||||
$$
|
||||
|
||||
Removing the assumptions:
|
||||
|
||||
Intrinsic assumptions:
|
||||
|
||||
- Unit aspect ratio
|
||||
- No skew
|
||||
|
||||
Extrinsic assumptions:
|
||||
|
||||
- No rotation
|
||||
- No translation
|
||||
|
||||
$$
|
||||
x=K[I\ 0]X\implies w\begin{bmatrix}u\\v\\1\end{bmatrix}=\begin{bmatrix}\alpha&0&u_0&0\\0&\beta&v_0&0\\0&0&1&0\end{bmatrix}\begin{bmatrix}x\\y\\z\\1\end{bmatrix}
|
||||
$$
|
||||
|
||||
Adding skew:
|
||||
|
||||
$$
|
||||
x=K[I\ 0]X\implies w\begin{bmatrix}u\\v\\1\end{bmatrix}=\begin{bmatrix}\alpha&s&u_0&0\\0&\beta&v_0&0\\0&0&1&0\end{bmatrix}\begin{bmatrix}x\\y\\z\\1\end{bmatrix}
|
||||
$$
|
||||
|
||||
Finally, adding camera rotation and translation:
|
||||
|
||||
$$
|
||||
x=K[I\ t]X\implies w\begin{bmatrix}u\\v\\1\end{bmatrix}=\begin{bmatrix}\alpha&s&u_0\\0&\beta&v_0\\0&0&1\end{bmatrix}\begin{bmatrix}r_{11}&r_{12}&r_{13}&t_x\\r_{21}&r_{22}&r_{23}&t_y\\r_{31}&r_{32}&r_{33}&t_z\end{bmatrix}\begin{bmatrix}x\\y\\z\\1\end{bmatrix}
|
||||
$$
|
||||
|
||||
What is the degrees of freedom of the camera matrix?
|
||||
|
||||
- rotation: 3
|
||||
- translation: 3
|
||||
- camera matrix: 5
|
||||
|
||||
Total: 11
|
||||
145
content/CSE559A/CSE559A_L20.md
Normal file
145
content/CSE559A/CSE559A_L20.md
Normal file
@@ -0,0 +1,145 @@
|
||||
# CSE559A Lecture 20
|
||||
|
||||
## Local feature descriptors
|
||||
|
||||
Detection: Identify the interest points
|
||||
|
||||
Description: Extract vector feature descriptor surrounding each interest point.
|
||||
|
||||
Matching: Determine correspondence between descriptors in two views
|
||||
|
||||
### Image representation
|
||||
|
||||
Histogram of oriented gradients (HOG)
|
||||
|
||||
- Quantization
|
||||
- Grids: fast but applicable only with few dimensions
|
||||
- Clustering: slower but can quantize data in higher dimensions
|
||||
- Matching
|
||||
- Histogram intersection or Euclidean may be faster
|
||||
- Chi-squared often works better
|
||||
- Earth mover’s distance is good for when nearby bins represent similar values
|
||||
|
||||
#### SIFT vector formation
|
||||
|
||||
Computed on rotated and scaled version of window according to computed orientation & scale
|
||||
|
||||
- resample the window
|
||||
|
||||
Based on gradients weighted by a Gaussian of variance half the window (for smooth falloff)
|
||||
|
||||
4x4 array of gradient orientation histogram weighted by magnitude
|
||||
|
||||
8 orientations x 4x4 array = 128 dimensions
|
||||
|
||||
Motivation: some sensitivity to spatial layout, but not too much.
|
||||
|
||||
For matching:
|
||||
|
||||
- Extraordinarily robust detection and description technique
|
||||
- Can handle changes in viewpoint
|
||||
- Up to about 60 degree out-of-plane rotation
|
||||
- Can handle significant changes in illumination
|
||||
- Sometimes even day vs. night
|
||||
- Fast and efficient—can run in real time
|
||||
- Lots of code available
|
||||
|
||||
#### SURF
|
||||
|
||||
- Fast approximation of SIFT idea
|
||||
- Efficient computation by 2D box filters & integral images
|
||||
- 6 times faster than SIFT
|
||||
- Equivalent quality for object identification
|
||||
|
||||
#### Shape context
|
||||
|
||||
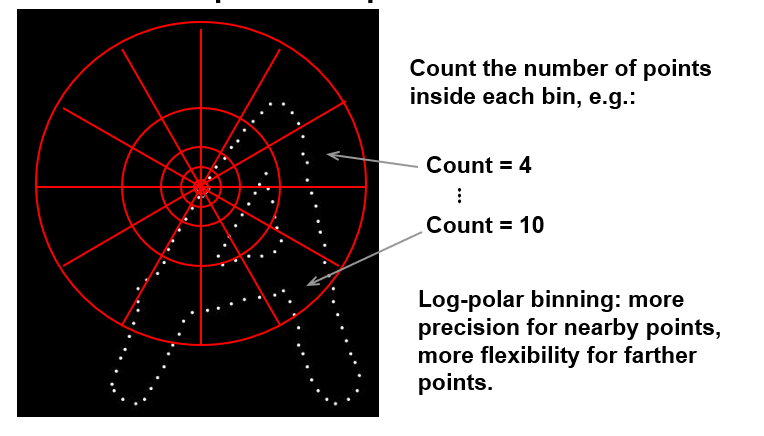
|
||||
|
||||
#### Self-similarity Descriptor
|
||||
|
||||
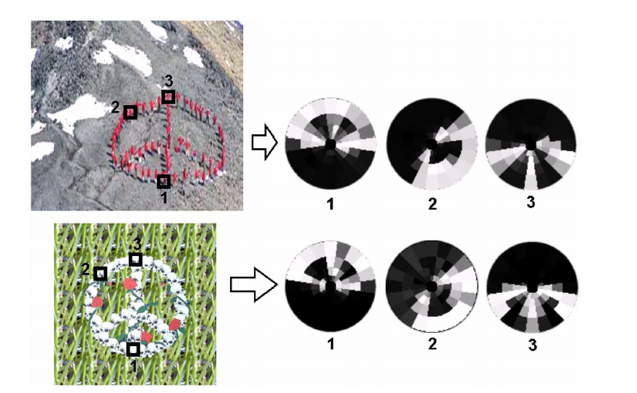
|
||||
|
||||
## Local feature matching
|
||||
|
||||
### Matching
|
||||
|
||||
Simplest approach: Pick the nearest neighbor. Threshold on absolute distance
|
||||
|
||||
Problem: Lots of self similarity in many photos
|
||||
|
||||
Solution: Nearest neighbor with low ratio test
|
||||
|
||||
|
||||
|
||||
## Deep Learning for Correspondence Estimation
|
||||
|
||||
|
||||
|
||||
## Optical Flow
|
||||
|
||||
### Field
|
||||
|
||||
Motion field: the projection of the 3D scene motion into the image
|
||||
Magnitude of vectors is determined by metric motion
|
||||
Only caused by motion
|
||||
|
||||
Optical flow: the apparent motion of brightness patterns in the image
|
||||
Magnitude of vectors is measured in pixels
|
||||
Can be caused by lightning
|
||||
|
||||
### Brightness constancy constraint, aperture problem
|
||||
|
||||
Machine Learning Approach
|
||||
|
||||
- Collect examples of inputs and outputs
|
||||
- Design a prediction model suitable for the task
|
||||
- Invariances, Equivariances; Complexity; Input and Output shapes and semantics
|
||||
- Specify loss functions and train model
|
||||
- Limitations: Requires training the model; Requires a sufficiently complete training dataset; Must re-learn known facts; Higher computational complexity
|
||||
|
||||
Optimization Approach
|
||||
|
||||
- Define properties we expect to hold for a correct solution
|
||||
- Translate properties into a cost function
|
||||
- Derive an algorithm to solve for the cost function
|
||||
- Limitations: Often requires making overly simple assumptions on properties; Some tasks can’t be easily defined
|
||||
|
||||
Given frames at times $t-1$ and $t$, estimate the apparent motion field $u(x,y)$ and $v(x,y)$ between them
|
||||
Brightness constancy constraint: projection of the same point looks the same in every frame
|
||||
|
||||
$$
|
||||
I(x,y,t-1) = I(x+u(x,y),y+v(x,y),t)
|
||||
$$
|
||||
|
||||
Additional assumptions:
|
||||
|
||||
- Small motion: points do not move very far
|
||||
- Spatial coherence: points move like their neighbors
|
||||
|
||||
Trick for solving:
|
||||
|
||||
Brightness constancy constraint:
|
||||
|
||||
$$
|
||||
I(x,y,t-1) = I(x+u(x,y),y+v(x,y),t)
|
||||
$$
|
||||
|
||||
Linearize the right-hand side using Taylor expansion:
|
||||
|
||||
$$
|
||||
I(x,y,t-1) \approx I(x,y,t) + I_x u(x,y) + I_y v(x,y)
|
||||
$$
|
||||
|
||||
$$
|
||||
I_x u(x,y) + I_y v(x,y) + I(x,y,t) - I(x,y,t-1) = 0
|
||||
$$
|
||||
|
||||
Hence,
|
||||
|
||||
$$
|
||||
I_x u(x,y) + I_y v(x,y) + I_t = 0
|
||||
$$
|
||||
|
||||
|
||||
|
||||
|
||||
215
content/CSE559A/CSE559A_L21.md
Normal file
215
content/CSE559A/CSE559A_L21.md
Normal file
@@ -0,0 +1,215 @@
|
||||
# CSE559A Lecture 21
|
||||
|
||||
## Continue on optical flow
|
||||
|
||||
### The brightness constancy constraint
|
||||
|
||||
$$
|
||||
I_x u(x,y) + I_y v(x,y) + I_t = 0
|
||||
$$
|
||||
Given the gradients $I_x, I_y$ and $I_t$, can we uniquely recover the motion $(u,v)$?
|
||||
|
||||
- Suppose $(u, v)$ satisfies the constraint: $\nabla I \cdot (u,v) + I_t = 0$
|
||||
- Then $\nabla I \cdot (u+u', v+v') + I_t = 0$ for any $(u', v')$ s.t. $\nabla I \cdot (u', v') = 0$
|
||||
- Interpretation: the component of the flow perpendicular to the gradient (i.e., parallel to the edge) cannot be recovered!
|
||||
|
||||
#### Aperture problem
|
||||
|
||||
- The brightness constancy constraint is only valid for a small patch in the image
|
||||
- For a large motion, the patch may look very different
|
||||
|
||||
Consider the barber pole illusion
|
||||
|
||||
### Estimating optical flow (Lucas-Kanade method)
|
||||
|
||||
- Consider a small patch in the image
|
||||
- Assume the motion is constant within the patch
|
||||
- Then we can solve for the motion $(u, v)$ by minimizing the error:
|
||||
|
||||
$$
|
||||
I_x u(x,y) + I_y v(x,y) + I_t = 0
|
||||
$$
|
||||
|
||||
How to get more equations for a pixel?
|
||||
Spatial coherence constraint: assume the pixel’s neighbors have the same (𝑢,𝑣)
|
||||
If we have 𝑛 pixels in the neighborhood, then we can set up a linear least squares system:
|
||||
|
||||
$$
|
||||
\begin{bmatrix}
|
||||
I_x(x_1, y_1) & I_y(x_1, y_1) \\
|
||||
\vdots & \vdots \\
|
||||
I_x(x_n, y_n) & I_y(x_n, y_n)
|
||||
\end{bmatrix}
|
||||
\begin{bmatrix}
|
||||
u \\ v
|
||||
\end{bmatrix} = -\begin{bmatrix}
|
||||
I_t(x_1, y_1) \\ \vdots \\ I_t(x_n, y_n)
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
#### Lucas-Kanade flow
|
||||
|
||||
Let $A=
|
||||
\begin{bmatrix}
|
||||
I_x(x_1, y_1) & I_y(x_1, y_1) \\
|
||||
\vdots & \vdots \\
|
||||
I_x(x_n, y_n) & I_y(x_n, y_n)
|
||||
\end{bmatrix}$
|
||||
|
||||
$b = \begin{bmatrix}
|
||||
I_t(x_1, y_1) \\ \vdots \\ I_t(x_n, y_n)
|
||||
\end{bmatrix}$
|
||||
|
||||
$d = \begin{bmatrix}
|
||||
u \\ v
|
||||
\end{bmatrix}$
|
||||
|
||||
The solution is $d=(A^T A)^{-1} A^T b$
|
||||
|
||||
Lucas-Kanade flow:
|
||||
|
||||
- Find $(u,v)$ minimizing $\sum_{i} (I(x_i+u,y_i+v,t)-I(x_i,y_i,t-1))^2$
|
||||
- use Taylor approximation of $I(x_i+u,y_i+v,t)$ for small shifts $(u,v)$ to obtain closed-form solution
|
||||
|
||||
### Refinement for Lucas-Kanade
|
||||
|
||||
In some cases, the Lucas-Kanade method may not work well:
|
||||
- The motion is large (larger than a pixel)
|
||||
- A point does not move like its neighbors
|
||||
- Brightness constancy does not hold
|
||||
|
||||
#### Iterative refinement (for large motion)
|
||||
|
||||
Iterative Lukas-Kanade Algorithm
|
||||
|
||||
1. Estimate velocity at each pixel by solving Lucas-Kanade equations
|
||||
2. Warp It towards It+1 using the estimated flow field
|
||||
- use image warping techniques
|
||||
3. Repeat until convergence
|
||||
|
||||
Iterative refinement is limited due to Aliasing
|
||||
|
||||
#### Coarse-to-fine refinement (for large motion)
|
||||
|
||||
- Estimate flow at a coarse level
|
||||
- Refine the flow at a finer level
|
||||
- Use the refined flow to warp the image
|
||||
- Repeat until convergence
|
||||
|
||||

|
||||
|
||||
#### Representing moving images with layers (for a point may not move like its neighbors)
|
||||
|
||||
- The image can be decomposed into a moving layer and a stationary layer
|
||||
- The moving layer is the layer that moves
|
||||
- The stationary layer is the layer that does not move
|
||||
|
||||
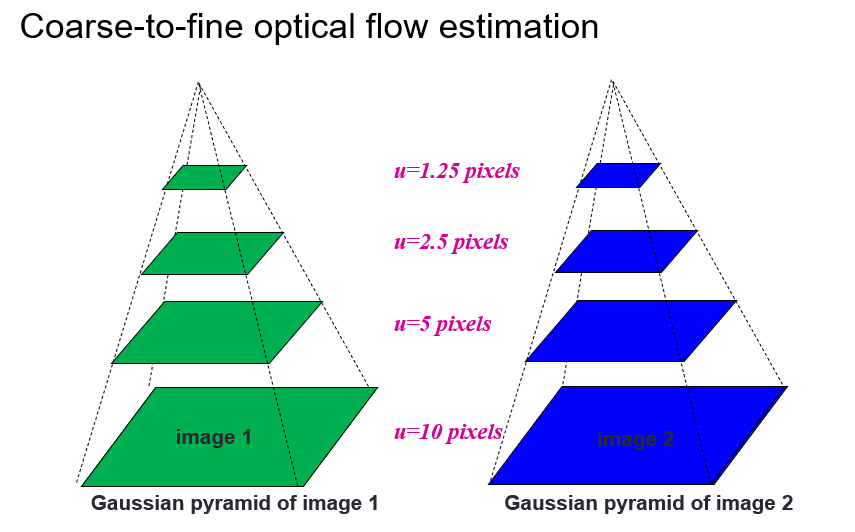
|
||||
|
||||
### SOTA models
|
||||
|
||||
#### 2009
|
||||
|
||||
Start with something similar to Lucas-Kanade
|
||||
|
||||
- gradient constancy
|
||||
- energy minimization with smoothing term
|
||||
- region matching
|
||||
- keypoint matching (long-range)
|
||||
|
||||
#### 2015
|
||||
|
||||
Deep neural networks
|
||||
|
||||
- Use a deep neural network to represent the flow field
|
||||
- Use synthetic data to train the network (floating chairs)
|
||||
|
||||
#### 2023
|
||||
|
||||
GMFlow
|
||||
|
||||
use Transformer to model the flow field
|
||||
|
||||
## Robust Fitting of parametric models
|
||||
|
||||
Challenges:
|
||||
|
||||
- Noise in the measured feature locations
|
||||
- Extraneous data: clutter (outliers), multiple lines
|
||||
- Missing data: occlusions
|
||||
|
||||
### Least squares fitting
|
||||
|
||||
Normal least squares fitting
|
||||
|
||||
$y=mx+b$ is not a good model for the data since there might be vertical lines
|
||||
|
||||
Instead we use total least squares
|
||||
|
||||
Line parametrization: $ax+by=d$
|
||||
|
||||
$(a,b)$ is the unit normal to the line (i.e., $a^2+b^2=1$)
|
||||
$d$ is the distance between the line and the origin
|
||||
Perpendicular distance between point $(x_i, y_i)$ and line $ax+by=d$ (assuming $a^2+b^2=1$):
|
||||
|
||||
$$
|
||||
|ax_i + by_i - d|
|
||||
$$
|
||||
|
||||
Objective function:
|
||||
|
||||
$$
|
||||
E = \sum_{i=1}^n (ax_i + by_i - d)^2
|
||||
$$
|
||||
|
||||
Solve for $d$ first: $d =a\bar{x}+b\bar{y}$
|
||||
Plugging back in:
|
||||
|
||||
$$
|
||||
E = \sum_{i=1}^n (a(x_i-\bar{x})+b(y_i-\bar{y}))^2 = \left\|\begin{bmatrix}x_1-\bar{x}&y_1-\bar{y}\\\vdots&\vdots\\x_n-\bar{x}&y_n-\bar{y}\end{bmatrix}\begin{pmatrix}a\\b\end{pmatrix}\right\|^2
|
||||
$$
|
||||
|
||||
We want to find $N$ that minimizes $\|UN\|^2$ subject to $\|N\|^2= 1$
|
||||
Solution is given by the eigenvector of $U^T U$ associated with the smallest eigenvalue
|
||||
|
||||
Drawbacks:
|
||||
|
||||
- Sensitive to outliers
|
||||
|
||||
### Robust fitting
|
||||
|
||||
General approach: find model parameters 𝜃 that minimize
|
||||
|
||||
$$
|
||||
\sum_{i} \rho_{\sigma}(r(x_i;\theta))
|
||||
$$
|
||||
|
||||
$r(x_i;\theta)$: residual of $x_i$ w.r.t. model parameters $\theta$
|
||||
$\rho_{\sigma}$: robust function with scale parameter $\sigma$, e.g., $\rho_{\sigma}(u)=\frac{u^2}{\sigma^2+u^2}$
|
||||
|
||||
Nonlinear optimization problem that must be solved iteratively
|
||||
|
||||
- Least squares solution can be used for initialization
|
||||
- Scale of robust function should be chosen carefully
|
||||
|
||||
Drawbacks:
|
||||
|
||||
- Need to manually choose the robust function and scale parameter
|
||||
|
||||
### RANSAC
|
||||
|
||||
Voting schemes
|
||||
|
||||
Random sample consensus: very general framework for model fitting in the presence of outliers
|
||||
|
||||
Outline:
|
||||
|
||||
- Randomly choose a small initial subset of points
|
||||
- Fit a model to that subset
|
||||
- Find all inlier points that are "close" to the model and reject the rest as outliers
|
||||
- Do this many times and choose the model with the most inliers
|
||||
|
||||
### Hough transform
|
||||
|
||||
|
||||
|
||||
260
content/CSE559A/CSE559A_L22.md
Normal file
260
content/CSE559A/CSE559A_L22.md
Normal file
@@ -0,0 +1,260 @@
|
||||
# CSE559A Lecture 22
|
||||
|
||||
## Continue on Robust Fitting of parametric models
|
||||
|
||||
### RANSAC
|
||||
|
||||
#### Definition: RANdom SAmple Consensus
|
||||
|
||||
RANSAC is a method to fit a model to a set of data points.
|
||||
|
||||
It is a non-deterministic algorithm that can be used to fit a model to a set of data points.
|
||||
|
||||
Pros:
|
||||
|
||||
- Simple and general
|
||||
- Applicable to many different problems
|
||||
- Often works well in practice
|
||||
|
||||
Cons:
|
||||
|
||||
- Lots of parameters to set
|
||||
- Number of iterations grows exponentially as outlier ratio increases
|
||||
- Can't always get a good initialization of the model based on the minimum number of samples.
|
||||
|
||||
### Hough Transform
|
||||
|
||||
Use point-line duality to find lines.
|
||||
|
||||
In practice, we don't use (m,b) parameterization.
|
||||
|
||||
Instead, we use polar parameterization:
|
||||
|
||||
$$
|
||||
\rho = x \cos \theta + y \sin \theta
|
||||
$$
|
||||
|
||||
Algorithm outline:
|
||||
|
||||
- Initialize accumulator $H$ to all zeros
|
||||
- For each feature point $(x,y)$
|
||||
- For $\theta = 0$ to $180$
|
||||
- $\rho = x \cos \theta + y \sin \theta$
|
||||
- $H(\theta, \rho) += 1$
|
||||
- Find the value(s) of $(\theta, \rho)$ where $H(\theta, \rho)$ is a local maximum (perform NMS on the accumulator array)
|
||||
- The detected line in the image is given by $\rho = x \cos \theta + y \sin \theta$
|
||||
|
||||
#### Effect of noise
|
||||
|
||||
|
||||
|
||||
Noise makes the peak fuzzy.
|
||||
|
||||
#### Effect of outliers
|
||||
|
||||
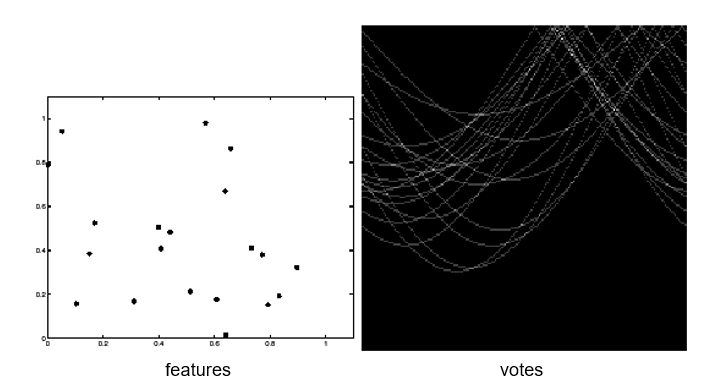
|
||||
|
||||
Outliers can break the peak.
|
||||
|
||||
#### Pros and Cons
|
||||
|
||||
Pros:
|
||||
|
||||
- Can deal with non-locality and occlusion
|
||||
- Can detect multiple instances of a model
|
||||
- Some robustness to noise: noise points unlikely to contribute consistently to any single bin
|
||||
- Leads to a surprisingly general strategy for shape localization (more on this next)
|
||||
|
||||
Cons:
|
||||
|
||||
- Complexity increases exponentially with the number of model parameters
|
||||
- In practice, not used beyond three or four dimensions
|
||||
- Non-target shapes can produce spurious peaks in parameter space
|
||||
- It's hard to pick a good grid size
|
||||
|
||||
### Generalize Hough Transform
|
||||
|
||||
Template representation: for each type of landmark point, store all possible displacement vectors towards the center
|
||||
|
||||
Detecting the template:
|
||||
|
||||
For each feature in a new image, look up that feature type in the model and vote for the possible center locations associated with that type in the model
|
||||
|
||||
#### Implicit shape models
|
||||
|
||||
Training:
|
||||
|
||||
- Build codebook of patches around extracted interest points using clustering
|
||||
- Map the patch around each interest point to closest codebook entry
|
||||
- For each codebook entry, store all positions it was found, relative to object center
|
||||
|
||||
Testing:
|
||||
|
||||
- Given test image, extract patches, match to codebook entry
|
||||
- Cast votes for possible positions of object center
|
||||
- Search for maxima in voting space
|
||||
- Extract weighted segmentation mask based on stored masks for the codebook occurrences
|
||||
|
||||
## Image alignment
|
||||
|
||||
### Affine transformation
|
||||
|
||||
Simple fitting procedure: linear least squares
|
||||
Approximates viewpoint changes for roughly planar objects and roughly orthographic cameras
|
||||
Can be used to initialize fitting for more complex models
|
||||
|
||||
Fitting an affine transformation:
|
||||
|
||||
$$
|
||||
\begin{bmatrix}
|
||||
&&&\cdots\\
|
||||
x_i & y_i & 0&0&1&0\\
|
||||
0&0&x_i&y_i&0&1\\
|
||||
&&&\cdots\\
|
||||
\end{bmatrix}
|
||||
\begin{bmatrix}
|
||||
m_1\\
|
||||
m_2\\
|
||||
m_3\\
|
||||
m_4\\
|
||||
t_1\\
|
||||
t_2\\
|
||||
\end{bmatrix}
|
||||
=
|
||||
\begin{bmatrix}
|
||||
\cdots\\
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
Only need 3 points to solve for 6 parameters.
|
||||
|
||||
### Homography
|
||||
|
||||
Recall that
|
||||
|
||||
$$
|
||||
x' = \frac{a x + b y + c}{g x + h y + i}, \quad y' = \frac{d x + e y + f}{g x + h y + i}
|
||||
$$
|
||||
|
||||
Use 2D homogeneous coordinates:
|
||||
|
||||
$(x,y) \rightarrow \begin{pmatrix}x \\ y \\ 1\end{pmatrix}$
|
||||
|
||||
$\begin{pmatrix}x\\y\\w\end{pmatrix} \rightarrow (x/w,y/w)$
|
||||
|
||||
Reminder: all homogeneous coordinate vectors that are (non-zero) scalar multiples of each other represent the same point
|
||||
|
||||
|
||||
Equation for homography in homogeneous coordinates:
|
||||
|
||||
$$
|
||||
\begin{pmatrix}
|
||||
x' \\
|
||||
y' \\
|
||||
1
|
||||
\end{pmatrix}
|
||||
\cong
|
||||
\begin{pmatrix}
|
||||
h_{11} & h_{12} & h_{13} \\
|
||||
h_{21} & h_{22} & h_{23} \\
|
||||
h_{31} & h_{32} & h_{33}
|
||||
\end{pmatrix}
|
||||
\begin{pmatrix}
|
||||
x \\
|
||||
y \\
|
||||
1
|
||||
\end{pmatrix}
|
||||
$$
|
||||
|
||||
Constraint from a match $(x_i,x_i')$, $x_i'\cong Hx_i$
|
||||
|
||||
How can we get rid of the scale ambiguity?
|
||||
|
||||
Cross product trick:$x_i' × Hx_i=0$
|
||||
|
||||
The cross product is defined as:
|
||||
|
||||
$$
|
||||
\begin{pmatrix}a\\b\\c\end{pmatrix} \times \begin{pmatrix}a'\\b'\\c'\end{pmatrix} = \begin{pmatrix}bc'-b'c\\ca'-c'a\\ab'-a'b\end{pmatrix}
|
||||
$$
|
||||
|
||||
Let $h_1^T, h_2^T, h_3^T$ be the rows of $H$. Then
|
||||
|
||||
$$
|
||||
x_i' × Hx_i=\begin{pmatrix}
|
||||
x_i' \\
|
||||
y_i' \\
|
||||
1
|
||||
\end{pmatrix} \times \begin{pmatrix}
|
||||
h_1^T x_i \\
|
||||
h_2^T x_i \\
|
||||
h_3^T x_i
|
||||
\end{pmatrix}
|
||||
=
|
||||
\begin{pmatrix}
|
||||
y_i' h_3^T x_i−h_2^T x_i \\
|
||||
h_1^T x_i−x_i' h_3^T x_i \\
|
||||
x_i' h_2^T x_i−y_i' h_1^T x_i
|
||||
\end{pmatrix}
|
||||
$$
|
||||
|
||||
Constraint from a match $(x_i,x_i')$:
|
||||
|
||||
$$
|
||||
x_i' × Hx_i=\begin{pmatrix}
|
||||
x_i' \\
|
||||
y_i' \\
|
||||
1
|
||||
\end{pmatrix} \times \begin{pmatrix}
|
||||
h_1^T x_i \\
|
||||
h_2^T x_i \\
|
||||
h_3^T x_i
|
||||
\end{pmatrix}
|
||||
=
|
||||
\begin{pmatrix}
|
||||
y_i' h_3^T x_i−h_2^T x_i \\
|
||||
h_1^T x_i−x_i' h_3^T x_i \\
|
||||
x_i' h_2^T x_i−y_i' h_1^T x_i
|
||||
\end{pmatrix}
|
||||
$$
|
||||
|
||||
Rearranging the terms:
|
||||
|
||||
$$
|
||||
\begin{bmatrix}
|
||||
0^T &-x_i^T &y_i' x_i^T \\
|
||||
x_i^T &0^T &-x_i' x_i^T \\
|
||||
y_i' x_i^T &x_i' x_i^T &0^T
|
||||
\end{bmatrix}
|
||||
\begin{bmatrix}
|
||||
h_1 \\
|
||||
h_2 \\
|
||||
h_3
|
||||
\end{bmatrix} = 0
|
||||
$$
|
||||
|
||||
These equations aren't independent! So, we only need two.
|
||||
|
||||
### Robust alignment
|
||||
|
||||
#### Descriptor-based feature matching
|
||||
|
||||
Extract features
|
||||
Compute putative matches
|
||||
Loop:
|
||||
|
||||
- Hypothesize transformation $T$
|
||||
- Verify transformation (search for other matches consistent with $T$)
|
||||
|
||||
#### RANSAC
|
||||
|
||||
Even after filtering out ambiguous matches, the set of putative matches still contains a very high percentage of outliers
|
||||
|
||||
RANSAC loop:
|
||||
|
||||
- Randomly select a seed group of matches
|
||||
- Compute transformation from seed group
|
||||
- Find inliers to this transformation
|
||||
- If the number of inliers is sufficiently large, re-compute least-squares estimate of transformation on all of the inliers
|
||||
|
||||
At the end, keep the transformation with the largest number of inliers
|
||||
15
content/CSE559A/CSE559A_L23.md
Normal file
15
content/CSE559A/CSE559A_L23.md
Normal file
@@ -0,0 +1,15 @@
|
||||
# CSE559A Lecture 23
|
||||
|
||||
## DUSt3r
|
||||
|
||||
Dense and Unconstrained Stereo 3D Reconstruction of arbitrary image collections.
|
||||
|
||||
[Github DUST3R](https://github.com/naver/dust3r)
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
1
content/CSE559A/CSE559A_L24.md
Normal file
1
content/CSE559A/CSE559A_L24.md
Normal file
@@ -0,0 +1 @@
|
||||
|
||||
217
content/CSE559A/CSE559A_L25.md
Normal file
217
content/CSE559A/CSE559A_L25.md
Normal file
@@ -0,0 +1,217 @@
|
||||
# CSE559A Lecture 25
|
||||
|
||||
## Geometry and Multiple Views
|
||||
|
||||
### Cues for estimating Depth
|
||||
|
||||
#### Multiple Views (the strongest depth cue)
|
||||
|
||||
Two common settings:
|
||||
|
||||
**Stereo vision**: a pair of cameras, usually with some constraints on the relative position of the two cameras.
|
||||
|
||||
**Structure from (camera) motion**: cameras observing a scene from different viewpoints
|
||||
|
||||
Structure and depth are inherently ambiguous from single views.
|
||||
|
||||
Other hints for depth:
|
||||
|
||||
- Occlusion
|
||||
- Perspective effects
|
||||
- Texture
|
||||
- Object motion
|
||||
- Shading
|
||||
- Focus/Defocus
|
||||
|
||||
#### Focus on Stereo and Multiple Views
|
||||
|
||||
Stereo correspondence: Given a point in one of the images, where could its corresponding points be in the other images?
|
||||
|
||||
Structure: Given projections of the same 3D point in two or more images, compute the 3D coordinates of that point
|
||||
|
||||
Motion: Given a set of corresponding points in two or more images, compute the camera parameters
|
||||
|
||||
#### A simple example of estimating depth with stereo:
|
||||
|
||||
Stereo: shape from "motion" between two views
|
||||
|
||||
We'll need to consider:
|
||||
|
||||
- Info on camera pose ("calibration")
|
||||
- Image point correspondences
|
||||
|
||||
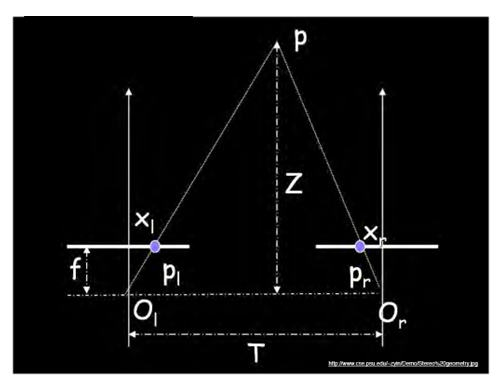
|
||||
|
||||
Assume parallel optical axes, known camera parameters (i.e., calibrated cameras). What is expression for Z?
|
||||
|
||||
Similar triangles $(p_l, P, p_r)$ and $(O_l, P, O_r)$:
|
||||
|
||||
$$
|
||||
\frac{T-x_l+x_r}{Z-f}=\frac{T}{Z}
|
||||
$$
|
||||
|
||||
$$
|
||||
Z = \frac{f \cdot T}{x_l-x_r}
|
||||
$$
|
||||
|
||||
### Camera Calibration
|
||||
|
||||
Use an scene with known geometry
|
||||
|
||||
- Correspond image points to 3d points
|
||||
- Get least squares solution (or non-linear solution)
|
||||
|
||||
Solving unknown camera parameters:
|
||||
|
||||
$$
|
||||
\begin{bmatrix}
|
||||
su\\
|
||||
sv\\
|
||||
s
|
||||
\end{bmatrix}
|
||||
= \begin{bmatrix}
|
||||
m_{11} & m_{12} & m_{13} & m_{14}\\
|
||||
m_{21} & m_{22} & m_{23} & m_{24}\\
|
||||
m_{31} & m_{32} & m_{33} & m_{34}
|
||||
\end{bmatrix}
|
||||
\begin{bmatrix}
|
||||
X\\
|
||||
Y\\
|
||||
Z\\
|
||||
1
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
Method 1: Homogenous linear system. Solve for m's entries using least squares.
|
||||
|
||||
$$
|
||||
\begin{bmatrix}
|
||||
X_1 & Y_1 & Z_1 & 1 & 0 & 0 & 0 & 0 & -u_1X_1 & -u_1Y_1 & -u_1Z_1 & -u_1 \\
|
||||
0 & 0 & 0 & 0 & X_1 & Y_1 & Z_1 & 1 & -v_1X_1 & -v_1Y_1 & -v_1Z_1 & -v_1 \\
|
||||
\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots\\
|
||||
X_n & Y_n & Z_n & 1 & 0 & 0 & 0 & 0 & -u_nX_n & -u_nY_n & -u_nZ_n & -u_n \\
|
||||
0 & 0 & 0 & 0 & X_n & Y_n & Z_n & 1 & -v_nX_n & -v_nY_n & -v_nZ_n & -v_n
|
||||
\end{bmatrix}
|
||||
\begin{bmatrix} m_{11} \\ m_{12} \\ m_{13} \\ m_{14} \\ m_{21} \\ m_{22} \\ m_{23} \\ m_{24} \\ m_{31} \\ m_{32} \\ m_{33} \\ m_{34} \end{bmatrix} = 0
|
||||
$$
|
||||
|
||||
Method 2: Non-homogenous linear system. Solve for m's entries using least squares.
|
||||
|
||||
**Advantages**
|
||||
|
||||
- Easy to formulate and solve
|
||||
- Provides initialization for non-linear methods
|
||||
|
||||
**Disadvantages**
|
||||
|
||||
- Doesn't directly give you camera parameters
|
||||
- Doesn't model radial distortion
|
||||
- Can't impose constraints, such as known focal length
|
||||
|
||||
**Non-linear methods are preferred**
|
||||
|
||||
- Define error as difference between projected points and measured points
|
||||
- Minimize error using Newton's method or other non-linear optimization
|
||||
|
||||
#### Triangulation
|
||||
|
||||
Given projections of a 3D point in two or more images (with known camera matrices), find the coordinates of the point
|
||||
|
||||
##### Approaches 1: Geometric approach
|
||||
|
||||
Find shortest segment connecting the two viewing rays and let $X$ be the midpoint of that segment
|
||||
|
||||
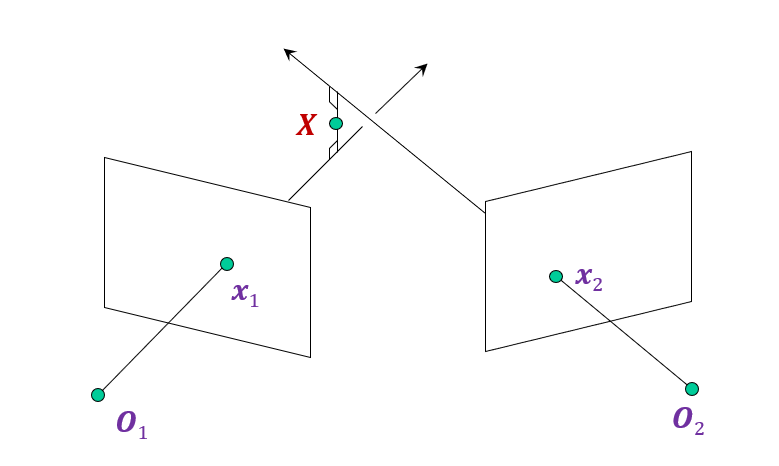
|
||||
|
||||
##### Approaches 2: Non-linear optimization
|
||||
|
||||
Minimize error between projected point and measured point
|
||||
|
||||
$$
|
||||
||\operatorname{proj}(P_1 X) - x_1||_2^2 + ||\operatorname{proj}(P_2 X) - x_2||_2^2
|
||||
$$
|
||||
|
||||
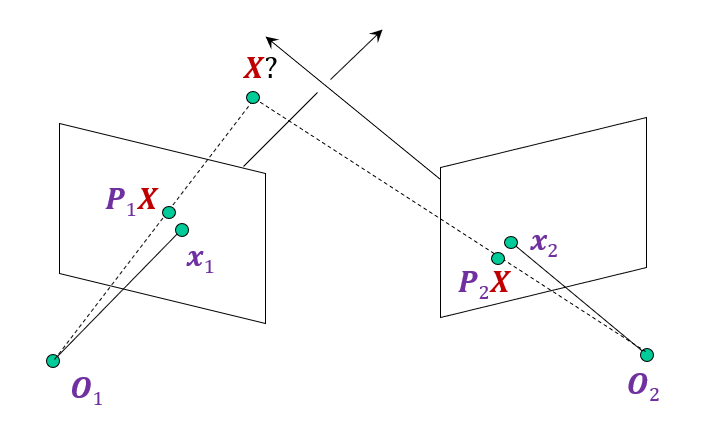
|
||||
|
||||
##### Approaches 3: Linear approach
|
||||
|
||||
$x_1\cong P_1X$ and $x_2\cong P_2X$
|
||||
|
||||
$x_1\times P_1X = 0$ and $x_2\times P_2X = 0$
|
||||
|
||||
$[x_{1_{\times}}]P_1X = 0$ and $[x_{2_{\times}}]P_2X = 0$
|
||||
|
||||
Rewrite as:
|
||||
|
||||
$$
|
||||
a\times b=\begin{bmatrix}
|
||||
0 & -a_3 & a_2\\
|
||||
a_3 & 0 & -a_1\\
|
||||
-a_2 & a_1 & 0
|
||||
\end{bmatrix}
|
||||
\begin{bmatrix}
|
||||
b_1\\
|
||||
b_2\\
|
||||
b_3
|
||||
\end{bmatrix}
|
||||
=[a_{\times}]b
|
||||
$$
|
||||
|
||||
Using **singular value decomposition**, we can solve for $X$
|
||||
|
||||
### Epipolar Geometry
|
||||
|
||||
What constraints must hold between two projections of the same 3D point?
|
||||
|
||||
Given a 2D point in one view, where can we find the corresponding point in the other view?
|
||||
|
||||
Given only 2D correspondences, how can we calibrate the two cameras, i.e., estimate their relative position and orientation and the intrinsic parameters?
|
||||
|
||||
Key ideas:
|
||||
|
||||
- We can answer all these questions without knowledge of the 3D scene geometry
|
||||
- Important to think about projections of camera centers and visual rays into the other view
|
||||
|
||||
#### Epipolar Geometry Setup
|
||||
|
||||
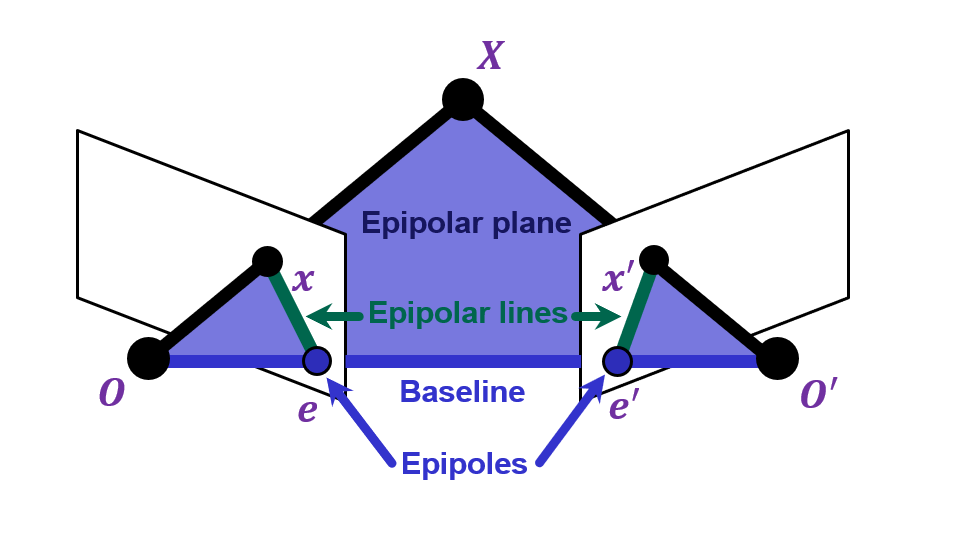
|
||||
|
||||
Suppose we have two cameras with centers $O,O'$
|
||||
|
||||
The baseline is the line connecting the origins
|
||||
|
||||
Epipoles $e,e'$ are where the baseline intersects the image planes, or projections of the other camera in each view
|
||||
|
||||
Consider a point $X$, which projects to $x$ and $x'$
|
||||
|
||||
The plane formed by $X,O,O'$ is called an epipolar plane
|
||||
There is a family of planes passing through $O$ and $O'$
|
||||
|
||||
Epipolar lines are projections of the baseline into the image planes
|
||||
|
||||
**Epipolar lines** connect the epipoles to the projections of $X$
|
||||
Equivalently, they are intersections of the epipolar plane with the image planes – thus, they come in matching pairs.
|
||||
|
||||
**Application**: This constraint can be used to find correspondences between points in two camera. by the epipolar line in one image, we can find the corresponding feature in the other image.
|
||||
|
||||
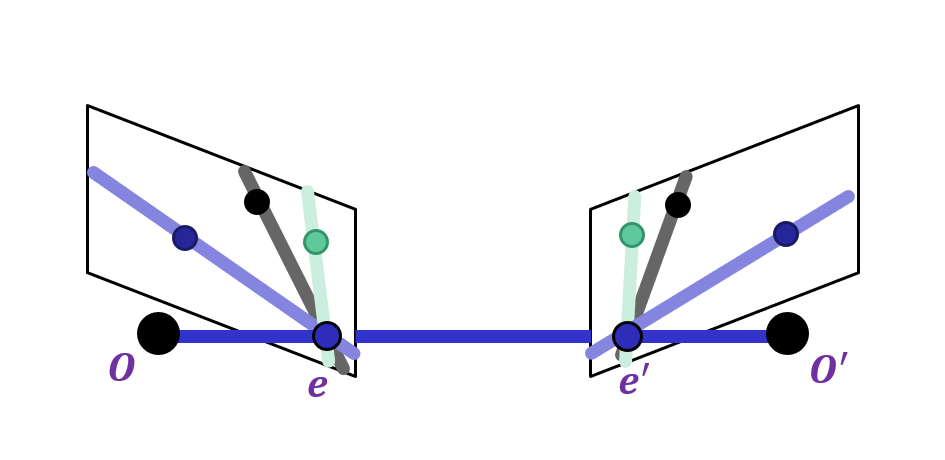
|
||||
|
||||
Epipoles are finite and may be visible in the image.
|
||||
|
||||
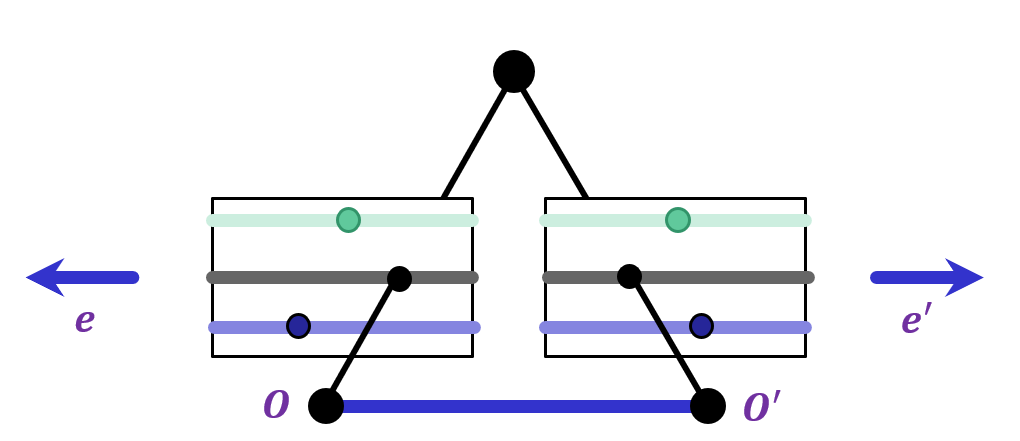
|
||||
|
||||
Epipoles are infinite, epipolar lines parallel.
|
||||
|
||||
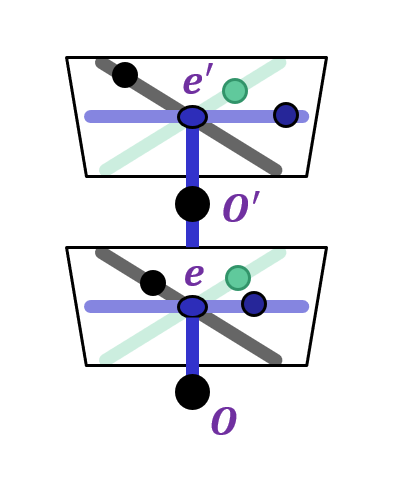
|
||||
|
||||
Epipole is "focus of expansion" and coincides with the principal point of the camera
|
||||
|
||||
Epipolar lines go out from principal point
|
||||
|
||||
Next class:
|
||||
|
||||
### The Essential and Fundamental Matrices
|
||||
|
||||
### Dense Stereo Matching
|
||||
|
||||
|
||||
177
content/CSE559A/CSE559A_L26.md
Normal file
177
content/CSE559A/CSE559A_L26.md
Normal file
@@ -0,0 +1,177 @@
|
||||
# CSE559A Lecture 26
|
||||
|
||||
## Continue on Geometry and Multiple Views
|
||||
|
||||
### The Essential and Fundamental Matrices
|
||||
|
||||
#### Math of the epipolar constraint: Calibrated case
|
||||
|
||||
Recall Epipolar Geometry
|
||||
|
||||

|
||||
|
||||
Epipolar constraint:
|
||||
|
||||
If we set the config for the first camera as the world origin and $[I|0]\begin{pmatrix}y\\1\end{pmatrix}=x$, and $[R|t]\begin{pmatrix}y\\1\end{pmatrix}=x'$, then
|
||||
|
||||
Notice that $x'\cdot [t\times (Ry)]=0$
|
||||
|
||||
$$
|
||||
x'^T E x_1 = 0
|
||||
$$
|
||||
|
||||
We denote the constraint defined by the Essential Matrix as $E$.
|
||||
|
||||
$E x$ is the epipolar line associated with $x$ ($l'=Ex$)
|
||||
|
||||
$E^T x'$ is the epipolar line associated with $x'$ ($l=E^T x'$)
|
||||
|
||||
$E e=0$ and $E^T e'=0$ ($x$ and $x'$ don't matter)
|
||||
|
||||
$E$ is singular (rank 2) and have five degrees of freedom.
|
||||
|
||||
#### Epipolar constraint: Uncalibrated case
|
||||
|
||||
If the calibration matrices $K$ and $K'$ are unknown, we can write the epipolar constraint in terms of unknown normalized coordinates:
|
||||
|
||||
$$
|
||||
x'^T_{norm} E x_{norm} = 0
|
||||
$$
|
||||
|
||||
where $x_{norm}=K^{-1} x$, $x'_{norm}=K'^{-1} x'$
|
||||
|
||||
$$
|
||||
x'^T_{norm} E x_{norm} = 0\implies x'^T_{norm} Fx=0
|
||||
$$
|
||||
|
||||
where $F=K'^{-1}EK^{-1}$ is the **Fundamental Matrix**.
|
||||
|
||||
$$
|
||||
(x',y',1)\begin{bmatrix}
|
||||
f_{11} & f_{12} & f_{13} \\
|
||||
f_{21} & f_{22} & f_{23} \\
|
||||
f_{31} & f_{32} & f_{33}
|
||||
\end{bmatrix}\begin{pmatrix}
|
||||
x\\y\\1
|
||||
\end{pmatrix}=0
|
||||
$$
|
||||
|
||||
Properties of $F$:
|
||||
|
||||
$F x$ is the epipolar line associated with $x$ ($l'=F x$)
|
||||
|
||||
$F^T x'$ is the epipolar line associated with $x'$ ($l=F^T x'$)
|
||||
|
||||
$F e=0$ and $F^T e'=0$
|
||||
|
||||
$F$ is singular (rank two) and has seven degrees of freedom
|
||||
|
||||
#### Estimating the fundamental matrix
|
||||
|
||||
Given: correspondences $x=(x,y,1)^T$ and $x'=(x',y',1)^T$
|
||||
|
||||
Constraint: $x'^T F x=0$
|
||||
|
||||
$$
|
||||
(x',y',1)\begin{bmatrix}
|
||||
f_{11} & f_{12} & f_{13} \\
|
||||
f_{21} & f_{22} & f_{23} \\
|
||||
f_{31} & f_{32} & f_{33}
|
||||
\end{bmatrix}\begin{pmatrix}
|
||||
x\\y\\1
|
||||
\end{pmatrix}=0
|
||||
$$
|
||||
|
||||
**Each pair of correspondences gives one equation (one constraint)**
|
||||
|
||||
At least 8 pairs of correspondences are needed to solve for the 9 elements of $F$ (The eight point algorithm)
|
||||
|
||||
We know $F$ needs to be singular/rank 2. How do we force it to be singular?
|
||||
|
||||
Solution: take SVD of the initial estimate and throw out the smallest singular value
|
||||
|
||||
$$
|
||||
F=U\begin{bmatrix}
|
||||
\sigma_1 & 0 \\
|
||||
0 & \sigma_2 \\
|
||||
0 & 0
|
||||
\end{bmatrix}V^T
|
||||
$$
|
||||
|
||||
## Structure from Motion
|
||||
|
||||
Not always uniquely solvable.
|
||||
|
||||
If we scale the entire scene by some factor $k$ and, at the same time, scale the camera matrices by the factor of $1/k$, the projections of the scene points remain exactly the same:
|
||||
$x\cong PX =(1/k P)(kX)$
|
||||
|
||||
Without a reference measurement, it is impossible to recover the absolute scale of the scene!
|
||||
|
||||
In general, if we transform the scene using a transformation $Q$ and apply the inverse transformation to the camera matrices, then the image observations do not change:
|
||||
|
||||
$x\cong PX =(P Q^{-1})(QX)$
|
||||
|
||||
### Types of Ambiguities
|
||||
|
||||
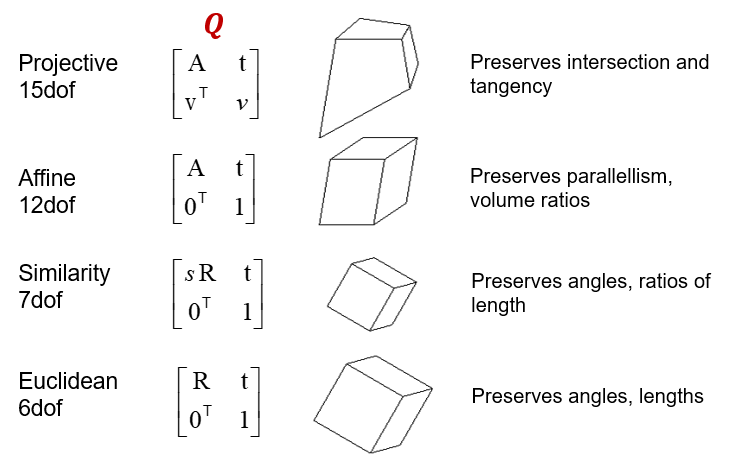
|
||||
|
||||
### Affine projection : more general than orthographic
|
||||
|
||||
A general affine projection is a 3D-to-2D linear mapping plus translation:
|
||||
|
||||
$$
|
||||
P=\begin{bmatrix}
|
||||
a_{11} & a_{12} & a_{13} & t_1 \\
|
||||
a_{21} & a_{22} & a_{23} & t_2 \\
|
||||
0 & 0 & 0 & 1
|
||||
\end{bmatrix}=\begin{bmatrix}
|
||||
A & t \\
|
||||
0^T & 1
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
In non-homogeneous coordinates:
|
||||
|
||||
$$
|
||||
\begin{pmatrix}
|
||||
x\\y\\1
|
||||
\end{pmatrix}=\begin{bmatrix}
|
||||
a_{11} & a_{12} & a_{13} \\
|
||||
a_{21} & a_{22} & a_{23}
|
||||
\end{bmatrix}\begin{pmatrix}
|
||||
X\\Y\\Z
|
||||
\end{pmatrix}+\begin{pmatrix}
|
||||
t_1\\t_2
|
||||
\end{pmatrix}=AX+t
|
||||
$$
|
||||
|
||||
### Affine Structure from Motion
|
||||
|
||||
Given: 𝑚 images of 𝑛 fixed 3D points such that
|
||||
|
||||
$$
|
||||
x_{ij}=A_iX_j+t_i, \quad i=1,\dots,m, \quad j=1,\dots,n
|
||||
$$
|
||||
|
||||
Problem: use the 𝑚𝑛 correspondences $x_{ij}$ to estimate 𝑚 projection matrices $A_i$ and translation vectors $t_i$, and 𝑛 points $X_j$
|
||||
|
||||
The reconstruction is defined up to an arbitrary affine transformation $Q$ (12 degrees of freedom):
|
||||
|
||||
$$
|
||||
\begin{bmatrix}
|
||||
A & t \\
|
||||
0^T & 1
|
||||
\end{bmatrix}\rightarrow\begin{bmatrix}
|
||||
A & t \\
|
||||
0^T & 1
|
||||
\end{bmatrix}Q^{-1}, \quad \begin{pmatrix}X_j\\1\end{pmatrix}\rightarrow Q\begin{pmatrix}X_j\\1\end{pmatrix}
|
||||
$$
|
||||
|
||||
How many constraints and unknowns for $m$ images and $n$ points?
|
||||
|
||||
$2mn$ constraints and $8m + 3n$ unknowns
|
||||
|
||||
To be able to solve this problem, we must have $2mn \geq 8m+3n-12$ (affine ambiguity takes away 12 dof)
|
||||
|
||||
E.g., for two views, we need four point correspondences
|
||||
|
||||
357
content/CSE559A/CSE559A_L3.md
Normal file
357
content/CSE559A/CSE559A_L3.md
Normal file
@@ -0,0 +1,357 @@
|
||||
# CSE559A Lecture 3
|
||||
|
||||
## Image formation
|
||||
|
||||
### Degrees of Freedom
|
||||
|
||||
$$
|
||||
x=K[R|t]X
|
||||
$$
|
||||
|
||||
$$
|
||||
w\begin{bmatrix}
|
||||
x\\
|
||||
y\\
|
||||
1
|
||||
\end{bmatrix}
|
||||
=
|
||||
\begin{bmatrix}
|
||||
\alpha & s & u_0 \\
|
||||
0 & \beta & v_0 \\
|
||||
0 & 0 & 1
|
||||
\end{bmatrix}
|
||||
\begin{bmatrix}
|
||||
r_{11} & r_{12} & r_{13} &t_x\\
|
||||
r_{21} & r_{22} & r_{23} &t_y\\
|
||||
r_{31} & r_{32} & r_{33} &t_z\\
|
||||
\end{bmatrix}
|
||||
\begin{bmatrix}
|
||||
x\\
|
||||
y\\
|
||||
z\\
|
||||
1
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
### Impact of translation of camera
|
||||
|
||||
$$
|
||||
p=K[R|t]\begin{bmatrix}
|
||||
x\\
|
||||
y\\
|
||||
z\\
|
||||
0
|
||||
\end{bmatrix}=K[R]\begin{bmatrix}
|
||||
x\\
|
||||
y\\
|
||||
z\\
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
Projection of a vanishing point or projection of a point at infinity is invariant to translation.
|
||||
|
||||
### Recover world coordinates from pixel coordinates
|
||||
|
||||
$$
|
||||
\begin{bmatrix}
|
||||
u\\
|
||||
v\\
|
||||
1
|
||||
\end{bmatrix}=K[R|t]^{-1}X
|
||||
$$
|
||||
|
||||
Key issue: where is the world origin $w$? Suppose $w=1/s$
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\begin{bmatrix}
|
||||
u\\
|
||||
v\\
|
||||
1
|
||||
\end{bmatrix}
|
||||
&=sK[R|t]X\\
|
||||
K^{-1}\begin{bmatrix}
|
||||
u\\
|
||||
v\\
|
||||
1
|
||||
\end{bmatrix}
|
||||
&=s[R|t]X\\
|
||||
R^{-1}K^{-1}\begin{bmatrix}
|
||||
u\\
|
||||
v\\
|
||||
1
|
||||
\end{bmatrix}&=s[I|R^{-1}t]X\\
|
||||
R^{-1}K^{-1}\begin{bmatrix}
|
||||
u\\
|
||||
v\\
|
||||
1
|
||||
\end{bmatrix}&=[I|R^{-1}t]sX\\
|
||||
R^{-1}K^{-1}\begin{bmatrix}
|
||||
u\\
|
||||
v\\
|
||||
1
|
||||
\end{bmatrix}&=sX+sR^{-1}t\\
|
||||
\frac{1}{s}R^{-1}K^{-1}\begin{bmatrix}
|
||||
u\\
|
||||
v\\
|
||||
1
|
||||
\end{bmatrix}-R^{-1}t&=X\\
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
## Projective Geometry
|
||||
|
||||
### Orthographic Projection
|
||||
|
||||
Special case of perspective projection when $f\to\infty$
|
||||
|
||||
- Distance for the center of projection is infinite
|
||||
- Also called parallel projection
|
||||
- Projection matrix is
|
||||
|
||||
$$
|
||||
w\begin{bmatrix}
|
||||
u\\
|
||||
v\\
|
||||
1
|
||||
\end{bmatrix}=
|
||||
\begin{bmatrix}
|
||||
f & 0 & 0 & 0\\
|
||||
0 & f & 0 & 0\\
|
||||
0 & 0 & 0 & s\\
|
||||
\end{bmatrix}
|
||||
\begin{bmatrix}
|
||||
x\\
|
||||
y\\
|
||||
z\\
|
||||
1
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
Continue in later part of the course
|
||||
|
||||
## Image processing foundations
|
||||
|
||||
### Motivation for image processing
|
||||
|
||||
Representational Motivation:
|
||||
|
||||
- We need more than raw pixel values
|
||||
|
||||
Computational Motivation:
|
||||
|
||||
- Many image processing operations must be run across many locations in a image
|
||||
- A loop in python is slow
|
||||
- High-level libraries reduce errors, developer time, and algorithm runtime
|
||||
- Two common libraries:
|
||||
- Torch+Torchvision: Focus on deep learning
|
||||
- scikit-image: Focus on classical image processing algorithms
|
||||
|
||||
### Operations on images
|
||||
|
||||
#### Point operations
|
||||
|
||||
Operations that are applied to one pixel at a time
|
||||
|
||||
Negative image
|
||||
|
||||
$$
|
||||
I_{neg}(x,y)=L-1-I(x,y)
|
||||
$$
|
||||
|
||||
Power law transformation:
|
||||
|
||||
$$
|
||||
I_{out}(x,y)=cI(x,y)^{\gamma}
|
||||
$$
|
||||
|
||||
- $c$ is a constant
|
||||
- $\gamma$ is the gamma value
|
||||
|
||||
Contrast stretching
|
||||
|
||||
use function to stretch the range of pixel values
|
||||
|
||||
$$
|
||||
I_{out}(x,y)=f(I(x,y))
|
||||
$$
|
||||
|
||||
- $f$ is a function that stretches the range of pixel values
|
||||
|
||||
Image histogram
|
||||
|
||||
- Histogram of an image is a plot of the frequency of each pixel value
|
||||
|
||||
Limitations:
|
||||
|
||||
- No spatial information
|
||||
- No information about the relationship between pixels
|
||||
|
||||
#### Linear filtering in spatial domain
|
||||
|
||||
Operations that are applied to a neighborhood at each position
|
||||
|
||||
Used to:
|
||||
|
||||
- Enhance image features
|
||||
- Denoise, sharpen, resize
|
||||
- Extract information about image structure
|
||||
- Edge detection, corner detection, blob detection
|
||||
- Detect image patterns
|
||||
- Template matching
|
||||
- Convolutional Neural Networks
|
||||
|
||||
Image filtering
|
||||
|
||||
Do dot product of the image with a kernel
|
||||
|
||||
$$
|
||||
h[m,n]=\sum_{k=0}^{m-i}\sum_{l=0}^{n-i}g[k,l]f[m+k,n+l]
|
||||
$$
|
||||
|
||||
```python
|
||||
def filter2d(image, kernel):
|
||||
"""
|
||||
Apply a 2D filter to an image, do not use this in practice
|
||||
"""
|
||||
for i in range(image.shape[0]):
|
||||
for j in range(image.shape[1]):
|
||||
image[i, j] = np.dot(kernel, image[i-1:i+2, j-1:j+2])
|
||||
return image
|
||||
```
|
||||
|
||||
Computational cost: $k^2mn$, assume $k$ is the size of the kernel and $m$ and $n$ are the dimensions of the image
|
||||
|
||||
Do not use this in practice, use built-in functions instead.
|
||||
|
||||
**Box filter**
|
||||
|
||||
$$
|
||||
\frac{1}{9}\begin{bmatrix}
|
||||
1 & 1 & 1\\
|
||||
1 & 1 & 1\\
|
||||
1 & 1 & 1
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
Smooths the image
|
||||
|
||||
**Identity filter**
|
||||
|
||||
$$
|
||||
\begin{bmatrix}
|
||||
0 & 0 & 0\\
|
||||
0 & 1 & 0\\
|
||||
0 & 0 & 0
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
Does not change the image
|
||||
|
||||
**Sharpening filter**
|
||||
|
||||
$$
|
||||
\begin{bmatrix}
|
||||
0 & 0 & 0 \\
|
||||
0 & 2 & 0 \\
|
||||
0 & 0 & 0
|
||||
\end{bmatrix}-
|
||||
\begin{bmatrix}
|
||||
1 & 1 & 1 \\
|
||||
1 & 1 & 1 \\
|
||||
1 & 1 & 1
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
Enhances the image edges
|
||||
|
||||
**Vertical edge detection**
|
||||
|
||||
$$
|
||||
\begin{bmatrix}
|
||||
1 & 0 & -1 \\
|
||||
2 & 0 & -2 \\
|
||||
1 & 0 & -1
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
Detects vertical edges
|
||||
|
||||
**Horizontal edge detection**
|
||||
|
||||
$$
|
||||
\begin{bmatrix}
|
||||
1 & 2 & 1 \\
|
||||
0 & 0 & 0 \\
|
||||
-1 & -2 & -1
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
Detects horizontal edges
|
||||
|
||||
Key property:
|
||||
|
||||
- Linear:
|
||||
- `filter(I,f_1+f_2)=filter(I,f_1)+filter(I,f_2)`
|
||||
- Scale invariant:
|
||||
- `filter(I,af)=a*filter(I,f)`
|
||||
- Shift invariant:
|
||||
- `filter(I,shift(f))=shift(filter(I,f))`
|
||||
- Commutative:
|
||||
- `filter(I,f_1)*filter(I,f_2)=filter(I,f_2)*filter(I,f_1)`
|
||||
- Associative:
|
||||
- `filter(I,f_1)*(filter(I,f_2)*filter(I,f_3))=(filter(I,f_1)*filter(I,f_2))*filter(I,f_3)`
|
||||
- Distributive:
|
||||
- `filter(I,f_1+f_2)=filter(I,f_1)+filter(I,f_2)`
|
||||
- Identity:
|
||||
- `filter(I,f_0)=I`
|
||||
|
||||
Important filter:
|
||||
|
||||
**Gaussian filter**
|
||||
|
||||
$$
|
||||
G(x,y)=\frac{1}{2\pi\sigma^2}e^{-\frac{x^2+y^2}{2\sigma^2}}
|
||||
$$
|
||||
|
||||
Smooths the image (Gaussian blur)
|
||||
|
||||
Common mistake: Make filter too large, visualize the filter before applying it (make the value on the edge $3\sigma$)
|
||||
|
||||
Properties of Gaussian filter:
|
||||
|
||||
- Remove high frequency components
|
||||
- Convolution with self is another Gaussian filter
|
||||
- Separable kernel:
|
||||
- `G(x,y)=G(x)G(y)` (factorable into the product of two 1D Gaussian filters)
|
||||
|
||||
##### Filter Separability
|
||||
|
||||
- Separable filter:
|
||||
- `f(x,y)=f(x)f(y)`
|
||||
|
||||
Example:
|
||||
|
||||
$$
|
||||
\begin{bmatrix}
|
||||
1 & 2 & 1 \\
|
||||
2 & 4 & 2 \\
|
||||
1 & 2 & 1
|
||||
\end{bmatrix}=
|
||||
\begin{bmatrix}
|
||||
1 \\
|
||||
2 \\
|
||||
1
|
||||
\end{bmatrix}\times
|
||||
\begin{bmatrix}
|
||||
1 & 2 & 1
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
Gaussian filter is separable
|
||||
|
||||
$$
|
||||
G(x,y)=\frac{1}{2\pi\sigma^2}e^{-\frac{x^2+y^2}{2\sigma^2}}=G(x)G(y)
|
||||
$$
|
||||
|
||||
This reduces the computational cost of the filter from $k^2mn$ to $2kmn$
|
||||
196
content/CSE559A/CSE559A_L4.md
Normal file
196
content/CSE559A/CSE559A_L4.md
Normal file
@@ -0,0 +1,196 @@
|
||||
# CSE559A Lecture 4
|
||||
|
||||
## Practical issues with filtering
|
||||
|
||||
$$
|
||||
h[m,n]=\sum_{k=0}^{m-i}\sum_{l=0}^{n-i}g[k,l]f[m+k,n+l]
|
||||
$$
|
||||
|
||||
Loss of information on edges of image
|
||||
|
||||
- The filter window falls off the edge of the image
|
||||
- Need to extrapolate
|
||||
- Methods:
|
||||
- clip filter
|
||||
- wrap around (extend the image periodically)
|
||||
- copy edge (extend the image by copying the edge pixels)
|
||||
- reflect across edge (extend the image by reflecting the edge pixels)
|
||||
|
||||
## Convolution vs Correlation
|
||||
|
||||
- Convolution:
|
||||
- The filter is flipped and convolved with the image
|
||||
|
||||
$$
|
||||
h[m,n]=\sum_{k=i}^{m}\sum_{l=i}^{n}g[k,l]f[m-k,n-l]
|
||||
$$
|
||||
|
||||
- Correlation:
|
||||
- The filter is not flipped and convolved with the image
|
||||
|
||||
$$
|
||||
h[m,n]=\sum_{k=0}^{m-i}\sum_{l=0}^{n-i}g[k,l]f[m+k,n+l]
|
||||
$$
|
||||
|
||||
does not matter for deep learning
|
||||
|
||||
```python
|
||||
scipy.signal.convolve2d(image, kernel, mode='same')
|
||||
scipy.signal.correlate2d(image, kernel, mode='same')
|
||||
```
|
||||
|
||||
but pytorch uses correlation for convolution, the convolution in pytorch is actually a correlation in scipy.
|
||||
|
||||
## Frequency domain representation of linear image filters
|
||||
|
||||
TL;DR: It can be helpful to think about linear spatial filters in terms fro their frequency domain representation
|
||||
|
||||
- Fourier transform and frequency domain
|
||||
- The convolution theorem
|
||||
|
||||
Hybrid image: More in homework 2
|
||||
|
||||
Human eye is sensitive to low frequencies in far field, high frequencies in near field
|
||||
|
||||
### Change of basis from an image perspective
|
||||
|
||||
For vectors:
|
||||
|
||||
- Vector -> Invertible matrix multiplication -> New vector
|
||||
- Normally we think of the standard/natural basis, with unit vectors in the direction of the axes
|
||||
|
||||
For images:
|
||||
|
||||
- Image -> Vector -> Invertible matrix multiplication -> New vector -> New image
|
||||
- Standard basis is just a collection of one-hot images
|
||||
|
||||
Use `im.flatten()` to convert an image to a vector
|
||||
|
||||
$$
|
||||
Image(M^{-1}GMVec(I))
|
||||
$$
|
||||
|
||||
- M is the change of basis matrix, $M^{-1}M=I$
|
||||
- G is the operation we want to perform
|
||||
- Vec(I) is the vectorized image
|
||||
|
||||
#### Lossy image compression (JPEG)
|
||||
|
||||
- JPEG is a lossy compression algorithm
|
||||
- It uses the DCT (Discrete Cosine Transform) to transform the image to the frequency domain
|
||||
- The DCT is a linear operation, so it can be represented as a matrix multiplication
|
||||
- The JPEG algorithm then quantizes the coefficients and entropy codes them (use Huffman coding)
|
||||
|
||||
## Thinking in frequency domain
|
||||
|
||||
### Fourier transform
|
||||
|
||||
Any univariate function can be represented as a weighted sum of sine and cosine functions
|
||||
|
||||
$$
|
||||
X[k]=\sum_{n=N-1}^{0}x[n]e^{-2\pi ikn/N}=\sum_{n=0}^{N-1}x[n]\left[\sin\left(\frac{2\pi}{N}kn\right)+i\cos\left(\frac{2\pi}{N}kn\right)\right]
|
||||
$$
|
||||
|
||||
- $X[k]$ is the Fourier transform of $x[n]$
|
||||
- $e^{-2\pi ikn/N}$ is the basis function
|
||||
- $x[n]$ is the original function
|
||||
|
||||
Real part:
|
||||
|
||||
$$
|
||||
\text{Re}(X[k])=\sum_{n=0}^{N-1}x[n]\cos\left(\frac{2\pi}{N}kn\right)
|
||||
$$
|
||||
|
||||
Imaginary part:
|
||||
|
||||
$$
|
||||
\text{Im}(X[k])=\sum_{n=0}^{N-1}x[n]\sin\left(\frac{2\pi}{N}kn\right)
|
||||
$$
|
||||
|
||||
Fourier transform stores the magnitude and phase of the sine and cosine function at each frequency
|
||||
|
||||
- Amplitude: encodes how much signal there is at a particular frequency
|
||||
- Phase: encodes the spacial information (indirectly)
|
||||
- For mathematical convenience, this is often written as a complex number
|
||||
|
||||
Amplitude: $A=\pm\sqrt{\text{Re}(\omega)^2+\text{Im}(\omega)^2}$
|
||||
|
||||
Phase: $\phi=\tan^{-1}\left(\frac{\text{Im}(\omega)}{\text{Re}(\omega)}\right)$
|
||||
|
||||
So use $A\sin(\omega+\phi)$ to represent the signal
|
||||
|
||||
Example:
|
||||
|
||||
$g(t)=\sin(2\pi ft)+\frac{1}{3}\sin(2\pi (3f)t)$
|
||||
|
||||
### Fourier analysis of images
|
||||
|
||||
Intensity image and Fourier image
|
||||
|
||||
Signals can be composed.
|
||||
|
||||

|
||||
|
||||
Note: frequency domain is often visualized using a log of the absolute value of the Fourier transform
|
||||
|
||||
Blurring the image is to delete the high frequency components (removing the center of the frequency domain)
|
||||
|
||||
## Convolution theorem
|
||||
|
||||
The Fourier transform of the convolution of two functions is the product of their Fourier transforms
|
||||
|
||||
$$
|
||||
F[f*g]=F[f]F[g]
|
||||
$$
|
||||
|
||||
- $F$ is the Fourier transform
|
||||
- $*$ is the convolution
|
||||
|
||||
Convolution in spatial domain is equivalent to multiplication in frequency domain
|
||||
|
||||
$$
|
||||
g*h=F^{-1}[F[g]F[h]]
|
||||
$$
|
||||
|
||||
- $F^{-1}$ is the inverse Fourier transform
|
||||
|
||||
### Is convolution invertible?
|
||||
|
||||
- Redo the convolution in the image domain is division in the frequency domain
|
||||
|
||||
$$
|
||||
g*h=F^{-1}\left[\frac{F[g]}{F[h]}\right]
|
||||
$$
|
||||
|
||||
- This is not always possible, because $F[h]$ may be zero and we may not know the filter
|
||||
|
||||
Small perturbations in the frequency domain can cause large perturbations in the spatial domain and vice versa
|
||||
|
||||
Deconvolution is hard and a active area of research
|
||||
|
||||
- Even if you know the filter, it is not always possible to invert the convolution, requires strong regularization
|
||||
- If you don't know the filter, it is even harder
|
||||
|
||||
## 2D image transformations
|
||||
|
||||
### Array slicing and image wrapping
|
||||
|
||||
Fast operation for extracting a subimage
|
||||
|
||||
- cropped image `image[10:20, 10:20]`
|
||||
- flipped image `image[::-1, ::-1]`
|
||||
|
||||
Image wrapping allows more flexible operations
|
||||
|
||||
#### Upsampling an image
|
||||
|
||||
- Upsampling an image is the process of increasing the resolution of the image
|
||||
|
||||
Bilinear interpolation:
|
||||
|
||||
- Use the average of the 4 nearest pixels to determine the value of the new pixel
|
||||
|
||||
Other interpolation methods:
|
||||
|
||||
- Bicubic interpolation: Use the average of the 16 nearest pixels to determine the value of the new pixel
|
||||
- Nearest neighbor interpolation: Use the value of the nearest pixel to determine the value of the new pixel
|
||||
222
content/CSE559A/CSE559A_L5.md
Normal file
222
content/CSE559A/CSE559A_L5.md
Normal file
@@ -0,0 +1,222 @@
|
||||
# CSE559A Lecture 5
|
||||
|
||||
## Continue on linear interpolation
|
||||
|
||||
- In linear interpolation, extreme values are at the boundary.
|
||||
- In bicubic interpolation, extreme values may be inside.
|
||||
|
||||
`scipy.interpolate.RegularGridInterpolator`
|
||||
|
||||
### Image transformations
|
||||
|
||||
Image warping is a process of applying transformation $T$ to an image.
|
||||
|
||||
Parametric (global) warping: $T(x,y)=(x',y')$
|
||||
|
||||
Geometric transformation: $T(x,y)=(x',y')$ This applies to each pixel in the same way. (global)
|
||||
|
||||
#### Translation
|
||||
|
||||
$T(x,y)=(x+a,y+b)$
|
||||
|
||||
matrix form:
|
||||
|
||||
$$
|
||||
\begin{pmatrix}
|
||||
x'\\y'
|
||||
\end{pmatrix}
|
||||
=
|
||||
\begin{pmatrix}
|
||||
1&0\\0&1
|
||||
\end{pmatrix}
|
||||
\begin{pmatrix}
|
||||
x\\y
|
||||
\end{pmatrix}
|
||||
+
|
||||
\begin{pmatrix}
|
||||
a\\b
|
||||
\end{pmatrix}
|
||||
$$
|
||||
|
||||
#### Scaling
|
||||
|
||||
$T(x,y)=(s_xx,s_yy)$ matrix form:
|
||||
|
||||
$$
|
||||
\begin{pmatrix}
|
||||
x'\\y'
|
||||
\end{pmatrix}
|
||||
=
|
||||
\begin{pmatrix}
|
||||
s_x&0\\0&s_y
|
||||
\end{pmatrix}
|
||||
\begin{pmatrix}
|
||||
x\\y
|
||||
\end{pmatrix}
|
||||
$$
|
||||
|
||||
#### Rotation
|
||||
|
||||
$T(x,y)=(x\cos\theta-y\sin\theta,x\sin\theta+y\cos\theta)$
|
||||
|
||||
matrix form:
|
||||
|
||||
$$
|
||||
\begin{pmatrix}
|
||||
x'\\y'
|
||||
\end{pmatrix}
|
||||
=
|
||||
\begin{pmatrix}
|
||||
\cos\theta&-\sin\theta\\\sin\theta&\cos\theta
|
||||
\end{pmatrix}
|
||||
\begin{pmatrix}
|
||||
x\\y
|
||||
\end{pmatrix}
|
||||
$$
|
||||
|
||||
To undo the rotation, we need to rotate the image by $-\theta$. This is equivalent to apply $R^T$ to the image.
|
||||
|
||||
#### Affine transformation
|
||||
|
||||
$T(x,y)=(a_1x+a_2y+a_3,b_1x+b_2y+b_3)$
|
||||
|
||||
matrix form:
|
||||
|
||||
$$
|
||||
\begin{pmatrix}
|
||||
x'\\y'
|
||||
\end{pmatrix}
|
||||
=
|
||||
\begin{pmatrix}
|
||||
a_1&a_2&a_3\\b_1&b_2&b_3
|
||||
\end{pmatrix}
|
||||
\begin{pmatrix}
|
||||
x\\y\\1
|
||||
\end{pmatrix}
|
||||
$$
|
||||
|
||||
Taking all the transformations together.
|
||||
|
||||
#### Projective homography
|
||||
|
||||
$T(x,y)=(\frac{ax+by+c}{gx+hy+i},\frac{dx+ey+f}{gx+hy+i})$
|
||||
|
||||
$$
|
||||
\begin{pmatrix}
|
||||
x'\\y'\\1
|
||||
\end{pmatrix}
|
||||
=
|
||||
\begin{pmatrix}
|
||||
a&b&c\\d&e&f\\g&h&i
|
||||
\end{pmatrix}
|
||||
\begin{pmatrix}
|
||||
x\\y\\1
|
||||
\end{pmatrix}
|
||||
$$
|
||||
|
||||
### Image warping
|
||||
|
||||
#### Forward warping
|
||||
|
||||
Send each pixel to its new position and do the matching.
|
||||
|
||||
- May cause gaps where the pixel is not mapped to any pixel.
|
||||
|
||||
#### Inverse warping
|
||||
|
||||
Send each new position to its original position and do the matching.
|
||||
|
||||
- Some mapping may not be invertible.
|
||||
|
||||
#### Which one is better?
|
||||
|
||||
- Inverse warping is better because it usually more efficient, doesn't have a problem with holes.
|
||||
- However, it may not always be possible to find the inverse mapping.
|
||||
|
||||
## Sampling and Aliasing
|
||||
|
||||
### Naive sampling
|
||||
|
||||
- Remove half of the rows and columns in the image.
|
||||
|
||||
Example:
|
||||
|
||||
When sampling a sine wave, the result may interpret as different wave.
|
||||
|
||||
#### Nyquist-Shannon sampling theorem
|
||||
|
||||
- A bandlimited signal can be uniquely determined by its samples if the sampling rate is greater than twice the maximum frequency of the signal.
|
||||
|
||||
- If the sampling rate is less than twice the maximum frequency of the signal, the signal will be aliased.
|
||||
|
||||
#### Anti-aliasing
|
||||
|
||||
- Sample more frequently. (not always possible)
|
||||
- Get rid of all frequencies that are greater than half of the new sampling frequency.
|
||||
- Use a low-pass filter to get rid of all frequencies that are greater than half of the new sampling frequency. (eg, Gaussian filter)
|
||||
|
||||
```python
|
||||
import scipy.ndimage as ndimage
|
||||
def down_sample(height, width, image):
|
||||
# Apply Gaussian blur to the image
|
||||
im_blur = ndimage.gaussian_filter(image, sigma=1)
|
||||
# Down sample the image by taking every second pixel
|
||||
return im_blur[::2, ::2]
|
||||
```
|
||||
|
||||
## Nonlinear filtering
|
||||
|
||||
### Median filter
|
||||
|
||||
Replace the value of a pixel with the median value of its neighbors.
|
||||
|
||||
- Good for removing salt and pepper noise. (black and white dot noise)
|
||||
|
||||
### Morphological operations
|
||||
|
||||
Binary image: image with only 0 and 1.
|
||||
|
||||
Let $B$ be a structuring element and $A$ be the original image (binary image).
|
||||
|
||||
- Erosion: $A\ominus B = \{p\mid B_p\subseteq A\}$, this is the set of all points that are completely covered by $B$.
|
||||
- Dilation: $A\oplus B = \{p\mid B_p\cap A\neq\emptyset\}$, this is the set of all points that are at least partially covered by $B$.
|
||||
- Opening: $A\circ B = (A\ominus B)\oplus B$, this is the set of all points that are at least partially covered by $B$ after erosion.
|
||||
- Closing: $A\bullet B = (A\oplus B)\ominus B$, this is the set of all points that are completely covered by $B$ after dilation.
|
||||
|
||||
Boundary extraction: use XOR operation on eroded image and original image.
|
||||
|
||||
Connected component labeling: label the connected components in the image. _use prebuild function in scipy.ndimage_
|
||||
|
||||
## Light,Camera/Eyes, and Color
|
||||
|
||||
### Principles of grouping and Gestalt Laws
|
||||
|
||||
- Proximity: objects that are close to each other are more likely to be grouped together.
|
||||
- Similarity: objects that are similar are more likely to be grouped together.
|
||||
- Closure: objects that form a closed path are more likely to be grouped together.
|
||||
- Continuity: objects that form a continuous path are more likely to be grouped together.
|
||||
|
||||
### Light and surface interactions
|
||||
|
||||
A photon's life choices:
|
||||
|
||||
- Absorption
|
||||
- Diffuse reflection (nice to model) (lambertian surface)
|
||||
- Specular reflection (mirror-like) (perfect mirror)
|
||||
- Transparency
|
||||
- Refraction
|
||||
- Fluorescence (returns different color)
|
||||
- Subsurface scattering (candles)
|
||||
- Photosphorescence
|
||||
- Interreflection
|
||||
|
||||
#### BRDF (Bidirectional Reflectance Distribution Function)
|
||||
|
||||
$$
|
||||
\rho(\theta_i,\phi_i,\theta_o,\phi_o)
|
||||
$$
|
||||
|
||||
- $\theta_i$ is the angle of incidence.
|
||||
- $\phi_i$ is the azimuthal angle of incidence.
|
||||
- $\theta_o$ is the angle of reflection.
|
||||
- $\phi_o$ is the azimuthal angle of reflection.
|
||||
213
content/CSE559A/CSE559A_L6.md
Normal file
213
content/CSE559A/CSE559A_L6.md
Normal file
@@ -0,0 +1,213 @@
|
||||
# CSE559A Lecture 6
|
||||
|
||||
## Continue on Light, eye/camera, and color
|
||||
|
||||
### BRDF (Bidirectional Reflectance Distribution Function)
|
||||
|
||||
$$
|
||||
\rho(\theta_i,\phi_i,\theta_o,\phi_o)
|
||||
$$
|
||||
|
||||
#### Diffuse Reflection
|
||||
|
||||
- Dull, matte surface like chalk or latex paint
|
||||
|
||||
- Most often used in computer vision
|
||||
- Brightness _does_ depend on direction of illumination
|
||||
|
||||
Diffuse reflection governed by Lambert's law: $I_d = k_d N\cdot L I_i$
|
||||
|
||||
- $N$: surface normal
|
||||
- $L$: light direction
|
||||
- $I_i$: incident light intensity
|
||||
- $k_d$: albedo
|
||||
|
||||
$$
|
||||
\rho(\theta_i,\phi_i,\theta_o,\phi_o)=k_d \cos\theta_i
|
||||
$$
|
||||
|
||||
#### Photometric Stereo
|
||||
|
||||
Suppose there are three light sources, $L_1, L_2, L_3$, and we have the following measurements:
|
||||
|
||||
$$
|
||||
I_1 = k_d N\cdot L_1
|
||||
$$
|
||||
|
||||
$$
|
||||
I_2 = k_d N\cdot L_2
|
||||
$$
|
||||
|
||||
$$
|
||||
I_3 = k_d N\cdot L_3
|
||||
$$
|
||||
|
||||
We can solve for $N$ by taking the dot product of $N$ and each light direction and then solving the system of equations.
|
||||
|
||||
Will not do this in the lecture.
|
||||
|
||||
#### Specular Reflection
|
||||
|
||||
- Mirror-like surface
|
||||
|
||||
$$
|
||||
I_e=\begin{cases}
|
||||
I_i & \text{if } V=R \\
|
||||
0 & \text{if } V\neq R
|
||||
\end{cases}
|
||||
$$
|
||||
|
||||
- $V$: view direction
|
||||
- $R$: reflection direction
|
||||
- $\theta_i$: angle between the incident light and the surface normal
|
||||
|
||||
Near-perfect mirror have a high light around $R$.
|
||||
|
||||
common model:
|
||||
|
||||
$$
|
||||
I_e=k_s (V\cdot R)^{n_s}I_i
|
||||
$$
|
||||
|
||||
- $k_s$: specular reflection coefficient
|
||||
- $n_s$: shininess (imperfection of the surface)
|
||||
- $I_i$: incident light intensity
|
||||
|
||||
#### Phong illumination model
|
||||
|
||||
- Phong approximation of surface reflectance
|
||||
- Assume reflectance is modeled by three compoents
|
||||
- Diffuse reflection
|
||||
- Specular reflection
|
||||
- Ambient reflection
|
||||
|
||||
$$
|
||||
I_e=k_a I_a + I_i \left[k_d (N\cdot L) + k_s (V\cdot R)^{n_s}\right]
|
||||
$$
|
||||
|
||||
- $k_a$: ambient reflection coefficient
|
||||
- $I_a$: ambient light intensity
|
||||
- $k_d$: diffuse reflection coefficient
|
||||
- $k_s$: specular reflection coefficient
|
||||
- $n_s$: shininess
|
||||
- $I_i$: incident light intensity
|
||||
|
||||
Many other models.
|
||||
|
||||
#### Measuring BRDF
|
||||
|
||||
Use Gonioreflectometer.
|
||||
|
||||
- Device for measuring the reflectance of a surface as a function of the incident and reflected angles.
|
||||
- Can be used to measure the BRDF of a surface.
|
||||
|
||||
BRDF dataset:
|
||||
|
||||
- MERL dataset
|
||||
- CURET dataset
|
||||
|
||||
### Camera/Eye
|
||||
|
||||
#### DSLR Camera
|
||||
|
||||
- Pinhole camera model
|
||||
- Lens
|
||||
- Aperture (the pinhole)
|
||||
- Sensor
|
||||
- ...
|
||||
|
||||
#### Digital Camera block diagram
|
||||
|
||||
|
||||
|
||||
Scanning protocols:
|
||||
|
||||
- Global shutter: all pixels are exposed at the same time
|
||||
- Interlaced: odd and even lines are exposed at different times
|
||||
- Rolling shutter: each line is exposed as it is read out
|
||||
|
||||
#### Eye
|
||||
|
||||
- Pupil
|
||||
- Iris
|
||||
- Retina
|
||||
- Rods and cones
|
||||
- ...
|
||||
|
||||
#### Eye Movements
|
||||
|
||||
- Saccade
|
||||
- Can be consciously controlled. Related to perceptual attention.
|
||||
- 200ms to initiation, 20 to 200ms to carry out. Large amplitude.
|
||||
- Smooth pursuit
|
||||
- Tracking an object
|
||||
- Difficult w/o an object to track!
|
||||
- Microsaccade and Ocular microtremor (OMT)
|
||||
- Involuntary. Smaller amplitude. Especially evident during prolonged
|
||||
fixation.
|
||||
|
||||
#### Contrast Sensitivity
|
||||
|
||||
- Uniform contrast image content, with increasing frequency
|
||||
- Why not uniform across the top?
|
||||
- Low frequencies: harder to see because of slower intensity changes
|
||||
- Higher frequencies: harder to see because of ability of our visual system to resolve fine features
|
||||
|
||||
### Color Perception
|
||||
|
||||
Visible light spectrum: 380 to 780 nm
|
||||
|
||||
- 400 to 500 nm: blue
|
||||
- 500 to 600 nm: green
|
||||
- 600 to 700 nm: red
|
||||
|
||||
#### HSV model
|
||||
|
||||
We use Gaussian functions to model the sensitivity of the human eye to different wavelengths.
|
||||
|
||||
- Hue: color (the wavelength of the highest peak of the sensitivity curve)
|
||||
- Saturation: color purity (the variance of the sensitivity curve)
|
||||
- Value: color brightness (the highest peak of the sensitivity curve)
|
||||
|
||||
#### Color Sensing in Camera (RGB)
|
||||
|
||||
- 3-chip vs. 1-chip: quality vs. cost
|
||||
|
||||
Bayer filter:
|
||||
|
||||
- Why more green?
|
||||
- Human eye is more sensitive to green light.
|
||||
|
||||
#### Color spaces
|
||||
|
||||
Images in python:
|
||||
|
||||
As matrix.
|
||||
|
||||
```python
|
||||
import matplotlib.pyplot as plt
|
||||
|
||||
from mpl_toolkits.mplot3d import Axes3D
|
||||
from skimage import io
|
||||
|
||||
def plot_rgb_3d(image_path):
|
||||
image = io.imread(image_path)
|
||||
r, g, b = image[:,:,0], image[:,:,1], image[:,:,2]
|
||||
fig = plt.figure()
|
||||
ax = fig.add_subplot(111, projection='3d')
|
||||
ax.scatter(r.flatten(), g.flatten(), b.flatten(), c=image.reshape(-1, 3)/255.0, marker='.')
|
||||
ax.set_xlabel('Red')
|
||||
ax.set_ylabel('Green')
|
||||
ax.set_zlabel('Blue')
|
||||
plt.show()
|
||||
|
||||
plot_rgb_3d('image.jpg')
|
||||
```
|
||||
|
||||
Other color spaces:
|
||||
|
||||
- YCbCr (fast to compute, usually used in TV)
|
||||
- HSV
|
||||
- L\*a\*b\* (CIELAB, perceptually uniform color space)
|
||||
|
||||
Most information is in the intensity channel.
|
||||
228
content/CSE559A/CSE559A_L7.md
Normal file
228
content/CSE559A/CSE559A_L7.md
Normal file
@@ -0,0 +1,228 @@
|
||||
# CSE559A Lecture 7
|
||||
|
||||
## Computer Vision (In Artificial Neural Networks for Image Understanding)
|
||||
|
||||
Early example of image understanding using Neural Networks: [Back propagation for zip code recognition]
|
||||
|
||||
Central idea; representation change, on each layer of feature.
|
||||
|
||||
Plan for next few weeks:
|
||||
|
||||
1. How do we train such models?
|
||||
2. What are those building blocks
|
||||
3. How should we combine those building blocks?
|
||||
|
||||
## How do we train such models?
|
||||
|
||||
CV is finally useful...
|
||||
|
||||
1. Image classification
|
||||
2. Image segmentation
|
||||
3. Object detection
|
||||
|
||||
ImageNet Large Scale Visual Recognition Challenge (ILSVRC)
|
||||
|
||||
- 1000 classes
|
||||
- 1.2 million images
|
||||
- 10000 test images
|
||||
|
||||
### Deep Learning (Just neural networks)
|
||||
|
||||
Bigger datasets, larger models, faster computers, lots of incremental improvements.
|
||||
|
||||
```python
|
||||
import torch
|
||||
import torch.nn as nn
|
||||
import torch.nn.functional as F
|
||||
|
||||
class Net(nn.Module):
|
||||
def __init__(self):
|
||||
super(Net, self).__init__()
|
||||
self.conv1 = nn.Conv2d(1, 6, 5)
|
||||
self.conv2 = nn.Conv2d(6, 16, 5)
|
||||
self.fc1 = nn.Linear(16 * 5 * 5, 120)
|
||||
self.fc2 = nn.Linear(120, 84)
|
||||
self.fc3 = nn.Linear(84, 10)
|
||||
|
||||
def forward(self, x):
|
||||
x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
|
||||
x = F.max_pool2d(F.relu(self.conv2(x)), 2)
|
||||
x = x.view(-1, self.num_flat_features(x))
|
||||
x = F.relu(self.fc1(x))
|
||||
x = F.relu(self.fc2(x))
|
||||
x = self.fc3(x)
|
||||
return x
|
||||
|
||||
def num_flat_features(self, x):
|
||||
size = x.size()[1:]
|
||||
num_features = 1
|
||||
for s in size:
|
||||
num_features *= s
|
||||
return num_features
|
||||
|
||||
# create pytorch dataset and dataloader
|
||||
dataset = torch.utils.data.TensorDataset(torch.randn(1000, 1, 28, 28), torch.randint(10, (1000,)))
|
||||
dataloader = torch.utils.data.DataLoader(dataset, batch_size=4, shuffle=True, num_workers=2)
|
||||
|
||||
# training process
|
||||
|
||||
net = Net()
|
||||
optimizer = optim.Adam(net.parameters(), lr=0.001)
|
||||
criterion = nn.CrossEntropyLoss()
|
||||
|
||||
# loop over the dataset multiple times
|
||||
for epoch in range(2):
|
||||
for i, data in enumerate(dataloader, 0):
|
||||
inputs, labels = data
|
||||
optimizer.zero_grad()
|
||||
outputs = net(inputs)
|
||||
loss = criterion(outputs, labels)
|
||||
loss.backward()
|
||||
optimizer.step()
|
||||
|
||||
print(f"Finished Training")
|
||||
```
|
||||
|
||||
Some generated code above.
|
||||
|
||||
### Supervised Learning
|
||||
|
||||
Training: given a dataset, learn a mapping from input to output.
|
||||
|
||||
Testing: given a new input, predict the output.
|
||||
|
||||
Example: Linear classification models
|
||||
|
||||
Find a linear function that separates the data.
|
||||
|
||||
$$
|
||||
f(x) = w^T x + b
|
||||
$$
|
||||
|
||||
[Linear classification models](http://cs231n.github.io/linear-classify/)
|
||||
|
||||
Simple representation of a linear classifier.
|
||||
|
||||
### Empirical loss minimization framework
|
||||
|
||||
Given a training set, find a model that minimizes the loss function.
|
||||
|
||||
Assume iid samples.
|
||||
|
||||
Example of loss function:
|
||||
|
||||
l1 loss:
|
||||
|
||||
$$
|
||||
\ell(f(x; w), y) = |f(x; w) - y|
|
||||
$$
|
||||
|
||||
l2 loss:
|
||||
|
||||
$$
|
||||
\ell(f(x; w), y) = (f(x; w) - y)^2
|
||||
$$
|
||||
|
||||
### Linear classification models
|
||||
|
||||
$$
|
||||
\hat{L}(w) = \frac{1}{n} \sum_{i=1}^n \ell(f(x_i; w), y_i)
|
||||
$$
|
||||
|
||||
hard to find the global minimum.
|
||||
|
||||
#### Linear regression
|
||||
|
||||
However, if we use l2 loss, we can find the global minimum.
|
||||
|
||||
$$
|
||||
\hat{L}(w) = \frac{1}{n} \sum_{i=1}^n (f(x_i; w) - y_i)^2
|
||||
$$
|
||||
|
||||
This is a convex function, so we can find the global minimum.
|
||||
|
||||
The gradient is:
|
||||
|
||||
$$
|
||||
\nabla_w||Xw-Y||^2 = 2X^T(Xw-Y)
|
||||
$$
|
||||
|
||||
Set the gradient to 0, we get:
|
||||
|
||||
$$
|
||||
w = (X^T X)^{-1} X^T Y
|
||||
$$
|
||||
|
||||
From the maximum likelihood perspective, we can also derive the same result.
|
||||
|
||||
#### Logistic regression
|
||||
|
||||
Sigmoid function:
|
||||
|
||||
$$
|
||||
\sigma(x) = \frac{1}{1 + e^{-x}}
|
||||
$$
|
||||
|
||||
The loss of logistic regression is not convex, so we cannot find the global minimum using normal equations.
|
||||
|
||||
#### Gradient Descent
|
||||
|
||||
Full batch gradient descent:
|
||||
|
||||
$$
|
||||
w \leftarrow w - \eta \nabla_w \hat{L}(w)
|
||||
$$
|
||||
|
||||
Stochastic gradient descent:
|
||||
|
||||
$$
|
||||
w \leftarrow w - \eta \nabla_w \hat{L}(w; x_i, y_i)
|
||||
$$
|
||||
|
||||
Mini-batch gradient descent:
|
||||
|
||||
$$
|
||||
w \leftarrow w - \eta \nabla_w \hat{L}(w; x_i, y_i)
|
||||
$$
|
||||
|
||||
Mini-batch Gradient Descent:
|
||||
|
||||
$$
|
||||
w \leftarrow w - \eta \nabla_w \hat{L}(w; x_i, y_i)
|
||||
$$
|
||||
|
||||
at each step, we update the weights using the average gradient of the mini-batch.
|
||||
|
||||
the mini-batch is selected randomly from the training set.
|
||||
|
||||
#### Multi-class classification
|
||||
|
||||
Use softmax function to convert the output to a probability distribution.
|
||||
|
||||
## Neural Networks
|
||||
|
||||
From linear to non-linear.
|
||||
|
||||
- Shadow approach:
|
||||
- Use feature transformation to make the data linearly separable.
|
||||
- Deep approach:
|
||||
- Stack multiple layers of linear models.
|
||||
|
||||
Common non-linear functions:
|
||||
|
||||
- ReLU:
|
||||
- $$
|
||||
\text{ReLU}(x) = \max(0, x)
|
||||
$$
|
||||
- Sigmoid:
|
||||
- $$
|
||||
\text{Sigmoid}(x) = \frac{1}{1 + e^{-x}}
|
||||
$$
|
||||
- Tanh:
|
||||
- $$
|
||||
\text{Tanh}(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}
|
||||
$$
|
||||
|
||||
|
||||
|
||||
### Backpropagation
|
||||
80
content/CSE559A/CSE559A_L8.md
Normal file
80
content/CSE559A/CSE559A_L8.md
Normal file
@@ -0,0 +1,80 @@
|
||||
# CSE559A Lecture 8
|
||||
|
||||
Paper review sharing.
|
||||
|
||||
## Recap: Three ways to think about linear classifiers
|
||||
|
||||
Geometric view: Hyperplanes in the feature space
|
||||
|
||||
Algebraic view: Linear functions of the features
|
||||
|
||||
Visual view: One template per class
|
||||
|
||||
## Continue on linear classification models
|
||||
|
||||
Two layer networks as combination of templates.
|
||||
|
||||
Interpretability is lost during the depth increase.
|
||||
|
||||
A two layer network is a **universal approximator** (we can approximate any continuous function to arbitrary accuracy). But the hidden layer may need to be huge.
|
||||
|
||||
[Multi-layer networks demo](https://playground.tensorflow.org)
|
||||
|
||||
### Supervised learning outline
|
||||
|
||||
1. Collect training data
|
||||
2. Specify model (select hyper-parameters)
|
||||
3. Train model
|
||||
|
||||
#### Hyper-parameters selection
|
||||
|
||||
- Number of layers, number of units per layer, learning rate, etc.
|
||||
- Type of non-linearity, regularization, etc.
|
||||
- Type of loss function, etc.
|
||||
- SGD settings: batch size, number of epochs, etc.
|
||||
|
||||
#### Hyper-parameter searching
|
||||
|
||||
Use validation set to evaluate the performance of the model.
|
||||
|
||||
Never peek the test set.
|
||||
|
||||
Use the training set to do K-fold cross validation.
|
||||
|
||||
### Backpropagation
|
||||
|
||||
#### Computation graphs
|
||||
|
||||
SGD update for each parameter
|
||||
|
||||
$$
|
||||
w_k\gets w_k-\eta\frac{\partial e}{\partial w_k}
|
||||
$$
|
||||
|
||||
$e$ is the error function.
|
||||
|
||||
#### Using the chain rule
|
||||
|
||||
Suppose $k=1$, $e=l(f_1(x,w_1),y)$
|
||||
|
||||
Example: $e=(f_1(x,w_1)-y)^2$
|
||||
|
||||
So $h_1=f_1(x,w_1)=w^T_1x$, $e=l(h_1,y)=(y-h_1)^2$
|
||||
|
||||
$$
|
||||
\frac{\partial e}{\partial w_1}=\frac{\partial e}{\partial h_1}\frac{\partial h_1}{\partial w_1}
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{\partial e}{\partial h_1}=2(h_1-y)
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{\partial h_1}{\partial w_1}=x
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{\partial e}{\partial w_1}=2(h_1-y)x
|
||||
$$
|
||||
|
||||
#### General backpropagation algorithm
|
||||
102
content/CSE559A/CSE559A_L9.md
Normal file
102
content/CSE559A/CSE559A_L9.md
Normal file
@@ -0,0 +1,102 @@
|
||||
# CSE559A Lecture 9
|
||||
|
||||
## Continue on ML for computer vision
|
||||
|
||||
### Backpropagation
|
||||
|
||||
#### Computation graphs
|
||||
|
||||
SGD update for each parameter
|
||||
|
||||
$$
|
||||
w_k\gets w_k-\eta\frac{\partial e}{\partial w_k}
|
||||
$$
|
||||
|
||||
$e$ is the error function.
|
||||
|
||||
#### Using the chain rule
|
||||
|
||||
Suppose $k=1$, $e=l(f_1(x,w_1),y)$
|
||||
|
||||
Example: $e=(f_1(x,w_1)-y)^2$
|
||||
|
||||
So $h_1=f_1(x,w_1)=w^T_1x$, $e=l(h_1,y)=(y-h_1)^2$
|
||||
|
||||
$$
|
||||
\frac{\partial e}{\partial w_1}=\frac{\partial e}{\partial h_1}\frac{\partial h_1}{\partial w_1}
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{\partial e}{\partial h_1}=2(h_1-y)
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{\partial h_1}{\partial w_1}=x
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{\partial e}{\partial w_1}=2(h_1-y)x
|
||||
$$
|
||||
|
||||
For the general cases,
|
||||
|
||||
$$
|
||||
\frac{\partial e}{\partial w_k}=\frac{\partial e}{\partial h_K}\frac{\partial h_K}{\partial h_{K-1}}\cdots\frac{\partial h_{k+2}}{\partial h_{k+1}}\frac{\partial h_{k+1}}{\partial h_k}\frac{\partial h_k}{\partial w_k}
|
||||
$$
|
||||
|
||||
Where the upstream gradient $\frac{\partial e}{\partial h_K}$ is known, and the local gradient $\frac{\partial h_k}{\partial w_k}$ is known.
|
||||
|
||||
#### General backpropagation algorithm
|
||||
|
||||
The adding layer is the gradient distributor layer.
|
||||
The multiplying layer is the gradient switcher layer.
|
||||
The max operation is the gradient router layer.
|
||||
|
||||
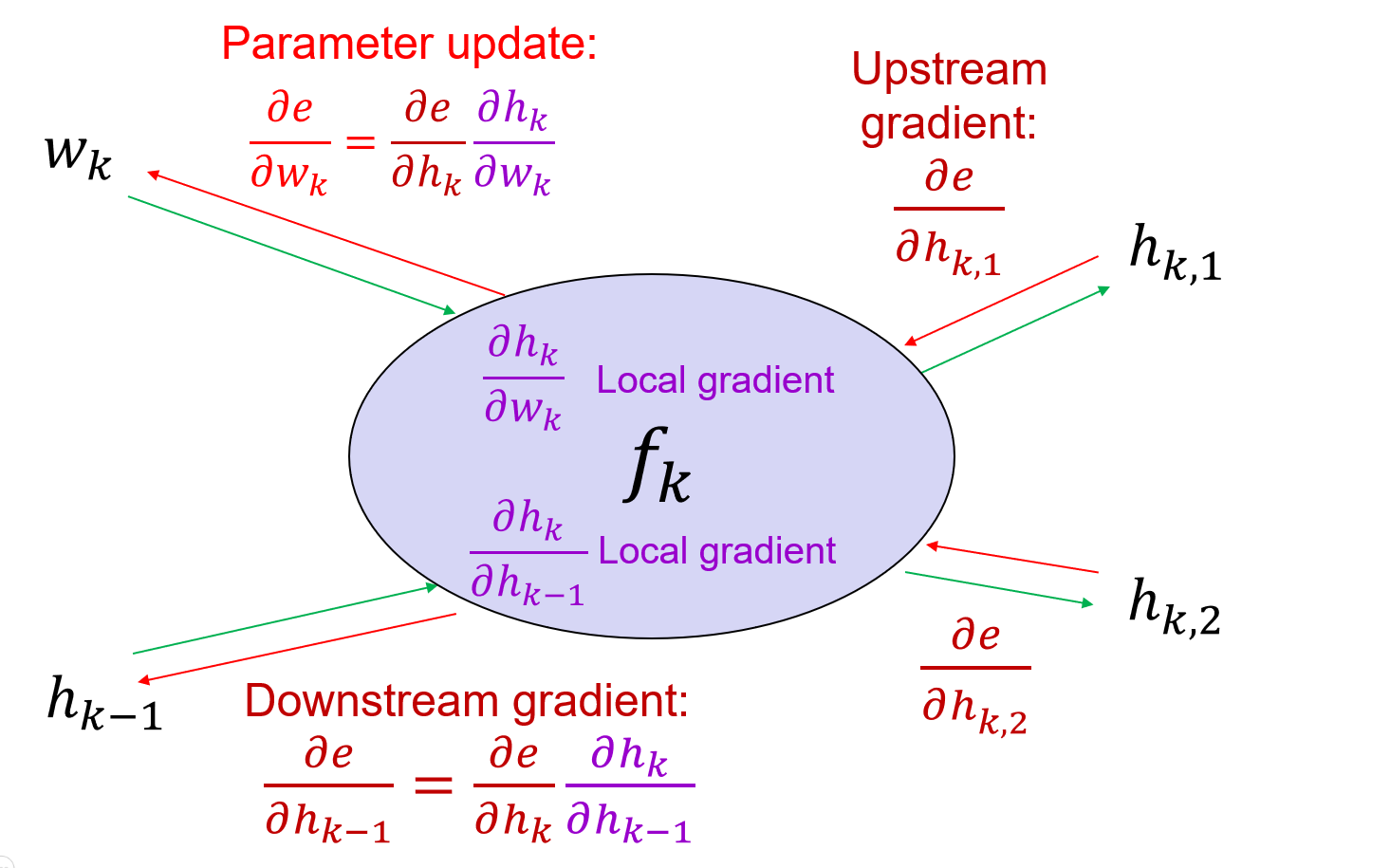
|
||||
|
||||
Simple example: Element-wise operation (ReLU)
|
||||
|
||||
$f(x)=ReLU(x)=max(0,x)$
|
||||
|
||||
$$
|
||||
\frac{\partial z}{\partial x}=\begin{pmatrix}
|
||||
\frac{\partial z_1}{\partial x_1} & 0 & \cdots & 0 \\
|
||||
0 & \frac{\partial z_2}{\partial x_2} & \cdots & 0 \\
|
||||
\vdots & \vdots & \ddots & \vdots \\
|
||||
0 & 0 & \cdots & \frac{\partial z_n}{\partial x_n}
|
||||
\end{pmatrix}
|
||||
$$
|
||||
|
||||
Where $\frac{\partial z_i}{\partial x_j}=1$ if $i=j$ and $z_i>0$, otherwise $\frac{\partial z_i}{\partial x_j}=0$.
|
||||
|
||||
When $\forall x_i<0$ then $\frac{\partial z}{\partial x}=0$ (dead ReLU)
|
||||
|
||||
Other examples on ppt.
|
||||
|
||||
## Convolutional Neural Networks
|
||||
|
||||
### Basic Convolutional layer
|
||||
|
||||
#### Flatten layer
|
||||
|
||||
Fully connected layer, operate on vectorized image.
|
||||
|
||||
With the multi-layer perceptron, the neural network trying to fit the templates.
|
||||
|
||||
|
||||
|
||||
#### Convolutional layer
|
||||
|
||||
Limit the receptive fields of units, tiles them over the input image, and share the weights.
|
||||
|
||||
Equivalent to sliding the learned filter over the image , computing dot products at each location.
|
||||
|
||||
|
||||
|
||||
Padding: Add a border of zeros around the image. (higher padding, larger output size)
|
||||
|
||||
Stride: The step size of the filter. (higher stride, smaller output size)
|
||||
|
||||
### Variants 1x1 convolutions, depthwise convolutions
|
||||
|
||||
### Backward pass
|
||||
32
content/CSE559A/_meta.js
Normal file
32
content/CSE559A/_meta.js
Normal file
@@ -0,0 +1,32 @@
|
||||
export default {
|
||||
//index: "Course Description",
|
||||
"---":{
|
||||
type: 'separator'
|
||||
},
|
||||
CSE559A_L1: "Computer Vision (Lecture 1)",
|
||||
CSE559A_L2: "Computer Vision (Lecture 2)",
|
||||
CSE559A_L3: "Computer Vision (Lecture 3)",
|
||||
CSE559A_L4: "Computer Vision (Lecture 4)",
|
||||
CSE559A_L5: "Computer Vision (Lecture 5)",
|
||||
CSE559A_L6: "Computer Vision (Lecture 6)",
|
||||
CSE559A_L7: "Computer Vision (Lecture 7)",
|
||||
CSE559A_L8: "Computer Vision (Lecture 8)",
|
||||
CSE559A_L9: "Computer Vision (Lecture 9)",
|
||||
CSE559A_L10: "Computer Vision (Lecture 10)",
|
||||
CSE559A_L11: "Computer Vision (Lecture 11)",
|
||||
CSE559A_L12: "Computer Vision (Lecture 12)",
|
||||
CSE559A_L13: "Computer Vision (Lecture 13)",
|
||||
CSE559A_L14: "Computer Vision (Lecture 14)",
|
||||
CSE559A_L15: "Computer Vision (Lecture 15)",
|
||||
CSE559A_L16: "Computer Vision (Lecture 16)",
|
||||
CSE559A_L17: "Computer Vision (Lecture 17)",
|
||||
CSE559A_L18: "Computer Vision (Lecture 18)",
|
||||
CSE559A_L19: "Computer Vision (Lecture 19)",
|
||||
CSE559A_L20: "Computer Vision (Lecture 20)",
|
||||
CSE559A_L21: "Computer Vision (Lecture 21)",
|
||||
CSE559A_L22: "Computer Vision (Lecture 22)",
|
||||
CSE559A_L23: "Computer Vision (Lecture 23)",
|
||||
CSE559A_L24: "Computer Vision (Lecture 24)",
|
||||
CSE559A_L25: "Computer Vision (Lecture 25)",
|
||||
CSE559A_L26: "Computer Vision (Lecture 26)",
|
||||
}
|
||||
4
content/CSE559A/index.md
Normal file
4
content/CSE559A/index.md
Normal file
@@ -0,0 +1,4 @@
|
||||
# CSE 559A: Computer Vision
|
||||
|
||||
## Course Description
|
||||
|
||||
Reference in New Issue
Block a user