upgrade structures and migrate to nextra v4
This commit is contained in:
148
content/CSE332S/CSE332S_L1.md
Normal file
148
content/CSE332S/CSE332S_L1.md
Normal file
@@ -0,0 +1,148 @@
|
||||
# CSE332S Lecture 1
|
||||
|
||||
## Today:
|
||||
|
||||
1. A bit about me
|
||||
2. A bit about the course
|
||||
3. A bit about C++
|
||||
4. How we will learn
|
||||
5. Canvas tour and course policies
|
||||
6. Piazza tour
|
||||
7. Studio: Setup our work environment
|
||||
|
||||
## A bit about me:
|
||||
|
||||
This is my 14th year at WashU.
|
||||
|
||||
- 5 as a graduate student advised by Dr. Cytron
|
||||
- Research focused on optimizing the memory system for garbage collected languages
|
||||
- My 9th as an instructor
|
||||
- Courses taught: 131, 247, 332S, 361S, 422S, 433S, 454A, 523S
|
||||
|
||||
## CSE 332S Overview:
|
||||
|
||||
This course has 3 high level goals:
|
||||
|
||||
1. Gain proficiency with a 2nd programming language
|
||||
2. Introduce important lower-level constructs that many high-level languages abstract away (pointers, explicit dynamic memory management, code compilation, stack management, static programming languages, etc.)
|
||||
3. Teach fundamental object-oriented programming principles and design
|
||||
|
||||
C++ allows us to accomplish all three goals above!
|
||||
|
||||
### An introduction to C++
|
||||
|
||||
C++ is a multi-paradigm language
|
||||
|
||||
- Procedural programming - functions
|
||||
- Object-oriented programming - classes and structs
|
||||
- Generic programming - templates
|
||||
|
||||
C++ is built upon C, keeping lower-level features of C while adding higher-level features
|
||||
|
||||
#### Evolution of C++
|
||||
|
||||
1. C is a procedural programming language primarily used to develop low-level systems software, such as operating systems.
|
||||
- designed to map efficiently to typical machine instructions, making compilation fairly straightforward and giving low-level access to memory
|
||||
- However, type safe code reuse is hard without high-level programming constructs such as objects and generics.
|
||||
2. Stroustrup first designed C++ with classes/objects, but kept procedural parts similar to C
|
||||
3. Templates (generics) were later added and the STL was developed
|
||||
4. C++ is now standardized, with the latest revision of the standard being C++23
|
||||
|
||||
### So, why C++? And an overview of the semester timeline...
|
||||
|
||||
1. C++ allows us to explore programming constructs such as low-level memory access (pointers and references), function calls (stack management), and explicit memory management (1st 1/3rd of the semester)
|
||||
2. We can then learn how those lower-level constructs are used to enable more abstract higher-level constructs, such as objects and the development of the C++ Standard Template Library (the STL) (middle 1/3rd of the semester)
|
||||
3. Finally, we will use C++ to study the fundamentals of object-oriented design (final 3rd of the semester)
|
||||
|
||||
### How we will learn (flipped classroom):
|
||||
|
||||
#### Prior to class
|
||||
|
||||
Lectures are pre-recorded and posted for you to view asynchronously before class
|
||||
|
||||
- Posted 72 hours before class on Canvas
|
||||
|
||||
Post-lecture tasks are posted alongside the lectures and should be completed before class
|
||||
|
||||
- Canvas discussion to ask questions, “like” already asked questions
|
||||
- A short quiz over the lecture content
|
||||
|
||||
#### During class
|
||||
|
||||
- Work on a studio within a group to build an understanding of the topic via hands-on exercises and discussion (10:30 - 11:20 AM, 1:30 - 2:20 PM)
|
||||
- Treat studio as a time to explore and test your understanding of a concept. Place emphasis on exploration.
|
||||
- TAs and I will be there to help guide you through and discuss the exercises.
|
||||
- Optional recitation for the first 30 minutes of each class - content generally based on questions posed in the discussion board. Recitations will be recorded.
|
||||
|
||||
#### Outside of class
|
||||
|
||||
- Readings provide further details on the topics covered in class
|
||||
- Lab assignments ask you to apply the concepts you have learned
|
||||
|
||||
### In-class studio policy
|
||||
|
||||
You should be in-class by 35 minutes after the official class start time (10 am -> 10:35 AM, 1 PM -> 1:35 PM) to receive credit
|
||||
|
||||
- Credit awarded for being in-class and working on studio. If you do not finish the studio, you will still get credit IF you are working on studio
|
||||
- All studio content is fair game on an exam. The exam is hard, the best way to prep is to spend class time efficiently working through studio
|
||||
- If instructors (myself or TAs) feel you are not working on studio, credit will be taken away. Old studios may be reviewed if this is a consistent problem
|
||||
- You should always commit and push the work you completed at the end of class. You should always accept the assignment link and join the team you are working with so you have access to the studio repository.
|
||||
|
||||
### Other options for studio
|
||||
|
||||
If studio must be missed for some reason:
|
||||
|
||||
- Complete the studio exercises in full (must complete all non-optional exercises) within 4 days of the assigned date to receive credit
|
||||
- Friday at 11:59 PM for Monday studios
|
||||
- Sunday at 11:59 PM for Wednesday studios
|
||||
- Ok to work asynchronously in a group
|
||||
|
||||
### Topics we will cover:
|
||||
|
||||
- C++ program basics
|
||||
- Variables, types, control statements, development environments
|
||||
- C++ functions
|
||||
- Parameters, the call stack, exception handling
|
||||
- C++ memory
|
||||
- Addressing, layout, management
|
||||
- C++ classes and structs
|
||||
- Encapsulation, abstraction, inheritance
|
||||
- C++ STL
|
||||
- Containers, iterators, algorithms, functors
|
||||
- OO design
|
||||
- Principles and Fundamentals, reusable design patterns
|
||||
|
||||
### Other details:
|
||||
|
||||
We will use Canvas to distribute lecture slides, studios, assignments, and announcements. Piazza will be used for discussion
|
||||
|
||||
### Lab details:
|
||||
|
||||
CSE 332 focuses on correctness, but also code readability and maintainability
|
||||
|
||||
- Labs graded on correctness as well as programming style
|
||||
- Each lab lists the programming guidelines that should be followed
|
||||
- Please review the CSE 332 programming guidelines before turning in each lab
|
||||
|
||||
Labs 1, 2, and 3 are individual assignments. You may work in groups of up to three on labs 4 and 5
|
||||
|
||||
### Academic Integrity
|
||||
|
||||
Cheating is the misrepresentation of someone else’s work as your own, or assisting someone else in cheating
|
||||
|
||||
- Providing or receiving answers on exams
|
||||
- Accessing unapproved sources of information on an exam
|
||||
- Submitting code written outside of this course in this semester, written by someone else not on your team (or taken from the internet)
|
||||
- Allowing another student to copy your solution
|
||||
- Do not host your projects in public repos
|
||||
|
||||
Please also refer to the McKelvey Academic Integrity Policy
|
||||
|
||||
Online resources may be used to lookup general purpose C++ information (libraries, etc.). They should not be used to lookup questions specific to a course assignment. Any online resources used, including generative AIs such as chatGPT must be cited, with a description of the prompt/question asked. A comment in your code works fine for this. You may use code from the textbook or from [cppreference.com](https://en.cppreference.com/w/) or [cplusplus.com](https://cplusplus.com/) without citations.
|
||||
|
||||
If you have any doubt at all, ask me!
|
||||
|
||||
### Studio: Setting up our working environment
|
||||
|
||||
Visit the course canvas page, sign up for the course piazza page, and get started on studio 1
|
||||
|
||||
274
content/CSE332S/CSE332S_L10.md
Normal file
274
content/CSE332S/CSE332S_L10.md
Normal file
@@ -0,0 +1,274 @@
|
||||
# CSE332S Lecture 10
|
||||
|
||||
## Associative Containers
|
||||
|
||||
| Container | Sorted | Unique Key | Allow duplicates |
|
||||
| -------------------- | ------ | ---------- | ---------------- |
|
||||
| `set` | Yes | Yes | No |
|
||||
| `multiset` | Yes | Yes | Yes |
|
||||
| `unordered_set` | No | Yes | No |
|
||||
| `unordered_multiset` | No | Yes | Yes |
|
||||
| `map` | Yes | Yes | No |
|
||||
| `multimap` | Yes | Yes | Yes |
|
||||
| `unordered_map` | No | Yes | No |
|
||||
| `unordered_multimap` | No | Yes | Yes |
|
||||
|
||||
Associative containers support efficient key lookup
|
||||
vs. sequence containers, which lookup by position
|
||||
Associative containers differ in 3 design dimensions
|
||||
|
||||
- Ordered vs. unordered (tree vs. hash structured)
|
||||
- We’ll look at ordered containers today, unordered next time
|
||||
- Set vs. map (just the key or the key and a mapped type)
|
||||
- Unique vs. multiple instances of a key
|
||||
|
||||
### Ordered Associative Containers
|
||||
|
||||
Example: `set`, `multiset`, `map`, `multimap`
|
||||
|
||||
Ordered associative containers are tree structured
|
||||
- Insert/delete maintain sorted order, e.g. `operator<`
|
||||
- Don’t use sequence algorithms like `sort` or `find` with them
|
||||
- Already sorted, so sorting unnecessary (or harmful)
|
||||
- `find` is more efficient (logarithmic time) as a container method
|
||||
Ordered associative containers are bidirectional
|
||||
- Can iterate through them in either direction, find sub-ranges
|
||||
- Can use as source or destination for algorithms like `copy`
|
||||
|
||||
### Set vs. Map
|
||||
|
||||
A set/multiset stores keys (the key is the entire value)
|
||||
|
||||
- Used to collect single-level information (e.g., a set of words to ignore)
|
||||
- Avoid in-place modification of keys (especially in a set or multiset)
|
||||
|
||||
A map/multimap associates keys with mapped types
|
||||
|
||||
- That style of data structure is sometimes called an associative array
|
||||
- Map subscripting operator takes key, returns reference to mapped type
|
||||
- E.g., `string s = employees[id]; // returns employee name`
|
||||
- If key does not exist, `[]` creates new entry with the key, value-initialized (0 if numeric, default initialized if class) instance of the mapped type
|
||||
|
||||
### Unique vs. Multiple Instances of a Key
|
||||
|
||||
In set and map containers, keys are unique
|
||||
|
||||
- In set, keys are the entire value, so every element is unique
|
||||
- In map, multiple keys may map to same value, but can’t duplicate keys
|
||||
- Attempt to insert a duplicate key is ignored by the container (returns false)
|
||||
|
||||
In multiset and multimap containers, duplicate keys ok
|
||||
|
||||
- Since containers are ordered, duplicates are kept next to each other
|
||||
- Insertion will always succeed, at appropriate place in the order
|
||||
|
||||
### Key Types, Comparators, Strict Weak Ordering
|
||||
|
||||
Like `sort` algorithm, can modify container’s order ...
|
||||
... with any callable object that can be used correctly for sort
|
||||
|
||||
Must establish a **strict weak ordering** over elements
|
||||
|
||||
- Two keys cannot both be less than each other (inequality), so comparison operator must return `false` if they are equal
|
||||
- If `a < b` and `b < c` then `a < c` (transitivity of inequality)
|
||||
- If `!(a < b)` and `! (b < a)` then `a == b` (equivalence)
|
||||
- If `a == b` and `b == c` then `a == c` (transitivity of eqivalence)
|
||||
|
||||
_Sounds like definition of order in math_
|
||||
|
||||
Type of the callable object is used in container type
|
||||
|
||||
- Cool example in LLM pp. 426 using `decltype` for a function
|
||||
- Could do this by declaring your own pointer to function type
|
||||
- But much easier to let compiler’s type inference figure it out for you
|
||||
|
||||
### Pairs
|
||||
|
||||
Maps use `pair` template to hold key, mapped type
|
||||
|
||||
- A `pair` can be used hold any two types
|
||||
- Maps use the key type as the 1st element of the pair (`p.first`)
|
||||
- Maps use the mapped type as the 2nd element of the pair (`p.second`)
|
||||
|
||||
Can compare `pair` variables using operators
|
||||
|
||||
- Equivalence, less than, other relational operators
|
||||
|
||||
Can declare `pair` variables several different ways
|
||||
|
||||
- Easiest uses initialization list (curly braces around values) (e.g. `pair<string, int> p = {"hello", 1};`)
|
||||
- Can also default construct (value initialization) (e.g. `pair<string, int> p;`)
|
||||
- Can also construct with two values (e.g. `pair<string, int> p("hello", 1);`)
|
||||
- Can also use special `make_pair` function (e.g. `pair<string, int> p = make_pair("hello", 1);`)
|
||||
|
||||
### Unordered Containers (UCs)
|
||||
|
||||
Example: `unordered_set`, `unordered_multiset`, `unordered_map`, `unordered_multimap`
|
||||
|
||||
UCs use `==` to compare elements instead of `<` to order them
|
||||
|
||||
- Types in unordered containers must be equality comparable
|
||||
- When you write your own structs, overload `==` as well as `<`
|
||||
|
||||
UCs store elements in indexed buckets instead of in a tree
|
||||
|
||||
- Useful for types that don’t have an obvious ordering relation over their values
|
||||
|
||||
UCs use hash functions to put and find elements in buckets
|
||||
|
||||
- May improve performance in some cases (if performance profiling suggests so)
|
||||
- Declare UCs with pluggable hash functions via callable objects, decltype, etc.
|
||||
- Or specialize the `std::hash()` template for your type, used by default
|
||||
|
||||
### Summary
|
||||
|
||||
Use associative containers for key based lookup
|
||||
|
||||
- Ordering of elements is maintained over the keys
|
||||
- Think ranges and ordering rather than position indexes
|
||||
- A sorted vector may be a better alternative (depends on which operations you will use most often, and their costs)
|
||||
|
||||
Ordered associative containers use strict weak order
|
||||
|
||||
- Operator `<` or any callable object that acts like `<` over `int` can be used
|
||||
|
||||
Maps allow two-level (dictionary-like) lookup
|
||||
|
||||
- Vs. sets which are used for “there or not there” lookup
|
||||
- Map uses a `pair` to associate key with mapped type
|
||||
|
||||
Can enforce uniqueness or allow duplicates
|
||||
|
||||
- Duplicates are still stored in order, creating “equal ranges”
|
||||
|
||||
## IO Libraries
|
||||
|
||||
### `std::copy()`
|
||||
|
||||
`std::copy()`
|
||||
|
||||
http://www.cplusplus.com/reference/algorithm/copy/
|
||||
|
||||
Takes 3 parameters:
|
||||
|
||||
- `copy(InputIterator first, InputIterator last, OutputIterator result);`
|
||||
- `[first, last)` specifies the range of elements to copy.
|
||||
- `result` specifies where we are copying to.
|
||||
|
||||
Example:
|
||||
|
||||
```cpp
|
||||
vector<int> v = {1, 2, 3, 4, 5};
|
||||
// copy v to cout
|
||||
std::copy(v.begin(), v.end(), std::ostream_iterator<int>(std::cout, " "));
|
||||
```
|
||||
|
||||
Some useful destination iterator types:
|
||||
|
||||
1. `ostream_iterator` - iterator over an output stream (like `cout`)
|
||||
2. `insert_iterator` - inserts elements directly into an STL container (will be practiced in studio)
|
||||
|
||||
```cpp
|
||||
#include <iostream>
|
||||
#include <string>
|
||||
#include <fstream>
|
||||
#include <iterator>
|
||||
#include <algorithm>
|
||||
|
||||
using namespace std;
|
||||
|
||||
int main(int argc, char *argv[]) {
|
||||
if (argc != 3) {
|
||||
cerr << "Usage: " << argv[0] << " <input file> <output file>" << endl;
|
||||
return 1;
|
||||
}
|
||||
|
||||
string input_file = argv[1];
|
||||
string output_file = argv[2];
|
||||
|
||||
ifstream input_file(input_file.c_str());
|
||||
ofstream output_file(output_file.c_str());
|
||||
|
||||
// don't skip whitespace
|
||||
input_file >> noskipws;
|
||||
|
||||
istream_iterator<char> i (input_file);
|
||||
ostream_iterator<char> o (output_file);
|
||||
|
||||
// copy the input file to the output file: copy(InputIterator first, InputIterator last, OutputIterator result);
|
||||
copy(i, istream_iterator<char>(), o);
|
||||
|
||||
cout << "Copied input file" << input_file << " to " << output_file << endl;
|
||||
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
### IO reviews
|
||||
|
||||
How to move data into and out of a program:
|
||||
|
||||
- Using `argc` and `argv` to pass command line args
|
||||
- Using `cout` to print data out to the terminal
|
||||
- Using `cin` to obtain data from the user at run-time
|
||||
- Using an `ifstream` to read data in from a file
|
||||
- Using an `ofstream` to write data out to a file
|
||||
|
||||
How to move data between strings, basic types
|
||||
|
||||
- Using an `istringstream` to extract formatted int values
|
||||
- Using an `ostringstream` to assemble a string
|
||||
|
||||
### Streams
|
||||
|
||||
Simply a buffer of data (array of bytes).
|
||||
|
||||
Insertion operator (`<<`) specifies how to move data from a variable into an output stream
|
||||
Extraction operator (`>>`) specifies how to pull data off of an input stream and store it into a variable
|
||||
|
||||
Both operators defined for built-in types:
|
||||
|
||||
- Numeric types
|
||||
- Pointers
|
||||
- Pointers to char (char *)
|
||||
|
||||
Cannot copy or assign stream objects
|
||||
|
||||
- Copy construction or assignment syntax using them results in a compile-time error
|
||||
|
||||
Extraction operator consumes data from input stream
|
||||
|
||||
- "Destructive read" that reads a different element each time
|
||||
- Use a variable if you want to read same value repeatedly
|
||||
|
||||
Need to test streams’ condition states
|
||||
|
||||
- E.g., calling the `is_open` method on a file stream
|
||||
- E.g., use the stream object in a while or if test
|
||||
- Insertion and extraction operators return a reference to a stream object, so can test them too
|
||||
|
||||
File stream destructor calls close automatically
|
||||
|
||||
### Flushing and stream manipulators
|
||||
|
||||
An output stream may hold onto data for a while, internally
|
||||
|
||||
- E.g., writing chunks of text rather than a character at a time is efficient
|
||||
- When it writes data out (e.g., to a file, the terminal window, etc.) is entirely up to the stream, **unless you tell it to flush out its buffers**
|
||||
- If a program crashes, any un-flushed stream data is lost
|
||||
- So, flushing streams reasonably often is an excellent debugging trick
|
||||
|
||||
Can tie an input stream directly to an output stream
|
||||
|
||||
- Output stream is then flushed by call to input stream extraction operator
|
||||
- E.g., `my_istream.tie(&my_ostream);`
|
||||
- `cout` is already tied to `cin` (useful for prompting the user, getting input)
|
||||
|
||||
Also can flush streams directly using stream manipulators
|
||||
|
||||
- E.g., `cout << flush;` or `cout << endl;` or `cout << unitbuf;`
|
||||
|
||||
Other stream manipulators are useful for formatting streams
|
||||
|
||||
- Field layout: `setwidth`, `setprecision`, etc.
|
||||
- Display notation: `oct`, `hex`, `dec`, `boolalpha`, `nobooleanalpha`, `scientific`, etc.
|
||||
171
content/CSE332S/CSE332S_L11.md
Normal file
171
content/CSE332S/CSE332S_L11.md
Normal file
@@ -0,0 +1,171 @@
|
||||
# CSE332S Lecture 11
|
||||
|
||||
## Operator overloading intro
|
||||
|
||||
> Insertion operator (`<<`) - pushes data from an object into an ostream
|
||||
>
|
||||
> Extraction operator (`>>`) - pulls data off of an istream and stores it into an object
|
||||
>
|
||||
> Defined for built-in types, but what about **user-defined types**?
|
||||
|
||||
**Operator overloading** - we can provide overloaded versions of operators to work with objects of our classes and structs
|
||||
|
||||
Example:
|
||||
|
||||
```cpp
|
||||
// declaration in point2d.h
|
||||
|
||||
struct Point2D {
|
||||
Point2d(int x, int y);
|
||||
int x_;
|
||||
int y_;
|
||||
}
|
||||
|
||||
// definition in point2d.cpp
|
||||
Point2D::Point2D(int x, int y): x_(x), y_(y) {}
|
||||
|
||||
// main function
|
||||
int main() {
|
||||
Point2D p1(5,5);
|
||||
cout << p1 << endl; // this is equivalent to calling `operator<<(ostream &, const Point2d &);` Not declared yet.
|
||||
cout << "enter 2 coordinates, separated by a space" << endl;
|
||||
cin >> p1; // this is equivalent to calling `operator>>(istream &, const Point2d &);` Not declared yet.
|
||||
cout << p1 << endl;
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
Example of declaration of operator:
|
||||
|
||||
```cpp
|
||||
// declaration in point2d.h
|
||||
struct Point2D {
|
||||
Point2D(int x, int y);
|
||||
int x_;
|
||||
int y_;
|
||||
}
|
||||
|
||||
istream & operator>> (istream
|
||||
&, Point2D &);
|
||||
|
||||
ostream & operator<< (ostream
|
||||
&, const Point2D &);
|
||||
|
||||
// definition in point2d.cpp
|
||||
Point2D::Point2D(int x, int y): x_(x), y_(y) {}
|
||||
|
||||
istream & operator>> (istream &i, Point2d &p) {
|
||||
// we will change p so don't put const on it
|
||||
i >> p.x_ >> p.y_;
|
||||
return i;
|
||||
}
|
||||
ostream & operator<< (ostream &o, const Point2D &p) {
|
||||
// we will not change p, so put const
|
||||
o << p.x_ << “ “ << p.y_;
|
||||
return o;
|
||||
}
|
||||
```
|
||||
|
||||
## Operator overloading: Containers
|
||||
|
||||
Require element type they hold to implement a certain interface:
|
||||
|
||||
- Containers take ownership of the elements they contain - a copy of the element is made and the copy is inserted into the container (implies element needs a **copy constructor**)
|
||||
- Ordered associative containers maintain order with elements `<` operator
|
||||
- Unordered containers compare elements for equivalence with `==` operator
|
||||
|
||||
```cpp
|
||||
// declaration in point2d.h
|
||||
struct Point2D {
|
||||
Point2D(int x, int y);
|
||||
bool operator< (const Point2D &) const;
|
||||
bool operator== (const Point2D &) const;
|
||||
int x_;
|
||||
int y_;
|
||||
}
|
||||
// must be a non-member
|
||||
operator istream & operator>> (istream &, Point2D &);
|
||||
// must be a non-member
|
||||
operator ostream & operator<< (ostrea &, const Point2D &);
|
||||
|
||||
// definition in point2d.cpp
|
||||
// order by x_ value, then y_
|
||||
bool Point2D::operator<(const Point2D & p) const {
|
||||
if(x_ < p,x_) {return true;}
|
||||
if(x_ == p.x_) {
|
||||
return y_ < p.y_;
|
||||
}
|
||||
return false;
|
||||
}
|
||||
```
|
||||
|
||||
## Operator overloading: Algorithms
|
||||
|
||||
Require elements to implement a specific **interface** - can find what this interface is via the cpp reference pages
|
||||
|
||||
Example: `std::sort()` requires elements implement `operator<`, `std::accumulate()`
|
||||
requires `operator+`
|
||||
|
||||
Suppose we want to calculate the centroid of all Point2D objects in a `vector<Point2D>`
|
||||
|
||||
We can use `accumulate()` to sum all x coordinates, and all y coordinates. Then divide each by the size of the vector.
|
||||
|
||||
By default, accumulate uses the elements `+` operator.
|
||||
|
||||
```cpp
|
||||
// declaration, within the struct Point2D declaration in point2d.h, used by accumulate algorithm
|
||||
Point2D operator+(const Point2D &) const;
|
||||
|
||||
// definition, in point2d.cpp
|
||||
Point2D Point2D::operator+ (const Point2D &p) const {
|
||||
return Point2D(x_ + p.x_, y_ + p.y_);
|
||||
}
|
||||
|
||||
// in main()
|
||||
// assume v is populated with points
|
||||
Point2D accumulated = accumulate(v.begin(), v.end(), Point2D(0,0));
|
||||
|
||||
Point2D centroid (accumulated.x_/v.size(), accumulated.y_/v.size());
|
||||
```
|
||||
|
||||
## Callable objects
|
||||
|
||||
Make the algorithms even more general
|
||||
|
||||
Can be used parameterize policy
|
||||
|
||||
- E.g., the order produced by a sorting algorithm
|
||||
- E.g., the order maintained by an associative containers
|
||||
|
||||
Each callable object does a single, specific operation
|
||||
|
||||
- E.g., returns true if first value is less than second value
|
||||
|
||||
Algorithms often have overloaded versions
|
||||
|
||||
- E.g., sort that takes two iterators (uses `operator<`)
|
||||
- E.g., sort that takes two iterators and a binary predicate, uses the binary predicate to compare elements in range
|
||||
|
||||
### Callable Objects
|
||||
|
||||
Callable objects support function call syntax
|
||||
|
||||
- A function or function pointer
|
||||
|
||||
```cpp
|
||||
// function pointer
|
||||
bool (*PF) (const string &, const string &);
|
||||
// function
|
||||
bool string_func (const string &, const string &);
|
||||
```
|
||||
|
||||
- A struct or class providing an overloaded `operator()`
|
||||
|
||||
```cpp
|
||||
// an example of self-defined operator
|
||||
struct strings_ok {
|
||||
bool operator() (const string &s, const string &t) {
|
||||
return (s != "quit") && (t != "quit");
|
||||
}
|
||||
};
|
||||
```
|
||||
427
content/CSE332S/CSE332S_L12.md
Normal file
427
content/CSE332S/CSE332S_L12.md
Normal file
@@ -0,0 +1,427 @@
|
||||
# CSE332S Lecture 12
|
||||
|
||||
## Object-Oriented Programming (OOP) in C++
|
||||
|
||||
Today:
|
||||
|
||||
1. Type vs. Class
|
||||
2. Subtypes and Substitution
|
||||
3. Polymorphism
|
||||
a. Parametric polymorphism (generic programming)
|
||||
b. Subtyping polymorphism (OOP)
|
||||
4. Inheritance and Polymorphism in C++
|
||||
a. construction/destruction order
|
||||
b. Static vs. dynamic type
|
||||
c. Dynamic binding via virtual functions
|
||||
d. Declaring interfaces via pure virtual functions
|
||||
|
||||
## Type vs. Class, substitution
|
||||
|
||||
### Type (interface) vs. Class
|
||||
|
||||
Each function/operator declared by an object has a signature: name, parameter list, and return value
|
||||
|
||||
The set of all public signatures defined by an object makes up the interface to the object, or its type
|
||||
|
||||
- An object’s type is known (what can we request of an object?)
|
||||
- Its implementation is not - different objects may implement an interface very differently
|
||||
- An object may have many types (think interfaces in Java)
|
||||
|
||||
An object’s class defines its implementation:
|
||||
|
||||
- Specifies its state (internal data and its representation)
|
||||
- Implements the functions/operators it declares
|
||||
|
||||
### Subtyping: Liskov Substitution Principle
|
||||
|
||||
An interface may contain other interfaces!
|
||||
|
||||
A type is a **subtype** if it contains the full interface of another type (its **supertype**) as a subset of its own interface. (subtype has more methods than supertype)
|
||||
|
||||
**Substitutability**: if S is a subtype of T, then objects of type T may be replaced with objects of type S
|
||||
|
||||
Substitutability leads to **polymorphism**: a single interface may have many different implementations
|
||||
|
||||
## Polymorphism
|
||||
|
||||
Parametric (interface) polymorphism (substitution applied to generic programming)
|
||||
|
||||
- Design algorithms or classes using **parameterized types** rather than specific concrete data types.
|
||||
- Any class that defines the full interface required of the parameterized type (is a **subtype** of the parameterized type) can be substituted in place of the type parameter **at compile-time**.
|
||||
- Allows substitution of **unrelated types**.
|
||||
|
||||
### Polymorphism in OOP
|
||||
|
||||
Subtyping (inheritance) polymorphism: (substitution applied to OOP)
|
||||
|
||||
- A derived class can inherit an interface from its parent (base) class
|
||||
- Creates a subtype/supertype relationship. (subclass/superclass)
|
||||
- All subclasses of a superclass inherit the superclass’s interface and its implementation of that interface.
|
||||
- Function overriding - subclasses may override the superclass’s implementation of an interface
|
||||
- Allows the implementation of an interface to be substituted at run-time via dynamic binding
|
||||
|
||||
## Inheritance in C++ - syntax
|
||||
|
||||
### Forms of Inheritance in C++
|
||||
|
||||
A derived class can inherit from a base class in one of 3 ways:
|
||||
|
||||
- Public Inheritance ("is a", creates a subtype)
|
||||
- Public part of base class remains public
|
||||
- Protected part of base class remains protected
|
||||
- Protected Inheritance ("contains a", **derived class is not a subtype**)
|
||||
- Public part of base class becomes protected
|
||||
- Protected part of base class remains protected
|
||||
- Private Inheritance ("contains a", **derived class is not a subtype**)
|
||||
- Public part of base class becomes private
|
||||
- Protected part of base class becomes private
|
||||
|
||||
So public inheritance is the only way to create a **subtype**.
|
||||
|
||||
```cpp
|
||||
class A {
|
||||
public:
|
||||
int i;
|
||||
protected:
|
||||
int j;
|
||||
private:
|
||||
int k;
|
||||
};
|
||||
class B : public A {
|
||||
// ...
|
||||
};
|
||||
class C : protected A {
|
||||
// ...
|
||||
};
|
||||
class D : private A {
|
||||
// ...
|
||||
};
|
||||
```
|
||||
|
||||
Class B uses public inheritance from A
|
||||
|
||||
- `i` remains public to all users of class B
|
||||
- `j` remains protected. It can be used by methods in class B or its derived classes
|
||||
|
||||
Class C uses protected inheritance from A
|
||||
|
||||
- `i` becomes protected in C, so the only users of class C that can access `i` are the methods of class C
|
||||
- `j` remains protected. It can be used by methods in class C or its derived classes
|
||||
|
||||
Class D uses private inheritance from A
|
||||
|
||||
- `i` and `j` become private in D, so only methods of class D can access them.
|
||||
|
||||
## Construction and Destruction Order of derived class objects
|
||||
|
||||
### Class and Member Construction Order
|
||||
|
||||
```cpp
|
||||
class A {
|
||||
public:
|
||||
A(int i) : m_i(i) {
|
||||
cout << "A" << endl;}
|
||||
~A() {cout<<"~A"<<endl;}
|
||||
private:
|
||||
int m_i;
|
||||
};
|
||||
class B : public A {
|
||||
public:
|
||||
B(int i, int j)
|
||||
: A(i), m_j(j) {
|
||||
cout << "B" << endl;}
|
||||
~B() {cout << "~B" << endl;}
|
||||
private:
|
||||
int m_j;
|
||||
};
|
||||
int main (int, char *[]) {
|
||||
B b(2,3);
|
||||
return 0;
|
||||
};
|
||||
```
|
||||
|
||||
In the main function, the B constructor is called on object b
|
||||
|
||||
- Passes in integer values 2 and 3
|
||||
|
||||
B constructor calls A constructor
|
||||
|
||||
- passes value 2 to A constructor via base/member initialization list
|
||||
|
||||
A constructor initializes `m_i` with the passed value 2
|
||||
|
||||
- Body of A constructor runs
|
||||
- Outputs "A"
|
||||
|
||||
B constructor initializes `m_j` with passed value 3
|
||||
|
||||
- Body of B constructor runs
|
||||
- outputs "B"
|
||||
|
||||
### Class and Member Destruction Order
|
||||
|
||||
```cpp
|
||||
class A {
|
||||
public:
|
||||
A(int i) : m_i(i) {
|
||||
cout << "A" << endl;}
|
||||
~A() {cout<<"~A"<<endl;}
|
||||
private:
|
||||
int m_i;
|
||||
};
|
||||
class B : public A {
|
||||
public:
|
||||
B(int i, int j)
|
||||
: A(i), m_j(j) {
|
||||
cout << "B" << endl;}
|
||||
~B() {cout << "~B" << endl;}
|
||||
private:
|
||||
int m_j;
|
||||
};
|
||||
int main (int, char *[]) {
|
||||
B b(2,3);
|
||||
return 0;
|
||||
};
|
||||
```
|
||||
|
||||
B destructor called on object b in main
|
||||
|
||||
- Body of B destructor runs
|
||||
- outputs "~B"
|
||||
|
||||
B destructor calls “destructor” of m_j
|
||||
|
||||
- int is a built-in type, so it’s a no-op
|
||||
|
||||
B destructor calls A destructor
|
||||
|
||||
- Body of A destructor runs
|
||||
- outputs "~A"
|
||||
|
||||
A destructor calls “destructor” of m_i
|
||||
|
||||
- again a no-op
|
||||
|
||||
At the level of each class, order of steps is reversed in constructor vs. destructor
|
||||
|
||||
- ctor: base class, members, body
|
||||
- dtor: body, members, base class
|
||||
|
||||
In short, cascading order is called when constructor is called, and reverse cascading order is called when destructor is called.
|
||||
|
||||
## Polymorphic function calls - function overriding
|
||||
|
||||
### Static vs. Dynamic type
|
||||
|
||||
The type of a variable is known statically (at compile time), based on its declaration
|
||||
|
||||
```cpp
|
||||
int i; int * p;
|
||||
Fish f; Mammal m;
|
||||
Fish * fp = &f;
|
||||
```
|
||||
|
||||
However, actual types of objects aliased by references & pointers to base classes vary dynamically (at run-time)
|
||||
|
||||
```cpp
|
||||
Fish f; Mammal m;
|
||||
Animal * ap = &f; // dynamic type is Fish
|
||||
ap = &m; // dynamic type is Mammal
|
||||
Animal & ar = get_animal(); // dynamic type is the type of the object returned by get_animal()
|
||||
```
|
||||
|
||||
A base class and its derived classes form a set of types
|
||||
|
||||
`type(*ap)` $\in$ `{Animal, Fish, Mammal}`
|
||||
`typeset(*fp)` $\subset$ `typeset(*ap)`
|
||||
|
||||
Each type set is **open**
|
||||
|
||||
- More subclasses can be added
|
||||
|
||||
### Supporting Function Overriding in C++: Virtual Functions
|
||||
|
||||
Static binding: A function/operator call is bound to an implementation at compile-time
|
||||
|
||||
Dynamic binding: A function/operator call is bound to an implementation at run-time. When dynamic binding is used:
|
||||
|
||||
1. Lookup the dynamic type of the object the function/operator is called on
|
||||
2. Bind the call to the implementation defined in that class
|
||||
|
||||
Function overriding requires dynamic binding!
|
||||
|
||||
In C++, virtual functions facilitate dynamic binding.
|
||||
|
||||
```cpp
|
||||
class A {
|
||||
public:
|
||||
A () {cout<<" A";}
|
||||
virtual ~A () {cout<<" ~A";} // tells compiler that this destructor might be overridden in a derived class (the destructor of the parent class is usually virtual)
|
||||
virtual void f(int); // tells compiler that this function might be overridden in a derived class
|
||||
};
|
||||
class B : public A {
|
||||
public:
|
||||
B () :A() {cout<<" B";}
|
||||
virtual ~B() {cout<<" ~B";}
|
||||
virtual void f(int) override; // tells compiler that this function might be overridden in a derived class, the parent function is virtual otherwise it will be an error
|
||||
//C++11
|
||||
};
|
||||
int main (int, char *[]) {
|
||||
// prints "A B"
|
||||
A *ap = new B;
|
||||
// prints "~B ~A" : would only
|
||||
// print "~A" if non-virtual
|
||||
delete ap;
|
||||
return 0;
|
||||
};
|
||||
```
|
||||
|
||||
Virtual functions:
|
||||
|
||||
- Declared virtual in a base class
|
||||
- Can override in derived classes
|
||||
- Overriding only happens when signatures are the same
|
||||
|
||||
- Otherwise it just overloads the function or operator name
|
||||
|
||||
When called through a pointer or reference to a base class:
|
||||
|
||||
- function/operator calls are resolved dynamically
|
||||
|
||||
Use `final` (C++11) to prevent overriding of a virtual method
|
||||
|
||||
Use `override` (C++11) in derived class to ensure that the signatures match (error if not)
|
||||
|
||||
```cpp
|
||||
class A {
|
||||
public:
|
||||
void x() {cout<<"A::x";};
|
||||
virtual void y() {cout<<"A::y";};
|
||||
};
|
||||
class B : public A {
|
||||
public:
|
||||
void x() {cout<<"B::x";};
|
||||
virtual void y() {cout<<"B::y";};
|
||||
};
|
||||
int main () {
|
||||
B b;
|
||||
A *ap = &b; B *bp = &b;
|
||||
b.x (); // prints "B::x": static binding always calls the x() function of the class of the object
|
||||
b.y (); // prints "B::y": static binding always calls the y() function of the class of the object
|
||||
bp->x (); // prints "B::x": lookup the type of bp, which is B, and x() is non-virtual so it is statically bound
|
||||
bp->y (); // prints "B::y": lookup the dynamic type of bp, which is B (at run-time), and call the overridden y() function
|
||||
ap->x (); // prints "A::x": lookup the type of ap, which is A, and x() is non-virtual so it is statically bound
|
||||
ap->y (); // prints "B::y": lookup the dynamic type of ap, which is B (at run-time), and call the overridden y() function of class B
|
||||
return 0;
|
||||
};
|
||||
```
|
||||
|
||||
Only matter with pointer or reference
|
||||
|
||||
- Calls on object itself resolved statically
|
||||
- E.g., `b.y();`
|
||||
|
||||
Look first at pointer/reference type
|
||||
|
||||
- If non-virtual there, resolve statically
|
||||
- E.g., `ap->x();`
|
||||
- If virtual there, resolve dynamically
|
||||
- E.g., `ap->y();`
|
||||
|
||||
Note that virtual keyword need not be repeated in derived classes
|
||||
|
||||
- But it’s good style to do so
|
||||
|
||||
Caller can force static resolution of a virtual function via scope operator
|
||||
|
||||
- E.g., `ap->A::y();` prints “A::y”
|
||||
|
||||
Potential Problem: Class Slicing
|
||||
|
||||
When a derived type may be caught by a catch block, passed into a function, or returned out of a function that expects a base type:
|
||||
|
||||
- Be sure to catch by reference
|
||||
- Pass by reference
|
||||
- Return by reference
|
||||
|
||||
Otherwise, a copy is made:
|
||||
|
||||
- Loses original object's "dynamic type"
|
||||
- Only the base parts of the object are copied, resulting in the class slicing problem
|
||||
|
||||
## Class (implementation) Inheritance VS. Interface
|
||||
|
||||
Inheritance
|
||||
Class is the implementation of a type.
|
||||
|
||||
- Class inheritance involves inheriting interface and implementation
|
||||
- Internal state and representation of an object
|
||||
|
||||
Interface is the set of operations that can be called on an object.
|
||||
|
||||
- Interface inheritance involves inheriting only a common interface
|
||||
- What operations can be called on an object of the type?
|
||||
- Subclasses are related by a common interface
|
||||
- But may have very different implementations
|
||||
|
||||
In C++, pure virtual functions make interface inheritance possible.
|
||||
|
||||
```cpp
|
||||
class A { // the abstract base class
|
||||
public:
|
||||
virtual void x() = 0; // pure virtual function, no default implementation
|
||||
virtual void y() = 0; // pure virtual function, no default implementation
|
||||
};
|
||||
class B : public A { // B is still an abstract class because it still has a pure virtual function y() that is not defined
|
||||
public:
|
||||
virtual void x();
|
||||
};
|
||||
class C : public B { // C is a concrete derived class because it has all the pure virtual functions defined
|
||||
public:
|
||||
virtual void y();
|
||||
};
|
||||
int main () {
|
||||
A * ap = new C; // ap is a pointer to an abstract class type, but it can point to a concrete derived class object, cannot create an object of an abstract class, for example, new A() will be an error.
|
||||
ap->x ();
|
||||
ap->y ();
|
||||
delete ap;
|
||||
return 0;
|
||||
};
|
||||
```
|
||||
|
||||
Pure Virtual Functions and Abstract Base Classes:
|
||||
|
||||
A is an **abstract (base) class**
|
||||
|
||||
- Similar to an interface in Java
|
||||
- Declares pure virtual functions (=0)
|
||||
- May also have non-virtual methods, as well as virtual methods that are not pure virtual
|
||||
|
||||
Derived classes override pure virtual methods
|
||||
|
||||
- B overrides `x()`, C overrides `y()`
|
||||
|
||||
Can't instantiate an abstract class
|
||||
|
||||
- class that declares pure virtual functions
|
||||
- or inherits ones that are not overridden
|
||||
|
||||
A and B are abstract, can create a C
|
||||
|
||||
Can still have a pointer or reference to an abstract class type
|
||||
|
||||
- Useful for polymorphism
|
||||
|
||||
## Review of Inheritance and Subtyping Polymorphism in C++
|
||||
|
||||
Create related subclasses via public inheritance from a common superclass
|
||||
|
||||
- All subclasses inherit the interface and its implementation from the superclass
|
||||
|
||||
Override superclass implementation via function overriding
|
||||
|
||||
- Relies on virtual functions to support dynamic binding of function/operator calls
|
||||
|
||||
Use pure virtual functions to declare a common interface that related subclasses can implement
|
||||
|
||||
- Client code uses the common interface, does not care how the interface is defined. Reduces complexity and dependencies between objects in a system.
|
||||
309
content/CSE332S/CSE332S_L13.md
Normal file
309
content/CSE332S/CSE332S_L13.md
Normal file
@@ -0,0 +1,309 @@
|
||||
# CSE332S Lecture 13
|
||||
|
||||
## Memory layout of a C++ program, variables and their lifetimes
|
||||
|
||||
### C++ Memory Overview
|
||||
|
||||
4 major memory segments
|
||||
|
||||
- Global: variables outside stack, heap
|
||||
- Code (a.k.a. text): the compiled program
|
||||
- Heap: dynamically allocated variables
|
||||
- Stack: parameters, automatic and temporary variables (all the variables that are declared inside a function, managed by the compiler, so must be fixed size)
|
||||
- _For the dynamically allocated variables, they will be allocated in the heap segment, but the pointer (fixed size) to them will be stored in the stack segment._
|
||||
|
||||
Key differences from Java
|
||||
|
||||
- Destructors of automatic variables called when stack frame where declared pops
|
||||
- No garbage collection: program must explicitly free dynamic memory
|
||||
|
||||
Heap and stack use varies dynamically
|
||||
|
||||
Code and global use is fixed
|
||||
|
||||
Code segment is "read-only"
|
||||
|
||||
```cpp
|
||||
int g_default_value = 1;
|
||||
|
||||
int main (int argc, char **argv) {
|
||||
Foo *f = new Foo;
|
||||
|
||||
f->setValue(g_default_value);
|
||||
|
||||
delete f; // programmer must explicitly free dynamic memory
|
||||
|
||||
return 0;
|
||||
}
|
||||
|
||||
void Foo::setValue(int v) {
|
||||
this->m_value = v;
|
||||
}
|
||||
```
|
||||
|
||||

|
||||
|
||||
### Memory, Lifetimes, and Scopes
|
||||
|
||||
Temporary variables
|
||||
|
||||
- Are scoped to an expression, e.g., `a = b + 3 * c;`
|
||||
|
||||
Automatic (stack) variables
|
||||
|
||||
- Are scoped to the duration of the function in which they are declared
|
||||
|
||||
Dynamically allocated variables
|
||||
|
||||
- Are scoped from explicit creation (new) to explicit destruction (delete)
|
||||
|
||||
Global variables
|
||||
|
||||
- Are scoped to the entire lifetime of the program
|
||||
- Includes static class and namespace members
|
||||
- May still have initialization ordering issues
|
||||
|
||||
Member variables
|
||||
|
||||
- Are scoped to the lifetime of the object within which they reside
|
||||
- Depends on whether object is temporary, automatic, dynamic, or global
|
||||
|
||||
**Lifetime of a pointer/reference can differ from the lifetime of the location to which it points/refers**
|
||||
|
||||
## Direct Dynamic Memory Allocation and Deallocation
|
||||
|
||||
```cpp
|
||||
#include <iostream>
|
||||
using namespace std;
|
||||
int main (int, char *[]) {
|
||||
int * i = new int; // any of these can throw bad_alloc
|
||||
int * j = new int(3);
|
||||
int * k = new int[*j];
|
||||
int * l = new int[*j];
|
||||
for (int m = 0; m < *j; ++m) { // fill the array with loop
|
||||
l[m] = m;
|
||||
}
|
||||
delete i; // call int destructor
|
||||
delete j; // single destructor call
|
||||
delete [] k; // call int destructor for each element
|
||||
delete [] l;
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
## Issues with direct memory management
|
||||
|
||||
### A Basic Issue: Multiple Aliasing
|
||||
|
||||
```cpp
|
||||
int main (int argc, char **argv) {
|
||||
Foo f;
|
||||
Foo *p = &f;
|
||||
Foo &r = f;
|
||||
delete p;
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
Multiple aliases for same object
|
||||
|
||||
- `f` is a simple alias, the object itself
|
||||
- `p` is a variable holding a pointer
|
||||
- `r` is a variable holding a reference
|
||||
|
||||
What happens when we call delete on p?
|
||||
|
||||
- Destroy a stack variable (may get a bus error there if we’re lucky)
|
||||
- If not, we may crash in destructor of f at function exit
|
||||
- Or worse, a local stack corruption that may lead to problems later
|
||||
|
||||
Problem: object destroyed but another alias to it was then used (**dangling pointer issue**)
|
||||
|
||||
### Memory Lifetime Errors
|
||||
|
||||
```cpp
|
||||
Foo *bad() {
|
||||
Foo f;
|
||||
return &f; // return address of local variable, f is destroyed after function returns
|
||||
}
|
||||
|
||||
Foo &alsoBad() {
|
||||
Foo f;
|
||||
return f; // return reference to local variable, f is destroyed after function returns
|
||||
}
|
||||
|
||||
Foo mediocre() {
|
||||
Foo f;
|
||||
return f; // return copy of local variable, f is destroyed after function returns, danger when f is a large object
|
||||
}
|
||||
|
||||
Foo * good() {
|
||||
Foo *f = new Foo;
|
||||
return f; // return pointer to local variable, with new we can return a pointer to a dynamically allocated object, but we must remember to delete it later
|
||||
}
|
||||
|
||||
int main() {
|
||||
Foo *f = &mediocre(); // f is a pointer to a temporary object, which is destroyed after function returns, f is invalid after function returns
|
||||
cout << good()->value() << endl; // good() returns a pointer to a dynamically allocated object, but we did not store the pointer, so it will be lost after function returns, making it impossible to delete it later.
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
Automatic variables
|
||||
|
||||
- Are destroyed on function return
|
||||
- But in bad, we return a pointer to a variable that no longer exists
|
||||
- Reference from also_bad similar
|
||||
- Like an un-initialized pointer
|
||||
|
||||
What if we returned a copy?
|
||||
|
||||
- Ok, we avoid the bad pointer, and end up with an actual object
|
||||
- But we do twice the work (why?)
|
||||
- And, it’s a temporary variable (more on this next)
|
||||
|
||||
We really want dynamic allocation here
|
||||
|
||||
Dynamically allocated variables
|
||||
|
||||
- Are not garbage collected
|
||||
- But are lost if no one refers to them: called a "**memory leak**"
|
||||
|
||||
Temporary variables
|
||||
|
||||
- Are destroyed at end of statement
|
||||
- Similar to problems w/ automatics
|
||||
|
||||
Can you spot 2 problems?
|
||||
|
||||
- One with a temporary variable
|
||||
- One with dynamic allocation
|
||||
|
||||
### Double Deletion Errors
|
||||
|
||||
```cpp
|
||||
int main (int argc, char **argv) {
|
||||
Foo *f = new Foo;
|
||||
delete f;
|
||||
// ... do other stuff
|
||||
delete f; // will throw an error because f is already deleted
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
What could be at this location?
|
||||
|
||||
- Another heap variable
|
||||
- Could corrupt heap
|
||||
|
||||
## Shared pointers and the RAII idiom
|
||||
|
||||
### A safer approach using smart pointers
|
||||
|
||||
C++11 provides two key dynamic allocation features
|
||||
|
||||
- `shared_ptr` : a reference counted pointer template to alias and manage objects allocated in dynamic memory (we’ll mostly use the shared_ptr smart pointer in this course)
|
||||
- `make_shared` : a function template that dynamically allocates and value initializes an object and then returns a shared pointer to it (hiding the object’s address, for safety)
|
||||
|
||||
C++11 provides 2 other smart pointers as well
|
||||
|
||||
- `unique_ptr` : a more complex but potentially very efficient way to transfer ownership of dynamic memory safely (implements C++11 “move semantics”)
|
||||
- `weak_ptr` : gives access to a resource that is guarded by a shared_ptr without increasing reference count (can be used to prevent memory leaks due to circular references)
|
||||
|
||||
### Resource Acquisition Is Initialization (RAII)
|
||||
|
||||
Also referred to as the "Guard Idiom"
|
||||
|
||||
- However, the term "RAII" is more widely used for C++
|
||||
|
||||
Relies on the fact that in C++ a stack object’s destructor is called when stack frame pops
|
||||
|
||||
Idea: we can use a stack object (usually a smart pointer) to hold the ownership of a heap object, or any other resource that requires explicit clean up
|
||||
|
||||
- Immediately initialize stack object with the allocated resource
|
||||
- De-allocate resource in the stack object’s destructor
|
||||
|
||||
### Example: Resource Acquisition Is Initialization (RAII)
|
||||
|
||||
```cpp
|
||||
shared_ptr<Foo> createAndInit() {
|
||||
shared_ptr<Foo> p =
|
||||
make_shared<Foo> ();
|
||||
init(p);// may throw exception
|
||||
return p;
|
||||
}
|
||||
|
||||
int run () {
|
||||
try {
|
||||
shared_ptr<Foo> spf =
|
||||
createAndInit();
|
||||
cout << “*spf is ” << *spf;
|
||||
} catch (...) {
|
||||
return -1
|
||||
}
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
RAII idiom example using shared_ptr
|
||||
|
||||
```cpp
|
||||
#include <memory>
|
||||
using namespace std;
|
||||
```
|
||||
|
||||
- `shared_ptr<X>` assumes and maintains ownership of aliased X
|
||||
- Can access the aliased X through it (*spf)
|
||||
- `shared_ptr<X>` destructor calls delete on address of owned X when it’s safe to do so (per reference counting idiom discussed next)
|
||||
- Combines well with other memory idioms
|
||||
|
||||
### Reference Counting
|
||||
|
||||
Basic Problem
|
||||
|
||||
- Resource sharing is often more efficient than copying
|
||||
- But it’s hard to tell when all are done using a resource
|
||||
- Must avoid early deletion
|
||||
- Must avoid leaks (non-deletion)
|
||||
|
||||
Solution Approach
|
||||
|
||||
- Share both the resource and a counter for references to it
|
||||
- Each new reference increments the counter
|
||||
- When a reference is done, it decrements the counter
|
||||
- If count drops to zero, also deletes resource and counter
|
||||
- "last one out shuts off the lights"
|
||||
|
||||
### Reference Counting Example
|
||||
|
||||
```cpp
|
||||
shared_ptr<Foo> createAndInit() {
|
||||
shared_ptr<Foo> p =
|
||||
make_shared<Foo> ();
|
||||
init(p);// may throw exception
|
||||
return p;
|
||||
}
|
||||
|
||||
int run () {
|
||||
try {
|
||||
shared_ptr<Foo> spf =
|
||||
createAndInit();
|
||||
shared_ptr<Foo> spf2 = spf;
|
||||
// object destroyed after
|
||||
// both spf and spf2 go away
|
||||
} catch (...) {
|
||||
return -1
|
||||
}
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
Again starts with RAII idiom via shared_ptr
|
||||
|
||||
- `spf` initially has sole ownership of aliased X
|
||||
- `spf.unique()` would return true
|
||||
- `spf.use_count` would return 1
|
||||
|
||||
`shared_ptr<X>` copy constructor increases count, and its destructor decreases count
|
||||
|
||||
`shared_ptr<X>` destructor calls delete on the pointer to the owned X when count drops to 0
|
||||
224
content/CSE332S/CSE332S_L14.md
Normal file
224
content/CSE332S/CSE332S_L14.md
Normal file
@@ -0,0 +1,224 @@
|
||||
# CSE332S Lecture 14
|
||||
|
||||
## Copy control
|
||||
|
||||
Copy control consists of 5 distinct operations
|
||||
|
||||
- A `copy constructor` initializes an object by duplicating the const l-value that was passed to it by reference
|
||||
- A `copy-assignment operator` (re)sets an object's value by duplicating the const l-value passed to it by reference
|
||||
- A `destructor` manages the destruction of an object
|
||||
- A `move constructor` initializes an object by transferring the implementation from the r-value reference passed to it (next lecture)
|
||||
- A `move-assignment operator` (re)sets an object's value by transferring the implementation from the r-value reference passed to it (next lecture)
|
||||
|
||||
Today we'll focus on the first 3 operations and will defer the others (introduced in C++11) until next time
|
||||
|
||||
- The others depend on the new C++11 `move semantics`
|
||||
|
||||
### Basic copy control operations
|
||||
|
||||
A copy constructor or copy-assignment operator takes a reference to a (usually const) instance of the class
|
||||
|
||||
- Copy constructor initializes a new object from it
|
||||
- Copy-assignment operator sets object's value from it
|
||||
- In either case, original the object is left unchanged (which differs from the move versions of these operations)
|
||||
- Destructor takes no arguments `~A()` (except implicit `this`)
|
||||
|
||||
Copy control operations for built-in types
|
||||
|
||||
- Copy construction and copy-assignment copy values
|
||||
- Destructor of built-in types does nothing (is a "no-op")
|
||||
|
||||
Compiler-synthesized copy control operations
|
||||
|
||||
- Just call that same operation on each member of the object
|
||||
- Uses defined/synthesized definition of that operation for user-defined types (see above for built-in types)
|
||||
|
||||
### Preventing or Allowing Basic Copy Control
|
||||
|
||||
Old (C++03) way to prevent compiler from generating a default constructor, copy constructor, destructor, or assignment operator was somewhat awkward
|
||||
|
||||
- Declare private, don't define, don't use within class
|
||||
- This works, but gives cryptic linker error if operation is used
|
||||
|
||||
New (C++11) way to prevent calls to any method
|
||||
|
||||
- End the declaration with `= delete` (and don't define)
|
||||
- Compiler will then give an intelligible error if a call is made
|
||||
|
||||
C++11 allows a constructor to call peer constructors
|
||||
|
||||
- Allows re-use of implementation (through delegation)
|
||||
- Object is fully constructed once any constructor finishes
|
||||
|
||||
C++11 lets you ask compiler to synthesize operations
|
||||
|
||||
- Explicitly, but only for basic copy control, default constructor
|
||||
- End the declaration with `= default` (and don't define) The compiler will then generate the operation or throw an error if it can't.
|
||||
|
||||
## Shallow vs Deep Copy
|
||||
|
||||
### Shallow Copy Construction
|
||||
|
||||
```cpp
|
||||
// just uses the array that's already in the other object
|
||||
IntArray::IntArray(const IntArray &a)
|
||||
:size_(a.size_),
|
||||
values_(a.values_) {
|
||||
// only memory address is copied, not the memory it points to
|
||||
}
|
||||
|
||||
int main(int argc, char * argv[]){
|
||||
IntArray arr = {0,1,2};
|
||||
IntArray arr2 = arr;
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
There are two ways to "copy"
|
||||
|
||||
- Shallow: re-aliases existing resources
|
||||
- E.g., by copying the address value from a pointer member variable
|
||||
- Deep: makes a complete and separate copy
|
||||
- I.e., by following pointers and deep copying what they alias
|
||||
|
||||
Version above shows shallow copy
|
||||
|
||||
- Efficient but may be risky (why?) The destructor will delete the memory that the other object is pointing to.
|
||||
- Usually want no-op destructor, aliasing via `shared_ptr` or a boolean value to check if the object is the original memory allocator for the resource.
|
||||
|
||||
### Deep Copy Construction
|
||||
|
||||
```cpp
|
||||
IntArray::IntArray(const IntArray &a)
|
||||
:size_(0), values_(nullptr) {
|
||||
|
||||
if (a.size_ > 0) {
|
||||
// new may throw bad_alloc,
|
||||
// set size_ after it succeeds
|
||||
values_ = new int[a.size_];
|
||||
size_ = a.size_;
|
||||
|
||||
// could use memcpy instead
|
||||
for (size_t i = 0;
|
||||
i < size_; ++i) {
|
||||
values_[i] = a.values_[i];
|
||||
}
|
||||
}
|
||||
}
|
||||
int main(int argc, char * argv[]){
|
||||
IntArray arr = {0,1,2};
|
||||
IntArray arr2 = arr;
|
||||
return 0;
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
This code shows deep copy
|
||||
|
||||
- Safe: no shared aliasing, exception aware initialization
|
||||
- But may not be as efficient as shallow copy in many cases
|
||||
|
||||
Note trade-offs with arrays
|
||||
|
||||
- Allocate memory once
|
||||
- More efficient than multiple calls to new (heap search)
|
||||
- Constructor and assignment called on each array element
|
||||
- Less efficient than block copy
|
||||
- E.g., using `memcpy()`
|
||||
- But sometimes necessary
|
||||
- i.e., constructors, destructors establish needed invariants
|
||||
|
||||
Each object is responsible for its own resources.
|
||||
|
||||
## Swap Trick for Copy-Assignment
|
||||
|
||||
The swap trick is a way to implement the copy-assignment operator, given that the `size_` and `values_` members are already defined in constructor.
|
||||
|
||||
```cpp
|
||||
class Array {
|
||||
public:
|
||||
Array(unsigned int) ; // assume constructor allocates memory
|
||||
Array(const Array &); // assume copy constructor makes a deep copy
|
||||
~Array(); // assume destructor calls delete on values_
|
||||
Array & operator=(const Array &a);
|
||||
private:
|
||||
size_t size_;
|
||||
int * values_;
|
||||
};
|
||||
|
||||
Array & Array::operator=(const Array &a) { // return ref lets us chain
|
||||
if (&a != this) { // note test for self-assignment (safe, efficient)
|
||||
Array temp(a); // copy constructor makes deep copy of a
|
||||
swap(temp.size_, size_); // note unqualified calls to swap
|
||||
swap(temp.values_, values_); // (do user-defined or std::swap)
|
||||
}
|
||||
return *this; // previous *values_ cleaned up by temp's destructor, which is the member variable of the current object
|
||||
}
|
||||
|
||||
int main(int argc, char * argv[]){
|
||||
IntArray arr = {0,1,2};
|
||||
IntArray arr2 = {3,4,5};
|
||||
arr2 = arr;
|
||||
return 0;
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
## Review: Construction/destruction order with inheritance, copy control with inheritance
|
||||
|
||||
### Constructor and Destructor are Inverses
|
||||
|
||||
```cpp
|
||||
IntArray::IntArray(unsigned int u)
|
||||
: size_(0), values_(nullptr) {
|
||||
// exception safe semantics
|
||||
values_ = new int [u];
|
||||
size_ = u;
|
||||
}
|
||||
|
||||
IntArray::~IntArray() {
|
||||
|
||||
// deallocates heap memory
|
||||
// that values_ points to,
|
||||
// so it's not leaked:
|
||||
// with deep copy, object
|
||||
// owns the memory
|
||||
delete [] values_;
|
||||
|
||||
// the size_ and values_
|
||||
// member variables are
|
||||
// themselves destroyed
|
||||
// after destructor body
|
||||
}
|
||||
```
|
||||
Constructors initialize
|
||||
|
||||
- At the start of each object's lifetime
|
||||
- Implicitly called when object is created
|
||||
|
||||
Destructors clean up
|
||||
|
||||
- Implicitly called when an object is destroyed
|
||||
- E.g., when stack frame where it was declared goes out of scope
|
||||
- E.g., when its address is passed to delete
|
||||
- E.g., when another object of which it is a member is being destroyed
|
||||
|
||||
### More on Initialization and Destruction
|
||||
|
||||
Initialization follows a well defined order
|
||||
|
||||
- Base class constructor is called
|
||||
- That constructor recursively follows this order, too
|
||||
- Member constructors are called
|
||||
- In order members were declared
|
||||
- Good style to list in that order (a good compiler may warn if not)
|
||||
- Constructor body is run
|
||||
|
||||
Destruction occurs in the reverse order
|
||||
|
||||
- Destructor body is run, then member destructors, then base class destructor (which recursively follows reverse order)
|
||||
|
||||
**Make destructor virtual if members are virtual**
|
||||
|
||||
- Or if class is part of an inheritance hierarchy
|
||||
- Avoids “slicing”: ensures destruction starts at the most derived class destructor (not at some higher base class)
|
||||
148
content/CSE332S/CSE332S_L15.md
Normal file
148
content/CSE332S/CSE332S_L15.md
Normal file
@@ -0,0 +1,148 @@
|
||||
# CSE332S Lecture 15
|
||||
|
||||
## Move semantics introduction and motivation
|
||||
|
||||
Review: copy control consists of 5 distinct operations
|
||||
|
||||
- A `copy constructor` initializes an object by duplicating the const l-value that was passed to it by reference
|
||||
- A `copy-assignment operator` (re)sets an object’s value by duplicating the const l-value passed to it by reference
|
||||
- A `destructor` manages the destruction of an object
|
||||
- A `move constructor` initializes an object by transferring the implementation from the r-value reference passed to it
|
||||
- A `move-assignment operator` (re)sets an object’s value by transferring the implementation from the r-value reference passed to it
|
||||
|
||||
Today we'll focus on the last 2 operations and other features (introduced in C++11) like r-value references
|
||||
I.e., features that support the new C++11 `move semantics`
|
||||
|
||||
### Motivation for move semantics
|
||||
|
||||
Copy construction and copy-assignment may be expensive due to time/memory for copying
|
||||
It would be more efficient to simply "take" the implementation from the passed object, if that's ok
|
||||
It's ok if the passed object won't be used afterward
|
||||
|
||||
- E.g., if it was passed by value and so is a temporary object
|
||||
- E.g., if a special r-value reference says it's ok to take from (as long as object remains in a state that's safe to destruct)
|
||||
|
||||
Note that some objects require move semantics
|
||||
|
||||
- I.e., types that don't allow copy construction/assignment
|
||||
- E.g., `unique_ptr`, `ifstream`, `thread`, etc.
|
||||
|
||||
New for C++11: r-value references and move function
|
||||
|
||||
- E.g., `int i; int &&rvri = std::move(i);`
|
||||
|
||||
### Synthesized move operations
|
||||
|
||||
Compiler will only synthesize a move operation if
|
||||
|
||||
- Class does not declare any copy control operations, and
|
||||
- Every non-static data member of the class can be moved
|
||||
|
||||
Members of built-in types can be moved
|
||||
|
||||
- E.g., by `std::move` etc.
|
||||
|
||||
User-defined types that have synthesized/defined version of the specific move operation can be moved
|
||||
L-values are always copied, r-values can be moved
|
||||
|
||||
- If there is no move constructor, r-values only can be copied
|
||||
|
||||
Can ask for a move operation to be synthesized
|
||||
|
||||
- I.e., by using `= default`
|
||||
- But if cannot move all members, synthesized as `= delete`
|
||||
|
||||
## Move constructor and assignment operator examples, more details on inheritance
|
||||
|
||||
### R-values, L-values, and Reference to Either
|
||||
|
||||
A variable is an l-value (has a location)
|
||||
|
||||
- E.g., `int i = 7;`
|
||||
|
||||
Can take a regular (l-value) reference to it
|
||||
|
||||
- E.g., `int & lvri = i;`
|
||||
|
||||
An expression is an r-value
|
||||
|
||||
- E.g., `i * 42`
|
||||
|
||||
Can only take an r-value reference to it (note syntax)
|
||||
|
||||
- E.g., `int && rvriexp = i * 42;`
|
||||
|
||||
Can only get r-value reference to l-value via move
|
||||
|
||||
- E.g., `int && rvri = std::move(i);`
|
||||
- Promises that i won’t be used for anything afterward
|
||||
- Also, must be safe to destroy i (could be stack/heap/global)
|
||||
|
||||
### Move Constructors
|
||||
|
||||
```cpp
|
||||
// takes implementation from a
|
||||
IntArray::IntArray(IntArray &&a)
|
||||
: size_(a.size_),
|
||||
values_(a.values_) {
|
||||
|
||||
// make a safe to destroy
|
||||
a.values_ = nullptr;
|
||||
a.size_ = 0;
|
||||
}
|
||||
```
|
||||
|
||||
Note r-value reference
|
||||
|
||||
- Says it's safe to take a's implementation from it
|
||||
- Promises only subsequent operation will be destruction
|
||||
|
||||
Note constructor design
|
||||
|
||||
- A lot like shallow copy constructor's implementation
|
||||
- Except, zeroes out state of `a`
|
||||
- No sharing, current object owns the implementation
|
||||
- Object `a` is now safe to destroy (but is not safe to do anything else with afterward)
|
||||
|
||||
### Move Assignment Operator
|
||||
|
||||
No allocation, so no exceptions to worry about
|
||||
|
||||
- Simply free existing implementation (delete `values_`)
|
||||
- Then copy over size and pointer values from `a`
|
||||
- Then zero out size and pointer in `a`
|
||||
|
||||
This leaves assignment complete, `a` safe to destroy
|
||||
|
||||
- Implementation is transferred from `a` to current object
|
||||
|
||||
```cpp
|
||||
Array & Array::operator=(Array &&a) { // Note r-value reference
|
||||
if (&a != this) { // still test for self-assignment
|
||||
delete [] values_; // safe to free first (if not self-assigning)
|
||||
size_ = a. size_; // take a’s size value
|
||||
values_ = a.values_; // take a’s pointer value
|
||||
a.size_ = 0; // zero out a’s size
|
||||
a.values_ = nullptr; // zero out a’s pointer (now safe to destroy)
|
||||
}
|
||||
return *this;
|
||||
}
|
||||
```
|
||||
|
||||
### Move Semantics and Inheritance
|
||||
|
||||
Base classes should declare/define move operations
|
||||
|
||||
- If it makes sense to do so at all
|
||||
- Derived classes then can focus on moving their members
|
||||
- E.g., calling `Base::operator=` from `Derived::operator=`
|
||||
|
||||
Containers further complicate these issues
|
||||
|
||||
- Containers hold their elements by value
|
||||
- Risks slicing, other inheritance and copy control problems
|
||||
|
||||
So, put (smart) pointers, not objects, into containers
|
||||
|
||||
- Access is polymorphic if destructors, other methods virtual
|
||||
- Smart pointers may help reduce need for copy control operations, or at least simplify cases where needed
|
||||
200
content/CSE332S/CSE332S_L16.md
Normal file
200
content/CSE332S/CSE332S_L16.md
Normal file
@@ -0,0 +1,200 @@
|
||||
# CSE332S Lecture 16
|
||||
|
||||
## Intro to OOP design and principles
|
||||
|
||||
### Review: Class Design
|
||||
|
||||
Designing a class to work well with the STL:
|
||||
|
||||
- What operators are required of our class?
|
||||
- `operator<` for ordered associative containers, `operator==` for unordered associative containers
|
||||
- `operator<<` and `operator>>` for interacting with iostreams
|
||||
- Algorithms require particular operators as well
|
||||
|
||||
Designing a class that manages dynamic resources:
|
||||
|
||||
- Must think about copy control
|
||||
- **Shallow copy** or **deep copy**?
|
||||
- When should the dynamic resources be cleaned up?
|
||||
- Move semantics for efficiency
|
||||
|
||||
### OOP Design: How do we combine objects to create complex software?
|
||||
|
||||
Goals - Software should be:
|
||||
|
||||
- Flexible
|
||||
- Extensible
|
||||
- Reusable
|
||||
|
||||
Today: 4 Principles of object-oriented programming
|
||||
|
||||
1. Encapsulation
|
||||
2. Abstraction
|
||||
3. Inheritance
|
||||
4. Polymorphism
|
||||
|
||||
#### Review: Client Code, interface vs. implementation
|
||||
|
||||
Today we will focus on a single class or family of classes related via a common
|
||||
base class and client code that interacts with it.
|
||||
|
||||
Next time: Combining objects to create more powerful and complex objects
|
||||
|
||||
**Client code**: code that has access to an object (via the object directly, a reference to the object, or a pointer/smart pointer to the object).
|
||||
|
||||
- Knows an object’s public interface only, not its implementation.
|
||||
|
||||
**Interface**: The set of all functions/operators (public member variables in C++ as well) a client can request of an object
|
||||
|
||||
**Implementation**: The definition of an object’s interface. State (member variables) and definitions of member functions/operators
|
||||
|
||||
#### Principle 1: Encapsulation
|
||||
|
||||
Data and behaviors are encapsulated together behind an interface
|
||||
|
||||
1. Member functions have direct access to the member variables of the object via “this”
|
||||
1. Benefit: Simplifies function calls (much smaller argument lists)
|
||||
|
||||
Proper encapsulation:
|
||||
|
||||
1. Data of a class remains internal (not enforced in C++)
|
||||
2. Client can only interact with the data of an object via its interface
|
||||
|
||||
**Benefit**:
|
||||
|
||||
(Flexible) Reduces impact of change - Easy to change how an object is stored
|
||||
without needing to modify client code that uses the object.
|
||||
|
||||
#### Principle 2: Abstraction
|
||||
|
||||
An object presents only the necessary interface to client code
|
||||
|
||||
1. Hides unnecessary implementation details from the client
|
||||
a. Member functions that client code does not need should be private or protected
|
||||
|
||||
We see abstraction everyday:
|
||||
|
||||
- TV
|
||||
- Cell phone
|
||||
- Coffee machine
|
||||
|
||||
Benefits:
|
||||
|
||||
1. Reduces code complexity, makes an object easier to use
|
||||
2. (Flexible) Reduces impact of change - internal implementation details can be
|
||||
modified without modification to client code
|
||||
|
||||
#### Principle 3: Inheritance (public inheritance in C++)
|
||||
|
||||
**"Implementation" inheritance - class inherits interface and implementation of
|
||||
its base class**
|
||||
|
||||
Benefits:
|
||||
|
||||
- Remove redundant code by placing it in a common base class.
|
||||
- (Reusable) Easily extend a class to add new functionality.
|
||||
|
||||
**"Interface" inheritance - inherit the interface of the base class only (abstract base class in C++, pure virtual functions)**
|
||||
|
||||
Benefits:
|
||||
|
||||
- Reduce dependencies between base/derived class
|
||||
- (Flexible, Extensible, Reusable) Program a client to depend on an interface rather than a specific implementation (more on this later)
|
||||
|
||||
#### One More Useful C++ Construct: Multiple Inheritance
|
||||
|
||||
C++ allows a class to inherit from more than one base class
|
||||
|
||||
```cpp
|
||||
class Bear: public ZooAnimal {/*...*/};
|
||||
class Panda: public Bear, public Endangered {/*...*/};
|
||||
```
|
||||
|
||||
Construction order - all base classes are constructed first:
|
||||
|
||||
- all base classes -> derived classes member variables -> constructor body
|
||||
|
||||
Destruction order - opposite of construction order:
|
||||
|
||||
- Destructor body -> derived classes member variables -> all base class
|
||||
destructors
|
||||
|
||||
**Rule of thumb**: When using multiple inheritance, a class should inherit
|
||||
implementation from a single base class only. Any number of interfaces may be
|
||||
inherited (this is enforced in Java)
|
||||
|
||||
#### Principle 4: Polymorphism
|
||||
|
||||
A single interface may have many different implementations (virtual functions and
|
||||
function overriding in C++)
|
||||
|
||||
Benefits:
|
||||
|
||||
1. Avoid nasty switch statements (function calls resolved dynamically)
|
||||
2. (Flexible) Allows the implementation of an interface to change at run-time
|
||||
|
||||
#### Program to an interface
|
||||
|
||||
Client should restrict variables to an interface only, not a specific implementation
|
||||
|
||||
- **Extensible, reusable**: New subclasses that define the interface can be created and used without modification to the client. Easy to add new functionality. Easy to reuse client.
|
||||
- **Reduce impact of change**: Decouples client from concrete classes it uses.
|
||||
- **Flexible**: The implementation of an interface used by the client can change at run-time.
|
||||
|
||||
In C++:
|
||||
|
||||
- Abstract base class using pure virtual functions to declare the interface
|
||||
- Implement the interface in subclasses via public inheritance
|
||||
- Client maintains reference or pointer to the base class
|
||||
- Calls through the reference or pointer are polymorphic
|
||||
|
||||
```cpp
|
||||
// declare printable interface
|
||||
class printable {
|
||||
public:
|
||||
virtual void print(ostream &o) = 0;
|
||||
};
|
||||
// derived classes defines printable
|
||||
// interface
|
||||
class smiley : public printable {
|
||||
public:
|
||||
virtual void print(ostream &o) {
|
||||
o << ":)" ;
|
||||
};
|
||||
};
|
||||
class frown : public printable {
|
||||
public:
|
||||
virtual void print(ostream &o) {
|
||||
o << ":(";
|
||||
};
|
||||
};
|
||||
int main(int argc, char * argv[]) {
|
||||
smiley s; // s restricted to
|
||||
// a smiley object
|
||||
s.print();
|
||||
// p may point to an object
|
||||
// of any class that defines
|
||||
// the printable interface
|
||||
printable * p =
|
||||
generateOutput();
|
||||
// Client unaware of the
|
||||
// implementation of print()
|
||||
p->print();
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
Program to an interface
|
||||
Allows easily extensible designs: anything that defines the printable interface can
|
||||
be used with our client
|
||||
|
||||
```cpp
|
||||
class Book : public printable {
|
||||
vector<string> pages;
|
||||
public:
|
||||
virtual void print(ostream &o) {
|
||||
for(unsigned int page = 0; page < pages.size(); ++page){
|
||||
o << "page: " << page << endl;
|
||||
o << pages[i] << endl;
|
||||
};
|
||||
};
|
||||
147
content/CSE332S/CSE332S_L17.md
Normal file
147
content/CSE332S/CSE332S_L17.md
Normal file
@@ -0,0 +1,147 @@
|
||||
# CSE332S Lecture 17
|
||||
|
||||
## Object Oriented Programming Building Blocks
|
||||
|
||||
OOP Building Blocks for Extensible, Flexible, and Reusable Code
|
||||
|
||||
Today: Techniques Commonly Used in Design Patterns
|
||||
|
||||
- **Program to an interface** (last time)
|
||||
- **Object composition and request forwarding** (today)
|
||||
- Composition vs. inheritance
|
||||
- **Run-time relationships between objects** (today)
|
||||
- Aggregate vs. acquaintance
|
||||
- **Delegation** (later...)
|
||||
|
||||
Next Time: Design Patterns
|
||||
|
||||
Describe the core of a repeatable solution to common design problems.
|
||||
|
||||
### Code Reuse: Two Ways to Reuse a Class
|
||||
|
||||
#### Inheritance
|
||||
|
||||
Code reuse by inheriting the implementation of a base class.
|
||||
|
||||
- **Pros:**
|
||||
- Inheritance relationships defined at compile-time - simple to understand.
|
||||
- **Cons:**
|
||||
- Subclass often inherits some implementation from superclass - derived class now depends on its base class implementation, leading to less flexible code.
|
||||
|
||||
#### Composition
|
||||
|
||||
Assemble multiple objects together to create new complex functionality, forward requests to the responsible assembled object.
|
||||
|
||||
- **Pros:**
|
||||
- Allows flexibility at run-time, composite objects often constructed dynamically by obtaining references/pointers to other objects (dependency injection).
|
||||
- Objects known only through their interface - increased flexibility, reduced impact of change.
|
||||
- **Cons:**
|
||||
- Code can be more difficult to understand, how objects interact may change dynamically.
|
||||
|
||||
### Example: Our First Design Pattern (Adapter Pattern)
|
||||
|
||||
**Problem:** We are given a class that we cannot modify for some reason - it provides functionality we need, but defines an interface that does not match our program (client code).
|
||||
|
||||
**Solution:** Create an adapter class, adapter declares the interface needed by our program, defines it by forwarding requests to the unmodifiable object.
|
||||
|
||||
Two ways to do this:
|
||||
|
||||
```cpp
|
||||
class unmodifiable {
|
||||
public:
|
||||
int func(); // does something useful, but doesn’t match the interface required by the client code
|
||||
};
|
||||
```
|
||||
|
||||
1. **Inheritance**
|
||||
|
||||
```cpp
|
||||
// Using inheritance:
|
||||
class adapter : protected unmodifiable {
|
||||
// open the access to the protected member func() for derived class
|
||||
public:
|
||||
int myFunc() {
|
||||
return func(); // forward request to encapsulated object
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
2. **Composition**
|
||||
|
||||
```cpp
|
||||
class adapterComp {
|
||||
unmodifiable var;
|
||||
public:
|
||||
int myFunc() {
|
||||
return var.func();
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
### Thinking About and Describing Run-time Relationships
|
||||
|
||||
Typically, composition is favored over inheritance! Object composition with programming to an interface allows relationships/interactions between objects to vary at run-time.
|
||||
|
||||
- **Aggregate:** Object is part of another. Its lifetime is the same as the object it is contained in. (similar to base class and derived class relationship)
|
||||
- **Acquaintance:** Objects know of each other, but are not responsible for each other. Lifetimes may be different.
|
||||
|
||||
```cpp
|
||||
// declare Printable Interface
|
||||
// declare printable interface
|
||||
class printable {
|
||||
public:
|
||||
virtual void print(ostream &o) = 0;
|
||||
};
|
||||
// derived classes defines printable
|
||||
// interface
|
||||
class smiley : public printable {
|
||||
public:
|
||||
virtual void print(ostream &o) {
|
||||
o << ":)";
|
||||
};
|
||||
};
|
||||
// second derived class defines
|
||||
// printable interface
|
||||
class frown : public printable {
|
||||
public:
|
||||
virtual void print(ostream &o) {o << ":(";
|
||||
};
|
||||
};
|
||||
```
|
||||
|
||||
1. **Aggregate**
|
||||
|
||||
```cpp
|
||||
// implementation 1:
|
||||
// Aggregate relationship
|
||||
class emojis {
|
||||
printable * happy;
|
||||
printable * sad;
|
||||
public:
|
||||
emojis() {
|
||||
happy = new smiley();
|
||||
sad = new frown();
|
||||
};
|
||||
~emojis() {
|
||||
delete happy;
|
||||
delete sad;
|
||||
};
|
||||
};
|
||||
```
|
||||
|
||||
2. **Acquaintance**
|
||||
|
||||
```cpp
|
||||
// implementation 2:
|
||||
// Acquaintances only
|
||||
class emojis {
|
||||
printable * happy;
|
||||
printable * sad;
|
||||
public:
|
||||
emojis();
|
||||
~emojis();
|
||||
// dependency injection
|
||||
void setHappy(printable *);
|
||||
void setSad(printable *);
|
||||
};
|
||||
```
|
||||
256
content/CSE332S/CSE332S_L2.md
Normal file
256
content/CSE332S/CSE332S_L2.md
Normal file
@@ -0,0 +1,256 @@
|
||||
# CSE332S Lecture 2
|
||||
|
||||
Today we'll talk generally about C++ development (plus a few platform specifics):
|
||||
|
||||
- We'll develop, submit, and grade code in Windows
|
||||
- It's also helpful to become familiar with Linux
|
||||
- E.g., on shell.cec.wustl.edu
|
||||
- For example, running code through two different compilers can catch a lot more "easy to make" errors
|
||||
|
||||
Extra credit on Lab 1: compile the cpp program in Linux.
|
||||
|
||||
## Writing C++
|
||||
|
||||
Makefile ASCII text
|
||||
|
||||
C++ course files, ASCII text, end it with .cpp
|
||||
|
||||
C++ header files, ASCII text, end it with .h
|
||||
|
||||
readme, ASCII text (show what program does)
|
||||
|
||||
## Parts of a C++ Program
|
||||
|
||||
### Declarations
|
||||
|
||||
data types, function signatures, class declarations
|
||||
|
||||
- This allows the compiler to check for type safety, correct syntax, and other errors
|
||||
- Usually kept in header files (e.g., .h)
|
||||
- Included as needed by other files (to make compiler happy)
|
||||
|
||||
```cpp
|
||||
// my_class.h
|
||||
class Simple {
|
||||
public:
|
||||
Simple (int i);
|
||||
void print_i();
|
||||
private:
|
||||
int i_;
|
||||
}
|
||||
|
||||
typedef unsigned int UNIT32;
|
||||
|
||||
int usage (char * program_name);
|
||||
|
||||
struct Point2D {
|
||||
double x_;
|
||||
double y_;
|
||||
};
|
||||
```
|
||||
|
||||
### Definitions
|
||||
|
||||
Static variables initialization, function implementation
|
||||
|
||||
- The part that turns into an executable program
|
||||
- Usually kept in source files (e.g., .cpp)
|
||||
|
||||
```cpp
|
||||
// my_class.cpp
|
||||
#include "my_class.h"
|
||||
|
||||
Simple::Simple (int i) : i_(i) {}
|
||||
|
||||
void Simple::print_i() {
|
||||
std::cout << i_ << std::endl;
|
||||
}
|
||||
```
|
||||
|
||||
### Directives
|
||||
|
||||
tell complier or preprocessor what to do
|
||||
|
||||
more on this later
|
||||
|
||||
## A Very Simple C++ Program
|
||||
|
||||
```cpp
|
||||
#include <iostream> // precompiler directive
|
||||
|
||||
using namespace std; // compiler directive
|
||||
|
||||
// definition of main function
|
||||
|
||||
int main(int, char *[]) {
|
||||
cout << "Hello, World!" << endl;
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
### What is `#include <iostream>`?
|
||||
|
||||
- `#include` tells the precompiler to include a file
|
||||
- Usually, we include header files that:
|
||||
- Contain declarations of structs, classes, functions
|
||||
- Sometimes contain template _definitions_ (template not included in this course)
|
||||
- Implementation varies from compiler to compiler (advanced topic covered later)
|
||||
- `<iostream>` is the C++ standard header file for input/output streams
|
||||
|
||||
### What is `using namespace std;`?
|
||||
|
||||
- The `using` directive tells the compiler to include code from libraries that have separate namespaces
|
||||
- Similar idea to "packages" in other languages
|
||||
- C++ provides a namespace for its standard library
|
||||
- Called the "standard namespace" (written as `std`)
|
||||
- Contains `cout`, `cin`, `cerr` standard iostreams, and much more
|
||||
- Namespaces reduce collisions between symbols
|
||||
- Rely on the `::` scoping operator to match symbols to them
|
||||
- If another library with namespace `mylib` defined `cout` we could say `std::cout` vs. `mylib::cout`
|
||||
- Can also apply `using` more selectively:
|
||||
- E.g., just `using std::cout`
|
||||
|
||||
### What is `int main(int, char *[]) { ... }`?
|
||||
|
||||
- Defines the main function of any C++ program, it is the entry point of the program
|
||||
|
||||
- Who calls main?
|
||||
- The runtime environment, specifically a function often called something like `crt0` or `crtexe`
|
||||
|
||||
- What about the stuff in parentheses?
|
||||
- A list of types of the input arguments to function `main`
|
||||
- With the function name, makes up its signature
|
||||
- Since this version of `main` ignores any inputs, we leave off names of the input variables, and only give their types
|
||||
|
||||
- What about the stuff in braces?
|
||||
- It's the body of function `main`, its definition
|
||||
|
||||
### What is `cout << "Hello, World!" << endl;`?
|
||||
|
||||
- Uses the standard output iostream, named `cout`
|
||||
- For standard input, use `cin`
|
||||
- For standard error, use `cerr`
|
||||
- `<<` is an operator for inserting into the stream
|
||||
- A member operator of the `ostream` class
|
||||
- Returns a reference to stream on which it's called
|
||||
- Can be applied repeatedly to references left-to-right
|
||||
- `"hello, world!"` is a C-style string
|
||||
- A 14-position character array terminated by `'\0'`
|
||||
- `endl` is an iostream manipulator
|
||||
- Ends the line by inserting end-of-line character(s)
|
||||
- Also flushes the stream
|
||||
|
||||
### What about `return 0;`?
|
||||
|
||||
- The `main` function must return an integer value
|
||||
- By convention:
|
||||
- Return `0` to indicate successful execution
|
||||
- Return non-zero value to indicate failure
|
||||
- The program should exit gracefully through `main`'s return
|
||||
- Other ways the program can terminate abnormally:
|
||||
- Uncaught exceptions propagating out of `main`
|
||||
- Division by zero
|
||||
- Dereferencing null pointers
|
||||
- Accessing memory not owned by the program
|
||||
- Array index out of bounds
|
||||
- Dereferencing invalid/"stray" pointers
|
||||
|
||||
## A slightly more complex program
|
||||
|
||||
```cpp
|
||||
#include <iostream>
|
||||
|
||||
using namespace std;
|
||||
|
||||
int main(int argc, char *argv[]) {
|
||||
for (int i = 0; i < argc; i++) {
|
||||
cout << argv[i] << endl;
|
||||
}
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
### `int argc, char *argv[]`
|
||||
|
||||
- A way to affect the program's behavior
|
||||
- Carry parameters with which program was called
|
||||
- Passed as parameters to main from crt0
|
||||
- Passed by value (we'll discuss what that means)
|
||||
|
||||
`argc`:
|
||||
|
||||
- An integer with the number of parameters (>=1)
|
||||
|
||||
`argv`:
|
||||
|
||||
- An array of pointers to C-style character strings
|
||||
- **Its array-length is the value stored in `argc`**
|
||||
- The name of the program is kept in `argv[0]`
|
||||
|
||||
### What is `for (int i = 0; i < argc; i++) { ... }`?
|
||||
|
||||
Standard C++ for loop syntax:
|
||||
|
||||
- Consists of 3 parts:
|
||||
1. Initialization statement (executed once at start)
|
||||
2. Test expression (checked before each iteration)
|
||||
3. Increment expression (executed after each iteration)
|
||||
|
||||
Let's break down each part:
|
||||
|
||||
`int i = 0`:
|
||||
|
||||
- Declares integer variable `i` (scoped to the loop)
|
||||
- Initializes `i` to 0 (initialization, not assignment)
|
||||
|
||||
`i < argc`:
|
||||
|
||||
- Tests if we're within array bounds
|
||||
- Critical for memory safety - accessing outside array can crash program
|
||||
|
||||
`++i`:
|
||||
|
||||
- Increments array position counter
|
||||
- Uses prefix increment operator
|
||||
|
||||
## Lifecycle of a C++ Program
|
||||
|
||||
Start from the makefile
|
||||
|
||||
- The makefile is a text file that tells the compiler how to build the program, it activates the 'make' utility to build the program
|
||||
- The make file turnin/checkin to the WebCAT E-mail
|
||||
- The makefile complies the gcc compiler to compile the cpp file
|
||||
- The makefile links the object files to create the executable file
|
||||
|
||||
The cpp file
|
||||
|
||||
- The cpp file is a text file that contains the source code of the program
|
||||
- The cpp file is compiled into an object file by the gcc compiler to combined with the link produced by the makefile with the runtime/util library
|
||||
|
||||
Finally, the object file is linked with the runtime/util library to create the executable program and ready to debug with Eclipse or Visual Studio.
|
||||
|
||||
## Development Environment Studio
|
||||
|
||||
### Course Format
|
||||
|
||||
- We'll follow a similar format most days in the course:
|
||||
- Around 30 minutes of lecture and discussion
|
||||
- Then about 60 minutes of studio time
|
||||
- Except for:
|
||||
- Open studio/lab days
|
||||
- Reviews before the midterm and final
|
||||
- The day of the midterm itself
|
||||
|
||||
### Studio Guidelines
|
||||
|
||||
- Work in groups of 2 or 3
|
||||
- Exercises are posted on the course web page
|
||||
- Record your answers and email them to the course account
|
||||
- Instructors will circulate to answer questions
|
||||
|
||||
### Purpose of Studios
|
||||
|
||||
- Develop skills and understanding
|
||||
- Explore ideas you can use for labs
|
||||
- Prepare for exams which test studio material
|
||||
- Encouraged to try variations beyond exercises
|
||||
308
content/CSE332S/CSE332S_L3.md
Normal file
308
content/CSE332S/CSE332S_L3.md
Normal file
@@ -0,0 +1,308 @@
|
||||
# CSE332S Lecture 3
|
||||
|
||||
## C++ basic data types
|
||||
|
||||
- int, long, short, char (signed, integer arithmetic)
|
||||
- char is only 1 byte for all platforms
|
||||
- other types are platform dependent
|
||||
- can determine the size of the type by using `sizeof()`, `<climits> INT_MAX`
|
||||
- float, double (floating point arithmetic)
|
||||
- more expensive in space and time
|
||||
- useful when you need to describe continuous quantities
|
||||
- bool (boolean logic)
|
||||
|
||||
### User-defined types
|
||||
|
||||
- (unscoped or scoped) enum
|
||||
- maps a sequence of integer values to named constants
|
||||
- function and operators
|
||||
- function is a named sequence of statements, for example `int main()`
|
||||
- struct and class
|
||||
- similar to abstractions in cpp, extend C struct
|
||||
|
||||
### struct and class
|
||||
|
||||
- struct is public by default
|
||||
- class is private by default
|
||||
- both can have
|
||||
- member variables
|
||||
- member functions
|
||||
- constructors
|
||||
- destructors
|
||||
- common practice:
|
||||
- use struct for simple data structures
|
||||
- use class for more complex data structures with non-trivial functionality
|
||||
|
||||
```cpp
|
||||
struct My_Data{
|
||||
My_Data(int x, int y): x_(x), y_(y) {}
|
||||
int x_;
|
||||
int y_;
|
||||
};
|
||||
```
|
||||
|
||||
```cpp
|
||||
class My_Data{
|
||||
public:
|
||||
My_Object(int x, int y): x_(x), y_(y) {}
|
||||
~My_Object(){}
|
||||
private:
|
||||
int x_;
|
||||
int y_;
|
||||
};
|
||||
```
|
||||
|
||||
### More about native and user-defined types
|
||||
|
||||
- Pointer
|
||||
- raw memory address of an object
|
||||
- its type constrains what types it can point to
|
||||
- can take on a value of 0 (null pointer)
|
||||
- Reference
|
||||
- alias for an existing object
|
||||
- its type constrains what types it can refer to
|
||||
- cannot take on a value of 0 (**always** refer to a valid object)
|
||||
- Mutable (default) vs. const types (read right to left)
|
||||
- `const int x;` is a read-only variable
|
||||
- `int j` is a read-write declaration
|
||||
|
||||
## Scopes
|
||||
|
||||
Each variable is associated with a scope, which is a region of the program where the variable is valid
|
||||
|
||||
- the entire program is a global scope
|
||||
- a namespace is a scope
|
||||
- member of a class is a scope
|
||||
- a function is a scope
|
||||
- a block is a scope
|
||||
|
||||
```cpp
|
||||
int g_x; // global scope
|
||||
namespace my_namespace{
|
||||
int n_x; // namespace scope
|
||||
}
|
||||
class My_Class{
|
||||
int c_x; // class scope
|
||||
int my_function(){
|
||||
int f_x; // function scope
|
||||
{
|
||||
int b_x; // block scope
|
||||
}
|
||||
return 0;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
A symbol is only visible within its scope
|
||||
|
||||
- helps hide unneeded details (abstraction)
|
||||
- helps avoid name collisions (encapsulation)
|
||||
|
||||
## Motivation for pointer and reference
|
||||
|
||||
We often need to _refer_ to an object, but don't want to copy it
|
||||
|
||||
There are two common ways to do this:
|
||||
|
||||
- Indirectly, via a pointer
|
||||
- This gives the address of the object
|
||||
- Requires the code to do extra work. eg, dereferencing
|
||||
- Like going to the address of the object
|
||||
- Directly, via a reference
|
||||
- Acts as an alias for the object
|
||||
- Code interacts with reference as if it were the object itself
|
||||
|
||||
## Pointer and reference syntax
|
||||
|
||||
### Pointer
|
||||
|
||||
A pointer is a variable that holds the address of an object
|
||||
|
||||
can be untyped. eg, `void *p;`
|
||||
|
||||
usually typed. eg, `int *p;` so that it can be checked by the compiler
|
||||
|
||||
If typed, the type constrains what it can point to, a int pointer can only point to an int. `int *p;`
|
||||
|
||||
A pointer can be null, eg, `int *p = nullptr;`
|
||||
|
||||
We can change to what it points to, eg, `p = &x;`
|
||||
|
||||
### Reference
|
||||
|
||||
A reference is an alias for an existing object, also holds the address of the object, but is only created on compile time.
|
||||
|
||||
Usually with nicer interface than pointers.
|
||||
|
||||
Must be typed, and its type constrains what types it can refer to. `int &r;`
|
||||
|
||||
Always refers to a valid object, so cannot be null. `int &r = nullptr;` is invalid.
|
||||
|
||||
Note: **reference cannot be reassigned to refer to a different object.**
|
||||
|
||||
|symbol|used in declaration|used in definition|
|
||||
|---|---|---|
|
||||
|unary `&`|reference, eg, `int &r;`|address-of, eg, `int &r = &x;`|
|
||||
|unary `*`|pointer, eg, `int *p;`|dereference, eg, `int *p = *q;`|
|
||||
|`->`|member access, eg, `p->x;`|member access via pointer, eg, `p->second;`|
|
||||
|`.`|member access, eg, `p.x;`|member access via reference, eg, `p.second;`|
|
||||
|
||||
## Aliasing via pointers and references
|
||||
|
||||
### Aliasing via reference
|
||||
|
||||
Example:
|
||||
|
||||
```cpp
|
||||
int main(int argc, char *argv[]){
|
||||
int i=0;
|
||||
int j=1;
|
||||
int &r = i;
|
||||
int &s = i;
|
||||
r = 8; // do not need to dereference r, just use it as an alias for i
|
||||
cout << "i: " << i << ", j: " << j << ", r: " << r << ", s: " << s << endl;
|
||||
// should print: i: 8, j: 1, r: 8, s: 8
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
### Aliasing via pointer
|
||||
|
||||
Example:
|
||||
|
||||
```cpp
|
||||
int main(int argc, char *argv[]){
|
||||
int i=0;
|
||||
int j=1;
|
||||
int *p = &i;
|
||||
int *q = &i;
|
||||
*q = 6; // need to dereference q to access the value of j
|
||||
cout << "i: " << i << ", j: " << j << ", p: " << *p << ", q: " << *q << endl;
|
||||
// should print: i: 6, j: 1, p: 6, q: 6
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
### Reference to Pointer
|
||||
|
||||
Example:
|
||||
|
||||
```cpp
|
||||
int main(int argc, char *argv[]){
|
||||
int j = 1;
|
||||
int &r = j; // r is a **reference** to j
|
||||
int *p = &r; // p is a **pointer** to the address of r, here & is the address-of operator, which returns the address of the object
|
||||
int * &t = p; // t is a **reference** to pointer p, here & is the reference operator, which returns the reference of the object.
|
||||
cout << "j: " << j << ", r: " << r << ", p: " << *p << ", t: " << *t << endl;
|
||||
// should print: j: 1, r: 1, p: 1, t: [address of p]
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
Notice that we cannot have a pointer to a reference. But we can have a reference to a pointer.
|
||||
|
||||
### Reference to Constant
|
||||
|
||||
Example:
|
||||
|
||||
```cpp
|
||||
int main(int argc, char *argv[]){
|
||||
const int i = 0;
|
||||
int j = 1;
|
||||
int &r = j; // r cannot refer to i, because i is a constant (if true, alter i through r should be valid)
|
||||
const int &s=i; // s can refer to i, because s is a constant reference (we don't reassign s)
|
||||
const int &t=j; // t can refer to j, because t is a constant reference (we don't reassign t)
|
||||
cout << "i: " << i << ", j: " << j << ", r: " << r << ", s: " << s << ", t: " << t << endl;
|
||||
// should print: i: 0, j: 1, r: 1, s: 0
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
Notice that we cannot have a non-constant reference to a constant object. But we can have a constant reference to a non-constant object.
|
||||
|
||||
### Pointer to Constant
|
||||
|
||||
Example:
|
||||
|
||||
```cpp
|
||||
int main(int argc, char *argv[]){
|
||||
const int i = 0;
|
||||
int j = 1;
|
||||
int k = 2;
|
||||
|
||||
// pointer to int
|
||||
int *w = &j;
|
||||
|
||||
// const pointer to int
|
||||
int *const x = &j;
|
||||
|
||||
// pointer to const int
|
||||
const int *y = &i;
|
||||
|
||||
// const pointer to const int, notice that we cannot change the value of the int that z is pointing to, in this case j **via pointer z**, nor the address that z is pointing to. But we can change the value of j via pointer w or j itself.
|
||||
const int *const z = &j;
|
||||
}
|
||||
```
|
||||
|
||||
- Read declaration from right to left, eg, `int *w = &j;` means `w` is a pointer to an `int` that is the address of `j`.
|
||||
- Make promises via the `const` keyword, two options:
|
||||
- `const int *p;` means `p` is a pointer to a constant `int`, so we cannot change the value of the `int` that `p` is pointing to, but we can change the address that `p` is pointing to.
|
||||
- `int *const p;` means `p` is a constant pointer to an `int`, so we cannot change the address that `p` is pointing to, but we can change the value of the `int` that `p` is pointing to.
|
||||
- A pointer to non-constant cannot point to a const variable.
|
||||
- neither `w = &i;` nor `x = &i;` is valid.
|
||||
- any of the pointer can points to `j`.
|
||||
|
||||
## Pass by value, pass by reference, and type inference
|
||||
|
||||
Example:
|
||||
|
||||
```cpp
|
||||
int main(int argc, char *argv[]){
|
||||
int h = -1;
|
||||
int i = 0;
|
||||
int j = 1;
|
||||
int k = 2;
|
||||
return func(h, i, j, &k);
|
||||
}
|
||||
|
||||
int func(int a, const int &b, int &c, int *d){
|
||||
++a; // [int] pass by value, a is a copy of h, so a is not the same as h
|
||||
c = b; // [int &] pass by reference, c is an alias for j, the value of c is the same as the value of b (or i), but we cannot change the value of b (or i) through c (const int &b)
|
||||
*d = a; // [int *] pass by value, d is a pointer to k, so *d is the value of k, a is assigned to value of k.
|
||||
++d; // d is a pointer to k, but pass by value, so ++d doesn't change the value of k.
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
### More type declaration keywords
|
||||
|
||||
`typedef` keyword introduces a "type alias" for a type.
|
||||
|
||||
```cpp
|
||||
typedef Foo * Foo_ptr; // Foo_ptr is a type alias for Foo *
|
||||
|
||||
// the following two variables are of the same type
|
||||
Foo_ptr p1 = 0;
|
||||
Foo *p2 = 0;
|
||||
```
|
||||
|
||||
`auto` keyword allows the compiler to deduce the type of a variable from the initializer.
|
||||
|
||||
```cpp
|
||||
int x = 0; // x is of type int
|
||||
float y = 1.0; // y is of type float
|
||||
auto z = x + y; // z is of type float, with initialized value 1.0
|
||||
```
|
||||
|
||||
`decltype` keyword allows the compiler to deduce the type of a variable from the type of an expression.
|
||||
|
||||
```cpp
|
||||
int x = 0;
|
||||
double y = 0.0;
|
||||
float z = 0.0f;
|
||||
|
||||
decltype(x) a; // a is of type int, value is not initialized
|
||||
decltype(y) b; // b is of type double, value is not initialized
|
||||
decltype(z) c; // c is of type float, value is not initialized
|
||||
```
|
||||
|
||||
478
content/CSE332S/CSE332S_L4.md
Normal file
478
content/CSE332S/CSE332S_L4.md
Normal file
@@ -0,0 +1,478 @@
|
||||
# CSE332S Lecture 4
|
||||
|
||||
## Namespace details
|
||||
|
||||
### Motivation
|
||||
|
||||
Classes encapsulate behavior (methods) and state (member data) behind an interface.
|
||||
|
||||
Structs are similar, but with state accessible.
|
||||
|
||||
Classes and structs are used to specify self contained, cohesive abstractions.
|
||||
|
||||
- Can say what class/struct does in one sentence.
|
||||
|
||||
What if we want to describe more loosely related collections of state and behavior?
|
||||
|
||||
Could use a class or struct
|
||||
|
||||
- But that dilutes their design intent.
|
||||
|
||||
### Namespace
|
||||
|
||||
Cpp offers an appropriate scoping mechanism for **loosely related** aggregates: Namespaces.
|
||||
|
||||
- Good for large function collections.
|
||||
- E.g. a set of related algorithms and function objects
|
||||
- Good for general purpose collections
|
||||
- E.g. program utilities, performance statistics, etc.
|
||||
|
||||
Declarative region
|
||||
|
||||
- Where a variable/function can be used
|
||||
- From where declared to end of declarative region
|
||||
|
||||
### Namespace Properties
|
||||
|
||||
Declared/(re)opend with `namespace` keyword.
|
||||
|
||||
- `namespace name { ... }`
|
||||
- `namespace name = namespace existing_name { ... };`
|
||||
|
||||
Access members using scoping `operator::`
|
||||
|
||||
- `std::cout << "Hello, World!" << std::endl;`
|
||||
|
||||
Everything not declared in another namespace is in the global namespace.
|
||||
|
||||
Can nest namespace declarations
|
||||
|
||||
- `namespace outer { namespace inner { ... } }`
|
||||
|
||||
### Using Namespaces
|
||||
|
||||
The `using` keyword make elements visible.
|
||||
|
||||
- Only apples to the current scope.
|
||||
|
||||
Can add entire name space to the current scope
|
||||
|
||||
- `using namespace std;`
|
||||
- `cout << "Hello, World!" << endl;`
|
||||
|
||||
Can also declare unnamed namespaces
|
||||
|
||||
- Elements are visible after the declaration
|
||||
- `namespace { int i = 42; }` will make `i` visible in the current file.
|
||||
|
||||
## C-style vs. C++ strings
|
||||
|
||||
### C++ string class
|
||||
|
||||
```cpp
|
||||
#include <iostream>
|
||||
#include <string>
|
||||
|
||||
using namespace std;
|
||||
|
||||
int main (int argc, char *argv[]) {
|
||||
string s = "Hello,";
|
||||
s += " World!";
|
||||
cout << s << endl; // prints "Hello, World!"
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
- Using `<string>` header
|
||||
- Various constructions
|
||||
- Assignment operator
|
||||
- Overloaded operators
|
||||
- Indexing operator, we can index cpp strings like arrays, `s[i]`
|
||||
### C-style strings
|
||||
|
||||
```cpp
|
||||
#include <iostream>
|
||||
#include <cstring>
|
||||
|
||||
using namespace std;
|
||||
|
||||
int main (int argc, char *argv[]) {
|
||||
char *h = "Hello, ";
|
||||
string sh = "Hello, ";
|
||||
char *w = "World!";
|
||||
string sw = "World!";
|
||||
cout << (h < w) << endl; // this returns 0 because we are comparing pointers
|
||||
cout << (sh < sw) << endl; // this returns 1 because we are comparing values of strings in alphabetical order
|
||||
h += w; // this operation is illegal because we are trying to add a pointer to a pointer
|
||||
sh += sw; // concatenates the strings
|
||||
cout << h << endl; // this prints char repeatedly till the termination char
|
||||
cout << sh << endl; // this prints the string
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
- C-style strings continguous arrays of char
|
||||
- Often accessed as `char *` by pointer.
|
||||
- Cpp string class provides a rich set of operations.
|
||||
- Cpp strings do "what you expected" as a programmer.
|
||||
- C-style strings do "what you expected" as a machine designer.
|
||||
|
||||
Use cpp strings for most string operations.
|
||||
|
||||
## Cpp native array
|
||||
|
||||
### Storing Other Data Types Besides `char`
|
||||
|
||||
There are many options to store non-char data in an array.
|
||||
|
||||
Native C-style arrays
|
||||
|
||||
- Cannot add or remove positions
|
||||
- Can index positions directly (constant time)
|
||||
- Not necessary zero-terminated (no null terminator as ending)
|
||||
|
||||
STL list container (bi-linked list)
|
||||
|
||||
- Add/remove position on either end
|
||||
- Cannot index positions directly
|
||||
|
||||
STL vector container ("back stack")
|
||||
|
||||
- Can add/remove position at the back
|
||||
- Can index positions directly
|
||||
|
||||
### Pointer and Arrays
|
||||
|
||||
```cpp
|
||||
#include <iostream>
|
||||
|
||||
using namespace std;
|
||||
|
||||
int main (int argc, char *argv[]) {
|
||||
int a[10];
|
||||
int *p = &a[0];
|
||||
int *q = a;
|
||||
// p and q are pointing to the same location
|
||||
++q; // q is now pointing to the second element of the array
|
||||
}
|
||||
```
|
||||
|
||||
An array holds a contiguous sequence of memory locations
|
||||
|
||||
- Can refer to locations using either array index or pointer location
|
||||
- `int a[0]` vs `int *p`
|
||||
- `a[i]` vs `*(a + i)`
|
||||
|
||||
Array variable essentially behaves like a const pointer
|
||||
|
||||
- Like `int * const arr;`
|
||||
- Cannot change where it points
|
||||
- Can change locations unless declared as const, eg `const int arr[10];`
|
||||
|
||||
Can initalize other pointers to the start of the array
|
||||
|
||||
- Using array name
|
||||
- `int *p = a;`
|
||||
- `int *p = &a[0];`
|
||||
|
||||
Adding or subtracting int pointer n moves a pointer by n of the type it points to
|
||||
|
||||
- `int *p = a;`
|
||||
- `p += 1;` moves pointer by 1 `sizeof(int)`
|
||||
- `p -= 1;` moves pointer by 1 `sizeof(int)`
|
||||
|
||||
Remember that cpp only guarantees `sizeof(char)` is 1.
|
||||
|
||||
### Array of (and Pointers to) Pointers
|
||||
|
||||
```cpp
|
||||
#include <iostream>
|
||||
|
||||
using namespace std;
|
||||
|
||||
int main (int argc, char *argv[]) {
|
||||
// could declare char ** argv
|
||||
for (int i = 0; i < argc; i++) {
|
||||
cout << argv[i] << endl;
|
||||
}
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
Can have array of pointers to pointers
|
||||
|
||||
Can also have an array of pointers to arrays
|
||||
|
||||
- `int (*a)[10];`
|
||||
- `a[0]` is an array of 10 ints
|
||||
- `a[0][0]` is the first int in the first array
|
||||
|
||||
### Rules for pointer arithmetic
|
||||
|
||||
```cpp
|
||||
#include <iostream>
|
||||
|
||||
using namespace std;
|
||||
|
||||
int main (int argc, char *argv[]) {
|
||||
int a[10];
|
||||
int *p = &a[0];
|
||||
int *q = p + 1;
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
You can subtract pointers to get the number of elements between them (no addition, multiplication, or division)
|
||||
|
||||
- `int n = q - p;`
|
||||
- `n` is the number of elements between `p` and `q`
|
||||
|
||||
You can add/subtract an integer to a pointer to get a new pointer
|
||||
|
||||
- `int *p2 = p + 1;`
|
||||
- `p2` is a pointer to the second element of the array
|
||||
- `p+(q-p)/2` is allowed but not `(p+q)/2`
|
||||
|
||||
Array and pointer arithmetic: Given a pointer `p` and integer `n`, `p[n]` is equivalent to `*(p+n)`.
|
||||
|
||||
Dereferencing a 0 pointer is undefined behavior.
|
||||
|
||||
Accessing memory outside of an array may
|
||||
|
||||
- Crash the program
|
||||
- Let you read/write memory you shouldn't (hard to debug)
|
||||
|
||||
Watch out for:
|
||||
|
||||
- Uninitialized pointers
|
||||
- Failing to check for null pointers
|
||||
- Accessing memory outside of an array
|
||||
- Error in loop initialization, termination, or increment
|
||||
|
||||
### Dynamic Memory Allocation
|
||||
|
||||
Aray can be allocated, and deallocated dynamically
|
||||
|
||||
Arrays have particular syntax for dynamic allocation
|
||||
|
||||
Don't leak, destroy safely.
|
||||
|
||||
```cpp
|
||||
Foo * baz (){
|
||||
// note the array form of new
|
||||
int * const a = new int[3];
|
||||
a[0] = 1; a[1] = 2; a[2] = 3;
|
||||
Foo *f = new Foo;
|
||||
f->reset(a);
|
||||
return f;
|
||||
}
|
||||
|
||||
void Foo::reset(int *a) {
|
||||
// ctor must initialize to 0
|
||||
delete [] this->array_ptr;
|
||||
this->array_ptr = a;
|
||||
}
|
||||
|
||||
void Foo::~Foo() {
|
||||
// note the array form of delete
|
||||
delete [] this->array_ptr;
|
||||
}
|
||||
```
|
||||
|
||||
## Vectors
|
||||
|
||||
```cpp
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
|
||||
using namespace std;
|
||||
|
||||
int main (int argc, char *argv[]) {
|
||||
vector<int> v;
|
||||
v.push_back(1);
|
||||
v.push_back(2);
|
||||
v.push_back(3);
|
||||
// note that size_t is an unsigned type that is guaranteed to be large enough to hold the size of v.size(), determined by the compiler.
|
||||
for (size_t i = 0; i < v.size(); i++) {
|
||||
cout << v[i] << endl;
|
||||
}
|
||||
// this will print 1, 2, 3
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
### Motivation to use vectors
|
||||
|
||||
Vector do a lot of (often tricky) dynamic memory management.
|
||||
|
||||
- use new[] and delete[] internally
|
||||
- resize, don't leak memory
|
||||
|
||||
Easier to pass to functions
|
||||
|
||||
- can tell you their size by `size()`
|
||||
- Don't have to pass a separate size argument
|
||||
- Don't need a pointer by reference in order to resize
|
||||
|
||||
Still have to pay attention
|
||||
|
||||
- `push_back` allocates more memory but `[]` does not
|
||||
- vectors copy and take ownership of elements
|
||||
|
||||
## IO classes
|
||||
|
||||
```cpp
|
||||
#include <iostream>
|
||||
|
||||
using namespace std;
|
||||
|
||||
int main (int argc, char *argv[]) {
|
||||
int i;
|
||||
// cout == std::ostream
|
||||
cout << "Enter an integer: ";
|
||||
// cin == std::istream
|
||||
cin >> i;
|
||||
cout << "You entered: " << i << endl;
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
`<iostream>` provides classes for input and output.
|
||||
|
||||
- Use `<istream>` for input
|
||||
- Use `<ostream>` for output
|
||||
|
||||
Overloaded operators
|
||||
|
||||
- `<<` for insertion
|
||||
- `>>` for extraction (terminates on whitespace)
|
||||
|
||||
Other methods
|
||||
|
||||
- `ostream`
|
||||
- `write`
|
||||
- `put`
|
||||
- `istream`
|
||||
- `get`
|
||||
- `eof`
|
||||
- `good`
|
||||
- `clear`
|
||||
|
||||
Stream manipulators
|
||||
|
||||
- `ostream`: `flush`, `endl`, `setwidth`, `setprecision`, `hex`, `boolalpha` (boolalpha is a manipulator that changes the way bools are printed from 0/1 to true/false).
|
||||
|
||||
### File I/O
|
||||
|
||||
```cpp
|
||||
#include <iostream>
|
||||
#include <fstream>
|
||||
|
||||
using namespace std;
|
||||
|
||||
int main (int argc, char *argv[]) {
|
||||
ifstream ifs;
|
||||
ifs.open("input.txt", ios::in);
|
||||
ofstream ofs ("output.txt", ios::out);
|
||||
if (!ifs.is_open() && ofs.is_open()) {
|
||||
int i;
|
||||
ifs >> i;
|
||||
ofs << i;
|
||||
}
|
||||
ifs.close();
|
||||
ofs.close();
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
`<fstream>` provides classes for file input and output.
|
||||
|
||||
- Use `<ifstream>` for input
|
||||
- Use `<ofstream>` for output
|
||||
|
||||
Other methods
|
||||
|
||||
- `open`
|
||||
- `close`
|
||||
- `is_open`
|
||||
- `getline` parses a line from the file, defaults to whitespace
|
||||
- `seekg`
|
||||
- `seekp`
|
||||
|
||||
File modes:
|
||||
|
||||
- `in` let you read from the file
|
||||
- `out` let you write to the file
|
||||
- `ate` let you write to the end of the file
|
||||
- `app` let you write to the end of the file
|
||||
- `trunc` let you truncate the file
|
||||
- `binary` let you read/write binary data
|
||||
|
||||
### String Streams Classes
|
||||
|
||||
```cpp
|
||||
#include <iostream>
|
||||
#include <fstream>
|
||||
#include <sstream>
|
||||
|
||||
using namespace std;
|
||||
|
||||
int main (int argc, char *argv[]) {
|
||||
ifstream ifs("input.txt", ios::in);
|
||||
if (!ifs.is_open()) {
|
||||
string line_1, word_1;
|
||||
getline(ifs, line_1);
|
||||
istringstream iss(line_1);
|
||||
iss >> word_1;
|
||||
cout << word_1 << endl;
|
||||
}
|
||||
ifs.close();
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
`<sstream>` provides classes for string streams.
|
||||
|
||||
- Use `<istringstream>` for input
|
||||
- Use `<ostringstream>` for output
|
||||
|
||||
Useful for scanning input
|
||||
|
||||
- Get a line form file into a string
|
||||
- Wrap a string into a stream
|
||||
- Pull words off the stream
|
||||
|
||||
```cpp
|
||||
#include <iostream>
|
||||
#include <sstream>
|
||||
|
||||
using namespace std;
|
||||
|
||||
int main (int argc, char *argv[]) {
|
||||
if (argc < 3) return 1;
|
||||
ostringstream argsout;
|
||||
argsout << argv[1] << " " << argv[2] << endl;
|
||||
istringstream argsin(argsout.str());
|
||||
float f,g;
|
||||
argsin >> f;
|
||||
argsin >> g;
|
||||
cout << f << "/" << g << "is" << f/g << endl;
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
Useful for formatting output
|
||||
|
||||
- Using string as format buffer
|
||||
- Wrapping a string into a stream
|
||||
- Push formatted values into the stream
|
||||
- Output the stream to file
|
||||
|
||||
Program gets arguments as C-style strings
|
||||
|
||||
Formatting is tedious and error prone in C-style strings (`sprintf`, etc.)
|
||||
|
||||
`iostream` formatting is friendly.
|
||||
|
||||
|
||||
|
||||
226
content/CSE332S/CSE332S_L5.md
Normal file
226
content/CSE332S/CSE332S_L5.md
Normal file
@@ -0,0 +1,226 @@
|
||||
# CSE332S Lecture 5
|
||||
|
||||
## Function and the Call Stack
|
||||
|
||||
### Function lifecycle
|
||||
|
||||
Read variable declaration from right to left
|
||||
|
||||
eg:
|
||||
|
||||
```c
|
||||
int i; // i is a integer variable
|
||||
int & r = i; // r is a reference to i
|
||||
int *p = &i; // p is a pointer to i
|
||||
const int * const q = &i; // q is a constant pointer to a constant integer
|
||||
```
|
||||
|
||||
Read function declaration from inside out
|
||||
|
||||
eg:
|
||||
|
||||
```c
|
||||
int f(int x); // f is a function that takes an integer argument and returns an integer
|
||||
```
|
||||
|
||||
Cpp use the "**program call stack**" to manage active function invocations
|
||||
|
||||
When a function is called:
|
||||
|
||||
1. A stack frame is "**pushed**" onto the call stack
|
||||
2. Execution jumps fro the calling functio's code block to the called function's code block
|
||||
|
||||
Then the function is executed the return value is pushed onto the stack
|
||||
|
||||
When a function returns:
|
||||
|
||||
1. The stack frame is "**popped**" off the call stack
|
||||
2. Execution jumps back to the calling function's code block
|
||||
|
||||
The compiler manages the program call stack
|
||||
|
||||
- Small performance overhead associated with stack frame management
|
||||
- Size of a stack frame must be known at compile time - cannot allocate dynamically sized objects on the stack
|
||||
|
||||
#### Stack frame
|
||||
|
||||
A stack frame represents the state of an active function call
|
||||
|
||||
Each frame contains:
|
||||
|
||||
- **Automatic variables** - variables local to the function. (automatic created and destroyed when the function is called and returns)
|
||||
- **Parameters** - values passed to the function
|
||||
- **A previous frame pointer** - used to access the caller's frame
|
||||
- **Return address** - the address of the instruction to execute after the function returns
|
||||
|
||||
### Recursion for free
|
||||
|
||||
An example of call stack:
|
||||
|
||||
```cpp
|
||||
void f(int x) {
|
||||
int y = x + 1;
|
||||
}
|
||||
void main(int argc, char *argv[]) {
|
||||
int z = 1;
|
||||
f(z);
|
||||
}
|
||||
```
|
||||
|
||||
when f is called, a stack frame is pushed onto the call stack:
|
||||
|
||||
- function `f`
|
||||
- parameter `x`
|
||||
- return address
|
||||
- function `main`
|
||||
- parameter `argc`
|
||||
- parameter `argv`
|
||||
- return address
|
||||
|
||||
On recursion, the call stack grows for each recursive call, and shrinks when each recursive call returns.
|
||||
|
||||
```cpp
|
||||
void f(int x) {
|
||||
if (x > 0) {
|
||||
f(x - 1);
|
||||
}
|
||||
}
|
||||
int main(int argc, char *argv[]) {
|
||||
f(10);
|
||||
}
|
||||
```
|
||||
|
||||
The function stack will look like this:
|
||||
|
||||
- function `f(0)`
|
||||
- parameter `x`
|
||||
- return address
|
||||
- function `f(1)`
|
||||
- parameter `x`
|
||||
- return address
|
||||
- ...
|
||||
- function `f(10)`
|
||||
- parameter `x`
|
||||
- return address
|
||||
- function `main`
|
||||
- parameter `argc`
|
||||
- parameter `argv`
|
||||
- return address
|
||||
|
||||
### Pass by reference and pass by value
|
||||
|
||||
However, when we call recursion with pass by reference.
|
||||
|
||||
```cpp
|
||||
void f(int & x) {
|
||||
if (x > 0) {
|
||||
f(x - 1);
|
||||
}
|
||||
}
|
||||
int main(int argc, char *argv[]) {
|
||||
int z = f(10);
|
||||
}
|
||||
```
|
||||
|
||||
The function stack will look like this:
|
||||
|
||||
- function `f(0)`
|
||||
- return address
|
||||
- function `f(1)`
|
||||
- return address
|
||||
- ...
|
||||
- function `f(10)`
|
||||
- return address
|
||||
- function `main`
|
||||
- parameter `z`
|
||||
- parameter `argc`
|
||||
- parameter `argv`
|
||||
- return address
|
||||
|
||||
This is because the reference is a pointer to the variable, so the function can modify the variable directly without creating a new variable.
|
||||
|
||||
### Function overloading and overload resolution
|
||||
|
||||
Function overloading is a feature that allows a function to have multiple definitions with the same name but **different parameters**.
|
||||
|
||||
Example:
|
||||
|
||||
```cpp
|
||||
void errMsg(int &x){
|
||||
cout << "Error with code: " << x << endl;
|
||||
}
|
||||
void errMsg(const int &x){
|
||||
cout << "Error with code: " << x << endl;
|
||||
}
|
||||
void errMsg(const string &x){
|
||||
cout << "Error with message: " << x << endl;
|
||||
}
|
||||
void errMsg(const int &x, const string &y){
|
||||
cout << "Error with code: " << x << " and message: " << y << endl;
|
||||
}
|
||||
int main(int argc, char *argv[]){
|
||||
int x = 10;
|
||||
const int y = 10;
|
||||
string z = "File not found";
|
||||
errMsg(x); // this is the first function (best match: int to int)
|
||||
errMsg(y); // this is the second function (best match: const int to const int)
|
||||
errMsg(z); // this is the third function (best match: string to const string)
|
||||
errMsg(x, z); // this is the fourth function (best match: int to const int, string to const string)
|
||||
}
|
||||
```
|
||||
|
||||
When the function is called, the compiler will automatically determine which function to use based on the arguments passed to the function.
|
||||
|
||||
BUT, there is still ambiguity when the function is called with the same type of arguments.
|
||||
|
||||
```cpp
|
||||
void errMsg(int &x);
|
||||
void errMsg(short &x);
|
||||
int main(int argc, char *argv[]){
|
||||
char x = 'a';
|
||||
errMsg(x); // this is ambiguous, cpp don't know which function to use since char can both be converted to int and short. This will throw an error.
|
||||
}
|
||||
```
|
||||
|
||||
#### Default arguments
|
||||
|
||||
Default arguments are arguments that are provided by the function caller, but if the caller does not provide a value for the argument, the function will use the default value.
|
||||
|
||||
```cpp
|
||||
void errMsg(int x = 0, string y = "Unknown error");
|
||||
```
|
||||
|
||||
If the caller does not provide a value for the argument, the function will use the default value.
|
||||
|
||||
```cpp
|
||||
errMsg(); // this will use the default value for both arguments
|
||||
errMsg(10); // this will use the default value for the second argument
|
||||
errMsg(10, "File not found"); // this will use the provided value for both arguments
|
||||
```
|
||||
|
||||
Overloading and default arguments
|
||||
|
||||
```cpp
|
||||
void errMsg(int x = 0, string y = "Unknown error");
|
||||
void errMsg(int x);
|
||||
```
|
||||
|
||||
This is ambiguous, because the compiler don't know which function to use. This will throw an error.
|
||||
|
||||
We can only default the rightmost arguments
|
||||
|
||||
```cpp
|
||||
void errMsg(int x = 0, string y = "Unknown error");
|
||||
void errMsg(int x, string y = "Unknown error"); // this is valid
|
||||
void errMsg(int x = 0, string y); // this is invalid
|
||||
```
|
||||
|
||||
Caller must supply leftmost arguments first, even they are same as default arguments
|
||||
|
||||
```cpp
|
||||
void errMsg(int x = 0, string y = "Unknown error");
|
||||
int main(int argc, char *argv[]){
|
||||
errMsg("File not found"); // this will throw an error, you need to provide the first argument
|
||||
errMsg(10, "File not found"); // this is valid
|
||||
}
|
||||
```
|
||||
231
content/CSE332S/CSE332S_L6.md
Normal file
231
content/CSE332S/CSE332S_L6.md
Normal file
@@ -0,0 +1,231 @@
|
||||
# CSE332S Lecture 6
|
||||
|
||||
## Expressions
|
||||
|
||||
### Expressions: Operators and Operands
|
||||
|
||||
- **Operators** obey arity, associativity, and precedence
|
||||
```cpp
|
||||
int result = 2 * 3 + 5; // assigns 11
|
||||
```
|
||||
- Operators are often overloaded for different types
|
||||
```cpp
|
||||
string name = first + last; // concatenation
|
||||
```
|
||||
- An **lvalue** gives a **location**; an **rvalue** gives a **value**
|
||||
- Left hand side of an assignment must be an lvalue
|
||||
- Prefix increment and decrement take and produce lvalues (e.g., `++a` and `--a`)
|
||||
- Postfix versions (e.g., `a++` and `a--`) take lvalues, produce rvalues
|
||||
- Beware accidentally using the “future equivalence” operator, e.g.,
|
||||
```cpp
|
||||
if (i = j) // instead of if (i == j)
|
||||
```
|
||||
- Avoid type conversions if you can, and only use **named** casts (if you must explicitly convert types)
|
||||
|
||||
When compiling an expression, the compiler uses the precedence of the operators to determine which subexpression to execute first. Operator precedence defines the order in which different operators in an expression are evaluated.
|
||||
|
||||
### Expressions are essentially function calls
|
||||
|
||||
```cpp
|
||||
int main(int argc, char *argv[]){
|
||||
string h="hello";
|
||||
string w="world";
|
||||
h=h+w;
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
Compiler will generate a function call for each expression.
|
||||
|
||||
The function name is `operator+` for the `+` operator.
|
||||
|
||||
```cpp
|
||||
string operator+(const string & a, const string & b){
|
||||
// implementation ignored.
|
||||
}
|
||||
```
|
||||
|
||||
### Initialization vs. Assignment
|
||||
|
||||
`=` has dual meaning
|
||||
|
||||
When used in declaration, it is an **initializer** (constructor is called)
|
||||
|
||||
```cpp
|
||||
int a = 1;
|
||||
```
|
||||
|
||||
When used in assignment, it is an **assignment**
|
||||
|
||||
```cpp
|
||||
a = 2;
|
||||
```
|
||||
|
||||
## Statements and exceptions
|
||||
|
||||
In C++, **statements** are the basic units of execution.
|
||||
|
||||
- Each statement ends with a semicolon (`;`) and can use expressions to compute values.
|
||||
- Statements introduce scopes, such as those for temporary variables.
|
||||
|
||||
A useful statement usually has a **side effect**:
|
||||
|
||||
- Stores a value for future use, e.g., `j = i + 5;`
|
||||
- Performs input or output, e.g., `cout << j << endl;`
|
||||
- Directs control flow, e.g., `if (j > 0) { ... } else { ... }`
|
||||
- Interrupts control flow, e.g., `throw out_of_range;`
|
||||
- Resumes control flow, e.g., `catch (RangeError &re) { ... }`
|
||||
|
||||
The `goto` statement is considered too low-level and is usually better replaced by `break` or `continue`.
|
||||
|
||||
- If you must use `goto`, you should comment on why it is necessary.
|
||||
|
||||
### Motivation for exceptions statements
|
||||
|
||||
Need to handle cases where program cannot behave normally
|
||||
|
||||
- E.g., zero denominator for division
|
||||
|
||||
Otherwise bad things happen
|
||||
|
||||
- Program crashes
|
||||
- Wrong results
|
||||
|
||||
Could set value to `Number::NaN`
|
||||
|
||||
- I.e., a special “not-a-number” value
|
||||
- Must avoid using a valid value…
|
||||
… which may be difficult (e.g., for int)
|
||||
- Anyway, caller might fail to check for it
|
||||
|
||||
Exceptions offer a better alternative
|
||||
|
||||
```cpp
|
||||
void Number::operator/(const Number & n){
|
||||
if (n.value == 0) throw DivisionByZero();
|
||||
// implementation ignored.
|
||||
return *this / n.value;
|
||||
}
|
||||
```
|
||||
|
||||
### Exceptions: Throw Statement Syntax
|
||||
|
||||
- Can throw any object
|
||||
- Can catch, inspect, user, refine, rethrow exceptions
|
||||
- By value makes local copy
|
||||
- By reference allows modification to be made to the original exception
|
||||
- Default catch block is indicated by `...`
|
||||
|
||||
```cpp
|
||||
void f(){
|
||||
throw 1;
|
||||
}
|
||||
|
||||
int main(int argc, char *argv[]){
|
||||
try{
|
||||
f();
|
||||
}
|
||||
catch (int &e){
|
||||
cout << "caught an exception: " << e << endl;
|
||||
}
|
||||
catch (...){
|
||||
cout << "caught an non int exception" << endl;
|
||||
}
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
### C++ 11: Library Exception Hierarchy
|
||||
|
||||
- **C++11 standardizes a hierarchy of exception classes**
|
||||
- To access these classes `#include <stdexcept>`
|
||||
- **Two main kinds (subclasses) of `exception`**
|
||||
- Run time errors (overflow errors and underflow errors)
|
||||
- Logic errors (invalid arguments, length error, out of range)
|
||||
- **Several other useful subclasses of `exception`**
|
||||
- Bad memory allocation
|
||||
- Bad cast
|
||||
- Bad type id
|
||||
- Bad exception
|
||||
- **You can also declare other subclasses of these**
|
||||
- Using the class and inheritance material in later lectures
|
||||
|
||||
## Exception behind the scenes
|
||||
|
||||
- **Normal program control flow is halted**
|
||||
- At the point where an exception is thrown
|
||||
|
||||
- **The program call stack "unwinds"**
|
||||
- Stack frame of each function in call chain "pops"
|
||||
- Variables in each popped frame are destroyed
|
||||
- This goes on until a matching try/catch scope is reached
|
||||
|
||||
- **Control passes to first matching catch block**
|
||||
- Can handle the exception and continue from there
|
||||
- Can free some resources and re-throw exception
|
||||
|
||||
- **Let's look at the call stack and how it behaves**
|
||||
- Good way to explain how exceptions work (in some detail)
|
||||
- Also a good way to understand normal function behavior
|
||||
|
||||
### Exceptions Manipulate the Function Call Stack
|
||||
|
||||
- **In general, the call stack’s structure is fairly basic**
|
||||
- A chunk of memory representing the state of an active function call
|
||||
- Pushed on program call stack at run-time (can observe in a debugger)
|
||||
|
||||
- **`g++ -s` generates machine code (in assembly language)**
|
||||
- A similar feature can give exact structure for most platforms/compilers
|
||||
|
||||
- **Each stack frame contains:**
|
||||
- A pointer to the previous stack frame
|
||||
- The return address (i.e., just after point from which function was called)
|
||||
- The parameters passed to the function (if any)
|
||||
- Automatic (local) variables for the function
|
||||
- Sometimes called “stack variables”
|
||||
|
||||
_basically, you can imageing the try/catch block as a function that is called when an exception is thrown._
|
||||
|
||||
## Additional Details about Exceptions
|
||||
|
||||
- Control jumps to the first matching catch block
|
||||
- Order matters if multiple possible matches
|
||||
- Especially with inheritance-related exception classes
|
||||
- Put more specific catch blocks before more general ones
|
||||
- Put catch blocks for more derived exception classes before catch blocks for their respective base classes
|
||||
- `catch(...)` is a catch-all block
|
||||
- Often should at least free resources, generate an error message, and else.
|
||||
- May rethrow exception for another handler to catch and do more
|
||||
- `throw`;
|
||||
- As of C++11, rethrows a caught exception
|
||||
|
||||
### Depreciated Exception Specifications
|
||||
|
||||
- **Exception specifications**
|
||||
- Used to specify which exceptions a function can throw
|
||||
- Depreciated in C++11
|
||||
- **Exception specifications are now deprecated**
|
||||
- **Use `noexcept` instead**
|
||||
- **`noexcept` is a type trait that indicates a function does not throw exceptions**
|
||||
|
||||
```cpp
|
||||
void f() throw(int, double); // prohibits throwing int or double
|
||||
```
|
||||
|
||||
```cpp
|
||||
void f() noexcept; // prohibits throwing any exceptions
|
||||
```
|
||||
|
||||
### Rule of Thumb for Using C++ Exceptions
|
||||
|
||||
- **Use exceptions to handle any cases where the program cannot behave normally**
|
||||
- Do not use exceptions as a way to control program execution under normal operating conditions
|
||||
|
||||
- **Don't let a thrown exception propagate out of the main function uncaught**
|
||||
- Instead, always catch any exceptions that propagate up
|
||||
- Then return a non-zero value to indicate program failure
|
||||
|
||||
- **Don’t rely on exception specifications**
|
||||
- May be a false promise, unless you have fully checked all the code used to implement that interface
|
||||
- No guarantees that they will work for templates, because a template parameter could leave them off and then fail
|
||||
|
||||
79
content/CSE332S/CSE332S_L7.md
Normal file
79
content/CSE332S/CSE332S_L7.md
Normal file
@@ -0,0 +1,79 @@
|
||||
# CSE332S Lecture 7
|
||||
|
||||
## Debugging
|
||||
|
||||
Debugger let’s us:
|
||||
|
||||
1. Execute code incrementally
|
||||
a. Line by line, function to function, breakpoint to breakpoint
|
||||
2. Examine state of executing program
|
||||
a. Examine program call stack
|
||||
b. Examine variables
|
||||
|
||||
When to debug:
|
||||
|
||||
1. Trace how a program runs
|
||||
2. Program crashes
|
||||
3. Incorrect result
|
||||
|
||||
### Basic debugging commands
|
||||
|
||||
Set breakpoints
|
||||
Run program - program stops on the first breakpoint it encounters
|
||||
From there:
|
||||
|
||||
- Execute one line at a time
|
||||
- Step into (step out can be useful if you step into a function outside of your code)
|
||||
- Step over
|
||||
|
||||
- Execute until the next breakpoint (continue)
|
||||
|
||||
While execution is stopped:
|
||||
|
||||
- Examine the state of the program
|
||||
- Call stack, variables, ...
|
||||
|
||||
### Lots of power, but where to start?
|
||||
|
||||
Stepping through the entire program is infeasible
|
||||
|
||||
Think first!!!
|
||||
|
||||
- What might be going wrong based on the output or crash message?
|
||||
- How can I test my hypothesis?
|
||||
- Can I narrow down the scope of my search?
|
||||
- Can I recreate the bug in a simpler test case/simpler code?
|
||||
- Set breakpoints in smart locations based on my hypothesis
|
||||
|
||||
### Today’s program
|
||||
|
||||
A simple lottery ticket game
|
||||
|
||||
1. User runs the program with 5 arguments, all integers (1-100)
|
||||
2. Program randomly generates 10 winning numbers
|
||||
3. User wins if they match 3 or more numbers
|
||||
|
||||
At least that’s how it should run, but you will have to find and fix a few issues first
|
||||
|
||||
First, let’s look at some things in the code
|
||||
|
||||
- Header guards/pragma once
|
||||
- Block comments: Who wrote this code? and what does it do?
|
||||
- Multiple files and including header files
|
||||
- **Do not define functions in header files, declarations only**
|
||||
- **Do not #include .cpp files**
|
||||
- Function or data type must be declared before it can be used
|
||||
|
||||
#### Header Guards
|
||||
|
||||
```cpp
|
||||
#pragma once // alternative to traditional header guards, don't need to do both.
|
||||
#ifndef ALGORITHMS_H
|
||||
#define ALGORITHMS_H
|
||||
#include<vector>
|
||||
void insertion_sort(std::vector<int> & v);
|
||||
bool binary_search(const std::vector<int> & v, int value);
|
||||
#endif // ALGORITHMS_H
|
||||
```
|
||||
|
||||
The header guard is used to prevent the header file from being included multiple times in the same file.
|
||||
236
content/CSE332S/CSE332S_L8.md
Normal file
236
content/CSE332S/CSE332S_L8.md
Normal file
@@ -0,0 +1,236 @@
|
||||
# CSE332S Lecture 8
|
||||
|
||||
## From procedural to object-oriented programming
|
||||
|
||||
Procedural programming
|
||||
|
||||
- Focused on **functions** and the call stack
|
||||
- Data and functions treated as **separate** abstractions
|
||||
- Data must be passed into/returned out of functions, functions work on any piece of data that can be passed in via parameters
|
||||
|
||||
Object-oriented programming
|
||||
|
||||
- Data and functions packaged **together** into a single abstraction
|
||||
- Data becomes more interesting (adds behavior)
|
||||
- Functions become more focused (restricts data scope)
|
||||
|
||||
## Object-oriented programming
|
||||
|
||||
- Data and functions packaged together into a single abstraction
|
||||
- Data becomes more interesting (adds behavior)
|
||||
- Functions become more focused (restricts data scope)
|
||||
|
||||
### Today:
|
||||
|
||||
- An introduction to classes and structs
|
||||
- Member variables (state of an object)
|
||||
- Constructors
|
||||
- Member functions/operators (behaviors)
|
||||
- Encapsulation
|
||||
- Abstraction
|
||||
|
||||
At a later date:
|
||||
|
||||
- Inheritance (class 12)
|
||||
- Polymorphism (12)
|
||||
- Developing reusable OO designs (16-21)
|
||||
|
||||
## Class and struct
|
||||
|
||||
### From C++ Functions to C++ Structs/Classes
|
||||
|
||||
C++ functions encapsulate behavior
|
||||
|
||||
- Data used/modified by a function must be passed in via parameters
|
||||
- Data produced by a function must be passed out via return type
|
||||
|
||||
Classes (and structs) encapsulate related data and behavior (**Encapsulation**)
|
||||
|
||||
- Member variables maintain each object’s state
|
||||
- Member functions (methods) and operators have direct access to member variables of the object on which they are called
|
||||
- Access to state of an object is often restricted
|
||||
- **Abstraction** - a class presents only the relevant details of an object, through its public interface.
|
||||
|
||||
### C++ Structs vs. C++ Classes?
|
||||
|
||||
Class members are **private** by default, struct members are **public** by default
|
||||
|
||||
When to use a struct
|
||||
|
||||
- Use a struct for things that are mostly about the data
|
||||
- **Add constructors and operators to work with STL containers/algorithms**
|
||||
|
||||
When to use a class
|
||||
|
||||
- Use a class for things where the behavior is the most important part
|
||||
- Prefer classes when dealing with encapsulation/polymorphism (later)
|
||||
|
||||
```cpp
|
||||
// point2d.h - struct declaration
|
||||
struct Point2D {
|
||||
Point2D(int x, int y);
|
||||
bool operator< (const Point2D &) const; // a const member function
|
||||
int x_; // promise a member variable
|
||||
int y_;
|
||||
};
|
||||
```
|
||||
|
||||
```cpp
|
||||
// point2d.cpp - methods functions
|
||||
#include "point2d.h"
|
||||
|
||||
Point2D::Point2D(int x, int y) :
|
||||
x_(x), y_(y) {}
|
||||
|
||||
bool Point2D::operator< (const Point2D &other) const {
|
||||
return x_ < other.x_ || (x_ == other.x_ && y_ < other.y_);
|
||||
}
|
||||
```
|
||||
|
||||
### Structure of a class
|
||||
|
||||
```cpp
|
||||
class Date {
|
||||
public: // public stores the member functions and variables accessible to the outside of class
|
||||
Date(); // default constructor
|
||||
Date (const Date &); // copy constructor
|
||||
Date(int year, int month, int day); // constructor with parameters
|
||||
virtual ~Date(); // (virtual) destructor
|
||||
Date& operator= (const Date &); // assignment operator
|
||||
int year() const; // accessor
|
||||
int month() const; // accessor
|
||||
int day() const; // accessor
|
||||
void year(int year); // mutator
|
||||
void month(int month); // mutator
|
||||
void day(int day); // mutator
|
||||
string yyymmdd() const; // generate a string representation of the date
|
||||
private: // private stores the member variables that only the class can access
|
||||
int year_;
|
||||
int month_;
|
||||
int day_;
|
||||
};
|
||||
```
|
||||
|
||||
#### Class constructor
|
||||
|
||||
- Same name as its class
|
||||
- Establishes invariants for objects of the class
|
||||
- **Base class/struct and member initialization list**
|
||||
- Used to initialize member variables
|
||||
- Used to construct base class when using inheritance
|
||||
- Must initialize const and reference members there
|
||||
- **Runs before the constructor body, object is fully initialized in constructor body**
|
||||
|
||||
```cpp
|
||||
// date.h
|
||||
class Date {
|
||||
public:
|
||||
Date();
|
||||
Date(const Date &);
|
||||
Date(int year, int month, int day);
|
||||
~Date();
|
||||
// ...
|
||||
private:
|
||||
int year_;
|
||||
int month_;
|
||||
int day_;
|
||||
};
|
||||
```
|
||||
|
||||
```cpp
|
||||
// date.cpp
|
||||
Date::Date() : year_(0), month_(0), day_(0) {} // initialize member variables, use pre-defined values as default values
|
||||
Date::Date(const Date &other) : year_(other.year_), month_(other.month_), day_(other.day_) {} // copy constructor
|
||||
Date::Date(int year, int month, int day) : year_(year), month_(month), day_(day) {} // constructor with parameters
|
||||
// ...
|
||||
```
|
||||
|
||||
#### More on constructors
|
||||
|
||||
Compiler defined constructors:
|
||||
|
||||
- Compiler only defines a default constructor if no other constructor is declared
|
||||
- Compiler defined constructors simply construct each member variable using the same operation
|
||||
|
||||
Default constructor for **built-in types** does nothing (leaves the variable uninitialized)!
|
||||
|
||||
It is an error to read an uninitialized variable
|
||||
|
||||
## Access control and friend declarations
|
||||
|
||||
Declaring access control scopes within a class - where is the member visible?
|
||||
|
||||
- `private`: visible only within the class
|
||||
- `protected`: also visible within derived classes (more later)
|
||||
- `public`: visible everywhere
|
||||
|
||||
Access control in a **class** is `private` by default
|
||||
|
||||
- It’s better style to label access control explicitly
|
||||
|
||||
A `struct` is the same as a `class`, except access control for a `struct` is `public` by default
|
||||
|
||||
- Usually used for things that are “mostly data”
|
||||
|
||||
### Issues with Encapsulation in C++
|
||||
|
||||
Encapsulation - state of an object is kept internally (private), state of an object can be changed via calls to its public interface (public member functions/operators)
|
||||
|
||||
Sometimes two classes are closely tied:
|
||||
|
||||
- One may need direct access to the other’s internal state
|
||||
- But, other classes should not have the same direct access
|
||||
- Containers and iterators are an example of this
|
||||
|
||||
We could:
|
||||
|
||||
1. Make the internal state public, but this violates **encapsulation**
|
||||
2. Use an inheritance relationship and make the internal state protected, but the inheritance relationship doesn’t make sense
|
||||
3. Create fine-grained accessors and mutators, but this clutters the interface and violates **abstraction**
|
||||
|
||||
### Friend declarations
|
||||
|
||||
Offer a limited way to open up class encapsulation
|
||||
|
||||
C++ allows a class to declare its “friends”
|
||||
|
||||
- Give access to specific classes or functions
|
||||
|
||||
Properties of the friend relation in C++
|
||||
|
||||
- Friendship gives complete access
|
||||
- Friend methods/functions behave like class members
|
||||
- public, protected, private scopes are all accessible by friends
|
||||
- Friendship is asymmetric and voluntary
|
||||
- A class gets to say what friends it has (giving permission to them)
|
||||
- But one cannot “force friendship” on a class from outside it
|
||||
- Friendship is not inherited
|
||||
- Specific friend relationships must be declared by each class
|
||||
- “Your parents’ friends are not necessarily your friends”
|
||||
|
||||
|
||||
```cpp
|
||||
// in Foo.h
|
||||
class Foo {
|
||||
friend ostream &operator<< (ostream &out, const Foo &f); // declare a friend function, can be added at any line of the class declaration
|
||||
public:
|
||||
Foo(int x);
|
||||
~Foo();
|
||||
// ...
|
||||
private:
|
||||
int baz_;
|
||||
};
|
||||
|
||||
ostream &operator<< (ostream &out, const Foo &f);
|
||||
```
|
||||
|
||||
```cpp
|
||||
// in Foo.cpp
|
||||
ostream &operator<< (ostream &out, const Foo &f) {
|
||||
out << f.baz_; // access private member variable via friend declaration
|
||||
return out;
|
||||
}
|
||||
|
||||
|
||||
```
|
||||
|
||||
199
content/CSE332S/CSE332S_L9.md
Normal file
199
content/CSE332S/CSE332S_L9.md
Normal file
@@ -0,0 +1,199 @@
|
||||
# CSE332S Lecture 9
|
||||
|
||||
## Sequential Containers
|
||||
|
||||
Hold elements of a parameterized type (specified when the container variable is
|
||||
declared): `vector<int> v; vector<string> v1;`
|
||||
|
||||
Elements are inserted/accessed based on their location (index)
|
||||
|
||||
- A single location cannot be in more than 1 container
|
||||
- Container owns elements it contains - copied in by value, contents of container are destroyed when the container is destroyed
|
||||
|
||||
Containers provide an appropriate interface to add, remove, and access elements
|
||||
|
||||
- Interface provided is determined by the specifics of the container - underlying data structure
|
||||
|
||||
_usually the provided interface of the container runs in constant time_
|
||||
|
||||
### Non-random access containers
|
||||
|
||||
Cannot access elements in constant time, must traverse the container to get to the desired element.
|
||||
|
||||
#### Forward list
|
||||
|
||||
- implemented as a singly linked list of elements
|
||||
- Elements are not contiguous in memory (no random access)
|
||||
- Contains a pointer to the first element (can only grow at front, supplies a `forward_iterator`)
|
||||
|
||||
#### List
|
||||
|
||||
- implemented as a doubly linked list of elements
|
||||
- Elements are not contiguous in memory (no random access)
|
||||
- Contains a pointer to front and back (can grow at front or back, supplies a `bidirectional_iterator`)
|
||||
|
||||
### Random access containers
|
||||
|
||||
Add, remove, and access elements in constant time.
|
||||
|
||||
#### Vector
|
||||
|
||||
- implemented as a dynamically sized array of elements
|
||||
- Elements are contiguous in memory (random access)
|
||||
- Can only grow at the back via `push_back()` (amortized constant time, _may expand the array takes linear time_)
|
||||
|
||||
#### Deque
|
||||
|
||||
- double-ended queue of elements
|
||||
- Elements do not have to be contiguous in memory, but must be accessible in constant time (random access)
|
||||
- Can grow at front or back of the queue
|
||||
|
||||
## Iterators and iterator types
|
||||
|
||||
Could use the subscript/indexing (operator[]) operator with a loop
|
||||
|
||||
- Not all containers supply an [] operator, but we should still be able to traverse and access their elements
|
||||
|
||||
Containers provide iterator types:
|
||||
|
||||
- `vector<int>::iterator i; // iterator over non-const elements`
|
||||
- `vector<int>::const_iterator ci; // iterator over const elements`
|
||||
|
||||
Containers provide functions for creating iterators to the beginning and just past
|
||||
the end of the container:
|
||||
|
||||
```cpp
|
||||
vector<int> v = { 1, 2, 3, 4, 5 };
|
||||
auto start = v.cbegin(); // cbegin() gives const iterator, you can't modify the elements, you can use .begin() to get a non-const iterator
|
||||
while (start != v.cend()) { // over const elements, v.cend() is not a valid element, it's just one pass the end.
|
||||
cout << *start << endl;
|
||||
++start;
|
||||
}
|
||||
```
|
||||
|
||||
### More on iterators
|
||||
|
||||
- Iterators generalize different uses of pointers
|
||||
- Most importantly, define left-inclusive intervals over the ranges of elements in a container `[begin, end)`
|
||||
- Iterators interface between algorithms and data structures (Iterator design pattern)
|
||||
- Algorithms manipulate iterators, not containers
|
||||
- An iterator’s value can represent 3 kinds of `states`:
|
||||
- `dereferencable` (points to a valid location in a range), eg `*start`
|
||||
- `past the end` (points just past last valid location in a range), eg `v.cend()`
|
||||
- `singular` (points to nothing), eg `nullptr`
|
||||
- Can construct, compare, copy, and assign iterators so that native and library types
|
||||
can inter-operate
|
||||
|
||||
### Properties of Iterator Intervals
|
||||
|
||||
- Valid intervals can be traversed safely with an iterator
|
||||
- An empty range `[p,p)` is valid
|
||||
- If `[first, last)` is valid and non-empty, then `[first+1, last)` is also valid
|
||||
- Proof: iterative induction on the interval
|
||||
- If `[first, last)` is valid
|
||||
- and position `mid` is reachable from `first`
|
||||
- and `last` is reachable from `mid`
|
||||
- then `[first, mid)` and `[mid, last)` are also valid
|
||||
- Proof: divide and conquer induction on the interval
|
||||
- If `[first, mid)` and `[mid, last)` are valid, then `[first, last)` is valid
|
||||
- Proof: divide and conquer induction on the interval
|
||||
|
||||
### Interface supplied by different iterator types
|
||||
|
||||
- Output iterators: used in output operations (write),
|
||||
- "destructive" read at head of stream (istream)
|
||||
- Input iterators: used in input operations (read),
|
||||
- "transient" write to stream (ostream)
|
||||
- Forward iterators: used in forward operations (read, write), common used in forward linked list
|
||||
- Value _persists_ after read/write
|
||||
- Bidirectional iterators: used in bidirectional operations (read, write), common used in doubly linked list
|
||||
- Value have _locations_
|
||||
- Random access iterators: used in random access operations (read, write), common used in vector
|
||||
- Can express _distance_ between two iterators
|
||||
|
||||
| Category/Operation | Output | Input | Forward | Bidirectional | Random Access |
|
||||
| ------------------ | -------------- | -------------- | -------------- | -------------- | ----------------- |
|
||||
| Read | N/A | `=*p`(r-value) | `=*p`(r-value) | `=*p`(r-value) | `=*p`(r-value) |
|
||||
| Access | N/A | `->` | `->` | `->` | `->,[]` |
|
||||
| Write | `*p=`(l-value) | N/A | `*p=`(l-value) | `*p=`(l-value) | `*p=`(l-value) |
|
||||
| Iteration | `++` | `++` | `++` | `++,--` | `++,--,+,-,+=,-=` |
|
||||
| Comparison | N/A | `==,!=` | `==,!=` | `==,!=` | `==,!=,<,>,<=,>=` |
|
||||
|
||||
## Generic algorithms in CPP
|
||||
|
||||
A standard collection of generic algorithms
|
||||
|
||||
- Applicable to various types and containers
|
||||
- E.g., sorting integers (`int`) vs. intervals (`pair<int, int>`)
|
||||
- E.g., sorting elements in a `vector` vs. in a C-style array
|
||||
- Polymorphic even without inheritance relationships - interface polymorphism
|
||||
- Types substituted need not have a common base class
|
||||
- Must only provide the interface the algorithm requires
|
||||
- Common iterator interfaces allow algorithms to work with many types of
|
||||
containers, without knowing the implementation details of the container
|
||||
- Significantly used with the sequence containers
|
||||
- To reorder elements within a container’s sequence
|
||||
- To store/fetch values into/from a container
|
||||
- To calculate various values and properties from it
|
||||
|
||||
### Organization of C++ Algorithm Libraries
|
||||
|
||||
The `<algorithm>` header file contains
|
||||
|
||||
- Non-modifying sequence operations
|
||||
- Do some calculation but don’t change sequence itself
|
||||
- Examples include `count`, `count_if`
|
||||
- Mutating sequence operations
|
||||
- Modify the order or values of the sequence elements
|
||||
- Examples include `copy`, `random_shuffle`
|
||||
- Sorting and related operations
|
||||
- Modify the order in which elements appear in a sequence
|
||||
- Examples include `sort`, `next_permutation`
|
||||
- The `<numeric>` header file contains
|
||||
- General numeric operations
|
||||
- Scalar and matrix algebra, especially used with `vector<T>`
|
||||
- Examples include `accumulate`, `inner_product`
|
||||
|
||||
### Using Algorithms
|
||||
|
||||
Example using `std::sort()`
|
||||
|
||||
- `sort` algorithm
|
||||
- Reorders a given range
|
||||
- Can also plug in a functor to change the ordering function
|
||||
- http://www.cplusplus.com/reference/algorithm/sort/
|
||||
|
||||
- Requires random access iterators.
|
||||
- Requires elements being sorted implement `operator<` (less than)
|
||||
|
||||
```cpp
|
||||
#include <algorithm>
|
||||
#include <vector>
|
||||
#include <iostream>
|
||||
|
||||
using namespace std;
|
||||
|
||||
int main(int argc, char* argv[]) {
|
||||
vector<int> v = { 3, 1, 4, 1, 5, 9 };
|
||||
sort(v.begin(), v.end()); // sort the vector
|
||||
for (int i : v) {
|
||||
cout << i << " ";
|
||||
}
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
Sort forward list of strings
|
||||
|
||||
```cpp
|
||||
forward_list<string> fl = { "hello", "world", "this", "is", "a", "test" };
|
||||
sort(fl.begin(), fl.end());
|
||||
```
|
||||
**This is not valid because forward list does not support random access iterators.**
|
||||
|
||||
Sort vector of strings
|
||||
|
||||
```cpp
|
||||
vector<string> v = { "hello", "world", "this", "is", "a", "test" };
|
||||
sort(v.begin(), v.end());
|
||||
```
|
||||
23
content/CSE332S/_meta.js
Normal file
23
content/CSE332S/_meta.js
Normal file
@@ -0,0 +1,23 @@
|
||||
export default {
|
||||
index: {type:"page",title:"Course Description",href:"/CSE332S/index.mdx"},
|
||||
"---":{
|
||||
type: 'separator'
|
||||
},
|
||||
CSE332S_L1: "Object-Oriented Programming Lab (Lecture 1)",
|
||||
CSE332S_L2: "Object-Oriented Programming Lab (Lecture 2)",
|
||||
CSE332S_L3: "Object-Oriented Programming Lab (Lecture 3)",
|
||||
CSE332S_L4: "Object-Oriented Programming Lab (Lecture 4)",
|
||||
CSE332S_L5: "Object-Oriented Programming Lab (Lecture 5)",
|
||||
CSE332S_L6: "Object-Oriented Programming Lab (Lecture 6)",
|
||||
CSE332S_L7: "Object-Oriented Programming Lab (Lecture 7)",
|
||||
CSE332S_L8: "Object-Oriented Programming Lab (Lecture 8)",
|
||||
CSE332S_L9: "Object-Oriented Programming Lab (Lecture 9)",
|
||||
CSE332S_L10: "Object-Oriented Programming Lab (Lecture 10)",
|
||||
CSE332S_L11: "Object-Oriented Programming Lab (Lecture 11)",
|
||||
CSE332S_L12: "Object-Oriented Programming Lab (Lecture 12)",
|
||||
CSE332S_L13: "Object-Oriented Programming Lab (Lecture 13)",
|
||||
CSE332S_L14: "Object-Oriented Programming Lab (Lecture 14)",
|
||||
CSE332S_L15: "Object-Oriented Programming Lab (Lecture 15)",
|
||||
CSE332S_L16: "Object-Oriented Programming Lab (Lecture 16)",
|
||||
CSE332S_L17: "Object-Oriented Programming Lab (Lecture 17)"
|
||||
}
|
||||
6
content/CSE332S/index.mdx
Normal file
6
content/CSE332S/index.mdx
Normal file
@@ -0,0 +1,6 @@
|
||||
# CSE332S
|
||||
|
||||
**Object-Oriented Software Development Laboratory**
|
||||
**Spring 2025**
|
||||
|
||||
Instructor: **Jon Shidal**
|
||||
245
content/CSE347/CSE347_L1.md
Normal file
245
content/CSE347/CSE347_L1.md
Normal file
@@ -0,0 +1,245 @@
|
||||
# Lecture 1
|
||||
|
||||
## Greedy Algorithms
|
||||
|
||||
* Builds up a solution by making a series of small decisions that optimize some objective.
|
||||
* Make one irrevocable choice at a time, creating smaller and smaller sub-problems of the same kind as the original problem.
|
||||
* There are many potential greedy strategies and picking the right one can be challenging.
|
||||
|
||||
### A Scheduling Problem
|
||||
|
||||
You manage a giant space telescope.
|
||||
|
||||
* There are $n$ research projects that want to use it to make observations.
|
||||
* Only one project can use the telescope at a time.
|
||||
* Project $p_i$ needs the telescope starting at time $s_i$ and running for a length of time $t_i$.
|
||||
* Goal: schedule as many as possible
|
||||
|
||||
Formally
|
||||
|
||||
Input:
|
||||
|
||||
* Given a set $P$ of projects, $|P|=n$
|
||||
* Each request $p_i\in P$ occupies interval $[s_i,f_i)$, where $f_i=s_i+t_i$
|
||||
|
||||
Goal: Choose a subset $\Pi\sqsubseteq P$ such that
|
||||
|
||||
1. No two projects in $\Pi$ have overlapping intervals.
|
||||
2. The number of selected projects $|\Pi|$ is maximized.
|
||||
|
||||
#### Shortest Interval
|
||||
|
||||
Counter-example: `[1,10],[9,12],[11,20]`
|
||||
|
||||
#### Earliest start time
|
||||
|
||||
Counter-example: `[1,10],[2,3],[4,5]`
|
||||
|
||||
#### Fewest Conflicts
|
||||
|
||||
Counter-example: `[1,2],[1,4],[1,4],[3,6],[7,8],[5,8],[5,8]`
|
||||
|
||||
#### Earliest finish time
|
||||
|
||||
Correct... but why
|
||||
|
||||
#### Theorem of Greedy Strategy (Earliest Finishing Time)
|
||||
|
||||
Say this greedy strategy (Earliest Finishing Time) picks a set $\Pi$ of intervals, some other strategy picks a set $O$ of intervals.
|
||||
|
||||
Assume sorted by finishing time
|
||||
|
||||
* $\Pi=\{i_1,i_2,...,i_k\},|\Pi|=k$
|
||||
* $O=\{j_1,j_2,...,j_m\},|O|=m$
|
||||
|
||||
We want to show that $|\Pi|\geq|O|,k>m$
|
||||
|
||||
#### Lemma: For all $r<k,f_{i_r}\leq f_{j_r}$
|
||||
|
||||
We proceed the proof by induction.
|
||||
|
||||
* Base Case, when r=1.
|
||||
$\Pi$ is the earliest finish time, and $O$ cannot pick a interval with earlier finish time, so $f_{i_r}\leq f_{j_r}$
|
||||
|
||||
* Inductive step, when r>1.
|
||||
Since $\Pi_r$ is the earliest finish time, so for any set in $O_r$, $f_{i_{r-1}}\leq f_{j_{r-1}}$, for any $j_r$ inserted to $O_r$, it can also be inserted to $\Pi_r$. So $O_r$ cannot pick an interval with earlier finish time than $Pi$ since it will also be picked by definition if $O_r$ is the optimal solution $OPT$.
|
||||
|
||||
#### Problem of “Greedy Stays Ahead” Proof
|
||||
|
||||
* Every problem has very different theorem.
|
||||
* It can be challenging to even write down the correct statement that you must prove.
|
||||
* We want a systematic approach to prove the correctness of greedy algorithms.
|
||||
|
||||
### Road Map to Prove Greedy Algorithm
|
||||
|
||||
#### 1. Make a Choice
|
||||
|
||||
Pick an interval based on greedy choice, say $q$
|
||||
|
||||
Proof: **Greedy Choice Property**: Show that using our first choice is not "fatal" – at least one optimal solution makes this choice.
|
||||
|
||||
Techniques: **Exchange Argument**: "If an optimal solution does not choose $q$, we can turn it into an equally good solution that does."
|
||||
|
||||
Let $\Pi^*$ be any optimal solution for project set $P$.
|
||||
- If $q\in \Pi^*$, we are done.
|
||||
- Otherwise, let $x$ be the optimal solution from $\Pi^*$ that does not pick $q$. We create another solution $\bar{\Pi^*}$ that replace $x$ with $q$, and prove that the $\bar{\Pi^*}$ is as optimal as $\Pi^*$
|
||||
|
||||
#### 2. Create a smaller instance $P'$ of the original problem
|
||||
|
||||
$P'$ has the same optimization criteria.
|
||||
|
||||
Proof: **Inductive Structure**: Show that after making the first choice, we're left with a smaller version of the same problem, whose solution we can safely combine with the first choice.
|
||||
|
||||
Let $P'$ be the subproblem left after making first choice $q$ in problem $P$ and let $\Pi'$ be an optimal solution to $P'$. Then $\Pi=\Pi^*\cup\{q\}$ is an optimal solution to $P$.
|
||||
|
||||
$P'=P-\{q\}-\{$projects conflicting with $q\}$
|
||||
|
||||
#### 3. Solution: Union of choices that we made
|
||||
|
||||
Union of choices that we made.
|
||||
|
||||
Proof: **Optimal Substructure**: Show that if we solve the subproblem optimally, adding our first choice creates an optimal solution to the *whole* problem.
|
||||
|
||||
Let $q$ be the first choice, $P'$ be the subproblem left after making $q$ in problem $P$, $\Pi'$ be an optimal solution to $P'$. We claim that $\Pi=\Pi'\cup \{q\}$ is an optimal solution to $P$.
|
||||
|
||||
We proceed the proof by contradiction.
|
||||
|
||||
Assume that $\Pi=\Pi'+\{q\}$ is not optimal.
|
||||
|
||||
|
||||
By Greedy choice property $GCP$. we already know that $\exists$ an optimal solution $\Pi^*$ for problem $P$ that contains $q$. If $\Pi$ is not optimal, $cost(\Pi^*)<cost(\Pi)$. Then since $\Pi^*-q$ is also a feasible solution to $P'$. $cost(\Pi^*-q)>cost(\Pi-q)=\Pi'$ which leads to contradiction that $\Pi'$ is an optimal solution to $P'$.
|
||||
|
||||
#### 4. Put 1-3 together to write an inductive proof of the Theorem
|
||||
|
||||
This is independent of problem, same for every problem.
|
||||
|
||||
Use scheduling problem as an example:
|
||||
|
||||
Theorem: given a scheduling problem $P$, if we repeatedly choose the remaining feasible project with the earliest finishing time, we will construct an optimal feasible solution to $P$.
|
||||
|
||||
Proof: We proceed by induction on $|P|$. (based on the size of problem $P$).
|
||||
|
||||
- Base case: $|P|=1$.
|
||||
- Inductive step.
|
||||
- Inductive hypothesis: For all problems of size $<n$, earliest finishing time (EFT) gives us an optimal solution.
|
||||
- EFT is optimal for problem of size $n$.
|
||||
- Proof: Once we pick q, because of greedy choice. $P'=P=\{q\} -\{$interval that conflict with $q\}$. $|P'|<n$, By Inductive hypothesis, EFT gives us an optimal solution to $P'$, but by inductive substructure, and optimal substructure. $\Pi'$ (optimal solution to $P'$), we have optimal solution to $P$.
|
||||
|
||||
_this step always holds as long as the previous three properties hold, and we don't usually write the whole proof._
|
||||
|
||||
```python
|
||||
# Algorithm construction for Interval scheduling problem
|
||||
def schedule(p):
|
||||
# sorting takes O(n)=nlogn
|
||||
p=sorted(p,key=lambda x:x[1])
|
||||
res=[P[0]]
|
||||
# O(n)=n
|
||||
for i in p[1:]:
|
||||
if res[-1][-1]<i[0]:
|
||||
res.append(i)
|
||||
return res
|
||||
```
|
||||
|
||||
## Extra Examples:
|
||||
|
||||
### File compression problem
|
||||
|
||||
You have $n$ files of different sizes $f_i$.
|
||||
|
||||
You want to merge them to create a single file. $merge(f_i,f_j)$ takes time $f_i+f_j$ and creates a file of size $f_k=f_i+f_j$.
|
||||
|
||||
Goal: Find the order of merges such that the total time to merge is minimized.
|
||||
|
||||
Thinking process: The merge process is a binary tree and each of the file is the leaf of the tree.
|
||||
|
||||
The total time required =$\sum^n_{i=1} d_if_i$, where $d_i$ is the depth of the file in the compression tree.
|
||||
|
||||
So compressing the smaller file first may yield a faster run time.
|
||||
|
||||
Proof:
|
||||
|
||||
#### Greedy Choice Property
|
||||
|
||||
Construct part of the solution by making a locally good decision.
|
||||
|
||||
Lemma: $\exist$ some optimal solution that merges the two smallest file first, lets say $[f_1,f_2]$
|
||||
|
||||
Proof: **Exchange argument**
|
||||
|
||||
* Case 1: Optimal choice already merges $f_1,f_2$, done. Time order does not matter in this problem at some point.
|
||||
* eg: [2,2,3], merge 2,3 and 2,2 first don't change the total cost
|
||||
* Case 2: Optimal choice does not merges $f_1$ and $f_2$.
|
||||
* Suppose the optimal solution merges $f_x,f_y$ as the deepest merge.
|
||||
* Then $d_x\geq d_1,d_y\geq d_2$. Exchanging $f_1,f_2$ with $f_x,f_y$ would yield a strictly less greater solution since $f_1,f_2$ already smallest.
|
||||
|
||||
#### Inductive Structure
|
||||
|
||||
* We can combine feasible solution to the subproblem $P'$ with the greedy choice to get a feasible solution to $P$
|
||||
* After making greedy choice $q$, we are left with a strictly smaller subproblem $P'$ with the same optimality criteria of the original problem
|
||||
*
|
||||
Proof: **Optimal Substructure**: Show that if we solve the subproblem optimally, adding our first choice creates an optimal solution to the *whole* problem.
|
||||
|
||||
Let $q$ be the first choice, $P'$ be the subproblem left after making $q$ in problem $P$, $\Pi^*$ be an optimal solution to $P'$. We claim that $\Pi=\Pi'\cup \{q\}$ is an optimal solution to $P$.
|
||||
|
||||
We proceed the proof by contradiction.
|
||||
|
||||
Assume that $\Pi=\Pi^*+\{q\}$ is not optimal.
|
||||
|
||||
By Greedy choice property $GCP$. we already know that $\Pi^*$ is optimal solution that contains $q$. Then $|\Pi^*|>|\Pi|$ $\Pi^*-q$ is also feasible solution to $P'$. $|\Pi^*-q|>|\Pi-q|=\Pi'$ which is an optimal solution to $P'$ which leads to contradiction.
|
||||
|
||||
Proof: **Smaller problem size**
|
||||
|
||||
After merging the smallest two files into one, we have strictly less files waiting to merge.
|
||||
|
||||
#### Optimal Substructure
|
||||
|
||||
* We can combine optimal solution to the subproblem $P'$ with the greedy choice to get a optimal solution to $P$
|
||||
|
||||
Step 4 ignored, same for all greedy problems.
|
||||
|
||||
### Conclusion: Greedy Algorithm
|
||||
|
||||
* Algorithm
|
||||
* Runtime Complexity
|
||||
* Proof
|
||||
* Greedy Choice Property
|
||||
* Construct part of the solution by making a locally good decision.
|
||||
* Inductive Structure
|
||||
* We can combine feasible solution to the subproblem $P'$ with the greedy choice to get a feasible solution to $P$
|
||||
* After making greedy choice $q$, we are left with a strictly smaller subproblem $P'$ with the same optimality criteria of the original problem
|
||||
* Optimal Substructure
|
||||
* We can combine optimal solution to the subproblem $P'$ with the greedy choice to get a optimal solution to $P$
|
||||
* Standard Contradiction Argument simplifies it
|
||||
|
||||
## Review:
|
||||
|
||||
### Essence of master method
|
||||
|
||||
Let $a\geq 1$ and $b>1$ be constants, let $f(n)$ be a function, and let $T(n)$ be defined on the nonnegative integers by the recurrence
|
||||
|
||||
$$
|
||||
T(n)=aT(\frac{n}{b})+f(n)
|
||||
$$
|
||||
|
||||
where we interpret $n/b$ to mean either ceiling or floor of $n/b$. $c_{crit}=\log_b a$ Then $T(n)$ has to following asymptotic bounds.
|
||||
|
||||
* Case I: if $f(n) = O(n^{c})$ ($f(n)$ "dominates" $n^{\log_b a-c}$) where $c<c_{crit}$, then $T(n) = \Theta(n^{c_{crit}})$
|
||||
|
||||
* Case II: if $f(n) = \Theta(n^{c_{crit}})$, ($f(n), n^{\log_b a-c}$ have no dominate) then $T(n) = \Theta(n^{\log_b a} \log_2 n)$
|
||||
|
||||
Extension for $f(n)=\Theta(n^{critical\_value}*(\log n)^k)$
|
||||
|
||||
* if $k>-1$
|
||||
|
||||
$T(n)=\Theta(n^{critical\_value}*(\log n)^{k+1})$
|
||||
|
||||
* if $k=-1$
|
||||
|
||||
$T(n)=\Theta(n^{critical\_value}*\log \log n)$
|
||||
|
||||
* if $k<-1$
|
||||
|
||||
$T(n)=\Theta(n^{critical\_value})$
|
||||
|
||||
* Case III: if $f(n) = \Omega(n^{log_b a+c})$ ($n^{log_b a-c}$ "dominates" $f(n)$) for some constant $c >0$, and if a $f(n/b)<= c f(n)$ for some constant $c <1$ then for all sufficiently large $n$, $T(n) = \Theta(n^{log_b a+c})$
|
||||
|
||||
320
content/CSE347/CSE347_L10.md
Normal file
320
content/CSE347/CSE347_L10.md
Normal file
@@ -0,0 +1,320 @@
|
||||
# Lecture 10
|
||||
|
||||
## Online Algorithms
|
||||
|
||||
### Example 1: Elevator
|
||||
|
||||
Problem: You've entered the lobby of a tall building, and want to go to the top floor as quickly as possible. There is an elevator which takes $E$ time to get to the top once it arrives. You can also take the stairs which takes $S$ time to climb (once you start) with $S>E$. However, you **do not know** when the elevator will arrive.
|
||||
|
||||
#### Offline (Clairvoyant) vs. Online
|
||||
|
||||
Offline: If you know that the elevator is arriving in $T$ time, the what will you do?
|
||||
|
||||
- Easy. I will computer $E+T$ with $S$ and take the smaller one.
|
||||
|
||||
Online: You do not know when the elevator will arrive.
|
||||
|
||||
- You can either wait for the elevator or take the stairs.
|
||||
|
||||
#### Strategies
|
||||
|
||||
**Always take the stairs.**
|
||||
|
||||
Your cost $S$,
|
||||
|
||||
Optimal Cost: $E$.
|
||||
|
||||
Your cost / Optimal cost = $\frac{S}{E}$.
|
||||
|
||||
$S$ would be arbitrary large. For example, the Empire State Building has $103$ floors.
|
||||
|
||||
**Wait for the elevator**
|
||||
|
||||
Your cost $T+E$
|
||||
|
||||
Optimal Cost: $S$ (if $T$ is large)
|
||||
|
||||
Your cost / Optimal cost = $\frac{T+E}{S}$.
|
||||
|
||||
$T$ could be arbitrary large. For out of service elevator, $T$ could be infinite.
|
||||
|
||||
#### Online Algorithms
|
||||
|
||||
Definition: An online algorithm must take decisions **without** full information about the problem instance [in this case $T$] and/or it does not know the future [e.g. makes decision immediately as jobs come in without knowing the future jobs].
|
||||
|
||||
An **offline algorithm** has the full information about the problem instance.
|
||||
|
||||
### Competitive Ratio
|
||||
|
||||
Quality of online algorithm is quantified by the **competitive ratio** (Idea is similar to the approximation ratio in optimization).
|
||||
|
||||
Consider a problem $L$ (minimization) and let $l$ be an instance of this problem.
|
||||
|
||||
$C^*(l)$ is the cost of the optimal offline solution with full information and unlimited computational power.
|
||||
|
||||
$A$ is the online algorithm for $L$.
|
||||
|
||||
$C_A(l)$ is the value of $A$'s solution on $l$.
|
||||
|
||||
An online algorithm $A$ is $\alpha$-competitive if
|
||||
|
||||
$$
|
||||
\frac{C_A(l)}{C^*(l)}\leq \alpha
|
||||
$$
|
||||
|
||||
for all instances $l$ of the problem.
|
||||
|
||||
In other words, $\alpha=\max_l\frac{C_A(l)}{C^*(l)}$.
|
||||
|
||||
For maximization problems, we want to minimize the comparative ratio.
|
||||
|
||||
### Back to the Elevator Problem
|
||||
|
||||
**Strategy 1**: Always take the stairs. Ratio is $\frac{S}{E}$. can be arbitrarily large.
|
||||
|
||||
**Strategy 2**: Wait for the elevator. Ratio is $\frac{T+E}{S}$. can be arbitrarily large.
|
||||
|
||||
**Strategy 3**: We do not make a decision immediately. Let's wait for $R$ times and then takes stairs if elevator does not arrive.
|
||||
|
||||
Question: What is the value of $R$? (how long to wait?)
|
||||
|
||||
Let's try $R=S$.
|
||||
|
||||
Claim: The comparative ratio is $2$.
|
||||
|
||||
Proof:
|
||||
|
||||
Case 1: The optimal offline solution takes the elevator, then $T+E\leq S$.
|
||||
|
||||
We also take the elevator.
|
||||
|
||||
Competitive ratio = $\frac{T+E}{T+E}=1$.
|
||||
|
||||
Case 2: The optimal offline solution takes the stairs, immediately.
|
||||
|
||||
We wait for $R$ times and then take the stairs. In worst case, we wait for $R$ times and then take the stairs for $R$.
|
||||
|
||||
Competitive ratio = $\frac{2R}{R}=2$.
|
||||
|
||||
QED
|
||||
|
||||
Let's try $R=S-E$ instead.
|
||||
|
||||
Claim: The comparative ratio is $max\{1,2-\frac{E}{S}\}$.
|
||||
|
||||
Proof:
|
||||
|
||||
Case 1: The optimal offline solution takes the elevator, then $T+E\leq S$.
|
||||
|
||||
We also take the elevator.
|
||||
|
||||
Competitive ratio = $\frac{T+E}{T+E}=1$.
|
||||
|
||||
Case 2: The optimal offline solution takes the stairs, immediately.
|
||||
|
||||
We wait for $R=S-E$ times and then take the stairs.
|
||||
|
||||
Competitive ratio = $\frac{S-E+S}{S}=2-\frac{E}{S}$.
|
||||
|
||||
QED
|
||||
|
||||
What if we wait less time? Let's try $R=S-E-\epsilon$ for some $\epsilon>0$
|
||||
|
||||
In the worst case, we take the stairs for $S-E-\epsilon$ times and then take the stairs for $S$.
|
||||
|
||||
Competitive ratio = $\frac{(S-E-\epsilon)+S}{S-E-\epsilon+E}=\frac{2S-E-\epsilon}{2S-E}>2-\frac{E}{S}$.
|
||||
|
||||
So the optimal competitive ratio is $max\{1,2-\frac{E}{S}\}$ when we wait for $S-E$ time.
|
||||
|
||||
### Example 2: Cache Replacement
|
||||
|
||||
Cache: Data in a cache is organized in blocks (also called pages or cache lines).
|
||||
|
||||
If CPU accesses data that is already in the cache, it is called **cache hit**, then access is fast.
|
||||
|
||||
If CPU accesses data that is not in the cache, it is called **cache miss**, This block if brought to cache from main memory. If the cache already has $k$ blocks (full), then another block need to be **kicked out** (eviction).
|
||||
|
||||
Global: Minimize the number of cache misses.
|
||||
|
||||
**Clairvoyant policy**: Knows that will be accessed in the future and the sequence of access.
|
||||
|
||||
FIF: Farthest in the future
|
||||
|
||||
Example: $k=3$, cache has $3$ blocks.
|
||||
|
||||
Sequence: $A B C D C A B$
|
||||
|
||||
Cache: $A B C$, the evict $B$ for $D$. then 3 warm up and 1 miss.
|
||||
|
||||
Online Algorithm: Least recently used (LRU)
|
||||
|
||||
LRU: least recently used.
|
||||
|
||||
Example: $A B C D C A B$
|
||||
|
||||
Cache: $A B C$, the evict $A$ for $D$. then 3 warm up and 1 miss.
|
||||
|
||||
Cache: $D B C$, the evict $B$ for $A$. 1 miss.
|
||||
|
||||
Cache: $D A C$, the evict $D$ for $B$. 1 miss.
|
||||
|
||||
#### Competitive Ratio for LRU
|
||||
|
||||
Claim: LRU is $k+1$-competitive.
|
||||
|
||||
Proof:
|
||||
|
||||
Split the sequence into subsequences such that each subsequence contains $k+1$ distinct blocks.
|
||||
|
||||
For example, suppose $k=3$, sequence $ABCDCEFGEA$, subsequences are $ABCDC$ and $EFGEA$.
|
||||
|
||||
LRU Cache: In each subsequence, it has at most $k+1$ misses.
|
||||
|
||||
The optimal offline solution: In each subsequence, must have at least $1$ miss.
|
||||
|
||||
So the competitive ratio is at most $k+1$.
|
||||
|
||||
QED
|
||||
|
||||
Using similar analysis, we can show that LRU is $k$ competitive.
|
||||
|
||||
Hint for the proof:
|
||||
|
||||
Split the sequence into subsequences such that each subsequence LRU has $k$ misses.
|
||||
|
||||
Argue that OPT has at least $1$ miss in each subsequence.
|
||||
|
||||
QED
|
||||
|
||||
#### Many sensible algorithms are $k$-competitive
|
||||
|
||||
**Lower Bound**: No deterministic online algorithm is better than $k$-competitive.
|
||||
|
||||
**Resource augmentation**: Offline algorithm (which knows the future) has $k$ cache lines in its cache and the online algorithm has $ck$ cache lines with $c>1$.
|
||||
|
||||
##### Lemma: Competitive Ratio is $\sim \frac{c}{c-1}$
|
||||
|
||||
Say $c=2$. LRU cache has twice as much as cache. LRU is $2$-competitive.
|
||||
|
||||
Proof:
|
||||
|
||||
LRU has cache of size $2k$.
|
||||
|
||||
Divide the sequence into subsequences such that you have $ck$ distinct pages.
|
||||
|
||||
In each subsequence, LRU has at most $ck$ misses.
|
||||
|
||||
The OPT has at least $(c-1)k$ misses.
|
||||
|
||||
So competitive ratio is at most $\frac{ck}{(c-1)k}=\frac{c}{c-1}$.
|
||||
|
||||
_Actual competitive ratio is $\sim \frac{c}{c-1+\frac{1}{k}}$._
|
||||
|
||||
QED
|
||||
|
||||
### Conclusion
|
||||
|
||||
- Definition: some information unknown
|
||||
- Clairvoyant vs. Online
|
||||
- Competitive Ratio
|
||||
- Example:
|
||||
- Elevator
|
||||
- Cache Replacement
|
||||
|
||||
### Example 3: Pessimal cache problem
|
||||
|
||||
Maximize number of cache misses.
|
||||
|
||||
Maximization problem: competitive ratio is $max\{\frac{\text{cost of the optimal online algorithm}}{\text{cost of our algorithm}}\}$.
|
||||
|
||||
Or get $min\{\frac{\text{cost of our algorithm}}{\text{cost of the optimal online algorithm}}\}$.
|
||||
|
||||
The size of the cache is $k$.
|
||||
|
||||
So if OPT has $X$ cache misses, we want $\geq \frac{X}{\alpha}$. cache misses where $\alpha$ is the competitive ratio.
|
||||
|
||||
Claim: The OPT could always miss (note quite) except when the page is accessed twice in a row.
|
||||
|
||||
Claim: No deterministic online algorithm has a bounded competitive ratio. (that is independent of the length of the sequence)
|
||||
|
||||
Proof:
|
||||
|
||||
Start with an empty cache. (size of cache is $k$)
|
||||
|
||||
Miss the first $k$ unique pages.
|
||||
|
||||
$P_1,P_2,\cdots,P_k|P_{k+1},P_{k+2},\cdots,P_{2k}$
|
||||
|
||||
Say your deterministic online algorithm choose to evict $P_i$ for $i\in\{1,2,\cdots,k\}$.
|
||||
|
||||
We want to choose $P_i$ for $i\in\{1,2,\cdots,k\}$ such that the number of misses is maximized.
|
||||
|
||||
The optimal offline solution: evict the page that will be accessed furthest in the future. Let's call it $\sigma$.
|
||||
|
||||
The online algorithm: evict $P_i$ for $i\in\{1,2,\cdots,k\}$. Will have $k+1$ misses in the worst case.
|
||||
|
||||
So the competitive ratio is at most $\frac{\sigma}{k+1}$, which is unbounded.
|
||||
|
||||
#### Randomized most recently used (RAND, MRU)
|
||||
|
||||
MRU without randomization is a deterministic algorithm, and thus, the competitive ration is bounded.
|
||||
|
||||
First $k$ unique accesses brings all pages to cache.
|
||||
|
||||
On the $k+1$th access, pick a random page from the cache and evict it.
|
||||
|
||||
After that evict the MRU no a miss.
|
||||
|
||||
Claim: RAND is $k$-competitive.
|
||||
|
||||
#### Lemma: After the first $k+1$ unique accesses at all times
|
||||
|
||||
1. 1 page is in the cache with probability 1 (the MRU one)
|
||||
2. There exists $k$ pages each of which is in the cache with probability $1-\frac{1}{k}$
|
||||
3. All other pages are in the cache with probability $0$.
|
||||
|
||||
Proof:
|
||||
|
||||
By induction.
|
||||
|
||||
Base case: right after the first $k+1$ unique accesses and before $k+2$th access.
|
||||
|
||||
1. $P_{k+1}$ is in the cache with probability $1$.
|
||||
2. When we brought $P_{k+1}$ to the cache, we evicted one page uniformly at random. (i.e. $P_i$ is evicted with probability $\frac{1}{k}$, $P_i$ is still in the cache with probability $1-\frac{1}{k}$)
|
||||
3. All other $r$ pages are definitely not in the cache because we did not see them yet.
|
||||
|
||||
Inductive cases:
|
||||
|
||||
Let $P$ be a page that is in the cache with probability $0$
|
||||
|
||||
Cache miss and RAND MRU evict $P'$ for another page with probability in this cache with probability $0$.
|
||||
|
||||
1. $P$ is in the cache with probability $1$.
|
||||
2. By induction, there exists a set of $k$ pages each of which is in the cache with probability $1-\frac{1}{k}$.
|
||||
3. All other pages are in the cache with probability $0$.
|
||||
|
||||
Let $P$ be a page in the cache with probability $1-\frac{1}{k}$.
|
||||
|
||||
With probability $\frac{1}{k}$, $P$ is not in the cache and RAND evicts $P'$ in the cache and brings $P$ to the cache.
|
||||
|
||||
QED
|
||||
|
||||
MRU is $k$-competitive.
|
||||
|
||||
Proof:
|
||||
|
||||
Case 1: Access MRU page.
|
||||
|
||||
Both OPT and our algorithm don't miss.
|
||||
|
||||
Case 2: Access some other 1 page
|
||||
|
||||
OPT definitely misses.
|
||||
|
||||
RAND MRU misses with probability $\geq \frac{1}{k}$.
|
||||
|
||||
Let's define the random variable $X$ as the number of misses of RAND MRU.
|
||||
|
||||
$E[X]\leq 1+\frac{1}{k}$.
|
||||
|
||||
QED
|
||||
152
content/CSE347/CSE347_L11.md
Normal file
152
content/CSE347/CSE347_L11.md
Normal file
@@ -0,0 +1,152 @@
|
||||
# Lecture 11
|
||||
|
||||
## More randomized algorithms
|
||||
|
||||
> Caching problem: You have a cache with $k$ blocks and a sequence of accesses, called $\sigma$. The cost of a randomized caching algorithm is the expected number of cache misses on $\sigma$.
|
||||
|
||||
### Randomized Marking Algorithm
|
||||
|
||||
> A phase $i$ has $n_i$ new pages.
|
||||
|
||||
Our goal is to optimize $m^*(\sigma)\geq \frac{1}{2}\sum_{i=1}^{n} n_j$ where $n_j$ is the number of new pages in phase $j$.
|
||||
|
||||
Marking algorithm:
|
||||
|
||||
- at a cache miss, evict an unmarked page uniformly at random
|
||||
- at the beginning of the algorithm, all the entries are unmarked
|
||||
- after $k$ unique accesses and one miss, all the entries are unmarked
|
||||
- old pages: pages in cache at the end of the previous phase
|
||||
- new pages: pages accessed in this phase that are not old.
|
||||
- new pages always cause a miss.
|
||||
- old pages can cause a miss if a new page was accessed and replaced that old page and then the old page was accessed again. This can also be caused by old pages replacing other old pages and creating this cascading effect.
|
||||
|
||||
Reminder: Competitive ratio for our randomized algorithm is
|
||||
|
||||
$$
|
||||
max_\sigma \{\frac{E[m(\sigma)]}{m^*(\sigma)}\}
|
||||
$$
|
||||
|
||||
```python
|
||||
def randomized_marking_algorithm(sigma, k):
|
||||
cache = set()
|
||||
marked = set()
|
||||
misses = 0
|
||||
for page in sigma:
|
||||
if page not in cache:
|
||||
# once all the blocks are marked, unmark all the blocks
|
||||
if len(marked) == k:
|
||||
marked.clear()
|
||||
# if the cache is full, randomly remove a page that is not marked
|
||||
if len(cache) == k:
|
||||
for page in cache:
|
||||
if page not in marked:
|
||||
cache.remove(page)
|
||||
misses += 1
|
||||
# add the new page to the cache and mark it
|
||||
cache.add(page)
|
||||
marked.add(page)
|
||||
return misses
|
||||
```
|
||||
|
||||
Example:
|
||||
|
||||
A cache on phase $i$ has $k$ blocks and miss on page $x$:
|
||||
|
||||
[$n_i$ new pages] [$o_i$ old pages] [$x$] [$\ldots$]
|
||||
|
||||
$P[x \text{ causes a miss}] = P[x\text{ was evicted earlier}] \leq \frac{n_j}{k-o_i}$
|
||||
|
||||
Proof:
|
||||
|
||||
**Warning: the first few line of the equation might be wrong.**
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
P\left[x \text{ was evicted earlier}\bigg\vert\begin{array}{c} n_j\text{ new pages}, \\ o_i\text{ old pages}, \\ k \text{ unmarked blocks} \end{array}\right] &=P[x\text{ was unmarked}]+P[x\text{ was marked}] \\
|
||||
&=P[x\text{ was unmarked (new page)}]+P[x\text{ was old page}]+P[x\text{ was in the remaining cache blocks}] \\
|
||||
&= \frac{1}{k}+\frac{o_i}{k} P\left[x \text{ was evicted earlier}\bigg\vert\begin{array}{c} n_j-1\text{ new pages}, \\ o_i-1\text{ old pages}, \\ k-1 \text{ unmarked blocks} \end{array}\right] +\frac{k-1-o_i}{k} P\left[x \text{ was evicted earlier}\bigg\vert\begin{array}{c} n_j-1\text{ new pages}, \\ o_i\text{ old pages}, \\ k-1 \text{ unmarked blocks} \end{array}\right] \\
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Let $P(n_j, o_i, k)$ be the probability that page $x$ causes a miss when the cache has $n_j$ new pages, $o_i$ old pages, and $k$ unmarked blocks.
|
||||
|
||||
Using $P(n_j, o_i, k)\leq \frac{n_j}{k-o_i}$, we have
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
P(n_j, o_i, k) &= \frac{1}{k}+\frac{o_i}{k} P(n_j-1, o_i-1, k-1)+\frac{k-1-o_i}{k} P(n_j-1, o_i, k-1) \\
|
||||
&\leq \frac{1}{k}+\frac{o_i}{k} \frac{n_j-1}{k-1-o_i-1}+\frac{k-1-o_i}{k} \frac{n_j-1}{k-1-o_i} \\
|
||||
&= \frac{1}{k}+\left(1+\frac{o_in}{k-o_i}+\frac{n_j-1}{k-o_i}\right)\\
|
||||
&=\frac{1}{k}\left(\frac{k-o_i+o_in+(n_j-1)(k-o_i)}{k-o_i}\right)\\
|
||||
&= \frac{n_j}{k-o_i}
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Fix a phase $j$, let $x_i$ be an indicator random variable
|
||||
|
||||
$$
|
||||
x_i=\begin{cases}
|
||||
1 & \text{if page } i \text{th old page causes a miss} \\
|
||||
0 & \text{otherwise}
|
||||
\end{cases}
|
||||
$$
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
P[x_i=1]&=P[i\text{th old page causes a miss}]\\
|
||||
&\leq \frac{n_j}{k-(i-1)}\\
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
E[x_i]&=E[\sum_{i=1}^{o_i} P[x_i=1]]\\
|
||||
&= E[n_j+\sum_{i=1}^{k-n_j}x_i]\\
|
||||
&=n_j+\sum_{i=1}^{k-n_j} E[x_i]\\
|
||||
&\leq n_j+\sum_{i=1}^{k-n_j} \frac{n_j}{k-(i-1)}\\
|
||||
&=n_j+\left(1+\frac{1}{k}+\frac{1}{k-1}+\cdots+\frac{1}{n_j}\right)\\
|
||||
&\leq n_j H_k\\
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Let $N$ be the total number of phases.
|
||||
|
||||
So the expected total number of misses is
|
||||
|
||||
$$
|
||||
E[\sum_{i=1}^{N} x_i]\leq \sum_{i=1}^{N} E[x_i]\leq\sum_{j=1}^{N} n_j H_k
|
||||
$$
|
||||
|
||||
So the competitive ratio is
|
||||
|
||||
$$
|
||||
\frac{E[\sum_{i=1}^{N} x_i]}{\frac{1}{2}\sum_{j=1}^{N} n_j}\leq 2H_k=O(\log k)
|
||||
$$
|
||||
|
||||
## Probabilistic boosting for decision problems
|
||||
|
||||
Assume that you have a randomized algorithm that gives you the correct answer with probability $\frac{1}{2}+\epsilon$. for some $\epsilon>0$.
|
||||
|
||||
I want to boost the probability of the correct decision to be $\geq 1-\delta$.
|
||||
|
||||
What we can do is to run the algorithm $x$ times independently with probability $\frac{1}{2}+\epsilon$ and take the majority vote.
|
||||
|
||||
The probability of the wrong decision is
|
||||
|
||||
$$
|
||||
\binom{x}{\lceil x/2\rceil} \left(\frac{1}{2}-\epsilon\right)^{\lceil x/2\rceil}
|
||||
$$
|
||||
|
||||
I want to choose $x$ such that this is $\leq \delta$.
|
||||
|
||||
> $$(1-p)^{\frac{1}{p}}\leq e^{-1}$$
|
||||
|
||||
So
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\binom{x}{\lceil x/2\rceil}\left(\frac{1}{2}-\epsilon\right)^{\lceil x/2\rceil}&\leq \left(\frac{xe}{x/2}\right)^{\lceil x/2\rceil}\left(\frac{1}{2}-\epsilon\right)^{-\lceil x/2\rceil\epsilon}
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
We use this to solve for $x$.
|
||||
334
content/CSE347/CSE347_L2.md
Normal file
334
content/CSE347/CSE347_L2.md
Normal file
@@ -0,0 +1,334 @@
|
||||
# Lecture 2
|
||||
|
||||
## Divide and conquer
|
||||
|
||||
Review of CSE 247
|
||||
|
||||
1. Divide the problem into (generally equal) smaller subproblems
|
||||
2. Recursively solve the subproblems
|
||||
3. Combine the solutions of subproblems to get the solution of the original problem
|
||||
- Examples: Merge Sort, Binary Search
|
||||
|
||||
Recurrence
|
||||
|
||||
Master Method:
|
||||
|
||||
$$
|
||||
T(n)=aT(\frac{n}{b})+\Theta(f(n))
|
||||
$$
|
||||
|
||||
### Example 1: Multiplying 2 numbers
|
||||
|
||||
Normal Algorithm:
|
||||
|
||||
```python
|
||||
def multiply(x,y):
|
||||
p=0
|
||||
for i in y:
|
||||
p+=x*y
|
||||
return p
|
||||
```
|
||||
|
||||
divide and conquer approach
|
||||
|
||||
```python
|
||||
def multiply(x,y):
|
||||
n=max(len(x),len(y))
|
||||
if n==1:
|
||||
return x*y
|
||||
xh,xl=x>>(n/2),x&((1<<n/2)-1)
|
||||
yh,yl=y>>(n/2),y&((1<<n/2)-1)
|
||||
return (multiply(xh,yh)<<n)+((multiply(xh,yl)+multiply(yh,xl))<<(n/2))+multiply(xl,yl)
|
||||
```
|
||||
|
||||
$$
|
||||
T(n)=4T(n/2)+\Theta(n)=\Theta(n^2)
|
||||
$$
|
||||
|
||||
Not a useful optimization
|
||||
|
||||
But,
|
||||
|
||||
$$
|
||||
multiply(xh,yl)+multiply(yh,xl)=multiply(xh-xl,yh-yl)+multiply(xh,yh)+multiply(xl,yl)
|
||||
$$
|
||||
|
||||
```python
|
||||
def multiply(x,y):
|
||||
n=max(len(x),len(y))
|
||||
if n==1:
|
||||
return x*y
|
||||
xh,xl=x>>(n/2),x&((1<<n/2)-1)
|
||||
yh,yl=y>>(n/2),y&((1<<n/2)-1)
|
||||
zhh=multiply(xh,yh)
|
||||
zll=multiply(xl,yl)
|
||||
return (zhh<<n)+((multiply(xh-xl,yh-yl)+zhh+zll)<<(n/2))+zll
|
||||
```
|
||||
|
||||
$$
|
||||
T(n)=3T(n/2)+\Theta(n)=\Theta(n^{\log_2 3})\approx \Theta(n^{1.58})
|
||||
$$
|
||||
|
||||
### Example 2: Closest Pairs
|
||||
|
||||
Input: $P$ is a set of $n$ points in the plane. $p_i=(x_i,y_i)$
|
||||
|
||||
$$
|
||||
d(p_i,p_j)=\sqrt{(x_i-x_j)^2+(y_i-y_j)^2}
|
||||
$$
|
||||
|
||||
Goal: Find the distance between the closest pair of points.
|
||||
|
||||
Naive algorithm: iterate all pairs ($O(n)=\Theta(n^2)$).
|
||||
|
||||
Divide and conquer algorithm:
|
||||
|
||||
Preprocessing: Sort $P$ by $x$ coordinate to get $P_x$.
|
||||
|
||||
Base case:
|
||||
|
||||
- 1 point: clostest d = inf
|
||||
- 2 points: clostest d = d(p_1,p_2)
|
||||
|
||||
Divide Step:
|
||||
|
||||
Compute mid point and get $Q, R$.
|
||||
|
||||
Recursive step:
|
||||
|
||||
- $d_l$ closest pair in $Q$
|
||||
- $d_r$ closest pair in $R$
|
||||
|
||||
Combine step:
|
||||
|
||||
Calculate $d_c$ closest point such that one point is on the left side and the other is on the right.
|
||||
|
||||
return $min(d_c,d_l,d_r)$
|
||||
|
||||
Total runtime:
|
||||
|
||||
$$
|
||||
T(n)=2T(n/2)+\Theta(n^2)
|
||||
$$
|
||||
|
||||
Still no change.
|
||||
|
||||
Important Insight: Can reduce the number of checks
|
||||
|
||||
**Lemma:** If all points within this square are at least $\delta=min\{d_r,d_l\}$ apart, there are at most 4 points in this square.
|
||||
|
||||
A better algorithm:
|
||||
|
||||
1. Divide $P_x$ into 2 halves using the mid point
|
||||
2. Recursively computer the $d_l$ and $d_r$, take $\delta=min(d_l,d_r)$.
|
||||
3. Filter points into y-strip: points which are within $(mid_x-\delta,mid_x+\delta)$
|
||||
4. Sort y-strip by y coordinate. For every point $p$, we look at this y-strip in sorted order starting at this point and stop when we see a point with y coordinate $>p_y +\delta$
|
||||
|
||||
```python
|
||||
# d is distance function
|
||||
def closestP(P,d):
|
||||
Px=sorted(P,key=lambda x:x[0])
|
||||
def closestPRec(P,d):
|
||||
n=len(P)
|
||||
if n==1:
|
||||
return float('inf')
|
||||
if n==2:
|
||||
return d(P[0],P[1])
|
||||
Q,R=Px[:n//2],Px[n//2:]
|
||||
midx=R[0][0]
|
||||
dl,dr=closestP(Q),closestP(R)
|
||||
dc=min(dl,dr)
|
||||
ys=[i if midx-dc<i[0]<midx+dc for i in P]
|
||||
ys.sort()
|
||||
yn=len(ys)
|
||||
# this step below checks at most 4 points, (but still runs O(n))
|
||||
for i in range(yn):
|
||||
for j in range(i,yn):
|
||||
curd=d(ys[i],ys[j])
|
||||
if curd>dc:
|
||||
break
|
||||
dc=min(dc,curd)
|
||||
return dc
|
||||
return closestPRec(Px,d):
|
||||
```
|
||||
|
||||
Runtime analysis:
|
||||
|
||||
$$
|
||||
T(n)=2T(n/2)+\Theta(n\log n)=\Theta(n\log^2 n)
|
||||
$$
|
||||
|
||||
We can do even better by presorting Y
|
||||
|
||||
1. Divide $P_x$ into 2 halves using the mid point
|
||||
2. Recursively computer the $d_l$ and $d_r$, take $\delta=min(d_l,d_r)$.
|
||||
3. Filter points into y-strip: points which are within $(mid_x-\delta,mid_x+\delta)$ by visiting presorted $P_y$
|
||||
|
||||
```python
|
||||
# d is distance function
|
||||
def closestP(P,d):
|
||||
Px=sorted(P,key=lambda x:x[0])
|
||||
Py=sorted(P,key=lambda x:x[1])
|
||||
def closestPRec(P,d):
|
||||
n=len(P)
|
||||
if n==1:
|
||||
return float('inf')
|
||||
if n==2:
|
||||
return d(P[0],P[1])
|
||||
Q,R=Px[:n//2],Px[n//2:]
|
||||
midx=R[0][0]
|
||||
dl,dr=closestP(Q),closestP(R)
|
||||
dc=min(dl,dr)
|
||||
ys=[i if midx-dc<i[0]<midx+dc for i in Py]
|
||||
yn=len(ys)
|
||||
# this step below checks at most 4 points, (but still runs O(n))
|
||||
for i in range(yn):
|
||||
for j in range(i,yn):
|
||||
curd=d(ys[i],ys[j])
|
||||
if curd>dc:
|
||||
break
|
||||
dc=min(dc,curd)
|
||||
return dc
|
||||
return closestPRec(Px,d):
|
||||
```
|
||||
|
||||
Runtime analysis:
|
||||
|
||||
$$
|
||||
T(n)=2T(n/2)+\Theta(n)=\Theta(n\log n)
|
||||
$$
|
||||
|
||||
## In-person lectures
|
||||
|
||||
$$
|
||||
T(n)=aT(n/b)+f(n)
|
||||
$$
|
||||
|
||||
$a$ is number of sub problems, $n/b$ is size of subproblems, $f(n)$ is the cost of divide and combine cost.
|
||||
|
||||
### Example 3: Max Contiguous Subsequence Sum (MCSS)
|
||||
|
||||
Given: array of integers (positive or negative), $S=[s_1,s_2,...,s_n]$
|
||||
|
||||
Return: $max\{\sum^i_{k=i} s_k|1\leq i\leq n, i\leq j\leq n\}$
|
||||
|
||||
Trivial solution:
|
||||
|
||||
brute force
|
||||
$O(n^3)$
|
||||
|
||||
A bit better solution:
|
||||
|
||||
$O(n^2)$ use prefix sum to reduce cost for sum.
|
||||
|
||||
Divide and conquer solution.
|
||||
|
||||
```python
|
||||
def MCSS(S):
|
||||
def MCSSMid(S,i,j,mid):
|
||||
res=S[j]
|
||||
for l in range(i,j):
|
||||
curS=0
|
||||
for r in range(l,j):
|
||||
curS+=S[r]
|
||||
res=max(res,curS)
|
||||
return res
|
||||
def MCSSRec(i,j):
|
||||
if i==j:
|
||||
return S[i]
|
||||
mid=(i+j)//2
|
||||
L,R=MCSSRec(i,mid),MCSSRec(mid,j)
|
||||
C=MCSSMid(i,j)
|
||||
return min([L,C,R])
|
||||
return MCSSRec(0,len(S))
|
||||
```
|
||||
|
||||
If `MCSSMid(S,i,j,mid)` use trivial solution, the running time is:
|
||||
|
||||
$$
|
||||
T(n)=2T(n/2)+O(n^2)=\Theta(n^2)
|
||||
$$
|
||||
|
||||
and we did nothing.
|
||||
|
||||
Observations: Any contiguous subsequence that starts on the left and ends on the right can be split into two parts as `sum(S[i:j])=sum(S[i:mid])+sum(S[mid,j])`
|
||||
|
||||
and let $LS$ be the subsequence that has the largest sum that ends at mid, and $RS$ be the subsequence that has the largest sum on the right that starts at mid.
|
||||
|
||||
**Lemma:** Biggest subsequence that contains `S[mid]` is $LS+RP$
|
||||
|
||||
Proof:
|
||||
|
||||
By contradiction,
|
||||
|
||||
Assume for the sake of contradiction that $y=L'+R'$ is a sum of such a subsequence that is larger than $x$ ($y>x$).
|
||||
|
||||
Let $z=LS+R'$, since $LS\geq L'$, by definition of $LS$, then $z\geq y$, WOLG, $RS\geq R'$, $x\geq y$, which contradicts that $y>x$.
|
||||
|
||||
Optimized function as follows:
|
||||
|
||||
```python
|
||||
def MCSS(S):
|
||||
def MCSSMid(S,i,j,mid):
|
||||
res=S[mid]
|
||||
LS,RS=0,0
|
||||
cl,cr=0,0
|
||||
for l in range(mid-1,i-1,-1):
|
||||
cl+=S[l]
|
||||
LS=max(LS,cl)
|
||||
for r in range(mid+1,j):
|
||||
cr+=S[r]
|
||||
RS=max(RS,cr)
|
||||
return res+LS+RS
|
||||
def MCSSRec(i,j):
|
||||
if i==j:
|
||||
return S[i]
|
||||
mid=(i+j)//2
|
||||
L,R=MCSSRec(i,mid),MCSSRec(mid,j)
|
||||
C=MCSSMid(i,j)
|
||||
return min([L,C,R])
|
||||
return MCSSRec(0,len(S))
|
||||
```
|
||||
|
||||
The running time is:
|
||||
|
||||
$$
|
||||
T(n)=2T(n/2)+O(n)=\Theta(n\log n)
|
||||
$$
|
||||
|
||||
Strengthening the recusions:
|
||||
|
||||
```python
|
||||
def MCSS(S):
|
||||
def MCSSRec(i,j):
|
||||
if i==j:
|
||||
return S[i],S[i],S[i],S[i]
|
||||
mid=(i+j)//2
|
||||
L,lp,ls,sl=MCSSRec(i,mid)
|
||||
R,rp,rs,sr=MCSSRec(mid,j)
|
||||
return min([L,R,ls+rp]),max(lp,sl+rp),max(rs,sr+ls),sl+sr
|
||||
return MCSSRec(0,len(S))
|
||||
```
|
||||
|
||||
Pre-computer version:
|
||||
|
||||
```python
|
||||
def MCSS(S):
|
||||
pfx,sfx=[0],[S[-1]]
|
||||
n=len(S)
|
||||
for i in range(n-1):
|
||||
pfx.append(pfx[-1]+S[i])
|
||||
sfx.insert(sfx[0]+S[n-i-2],0)
|
||||
def MCSSRec(i,j):
|
||||
if i==j:
|
||||
return S[i],pfx[i],sfx[i]
|
||||
mid=(i+j)//2
|
||||
L,lp,ls=MCSSRec(i,mid)
|
||||
R,rp,rs=MCSSRec(mid,j)
|
||||
return min([L,R,ls+rp]),max(lp,sfx[mid]-sfx[i]+rp),max(rs,sfx[j]-sfx[mid]+ls)
|
||||
return MCSSRec(0,n)
|
||||
```
|
||||
|
||||
$$
|
||||
T(n)=2T(n/2)+O(1)=\Theta(n)
|
||||
$$
|
||||
161
content/CSE347/CSE347_L3.md
Normal file
161
content/CSE347/CSE347_L3.md
Normal file
@@ -0,0 +1,161 @@
|
||||
# Lecture 3
|
||||
|
||||
## Dynamic programming
|
||||
|
||||
When we cannot find a good Greedy Choice, the only thing we can do is to iterate all choices.
|
||||
|
||||
### Example 1: Edit distance
|
||||
|
||||
Input: 2 sequences of some character set, e.g.
|
||||
|
||||
$S=ABCADA$, $T=ABADC$
|
||||
|
||||
Goal: Computer the minimum number of **insertions or deletions** you could do to convert $S$ into $T$
|
||||
|
||||
We will call it `Edit Distance(S[1...n],T[1...m])`. where `n` and `m` be the length of `S` and `T` respectively.
|
||||
|
||||
Idea: computer difference between the sequences.
|
||||
|
||||
Observe: The difference we observed appears at index 3, and in this example where the sequences are short, it is obvious that it is better to delete 'C'. But for long sequence, we donot know that the later sequence looks like so it is hard to make a decision on whether to insert 'A' or delete 'C'.
|
||||
|
||||
Use branching algorithm:
|
||||
|
||||
```python
|
||||
def editDist(S,T,i,j):
|
||||
if len(S)<=i:
|
||||
return len(T)
|
||||
if len(T)<=j:
|
||||
return len(S)
|
||||
if S[i]==T[j]:
|
||||
return editDist(S,T,i+1,j+1)
|
||||
else:
|
||||
return min(editDist(S,T,i+1,j),editDist(S,T,i,j+1))
|
||||
```
|
||||
|
||||
Correctness Proof Outline:
|
||||
|
||||
- ~~Greedy Choice Property~~
|
||||
|
||||
- Complete Choice Property:
|
||||
- The optimal solution makes **one** of the choices that we consider
|
||||
- Inductive Structure:
|
||||
- Once you make **any** choice, you are left with a smaller problem of the same type. **Any** first choice + **feasible** solution to the subproblem = feasible solution to the entire problem.
|
||||
- Optimal Substructure:
|
||||
- If we optimally solve the subproblem for **a particular choice c**, and combine it with c, resulting solution is the **optimal solution that makes choice c**.
|
||||
|
||||
Correctness Proof:
|
||||
|
||||
Claim: For any problem $P$, the branking algorithm finds the optimal solution.
|
||||
|
||||
Proof: Induct on problem size
|
||||
|
||||
- Base case: $|S|=0$ or $|T|=0$, obvious
|
||||
- Inductive Case: By inductive hypothesis: Branching algorithm works for all smaller problems, either $S$ is smaller or $T$ is smaller or both
|
||||
- For each choice we make, we got a strictly smaller problem: by inductive structure, and the answer is correct by inductive hypothesis.
|
||||
- By Optimal substructure, we know for any choice, the solution of branching algorithm for subproblem and the choice we make is an optimal solution for that problem.
|
||||
- Using Complete choice property, we considered all the choices.
|
||||
|
||||
Using tree graph, the left and right part of the tree has height n, but the middle part of the tree has height 2n. So the running time is $\Omega(2^n)$, at least $2^n$.
|
||||
|
||||
#### How could we reduce the complexity?
|
||||
|
||||
There are **overlapping subproblems** that we compute more than once! Number of distinct subproblems is polynomial, we can **share the solution** that we have already computed!
|
||||
|
||||
**store the result of subprolem in 2D array**
|
||||
|
||||
Use dp:
|
||||
|
||||
```python
|
||||
def editDist(S,T,i,j):
|
||||
m,n=len(S),len(T)
|
||||
dp=[[0]*(n+1) for _ in range(m+1)]
|
||||
for i in range(n):
|
||||
dp[i][m]=n-i
|
||||
for i in range(m):
|
||||
dp[n][j]=m-i
|
||||
for i in range(m):
|
||||
for j in range(n):
|
||||
if S[i]==T[j]:
|
||||
dp[i][j]=dp[i+1][j+1]
|
||||
else:
|
||||
# assuming the cost of insertion and deletion is 1
|
||||
dp[i][j]=min(1+dp[i][j+1],1+dp[i+1][j])
|
||||
```
|
||||
|
||||
We can use backtracking to find out how do we reach our final answer. Then the new runtime will be the time used to complete the table, which is $T(n,m)=\Theta(mn)$
|
||||
|
||||
### Example 2: Weighted Interval Scheduling (IS)
|
||||
|
||||
Input: $P=\{p_1,p_2,...,p_n\}$, $p_i=\{s_i,f_i,w_i\}$
|
||||
$s_i$ is the start time, $f_i$ is the finish time, $w_i$ is the weight of the task for job $i$
|
||||
|
||||
Goal: Pick a set of **non-overlapping** intervals $\Pi$ such that $\sum_{p_i\in \Pi} w_i$ is maximized.
|
||||
|
||||
Trivial solution ($T(n)=O(2^n)$)
|
||||
|
||||
```python
|
||||
# p=[[s_i,f_i,w_i],...]
|
||||
p=[]
|
||||
p.sort()
|
||||
n=len(p)
|
||||
def intervalScheduling(idx):
|
||||
res=0
|
||||
if i>=n:
|
||||
return res
|
||||
for i in range(idx,n):
|
||||
# pick when end
|
||||
if p[idx][1]>p[i][0]:
|
||||
continue
|
||||
res=max(intervalScheduling(i+1)+p[i][2],res)
|
||||
return intervalScheduling(0)
|
||||
```
|
||||
|
||||
Using dp ($T(n)=O(n^2)$)
|
||||
|
||||
```python
|
||||
def intervalScheduling(p):
|
||||
p.sort()
|
||||
n=len(p)
|
||||
dp=[0]*(n+1)
|
||||
for i in range(n-1,-1,-1):
|
||||
# load initial best case: do nothing
|
||||
dp[i]=dp[i+1]
|
||||
_,e,w=p[i]
|
||||
for j in range(bisect.bisect_left(p,e,key=lambda x:x[0]),n+1):
|
||||
dp[i]=max(dp[i],w+dp[j])
|
||||
return dp[0]
|
||||
```
|
||||
|
||||
### Example 3: Subset sums
|
||||
|
||||
Input: a set $S$ of positive and unique integers and another integer $K$.
|
||||
|
||||
Problem: Is there a subset $X\subseteq S$ such that $sum(X)=K$
|
||||
|
||||
Brute force takes $O(2^n)$.
|
||||
|
||||
```python
|
||||
def subsetSum(arr,i,k)->bool:
|
||||
if i>=len(arr):
|
||||
if k==0:
|
||||
return True
|
||||
return False
|
||||
return subsetSum(i+1,k-arr[i]) or subsetSum(i+1,k)
|
||||
```
|
||||
|
||||
Using dp $O(nk)$
|
||||
|
||||
```python
|
||||
def subsetSum(arr,k)->bool:
|
||||
n=len(arr)
|
||||
dp=[False]*(k+1)
|
||||
dp[0]=True
|
||||
for e in arr:
|
||||
ndp=[]
|
||||
for i in range(k+1):
|
||||
ndp.append(dp[i])
|
||||
if i-e>=0:
|
||||
ndp[i]|=dp[i-e]
|
||||
dp=ndp
|
||||
return dp[-1]
|
||||
```
|
||||
321
content/CSE347/CSE347_L4.md
Normal file
321
content/CSE347/CSE347_L4.md
Normal file
@@ -0,0 +1,321 @@
|
||||
# Lecture 4
|
||||
|
||||
## Maximum Flow
|
||||
|
||||
### Example 1: Ship cement from factory to building
|
||||
|
||||
Input $s$: source, $t$: destination
|
||||
|
||||
Graph with **directed** edges weights on each edge: **capacity**
|
||||
|
||||
**Goal:** Ship as much stuff as possible while obeying capacity constrains.
|
||||
|
||||
Graph: $(V,E)$ directed and weighted
|
||||
|
||||
- Unique source and sink nodes $\to s, t$
|
||||
- Each edge has capacity $c(e)$ [Integer]
|
||||
|
||||
A valid flow assignment assigns an integer $f(e)$ to each edge s.t.
|
||||
|
||||
Capacity constraint: $0\leq f(e)\leq c(e)$
|
||||
|
||||
Flow conservation:
|
||||
|
||||
$$
|
||||
\sum_{e\in E_{in}(v)}f(e)=\sum_{e\in E_{out}(v)}f(e),\forall v\in V-{s,t}
|
||||
$$
|
||||
|
||||
$E_{in}(v)$: set of incoming edges to $v$
|
||||
$E_{out}(v)$: set of outgoing edges from $v$
|
||||
|
||||
Compute: Maximum Flow: Find a valid flow assignment to
|
||||
|
||||
Maximize $|F|=\sum_{e\in E_{in}(t)}f(e)=\sum_{e\in E_{out}(s)}f(e)$ (total units received by end and sent by source)
|
||||
|
||||
Additional assumptions
|
||||
|
||||
1. $s$ has no incoming edges, $t$ has no outgoing edges
|
||||
2. You do not have a cycle of 2 nodes
|
||||
|
||||
A proposed algorithm:
|
||||
|
||||
1. Find a path from $s$ to $t$
|
||||
2. Push as much flow along the path as possible
|
||||
3. Adjust the capacities
|
||||
4. Repeat until we cannot find a path
|
||||
|
||||
**Residual Graph:** If there is an edge $e=(u,v)$ in $G$, we will add a back edge $\bar{e}=(v,u)$. Capacity of $\bar{e}=$ flow on $e$. Call this graph $G_R$.
|
||||
|
||||
Algorithm:
|
||||
|
||||
- Find an "augmenting path" $P$.
|
||||
- $P$ can contain forward or backward edges!
|
||||
- Say the smallest residual capacity along the path is $k$.
|
||||
- Push $k$ flow on the path ($f(e) =f(e) + k$ for all edges on path $P$)
|
||||
- Reduce the capacity of all edges on the path $P$ by $k$
|
||||
- **Increase** the capacity of the corresponding mirror/back edges
|
||||
- Repeat until there are no augmenting paths
|
||||
|
||||
### Formalize: Ford-Fulkerson (FF) Algorithm
|
||||
|
||||
1. Initialize the residual graph $G_R=G$
|
||||
2. Find an augmenting path $P$ with capacity $k$ (min capacity of any edge on $P$)
|
||||
3. Fix up the residual capacities in $G_R$
|
||||
- $c(e)=c(e)-k,\forall e\in P$
|
||||
- $c(\bar{e})=c(\bar{e})+k,\forall \bar{e}\in P$
|
||||
4. Repeat 2 and 3 until no augmenting path can be found in $G_R$.
|
||||
|
||||
```python
|
||||
def ford_fulkerson_algo(G,n,s,t):
|
||||
"""
|
||||
Args:
|
||||
G: is the graph for max_flow
|
||||
n: is the number of vertex in the graph
|
||||
s: start vertex of flow
|
||||
t: end vertex of flow
|
||||
Returns:
|
||||
the max flow in graph from s to t
|
||||
"""
|
||||
# Initialize the residual graph $G_R=G$
|
||||
GR=[defaultdict(int) for i in range(n)]
|
||||
for i in range(n):
|
||||
for v,_ in enumerate(G[i]):
|
||||
# weight w is unused
|
||||
GR[v][i]=0
|
||||
path=set()
|
||||
def augP(cur):
|
||||
# Find an augumentting path $P$ with capacity $k$ (min capacity of any edge on $P$)
|
||||
if cur==t: return True
|
||||
# true for edge in residual path, false for edge in graph
|
||||
for v,w in G[cur]:
|
||||
if w==0 or (cur,v,False) in path: continue
|
||||
path.add((cur,v,False))
|
||||
if augP(v): return True
|
||||
path.remove((cur,v,False))
|
||||
for v,w in GR[cur]:
|
||||
if w==0 or (cur,v,True) in path: continue
|
||||
path.add((cur,v,True))
|
||||
if augP(v): return True
|
||||
path.remove((cur,v,True))
|
||||
return False
|
||||
while augP(s):
|
||||
k=min([GR[a][b] if isR else G[a][b] for a,b,isR in path])
|
||||
# Fix up the residual capacities in $G_R$
|
||||
# - $c(e)=c(e)-k,\forall e\in P$
|
||||
# - $c(\bar{e})=c(\bar{e})+k,\forall \bar{e}\in P$
|
||||
for a,b,isR in path:
|
||||
if isR:
|
||||
GR[a][b]+=k
|
||||
else:
|
||||
G[a][b]-=k
|
||||
return sum(GR[s].values())
|
||||
```
|
||||
|
||||
#### Proof of Correctness: Valid Flow
|
||||
|
||||
**Lemma 1:** FF finds a valid flow
|
||||
|
||||
- Capacity and conservation constrains are not violated
|
||||
- Capacity constraint: $0\leq f(e)\leq c(e)$
|
||||
- Flow conservation: $\sum_{e\in E_{in}(v)}f(e)=\sum_{e\in E_{out}(v)}f(e),\forall v\in V-\{s,t\}$
|
||||
|
||||
Proof: We proceed by induction on **augmenting paths**
|
||||
|
||||
##### Base Case
|
||||
|
||||
$f(e)=0$ on all edges
|
||||
|
||||
##### Inductive Case
|
||||
|
||||
By inductive hypothesis, we have a valid flow and the corresponding residual graph $G_R$.
|
||||
|
||||
Inductive Step:
|
||||
|
||||
Now we find an augmented path $P$ in $GR$, pushed $k$ (which is the smallest edge capacity on $P$). Argue that the constraints are not violated.
|
||||
|
||||
**Capacity Constrains:** Consider an edge $e$ in $P$.
|
||||
|
||||
- If $e$ is an forward edge (in the original graph)
|
||||
- by construction of $G_R$, it had left over capacities.
|
||||
- If $e$ is an back edge with residual capacity $\geq k$
|
||||
- flow on real edge reduces, but the real capacity is still $\geq 0$, no capacity constrains violation.
|
||||
|
||||
**Conservation Constrains:** Consider a vertex $v$ on path $P$
|
||||
|
||||
1. Both forward edges
|
||||
- No violation, push $k$ flow into $v$ and out.
|
||||
2. Both back edges
|
||||
- No violation, push $k$ less flow into $v$ and out.
|
||||
3. Redirecting flow
|
||||
- No violation, change of $0$ by $k-k$ on $v$.
|
||||
|
||||
#### Proof of Correctness: Termination
|
||||
|
||||
**Lemma 2:** FF terminate
|
||||
|
||||
Proof:
|
||||
|
||||
Every time it finds an augmenting path that increases the total flow.
|
||||
|
||||
Must terminate either when it finds a max flow or before.
|
||||
|
||||
Each iteration we use $\Theta(m+n)$ to find a valid path.
|
||||
|
||||
The number of iteration $\leq |F|$, the total is $\Theta(|F|(m+n))$ (not polynomial time)
|
||||
|
||||
#### Proof of Correctness: Optimality
|
||||
|
||||
From Lemma 1 and 2, we know that FF returns a feasible solution, but does it return the **maximum** flow?
|
||||
|
||||
##### Max-flow Min-cut Theorem
|
||||
|
||||
Given a graph $G(V,E)$, a **graph cut** is a partition of vertices into 2 subsets.
|
||||
|
||||
- $S$: $s$ + maybe some other vertices
|
||||
- $V-S$: $t$ + maybe some other vertices
|
||||
|
||||
Define capacity of the cut be the sum of capacity of edges that go from a vertex in $S$ to a vertex in $T$.
|
||||
|
||||
**Lemma 3:** For all valid flows $f$, $|f|\leq C(S)$ for all cut $S$ (Max-flow $\leq$ Min-cut)
|
||||
|
||||
Proof: all flow must go through one of the cut edges.
|
||||
|
||||
**Min-cut:** cut of smallest capacity, $S^*$. $|f|\leq C(S^*)$
|
||||
|
||||
**Lemma 4:** FF produces a flow $=C(S^*)$
|
||||
|
||||
Proof: Let $\hat{f}$ be the flow found by FF. Mo augmenting paths in $G_R$.
|
||||
|
||||
Let $\hat{S}$ be all vertices that can be reached from $s$ using edges with capacities $>0$.
|
||||
|
||||
and all the forward edges going out of the cut are saturated. Since back edges have capacity 0, no flow is going into the cut $S$.
|
||||
|
||||
If some flow was coming from $V-\hat{S}$, then there must be some edges with capacity $>0$. So, $|f|\leq C(S^*)$
|
||||
|
||||
### Example 2: Bipartite Matching
|
||||
|
||||
input: Given $n$ classes and $n$ rooms; we want to match classes to rooms.
|
||||
|
||||
Bipartite graph $G=(V,E)$ (unweighted and undirected)
|
||||
|
||||
- Vertices are either in set $L$ or $R$
|
||||
- Edges only go between vertices of different sets
|
||||
|
||||
Matching: A subset of edges $M\subseteq E$ s.t.
|
||||
|
||||
- Each vertex has at most one edge from $M$ incident on it.
|
||||
|
||||
Maximum Matching: matching of the largest size.
|
||||
|
||||
We will reduce the problem to the problem of finding the maximum flow
|
||||
|
||||
#### Reduction
|
||||
|
||||
Given a bipartite graph $G=(V,E)$, construct a graph $G'=(V',E')$ such that
|
||||
|
||||
$$
|
||||
|max-flow (G')|=|max-flow(G)|
|
||||
$$
|
||||
|
||||
Let $s$ connects to all vertices in $L$ and all vertex in $R$ connects to $t$.
|
||||
|
||||
$G'=G+s+t+$added edges form $S$ to $T$ and added capacities.
|
||||
|
||||
#### Proof of correctness
|
||||
|
||||
Claim: $G'$ has a flow of $k$ iff $G$ has a matching of size $k$
|
||||
|
||||
Proof: Two directions:
|
||||
|
||||
1. Say $G$ has a matching of size $k$, we want to prove $G'$ has a flow of size $k$.
|
||||
2. Say $G'$ has a flow of size $k$, we want to prove $G$ has a matching of size $k$.
|
||||
|
||||
## Conclusion: Maximum Flow
|
||||
|
||||
Problem input and target
|
||||
|
||||
Ford-Fulkerson Algorithm
|
||||
|
||||
- Execution: residual graph
|
||||
- Runtime
|
||||
|
||||
FF correctness proof
|
||||
|
||||
- Max-flow Min-cut Theorem
|
||||
- Graph Cut definition
|
||||
- Capacity of cut
|
||||
|
||||
Reduction to Bipartite Matching
|
||||
|
||||
### Example 3: Image Segmentation: (reduction from min-cut)
|
||||
|
||||
Given:
|
||||
|
||||
- Image consisting of an object and a background.
|
||||
- the object occupies some set of pixels $A$, while the background occupies the remaining pixels $B$.
|
||||
|
||||
Required:
|
||||
|
||||
- Separate $A$ from $B$ but if doesn't know which pixels are each.
|
||||
- For each pixel $i,p_i$ is the probability that $i\in A$
|
||||
- For each pair of adjacent pixels $i,j,c_{ij}$ is the cost of placing the object boundary between them. i.e. putting $i$ in $A$ and $j$ in $B$.
|
||||
- A segmentation of the image is an assignment of each pixel to $A$ or $B$.
|
||||
- The goal is to find a segmentation that maximizes
|
||||
|
||||
$$
|
||||
\sum_{i\in A}p_i+\sum_{i\in B}(1-p_i)-\sum_{i,j\ on \ boundary}c_{ij}
|
||||
$$
|
||||
|
||||
Solution:
|
||||
|
||||
- Let's turn our maximization into a minimization
|
||||
- If the image has $N$ pixels, then we can rewrite the objective as
|
||||
|
||||
$$
|
||||
N-\sum_{i\in A}(1-p_i)-\sum_{i\in B}p_i-\sum_{i,j\ on \ boundary}c_{ij}
|
||||
$$
|
||||
|
||||
because $N=\sum_{i\in A}p_i+\sum_{i\in A}(1-p_i)+\sum_{i\in B}p_i+\sum_{i\in B}(1-p_i)$ boundary
|
||||
|
||||
New maximization problem:
|
||||
|
||||
$$
|
||||
Max\left( N-\sum_{i\in A}(1-p_i)-\sum_{i\in B}p_i-\sum_{i,j\ on \ boundary}c_{ij}\right)
|
||||
$$
|
||||
|
||||
Now, this is equivalent ot minimizing
|
||||
|
||||
$$
|
||||
\sum_{i\in A}(1-p_i)+\sum_{i\in B}p_i+\sum_{i,j\ on \ boundary}c_{ij}
|
||||
$$
|
||||
|
||||
Second steps
|
||||
|
||||
- Form a graph with $n$ vertices, $v_i$ on for each pixel
|
||||
- Add vertices $s$ and $t$
|
||||
- For each $v_i$, add edges $S-T$ cut of $G$ assigned each $v_i$ to either $S$ side or $T$ side.
|
||||
- The $S$ side of an $S-T$ is the $A$ side, while the $T$ side of the cur is the $B$ side.
|
||||
- Observer that if $v_i$ goes on the $S$ side, it becomes part of $A$, so the cut increases by $1-p$. Otherwise, it become part of $B$, so the cut increases by $p_i$ instead.
|
||||
- Now add edges $v_i\to v_j$ with capacity $c_{ij}$ for all adjacent pixels pairs $i,j$
|
||||
- If $v_i$ and $v_j$ end up on opposite sides of the cut (boundary), then the cut increases by $c_{ij}$.
|
||||
- Conclude that any $S-T$ cut that assigns $S\subseteq V$ to the $A$ side and $V\backslash S$ to the $B$ side pays a total of
|
||||
1. $1-p_i$ for each $v_i$ on the $A$ side
|
||||
2. $p_i$ for each $v_i$ on the $B$ side
|
||||
3. $c_{ij}$ for each adjacent pair $i,j$ that is at the boundary. i.e. $i\in S\ and\ j\in V\backslash S$
|
||||
- Conclude that a cut with a capacity $c$ implies a segmentation with objective value $cs$.
|
||||
- The converse can (and should) be also checked: a segmentation with subjective value $c$ implies a $S-T$ cut with capacity $c$.
|
||||
|
||||
#### Algorithm
|
||||
|
||||
- Given an image with $N$ pixels, build the graph $G$ as desired.
|
||||
- Use the FF algorithm to find a minimum $S-T$ cut of $G$
|
||||
- Use this cut to assign each pixel to $A$ or $B$ as described, i.e pixels that correspond to vertices on the $S$ side are assigned to $A$ and those corresponding to vertices on the $T$ side to $B$.
|
||||
- Minimizing the cut capacity minimizes our transformed minimization objective function.
|
||||
|
||||
#### Running time
|
||||
|
||||
The graph $G$ contains $\Theta(N)$ edges, because each pixel is adjacent to a maximum of of 4 neighbors and $S$ and $T$.
|
||||
|
||||
FF algorithm has running time $O((m+n)|F|)$, where $|F|\leq |n|$ is the size of set of min-cut. The edge count is $m=6n$.
|
||||
|
||||
So the total running time is $O(n^2)$
|
||||
341
content/CSE347/CSE347_L5.md
Normal file
341
content/CSE347/CSE347_L5.md
Normal file
@@ -0,0 +1,341 @@
|
||||
# Lecture 5
|
||||
|
||||
## Takeaway from Bipartite Matching
|
||||
|
||||
- We saw how to solve a problem (bi-partite matching and others) by reducing it to another problem (maximum flow).
|
||||
- In general, we can design an algorithm to map instances of a new problem to instances of known solvable problem (e.g., max-flow) to solve this new problem!
|
||||
- Mapping from one problem to another which preserves solutions is called reduction.
|
||||
|
||||
## Reduction: Basic Ideas
|
||||
|
||||
Convert solutions to the known problem to the solutions to the new problem
|
||||
|
||||
- Instance of new problem
|
||||
- Instance of known problem
|
||||
- Solution of known problem
|
||||
- Solution of new problem
|
||||
|
||||
## Reduction: Formal Definition
|
||||
|
||||
Problems $L,K$.
|
||||
|
||||
$L$ reduces to $K$ ($L\leq K$) if there is a mapping $\phi$ from **any** instance $l\in L$ to some instance $\phi(l)\in K'\subset K$, such that the solution for $\phi(l)$ yields a solution for $l$.
|
||||
|
||||
This means that **L is no harder than K**
|
||||
|
||||
### Using reduction to design algorithms
|
||||
|
||||
In the example of reduction to solve Bipartite Matching:
|
||||
|
||||
$L:$ Bipartite Matching
|
||||
|
||||
$K:$ Max-flow Problem
|
||||
|
||||
Efficiency:
|
||||
|
||||
1. Reduction: $\phi:l\to\phi(l)$ (Polynomial time reduction $\phi(l)$)
|
||||
2. Solve prom $\phi(l)$ (Polynomial time to solve $poly(g)$)
|
||||
3. Convert the solution for $\phi(l)$ to a solution to $l$ (Polynomial time to solve $poly(g)$)
|
||||
|
||||
### Efficient Reduction
|
||||
|
||||
A reduction $\phi:l\to\phi(l)$ is efficient ($L\leq p(k)$) if for any $l\in L$:
|
||||
|
||||
1. $\phi(l)$ is computable from $l$ in polynomial ($|l|$) time.
|
||||
2. Solution to $l$ is computable from solution of $\phi(l)$ in polynomial ($|l|$) time.
|
||||
|
||||
We call $L$ is **poly-time reducible** to $K$, or $L$ poly-time
|
||||
reduces to $K$.
|
||||
|
||||
### Which problem is harder?
|
||||
|
||||
Theorem: If $L\leq p(k)$ and there is a polynomial time algorithm to solve $K$, then there is a polynomial time algorithm to solve $L$.
|
||||
|
||||
Proof: Given an instance of $l\in L$ If we can convert the problem in polynomial time with respect to the original problem $l$.
|
||||
|
||||
1. Compute $\phi(l)$: $p(l)$
|
||||
2. Solve $\phi(l)$: $p(\phi(l))$
|
||||
3. Convert solution: $p(\phi(l))$
|
||||
|
||||
Total time: $p(l)+p(\phi(l))+p(\phi(l))=p(l)+p(\phi(l))$
|
||||
Need to show: $|\phi(l)|=poly(|l|)$
|
||||
|
||||
Proof:
|
||||
|
||||
Since we can convert $\phi(l)$ in $p(l)$ time, and on every time step, (constant step) we can only write constant amount of data.
|
||||
|
||||
So $|\phi(l)|=poly(|l|)$
|
||||
|
||||
## Hardness Problems
|
||||
|
||||
Reductions show the relationship between problem hardness!
|
||||
|
||||
Question: Could you solve a problem in polynomial time?
|
||||
|
||||
Easy: polynomial time solution
|
||||
Hard: No polynomial time solution (as far as we know)
|
||||
|
||||
### Types of Problems
|
||||
|
||||
Decision Problem: Yes/No answer
|
||||
|
||||
Examples: Subset sums
|
||||
|
||||
1. Is the there a flow of size $F$
|
||||
2. Is there a shortest path of length $L$ from vertex $u$ to vertex $v$.
|
||||
3. Given a set of intercal, can you schedule $k$ of them.
|
||||
|
||||
Optimization Problem: What is the value of an optimal feasible solution of a problem?
|
||||
|
||||
- Minimization: Minimize cost
|
||||
- min cut
|
||||
- minimal spanning tree
|
||||
- shortest path
|
||||
- Maximization: Maximize profit
|
||||
- interval scheduling
|
||||
- maximum flow
|
||||
- maximum matching
|
||||
|
||||
#### Canonical Decision Problem
|
||||
|
||||
Does the instance $l\in L$ (an optimization problem) have a feasible solution with objective value $k$:
|
||||
|
||||
Objective value $\geq k$ (maximization) $\leq k$ (minimization)
|
||||
|
||||
$DL$ is the reduced Canonical Decision problem $L$
|
||||
|
||||
##### Hardness of Canonical Decision Problems
|
||||
|
||||
Lemma 1: $DL\leq p(L)$ ($DL$ is no harder than $L$)
|
||||
|
||||
Proof: Assume $L$ **maximization** problem $DL(l)$: does have a solution $\geq k$.
|
||||
|
||||
Example: Does graph $G$ have flow $\geq k$.
|
||||
|
||||
Let $v^∗$ be the maximum objective on $l$ by solving $l$.
|
||||
|
||||
Let the instance of $DL:(l,k)$ and $l$ be the problem and $k$ be the objective
|
||||
|
||||
1. $l\to \phi(l)\in L$ (optimization problem) $\phi(l,k)=l$
|
||||
2. Is $v^*(l)\geq k$? If so, return true, else return false.
|
||||
|
||||
Lemma 2: If $v^* =O(c^{|l|})$ for any constant $c$, then $L\leq p(DL)$.
|
||||
|
||||
Proof: First we could show $L\leq DL$. Suppose maximization problem, canonical decision problem is is there a solution $\geq k$.
|
||||
|
||||
Naïve Linear Search: Ask $DL(l,k)$, if returns false, ask $DL(l,k+1)$ until returns true
|
||||
|
||||
Runtime: At most $k$ search to iterate all possibilities.
|
||||
|
||||
This is exponential! How to reduce it?
|
||||
|
||||
Our old friend Binary (exponential) Search is back!
|
||||
|
||||
You gets a no at some value: try power of 2 until you get a no, then do binary search
|
||||
|
||||
\# questions: $=log_2(v^*(l))=poly(l)$
|
||||
|
||||
Binary search in area: from last yes to first no.
|
||||
|
||||
Runtime: Binary search ($O(n)=\log(v^*(l))$)
|
||||
|
||||
### Reduction for Algorithm Design vs Hardness
|
||||
|
||||
For problems $L,K$
|
||||
|
||||
If $K$ is “easy” (exists a poly-time solution), then $L$ is also easy.
|
||||
|
||||
If $L$ is “hard” (no poly-time solution), then $k$ is also hard.
|
||||
|
||||
Every problem that we worked on so far, $K$ is “easy”, so we reduce from new problem to known problem (e.g., max-flow).
|
||||
|
||||
#### Reduction for Hardness: Independent Set (ISET)
|
||||
|
||||
Input: Given an undirected graph $G = (V,E)$,
|
||||
|
||||
A subset of vertices $S\subset V$ is called an **independent set** if no two vertices of are connected by an edge.
|
||||
|
||||
Problem: Does $G$ contain an independent set of size $\geq k$?
|
||||
|
||||
$ISET(G,k)$ returns true if $G$ contains an independent set of size $\geq k$, and false otherwise.
|
||||
|
||||
Algorithm? NO! We think that this is a hard problem.
|
||||
|
||||
A lot of pQEDle have tried and could not find a poly-time solution
|
||||
|
||||
### Example: Vertex Cover (VC)
|
||||
|
||||
Input: Given an undirected graph $G = (V,E)$
|
||||
|
||||
A subset of vertices $C\subset V$ is called a **vertex cover** if contains at least one end point of every edge.
|
||||
|
||||
Formally, for all edges $(u,v)\in E$, either $u\in C$, or $v\in C$.
|
||||
|
||||
Problem: $VC(G,j)$ returns true if has a vertex cover of size $\leq j$, and false otherwise (minimization problem)
|
||||
|
||||
Example:
|
||||
|
||||
#### How hard is Vertex Cover?
|
||||
|
||||
Claim: $ISET\leq p(VC)$
|
||||
Side Note: when we prove $VC$ is hard, we prove it is no easier than $ISET$.
|
||||
|
||||
DO NOT: $VC\leq p(ISET)$
|
||||
|
||||
Proof: Show that $G=(V,E)$ has an independent set of $k$ **if and only if** the same graph (not always!) has a vertex cover of size $|V|-k$.
|
||||
|
||||
Map:
|
||||
|
||||
$$
|
||||
ISET(G,k)\to VC(g,|v|-k)
|
||||
$$
|
||||
|
||||
$G'=G$
|
||||
|
||||
##### Proof of reduction: Direction 1
|
||||
|
||||
Claim 1: $ISET$ of size $k\to$ $VC$ of size $|V|-k$
|
||||
|
||||
Proof: Assume $G$ has an $ISET$ of size $k:S$, consider $C = V-S,|C|=|V|-k$
|
||||
|
||||
Claim: $C$ is a vertex cover
|
||||
|
||||
##### Proof of reduction: Direction 2
|
||||
|
||||
|
||||
Claim 2: $VC$ of size $|V|-k\to ISET$ of size $k$
|
||||
|
||||
Proof: Assume $G$ has an $VC$ of size $|V| −k:C$, consider $S = V − C, |S| =k$
|
||||
|
||||
Claim: $S$ is an independent set
|
||||
|
||||
### What does poly-time mean?
|
||||
|
||||
Algorithm runs in time polynomial to input size.
|
||||
|
||||
- If the input has items, algorithm runs in $\Theta(n^c)$ for any constant is poly-time.
|
||||
- Examples: intervals to schedule, number of integers to sort, # vertices + # edges in a graph
|
||||
- Numerical Value (Integer $n$), what is the input size?
|
||||
- Examples: weights, capacity, total time, flow constraints
|
||||
- It is not straightforward!
|
||||
|
||||
### Real time complexity of F-F?
|
||||
|
||||
In class: $O(F( |V| + |E|))$
|
||||
|
||||
- $|V| + |E|$ = this much space to represent the graph
|
||||
- $F$ : size of the maximum flow.
|
||||
|
||||
If every edge has capacity , then $F = O(CE)$
|
||||
Running time:$O(C|E|(|V| + |E| )))$
|
||||
|
||||
### What is the actual input size?
|
||||
|
||||
Each edge ($|E|$ edges):
|
||||
|
||||
- 2 vertices: $|V|$ distinct symbol, $\log |V|$ bits per symbol
|
||||
- 1 capacity: $\log C$
|
||||
|
||||
Size of graph:
|
||||
|
||||
- $O(|E|(|V| + \log C))$
|
||||
- $p( |E| , |V| , \log C)$
|
||||
|
||||
Running time:
|
||||
|
||||
- $P( |E| , |V| , |C| )$
|
||||
- Exponential if is exponential in $|V|+|E|$
|
||||
|
||||
### Pseudo-polynomial
|
||||
|
||||
Naïve Ford-Fulkerson is bad!
|
||||
|
||||
Problem ’s inputs contain some numerical values, say $|W|$. We need only log bits to store . If algorithms runs in $p(W)$, then it is exponential, or **pseudopolynomial**.
|
||||
|
||||
In homework, you improved F-F to make it work in
|
||||
$p( |V| ,|E| , \log C)$, to make it a real polynomial algorithm.
|
||||
|
||||
## Conclusion: Reductions
|
||||
|
||||
- Reduction
|
||||
- Construction of mapping with runtime
|
||||
- Bidirectional proof
|
||||
- Efficient Reduction $L\leq p(K)$
|
||||
- Which problem is harder?
|
||||
- If $L$ is hard, then $K$ is hard. $\to$ Used to show hardness
|
||||
- If $K$ is easy, then $L$ is easy. $\to$ Used for design algorithms
|
||||
- Canonical Decision Problem
|
||||
- Reduction to and from the optimization problem
|
||||
- Reduction for hardness
|
||||
- Independent Set$leq p$ Vertex Cover
|
||||
|
||||
## On class
|
||||
|
||||
Reduction: $V^* = O(c^k)$
|
||||
|
||||
OPT: Find max flow of at least one instance $(G,s,t)$
|
||||
|
||||
DEC: Is there a flow of size $pK$, given $G,s,t \implies$ the instance is defined by the tuple $(G,s,t,k)$
|
||||
|
||||
Yes, if there exists one
|
||||
No, otherwise
|
||||
|
||||
Forget about F-F and assume that you have an oracle that solves the decision problem.
|
||||
|
||||
First solution (the naive solution): iterate over $k = 1, 2, \dots$ until the oracle returns false and the last one returns true would be the max flow.
|
||||
|
||||
Time complexity: $K\cdot X$, where $X$ is the time complexity of the oracle
|
||||
Input size: $poly(||V|,|E|, |E|log(max-capacity))$, and $V^* \leq \sum$ capacities
|
||||
|
||||
A better solution: do a binary search. If there is no upper bound, we use exponential binary search instead. Then,
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
log(V^*) &\leq X\cdot log(\sum capacities)\\
|
||||
&\leq X\cdot log(|E|\cdot maxCapacity)\\
|
||||
&\leq X\cdot (log(|E| + log(maxCapacity)))
|
||||
\end{aligned}
|
||||
$$
|
||||
As $\log(maxCapacity)$ is linear in the size of the input, the running time is polynomial to the solution of the original problem.
|
||||
|
||||
Assume that ISET is a hard problem, i.e. we don't know of any polynomial time solution. We want to show that vertex cover is also a hard problem here:
|
||||
|
||||
$ISET \leq_{p} VC$
|
||||
|
||||
1. Given an instance of ISET, construct an instance of VC
|
||||
2. Show that the construction can be done in polynomial time
|
||||
3. Show that if the ISET instance is true than the CV instance is true
|
||||
4. Show that if the VC instance is true then the ISET instance is true.
|
||||
|
||||
> ISET: given $(G,K)$, is there a set of vertices that do not share edges of size $K$
|
||||
> VC: given $(G,K)$, is there a set of vertices that cover all edges of size $K$
|
||||
|
||||
1. Given $l: (G,K)$ being an instance of ISET, we construct $\phi(l): (G',K')$ as an instance of VC. $\phi(l): (G, |V|-K), \textup{i.e., } G' = G \cup K' = |V| - K$
|
||||
2. It is obvious that it is a polynomial time construction since copying the graph is linear, in the size of the graph and the subtraction of integers is constant time.
|
||||
|
||||
**Direction 1**: ISET of size k $\implies$ VC of size $|V| - K$ Assume that ISET(G,K) returns true, show that $VC(G, |V|-K)$ returns true
|
||||
|
||||
Let $S$ be an independent set of size $K$ and $C = V-S$
|
||||
|
||||
We claim that $C$ is a vertex cover of size $|V|-K$
|
||||
|
||||
Proof:
|
||||
|
||||
We proceed by contradiction. Assume that $C$ is NOT a vertex cover, and it means that there is an edge $(u,v)$ such that $u\notin c , v\notin C$. And it implies that $u\in S , v\in S$, which contradicts with the assumption that S is an independent set.
|
||||
Therefore, $c$ is an vertex cover
|
||||
|
||||
**Direction 2**: VC of size $|V|-K \implies$ ISET of size $K$
|
||||
|
||||
Let $C$ be a vertex cover of size $|V|-K$ , let $s = |v| - c$
|
||||
|
||||
We claim that $S$ is an independent set of size $K$.
|
||||
|
||||
Again, assume, for the sake of contradiction, that $S$ is not an independent set. And we get
|
||||
|
||||
$\exists (u,v) \textup{such that } u\in S, v \in S$
|
||||
|
||||
$u,v \notin C$
|
||||
|
||||
$C \textup{ is not a vertex cover}$
|
||||
|
||||
And this is a contradiction with our assumption.
|
||||
287
content/CSE347/CSE347_L6.md
Normal file
287
content/CSE347/CSE347_L6.md
Normal file
@@ -0,0 +1,287 @@
|
||||
# Lecture 6
|
||||
|
||||
## NP-completeness
|
||||
|
||||
### $P$: Polynomial-time Solvable
|
||||
|
||||
$P$: Class of decision problems $L$ such that there is a polynomial-time algorithm that correctly answers yes or not for every instance $l\in L$.
|
||||
|
||||
Algorithm "$A$ decides $L$". If algorithm $A$ always correctly answers for any instance $l\in L$.
|
||||
|
||||
Example:
|
||||
|
||||
Is the number $n$ prime? Best algorithm so far: $O(\log^6 n)$, 2002
|
||||
|
||||
## Introduction to NP
|
||||
|
||||
- NP$\neq$ Non-polynomial (Non-deterministic polynomial time)
|
||||
- Let $L$ be a decision problem.
|
||||
- Let $l$ be an instance of the problem that the answer happens to be "yes".
|
||||
- A **certificate** c(l) for $l$ is a "proof" that the answer for $l$ is true. [$l$ is a true instance]
|
||||
- For canonical decision problems for optimization problems, the certificate is often a feasible solution for the corresponding optimization problem.
|
||||
|
||||
### Example of certificates
|
||||
|
||||
- Problem: Is there a path from $s$ to $t$
|
||||
- Instance: graph $G(V,E),s,t$.
|
||||
- Certificate: path from $s$ to $t$.
|
||||
- Problem: Can I schedule $k$ intervals in the room so that they do not conflict.
|
||||
- Instance: $l:(I,k)$
|
||||
- Certificate: set of $k$ non-conflicting intervals.
|
||||
- Problem: ISET
|
||||
- Instance: $G(V,E),k$.
|
||||
- Certificate: $k$ vertices with no edges between them.
|
||||
|
||||
If the answer to the problem is NO, you don't need to provide anything to prove that.
|
||||
|
||||
### Useful certificates
|
||||
|
||||
For a problem to be in NP, the problem need to have "useful" certificates. What is considered a good certificate?
|
||||
|
||||
- Easy to check
|
||||
- Verifying algorithm which can check a YES answer and a certificate in $poly(l)$
|
||||
- Not too long: [$poly(l)$]
|
||||
|
||||
### Verifier Algorithm
|
||||
|
||||
**Verifier algorithm** is one that takes an instance $l\in L$ and a certificate $c(l)$ and says yes if the certificate proves that $l$ is a true instance and false otherwise.
|
||||
|
||||
$V$ is a poly-time verifier for $L$ is it is a verifier and runs in $poly(|l|,|c|)$ time. (c=$poly(l)$)
|
||||
|
||||
- The runtime must be polynomial
|
||||
- Must check **every** problem constraint
|
||||
- Not always trivial
|
||||
|
||||
## Class NP
|
||||
|
||||
**NP:** A class of decision problems such that exists a certificate schema $c$ and a verifier algorithm $V$ such that:
|
||||
|
||||
1. certificate is $poly(l)$ in size.
|
||||
2. $V:poly(l)$ in time.
|
||||
|
||||
**P:** is a class of problems that you can **solve** in polynomial time
|
||||
|
||||
**NP:** is a class of problems that you can **verify** TRUE instances in polynomial time given a poly-size certificate
|
||||
|
||||
**Millennium question**
|
||||
|
||||
$P\subseteq NP$? $NP\subseteq P$?
|
||||
|
||||
$P\subseteq NP$ is true.
|
||||
|
||||
Proof: Let $L$ be a problem in $P$, we want to show that there is a polynomial size certificate with a poly-time verifier.
|
||||
|
||||
There is an algorithm $A$ which solves $L$ in polynomial time.
|
||||
|
||||
**Certificate:** empty thing.
|
||||
|
||||
**Verifier:** $(l,c)$
|
||||
|
||||
1. Discard $c$.
|
||||
2. Run $A$ on $l$ and return the answer.
|
||||
|
||||
Nobody knows the solution $NP\subseteq P$. Sad.
|
||||
|
||||
### Class of problem: NP complete
|
||||
|
||||
Informally: hardest problem in NP
|
||||
|
||||
Consider a problem $L$.
|
||||
|
||||
- We want to show if $L\subseteq P$, then $NP\subseteq P$
|
||||
|
||||
**NP-hard**: A decision problem $L$ is NP-hard if for any problem $K\in NP$, $K\leq_p L$.
|
||||
|
||||
$L$ is at least as hard as all the problems in NP. If we have an algorithm for $L$, we have an algorithm for any problem in NP with only polynomial time extra cost.
|
||||
|
||||
MindMap:
|
||||
|
||||
$K\implies L\implies sol(L)\implies sol(K)$
|
||||
|
||||
#### Lemma $P=NP$
|
||||
|
||||
Let $L$ be an NP-hard problem. If $L\in P$, then $P=NP$.
|
||||
|
||||
Proof:
|
||||
|
||||
Say $L$ has a poly-time solution, some problem $K$ in $NP$.
|
||||
|
||||
For any $K\in NP$, $NP\subset P$, $P\subset NP$, then $P=NP$.
|
||||
|
||||
**NP-complete:** $L$ is **NP-complete** if it is both NP-hard and $L\in NP$.
|
||||
|
||||
**NP-optimization:** $L$ is **NP-optimization** problem if the canonical decision problem is NP-complete.
|
||||
|
||||
**Claim:** If any NP-optimization problem have polynomial-time solution, then $P=NP$.
|
||||
|
||||
### Is $P=NP$?
|
||||
|
||||
- Answering this problem is hard.
|
||||
- But for any NP-complete problem, if you could find a poly-time algorithm for $L$, then you would have answered this question.
|
||||
- Therefore, finding a poly-time algorithm for $L$ is hard.
|
||||
|
||||
## NP-Complete problem
|
||||
|
||||
### Satisfiability (SAT)
|
||||
|
||||
Boolean Formulas:
|
||||
|
||||
A set of Boolean variables:
|
||||
|
||||
$x,y,a,b,c,w,z,...$ they take values true or false.
|
||||
|
||||
A boolean formula is a formula of Boolean variables with and, or and not.
|
||||
|
||||
Examples:
|
||||
|
||||
$\phi:x\land (\neg y \lor z)\land\neg(y\lor w)$
|
||||
|
||||
$x=1,y=0,z=1,w=0$, the formula is $1$.
|
||||
|
||||
**SAT:** given a formula $\phi$, is there a setting $M$ of variables such that the $\phi$ evaluates to True under this setting.
|
||||
|
||||
If there is such assignment, then $\phi$ is satisfiable. Otherwise, it is not.
|
||||
|
||||
Example: $x\land y\land \neg(x\lor y)$ is not satisfiable.
|
||||
|
||||
A seminar paper by Cook and Levin in 1970 showed that SAT is NP-complete.
|
||||
|
||||
1. SAT is in NP
|
||||
Proof:
|
||||
$\exists$ a certificate schema and a poly-time verifier.
|
||||
$c$ satisfying assignment $M$ and $v$ check that $M$ makes $\phi$ true.
|
||||
2. SAT is NP-hard. we can just accept it has a fact.
|
||||
|
||||
#### How to show a problem is NP-complete?
|
||||
|
||||
Say we have a problem $L$.
|
||||
|
||||
1. Show that $L\in NP$.
|
||||
Exists certificate schema and verification algorithm in polynomial time.
|
||||
2. Prove that we can reduce SAT to $L$. $SAT\leq_p L$ **(NOT $L\leq_p SAT$)**
|
||||
Solving $L$ also solve SAT.
|
||||
|
||||
### CNF-SAT
|
||||
|
||||
**CNF:** Conjugate normal form of SAT
|
||||
|
||||
The formula $\phi$ must be an "and of ors"
|
||||
|
||||
$$
|
||||
\phi=\land_{i=1}^n(\lor^{m_i}_{j=1}l_{i,j})
|
||||
$$
|
||||
|
||||
$l_{i,j}$: clause
|
||||
|
||||
### 3-CNF-SAT
|
||||
|
||||
**3-CNF-SAT:** where every clauses has exactly 3 literals.
|
||||
|
||||
is NP complete [not all version of them are, 2-CNF-SAT is in P]
|
||||
|
||||
Input: 3-CNF expression with $n$ variables and $m$ clauses in the form:
|
||||
|
||||
number of total literals: $3m$
|
||||
|
||||
Output: An assignment of the $n$ variables such that at least one literal from each clauses evaluates to true.
|
||||
|
||||
Note:
|
||||
|
||||
1. One variable can be used to satisfy multiple clauses.
|
||||
2. $x_i$ and $\neg x_i$ cannot both evaluate to true.
|
||||
|
||||
Example: ISET is NP-complete.
|
||||
|
||||
Proof:
|
||||
|
||||
Say we have a problem $L$
|
||||
|
||||
1. Show that $ISET\in NP$
|
||||
Certificate: set of $k$ vertices: $|S|=k\in poly(g)$\
|
||||
Verifier: checks that there are no edges between them $O(E k^2)$
|
||||
2. ISET is NP-hard. We need to prove $3SAT\leq_p ISET$
|
||||
- Construct a reduction from $3SAT$ to $ISET$.
|
||||
- Show that $ISET$ is harder than $3SAT$.
|
||||
|
||||
We need to prove $\phi\in 3SAT$ is satisfiable if and only if the constructed $G$ has an $ISET$ of size $\geq k=m$
|
||||
|
||||
#### Reduction mapping construction
|
||||
|
||||
We construct an ISET instance from $3-SAT$.
|
||||
|
||||
Suppose the formula has $n$ variables and $m$ clauses
|
||||
|
||||
1. for each clause, we construct vertex for each literal and connect them (for $x\lor \neg y\lor z$, we connect $x,\neg y,z$ together)
|
||||
2. then we connect all the literals with their negations (connects $x$ and $\neg x$)
|
||||
|
||||
$\implies$
|
||||
|
||||
If $\phi$ has a satisfiable assignment, then $G$ has an independent set of size $\geq m$,
|
||||
|
||||
For a set $S$ we pick exactly one true literal from every clause and take the corresponding vertex to that clause, $|S|=m$
|
||||
|
||||
Must also argue that $S$ is an independent set.
|
||||
|
||||
Example: picked a set of vertices $|S|=4$.
|
||||
|
||||
A literal has edges:
|
||||
|
||||
- To all literals in the same clause: We never pick two literals form the same clause.
|
||||
- To its negation.
|
||||
|
||||
Since it is a satisfiable 3-SAT assignment, $x$ and $\neg x$ cannot both evaluate to true, those edges are not a problem, so $S$ is an independent set.
|
||||
|
||||
$\impliedby$
|
||||
|
||||
If $G$ has an independent set of size $\geq m$, then $\phi$ is satisfiable.
|
||||
|
||||
Say that $S$ is an independent set of $m$, we need to construct a satisfiable assignment for the original $\phi$.
|
||||
|
||||
- If $S$ contains a vertex corresponding to literal $x_i$, then set $x_i$ to true.
|
||||
- If contains a vertex corresponding to literal $\neg x_i$, then set $x_i$ to false.
|
||||
- Other variables can be set arbitrarily
|
||||
|
||||
Question: Is it a valid 3-SAT assignment?
|
||||
|
||||
Your ISET $S$ can contain at most $1$ vertex from each clause. Since vertices in a clause are connected by edges.
|
||||
|
||||
- Since $S$ contains $m$ vertices, it must contain exactly $1$ vertex from each clause.
|
||||
- Therefore, we will make at least $1$ literals form each clause to be true.
|
||||
- Therefore, all the clauses are true and $\phi$ is satisfied.
|
||||
|
||||
## Conclusion: NP-completeness
|
||||
|
||||
- Prove NP-Complete:
|
||||
- If NP-optimization, convert to canonical decision problem
|
||||
- Certificate, Verification algorithm
|
||||
- Prove NP-hard: reduce from existing NP-Complete
|
||||
problems
|
||||
- 3-SAT Problem:
|
||||
- Input, output, constraints
|
||||
- A well-known NP-Complete problem
|
||||
- Reduce from 3-SAT to ISET to show ISET is NP-Complete
|
||||
|
||||
## On class
|
||||
|
||||
### NP-complete
|
||||
|
||||
$p\in NP$, if we have a certificate schema and a verifier algorithm.
|
||||
|
||||
### NP-complete proof
|
||||
|
||||
#### P is in NP
|
||||
|
||||
what a certificate would looks like, show that if has a polynomial time o the problem size.
|
||||
|
||||
design a verifier algorithm that checks a certificate if it indeed prove tha the answer is YES and has a polynomial time complexity. Inputs: certificate and the problem input $poly(|l|,|c|)=poly(|p|)$
|
||||
|
||||
#### P is NP hard
|
||||
|
||||
select an already known NP-hard problem: eg. 3-SAT, ISET, VC,...
|
||||
|
||||
show that $3-SAT\leq_p p$
|
||||
|
||||
- present an algorithm that given any instance of 3-SAT (on the chosen NP hard problem) to an instance of $p$.
|
||||
- show that the construction is done in polynomial time.
|
||||
- show that if $p$'s instance answer is YES, then the instance of 3-SAT is YES.
|
||||
- show that if 3-SAT's instance answer is YES then the instance of $p$ is YES.
|
||||
312
content/CSE347/CSE347_L7.md
Normal file
312
content/CSE347/CSE347_L7.md
Normal file
@@ -0,0 +1,312 @@
|
||||
# Lecture 7
|
||||
|
||||
## Known NP-Complete Problems
|
||||
|
||||
- SAT and 3-SAT
|
||||
- Vertex Cover
|
||||
- Independent Set
|
||||
|
||||
## How to show a problem $L$ is NP-Complete
|
||||
|
||||
- Show $L \in$ NP
|
||||
- Give a polynomial time certificate
|
||||
- Give a polynomial time verifier
|
||||
- Show $L$ is NP-Hard: for some known NP-Complete problem $K$, show $K \leq_p L$
|
||||
- Construct a mapping $\phi$ from instance in $K$ to instance in $L$, given an instance $k\in K$, $\phi(k)\in L$.
|
||||
- Show that you can compute $\phi(k)$ in polynomial time.
|
||||
- Show that $k \in K$ is true if and only if $\phi(k) \in L$ is true.
|
||||
|
||||
### Example 1: Subset Sum
|
||||
|
||||
Input: A set $S$ of integers and a target positive integer $t$.
|
||||
|
||||
Problem: Determine if there exists a subset $S' \subseteq S$ such that $\sum_{a_i\in S'} a_i = t$.
|
||||
|
||||
We claim that Subset Sum is NP-Complete.
|
||||
|
||||
Step 1: Subset Sum $\in$ NP
|
||||
|
||||
- Certificate: $S' \subseteq S$
|
||||
- Verifier: Check that $\sum_{a_i\in S'} a_i = t$
|
||||
|
||||
Step 2: Subset Sum is NP-Hard
|
||||
|
||||
We claim that 3-SAT $\leq_p$ Subset Sum
|
||||
|
||||
Given any $3$-CNF formula $\Psi$, we will construct an instance $(S, t)$ of Subset Sum such that $\Psi$ is satisfiable if and only if there exists a subset $S' \subseteq S$ such that $\sum_{a_i\in S'} a_i = t$.
|
||||
|
||||
#### How to construct $\Psi$?
|
||||
|
||||
Reduction construction:
|
||||
|
||||
Assumption: No clause contains both a literal and its negation.
|
||||
|
||||
3-SAT problem: $\Psi$ has $n$ variables and $m$ clauses.
|
||||
|
||||
Need to: construct $S$ of positive numbers and a target $t$
|
||||
|
||||
Ideas of construction:
|
||||
|
||||
For 3-SAT instance $\Psi$:
|
||||
|
||||
- At least one literal in each clause is true
|
||||
- A variable and its negation cannot both be true
|
||||
|
||||
$S$ contains integers with $n+m$ digits (base 10)
|
||||
|
||||
$$
|
||||
p_1p_2\cdots p_n q_1 q_2 \cdots q_m
|
||||
$$
|
||||
|
||||
where $p_i$ are representations of variables that are either $0$ or $1$ and $q_j$ are representations of clauses.
|
||||
|
||||
For each variable $x_i$, we will have two integers in $S$, called $v_i$ and $\overline{v_i}$.
|
||||
|
||||
- For each variable $x_i$, both $v_i$ and $\overline{v_i}$ have digits $p_i=1$. all other $p$ positions are zero
|
||||
|
||||
- Each digit $q_j$ in $v_i$ is $1$ if $x_i$ appears in clause $j$; otherwise $q_j=0$
|
||||
|
||||
For example:
|
||||
|
||||
$\Psi=(x_1\lor \neg x_2 \lor x_3) \land (\neg x_1 \lor x_2 \lor x_3)$
|
||||
|
||||
| | $p_1$ | $p_2$ | $p_3$ | $q_1$ | $q_2$ |
|
||||
| ---------------- | ----- | ----- | ----- | ----- | ----- |
|
||||
| $v_1$ | 1 | 0 | 0 | 1 | 0 |
|
||||
| $\overline{v_1}$ | 1 | 0 | 0 | 0 | 1 |
|
||||
| $v_2$ | 0 | 1 | 0 | 0 | 1 |
|
||||
| $\overline{v_2}$ | 0 | 1 | 0 | 1 | 0 |
|
||||
| $v_3$ | 0 | 0 | 1 | 1 | 1 |
|
||||
| $\overline{v_3}$ | 0 | 0 | 1 | 0 | 0 |
|
||||
| t | 1 | 1 | 1 | 1 | 1 |
|
||||
|
||||
Let's try to prove correctness of the reduction.
|
||||
|
||||
Direction 1: Say subset sum has a solution $S'$.
|
||||
|
||||
We must prove that there is a satisfying assignment for $\Psi$.
|
||||
|
||||
Set $x_i=1$ if $v_i\in S'$
|
||||
|
||||
Set $x_i=0$ if $\overline{v_i}\in S'$
|
||||
|
||||
1. We want set $x_i$ to be both true and false, we will pick (in $S'$) either $v_i$ or $\overline{v_i}$
|
||||
2. For each clause we have at least one literal that is true since $q_j$ has a $1$ in the clause.
|
||||
|
||||
Direction 2: Say $\Psi$ has a satisfying assignment.
|
||||
|
||||
We must prove that there is a subset $S'$ such that $\sum_{a_i\in S'} a_i = t$.
|
||||
|
||||
If $x_i=1$, then $v_i\in S'$
|
||||
|
||||
If $x_i=0$, then $\overline{v_i}\in S'$
|
||||
|
||||
Problem: 1,2 or 3 literals in every clause can be true.
|
||||
|
||||
Fix
|
||||
|
||||
Add 2 numbers to $S$ for each clause $j$. We add $y_j,z_j$.
|
||||
|
||||
- All $p$ digits are zero
|
||||
- $q_j$ of $y_j$ is $1$, $q_j$ of $z_j$ is $2$, for all $j$, other digits are zero.
|
||||
- Intuitively, these numbers account for the number of literals in clause $j$ that are true.
|
||||
|
||||
New target are as follows:
|
||||
|
||||
| | $p_1$ | $p_2$ | $p_3$ | $q_1$ | $q_2$ |
|
||||
| ----- | ----- | ----- | ----- | ----- | ----- |
|
||||
| $y_1$ | 0 | 0 | 0 | 1 | 0 |
|
||||
| $z_1$ | 0 | 0 | 0 | 2 | 0 |
|
||||
| $y_2$ | 0 | 0 | 0 | 0 | 1 |
|
||||
| $z_2$ | 0 | 0 | 0 | 0 | 2 |
|
||||
| $t$ | 1 | 1 | 1 | 4 | 4 |
|
||||
|
||||
#### Time Complexity of construction for Subset Sum
|
||||
|
||||
- $O(n+m)$
|
||||
- $n$ is the number of variables
|
||||
- $m$ is the number of clauses
|
||||
|
||||
How many integers are in $S$?
|
||||
|
||||
- $2n$ for variables
|
||||
- $2m$ for new numbers
|
||||
- Total: $2n+2m$ integers
|
||||
|
||||
How many digits are in each integer?
|
||||
|
||||
- $n+m$ digits
|
||||
- Time complexity: $O((n+m)^2)$
|
||||
|
||||
#### Proof of reduction for Subset Sum
|
||||
|
||||
Claim 1: If Subset Sum has a solution, then $\Psi$ is satisfiable.
|
||||
|
||||
Proof:
|
||||
|
||||
Say $S'$ is a solution to Subset Sum. Then there exists a subset $S' \subseteq S$ such that $\sum_{a_i\in S'} a_i = t$. Here is an assignment of truth values to variables in $\Psi$ that satisfies $\Psi$:
|
||||
|
||||
- Set $x_i=1$ if $v_i\in S'$
|
||||
- Set $x_i=0$ if $\overline{v_i}\in S'$
|
||||
|
||||
This is a valid assignment since:
|
||||
|
||||
- We pick either $v_i$ or $\overline{v_i}$
|
||||
- For each clause, at least one literal is true
|
||||
|
||||
QED
|
||||
|
||||
Claim 2: If $\Psi$ is satisfiable, then Subset Sum has a solution.
|
||||
|
||||
Proof:
|
||||
|
||||
If $A$ is a satisfiable assignment for $\Psi$, then we can construct a subset $S'$ of $S$ such that $\sum_{a_i\in S'} a_i = t$.
|
||||
|
||||
If $x_i=1$, then $v_i\in S'$
|
||||
|
||||
If $x_i=0$, then $\overline{v_i}\in S'$
|
||||
|
||||
Say $t=\sum$ elements we picked from $S$.
|
||||
|
||||
- All $p_i$ in $t$ are $1$
|
||||
- All $q_j$ in $t$ are either $1$ or $2$ or $3$.
|
||||
- If $q_j=1$, then $y_j,z_j\in S'$
|
||||
- If $q_j=2$, then $z_j\in S'$
|
||||
- If $q_j=3$, then $y_j\in S'$
|
||||
|
||||
QED
|
||||
|
||||
### Example 2: 3 Color
|
||||
|
||||
Input: Graph $G$
|
||||
|
||||
Problem: Determine if $G$ is 3-colorable.
|
||||
|
||||
We claim that 3-Color is NP-Complete.
|
||||
|
||||
#### Proof of NP for 3-Color
|
||||
|
||||
Homework
|
||||
|
||||
#### Proof of NP-Hard for 3-Color
|
||||
|
||||
We claim that 3-SAT $\leq_p$ 3-Color
|
||||
|
||||
Given a 3-CNF formula $\Psi$, we will construct a graph $G$ such that $\Psi$ is satisfiable if and only if $G$ is 3-colorable.
|
||||
|
||||
Construction:
|
||||
|
||||
1. Construct a core triangle (3 vertices for 3 colors)
|
||||
2. 2 vertices for each variable $x_i:v_i,\overline{v_i}$
|
||||
3. Clause widget
|
||||
|
||||
Clause widget:
|
||||
|
||||
- 3 vertices for each clause $C_j:y_j,z_j,t_j$ (clause widget)
|
||||
- 3 edges extended from clause widget
|
||||
- variable vertex connected to extended edges
|
||||
|
||||
Key for dangler design:
|
||||
|
||||
Connect to all $v_i$ with true to the same color. and connect to all $v_i$ with false to another color.
|
||||
|
||||
'''
|
||||
TODO: Add dangler design image here.
|
||||
'''
|
||||
|
||||
#### Proof of reduction for 3-Color
|
||||
|
||||
Direction 1: If $\Psi$ is satisfiable, then $G$ is 3-colorable.
|
||||
|
||||
Proof:
|
||||
|
||||
Say $\Psi$ is satisfiable. Then $v_i$ and $\overline{v_i}$ are in different colors.
|
||||
|
||||
For the color in central triangle, we can pick any color.
|
||||
|
||||
For each dangler color is connected to blue, all literals cannot be blue.
|
||||
|
||||
...
|
||||
|
||||
QED
|
||||
|
||||
Direction 2: If $G$ is 3-colorable, then $\Psi$ is satisfiable.
|
||||
|
||||
Proof:
|
||||
|
||||
QED
|
||||
|
||||
### Example 3:Hamiltonian cycle problem (HAMCYCLE)
|
||||
|
||||
Input: $G(V,E)$
|
||||
|
||||
Output: Does $G$ have a Hamiltonian cycle? (A cycle that visits each vertex exactly once.)
|
||||
|
||||
Proof is too hard.
|
||||
|
||||
but it is an existing NP-complete problem.
|
||||
|
||||
## On lecture
|
||||
|
||||
### Example 4: Scheduling problem (SCHED)
|
||||
|
||||
scheduling with release time, deadline and execution times.
|
||||
|
||||
Given $n$ jobs, where job $i$ has release time $r_i$, deadline $d_i$, and execution time $t_i$.
|
||||
|
||||
Example:
|
||||
|
||||
$S=\{2,3,7,5,4\}$. we created 5 jobs release time is 0, deadline is 26, execution time is $1$.
|
||||
|
||||
Problem: Can you schedule these jobs so that each job starts after its release time and finishes before its deadline, and executed for $t_i$ time units?
|
||||
|
||||
#### Proof of NP-completeness
|
||||
|
||||
Step 1: Show that the problem is in NP.
|
||||
|
||||
Certificate: $\langle (h_i,j_i),(h_2,j_2),\cdots,(h_n,j_n)\rangle$, where $h_i$ is the start time of job $i$ and $j_i$ is the machine that job $i$ is assigned to.
|
||||
|
||||
Verifier: Check that $h_i + t_i \leq d_i$ for all $i$.
|
||||
|
||||
Step 2: Show that the problem is NP-hard.
|
||||
|
||||
We proceed by proving that $SSS\leq_p$ Scheduling.
|
||||
|
||||
Consider an instance of SSS: $\{ a_1,a_2,\cdots,a_n\}$ and sum $b$. We can create a scheduling instance with release time 0, deadline $b$, and execution time $1$.
|
||||
|
||||
Then we prove that the scheduling instance is a "yes" instance if and only if the SSS instance is a "yes" instance.
|
||||
|
||||
Ideas of proof:
|
||||
|
||||
If there is a subset of $\{a_1,a_2,\cdots,a_n\}$ that sums to $b$, then we can schedule the jobs in that order on one machine.
|
||||
|
||||
If there is a schedule where all jobs are finished by time $b$, then the sum of the scheduled jobs is exactly $b$.
|
||||
|
||||
### Example 5: Component grouping problem (CG)
|
||||
|
||||
Given an undirected graph which is not necessarily connected. (A component is a subgraph that is connected.)
|
||||
|
||||
Problem: Component Grouping: Give a graph $G$ that is not connected, and a positive integer $k$, is there a subset of its components that sums up to $k$?
|
||||
|
||||
Denoted as $CG(G,k)$.
|
||||
|
||||
#### Proof of NP-completeness for Component Grouping
|
||||
|
||||
Step 1: Show that the problem is in NP.
|
||||
|
||||
Certificate: $\langle S\rangle$, where $S$ is the subset of components that sums up to $k$.
|
||||
|
||||
Verifier: Check that the sum of the sizes of the components in $S$ is $k$. This can be done in polynomial time using breadth-first search.
|
||||
|
||||
Step 2: Show that the problem is NP-hard.
|
||||
|
||||
We proceed by proving that $SSS\leq_p CG$. (Subset Sum $\leq_p$ Component Grouping)
|
||||
|
||||
Consider an instance of SSS: $\langle a_1,a_2,\cdots,a_n,b\rangle$.
|
||||
|
||||
We construct an instance of CG as follows:
|
||||
|
||||
For each $a_i\in S$, we create a chain of $a_i$ vertices.
|
||||
|
||||
WARNING: this is not a valid proof for NP hardness since the reduction is not polynomial for $n$, where $n$ is the number of vertices in the SSS instance.
|
||||
|
||||
353
content/CSE347/CSE347_L8.md
Normal file
353
content/CSE347/CSE347_L8.md
Normal file
@@ -0,0 +1,353 @@
|
||||
# Lecture 8
|
||||
|
||||
## NP-optimization problem
|
||||
|
||||
Cannot be solved in polynomial time.
|
||||
|
||||
Example:
|
||||
|
||||
- Maximum independent set
|
||||
- Minimum vertex cover
|
||||
|
||||
What can we do?
|
||||
|
||||
- solve small instances
|
||||
- hard instances are rare - average case analysis
|
||||
- solve special cases
|
||||
- find an approximate solution
|
||||
|
||||
## Approximation algorithms
|
||||
|
||||
We find a "good" solution in polynomial time, but may not be optimal.
|
||||
|
||||
Example:
|
||||
|
||||
- Minimum vertex cover: we will find a small vertex cover, but not necessarily the smallest one.
|
||||
- Maximum independent set: we will find a large independent set, but not necessarily the largest one.
|
||||
|
||||
Question: How do we quantify the quality of the solution?
|
||||
|
||||
### Approximation ratio
|
||||
|
||||
Intuition:
|
||||
|
||||
How good is an algorithm $A$ compared to an optimal solution in the worst case?
|
||||
|
||||
Definition:
|
||||
|
||||
Consider algorithm $A$ for an NP-optimization problem $L$. Say for **any** instance $l$, $A$ finds a solution output $c_A(l)$ and the optimal solution is $c^*(l)$.
|
||||
|
||||
Approximation ratio is either:
|
||||
|
||||
$$
|
||||
\max_{l \in L} \frac{c_A(l)}{c^*(l)}=\alpha
|
||||
$$
|
||||
|
||||
for maximization problems, or
|
||||
|
||||
$$
|
||||
\min_{l \in L} \frac{c^A(l)}{c_*(l)}=\alpha
|
||||
$$
|
||||
|
||||
for minimization problems.
|
||||
|
||||
Example:
|
||||
|
||||
Alice's Algorithm, $A$, finds a vertex cover of size $c_A(l)$ for instance $l(G)$. The optimal vertex cover has size $c^*(l)$.
|
||||
|
||||
We want approximation ratio to be as close to 1 as possible.
|
||||
|
||||
> Vertex cover:
|
||||
>
|
||||
> A vertex cover is a set of vertices that touches all edges.
|
||||
|
||||
Let's try an approximation algorithm for the vertex cover problem, called Greedy cover.
|
||||
|
||||
#### Greedy cover
|
||||
|
||||
Pick any uncovered edge, both its endpoints are added to the cover $C$, until all edges are covered.
|
||||
|
||||
Runtime: $O(m)$
|
||||
|
||||
Claim: Greedy cover is correct, and it finds a vertex cover.
|
||||
|
||||
Proof:
|
||||
|
||||
Algorithm only terminates when all edges are covered.
|
||||
|
||||
Claim: Greedy cover is a 2-approximation algorithm.
|
||||
|
||||
Proof:
|
||||
|
||||
Look at the two edges we picked.
|
||||
|
||||
Either it is covered by Greedy cover, or it is not.
|
||||
|
||||
If it is not covered by Greedy cover, then we will add both endpoints to the cover.
|
||||
|
||||
In worst case, Greedy cover will add both endpoints of each edge to the cover. (Consider the graph with disjoint edges.)
|
||||
|
||||
Thus, the size of the vertex cover found by Greedy cover is at most twice the size of the optimal vertex cover.
|
||||
|
||||
Thus, Greedy cover is a 2-approximation algorithm.
|
||||
|
||||
> Min-cut:
|
||||
>
|
||||
> Given a graph $G$ and two vertices $s$ and $t$, find the minimum cut between $s$ and $t$.
|
||||
>
|
||||
> Max-cut:
|
||||
>
|
||||
> Given a graph $G$, find the maximum cut.
|
||||
|
||||
#### Local cut
|
||||
|
||||
Algorithm:
|
||||
|
||||
- start with an arbitrary cut of $G$.
|
||||
- While you can move a vertex from one side to the other side while increasing the size of the cut, do so.
|
||||
- Return the cut found.
|
||||
|
||||
We will prove its:
|
||||
|
||||
- Runtime
|
||||
- Feasibility
|
||||
- Approximation ratio
|
||||
|
||||
##### Runtime for local cut
|
||||
|
||||
Since size of cut is at most $|E|$, the runtime is $O(m)$.
|
||||
|
||||
When we move a vertex from one side to the other side, the size of the cut increases by at least 1.
|
||||
|
||||
Thus, the algorithm terminates in at most $|V|$ steps.
|
||||
|
||||
So the runtime is $O(|E||V|^2)$.
|
||||
|
||||
##### Feasibility for local cut
|
||||
|
||||
The algorithm only terminates when no more vertices can be moved.
|
||||
|
||||
Thus, the cut found is a feasible solution.
|
||||
|
||||
##### Approximation ratio for local cut
|
||||
|
||||
This is a half-approximation algorithm.
|
||||
|
||||
We need to show that the size of the cut found is at least half of the size of the optimal cut.
|
||||
|
||||
We could first upper bound the size of the optimal cut is at most $|E|$.
|
||||
|
||||
We will then prove that solution we found is at least half of the optimal cut $\frac{|E|}{2}$ for any graph $G$.
|
||||
|
||||
Proof:
|
||||
|
||||
When we terminate, no vertex could be moved
|
||||
|
||||
Therefore, **The number of crossing edges is at least the number of non-crossing edges**.
|
||||
|
||||
Let $d(u)$ be the degree of vertex $u\in V$.
|
||||
|
||||
The total number of crossing edges for vertex $u$ is at least $\frac{1}{2}d(u)$.
|
||||
|
||||
Summing over all vertices, the total number of crossing edges is at least $\frac{1}{2}\sum_{u\in V}d(u)=\frac{1}{2}|E|$.
|
||||
|
||||
So the total number of non-crossing edges is at most $\frac{|E|}{2}$.
|
||||
|
||||
QED
|
||||
|
||||
#### Set cover
|
||||
|
||||
Problem:
|
||||
|
||||
You are collecting a set of magic cards.
|
||||
|
||||
$X$ is the set of all possible cards. You want at least one of each card.
|
||||
|
||||
Each dealer $j$ has a pack $S_j\subseteq X$ of cards. You have to buy entire pack or none from dealer $j$.
|
||||
|
||||
Goal: What is the least number of packs you need to buy to get all cards?
|
||||
|
||||
Formally:
|
||||
|
||||
Input $X$ is a universe of $n$ elements, and a collection of subsets of $X$, $Y=\{S_1, S_2, \ldots, S_m\}\subseteq X$.
|
||||
|
||||
Goal: Pick $C\subseteq Y$ such that $\bigcup_{S_i\in C}S_i=X$, and $|C|$ is minimized.
|
||||
|
||||
Set cover is an NP-optimization problem. It is a generalization of the vertex cover problem.
|
||||
|
||||
#### Greedy set cover
|
||||
|
||||
Algorithm:
|
||||
|
||||
- Start with empty set $C$.
|
||||
- While there is an element $x$ in $X$ that is not covered, pick one such element $x\in S_i$ where $S_i$ is the set that has not been picked before.
|
||||
- Add $S_i$ to $C$.
|
||||
- Return $C$.
|
||||
|
||||
```python
|
||||
def greedy_set_cover(X, Y):
|
||||
# X is the set of elements
|
||||
# Y is the collection of sets, hashset by default
|
||||
C = []
|
||||
def non_covered_elements(X, C):
|
||||
# return the elements in X that are not covered by C
|
||||
# O(|X|)
|
||||
return [x for x in X if not any(x in c for c in C)]
|
||||
non_covered = non_covered_elements(X, C)
|
||||
# O(|X|) every loop reduce the size of non_covered by 1
|
||||
while non_covered:
|
||||
max_cover,max_set = 0,None
|
||||
# O(|Y|)
|
||||
for S in Y:
|
||||
# Intersection of two sets is O(min(|X|,|S|))
|
||||
cur_cover = len(set(non_covered) & set(S))
|
||||
if cur_cover > max_cover:
|
||||
max_cover,max_set = cur_cover,S
|
||||
C.append(max_set)
|
||||
non_covered = non_covered_elements(X, C)
|
||||
return C
|
||||
```
|
||||
|
||||
It is not optimal.
|
||||
|
||||
Need to prove its:
|
||||
|
||||
- Correctness:
|
||||
Keep picking until all elements are covered.
|
||||
- Runtime:
|
||||
$O(|X||Y|^2)$
|
||||
- Approximation ratio:
|
||||
|
||||
##### Approximation ratio for greedy set cover
|
||||
|
||||
> Harmonic number:
|
||||
>
|
||||
> $H_n=\sum_{i=1}^n\frac{1}{i}=\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n}=\Theta(\log n)$
|
||||
|
||||
We claim that the size of the set cover found is at most $H_n\log n$ times the size of the optimal set cover.
|
||||
|
||||
###### First bound:
|
||||
|
||||
Proof:
|
||||
|
||||
If the optimal picks $k$ sets, then the size of the set cover found is at most $(1+\log n)k$ sets.
|
||||
|
||||
Let $n=|X|$.
|
||||
|
||||
Observe that
|
||||
|
||||
For the first round, the elements that we not covered is $n$.
|
||||
$$
|
||||
|U_0|=n
|
||||
$$
|
||||
|
||||
In the second round, the elements that we not covered is at most $|U_0|-x$ where $x=|S_1|$ is the number of elements in the set picked in the first round.
|
||||
|
||||
$$
|
||||
|U_1|=|U_0|-|S_1|
|
||||
$$
|
||||
|
||||
...
|
||||
|
||||
So $x_i\geq \frac{|U_{i-1}|}{k}$.
|
||||
|
||||
We proceed by contradiction.
|
||||
|
||||
Suppose all sets in the optimal solution are $< \frac{|U_0|}{k}$. Then the sum of the sizes of the sets in the optimal solution is $< |U_0|=n$.
|
||||
|
||||
_There exists a least ratio of selection of sets determined by $k_i$. Otherwise the function (selecting the set cover) will not terminate (no such sets exists)_
|
||||
|
||||
> Some math magics:
|
||||
> $$(1-\frac{1}{k})^k\leq \frac{1}{e}$$
|
||||
|
||||
So $n(1-\frac{1}{k})^{|C|-1}=1$, $|C|\leq 1+k\ln n$.
|
||||
|
||||
So the size of the set cover found is at most $(1+\ln n)k$.
|
||||
|
||||
QED
|
||||
|
||||
So the greedy set cover is not too bad...
|
||||
|
||||
###### Second bound:
|
||||
|
||||
Greedy set cover is a $H_d$-approximation algorithm of set cover.
|
||||
|
||||
Proof:
|
||||
|
||||
Assign a cost to the elements of $X$ according to the decisions of the greedy set cover.
|
||||
|
||||
Let $\delta(S^i)$ be the new number of elements covered by set $S^i$.
|
||||
|
||||
$$
|
||||
\delta(S^i)=|S_i\cap U_{i-1}|
|
||||
$$
|
||||
|
||||
If the element $x$ is added by step $i$, when set $S_i$ is picked, then the cost of $x$ to
|
||||
|
||||
$$
|
||||
\frac{1}{\delta(S^i)}=\frac{1}{x_i}
|
||||
$$
|
||||
|
||||
Example:
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
X&=\{A,B,C,D,E,F,G\}\\
|
||||
S_1&=\{A,C,E\}\\
|
||||
S_2&=\{B,C,F,G\}\\
|
||||
S_3&=\{B,D,F,G\}\\
|
||||
S_4&=\{D,G\}
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
First we select $S_2$, then $cost(B)=cost(C)=cost(F)=cost(G)=\frac{1}{4}$.
|
||||
|
||||
Then we select $S_1$, then $cost(A)=cost(E)=\frac{1}{2}$.
|
||||
|
||||
Then we select $S_3$, then $cost(D)=1$.
|
||||
|
||||
If element $x$ was covered by greedy set cover due to the addition of set $S^i$ at step $i$, then the cost of $x$ is $\frac{1}{\delta(S^i)}$.
|
||||
|
||||
$$
|
||||
\textup{Total cost of GSC}=\sum_{x\in X}c(x)=\sum_{i=1}^{|C|}\sum_{X\textup{ covered at iteration }i}c(x)=\sum_{i=1}^{|C|}\delta(S^i)\frac{1}{\delta(S^i)}=|C|
|
||||
$$
|
||||
|
||||
Claim: Consider any set $S$ that is a subset of $X$. The cost paid by the greedy set cover for $S$ is at most $H_{|S|}$.
|
||||
|
||||
Suppose that the greedy set covers $S$ in order $x_1,x_2,\ldots,x_{|S|}$, where $\{x_1,x_2,\ldots,x_{|S|}\}=S$.
|
||||
|
||||
When GSC covers $x_j$, $\{x_j,x_{j+1},\ldots,x_{|S|}\}$ are not covered.
|
||||
|
||||
At this point, the GSC has the option of picking $S$
|
||||
|
||||
This implies that the $\delta(S)$ is at least $|S|-j+1$.
|
||||
|
||||
Assume that $S$ is picked $\hat{S}$ for which $\delta(\hat{S})$ is maximized ($\hat{S}$ may be $S$ or other sets that have not covered $x_j$).
|
||||
|
||||
So, $\delta(\hat{S})\geq \delta(S)\geq |S|-j+1$.
|
||||
|
||||
So the cost of $x_j$ is $\delta(\hat{S})\leq \frac{1}{\delta(S)}\leq \frac{1}{|S|-j+1}$.
|
||||
|
||||
Summing over all $j$, the cost of $S$ is at most $\sum_{j=1}^{|S|}\frac{1}{|S|-j+1}=H_{|S|}$.
|
||||
|
||||
Back to the proof of approximation ratio:
|
||||
|
||||
Let $C^*$ be optimal set cover.
|
||||
|
||||
$$
|
||||
|C|=\sum_{x\in X}c(x)\leq \sum_{S_j\in C^*}\sum_{x\in S_j}c(x)
|
||||
$$
|
||||
|
||||
This inequality holds because of counting element that is covered by more than one set.
|
||||
|
||||
Since $\sum_{x\in S_j}c(x)\leq H_{|S_j|}$, by our claim.
|
||||
|
||||
Let $d$ be the largest cardinality of any set in $C^*$.
|
||||
|
||||
$$
|
||||
|C|\leq \sum_{S_j\in C^*}H_{|S_j|}\leq \sum_{S_j\in C^*}H_d=H_d|C^*|
|
||||
$$
|
||||
|
||||
So the approximation ratio for greedy set cover is $H_d$.
|
||||
|
||||
QED
|
||||
349
content/CSE347/CSE347_L9.md
Normal file
349
content/CSE347/CSE347_L9.md
Normal file
@@ -0,0 +1,349 @@
|
||||
# Lecture 9
|
||||
|
||||
## Randomized Algorithms
|
||||
|
||||
### Hashing
|
||||
|
||||
Hashing with chaining:
|
||||
|
||||
Input: We have integers in range $[1,n-1]=U$. We want to map them to a hash table $T$ with $m$ slots.
|
||||
|
||||
Hash function: $h:U\rightarrow [m]$
|
||||
|
||||
Goal: Hashing a set $S\subseteq U$, $|S|=n$ into $T$ such that the number of elements in each slot is at most $1$.
|
||||
|
||||
#### Collisions
|
||||
|
||||
When multiple keys are mapped to the same slot, we call it a collision, we keep a linked list of all the keys that map to the same slot.
|
||||
|
||||
**Runtime** of insert, query, delete of elements $=\Theta(\textup{length of the chain})$
|
||||
|
||||
**Worst-case** runtime of insert, query, delete of elements $=\Theta(n)$
|
||||
|
||||
Therefore, we want chains to be short, or $\Theta(1)$, as long as $|S|$ is reasonably sized, or equivalently, we want the number in any set $S$ to hash **uniformly** across all slots.
|
||||
|
||||
#### Simple Uniform Hashing Assumptions
|
||||
|
||||
The $n$ elements we want to hash (the set $S$) is picked uniformly at random from $U$. Therefore, we could see that this simple hash function works fine:
|
||||
|
||||
$$
|
||||
h(x)=x\mod m
|
||||
$$
|
||||
|
||||
Question: What happens if an adversary knows this function and designs $S$ to make the worst-case runtime happen?
|
||||
|
||||
Answer: The adversary can make the runtime of each operation $\Theta(n)$ by simply making all the elements hash to the same slot.
|
||||
|
||||
#### Randomization to the rescue
|
||||
|
||||
We don't want the adversary to know the hash function based on just looking at the code.
|
||||
|
||||
Ideas: Randomize the choice of the hash function.
|
||||
|
||||
### Randomized Algorithm
|
||||
|
||||
#### Definition
|
||||
|
||||
A randomized algorithm is an algorithm the algorithm makes internal random choices.
|
||||
|
||||
2 kinds of randomized algorithms:
|
||||
|
||||
1. Las Vegas: The runtime is random, but the output is always correct.
|
||||
2. Monte Carlo: The runtime is fixed, but the output is sometimes incorrect.
|
||||
|
||||
We will focus on Las Vegas algorithms in this course.
|
||||
|
||||
$$O(n)=E[T(n)]$$ or some other probabilistic quantity.
|
||||
|
||||
#### Randomization can help
|
||||
|
||||
Ideas: Randomize the choice of hash function $h$ from a family of hash functions, $H$.
|
||||
|
||||
If we randomly pick a hash function from this family, then the probability that the hash function is bad on **any particular** set $S$ is small.
|
||||
|
||||
Intuitively, the adversary can not pick a bad input since most hash functions are good for any particular input $S$.
|
||||
|
||||
#### Universal Hashing: Goal
|
||||
|
||||
We want to design a universal family of hash functions, $H$, such that the probability that the hash table behaves badly on any input $S$ is small.
|
||||
|
||||
#### Universal Hashing: Definition
|
||||
|
||||
Suppose we have $m$ buckets in the hash table. We also have $2$ inputs $x\neq y$ and $x,y\in U$. We want $x$ and $y$ to be unlikely to hash to the same bucket.
|
||||
|
||||
$H$ is a universal **family** of hash functions if for any two elements $x\neq y$,
|
||||
|
||||
$$
|
||||
Pr_{h\in H}[h(x)=h(y)]=\frac{1}{m}
|
||||
$$
|
||||
|
||||
where $h$ is picked uniformly at random from the family $H$.
|
||||
|
||||
#### Universal Hashing: Analysis
|
||||
|
||||
Claim: If we choose $h$ randomly from a universal family of hash functions, $H$, then the hash table will exhibit good behavior on any set $S$ of size $n$ with high probability.
|
||||
|
||||
Question: What are some good properties and what does it mean by with high probability?
|
||||
|
||||
Claim: Given a universal family of hash functions, $H$, $S=\{a_1,a_2,\cdots,a_n\}\subset \mathbb{N}$. For any probability $0\leq \delta\leq 1$, if $n\leq \sqrt{2m\delta}$, the chance that no two keys hash to the same slot is $\geq1-\delta$.
|
||||
|
||||
Example: If we pick $\delta=\frac{1}{2}$. As long as $n<\sqrt{2m}$, the chance that no two keys hash to the same slot is $\geq\frac{1}{2}$.
|
||||
|
||||
If we pick $\delta=\frac{1}{3}$. As long as $n<\sqrt{\frac{4}{3}m}$, the chance that no two keys hash to the same slot is $\geq\frac{2}{3}$.
|
||||
|
||||
Proof Strategy:
|
||||
|
||||
1. Compute the **expected value** of collisions. Note that collisions occurs when two different values are hashed to the same slot. (Indicator random variables)
|
||||
2. Apply a "tail" bound that converts the expected value to probability. (Markov's inequality)
|
||||
|
||||
##### Compute the expected number of collisions
|
||||
|
||||
Let $m$ be the size of the hash table. $n$ is the number of keys in the set $S$. $N$ is the size of the universe.
|
||||
|
||||
For inputs $x,y\in S,x\neq y$, we define a random variable
|
||||
|
||||
$$
|
||||
C_{xy}=
|
||||
\begin{cases}
|
||||
1 & \text{if } h(x)=h(y) \\
|
||||
0 & \text{otherwise}
|
||||
\end{cases}
|
||||
$$
|
||||
|
||||
$C_{xy}$ is called an indicator random variable, that takes value $0$ or $1$.
|
||||
|
||||
The expected number of collisions is
|
||||
|
||||
$$
|
||||
E[C_{xy}]=1\times Pr[C_{xy}=1]+0\times Pr[C_{xy}=0]=Pr[C_{xy}=1]=\frac{1}{m}
|
||||
$$
|
||||
|
||||
Define $C_x$: random variable that represents the cost of inserting/searching/deleting $x$ from the hash table.
|
||||
|
||||
$C_x\leq$ total number of elements that collide with $x$ (= number of elements $y$ such that $h(x)=h(y)$).
|
||||
|
||||
$$
|
||||
C_x=\sum_{y\in S,y\neq x,h(x)=h(y)}1
|
||||
$$
|
||||
|
||||
So, $C_x=\sum_{y\in S,y\neq x}C_{xy}$.
|
||||
|
||||
By linearity of expectation,
|
||||
|
||||
$$
|
||||
E[C_x]=\sum_{y\in S,y\neq x}E[C_{xy}]=\sum_{y\in S,y\neq x}\frac{1}{m}=\frac{n-1}{m}
|
||||
$$
|
||||
|
||||
$E[C]=\Theta(1)$ if $n=O(m)$. Total cost of $K$ insert/search operations is $O(k)$. by linearity of expectation.
|
||||
|
||||
Say $C$ is the total number of collisions.
|
||||
|
||||
$C=\frac{\sum_{x\in S}C_x}{2}$ because each collision is counted twice.
|
||||
|
||||
$$
|
||||
E[C]=\frac{1}{2}\sum_{x\in S}E[C_x]=\frac{1}{2}\sum_{x\in S}\frac{n-1}{m}=\frac{n(n-1)}{2m}
|
||||
$$
|
||||
|
||||
If we want $E[C]\leq \delta$, then we need $n=\sqrt{2m\delta}$.
|
||||
|
||||
#### The probability of no collisions $C=0$
|
||||
|
||||
We know that the expected value of number of collisions is now $\leq \delta$, but what about the probability of **NO** collisions?
|
||||
|
||||
> Markov's inequality: $$P[X\geq k]\leq\frac{E[X]}{k}$$
|
||||
> For non-negative random variable $X$, $Pr[X\geq k\cdot E[X]]\leq \frac{1}{k}$.
|
||||
|
||||
Use Markov's inequality: For non-negative random variable $X$, $Pr[X\geq k\cdot E[X]]\leq \frac{1}{k}$.
|
||||
|
||||
Apply this to $C$:
|
||||
|
||||
$$
|
||||
Pr[C\geq \frac{1}{\delta}E[C]]<\delta\Rightarrow Pr[C\geq 1]<\delta
|
||||
$$
|
||||
|
||||
So, if we want $Pr[C=0]>1-\delta$, $n<\sqrt{2m\delta}$ with probability $1-\delta$, you will have no collisions.
|
||||
|
||||
#### More general conclusion
|
||||
|
||||
Claim: For a universal hash function family $H$, if number of keys $n\leq \sqrt{Bm\delta}$, then the probability that at most $B+1$ keys hash to the same slot is $> 1-\delta$.
|
||||
|
||||
### Example: Quicksort
|
||||
|
||||
Based on partitioning [assume all elements are distinct]: Partition($A[p\cdots r]$)
|
||||
|
||||
- Rearranges $A$ into $A[p\cdots q-1],A[q],A[q+1\cdots r]$
|
||||
|
||||
Runtime: $O(r-p)$, linear time.
|
||||
|
||||
```python
|
||||
def partition(A,p,r):
|
||||
x=A[r]
|
||||
lo=p
|
||||
for i in range(p,r):
|
||||
if A[i]<x:
|
||||
A[lo],A[i]=A[i],A[lo]
|
||||
lo+=1
|
||||
A[lo],A[r]=A[r],A[lo]
|
||||
return lo
|
||||
|
||||
def quicksort(A,p,r):
|
||||
if p<r:
|
||||
q=partition(A,p,r)
|
||||
quicksort(A,p,q-1)
|
||||
quicksort(A,q+1,r)
|
||||
```
|
||||
|
||||
#### Runtime analysis
|
||||
|
||||
Let the number of element in $A_{low}$ be $k$.
|
||||
|
||||
$$
|
||||
T(n)=\Theta(n)+T(k)+T(n-k-1)
|
||||
$$
|
||||
|
||||
By even split assumption, $k=\frac{n}{2}$.
|
||||
|
||||
$$
|
||||
T(n)=T(\frac{n}{2})+T(\frac{n}{2}-1)+\Theta(n)\approx \Theta(n\log n)
|
||||
$$
|
||||
|
||||
Which is approximately the same as merge sort.
|
||||
|
||||
_Average case analysis is always suspicious._
|
||||
|
||||
### Randomized Quicksort
|
||||
|
||||
- Pick a random pivot element.
|
||||
- Analyze the expected runtime. over the random choices of pivot.
|
||||
|
||||
```python
|
||||
|
||||
def randomized_partition(A,p,r):
|
||||
ix=random.randint(p,r)
|
||||
x=A[ix]
|
||||
A[r],A[ix]=A[ix],A[r]
|
||||
lo=p
|
||||
for i in range(p,r):
|
||||
if A[i]<x:
|
||||
A[lo],A[i]=A[i],A[lo]
|
||||
lo+=1
|
||||
A[lo],A[r]=A[r],A[lo]
|
||||
return lo
|
||||
|
||||
def randomized_quicksort(A,p,r):
|
||||
if p<r:
|
||||
q=randomized_partition(A,p,r)
|
||||
randomized_quicksort(A,p,q-1)
|
||||
randomized_quicksort(A,q+1,r)
|
||||
```
|
||||
|
||||
$$
|
||||
E[T(n)]=E(T(n-k-1)+T(k)+cn)=E(T(n-k-1))+E(T(k))+cn
|
||||
$$
|
||||
|
||||
by linearity of expectation.
|
||||
|
||||
$$
|
||||
Pr[\textup{pivot has rank }k]=\frac{1}{n}
|
||||
$$
|
||||
|
||||
So,
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
E[T(n)]&=\frac{1}{n}\sum_{k=0}^{n-1}(E[T(k)]+E[T(n-k-1)])+cn\\
|
||||
&=cn+\sum_{k=0}^{n-1}Pr[n-k-1=j]T(j)+\sum_{k=0}^{n-1}Pr[k=j]T(j)\\
|
||||
&=cn+\sum_{k=0}^{n-1}\frac{1}{n}T(j)+\sum_{k=0}^{n-1}\frac{1}{n}T(j)\\
|
||||
&=cn+\frac{2}{n}\sum_{k=0}^{n-1}T(j)
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Claim: the solution to this recurrence is $E[T(n)]=O(n\log n)$ or $T(n)=c'n\log n+1$.
|
||||
|
||||
Proof:
|
||||
|
||||
We prove by induction.
|
||||
|
||||
Base case: $n=1,T(n)=T(1)=c$
|
||||
|
||||
Inductive step: Assume that $T(k)=c'k\log k+1$ for all $k<n$.
|
||||
|
||||
Then,
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
T(n)&=cn+\frac{2}{n}\sum_{k=0}^{n-1}T(k)\\
|
||||
&=cn+\frac{2}{n}\sum_{k=0}^{n-1}(c'k\log k+1)\\
|
||||
&=cn+\frac{2c'}{n}\sum_{k=0}^{n-1}k\log k+\frac{2}{n}\sum_{k=0}^{n-1}1
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Then we use the fact that $\sum_{k=0}^{n-1}k\log k\leq \frac{n^2\log n}{2}-\frac{n^2}{8}$ (can be proved by induction).
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
T(n)&=cn+\frac{2c'}{n}\left(\frac{n^2\log n}{2}-\frac{n^2}{8}\right)+\frac{2}{n}n\\
|
||||
&=c'n\log n-\frac{1}{4}c'n+cn+2\\
|
||||
&=(c'n\log n+1)-\left(\frac{1}{4}c'n-cn-1\right)
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
We need to prove that $\frac{1}{4}c'n-cn-1\geq 0$.
|
||||
|
||||
Choose $c'$ and $c$ such that $\frac{1}{4}c'n\geq cn+1$ for all $n\geq 2$.
|
||||
|
||||
If $c'\geq 8c$, then $T(n)\leq c'n\log n+1$.
|
||||
|
||||
$E[T(n)]\leq c'n\log n+1=O(n\log n)$
|
||||
|
||||
QED
|
||||
|
||||
A more elegant proof:
|
||||
|
||||
Let $X_{ij}$ be an indicator random variable that is $1$ if element of rank $i$ is compared to element of rank $j$.
|
||||
|
||||
Running time: $$X=\sum_{i=0}^{n-2}\sum_{j=i+1}^{n-1}X_{ij}$$
|
||||
|
||||
So, the expected number of comparisons is
|
||||
|
||||
$$
|
||||
E[X_{ij}]=Pr[X_{ij}=1]\times 1+Pr[X_{ij}=0]\times 0=Pr[X_{ij}=1]
|
||||
$$
|
||||
|
||||
This is equivalent to the expected number of comparisons in randomized quicksort.
|
||||
|
||||
The expected number of running time is
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
E[X]&=E[\sum_{i=0}^{n-2}\sum_{j=i+1}^{n-1}X_{ij}]\\
|
||||
&=\sum_{i=0}^{n-2}\sum_{j=i+1}^{n-1}E[X_{ij}]\\
|
||||
&=\sum_{i=0}^{n-2}\sum_{j=i+1}^{n-1}Pr[X_{ij}=1]
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
For any two elements $z_i,z_j\in S$, the probability that $z_i$ is compared to $z_j$ is (either $z_i$ or $z_j$ is picked first as the pivot before the any elements of the ranks larger than $i$ and less than $j$)
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
Pr[X_{ij}=1]&=Pr[z_i\text{ is picked first}]+Pr[z_j\text{ is picked first}]\\
|
||||
&=\frac{1}{j-i+1}+\frac{1}{j-i+1}\\
|
||||
&=\frac{2}{j-i+1}
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
So, with harmonic number, $H_n=\sum_{k=1}^{n}\frac{1}{k}$,
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
E[X]&=\sum_{i=0}^{n-2}\sum_{j=i+1}^{n-1}\frac{2}{j-i+1}\\
|
||||
&\leq 2\sum_{i=0}^{n-2}\sum_{k=1}^{n-i-1}\frac{1}{k}\\
|
||||
&\leq 2\sum_{i=0}^{n-2}c\log(n)\\
|
||||
&=2c\log(n)\sum_{i=0}^{n-2}1\\
|
||||
&=\Theta(n\log n)
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
|
||||
QED
|
||||
|
||||
34
content/CSE347/Exam_reviews/CSE347_E1.md
Normal file
34
content/CSE347/Exam_reviews/CSE347_E1.md
Normal file
@@ -0,0 +1,34 @@
|
||||
# Exam 1 review
|
||||
|
||||
## Greedy
|
||||
|
||||
A Greedy Algorithm is an algorithm whose solution applies the same choice rule at each step over and over until no more choices can be made.
|
||||
|
||||
- Stating and Proving a Greedy Algorithm
|
||||
- State your algorithm (“at this step, make this choice”)
|
||||
- Greedy Choice Property (Exchange Argument)
|
||||
- Inductive Structure
|
||||
- Optimal Substructure
|
||||
- "Simple Induction"
|
||||
- Asymptotic Runtime
|
||||
|
||||
## Divide and conquer
|
||||
|
||||
Stating and Proving a Dividing and Conquer Algorithm
|
||||
|
||||
- Describe the divide, conquer, and combine steps of your algorithm.
|
||||
- The combine step is the most important part of a divide and conquer algorithm, and in your recurrence this step is the "f (n)", or work done at each subproblem level. You need to show that you can combine the results of your subproblems somehow to get the solution for the entire problem.
|
||||
- Provide and prove a base case (when you can divide no longer)
|
||||
- Prove your induction step: suppose subproblems (two problems of size n/2, usually) of the same kind are solved optimally. Then, because of the combine step, the overall problem (of size n) will be solved optimally.
|
||||
- Provide recurrence and solve for its runtime (Master Method)
|
||||
|
||||
## Maximum Flow
|
||||
Given a weighted directed acyclic graph with a source and a sink node, the goal is to see how much "flow" you can push from the source to the sink simultaneously.
|
||||
|
||||
Finding the maximum flow can be solved by the Ford-Fulkerson Algorithm. Runtime (from lecture slides): $O(F (|V | + |E |))$.
|
||||
|
||||
Fattest Path improvement: $O(log |V |(|V | + |E |))$
|
||||
|
||||
Min Cut-Max Flow: the maximum flow from source $s$ to sink $t$ is equal to the minimum sum of an $s-t$ cut.
|
||||
|
||||
A cut is a partition of a graph into two disjoint sets by removing edges connecting the two parts. An $s-t$ cut will put $s$ and $t$ into the different sets.
|
||||
139
content/CSE347/Exam_reviews/CSE347_E2.md
Normal file
139
content/CSE347/Exam_reviews/CSE347_E2.md
Normal file
@@ -0,0 +1,139 @@
|
||||
# Exam 2 Review
|
||||
|
||||
## Reductions
|
||||
|
||||
We say that a problem $A$ reduces to a problem $B$ if there is a **polynomial time** reduction function $f$ such that for all $x$, $x \in A \iff f(x) \in B$.
|
||||
|
||||
To prove a reduction, we need to show that the reduction function $f$:
|
||||
|
||||
1. runs in polynomial time
|
||||
2. $x \in A \iff f(x) \in B$.
|
||||
|
||||
### Useful results from reductions
|
||||
|
||||
1. $B$ is at least as hard as $A$ if $A \leq B$.
|
||||
2. If we can solve $B$ in polynomial time, then we can solve $A$ in polynomial time.
|
||||
3. If we want to solve problem $A$, and we already know an efficient algorithm for $B$, then we can use the reduction $A \leq B$ to solve $A$ efficiently.
|
||||
4. If we want to show that $B$ is NP-hard, we can do this by showing that $A \leq B$ for some known NP-hard problem $A$.
|
||||
|
||||
$P$ is the class of problems that can be solved in polynomial time. $NP$ is the class of problems that can be verified in polynomial time.
|
||||
|
||||
We know that $P \subseteq NP$.
|
||||
|
||||
### NP-complete problems
|
||||
|
||||
A problem is NP-complete if it is in $NP$ and it is also NP-hard.
|
||||
|
||||
#### NP
|
||||
|
||||
A problem is in $NP$ if
|
||||
|
||||
1. there is a polynomial size certificate for the problem, and
|
||||
2. there is a polynomial time verifier for the problem that takes the certificate and checks whether it is a valid solution.
|
||||
|
||||
#### NP-hard
|
||||
|
||||
A problem is NP-hard if every instance of $NP$ hard problem can be reduced to it in polynomial time.
|
||||
|
||||
List of known NP-hard problems:
|
||||
|
||||
1. 3-SAT (or SAT):
|
||||
- Statement: Given a boolean formula in CNF with at most 3 literals per clause, is there an assignment of truth values to the variables that makes the formula true?
|
||||
2. Independent Set:
|
||||
- Statement: Given a graph $G$ and an integer $k$, does $G$ contain a set of $k$ vertices such that no two vertices in the set are adjacent?
|
||||
3. Vertex Cover:
|
||||
- Statement: Given a graph $G$ and an integer $k$, does $G$ contain a set of $k$ vertices such that every edge in $G$ is incident to at least one vertex in the set?
|
||||
4. 3-coloring:
|
||||
- Statement: Given a graph $G$, can each vertex be assigned one of 3 colors such that no two adjacent vertices have the same color?
|
||||
5. Hamiltonian Cycle:
|
||||
- Statement: Given a graph $G$, does $G$ contain a cycle that visits every vertex exactly once?
|
||||
6. Hamiltonian Path:
|
||||
- Statement: Given a graph $G$, does $G$ contain a path that visits every vertex exactly once?
|
||||
|
||||
## Approximation Algorithms
|
||||
|
||||
- Consider optimization problems whose decision problem variant is NP-hard. Unless P=NP, finding an optimal solution to these problems cannot be done in polynomial time.
|
||||
- In approximation algorithms, we make a trade-o↵: we’re willing to accept sub-optimal solutions in exchange for polynomial runtime.
|
||||
- The Approximation Ratio of our algorithm is the worst-case ratio of our solution to the optimal solution.
|
||||
- For minimization problems, this ratio is $$\max_{l\in L}\left(\frac{c_A(l)}{c_{OPT}(l)}\right)$$, since our solution will be larger than OPT.
|
||||
- For maximization problems, this ratio is $$\min_{l\in L}\left(\frac{c_{OPT}(l)}{c_A(l)}\right)$$, since our solution will be smaller than OPT.
|
||||
- If given an algorithm, and you need to show it has some desired approximation ratio, there are a few approaches.
|
||||
- In recitation, we saw Max-Subset Sum. We found upper bounds on the optimal solution and showed that the given algorithm would always give a solution with value at least half of the upper bound, giving our approximation ratio of 2.
|
||||
- In lecture, you saw the Vertex Cover 2-approximation. Here, you would select any uncovered edge $(u, v)$ and add both u and v to the cover. We argued that at least one of u or v must be in the optimal cover, as the edge must be covered, so at every step we added at least one vertex from an optimal solution, and potentially one extra. So, the size of our cover could not be any larger than twice the optimal.
|
||||
|
||||
## Randomized Algorithms
|
||||
|
||||
Sometimes, we can get better expected performance from an algorithm by introducing randomness.
|
||||
|
||||
We make the tradeoff _guarantee_ runtime and solution quality from a deterministic algorithm, to _expected_ runtime and _quality_ from randomized algorithms.
|
||||
|
||||
We can make various bounds and tricks to calculate and amplify the probability of succeeding.
|
||||
|
||||
### Chernoff Bound
|
||||
|
||||
Statement:
|
||||
|
||||
$$
|
||||
Pr[X < (1-\delta)E[x]] \leq e^{-\frac{\delta^2 E[x]}{2}}
|
||||
$$
|
||||
|
||||
Requirements:
|
||||
|
||||
- $X$ is the sum of $n$ independent random variables
|
||||
- You used the Chernoff bound to bound the probability of getting less than $d$ good partitions, since the probability of each partition being good is independent – the quality of one partition does not affect the quality of the next.
|
||||
- Usage: If you have some probability $Pr[X < \text{something}]$ that you want to bound, you must find $E[X]$, and find a value for $\delta$ such that $(1-\delta)E[X] = \text{something}$. You can then plug in and $E[X]$ into the Chernoff bound.
|
||||
|
||||
### Markov's Inequality
|
||||
|
||||
Statement:
|
||||
|
||||
$$
|
||||
Pr[X \geq a] \leq \frac{E[X]}{a}
|
||||
$$
|
||||
|
||||
Requirements:
|
||||
|
||||
- $X$ is a non-negative random variable
|
||||
- No assumptions about independence
|
||||
- Usage: If you have some probability $Pr[X \geq \text{something}]$ that you want to bound, you must find $E[X]$, and find a value for $a$ such that $a = \text{something}$. You can then plug in and $E[X]$ into Markov's inequality.
|
||||
|
||||
### Union Bound
|
||||
|
||||
Statement:
|
||||
|
||||
$$
|
||||
Pr[\bigcup_{i=1}^n e_i] \leq \sum_{i=1}^n Pr[e_i]
|
||||
$$
|
||||
|
||||
- Conceptually, it's saying that at least one event out of a collection will occur is no more than the sum of the probabilities of each event.
|
||||
- Usage: To bound some bad event $e$, we can use the union bound to sum up the probabilities of each of the bad events $e_i$ and use that to bound $Pr[e]$.
|
||||
|
||||
#### Probabilistic Boosting via Repeated Trials
|
||||
|
||||
- If we want to reduce the probability of some bad event $e$ to some value $p$, we can run the algorithm repeatedly and make majority votes for the decision.
|
||||
- Assume we run the algorithm $k$ times, and the probability of success is $\frac{1}{2} + \epsilon$.
|
||||
- The probability that all trials fail is at most $(1-\epsilon)^k$.
|
||||
- The majority vote of $k$ runs is wrong is the same as probability that more than $\frac{k}{2}+1$ trials fail.
|
||||
- So, the probability is
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
Pr[\text{majority fails}] &=\sum_{i=\frac{k}{2}+1}^{k}\binom{k}{i}(\frac{1}{2}-\epsilon)^i(\frac{1}{2}+\epsilon)^{k-i}\\
|
||||
&= \binom{k}{\frac{k}{2}+1}(\frac{1}{2}-\epsilon)^{\frac{k}{2}+1}
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
|
||||
- If we want this probability to be at most $p$, we can just solve for $k$ in the inequality make it less than some $\delta$. Then we solve for $k$ in the inequality $\binom{k}{\frac{k}{2}+1}(\frac{1}{2}-\epsilon)^{\frac{k}{2}+1} \leq \delta$.
|
||||
|
||||
## Online Algorithms
|
||||
|
||||
- We make decisions on the fly, without knowing the future.
|
||||
- The _offline optimum_ is the optimal solution that knows the future.
|
||||
- The _competitive ratio_ of an online algorithm is the worst-case ratio of the cost of the online algorithm to the cost of the offline optimum. (when offline problem is NP-complete, an online algorithm for the problem is also an approximation algorithm) $$\text{Competitive Ratio} = \frac{C_{online}}{C_{offline}}$$
|
||||
- We do case by case analysis to show that the competitive ratio is at most some value. Just like approximation ratio proofs.
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
18
content/CSE347/_meta.js
Normal file
18
content/CSE347/_meta.js
Normal file
@@ -0,0 +1,18 @@
|
||||
export default {
|
||||
//index: "Course Description",
|
||||
"---":{
|
||||
type: 'separator'
|
||||
},
|
||||
Exam_reviews: "Exam reviews",
|
||||
CSE347_L1: "Analysis of Algorithms (Lecture 1)",
|
||||
CSE347_L2: "Analysis of Algorithms (Lecture 2)",
|
||||
CSE347_L3: "Analysis of Algorithms (Lecture 3)",
|
||||
CSE347_L4: "Analysis of Algorithms (Lecture 4)",
|
||||
CSE347_L5: "Analysis of Algorithms (Lecture 5)",
|
||||
CSE347_L6: "Analysis of Algorithms (Lecture 6)",
|
||||
CSE347_L7: "Analysis of Algorithms (Lecture 7)",
|
||||
CSE347_L8: "Analysis of Algorithms (Lecture 8)",
|
||||
CSE347_L9: "Analysis of Algorithms (Lecture 9)",
|
||||
CSE347_L10: "Analysis of Algorithms (Lecture 10)",
|
||||
CSE347_L11: "Analysis of Algorithms (Lecture 11)"
|
||||
}
|
||||
21
content/CSE347/index.md
Normal file
21
content/CSE347/index.md
Normal file
@@ -0,0 +1,21 @@
|
||||
# CSE 347
|
||||
|
||||
This is a course about fancy algorithms.
|
||||
|
||||
Topics include:
|
||||
|
||||
1. Greedy Algorithms
|
||||
2. Dynamic Programming
|
||||
3. Divide and Conquer
|
||||
4. Maximum Flows
|
||||
5. Reductions
|
||||
6. NP-Complete Problems
|
||||
7. Approximation Algorithms
|
||||
8. Randomized Algorithms
|
||||
9. Online Algorithms
|
||||
|
||||
It's hard if you don't know the tricks for solving leetcode problems.
|
||||
|
||||
I've been doing leetcode daily problems for almost 2 years when I get into the course.
|
||||
|
||||
It's relatively easy for me but I do have a hard time to get every proof right.
|
||||
127
content/CSE442T/CSE442T_L1.md
Normal file
127
content/CSE442T/CSE442T_L1.md
Normal file
@@ -0,0 +1,127 @@
|
||||
# Lecture 1
|
||||
|
||||
## Chapter 1: Introduction
|
||||
|
||||
### Alice sending information to Bob
|
||||
|
||||
Assuming _Eve_ can always listen
|
||||
|
||||
Rule 1. Message, Encryption to Code and Decryption to original Message.
|
||||
|
||||
### Kerckhoffs' principle
|
||||
|
||||
It states that the security of a cryptographic system shouldn't rely on the secrecy of the algorithm (Assuming Eve knows how everything works.)
|
||||
|
||||
**Security is due to the security of the key.**
|
||||
|
||||
### Private key encryption scheme
|
||||
|
||||
Let $M$ be the set of message that Alice will send to Bob. (The message space) "plaintext"
|
||||
|
||||
Let $K$ be the set of key that will ever be used. (The key space)
|
||||
|
||||
$Gen$ be the key generation algorithm.
|
||||
|
||||
$k\gets Gen(K)$
|
||||
|
||||
$c\gets Enc_k(m)$ denotes cipher encryption.
|
||||
|
||||
$m'\gets Dec_k(c')$ $m'$ might be null for incorrect $c'$.
|
||||
|
||||
$P[k\gets K:Dec_k(Enc_k(M))=m]=1$ The probability of decryption of encrypted message is original message is 1.
|
||||
|
||||
*_in some cases we can allow the probability not be 1_
|
||||
|
||||
### Some examples of crypto system
|
||||
|
||||
Let $M=\text{all five letter strings}$.
|
||||
|
||||
And $K=[1,10^{10}]$
|
||||
|
||||
Example:
|
||||
|
||||
$P[k=k']=\frac{1}{10^{10}}$
|
||||
|
||||
$Enc_{1234567890}("brion")="brion1234567890"$
|
||||
|
||||
$Dec_{1234567890}(brion1234567890)="brion"$
|
||||
|
||||
Seems not very secure but valid crypto system.
|
||||
|
||||
### Early attempts for crypto system
|
||||
|
||||
#### Caesar cipher
|
||||
|
||||
$M=\text{finite string of texts}$
|
||||
|
||||
$K=[1,26]$
|
||||
|
||||
$Enc_k=[(i+K)\% 26\ for\ i \in m]=c$
|
||||
|
||||
$Dec_k=[(i+26-K)\% 26\ for\ i \in c]$
|
||||
|
||||
```python
|
||||
def caesar_cipher_enc(s: str, k:int):
|
||||
return ''.join([chr((ord(i)-ord('a')+k)%26+ord('a')) for i in s])
|
||||
|
||||
def caesar_cipher_dec(s: str, k:int):
|
||||
return ''.join([chr((ord(i)-ord('a')+26-k)%26+ord('a')) for i in s])
|
||||
```
|
||||
|
||||
#### Substitution cipher
|
||||
|
||||
$M=\text{finite string of texts}$
|
||||
|
||||
$K=\text{set of all bijective linear transformations (for English alphabet},|K|=26!\text{)}$
|
||||
|
||||
$Enc_k=[iK\ for\ i \in m]=c$
|
||||
|
||||
$Dec_k=[iK^{-1}\ for\ i \in c]$
|
||||
|
||||
Fails to frequency analysis
|
||||
|
||||
#### Vigenere Cipher
|
||||
|
||||
$M=\text{finite string of texts with length }m$
|
||||
|
||||
$K=\text{[0,26]}^n$ (assuming English alphabet)
|
||||
|
||||
```python
|
||||
def viginere_cipher_enc(s: str, k: List[int]):
|
||||
res=''
|
||||
n,m=len(s),len(k)
|
||||
j=0
|
||||
for i in s:
|
||||
res+=caesar_cipher_enc(i,k[j])
|
||||
j=(j+1)%m
|
||||
return res
|
||||
|
||||
def viginere_cipher_dec(s: str, k: List[int]):
|
||||
res=''
|
||||
n,m=len(s),len(k)
|
||||
j=0
|
||||
for i in s:
|
||||
res+=caesar_cipher_dec(i,k[j])
|
||||
j=(j+1)%m
|
||||
return res
|
||||
```
|
||||
|
||||
#### One time pad
|
||||
|
||||
Completely random string, sufficiently long.
|
||||
|
||||
$M=\text{finite string of texts with length }n$
|
||||
|
||||
$K=\text{[0,26]}^n$ (assuming English alphabet)$
|
||||
|
||||
$Enc_k=m\oplus k$
|
||||
|
||||
$Dec_k=c\oplus k$
|
||||
|
||||
```python
|
||||
def one_time_pad_enc(s: str, k: List[int]):
|
||||
return ''.join([chr((ord(i)-ord('a')+k[j])%26+ord('a')) for j,i in enumerate(s)])
|
||||
|
||||
def one_time_pad_dec(s: str, k: List[int]):
|
||||
return ''.join([chr((ord(i)-ord('a')+26-k[j])%26+ord('a')) for j,i in enumerate(s)])
|
||||
```
|
||||
210
content/CSE442T/CSE442T_L10.md
Normal file
210
content/CSE442T/CSE442T_L10.md
Normal file
@@ -0,0 +1,210 @@
|
||||
# Lecture 10
|
||||
|
||||
## Chapter 2: Computational Hardness
|
||||
|
||||
### Discrete Log Assumption (Assumption 52.2)
|
||||
|
||||
This is collection of one-way functions
|
||||
|
||||
$$
|
||||
p\gets \tilde\Pi_n(\textup{ safe primes }), p=2q+1
|
||||
$$
|
||||
|
||||
$$
|
||||
a\gets \mathbb{Z}*_{p};g=a^2(\textup{ make sure }g\neq 1)
|
||||
$$
|
||||
|
||||
$$
|
||||
f_{g,p}(x)=g^x\mod p
|
||||
$$
|
||||
|
||||
$$
|
||||
f:\mathbb{Z}_q\to \mathbb{Z}^*_p
|
||||
$$
|
||||
|
||||
#### Evidence for Discrete Log Assumption
|
||||
|
||||
Best known algorithm to always solve discrete log mod p, $p\in \Pi_n$
|
||||
|
||||
$$
|
||||
O(2^{\sqrt{2}\sqrt{\log(n)}})
|
||||
$$
|
||||
|
||||
### RSA Assumption
|
||||
|
||||
Let $e$ be the exponents
|
||||
|
||||
$$
|
||||
P[p,q\gets \Pi_n;N\gets p\cdot q;e\gets \mathbb{Z}_{\phi(N)}^*;y\gets \mathbb{N}_n;x\gets \mathcal{A}(N,e,y);x^e=y\mod N]<\epsilon(n)
|
||||
$$
|
||||
|
||||
#### Theorem 53.2 (RSA Algorithm)
|
||||
|
||||
This is a collection of one-way functions
|
||||
|
||||
$I=\{(N,e):N=p\cdot q,p,q\in \Pi_n \textup{ and } e\in \mathbb{Z}_{\phi(N)}^*\}$
|
||||
|
||||
$D_{(N,e)}=\mathbb{Z}_N^*$
|
||||
|
||||
$R_{(N,e)}=\mathbb{Z}_N^*$
|
||||
|
||||
$f_{(N,e)}(x)=x^e\mod N$
|
||||
|
||||
Example:
|
||||
|
||||
On encryption side
|
||||
|
||||
$p=5,q=11,N=5\times 11=55$, $\phi(N)=4*10=40$
|
||||
|
||||
pick $e\in \mathbb{Z}_{40}^*$. say $e=3$, and $f(x)=x^3\mod 55$
|
||||
|
||||
pick $y\in \mathbb{Z}_{55}^*$. say $y=17$. We have $(55,3,17)$
|
||||
|
||||
$x^{40}\equiv 1\mod 55$
|
||||
|
||||
$x^{41}\equiv x\mod 55$
|
||||
|
||||
$x^{40k+1}\equiv x \mod 55$
|
||||
|
||||
Since $x^a\equiv x^{a\mod 40}\mod 55$ (by corollary of Fermat's little Theorem: $a^x\mod N=a^{x\mod \Phi(N)}\mod N$
|
||||
s )
|
||||
|
||||
The problem is, what can we multiply by $3$ to get $1\mod \phi(N)=1\mod 40$.
|
||||
|
||||
by computing the multiplicative inverse using extended Euclidean algorithm we have $3\cdot 27\equiv 1\mod 40$.
|
||||
|
||||
$x^3\equiv 17\mod 55$
|
||||
|
||||
$x\equiv 17^{27}\mod 55$
|
||||
|
||||
On adversary side.
|
||||
|
||||
they don't know $\phi(N)=40$
|
||||
|
||||
$$
|
||||
f(N,e):\mathbb{Z}_N^*\to \mathbb{Z}_N^*
|
||||
$$
|
||||
is a bijection.
|
||||
|
||||
Proof: Suppose $x_1^e\equiv x_2^e\mod n$
|
||||
|
||||
Then let $d=e^{-1}\mod \phi(N)$ (exists b/c $e\in\phi(N)^*$)
|
||||
|
||||
So $(x_1^e)^d\equiv (x_2^e)^d\mod N$
|
||||
|
||||
So $x_1^{e\cdot d\mod \phi(N)}\equiv x_2^{e\cdot d\mod \phi(N)}\mod N$ (Euler's Theorem)
|
||||
|
||||
$x_1\equiv x_2\mod N$
|
||||
|
||||
So it's one-to-one.
|
||||
|
||||
QED
|
||||
|
||||
Let $y\in \mathbb{Z}_N^*$, letting $x=y^d\mod N$, where $d\equiv e^{-1}\mod \phi(N)$
|
||||
|
||||
$x^e\equiv (y^d)^e \equiv y\mod n$
|
||||
|
||||
Proof:
|
||||
|
||||
It's easy to sample from $I$:
|
||||
|
||||
* pick $p,q\in \Pi_n$. $N=p\cdot q$
|
||||
* compute $\phi(N)=(p-1)(q-1)$
|
||||
* pick $e\gets \mathbb{Z}^*_N$. If $gcd(e,\phi(N))\neq 1$, pick again ($\mathbb{Z}_{\phi_(N)}^*$ has plenty of elements.)
|
||||
|
||||
Easy to sample $\mathbb{\mathbb{Z}_N^*}$ (domain).
|
||||
|
||||
Easy to compute $x^e\mod N$.
|
||||
|
||||
Hard to invert:
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
&~~~~P[(N,e)\in I;x\gets \mathbb{Z}_N^*;y=x^e\mod N:f(\mathcal{A}((N,e),y))=y]\\
|
||||
&=P[(N,e)\in I;x\gets \mathbb{Z}_N^*;y=x^e\mod N:x\gets \mathcal{A}((N,e),y)]\\
|
||||
&=P[(N,e)\in I;y\gets \mathbb{Z}_N^*;y=x^e\mod N:x\gets \mathcal{A}((N,e),y),x^e\equiv y\mod N]\\
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
By RSA assumption
|
||||
|
||||
The second equality follows because for any finite $D$ and bijection $f:D\to D$, sampling $y\in D$ directly is equivalent to sampling $x\gets D$, then computing $y=f(x)$.
|
||||
|
||||
QED
|
||||
|
||||
#### Theorem If inverting RSA is hard, then factoring is hard.
|
||||
|
||||
$$
|
||||
\textup{ RSA assumption }\implies \textup{ Factoring assumption}
|
||||
$$
|
||||
|
||||
If inverting RSA is hard, then factoring is hard.
|
||||
|
||||
i.e If factoring is easy, then inverting RSA is easy.
|
||||
|
||||
Proof:
|
||||
|
||||
Suppose $\mathcal{A}$ is an adversary that breaks the factoring assumption, then
|
||||
|
||||
$$
|
||||
P[p\gets \Pi_n;q\gets \Pi_n;N=p\cdot q;\mathcal{A}(N)=(p,q)]>\frac{1}{p(n)}
|
||||
$$
|
||||
|
||||
infinitely often.for a polynomial $p$.
|
||||
|
||||
Then we designing $B$ to invert RSA.
|
||||
|
||||
Suppose
|
||||
|
||||
$p,q\gets \Pi_n;N=p\cdot q;e\gets \mathbb{Z}_{\phi(N)}^*;x\gets \mathbb{Z}^n;y=x^e\mod N$
|
||||
|
||||
``` python
|
||||
def B(N,e,y):
|
||||
"""
|
||||
Goal: find x
|
||||
"""
|
||||
p,q=A(N)
|
||||
if n!=p*q:
|
||||
return None
|
||||
phiN=(p-1)*(q-1)
|
||||
# find modular inverse of e \mod N
|
||||
d=extended_euclidean_algorithm(e,phiN)
|
||||
# returns (y**d)%N
|
||||
x=fast_modular_exponent(y,d,N)
|
||||
return x
|
||||
```
|
||||
|
||||
So the probability of B succeeds is equal to A succeeds, which $>\frac{1}{p(n)}$ infinitely often, breaking RSA assumption.
|
||||
|
||||
Remaining question: Can $x$ be found without factoring $N$? $y=x^e\mod N$
|
||||
|
||||
### One-way permutation (Definition 55.1)
|
||||
|
||||
A collection function $\mathcal{F}=\{f_i:D_i\to R_i\}_{i\in I}$ is a one-way permutation if
|
||||
|
||||
1. $\forall i,f_i$ is a permutation
|
||||
2. $\mathcal{F}$ is a collection of one-way functions
|
||||
|
||||
_basically, a one-way permutation is a collection of one-way functions that maps $\{0,1\}^n$ to $\{0,1\}^n$ in a bijection way._
|
||||
|
||||
### Trapdoor permutations
|
||||
|
||||
Idea: $f:D\to R$ is a one-way permutation.
|
||||
|
||||
$y\gets R$.
|
||||
|
||||
* Finding $x$ such that $f(x)=y$ is hard.
|
||||
* With some secret info about $f$, finding $x$ is easy.
|
||||
|
||||
$\mathcal{F}=\{f_i:D_i\to R_i\}_{i\in I}$
|
||||
|
||||
1. $\forall i,f_i$ is a permutation
|
||||
2. $(i,t)\gets Gen(1^n)$ efficient. ($i\in I$ paired with $t$), $t$ is the "trapdoor info"
|
||||
3. $\forall i,D_i$ can be sampled efficiently.
|
||||
4. $\forall i,\forall x,f_i(x)$ can be computed in polynomial time.
|
||||
5. $P[(i,t)\gets Gen(1^n);y\gets R_i:f_i(\mathcal{A}(1^n,i,y))=y]<\epsilon(n)$ (note: $\mathcal{A}$ is not given $t$)
|
||||
6. (trapdoor) There is a p.p.t. $B$ such that given $i,y,t$, B always finds x such that $f_i(x)=y$. $t$ is the "trapdoor info"
|
||||
|
||||
#### Theorem RSA is a trapdoor
|
||||
|
||||
RSA collection of trapdoor permutation with factorization $(p,q)$ of $N$, or $\phi(N)$, as trapdoor info $f$.
|
||||
114
content/CSE442T/CSE442T_L11.md
Normal file
114
content/CSE442T/CSE442T_L11.md
Normal file
@@ -0,0 +1,114 @@
|
||||
# Lecture 11
|
||||
|
||||
Exam info posted tonight.
|
||||
|
||||
## Chapter 3: Indistinguishability and pseudo-randomness
|
||||
|
||||
### Pseudo-randomness
|
||||
|
||||
Idea: **Efficiently** produce many bits
|
||||
|
||||
which "appear" truly random.
|
||||
|
||||
#### One-time pad
|
||||
|
||||
$m\in\{0,1\}^n$
|
||||
|
||||
$Gen(1^n):k\gets \{0,1\}^N$
|
||||
|
||||
$Enc_k(m)=m\oplus k$
|
||||
|
||||
$Dec_k(c)=c\oplus k$
|
||||
|
||||
Advantage: Perfectly secret
|
||||
|
||||
Disadvantage: Impractical
|
||||
|
||||
The goal of pseudo-randomness is to make the algorithm, computationally secure, and practical.
|
||||
|
||||
Let $\{X_n\}$ be a sequence of distributions over $\{0,1\}^{l(n)}$, where $l(n)$ is a polynomial of $n$.
|
||||
|
||||
"Probability ensemble"
|
||||
|
||||
Example:
|
||||
|
||||
Let $U_n$ be the uniform distribution over $\{0,1\}^n$
|
||||
|
||||
For all $x\in \{0,1\}^n$
|
||||
|
||||
$P[x\gets U_n]=\frac{1}{2^n}$
|
||||
|
||||
For $1\leq i\leq n$, $P[x_i=1]=\frac{1}{2}$
|
||||
|
||||
For $1\leq i<j\leq n,P[x_i=1 \textup{ and } x_j=1]=\frac{1}{4}$ (by independence of different bits.)
|
||||
|
||||
Let $\{X_n\}_n$ and $\{Y_n\}_n$ be probability ensembles (separate of dist over $\{0,1\}^{l(n)}$)
|
||||
|
||||
$\{X_n\}_n$ and $\{Y_n\}_n$ are computationally **in-distinguishable** if for all non-uniform p.p.t adversary $\mathcal{D}$ ("distinguishers")
|
||||
|
||||
$$
|
||||
|P[x\gets X_n:\mathcal{D}(x)=1]-P[y\gets Y_n:\mathcal{D}(y)=1]|<\epsilon(n)
|
||||
$$
|
||||
|
||||
this basically means that the probability of finding any pattern in the two array is negligible.
|
||||
|
||||
If there is a $\mathcal{D}$ such that
|
||||
|
||||
$$
|
||||
|P[x\gets X_n:\mathcal{D}(x)=1]-P[y\gets Y_n:\mathcal{D}(y)=1]|\geq \mu(n)
|
||||
$$
|
||||
|
||||
then $\mathcal{D}$ is distinguishing with probability $\mu(n)$
|
||||
|
||||
If $\mu(n)\geq\frac{1}{p(n)}$, then $\mathcal{D}$ is distinguishing the two $\implies X_n\cancel{\approx} Y_n$
|
||||
|
||||
### Prediction lemma
|
||||
|
||||
$X_n^0$ and $X_n^1$ ensembles over $\{0,1\}^{l(n)}$
|
||||
|
||||
Suppose $\exists$ distinguisher $\mathcal{D}$ which distinguish by $\geq \mu(n)$. Then $\exists$ adversary $\mathcal{A}$ such that
|
||||
|
||||
$$
|
||||
P[b\gets\{0,1\};t\gets X_n^b]:\mathcal{A}(t)=b]\geq \frac{1}{2}+\frac{\mu(n)}{2}
|
||||
$$
|
||||
|
||||
Proof:
|
||||
|
||||
Without loss of generality, suppose
|
||||
|
||||
$$
|
||||
P[t\gets X^1_n:\mathcal{D}(t)=1]-P[t\gets X_n^0:\mathcal{D}(t)=1]\geq \mu(n)
|
||||
$$
|
||||
|
||||
$\mathcal{A}=\mathcal{D}$ (Outputs 1 if and only if $D$ outputs 1, otherwise 0.)
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
&~~~~~P[b\gets \{0,1\};t\gets X_n^b:\mathcal{A}(t)=b]\\
|
||||
&=P[t\gets X_n^1;\mathcal{A}=1]\cdot P[b=1]+P[t\gets X_n^0;\mathcal{A}(t)=0]\cdot P[b=0]\\
|
||||
&=\frac{1}{2}P[t\gets X_n^1;\mathcal{A}(t)=1]+\frac{1}{2}(1-P[t\gets X_n^0;\mathcal{A}(t)=1])\\
|
||||
&=\frac{1}{2}+\frac{1}{2}(P[t\gets X_n^1;\mathcal{A}(t)=1]-P[t\gets X_n^0;\mathcal{A}(t)=1])\\
|
||||
&\geq\frac{1}{2}+\frac{1}{2}\mu(n)\\
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
### Pseudo-random
|
||||
|
||||
$\{X_n\}$ over $\{0,1\}^{l(n)}$ is **pseudorandom** if $\{X_n\}\approx\{U_{l(n)}\}$. i.e. indistinguishable from the true randomness.
|
||||
|
||||
Example:
|
||||
|
||||
Building distinguishers
|
||||
|
||||
1. $X_n$: always outputs $0^n$, $\mathcal{D}$: [outputs $1$ if $t=0^n$]
|
||||
$$
|
||||
\vert P[t\gets X_n:\mathcal{D}(t)=1]-P[t\gets U_n:\mathcal{D}(t)=1]\vert=1-\frac{1}{2^n}\approx 1
|
||||
$$
|
||||
2. $X_n$: 1st $n-1$ bits are truly random $\gets U_{n-1}$ nth bit is $1$ with probability 0.50001 and $0$ with 0.49999, $D$: [outputs $1$ if $X_n=1$]
|
||||
$$
|
||||
\vert P[t\gets X_n:\mathcal{D}(t)=1]-P[t\gets U_n:\mathcal{D}(t)=1]\vert=0.5001-0.5=0.001\neq 0
|
||||
$$
|
||||
3. $X_n$: For each bit $x_i\gets\{0,1\}$ **unless** there have been 1 million $0$'s. in a row. Then outputs $1$, $D$: [outputs $1$ if $x_1=x_2=...=x_{1000001}=0$]
|
||||
$$
|
||||
\vert P[t\gets X_n:\mathcal{D}(t)=1]-P[t\gets U_n:\mathcal{D}(t)=1]\vert=|0-\frac{1}{2^{1000001}}|\neq 0
|
||||
$$
|
||||
152
content/CSE442T/CSE442T_L12.md
Normal file
152
content/CSE442T/CSE442T_L12.md
Normal file
@@ -0,0 +1,152 @@
|
||||
# Lecture 12
|
||||
|
||||
## Chapter 3: Indistinguishability and Pseudorandomness
|
||||
|
||||
$\{X_n\}$ and $\{Y_n\}$ are distinguishable by $\mu(n)$ if $\exists$ distinguisher $\mathcal{D}$
|
||||
|
||||
$$
|
||||
|P[x\gets X_n:\mathcal{D}(x)=1]-P[y\gets Y_n:\mathcal{D}(y)=1]|\geq \mu(n)
|
||||
$$
|
||||
|
||||
- If $\mu(n)\geq \frac{1}{p(n)}\gets poly(n)$ for infinitely many n, then $\{X_n\}$ and $\{Y_n\}$ are distinguishable.
|
||||
- Otherwise, indistinguishable ($|diff|<\epsilon(n)$)
|
||||
|
||||
Property: Closed under efficient procedures.
|
||||
|
||||
If $M$ is any n.u.p.p.t. which can take a ample from $t$ from $X_n,Y_n$ as input $M(X_n)$
|
||||
|
||||
If $\{X_n\}\approx\{Y_n\}$, then so are $\{M(X_n)\}\approx\{M(Y_n)\}$
|
||||
|
||||
Proof:
|
||||
|
||||
If $\mathcal{D}$ distinguishes $M(X_n)$ and $M(Y_n)$ by $\mu(n)$ then $\mathcal{D}(M(\cdot))$ is also a polynomial-time distinguisher of $X_n,Y_n$.
|
||||
|
||||
### Hybrid Lemma
|
||||
|
||||
Let $X^0_n,X^1_n,\dots,X^m_n$ are ensembles indexed from $1,..,m$
|
||||
|
||||
If $\mathcal{D}$ distinguishes $X_n^0$ and $X_n^m$ by $\mu(n)$, then $\exists i,1\leq i\leq m$ where $X_{n}^{i-1}$ and $X_n^i$ are distinguished by $\mathcal{D}$ by $\frac{\mu(n)}{m}$
|
||||
|
||||
Proof: (we use triangle inequality.) Let $p_i=P[t\gets X_n^i:\mathcal{D}(t)=1],0\leq i\leq m$. We have $|p_0-p_m|\geq m(n)$
|
||||
|
||||
Using telescoping tricks:
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
|p_0-p_m|&=|p_0-p_1+p_1-p_2+\dots +p_{m-1}-p_m|\\
|
||||
&\leq |p_0-p_1|+|p_1-p_2|+\dots+|p_{m-1}-p_m|\\
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
If all $|p_{i-1}-p_i|<\frac{\mu(n)}{m},|p_0-p_m|<\mu_n$ contradiction.
|
||||
|
||||
In applications, only useful if $m\leq q(n)$ polynomial
|
||||
|
||||
If $X^0_n$ and $X^m_n$ are distinguishable by $\frac{1}{p(n)}$, then $2$ inner "hybrids" are distinguishable $\frac{1}{p(n)q(n)}=\frac{1}{poly(n)}$
|
||||
|
||||
Example:
|
||||
|
||||
For some Brian in Week 1 and Week 50, a distinguisher $\mathcal{D}$ outputs 1 if hair is considered "long".
|
||||
|
||||
There is some week $i,1\leq i\leq 50$ $|p_{i-1}-p_i|\geq 0.02$
|
||||
|
||||
By prediction lemma, there is a machine that could
|
||||
|
||||
$$
|
||||
P[b\to \{0,1\};pic\gets X^{i-1+b}:\mathcal{A}(pic)=b]\geq \frac{1}{2}+\frac{0.02}{2}=0.51
|
||||
$$
|
||||
|
||||
### Next bit test (NBT)
|
||||
|
||||
We say $\{X_n\}$ passes the next bit test if $\forall i\in\{0,1,...,l(n)-1\}$ on $\{0,1\}^{l(n)}$ and for all adversaries $\mathcal{A}:P[t\gets X_n:\mathcal{A}(t_1,t_2,...,t_i)=t_{i+1}]\leq \frac{1}{2}+\epsilon(n)$ (given first $i$ bit, the probability of successfully predicts $i+1$ th bit is almost random $\frac{1}{2}$)
|
||||
|
||||
Note that for any $\mathcal{A}$, and any $i$,
|
||||
|
||||
$$
|
||||
P[t\gets U_{l(n)}:\mathcal{A}(t_1,...t_i)=t_{i+1}]=\frac{1}{2}
|
||||
$$
|
||||
|
||||
If $\{X_n\}\approx\{U_{l(n)}\}$ (pseudorandom), then $X_n$ must pass NBT for all $i$.
|
||||
|
||||
Otherwise $\exists \mathcal{A},i$ where for infinitely many $n$,
|
||||
|
||||
$$
|
||||
P[t\gets X_n:\mathcal{A}(t_1,t_2,...,t_i)=t_{i+1}]\leq \frac{1}{2}+\epsilon(n)
|
||||
$$
|
||||
|
||||
We can build a distinguisher $\mathcal{D}$ from $\mathcal{A}$.
|
||||
|
||||
The converse if True!
|
||||
|
||||
The NBT(Next bit test) is complete.
|
||||
|
||||
If $\{X_n\}$ on $\{0,1\}^{l(n)}$ passes NBT, then it's pseudorandom.
|
||||
|
||||
Ideas of proof: full proof is on the text.
|
||||
|
||||
Our idea is that we want to create $H^{l(n)}_n=\{X_n\}$ and $H^0_n=\{U_{l(n)}\}$
|
||||
|
||||
We construct "random" bit stream:
|
||||
|
||||
$$
|
||||
H_n^i=\{x\gets X_n;u\gets U_{l(n)};t=x_1x_2\dots x_i u_{i+1}u_{i+2}\dots u_{l(n)}\}
|
||||
$$
|
||||
|
||||
If $\{X_n\}$ were not pseudorandom, there is a $D$
|
||||
|
||||
$$
|
||||
|P[x\gets X_n:\mathcal{D}(x)=1]-P[u\gets U_{l(n)}:\mathcal{D}(u)=1]|=\mu(n)\geq \frac{1}{p(n)}
|
||||
$$
|
||||
|
||||
By hybrid lemma, there is $i,1\leq i\leq l(n)$ where:
|
||||
|
||||
$$
|
||||
|P[t\gets H^{i-1}:\mathcal{D}(t)=1]-P[t\gets H^i:\mathcal{D}(t)=1]|\geq \frac{1}{p(n)l(n)}=\frac{1}{poly(n)}
|
||||
$$
|
||||
|
||||
$l(n)$ is the step we need to take transform $X$ to $X^n$
|
||||
|
||||
Let,
|
||||
|
||||
$$
|
||||
H^i=x_1\dots x_i u_{i+1}\dots u_{l(n)}\\
|
||||
H^i=x_1\dots x_i x_{i+1}\dots u_{l(n)}
|
||||
$$
|
||||
|
||||
notice that only two bits are distinguished in the procedure.
|
||||
|
||||
$\mathcal{D}$ can distinguish $x_{i+1}$ from a truly random $U_{i+1}$, knowing the first $i$ bits $x_i\dots x_i$ came from $x\gets x_n$
|
||||
|
||||
So $\mathcal{D}$ can predict $x_{i+1}$ from $x_1\dots x_i$ (contradicting with that $X$ passes NBT)
|
||||
|
||||
QED
|
||||
|
||||
## Pseudorandom Generator
|
||||
|
||||
Suppose $G:\{0,1\}^*\to\{0,1\}^*$ is a pseudorandom generator if the following is true:
|
||||
|
||||
1. $G$ is efficiently computable.
|
||||
2. $|G(x)|\geq |x|\forall x$ (expansion)
|
||||
3. $\{x\gets U_n:G(x)\}_n$ is pseudorandom
|
||||
|
||||
$n$ truly random bits $\to$ $n^2$ pseudorandom bits
|
||||
|
||||
### PRG exists if and only if one-way function exists
|
||||
|
||||
The other part of proof will be your homework, damn.
|
||||
|
||||
If one-way function exists, then Pseudorandom Generator exists.
|
||||
|
||||
Ideas of proof:
|
||||
|
||||
Let $f:\{0,1\}^n\to \{0,1\}^n$ be a strong one-way permutation (bijection).
|
||||
|
||||
$x\gets U_n$
|
||||
|
||||
$f(x)||x$
|
||||
|
||||
Not all bits of $x$ would be hard to predict.
|
||||
|
||||
**Hard-core bit:** One bit of information about $x$ which is hard to determine from $f(x)$. $P[\text{success}]\leq \frac{1}{2}+\epsilon(n)$
|
||||
|
||||
Depends on $f(x)$
|
||||
161
content/CSE442T/CSE442T_L13.md
Normal file
161
content/CSE442T/CSE442T_L13.md
Normal file
@@ -0,0 +1,161 @@
|
||||
# Lecture 13
|
||||
|
||||
## Chapter 3: Indistinguishability and Pseudorandomness
|
||||
|
||||
### Pseudorandom Generator (PRG)
|
||||
|
||||
#### Definition 77.1 (Pseudorandom Generator)
|
||||
|
||||
$G:\{0,1\}^n\to\{0,1\}^{l(n)}$ is a pseudorandom generator if the following is true:
|
||||
|
||||
1. $G$ is efficiently computable.
|
||||
2. $l(n)> n$ (expansion)
|
||||
3. $\{x\gets \{0,1\}^n:G(x)\}_n\approx \{u\gets \{0,1\}^{l(n)}\}$
|
||||
|
||||
#### Definition 78.3 (Hard-core bit (predicate) (HCB))
|
||||
|
||||
Hard-core bit (predicate) (HCB): $h:\{0,1\}^n\to \{0,1\}$ is a hard-core bit of $f:\{0,1\}^n\to \{0,1\}^*$ if for every adversary $A$,
|
||||
|
||||
$$
|
||||
Pr[x\gets \{0,1\}^n;y=f(x);A(1^n,y)=h(x)]\leq \frac{1}{2}+\epsilon(n)
|
||||
$$
|
||||
|
||||
Ideas: $f:\{0,1\}^n\to \{0,1\}^*$ is a one-way function.
|
||||
|
||||
Given $y=f(x)$, it is hard to recover $x$. A cannot produce all of $x$ but can know some bits of $x$.
|
||||
|
||||
$h(x)$ is just a yes/no question regarding $x$.
|
||||
|
||||
Example:
|
||||
|
||||
In RSA function, we pick $p,q\in \Pi^n$ as primes and $N=pq$. $e\gets \mathbb{Z}_N^*$ and $f(x)=x^e\mod N$.
|
||||
|
||||
$h(x)=x_n$ is a HCB of $f$. Given RSA assumption.
|
||||
|
||||
**h(x) is not necessarily one of the bits of $x=x_1x_2\cdots x_n$.**
|
||||
|
||||
#### Theorem Any one-way function has a HCB.
|
||||
|
||||
A HCB can be produced for any one-way function.
|
||||
|
||||
Let $f:\{0,1\}^n\to \{0,1\}^*$ be a strong one-way function.
|
||||
|
||||
Define $g:\{0,1\}^{2n}\to \{0,1\}^*$ as $g(x,r)=(f(x), r),x\in \{0,1\}^n,r\in \{0,1\}^n$. $g$ is a strong one-way function. (proved in homework)
|
||||
|
||||
$$
|
||||
h(x,r)=\langle x,r\rangle=x_1r_1+ x_2r_2+\cdots + x_nr_n\mod 2
|
||||
$$
|
||||
|
||||
$\langle x,1^n\rangle=x_1+x_2+\cdots +x_n\mod 2$
|
||||
|
||||
$\langle x,0^{n-1}1\rangle=x_ n$
|
||||
|
||||
Ideas of proof:
|
||||
|
||||
If A could reliably find $\langle x,1^n\rangle$, with $r$ being completely random, then it could find $x$ too often.
|
||||
|
||||
### Pseudorandom Generator from HCB
|
||||
|
||||
1. $G(x)=\{0,1\}^n\to \{0,1\}^{n+1}$
|
||||
2. $G(x)=\{0,1\}^n\to \{0,1\}^{l(n)}$
|
||||
|
||||
For (1),
|
||||
|
||||
#### Theorem HCB generates PRG
|
||||
|
||||
Let $f:\{0,1\}^n\to \{0,1\}^n$ be a one-way permutation (bijective) with a HCB $h$. Then $G(x)=f(x)|| h(x)$ is a PRG.
|
||||
|
||||
Proof:
|
||||
|
||||
Efficiently computable: $f$ is one-way so $h$ is efficiently computable.
|
||||
|
||||
Expansion: $n<n+1$
|
||||
|
||||
Pseudorandomness:
|
||||
|
||||
We proceed by contradiction.
|
||||
|
||||
Suppose $\{G(U_n)\}\cancel{\approx} \{U_{n+1}\}$. Then there would be a next-bit predictor $A$ such that for some bit $i$.
|
||||
|
||||
$$
|
||||
Pr[x\gets \{0,1\}^n;t=G(x);A(t_1t_2\cdots t_{i-1})=t_i]\geq \frac{1}{2}+\epsilon(n)
|
||||
$$
|
||||
|
||||
Since $f$ is a bijection, $x\gets U_n$ and $f(x)\gets U_n$.
|
||||
|
||||
$G(x)=f(x)|| h(x)$
|
||||
|
||||
So $A$ could not predict $t_i$ with advantage $\frac{1}{2}+\epsilon(n)$ given any first $n$ bits.
|
||||
|
||||
$$
|
||||
Pr[t_i=1|t_1t_2\cdots t_{i-1}]= \frac{1}{2}
|
||||
$$
|
||||
|
||||
So $i=n+1$ the last bit, $A$ could predict.
|
||||
|
||||
$$
|
||||
Pr[x\gets \{0,1\}^n;y=f(x);A(y)=h(x)]>\frac{1}{2}+\epsilon(n)
|
||||
$$
|
||||
|
||||
This contradicts the HCB definition of $h$.
|
||||
|
||||
### Construction of PRG
|
||||
|
||||
$G'=\{0,1\}^n\to \{0,1\}^{l(n)}$
|
||||
|
||||
using PRG $G:\{0,1\}^n\to \{0,1\}^{n+1}$
|
||||
|
||||
Let $s\gets \{0,1\}^n$ be a random string.
|
||||
|
||||
We proceed by the following construction:
|
||||
|
||||
$G(s)=X_1||b_1$
|
||||
|
||||
$G(X_1)=X_2||b_2$
|
||||
|
||||
$G(X_2)=X_3||b_3$
|
||||
|
||||
$\cdots$
|
||||
|
||||
$G(X_{l(n)-1})=X_{l(n)}||b_{l(n)}$
|
||||
|
||||
$G'(s)=b_1b_2b_3\cdots b_{l(n)}$
|
||||
|
||||
We claim $G':\{0,1\}^n\to \{0,1\}^{l(n)}$ is a PRG.
|
||||
|
||||
#### Corollary: Combining constructions
|
||||
|
||||
$f:\{0,1\}^n\to \{0,1\}^n$ is a one-way permutation with a HCB $h: \{0,1\}^n\to \{0,1\}$.
|
||||
|
||||
$G(s)=h(x)||h(f(x))||h(f^2(x))\cdots h(f^{l(n)-1}(x))$ is a PRG. Where $f^a(x)=f(f^{a-1}(x))$.
|
||||
|
||||
Proof:
|
||||
|
||||
$G'$ is a PRG:
|
||||
|
||||
1. Efficiently computable: since we are computing $G'$ by applying $G$ multiple times (polynomial of $l(n)$ times).
|
||||
2. Expansion: $n<l(n)$.
|
||||
3. Pseudorandomness: We proceed by contradiction. Suppose the output is not pseudorandom. Then there exists a distinguisher $\mathcal{D}$ that can distinguish $G'$ from $U_{l(n)}$ with advantage $\frac{1}{2}+\epsilon(n)$.
|
||||
|
||||
Strategy: use hybrid argument to construct distributions.
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
H^0&=U_{l(n)}=u_1u_2\cdots u_{l(n)}\\
|
||||
H^1&=u_1u_2\cdots u_{l(n)-1}b_{l(n)}\\
|
||||
H^2&=u_1u_2\cdots u_{l(n)-2}b_{l(n)-1}b_{l(n)}\\
|
||||
&\cdots\\
|
||||
H^{l(n)}&=b_1b_2\cdots b_{l(n)}
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
By the hybrid argument, there exists an $i$ such that $\mathcal{D}$ can distinguish $H^i$ and $H^{i+1}$ $0\leq i\leq l(n)-1$ by $\frac{1}{p(n)l(n)}$
|
||||
|
||||
Show that there exists $\mathcal{D}$ for
|
||||
|
||||
$$
|
||||
\{u\gets U_{n+1}\}\text{ vs. }\{x\gets U_n;G(x)=u\}
|
||||
$$
|
||||
|
||||
with advantage $\frac{1}{2}+\epsilon(n)$. (contradiction)
|
||||
|
||||
176
content/CSE442T/CSE442T_L14.md
Normal file
176
content/CSE442T/CSE442T_L14.md
Normal file
@@ -0,0 +1,176 @@
|
||||
# Lecture 14
|
||||
|
||||
## Recap
|
||||
|
||||
$\exists$ one-way functions $\implies$ $\exists$ PRG expand by any polynomial amount
|
||||
|
||||
$\exists G:\{0,1\}^n \to \{0,1\}^{l(n)}$ s.t. $G$ is efficiently computable, $l(n) > n$, and $G$ is pseudorandom
|
||||
|
||||
$$
|
||||
\{G(U_n)\}\approx \{U_{l(n)}\}
|
||||
$$
|
||||
|
||||
Back to the experiment we did long time ago:
|
||||
|
||||
||Group 1|Group 2|
|
||||
|---|---|---|
|
||||
|$00000$ or $11111$|3|16|
|
||||
|4 of 1's|42|56|
|
||||
|balanced|too often|usual|
|
||||
|consecutive repeats|0|4|
|
||||
|
||||
So Group 1 is human, Group 2 is computer.
|
||||
|
||||
## Chapter 3: Indistinguishability and Pseudorandomness
|
||||
|
||||
### Computationally secure encryption
|
||||
|
||||
Recall with perfect security,
|
||||
|
||||
$$
|
||||
P[k\gets Gen(1^n):Enc_k(m_1)=c] = P[k\gets Gen(1^n):Enc_k(m_2)=c]
|
||||
$$
|
||||
|
||||
for all $m_1,m_2\in M$ and $c\in C$.
|
||||
|
||||
$(Gen,Enc,Dec)$ is **single message secure** if $\forall n.u.p.p.t \mathcal{D}$ and for all $n\in \mathbb{N}$, $\forall m_1,m_2\gets \{0,1\}^n \in M^n$, $\mathcal{D}$ distinguishes $Enc_k(m_1)$ and $Enc_k(m_2)$ with at most negligble probability.
|
||||
|
||||
$$
|
||||
P[k\gets Gen(1^n):\mathcal{D}(Enc_k(m_1),Enc_k(m_2))=1] \leq \epsilon(n)
|
||||
$$
|
||||
|
||||
By the prediction lemma, ($\mathcal{A}$ is a ppt, you can also name it as $\mathcal{D}$)
|
||||
|
||||
$$
|
||||
P[b\gets \{0,1\}:k\gets Gen(1^n):\mathcal{A}(Enc_k(m_b)) = b] \leq \frac{1}{2} + \frac{\epsilon(n)}{2}
|
||||
$$
|
||||
|
||||
and the above equation is $\frac{1}{2}$ for perfect secrecy.
|
||||
|
||||
### Construction of single message secure cryptosystem
|
||||
|
||||
cryptosystem with shorter keys. Mimic OTP(one time pad) with shorter keys with pseudorandom randomness.
|
||||
|
||||
$K=\{0,1\}^n$, $\mathcal{M}=\{0,1\}^{l(n)}$, $G:K \to \mathcal{M}$ is a PRG.
|
||||
|
||||
$Gen(1^n)$: $k\gets \{0,1\}^n$; output $k$.
|
||||
|
||||
$Enc_k(m)$: $r\gets \{0,1\}^{l(n)}$; output $G(k)\oplus m$.
|
||||
|
||||
$Dec_k(c)$: output $G(k)\oplus c$.
|
||||
|
||||
Proof of security:
|
||||
|
||||
Let $m_0,m_1\in \mathcal{M}$ be two messages, and $\mathcal{D}$ is a n.u.p.p.t distinguisher.
|
||||
|
||||
Suppose $\{K\gets Gen(1^n):Enc_k(m_i)\}$ is distinguished for $i=0,1$ by $\mathcal{D}$ and by $\mu(n)\geq\frac{1}{poly(n)}$.
|
||||
|
||||
Strategy: Move to OTP, then flip message.
|
||||
|
||||
$$
|
||||
H_0(Enc_k(m_0)) = \{k\gets \{0,1\}^n: m_0\oplus G(k)\}
|
||||
$$
|
||||
$$
|
||||
H_1(OTP(m_1)) = \{u\gets U_{l(n)}: m_o\oplus u\}
|
||||
$$
|
||||
$$
|
||||
H_2(OTP(m_1)) = \{u\gets U_{l(n)}: m_1\oplus u\}
|
||||
$$
|
||||
$$
|
||||
H_3(Enc_k(m_0)) = \{k\gets \{0,1\}^n: m_1\oplus G(k)\}
|
||||
$$
|
||||
|
||||
By hybrid argument, 2 neighboring messages are indistinguishable.
|
||||
|
||||
However, $H_0$ and $H_1$ are indistinguishable since $G(U_n)$ and $U_{l(n)}$ are indistinguishable.
|
||||
|
||||
$H_1$ and $H_2$ are indistinguishable by perfect secrecy of OTP.
|
||||
|
||||
$H_2$ and $H_3$ are indistinguishable since $G(U_n)$ and $U_{l(n)}$ are indistinguishable.
|
||||
|
||||
Which leads to a contradiction.
|
||||
|
||||
### Multi-message secure encryption
|
||||
|
||||
$(Gen,Enc,Dec)$ is multi-message secure if $\forall n.u.p.p.t \mathcal{D}$ and for all $n\in \mathbb{N}$, and $q(n)\in poly(n)$.
|
||||
|
||||
$$
|
||||
\overline{m}=(m_1,\dots,m_{q(n)})
|
||||
$$
|
||||
$$
|
||||
\overline{m}'=(m_1',\dots,m_{q(n)}')
|
||||
$$
|
||||
|
||||
are list of $q(n)$ messages in $\{0,1\}^n$.
|
||||
|
||||
$\mathcal{D}$ distinguishes $Enc_k(\overline{m})$ and $Enc_k(\overline{m}')$ with at most negligble probability.
|
||||
|
||||
$$
|
||||
P[k\gets Gen(1^n):\mathcal{D}(Enc_k(\overline{m}),Enc_k(\overline{m}'))=1] \leq \frac{1}{2} + \epsilon(n)
|
||||
$$
|
||||
|
||||
**THIS IS NOT MULTI-MESSAGE SECURE.**
|
||||
|
||||
We can take $\overline{m}=(0^n,0^n)\to (G(k),G(k))$ and $\overline{m}'=(0^n,1^n)\to (G(k),G(k)+1^n)$ the distinguisher can easily distinguish if some message was sent twice.
|
||||
|
||||
What we need is that the distinguisher cannot distinguish if some message was sent twice. To achieve multi-message security, we need our encryption function to use randomness (or change states) for each message, otherwise $Enc_k(0^n)$ will return the same on consecutive messages.
|
||||
|
||||
Our fix is, if we can agree on a random function $F:\{0,1\}^n\to \{0,1\}^n$ satisfied that: for each input $x\in\{0,1\}^n$, $F(x)$ is chosen uniformly at random.
|
||||
|
||||
$Gen(1^n):$ Choose random function $F:\{0,1\}^n\to \{0,1\}^n$.
|
||||
|
||||
$Enc_F(m):$ let $r\gets U_n$; output $(r,F(r)\oplus m)$.
|
||||
|
||||
$Dec_F(m):$ Given $(r,c)$, output $m=F(r)\oplus c$.
|
||||
|
||||
Ideas: Adversary sees $r$ but has no Ideas about $F(r)$. (we choose all outputs at random)
|
||||
|
||||
If we could do this, this is MMS (multi-message secure).
|
||||
|
||||
Proof:
|
||||
|
||||
Suppose $m_1,m_2,\dots,m_{q(n)}$, $m_1',\dots,m_{q(n)}'$ are sent to the encryption oracle.
|
||||
|
||||
Suppose the encryption are distinguished by $\mathcal{D}$ with probability $\frac{1}{2}+\epsilon(n)$.
|
||||
|
||||
Strategy: move to OTP with hybrid argument.
|
||||
|
||||
Suppose we choose a random function
|
||||
|
||||
$$
|
||||
H_0:\{F\gets RF_n:((r_1,m_1\oplus F(r_1)),(r_2,m_2\oplus F(r_2)),\dots,(r_{q(n)},m_{q(n)}\oplus F(r_{q(n)})))\}
|
||||
$$
|
||||
|
||||
and
|
||||
|
||||
$$
|
||||
H_1:\{OTP:(r_1,m_1\oplus u_1),(r_2,m_2\oplus u_2),\dots,(r_{q(n)},m_{q(n)}\oplus u_{q(n)})\}
|
||||
$$
|
||||
|
||||
$r_i,u_i\in U_n$.
|
||||
|
||||
By hybrid argument, $H_0$ and $H_1$ are indistinguishable if $r_1,\dots,r_{q(n)}$ are different, these are the same.
|
||||
|
||||
$F(r_1),\dots,F(r_{q(n)})$ are chosen uniformly and independently at random.
|
||||
|
||||
only possible problem is $r_i=r_j$ for some $i\neq j$, and $P[r_i=r_j]=\frac{1}{2^n}$.
|
||||
|
||||
And the probability that at least one pair are equal
|
||||
|
||||
$$
|
||||
P[\text{at least one pair are equal}] =P[\bigcup_{i\neq j}\{r_i=r_j\}] \leq \sum_{i\neq j}P[r_i=r_j]=\binom{n}{2}\frac{1}{2^n} < \frac{n^2}{2^{n+1}}
|
||||
$$
|
||||
|
||||
which is negligible.
|
||||
|
||||
Unfortunately, we cannot do this in practice.
|
||||
|
||||
How many random functions are there?
|
||||
|
||||
The length of description of $F$ is $n 2^n$.
|
||||
|
||||
For each $x\in \{0,1\}^n$, there are $2^n$ possible values for $F(x)$.
|
||||
|
||||
So the total number of random functions is $(2^n)^{2^n}=2^{n2^n}$.
|
||||
|
||||
|
||||
189
content/CSE442T/CSE442T_L15.md
Normal file
189
content/CSE442T/CSE442T_L15.md
Normal file
@@ -0,0 +1,189 @@
|
||||
# Lecture 15
|
||||
|
||||
## Chapter 3: Indistinguishability and Pseudorandomness
|
||||
|
||||
### Random Function
|
||||
|
||||
$F:\{0,1\}^n\to \{0,1\}^n$
|
||||
|
||||
For each $x\in \{0,1\}^n$, there are $2^n$ possible values for $F(x)$.
|
||||
|
||||
pick $y=F(x)\gets \{0,1\}^n$ independently at random. ($n$ bits)
|
||||
|
||||
This generates $n\cdot 2^n$ random bits to specify $F$.
|
||||
|
||||
### Equivalent description of $F$
|
||||
|
||||
```python
|
||||
# initialized empty list L
|
||||
L=collections.defaultdict(int)
|
||||
# initialize n bits constant
|
||||
n=10
|
||||
def F(x):
|
||||
""" simulation of random function
|
||||
param:
|
||||
x: n bits
|
||||
return:
|
||||
y: n bits
|
||||
"""
|
||||
if L[x] is not None:
|
||||
return L[x]
|
||||
else:
|
||||
# y is a random n-bit string
|
||||
y=random.randbits(n)
|
||||
L[x]=y
|
||||
return y
|
||||
```
|
||||
|
||||
However, this is not a good random function since two communicator may not agree on the same $F$.
|
||||
|
||||
### Pseudorandom Function
|
||||
|
||||
$f:\{0,1\}^n\to \{0,1\}^n$
|
||||
|
||||
#### Oracle Access (for function $g$)
|
||||
|
||||
$O_g$ is a p.p.t. that given $x\in \{0,1\}^n$ outputs $g(x)$.
|
||||
|
||||
The distinguisher $D$ is given oracle access to $O_g$ and outputs $1$ if $g$ is random and $0$ otherwise. It can make polynomially many queries.
|
||||
|
||||
### Oracle indistinguishability
|
||||
|
||||
$\{F_n\}$ and $\{G_n\}$ are sequence of distribution on functions
|
||||
|
||||
$$
|
||||
f:\{0,1\}^{l_1(n)}\to \{0,1\}^{l_2(n)}
|
||||
$$
|
||||
|
||||
that are computationally indistinguishable
|
||||
|
||||
$$
|
||||
\{f_n\}\sim \{g_n\}
|
||||
$$
|
||||
|
||||
if for all p.p.t. $D$ (with oracle access to $F_n$ and $G_n$),
|
||||
|
||||
$$
|
||||
\left|P[f\gets F_n:D^f(1^n)=1]-P[g\gets G_n:D^g(1^n)=1]\right|< \epsilon(n)
|
||||
$$
|
||||
|
||||
where $\epsilon(n)$ is negligible.
|
||||
|
||||
Under this property, we still have:
|
||||
|
||||
- Closure properties. under efficient procedures.
|
||||
- Prediction lemma.
|
||||
- Hybrid lemma.
|
||||
|
||||
### Pseudorandom Function Family
|
||||
|
||||
Definition: $\{f_s:\{0,1\}^\{0.1\}^{|S|}\to \{0,1\}^P$ $t_0s\in \{0,1\}^n\}$ is a pseudorandom function family if $\{f_s\}_{s\in \{0,1\}^n}$ are oracle indistinguishable.
|
||||
|
||||
- It is easy to compute for every $x\in \{0,1\}^{|S|}$.
|
||||
- $\{s \gets\{0,1\}^n\}_n\approx \{F\gets RF_n,F\}$ is indistinguishable from the uniform distribution over $\{0,1\}^P$.
|
||||
- $R$ is truly random function.
|
||||
|
||||
Example:
|
||||
|
||||
For $s\in \{0,1\}^n$, define $f_s:\overline{x}\mapsto s\cdot \overline{s}$.
|
||||
|
||||
$\mathcal{D}$ gives oracle access to $g(0^n)=\overline{y_0}$, $g(1^n)=\overline{y_1}$. If $\overline{y_0}+\overline{y_1}=1^n$, then $\mathcal{D}$ outputs $1$ otherwise $0$.
|
||||
|
||||
```python
|
||||
def O_g(x):
|
||||
pass
|
||||
|
||||
def D():
|
||||
# bit_stream(0,n) is a n-bit string of 0s
|
||||
y0=O_g(bit_stream(0,n))
|
||||
y1=O_g(bit_stream(1,n))
|
||||
if y0+y1==bit_stream(1,n):
|
||||
return 1
|
||||
else:
|
||||
return 0
|
||||
```
|
||||
|
||||
If $g=f_s$, then $D$ returns $\overline{s}+\overline{s}+1^n =1^n$.
|
||||
|
||||
$$
|
||||
P[f_s\gets D^{f_s}(1^n)=1]=1
|
||||
$$
|
||||
|
||||
$$
|
||||
P[F\gets RF^n,D^F(1^n)=1]=\frac{1}{2^n}
|
||||
$$
|
||||
|
||||
#### Theorem PRG exists then PRF family exists.
|
||||
|
||||
Proof:
|
||||
|
||||
Let $g:\{0,1\}^n\to \{0,1\}^{2n}$ be a PRG.
|
||||
|
||||
$$
|
||||
g(\overline{x})=[g_0(\overline{x})] [g_1(\overline{x})]
|
||||
$$
|
||||
|
||||
Then we choose a random $s\in \{0,1\}^n$ (initial seed) and define $\overline{x}\gets \{0,1\}^n$, $\overline{x}=x_1\cdots x_n$.
|
||||
|
||||
$$
|
||||
f_s(\overline{x})=f_s(x_1\cdots x_n)=g_{x_n}(\dots (g_{x_2}(g_{x_1}(s))))
|
||||
$$
|
||||
|
||||
```python
|
||||
s=random.randbits(n)
|
||||
|
||||
#????
|
||||
|
||||
def g(x):
|
||||
if x[0]==0:
|
||||
return g(f_s(x[1:]))
|
||||
else:
|
||||
return g(f_s(x[1:]))
|
||||
|
||||
def f_s(x):
|
||||
return g(x)
|
||||
|
||||
```
|
||||
|
||||
Suppose $g:\{0,1\}^3\to \{0,1\}^6$ is a PRG.
|
||||
|
||||
| $x$ | $f_s(x)$ |
|
||||
| --- | -------- |
|
||||
| 000 | 110011 |
|
||||
| 001 | 010010 |
|
||||
| 010 | 001001 |
|
||||
| 011 | 000110 |
|
||||
| 100 | 100000 |
|
||||
| 101 | 110110 |
|
||||
| 110 | 000111 |
|
||||
| 111 | 001110 |
|
||||
|
||||
Suppose the initial seed is $011$, then the constructed function tree goes as follows:
|
||||
|
||||
Example:
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
f_s(110)&=g_0(g_1(g_1(s)))\\
|
||||
&=g_0(g_1(110))\\
|
||||
&=g_0(111)\\
|
||||
&=001
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
f_s(010)&=g_0(g_1(g_0(s)))\\
|
||||
&=g_0(g_1(000))\\
|
||||
&=g_0(001)\\
|
||||
&=010
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Assume that $D$ distinguishes $f_s$ and $F\gets RF_n$ with non-negligible probability.
|
||||
|
||||
By hybrid argument, there exists a hybrid $H_i$ such that $D$ distinguishes $H_i$ and $H_{i+1}$ with non-negligible probability.
|
||||
|
||||
For $H_0$,
|
||||
|
||||
QED
|
||||
134
content/CSE442T/CSE442T_L16.md
Normal file
134
content/CSE442T/CSE442T_L16.md
Normal file
@@ -0,0 +1,134 @@
|
||||
# Lecture 16
|
||||
|
||||
## Chapter 3: Indistinguishability and Pseudorandomness
|
||||
|
||||
PRG exists $\implies$ Pseudorandom function family exists.
|
||||
|
||||
### Multi-message secure encryption
|
||||
|
||||
$Gen(1^n):$ Output $f_i:\{0,1\}^n\to \{0,1\}^n$ from PRF family
|
||||
|
||||
$Enc_i(m):$ Random $r\gets \{0,1\}^n$
|
||||
Ouput $(r,m\oplus f_i(r))$
|
||||
|
||||
$Dec_i(r,c):$ Output $c\oplus f_i(r)$
|
||||
|
||||
Proof of security:
|
||||
|
||||
Suppose $D$ distinguishes, for infinitly many $n$.
|
||||
|
||||
The encryption of $a$ pair of lists
|
||||
|
||||
(1) $\{i\gets Gen(1^n):(r_1,m_1\oplus f_i(r_1)),(r_2,m_2\oplus f_i(r_2)),(r_3,m_3\oplus f_i(r_3)),\ldots,(r_q,m_q\oplus f_i(r_q)), \}$
|
||||
|
||||
(2) $\{F\gets RF_n: (r_1,m_1\oplus F(r_1))\ldots\}$
|
||||
|
||||
(3) One-time pad $\{(r_1,m_1\oplus s_1)\}$
|
||||
|
||||
(4) One-time pad $\{(r_1,m_1'\oplus s_1)\}$
|
||||
|
||||
If (1) (2) distinguished,
|
||||
|
||||
$(r_1,f_i(r_1)),\ldots,(r_q,f_i(r_q))$ is distinguished from
|
||||
|
||||
$(r_1,F(r_1)),\ldots, (r_q,F(r_q))$
|
||||
|
||||
So $D$ distinguishing output of $r_1,\ldots, r_q$ of PRF from the RF, this contradicts with definition of PRF.
|
||||
|
||||
QED
|
||||
|
||||
Noe we have
|
||||
|
||||
(RSA assumption and Discrete log assumption for one-way function exists.)
|
||||
|
||||
One-way function exists $\implies$
|
||||
|
||||
Pseudo random generator exists $\implies$
|
||||
|
||||
Pseudo random function familiy exists $\implies$
|
||||
|
||||
Mult-message secure encryption exists.
|
||||
|
||||
### Public key cryptography
|
||||
|
||||
1970s.
|
||||
|
||||
The goal was to agree/share a key without meeting in advance
|
||||
|
||||
#### Diffie-Helmann Key exchange
|
||||
|
||||
A and B create a secret key together without meeting.
|
||||
|
||||
Rely on discrete log assumption.
|
||||
|
||||
They pulicly agree on modulus $p$ and generator $g$.
|
||||
|
||||
Alice picks random exponent $a$ and computes $g^a\mod p$
|
||||
|
||||
Bob picks random exponent $b$ and computes $g^b\mod p$
|
||||
|
||||
and they send result to each other.
|
||||
|
||||
And Alice do $(g^b)^a$ where Bob do $(g^a)^b$.
|
||||
|
||||
#### Diffie-Helmann assumption
|
||||
|
||||
With $g^a,g^b$ no one can compute $g^{ab}$.
|
||||
|
||||
#### Public key encryption scheme
|
||||
|
||||
Ideas: The recipient Bob distributes opened Bob-locks
|
||||
|
||||
- Once closed, only Bob can open it.
|
||||
|
||||
Public-key encryption scheme:
|
||||
|
||||
1. $Gen(1^n):$ Outputs $(pk,sk)$
|
||||
2. $Enc_{pk}(m):$ Efficient for all $m,pk$
|
||||
3. $Dec_{sk}(c):$ Efficient for all $c,sk$
|
||||
4. $P[(pk,sk)\gets Gen(1^n):Dec_{sk}(Enc_{pk}(m))=m]=1$
|
||||
|
||||
Let $A, E$ knows $pk$ not $sk$ and $B$ knows $pk,sk$.
|
||||
|
||||
Adversary can now encrypt any message $m$ with the public key.
|
||||
|
||||
- Perfect secrecy impossible
|
||||
- Randomness necessary
|
||||
|
||||
#### Security of public key
|
||||
|
||||
$\forall n.u.p.p.t D,\exists \epsilon(n)$ such that $\forall n,m_0,m_1\in \{0,1\}^n$
|
||||
|
||||
$$
|
||||
\{(pk,sk)\gets Gen(1^n):(pk,Enc_{pk}(m_0))\} \{(pk,sk)\gets Gen(1^n):(pk,Enc_{pk}(m_1))\}
|
||||
$$
|
||||
|
||||
are distinguished by at most $\epsilon (n)$
|
||||
|
||||
This "single" message security implies multi-message security!
|
||||
|
||||
_Left as exercise_
|
||||
|
||||
We will achieve security in sending a single bit $0,1$
|
||||
|
||||
Time for trapdoor permutation. (EX. RSA)
|
||||
|
||||
#### Encryption Scheme via Trapdoor Permutation
|
||||
|
||||
Given family of trapdoor permutation $\{f_i\}$ with hardcore bit $h(i)$
|
||||
|
||||
$Gen(1^n):(f_i,f_i^{-1})$, where $f_i^{-1}$ uses trapdoor permutation of $t$
|
||||
|
||||
$Output ((f_i,h_i),f_i^{-1})$
|
||||
|
||||
$m=0$ or $1$.
|
||||
|
||||
$Enc_{pk}(m):r\gets\{0,1\}^n$
|
||||
|
||||
$Output (f_i(r),h_i(r)+m)$
|
||||
|
||||
$Dec_{sk}(c_1,c_2)$
|
||||
|
||||
$r=f_i^{-1}(c_1)$
|
||||
|
||||
$m=c_2+h_1(r)$
|
||||
159
content/CSE442T/CSE442T_L17.md
Normal file
159
content/CSE442T/CSE442T_L17.md
Normal file
@@ -0,0 +1,159 @@
|
||||
# Lecture 17
|
||||
|
||||
## Chapter 3: Indistinguishability and Pseudorandomness
|
||||
|
||||
### Public key encryption scheme (1-bit)
|
||||
|
||||
$Gen(1^n):(f_i, f_i^{-1})$
|
||||
|
||||
$f_i$ is the trapdoor permutation. (eg. RSA)
|
||||
|
||||
$Output((f_i, h_i), f_i^{-1})$, where $(f_i, h_i)$ is the public key and $f_i^{-1}$ is the secret key.
|
||||
|
||||
$Enc_{pk}(m):r\gets \{0, 1\}^n$
|
||||
|
||||
$Output(f_i(r), h_i(r)\oplus m)$
|
||||
|
||||
where $f_i(r)$ is denoted as $c_1$ and $h_i(r)\oplus m$ is the tag $c_2$.
|
||||
|
||||
The decryption function is:
|
||||
|
||||
$Dec_{sk}(c_1, c_2)$:
|
||||
|
||||
$r=f_i^{-1}(c_1)$
|
||||
|
||||
$m=c_2\oplus h_i(r)$
|
||||
|
||||
#### Validity of the decryption
|
||||
|
||||
Proof of the validity of the decryption: Exercise.
|
||||
|
||||
#### Security of the encryption scheme
|
||||
|
||||
The encryption scheme is secure under this construction (Trapdoor permutation (TDP), Hardcore bit (HCB)).
|
||||
|
||||
Proof:
|
||||
|
||||
We proceed by contradiction. (Constructing contradiction with definition of hardcore bit.)
|
||||
|
||||
Assume that there exists a distinguisher $\mathcal{D}$ that can distinguish the encryption of $0$ and $1$ with non-negligible probability $\mu(n)$.
|
||||
|
||||
$$
|
||||
\{(pk,sk)\gets Gen(1^n):(pk,Enc_{pk}(0))\} v.s.\{(pk,sk)\gets Gen(1^n):(pk,Enc_{pk}(1))\} \geq \mu(n)
|
||||
$$
|
||||
|
||||
By prediction lemma (the distinguisher can be used to create and adversary that can break the security of the encryption scheme with non-negligible probability $\mu(n)$).
|
||||
|
||||
$$
|
||||
P[m\gets \{0,1\}; (pk,sk)\gets Gen(1^n):\mathcal{A}(pk,Enc_{pk}(m))=m]\geq \frac{1}{2}+\mu(n)
|
||||
$$
|
||||
|
||||
We will use this to construct an agent $B$ which can determine the hardcore bit $h_i(r)$ of the trapdoor permutation $f_i(r)$ with non-negligible probability.
|
||||
|
||||
$f_i,h_i$ are determined.
|
||||
|
||||
$B$ is given $f_i(r)$ and $h_i(r)$ and outputs $b\in \{0,1\}$.
|
||||
|
||||
- $r\gets \{0,1\}^n$ is chosen uniformly at random.
|
||||
- $y=f_i(r)$ is given to $B$.
|
||||
- $b=h_i(r)$ is given to $B$.
|
||||
- Choose $c_2\gets \{0,1\}= h_i(r)\oplus m$ uniformly at random.
|
||||
- Then use $\mathcal{A}$ with $pk=(f_i, h_i),Enc_{pk}(m)=(f_i(r), h_i(r)\oplus m)$ to determine whether $r$ is $0$ or $1$.
|
||||
- Let $m'\gets \mathcal{A}(pk,(y,c_2))$.
|
||||
- Since $c_2=h_i(r)\oplus m$, we have $m=b\oplus c_2$, $b=m'\oplus c_2$.
|
||||
- Output $b=m'\oplus c_2$.
|
||||
|
||||
The probability that $B$ correctly guesses $b$ given $f_i,h_i$ is:
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
&~~~~~P[r\gets \{0,1\}^n: y=f_i(r), b=h_i(r): B(f_i,h_i,y)=b]\\
|
||||
&=P[r\gets \{0,1\}^n,c_2\gets \{0,1\}: y=f_i(r), b=h_i(r):\mathcal{A}((f_i,h_i),(y,c_2))=(c_2+b)]\\
|
||||
&=P[r\gets \{0,1\}^n,m\gets \{0,1\}: y=f_i(r), b=h_i(r):\mathcal{A}((f_i,h_i),(y,b\oplus m))=m]\\
|
||||
&>\frac{1}{2}+\mu(n)
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
This contradicts the definition of hardcore bit.
|
||||
|
||||
QED
|
||||
|
||||
### Public key encryption scheme (multi-bit)
|
||||
|
||||
Let $m\in \{0,1\}^k$.
|
||||
|
||||
We can choose random $r_i\in \{0,1\}^n$, $y_i=f_i(r_i)$, $b_i=h_i(r_i),c_i=m_i\oplus b_i$.
|
||||
|
||||
$Enc_{pk}(m)=((y_1,c_1),\cdots,(y_k,c_k)),c\in \{0,1\}^k$
|
||||
|
||||
$Dec_{sk}:r_k=f_i^{-1}(y_k),h_i(r_k)\oplus c_k=m_k$
|
||||
|
||||
### Special public key cryptosystem: El-Gamal (based on Diffie-Hellman Assumption)
|
||||
|
||||
#### Definition 105.1 Decisional Diffie-Hellman Assumption (DDH)
|
||||
|
||||
> Define the group of squares mod $p$ as follows:
|
||||
>
|
||||
> $p=2q+1$, $q\in \Pi_{n-1}$, $g\gets \mathbb{Z}_p^*/\{1\}$, $y=g^2$
|
||||
>
|
||||
> $G=\{y,y^2,\cdots,y^q=1\}\mod p$
|
||||
|
||||
These two listed below are indistinguishable.
|
||||
|
||||
$\{p\gets \tilde{\Pi_n};y\gets Gen_q;a,b\gets \mathbb{Z}_q:(p,y,y^a,y^b,y^{ab})\}_n$
|
||||
|
||||
$\{p\gets \tilde{\Pi_n};y\gets Gen_q;a,b,\bold{z}\gets \mathbb{Z}_q:(p,y,y^a,y^b,y^\bold{z})\}_n$
|
||||
|
||||
> (Computational) Diffie-Hellman Assumption:
|
||||
>
|
||||
> Hard to compute $y^{ab}$ given $p,y,y^a,y^b$.
|
||||
|
||||
So DDH assumption implies discrete logarithm assumption.
|
||||
|
||||
Ideas:
|
||||
|
||||
If one can find $a,b$ from $y^a,y^b$, then one can find $ab$ from $y^{ab}$ and compare to $\bold{z}$ to check whether $y^\bold{z}$ is a valid DDH tuple.
|
||||
|
||||
#### El-Gamal encryption scheme (public key cryptosystem)
|
||||
|
||||
$Gen(1^n)$:
|
||||
|
||||
$p\gets \tilde{\Pi_n},g\gets \mathbb{Z}_p^*/\{1\},y\gets Gen_q,a\gets \mathbb{Z}_q$
|
||||
|
||||
Output:
|
||||
|
||||
$pk=(p,y,y^a\mod p)$ (public key)
|
||||
|
||||
$sk=(p,y,a)$ (secret key)
|
||||
|
||||
**Message space:** $G_q=\{y,y^2,\cdots,y^q=1\}$
|
||||
|
||||
$Enc_{pk}(m)$:
|
||||
|
||||
$b\gets \mathbb{Z}_q$
|
||||
|
||||
$c_1=y^b\mod p,c_2=(y^{ab}\cdot m)\mod p$
|
||||
|
||||
Output: $(c_1,c_2)$
|
||||
|
||||
$Dec_{sk}(c_1,c_2)$:
|
||||
|
||||
Since $c_2=(y^{ab}\cdot m)\mod p$, we have $m=\frac{c_2}{c_1^a}\mod p$
|
||||
|
||||
Output: $m$
|
||||
|
||||
#### Security of El-Gamal encryption scheme
|
||||
|
||||
Proof:
|
||||
|
||||
If not secure, then there exists a distinguisher $\mathcal{D}$ that can distinguish the encryption of $m_1,m_2\in G_q$ with non-negligible probability $\mu(n)$.
|
||||
|
||||
$$
|
||||
\{(pk,sk)\gets Gen(1^n):D(pk,Enc_{pk}(m_1))\}\text{ vs. }\\
|
||||
\{(pk,sk)\gets Gen(1^n):D(pk,Enc_{pk}(m_2))\}\geq \mu(n)
|
||||
$$
|
||||
|
||||
And proceed by contradiction. This contradicts the DDH assumption.
|
||||
|
||||
QED
|
||||
|
||||
148
content/CSE442T/CSE442T_L18.md
Normal file
148
content/CSE442T/CSE442T_L18.md
Normal file
@@ -0,0 +1,148 @@
|
||||
# Lecture 18
|
||||
|
||||
## Chapter 5: Authentication
|
||||
|
||||
### 5.1 Introduction
|
||||
|
||||
Signatures
|
||||
|
||||
**private key**
|
||||
|
||||
Alice and Bob share a secret key $k$.
|
||||
|
||||
Message Authentication Codes (MACs)
|
||||
|
||||
**public key**
|
||||
|
||||
Any one can verify the signature.
|
||||
|
||||
Digital Signatures
|
||||
|
||||
#### Definitions 134.1
|
||||
|
||||
A message authentication codes (MACs) is a triple $(Gen, Tag, Ver)$ where
|
||||
|
||||
- $k\gets Gen(1^k)$ is a p.p.t. algorithm that takes as input a security parameter $k$ and outputs a key $k$.
|
||||
- $\sigma\gets Tag_k(m)$ is a p.p.t. algorithm that takes as input a key $k$ and a message $m$ and outputs a tag $\sigma$.
|
||||
- $Ver_k(m, \sigma)$ is a deterministic algorithm that takes as input a key $k$, a message $m$, and a tag $\sigma$ and outputs "Accept" if $\sigma$ is a valid tag for $m$ under $k$ and "Reject" otherwise.
|
||||
|
||||
For all $n\in\mathbb{N}$, all $m\in\mathcal{M}_n$.
|
||||
|
||||
$$
|
||||
P[k\gets Gen(1^k):Ver_k(m, Tag_k(m))=\textup {``Accept''}]=1
|
||||
$$
|
||||
|
||||
#### Definition 134.2 (Security of MACs)
|
||||
|
||||
Security: Prevent an adversary from producing any accepted $(m, \sigma)$ pair that they haven't seen before.
|
||||
|
||||
- Assume they have seen some history of signed messages. $(m_1, \sigma_1), (m_2, \sigma_2), \ldots, (m_q, \sigma_q)$.
|
||||
- Adversary $\mathcal{A}$ has oracle access to $Tag_k$. Goal is to produce a new $(m, \sigma)$ pair that is accepted but none of $(m_1, \sigma_1), (m_2, \sigma_2), \ldots, (m_q, \sigma_q)$.
|
||||
|
||||
$\forall$ n.u.p.p.t. adversary $\mathcal{A}$ with oracle access to $Tag_k(\cdot)$,
|
||||
|
||||
$$
|
||||
\Pr[k\gets Gen(1^k);(m, \sigma)\gets\mathcal{A}^{Tag_k(\cdot)}(1^k);\mathcal{A}\textup{ did not query }m \textup{ and } Ver_k(m, \sigma)=\textup{``Accept''}]<\epsilon(n)
|
||||
$$
|
||||
|
||||
#### MACs scheme
|
||||
|
||||
$F=\{f_s\}$ is a PRF family.
|
||||
|
||||
$f_s:\{0,1\}^{|S|}\to\{0,1\}^{|S|}$
|
||||
|
||||
$Gen(1^k): s\gets \{0,1\}^n$
|
||||
|
||||
$Tag_k(m)$ outputs $f_s(m)$.
|
||||
|
||||
$Ver_s(m, \sigma)$ outputs "Accept" if $f_s(m)=\sigma$ and "Reject" otherwise.
|
||||
|
||||
Proof of security (Outline):
|
||||
|
||||
Suppose we used $F\gets RF_n$ (true random function).
|
||||
|
||||
If $\mathcal{A}$ wants $F(m)$ for $m\in \{m_1, \ldots, m_q\}$. $F(m)\gets U_n$.
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
&P[F\gets RF_n; (m, \sigma)\gets\mathcal{A}^{F(\cdot)}(1^k);\mathcal{A}\textup{ did not query }m \textup{ and } Ver_k(m, \sigma)=\textup{``Accept''}]\\
|
||||
&=P[F\gets RF_n; (m, \sigma)\gets F(m)]\\
|
||||
&=\frac{1}{2^n}<\epsilon(n)
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Suppose an adversary $\mathcal{A}$ has $\frac{1}{p(n)}$ chance of success with our PRF-based scheme...
|
||||
|
||||
This could be used to distinguish PRF $f_s$ from a random function.
|
||||
|
||||
The distinguisher runs as follows:
|
||||
|
||||
- Runs $\mathcal{A}(1^n)$
|
||||
- Whenever $\mathcal{A}$ asks for $Tag_k(m)$, we ask our oracle for $f(m)$
|
||||
- $(m, \sigma)\gets\mathcal{A}^{F(\cdot)}(1^n)$
|
||||
- Query oracle for $f(m)$
|
||||
- If $\sigma=f(m)$, output 1
|
||||
- Otherwise, output 0
|
||||
|
||||
$D$ will output 1 for PRF with probability $\frac{1}{p(n)}$ and for RF with probability $\frac{1}{2^n}$.
|
||||
|
||||
#### Definition 135.1(Digital Signature D.S. over $\{M_n\}_n$)
|
||||
|
||||
A digital signature scheme is a triple $(Gen, Sign, Ver)$ where
|
||||
|
||||
- $(pk,sk)\gets Gen(1^k)$ is a p.p.t. algorithm that takes as input a security parameter $k$ and outputs a public key $pk$ and a secret key $sk$.
|
||||
- $\sigma\gets Sign_{sk}(m)$ is a p.p.t. algorithm that takes as input a secret key $sk$ and a message $m$ and outputs a signature $\sigma$.
|
||||
- $Ver_{pk}(m, \sigma)$ is a deterministic algorithm that takes as input a public key $pk$, a message $m$, and a signature $\sigma$ and outputs "Accept" if $\sigma$ is a valid signature for $m$ under $pk$ and "Reject" otherwise.
|
||||
|
||||
For all $n\in\mathbb{N}$, all $m\in\mathcal{M}_n$.
|
||||
|
||||
$$
|
||||
P[(pk,sk)\gets Gen(1^k); \sigma\gets Sign_{sk}(m); Ver_{pk}(m, \sigma)=\textup{``Accept''}]=1
|
||||
$$
|
||||
|
||||
#### Security of Digital Signature
|
||||
|
||||
$$
|
||||
P[(pk,sk)\gets Gen(1^k); (m, \sigma)\gets\mathcal{A}^{Sign_{sk}(\cdot)}(1^k);\mathcal{A}\textup{ did not query }m \textup{ and } Ver_{pk}(m, \sigma)=\textup{``Accept''}]<\epsilon(n)
|
||||
$$
|
||||
|
||||
For all n.u.p.p.t. adversary $\mathcal{A}$ with oracle access to $Sign_{sk}(\cdot)$.
|
||||
|
||||
### 5.4 One time security: $\mathcal{A}$ can only use oracle once.
|
||||
|
||||
Output $(m, \sigma)$ if $m\neq m$
|
||||
|
||||
Security parameter $n$
|
||||
|
||||
One time security on $\{0,1\}^n$
|
||||
|
||||
One time security on $\{0,1\}^*$
|
||||
|
||||
Regular security on $\{0,1\}^*$
|
||||
|
||||
Note: the adversary automatically has access to $Ver_{pk}(\cdot)$
|
||||
|
||||
#### One time security scheme (Lamport Scheme on $\{0,1\}^n$)
|
||||
|
||||
$Gen(1^k)$: $\mathbb{Z}_n$ random n-bit string
|
||||
|
||||
$sk$: List 0: $\bar{x_1}^0, \bar{x_2}^0, \ldots, \bar{x_n}^0$
|
||||
|
||||
List 1: $\bar{x_1}^1, \bar{x_2}^1, \ldots, \bar{x_n}^1$
|
||||
|
||||
All $\bar{x_i}^j\in\{0,1\}^n$
|
||||
|
||||
$pk$: For a strong one-way function $f$
|
||||
|
||||
List 0: $f(\bar{x_1}^0), f(\bar{x_2}^0), \ldots, f(\bar{x_n}^0)$
|
||||
|
||||
List 1: $f(\bar{x_1}^1), f(\bar{x_2}^1), \ldots, f(\bar{x_n}^1)$
|
||||
|
||||
$Sign_{sk}(m):(m_1, m_2, \ldots, m_n)\mapsto(\bar{x_1}^{m_1}, \bar{x_2}^{m_2}, \ldots, \bar{x_n}^{m_n})$
|
||||
|
||||
$Ver_{pk}(m, \sigma)$: output "Accept" if $\sigma$ is a prefix of $f(m)$ and "Reject" otherwise.
|
||||
|
||||
> Example: When we sign a message $01100$, $$Sign_{sk}(01100)=(\bar{x_1}^0, \bar{x_2}^1, \bar{x_3}^1, \bar{x_4}^0, \bar{x_5}^0)$$
|
||||
> We only reveal the $x_1^0, x_2^1, x_3^1, x_4^0, x_5^0$
|
||||
> For the second signature, we need to reveal exactly different bits.
|
||||
> The adversary can query the oracle for $f(0^n)$ (reveals list0) and $f(1^n)$ (reveals list1) to produce any valid signature they want.
|
||||
124
content/CSE442T/CSE442T_L19.md
Normal file
124
content/CSE442T/CSE442T_L19.md
Normal file
@@ -0,0 +1,124 @@
|
||||
# Lecture 19
|
||||
|
||||
## Chapter 5: Authentication
|
||||
|
||||
### One-Time Secure Digital Signature
|
||||
|
||||
#### Definition 136.2 (Security of Digital Signature)
|
||||
|
||||
A digital signature scheme is $(Gen, Sign, Ver)$ is secure if for all n.u.p.p.t. $\mathcal{A}$, there exists a negligible function $\epsilon(n)$ such that $\forall n\in\mathbb{N}$,
|
||||
|
||||
$$
|
||||
P[(pk,sk)\gets Gen(1^n); (m,\sigma)\gets\mathcal{A}^{Sign_{sk}(\cdot)}(1^n); \mathcal{A}\textup{ did not query }m\textup{ and } Ver_{pk}(m,\sigma)=\textup{``Accept''}]\leq \frac{1}{p(n)}+\epsilon(n)
|
||||
$$
|
||||
|
||||
A digital signature scheme is one-time secure if it is secure and the adversary makes only one query to the signing oracle.
|
||||
|
||||
### Lamport's One-Time Signature
|
||||
|
||||
Given a one-way function $f$, we can create a signature scheme as follows:
|
||||
|
||||
We construct a key pair $(sk, pk)$ as follows:
|
||||
|
||||
$sk$ is two list of random bits,
|
||||
|
||||
where $sk_0=\{\bar{x_1}^0, \bar{x_2}^0, \ldots, \bar{x_n}^0\}$
|
||||
|
||||
and $sk_1=\{\bar{x_1}^1, \bar{x_2}^1, \ldots, \bar{x_n}^1\}$.
|
||||
|
||||
$pk$ is the image of $sk$ under $f$, i.e. $pk = f(sk)$.
|
||||
|
||||
where $pk_0 = \{f(\bar{x_1}^0), f(\bar{x_2}^0), \ldots, f(\bar{x_n}^0)\}$
|
||||
|
||||
and $pk_1 = \{f(\bar{x_1}^1), f(\bar{x_2}^1), \ldots, f(\bar{x_n}^1)\}$.
|
||||
|
||||
To sign a message $m\in\{0,1\}^n$, we output the signature $Sign_{sk}(m=m_1m_2\ldots m_n) = \{\bar{x_1}^{m_1}, \bar{x_2}^{m_2}, \ldots, \bar{x_n}^{m_n}\}$.
|
||||
|
||||
To verify a signature $\sigma$ on $m$, we check if $f(\sigma) = pk_m$.
|
||||
|
||||
This is not more than one-time secure since the adversary can ask oracle for $Sign_{sk}(0^n)$ and $Sign_{sk}(1^n)$ to reveal list $pk_0$ and $pk_1$ to sign any message.
|
||||
|
||||
We will show it is one-time secure
|
||||
|
||||
Ideas of proof:
|
||||
|
||||
Say their query is $Sign_{sk}(0^n)$ and reveals $pk_0$.
|
||||
|
||||
Now must sign $m\neq 0^n$. There must be a 1, somewhere in the message. Say the $i$th bit is the first 1. then they need to produce $x'$ such that $f(x_i)=f(x_i')$, which inverts the one-way function.
|
||||
|
||||
Proof of one-time security:
|
||||
|
||||
Suppose there exists an adversary $\mathcal{A}$ that can produce a valid signature on a different message after one query to oracle with non-negligible probability $\mu>\frac{1}{p(n)}$.
|
||||
|
||||
We will design a function $B$ which use $\mathcal{A}$ to invert the one-way function with non-negligible probability.
|
||||
|
||||
Let $x\gets \{0,1\}^n$ be a random variable, $y=f(x)$.
|
||||
|
||||
B: input is $y$ and $1^n$. Our goal is to find $x'$ such that $f(x')=y$.
|
||||
|
||||
Create 2 lists:
|
||||
|
||||
$sk_0=\{x_0^0, x_1^0, \ldots, x_{n-1}^0\}$
|
||||
|
||||
$sk_1=\{x_0^1, x_1^1, \ldots, x_{n-1}^1\}$
|
||||
|
||||
Then we pick a random $(c,i)\gets \{0,1\}^n\times [n]$. ($2n$ possibilities)
|
||||
|
||||
Replace $f(x_i^c)$ with $y$.
|
||||
|
||||
Return $sk_c$ with None.
|
||||
|
||||
Run $\mathcal{A}$ on input $y$ and $1^n$. It will query $Sign_{sk}$ on some message $m$.
|
||||
|
||||
Case 1: $m_i=1-c$
|
||||
|
||||
We can answer with all of $x_1^{m_1}, x_2^{m_2}, \ldots, x_{1-c}^{m_{1-c}}, \ldots, x_n^{m_n}$
|
||||
|
||||
Case 2: $m_i=c$
|
||||
|
||||
We must abort we don't know what to do.
|
||||
|
||||
Since $\mathcal{A}$ outputs $(m',\sigma)$ with non-negligible probability, we are hoping that $m_i'=c$. Then it's attempting to provide $x\to y$
|
||||
|
||||
Since $m'$ differs at most 1 bit from $m$, we have $x\to y$ with probability $P[m_i'=c]\geq \frac{1}{n}$.
|
||||
|
||||
$\sigma=(x_1^1,x_2^1,\ldots,x_n^1)$
|
||||
|
||||
Check if $f(\sigma)=y$. If so, output $x'$. (all correct with prob $\geq \frac{1}{p(n)}$)
|
||||
|
||||
If not, try again.
|
||||
|
||||
$B$ inverts $f$ with prob $\geq \frac{1}{p(n)}$
|
||||
|
||||
### Collision Resistant Hash Functions (CRHF)
|
||||
|
||||
We now have one-time secure signature scheme.
|
||||
|
||||
We want one-time secure signature scheme that increase the size of messages relative to the keys.
|
||||
|
||||
Let $H:\{h_i:D_i\to R_i\}_{i\in I}$ be a family of CRHF if
|
||||
|
||||
Easy to pick:
|
||||
|
||||
$Gen(1^n)$: outputs $i\in I$ (p,p,t)
|
||||
|
||||
Compression
|
||||
|
||||
$|R_i|<|D_i|$ for each $i\in I$
|
||||
|
||||
Easy to compute:
|
||||
|
||||
Can computer $h_i(x),\forall i,x\in D_i$ with a p.p.t
|
||||
|
||||
Collision resistant:
|
||||
|
||||
$\forall n.u.p.p.t \mathcal{A}$, $\forall n$,
|
||||
|
||||
$$
|
||||
P[i\gets Gen(1^n); (x_1,x_2)\gets \mathcal{A}(1^n,i): h_i(x_1)=h_i(x_2)\land x_1\neq x_2]\leq \epsilon(n)
|
||||
$$
|
||||
|
||||
CRHF implies one-way function.
|
||||
|
||||
But not the other way around. (CRHF is a stronger notion than one-way function.)
|
||||
|
||||
97
content/CSE442T/CSE442T_L2.md
Normal file
97
content/CSE442T/CSE442T_L2.md
Normal file
@@ -0,0 +1,97 @@
|
||||
# Lecture 2
|
||||
|
||||
## Probability review
|
||||
|
||||
Sample space $S=\text{set of outcomes (possible results of experiments)}$
|
||||
|
||||
Event $A\subseteq S$
|
||||
|
||||
$P[A]=P[$ outcome $x\in A]$
|
||||
|
||||
$P[\{x\}]=P[x]$
|
||||
|
||||
Conditional probability:
|
||||
|
||||
$P[A|B]={P[A\cap B]\over P[B]}$
|
||||
|
||||
Assuming $B$ is the known information. Moreover, $P[B]>0$
|
||||
|
||||
Probability that $A$ and $B$ occurring: $P[A\cap B]=P[A|B]\cdot P[B]$
|
||||
|
||||
$P[B\cap A]=P[B|A]\cdot P[A]$
|
||||
|
||||
So $P[A|B]={P[B|A]\cdot P[A]\over P[B]}$ (Bayes Theorem)
|
||||
|
||||
**There is always a chance that random guess would be the password... Although really, really, low...**
|
||||
|
||||
### Law of total probability
|
||||
|
||||
Let $S=\bigcup_{i=1}^n B_i$. and $B_i$ are disjoint events.
|
||||
|
||||
$A=\bigcup_{i=1}^n A\cap B_i$ ($A\cap B_i$ are all disjoint)
|
||||
|
||||
$P[A]=\sum^n_{i=1} P[A|B_i]\cdot P[B_i]$
|
||||
|
||||
## Chapter 1: Introduction
|
||||
|
||||
### Defining security
|
||||
|
||||
#### Perfect Secrecy (Shannon Secrecy)
|
||||
|
||||
$k\gets Gen()$ $k\in K$
|
||||
|
||||
$c\gets Enc_k(m)$ or we can also write as $c\gets Enc(k,m)$ for $m\in M$
|
||||
|
||||
And the decryption procedure:
|
||||
|
||||
$m'\gets Dec_k(c')$, $m'$ might be null.
|
||||
|
||||
$P[k\gets Gen(): Dec_k(Enc_k(m))=m]=1$
|
||||
|
||||
#### Definition 11.1 (Shannon Secrecy)
|
||||
|
||||
Distribution $D$ over the message space $M$
|
||||
|
||||
$P[k\gets Gen;m\gets D: m=m'|c\gets Enc_k(m)]=P[m\gets D: m=m']$
|
||||
|
||||
Basically, we cannot gain any information from the encoded message.
|
||||
|
||||
Code shall not contain any information changing the distribution of expectation of message after viewing the code.
|
||||
|
||||
**NO INFO GAINED**
|
||||
|
||||
#### Definition 11.2 (Perfect Secrecy)
|
||||
|
||||
For any 2 messages, say $m_1,m_2\in M$ and for any possible cipher $c$,
|
||||
|
||||
$P[k\gets Gen:c\gets Enc_k(m_1)]=P[k\gets Gen():c\gets Enc_k(m_2)]$
|
||||
|
||||
For a fixed $c$, any message (have a equal probability) could be encrypted to that...
|
||||
|
||||
#### Theorem 12.3
|
||||
|
||||
Shannon secrecy is equivalent to perfect secrecy.
|
||||
|
||||
Proof:
|
||||
|
||||
If a crypto-system satisfy perfect secrecy, then it also satisfy Shannon secrecy.
|
||||
|
||||
Let $(Gen,Enc,Dec)$ be a perfectly secret crypto-system with $K$ and $M$.
|
||||
|
||||
Let $D$ be any distribution over messages.
|
||||
|
||||
Let $m'\in M$.
|
||||
|
||||
$$
|
||||
={P_k[c\gets Enc_k(m')]\cdot P[m=m']\over P_{k,m}[c\gets Enc_k(m)]}\\
|
||||
$$
|
||||
|
||||
$$
|
||||
P[k\gets Gen();m\gets D:m=m'|c\gets Enc_k(m)]={P_{k,m}[c\gets Enc_k(m)\vert m=m']\cdot P[m=m']\over P_{k,m}[c\gets Enc_k(m)]}\\
|
||||
P_{k,m}[c\gets Enc_k(m)]=\sum^n_{i=1}P_{k,m}[c\gets Enc_k(m)|m=m_i]\cdot P[m=m_i]\\
|
||||
=\sum^n_{i=1}P_{K,m_i}[c\gets Enc_k(m_i)]\cdot P[m=m_i]
|
||||
$$
|
||||
|
||||
and $P_{k,m_i}[c\gets Enc_k(m_i)]$ is constant due to perfect secrecy
|
||||
|
||||
$\sum^n_{i=1}P_{k,m_i}[c\gets Enc_k(m_i)]\cdot P[m=m_i]=\sum^n_{i=1} P[m=m_i]=1$
|
||||
176
content/CSE442T/CSE442T_L20.md
Normal file
176
content/CSE442T/CSE442T_L20.md
Normal file
@@ -0,0 +1,176 @@
|
||||
# Lecture 20
|
||||
|
||||
## Chapter 5: Authentication
|
||||
|
||||
### Construction of CRHF (Collision Resistant Hash Function)
|
||||
|
||||
Let $h: \{0, 1\}^{n+1} \to \{0, 1\}^n$ be a CRHF.
|
||||
|
||||
Base on the discrete log assumption, we can construct a CRHF $H: \{0, 1\}^{n+1} \to \{0, 1\}^n$ as follows:
|
||||
|
||||
$Gen(1^n):(g,p,y)$
|
||||
|
||||
$p\in \tilde{\Pi}_n(p=2q+1)$
|
||||
|
||||
$g$ generator for group of sequence $\mod p$ (G_q)
|
||||
|
||||
$y$ is a random element in $G_q$
|
||||
|
||||
$h_{g,p,y}(x,b)=y^bg^x\mod p$, $y^bg^x\mod p \in \{0,1\}^n$
|
||||
|
||||
$g^x\mod p$ if $b=0$, $y\cdot g^x\mod p$ if $b=1$.
|
||||
|
||||
Under the discrete log assumption, $H$ is a CRHF.
|
||||
|
||||
- It is easy to sample $(g,p,y)$
|
||||
- It is easy to compute
|
||||
- Compressing by 1 bit
|
||||
|
||||
Proof:
|
||||
|
||||
The hash function $h$ is a CRHF
|
||||
|
||||
Suppose there exists an adversary $\mathcal{A}$ that can break $h$ with non-negligible probability $\mu$.
|
||||
|
||||
$$
|
||||
P[(p,g,y)\gets Gen(1^n);(x_1,b_1),(x_2,b_2)\gets \mathcal{A}(p,g,y):y^{b_1}g^{x_1}\equiv y^{b_2}g^{x_2}\mod p\land (x_1,b_1)\neq (x_2,b_2)]=\mu(n)>\frac{1}{p(n)}
|
||||
$$
|
||||
|
||||
Where $y^{b_1}g^{x_1}=y^{b_2}g^{x_2}\mod p$ is the collision of $H$.
|
||||
|
||||
Suppose $b_1=b_2$.
|
||||
|
||||
Then $y^{b_1}g^{x_1}\equiv y^{b_2}g^{x_2}\mod p$ implies $g^{x_1}\equiv g^{x_2}\mod p$.
|
||||
|
||||
So $x_1=x_2$ and $(x_1,b_1)=(x_2,b_2)$.
|
||||
|
||||
So $b_1\neq b_2$, Without loss of generality, say $b_1=1$ and $b_2=0$.
|
||||
|
||||
$y\cdot g^{x_1}\equiv g^{x_2}\mod p$ implies $y\equiv g^{x_2-x_1}\mod p$.
|
||||
|
||||
We can create a adversary $\mathcal{B}$ that can break the discrete log assumption with non-negligible probability $\mu(n)$ using $\mathcal{A}$.
|
||||
|
||||
Let $g,p$ be chosen and set random $x$ such that $y=g^x\mod p$.
|
||||
|
||||
Let the algorithm $\mathcal{B}$ defined as follows:
|
||||
|
||||
```pseudocode
|
||||
function B(p,g,y):
|
||||
(x_1,b_1),(x_2,b_2)\gets \mathcal{A}(p,g,y)
|
||||
If (x_1,1) and (x_2,0) and there is a collision:
|
||||
y=g^{x_2-x_1}\mod p
|
||||
return x_2-x_1 for b=1
|
||||
Else:
|
||||
return "Failed"
|
||||
```
|
||||
|
||||
$$
|
||||
P[B\text{ succeeds}]\geq P[A\text{ succeeds}]-\frac{1}{p(n)}>\frac{1}{p(n)}
|
||||
$$
|
||||
|
||||
So $\mathcal{B}$ can break the discrete log assumption with non-negligible probability $\mu(n)$, which contradicts the discrete log assumption.
|
||||
|
||||
So $h$ is a CRHF.
|
||||
|
||||
QED
|
||||
|
||||
To compress by more, say $h_k:{0,1}^n\to \{0,1\}^{n-k},k\geq 1$, then we can use $h: \{0,1\}^{n+1}\to \{0,1\}^n$ multiple times.
|
||||
|
||||
$$
|
||||
h_k(x)=h(h(\cdots(h(x)))\cdots)=h^{k}(x)
|
||||
$$
|
||||
|
||||
To find a collision of $h_k$, the adversary must find a collision of $h$.
|
||||
|
||||
### Application of CRHF to Digital Signature
|
||||
|
||||
Digital signature scheme on $\{0,1\}^*$ for a fixed security parameter $n$. (one-time secure)
|
||||
|
||||
- Use Digital Signature Scheme on $\{0,1\}^{n}$: $Gen, Sign, Ver$.
|
||||
- Use CRHF family $\{h_i:\{0,1\}^*\to \{0,1\}^n\}_{i\in I}$
|
||||
|
||||
$Gen'(1^n):(pk,sk)\gets Gen(1^n)$, choose $i\in I$ uniformly at random.
|
||||
|
||||
$sk'=(sk,i)$
|
||||
|
||||
$Sign'_{sk'}(m):\sigma\gets Sign_{sk}(h_i(m))$, return $(i,\sigma)$
|
||||
|
||||
$pk'=(pk,i)$
|
||||
|
||||
$Ver'_{pk'}(m,(i,\sigma)):Ver_{pk}(m,\sigma)$ and $i\in I$
|
||||
|
||||
One-time secure:
|
||||
|
||||
- Given that ($Gen,Sign,Ver$) is one-time secure
|
||||
- $h$ is a CRHF
|
||||
|
||||
Then ($Gen',Sign',Ver'$) is one-time secure.
|
||||
|
||||
Ideas of Proof:
|
||||
|
||||
If the digital signature scheme ($Gen',Sign',Ver'$) is not one-time secure, then there exists an adversary $\mathcal{A}$ which can ask oracle for one signature on $m_1$ and receive $\sigma_1=Sign'_{sk'}(m_1)=Sign_{sk}(h_i(m_1))$.
|
||||
|
||||
- It outputs $m_2\neq m_1$ and receives $\sigma_2=Sign'_{sk'}(m_2)=Sign_{sk}(h_i(m_2))$.
|
||||
- If $Ver'_{pk'}(m_2,\sigma_2)$ is accepted, then $Ver_{pk}(h_i(m_2),\sigma_2)$ is accepted and $i\in I$.
|
||||
|
||||
There are two cases to consider:
|
||||
|
||||
Case 1: $h_i(m_1)=h_i(m_2)$, Then $\mathcal{A}$ finds a collision of $h$.
|
||||
|
||||
Case 2: $h_i(m_1)\neq h_i(m_2)$, Then $\mathcal{A}$ produced valid signature on $h_i(m_2)$ after only seeing $Sign'_{sk'}(m_1)\neq Sign'_{sk'}(m_2)$. This contradicts the one-time secure of ($Gen,Sign,Ver$).
|
||||
|
||||
QED
|
||||
|
||||
### Many-time Secure Digital Signature
|
||||
|
||||
Using one-time secure digital signature scheme on $\{0,1\}^*$ to construct many-time secure digital signature scheme on $\{0,1\}^*$.
|
||||
|
||||
Let $Gen,Sign,Ver$ defined as follows:
|
||||
|
||||
$Gen(1^n):(pk,sk)\gets (pk_0,sk_0)
|
||||
|
||||
For the first message:
|
||||
|
||||
$(pk_1,sk_1)\gets Gen'(1^n)$
|
||||
|
||||
$Sign_{sk}(m_1):\sigma_1\gets Sign_{sk_0}(m_1||pk_1)$, return $\sigma_1'=(1,m_1,pk_1,\sigma_1)$
|
||||
|
||||
We need to remember state $\sigma_1'$ and $sk_1$ for the second message.
|
||||
|
||||
For the second message:
|
||||
|
||||
$(pk_2,sk_2)\gets Gen'(1^n)$
|
||||
|
||||
$Sign_{sk}(m_2):\sigma_2\gets Sign_{sk_1}(m_2||pk_0)$, return $\sigma_2'=(0,m_2,pk_0,\sigma_1')$
|
||||
|
||||
We need to remember state $\sigma_2'$ and $sk_2$ for the third message.
|
||||
|
||||
...
|
||||
|
||||
For the $i$-th message:
|
||||
|
||||
$(pk_i,sk_i)\gets Gen'(1^n)$
|
||||
|
||||
$Sign_{sk}(m_i):\sigma_i\gets Sign_{sk_{i-1}}(m_i||pk_{i-1})$, return $\sigma_i'=(i-1,m_i,pk_{i-1},\sigma_{i-1}')$
|
||||
|
||||
We need to remember state $\sigma_i'$ and $sk_i$ for the $(i+1)$-th message.
|
||||
|
||||
$Ver_{pk}:(m_i,(i,m_i,p_k,\sigma_i,\sigma_{i-1}))$ Will need to verify all the states public keys so far.
|
||||
|
||||
$$
|
||||
Ver_{pk_0}(m_1||pk_1, \sigma_1) = \text{ Accept}\\
|
||||
Ver_{pk_1}(m_2||pk_2, \sigma_2) = \text{ Accept}\\
|
||||
\vdots\\
|
||||
Ver_{pk_i}(m_i||pk_i, \sigma_i) = \text{ Accept}
|
||||
$$
|
||||
|
||||
Proof on homework.
|
||||
|
||||
Drawbacks:
|
||||
|
||||
- Signature size and verification time grows linearly with the number of messages.
|
||||
- Memory for signing grows linearly with the number of messages.
|
||||
|
||||
These can be fixed.
|
||||
|
||||
Question: Note that the signature signing message longer than the public key, which is impossible in Lamport Scheme.
|
||||
147
content/CSE442T/CSE442T_L21.md
Normal file
147
content/CSE442T/CSE442T_L21.md
Normal file
@@ -0,0 +1,147 @@
|
||||
# Lecture 21
|
||||
|
||||
## Chapter 5: Authentication
|
||||
|
||||
### Digital Signature Scheme
|
||||
|
||||
"Chain based approach".
|
||||
|
||||
$pk_0\to m_1||pk_1\to m_2||pk_2\to m_3||pk_3\to m_4\dots$
|
||||
|
||||
The signature size grows linearly with the message size $n$.
|
||||
|
||||
Improvement:
|
||||
|
||||
Use "Tree based approach".
|
||||
|
||||
Instead of creating 1 public key, we create 2 public keys each time and use the shorter one to sign the next message.
|
||||
|
||||
For example, let $n=4$, and we want to sign $m=1100$.
|
||||
|
||||
Every verifier knows the public key.
|
||||
|
||||
Then we generates $(pk_0,sk_0),(pk_1,sk_1)$ and store $\sigma, sk_0,sk_1$
|
||||
|
||||
$\sigma=Sign_{sk_0}(pk_0||pk_1)$
|
||||
|
||||
and generates $\to (pk_2,sk_2)\to (pk_3,sk_3)\to (pk_4,sk_4)$
|
||||
|
||||
$\sigma_1=Sign_{sk_1}(pk_{10}||pk_{11})$
|
||||
|
||||
$\sigma_{11}=Sign_{sk_{11}}(pk_{110}||pk_{111})$
|
||||
|
||||
$\sigma_{110}=Sign_{sk_{110}}(pk_{1100}||pk_{1101})$
|
||||
|
||||
$\sigma_{1100}=Sign_{sk_{1100}}(m)$
|
||||
|
||||
So we sign $m=1100$ as $\sigma_{1100}$.
|
||||
|
||||
The final signature is $\sigma'=(pk,\sigma,pk_1,\sigma_1,pk_{11},\sigma_{11},pk_{110},\sigma_{110},pk_{1100},\sigma_{1100})$.
|
||||
|
||||
The verifier can verify the signature by checking the authenticity of each public key.
|
||||
|
||||
Outputs $m,\sigma'_m$
|
||||
|
||||
The signature size grows logarithmically with the message size $n$.
|
||||
|
||||
If we want to sign $m=1110$ for next message, we can just append $1110$ to the end of the previous signature since $pk_1,pk_{11},pk_{110}$ are all stored in the previous signature tree.
|
||||
|
||||
So the next signature is $\sigma'_{1110}=(pk,\sigma,pk_1,\sigma_1,pk_{11},\sigma_{11},pk_{111},\sigma_{111},pk_{1110},\sigma_{1110})$.
|
||||
|
||||
The size of the next signature is still $O(\log n)$.
|
||||
|
||||
Advantages:
|
||||
|
||||
1. The signature size is small (do not grow linearly as the number of messages grows).
|
||||
2. The verification is efficient (do not need to check all the previous messages).
|
||||
3. The signature is secure.
|
||||
|
||||
Disadvantages:
|
||||
|
||||
1. Have to store all the public keys securely pair as you go.
|
||||
|
||||
Fix: Psudo-randomness.
|
||||
|
||||
Use a Pseudo-random number generator to generate random pk/sk pairs.
|
||||
|
||||
Since the PRG is deterministic, we don't need to store the public keys anymore.
|
||||
|
||||
We can use a random seed to generate all the pk/sk pairs.
|
||||
|
||||
### Trapdoor-based Signature Scheme
|
||||
|
||||
Idea: use RSA to create
|
||||
|
||||
$N=p\cdot q$, $e\in\mathbb{Z}_{\phi(N)}^*$, $d=e^{-1}\mod\phi(N)$ (secret key)
|
||||
|
||||
We do the "flip" encryption as follows:
|
||||
|
||||
Let $c=Enc_{pk}(m)=m^e\mod N$
|
||||
|
||||
Then $Dec_{sk}(c)=c^d\mod N=m'\mod N$.
|
||||
|
||||
$\sigma=Sign_{sk}(m)=m^d\mod N$
|
||||
|
||||
$Verify_{pk}(m,\sigma)=1\iff \sigma^e=(m^d)^e\mod N=m$
|
||||
|
||||
#### Forgery 1:
|
||||
|
||||
Ask oracle nothing.
|
||||
|
||||
Pick random $\sigma$ let $m=\sigma^e$.
|
||||
|
||||
Although in this case, the adversary has no control over $m$, it is still not very good.
|
||||
|
||||
#### Forgery 2:
|
||||
|
||||
They want to sign $m$.
|
||||
|
||||
Pick $m_1,m_2$ and $m=m_1\cdot m_2$.
|
||||
|
||||
Ask oracle for $Enc_{pk}(m_1)=\sigma_1$ and $Enc_{pk}(m_2)=\sigma_2$.
|
||||
|
||||
Output $\sigma=\sigma_1\cdot\sigma_2$, since $\sigma_1\cdot\sigma_2=(m_1^d\mod N)\cdot(m_2^d\mod N)=(m_1\cdot m_2)^d\mod N=m^d=\sigma$.
|
||||
|
||||
This is a valid signature for $m$.
|
||||
|
||||
That's very bad.
|
||||
|
||||
This means if we signed two messages $m_1,m_2$, we can get a valid signature for $m_1\cdot m_2$. If unfortunately $m_1\cdot m_2$ is the message we want to sign, the adversary can produce a fake signature for free.
|
||||
|
||||
#### Fix for forgeries
|
||||
|
||||
Pick a "random"-looking function $h:\mathcal{M}\to\mathbb{Z}_N^*$. ($h(\cdot)$ is collision-resistant)
|
||||
|
||||
$pk=(h,N,e)$, $sk=(h,N,d)$
|
||||
|
||||
$Sign_{sk}(m)=h(m)^d\mod N$
|
||||
|
||||
$Verify_{pk}(m,\sigma)=1\iff \sigma^e=h(m)\mod N$
|
||||
|
||||
If $h$ is truly random, this would be secure.
|
||||
|
||||
$\sigma^e=m$ and $\sigma^e=h(m)\cancel{\to}m$
|
||||
|
||||
So $\sigma_1=h(m_1)^d$ and $\sigma_2=h(m_2)^d$, If $m=m_1\cdot m_2$, then $\sigma_1\cdot\sigma_2=h(m_1)^d\cdot h(m_2)^d\neq h(m)^d=\sigma$. (the equality is very unlikely to happen)
|
||||
|
||||
This is secure.
|
||||
|
||||
Choices of $h$:
|
||||
|
||||
1. $h$ is random function. Not practical since we need the verifier to know $h$.
|
||||
2. $h$ is pseudo-random function. Verifier needs to use $h$, with full access to the random oracle. If we use $f_k$ for a random key $k$, they need $k$. No more pseudo-random security guarantee.
|
||||
3. $h$ is a collision-resistant hash function. We can't be sure it doesn't have any patterns like $h(m_1\cdot m_2)=h(m_1)\cdot h(m_2)$.
|
||||
|
||||
Here we present our silly solution:
|
||||
|
||||
#### Random oracle model:
|
||||
|
||||
Assume we have a true random function $h$, the adversary only has oracle access to $h$.
|
||||
|
||||
And $h$ is practical to use.
|
||||
|
||||
This RSA scheme under the random oracle model is secure. (LOL)
|
||||
|
||||
This requires a proof.
|
||||
|
||||
In practice, SHA-256 is used as $h$. Fun, no one really finds a collision yet.
|
||||
201
content/CSE442T/CSE442T_L22.md
Normal file
201
content/CSE442T/CSE442T_L22.md
Normal file
@@ -0,0 +1,201 @@
|
||||
# Lecture 22
|
||||
|
||||
## Chapter 7: Composability
|
||||
|
||||
So far we've sought security against
|
||||
|
||||
$$
|
||||
c\gets Enc_k(m)
|
||||
$$
|
||||
|
||||
Adversary knows $c$, but nothing else.
|
||||
|
||||
### Attack models
|
||||
|
||||
#### Known plaintext attack (KPA)
|
||||
|
||||
Adversary has seen $(m_1,Enc_k(m_1)),(m_2,Enc_k(m_2)),\cdots,(m_q,Enc_k(m_q))$.
|
||||
|
||||
$m_1,\cdots,m_q$ are known to the adversary.
|
||||
|
||||
Given new $c=Enc_k(m)$, is previous knowledge helpful?
|
||||
|
||||
#### Chosen plaintext attack (CPA)
|
||||
|
||||
Adversary can choose $m_1,\cdots,m_q$ and obtain $Enc_k(m_1),\cdots,Enc_k(m_q)$.
|
||||
|
||||
Then adversary see new encryption $c=Enc_k(m)$. with the same key.
|
||||
|
||||
Example:
|
||||
|
||||
In WWII, Japan planned to attack "AF", but US suspected it means Midway.
|
||||
|
||||
So US use Axis: $Enc_k(AF)$ and ran out of supplies.
|
||||
|
||||
Then US know Japan will attack Midway.
|
||||
|
||||
#### Chosen ciphertext attack (CCA)
|
||||
|
||||
Adversary can choose $c_1,\cdots,c_q$ and obtain $Dec_k(c_1),\cdots,Dec_k(c_q)$.
|
||||
|
||||
|
||||
#### Definition 168.1 (Secure private key encryption against attacks)
|
||||
|
||||
Capture these ideas with the adversary having oracle access.
|
||||
|
||||
Let $\Pi=(Gen,Enc,Dec)$ be a private key encryption scheme. Let a random variable $IND_b^{O_1,O_2}(\Pi,\mathcal{A},n)$ where $\mathcal{A}$ is an n.u.p.p.t. The security parameter is $n\in \mathbb{N}$, $b\in\{0,1\}$ denoting the real scheme or the adversary's challenge.
|
||||
|
||||
The experiment is the following:
|
||||
|
||||
- Key $k\gets Gen(1^n)$
|
||||
- Adversary $\mathcal{A}^{O_1(k)}(1^n)$ queries oracle $O_1$
|
||||
- $m_0,m_1\gets \mathcal{A}^{O_1(k)}(1^n)$
|
||||
- $c\gets Enc_k(m_b)$
|
||||
- $\mathcal{A}^{O_2(c)}(1^n,c)$ queries oracle $O_2$ to distinguish $c$ is encryption of $m_0$ or $m_1$
|
||||
- $\mathcal{A}$ outputs bit $b'$ which is either zero or one
|
||||
|
||||
$\Pi$ is CPA/CCA1/CCA2 secure if for all PPT adversaries $\mathcal{A}$,
|
||||
|
||||
$$
|
||||
\{IND_0^{O_1,O_2}(\Pi,\mathcal{A},n)\}_n\approx\{IND_1^{O_1,O_2}(\Pi,\mathcal{A},n)\}_n
|
||||
$$
|
||||
|
||||
where $\approx$ is statistical indistinguishability.
|
||||
|
||||
|Security|$O_1$|$O_2$|
|
||||
|:---:|:---:|:---:|
|
||||
|CPA|$Enc_k$|$Enc_k$|
|
||||
|CCA1|$Enc_k,Dec_k$|$Enc_k$|
|
||||
|CCA2 (or full CCA)|$Enc_k,Dec_k$|$Enc_k,Dec_k^*$|
|
||||
|
||||
Note that $Dec_k^*$ will not allowed to query decryption of a functioning ciphertext.
|
||||
|
||||
You can imagine the experiment is a class as follows:
|
||||
|
||||
```python
|
||||
n = 1024
|
||||
|
||||
@lru_cache(None)
|
||||
def oracle_1(m,key,**kwargs):
|
||||
"""
|
||||
Query oracle 1
|
||||
"""
|
||||
pass
|
||||
|
||||
@lru_cache(None)
|
||||
def oracle_2(c,key,**kwargs):
|
||||
"""
|
||||
Query oracle 2
|
||||
"""
|
||||
pass
|
||||
|
||||
class Experiment:
|
||||
def __init__(self, key, oracle_1, oracle_2):
|
||||
self.key = key
|
||||
self.oracle_1 = oracle_1
|
||||
self.oracle_2 = oracle_2
|
||||
|
||||
def sufficient_trial(self):
|
||||
pass
|
||||
|
||||
def generate_test_message(self):
|
||||
pass
|
||||
|
||||
def set_challenge(self, c):
|
||||
self.challenge = c
|
||||
|
||||
def query_1(self):
|
||||
while not self.sufficient_trial():
|
||||
self.oracle_1(m,self.key,**kwargs)
|
||||
|
||||
def challenge(self):
|
||||
"""
|
||||
Return m_0, m_1 for challenge
|
||||
"""
|
||||
m_0, m_1 = self.generate_test_message()
|
||||
self.m_0 = m_0
|
||||
self.m_1 = m_1
|
||||
return m_0, m_1
|
||||
|
||||
def query_2(self, c):
|
||||
while not self.sufficient_trial():
|
||||
self.oracle_2(c,self.key,**kwargs)
|
||||
|
||||
def output(self):
|
||||
return 0 if self.challenge==m_0 else 1
|
||||
|
||||
if __name__ == "__main__":
|
||||
key = random.randint(0, 2**n)
|
||||
exp = Experiment(key, oracle_1, oracle_2)
|
||||
exp.query_1()
|
||||
m_0, m_1 = exp.challenge()
|
||||
choice = random.choice([m_0, m_1])
|
||||
exp.set_challenge(choice)
|
||||
exp.query_2()
|
||||
b_prime = exp.output()
|
||||
print(f"b'={b_prime}, b={choice==m_0}")
|
||||
```
|
||||
|
||||
#### Theorem: Our mms private key encryption scheme is CPA, CCA1 secure.
|
||||
|
||||
Have a PRF family $\{f_k\}:\{0,1\}^{|k|}\to\{0,1\}^{|k|}$
|
||||
|
||||
$Gen(1^n)$ outputs $k\in\{0,1\}^n$ and samples $f_k$ from the PRF family.
|
||||
|
||||
$Enc_k(m)$ samples $r\in\{0,1\}^n$ and outputs $(r,f_k(r)\oplus m)$. For multi-message security, we need to encrypt $m_1,\cdots,m_q$ at once.
|
||||
|
||||
$Dec_k(r,c)$ outputs $f_k(r)\oplus c$.
|
||||
|
||||
Familiar Theme:
|
||||
|
||||
- Show the R.F. version is secure.
|
||||
- $F\gets RF_n$
|
||||
- If the PRF version were insecure, then the PRF can be distinguished from a random function...
|
||||
|
||||
$IND_b^{O_1,O_2}(\Pi,\mathcal{A},n), F\gets RF_n$
|
||||
|
||||
- $Enc$ queries $(m_1,(r_1,m_1\oplus F_k(r_1))),\cdots,(m_{q_1},(r_{q_1},m_{q_1}\oplus F_k(r_{q_1})))$
|
||||
- $Dec$ queries $(s_1,c_1),\cdots,(s_{q_2},c_{q_2})$, where $m_i=c_i-F_k(s_i)$
|
||||
- $m_0,m_1\gets \mathcal{A}^{O_2(k)}(1^n)$, $Enc_F(m_b)=(R,M_b+F(R))$
|
||||
- Query round similar to above.
|
||||
|
||||
As long as $R$ was never seen in querying rounds, $P[\mathcal{A} \text{ guesses correctly}]=1/2$.
|
||||
|
||||
$P[R\text{ was seen before}]\leq \frac{p(n)}{2^n}$ (by the total number of queries in all rounds.)
|
||||
|
||||
**This encryption scheme is not CCA2 secure.**
|
||||
|
||||
After round 1, $O^n,1^n\gets \mathcal{A}^{O_1(k)}(1^n)$,
|
||||
|
||||
$(r,m+F(r))=(r,c)$ in round 2.
|
||||
|
||||
Query $Dec_F(r,c+0\ldots 01)=0\ldots 01 \text{ or } 1\ldots 10$.
|
||||
|
||||
$c+0\ldots 01-F(r)=M+0\ldots 01$
|
||||
|
||||
### Encrypt then authenticate
|
||||
|
||||
Have a PRF family $\{f_k\}:\{0,1\}^|k|\to\{0,1\}^{|k|}$
|
||||
|
||||
$Gen(1^n)$ outputs $k_1,k_2\in\{0,1\}^n$ and samples $f_k$ from the PRF family.
|
||||
|
||||
$Enc_{k_1,k_2}(m)$ samples $r\in\{0,1\}^n$ and let $c_1=f_{k_1}(r)\oplus m$ and $c_2=f_{k_2}(c_1)$. Then we output $(r,c_1,c_2)$. where $c_1$ is the encryption, and $c_2$ is the tag. For multi-message security, we need to encrypt $m_1,\cdots,m_q$ at once.
|
||||
|
||||
$Dec_{k_1,k_2}(r,c_1,c_2)$ checks if $c_2=f_{k_2}(c_1)$. If so, output $c_1-f_{k_1}(r)$. Otherwise, output $\bot$.
|
||||
|
||||
Show that this scheme is CPA secure.
|
||||
|
||||
1. Show that the modifier version $\Pi'^{RF}$ where $f_{k_2}$ is replaced with a random function is CCA2 secure.
|
||||
2. If ours isn't, then PRF detector can be created.
|
||||
|
||||
Suppose $\Pi^RF$ is not secure, then $\exists \mathcal{A}$ which can distinguish $IND_i^{O_1,O_2}(\Pi'^{RF},\mathcal{A},n)$ with non-negligible probability. We will use this to construct $B$ which breaks the CPA security of $\Pi$.
|
||||
|
||||
Let $B$ be the PPT algorithm that on input $1^n$, does the following:
|
||||
|
||||
- Run $\mathcal{A}^{O_1,O_2}(\Pi'^{RF},\mathcal{A},n)$
|
||||
- Let $m_0,m_1$ be the messages that $\mathcal{A}$ asked for in the second round.
|
||||
- Choose $b\in\{0,1\}$ uniformly at random.
|
||||
- Query $Enc_{k_1,k_2}(m_b)$ to the oracle.
|
||||
- Let $c$ be the challenge ciphertext.
|
||||
- Return whatever $\mathcal{A}$ outputs.
|
||||
|
||||
125
content/CSE442T/CSE442T_L23.md
Normal file
125
content/CSE442T/CSE442T_L23.md
Normal file
@@ -0,0 +1,125 @@
|
||||
# Lecture 23
|
||||
|
||||
## Chapter 7: Composability
|
||||
|
||||
### Zero-knowledge proofs
|
||||
|
||||
Let the Prover Peggy and the Verifier Victor.
|
||||
|
||||
Peggy wants to prove to Victor that she knows a secret $x$ without revealing anything about $x$. (e.g. $x$ such that $g^x=y\mod p$)
|
||||
|
||||
#### Zero-knowledge proofs protocol
|
||||
|
||||
The protocol should satisfy the following properties:
|
||||
|
||||
- **Completeness**: If Peggy knows $x$, she can always make Victor accept.
|
||||
- **Soundness**: If a malicious Prover $P^*$ does not know $x$, then $V$ accepts with probability at most $\epsilon(n)$.
|
||||
- **Zero-knowledge**: After the process, $V^*$ (possibly dishonest Verifier) knows no more about $x$ than he did before.
|
||||
|
||||
[The interaction could have been faked without $P$]
|
||||
|
||||
#### Example: Hair counting magician
|
||||
|
||||
"Magician" who claims they can count the number of hairs on your head.
|
||||
|
||||
secret info: the method of counting.
|
||||
|
||||
Repeat the following process for $k$ times:
|
||||
|
||||
1. "Magician" tells the number of hairs
|
||||
2. You remove some hair $b\in \{0,1\}$ from your head.
|
||||
3. "Magician" tells the number of hairs left.
|
||||
4. Reject if the number of hairs is incorrect. Accept after $k$ times. (to our desired certainty)
|
||||
|
||||
#### Definition
|
||||
|
||||
Let $P$ and $V$ be two interactive Turing machines.
|
||||
|
||||
Let $x$ be the shared input, $y$ be the secret knowledge, $z$ be the existing knowledge about $y$, with $r_1,r_2,\cdots,r_k$ being the random tapes.
|
||||
|
||||
$V$ should output accept or reject after the interaction for $q$ times.
|
||||
|
||||
```python
|
||||
class P(TuringMachine):
|
||||
"""
|
||||
:param x: the shared input with V
|
||||
:param y: auxiliary input (the secret knowledge)
|
||||
:param z: auxiliary input (could be existing knowledge about y)
|
||||
:param r_i: random message
|
||||
"""
|
||||
def run(self, x)->str:
|
||||
"""
|
||||
:return: the message to be sent to V $m_p$
|
||||
"""
|
||||
|
||||
class V(TuringMachine):
|
||||
"""
|
||||
The verifier will output accept or reject after the interaction for $q$ times.
|
||||
|
||||
:param x: the shared input with P
|
||||
:param y: auxiliary input (the secret knowledge)
|
||||
:param z: auxiliary input (could be existing knowledge about y)
|
||||
:param r_i: random message
|
||||
"""
|
||||
def run(self, q: int)->bool:
|
||||
"""
|
||||
:param q: the number of rounds
|
||||
:return: accept or reject
|
||||
"""
|
||||
for i in range(q):
|
||||
m_v = V.run(i)
|
||||
m_p = P.run(m_v)
|
||||
if m_p!=m_v:
|
||||
return False
|
||||
return True
|
||||
```
|
||||
|
||||
Let the transcript be the sequence of messages exchanged between $P$ and $V$. $\text{Transcript} = (m_1^p,m_1^v,m_2^p,m_2^v,\cdots,m_q^p,m_q^v)$.
|
||||
|
||||
Define $(P,V)$ be the zero-knowledge proof protocol. For a **language** $L$, $(P,V)$ is a zero-knowledge proof for $L$ if:
|
||||
|
||||
> Language $L$ is a set of pairs of isomorphic graphs (where two graphs are isomorphic if there exists a bijection between their vertices).
|
||||
|
||||
- $(P,V)$ is complete for $L$: $\forall x\in L$, $\exists$ "witness" $y$ such that $\forall z\in \{0,1\}^n$, $Pr[out_v[P(x,y)\longleftrightarrow V(x,z)]=\text{accept}]=1$.
|
||||
- $(P,V)$ is sound for $L$: $\forall x\notin L$, $\forall P^*$, $Pr[out_v[P^*(x)\longleftrightarrow V(x,z)]=\text{accept}]< \epsilon(n)$.
|
||||
- $(P,V)$ is zero-knowledge for $L$: $\forall V^*$, $\exists$ p.p.t. simulator $S$ such that the following distributions are indistinguishable:
|
||||
|
||||
$$
|
||||
\{\text{Transcript}[P(x,y)\leftrightarrow V^*(x,z)\mid x\in L,y\leftarrow \{0,1\}^n]\}\quad\text{and}\quad\{S(x,z)\mid x\notin L\}.
|
||||
$$
|
||||
|
||||
*If these distributions are indistinguishable, then $V^*$ learns nothing from the interaction.*
|
||||
|
||||
#### Example: Graph isomorphism
|
||||
|
||||
Let $G_0$ and $G_1$ be two graphs.
|
||||
|
||||
$V$ picks a random permutation $\pi\in S_n$ and sends $G_\pi$ to $P$.
|
||||
|
||||
$P$ needs to determine if $G_\pi=G_0$ or $G_\pi=G_1$.
|
||||
|
||||
If they are isomorphic, then $\exists$ permutation $\sigma:\{1,\cdots,n\}\rightarrow \{1,\cdots,n\}$ such that $G_0=\{(i,j)\mid (i,j)\in G_1\}$.
|
||||
|
||||
Protocol:
|
||||
|
||||
Shared input $\overline{x}=(G_0,G_1)$ witness $\overline{y}=\sigma$. Repeat the following process for $n$ times, where $n$ is the number of vertices.
|
||||
|
||||
1. $P$ picks a random permutation $\pi\in \mathbb{P}_n$ and sends $G_\pi=\pi(G_0)$ to $V$.
|
||||
2. $V$ picks a random $b\in \{0,1\}$ and sends $b$ to $P$.
|
||||
3. If $b=1$, $P$ sends $\sigma=\pi^{-1}$ to $V$.
|
||||
4. If $b=0$, $P$ sends $\sigma=\pi$ to $V$.
|
||||
5. $V$ receives $\phi$ and checks if $b=0$ and $G_\sigma=\phi(G_0)$ or $b=1$ and $G_\sigma =\phi(G_1)$. Return accept if true.
|
||||
|
||||
If they are not isomorphic, $P$ rejects with probability 1.
|
||||
|
||||
If they are isomorphic, $P$ accepts with probability $\frac{1}{n!}$.
|
||||
|
||||
Proof:
|
||||
|
||||
- Completeness: If $G_0$ and $G_1$ are isomorphic, then $P$ can always find a permutation $\sigma$ such that $G_\sigma=G_0$ or $G_\sigma=G_1$.
|
||||
- Soundness:
|
||||
- If $P^*$ knows that $V$ was going to send $b=0$, then they will pick $\Pi$ and send $G=\Pi(G_0)$ to $V$. However, if we thought they would send $0$ but they sent $1$, then $G=\Pi(G_1)$ and they would reject.
|
||||
- If $P^*$ knows that $V$ was going to send $b=1$, then they will pick $\Pi$ and send $G=\Pi(G_1)$ to $V$. However, if we thought they would send $1$ but they sent $0$, then $G=\Pi(G_0)$ and they would reject.
|
||||
- The key is that $P^*$ can only response correctly with probability at most $\frac{1}{2}$ each time.
|
||||
|
||||
Continue on the next lecture. (The key is that $P^*$ can only get a random permutation)
|
||||
45
content/CSE442T/CSE442T_L24.md
Normal file
45
content/CSE442T/CSE442T_L24.md
Normal file
@@ -0,0 +1,45 @@
|
||||
# Lecture 24
|
||||
|
||||
## Chapter 7: Composability
|
||||
|
||||
### Continue on zero-knowledge proof
|
||||
|
||||
Let $X=(G_0,G_1)$ and $y=\sigma$ permutation. $\sigma(G_0)=G_1$.
|
||||
|
||||
$P$ is a random $\Pi$ permutation and $H=\Pi(G_0)$.
|
||||
|
||||
$P$ sends $H$ to $V$.
|
||||
|
||||
$V$ sends a random $b\in\{0,1\}$ to $P$.
|
||||
|
||||
$P$ sends $\phi=\Pi$ if $b=0$ and $\phi=\Pi\phi^{-1}$ if $b=1$.
|
||||
|
||||
$V$ outputs accept if $\phi(G_0)=G_1$ and reject otherwise.
|
||||
|
||||
### Message transfer protocol
|
||||
|
||||
The message transfer protocol is defined as follow.
|
||||
|
||||
Construct a simulator $S(x,z)$ based on $V^*(x,z)$.
|
||||
|
||||
Pick $b'\gets\{0,1\}$.
|
||||
|
||||
$\Pi\gets \mathbb{P}_n$ and $H\gets \Pi(G_0)$.
|
||||
|
||||
If $V^*$ sends $b=b'$, we send $\Pi$/ output $V^*$'s output
|
||||
|
||||
Otherwise, we start over. Go back to the beginning state. Do this until "n" successive accept.'
|
||||
|
||||
### Zero-knowledge definition (Cont.)
|
||||
|
||||
In zero-knowledge definition. We need the simulator $S$ to have expected running time polynomial in $n$.
|
||||
|
||||
Expected two trials for each "success"
|
||||
|
||||
2*n running time (one interaction)
|
||||
|
||||
$$
|
||||
\{Out_{V^*}[S(x,z)\leftrightarrow V^*(x,z)]\}=\{Out_{V^*}[P(x,y)\leftrightarrow V^*(x,z)]\}
|
||||
$$
|
||||
|
||||
If $G_0$ and $G_1$ are indistinguishable, $H_s=\Pi(G_{b'})$ same distribution as $H_p=\Pi(G_0)$. (random permutation of $G_1$ is a random permutation of $G_0$)
|
||||
115
content/CSE442T/CSE442T_L3.md
Normal file
115
content/CSE442T/CSE442T_L3.md
Normal file
@@ -0,0 +1,115 @@
|
||||
# Lecture 3
|
||||
|
||||
All algorithms $C(x)\to y$, $x,y\in \{0,1\}^*$
|
||||
|
||||
P.P.T= Probabilistic Polynomial-time Turing Machine.
|
||||
|
||||
## Chapter 2: Computational Hardness
|
||||
|
||||
### Turing Machine: Mathematical model for a computer program
|
||||
|
||||
A machine that can:
|
||||
|
||||
1. Read in put
|
||||
2. Read/Write working tape move left/right
|
||||
3. Can change state
|
||||
|
||||
### Assumptions
|
||||
|
||||
Anything can be accomplished by a real computer program can be accomplished by a "sufficiently complicated" Turing Machine (TM).
|
||||
|
||||
### Polynomial time
|
||||
|
||||
We say $C(x),|x|=n,n\to \infty$ runs in polynomial time if it uses at most $T(n)$ operations bounded by some polynomials. $\exist c>0$ such that $T(n)=O(n^c)$
|
||||
|
||||
If we can argue that algorithm runs in polynomially-many constant-time operations, then this is true for the T.M.
|
||||
|
||||
$p,q$ are polynomials in $n$,
|
||||
|
||||
$p(n)+q(n),p(n)q(n),p(q(n))$ are polynomial of $n$.
|
||||
|
||||
Polynomial-time $\approx$ "efficient" for this course.
|
||||
|
||||
### Probabilistic
|
||||
|
||||
Our algorithm's have access to random "coin-flips" we can produce poly(n) random bits.
|
||||
|
||||
$P[C(x)\text{ takes at most }T(n)\text{ steps }]=1$
|
||||
|
||||
Our adversary $a(x)$ will be a P.P.T which is non-uniform (n.u.) (programs description size can grow polynomially in n)
|
||||
|
||||
### Efficient private key encryption scheme
|
||||
|
||||
#### Definition 3.2 (Efficient private key encryption scheme)
|
||||
|
||||
The triple $(Gen,Enc,Dec)$ is an efficient private key encryption scheme over the message space $M$ and key space $K$ if:
|
||||
|
||||
1. $Gen(1^n)$ is a randomized p.p.t that outputs $k\in K$
|
||||
2. $Enc_k(m)$ is a potentially randomized p.p.t that outputs $c$ given $m\in M$
|
||||
3. $Dec_k(c')$ is a deterministic p.p.t that outputs $m$ or "null"
|
||||
4. $P_k[Dec_k(Enc_k(m))=m]=1,\forall m\in M$
|
||||
|
||||
### Negligible function
|
||||
|
||||
$\epsilon:\mathbb{N}\to \mathbb{R}$ is a negligible function if $\forall c>0$, $\exists N\in\mathbb{N}$ such that $\forall n\geq N, \epsilon(n)<\frac{1}{n^c}$ (looks like definition of limits huh) (Definition 27.2)
|
||||
|
||||
Idea: for any polynomial, even $n^{100}$, in the long run $\epsilon(n)\leq \frac{1}{n^{100}}$
|
||||
|
||||
Example: $\epsilon (n)=\frac{1}{2^n}$, $\epsilon (n)=\frac{1}{n^{\log (n)}}$
|
||||
|
||||
Non-example: $\epsilon (n)=O(\frac{1}{n^c})\forall c$
|
||||
|
||||
### One-way function
|
||||
|
||||
Idea: We are always okay with our chance of failure being negligible.
|
||||
|
||||
Foundational concept of cryptography
|
||||
|
||||
Goal: making $Enc_k(m),Dec_k(c')$ easy and $Dec^{-1}(c')$ hard.
|
||||
|
||||
#### Definition 27.3 (Strong one-way function)
|
||||
|
||||
$$
|
||||
f:\{0,1\}^n\to \{0,1\}^*(n\to \infty)
|
||||
$$
|
||||
|
||||
There is a negligible function $\epsilon (n)$ such that for any adversary $\mathcal{A}$ (n.u.p.p.t)
|
||||
|
||||
$$
|
||||
P[x\gets\{0,1\}^n;y=f(x):f(\mathcal{A}(y))=y]\leq\epsilon(n)
|
||||
$$
|
||||
|
||||
_Probability of guessing a message $x'$ with the same output as the correct message $x$ is negligible_
|
||||
|
||||
and
|
||||
|
||||
there is a p.p.t which computes $f(x)$ for any $x$.
|
||||
|
||||
- Hard to go back from output
|
||||
- Easy to find output
|
||||
|
||||
$a$ sees output y, they wan to find some $x'$ such that $f(x')=y$.
|
||||
|
||||
Example: Suppose $f$ is one-to-one, then $a$ must find our $x$, $P[x'=x]=\frac{1}{2^n}$, which is negligible.
|
||||
|
||||
Why do we allow $a$ to get a different $x'$?
|
||||
|
||||
> Suppose the definition is $P[x\gets\{0,1\}^n;y=f(x):\mathcal{A}(y)=x]\neq\epsilon(n)$, then a trivial function $f(x)=x$ would also satisfy the definition.
|
||||
|
||||
To be technically fair, $\mathcal{A}(y)=\mathcal{A}(y,1^n)$, size of input $\approx n$, let them use $poly(n)$ operations. (we also tells the input size is $n$ to $\mathcal{A}$)
|
||||
|
||||
#### Do one-way function exists?
|
||||
|
||||
Unknown, actually...
|
||||
|
||||
But we think so!
|
||||
|
||||
We will need to use various assumptions. one that we believe very strongly based on evidence/experience
|
||||
|
||||
Example:
|
||||
|
||||
$p,q$ are large random primes
|
||||
|
||||
$N=p\cdot q$
|
||||
|
||||
Factoring $N$ is hard. (without knowing $p,q$)
|
||||
140
content/CSE442T/CSE442T_L4.md
Normal file
140
content/CSE442T/CSE442T_L4.md
Normal file
@@ -0,0 +1,140 @@
|
||||
# Lecture 4
|
||||
|
||||
## Recap
|
||||
|
||||
Negligible function $\epsilon(n)$ if $\forall c>0,\exist N$ such that $n>N$, $\epsilon (n)<\frac{1}{n^c}$
|
||||
|
||||
Example:
|
||||
|
||||
$\epsilon(n)=2^{-n},\epsilon(n)=\frac{1}{n^{\log (\log n)}}$
|
||||
|
||||
## Chapter 2: Computational Hardness
|
||||
|
||||
### One-way function
|
||||
|
||||
#### Strong One-Way Function
|
||||
|
||||
1. $\exists$ a P.P.T. that computes $f(x),\forall x\in\{0,1\}^n$
|
||||
2. $\forall \mathcal{A}$ adversaries, $\exists \epsilon(n),\forall n$.
|
||||
|
||||
$$
|
||||
P[x\gets \{0,1\}^n;y=f(x):f(\mathcal{A}(y,1^n))=y]<\epsilon(n)
|
||||
$$
|
||||
|
||||
_That is, the probability of success guessing should decreasing (exponentially) as encrypted message increase (linearly)..._
|
||||
|
||||
To negate statement 2:
|
||||
|
||||
$$
|
||||
P[x\gets \{0,1\}^n;y=f(x):f(\mathcal{A}(y,1^n))=y]=\mu(n)
|
||||
$$
|
||||
|
||||
is a negligible function.
|
||||
|
||||
Negation:
|
||||
|
||||
$\exists \mathcal{A}$, $P[x\gets \{0,1\}^n;y=f(x):f(\mathcal{A}(y,1^n))=y]=\mu(n)$ is not a negligible function.
|
||||
|
||||
That is, $\exists c>0,\forall N \exists n>N \epsilon(n)>\frac{1}{n^c}$
|
||||
|
||||
$\mu(n)>\frac{1}{n^c}$ for infinitely many $n$. or infinitely often.
|
||||
|
||||
> Keep in mind: $P[success]=\frac{1}{n^c}$, it can try $O(n^c)$ times and have a good chance of succeeding at least once.
|
||||
|
||||
#### Definition 28.4 (Weak one-way function)
|
||||
|
||||
$f:\{0,1\}^n\to \{0,1\}^*$
|
||||
|
||||
1. $\exists$ a P.P.T. that computes $f(x),\forall x\in\{0,1\}^n$
|
||||
2. $\forall \mathcal{A}$ adversaries, $\exists \epsilon(n),\forall n$.
|
||||
|
||||
$$
|
||||
P[x\gets \{0,1\}^n;y=f(x):f(\mathcal{A}(y,1^n))=y]<1-\frac{1}{p(n)}
|
||||
$$
|
||||
|
||||
_The probability of success should not be too close to 1_
|
||||
|
||||
### Probability
|
||||
|
||||
#### Useful bound $0<p<1$
|
||||
|
||||
$1-p<e^{-p}$
|
||||
|
||||
(most useful when $p$ is small)
|
||||
|
||||
For an experiment has probability $p$ of failure and $1-p$ of success.
|
||||
|
||||
We run experiment $n$ times independently.
|
||||
|
||||
$P[\text{success all n times}]=(1-p)^n<(e^{-p})^n=e^{-np}$
|
||||
|
||||
#### Theorem 35.1 (Strong one-way function from weak one-way function)
|
||||
|
||||
If there exists a weak one-way function, there there exists a strong one-way function
|
||||
|
||||
In particular, if $f:\{0,1\}^n\to \{0,1\}^*$ is weak one-way function.
|
||||
|
||||
$\exists$ polynomial $q(n)$ such that
|
||||
|
||||
$$
|
||||
g(x):\{0,1\}^{nq(n)}\to \{0,1\}^*
|
||||
$$
|
||||
|
||||
and for every $n$ bits $x_i$
|
||||
|
||||
$$
|
||||
g(x_1,x_2,..,x_{q(n)})=(f(x_1),f(x_2),...,f(x_{q(n)}))
|
||||
$$
|
||||
|
||||
is a strong one-way function.
|
||||
|
||||
Proof:
|
||||
|
||||
1. Since $\exist P.P.T.$ that computes $f(x),\forall x$ we use this $q(n)$ polynomial times to compute $g$.
|
||||
2. (Idea) $a$ has to succeed in inverting $f$ all $q(n)$ times.
|
||||
Since $x$ is a weak one-way, $\exists$ polynomial $p(n)$. $\forall q, P[q$ inverts $f]<1-\frac{1}{p(n)}$ (Here we use $<$ since we can always find a polynomial that works)
|
||||
|
||||
Let $q(n)=np(n)$.
|
||||
|
||||
Then $P[a$ inverting $g]\sim P[a$ inverts $f$ all $q(n)]$ times. $<(1-\frac{1}{p(n)})^{q(n)}=(1-\frac{1}{p(n)})^{np(n)}<(e^{-\frac{1}{p(n)}})^{np(n)}=e^{-n}$ which is negligible function.
|
||||
|
||||
QED
|
||||
|
||||
_we can always force the adversary to invert the weak one-way function for polynomial time to reach the property of strong one-way function_
|
||||
|
||||
Example: $(1-\frac{1}{n^2})^{n^3}<e^{-n}$
|
||||
|
||||
### Some candidates of one-way function
|
||||
|
||||
#### Multiplication
|
||||
|
||||
$$
|
||||
Mult(m_1,m_2)=\begin{cases}
|
||||
1,m_1=1 | m_2=1\\
|
||||
m_1\cdot m_2
|
||||
\end{cases}
|
||||
$$
|
||||
|
||||
But we don't want trivial answers like (1,1000000007)
|
||||
|
||||
Idea: Our "secret" is 373 and 481, Eve can see the product 179413.
|
||||
|
||||
Not strong one-way for all integer inputs because there are trivial answer for $\frac{3}{4}$ of all outputs. `Mult(2,y/2)`
|
||||
|
||||
Factoring Assumption:
|
||||
|
||||
The only way to efficiently factorizing the product of prime is to iterate all the primes.
|
||||
|
||||
In other words:
|
||||
|
||||
$\forall a\exists \epsilon(n)$ such that $\forall n$. $P[p_1\gets \prod n_j]$
|
||||
|
||||
We'll show this is a weak one-way function under the Factoring Assumption.
|
||||
|
||||
$\forall a,\exists \epsilon(n)$ such that $\forall n$,
|
||||
|
||||
$$
|
||||
P[p_1\gets \Pi_n;p_2\gets \Pi_n;N=p_1\cdot p_2:a(n)=\{p_1,p_2\}]<\epsilon(n)
|
||||
$$
|
||||
|
||||
where $\Pi_n=\{p\text{ all primes }p<2^n\}$
|
||||
116
content/CSE442T/CSE442T_L5.md
Normal file
116
content/CSE442T/CSE442T_L5.md
Normal file
@@ -0,0 +1,116 @@
|
||||
# Lecture 5
|
||||
|
||||
## Chapter 2: Computational Hardness
|
||||
|
||||
Proving that there are one-way functions relies on assumptions.
|
||||
|
||||
Factoring Assumption: $\forall \mathcal{A}, \exist \epsilon (n)$, let $p,q\in \Pi_n,p,q<2^n$
|
||||
|
||||
$$
|
||||
P[p\gets \Pi_n;q\gets \Pi_n;N=p\cdot q:\mathcal{A}(N)\in \{p,q\}]<\epsilon(n)
|
||||
$$
|
||||
|
||||
Evidence: To this point, best known procedure to always factor has run time $O(2^{\sqrt{n}\sqrt{log(n)}})$
|
||||
|
||||
Distribution of prime numbers:
|
||||
|
||||
- We have infinitely many prime
|
||||
- Prime Number Theorem $\pi(n)\approx\frac{n}{\ln(n)}$, that means, $\frac{1}{\ln n}$ of all integers are prime.
|
||||
|
||||
We want to (guaranteed to) find prime:
|
||||
|
||||
$\pi(n)>\frac{2^n}{2n}$
|
||||
|
||||
e.g.
|
||||
$$
|
||||
P[x\gets \{0,1\}^n:x\in prime]\geq {\frac{2^n}{2n}\over 2^n}=\frac{1}{2n}
|
||||
$$
|
||||
|
||||
Theorem:
|
||||
|
||||
$$
|
||||
f_{mult}:\{0,1\}^{2n}\to \{0,1\}^{2n},f_{mult}(x_1,x_2)=x_1\cdot x_2
|
||||
$$
|
||||
|
||||
Idea: There are enough pairs of primes to make this difficult.
|
||||
|
||||
> Reminder: Weak on-way if easy to compute and $\exist p(n)$,
|
||||
> $P[\mathcal{A}\ \text{inverts=success}]<1-\frac{1}{p(n)}$
|
||||
> $P[\mathcal{A}\ \text{inverts=failure}]>\frac{1}{p(n)}$ high enough
|
||||
|
||||
### Prove one-way function (under assumptions)
|
||||
|
||||
To prove $f$ is on-way (under assumption)
|
||||
|
||||
1. Show $\exists p.p.t$ solves $f(x),\forall x$.
|
||||
2. Proof by contradiction.
|
||||
- For weak: Provide $p(n)$ that we know works.
|
||||
- Assume $\exists \mathcal{A}$ such that $P[\mathcal{A}\ \text{inverts}]>1-\frac{1}{p(n)}$
|
||||
- For strong: Provide $p(n)$ that we know works.
|
||||
- Assume $\exists \mathcal{A}$ such that $P[\mathcal{A}\ \text{inverts}]>\frac{1}{p(n)}$
|
||||
|
||||
Construct p.p.t $\mathcal{B}$
|
||||
which uses $\mathcal{A}$ to solve a problem, which contradicts assumption or known fact.
|
||||
|
||||
Back to Theorem:
|
||||
|
||||
We will show that $p(n)=8n^2$ works.
|
||||
|
||||
We claim $\forall \mathcal{A}$,
|
||||
|
||||
$$
|
||||
P[(x_1,x_2)\gets \{0,1\}^{2n};y=f_{mult}(x_1,x_2):f(\mathcal{A}(y))=y]<1-\frac{1}{8n^2}
|
||||
$$
|
||||
|
||||
For the sake of contradiction, suppose
|
||||
|
||||
$$
|
||||
\exists \mathcal{A} \textup{ such that} P[\mathcal{A}\ \text{inverts}]>1-\frac{1}{8n^2}
|
||||
$$
|
||||
|
||||
We will use this $\mathcal{A}$ to design p.p.t $B$ which can factor 2 random primes with non-negligible prob.
|
||||
|
||||
```python
|
||||
def A(y):
|
||||
# the adversary algorithm
|
||||
# expecting N to be product of random integer, don't need to be prime
|
||||
|
||||
def is_prime(x):
|
||||
# test if x is a prime
|
||||
|
||||
def gen(n):
|
||||
# generate number up to n bits
|
||||
|
||||
def B(y):
|
||||
# N is the input cipher
|
||||
x1,x2=gen(n),gen(n)
|
||||
p=x1*x2
|
||||
if is_prime(x1) and is_prime(x2):
|
||||
return A(p)
|
||||
return A(y)
|
||||
```
|
||||
|
||||
How often does $\mathcal{B}$ succeed/fail?
|
||||
|
||||
$\mathcal{B}$ fails to factor $N=p\dot q$, if:
|
||||
|
||||
- $x$ and $y$ are not both prime
|
||||
- $P_e=1-P(x\in \Pi_n)P(y\in \Pi_n)\leq 1-(\frac{1}{2n})^2=1-\frac{1}{4n^2}$
|
||||
- if $\mathcal{A}$ fails to factor
|
||||
- $P_f<\frac{1}{8n^2}$
|
||||
|
||||
So
|
||||
|
||||
$$
|
||||
P[\mathcal{B} \text{ fails}]\leq P[E\cup F]\leq P[E]+P[F]\leq (1-\frac{1}{4n^2}+\frac{1}{8n^2})=1-\frac{1}{8n^2}
|
||||
$$
|
||||
|
||||
So
|
||||
|
||||
$$
|
||||
P[\mathcal{B} \text{ succeed}]\geq \frac{1}{8n^2} (\text{non-negligible})
|
||||
$$
|
||||
|
||||
This contradicting factoring assumption. Therefore, our assumption that $\mathcal{A}$ exists was wrong.
|
||||
|
||||
Therefore $\forall \mathcal{A}$, $P[(x_1,x_2)\gets \{0,1\}^{2n};y=f_{mult}(x_1,x_2):f(\mathcal{A}(y))=y]<1-\frac{1}{8n^2}$ is wrong.
|
||||
114
content/CSE442T/CSE442T_L6.md
Normal file
114
content/CSE442T/CSE442T_L6.md
Normal file
@@ -0,0 +1,114 @@
|
||||
# Lecture 6
|
||||
|
||||
## Review
|
||||
|
||||
$$
|
||||
f_{mult}:\{0,1\}^{2n}\to \{0,1\}^{2n}
|
||||
$$
|
||||
|
||||
is a weak one-way.
|
||||
|
||||
$P[\mathcal{A}\ \text{invert}]\leq 1-\frac{1}{8n^2}$ over $x,y\in$ random integers $\{0,1\}^n$
|
||||
|
||||
## Chapter 2: Computational Hardness
|
||||
|
||||
### Converting weak one-way function to strong one-way function
|
||||
|
||||
By factoring assumptions, $\exists$ strong one-way function
|
||||
|
||||
$f:\{0,1\}^N\to \{0,1\}^N$ for infinitely many $N$.
|
||||
|
||||
$f=\left(f_{mult}(x_1,y_1),f_{mult}(x_2,y_2),\dots,f_{mult}(x_q,y_q)\right)$, $x_i,y_i\in \{0,1\}^n$.
|
||||
|
||||
$f:\{0,1\}^{8n^4}\to \{0,1\}^{8n^4}$
|
||||
|
||||
Idea: With high probability, at least one pair $(x_i,y_i)$ are both prime.
|
||||
|
||||
Factoring assumption: $\mathcal{A}$ has low chance of factoring $f_{mult}(x_i,y_i)$
|
||||
|
||||
Use $P[x \textup{ is prime}]\geq\frac{1}{2n}$
|
||||
|
||||
$$
|
||||
P[\forall p,q \in x_i,y_i, p\textup{ and } q \textup{ is not prime }]=P[p,q \in x_i,y_i, p\textup{ and } q \textup{ is not prime }]^q
|
||||
$$
|
||||
|
||||
$$
|
||||
P[\forall p,q \in x_i,y_i, p\textup{ and } q \textup{ is not prime }]\leq(1-\frac{1}{4n^2})^{4n^3}\leq (e^{-\frac{1}{4n^2}})^{4n^3}=e^{-n}
|
||||
$$
|
||||
|
||||
### Proof of strong one-way function
|
||||
|
||||
1. $f_{mult}$ is efficiently computable, and we compute it poly-many times.
|
||||
2. Suppose it's not hard to invert. Then
|
||||
$\exists \text{n.u.p.p.t.}\ \mathcal{A}$such that $P[w\gets \{0,1\}^{8n^4};z=f(w):f(\mathcal{A}(z))=0]=\mu (n)>\frac{1}{p(n)}$
|
||||
|
||||
We will use this to construct $\mathcal{B}$ that breaks factoring assumption.
|
||||
|
||||
$p\gets \Pi_n,q\gets \Pi_n,N=p\cdot q$
|
||||
|
||||
```psudocode
|
||||
function B:
|
||||
Receives N
|
||||
Sample (x,y) q times
|
||||
Compute z_i = f_mult(x_i,y_i) for each i
|
||||
From i=1 to q
|
||||
check if both x_i y_i are prime
|
||||
If yes,
|
||||
z_i = N
|
||||
break // replace first instance
|
||||
Let z = (z_1,z_2,...,z_q) // z_k = N hopefully
|
||||
((x_1,y_1),...,(x_k,y_k),...,(x_q,y_q)) <- a(z)
|
||||
if (x_k,y_k) was replaced
|
||||
return x_k,y_k
|
||||
else
|
||||
return null
|
||||
```
|
||||
|
||||
Let $E$ be the event that all pairs of sampled integers were not both prime.
|
||||
|
||||
Let $F$ be the event that $\mathcal{A}$ failed to invert
|
||||
|
||||
$P[\mathcal{B} \text{ fails}]\leq P[E\cup F]\leq P[E]+P[F]\leq e^{-n}+(1-\frac{1}{p(n)})=1-(\frac{1}{p(n)}-e^{-n})\leq 1-\frac{1}{2p(n)}$
|
||||
|
||||
$P[\mathcal{B} \text{ succeeds}]=P[p\gets \Pi_n,q\gets \Pi_n,N=p\cdot q:\mathcal{B}(N)\in \{p,q\}]\geq \frac{1}{2p(n)}$
|
||||
|
||||
Contradicting factoring assumption
|
||||
|
||||
We've defined one-way functions to hae domain $\{0,1\}^n$ for some $n$.
|
||||
|
||||
Our strong one-way function $f(n)$
|
||||
|
||||
- Takes $4n^3$ pairs of random integers
|
||||
- Multiplies all pairs
|
||||
- Hope at least pair are both prime $p,q$ b/c we know $N=p\cdot q$ is hard to factor
|
||||
|
||||
### General collection of strong one-way functions
|
||||
|
||||
$F=\{f_i:D_i\to R_i\},i\in I$, $I$ is the index set.
|
||||
|
||||
1. We can effectively choose $i\gets I$ using $Gen$.
|
||||
2. $\forall i$ we ca efficiently sample $x\gets D_i$.
|
||||
3. $\forall i\forall x\in D_i,f_i(x)$ is efficiently computable
|
||||
4. For any n.u.p.p.t $\mathcal{A}$, $\exists$ negligible function $\epsilon (n)$.
|
||||
$P[i\gets Gen(1^n);x\gets D_i;y=f_i(x):f(\mathcal{A}(y,i,1^n))=y]\leq \epsilon(n)$
|
||||
|
||||
#### An instance of strong one-way function under factoring assumption
|
||||
|
||||
$f_{mult,n}:(\Pi_n\times \Pi_n)\to \{0,1\}^{2n}$ is a collection of strong one way function.
|
||||
|
||||
Ideas of proof:
|
||||
|
||||
1. $n\gets Gen(1^n)$
|
||||
2. We can efficiently sample $p,q$ (with justifications)
|
||||
3. Factoring assumption
|
||||
|
||||
Algorithm for sampling a random prime $p\gets \Pi_n$
|
||||
|
||||
1. $x\gets \{0,1\}^n$ (n bit integer)
|
||||
2. Check if $x$ is prime.
|
||||
- Deterministic poly-time procedure
|
||||
- In practice, a much faster randomized procedure (Miller-Rabin) used
|
||||
|
||||
$P[x\cancel{\in} \text{prime}|\text{test said x prime}]<\epsilon(n)$
|
||||
|
||||
3. If not, repeat. Do this for polynomial number of times
|
||||
120
content/CSE442T/CSE442T_L7.md
Normal file
120
content/CSE442T/CSE442T_L7.md
Normal file
@@ -0,0 +1,120 @@
|
||||
# Lecture 7
|
||||
|
||||
## Chapter 2: Computational Hardness
|
||||
|
||||
### Letter choosing experiment
|
||||
|
||||
For 100 letter tiles,
|
||||
|
||||
$p_1,...,p_{27}$ (with one blank)
|
||||
|
||||
$(p_1)^2+\dots +(p_{27})^2\geq\frac{1}{27}$
|
||||
|
||||
For any $p_1,...,p_n$, $0\leq p_i\leq 1$.
|
||||
|
||||
$\sum p_i=1$
|
||||
|
||||
$P[\text{the same event twice in a row}]=p_1^2+p_2^2....+p_n^2$
|
||||
|
||||
By Cauchy-Schwarz: $|u\cdot v|^2 \leq ||u||\cdot ||v||^2$.
|
||||
|
||||
let $\vec{u}=(p_1,...,p_n)$, $\vec{v}=(1,..,1)$, so $(p_1^2+p_2^2....+p_n)^2\leq (p_1^2+p_2^2....+p_n^2)\cdot n$. So $p_1^2+p_2^2....+p_n^2\geq \frac{1}{n}$
|
||||
|
||||
So for an adversary $\mathcal{A}$, who random choose $x'$ and output $f(x')=f(x)$ if matched. $P[f(x)=f(x')]\geq\frac{1}{|Y|}$
|
||||
|
||||
So $P[x\gets f(x);y=f(x):\mathcal{A}(y,1^n)=y]\geq \frac{1}{|Y|}$
|
||||
|
||||
### Modular arithmetic
|
||||
|
||||
For $a,b\in \mathbb{Z}$, $N\in \mathbb{Z}^2$
|
||||
|
||||
$a\equiv b \mod N\iff N|(a-b)\iff \exists k\in \mathbb{Z}, a-b=kN,a=kN+b$
|
||||
|
||||
Ex: $N=23$, $-20\equiv 3\equiv 26\equiv 49\equiv 72\mod 23$.
|
||||
|
||||
#### Equivalent relations for any $N$ on $\mathbb{Z}$
|
||||
|
||||
$a\equiv a\mod N$
|
||||
|
||||
$a\equiv b\mod N\iff b\equiv a\mod N$
|
||||
|
||||
$a\equiv b\mod N$ and $b\equiv c\mod N\implies a\equiv c\mod N$
|
||||
|
||||
#### Division Theorem
|
||||
|
||||
For any $a\in \mathbb{Z}$, and $N\in\mathbb{Z}^+$, $\exists unique\ r,0\leq r<N$.
|
||||
|
||||
$\mathbb{Z}_N=\{0,1,2,...,N-1\}$ with modular arithmetic.
|
||||
|
||||
$a+b\mod N,a\cdot b\mod N$
|
||||
|
||||
Theorem: If $a\equiv b\mod N$ and$c\equiv d\mod N$, then $a\cdot c\equiv b\cdot d\mod N$.
|
||||
|
||||
Definition: $gcd(a,b)=d,a,b\in \mathbb{Z}^+$, is the maximum number such that $d|a$ and $d|b$.
|
||||
|
||||
Using normal factoring is slow... (Example: large $p,q,r$, $N=p\cdot q,,M=p\cdot r$)
|
||||
|
||||
##### Euclidean algorithm
|
||||
|
||||
Recursively relying on fact that $(a>b>0)$
|
||||
|
||||
$gcd(a,b)=gcd(b,a\mod b)$
|
||||
|
||||
```python
|
||||
def euclidean_algorithm(a,b):
|
||||
if a<b: return euclidean_algorithm(b,a)
|
||||
if b==0: return a
|
||||
return euclidean_algorithm(b,a%b)
|
||||
```
|
||||
|
||||
Proof:
|
||||
|
||||
We'll show $d|a$ and $d|b\iff d|b$ and $d|(a\mod b)$
|
||||
|
||||
$\impliedby$ $a=q\cdot b+r$, $r=a\mod b$
|
||||
|
||||
$\implies$ $d|r$, $r=a\mod b$
|
||||
|
||||
Runtime analysis:
|
||||
|
||||
Fact: $b_{i+2}<\frac{1}{2}b_i$
|
||||
|
||||
Proof:
|
||||
|
||||
Since $a_i=q_i\cdot b_i+b_{i+1}$, and $b_1=q_2\cdot b_2+b_3$, $b_2>b_3$, and $q_2$ in worst case is $1$, so $b_3<\frac{b_1}{2}$
|
||||
|
||||
$T(n)=2\Theta(\log b)=O(\log n)$ (linear in size of bits input)
|
||||
|
||||
##### Extended Euclidean algorithm
|
||||
|
||||
Our goal is to find $x,y$ such that $ax+by=gcd(a,b)$
|
||||
|
||||
Given $a\cdot x\equiv b\mod N$, we do euclidean algorithm to find $gcd(a,b)=d$, then reverse the steps to find $x,y$ such that $ax+by=d$
|
||||
|
||||
```python
|
||||
def extended_euclidean_algorithm(a,b):
|
||||
if a%b==0: return (0,1)
|
||||
x,y=extended_euclidean_algorithm(b,a%b)
|
||||
return (y,x-y*(a//b))
|
||||
```
|
||||
|
||||
Example: $a=12,b=43$, $gcd(12,43)=1$
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
43&=3\cdot 12+7\\
|
||||
12&=1\cdot 7+5\\
|
||||
7&=1\cdot 5+2\\
|
||||
5&=2\cdot 2+1\\
|
||||
2&=2\cdot 1+0\\
|
||||
1&=1\cdot 5-2\cdot 2\\
|
||||
1&=1\cdot 5-2\cdot (7-1\cdot 5)\\
|
||||
1&=3\cdot 5-2\cdot 7\\
|
||||
1&=3\cdot (12-1\cdot 7)-2\cdot 7\\
|
||||
1&=3\cdot 12-5\cdot 7\\
|
||||
1&=3\cdot 12-5\cdot (43-3\cdot 12)\\
|
||||
1&=-5\cdot 43+18\cdot 12\\
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
So $x=-5,y=18$
|
||||
74
content/CSE442T/CSE442T_L8.md
Normal file
74
content/CSE442T/CSE442T_L8.md
Normal file
@@ -0,0 +1,74 @@
|
||||
# Lecture 8
|
||||
|
||||
## Chapter 2: Computational Hardness
|
||||
|
||||
### Computational number theory/arithmetic
|
||||
|
||||
We want to have a easy-to-use one-way functions for cryptography.
|
||||
|
||||
How to find $a^x\mod N$ quickly. $a,x,N$ are positive integers. We want to reduce $[a\mod N]$
|
||||
|
||||
Example: $129^{39}\mod 41\equiv (129\mod 41)^{39}\mod 41=6^{39}\mod 41$
|
||||
|
||||
Find the binary representation of $x$. e.g. express as sums of powers of 2.
|
||||
|
||||
`x=39=bin(1,0,0,1,1,1)`
|
||||
|
||||
Repeatedly square $floor(\log_2(x))$ times.
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
6^{39}\mod 41&=6^{32+4+2+1}\mod 41\\
|
||||
&=(6^{32}\mod 41)(6^{4}\mod 41)(6^{2}\mod 41)(6^{1}\mod 41)\mod 41\\
|
||||
&=(-4)(25)(-5)(6)\mod 41\\
|
||||
&=7
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
The total multiplication steps is $floor(\log_2(x))$
|
||||
|
||||
_looks like fast exponentiation right?_
|
||||
|
||||
Goal: $f_{g,p}(x)=g^x\mod p$ is a one-way function, for certain choice of $p,g$ (and assumptions)
|
||||
|
||||
#### A group (Nice day one for MODERN ALGEBRA)
|
||||
|
||||
A group $G$ is a set with, a binary operation $\oplus$. and $\forall a,b\in G$, $a \oplus b\to c$
|
||||
|
||||
1. $a,b\in G,a\oplus b\in G$ (closure)
|
||||
2. $(a\oplus b)\oplus c=a\oplus(b\oplus c)$ (associativity)
|
||||
3. $\exists e$ such that $\forall a\in G, e\oplus g=g=g\oplus e$ (identity element)
|
||||
4. $\exists g^{-1}\in G$ such that $g\oplus g^{-1}=e$ (inverse element)
|
||||
|
||||
Example:
|
||||
|
||||
- $\mathbb{Z}_N=\{0,1,2,3,...,N-1\}$ with addition $\mod N$, with identity element $0$. $a\in \mathbb{Z}_N, a^{-1}=N-a$.
|
||||
- A even simpler group is $\Z$ with addition.
|
||||
- $\mathbb{Z}_N^*=\{x:x\in \mathbb{Z},1 \leq x\leq N: gcd(x,N)=1\}$ with multiplication $\mod N$ (we can do division here! yeah...).
|
||||
- If $N=p$ is prime, then $\mathbb{Z}_p^*=\{1,2,3,...,p-1\}$
|
||||
- If $N=24$, then $\mathbb{Z}_{24}^*=\{1,5,7,11,13,17,19,23\}$
|
||||
- Identity is $1$.
|
||||
- Let $a\in \mathbb{Z}_N^*$, by Euclidean algorithm, $gcd(a,N)=1$,$\exists x,y \in Z$ such that $ax+Ny=1,ax\equiv 1\mod N,x=a^{-1}$
|
||||
- $a,b\in \mathbb{Z}_N^*$. Want to show $gcd(ab,N)=1$. If $gcd(ab,N)=d>1$, then some prime $p|d$. so $p|(a,b)$, which means $p|a$ or $p|b$. In either case, $gcd(a,N)>d$ or $gcd(b,N)>d$, which contradicts that $a,b\in \mathbb{C}_N^*$
|
||||
|
||||
#### Euler's totient function
|
||||
|
||||
$\phi:\mathbb{Z}^+\to \mathbb{Z}^+,\phi(N)=|\mathbb{Z}_N^*|=|\{1\leq x\leq N:gcd(x,N)=1\}|$
|
||||
|
||||
Example: $\phi(1)=1$, $\phi(24)=8$, $\phi (p)=p-1$, $\phi(p\cdot q)=(p-1)(q-1)$
|
||||
|
||||
#### Euler's Theorem
|
||||
|
||||
For any $a\in \mathbb{Z}_N^*$, $a^{\phi(N)}\equiv 1\mod N$
|
||||
|
||||
Consequence: $a^x\mod N$, $x=K\cdot \phi(N)+r,0\leq r\leq \phi(N)$
|
||||
|
||||
$$
|
||||
a^x\equiv a^{K \cdot \phi (N) +r}\equiv ( a^{\phi(n)} )^K \cdot a^r \mod N$
|
||||
$$
|
||||
|
||||
So computing $a^x\mod N$ is polynomial in $\log (N)$ by reducing $a\mod N$ and $x\mod \phi(N)<N$
|
||||
|
||||
Corollary: Fermat's little theorem:
|
||||
|
||||
$1\leq a\leq p-1,a^{p-1}\equiv 1 \mod p$
|
||||
118
content/CSE442T/CSE442T_L9.md
Normal file
118
content/CSE442T/CSE442T_L9.md
Normal file
@@ -0,0 +1,118 @@
|
||||
# Lecture 9
|
||||
|
||||
## Chapter 2: Computational Hardness
|
||||
|
||||
### Continue on Cyclic groups
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
107^{662}\mod 51&=(107\mod 51)^{662}\mod 51\\
|
||||
&=5^{662}\mod 51
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Remind that $\phi(p),p\in\Pi,\phi(p)=p-1$.
|
||||
|
||||
$51=3\times 17,\phi(51)=\phi(3)\times \phi(17)=2\times 16=32$, So $5^{32}\mod 1$
|
||||
|
||||
$5^2\equiv 25\mod 51=25$
|
||||
$5^4\equiv (5^2)^2\equiv(25)^2 \mod 51\equiv 625\mod 51=13$
|
||||
$5^8\equiv (5^4)^2\equiv(13)^2 \mod 51\equiv 169\mod 51=16$
|
||||
$5^16\equiv (5^8)^2\equiv(16)^2 \mod 51\equiv 256\mod 51=1$
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
5^{662}\mod 51&=107^{662\mod 32}\mod 51\\
|
||||
&=5^{22}\mod 51\\
|
||||
&=5^{16}\cdot 5^4\cdot 5^2\mod 51\\
|
||||
&=19
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
For $a\in \mathbb{Z}_N^*$, the order of $a$, $o(a)$ is the smallest positive $k$ such that $a^k\equiv 1\mod N$. $o(a)\leq \phi(N),o(a)|\phi (N)$
|
||||
|
||||
In a general finite group
|
||||
|
||||
$g^{|G|}=e$ (identity)
|
||||
|
||||
$o(g)\vert |G|$
|
||||
|
||||
If a group $G=\{a,a^2,a^3,...,e\}$ $G$ is cyclic
|
||||
|
||||
In a cyclic group, if $o(a)=|G|$, then a is a generator of $G$.
|
||||
|
||||
Fact: $\mathbb{Z}^*_p$ is cyclic
|
||||
|
||||
$|\mathbb{Z}^*_p|=p-1$, so $\exists$ generator $g$, and $\mathbb{Z}$, $\phi(\mathbb{Z}_{13}^*)=12$
|
||||
|
||||
For example, $2$ is a generator for $\mathbb{Z}_{13}^*$ with $2,4,8,3,6,12,11,9,5,10,7,1$.
|
||||
|
||||
If $g$ is a generator, $f:\mathbb{Z}_p^*\to \mathbb{Z}_p^*$, $f(x)=g^x \mod p$ is onto.
|
||||
|
||||
What type of prime $p$?
|
||||
|
||||
- Large prime.
|
||||
- If $p-1$ is very factorable, that is very bad.
|
||||
- Pohlig-Hellman algorithm
|
||||
- $p=2^n+1$ only need polynomial time to invert
|
||||
- We want $p=2q+1$, where $q$ is prime. (Sophie Germain primes, or safe primes)
|
||||
|
||||
There are _probably_ infinitely many safe prime and efficient to sample as well.
|
||||
|
||||
If $p$ is safe, $g$ generator.
|
||||
|
||||
$$
|
||||
\mathbb{Z}_p^*=\{g,g^2,..,e\}
|
||||
$$
|
||||
|
||||
Then $\{g^2,...g^{2q}\}S_{g,p}\subseteq \mathbb{Z}_p^*$ is a subgroup; $g^{2k}\cdot g^{2l}=g^{2(k+l)}\in S_{g,p}$
|
||||
|
||||
It is cyclic with generator $g^2$.
|
||||
|
||||
It is easy to find a generator.
|
||||
|
||||
- Pick $a\in \mathbb{Z}_p^*$
|
||||
- Let $x=a^2$. If $x\neq 1$, it is a generator of subgroup $S_p$
|
||||
- $S_p=\{x,x^2,...,x^q\}\mod p$
|
||||
|
||||
Example: $p=2\cdot 11+1=23$
|
||||
|
||||
we have a subgroup with generator $4$ and $S_4=\{4,16,18,3,12,2,8,9,13,6,1\}$
|
||||
|
||||
```python
|
||||
def get_generator(p):
|
||||
"""
|
||||
p should be a prime, or you need to do factorization
|
||||
"""
|
||||
g=[]
|
||||
for i in range(2,p-1):
|
||||
k=i
|
||||
sg=[]
|
||||
step=p
|
||||
while k!=1 and step>0:
|
||||
if k==0:
|
||||
raise ValueError(f"Damn, {i} generates 0 for group {p}")
|
||||
sg.append(k)
|
||||
k=(k*i)%p
|
||||
step-=1
|
||||
sg.append(1)
|
||||
# if len(sg)!=(p-1): continue
|
||||
g.append((i,[j for j in sg]))
|
||||
return g
|
||||
```
|
||||
|
||||
### (Computational) Diffie-Hellman assumption
|
||||
|
||||
If $p$ is a randomly sampled safe prime.
|
||||
|
||||
Denote safe prime as $\tilde{\Pi}_n=\{p\in \Pi_n:q=\frac{p-1}{2}\in \Pi_{n-1}\}$
|
||||
|
||||
Then
|
||||
|
||||
$$
|
||||
P\left[p\gets \tilde{\Pi_n};a\gets\mathbb{Z}_p^*;g=a^2\neq 1;x\gets \mathbb{Z}_q;y=g^x\mod p:\mathcal{A}(y)=x\right]\leq \epsilon(n)
|
||||
$$
|
||||
|
||||
$p\gets \tilde{\Pi_n};a\gets\mathbb{Z}_p^*;g=a^2\neq 1$ is the function condition when we do the encryption on cyclic groups.
|
||||
|
||||
Notes: $f:\Z_q\to \mathbb{Z}_p^*$ is one-to-one, so $f(\mathcal{A}(y))\iff \mathcal{A}(y)=x$
|
||||
215
content/CSE442T/Exam_reviews/CSE442T_E1.md
Normal file
215
content/CSE442T/Exam_reviews/CSE442T_E1.md
Normal file
@@ -0,0 +1,215 @@
|
||||
# System check for exam list
|
||||
|
||||
**The exam will take place in class on Monday, October 21.**
|
||||
|
||||
The topics will cover Chapters 1 and 2, as well as the related probability discussions we've had (caveats below). Assignments 1 through 3 span this material.
|
||||
|
||||
## Specifics on material:
|
||||
|
||||
NOT "match-making game" in 1.2 (seems fun though)
|
||||
|
||||
NOT the proof of Theorem 31.3 (but definitely the result!)
|
||||
|
||||
NOT 2.4.3 (again, definitely want to know this result, and we have discussed the idea behind it)
|
||||
|
||||
NOT 2.6.5, 2.6.6
|
||||
|
||||
NOT 2.12, 2.13
|
||||
|
||||
The probability knowledge/techniques I've expanded on include conditional probability, independence, law of total probability, Bayes' Theorem, union bound, 1-p bound (or "useful bound"), collision
|
||||
|
||||
I expect you to demonstrate understanding of the key definitions, theorems, and proof techniques. The assignments are designed to reinforce all of these. However, exam questions will be written with the understanding of the time limitations.
|
||||
|
||||
The exam is "closed-book," with no notes of any kind allowed. The advantage of this is that some questions might be very basic. However, I will expect that you will have not just memorized definitions and theorems, but you can also explain their meaning and apply them.
|
||||
|
||||
## Chapter 1
|
||||
|
||||
### Prove security
|
||||
|
||||
#### Definition 11.1 Shannon secrecy
|
||||
|
||||
$(\mathcal{M},\mathcal{K}, Gen, Enc, Dec)$ (A crypto-system) is said to be private-key encryption scheme that is *Shannon-secrete with respect to distribution $D$ over the message space $\mathcal{M}$* if for all $m'\in \mathcal{M}$ and for all $c$,
|
||||
|
||||
$$
|
||||
P[k\gets Gen;m\gets D:m=m'|Enc_k(m)=c]=P[m\gets D:m=m']
|
||||
$$
|
||||
|
||||
(The adversary cannot learn all, part of, any letter of, any function off, or any partial information about the plaintext)
|
||||
|
||||
#### Definition 11.2 Perfect Secrecy
|
||||
|
||||
$(\mathcal{M},\mathcal{K}, Gen, ENc, Dec)$ (A crypto-system) is said to be private-key encryption scheme that is *perfectly secret* if forall $m_1,m_2\in \mathcal{M},\forall c$:
|
||||
|
||||
$$
|
||||
P[k\gets Gen:Enc_k(m_1)=c]=P[k\gets Gen:Enc_k(m_2)=c]
|
||||
$$
|
||||
|
||||
(For all coding scheme in the crypto system, for any two different message, they are equally likely to be mapped to $c$)
|
||||
|
||||
#### Definition 12.3
|
||||
|
||||
A private-key encryption scheme is perfectly secret if and only if it is Shannon secret.
|
||||
|
||||
## Chapter 2
|
||||
|
||||
### Efficient Private-key Encryption
|
||||
|
||||
#### Definition 24.7
|
||||
|
||||
A triplet of algorithms $(Gen,Enc,Dec)$ is called an efficient private-key encryption scheme if the following holds.
|
||||
|
||||
1. $k\gets Gen(1^n)$ is a p.p.t. such that for every $n\in \mathbb{N}$, it samples a key $k$.
|
||||
2. $c\gets Enc_k(m)$ is a p.p.t. that given $k$ and $m\in \{0,1\}^n$ produces a ciphertext $c$.
|
||||
3. $m\gets Dec_c(c)$ is a p.p.t. that given a ciphertext $c$ and key $k$ produces a message $m\in \{0,1\}^n\cup \perp$.
|
||||
4. For all $n\in \mathbb{N},m\in \{0,1\}^n$
|
||||
|
||||
$$
|
||||
Pr[k\gets Gen(1^n);Dec_k(Enc_k(m))=m]=1
|
||||
$$
|
||||
|
||||
### One-Way functions
|
||||
|
||||
#### Definition 26.1
|
||||
|
||||
A function $f:\{0,1\}^*\to\{0,1\}^*$ is worst-case one-way if the function is:
|
||||
|
||||
1. Easy to compute. There is a p.p.t $C$ that computes $f(x)$ on all inputs $x\in \{0,1\}^*$, and
|
||||
2. Hard to invert. There is no adversary $\mathcal{A}$ such that
|
||||
|
||||
$$
|
||||
\forall x,P[\mathcal{A}(f(x))\in f^{-1}(f(x))]=1
|
||||
$$
|
||||
|
||||
#### Definition 27.2 Negligible function
|
||||
|
||||
A function $\epsilon(n)$ is negligible if for every $c$. there exists some $n_0$ such that for all $n>n_0$, $\epsilon (n)\leq \frac{1}{n^c}$.
|
||||
|
||||
#### Definition 27.3 Strong One-Way Function
|
||||
|
||||
A function mapping strings to strings $f:\{0,1\}^*\to \{0,1\}^*$ is a strong one-way function if it satisfies the following two conditions:
|
||||
|
||||
1. Easy to compute. There is a p.p.t $C$ that computes $f(x)$ on all inputs $x\in \{0,1\}^*$, and
|
||||
2. Hard to invert. There is no adversary $\mathcal{A}$ such that
|
||||
|
||||
$$
|
||||
P[x\gets\{0,1\}^n;y\gets f(x):f(\mathcal{A}(1^n,y))=y]\leq \epsilon(n)
|
||||
$$
|
||||
|
||||
#### Definition 28.4 (Weak One-Way Function)
|
||||
|
||||
A function mapping strings to strings $f:\{0,1\}^*\to \{0,1\}^*$ is a strong one-way function if it satisfies the following two conditions:
|
||||
|
||||
1. Easy to compute. There is a p.p.t $C$ that computes $f(x)$ on all inputs $x\in \{0,1\}^*$, and
|
||||
2. Hard to invert. There is no adversary $\mathcal{A}$ such that
|
||||
|
||||
$$
|
||||
P[x\gets\{0,1\}^n;y\gets f(x):f(\mathcal{A}(1^n,y))=y]\leq 1-\frac{1}{q(n)}
|
||||
$$
|
||||
|
||||
#### Notation for prime numbers
|
||||
|
||||
Denote the (finite) set of primes that are smaller than $2^n$ as
|
||||
|
||||
$$
|
||||
\Pi_n=\{q|q<2^n\textup{ and } q \textup{ is prime}\}
|
||||
$$
|
||||
|
||||
#### Assumption 30.1 (Factoring)
|
||||
|
||||
For every adversary $\mathcal{A}$, there exists a negligible function $\epsilon$ such that
|
||||
|
||||
$$
|
||||
P[p\gets \Pi_n;q\gets \Pi_n;N\gets pq:\mathcal{A}(N)\in \{p,q\}]<\epsilon(n)
|
||||
$$
|
||||
|
||||
(For every product of random 2 primes, the probability for any adversary to find the prime factors is negligible.)
|
||||
|
||||
(There is no polynomial function that can decompose the product of two $n$ bit prime, the best function is $2^{O(n^{\frac{1}{3}}\log^{\frac{2}{3}}n)}$)
|
||||
|
||||
#### Theorem 35.1
|
||||
|
||||
For any weak one-way function $f:\{0,1\}^n\to \{0,1\}^*$, there exists a polynomial $m(\cdot)$ such that function
|
||||
|
||||
$$
|
||||
f'(x_1,x_2,\dots, x_{m(n)})=(f(x_1),f(x_2),\dots, f(x_{m(n)})).
|
||||
$$
|
||||
|
||||
from $f'=(\{0,1\}^n)^{m(n)}\to(\{0,1\}^*)^{m(n)}$ is strong one-way.
|
||||
|
||||
### RSA
|
||||
|
||||
#### Definition 46.7
|
||||
|
||||
A group $G$ is a set of elements with a binary operator $\oplus:G\times G\to G$ that satisfies the following properties
|
||||
|
||||
1. Closure: $\forall a,b\in G, a\oplus b\in G$
|
||||
2. Identity: $\exists i\in G$ such that $\forall a\in G, i\oplus a=a\oplus i=a$
|
||||
3. Associativity: $\forall a,b,c\in G,(a\oplus b)\oplus c=a\oplus(b\oplus c)$.
|
||||
4. Inverse: $\forall a\in G$, there is an element $b\in G$ such that $a\oplus b=b\oplus a=i$
|
||||
|
||||
#### Definition Euler totient function $\Phi(N)$.
|
||||
|
||||
$$
|
||||
\Phi(p)=p-1
|
||||
$$
|
||||
|
||||
if $p$ is prime
|
||||
|
||||
$$
|
||||
\Phi(N)=(p-1)(q-1)
|
||||
$$
|
||||
|
||||
if $N=pq$ and $p,q$ are primes
|
||||
|
||||
#### Theorem 47.10
|
||||
|
||||
$\forall a\in \mathbb{Z}_N^*,a^{\Phi(N)}=1\mod N$
|
||||
|
||||
#### Corollary 48.11
|
||||
|
||||
$\forall a\in \mathbb{Z}_p^*,a^{p-1}\equiv 1\mod p$.
|
||||
|
||||
#### Corollary 48.12
|
||||
|
||||
$a^x\mod N=a^{x\mod \Phi(N)}\mod N$
|
||||
|
||||
## Some other important results
|
||||
|
||||
### Exponent
|
||||
|
||||
$$
|
||||
(1-\frac{1}{n})^n\approx e
|
||||
$$
|
||||
when $n$ is large.
|
||||
|
||||
### Primes
|
||||
|
||||
Let $\pi(x)$ be the lower-bounds for prime less than or equal to $x$.
|
||||
|
||||
#### Theorem 31.3 Chebyshev
|
||||
|
||||
For $x>1$,$\pi(x)>\frac{x}{2\log x}$
|
||||
|
||||
#### Corollary 31.3
|
||||
|
||||
For $2^n>1$, $p(n)>\frac{1}{n}$
|
||||
|
||||
(The probability that a uniformly sampled n-bit integer is prime is greater than $\frac{1}{n}$)
|
||||
|
||||
### Modular Arithmetic
|
||||
|
||||
#### Extended Euclid Algorithm
|
||||
|
||||
```python
|
||||
def eea(a,b)->tuple(int):
|
||||
# assume a>b
|
||||
# return x,y such that ax+by=gcd(a,b)=d.
|
||||
# so y is the modular inverse of b mod a
|
||||
# so x is the modular inverse of a mod b
|
||||
# so gcd(a,b)=ax+by
|
||||
if a%b==0:
|
||||
return (0,1)
|
||||
x,y=eea(b,a%b)
|
||||
return (y,x-y(a//b))
|
||||
```
|
||||
|
||||
222
content/CSE442T/Exam_reviews/CSE442T_E2.md
Normal file
222
content/CSE442T/Exam_reviews/CSE442T_E2.md
Normal file
@@ -0,0 +1,222 @@
|
||||
# CSE442T Exam 2 Review
|
||||
|
||||
## Review
|
||||
|
||||
### Assumptions used in cryptography (this course)
|
||||
|
||||
#### Diffie-Hellman assumption
|
||||
|
||||
The Diffie-Hellman assumption is that the following problem is hard.
|
||||
|
||||
$$
|
||||
\text{Given } g,g^a,g^b\text{, it is hard to compute } g^{ab}.
|
||||
$$
|
||||
|
||||
More formally,
|
||||
|
||||
If $p$ is a randomly sampled safe prime.
|
||||
|
||||
Denote safe prime as $\tilde{\Pi}_n=\{p\in \Pi_n:q=\frac{p-1}{2}\in \Pi_{n-1}\}$
|
||||
|
||||
Then
|
||||
|
||||
$$
|
||||
P\left[p\gets \tilde{\Pi_n};a\gets\mathbb{Z}_p^*;g=a^2\neq 1;x\gets \mathbb{Z}_q;y=g^x\mod p:\mathcal{A}(y)=x\right]\leq \varepsilon(n)
|
||||
$$
|
||||
|
||||
$p\gets \tilde{\Pi_n};a\gets\mathbb{Z}_p^*;g=a^2\neq 1$ is the function condition when we do the encryption on cyclic groups.
|
||||
|
||||
#### Discrete logarithm assumption
|
||||
|
||||
> If Diffie-Hellman assumption holds, then discrete logarithm assumption holds.
|
||||
|
||||
This is a corollary of the Diffie-Hellman assumption, it states as follows.
|
||||
|
||||
This is collection of one-way functions
|
||||
|
||||
$$
|
||||
p\gets \tilde\Pi_n(\textup{ safe primes }), p=2q+1
|
||||
$$
|
||||
$$
|
||||
a\gets \mathbb{Z}*_{p};g=a^2(\textup{ make sure }g\neq 1)
|
||||
$$
|
||||
$$
|
||||
f_{g,p}(x)=g^x\mod p
|
||||
$$
|
||||
$$
|
||||
f:\mathbb{Z}_q\to \mathbb{Z}^*_p
|
||||
$$
|
||||
|
||||
#### RSA assumption
|
||||
|
||||
The RSA assumption is that it is hard to factorize a product of two large primes. (no polynomial time algorithm for factorization product of two large primes with $n$ bits)
|
||||
|
||||
Let $e$ be the exponents
|
||||
|
||||
$$
|
||||
P[p,q\gets \Pi_n;N\gets p\cdot q;e\gets \mathbb{Z}_{\phi(N)}^*;y\gets \mathbb{N}_n;x\gets \mathcal{A}(N,e,y);x^e=y\mod N]<\varepsilon(n)
|
||||
$$
|
||||
|
||||
#### Factoring assumption
|
||||
|
||||
> If RSA assumption holds, then factoring assumption holds.
|
||||
|
||||
The only way to efficiently factorize the product of prime is to iterate all the primes.
|
||||
|
||||
### Fancy product of these assumptions
|
||||
|
||||
#### Trapdoor permutation
|
||||
|
||||
> RSA assumption $\implies$ Trapdoor permutation exists.
|
||||
|
||||
Idea: $f:D\to R$ is a one-way permutation.
|
||||
|
||||
$y\gets R$.
|
||||
|
||||
* Finding $x$ such that $f(x)=y$ is hard.
|
||||
* With some secret info about $f$, finding $x$ is easy.
|
||||
|
||||
$\mathcal{F}=\{f_i:D_i\to R_i\}_{i\in I}$
|
||||
|
||||
1. $\forall i,f_i$ is a permutation
|
||||
2. $(i,t)\gets Gen(1^n)$ efficient. ($i\in I$ paired with $t$), $t$ is the "trapdoor info"
|
||||
3. $\forall i,D_i$ can be sampled efficiently.
|
||||
4. $\forall i,\forall x,f_i(x)$ can be computed in polynomial time.
|
||||
5. $P[(i,t)\gets Gen(1^n);y\gets R_i:f_i(\mathcal{A}(1^n,i,y))=y]<\varepsilon(n)$ (note: $\mathcal{A}$ is not given $t$)
|
||||
6. (trapdoor) There is a p.p.t. $B$ such that given $i,y,t$, B always finds x such that $f_i(x)=y$. $t$ is the "trapdoor info"
|
||||
|
||||
_There is one bit of trapdoor info that without it, finding $x$ is hard._
|
||||
|
||||
#### Collision resistance hash function
|
||||
|
||||
> If discrete logarithm assumption holds, then collision resistance hash function exists.
|
||||
|
||||
Let $h: \{0, 1\}^{n+1} \to \{0, 1\}^n$ be a CRHF.
|
||||
|
||||
Base on the discrete log assumption, we can construct a CRHF $H: \{0, 1\}^{n+1} \to \{0, 1\}^n$ as follows:
|
||||
|
||||
$Gen(1^n):(g,p,y)$
|
||||
|
||||
$p\in \tilde{\Pi}_n(p=2q+1)$
|
||||
|
||||
$g$ generator for group of sequence $\mod p$ (G_q)
|
||||
|
||||
$y$ is a random element in $G_q$
|
||||
|
||||
$h_{g,p,y}(x,b)=y^bg^x\mod p$, $y^bg^x\mod p \in \{0,1\}^n$
|
||||
|
||||
$g^x\mod p$ if $b=0$, $y\cdot g^x\mod p$ if $b=1$.
|
||||
|
||||
Under the discrete log assumption, $H$ is a CRHF.
|
||||
|
||||
- It is easy to sample $(g,p,y)$
|
||||
- It is easy to compute
|
||||
- Compressing by 1 bit
|
||||
|
||||
#### One-way permutation
|
||||
|
||||
> If trapdoor permutation exists, then one-way permutation exists.
|
||||
|
||||
A one-way permutation is a function that is one-way and returns a permutation of the input.
|
||||
|
||||
#### One-way function
|
||||
|
||||
> If one-way permutation exists, then one-way function exists.
|
||||
|
||||
One-way function is a class of functions that are easy to compute but hard to invert.
|
||||
|
||||
##### Weak one-way function
|
||||
|
||||
A weak one-way function is
|
||||
|
||||
$$
|
||||
f:\{0,1\}^n\to \{0,1\}^*
|
||||
$$
|
||||
|
||||
1. $\exists$ a P.P.T. that computes $f(x),\forall x\in\{0,1\}^n$
|
||||
2. $\forall a$ adversaries, $\exists \varepsilon(n),\forall n$.
|
||||
|
||||
$$
|
||||
P[x\gets \{0,1\}^n;y=f(x):f(a(y,1^n))=y]<1-\frac{1}{p(n)}
|
||||
$$
|
||||
_The probability of success should not be too close to 1_
|
||||
|
||||
|
||||
##### Strong one-way function
|
||||
|
||||
> If weak one-way function exists, then strong one-way function exists.
|
||||
|
||||
A strong one-way function is
|
||||
|
||||
$$
|
||||
f:\{0,1\}^n\to \{0,1\}^*(n\to \infty)
|
||||
$$
|
||||
|
||||
There is a negligible function $\varepsilon (n)$ such that for any adversary $a$ (n.u.p.p.t)
|
||||
|
||||
$$
|
||||
P[x\gets\{0,1\}^n;y=f(x):f(a(y))=y,a(y)=x']\leq\varepsilon(n)
|
||||
$$
|
||||
|
||||
_Probability of guessing correct message is negligible_
|
||||
|
||||
#### Hard-core bits
|
||||
|
||||
> Strong one-way function $\iff$ hard-core bits exists.
|
||||
|
||||
A hard-core bit is a bit that is hard to predict given the output of a one-way function.
|
||||
|
||||
#### Pseudorandom generator
|
||||
|
||||
> If one-way permutation exists, then pseudorandom generator exists.
|
||||
|
||||
We can also use pseudorandom generator to construct one-way function.
|
||||
|
||||
And hard-core bits can be used to construct pseudorandom generator.
|
||||
|
||||
#### Pseudorandom function
|
||||
|
||||
> If pseudorandom generator exists, then pseudorandom function exists.
|
||||
|
||||
A pseudorandom function is a function that is indistinguishable from a true random function.
|
||||
|
||||
### Multi-message secure private-key encryption
|
||||
|
||||
> If pseudorandom function exists, then multi-message secure private-key encryption exists.
|
||||
|
||||
A multi-message secure private-key encryption is a function that is secure against an adversary who can see multiple messages.
|
||||
|
||||
#### Single message secure private-key encryption
|
||||
|
||||
> If multi-message secure private-key encryption exists, then single message secure private-key encryption exists.
|
||||
|
||||
#### Message-authentication code
|
||||
|
||||
> If pseudorandom function exists, then message-authentication code exists.
|
||||
|
||||
|
||||
### Public-key encryption
|
||||
|
||||
> If Diffie-Hellman assumption holds, and Trapdoor permutation exists, then public-key encryption exists.
|
||||
|
||||
### Digital signature
|
||||
|
||||
A digital signature scheme is a triple $(Gen, Sign, Ver)$ where
|
||||
|
||||
- $(pk,sk)\gets Gen(1^k)$ is a p.p.t. algorithm that takes as input a security parameter $k$ and outputs a public key $pk$ and a secret key $sk$.
|
||||
- $\sigma\gets Sign_{sk}(m)$ is a p.p.t. algorithm that takes as input a secret key $sk$ and a message $m$ and outputs a signature $\sigma$.
|
||||
- $Ver_{pk}(m, \sigma)$ is a deterministic algorithm that takes as input a public key $pk$, a message $m$, and a signature $\sigma$ and outputs "Accept" if $\sigma$ is a valid signature for $m$ under $pk$ and "Reject" otherwise.
|
||||
|
||||
For all $n\in\mathbb{N}$, all $m\in\mathcal{M}_n$.
|
||||
|
||||
$$
|
||||
P[(pk,sk)\gets Gen(1^k); \sigma\gets Sign_{sk}(m); Ver_{pk}(m, \sigma)=\textup{``Accept''}]=1
|
||||
$$
|
||||
|
||||
#### One-time secure digital signature
|
||||
|
||||
#### Fixed-length one-time secure digital signature
|
||||
|
||||
> If one-way function exists, then fixed-length one-time secure digital signature exists.
|
||||
|
||||
|
||||
4
content/CSE442T/Exam_reviews/_meta.js
Normal file
4
content/CSE442T/Exam_reviews/_meta.js
Normal file
@@ -0,0 +1,4 @@
|
||||
export default {
|
||||
CSE442T_E1: "CSE442T Exam 1 Review",
|
||||
CSE442T_E2: "CSE442T Exam 2 Review"
|
||||
}
|
||||
31
content/CSE442T/_meta.js
Normal file
31
content/CSE442T/_meta.js
Normal file
@@ -0,0 +1,31 @@
|
||||
export default {
|
||||
//index: "Course Description",
|
||||
"---":{
|
||||
type: 'separator'
|
||||
},
|
||||
Exam_reviews: "Exam reviews",
|
||||
CSE442T_L1: "Introduction to Cryptography (Lecture 1)",
|
||||
CSE442T_L2: "Introduction to Cryptography (Lecture 2)",
|
||||
CSE442T_L3: "Introduction to Cryptography (Lecture 3)",
|
||||
CSE442T_L4: "Introduction to Cryptography (Lecture 4)",
|
||||
CSE442T_L5: "Introduction to Cryptography (Lecture 5)",
|
||||
CSE442T_L6: "Introduction to Cryptography (Lecture 6)",
|
||||
CSE442T_L7: "Introduction to Cryptography (Lecture 7)",
|
||||
CSE442T_L8: "Introduction to Cryptography (Lecture 8)",
|
||||
CSE442T_L9: "Introduction to Cryptography (Lecture 9)",
|
||||
CSE442T_L10: "Introduction to Cryptography (Lecture 10)",
|
||||
CSE442T_L11: "Introduction to Cryptography (Lecture 11)",
|
||||
CSE442T_L12: "Introduction to Cryptography (Lecture 12)",
|
||||
CSE442T_L13: "Introduction to Cryptography (Lecture 13)",
|
||||
CSE442T_L14: "Introduction to Cryptography (Lecture 14)",
|
||||
CSE442T_L15: "Introduction to Cryptography (Lecture 15)",
|
||||
CSE442T_L16: "Introduction to Cryptography (Lecture 16)",
|
||||
CSE442T_L17: "Introduction to Cryptography (Lecture 17)",
|
||||
CSE442T_L18: "Introduction to Cryptography (Lecture 18)",
|
||||
CSE442T_L19: "Introduction to Cryptography (Lecture 19)",
|
||||
CSE442T_L20: "Introduction to Cryptography (Lecture 20)",
|
||||
CSE442T_L21: "Introduction to Cryptography (Lecture 21)",
|
||||
CSE442T_L22: "Introduction to Cryptography (Lecture 22)",
|
||||
CSE442T_L23: "Introduction to Cryptography (Lecture 23)",
|
||||
CSE442T_L24: "Introduction to Cryptography (Lecture 24)"
|
||||
}
|
||||
55
content/CSE442T/index.md
Normal file
55
content/CSE442T/index.md
Normal file
@@ -0,0 +1,55 @@
|
||||
# CSE 442T
|
||||
|
||||
## Course Description
|
||||
|
||||
This course is an introduction to the theory of cryptography. Topics include:
|
||||
|
||||
One-way functions, Pseudorandomness, Private-key cryptography, Public-key cryptography, Authentication, and etc.
|
||||
|
||||
### Instructor:
|
||||
|
||||
[Brian Garnett](bcgarnett@wustl.edu)
|
||||
|
||||
Math Phd… Great!
|
||||
|
||||
Proof based course and write proofs.
|
||||
|
||||
CSE 433 for practical applications.
|
||||
|
||||
### Office Hours:
|
||||
|
||||
Right after class! 4-5 Mon, Urbaur Hall 227
|
||||
|
||||
### Textbook:
|
||||
|
||||
[A course in cryptography Lecture Notes](https://www.cs.cornell.edu/courses/cs4830/2010fa/lecnotes.pdf)
|
||||
|
||||
### Comments:
|
||||
|
||||
Most proofs are not hard to understand.
|
||||
|
||||
Many definitions to remember. They are long and tedious.
|
||||
|
||||
For example, I have to read the book to understand the definition of "hybrid argument". It was given as follows:
|
||||
|
||||
>Let $X^0_n,X^1_n,\dots,X^m_n$ are ensembles indexed from $1,..,m$
|
||||
> If $\mathcal{D}$ distinguishes $X_n^0$ and $X_n^m$ by $\mu(n)$, then $\exists i,1\leq i\leq m$ where $X_{n}^{i-1}$ and $X_n^i$ are distinguished by $\mathcal{D}$ by $\frac{\mu(n)}{m}$
|
||||
|
||||
I'm having a hard time to recover them without reading the book.
|
||||
|
||||
The lecturer's explanation is good but you'd better always pay attention in class or you'll having a hard time to catch up with the proof.
|
||||
|
||||
### Notations used in this course
|
||||
|
||||
The notations used in this course is very complicated. However, since we need to defined those concepts mathematically, we have to use those notations. Here are some notations I changed or emphasized for better readability at least for myself.
|
||||
|
||||
- I changed all the element in set to lowercase letters. I don't know why K is capitalized in the book.
|
||||
- I changed the message space notation $\mathcal{M}$ to $M$, and key space notation $\mathcal{K}$ to $K$ for better readability.
|
||||
- All the $\mathcal{A}$ denotes a algorithm. For example, $\mathcal{A}$ is the adversary algorithm, and $\mathcal{D}$ is the distinguisher algorithm.
|
||||
- As always, $[1,n]$ denotes the set of integers from 1 to n.
|
||||
- $P[A]$ denotes the probability of event $A$.
|
||||
- $\{0,1\}^n$ denotes the set of all binary strings of length $n$.
|
||||
- $1^n$ denotes the string of length $n$ with all bits being 1.
|
||||
- $0^n$ denotes the string of length $n$ with all bits being 0.
|
||||
- $;$ means and, $:$ means given that.
|
||||
- $\Pi_n$ denotes the set of all primes less than $2^n$.
|
||||
59
content/CSE559A/CSE559A_L1.md
Normal file
59
content/CSE559A/CSE559A_L1.md
Normal file
@@ -0,0 +1,59 @@
|
||||
# CSE559A Lecture 1
|
||||
|
||||
## Introducing the syllabus
|
||||
|
||||
See the syllabus on Canvas.
|
||||
|
||||
## Motivational introduction for computer vision
|
||||
|
||||
Computer vision is the study of manipulating images.
|
||||
|
||||
Automatic understanding of images and videos
|
||||
|
||||
1. vision for measurement (measurement, segmentation)
|
||||
2. vision for perception, interpretation (labeling)
|
||||
3. search and organization (retrieval, image or video archives)
|
||||
|
||||
### What is image
|
||||
|
||||
A 2d array of numbers.
|
||||
|
||||
### Vision is hard
|
||||
|
||||
connection to graphics.
|
||||
|
||||
computer vision need to generate the model from the image.
|
||||
|
||||
#### Are A and B the same color?
|
||||
|
||||
It depends on the context what you mean by "the same".
|
||||
|
||||
todo
|
||||
|
||||
#### Chair detector example.
|
||||
|
||||
double for loops.
|
||||
|
||||
#### Our visual system is not perfect.
|
||||
|
||||
Some optical illusion images.
|
||||
|
||||
todo, embed images here.
|
||||
|
||||
### Ridiculously brief history of computer vision
|
||||
|
||||
1960s: interpretation of synthetic worlds
|
||||
1970s: some progress on interpreting selected images
|
||||
1980s: ANNs come and go; shift toward geometry and increased mathematical rigor
|
||||
1990s: face recognition; statistical analysis in vogue
|
||||
2000s: becoming useful; significant use of machine learning; large annotated datasets available; video processing starts.
|
||||
2010s: Deep learning with ConvNets
|
||||
2020s: String synthesis; continued improvement across tasks, vision-language models.
|
||||
|
||||
## How computer vision is used now
|
||||
|
||||
### OCR, Optical Character Recognition
|
||||
|
||||
Technology to convert scanned docs to text.
|
||||
|
||||
|
||||
148
content/CSE559A/CSE559A_L10.md
Normal file
148
content/CSE559A/CSE559A_L10.md
Normal file
@@ -0,0 +1,148 @@
|
||||
# CSE559A Lecture 10
|
||||
|
||||
## Convolutional Neural Networks
|
||||
|
||||
### Convolutional Layer
|
||||
|
||||
Output feature map resolution depends on padding and stride
|
||||
|
||||
Padding: add zeros around the input image
|
||||
|
||||
Stride: the step of the convolution
|
||||
|
||||
Example:
|
||||
|
||||
1. Convolutional layer for 5x5 image with 3x3 kernel, padding 1, stride 1 (no skipping pixels)
|
||||
- Input: 5x5 image
|
||||
- Output: 3x3 feature map, (5-3+2*1)/1+1=5
|
||||
2. Convolutional layer for 5x5 image with 3x3 kernel, padding 1, stride 2 (skipping pixels)
|
||||
- Input: 5x5 image
|
||||
- Output: 2x2 feature map, (5-3+2*1)/2+1=2
|
||||
|
||||
_Learned weights can be thought of as local templates_
|
||||
|
||||
```python
|
||||
import torch
|
||||
import torch.nn as nn
|
||||
|
||||
# suppose input image is HxWx3 (assume RGB image)
|
||||
|
||||
conv_layer = nn.Conv2d(in_channels=3, # input channel, input is HxWx3
|
||||
out_channels=64, # output channel (number of filters), output is HxWx64
|
||||
kernel_size=3, # kernel size
|
||||
padding=1, # padding, this ensures that the output feature map has the same resolution as the input image, H_out=H_in, W_out=W_in
|
||||
stride=1) # stride
|
||||
```
|
||||
|
||||
Usually followed by a ReLU activation function
|
||||
|
||||
```python
|
||||
conv_layer = nn.Conv2d(in_channels=3, out_channels=64, kernel_size=3, padding=1, stride=1)
|
||||
relu = nn.ReLU()
|
||||
```
|
||||
|
||||
Suppose input image is $H\times W\times K$, the output feature map is $H\times W\times L$ with kernel size $F\times F$, this takes $F^2\times K\times L\times H\times W$ parameters
|
||||
|
||||
Each operation $D\times (K^2C)$ matrix with $(K^2C)\times N$ matrix, assume $D$ filters and $C$ output channels.
|
||||
|
||||
### Variants 1x1 convolutions, depthwise convolutions
|
||||
|
||||
#### 1x1 convolutions
|
||||
|
||||
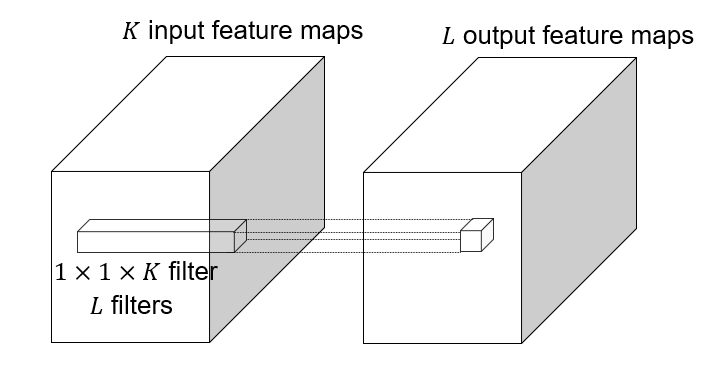
|
||||
|
||||
1x1 convolution: $F=1$, this layer do convolution in the pixel level, it is **pixel-wise** convolution for the feature.
|
||||
|
||||
Used to save computation, reduce the number of parameters.
|
||||
|
||||
Example: 3x3 conv layer with 256 channels at input and output.
|
||||
|
||||
Option 1: naive way:
|
||||
|
||||
```python
|
||||
conv_layer = nn.Conv2d(in_channels=256, out_channels=256, kernel_size=3, padding=1, stride=1)
|
||||
```
|
||||
|
||||
This takes $256\times 3 \times 3\times 256=524,288$ parameters.
|
||||
|
||||
Option 2: 1x1 convolution:
|
||||
|
||||
```python
|
||||
conv_layer = nn.Conv2d(in_channels=256, out_channels=64, kernel_size=1, padding=0, stride=1)
|
||||
conv_layer = nn.Conv2d(in_channels=64, out_channels=64, kernel_size=3, padding=1, stride=1)
|
||||
conv_layer = nn.Conv2d(in_channels=64, out_channels=256, kernel_size=1, padding=0, stride=1)
|
||||
```
|
||||
|
||||
This takes $256\times 1\times 1\times 64 + 64\times 3\times 3\times 64 + 64\times 1\times 1\times 256 = 16,384 + 36,864 + 16,384 = 69,632$ parameters.
|
||||
|
||||
This lose some information, but save a lot of parameters.
|
||||
|
||||
#### Depthwise convolutions
|
||||
|
||||
Depthwise convolution: $K\to K$ feature map, save computation, reduce the number of parameters.
|
||||
|
||||
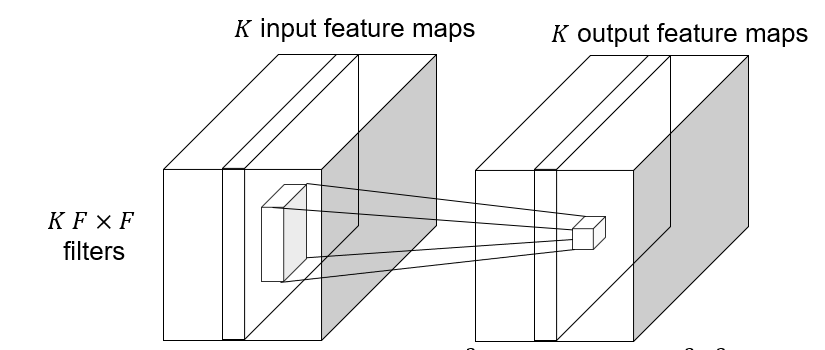
|
||||
|
||||
#### Grouped convolutions
|
||||
|
||||
Self defined convolution on the feature map following the similar manner.
|
||||
|
||||
### Backward pass
|
||||
|
||||
Vector-matrix form:
|
||||
|
||||
$$
|
||||
\frac{\partial e}{\partial x}=\frac{\partial e}{\partial z}\frac{\partial z}{\partial x}
|
||||
$$
|
||||
|
||||
Suppose the kernel is 3x3, the feature map is $\ldots, x_{i-1}, x_i, x_{i+1}, \ldots$, and $\ldots, z_{i-1}, z_i, z_{i+1}, \ldots$ is the output feature map, then:
|
||||
|
||||
The convolution operation can be written as:
|
||||
|
||||
$$
|
||||
z_i = w_1x_{i-1} + w_2x_i + w_3x_{i+1}
|
||||
$$
|
||||
|
||||
The gradient of the kernel is:
|
||||
|
||||
$$
|
||||
\frac{\partial e}{\partial x_i} = \sum_{j=-1}^{1}\frac{\partial e}{\partial z_i}\frac{\partial z_i}{\partial x_i} = \sum_{j=-1}^{1}\frac{\partial e}{\partial z_i}w_j
|
||||
$$
|
||||
|
||||
### Max-pooling
|
||||
|
||||
Get max value in the local region.
|
||||
|
||||
#### Receptive field
|
||||
|
||||
The receptive field of a unit is the region of the input feature map whose values contribute to the response of that unit (either in the previous layer or in the initial image)
|
||||
|
||||
## Architecture of CNNs
|
||||
|
||||
### AlexNet (2012-2013)
|
||||
|
||||
Successor of LeNet-5, but with a few significant changes
|
||||
|
||||
- Max pooling, ReLU nonlinearity
|
||||
- Dropout regularization
|
||||
- More data and bigger model (7 hidden layers, 650K units, 60M params)
|
||||
- GPU implementation (50x speedup over CPU)
|
||||
- Trained on two GPUs for a week
|
||||
|
||||
#### Key points
|
||||
|
||||
Most floating point operations occur in the convolutional layers.
|
||||
|
||||
Most of the memory usage is in the early convolutional layers.
|
||||
|
||||
Nearly all parameters are in the fully-connected layers.
|
||||
|
||||
### VGGNet (2014)
|
||||
|
||||
### GoogLeNet (2014)
|
||||
|
||||
### ResNet (2015)
|
||||
|
||||
### Beyond ResNet (2016 and onward): Wide ResNet, ResNeXT, DenseNet
|
||||
|
||||
|
||||
141
content/CSE559A/CSE559A_L11.md
Normal file
141
content/CSE559A/CSE559A_L11.md
Normal file
@@ -0,0 +1,141 @@
|
||||
# CSE559A Lecture 11
|
||||
|
||||
## Continue on Architecture of CNNs
|
||||
|
||||
### AlexNet (2012-2013)
|
||||
|
||||
Successor of LeNet-5, but with a few significant changes
|
||||
|
||||
- Max pooling, ReLU nonlinearity
|
||||
- Dropout regularization
|
||||
- More data and bigger model (7 hidden layers, 650K units, 60M params)
|
||||
- GPU implementation (50x speedup over CPU)
|
||||
- Trained on two GPUs for a week
|
||||
|
||||
#### Architecture for AlexNet
|
||||
|
||||
- Input: 224x224x3
|
||||
- 11x11 conv, stride 4, 96 filters
|
||||
- 3x3 max pooling, stride 2
|
||||
- 5x5 conv, 256 filters, padding 2
|
||||
- 3x3 max pooling, stride 2
|
||||
- 3x3 conv, 384 filters, padding 1
|
||||
- 3x3 conv, 384 filters, padding 1
|
||||
- 3x3 conv, 256 filters, padding 1
|
||||
- 3x3 max pooling, stride 2
|
||||
- 4096-unit FC, ReLU
|
||||
- 4096-unit FC, ReLU
|
||||
- 1000-unit FC, softmax
|
||||
|
||||
#### Key points for AlexNet
|
||||
|
||||
Most floating point operations occur in the convolutional layers.
|
||||
|
||||
Most of the memory usage is in the early convolutional layers.
|
||||
|
||||
Nearly all parameters are in the fully-connected layers.
|
||||
|
||||
#### Further refinement (ZFNet, 2013)
|
||||
|
||||
Best paper award at ILSVRC 2013.
|
||||
|
||||
Nicely visualizes the feature maps.
|
||||
|
||||
### VGGNet (2014)
|
||||
|
||||
All the cov layers are 3x3 filters with stride 1 and padding 1. Take advantage of pooling to reduce the spatial dimensionality.
|
||||
|
||||
#### Architecture for VGGNet
|
||||
|
||||
- Input: 224x224x3
|
||||
- 3x3 conv, 64 filters, padding 1
|
||||
- 3x3 conv, 64 filters, padding 1
|
||||
- 2x2 max pooling, stride 2
|
||||
- 3x3 conv, 128 filters, padding 1
|
||||
- 3x3 conv, 128 filters, padding 1
|
||||
- 2x2 max pooling, stride 2
|
||||
- 3x3 conv, 256 filters, padding 1
|
||||
- 3x3 conv, 256 filters, padding 1
|
||||
- 2x2 max pooling, stride 2
|
||||
- 3x3 conv, 512 filters, padding 1
|
||||
- 3x3 conv, 512 filters, padding 1
|
||||
- 3x3 conv, 512 filters, padding 1
|
||||
- 2x2 max pooling, stride 2
|
||||
- 3x3 conv, 512 filters, padding 1
|
||||
- 3x3 conv, 512 filters, padding 1
|
||||
- 3x3 conv, 512 filters, padding 1
|
||||
- 2x2 max pooling, stride 2
|
||||
- 4096-unit FC, ReLU
|
||||
- 4096-unit FC, ReLU
|
||||
- 1000-unit FC, softmax
|
||||
|
||||
#### Key points for VGGNet
|
||||
|
||||
- Sequence of deeper networks trained progressively
|
||||
- Large receptive fields replaced by successive layer of 3x3 convs with relu in between
|
||||
- 7x7 takes $49K^2$ parameters, 3x3 takes $27K^2$ parameters
|
||||
|
||||
#### Pretrained models
|
||||
|
||||
- Use pretrained-network as feature extractor (removing the last layer and training a new linear layer) (transfer learning)
|
||||
- Add RNN layers to generate captions
|
||||
- Fine-tune the model for the new task (finetuning)
|
||||
- Keep the earlier layers fixed and only train the new prediction layer
|
||||
|
||||
### GoogLeNet (2014)
|
||||
|
||||
Stem network at the start aggressively downsamples input.
|
||||
|
||||
#### Key points for GoogLeNet
|
||||
|
||||
- Parallel paths with different receptive field size and operations are means to capture space patterns of correlations in the stack of feature maps
|
||||
- Use 1x1 convs to reduce dimensionality
|
||||
- Use Global Average Pooling (GAP) to replace the fully connected layer
|
||||
- Auxiliary classifiers to improve training
|
||||
- Training using loss at the end of the network didn't work well: network is too deep, gradient don't provide useful model updates
|
||||
- As a hack, attach "auxiliary classifiers" at several intermediate points in the network that also try to classify the image and receive loss
|
||||
- _GooLeNet was before batch normalization, with batch normalization, the auxiliary classifiers were removed._
|
||||
|
||||
### ResNet (2015)
|
||||
|
||||
152 layers
|
||||
|
||||
[ResNet paper](https://arxiv.org/abs/1512.03385)
|
||||
|
||||
#### Key points for ResNet
|
||||
|
||||
- The residual module
|
||||
- Introduce `skip` or `shortcut` connections to avoid the degradation problem
|
||||
- Make it easy for network layers to represent the identity mapping
|
||||
- Directly performing 3×3 convolutions with 256 feature maps at input and output:
|
||||
- $256 \times 256 \times 3 \times 3 \approx 600K$ operations
|
||||
- Using 1×1 convolutions to reduce 256 to 64 feature maps, followed by 3×3 convolutions, followed by 1×1 convolutions to expand back to 256 maps:
|
||||
- $256 \times 64 \times 1 \times 1 \approx 16K$
|
||||
- $64 \times 64 \times 3 \times 3 \approx 36K$
|
||||
- $64 \times 256 \times 1 \times 1 \approx 16K$
|
||||
- Total $\approx 70K$
|
||||
|
||||
_Possibly the first model with top-5 error rate better than human performance._
|
||||
|
||||
### Beyond ResNet (2016 and onward): Wide ResNet, ResNeXT, DenseNet
|
||||
|
||||
#### Wide ResNet
|
||||
|
||||
Reduce number of residual blocks, but increase number of feature maps in each block
|
||||
|
||||
- More parallelizable, better feature reuse
|
||||
- 16-layer WRN outperforms 1000-layer ResNets, though with much larger # of parameters
|
||||
|
||||
#### ResNeXt
|
||||
|
||||
- Propose “cardinality” as a new factor in network design, apart from depth and width
|
||||
- Claim that increasing cardinality is a better way to increase capacity than increasing depth or width
|
||||
|
||||
#### DenseNet
|
||||
|
||||
- Use Dense block between conv layers
|
||||
- Less parameters than ResNet
|
||||
|
||||
Next class:
|
||||
|
||||
Transformer architectures
|
||||
159
content/CSE559A/CSE559A_L12.md
Normal file
159
content/CSE559A/CSE559A_L12.md
Normal file
@@ -0,0 +1,159 @@
|
||||
# CSE559A Lecture 12
|
||||
|
||||
## Transformer Architecture
|
||||
|
||||
### Outline
|
||||
|
||||
**Self-Attention Layers**: An important network module, which often has a global receptive field
|
||||
|
||||
**Sequential Input Tokens**: Breaking the restriction to 2d input arrays
|
||||
|
||||
**Positional Encodings**: Representing the metadata of each input token
|
||||
|
||||
**Exemplar Architecture**: The Vision Transformer (ViT)
|
||||
|
||||
**Moving Forward**: What does this new module enable? Who wins in the battle between transformers and CNNs?
|
||||
|
||||
### The big picture
|
||||
|
||||
CNNs
|
||||
|
||||
- Local receptive fields
|
||||
- Struggles with global content
|
||||
- Shape of intermediate layers is sometimes a pain
|
||||
|
||||
Things we might want:
|
||||
|
||||
- Use information from across the image
|
||||
- More flexible shape handling
|
||||
- Multiple modalities
|
||||
|
||||
Our Hero: MultiheadAttention
|
||||
|
||||
Use positional encodings to represent the metadata of each input token
|
||||
|
||||
## Self-Attention layers
|
||||
|
||||
### Comparing with ways to handling sequential data
|
||||
|
||||
#### RNN
|
||||
|
||||
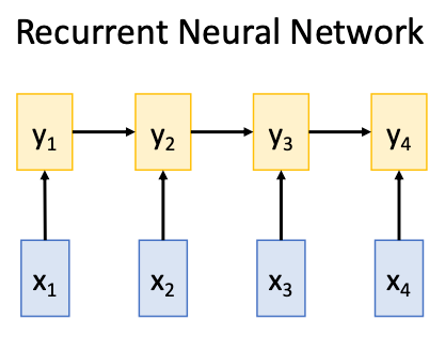
|
||||
|
||||
Works on **Ordered Sequences**
|
||||
|
||||
- Good at long sequences: After one RNN layer $h_r$ sees the whole sequence
|
||||
- Bad at parallelization: need to compute hidden states sequentially
|
||||
|
||||
#### 1D conv
|
||||
|
||||
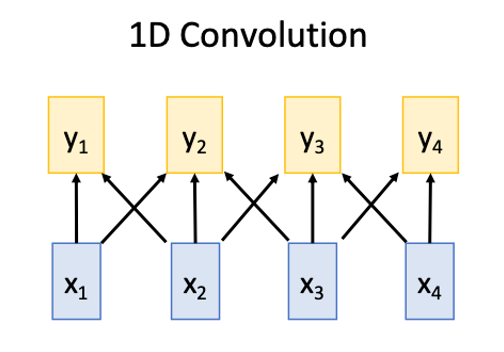
|
||||
|
||||
Works on **Multidimensional Grids**
|
||||
|
||||
- Bad at long sequences: Need to stack may conv layers or outputs to see the whole sequence
|
||||
- Good at parallelization: Each output can be computed in parallel
|
||||
|
||||
#### Self-Attention
|
||||
|
||||
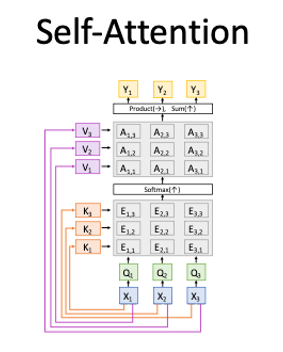
|
||||
|
||||
Works on **Set of Vectors**
|
||||
|
||||
- Good at Long sequences: Each output can attend to all inputs
|
||||
- Good at parallelization: Each output can be computed in parallel
|
||||
- Bad at saving memory: Need to store all inputs in memory
|
||||
|
||||
### Encoder-Decoder Architecture
|
||||
|
||||
The encoder is constructed by stacking multiple self-attention layers and feed-forward networks.
|
||||
|
||||
#### Word Embeddings
|
||||
|
||||
Translate tokens to vector space
|
||||
|
||||
```python
|
||||
class Embedder(nn.Module):
|
||||
def __init__(self, vocab_size, d_model):
|
||||
super().__init__()
|
||||
self.embed=nn.Embedding(vocab_size, d_model)
|
||||
|
||||
def forward(self, x):
|
||||
return self.embed(x)
|
||||
```
|
||||
|
||||
#### Positional Embeddings
|
||||
|
||||
The positional encodings are a way to represent the position of each token in the sequence.
|
||||
|
||||
Combined with the word embeddings, we get the input to the self-attention layer with information about the position of each token in the sequence.
|
||||
|
||||
> The reason why we just add the positional encodings to the word embeddings is _perhaps_ that we want the model to self-assign weights to the word-token and positional-token.
|
||||
|
||||
#### Query, Key, Value
|
||||
|
||||
The query, key, and value are the three components of the self-attention layer.
|
||||
|
||||
They are used to compute the attention weights.
|
||||
|
||||
```python
|
||||
class SelfAttention(nn.Module):
|
||||
def __init__(self, d_model, num_heads):
|
||||
super().__init__()
|
||||
self.d_model = d_model
|
||||
self.d_k = d_k
|
||||
self.q_linear = nn.Linear(d_model, d_k)
|
||||
self.k_linear = nn.Linear(d_model, d_k)
|
||||
self.v_linear = nn.Linear(d_model, d_k)
|
||||
self.dropout = nn.Dropout(dropout)
|
||||
self.out = nn.Linear(d_k, d_k)
|
||||
|
||||
def forward(self, q, k, v, mask=None):
|
||||
|
||||
bs = q.size(0)
|
||||
|
||||
k = self.k_linear(k)
|
||||
q = self.q_linear(q)
|
||||
v = self.v_linear(v)
|
||||
|
||||
# calculate attention weights
|
||||
outputs = attention(q, k, v, self.d_k, mask, self.dropout)
|
||||
|
||||
# apply output linear transformation
|
||||
outputs = self.out(outputs)
|
||||
|
||||
return outputs
|
||||
```
|
||||
|
||||
#### Attention
|
||||
|
||||
```python
|
||||
def attention(q, k, v, d_k, mask=None, dropout=None):
|
||||
scores = torch.matmul(q, k.transpose(-2, -1)) / math.sqrt(d_k)
|
||||
|
||||
if mask is not None:
|
||||
mask = mask.unsqueeze(1)
|
||||
scores = scores.masked_fill(mask == 0, -1e9)
|
||||
|
||||
scores = F.softmax(scores, dim=-1)
|
||||
|
||||
if dropout is not None:
|
||||
scores = dropout(scores)
|
||||
|
||||
outputs = torch.matmul(scores, v)
|
||||
|
||||
return outputs
|
||||
```
|
||||
|
||||
The query, key are used to compute the attention map, and the value is used to compute the attention output.
|
||||
|
||||
#### Multi-Head self-attention
|
||||
|
||||
The multi-head self-attention is a self-attention layer that has multiple heads.
|
||||
|
||||
Each head has its own query, key, and value.
|
||||
|
||||
### Computing Attention Efficiency
|
||||
|
||||
- the standard attention has a complexity of $O(n^2)$
|
||||
- We can use sparse attention to reduce the complexity to $O(n)$
|
||||
59
content/CSE559A/CSE559A_L13.md
Normal file
59
content/CSE559A/CSE559A_L13.md
Normal file
@@ -0,0 +1,59 @@
|
||||
# CSE559A Lecture 13
|
||||
|
||||
## Positional Encodings
|
||||
|
||||
### Fixed Positional Encodings
|
||||
|
||||
Set of sinusoids of different frequencies.
|
||||
|
||||
$$
|
||||
f(p,2i)=\sin(\frac{p}{10000^{2i/d}})\quad f(p,2i+1)=\cos(\frac{p}{10000^{2i/d}})
|
||||
$$
|
||||
|
||||
[source](https://kazemnejad.com/blog/transformer_architecture_positional_encoding/)
|
||||
|
||||
### Positional Encodings in Reconstruction
|
||||
|
||||
MLP is hard to learn high-frequency information from scaler input $(x,y)$.
|
||||
|
||||
Example: network mapping from $(x,y)$ to $(r,g,b)$.
|
||||
|
||||
### Generalized Positional Encodings
|
||||
|
||||
- Dependence on location, scaler, metadata, etc.
|
||||
- Can just be fully learned (use `nn.Embedding` and optimize based on a categorical input.)
|
||||
|
||||
## Vision Transformer (ViT)
|
||||
|
||||
### Class Token
|
||||
|
||||
In Vision Transformers, a special token called the class token is added to the input sequence to aggregate information for classification tasks.
|
||||
|
||||
### Hidden CNN Modules
|
||||
|
||||
- PxP convolution with stride P (split the image into patches and use positional encoding)
|
||||
|
||||
### ViT + ResNet Hybrid
|
||||
|
||||
Build a hybrid model that combines the vision transformer after 50 layer of ResNet.
|
||||
|
||||
## Moving Forward
|
||||
|
||||
At least for now, CNN and ViT architectures have similar performance at least in ImageNet.
|
||||
|
||||
- General Consensus: once the architecture is big enough, and not designed terribly, it can do well.
|
||||
- Differences remain:
|
||||
- Computational efficiency
|
||||
- Ease of use in other tasks and with other input data
|
||||
- Ease of training
|
||||
|
||||
## Wrap up
|
||||
|
||||
Self attention as a key building block
|
||||
|
||||
Flexible input specification using tokens with positional encodings
|
||||
|
||||
A wide variety of architectural styles
|
||||
|
||||
Up Next:
|
||||
Training deep neural networks
|
||||
73
content/CSE559A/CSE559A_L14.md
Normal file
73
content/CSE559A/CSE559A_L14.md
Normal file
@@ -0,0 +1,73 @@
|
||||
# CSE559A Lecture 14
|
||||
|
||||
## Object Detection
|
||||
|
||||
AP (Average Precision)
|
||||
|
||||
### Benchmarks
|
||||
|
||||
#### PASCAL VOC Challenge
|
||||
|
||||
20 Challenge classes.
|
||||
|
||||
CNN increases the accuracy of object detection.
|
||||
|
||||
#### COCO dataset
|
||||
|
||||
Common objects in context.
|
||||
|
||||
Semantic segmentation. Every pixel is classified to tags.
|
||||
|
||||
Instance segmentation. Every pixel is classified and grouped into instances.
|
||||
|
||||
### Object detection: outline
|
||||
|
||||
Proposal generation
|
||||
|
||||
Object recognition
|
||||
|
||||
#### R-CNN
|
||||
|
||||
Proposal generation
|
||||
|
||||
Use CNN to extract features from proposals.
|
||||
|
||||
with SVM to classify proposals.
|
||||
|
||||
Use selective search to generate proposals.
|
||||
|
||||
Use AlexNet finetuned on PASCAL VOC to extract features.
|
||||
|
||||
Pros:
|
||||
|
||||
- Much more accurate than previous approaches
|
||||
- Andy deep architecture can immediately be "plugged in"
|
||||
|
||||
Cons:
|
||||
|
||||
- Not a single end-to-end trainable system
|
||||
- Fine-tune network with softmax classifier (log loss)
|
||||
- Train post-hoc linear SVMs (hinge loss)
|
||||
- Train post-hoc bounding box regressors (least squares)
|
||||
- Training is slow 2000CNN passes for each image
|
||||
- Inference (detection) was slow
|
||||
|
||||
#### Fast R-CNN
|
||||
|
||||
Proposal generation
|
||||
|
||||
Use CNN to extract features from proposals.
|
||||
|
||||
##### ROI pooling and ROI alignment
|
||||
|
||||
ROI pooling:
|
||||
|
||||
- Pooling is applied to the feature map.
|
||||
- Pooling is applied to the proposal.
|
||||
|
||||
ROI alignment:
|
||||
|
||||
- Align the proposal to the feature map.
|
||||
- Align the proposal to the feature map.
|
||||
|
||||
Use bounding box regression to refine the proposal.
|
||||
131
content/CSE559A/CSE559A_L15.md
Normal file
131
content/CSE559A/CSE559A_L15.md
Normal file
@@ -0,0 +1,131 @@
|
||||
# CSE559A Lecture 15
|
||||
|
||||
## Continue on object detection
|
||||
|
||||
### Two strategies for object detection
|
||||
|
||||
#### R-CNN: Region proposals + CNN features
|
||||
|
||||
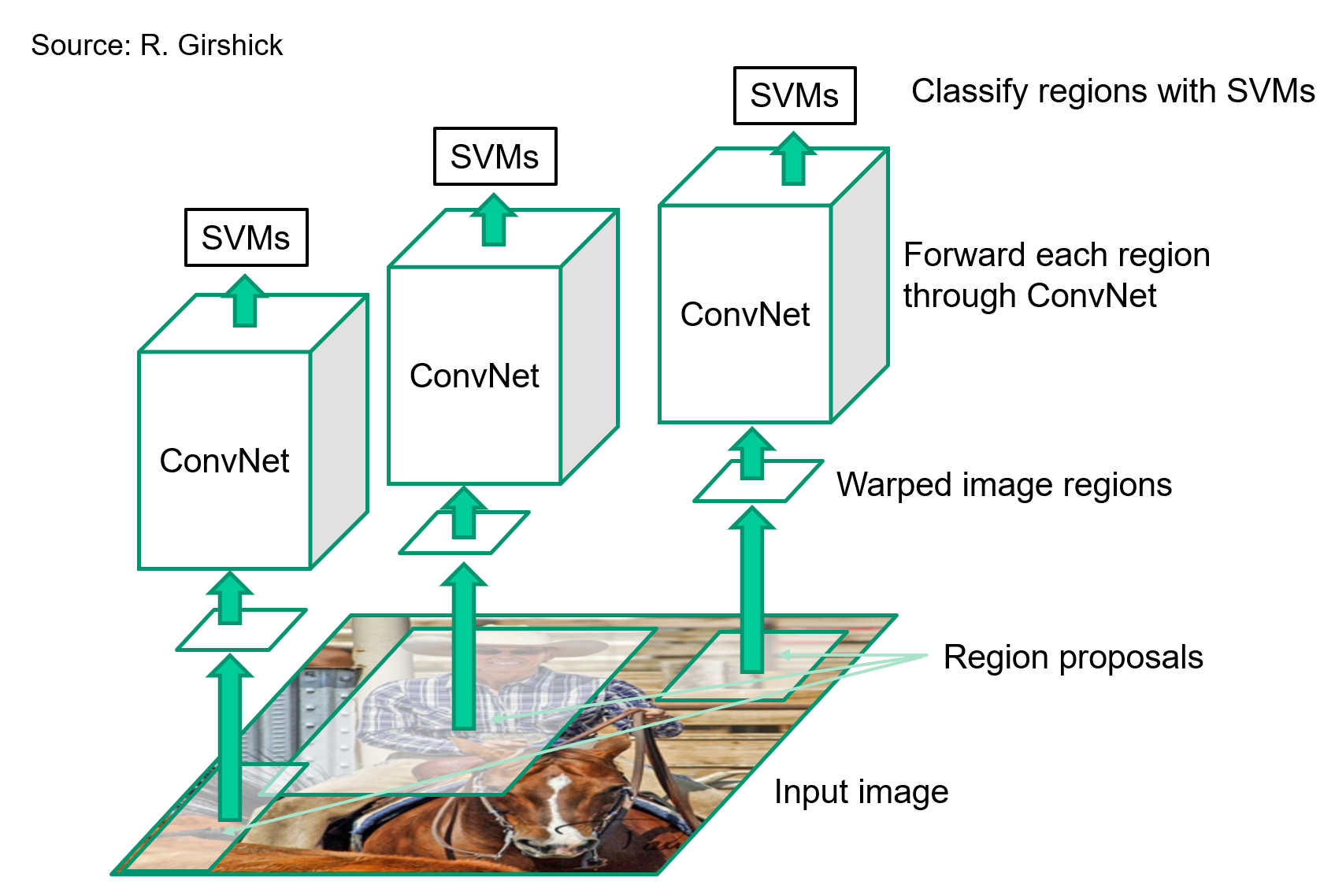
|
||||
|
||||
#### Fast R-CNN: CNN features + RoI pooling
|
||||
|
||||
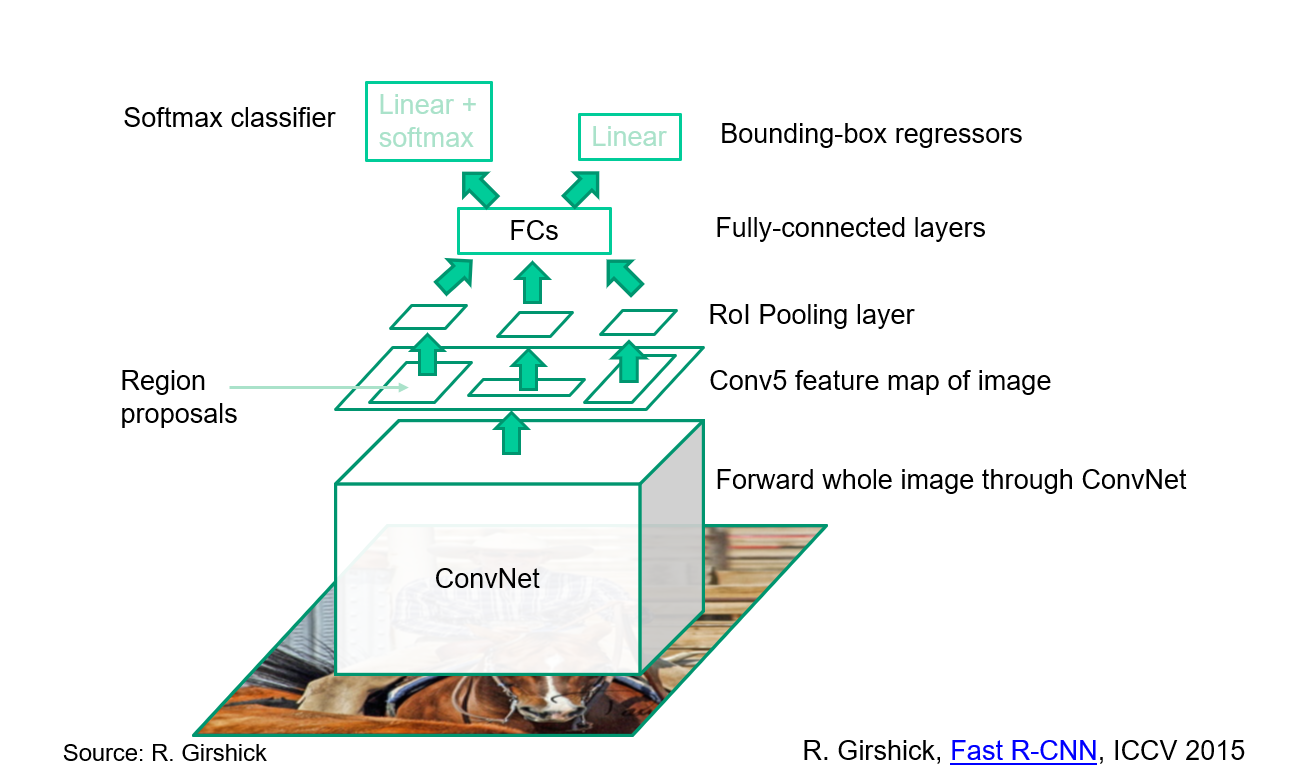
|
||||
|
||||
Use bilinear interpolation to get the features of the proposal.
|
||||
|
||||
#### Region of interest pooling
|
||||
|
||||
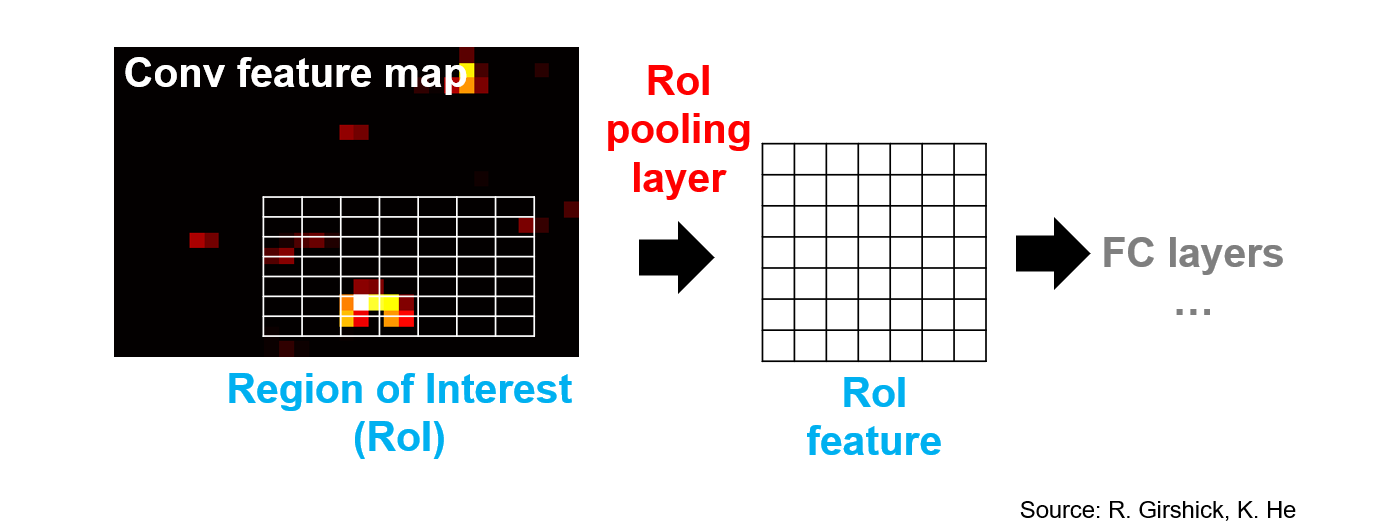
|
||||
|
||||
Use backpropagation to get the gradient of the proposal.
|
||||
|
||||
### New materials
|
||||
|
||||
#### Faster R-CNN
|
||||
|
||||
Use one CNN to generate region proposals. And use another CNN to classify the proposals.
|
||||
|
||||
##### Region proposal network
|
||||
|
||||
Idea: put an "anchor box" of fixed size over each position in the feature map and try to predict whether this box is likely to contain an object.
|
||||
|
||||
Introduce anchor boxes at multiple scales and aspect ratios to handle a wider range of object sizes and shapes.
|
||||
|
||||
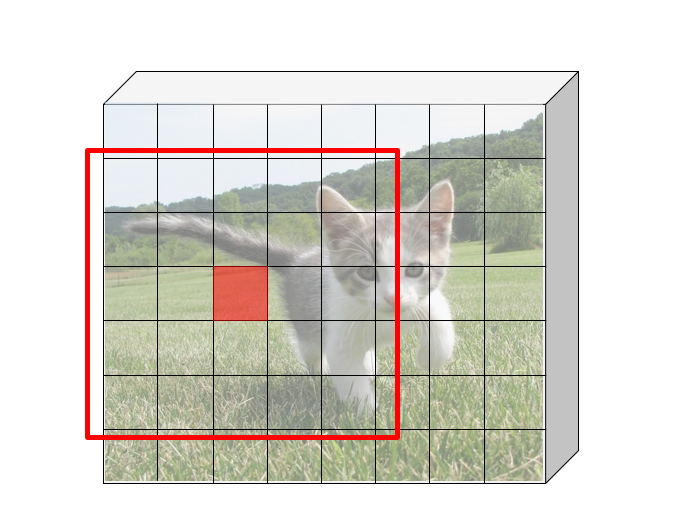
|
||||
|
||||
### Single-stage and multi-resolution detection
|
||||
|
||||
#### YOLO
|
||||
|
||||
You only look once (YOLO) is a state-of-the-art, real-time object detection system.
|
||||
|
||||
1. Take conv feature maps at 7x7 resolution
|
||||
2. Add two FC layers to predict, at each location, a score for each class and 2 bboxes with confidences
|
||||
|
||||
For PASCAL, output is 7×7×30 (30=20 + 2∗(4+1))
|
||||
|
||||
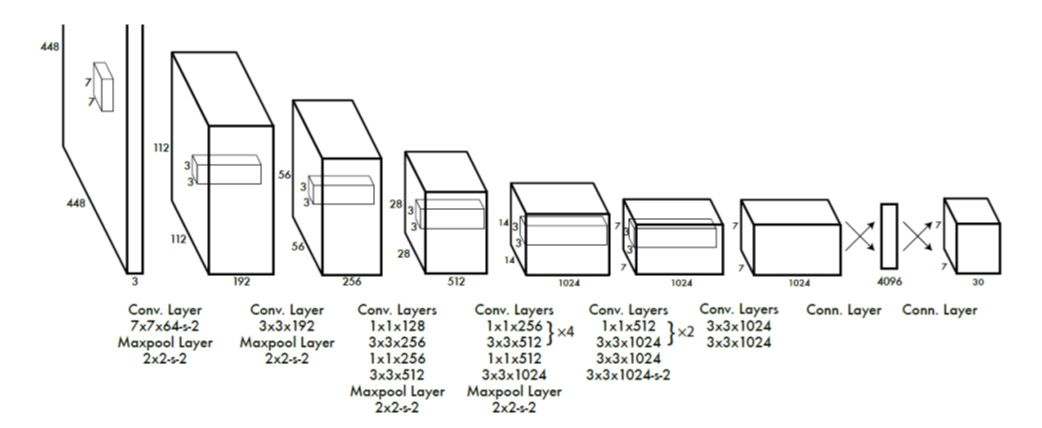
|
||||
|
||||
##### YOLO Network Head
|
||||
|
||||
```python
|
||||
model.add(Conv2D(1024, (3, 3), activation='lrelu', kernel_regularizer=l2(0.0005)))
|
||||
model.add(Conv2D(1024, (3, 3), activation='lrelu', kernel_regularizer=l2(0.0005)))
|
||||
# use flatten layer for global reasoning
|
||||
model.add(Flatten())
|
||||
model.add(Dense(512))
|
||||
model.add(Dense(1024))
|
||||
model.add(Dropout(0.5))
|
||||
model.add(Dense(7 * 7 * 30, activation='sigmoid'))
|
||||
model.add(YOLO_Reshape(target_shape=(7, 7, 30)))
|
||||
model.summary()
|
||||
```
|
||||
|
||||
#### YOLO results
|
||||
|
||||
1. Each grid cell predicts only two boxes and can only have one class – this limits the number of nearby objects that can be predicted
|
||||
2. Localization accuracy suffers compared to Fast(er) R-CNN due to coarser features, errors on small boxes
|
||||
3. 7x speedup over Faster R-CNN (45-155 FPS vs. 7-18 FPS)
|
||||
|
||||
#### YOLOv2
|
||||
|
||||
1. Remove FC layer, do convolutional prediction with anchor boxes instead
|
||||
2. Increase resolution of input images and conv feature maps
|
||||
3. Improve accuracy using batch normalization and other tricks
|
||||
|
||||
#### SSD
|
||||
|
||||
SSD is a multi-resolution object detection
|
||||
|
||||
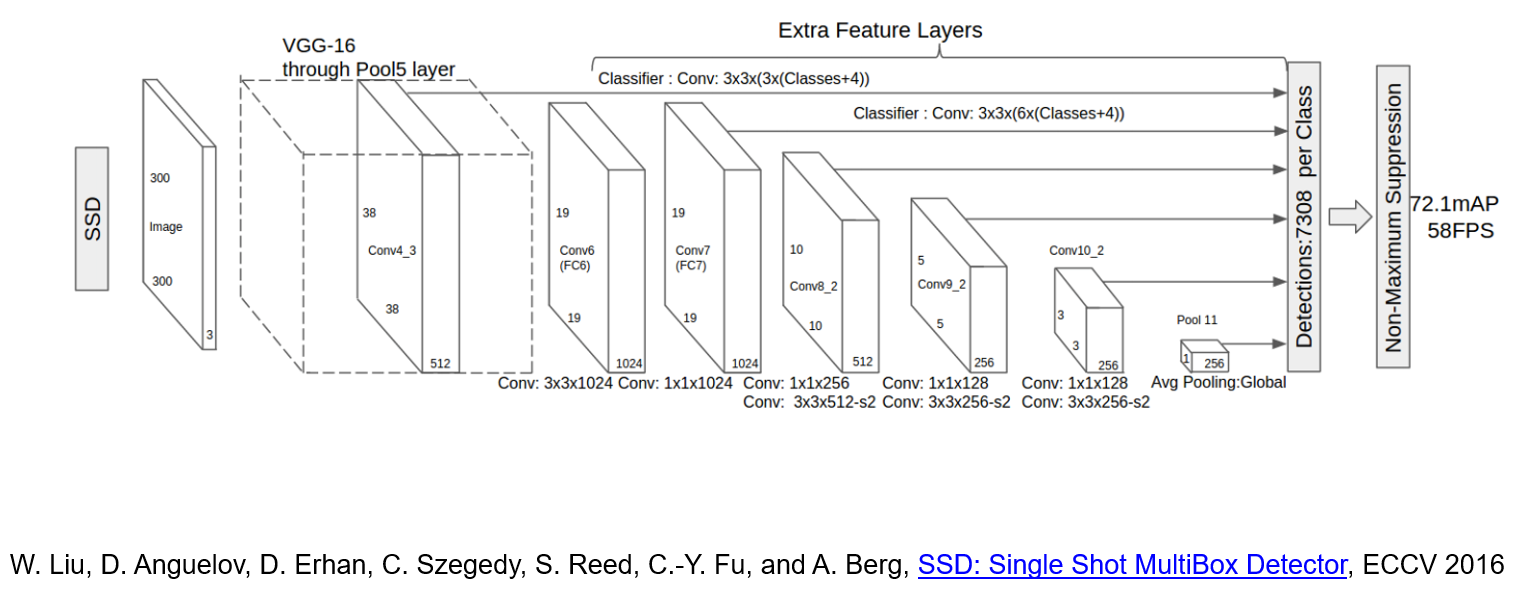
|
||||
|
||||
1. Predict boxes of different size from different conv maps
|
||||
2. Each level of resolution has its own predictor
|
||||
|
||||
##### Feature Pyramid Network
|
||||
|
||||
- Improve predictive power of lower-level feature maps by adding contextual information from higher-level feature maps
|
||||
- Predict different sizes of bounding boxes from different levels of the pyramid (but share parameters of predictors)
|
||||
|
||||
#### RetinaNet
|
||||
|
||||
RetinaNet combine feature pyramid network with focal loss to reduce the standard cross-entropy loss for well-classified examples.
|
||||
|
||||
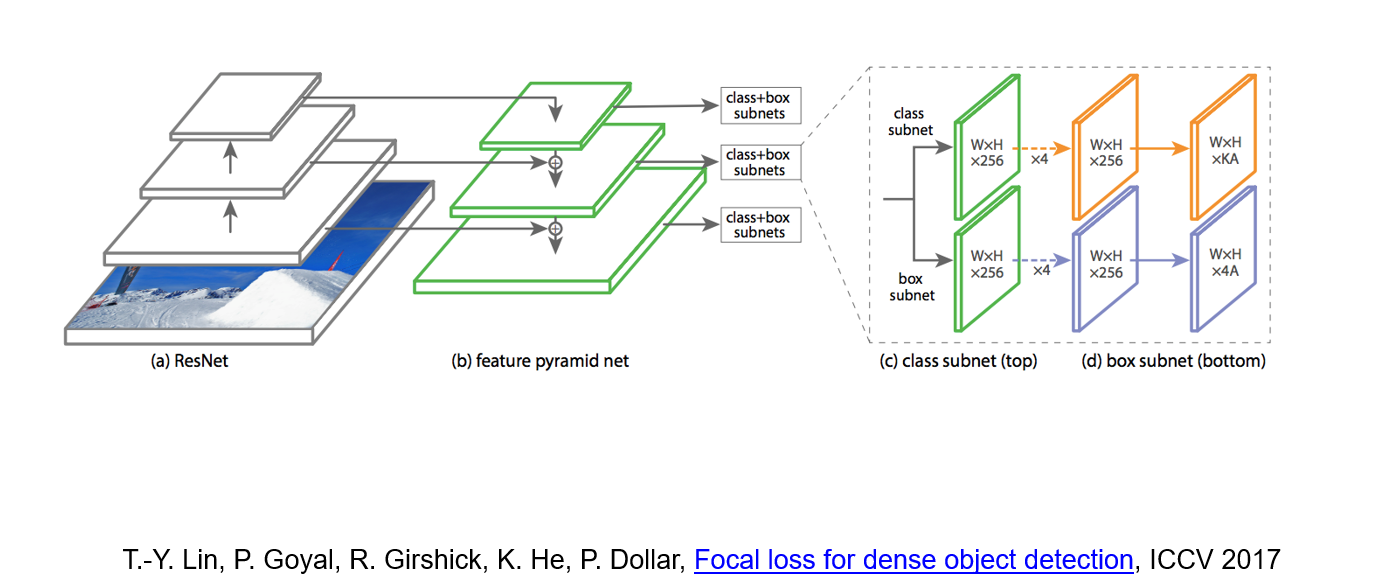
|
||||
|
||||
> Cross-entropy loss:
|
||||
> $$CE(p_t) = - \log(p_t)$$
|
||||
|
||||
The focal loss is defined as:
|
||||
|
||||
$$
|
||||
FL(p_t) = - (1 - p_t)^{\gamma} \log(p_t)
|
||||
$$
|
||||
|
||||
We can increase $\gamma$ to reduce the loss for well-classified examples.
|
||||
|
||||
#### YOLOv3
|
||||
|
||||
Minor refinements
|
||||
|
||||
### Alternative approaches
|
||||
|
||||
#### CornerNet
|
||||
|
||||
Use a pair of corners to represent the bounding box.
|
||||
|
||||
Use hourglass network to accumulate the information of the corners.
|
||||
|
||||
#### CenterNet
|
||||
|
||||
Use a center point to represent the bounding box.
|
||||
|
||||
#### Detection Transformer
|
||||
|
||||
Use transformer architecture to detect the object.
|
||||
|
||||
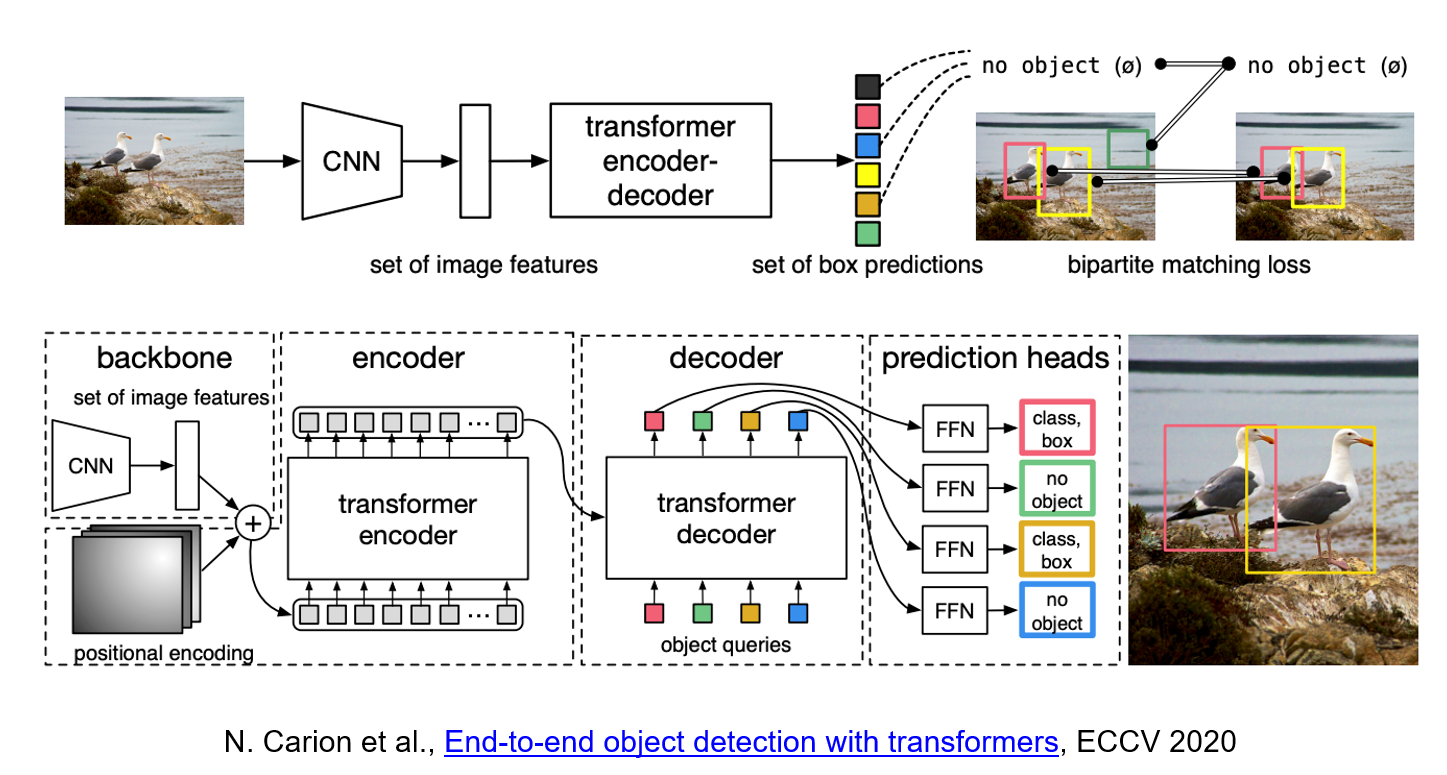
|
||||
|
||||
DETR uses a conventional CNN backbone to learn a 2D representation of an input image. The model flattens it and supplements it with a positional encoding before passing it into a transformer encoder. A transformer decoder then takes as input a small fixed number of learned positional embeddings, which we call object queries, and additionally attends to the encoder output. We pass each output embedding of the decoder to a shared feed forward network (FFN) that predicts either a detection (class and bounding box) or a "no object" class.
|
||||
|
||||
114
content/CSE559A/CSE559A_L16.md
Normal file
114
content/CSE559A/CSE559A_L16.md
Normal file
@@ -0,0 +1,114 @@
|
||||
# CSE559A Lecture 16
|
||||
|
||||
## Dense image labelling
|
||||
|
||||
### Semantic segmentation
|
||||
|
||||
Use one-hot encoding to represent the class of each pixel.
|
||||
|
||||
### General Network design
|
||||
|
||||
Design a network with only convolutional layers, make predictions for all pixels at once.
|
||||
|
||||
Can the network operate at full image resolution?
|
||||
|
||||
Practical solution: first downsample, then upsample
|
||||
|
||||
### Outline
|
||||
|
||||
- Upgrading a Classification Network to Segmentation
|
||||
- Operations for dense prediction
|
||||
- Transposed convolutions, unpooling
|
||||
- Architectures for dense prediction
|
||||
- DeconvNet, U-Net, "U-Net"
|
||||
- Instance segmentation
|
||||
- Mask R-CNN
|
||||
- Other dense prediction problems
|
||||
|
||||
### Fully Convolutional Networks
|
||||
|
||||
"upgrading" a classification network to a dense prediction network
|
||||
|
||||
1. Covert "fully connected" layers to 1x1 convolutions
|
||||
2. Make the input image larger
|
||||
3. Upsample the output
|
||||
|
||||
Start with an existing classification CNN ("an encoder")
|
||||
|
||||
Then use bilinear interpolation and transposed convolutions to make full resolution.
|
||||
|
||||
### Operations for dense prediction
|
||||
|
||||
#### Transposed Convolutions
|
||||
|
||||
Use the filter to "paint" in the output: place copies of the filter on the output, multiply by corresponding value in the input, sum where copies of the filter overlap
|
||||
|
||||
We can increase the resolution of the output by using a larger stride in the convolution.
|
||||
|
||||
- For stride 2, dilate the input by inserting rows and columns of zeros between adjacent entries, convolve with flipped filter
|
||||
- Sometimes called convolution with fractional input stride 1/2
|
||||
|
||||
#### Unpooling
|
||||
|
||||
Max unpooling:
|
||||
|
||||
- Copy the maximum value in the input region to all locations in the output
|
||||
- Use the location of the maximum value to know where to put the value in the output
|
||||
|
||||
Nearest neighbor unpooling:
|
||||
|
||||
- Copy the maximum value in the input region to all locations in the output
|
||||
- Use the location of the maximum value to know where to put the value in the output
|
||||
|
||||
### Architectures for dense prediction
|
||||
|
||||
#### DeconvNet
|
||||
|
||||
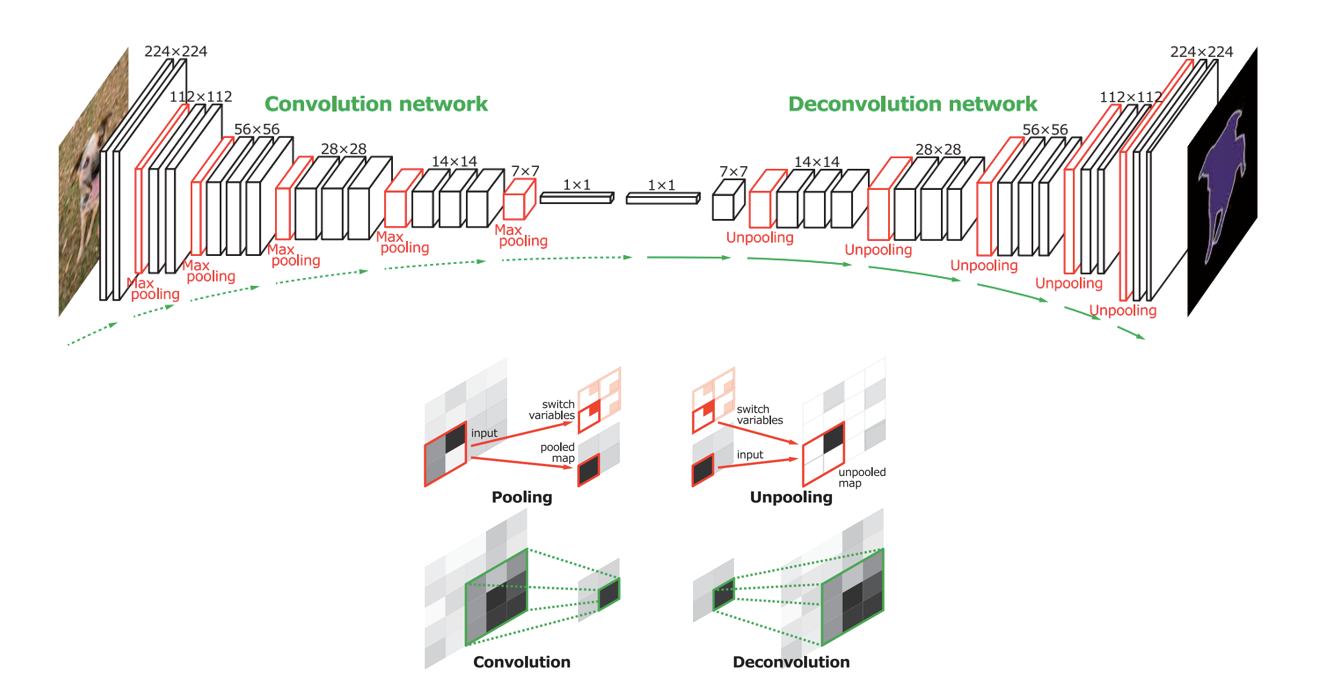
|
||||
|
||||
_How the information about location is encoded in the network?_
|
||||
|
||||
#### U-Net
|
||||
|
||||
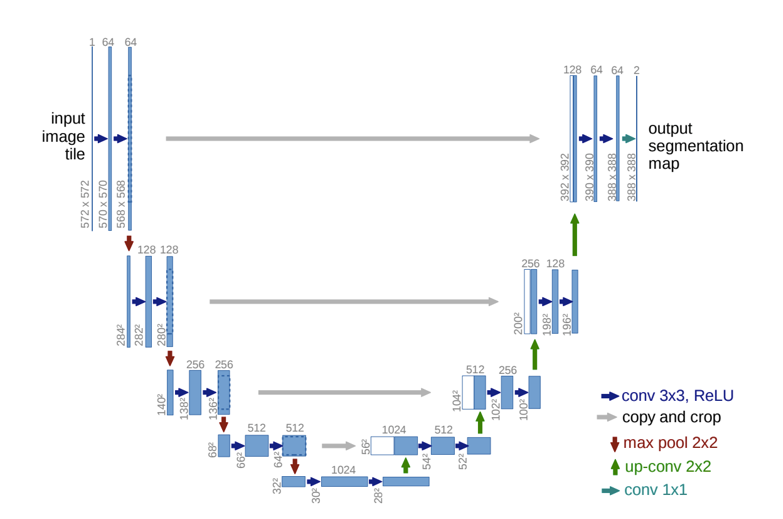
|
||||
|
||||
- Like FCN, fuse upsampled higher-level feature maps with higher-res, lower-level feature maps (like residual connections)
|
||||
- Unlike FCN, fuse by concatenation, predict at the end
|
||||
|
||||
#### Extended U-Net Architecture
|
||||
|
||||
Many variants of U-Net would replace the "encoder" of the U-Net with other architectures.
|
||||
|
||||
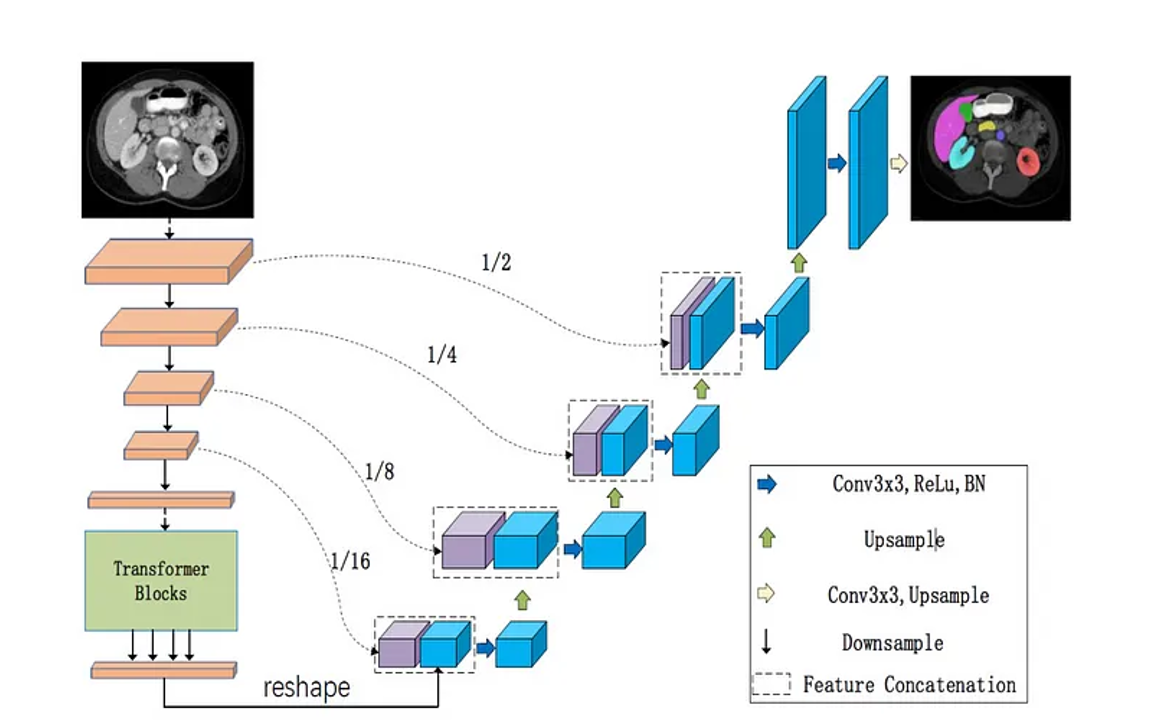
|
||||
|
||||
##### Encoder/Decoder v.s. U-Net
|
||||
|
||||
|
||||
|
||||
### Instance Segmentation
|
||||
|
||||
#### Mask R-CNN
|
||||
|
||||
Mask R-CNN = Faster R-CNN + FCN on Region of Interest
|
||||
|
||||
### Extend to keypoint prediction?
|
||||
|
||||
- Use a similar architecture to Mask R-CNN
|
||||
|
||||
_Continue on Tuesday_
|
||||
|
||||
### Other tasks
|
||||
|
||||
#### Panoptic feature pyramid network
|
||||
|
||||
|
||||
|
||||
#### Depth and normal estimation
|
||||
|
||||
|
||||
|
||||
D. Eigen and R. Fergus, Predicting Depth, Surface Normals and Semantic Labels with a Common Multi-Scale Convolutional Architecture, ICCV 2015
|
||||
|
||||
#### Colorization
|
||||
|
||||
R. Zhang, P. Isola, and A. Efros, Colorful Image Colorization, ECCV 2016
|
||||
184
content/CSE559A/CSE559A_L17.md
Normal file
184
content/CSE559A/CSE559A_L17.md
Normal file
@@ -0,0 +1,184 @@
|
||||
# CSE559A Lecture 17
|
||||
|
||||
## Local Features
|
||||
|
||||
### Types of local features
|
||||
|
||||
#### Edge
|
||||
|
||||
Goal: Identify sudden changes in image intensity
|
||||
|
||||
Generate edge map as human artists.
|
||||
|
||||
An edge is a place of rapid change in the image intensity function.
|
||||
|
||||
Take the absolute value of the first derivative of the image intensity function.
|
||||
|
||||
For 2d functions, $\frac{\partial f}{\partial x}=\lim_{\Delta x\to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}$
|
||||
|
||||
For discrete images data, $\frac{\partial f}{\partial x}\approx \frac{f(x+1)-f(x)}{1}$
|
||||
|
||||
Run convolution with kernel $[1,0,-1]$ to get the first derivative in the x direction, without shifting. (generic kernel is $[1,-1]$)
|
||||
|
||||
Prewitt operator:
|
||||
|
||||
$$
|
||||
M_x=\begin{bmatrix}
|
||||
1 & 0 & -1 \\
|
||||
1 & 0 & -1 \\
|
||||
1 & 0 & -1 \\
|
||||
\end{bmatrix}
|
||||
\quad
|
||||
M_y=\begin{bmatrix}
|
||||
1 & 1 & 1 \\
|
||||
0 & 0 & 0 \\
|
||||
-1 & -1 & -1 \\
|
||||
\end{bmatrix}
|
||||
$$
|
||||
Sobel operator:
|
||||
|
||||
$$
|
||||
M_x=\begin{bmatrix}
|
||||
1 & 0 & -1 \\
|
||||
2 & 0 & -2 \\
|
||||
1 & 0 & -1 \\
|
||||
\end{bmatrix}
|
||||
\quad
|
||||
M_y=\begin{bmatrix}
|
||||
1 & 2 & 1 \\
|
||||
0 & 0 & 0 \\
|
||||
-1 & -2 & -1 \\
|
||||
\end{bmatrix}
|
||||
$$
|
||||
Roberts operator:
|
||||
|
||||
$$
|
||||
M_x=\begin{bmatrix}
|
||||
1 & 0 \\
|
||||
0 & -1 \\
|
||||
\end{bmatrix}
|
||||
\quad
|
||||
M_y=\begin{bmatrix}
|
||||
0 & 1 \\
|
||||
-1 & 0 \\
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
Image gradient:
|
||||
|
||||
$$
|
||||
\nabla f = \left(\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}\right)
|
||||
$$
|
||||
|
||||
Gradient magnitude:
|
||||
|
||||
$$
|
||||
||\nabla f|| = \sqrt{\left(\frac{\partial f}{\partial x}\right)^2 + \left(\frac{\partial f}{\partial y}\right)^2}
|
||||
$$
|
||||
|
||||
Gradient direction:
|
||||
|
||||
$$
|
||||
\theta = \tan^{-1}\left(\frac{\frac{\partial f}{\partial y}}{\frac{\partial f}{\partial x}}\right)
|
||||
$$
|
||||
|
||||
The gradient points in the direction of the most rapid increase in intensity.
|
||||
|
||||
> Application: Gradient-domain image editing
|
||||
>
|
||||
> Goal: solve for pixel values in the target region to match gradients of the source region while keeping the rest of the image unchanged.
|
||||
>
|
||||
> [Poisson Image Editing](http://www.cs.virginia.edu/~connelly/class/2014/comp_photo/proj2/poisson.pdf)
|
||||
|
||||
Noisy edge detection:
|
||||
|
||||
When the intensity function is very noisy, we can use a Gaussian smoothing filter to reduce the noise before taking the gradient.
|
||||
|
||||
Suppose pixels of the true image $f_{i,j}$ are corrupted by Gaussian noise $n_{i,j}$ with mean 0 and variance $\sigma^2$.
|
||||
Then the noisy image is $g_{i,j}=(f_{i,j}+n_{i,j})-(f_{i,j+1}+n_{i,j+1})\approx N(0,2\sigma^2)$
|
||||
|
||||
To find edges, look for peaks in $\frac{d}{dx}(f\circ g)$ where $g$ is the Gaussian smoothing filter.
|
||||
|
||||
or we can directly use the Derivative of Gaussian (DoG) filter:
|
||||
|
||||
$$
|
||||
\frac{d}{dx}g(x,\sigma)=\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{x^2}{2\sigma^2}}
|
||||
$$
|
||||
|
||||
##### Separability of Gaussian filter
|
||||
|
||||
A Gaussian filter is separable if it can be written as a product of two 1D filters.
|
||||
|
||||
$$
|
||||
\frac{d}{dx}g(x,\sigma)=\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{x^2}{2\sigma^2}}
|
||||
\quad \frac{d}{dy}g(y,\sigma)=\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{y^2}{2\sigma^2}}
|
||||
$$
|
||||
|
||||
##### Separable Derivative of Gaussian (DoG) filter
|
||||
|
||||
$$
|
||||
\frac{d}{dx}g(x,y)\propto -x\exp\left(-\frac{x^2+y^2}{2\sigma^2}\right)
|
||||
\quad \frac{d}{dy}g(x,y)\propto -y\exp\left(-\frac{x^2+y^2}{2\sigma^2}\right)
|
||||
$$
|
||||
|
||||
##### Derivative of Gaussian: Scale
|
||||
|
||||
Using Gaussian derivatives with different values of 𝜎 finds structures at different scales or frequencies
|
||||
|
||||
(Take the hybrid image as an example)
|
||||
|
||||
##### Canny edge detector
|
||||
|
||||
1. Smooth the image with a Gaussian filter
|
||||
2. Compute the gradient magnitude and direction of the smoothed image
|
||||
3. Thresholding gradient magnitude
|
||||
4. Non-maxima suppression
|
||||
- For each location `q` above the threshold, check that the gradient magnitude is higher than at adjacent points `p` and `r` in the direction of the gradient
|
||||
5. Thresholding the non-maxima suppressed gradient magnitude
|
||||
6. Hysteresis thresholding
|
||||
- Use two thresholds: high and low
|
||||
- Start with a seed edge pixel with a gradient magnitude greater than the high threshold
|
||||
- Follow the gradient direction to find all connected pixels with a gradient magnitude greater than the low threshold
|
||||
|
||||
##### Top-down segmentation
|
||||
|
||||
Data-driven top-down segmentation:
|
||||
|
||||
#### Interest point
|
||||
|
||||
Key point matching:
|
||||
|
||||
1. Find a set of distinctive keypoints in the image
|
||||
2. Define a region of interest around each keypoint
|
||||
3. Compute a local descriptor from the normalized region
|
||||
4. Match local descriptors between images
|
||||
|
||||
Characteristic of good features:
|
||||
|
||||
- Repeatability
|
||||
- The same feature can be found in several images despite geometric and photometric transformations
|
||||
- Saliency
|
||||
- Each feature is distinctive
|
||||
- Compactness and efficiency
|
||||
- Many fewer features than image pixels
|
||||
- Locality
|
||||
- A feature occupies a relatively small area of the image; robust to clutter and occlusion
|
||||
|
||||
##### Harris corner detector
|
||||
|
||||
### Applications of local features
|
||||
|
||||
#### Image alignment
|
||||
|
||||
#### 3D reconstruction
|
||||
|
||||
#### Motion tracking
|
||||
|
||||
#### Robot navigation
|
||||
|
||||
#### Indexing and database retrieval
|
||||
|
||||
#### Object recognition
|
||||
|
||||
|
||||
|
||||
68
content/CSE559A/CSE559A_L18.md
Normal file
68
content/CSE559A/CSE559A_L18.md
Normal file
@@ -0,0 +1,68 @@
|
||||
# CSE559A Lecture 18
|
||||
|
||||
## Continue on Harris Corner Detector
|
||||
|
||||
Goal: Descriptor distinctiveness
|
||||
|
||||
- We want to be able to reliably determine which point goes with which.
|
||||
- Must provide some invariance to geometric and photometric differences.
|
||||
|
||||
Harris corner detector:
|
||||
|
||||
> Other existing variants:
|
||||
> - Hessian & Harris: [Beaudet '78], [Harris '88]
|
||||
> - Laplacian, DoG: [Lindeberg '98], [Lowe 1999]
|
||||
> - Harris-/Hessian-Laplace: [Mikolajczyk & Schmid '01]
|
||||
> - Harris-/Hessian-Affine: [Mikolajczyk & Schmid '04]
|
||||
> - EBR and IBR: [Tuytelaars & Van Gool '04]
|
||||
> - MSER: [Matas '02]
|
||||
> - Salient Regions: [Kadir & Brady '01]
|
||||
> - Others…
|
||||
|
||||
### Deriving a corner detection criterion
|
||||
|
||||
- Basic idea: we should easily recognize the point by looking through a small window
|
||||
- Shifting a window in any direction should give a large change in intensity
|
||||
|
||||
Corner is the point where the intensity changes in all directions.
|
||||
|
||||
Criterion:
|
||||
|
||||
Change in appearance of window $W$ for the shift $(u,v)$:
|
||||
|
||||
$$
|
||||
E(u,v) = \sum_{x,y\in W} [I(x+u,y+v) - I(x,y)]^2
|
||||
$$
|
||||
|
||||
First-order Taylor approximation for small shifts $(u,v)$:
|
||||
|
||||
$$
|
||||
I(x+u,y+v) \approx I(x,y) + I_x u + I_y v
|
||||
$$
|
||||
|
||||
plug into $E(u,v)$:
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
E(u,v) &= \sum_{(x,y)\in W} [I(x+u,y+v) - I(x,y)]^2 \\
|
||||
&\approx \sum_{(x,y)\in W} [I(x,y) + I_x u + I_y v - I(x,y)]^2 \\
|
||||
&= \sum_{(x,y)\in W} [I_x u + I_y v]^2 \\
|
||||
&= \sum_{(x,y)\in W} [I_x^2 u^2 + 2 I_x I_y u v + I_y^2 v^2]
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
Consider the second moment matrix:
|
||||
|
||||
$$
|
||||
M = \begin{bmatrix}
|
||||
I_x^2 & I_x I_y \\
|
||||
I_x I_y & I_y^2
|
||||
\end{bmatrix}=\begin{bmatrix}
|
||||
a & 0 \\
|
||||
0 & b
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
If either $a$ or $b$ is small, then the window is not a corner.
|
||||
|
||||
|
||||
71
content/CSE559A/CSE559A_L19.md
Normal file
71
content/CSE559A/CSE559A_L19.md
Normal file
@@ -0,0 +1,71 @@
|
||||
# CSE559A Lecture 19
|
||||
|
||||
## Feature Detection
|
||||
|
||||
### Behavior of corner features with respect to Image Transformations
|
||||
|
||||
To be useful for image matching, “the same” corner features need to show up despite geometric and photometric transformations
|
||||
|
||||
We need to analyze how the corner response function and the corner locations change in response to various transformations
|
||||
|
||||
#### Affine intensity change
|
||||
|
||||
Solution:
|
||||
|
||||
- Only derivative of intensity are used (invariant to intensity change)
|
||||
- Intensity scaling
|
||||
|
||||
#### Image translation
|
||||
|
||||
Solution:
|
||||
|
||||
- Derivatives and window function are shift invariant
|
||||
|
||||
#### Image rotation
|
||||
|
||||
Second moment ellipse rotates but its shape (i.e. eigenvalues) remains the same
|
||||
|
||||
#### Scaling
|
||||
|
||||
Classify edges instead of corners
|
||||
|
||||
## Automatic Scale selection for interest point detection
|
||||
|
||||
### Scale space
|
||||
|
||||
We want to extract keypoints with characteristic scales that are equivariant (or covariant) with respect to scaling of the image
|
||||
|
||||
Approach: compute a scale-invariant response function over neighborhoods centered at each location $(x,y)$ and a range of scales $\sigma$, find scale-space locations $(x,y,\sigma)$ where this function reaches a local maximum
|
||||
|
||||
A particularly convenient response function is given by the scale-normalized Laplacian of Gaussian (LoG) filter:
|
||||
|
||||
$$
|
||||
\nabla^2_{norm}=\sigma^2\nabla^2\left(\frac{\partial^2}{\partial x^2}g+\frac{\partial^2}{\partial y^2}g\right)
|
||||
$$
|
||||
|
||||
|
||||
|
||||
#### Edge detection with LoG
|
||||
|
||||
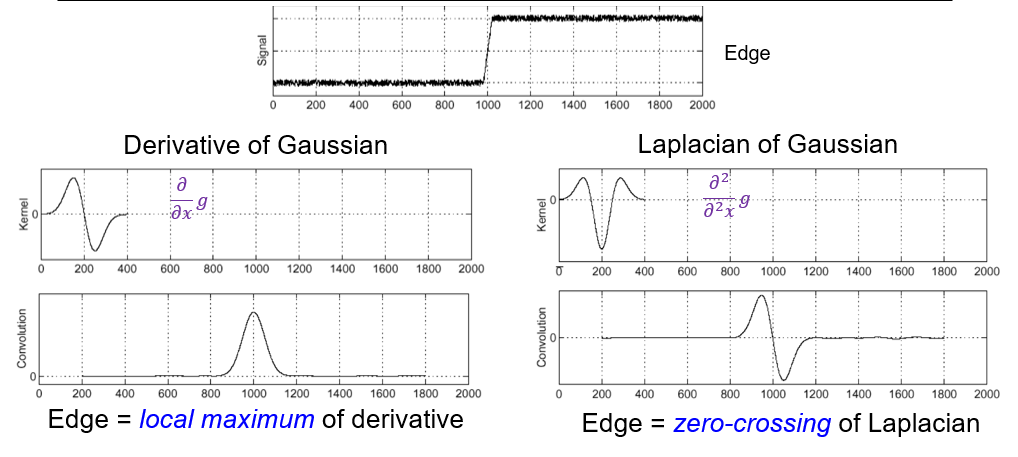
|
||||
|
||||
#### Blob detection with LoG
|
||||
|
||||
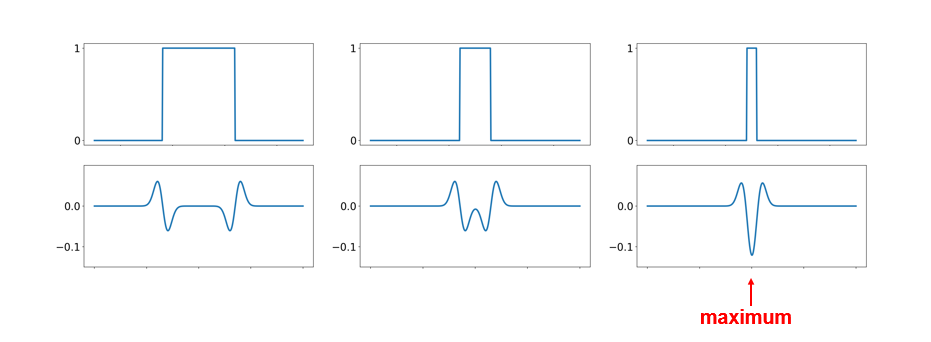
|
||||
|
||||
### Difference of Gaussians (DoG)
|
||||
|
||||
DoG has a little more flexibility, since you can select the scales of the Gaussians.
|
||||
|
||||
### Scale-invariant feature transform (SIFT)
|
||||
|
||||
The main goal of SIFT is to enable image matching in the presence of significant transformations
|
||||
|
||||
- To recognize the same keypoint in multiple images, we need to match appearance descriptors or "signatures" in their neighborhoods
|
||||
- Descriptors that are locally invariant w.r.t. scale and rotation can handle a wide range of global transformations
|
||||
|
||||
### Maximum stable extremal regions (MSER)
|
||||
|
||||
Based on Watershed segmentation algorithm
|
||||
|
||||
Select regions that are stable over a large parameter range
|
||||
165
content/CSE559A/CSE559A_L2.md
Normal file
165
content/CSE559A/CSE559A_L2.md
Normal file
@@ -0,0 +1,165 @@
|
||||
# CSE559A Lecture 2
|
||||
|
||||
## The Geometry of Image Formation
|
||||
|
||||
Mapping between image and world coordinates.
|
||||
|
||||
Today's focus:
|
||||
|
||||
$$
|
||||
x=K[R\ t]X
|
||||
$$
|
||||
|
||||
### Pinhole Camera Model
|
||||
|
||||
Add a barrier to block off most of the rays.
|
||||
|
||||
- Reduce blurring
|
||||
- The opening known as the **aperture**
|
||||
|
||||
$f$ is the focal length.
|
||||
$c$ is the center of the aperture.
|
||||
|
||||
#### Focal length/ Field of View (FOV)/ Zoom
|
||||
|
||||
- Focal length: distance between the aperture and the image plane.
|
||||
- Field of View (FOV): the angle between the two rays that pass through the aperture and the image plane.
|
||||
- Zoom: the ratio of the focal length to the image plane.
|
||||
|
||||
#### Other types of projection
|
||||
|
||||
Beyond the pinhole/perspective camera model, there are other types of projection.
|
||||
|
||||
- Radial distortion
|
||||
- 360-degree camera
|
||||
- Equirectangular Panoramas
|
||||
- Random lens
|
||||
- Rotating sensors
|
||||
- Photofinishing
|
||||
- Tiltshift lens
|
||||
|
||||
### Perspective Geometry
|
||||
|
||||
Length and area are not preserved.
|
||||
|
||||
Angle is not preserved.
|
||||
|
||||
But straight lines are still straight.
|
||||
|
||||
Parallel lines in the world intersect at a **vanishing point** on the image plane.
|
||||
|
||||
Vanishing lines: the set of all vanishing points of parallel lines in the world on the same plane in the world.
|
||||
|
||||
Vertical vanishing point at infinity.
|
||||
|
||||
### Camera/Projection Matrix
|
||||
|
||||
Linear projection model.
|
||||
|
||||
$$
|
||||
x=K[R\ t]X
|
||||
$$
|
||||
|
||||
- $x$: image coordinates 2d (homogeneous coordinates)
|
||||
- $X$: world coordinates 3d (homogeneous coordinates)
|
||||
- $K$: camera matrix (3x3 and invertible)
|
||||
- $R$: camera rotation matrix (3x3)
|
||||
- $t$: camera translation vector (3x1)
|
||||
|
||||
#### Homogeneous coordinates
|
||||
|
||||
- 2D: $$(x, y)\to\begin{bmatrix}x\\y\\1\end{bmatrix}$$
|
||||
- 3D: $$(x, y, z)\to\begin{bmatrix}x\\y\\z\\1\end{bmatrix}$$
|
||||
|
||||
converting from homogeneous to inhomogeneous coordinates:
|
||||
|
||||
- 2D: $$\begin{bmatrix}x\\y\\w\end{bmatrix}\to(x/w, y/w)$$
|
||||
- 3D: $$\begin{bmatrix}x\\y\\z\\w\end{bmatrix}\to(x/w, y/w, z/w)$$
|
||||
|
||||
When $w=0$, the point is at infinity.
|
||||
|
||||
Homogeneous coordinates are invariant under scaling (non-zero scalar).
|
||||
|
||||
$$
|
||||
k\begin{bmatrix}x\\y\\w\end{bmatrix}=\begin{bmatrix}kx\\ky\\kw\end{bmatrix}\implies\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}x/k\\y/k\end{bmatrix}
|
||||
$$
|
||||
|
||||
A convenient way to represent a point at infinity is to use a unit vector.
|
||||
|
||||
Line equation: $ax+by+c=0$
|
||||
|
||||
$$
|
||||
line_i=\begin{bmatrix}a_i\\b_i\\c_i\end{bmatrix}
|
||||
$$
|
||||
|
||||
|
||||
Append a 1 to pixel coordinates to get homogeneous coordinates.
|
||||
|
||||
$$
|
||||
pixel_i=\begin{bmatrix}u_i\\v_i\\1\end{bmatrix}
|
||||
$$
|
||||
|
||||
Line given by cross product of two points:
|
||||
|
||||
$$
|
||||
line_i=pixel_1\times pixel_2
|
||||
$$
|
||||
|
||||
Intersection of two lines given by cross product of the lines:
|
||||
|
||||
$$
|
||||
pixel_i=line_1\times line_2
|
||||
$$
|
||||
|
||||
#### Pinhole Camera Projection Matrix
|
||||
|
||||
Intrinsic Assumptions:
|
||||
|
||||
- Unit aspect ratio
|
||||
- No skew
|
||||
- Optical center at (0,0)
|
||||
|
||||
Extrinsic Assumptions:
|
||||
|
||||
- No rotation
|
||||
- No translation (camera at world origin)
|
||||
|
||||
$$
|
||||
x=K[I\ 0]X\implies w\begin{bmatrix}u\\v\\1\end{bmatrix}=\begin{bmatrix}f&0&0&0\\0&f&0&0\\0&0&1&0\end{bmatrix}\begin{bmatrix}x\\y\\z\\1\end{bmatrix}
|
||||
$$
|
||||
|
||||
Removing the assumptions:
|
||||
|
||||
Intrinsic assumptions:
|
||||
|
||||
- Unit aspect ratio
|
||||
- No skew
|
||||
|
||||
Extrinsic assumptions:
|
||||
|
||||
- No rotation
|
||||
- No translation
|
||||
|
||||
$$
|
||||
x=K[I\ 0]X\implies w\begin{bmatrix}u\\v\\1\end{bmatrix}=\begin{bmatrix}\alpha&0&u_0&0\\0&\beta&v_0&0\\0&0&1&0\end{bmatrix}\begin{bmatrix}x\\y\\z\\1\end{bmatrix}
|
||||
$$
|
||||
|
||||
Adding skew:
|
||||
|
||||
$$
|
||||
x=K[I\ 0]X\implies w\begin{bmatrix}u\\v\\1\end{bmatrix}=\begin{bmatrix}\alpha&s&u_0&0\\0&\beta&v_0&0\\0&0&1&0\end{bmatrix}\begin{bmatrix}x\\y\\z\\1\end{bmatrix}
|
||||
$$
|
||||
|
||||
Finally, adding camera rotation and translation:
|
||||
|
||||
$$
|
||||
x=K[I\ t]X\implies w\begin{bmatrix}u\\v\\1\end{bmatrix}=\begin{bmatrix}\alpha&s&u_0\\0&\beta&v_0\\0&0&1\end{bmatrix}\begin{bmatrix}r_{11}&r_{12}&r_{13}&t_x\\r_{21}&r_{22}&r_{23}&t_y\\r_{31}&r_{32}&r_{33}&t_z\end{bmatrix}\begin{bmatrix}x\\y\\z\\1\end{bmatrix}
|
||||
$$
|
||||
|
||||
What is the degrees of freedom of the camera matrix?
|
||||
|
||||
- rotation: 3
|
||||
- translation: 3
|
||||
- camera matrix: 5
|
||||
|
||||
Total: 11
|
||||
145
content/CSE559A/CSE559A_L20.md
Normal file
145
content/CSE559A/CSE559A_L20.md
Normal file
@@ -0,0 +1,145 @@
|
||||
# CSE559A Lecture 20
|
||||
|
||||
## Local feature descriptors
|
||||
|
||||
Detection: Identify the interest points
|
||||
|
||||
Description: Extract vector feature descriptor surrounding each interest point.
|
||||
|
||||
Matching: Determine correspondence between descriptors in two views
|
||||
|
||||
### Image representation
|
||||
|
||||
Histogram of oriented gradients (HOG)
|
||||
|
||||
- Quantization
|
||||
- Grids: fast but applicable only with few dimensions
|
||||
- Clustering: slower but can quantize data in higher dimensions
|
||||
- Matching
|
||||
- Histogram intersection or Euclidean may be faster
|
||||
- Chi-squared often works better
|
||||
- Earth mover’s distance is good for when nearby bins represent similar values
|
||||
|
||||
#### SIFT vector formation
|
||||
|
||||
Computed on rotated and scaled version of window according to computed orientation & scale
|
||||
|
||||
- resample the window
|
||||
|
||||
Based on gradients weighted by a Gaussian of variance half the window (for smooth falloff)
|
||||
|
||||
4x4 array of gradient orientation histogram weighted by magnitude
|
||||
|
||||
8 orientations x 4x4 array = 128 dimensions
|
||||
|
||||
Motivation: some sensitivity to spatial layout, but not too much.
|
||||
|
||||
For matching:
|
||||
|
||||
- Extraordinarily robust detection and description technique
|
||||
- Can handle changes in viewpoint
|
||||
- Up to about 60 degree out-of-plane rotation
|
||||
- Can handle significant changes in illumination
|
||||
- Sometimes even day vs. night
|
||||
- Fast and efficient—can run in real time
|
||||
- Lots of code available
|
||||
|
||||
#### SURF
|
||||
|
||||
- Fast approximation of SIFT idea
|
||||
- Efficient computation by 2D box filters & integral images
|
||||
- 6 times faster than SIFT
|
||||
- Equivalent quality for object identification
|
||||
|
||||
#### Shape context
|
||||
|
||||
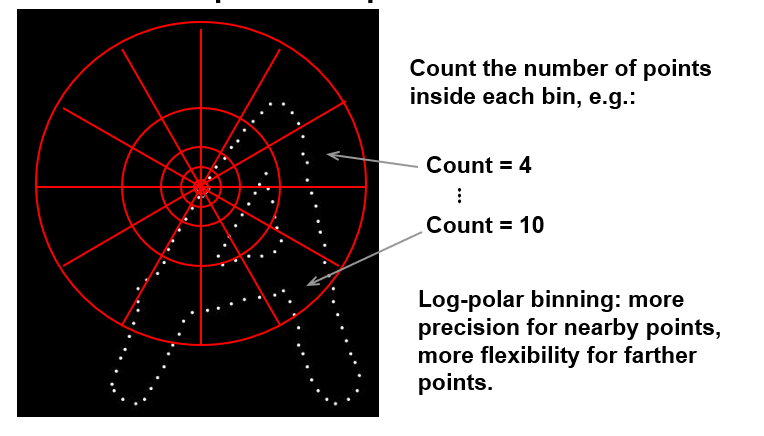
|
||||
|
||||
#### Self-similarity Descriptor
|
||||
|
||||
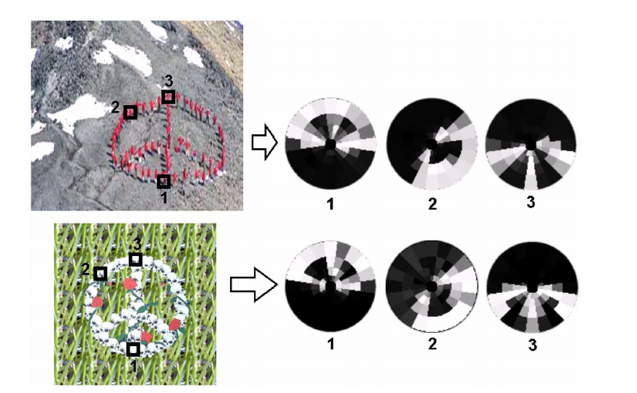
|
||||
|
||||
## Local feature matching
|
||||
|
||||
### Matching
|
||||
|
||||
Simplest approach: Pick the nearest neighbor. Threshold on absolute distance
|
||||
|
||||
Problem: Lots of self similarity in many photos
|
||||
|
||||
Solution: Nearest neighbor with low ratio test
|
||||
|
||||
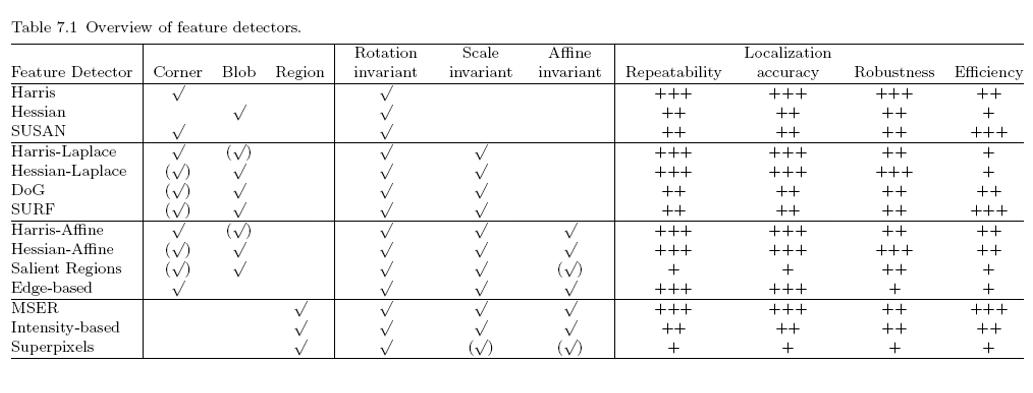
|
||||
|
||||
## Deep Learning for Correspondence Estimation
|
||||
|
||||
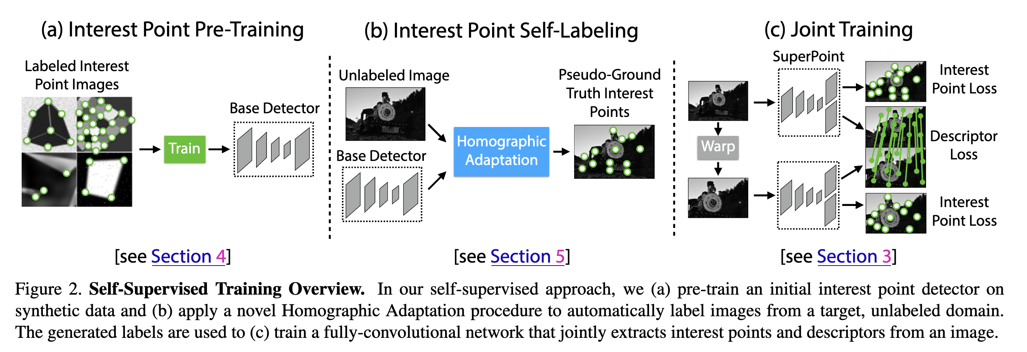
|
||||
|
||||
## Optical Flow
|
||||
|
||||
### Field
|
||||
|
||||
Motion field: the projection of the 3D scene motion into the image
|
||||
Magnitude of vectors is determined by metric motion
|
||||
Only caused by motion
|
||||
|
||||
Optical flow: the apparent motion of brightness patterns in the image
|
||||
Magnitude of vectors is measured in pixels
|
||||
Can be caused by lightning
|
||||
|
||||
### Brightness constancy constraint, aperture problem
|
||||
|
||||
Machine Learning Approach
|
||||
|
||||
- Collect examples of inputs and outputs
|
||||
- Design a prediction model suitable for the task
|
||||
- Invariances, Equivariances; Complexity; Input and Output shapes and semantics
|
||||
- Specify loss functions and train model
|
||||
- Limitations: Requires training the model; Requires a sufficiently complete training dataset; Must re-learn known facts; Higher computational complexity
|
||||
|
||||
Optimization Approach
|
||||
|
||||
- Define properties we expect to hold for a correct solution
|
||||
- Translate properties into a cost function
|
||||
- Derive an algorithm to solve for the cost function
|
||||
- Limitations: Often requires making overly simple assumptions on properties; Some tasks can’t be easily defined
|
||||
|
||||
Given frames at times $t-1$ and $t$, estimate the apparent motion field $u(x,y)$ and $v(x,y)$ between them
|
||||
Brightness constancy constraint: projection of the same point looks the same in every frame
|
||||
|
||||
$$
|
||||
I(x,y,t-1) = I(x+u(x,y),y+v(x,y),t)
|
||||
$$
|
||||
|
||||
Additional assumptions:
|
||||
|
||||
- Small motion: points do not move very far
|
||||
- Spatial coherence: points move like their neighbors
|
||||
|
||||
Trick for solving:
|
||||
|
||||
Brightness constancy constraint:
|
||||
|
||||
$$
|
||||
I(x,y,t-1) = I(x+u(x,y),y+v(x,y),t)
|
||||
$$
|
||||
|
||||
Linearize the right-hand side using Taylor expansion:
|
||||
|
||||
$$
|
||||
I(x,y,t-1) \approx I(x,y,t) + I_x u(x,y) + I_y v(x,y)
|
||||
$$
|
||||
|
||||
$$
|
||||
I_x u(x,y) + I_y v(x,y) + I(x,y,t) - I(x,y,t-1) = 0
|
||||
$$
|
||||
|
||||
Hence,
|
||||
|
||||
$$
|
||||
I_x u(x,y) + I_y v(x,y) + I_t = 0
|
||||
$$
|
||||
|
||||
|
||||
|
||||
|
||||
215
content/CSE559A/CSE559A_L21.md
Normal file
215
content/CSE559A/CSE559A_L21.md
Normal file
@@ -0,0 +1,215 @@
|
||||
# CSE559A Lecture 21
|
||||
|
||||
## Continue on optical flow
|
||||
|
||||
### The brightness constancy constraint
|
||||
|
||||
$$
|
||||
I_x u(x,y) + I_y v(x,y) + I_t = 0
|
||||
$$
|
||||
Given the gradients $I_x, I_y$ and $I_t$, can we uniquely recover the motion $(u,v)$?
|
||||
|
||||
- Suppose $(u, v)$ satisfies the constraint: $\nabla I \cdot (u,v) + I_t = 0$
|
||||
- Then $\nabla I \cdot (u+u', v+v') + I_t = 0$ for any $(u', v')$ s.t. $\nabla I \cdot (u', v') = 0$
|
||||
- Interpretation: the component of the flow perpendicular to the gradient (i.e., parallel to the edge) cannot be recovered!
|
||||
|
||||
#### Aperture problem
|
||||
|
||||
- The brightness constancy constraint is only valid for a small patch in the image
|
||||
- For a large motion, the patch may look very different
|
||||
|
||||
Consider the barber pole illusion
|
||||
|
||||
### Estimating optical flow (Lucas-Kanade method)
|
||||
|
||||
- Consider a small patch in the image
|
||||
- Assume the motion is constant within the patch
|
||||
- Then we can solve for the motion $(u, v)$ by minimizing the error:
|
||||
|
||||
$$
|
||||
I_x u(x,y) + I_y v(x,y) + I_t = 0
|
||||
$$
|
||||
|
||||
How to get more equations for a pixel?
|
||||
Spatial coherence constraint: assume the pixel’s neighbors have the same (𝑢,𝑣)
|
||||
If we have 𝑛 pixels in the neighborhood, then we can set up a linear least squares system:
|
||||
|
||||
$$
|
||||
\begin{bmatrix}
|
||||
I_x(x_1, y_1) & I_y(x_1, y_1) \\
|
||||
\vdots & \vdots \\
|
||||
I_x(x_n, y_n) & I_y(x_n, y_n)
|
||||
\end{bmatrix}
|
||||
\begin{bmatrix}
|
||||
u \\ v
|
||||
\end{bmatrix} = -\begin{bmatrix}
|
||||
I_t(x_1, y_1) \\ \vdots \\ I_t(x_n, y_n)
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
#### Lucas-Kanade flow
|
||||
|
||||
Let $A=
|
||||
\begin{bmatrix}
|
||||
I_x(x_1, y_1) & I_y(x_1, y_1) \\
|
||||
\vdots & \vdots \\
|
||||
I_x(x_n, y_n) & I_y(x_n, y_n)
|
||||
\end{bmatrix}$
|
||||
|
||||
$b = \begin{bmatrix}
|
||||
I_t(x_1, y_1) \\ \vdots \\ I_t(x_n, y_n)
|
||||
\end{bmatrix}$
|
||||
|
||||
$d = \begin{bmatrix}
|
||||
u \\ v
|
||||
\end{bmatrix}$
|
||||
|
||||
The solution is $d=(A^T A)^{-1} A^T b$
|
||||
|
||||
Lucas-Kanade flow:
|
||||
|
||||
- Find $(u,v)$ minimizing $\sum_{i} (I(x_i+u,y_i+v,t)-I(x_i,y_i,t-1))^2$
|
||||
- use Taylor approximation of $I(x_i+u,y_i+v,t)$ for small shifts $(u,v)$ to obtain closed-form solution
|
||||
|
||||
### Refinement for Lucas-Kanade
|
||||
|
||||
In some cases, the Lucas-Kanade method may not work well:
|
||||
- The motion is large (larger than a pixel)
|
||||
- A point does not move like its neighbors
|
||||
- Brightness constancy does not hold
|
||||
|
||||
#### Iterative refinement (for large motion)
|
||||
|
||||
Iterative Lukas-Kanade Algorithm
|
||||
|
||||
1. Estimate velocity at each pixel by solving Lucas-Kanade equations
|
||||
2. Warp It towards It+1 using the estimated flow field
|
||||
- use image warping techniques
|
||||
3. Repeat until convergence
|
||||
|
||||
Iterative refinement is limited due to Aliasing
|
||||
|
||||
#### Coarse-to-fine refinement (for large motion)
|
||||
|
||||
- Estimate flow at a coarse level
|
||||
- Refine the flow at a finer level
|
||||
- Use the refined flow to warp the image
|
||||
- Repeat until convergence
|
||||
|
||||

|
||||
|
||||
#### Representing moving images with layers (for a point may not move like its neighbors)
|
||||
|
||||
- The image can be decomposed into a moving layer and a stationary layer
|
||||
- The moving layer is the layer that moves
|
||||
- The stationary layer is the layer that does not move
|
||||
|
||||
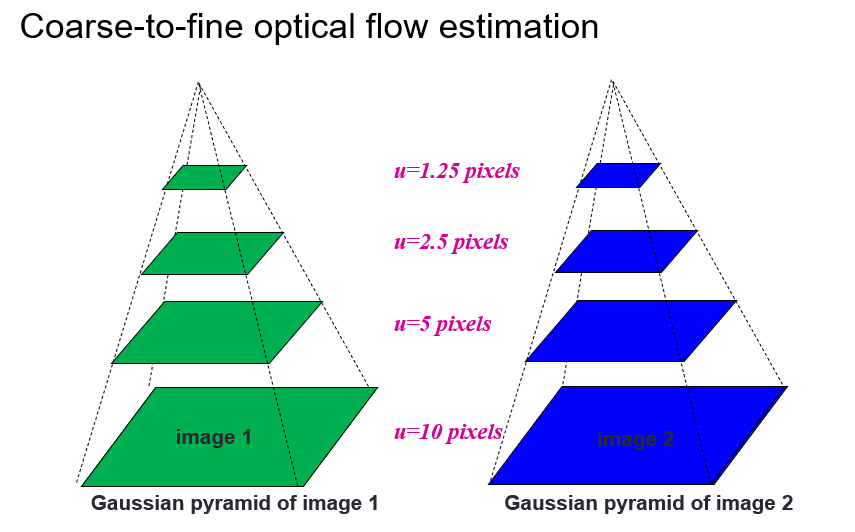
|
||||
|
||||
### SOTA models
|
||||
|
||||
#### 2009
|
||||
|
||||
Start with something similar to Lucas-Kanade
|
||||
|
||||
- gradient constancy
|
||||
- energy minimization with smoothing term
|
||||
- region matching
|
||||
- keypoint matching (long-range)
|
||||
|
||||
#### 2015
|
||||
|
||||
Deep neural networks
|
||||
|
||||
- Use a deep neural network to represent the flow field
|
||||
- Use synthetic data to train the network (floating chairs)
|
||||
|
||||
#### 2023
|
||||
|
||||
GMFlow
|
||||
|
||||
use Transformer to model the flow field
|
||||
|
||||
## Robust Fitting of parametric models
|
||||
|
||||
Challenges:
|
||||
|
||||
- Noise in the measured feature locations
|
||||
- Extraneous data: clutter (outliers), multiple lines
|
||||
- Missing data: occlusions
|
||||
|
||||
### Least squares fitting
|
||||
|
||||
Normal least squares fitting
|
||||
|
||||
$y=mx+b$ is not a good model for the data since there might be vertical lines
|
||||
|
||||
Instead we use total least squares
|
||||
|
||||
Line parametrization: $ax+by=d$
|
||||
|
||||
$(a,b)$ is the unit normal to the line (i.e., $a^2+b^2=1$)
|
||||
$d$ is the distance between the line and the origin
|
||||
Perpendicular distance between point $(x_i, y_i)$ and line $ax+by=d$ (assuming $a^2+b^2=1$):
|
||||
|
||||
$$
|
||||
|ax_i + by_i - d|
|
||||
$$
|
||||
|
||||
Objective function:
|
||||
|
||||
$$
|
||||
E = \sum_{i=1}^n (ax_i + by_i - d)^2
|
||||
$$
|
||||
|
||||
Solve for $d$ first: $d =a\bar{x}+b\bar{y}$
|
||||
Plugging back in:
|
||||
|
||||
$$
|
||||
E = \sum_{i=1}^n (a(x_i-\bar{x})+b(y_i-\bar{y}))^2 = \left\|\begin{bmatrix}x_1-\bar{x}&y_1-\bar{y}\\\vdots&\vdots\\x_n-\bar{x}&y_n-\bar{y}\end{bmatrix}\begin{pmatrix}a\\b\end{pmatrix}\right\|^2
|
||||
$$
|
||||
|
||||
We want to find $N$ that minimizes $\|UN\|^2$ subject to $\|N\|^2= 1$
|
||||
Solution is given by the eigenvector of $U^T U$ associated with the smallest eigenvalue
|
||||
|
||||
Drawbacks:
|
||||
|
||||
- Sensitive to outliers
|
||||
|
||||
### Robust fitting
|
||||
|
||||
General approach: find model parameters 𝜃 that minimize
|
||||
|
||||
$$
|
||||
\sum_{i} \rho_{\sigma}(r(x_i;\theta))
|
||||
$$
|
||||
|
||||
$r(x_i;\theta)$: residual of $x_i$ w.r.t. model parameters $\theta$
|
||||
$\rho_{\sigma}$: robust function with scale parameter $\sigma$, e.g., $\rho_{\sigma}(u)=\frac{u^2}{\sigma^2+u^2}$
|
||||
|
||||
Nonlinear optimization problem that must be solved iteratively
|
||||
|
||||
- Least squares solution can be used for initialization
|
||||
- Scale of robust function should be chosen carefully
|
||||
|
||||
Drawbacks:
|
||||
|
||||
- Need to manually choose the robust function and scale parameter
|
||||
|
||||
### RANSAC
|
||||
|
||||
Voting schemes
|
||||
|
||||
Random sample consensus: very general framework for model fitting in the presence of outliers
|
||||
|
||||
Outline:
|
||||
|
||||
- Randomly choose a small initial subset of points
|
||||
- Fit a model to that subset
|
||||
- Find all inlier points that are "close" to the model and reject the rest as outliers
|
||||
- Do this many times and choose the model with the most inliers
|
||||
|
||||
### Hough transform
|
||||
|
||||
|
||||
|
||||
260
content/CSE559A/CSE559A_L22.md
Normal file
260
content/CSE559A/CSE559A_L22.md
Normal file
@@ -0,0 +1,260 @@
|
||||
# CSE559A Lecture 22
|
||||
|
||||
## Continue on Robust Fitting of parametric models
|
||||
|
||||
### RANSAC
|
||||
|
||||
#### Definition: RANdom SAmple Consensus
|
||||
|
||||
RANSAC is a method to fit a model to a set of data points.
|
||||
|
||||
It is a non-deterministic algorithm that can be used to fit a model to a set of data points.
|
||||
|
||||
Pros:
|
||||
|
||||
- Simple and general
|
||||
- Applicable to many different problems
|
||||
- Often works well in practice
|
||||
|
||||
Cons:
|
||||
|
||||
- Lots of parameters to set
|
||||
- Number of iterations grows exponentially as outlier ratio increases
|
||||
- Can't always get a good initialization of the model based on the minimum number of samples.
|
||||
|
||||
### Hough Transform
|
||||
|
||||
Use point-line duality to find lines.
|
||||
|
||||
In practice, we don't use (m,b) parameterization.
|
||||
|
||||
Instead, we use polar parameterization:
|
||||
|
||||
$$
|
||||
\rho = x \cos \theta + y \sin \theta
|
||||
$$
|
||||
|
||||
Algorithm outline:
|
||||
|
||||
- Initialize accumulator $H$ to all zeros
|
||||
- For each feature point $(x,y)$
|
||||
- For $\theta = 0$ to $180$
|
||||
- $\rho = x \cos \theta + y \sin \theta$
|
||||
- $H(\theta, \rho) += 1$
|
||||
- Find the value(s) of $(\theta, \rho)$ where $H(\theta, \rho)$ is a local maximum (perform NMS on the accumulator array)
|
||||
- The detected line in the image is given by $\rho = x \cos \theta + y \sin \theta$
|
||||
|
||||
#### Effect of noise
|
||||
|
||||
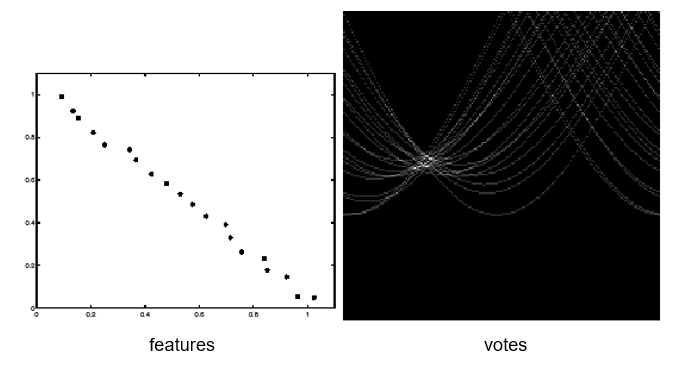
|
||||
|
||||
Noise makes the peak fuzzy.
|
||||
|
||||
#### Effect of outliers
|
||||
|
||||
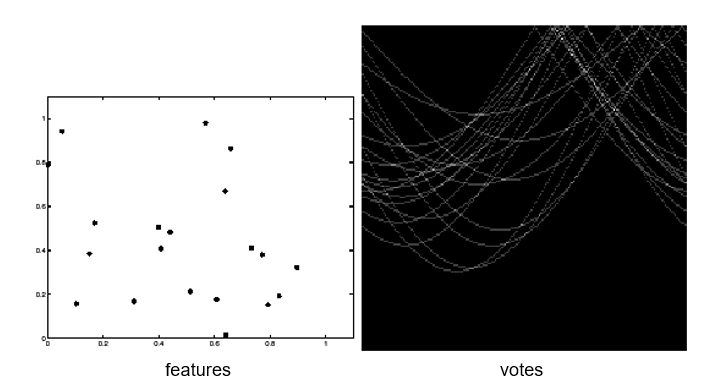
|
||||
|
||||
Outliers can break the peak.
|
||||
|
||||
#### Pros and Cons
|
||||
|
||||
Pros:
|
||||
|
||||
- Can deal with non-locality and occlusion
|
||||
- Can detect multiple instances of a model
|
||||
- Some robustness to noise: noise points unlikely to contribute consistently to any single bin
|
||||
- Leads to a surprisingly general strategy for shape localization (more on this next)
|
||||
|
||||
Cons:
|
||||
|
||||
- Complexity increases exponentially with the number of model parameters
|
||||
- In practice, not used beyond three or four dimensions
|
||||
- Non-target shapes can produce spurious peaks in parameter space
|
||||
- It's hard to pick a good grid size
|
||||
|
||||
### Generalize Hough Transform
|
||||
|
||||
Template representation: for each type of landmark point, store all possible displacement vectors towards the center
|
||||
|
||||
Detecting the template:
|
||||
|
||||
For each feature in a new image, look up that feature type in the model and vote for the possible center locations associated with that type in the model
|
||||
|
||||
#### Implicit shape models
|
||||
|
||||
Training:
|
||||
|
||||
- Build codebook of patches around extracted interest points using clustering
|
||||
- Map the patch around each interest point to closest codebook entry
|
||||
- For each codebook entry, store all positions it was found, relative to object center
|
||||
|
||||
Testing:
|
||||
|
||||
- Given test image, extract patches, match to codebook entry
|
||||
- Cast votes for possible positions of object center
|
||||
- Search for maxima in voting space
|
||||
- Extract weighted segmentation mask based on stored masks for the codebook occurrences
|
||||
|
||||
## Image alignment
|
||||
|
||||
### Affine transformation
|
||||
|
||||
Simple fitting procedure: linear least squares
|
||||
Approximates viewpoint changes for roughly planar objects and roughly orthographic cameras
|
||||
Can be used to initialize fitting for more complex models
|
||||
|
||||
Fitting an affine transformation:
|
||||
|
||||
$$
|
||||
\begin{bmatrix}
|
||||
&&&\cdots\\
|
||||
x_i & y_i & 0&0&1&0\\
|
||||
0&0&x_i&y_i&0&1\\
|
||||
&&&\cdots\\
|
||||
\end{bmatrix}
|
||||
\begin{bmatrix}
|
||||
m_1\\
|
||||
m_2\\
|
||||
m_3\\
|
||||
m_4\\
|
||||
t_1\\
|
||||
t_2\\
|
||||
\end{bmatrix}
|
||||
=
|
||||
\begin{bmatrix}
|
||||
\cdots\\
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
Only need 3 points to solve for 6 parameters.
|
||||
|
||||
### Homography
|
||||
|
||||
Recall that
|
||||
|
||||
$$
|
||||
x' = \frac{a x + b y + c}{g x + h y + i}, \quad y' = \frac{d x + e y + f}{g x + h y + i}
|
||||
$$
|
||||
|
||||
Use 2D homogeneous coordinates:
|
||||
|
||||
$(x,y) \rightarrow \begin{pmatrix}x \\ y \\ 1\end{pmatrix}$
|
||||
|
||||
$\begin{pmatrix}x\\y\\w\end{pmatrix} \rightarrow (x/w,y/w)$
|
||||
|
||||
Reminder: all homogeneous coordinate vectors that are (non-zero) scalar multiples of each other represent the same point
|
||||
|
||||
|
||||
Equation for homography in homogeneous coordinates:
|
||||
|
||||
$$
|
||||
\begin{pmatrix}
|
||||
x' \\
|
||||
y' \\
|
||||
1
|
||||
\end{pmatrix}
|
||||
\cong
|
||||
\begin{pmatrix}
|
||||
h_{11} & h_{12} & h_{13} \\
|
||||
h_{21} & h_{22} & h_{23} \\
|
||||
h_{31} & h_{32} & h_{33}
|
||||
\end{pmatrix}
|
||||
\begin{pmatrix}
|
||||
x \\
|
||||
y \\
|
||||
1
|
||||
\end{pmatrix}
|
||||
$$
|
||||
|
||||
Constraint from a match $(x_i,x_i')$, $x_i'\cong Hx_i$
|
||||
|
||||
How can we get rid of the scale ambiguity?
|
||||
|
||||
Cross product trick:$x_i' × Hx_i=0$
|
||||
|
||||
The cross product is defined as:
|
||||
|
||||
$$
|
||||
\begin{pmatrix}a\\b\\c\end{pmatrix} \times \begin{pmatrix}a'\\b'\\c'\end{pmatrix} = \begin{pmatrix}bc'-b'c\\ca'-c'a\\ab'-a'b\end{pmatrix}
|
||||
$$
|
||||
|
||||
Let $h_1^T, h_2^T, h_3^T$ be the rows of $H$. Then
|
||||
|
||||
$$
|
||||
x_i' × Hx_i=\begin{pmatrix}
|
||||
x_i' \\
|
||||
y_i' \\
|
||||
1
|
||||
\end{pmatrix} \times \begin{pmatrix}
|
||||
h_1^T x_i \\
|
||||
h_2^T x_i \\
|
||||
h_3^T x_i
|
||||
\end{pmatrix}
|
||||
=
|
||||
\begin{pmatrix}
|
||||
y_i' h_3^T x_i−h_2^T x_i \\
|
||||
h_1^T x_i−x_i' h_3^T x_i \\
|
||||
x_i' h_2^T x_i−y_i' h_1^T x_i
|
||||
\end{pmatrix}
|
||||
$$
|
||||
|
||||
Constraint from a match $(x_i,x_i')$:
|
||||
|
||||
$$
|
||||
x_i' × Hx_i=\begin{pmatrix}
|
||||
x_i' \\
|
||||
y_i' \\
|
||||
1
|
||||
\end{pmatrix} \times \begin{pmatrix}
|
||||
h_1^T x_i \\
|
||||
h_2^T x_i \\
|
||||
h_3^T x_i
|
||||
\end{pmatrix}
|
||||
=
|
||||
\begin{pmatrix}
|
||||
y_i' h_3^T x_i−h_2^T x_i \\
|
||||
h_1^T x_i−x_i' h_3^T x_i \\
|
||||
x_i' h_2^T x_i−y_i' h_1^T x_i
|
||||
\end{pmatrix}
|
||||
$$
|
||||
|
||||
Rearranging the terms:
|
||||
|
||||
$$
|
||||
\begin{bmatrix}
|
||||
0^T &-x_i^T &y_i' x_i^T \\
|
||||
x_i^T &0^T &-x_i' x_i^T \\
|
||||
y_i' x_i^T &x_i' x_i^T &0^T
|
||||
\end{bmatrix}
|
||||
\begin{bmatrix}
|
||||
h_1 \\
|
||||
h_2 \\
|
||||
h_3
|
||||
\end{bmatrix} = 0
|
||||
$$
|
||||
|
||||
These equations aren't independent! So, we only need two.
|
||||
|
||||
### Robust alignment
|
||||
|
||||
#### Descriptor-based feature matching
|
||||
|
||||
Extract features
|
||||
Compute putative matches
|
||||
Loop:
|
||||
|
||||
- Hypothesize transformation $T$
|
||||
- Verify transformation (search for other matches consistent with $T$)
|
||||
|
||||
#### RANSAC
|
||||
|
||||
Even after filtering out ambiguous matches, the set of putative matches still contains a very high percentage of outliers
|
||||
|
||||
RANSAC loop:
|
||||
|
||||
- Randomly select a seed group of matches
|
||||
- Compute transformation from seed group
|
||||
- Find inliers to this transformation
|
||||
- If the number of inliers is sufficiently large, re-compute least-squares estimate of transformation on all of the inliers
|
||||
|
||||
At the end, keep the transformation with the largest number of inliers
|
||||
15
content/CSE559A/CSE559A_L23.md
Normal file
15
content/CSE559A/CSE559A_L23.md
Normal file
@@ -0,0 +1,15 @@
|
||||
# CSE559A Lecture 23
|
||||
|
||||
## DUSt3r
|
||||
|
||||
Dense and Unconstrained Stereo 3D Reconstruction of arbitrary image collections.
|
||||
|
||||
[Github DUST3R](https://github.com/naver/dust3r)
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
1
content/CSE559A/CSE559A_L24.md
Normal file
1
content/CSE559A/CSE559A_L24.md
Normal file
@@ -0,0 +1 @@
|
||||
|
||||
217
content/CSE559A/CSE559A_L25.md
Normal file
217
content/CSE559A/CSE559A_L25.md
Normal file
@@ -0,0 +1,217 @@
|
||||
# CSE559A Lecture 25
|
||||
|
||||
## Geometry and Multiple Views
|
||||
|
||||
### Cues for estimating Depth
|
||||
|
||||
#### Multiple Views (the strongest depth cue)
|
||||
|
||||
Two common settings:
|
||||
|
||||
**Stereo vision**: a pair of cameras, usually with some constraints on the relative position of the two cameras.
|
||||
|
||||
**Structure from (camera) motion**: cameras observing a scene from different viewpoints
|
||||
|
||||
Structure and depth are inherently ambiguous from single views.
|
||||
|
||||
Other hints for depth:
|
||||
|
||||
- Occlusion
|
||||
- Perspective effects
|
||||
- Texture
|
||||
- Object motion
|
||||
- Shading
|
||||
- Focus/Defocus
|
||||
|
||||
#### Focus on Stereo and Multiple Views
|
||||
|
||||
Stereo correspondence: Given a point in one of the images, where could its corresponding points be in the other images?
|
||||
|
||||
Structure: Given projections of the same 3D point in two or more images, compute the 3D coordinates of that point
|
||||
|
||||
Motion: Given a set of corresponding points in two or more images, compute the camera parameters
|
||||
|
||||
#### A simple example of estimating depth with stereo:
|
||||
|
||||
Stereo: shape from "motion" between two views
|
||||
|
||||
We'll need to consider:
|
||||
|
||||
- Info on camera pose ("calibration")
|
||||
- Image point correspondences
|
||||
|
||||
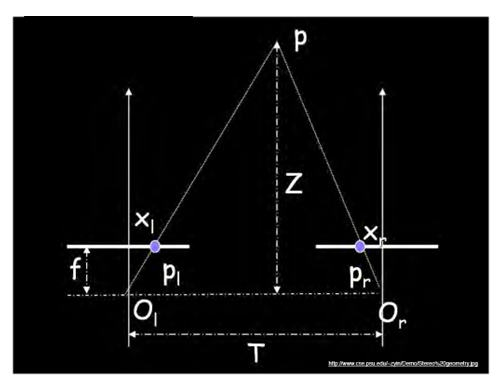
|
||||
|
||||
Assume parallel optical axes, known camera parameters (i.e., calibrated cameras). What is expression for Z?
|
||||
|
||||
Similar triangles $(p_l, P, p_r)$ and $(O_l, P, O_r)$:
|
||||
|
||||
$$
|
||||
\frac{T-x_l+x_r}{Z-f}=\frac{T}{Z}
|
||||
$$
|
||||
|
||||
$$
|
||||
Z = \frac{f \cdot T}{x_l-x_r}
|
||||
$$
|
||||
|
||||
### Camera Calibration
|
||||
|
||||
Use an scene with known geometry
|
||||
|
||||
- Correspond image points to 3d points
|
||||
- Get least squares solution (or non-linear solution)
|
||||
|
||||
Solving unknown camera parameters:
|
||||
|
||||
$$
|
||||
\begin{bmatrix}
|
||||
su\\
|
||||
sv\\
|
||||
s
|
||||
\end{bmatrix}
|
||||
= \begin{bmatrix}
|
||||
m_{11} & m_{12} & m_{13} & m_{14}\\
|
||||
m_{21} & m_{22} & m_{23} & m_{24}\\
|
||||
m_{31} & m_{32} & m_{33} & m_{34}
|
||||
\end{bmatrix}
|
||||
\begin{bmatrix}
|
||||
X\\
|
||||
Y\\
|
||||
Z\\
|
||||
1
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
Method 1: Homogenous linear system. Solve for m's entries using least squares.
|
||||
|
||||
$$
|
||||
\begin{bmatrix}
|
||||
X_1 & Y_1 & Z_1 & 1 & 0 & 0 & 0 & 0 & -u_1X_1 & -u_1Y_1 & -u_1Z_1 & -u_1 \\
|
||||
0 & 0 & 0 & 0 & X_1 & Y_1 & Z_1 & 1 & -v_1X_1 & -v_1Y_1 & -v_1Z_1 & -v_1 \\
|
||||
\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots\\
|
||||
X_n & Y_n & Z_n & 1 & 0 & 0 & 0 & 0 & -u_nX_n & -u_nY_n & -u_nZ_n & -u_n \\
|
||||
0 & 0 & 0 & 0 & X_n & Y_n & Z_n & 1 & -v_nX_n & -v_nY_n & -v_nZ_n & -v_n
|
||||
\end{bmatrix}
|
||||
\begin{bmatrix} m_{11} \\ m_{12} \\ m_{13} \\ m_{14} \\ m_{21} \\ m_{22} \\ m_{23} \\ m_{24} \\ m_{31} \\ m_{32} \\ m_{33} \\ m_{34} \end{bmatrix} = 0
|
||||
$$
|
||||
|
||||
Method 2: Non-homogenous linear system. Solve for m's entries using least squares.
|
||||
|
||||
**Advantages**
|
||||
|
||||
- Easy to formulate and solve
|
||||
- Provides initialization for non-linear methods
|
||||
|
||||
**Disadvantages**
|
||||
|
||||
- Doesn't directly give you camera parameters
|
||||
- Doesn't model radial distortion
|
||||
- Can't impose constraints, such as known focal length
|
||||
|
||||
**Non-linear methods are preferred**
|
||||
|
||||
- Define error as difference between projected points and measured points
|
||||
- Minimize error using Newton's method or other non-linear optimization
|
||||
|
||||
#### Triangulation
|
||||
|
||||
Given projections of a 3D point in two or more images (with known camera matrices), find the coordinates of the point
|
||||
|
||||
##### Approaches 1: Geometric approach
|
||||
|
||||
Find shortest segment connecting the two viewing rays and let $X$ be the midpoint of that segment
|
||||
|
||||
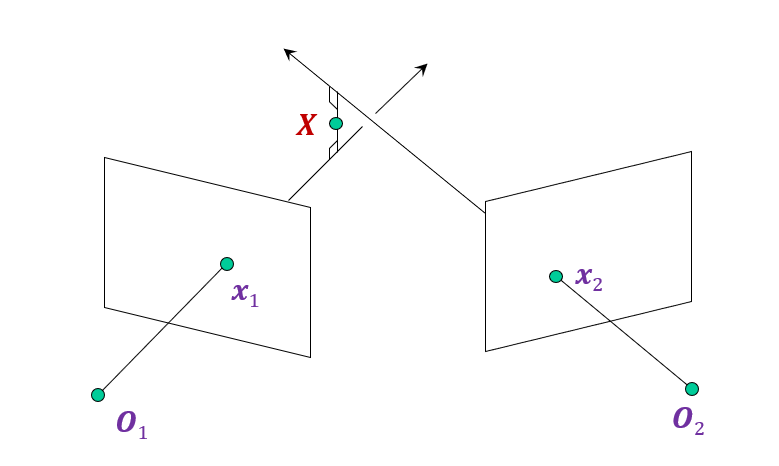
|
||||
|
||||
##### Approaches 2: Non-linear optimization
|
||||
|
||||
Minimize error between projected point and measured point
|
||||
|
||||
$$
|
||||
||\operatorname{proj}(P_1 X) - x_1||_2^2 + ||\operatorname{proj}(P_2 X) - x_2||_2^2
|
||||
$$
|
||||
|
||||
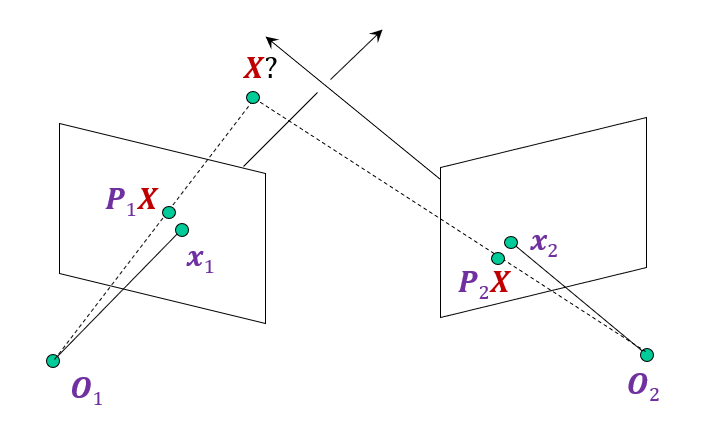
|
||||
|
||||
##### Approaches 3: Linear approach
|
||||
|
||||
$x_1\cong P_1X$ and $x_2\cong P_2X$
|
||||
|
||||
$x_1\times P_1X = 0$ and $x_2\times P_2X = 0$
|
||||
|
||||
$[x_{1_{\times}}]P_1X = 0$ and $[x_{2_{\times}}]P_2X = 0$
|
||||
|
||||
Rewrite as:
|
||||
|
||||
$$
|
||||
a\times b=\begin{bmatrix}
|
||||
0 & -a_3 & a_2\\
|
||||
a_3 & 0 & -a_1\\
|
||||
-a_2 & a_1 & 0
|
||||
\end{bmatrix}
|
||||
\begin{bmatrix}
|
||||
b_1\\
|
||||
b_2\\
|
||||
b_3
|
||||
\end{bmatrix}
|
||||
=[a_{\times}]b
|
||||
$$
|
||||
|
||||
Using **singular value decomposition**, we can solve for $X$
|
||||
|
||||
### Epipolar Geometry
|
||||
|
||||
What constraints must hold between two projections of the same 3D point?
|
||||
|
||||
Given a 2D point in one view, where can we find the corresponding point in the other view?
|
||||
|
||||
Given only 2D correspondences, how can we calibrate the two cameras, i.e., estimate their relative position and orientation and the intrinsic parameters?
|
||||
|
||||
Key ideas:
|
||||
|
||||
- We can answer all these questions without knowledge of the 3D scene geometry
|
||||
- Important to think about projections of camera centers and visual rays into the other view
|
||||
|
||||
#### Epipolar Geometry Setup
|
||||
|
||||
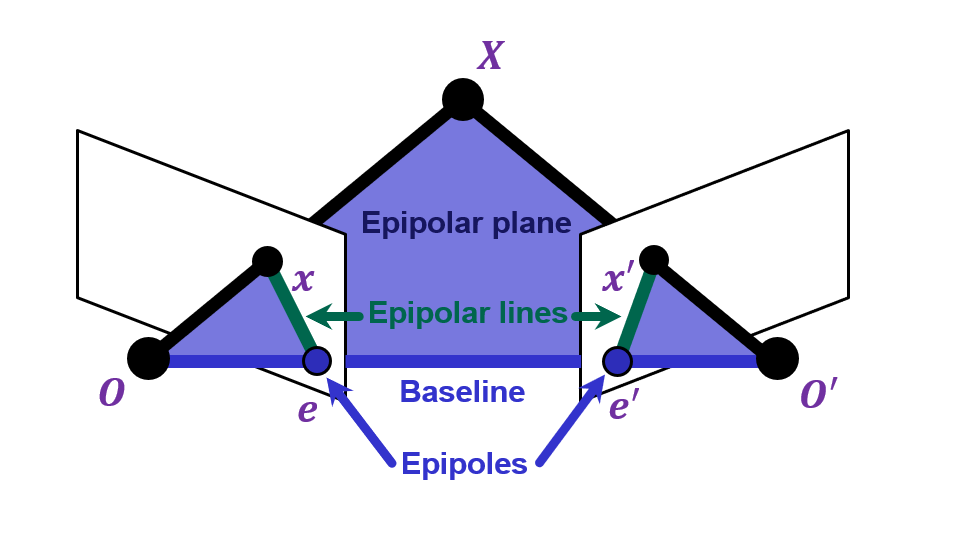
|
||||
|
||||
Suppose we have two cameras with centers $O,O'$
|
||||
|
||||
The baseline is the line connecting the origins
|
||||
|
||||
Epipoles $e,e'$ are where the baseline intersects the image planes, or projections of the other camera in each view
|
||||
|
||||
Consider a point $X$, which projects to $x$ and $x'$
|
||||
|
||||
The plane formed by $X,O,O'$ is called an epipolar plane
|
||||
There is a family of planes passing through $O$ and $O'$
|
||||
|
||||
Epipolar lines are projections of the baseline into the image planes
|
||||
|
||||
**Epipolar lines** connect the epipoles to the projections of $X$
|
||||
Equivalently, they are intersections of the epipolar plane with the image planes – thus, they come in matching pairs.
|
||||
|
||||
**Application**: This constraint can be used to find correspondences between points in two camera. by the epipolar line in one image, we can find the corresponding feature in the other image.
|
||||
|
||||
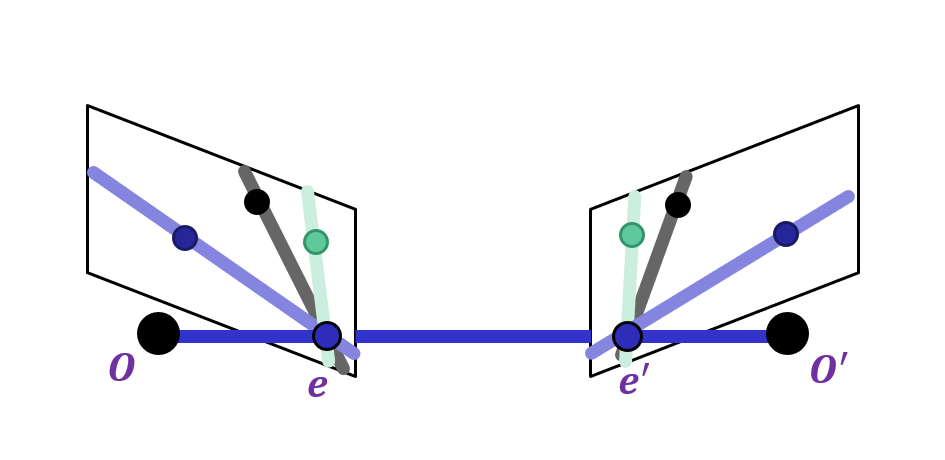
|
||||
|
||||
Epipoles are finite and may be visible in the image.
|
||||
|
||||
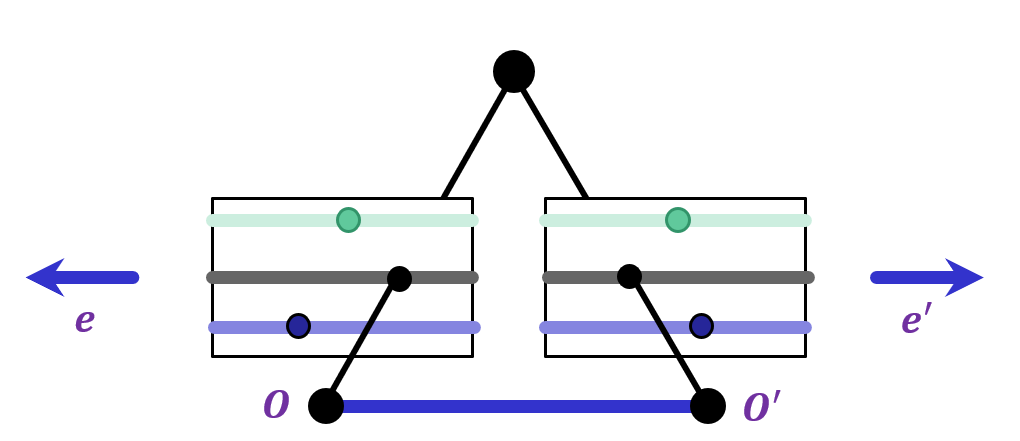
|
||||
|
||||
Epipoles are infinite, epipolar lines parallel.
|
||||
|
||||
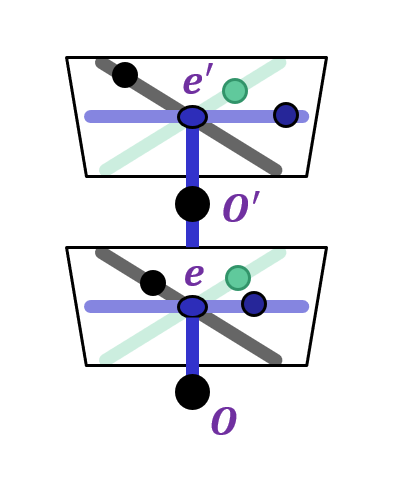
|
||||
|
||||
Epipole is "focus of expansion" and coincides with the principal point of the camera
|
||||
|
||||
Epipolar lines go out from principal point
|
||||
|
||||
Next class:
|
||||
|
||||
### The Essential and Fundamental Matrices
|
||||
|
||||
### Dense Stereo Matching
|
||||
|
||||
|
||||
177
content/CSE559A/CSE559A_L26.md
Normal file
177
content/CSE559A/CSE559A_L26.md
Normal file
@@ -0,0 +1,177 @@
|
||||
# CSE559A Lecture 26
|
||||
|
||||
## Continue on Geometry and Multiple Views
|
||||
|
||||
### The Essential and Fundamental Matrices
|
||||
|
||||
#### Math of the epipolar constraint: Calibrated case
|
||||
|
||||
Recall Epipolar Geometry
|
||||
|
||||

|
||||
|
||||
Epipolar constraint:
|
||||
|
||||
If we set the config for the first camera as the world origin and $[I|0]\begin{pmatrix}y\\1\end{pmatrix}=x$, and $[R|t]\begin{pmatrix}y\\1\end{pmatrix}=x'$, then
|
||||
|
||||
Notice that $x'\cdot [t\times (Ry)]=0$
|
||||
|
||||
$$
|
||||
x'^T E x_1 = 0
|
||||
$$
|
||||
|
||||
We denote the constraint defined by the Essential Matrix as $E$.
|
||||
|
||||
$E x$ is the epipolar line associated with $x$ ($l'=Ex$)
|
||||
|
||||
$E^T x'$ is the epipolar line associated with $x'$ ($l=E^T x'$)
|
||||
|
||||
$E e=0$ and $E^T e'=0$ ($x$ and $x'$ don't matter)
|
||||
|
||||
$E$ is singular (rank 2) and have five degrees of freedom.
|
||||
|
||||
#### Epipolar constraint: Uncalibrated case
|
||||
|
||||
If the calibration matrices $K$ and $K'$ are unknown, we can write the epipolar constraint in terms of unknown normalized coordinates:
|
||||
|
||||
$$
|
||||
x'^T_{norm} E x_{norm} = 0
|
||||
$$
|
||||
|
||||
where $x_{norm}=K^{-1} x$, $x'_{norm}=K'^{-1} x'$
|
||||
|
||||
$$
|
||||
x'^T_{norm} E x_{norm} = 0\implies x'^T_{norm} Fx=0
|
||||
$$
|
||||
|
||||
where $F=K'^{-1}EK^{-1}$ is the **Fundamental Matrix**.
|
||||
|
||||
$$
|
||||
(x',y',1)\begin{bmatrix}
|
||||
f_{11} & f_{12} & f_{13} \\
|
||||
f_{21} & f_{22} & f_{23} \\
|
||||
f_{31} & f_{32} & f_{33}
|
||||
\end{bmatrix}\begin{pmatrix}
|
||||
x\\y\\1
|
||||
\end{pmatrix}=0
|
||||
$$
|
||||
|
||||
Properties of $F$:
|
||||
|
||||
$F x$ is the epipolar line associated with $x$ ($l'=F x$)
|
||||
|
||||
$F^T x'$ is the epipolar line associated with $x'$ ($l=F^T x'$)
|
||||
|
||||
$F e=0$ and $F^T e'=0$
|
||||
|
||||
$F$ is singular (rank two) and has seven degrees of freedom
|
||||
|
||||
#### Estimating the fundamental matrix
|
||||
|
||||
Given: correspondences $x=(x,y,1)^T$ and $x'=(x',y',1)^T$
|
||||
|
||||
Constraint: $x'^T F x=0$
|
||||
|
||||
$$
|
||||
(x',y',1)\begin{bmatrix}
|
||||
f_{11} & f_{12} & f_{13} \\
|
||||
f_{21} & f_{22} & f_{23} \\
|
||||
f_{31} & f_{32} & f_{33}
|
||||
\end{bmatrix}\begin{pmatrix}
|
||||
x\\y\\1
|
||||
\end{pmatrix}=0
|
||||
$$
|
||||
|
||||
**Each pair of correspondences gives one equation (one constraint)**
|
||||
|
||||
At least 8 pairs of correspondences are needed to solve for the 9 elements of $F$ (The eight point algorithm)
|
||||
|
||||
We know $F$ needs to be singular/rank 2. How do we force it to be singular?
|
||||
|
||||
Solution: take SVD of the initial estimate and throw out the smallest singular value
|
||||
|
||||
$$
|
||||
F=U\begin{bmatrix}
|
||||
\sigma_1 & 0 \\
|
||||
0 & \sigma_2 \\
|
||||
0 & 0
|
||||
\end{bmatrix}V^T
|
||||
$$
|
||||
|
||||
## Structure from Motion
|
||||
|
||||
Not always uniquely solvable.
|
||||
|
||||
If we scale the entire scene by some factor $k$ and, at the same time, scale the camera matrices by the factor of $1/k$, the projections of the scene points remain exactly the same:
|
||||
$x\cong PX =(1/k P)(kX)$
|
||||
|
||||
Without a reference measurement, it is impossible to recover the absolute scale of the scene!
|
||||
|
||||
In general, if we transform the scene using a transformation $Q$ and apply the inverse transformation to the camera matrices, then the image observations do not change:
|
||||
|
||||
$x\cong PX =(P Q^{-1})(QX)$
|
||||
|
||||
### Types of Ambiguities
|
||||
|
||||
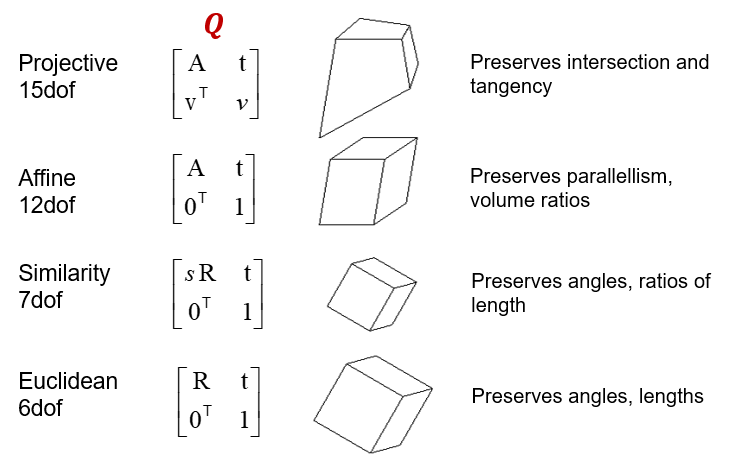
|
||||
|
||||
### Affine projection : more general than orthographic
|
||||
|
||||
A general affine projection is a 3D-to-2D linear mapping plus translation:
|
||||
|
||||
$$
|
||||
P=\begin{bmatrix}
|
||||
a_{11} & a_{12} & a_{13} & t_1 \\
|
||||
a_{21} & a_{22} & a_{23} & t_2 \\
|
||||
0 & 0 & 0 & 1
|
||||
\end{bmatrix}=\begin{bmatrix}
|
||||
A & t \\
|
||||
0^T & 1
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
In non-homogeneous coordinates:
|
||||
|
||||
$$
|
||||
\begin{pmatrix}
|
||||
x\\y\\1
|
||||
\end{pmatrix}=\begin{bmatrix}
|
||||
a_{11} & a_{12} & a_{13} \\
|
||||
a_{21} & a_{22} & a_{23}
|
||||
\end{bmatrix}\begin{pmatrix}
|
||||
X\\Y\\Z
|
||||
\end{pmatrix}+\begin{pmatrix}
|
||||
t_1\\t_2
|
||||
\end{pmatrix}=AX+t
|
||||
$$
|
||||
|
||||
### Affine Structure from Motion
|
||||
|
||||
Given: 𝑚 images of 𝑛 fixed 3D points such that
|
||||
|
||||
$$
|
||||
x_{ij}=A_iX_j+t_i, \quad i=1,\dots,m, \quad j=1,\dots,n
|
||||
$$
|
||||
|
||||
Problem: use the 𝑚𝑛 correspondences $x_{ij}$ to estimate 𝑚 projection matrices $A_i$ and translation vectors $t_i$, and 𝑛 points $X_j$
|
||||
|
||||
The reconstruction is defined up to an arbitrary affine transformation $Q$ (12 degrees of freedom):
|
||||
|
||||
$$
|
||||
\begin{bmatrix}
|
||||
A & t \\
|
||||
0^T & 1
|
||||
\end{bmatrix}\rightarrow\begin{bmatrix}
|
||||
A & t \\
|
||||
0^T & 1
|
||||
\end{bmatrix}Q^{-1}, \quad \begin{pmatrix}X_j\\1\end{pmatrix}\rightarrow Q\begin{pmatrix}X_j\\1\end{pmatrix}
|
||||
$$
|
||||
|
||||
How many constraints and unknowns for $m$ images and $n$ points?
|
||||
|
||||
$2mn$ constraints and $8m + 3n$ unknowns
|
||||
|
||||
To be able to solve this problem, we must have $2mn \geq 8m+3n-12$ (affine ambiguity takes away 12 dof)
|
||||
|
||||
E.g., for two views, we need four point correspondences
|
||||
|
||||
357
content/CSE559A/CSE559A_L3.md
Normal file
357
content/CSE559A/CSE559A_L3.md
Normal file
@@ -0,0 +1,357 @@
|
||||
# CSE559A Lecture 3
|
||||
|
||||
## Image formation
|
||||
|
||||
### Degrees of Freedom
|
||||
|
||||
$$
|
||||
x=K[R|t]X
|
||||
$$
|
||||
|
||||
$$
|
||||
w\begin{bmatrix}
|
||||
x\\
|
||||
y\\
|
||||
1
|
||||
\end{bmatrix}
|
||||
=
|
||||
\begin{bmatrix}
|
||||
\alpha & s & u_0 \\
|
||||
0 & \beta & v_0 \\
|
||||
0 & 0 & 1
|
||||
\end{bmatrix}
|
||||
\begin{bmatrix}
|
||||
r_{11} & r_{12} & r_{13} &t_x\\
|
||||
r_{21} & r_{22} & r_{23} &t_y\\
|
||||
r_{31} & r_{32} & r_{33} &t_z\\
|
||||
\end{bmatrix}
|
||||
\begin{bmatrix}
|
||||
x\\
|
||||
y\\
|
||||
z\\
|
||||
1
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
### Impact of translation of camera
|
||||
|
||||
$$
|
||||
p=K[R|t]\begin{bmatrix}
|
||||
x\\
|
||||
y\\
|
||||
z\\
|
||||
0
|
||||
\end{bmatrix}=K[R]\begin{bmatrix}
|
||||
x\\
|
||||
y\\
|
||||
z\\
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
Projection of a vanishing point or projection of a point at infinity is invariant to translation.
|
||||
|
||||
### Recover world coordinates from pixel coordinates
|
||||
|
||||
$$
|
||||
\begin{bmatrix}
|
||||
u\\
|
||||
v\\
|
||||
1
|
||||
\end{bmatrix}=K[R|t]^{-1}X
|
||||
$$
|
||||
|
||||
Key issue: where is the world origin $w$? Suppose $w=1/s$
|
||||
|
||||
$$
|
||||
\begin{aligned}
|
||||
\begin{bmatrix}
|
||||
u\\
|
||||
v\\
|
||||
1
|
||||
\end{bmatrix}
|
||||
&=sK[R|t]X\\
|
||||
K^{-1}\begin{bmatrix}
|
||||
u\\
|
||||
v\\
|
||||
1
|
||||
\end{bmatrix}
|
||||
&=s[R|t]X\\
|
||||
R^{-1}K^{-1}\begin{bmatrix}
|
||||
u\\
|
||||
v\\
|
||||
1
|
||||
\end{bmatrix}&=s[I|R^{-1}t]X\\
|
||||
R^{-1}K^{-1}\begin{bmatrix}
|
||||
u\\
|
||||
v\\
|
||||
1
|
||||
\end{bmatrix}&=[I|R^{-1}t]sX\\
|
||||
R^{-1}K^{-1}\begin{bmatrix}
|
||||
u\\
|
||||
v\\
|
||||
1
|
||||
\end{bmatrix}&=sX+sR^{-1}t\\
|
||||
\frac{1}{s}R^{-1}K^{-1}\begin{bmatrix}
|
||||
u\\
|
||||
v\\
|
||||
1
|
||||
\end{bmatrix}-R^{-1}t&=X\\
|
||||
\end{aligned}
|
||||
$$
|
||||
|
||||
## Projective Geometry
|
||||
|
||||
### Orthographic Projection
|
||||
|
||||
Special case of perspective projection when $f\to\infty$
|
||||
|
||||
- Distance for the center of projection is infinite
|
||||
- Also called parallel projection
|
||||
- Projection matrix is
|
||||
|
||||
$$
|
||||
w\begin{bmatrix}
|
||||
u\\
|
||||
v\\
|
||||
1
|
||||
\end{bmatrix}=
|
||||
\begin{bmatrix}
|
||||
f & 0 & 0 & 0\\
|
||||
0 & f & 0 & 0\\
|
||||
0 & 0 & 0 & s\\
|
||||
\end{bmatrix}
|
||||
\begin{bmatrix}
|
||||
x\\
|
||||
y\\
|
||||
z\\
|
||||
1
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
Continue in later part of the course
|
||||
|
||||
## Image processing foundations
|
||||
|
||||
### Motivation for image processing
|
||||
|
||||
Representational Motivation:
|
||||
|
||||
- We need more than raw pixel values
|
||||
|
||||
Computational Motivation:
|
||||
|
||||
- Many image processing operations must be run across many locations in a image
|
||||
- A loop in python is slow
|
||||
- High-level libraries reduce errors, developer time, and algorithm runtime
|
||||
- Two common libraries:
|
||||
- Torch+Torchvision: Focus on deep learning
|
||||
- scikit-image: Focus on classical image processing algorithms
|
||||
|
||||
### Operations on images
|
||||
|
||||
#### Point operations
|
||||
|
||||
Operations that are applied to one pixel at a time
|
||||
|
||||
Negative image
|
||||
|
||||
$$
|
||||
I_{neg}(x,y)=L-1-I(x,y)
|
||||
$$
|
||||
|
||||
Power law transformation:
|
||||
|
||||
$$
|
||||
I_{out}(x,y)=cI(x,y)^{\gamma}
|
||||
$$
|
||||
|
||||
- $c$ is a constant
|
||||
- $\gamma$ is the gamma value
|
||||
|
||||
Contrast stretching
|
||||
|
||||
use function to stretch the range of pixel values
|
||||
|
||||
$$
|
||||
I_{out}(x,y)=f(I(x,y))
|
||||
$$
|
||||
|
||||
- $f$ is a function that stretches the range of pixel values
|
||||
|
||||
Image histogram
|
||||
|
||||
- Histogram of an image is a plot of the frequency of each pixel value
|
||||
|
||||
Limitations:
|
||||
|
||||
- No spatial information
|
||||
- No information about the relationship between pixels
|
||||
|
||||
#### Linear filtering in spatial domain
|
||||
|
||||
Operations that are applied to a neighborhood at each position
|
||||
|
||||
Used to:
|
||||
|
||||
- Enhance image features
|
||||
- Denoise, sharpen, resize
|
||||
- Extract information about image structure
|
||||
- Edge detection, corner detection, blob detection
|
||||
- Detect image patterns
|
||||
- Template matching
|
||||
- Convolutional Neural Networks
|
||||
|
||||
Image filtering
|
||||
|
||||
Do dot product of the image with a kernel
|
||||
|
||||
$$
|
||||
h[m,n]=\sum_{k=0}^{m-i}\sum_{l=0}^{n-i}g[k,l]f[m+k,n+l]
|
||||
$$
|
||||
|
||||
```python
|
||||
def filter2d(image, kernel):
|
||||
"""
|
||||
Apply a 2D filter to an image, do not use this in practice
|
||||
"""
|
||||
for i in range(image.shape[0]):
|
||||
for j in range(image.shape[1]):
|
||||
image[i, j] = np.dot(kernel, image[i-1:i+2, j-1:j+2])
|
||||
return image
|
||||
```
|
||||
|
||||
Computational cost: $k^2mn$, assume $k$ is the size of the kernel and $m$ and $n$ are the dimensions of the image
|
||||
|
||||
Do not use this in practice, use built-in functions instead.
|
||||
|
||||
**Box filter**
|
||||
|
||||
$$
|
||||
\frac{1}{9}\begin{bmatrix}
|
||||
1 & 1 & 1\\
|
||||
1 & 1 & 1\\
|
||||
1 & 1 & 1
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
Smooths the image
|
||||
|
||||
**Identity filter**
|
||||
|
||||
$$
|
||||
\begin{bmatrix}
|
||||
0 & 0 & 0\\
|
||||
0 & 1 & 0\\
|
||||
0 & 0 & 0
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
Does not change the image
|
||||
|
||||
**Sharpening filter**
|
||||
|
||||
$$
|
||||
\begin{bmatrix}
|
||||
0 & 0 & 0 \\
|
||||
0 & 2 & 0 \\
|
||||
0 & 0 & 0
|
||||
\end{bmatrix}-
|
||||
\begin{bmatrix}
|
||||
1 & 1 & 1 \\
|
||||
1 & 1 & 1 \\
|
||||
1 & 1 & 1
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
Enhances the image edges
|
||||
|
||||
**Vertical edge detection**
|
||||
|
||||
$$
|
||||
\begin{bmatrix}
|
||||
1 & 0 & -1 \\
|
||||
2 & 0 & -2 \\
|
||||
1 & 0 & -1
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
Detects vertical edges
|
||||
|
||||
**Horizontal edge detection**
|
||||
|
||||
$$
|
||||
\begin{bmatrix}
|
||||
1 & 2 & 1 \\
|
||||
0 & 0 & 0 \\
|
||||
-1 & -2 & -1
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
Detects horizontal edges
|
||||
|
||||
Key property:
|
||||
|
||||
- Linear:
|
||||
- `filter(I,f_1+f_2)=filter(I,f_1)+filter(I,f_2)`
|
||||
- Scale invariant:
|
||||
- `filter(I,af)=a*filter(I,f)`
|
||||
- Shift invariant:
|
||||
- `filter(I,shift(f))=shift(filter(I,f))`
|
||||
- Commutative:
|
||||
- `filter(I,f_1)*filter(I,f_2)=filter(I,f_2)*filter(I,f_1)`
|
||||
- Associative:
|
||||
- `filter(I,f_1)*(filter(I,f_2)*filter(I,f_3))=(filter(I,f_1)*filter(I,f_2))*filter(I,f_3)`
|
||||
- Distributive:
|
||||
- `filter(I,f_1+f_2)=filter(I,f_1)+filter(I,f_2)`
|
||||
- Identity:
|
||||
- `filter(I,f_0)=I`
|
||||
|
||||
Important filter:
|
||||
|
||||
**Gaussian filter**
|
||||
|
||||
$$
|
||||
G(x,y)=\frac{1}{2\pi\sigma^2}e^{-\frac{x^2+y^2}{2\sigma^2}}
|
||||
$$
|
||||
|
||||
Smooths the image (Gaussian blur)
|
||||
|
||||
Common mistake: Make filter too large, visualize the filter before applying it (make the value on the edge $3\sigma$)
|
||||
|
||||
Properties of Gaussian filter:
|
||||
|
||||
- Remove high frequency components
|
||||
- Convolution with self is another Gaussian filter
|
||||
- Separable kernel:
|
||||
- `G(x,y)=G(x)G(y)` (factorable into the product of two 1D Gaussian filters)
|
||||
|
||||
##### Filter Separability
|
||||
|
||||
- Separable filter:
|
||||
- `f(x,y)=f(x)f(y)`
|
||||
|
||||
Example:
|
||||
|
||||
$$
|
||||
\begin{bmatrix}
|
||||
1 & 2 & 1 \\
|
||||
2 & 4 & 2 \\
|
||||
1 & 2 & 1
|
||||
\end{bmatrix}=
|
||||
\begin{bmatrix}
|
||||
1 \\
|
||||
2 \\
|
||||
1
|
||||
\end{bmatrix}\times
|
||||
\begin{bmatrix}
|
||||
1 & 2 & 1
|
||||
\end{bmatrix}
|
||||
$$
|
||||
|
||||
Gaussian filter is separable
|
||||
|
||||
$$
|
||||
G(x,y)=\frac{1}{2\pi\sigma^2}e^{-\frac{x^2+y^2}{2\sigma^2}}=G(x)G(y)
|
||||
$$
|
||||
|
||||
This reduces the computational cost of the filter from $k^2mn$ to $2kmn$
|
||||
196
content/CSE559A/CSE559A_L4.md
Normal file
196
content/CSE559A/CSE559A_L4.md
Normal file
@@ -0,0 +1,196 @@
|
||||
# CSE559A Lecture 4
|
||||
|
||||
## Practical issues with filtering
|
||||
|
||||
$$
|
||||
h[m,n]=\sum_{k=0}^{m-i}\sum_{l=0}^{n-i}g[k,l]f[m+k,n+l]
|
||||
$$
|
||||
|
||||
Loss of information on edges of image
|
||||
|
||||
- The filter window falls off the edge of the image
|
||||
- Need to extrapolate
|
||||
- Methods:
|
||||
- clip filter
|
||||
- wrap around (extend the image periodically)
|
||||
- copy edge (extend the image by copying the edge pixels)
|
||||
- reflect across edge (extend the image by reflecting the edge pixels)
|
||||
|
||||
## Convolution vs Correlation
|
||||
|
||||
- Convolution:
|
||||
- The filter is flipped and convolved with the image
|
||||
|
||||
$$
|
||||
h[m,n]=\sum_{k=i}^{m}\sum_{l=i}^{n}g[k,l]f[m-k,n-l]
|
||||
$$
|
||||
|
||||
- Correlation:
|
||||
- The filter is not flipped and convolved with the image
|
||||
|
||||
$$
|
||||
h[m,n]=\sum_{k=0}^{m-i}\sum_{l=0}^{n-i}g[k,l]f[m+k,n+l]
|
||||
$$
|
||||
|
||||
does not matter for deep learning
|
||||
|
||||
```python
|
||||
scipy.signal.convolve2d(image, kernel, mode='same')
|
||||
scipy.signal.correlate2d(image, kernel, mode='same')
|
||||
```
|
||||
|
||||
but pytorch uses correlation for convolution, the convolution in pytorch is actually a correlation in scipy.
|
||||
|
||||
## Frequency domain representation of linear image filters
|
||||
|
||||
TL;DR: It can be helpful to think about linear spatial filters in terms fro their frequency domain representation
|
||||
|
||||
- Fourier transform and frequency domain
|
||||
- The convolution theorem
|
||||
|
||||
Hybrid image: More in homework 2
|
||||
|
||||
Human eye is sensitive to low frequencies in far field, high frequencies in near field
|
||||
|
||||
### Change of basis from an image perspective
|
||||
|
||||
For vectors:
|
||||
|
||||
- Vector -> Invertible matrix multiplication -> New vector
|
||||
- Normally we think of the standard/natural basis, with unit vectors in the direction of the axes
|
||||
|
||||
For images:
|
||||
|
||||
- Image -> Vector -> Invertible matrix multiplication -> New vector -> New image
|
||||
- Standard basis is just a collection of one-hot images
|
||||
|
||||
Use `im.flatten()` to convert an image to a vector
|
||||
|
||||
$$
|
||||
Image(M^{-1}GMVec(I))
|
||||
$$
|
||||
|
||||
- M is the change of basis matrix, $M^{-1}M=I$
|
||||
- G is the operation we want to perform
|
||||
- Vec(I) is the vectorized image
|
||||
|
||||
#### Lossy image compression (JPEG)
|
||||
|
||||
- JPEG is a lossy compression algorithm
|
||||
- It uses the DCT (Discrete Cosine Transform) to transform the image to the frequency domain
|
||||
- The DCT is a linear operation, so it can be represented as a matrix multiplication
|
||||
- The JPEG algorithm then quantizes the coefficients and entropy codes them (use Huffman coding)
|
||||
|
||||
## Thinking in frequency domain
|
||||
|
||||
### Fourier transform
|
||||
|
||||
Any univariate function can be represented as a weighted sum of sine and cosine functions
|
||||
|
||||
$$
|
||||
X[k]=\sum_{n=N-1}^{0}x[n]e^{-2\pi ikn/N}=\sum_{n=0}^{N-1}x[n]\left[\sin\left(\frac{2\pi}{N}kn\right)+i\cos\left(\frac{2\pi}{N}kn\right)\right]
|
||||
$$
|
||||
|
||||
- $X[k]$ is the Fourier transform of $x[n]$
|
||||
- $e^{-2\pi ikn/N}$ is the basis function
|
||||
- $x[n]$ is the original function
|
||||
|
||||
Real part:
|
||||
|
||||
$$
|
||||
\text{Re}(X[k])=\sum_{n=0}^{N-1}x[n]\cos\left(\frac{2\pi}{N}kn\right)
|
||||
$$
|
||||
|
||||
Imaginary part:
|
||||
|
||||
$$
|
||||
\text{Im}(X[k])=\sum_{n=0}^{N-1}x[n]\sin\left(\frac{2\pi}{N}kn\right)
|
||||
$$
|
||||
|
||||
Fourier transform stores the magnitude and phase of the sine and cosine function at each frequency
|
||||
|
||||
- Amplitude: encodes how much signal there is at a particular frequency
|
||||
- Phase: encodes the spacial information (indirectly)
|
||||
- For mathematical convenience, this is often written as a complex number
|
||||
|
||||
Amplitude: $A=\pm\sqrt{\text{Re}(\omega)^2+\text{Im}(\omega)^2}$
|
||||
|
||||
Phase: $\phi=\tan^{-1}\left(\frac{\text{Im}(\omega)}{\text{Re}(\omega)}\right)$
|
||||
|
||||
So use $A\sin(\omega+\phi)$ to represent the signal
|
||||
|
||||
Example:
|
||||
|
||||
$g(t)=\sin(2\pi ft)+\frac{1}{3}\sin(2\pi (3f)t)$
|
||||
|
||||
### Fourier analysis of images
|
||||
|
||||
Intensity image and Fourier image
|
||||
|
||||
Signals can be composed.
|
||||
|
||||

|
||||
|
||||
Note: frequency domain is often visualized using a log of the absolute value of the Fourier transform
|
||||
|
||||
Blurring the image is to delete the high frequency components (removing the center of the frequency domain)
|
||||
|
||||
## Convolution theorem
|
||||
|
||||
The Fourier transform of the convolution of two functions is the product of their Fourier transforms
|
||||
|
||||
$$
|
||||
F[f*g]=F[f]F[g]
|
||||
$$
|
||||
|
||||
- $F$ is the Fourier transform
|
||||
- $*$ is the convolution
|
||||
|
||||
Convolution in spatial domain is equivalent to multiplication in frequency domain
|
||||
|
||||
$$
|
||||
g*h=F^{-1}[F[g]F[h]]
|
||||
$$
|
||||
|
||||
- $F^{-1}$ is the inverse Fourier transform
|
||||
|
||||
### Is convolution invertible?
|
||||
|
||||
- Redo the convolution in the image domain is division in the frequency domain
|
||||
|
||||
$$
|
||||
g*h=F^{-1}\left[\frac{F[g]}{F[h]}\right]
|
||||
$$
|
||||
|
||||
- This is not always possible, because $F[h]$ may be zero and we may not know the filter
|
||||
|
||||
Small perturbations in the frequency domain can cause large perturbations in the spatial domain and vice versa
|
||||
|
||||
Deconvolution is hard and a active area of research
|
||||
|
||||
- Even if you know the filter, it is not always possible to invert the convolution, requires strong regularization
|
||||
- If you don't know the filter, it is even harder
|
||||
|
||||
## 2D image transformations
|
||||
|
||||
### Array slicing and image wrapping
|
||||
|
||||
Fast operation for extracting a subimage
|
||||
|
||||
- cropped image `image[10:20, 10:20]`
|
||||
- flipped image `image[::-1, ::-1]`
|
||||
|
||||
Image wrapping allows more flexible operations
|
||||
|
||||
#### Upsampling an image
|
||||
|
||||
- Upsampling an image is the process of increasing the resolution of the image
|
||||
|
||||
Bilinear interpolation:
|
||||
|
||||
- Use the average of the 4 nearest pixels to determine the value of the new pixel
|
||||
|
||||
Other interpolation methods:
|
||||
|
||||
- Bicubic interpolation: Use the average of the 16 nearest pixels to determine the value of the new pixel
|
||||
- Nearest neighbor interpolation: Use the value of the nearest pixel to determine the value of the new pixel
|
||||
222
content/CSE559A/CSE559A_L5.md
Normal file
222
content/CSE559A/CSE559A_L5.md
Normal file
@@ -0,0 +1,222 @@
|
||||
# CSE559A Lecture 5
|
||||
|
||||
## Continue on linear interpolation
|
||||
|
||||
- In linear interpolation, extreme values are at the boundary.
|
||||
- In bicubic interpolation, extreme values may be inside.
|
||||
|
||||
`scipy.interpolate.RegularGridInterpolator`
|
||||
|
||||
### Image transformations
|
||||
|
||||
Image warping is a process of applying transformation $T$ to an image.
|
||||
|
||||
Parametric (global) warping: $T(x,y)=(x',y')$
|
||||
|
||||
Geometric transformation: $T(x,y)=(x',y')$ This applies to each pixel in the same way. (global)
|
||||
|
||||
#### Translation
|
||||
|
||||
$T(x,y)=(x+a,y+b)$
|
||||
|
||||
matrix form:
|
||||
|
||||
$$
|
||||
\begin{pmatrix}
|
||||
x'\\y'
|
||||
\end{pmatrix}
|
||||
=
|
||||
\begin{pmatrix}
|
||||
1&0\\0&1
|
||||
\end{pmatrix}
|
||||
\begin{pmatrix}
|
||||
x\\y
|
||||
\end{pmatrix}
|
||||
+
|
||||
\begin{pmatrix}
|
||||
a\\b
|
||||
\end{pmatrix}
|
||||
$$
|
||||
|
||||
#### Scaling
|
||||
|
||||
$T(x,y)=(s_xx,s_yy)$ matrix form:
|
||||
|
||||
$$
|
||||
\begin{pmatrix}
|
||||
x'\\y'
|
||||
\end{pmatrix}
|
||||
=
|
||||
\begin{pmatrix}
|
||||
s_x&0\\0&s_y
|
||||
\end{pmatrix}
|
||||
\begin{pmatrix}
|
||||
x\\y
|
||||
\end{pmatrix}
|
||||
$$
|
||||
|
||||
#### Rotation
|
||||
|
||||
$T(x,y)=(x\cos\theta-y\sin\theta,x\sin\theta+y\cos\theta)$
|
||||
|
||||
matrix form:
|
||||
|
||||
$$
|
||||
\begin{pmatrix}
|
||||
x'\\y'
|
||||
\end{pmatrix}
|
||||
=
|
||||
\begin{pmatrix}
|
||||
\cos\theta&-\sin\theta\\\sin\theta&\cos\theta
|
||||
\end{pmatrix}
|
||||
\begin{pmatrix}
|
||||
x\\y
|
||||
\end{pmatrix}
|
||||
$$
|
||||
|
||||
To undo the rotation, we need to rotate the image by $-\theta$. This is equivalent to apply $R^T$ to the image.
|
||||
|
||||
#### Affine transformation
|
||||
|
||||
$T(x,y)=(a_1x+a_2y+a_3,b_1x+b_2y+b_3)$
|
||||
|
||||
matrix form:
|
||||
|
||||
$$
|
||||
\begin{pmatrix}
|
||||
x'\\y'
|
||||
\end{pmatrix}
|
||||
=
|
||||
\begin{pmatrix}
|
||||
a_1&a_2&a_3\\b_1&b_2&b_3
|
||||
\end{pmatrix}
|
||||
\begin{pmatrix}
|
||||
x\\y\\1
|
||||
\end{pmatrix}
|
||||
$$
|
||||
|
||||
Taking all the transformations together.
|
||||
|
||||
#### Projective homography
|
||||
|
||||
$T(x,y)=(\frac{ax+by+c}{gx+hy+i},\frac{dx+ey+f}{gx+hy+i})$
|
||||
|
||||
$$
|
||||
\begin{pmatrix}
|
||||
x'\\y'\\1
|
||||
\end{pmatrix}
|
||||
=
|
||||
\begin{pmatrix}
|
||||
a&b&c\\d&e&f\\g&h&i
|
||||
\end{pmatrix}
|
||||
\begin{pmatrix}
|
||||
x\\y\\1
|
||||
\end{pmatrix}
|
||||
$$
|
||||
|
||||
### Image warping
|
||||
|
||||
#### Forward warping
|
||||
|
||||
Send each pixel to its new position and do the matching.
|
||||
|
||||
- May cause gaps where the pixel is not mapped to any pixel.
|
||||
|
||||
#### Inverse warping
|
||||
|
||||
Send each new position to its original position and do the matching.
|
||||
|
||||
- Some mapping may not be invertible.
|
||||
|
||||
#### Which one is better?
|
||||
|
||||
- Inverse warping is better because it usually more efficient, doesn't have a problem with holes.
|
||||
- However, it may not always be possible to find the inverse mapping.
|
||||
|
||||
## Sampling and Aliasing
|
||||
|
||||
### Naive sampling
|
||||
|
||||
- Remove half of the rows and columns in the image.
|
||||
|
||||
Example:
|
||||
|
||||
When sampling a sine wave, the result may interpret as different wave.
|
||||
|
||||
#### Nyquist-Shannon sampling theorem
|
||||
|
||||
- A bandlimited signal can be uniquely determined by its samples if the sampling rate is greater than twice the maximum frequency of the signal.
|
||||
|
||||
- If the sampling rate is less than twice the maximum frequency of the signal, the signal will be aliased.
|
||||
|
||||
#### Anti-aliasing
|
||||
|
||||
- Sample more frequently. (not always possible)
|
||||
- Get rid of all frequencies that are greater than half of the new sampling frequency.
|
||||
- Use a low-pass filter to get rid of all frequencies that are greater than half of the new sampling frequency. (eg, Gaussian filter)
|
||||
|
||||
```python
|
||||
import scipy.ndimage as ndimage
|
||||
def down_sample(height, width, image):
|
||||
# Apply Gaussian blur to the image
|
||||
im_blur = ndimage.gaussian_filter(image, sigma=1)
|
||||
# Down sample the image by taking every second pixel
|
||||
return im_blur[::2, ::2]
|
||||
```
|
||||
|
||||
## Nonlinear filtering
|
||||
|
||||
### Median filter
|
||||
|
||||
Replace the value of a pixel with the median value of its neighbors.
|
||||
|
||||
- Good for removing salt and pepper noise. (black and white dot noise)
|
||||
|
||||
### Morphological operations
|
||||
|
||||
Binary image: image with only 0 and 1.
|
||||
|
||||
Let $B$ be a structuring element and $A$ be the original image (binary image).
|
||||
|
||||
- Erosion: $A\ominus B = \{p\mid B_p\subseteq A\}$, this is the set of all points that are completely covered by $B$.
|
||||
- Dilation: $A\oplus B = \{p\mid B_p\cap A\neq\emptyset\}$, this is the set of all points that are at least partially covered by $B$.
|
||||
- Opening: $A\circ B = (A\ominus B)\oplus B$, this is the set of all points that are at least partially covered by $B$ after erosion.
|
||||
- Closing: $A\bullet B = (A\oplus B)\ominus B$, this is the set of all points that are completely covered by $B$ after dilation.
|
||||
|
||||
Boundary extraction: use XOR operation on eroded image and original image.
|
||||
|
||||
Connected component labeling: label the connected components in the image. _use prebuild function in scipy.ndimage_
|
||||
|
||||
## Light,Camera/Eyes, and Color
|
||||
|
||||
### Principles of grouping and Gestalt Laws
|
||||
|
||||
- Proximity: objects that are close to each other are more likely to be grouped together.
|
||||
- Similarity: objects that are similar are more likely to be grouped together.
|
||||
- Closure: objects that form a closed path are more likely to be grouped together.
|
||||
- Continuity: objects that form a continuous path are more likely to be grouped together.
|
||||
|
||||
### Light and surface interactions
|
||||
|
||||
A photon's life choices:
|
||||
|
||||
- Absorption
|
||||
- Diffuse reflection (nice to model) (lambertian surface)
|
||||
- Specular reflection (mirror-like) (perfect mirror)
|
||||
- Transparency
|
||||
- Refraction
|
||||
- Fluorescence (returns different color)
|
||||
- Subsurface scattering (candles)
|
||||
- Photosphorescence
|
||||
- Interreflection
|
||||
|
||||
#### BRDF (Bidirectional Reflectance Distribution Function)
|
||||
|
||||
$$
|
||||
\rho(\theta_i,\phi_i,\theta_o,\phi_o)
|
||||
$$
|
||||
|
||||
- $\theta_i$ is the angle of incidence.
|
||||
- $\phi_i$ is the azimuthal angle of incidence.
|
||||
- $\theta_o$ is the angle of reflection.
|
||||
- $\phi_o$ is the azimuthal angle of reflection.
|
||||
213
content/CSE559A/CSE559A_L6.md
Normal file
213
content/CSE559A/CSE559A_L6.md
Normal file
@@ -0,0 +1,213 @@
|
||||
# CSE559A Lecture 6
|
||||
|
||||
## Continue on Light, eye/camera, and color
|
||||
|
||||
### BRDF (Bidirectional Reflectance Distribution Function)
|
||||
|
||||
$$
|
||||
\rho(\theta_i,\phi_i,\theta_o,\phi_o)
|
||||
$$
|
||||
|
||||
#### Diffuse Reflection
|
||||
|
||||
- Dull, matte surface like chalk or latex paint
|
||||
|
||||
- Most often used in computer vision
|
||||
- Brightness _does_ depend on direction of illumination
|
||||
|
||||
Diffuse reflection governed by Lambert's law: $I_d = k_d N\cdot L I_i$
|
||||
|
||||
- $N$: surface normal
|
||||
- $L$: light direction
|
||||
- $I_i$: incident light intensity
|
||||
- $k_d$: albedo
|
||||
|
||||
$$
|
||||
\rho(\theta_i,\phi_i,\theta_o,\phi_o)=k_d \cos\theta_i
|
||||
$$
|
||||
|
||||
#### Photometric Stereo
|
||||
|
||||
Suppose there are three light sources, $L_1, L_2, L_3$, and we have the following measurements:
|
||||
|
||||
$$
|
||||
I_1 = k_d N\cdot L_1
|
||||
$$
|
||||
|
||||
$$
|
||||
I_2 = k_d N\cdot L_2
|
||||
$$
|
||||
|
||||
$$
|
||||
I_3 = k_d N\cdot L_3
|
||||
$$
|
||||
|
||||
We can solve for $N$ by taking the dot product of $N$ and each light direction and then solving the system of equations.
|
||||
|
||||
Will not do this in the lecture.
|
||||
|
||||
#### Specular Reflection
|
||||
|
||||
- Mirror-like surface
|
||||
|
||||
$$
|
||||
I_e=\begin{cases}
|
||||
I_i & \text{if } V=R \\
|
||||
0 & \text{if } V\neq R
|
||||
\end{cases}
|
||||
$$
|
||||
|
||||
- $V$: view direction
|
||||
- $R$: reflection direction
|
||||
- $\theta_i$: angle between the incident light and the surface normal
|
||||
|
||||
Near-perfect mirror have a high light around $R$.
|
||||
|
||||
common model:
|
||||
|
||||
$$
|
||||
I_e=k_s (V\cdot R)^{n_s}I_i
|
||||
$$
|
||||
|
||||
- $k_s$: specular reflection coefficient
|
||||
- $n_s$: shininess (imperfection of the surface)
|
||||
- $I_i$: incident light intensity
|
||||
|
||||
#### Phong illumination model
|
||||
|
||||
- Phong approximation of surface reflectance
|
||||
- Assume reflectance is modeled by three compoents
|
||||
- Diffuse reflection
|
||||
- Specular reflection
|
||||
- Ambient reflection
|
||||
|
||||
$$
|
||||
I_e=k_a I_a + I_i \left[k_d (N\cdot L) + k_s (V\cdot R)^{n_s}\right]
|
||||
$$
|
||||
|
||||
- $k_a$: ambient reflection coefficient
|
||||
- $I_a$: ambient light intensity
|
||||
- $k_d$: diffuse reflection coefficient
|
||||
- $k_s$: specular reflection coefficient
|
||||
- $n_s$: shininess
|
||||
- $I_i$: incident light intensity
|
||||
|
||||
Many other models.
|
||||
|
||||
#### Measuring BRDF
|
||||
|
||||
Use Gonioreflectometer.
|
||||
|
||||
- Device for measuring the reflectance of a surface as a function of the incident and reflected angles.
|
||||
- Can be used to measure the BRDF of a surface.
|
||||
|
||||
BRDF dataset:
|
||||
|
||||
- MERL dataset
|
||||
- CURET dataset
|
||||
|
||||
### Camera/Eye
|
||||
|
||||
#### DSLR Camera
|
||||
|
||||
- Pinhole camera model
|
||||
- Lens
|
||||
- Aperture (the pinhole)
|
||||
- Sensor
|
||||
- ...
|
||||
|
||||
#### Digital Camera block diagram
|
||||
|
||||
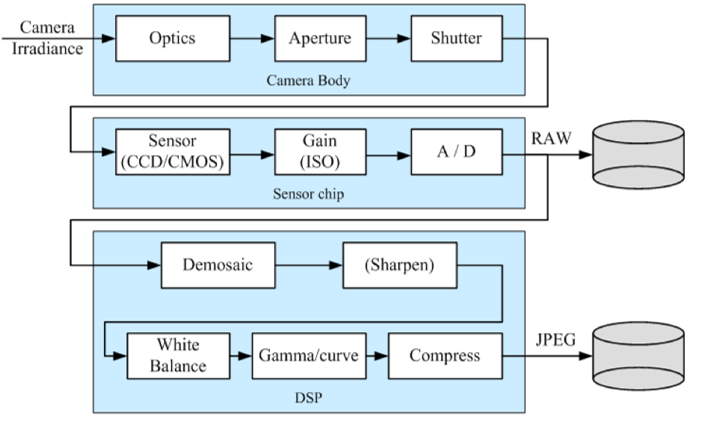
|
||||
|
||||
Scanning protocols:
|
||||
|
||||
- Global shutter: all pixels are exposed at the same time
|
||||
- Interlaced: odd and even lines are exposed at different times
|
||||
- Rolling shutter: each line is exposed as it is read out
|
||||
|
||||
#### Eye
|
||||
|
||||
- Pupil
|
||||
- Iris
|
||||
- Retina
|
||||
- Rods and cones
|
||||
- ...
|
||||
|
||||
#### Eye Movements
|
||||
|
||||
- Saccade
|
||||
- Can be consciously controlled. Related to perceptual attention.
|
||||
- 200ms to initiation, 20 to 200ms to carry out. Large amplitude.
|
||||
- Smooth pursuit
|
||||
- Tracking an object
|
||||
- Difficult w/o an object to track!
|
||||
- Microsaccade and Ocular microtremor (OMT)
|
||||
- Involuntary. Smaller amplitude. Especially evident during prolonged
|
||||
fixation.
|
||||
|
||||
#### Contrast Sensitivity
|
||||
|
||||
- Uniform contrast image content, with increasing frequency
|
||||
- Why not uniform across the top?
|
||||
- Low frequencies: harder to see because of slower intensity changes
|
||||
- Higher frequencies: harder to see because of ability of our visual system to resolve fine features
|
||||
|
||||
### Color Perception
|
||||
|
||||
Visible light spectrum: 380 to 780 nm
|
||||
|
||||
- 400 to 500 nm: blue
|
||||
- 500 to 600 nm: green
|
||||
- 600 to 700 nm: red
|
||||
|
||||
#### HSV model
|
||||
|
||||
We use Gaussian functions to model the sensitivity of the human eye to different wavelengths.
|
||||
|
||||
- Hue: color (the wavelength of the highest peak of the sensitivity curve)
|
||||
- Saturation: color purity (the variance of the sensitivity curve)
|
||||
- Value: color brightness (the highest peak of the sensitivity curve)
|
||||
|
||||
#### Color Sensing in Camera (RGB)
|
||||
|
||||
- 3-chip vs. 1-chip: quality vs. cost
|
||||
|
||||
Bayer filter:
|
||||
|
||||
- Why more green?
|
||||
- Human eye is more sensitive to green light.
|
||||
|
||||
#### Color spaces
|
||||
|
||||
Images in python:
|
||||
|
||||
As matrix.
|
||||
|
||||
```python
|
||||
import matplotlib.pyplot as plt
|
||||
|
||||
from mpl_toolkits.mplot3d import Axes3D
|
||||
from skimage import io
|
||||
|
||||
def plot_rgb_3d(image_path):
|
||||
image = io.imread(image_path)
|
||||
r, g, b = image[:,:,0], image[:,:,1], image[:,:,2]
|
||||
fig = plt.figure()
|
||||
ax = fig.add_subplot(111, projection='3d')
|
||||
ax.scatter(r.flatten(), g.flatten(), b.flatten(), c=image.reshape(-1, 3)/255.0, marker='.')
|
||||
ax.set_xlabel('Red')
|
||||
ax.set_ylabel('Green')
|
||||
ax.set_zlabel('Blue')
|
||||
plt.show()
|
||||
|
||||
plot_rgb_3d('image.jpg')
|
||||
```
|
||||
|
||||
Other color spaces:
|
||||
|
||||
- YCbCr (fast to compute, usually used in TV)
|
||||
- HSV
|
||||
- L\*a\*b\* (CIELAB, perceptually uniform color space)
|
||||
|
||||
Most information is in the intensity channel.
|
||||
228
content/CSE559A/CSE559A_L7.md
Normal file
228
content/CSE559A/CSE559A_L7.md
Normal file
@@ -0,0 +1,228 @@
|
||||
# CSE559A Lecture 7
|
||||
|
||||
## Computer Vision (In Artificial Neural Networks for Image Understanding)
|
||||
|
||||
Early example of image understanding using Neural Networks: [Back propagation for zip code recognition]
|
||||
|
||||
Central idea; representation change, on each layer of feature.
|
||||
|
||||
Plan for next few weeks:
|
||||
|
||||
1. How do we train such models?
|
||||
2. What are those building blocks
|
||||
3. How should we combine those building blocks?
|
||||
|
||||
## How do we train such models?
|
||||
|
||||
CV is finally useful...
|
||||
|
||||
1. Image classification
|
||||
2. Image segmentation
|
||||
3. Object detection
|
||||
|
||||
ImageNet Large Scale Visual Recognition Challenge (ILSVRC)
|
||||
|
||||
- 1000 classes
|
||||
- 1.2 million images
|
||||
- 10000 test images
|
||||
|
||||
### Deep Learning (Just neural networks)
|
||||
|
||||
Bigger datasets, larger models, faster computers, lots of incremental improvements.
|
||||
|
||||
```python
|
||||
import torch
|
||||
import torch.nn as nn
|
||||
import torch.nn.functional as F
|
||||
|
||||
class Net(nn.Module):
|
||||
def __init__(self):
|
||||
super(Net, self).__init__()
|
||||
self.conv1 = nn.Conv2d(1, 6, 5)
|
||||
self.conv2 = nn.Conv2d(6, 16, 5)
|
||||
self.fc1 = nn.Linear(16 * 5 * 5, 120)
|
||||
self.fc2 = nn.Linear(120, 84)
|
||||
self.fc3 = nn.Linear(84, 10)
|
||||
|
||||
def forward(self, x):
|
||||
x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
|
||||
x = F.max_pool2d(F.relu(self.conv2(x)), 2)
|
||||
x = x.view(-1, self.num_flat_features(x))
|
||||
x = F.relu(self.fc1(x))
|
||||
x = F.relu(self.fc2(x))
|
||||
x = self.fc3(x)
|
||||
return x
|
||||
|
||||
def num_flat_features(self, x):
|
||||
size = x.size()[1:]
|
||||
num_features = 1
|
||||
for s in size:
|
||||
num_features *= s
|
||||
return num_features
|
||||
|
||||
# create pytorch dataset and dataloader
|
||||
dataset = torch.utils.data.TensorDataset(torch.randn(1000, 1, 28, 28), torch.randint(10, (1000,)))
|
||||
dataloader = torch.utils.data.DataLoader(dataset, batch_size=4, shuffle=True, num_workers=2)
|
||||
|
||||
# training process
|
||||
|
||||
net = Net()
|
||||
optimizer = optim.Adam(net.parameters(), lr=0.001)
|
||||
criterion = nn.CrossEntropyLoss()
|
||||
|
||||
# loop over the dataset multiple times
|
||||
for epoch in range(2):
|
||||
for i, data in enumerate(dataloader, 0):
|
||||
inputs, labels = data
|
||||
optimizer.zero_grad()
|
||||
outputs = net(inputs)
|
||||
loss = criterion(outputs, labels)
|
||||
loss.backward()
|
||||
optimizer.step()
|
||||
|
||||
print(f"Finished Training")
|
||||
```
|
||||
|
||||
Some generated code above.
|
||||
|
||||
### Supervised Learning
|
||||
|
||||
Training: given a dataset, learn a mapping from input to output.
|
||||
|
||||
Testing: given a new input, predict the output.
|
||||
|
||||
Example: Linear classification models
|
||||
|
||||
Find a linear function that separates the data.
|
||||
|
||||
$$
|
||||
f(x) = w^T x + b
|
||||
$$
|
||||
|
||||
[Linear classification models](http://cs231n.github.io/linear-classify/)
|
||||
|
||||
Simple representation of a linear classifier.
|
||||
|
||||
### Empirical loss minimization framework
|
||||
|
||||
Given a training set, find a model that minimizes the loss function.
|
||||
|
||||
Assume iid samples.
|
||||
|
||||
Example of loss function:
|
||||
|
||||
l1 loss:
|
||||
|
||||
$$
|
||||
\ell(f(x; w), y) = |f(x; w) - y|
|
||||
$$
|
||||
|
||||
l2 loss:
|
||||
|
||||
$$
|
||||
\ell(f(x; w), y) = (f(x; w) - y)^2
|
||||
$$
|
||||
|
||||
### Linear classification models
|
||||
|
||||
$$
|
||||
\hat{L}(w) = \frac{1}{n} \sum_{i=1}^n \ell(f(x_i; w), y_i)
|
||||
$$
|
||||
|
||||
hard to find the global minimum.
|
||||
|
||||
#### Linear regression
|
||||
|
||||
However, if we use l2 loss, we can find the global minimum.
|
||||
|
||||
$$
|
||||
\hat{L}(w) = \frac{1}{n} \sum_{i=1}^n (f(x_i; w) - y_i)^2
|
||||
$$
|
||||
|
||||
This is a convex function, so we can find the global minimum.
|
||||
|
||||
The gradient is:
|
||||
|
||||
$$
|
||||
\nabla_w||Xw-Y||^2 = 2X^T(Xw-Y)
|
||||
$$
|
||||
|
||||
Set the gradient to 0, we get:
|
||||
|
||||
$$
|
||||
w = (X^T X)^{-1} X^T Y
|
||||
$$
|
||||
|
||||
From the maximum likelihood perspective, we can also derive the same result.
|
||||
|
||||
#### Logistic regression
|
||||
|
||||
Sigmoid function:
|
||||
|
||||
$$
|
||||
\sigma(x) = \frac{1}{1 + e^{-x}}
|
||||
$$
|
||||
|
||||
The loss of logistic regression is not convex, so we cannot find the global minimum using normal equations.
|
||||
|
||||
#### Gradient Descent
|
||||
|
||||
Full batch gradient descent:
|
||||
|
||||
$$
|
||||
w \leftarrow w - \eta \nabla_w \hat{L}(w)
|
||||
$$
|
||||
|
||||
Stochastic gradient descent:
|
||||
|
||||
$$
|
||||
w \leftarrow w - \eta \nabla_w \hat{L}(w; x_i, y_i)
|
||||
$$
|
||||
|
||||
Mini-batch gradient descent:
|
||||
|
||||
$$
|
||||
w \leftarrow w - \eta \nabla_w \hat{L}(w; x_i, y_i)
|
||||
$$
|
||||
|
||||
Mini-batch Gradient Descent:
|
||||
|
||||
$$
|
||||
w \leftarrow w - \eta \nabla_w \hat{L}(w; x_i, y_i)
|
||||
$$
|
||||
|
||||
at each step, we update the weights using the average gradient of the mini-batch.
|
||||
|
||||
the mini-batch is selected randomly from the training set.
|
||||
|
||||
#### Multi-class classification
|
||||
|
||||
Use softmax function to convert the output to a probability distribution.
|
||||
|
||||
## Neural Networks
|
||||
|
||||
From linear to non-linear.
|
||||
|
||||
- Shadow approach:
|
||||
- Use feature transformation to make the data linearly separable.
|
||||
- Deep approach:
|
||||
- Stack multiple layers of linear models.
|
||||
|
||||
Common non-linear functions:
|
||||
|
||||
- ReLU:
|
||||
- $$
|
||||
\text{ReLU}(x) = \max(0, x)
|
||||
$$
|
||||
- Sigmoid:
|
||||
- $$
|
||||
\text{Sigmoid}(x) = \frac{1}{1 + e^{-x}}
|
||||
$$
|
||||
- Tanh:
|
||||
- $$
|
||||
\text{Tanh}(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}
|
||||
$$
|
||||
|
||||
|
||||
|
||||
### Backpropagation
|
||||
80
content/CSE559A/CSE559A_L8.md
Normal file
80
content/CSE559A/CSE559A_L8.md
Normal file
@@ -0,0 +1,80 @@
|
||||
# CSE559A Lecture 8
|
||||
|
||||
Paper review sharing.
|
||||
|
||||
## Recap: Three ways to think about linear classifiers
|
||||
|
||||
Geometric view: Hyperplanes in the feature space
|
||||
|
||||
Algebraic view: Linear functions of the features
|
||||
|
||||
Visual view: One template per class
|
||||
|
||||
## Continue on linear classification models
|
||||
|
||||
Two layer networks as combination of templates.
|
||||
|
||||
Interpretability is lost during the depth increase.
|
||||
|
||||
A two layer network is a **universal approximator** (we can approximate any continuous function to arbitrary accuracy). But the hidden layer may need to be huge.
|
||||
|
||||
[Multi-layer networks demo](https://playground.tensorflow.org)
|
||||
|
||||
### Supervised learning outline
|
||||
|
||||
1. Collect training data
|
||||
2. Specify model (select hyper-parameters)
|
||||
3. Train model
|
||||
|
||||
#### Hyper-parameters selection
|
||||
|
||||
- Number of layers, number of units per layer, learning rate, etc.
|
||||
- Type of non-linearity, regularization, etc.
|
||||
- Type of loss function, etc.
|
||||
- SGD settings: batch size, number of epochs, etc.
|
||||
|
||||
#### Hyper-parameter searching
|
||||
|
||||
Use validation set to evaluate the performance of the model.
|
||||
|
||||
Never peek the test set.
|
||||
|
||||
Use the training set to do K-fold cross validation.
|
||||
|
||||
### Backpropagation
|
||||
|
||||
#### Computation graphs
|
||||
|
||||
SGD update for each parameter
|
||||
|
||||
$$
|
||||
w_k\gets w_k-\eta\frac{\partial e}{\partial w_k}
|
||||
$$
|
||||
|
||||
$e$ is the error function.
|
||||
|
||||
#### Using the chain rule
|
||||
|
||||
Suppose $k=1$, $e=l(f_1(x,w_1),y)$
|
||||
|
||||
Example: $e=(f_1(x,w_1)-y)^2$
|
||||
|
||||
So $h_1=f_1(x,w_1)=w^T_1x$, $e=l(h_1,y)=(y-h_1)^2$
|
||||
|
||||
$$
|
||||
\frac{\partial e}{\partial w_1}=\frac{\partial e}{\partial h_1}\frac{\partial h_1}{\partial w_1}
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{\partial e}{\partial h_1}=2(h_1-y)
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{\partial h_1}{\partial w_1}=x
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{\partial e}{\partial w_1}=2(h_1-y)x
|
||||
$$
|
||||
|
||||
#### General backpropagation algorithm
|
||||
102
content/CSE559A/CSE559A_L9.md
Normal file
102
content/CSE559A/CSE559A_L9.md
Normal file
@@ -0,0 +1,102 @@
|
||||
# CSE559A Lecture 9
|
||||
|
||||
## Continue on ML for computer vision
|
||||
|
||||
### Backpropagation
|
||||
|
||||
#### Computation graphs
|
||||
|
||||
SGD update for each parameter
|
||||
|
||||
$$
|
||||
w_k\gets w_k-\eta\frac{\partial e}{\partial w_k}
|
||||
$$
|
||||
|
||||
$e$ is the error function.
|
||||
|
||||
#### Using the chain rule
|
||||
|
||||
Suppose $k=1$, $e=l(f_1(x,w_1),y)$
|
||||
|
||||
Example: $e=(f_1(x,w_1)-y)^2$
|
||||
|
||||
So $h_1=f_1(x,w_1)=w^T_1x$, $e=l(h_1,y)=(y-h_1)^2$
|
||||
|
||||
$$
|
||||
\frac{\partial e}{\partial w_1}=\frac{\partial e}{\partial h_1}\frac{\partial h_1}{\partial w_1}
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{\partial e}{\partial h_1}=2(h_1-y)
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{\partial h_1}{\partial w_1}=x
|
||||
$$
|
||||
|
||||
$$
|
||||
\frac{\partial e}{\partial w_1}=2(h_1-y)x
|
||||
$$
|
||||
|
||||
For the general cases,
|
||||
|
||||
$$
|
||||
\frac{\partial e}{\partial w_k}=\frac{\partial e}{\partial h_K}\frac{\partial h_K}{\partial h_{K-1}}\cdots\frac{\partial h_{k+2}}{\partial h_{k+1}}\frac{\partial h_{k+1}}{\partial h_k}\frac{\partial h_k}{\partial w_k}
|
||||
$$
|
||||
|
||||
Where the upstream gradient $\frac{\partial e}{\partial h_K}$ is known, and the local gradient $\frac{\partial h_k}{\partial w_k}$ is known.
|
||||
|
||||
#### General backpropagation algorithm
|
||||
|
||||
The adding layer is the gradient distributor layer.
|
||||
The multiplying layer is the gradient switcher layer.
|
||||
The max operation is the gradient router layer.
|
||||
|
||||
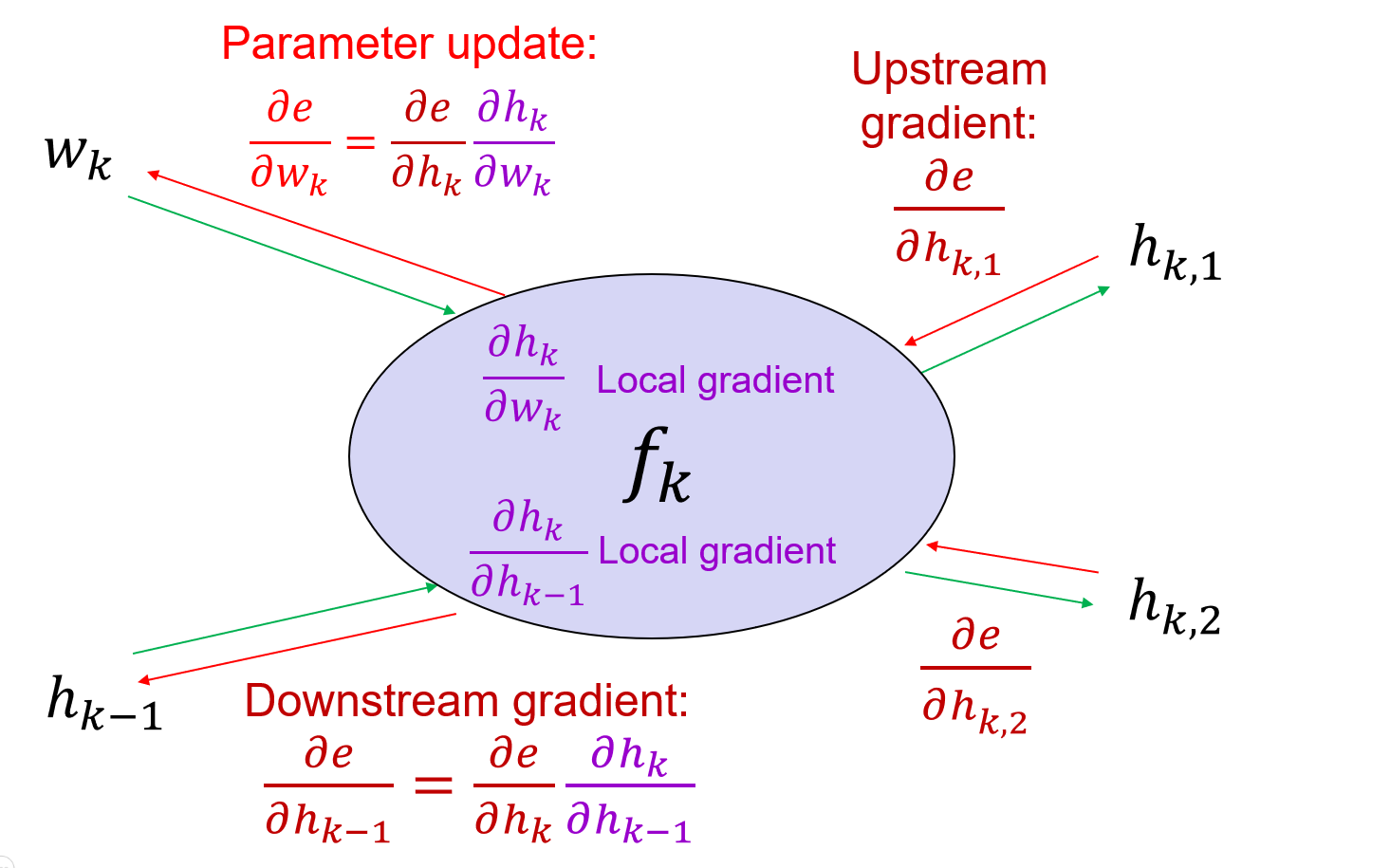
|
||||
|
||||
Simple example: Element-wise operation (ReLU)
|
||||
|
||||
$f(x)=ReLU(x)=max(0,x)$
|
||||
|
||||
$$
|
||||
\frac{\partial z}{\partial x}=\begin{pmatrix}
|
||||
\frac{\partial z_1}{\partial x_1} & 0 & \cdots & 0 \\
|
||||
0 & \frac{\partial z_2}{\partial x_2} & \cdots & 0 \\
|
||||
\vdots & \vdots & \ddots & \vdots \\
|
||||
0 & 0 & \cdots & \frac{\partial z_n}{\partial x_n}
|
||||
\end{pmatrix}
|
||||
$$
|
||||
|
||||
Where $\frac{\partial z_i}{\partial x_j}=1$ if $i=j$ and $z_i>0$, otherwise $\frac{\partial z_i}{\partial x_j}=0$.
|
||||
|
||||
When $\forall x_i<0$ then $\frac{\partial z}{\partial x}=0$ (dead ReLU)
|
||||
|
||||
Other examples on ppt.
|
||||
|
||||
## Convolutional Neural Networks
|
||||
|
||||
### Basic Convolutional layer
|
||||
|
||||
#### Flatten layer
|
||||
|
||||
Fully connected layer, operate on vectorized image.
|
||||
|
||||
With the multi-layer perceptron, the neural network trying to fit the templates.
|
||||
|
||||
|
||||
|
||||
#### Convolutional layer
|
||||
|
||||
Limit the receptive fields of units, tiles them over the input image, and share the weights.
|
||||
|
||||
Equivalent to sliding the learned filter over the image , computing dot products at each location.
|
||||
|
||||
|
||||
|
||||
Padding: Add a border of zeros around the image. (higher padding, larger output size)
|
||||
|
||||
Stride: The step size of the filter. (higher stride, smaller output size)
|
||||
|
||||
### Variants 1x1 convolutions, depthwise convolutions
|
||||
|
||||
### Backward pass
|
||||
32
content/CSE559A/_meta.js
Normal file
32
content/CSE559A/_meta.js
Normal file
@@ -0,0 +1,32 @@
|
||||
export default {
|
||||
//index: "Course Description",
|
||||
"---":{
|
||||
type: 'separator'
|
||||
},
|
||||
CSE559A_L1: "Computer Vision (Lecture 1)",
|
||||
CSE559A_L2: "Computer Vision (Lecture 2)",
|
||||
CSE559A_L3: "Computer Vision (Lecture 3)",
|
||||
CSE559A_L4: "Computer Vision (Lecture 4)",
|
||||
CSE559A_L5: "Computer Vision (Lecture 5)",
|
||||
CSE559A_L6: "Computer Vision (Lecture 6)",
|
||||
CSE559A_L7: "Computer Vision (Lecture 7)",
|
||||
CSE559A_L8: "Computer Vision (Lecture 8)",
|
||||
CSE559A_L9: "Computer Vision (Lecture 9)",
|
||||
CSE559A_L10: "Computer Vision (Lecture 10)",
|
||||
CSE559A_L11: "Computer Vision (Lecture 11)",
|
||||
CSE559A_L12: "Computer Vision (Lecture 12)",
|
||||
CSE559A_L13: "Computer Vision (Lecture 13)",
|
||||
CSE559A_L14: "Computer Vision (Lecture 14)",
|
||||
CSE559A_L15: "Computer Vision (Lecture 15)",
|
||||
CSE559A_L16: "Computer Vision (Lecture 16)",
|
||||
CSE559A_L17: "Computer Vision (Lecture 17)",
|
||||
CSE559A_L18: "Computer Vision (Lecture 18)",
|
||||
CSE559A_L19: "Computer Vision (Lecture 19)",
|
||||
CSE559A_L20: "Computer Vision (Lecture 20)",
|
||||
CSE559A_L21: "Computer Vision (Lecture 21)",
|
||||
CSE559A_L22: "Computer Vision (Lecture 22)",
|
||||
CSE559A_L23: "Computer Vision (Lecture 23)",
|
||||
CSE559A_L24: "Computer Vision (Lecture 24)",
|
||||
CSE559A_L25: "Computer Vision (Lecture 25)",
|
||||
CSE559A_L26: "Computer Vision (Lecture 26)",
|
||||
}
|
||||
4
content/CSE559A/index.md
Normal file
4
content/CSE559A/index.md
Normal file
@@ -0,0 +1,4 @@
|
||||
# CSE 559A: Computer Vision
|
||||
|
||||
## Course Description
|
||||
|
||||
1
content/Math3200/Lecture_1.mdx
Normal file
1
content/Math3200/Lecture_1.mdx
Normal file
@@ -0,0 +1 @@
|
||||
<div style={{ width: '100%', height: '25px'}}></div><iframe src="https://notenextra.trance-0.com/Math3200/Lecture_1.html" title="Math 3200 Lecture 1" style={{ width: '100%', height: '100vh', border: 'none' }}/>
|
||||
1
content/Math3200/Lecture_10.mdx
Normal file
1
content/Math3200/Lecture_10.mdx
Normal file
@@ -0,0 +1 @@
|
||||
<div style={{ width: '100%', height: '25px'}}></div><iframe src="https://notenextra.trance-0.com/Math3200/Lecture_10.html" title="Math 3200 Lecture 10" style={{ width: '100%', height: '100vh', border: 'none' }}/>
|
||||
1
content/Math3200/Lecture_11.mdx
Normal file
1
content/Math3200/Lecture_11.mdx
Normal file
@@ -0,0 +1 @@
|
||||
<div style={{ width: '100%', height: '25px'}}></div><iframe src="https://notenextra.trance-0.com/Math3200/Lecture_11.html" title="Math 3200 Lecture 11" style={{ width: '100%', height: '100vh', border: 'none' }}/>
|
||||
1
content/Math3200/Lecture_12.mdx
Normal file
1
content/Math3200/Lecture_12.mdx
Normal file
@@ -0,0 +1 @@
|
||||
<div style={{ width: '100%', height: '25px'}}></div><iframe src="https://notenextra.trance-0.com/Math3200/Lecture_12.html" title="Math 3200 Lecture 12" style={{ width: '100%', height: '100vh', border: 'none' }}/>
|
||||
1
content/Math3200/Lecture_13.mdx
Normal file
1
content/Math3200/Lecture_13.mdx
Normal file
@@ -0,0 +1 @@
|
||||
<div style={{ width: '100%', height: '25px'}}></div><iframe src="https://notenextra.trance-0.com/Math3200/Lecture_13.html" title="Math 3200 Lecture 13" style={{ width: '100%', height: '100vh', border: 'none' }}/>
|
||||
1
content/Math3200/Lecture_14.mdx
Normal file
1
content/Math3200/Lecture_14.mdx
Normal file
@@ -0,0 +1 @@
|
||||
<div style={{ width: '100%', height: '25px'}}></div><iframe src="https://notenextra.trance-0.com/Math3200/Lecture_14.html" title="Math 3200 Lecture 14" style={{ width: '100%', height: '100vh', border: 'none' }}/>
|
||||
1
content/Math3200/Lecture_15.mdx
Normal file
1
content/Math3200/Lecture_15.mdx
Normal file
@@ -0,0 +1 @@
|
||||
<div style={{ width: '100%', height: '25px'}}></div><iframe src="https://notenextra.trance-0.com/Math3200/Lecture_15.html" title="Math 3200 Lecture 15" style={{ width: '100%', height: '100vh', border: 'none' }}/>
|
||||
1
content/Math3200/Lecture_16.mdx
Normal file
1
content/Math3200/Lecture_16.mdx
Normal file
@@ -0,0 +1 @@
|
||||
<div style={{ width: '100%', height: '25px'}}></div><iframe src="https://notenextra.trance-0.com/Math3200/Lecture_16.html" title="Math 3200 Lecture 16" style={{ width: '100%', height: '100vh', border: 'none' }}/>
|
||||
1
content/Math3200/Lecture_17.mdx
Normal file
1
content/Math3200/Lecture_17.mdx
Normal file
@@ -0,0 +1 @@
|
||||
<div style={{ width: '100%', height: '25px'}}></div><iframe src="https://notenextra.trance-0.com/Math3200/Lecture_17.html" title="Math 3200 Lecture 17" style={{ width: '100%', height: '100vh', border: 'none' }}/>
|
||||
Some files were not shown because too many files have changed in this diff Show More
Reference in New Issue
Block a user